Determination of tissue optical properties in PDT treated Head & Neck patients

Abstract

Determination of optical properties (absorption (μ_a) and scattering (μ_s′) coefficients) in human tissue is important when it comes to accurate calculation of fluence rate in and around tissue area. ALA application to the tissue induces production of protoporphyrin IX when activated by red light. Changes in the tissue optical properties can send information such as treatment outcome and tissue drug concentration.

Patients in this study were treated with PDT for head and neck mucosal dysplasia. They were enrolled in a phase I study of escalating light doses and oral ALA with 60mg/kg. Red light at 630nm was administered to the tumor from a laser. The light dose was escalated from 50–200J/cm² with a measured fluence rate at tissue surface of 100mW/cm².

We developed a light detection device for the purpose of determining optical properties in vivo using the semi-infinite method. The light detection device consists of two parallel, placed 5mm apart. In one of the catheters a 2 mm long linear diffusing light source is placed while in the second catheter, a calibrated isotropic detector is placed. The detector is scanned along the length of the light source containing catheter. Scans are done with the device placed on the treatment area (tumor) and on the normal tissue. Optical properties were measured in-vivo before and after PDT delivery for both normal tissue and tumor.

1. INTRODUCTION

There are several studies reporting excellent results for patients treated with PDT for early stage cancer of head and neck region (Biel et al., 2010). Early superficial lesions in the oral cavity, larynx and pharynx are ideal targets for PDT (Agostinis et al., 2011). The advantage of PDT over other conventional modalities of surgery, radiation, and chemotherapy is that is a minimally invasive treatment technique with selective tumor destruction and normal tissue preservation. Often, with surgery and radiotherapy control is achieved at the expense of functional disturbance as well as disfigurement and other long lasting complications. PDT has little effect on underlying functional structures and has excellent cosmetic outcome, making it a well suited treatment modality for lesions of head, neck and oral cavity.

The current study is part of a study of ALA-mediated PDT for head and neck mucosal dysplasia the oral cavity. Patients were enrolled in this phase I light-dose-escalation study using oral ALA with 60mg/kg. Red light at 630nm was administered to the target from a diode laser. The light dose was escalated from 50–200J/cm², in fractionated and non-fractionated arms. The photosensitizer used was 5-aminolevulinic acid (5-ALA) [9, 10], an agent with no photosensitizing properties that is converted in situ to the photosensitizer protoporphyrin IX. ALA can be administered orally, topically or intravenously.

The success of the light therapy depends on the accuracy of the prescribed light delivered to the tumor. By knowing the optical properties of tissue before and after light delivery we can determine the efficacy of the treatment. The main purpose of this study was to determine the optical properties (scattering and absorption coefficients) in vivo by superficial measurements using a light detection device made for this purpose.

2. METHODS

2.1 Description of the measuring probe

The light detection device (fig 1a) consists of two parallel, 2mm (OD) light transmitting catheters (Flexi-needle, Best medical International, Springfield, VA) placed 5mm apart. One side of the device was covered with a black carbon sheet, in order to avoid detection of light incident from the outside. The two parallel catheters hold a 2 mm long linear diffusing light and a calibrated isotropic detector (fig 1b), respectively. The detector is scanned along the length of the light source-containing catheter. Scans were done with the device placed on the surface of the treatment area (fig 1c) and on the normal oral cavity tissue, with the catheters touching surface tissue.

Figure 1.

(a) Two parallel catheter light detection device, (b) Optical fiber-based isotropic detector, (c) Light detection device placed on phantom surface for semi-infinite measurement

The detectors used in this study are optical fiber-based isotropic detectors (Rare Earth Medical, West Yarmouth, MA) of the scattering-tip type [1]. The light collected by the detector was digitized using a photodiode-based in-vivo light dosimetry system [2]. The detectors were calibrated to measure absolute fluence rate in air.

2.2 Model and fitting algorithm

A diffusion theory based on light source on semi-infinite medium has been developed to model the measured data [3]:

$$\varphi (\rho ,{\mu }_a,{{\mu }_s}^{\prime })=C_1\mathrm{\Psi }(\rho )+C_2{j}_z(\rho )$$ (1)

$$\mathrm{\Psi }(\rho )=\frac{1}{4\pi D}\left(\frac{e^{-{\mu }_{\mathit{eff}}{r}_1}}{r_1}-\frac{e^{-{\mu }_{\mathit{eff}}{r}_2}}{r_2}\right)$$ (2)

$$j_z=\frac{1}{4\pi }\left[\frac{1}{{\mu }_t^{\prime }}\left({\mu }_{\mathit{eff}}+\frac{1}{r_1}\right)\frac{e^{-{\mu }_{\mathit{eff}}{r}_1}}{r_1^2}+\left(\frac{1}{{\mu }_t^{\prime }}+2z_b\right)\left({\mu }_{\mathit{eff}}+\frac{1}{r_2}\right)\frac{e^{-{\mu }_{\mathit{eff}}{r}_2}}{r_2^2}\right]$$ (3)

where Ψ(ρ) and j_z(ρ) are photon fluence and flux rate respectively and are functions of ρ, μ_s′(λ) and μ_a(λ)The parameter z_b, r₁, and r₂ are from the extrapolated boundary condition that was adapted to solve diffusion equation of semi-infinite media. In brief, the analytical solution of semi-infinite turbid media is equivalent to that of infinite turbid media with two sources. One source is positioned at $1/{\mu }_t^{\prime }$ below the medium surface or $z_b+1/{\mu }_t^{\prime }$ below the ‘extrapolated boundary’. The other source, or the image source, is positioned at $z_b+1/{\mu }_t^{\prime }$ above the extrapolated boundary. r₁ is the distance between the source and the detector. r₂ is the distance between the image source and the detector. C₁ and C₂ are constants that depend on the relative refractive index of tissues and air [4]. In addition to the diffusion model, a model based on the P₃ approximation to radiative transport has also been developed and implemented [5, 6].

Adapting the previously developed expressions for optical fiber-based probes requires three modifications: First, the source term commonly used for optical fiber sources replaces the incident pencil beam with an isotropic source placed one scattering mean free path below the fiber. Here, the source is fundamentally isotropic, so we model it as an isotropic point source at z=0. The image sources are placed at z=−2zb.

Second, the standard model of detection treats the detector (typically the face of an optical fiber) as a plane detector, so the signal it collects is proportional to the cosine of the irradiance normal to the surface. This is accounted for by including a cosine of the incident angle in the integrals used to calculate C₁ and C₂ in equation 1. In this case, our detector is isotropic: its response is proportional to fluence rate rather than irradiance, so the corresponding integrals omit the cosine factor.

Third, unlike fiber-based probes or catheter-based probes in infinite media [7], it is possible in this case for light emitted by the source to reach the detector without passing through the diffusing medium. We refer to this component as ‘non-diffuse light’. To assess the shape of the non-diffuse light component, we have made measurements using the probe with no diffusing medium. The amplitude of the nondifuse light component was determined by measuring the total detected signal in phantoms of known optical properties, and subtracting the calculated diffuse light component. The resulting dependence of the non-diffuse light component on optical properties was fit with an empirical formula.

The fitting algorithm (fig 2) we employ is a differential evolution algorithm modified from that proposed by [8] implemented in Matlab as reported previously[7]. In this case, the fit uses a model which includes both the diffuse and direct components. The free parameters in the fit are μ_a and μ_s′. Fitting with fixed μ_s′ is also a supported option.

Figure 2.

The GUI of the fitting program for the determination of optical properties in semi-infinite medium. Dotted line is the measured data, solid line the fit of the measured data, dashed line represents the scattered light and the green line is the fit to the scattered light.

2.3 Phantom measurements

To validate our theory, the optical properties were measured in liquid tissue simulating phantoms with known reduced scattering coefficient (μ_s′) and absorption coefficient (μ_a). The liquid phantoms were made with known optical properties, consisting of Liposyn (Liposyn III, 30% Abbott Lab, North Chicago, IL) – as scattering medium and black India ink (Higgins black India ink #4418, Bellwood, IL) – as absorbing medium. The Intralipid and Ink concentrations varied from 0.23 to 1.14% and 0.002 to 0.023%, respectively. The phantom surface was covered by a transparent plastic foil, in order to better simulate measurements done on tissue surface and to avoid liquid filling the space in between the two catheters. The fluence rate was measured using a 0.5mm scattering tip isotropic detector that was moved along the parallel catheter using the motorized probe described previously (fig 3). The optical properties were independently measured using an established method to validate the results.

Figure 3.

(a) Schematics of the semi-infinite type measurement, showing the placement of the parallel catheter device, liquid phantom and positioning device.

2.4 Clinical measurements

2.4.1 Patients

The patients studied here were enrolled in a phase I dose escalation study of photodynamic therapy for the treatment of pre-malignant tumors and superficial microinvasive disease of the head and neck. Patients were given 60mg/kg body weight of Levulan (DUSA Pharmaceuticals, Wilmington, MA) photosensitizer orally. The prescribed start time for light delivery after ALA administration was 4 to 6 hours. Light doses for the treated lesions varied from 50–200 J/cm². Light was delivered at a dose rate of 100mW/cm².

2.4.2 Light delivery systems

Treatment light was generated by a Ceralas Series GaAlAs diode laser (Biolitech, Inc.). This laser has a peak wavelength of 632nm and produces up to 4W. The light was delivered by a microlens diffuser (Medlight SA) or a balloon applicator consisting of a balloon catheter (model CDB-LB20 to CDB-LB50) and cylindrical diffuser.

2.5 Isotropic detector calibration accuracy

2.5.1. Integrating sphere calibration accuracy

The integrating sphere was calibrated for the light fluence rate. The variation of the calibration factor, α, over a period of time is plotted for 630nm (Figure 4) and summarized in Table 1. The average CF is plotted as a solid red line.

Figure 4.

Fluence rate calibration in an integrating sphere at 630nm.

Table 1.

Variation over time of fluence rate calibration factor, α, for 630nm.

Date	10.6.08	10.27.08	10.31.08	11.14.08	12.16.09	3.24.10	10.28.10	8.22.11
α	57.15	51	52.74	45.7	42.75	44.68	47.26	51.51
Date	12.19.11	4.25.12	7.25.12	10.18.12	2.18.13	7.18.13	10.10.13
α	39.69	30.55	48.85	39.05	45.49	47.73	46.13

2.5.2 Angular dependence of the isotropic detectors

The angular response of the detectors was measured in two planes: horizontal and vertical, as shown in figure 5. The response of each detector was measured for every ten degree in each plane. Normalized angular response to 0 degree correction factor of eleven 0.5mm isotropic detectors in the vertical plane is shown in figure 5a and normalized angular response to 90 degrees in the horizontal plane is shown in figure 5b. A summary of the variation of the normalized calibration factors, a/a_avr, for the eight detectors used is shown in Table 2.

Figure 5.

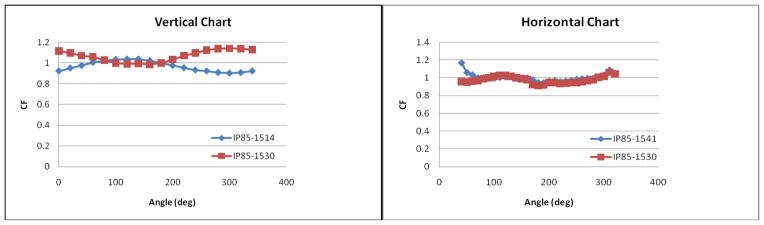
Angular response of the detectors in: (a) vertical plane and (b) horizontal plane.

Table 2.

Time variation of the normalized calibration factors, a/a_avr, for the isotropic detectors over time.

Ch	S/N	5.14.10	7.22.10	8.9.10	10.7.10	11.3.10	3.21.11	10.10.12	12.4.12	2.18.13	Stdev	Avr
1	C0104.111	0.93	1.05	1.06	0.94	1.03	0.98	1.02	0.98	1.01	0.05	1.00
2	IP85-1514	0.97	1.02	1.03	1.03	0.98	0.98	1.05	0.99	0.96	0.03	1.00
3	IP85-1530	0.92	0.99	1.04	0.98	1.07	1.01	0.99	1.01	1.00	0.04	1.00

3. RESULTS AND DISCUSSION

3.2. Determination of optical properties

3.2.1 Correction for non-diffuse light

To correct for the effects of non-diffuse light, we used an empirical correction based on a comparison between the signal measured in the detector for a phantom of known optical properties, and the corresponding predicted diffuse light profile. This correction takes the form of an additive component of fixed profile (shown in figure 6 (a)) given by:

$$\mathrm{\Phi }(r)=\frac{f({\mu }_{\mathit{eff}})S}{a+{br}^2+{cr}^4}$$ (4)

Figure 6.

(a) Normalized profile for “non-diffuse” components obtained in optical phantoms with known optical properties (solid lines) along with profile measured in air (air 1,2,3,4 as shown in dotted lines). Two fits are shown: one (“non-diffuse fit”) uses Eqs. 4–5, and the other (“direct light fit”) uses Eq. 6 with r² = (x²+0.5²). (b) Non-diffuse light f/S at source peak vs. effective attenuation coefficient. Symbols are measurements. Solid line is the fit using Eq. 5 and dashed line is Eq. 6 with r = 0.5 cm (or x = 0 cm).

The intensity of this “non-diffuse” component depends on the optical properties of the phantom, as shown in figure 6(b). This dependence is approximated by

$$f({\mu }_{\mathit{eff}})=\{\begin{array}{cc}0.20& {\mu }_{\mathit{eff}}<3.0\\ 0.0667·{\mu }_{\mathit{eff}}& {\mu }_{\mathit{eff}}\ge 3.0\end{array}$$ (5)

In comparison, the direct light is expressed as:

$${\left(\frac{\mathrm{\Phi }}{S}\right)}_{\mathit{dir}}=\frac{1}{4\pi r^2}$$ (6)

3.2.2 Optical property determination in liquid phantoms

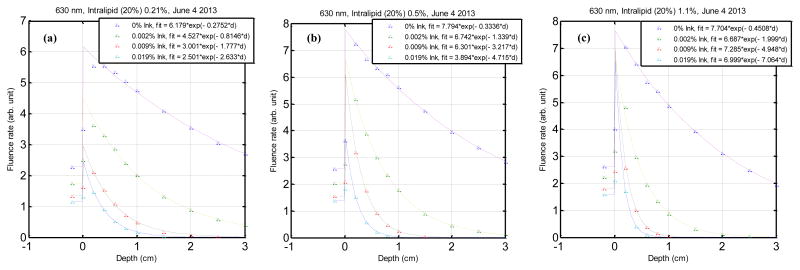
Optical properties were determined in liquid tissue simulating phantoms with known optical properties. They were also independently measured using vertical scans in a broad illumination beam in order to validate the results (Figure 7). The optical properties obtained from the two methods were than compared for accuracy. The results of the broad beam method and the parallel-catheter method are shown in Table 3.

Figure 7.

Fluence rate as a function of depth in a series of liquid phantoms illuminated by a broad light beam. Optical properties of liquid tissue simulating phantoms of different scattering coefficients. The phantoms were made of intralipid concentrations of (a) 0.21%, (b) 0.5% and (c) 1.1% and variable ink concentration as indicated in the legend.

Table 3.

A comparison between optical properties (μ_a, μ_s′ and μ_eff) determined by broad-beam and parallel-catheter methods for three different measurements done for optical phantoms with Liposyn concentration of 0.53% and ink concentrations of 0.002%, 0.012% and 0.023%.

Collimated beam			Semi-infinite
μa	μs′	μeff	μa	μs′	μeff	μa	μs′	μeff
0.098	2.26	0.815	0.089	2.31	0.78	−10	2	−4
0.466	1.6	1.496	0.605	1.5	1.65	23	−7	9
1.023	2.26	2.633	1.375	2.88	3.44	26	22	23
0.086	5.23	1.162	0.104	5.02	1.25	17	−4	7
0.486	7.102	3.217	0.584	8.84	3.94	17	20	18
1.043	7.102	4.715	1.219	8.5	5.58	14	16	16
0.121	8.12	1.72	0.113	6.49	1.48	−7	−25	−16
0.474	8.71	3.519	0.607	8.47	3.93	22	−3	10
1.016	14.37	7.064	1.23	17.84	8.11	17	19	13

3.2.3 Determination of optical properties in tissue

Table 4 lists the subject number, PDT light delivery modality, treated site, time of light delivery and tissue information. Optical properties were measured in-vivo before and after PDT delivery for both normal tissue and tumor whenever possible.

Table 4.

Summary of measured in-vivo optical properties pre and post PDT, for tumor and normal tissue.

Subject	Treatment modality		Treated site	pre PDT		post PDT
				normal	tumor	normal	tumor
16	Collimated beam	Oral Cavity	tongue	✓	✓	✘	✓
18	Collimated beam	Oral Cavity	R lateral tongue and floor of mouth	✓	✓	✓	✓
19	Collimated beam	Oral Cavity	base of tongue L partial pharynx	✓	✓	✓	✓
20	Baloon	Oral Cavity	tongue and floor of mouth	✓	✓	✘	✘
21	Collimated beam	Oral Cavity	tongue, floor of mouth	✓	✓	✓	✓
22	Baloon	Larynx	vocal cord	✘	✓	✘	✘
24	Baloon	Nasal Cavity	nasal cavity	✓	✓	✓	✓
26	Collimated beam	Not treated	oral cavity	✓	✓	✓	✓
28	Collimated beam	Oral Cavity	R buccal mucosa/maxillary area R tongue	✓	✓	✓	✓
29	Collimated beam	Oral Cavity	left lower lip	✘	✘	✘	✓

Typical in-vivo fluence rate profiles measured in patient tumor and normal tissues are shown in figures 8 (a) and (b), respectively. The overall fit is indicated by the line that closely fits the data. The fit inherently separates the diffuse and non-diffuse components, and shows the best fit to the diffuse component, which is used to determine the tissue optical properties. For most patient data, fits in reasonable agreement with the measured data were obtained. In cases of high μ_eff, the majority of the signal was due to the non-diffuse component. In extreme cases, this may lead to a low signal-to-noise ratio (SNR) in the diffuse component, increasing the uncertainty of the fit in these cases.

Figure 8.

Optical properties determination for (a) normal tissue and (b) tumor post-PDT light delivery.

The resulting optical properties are summarized in table 5.

Table 5.

Summary of measured in–vivo optical properties pre/post PDT for tumor and normal tissue. For the patients in whom measurements could be made.

			pre PDT normal			pre PDT tumor			post PDT normal			post PDT tumor
Case #	Site	Method	μa	μs′	μeff	μa	μs′	μeff	μa	μs′	μeff	μa	μs′	μeff
29	oral cavity	Collimated beam	✘	✘	✘	✘	✘	✘	✘	✘	✘	0.39	13.82	3.99
28	oral cavity	Collimated beam	0.11	26.18	2.84	0.15	26.64	3.42	0.49	10.68	3.83	4.23	0.74	3.00
26	oral cavity	Collimated beam	0.32	4.65	2.09	1.76	2.01	3.25	0.07	5.52	1.02	0.05	4.82	0.80
21	oral cavity	Collimated beam	0.16	17.89	2.96	✘	✘	✘	1.46	1.83	2.74	0.91	4.69	3.18
19	oral cavity	Collimated beam	0.15	19.88	3.00	0.16	2.93	3.54	0.41	3.11	1.86	0.15	1.79	0.87
18	oral cavity	Collimated beam	0.13	4.20	1.29	0.12	3.43	1.12	0.10	4.91	1.18	0.23	0.91	0.80
16	oral cavity	Collimated beam	0.46	3.28	1.98	✘	✘	✘	✘	✘	✘	2.10	6.55	4.04
24	nasal cavity	Baloon	0.02	4.27	0.45	✘	✘	✘	0.38	5.52	2.24	0.19	6.48	1.90
22	larynx	Baloon	✘	✘	✘	0.31	11.67	3.23	✘	✘	✘	✘	✘	✘
20	oral cavity	Baloon	0.16	18.95	3.00	0.39	13.24	3.98	0.09	8.13	1.51	0.79	15.19	6.08
			AVR	0.19	12.41	2.20	0.48	9.99	3.09	0.43	5.67	2.05	1.00	6.11

4. CONCLUSIONS

We have proposed a method to determine the tissue optical properties using two parallel catheters and a point source in a semi-infinite medium condition. The algorithm is validated in phantom with known optical properties with a maximum uncertainty of 22% for μ_a and 26% for μ_s’ for the typical range of tissue optical properties: ma between 0.1 to 1 cm⁻¹ and ms′ between 2 and 14 cm⁻¹. We found that the effective attenuation coefficient in ALA-mediated HN patients to be 2.1 +/− 0.9 cm⁻¹ and 2.9 +/− 1.3 cm⁻¹ for normal tissue and tumor, respectively, corresponding to optical penetration depths of 0.5 and 0.34 cm, for normal skin and tumor, respectively.