Functionally dissociable influences on learning rate in a dynamic environment

Summary

Maintaining accurate beliefs in a changing environment requires dynamically adapting the rate at which one learns from new experiences. Beliefs should be stable in the face of noisy data, but malleable in periods of change or uncertainty. Here we used computational modeling, psychophysics and fMRI to show that adaptive learning is not a unitary phenomenon in the brain. Rather, it can be decomposed into three computationally and neuroanatomically distinct factors that were evident in human subjects performing a spatial-prediction task: (1) surprise-driven belief updating, related to BOLD activity in visual cortex; (2) uncertainty-driven belief updating, related to anterior prefrontal and parietal activity; and (3) reward-driven belief updating, a context-inappropriate behavioral tendency related to activity in ventral striatum. These distinct factors converged in a core system governing adaptive learning. This system, which included dorsomedial frontal cortex, responded to all three factors and predicted belief updating both across trials and across individuals.

Introduction

Decisions are often guided by beliefs about states of the world that can be used to predict desirable or undesirable outcomes. Some states, like the location of a restaurant, are stable and directly observable. Conversely, other states, like the quality of that restaurant, can change unexpectedly and must be inferred from noisy data. In the latter scenario a key question is how much to adjust beliefs in response to a new observation (e.g., Rushworth and Behrens, 2008). The answer to this question can be different for each new observation and depends critically on both the unexpectedness of the observation (“surprise”) and the uncertainty of the preexisting belief (“belief uncertainty”). The goal of this study was to identify brain activity associated with these computationally distinct influences on flexible belief adjustment.

Flexible belief adjustment that is sensitive to surprise and uncertainty is evident in human learning behavior. Under certain conditions, these factors are used to scale the influence of prediction errors—new observations that are inconsistent with existing beliefs—on subsequent changes in belief (Li et al., 2011; Nassar et al., 2012; Nassar et al., 2010; O’Reilly et al., 2013; see Fig. 1). This scaling can be formalized as a learning rate in a delta rule and can also be influenced by uninformative contextual factors such as reward and arousal (Hayden et al., 2009; Nassar et al., 2012).

Figure 1.

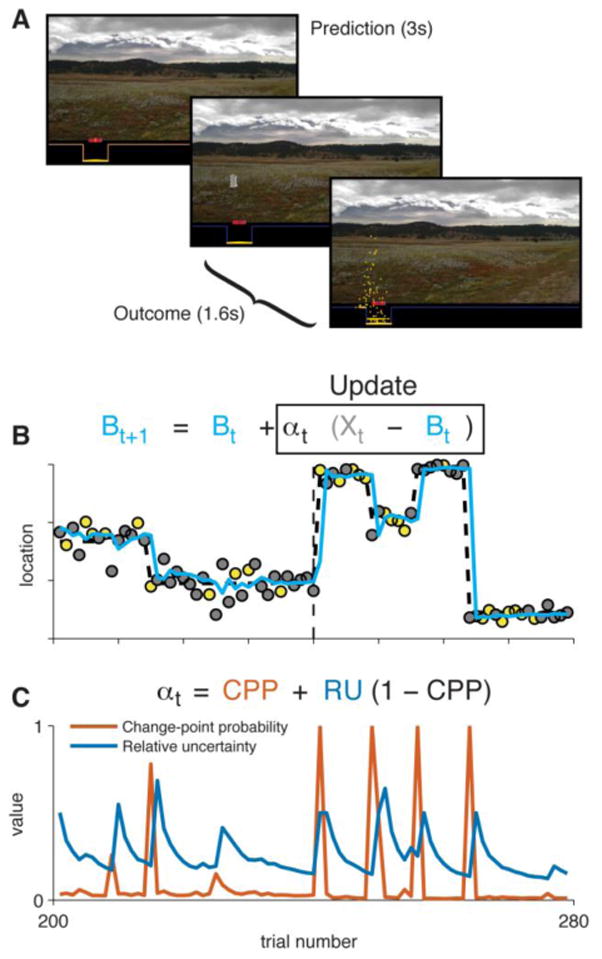
Task overview and theoretical predictions. A: Screenshots of the experimental task. Participants positioned a bucket, trying to predict where a bag would drop from an occluded helicopter. B: An example sequence of trials. Data points mark the location at which successive bags fell (yellow = rewarding outcome, gray = neutral outcome). Heavy dashed line marks the true generative mean, which had periods of stability with occasional change points. Cyan line marks the predictions of an approximate Bayesian model. Inset equation presents the model’s belief-updating rule (B_t = belief, X_t = observed outcome, α_t = learning rate on trial t). Vertical dashed line marks the boundary between a high-noise condition (left) and low-noise condition (right), reflected in different levels of stochastic variance around the generative mean. C: Two theoretical influences on learning rate across trials. Change-point probability (CPP) is elevated when an unexpectedly large prediction error occurs. Relative uncertainty (RU) is elevated subsequently and slowly decays as a more precise estimate of the current mean is reached. Inset equation shows how CPP and RU jointly determine the adaptive learning rate.

Despite these known behavioral effects, the neural mechanisms that govern how these distinct factors influence belief updating are not well understood. Rather than distinguishing these different influences, human neuroimaging and monkey electrophysiology studies have focused on a common mechanism of belief updating, typically localized to dorsomedial frontal cortex (DMFC; Behrens et al., 2007; Hayden et al., 2009; O’Reilly et al., 2013). However, other lines of evidence implicate a broader system of brain regions in learning-rate modulation or suggest that DMFC may be sensitive to only a subset of the computational factors that impact learning rate (Fischer and Ullsperger, 2013; Payzan-LeNestour et al., 2013; Vilares et al., 2012).

We used functional magnetic resonance imaging (fMRI) to measure neural activity during a task in which belief updating can be observed directly and decomposed into factors related to surprise, belief uncertainty, and reward. As detailed below, we found that these distinct computational factors have dissociable neural representations that provide insight into how individual variables governing learning might be computed in the brain. We also identify the convergence of these factors in a core set of regions, including DMFC, which appear to govern adaptive learning.

Results

We used fMRI to measure blood-oxygenation-level-dependent (BOLD) signal in 32 participants as they performed a modified predictive-inference task (Nassar et al., 2010). Predictions were made in the context of a video game that required repeatedly positioning a bucket to catch bags of money that subsequently dropped from an unseen helicopter (Fig. 1). We used two manipulations to affect both surprise and belief uncertainty: (1) Bag locations were sampled on each trial from a Gaussian distribution, with a standard deviation (noise) that was fixed to a high or low value in each 120-trial run; and (2) the mean of this distribution, representing the location of the helicopter, usually remained stable across trials but was occasionally resampled from a uniform distribution. In addition, each bag had either a high or neutral reward value (sampled with equal probability independently on each trial), which was revealed only after the prediction had been made. Participants could maximize their overall earnings by inferring the location of the helicopter and placing their bucket directly beneath it. Successful inference required flexible belief updating in response to changes in the helicopter’s location but stable belief maintenance across trials in which the helicopter remained stationary.

Behavioral results

Multiple factors influenced belief-updating behavior. We measured belief updating as the adjustment in bucket position from one trial to the next. This update, when expressed as a fraction of the spatial prediction error—i.e., the difference between the previous, chosen bucket position and the subsequent bag position, or δ—can be thought of as a direct measure of learning rate (cf. Nassar et al., 2010). We analyzed behavior using linear regression models of belief updating. One explanatory variable was the trial-wise prediction error δ, which could account for a tendency to update bucket position toward the most recent bag location as a fixed fraction of δ (i.e., a fixed learning rate). Additional explanatory variables encoded trial-to-trial adjustments in learning rate based on both normative and incidental factors.

Two normative factors were computed by applying an approximately Bayesian learning model to the sequence of observations experienced by each participant (Fig. 1B; Nassar et al., 2012; Nassar et al., 2010). The first factor was change-point probability (CPP), which is elevated transiently upon observation of a surprising outcome and reflects the probability that the helicopter has moved (Fig. 1C). The second factor was relative uncertainty (RU), which reflects the uncertainty in one’s belief about the environment. RU depends inversely on the number of prior observations attributable to the current environmental state. It is maximal on the trial after a likely change point and decays gradually as a function of trials thereafter (see Fig. 1C). The regression also included a term for the current reward value. Reward value carried no predictive information and therefore played no role in our computational model, although reward information can, of course, be relevant in other situations.

Regression fits showed that participants flexibly adapted their learning rates as predicted by the computational model while also deviating from the model in systematic ways. Consistent with previous work, participants learned more when outcomes were surprising as indexed by CPP (median coefficient=0.53, IQR 0.40 to 0.76, signed-rank p<0.001) and when beliefs were more uncertain as indexed by RU (median=0.32, IQR 0.11 to 0.44, signed-rank p<0.001; Fig. 2C; Nassar et al., 2012). However, there was considerable heterogeneity across participants, with some behaving like the computational model (CPP and RU coefficients near one) and others less so (coefficients near zero). On average, participants also deviated from the model with a tendency to use less-flexible learning rates (median fixed learning-rate coefficient=0.39, IQR 0.22 to 0.48, signed-rank p<0.001) and to modulate learning based on the irrelevant factor of reward value (median reward coefficient=0.03, IQR 0 to 0.05, signed-rank p<0.001; Fig. 2C). The overall regression fit behavior very well (median r²=0.967, inter-quartile range [IQR] 0.949 to 0.979). Secondary analyses showed that (1) effects of CPP and RU could also be observed using single-trial estimates of learning rate, and (2) the effect of CPP varied adaptively with noise level across runs (see Fig. S1).

Figure 2.

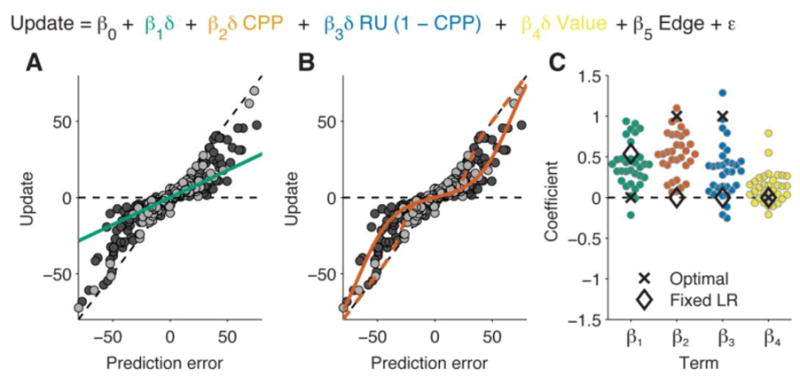
Behavioral results. A: Example data from one participant, illustrating the fit obtained using only a fixed-learning-rate term. Each data point represents a trial. A fixed learning rate implies a linear relationship between prediction error (current outcome minus previous prediction) and update (next prediction minus previous prediction), regardless of noise (light gray = low noise; dark gray = high noise). B: Illustration of the fit obtained with a change-point probability term, using the same data as in panel A. Here the learning rate is adaptive (non-linear) and depends on noise. C: Coefficients from the full regression-based analysis of behavioral data (see inset equation), with coefficients estimated for each participant individually. The four plotted coefficients correspond to a fixed learning rate (β₁, panel A), change-point probability (β₂, panel B), relative uncertainty (β₃), and reward value (β₄). Estimates of β₄ are scaled by a factor of 5 for visibility. Black markers show the results of fitting the regression model to simulated data generated by the approximate Bayesian model (“Optimal”) or by a model with a fixed learning rate (“Fixed LR”).

fMRI results

Individual learning-rate variables

Each of the three distinct influences on learning rate identified from behavior—CPP, RU, and reward value—was associated with modulation of BOLD activity during task performance (Fig. 3 and Table S1). We included all three variables as amplitude modulators of trial-related BOLD responses in a general linear model (GLM). CPP was associated with positive effects in a large posterior cluster including both primary and higher-level visual regions in occipital, inferior temporal, and posterior parietal cortex. Positive effects also appeared in DMFC, posterior cingulate cortex (PCC), superior frontal sulci, and bilateral anterior insula. Negative effects of CPP were observed in ventral striatum, medial temporal lobes (MTL), superior temporal gyri, and left lateral PFC. RU was associated with positive BOLD effects in intraparietal sulci and posterior parietal cortex, cerebellum, DMFC, anterior and lateral PFC, superior frontal sulci, and bilateral anterior insula. RU had negative effects in ventromedial PFC (vmPFC) and MTL. Reward value had positive effects in ventral striatum, DMFC, bilateral anterior insula, and parietal cortex.

Figure 3.

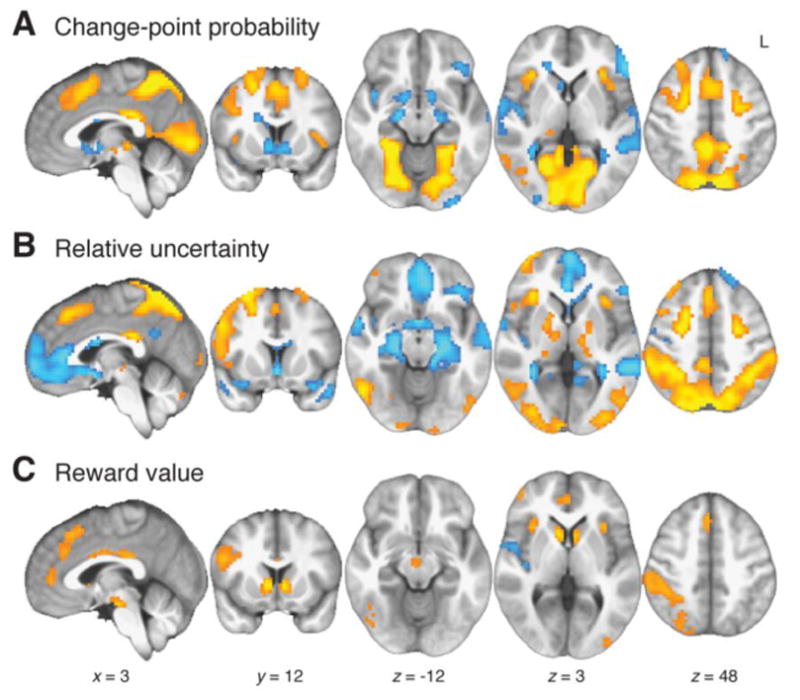
Effects of individual learning-rate variables on BOLD, tested concurrently in the same GLM (see text and Table S1).

Selective effects of learning-rate variables

A subset of these brain regions showed selectivity for just one of the three learning-rate variables (Fig. 4 and Table 1). We imposed three criteria for selectivity: the effect had to differ from zero for that variable individually and had to differ in the same direction from the same region’s response to each of the other two variables. For example, CPP-selective regions were identified based on a three-way conjunction of whole-brain effects for CPP>0, CPP>RU, and CPP>reward. This approach can detect selective effects that are either positive or negative. For example, a region showing a selective negative effect of CPP would show negative modulation by CPP, and greater negative modulation by CPP than by RU or reward. Interpreting contrasts between regression coefficients requires that the predictors be comparably scaled; our approach was to z-score each variable across trials (within each participant) before convolution with the hemodynamic response function (HRF).

Figure 4.

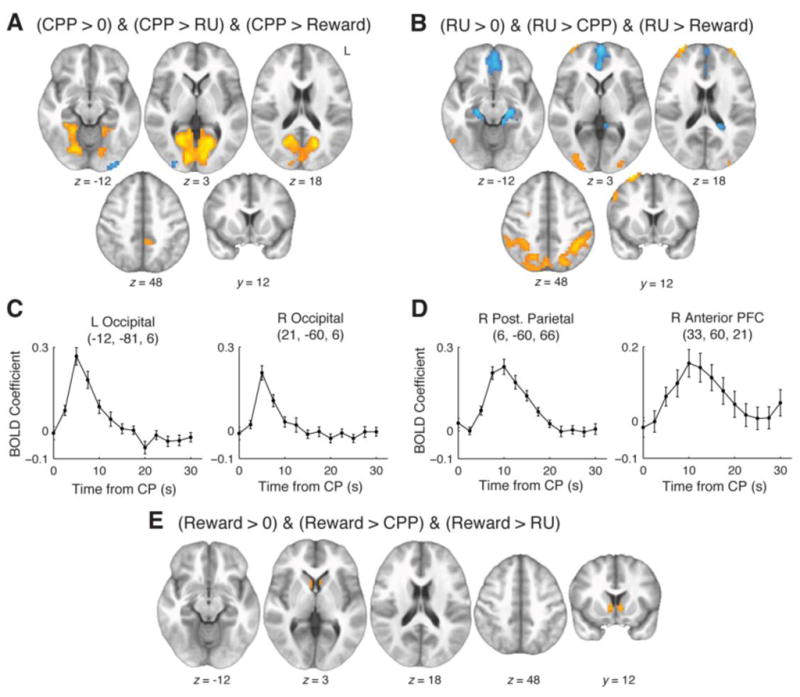
Brain regions selectively sensitive to CPP, RU, or reward. A: Regions showing significant effects (corrected p<0.05, whole-brain permutation test) in the same direction for contrasts of CPP versus 0, CPP versus RU, and CPP versus reward. Warm colors represent positive effects and cool colors represent negative effects. B: Regions showing significant effects in the same direction for contrasts of RU versus 0, RU versus CPP, and RU versus reward. C: Mean±SEM BOLD time courses relative to large change points (CPP>0.5), obtained from 33-voxel spheres centered at peak voxels in Panel A. Sensitivity to CPP entails a response that peaks soon after a change point and then decays rapidly (see Fig. 1C and S2). D: Equivalent time courses for peak locations in Panel B. See Movie S1 for further details of change-point-aligned time courses. E: Regions showing significant effects in the same direction for contrasts of reward versus 0, reward versus CPP, and reward versus RU.

Table 1.

Selective effects of CPP, RU, or reward.

#Voxels	Region	Peak t	Peak x	Peak y	Peak z
Selective response to changepoint probability: Positive effects
1951	L calcarine sulcus	8.57	−12	−81	6
	R calcarine sulcus	8.52	21	−60	6
35	posterior cingulate cortex	4.87	−6	−42	48
18	L occipital cortex	4.41	−12	−96	24
Selective response to changepoint probability: Negative effects
62	L lateral occipital cortex	−6.06	−27	−96	−6
45	R lateral occipital cortex	−6.09	33	−93	−3
Selective response to relative uncertainty: Positive effects
1733	posterior parietal cortex	10.43	6	−60	66
703	L cerebellum	9.49	−27	−42	−42
362	R cerebellum	8.52	30	−45	−48
219	R anterior PFC	6.76	33	60	18
152	R superior frontal gyrus	9.13	30	3	66
88	R lateral occipital cortex	5.63	33	−90	6
52	R occipitotemporal cortex	4.92	57	−60	−3
47	L lateral occipital cortex	4.84	−30	−93	12
43	L occipitotemporal cortex	5.03	−48	−63	−3
21	R inferior frontal junction	5.22	54	12	39
20	L anterior PFC	5.44	−36	57	18
Selective response to relative uncertainty: Negative effects
460	ventromedial PFC	−7.58	0	60	0
77	L medial temporal lobe	−7.70	−21	−24	−12
45	R medial temporal lobe	−6.80	24	−21	−15
26	L posterior peri-ventricular	−5.20	−21	−42	18
13	posterior cingulate cortex	−4.25	−3	−48	36
11	R posterior peri-ventricular	−5.08	30	−54	6
Selective response to reward value: Positive effects
26	R ventral striatum	5.67	6	9	0
21	L ventral striatum	5.53	−6	12	−3

CPP-selective positive effects were identified in visual cortex and PCC; negative effects were seen in bilateral areas of lateral occipital cortex (Fig. 4A and Table 1). RU-selective positive effects were found in posterior parietal cortex extending to intraparietal sulcus bilaterally, as well as bilateral cerebellum, lateral occipital cortex, and anterior PFC (aPFC). RU-selective negative effects were found in regions including vmPFC, medial parietal, and bilateral MTL (Fig. 4B and Table 1). Reward-selective positive effects were observed in bilateral ventral striatum (Fig. 4E and Table 1). There were no reward-selective negative effects.

A key driver of regional selectivity for CPP or RU was the time course of BOLD activity after large change points. Although theoretical BOLD time courses for CPP and RU were largely uncorrelated (computing these terms from the normative model and then convolving with the HRF, median r=0.10, IQR 0.08 to 0.13), the two factors have a strong time-lagged interdependence. Points of rapid change in the environment (high CPP) tend to be followed by periods in which the new state has not yet been well sampled (high RU; Fig. 1C and Fig. S2). As a result, a useful way to visualize the distinction between these two variables is to examine time courses aligned to the occurrence of large change points (Fig. 4C–D and Movie S1). An area will appear CPP selective if the BOLD change has a rapid onset, peaks around 5s after the change point, and decays quickly (Fig. 4C). Conversely, an area will appear RU selective if the BOLD signal rises and then falls more gradually, peaking ~10s after the change point (Fig. 4D).

Timing differences on this scale have often been utilized in previous fMRI research (e.g., Zarahn et al., 1999), and appear unlikely to emerge artificially from interregional variability in neurovascular response properties. HRF peak latencies can vary from approximately 2.5–6s across individuals (Aguirre et al., 1998; Handwerker et al., 2004), but systematic differences across brain regions seldom exceed ~1s (Bright et al., 2009; Chang et al., 2008; Handwerker et al., 2004). The few observations of larger differences involve especially fast hemodynamic responses to respiratory manipulations in certain regions (Bright et al., 2009). Thus, although the temporal properties of neurovascular coupling remain an area of active inquiry, current evidence suggests the ~10s lags that characterize RU-selective regions are likely neural rather than solely vascular in origin.

Conjunction of learning-rate effects

In addition to their dissociable effects, the three influences on learning rate (CPP, RU, and reward) also converged on a set of common regions. A conjunction analysis showed three-way overlap in bilateral occipitoparietal regions, bilateral anterior insula, DMFC, PCC, and right lateral PFC. Control analyses together with a follow-up eye-tracking study ruled out the possibility of an oculomotor confound and confirmed that activity in each of these regions reflected adaptive learning (see Fig. S3–S4). We refer to these areas as common adaptive learning-rate regions. There were also small areas of overlapping negative effects in right posterior insula (Fig. 5 and Table 2).

Figure 5.

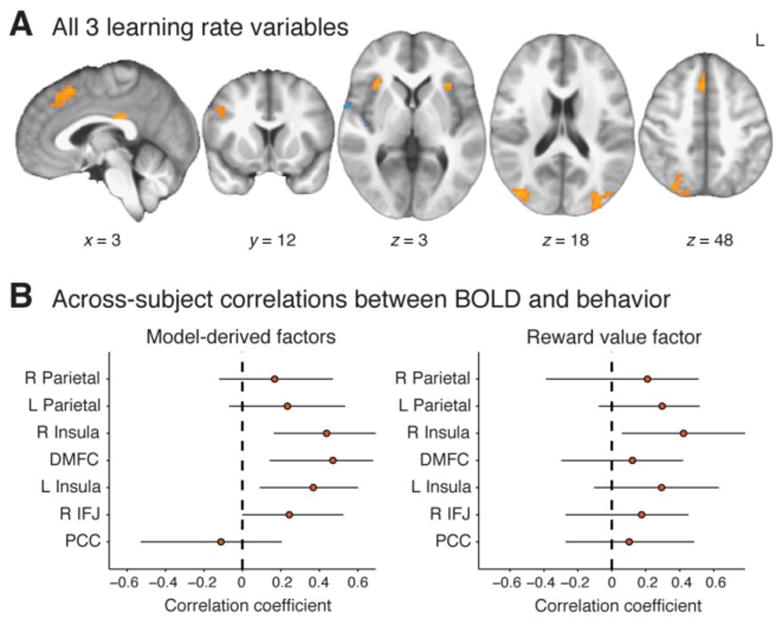
Conjunction of BOLD effects for multiple influences on learning rate. A: Regions showing significant effects (corrected p<0.05, whole-brain permutation test) of all three learning-rate-related variables: CPP, RU, and reward value. B: Across-participant relationship between behavioral effects and BOLD effects in each conjunction region. Results are plotted for the effects of normative factors (the sum of CPP and RU parameters; left) and effects of reward value (right). Points represent across-participant Pearson correlations (with bootstrapped 95% CIs) between the behavioral parameter and the BOLD effect in each ROI.

Table 2.

Conjunction of CPP, RU, and reward value BOLD effects.

#Voxels	Region	Peak t	Peak x	Peak y	Peak z
Conjunction of positive effects
212	R occipitoparietal cortex	5.46	33	−69	30
93	L occipitoparietal cortex	5.13	−30	−93	15
49	R anterior insula	6.49	33	21	6
38	DMFC	4.97	3	18	51
28	L anterior insula	5.29	−30	18	6
23	R inferior frontal junction	4.17	48	12	33
15	posterior cingulate cortex	5.05	3	−27	27
Conjunction of negative effects
14	R posterior insula	−4.71	48	−6	−6
13	R posterior insula	−5.35	63	0	6

Functional connectivity between factor-specific regions and common adaptive learning-rate regions

We speculated that functional connectivity between the common adaptive learning-rate regions and factor-specific regions might vary from trial to trial, depending on which factor made a greater relative contribution to the overall learning rate. For example, an RU-selective region might share more variance with the common regions when RU is high and CPP is low than when the opposite is true. We tested this idea using psychophysiological interaction (PPI) analysis (Friston et al., 1997). We set up a regression model for each participant that contained four interaction terms defined by crossing two psychological variables (CPP and RU) with two physiological variables (trial-wise BOLD amplitudes from the occipital cluster selective for CPP and the right aPFC cluster selective for RU) and fit the model to BOLD amplitudes from the common adaptive learning-rate regions. Consistent with the hypothesis of task-dependent functional connectivity, coefficients for the matched PPI terms (CPP×Occipital, RU×aPFC) significantly exceeded coefficients for the mismatched PPI terms (CPP×aPFC, RU×Occipital; median contrast coefficient=0.031; signed-rank p=0.002; see Fig. S5 for details and further results).

Individual differences

Supporting the functional relevance of the common adaptive learning-rate regions, individual differences in these regions’ BOLD responsiveness to model-derived factors (CPP and RU) predicted behavioral sensitivity to these same factors. Because behavioral regression coefficients for CPP and RU were highly correlated across participants (r²=0.64; p<0.001), we took the sum of these coefficients as a measure of an individual’s normative learning-rate adjustment for both the behavioral and BOLD data. BOLD coefficients from the seven common adaptive learning-rate ROIs, when included as predictors in a multiple regression analysis, collectively explained a significant fraction of the between-participant behavioral variance (r²=0.44, F=2.74, p<0.030). Bivariate correlations between individual ROIs and behavior were generally positive (Fig. 5B), although this positive relationship survived Bonferroni correction for 7 tests only in DMFC (r=0.47). We found only a marginal relationship between individual differences in the BOLD response to reward value and reward-related behavioral effects (r²=0.40, F=2.31, p=0.060). None of the bivariate correlations for reward value were significant after Bonferroni correction, although the effects tended to be positive across ROIs (Fig. 5C).

Residual learning-rate modulation

Two regions of DMFC correlated with the residual fluctuations in learning rate not captured by our behavioral model. We converted the residual term from our behavioral regression analysis into an additional predictor in the GLM analysis of BOLD effects. This term modeled BOLD modulation based on whether the learning rate on each trial was higher or lower than predicted by the behavioral regression. A whole-brain analysis showed that residual learning rate was associated with BOLD fluctuations in two clusters in DMFC (Fig. 6A). The more superior cluster was close to, but not overlapping, the DMFC cluster identified above as a common adaptive learning-rate region. The second cluster was rostral/inferior and centered in the cingulate sulcus. These two residual-related clusters did not show significant effects of CPP, RU, or reward, even when tested as ROIs.

Figure 6.

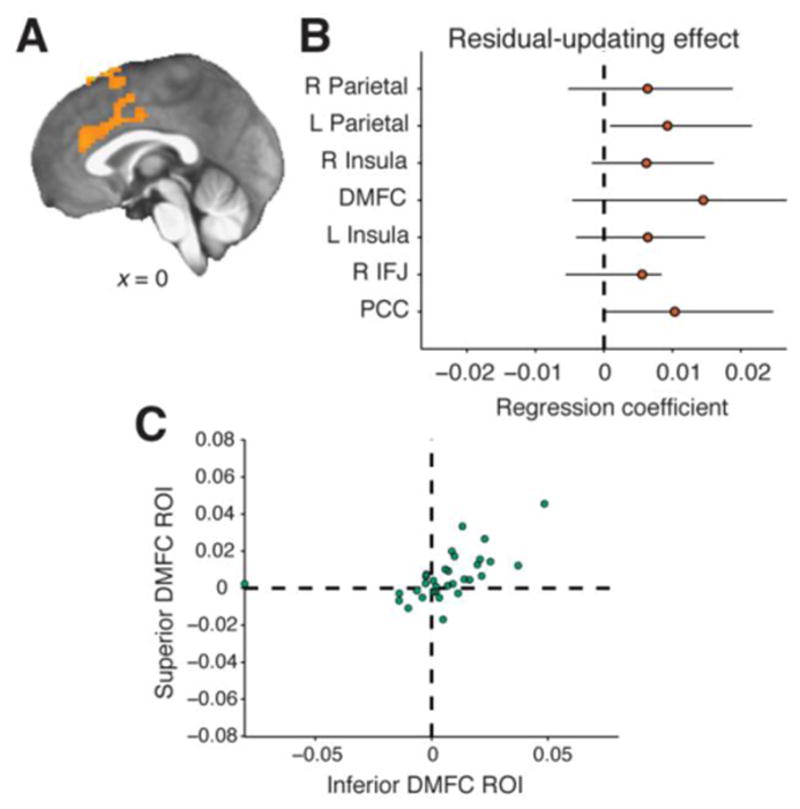
BOLD response correlated with residual variability in prediction-updating behavior. A: Significant clusters for residual behavioral update (corrected p<0.05, whole-brain permutation test) were seen in both inferior and superior DMFC. B: The same effect was tested in common adaptive learning-rate regions (see Fig. 5). Points show the median residual update effect in each region with bootstrapped 95% CIs. C: Trial-by-trial BOLD amplitudes from the regions in Panel A were significant predictors of belief-updating behavior. BOLD amplitudes from either superior or inferior DMFC were added to a behavioral regression model that also contained all other hypothesized predictors of belief updating (see Fig. 2), and regression coefficients were estimated separately for each participant. The BOLD term tended to receive positive coefficients across participants, both for amplitudes extracted from the superior DMFC region (vertical axis) and from the inferior DMFC region (horizontal axis).

Residual learning-rate effects were also weakly present in the common adaptive learning-rate ROIs. Although coefficients tended to be positive, a test against zero was significant only in the left parietal cluster after Bonferroni correction for 7 tests (corrected p=0.030; Fig. 6B).

BOLD measurements from DMFC predicted participants’ behavior over and above the factors identified previously. We extracted trial-specific BOLD amplitudes from residual-learning-rate ROIs in DMFC, using an iterative leave-one-participant-out procedure to ensure independence. We entered these BOLD amplitudes as additional predictors in participant-wise behavioral regression models. A model containing the inferior DMFC ROI, but not one containing the superior DMFC ROI, explained a significant amount of variance beyond the original behavioral model (inferior ROI: median z-transformed F-statistic=0.68, signed-rank p=0.002; superior ROI: 0.34, p=0.096). The regression coefficient for the BOLD term was significantly greater than zero in each model, suggesting that either ROI could account for variability in behavior (inferior: median β=0.01, IQR 0.00 to 0.02, signed-rank p=0.014; superior: 0.00, 0.00 to 0.01, p=0.010; Fig. 6C).

Similar improvement in our behavioral model could be obtained by including trial-wise BOLD coefficients extracted from the common adaptive learning-rate regions shown in Fig. 5A. We added each of the seven ROIs individually to the behavioral model (all median z-transformed Fs>0.33; signed-rank ps<0.05 for six ROIs and p=0.08 for the right lateral PFC ROI). Coefficients indicated greater learning on trials with higher BOLD activity (all median coefficients >0) but this trend only reached statistical significance in three ROIs (signed-rank p<0.05 in right and left parietal and PCC; 0.06<p<0.2 for all other ROIs).

Discussion

The present study examined the neural representation of factors that the brain uses to adjust the influence of new observations on internal beliefs. We developed a novel task that allowed measurement of the specific contributions of surprise, belief uncertainty, and reward value to trial-by-trial adjustments in learning rate. Consistent with previous work, we found surprise and belief uncertainty to increase the influence of new observations on subsequent beliefs (Nassar et al., 2012; Nassar et al., 2010). In addition, participants showed a context-inappropriate tendency to be more influenced by observations associated with reward.

We would expect these distinct computational factors to be linked to dissociable neural patterns, but also to converge in regions that drive adaptive learning. This is exactly what we found. We first discuss the dissociable activity patterns related to each factor, as well as signals associated with residual variability in belief-updating behavior not attributable to any of these factors. We then discuss the convergence of these influences in a core set of brain regions and the further evidence that this core system governs adaptive learning.

Change-point probability (CPP)

Participants exhibited surprise-driven learning, updating beliefs by a proportionally larger amount when observations signaled a higher probability of a change point in the environment. CPP is positively related to prediction error magnitude: larger error magnitudes would be less likely if the environment had remained stable and therefore imply a greater posterior probability of a change point. High CPP is expected to bring about a rapid and reactive increase in learning rate.

We observed CPP-specific effects in primary and higher-order visual regions (Fig. 4A), consistent with the notion that CPP is inferred based on the unexpectedness of new sensory representations. A key question for future work is to what extent this early sensory representation of surprise can flexibly change to account for changes in stimulus statistics.

Relative uncertainty (RU)

Whereas CPP enhances learning from surprising external events, RU drives learning based on the imprecision of one’s current internal belief. Unlike CPP, the level of RU is determined in advance of each observation. In this sense RU can be regarded as a proactive (rather than reactive) modulatory influence (cf. Braver, 2012). In our experimental task, RU is elevated for several trials after a large change point has been detected (Fig. 1C), while beliefs are being refined for the new environmental regime.

We observed positive BOLD effects specific to RU in parietal regions, aPFC, and cerebellum. This finding partly overlaps with reported effects of estimation uncertainty in parietal cortex in other task paradigms (Payzan-LeNestour et al., 2013) and is consistent with previous studies linking learning rate with parietal mechanisms (Collins and Frank, 2012; Fischer and Ullsperger, 2013). The involvement of aPFC is consistent with this region’s roles in subjective uncertainty, uncertainty-driven exploration, exploratory action selection, and in representing the value of alternative courses of action (Badre et al., 2012; Boorman et al., 2011; Cavanagh et al., 2012; Daw et al., 2006; Fleming et al., 2012). Similarly, our finding of RU effects in cerebellum is broadly consistent with the hypothesis that cerebellum plays a highly general role in maintaining and updating internal models (Moberget et al., 2014).

We also found that bilateral MTL and vmPFC were consistently less active during periods of high RU. The effects were directionally consistent with previously reported BOLD effects of subjective confidence in these regions (De Martino et al., 2013; Kim and Cabeza, 2007) and might be related to findings hinting at mutually antagonistic interactions between feedback-driven learning and MTL-mediated episodic memory (Foerde et al., 2013). In this case, MTL engagement could serve to render beliefs more resistant to noisy observations during periods of environmental stability.

Reward value

Behavioral learning rates were influenced by a randomized manipulation of reward value. This effect was not predicted by our computational model because trial-by-trial rewards were irrelevant to predicting the spatial locations of future outcomes. However, previous work involving nonhuman primates has similarly found that incentive-laden observations had a greater impact on subsequent behavior than neutral observations with equivalent predictive relevance (Hayden et al., 2009). The reward effect might be explained from a normative perspective as an overgeneralization from situations in which (unlike our task) preferential learning from potential rewards is beneficial. The reward effect also might reflect a more general influence of physiologically arousing events on learning (cf. Nassar et al., 2012); future work could assess this idea by testing whether penalties (relative to neutral outcomes) would also drive increases in learning.

We observed BOLD effects of the reward manipulation in ventral striatum, consistent with this structure’s known role in encoding subjective value and reward prediction error (Bartra et al., 2013; Berns et al., 2001). A reward-sensitive region would also be expected to show a negative effect of CPP, given that CPP was associated with large spatial error and earnings depended on accuracy. A negative effect of CPP was indeed observed in ventral striatum (Fig. 3A). By contrast, other brain regions responded positively to both CPP and reward value (e.g., Fig. 5A), implicating these regions in learning-rate modulation rather than direct registration of reward.

Common adaptive learning-rate regions

Our results provide rigorous support for the previously proposed link between DMFC activity and adaptive belief updating (Behrens et al., 2007; Hayden et al., 2009; O’Reilly et al., 2013; Payzan-LeNestour et al., 2013). By decomposing the different influences on learning rate, we were able to show that each of three computationally distinct influences—CPP, RU, and reward—was associated with increased DMFC activity. However, these common adaptive learning-rate effects were not confined to DMFC, but rather appeared in a distributed system that also included anterior insula, PCC, and occipitoparietal cortex (Fig. 5). A question for future research is whether individual regions in this ensemble perform distinct roles in the neural implementation of adaptive learning, or whether, alternatively, their joint activity might reflect a common source of neural input such as the noradrenergic neuromodulatory system (Aston-Jones and Cohen, 2005; Nieuwenhuis et al., 2005; Payzan-LeNestour et al., 2013; Yu and Dayan, 2005).

Several findings support the interpretation that these regions jointly constitute a common pathway governing learning rate, which can be modulated via multiple factor-specific input channels. First, the common adaptive learning-rate regions exhibited task-dependent functional connectivity with factor-specific brain regions. BOLD activity in the common regions was more similar to the RU-selective aPFC region when modeled learning rates were driven by RU but more similar to the CPP-selective occipital region when modeled learning rates were driven by CPP (Fig. S5). Such a pattern of functional connectivity is consistent with the idea that information about belief uncertainty and surprise converges in the common adaptive learning-rate regions to facilitate effective inference in noisy and changing environments. Second, BOLD activity in these regions covaried with behavior across participants. The more that activity in the common adaptive learning-rate regions was modulated by the normative factors of RU and CPP, the more a subject’s behavior exhibited the influence of these factors. Third, BOLD activity in these regions covaried with behavior across trials. Greater activity in the common adaptive learning-rate regions on a given trial was associated with a larger subsequent update in beliefs.

The common adaptive learning-rate region we identified in DMFC appears somewhat dorsal to the area of anterior cingulate cortex (ACC) that has been linked to adaptive learning in previous work (Behrens et al., 2007). Although effects of individual factors extended ventrally into the cingulate sulcus (in different locations for CPP and reward value; Fig. 3), the area of overlap was centered near pre-supplementary motor area (pre-SMA; Fig. 5). Pre-SMA responds to a broad array of cognitive manipulations irrespective of motor demands, including belief updating (Fedorenko et al., 2013; O’Reilly et al., 2013; Payzan-LeNestour et al., 2013), and the cytoarchitectural locus of ACC BOLD effects can extend dorsally on the medial surface in many individuals (Cole et al., 2009). Given these considerations, we regard our results as compatible with previous demonstrations of adaptive learning effects in DMFC.

Arousal systems and residual updating behavior

Adaptive learning-rate modulation is thought to be influenced by physiological arousal systems, with previous work linking both pupillary and electrodermal arousal measures to rates of belief updating (Li et al., 2011; Nassar et al., 2012; O’Reilly et al., 2013). We obtained indirect evidence for such an association in our analysis of residual updating behavior. By eliciting an explicit prediction on every trial we could quantify whether participants updated their belief to a greater or lesser degree than predicted by our participant-specific behavioral regression model. These residual fluctuations in learning rate correlated with BOLD signal in both superior and inferior DMFC. Both of these areas are part of a connectivity-defined “salience network” (Seeley et al., 2007), and the inferior area has additionally been implicated in sympathetic outflow as indexed by pupil diameter (Critchley et al., 2005). Trial-specific BOLD amplitudes in these regions provided incremental information about belief updating even beyond our full set of behavioral predictors. It is therefore appealing, albeit speculative, to interpret these residual belief-updating effects in terms of task-unrelated fluctuations in physiological arousal. An important goal for future work is to examine how arousal might combine with other factors to influence belief updating, and how DMFC might regulate some or all of these influences (O’Reilly et al., 2013). Future studies with concurrent fMRI and physiological recordings would be well positioned to address this question.

Conclusions

We found that decision makers estimating a non-stationary feature of the environment could adapt the rate at which they learned from new experiences, and that adaptive learning was influenced by multiple computationally distinct factors. Two such factors, CPP and RU, were identified on the basis of an approximately Bayesian model of adaptive belief updating. CPP reflected a reactive response to observations signifying environmental change, whereas RU drove a more gradual and proactive response based on imprecision in one’s current belief. Learning was also affected by outcome reward value even though this quantity played no role in a normative model of task performance.

Using this computational decomposition of adaptive learning we were able to identify BOLD effects uniquely associated with each factor, suggesting that multiple distinct neural processes modulate belief updating. A region of visual cortex responded uniquely to CPP; regions of aPFC, parietal cortex, and cerebellum responded uniquely to RU; and ventral striatum responded uniquely to reward value. Next, we were able to identify the convergence of all three influences in a set of regions including DMFC, insula, parietal cortex and PCC. These regions showed task-dependent functional connectivity to the factor-specific regions and their activity predicted adaptive learning both across trials and across participants. These findings are compatible with the idea that a common mechanism—which may also be influenced by physiological arousal—underlies diverse influences on learning in volatile settings.

Experimental procedures

Participants

Human-participant procedures were approved by the University of Pennsylvania Internal Review Board; informed consent was obtained from all participants. Participants were recruited from the University of Pennsylvania community: n=32, 17 female, mean age=22.4 (SD=3.0; range 18–30). Two additional participants were excluded from analyses: one for head movement during MRI scanning (shifts of at least 0.5mm between >5% of adjacent timepoints), and one for trial-wise learning rates consistently >1 (median=1.19), suggesting a misunderstanding of the task structure. After the study concluded, all participants were invited to return for a follow-up eye-tracking session and 13 did so. Three participants were excluded from eye-tracking analyses because of insufficient valid eye-tracking data (see Fig. S4 legend for details), resulting in an eye-tracking sample of n=10 (age 20–28, 6 female).

Task

Participants performed a predictive-inference task, programmed in Matlab (The MathWorks, Natick, MA) using MGL (http://justingardner.net/mgl) and SnowDots (http://code.google.com/p/snow-dots) extensions. Conceptually, the task involved repeatedly predicting the next in a sequence of numbers (Nassar et al., 2012; Nassar et al., 2010). The inference problem was embedded in a cover task in which the number corresponded to the horizontal position at which a bag of money would drop from a helicopter concealed behind clouds.

The objective of the task was to catch coins in a bucket by predicting where the bag would land, which was equivalent to inferring the generative mean (i.e., the position of the helicopter) and centering the bucket at that position. For each trial we could directly observe the state prediction error, denoted δ and defined as the distance between the previous prediction and outcome. We could also observe the update, defined as the subsequent shift in the participant’s prediction. These two variables together provide trial-wise estimates of the participant’s learning rate.

Participants used a joystick to control the left/right position of the bucket. On each trial the participant had 3s to place the bucket, which was then locked in place as a bag dropped and exploded into a cloud of coins. A new trial began immediately after the outcome display was complete, resulting in a 4.6s trial-onset asynchrony. Bag positions were drawn from a Gaussian distribution whose mean usually remained fixed from trial to trial. On occasional change points the mean was redrawn from a uniform distribution spanning the width of the display. The probability of a change point was zero for the first three trials after the previous change point and 0.125 on each trial thereafter. Participants were told that the helicopter usually stayed in one place but moved occasionally. Participants also could directly observe the helicopter’s position during preliminary practice (see below).

At the beginning of each trial the participant had to move the joystick to a “home position” at the right-hand edge of the display to collect the bucket before moving it to the desired position. This procedure was used to decouple the degree of belief updating on each trial from the amplitude of the associated motor response. Motor amplitude depended on the selected left/right position, which had no correlation with update magnitude (median r=0.00, IQR −0.02 to 0.04). After each bag fell, a red bar marked the interval between the bag position and the participant’s previous prediction. Theoretically, the subsequent prediction is expected to fall within that interval (which represents a learning rate between 0 and 1), although participants were free to place the bucket anywhere they chose.

Left/right position was internally mapped to a value from 0 to 300 screen units to correspond with previous numerical instantiations of the task (Nassar et al., 2012). The Gaussian distribution governing bag positions had SD=10 in “low-noise” runs and SD=25 in “high-noise” runs. “Noise” here refers to non-predictive stochasticity across observations, elsewhere denoted “expected uncertainty” (Yu and Dayan, 2005) or “risk” (Payzan-LeNestour et al., 2013). The width of the bucket was set to 3 × SD in order to equate earnings in the two noise conditions. Each participant performed four 120-trial runs during functional scanning. Runs alternated between the low-noise and high-noise conditions, with the order counterbalanced across participants.

As an independent manipulation of reward, the coins that issued from each bag had either positive or neutral monetary value, randomized independently on each trial. Participants’ final earnings depended on the number of positive-value coins they caught but both outcome types were equally informative for future spatial predictions. For half the participants, positive and neutral coins were colored yellow and gray, respectively, and described as “gold” and “rocks.” For the remaining participant the colors were reversed and described as “coins” and “sand.”

Each participant completed a one-hour behavioral practice session in advance of MRI scanning. Practice began with four 40-trial runs of a version of the task in which the helicopter was visible. This initial phase: (1) made explicit the structure of the task, with the helicopter staying stable for periods of time and sometimes randomly repositioning; (2) let participants observe the frequency of change points; and (3) served to emphasize that the best strategy was to set the prediction to the generative mean. The practice session continued with four 80-trial runs with the helicopter hidden. Participants were explicitly instructed during practice to place the bucket directly underneath the helicopter (whether visible or not), which was the optimal strategy. At the beginning of the MRI session (during anatomical scanning), participants performed two 40-trial practice runs with the helicopter visible.

The follow-up eye-tracking session used the same task as the MRI session and consisted of two 40-trial practice runs with the helicopter visible followed by four 120-trial runs with the helicopter hidden.

Normative model

Overview

Optimal task performance required inferring the location of the helicopter based on the locations of bags dropped on previous trials:

$$p\left({\mu }_t|X_{1:t}\right)=\frac{p\left(X_{1:t}|{\mu }_t\right)p\left({\mu }_t\right)}{p\left(X_{1:t}\right)}$$ (1)

where μ_t is the location of the helicopter on trial t and X_1:t represents the locations of bags dropped from trials 1 through t. Exact inference over μ_t is computationally costly in the presence of change points (Adams and MacKay, 2007; Behrens et al., 2007; Fearnhead and Liu, 2007; Wilson et al., 2010). However, the computational complexity of optimal inference can be reduced dramatically by approximating the prior distribution over possible means as a weighted mixture of two components: (1) a Gaussian distribution with mean and variance matched to the true mixture of Gaussians, and (2) a uniform distribution accounting for the possibility of the mean being resampled according to a change-point process (Nassar et al., 2012). This reduced form of the Bayesian model achieves similar performance to the optimal inference algorithm at a fraction of the cost, provides a parsimonious description of the main features of participants’ learning behavior, and can be implemented as delta-rule (Nassar et al., 2012; Nassar et al., 2010):

$$B_{t+1}=B_t+{\alpha }_t+{\delta }_t$$ (2)

$${\delta }_t=X_t-B_t$$ (3)

where B_t+1 is a belief about the location of the helicopter on the next trial, δ_t is the error made in predicting the current bag location (X_t), and α_t is the learning rate. Learning rate is determined separately for each trial and depends critically on two factors. The first factor, CPP, is a measure of how likely it is, given the current observation, that the position of the helicopter has changed since the previous time step. The second factor, RU, is the fraction of overall predictive uncertainty that is due to imprecise knowledge about the location of the helicopter. RU is analogous to the gain in a Kalman filter and is also similar to estimation uncertainty as formulated in choice tasks (Payzan-LeNestour et al., 2013).

In what follows we use Ω_t to denote CPP on trial t, and τ_t to denote RU on trial t, to match notation used previously (Nassar et al., 2012). Trial-wise learning rate is computed as follows:

$${\alpha }_t={\mathrm{\Omega }}_t+{\tau }_t\times (1-{\mathrm{\Omega }}_t)$$ (4)

Thus, new data are more influential when the model believes that the location of the helicopter has changed or is less sure about the true location of the helicopter.

Computation of model variables

The model computes Ω_t on each trial according to the relative likelihood of the newest observation (X_t) under either the current belief distribution (which is Gaussian, centered at the inferred position of the helicopter, B_t) or the change-point distribution (which is uniform from 0 to 300 screen units; see above):

$${\mathrm{\Omega }}_t=\frac{\mathcal{U}\left(X_t|0,300\right)H}{\mathcal{U}\left(X_t|0,300\right)H+\mathcal{N}\left(X_t|B_t,{\sigma }_t^2\right)(1-H)}$$ (5)

where H is the hazard rate (the probability of a change point on each trial) and σ_t is the standard deviation on the predictive distribution over future bag locations. Thus, Ω_t is higher when change points are expected to be more frequent (H is high) or when the observed datum is surprising ( $\mathcal{N}\left(X_t|B_t,{\sigma }_t^2\right)$ is low). The model was equipped with a fixed hazard rate corresponding to the observed rate of change points across all trials in our dataset (H=0.1). Thus, in our implementation of the model, change-point probability was driven only by a mismatch between the newest bag location and prior expectations.

Unlike Ω_t, τ_t does not depend on the current observation X_t. The model computes τ_t+1 at the end of trial t according to the fraction of total uncertainty about the next bag location that is attributable to an imprecise estimate of the helicopter location (as opposed to uncertainty resulting from noise; i.e., the variance of the Gaussian distribution from which bag locations are picked, σ²_N):

$${\tau }_{t+1}=\frac{{\mathrm{\Omega }}_t{\sigma }_N^2+\left(1-{\mathrm{\Omega }}_t\right){\tau }_t{\sigma }_N^2+{\mathrm{\Omega }}_t\left(1-{\mathrm{\Omega }}_t\right){\left({\delta }_t\left(1-{\tau }_t\right)\right)}^2}{{\mathrm{\Omega }}_t{\sigma }_N^2+\left(1-{\mathrm{\Omega }}_t\right){\tau }_t{\sigma }_N^2+{\mathrm{\Omega }}_t\left(1-{\mathrm{\Omega }}_t\right){\left({\delta }_t\left(1-{\tau }_t\right)\right)}^2+{\sigma }_N^2}$$ (6)

where the numerator includes a weighted average of the variance on the helicopter distribution conditional on a change point (first term) and the variance on the helicopter distribution conditional on no change point (second term). In addition, it contains a term that accounts for variance emerging from the difference in the means of these two conditional distributions (third term). The denominator is the same as the numerator, but contains an additional term to account for uncertainty arising from noise (σ²_N). Relative uncertainty computed in this way factors into the learning rate computed by the model for the subsequent trial via Equation 4.

In contrast to previous work with this model, our implementation did not involve fitting its parameters directly to behavioral data. Instead, we fixed free parameters to the appropriate value for each noise condition (H=0.1; σ_N =10 or 25) and simulated behavior from this normative model over each sequence of stimuli observed by our participants. Trial-by-trial estimates of CPP and RU were extracted from these runs and used as normative prescriptions for surprise-driven and uncertainty-driven influences on learning, respectively. Participants may have had imprecise subjective estimates of H (Nassar et al., 2010) but our estimated CPP and RU time courses were robust to either halving or doubling the assumed hazard rate (median rs≥0.98 for true versus alternative hazard rates).

Behavioral analysis

Regression model

We formally tested our behavioral predictions using a linear regression framework, with trial-wise update (B_t+1 − B_t) as the dependent variable. Regression models were fit separately for each participant, with coefficients then tested against zero at the group level. For comparisons between nested models, z-transformed F statistics were computed for the model comparison within each individual, and were tested against zero at the group level. All behavioral regression models included an intercept (modeling any tendency to update preferentially leftward or rightward) and a quadratic-weighted term modeling an observed tendency to avoid the edges of the display. Results showed a positive effect for the intercept term (median=0.32, IQR −0.04 to 0.73, signed-rank p=0.004), indicating a rightward bias (toward the joystick’s home position). The edge-effect term also received positive coefficients (median=1.37, IQR 0.42 to 3.22, signed-rank p<0.001). Because learning rate in the normative model is linearly dependent on CPP (Fig. 1C), trial-wise update was modeled as a function of CPP × δ. The theoretical effect of RU on belief updating prescribed by the normative model was modeled as RU × (1 − CPP) × δ. We obtained results equivalent to those reported in the Behavioral Results section using variants of the model that: (1) included a main effect for each term in addition to its interaction with δ, (2) mean-centered the predictors before constructing the interactions, or (3) analyzed high-noise and low-noise runs separately.

MRI data acquisition and preprocessing

MRI data were acquired on a 3T Siemens Trio with a 32-channel head coil. We first collected a T1-weighted MPRAGE structural image (0.9375 × 0.9375 × 1mm voxels, 192 × 256 matrix, 160 axial slices, TI=1100ms, TR=1630ms, TE=3.11ms, flip angle=15°). Functional data were acquired using a gradient-echo echoplanar imaging (EPI) sequence (3mm isotropic voxels, 64 × 64 matrix, 42 axial slices tilted 30° from the AC-PC plane, TR=2500ms, TE=25ms, flip angle=75°). There were 4 runs, each with 226 images (9 min, 25s). At the end of the session we acquired matched fieldmap images (TR=1000ms, TE=2.69 and 5.27ms, flip angle=60°).

Data were preprocessed using FSL (Jenkinson et al., 2002; Jenkinson et al., 2012; Jenkinson and Smith, 2001; Smith et al., 2004) and AFNI (Cox, 1996; Cox, 2012) software. Functional data were temporally aligned to midpoint of each acquisition (AFNI’s 3dTshift), motion corrected (FSL’s MCFLIRT), undistorted and warped to MNI space (see below), outlier-attenuated (AFNI’s 3dDespike), smoothed with a 6 mm FWHM Gaussian kernel (FSL’s fslmaths), and intensity-scaled by a single grand-mean value per run. To warp the data to MNI space, functional data were aligned to the structural image (FSL’s FLIRT), using boundary-based registration (Greve and Fischl, 2009) simultaneously incorporating fieldmap-based geometric undistortion. Separately, the structural image was nonlinearly coregistered to the MNI template (FSL’s FLIRT and FNIRT). The two transformations were concatenated and applied to the functional data.

fMRI analysis

Voxelwise general linear models (GLMs) were fit using ordinary least squares (AFNI’s 3dDeconvolve). GLMs were estimated for each participant individually using data concatenated across the 4 runs. There were 11 baseline terms per run: a constant, 4 low-frequency drift terms (first-through-fourth-order Legendre polynomials), and 6 motion parameters.

The primary GLM modeled each bag drop as a 1s event convolved with an HRF. Together with the constant effect we included 5 mean-centered amplitude modulators of the outcome-related BOLD response: (1) the outcome’s left/right position on the screen (included as a nuisance term), (2) model-derived CPP, (3) model-derived RU, (4) reward value (a binary term contrasting high-value versus neutral-value outcomes), and (5) residual update from the behavioral analysis. The residual term represents the extent to which the participant’s update on a given trial was different than predicted by a regression model that included all of the hypothesized influences on learning rate. We also computed all pairwise contrasts among the CPP, RU, and reward value terms for each participant. Each modulator was z-scored across trials for a given participant (prior to HRF convolution) to place the GLM coefficients on a comparable scale and facilitate contrasts between modulator variables.

Single-trial nuisance regressors were included for the first and last trial of each run as well as invalid trials. A trial was deemed invalid if the participant either failed to collect the bucket from the home position or made an obvious response error (placing the bucket >30 screen units outside the range between the last prediction and outcome). Trials immediately following either of these events were also deemed invalid. The percentage of invalid trials was zero for 18 participants, 0.2–2.8% for 13 participants, and 10.2% for one participant.

Whole-brain, group-level analyses assessed statistical significance on the basis of cluster mass, with the cluster-defining threshold set to the nominal p<0.001 level. Corrected p-values were determined via permutation testing (Nichols and Holmes, 2002) using FSL’s randomise with 5000 iterations. Each iteration involved sign-flipping the entire coefficient map for a random subset of participants, computing the group-level t-map, and adding the maximum suprathreshold cluster mass to an empirical null distribution. This method estimates the distribution for image-wise maximum cluster mass under the null hypothesis that coefficients are centered on zero, while preserving the spatial autocorrelation of the data. The empirical null distribution was then used to assign p-values to clusters in the non-permuted data, affording whole-brain control of the family-wise error rate. Results were thresholded at corrected p<0.05, two-tailed. Conjunction analyses identified regions that passed this threshold with effects of the same sign in each of the constituent analyses. A cluster extent threshold of 10 contiguous voxels (270μL) was applied to conjunction results. For significant voxels, conjunction t statistics were defined as the minimum-absolute-value t statistic across the constituent analyses.

Further analyses tested whether trial-by-trial BOLD measurements from the two DMFC residual-update regions (Fig. 6A) or the seven common adaptive learning-rate regions (Fig. 5) improved our predictive modeling of updating behavior. We extracted the BOLD time course from each ROI, regressed out effects of baseline, CPP, RU, and reward value, and estimated a series of single-trial BOLD amplitudes (Mumford et al., 2012). Nine new behavioral regression models were created, one for each ROI, that included all the original predictors (Fig. 2) plus a term that allowed the impact of prediction errors to be adjusted according to trial-wise BOLD amplitudes. For the residual-update regions in DMFC, the BOLD amplitudes were extracted using a leave-one-participant-out procedure to avoid circularity. On each iteration we defined two ROIs as 15mm-radius spheres centered at local peaks for the residual effect in inferior and superior DMFC using a subsample of n=31 (which in practice resulted in identical ROIs in 30 of the 32 iterations), and extracted BOLD time courses from these ROIs for the held-out participant.

Supplementary Material

1

Figure S1. Additional behavioral analyses further supported our conclusion that participants flexibly adapted their learning rates as predicted by the normative model.

A: Direct estimation of trial-wise learning rate (LR). In addition to the regression-based behavioral analyses described in the main text, we also performed descriptive analyses directly on empirical trial-wise learning rate (cf. Nassar et al., 2010). The learning rate on trial t can be estimated as the subsequent update in bucket position (B_t+1 − B_t) expressed as a fraction of the current spatial prediction error (δ_t). This estimate will be affected by motor noise in joystick placement and will be less precise when δ_t is small; we therefore omitted trials with δ_t < 5 screen units (see Experimental Procedures).

The overall trial-wise learning rate (median of medians from individual participants) was 0.55 (IQR 0.43 to 0.76). Learning rate was greater after change points (median=0.94, IQR 0.88 to 0.95) than otherwise (median=0.51, IQR 0.40 to 0.73; median difference=0.34, IQR 0.15 to 0.46, signed-rank p<0.001), consistent with increased learning from surprisingly large errors. Learning rates also tended to decrease across successive non-change-point trials, mirroring the decrease in belief uncertainty (see Fig. 1C; the median within-participant Spearman correlation between lag and learning rate across non-change-point trials ρ=−0.11, IQR −0.19 to 0.00, signed-rank p<0.001). Plotted points and error bars represent median and IQR.

B: Context-sensitive estimation of change-point probability (CPP). Theoretical CPP increases as an approximately sigmoidal function of |δ_t| but also depends on the level of observation noise. Our experimental task dissociated CPP from physical values of δ_t by manipulating the noise level across runs. A moderate-sized prediction error might imply high CPP if it occurred in a low-noise context (dashed line) but low CPP if it occurred in a high-noise context (solid line). We used additional regression-based analyses to demonstrate that behavior showed the expected noise sensitivity.

For these analyses, we estimated approximate CPP as a function of δ_t (holding RU fixed at its median value for simplicity), separately for the low-noise context (CPP_σ=10[δ_t]) and the high-noise context (CPP_σ=25[δ_t]). We then defined a new participant-wise regression model with 3 terms of interest. The first regressor was based on the average of these functions: δ_t × [CPP_σ=10(δ_t) + CPP_σ=25(δ_t)]/2. Coefficients were significantly positive for this term (median=0.48, IQR 0.28 to 0.67, signed-rank p<0.001), reflecting the general tendency for learning rate to rise with |δ_t|. The other two terms were based on the difference between the two functions: δ_t × [CPP_σ=10(δ_t) − CPP_σ=25(δ_t)], defined separately for low-noise and high-noise runs only. These difference terms have values near zero for small prediction errors (which do not signify a change point in either noise condition) and for large prediction errors (which signify a change point in both conditions). They have positive values for intermediate prediction errors (approximately 25–100 screen units), which are more indicative of a change point in the low-noise condition than in the high-noise condition. The two difference regressors should receive similar coefficients if learning rate depends solely on δ_t and coefficients of opposite sign if learning rate is influenced by the noise context. Our results showed that learning rate demonstrated the appropriate noise sensitivity: coefficients were significantly positive for the second term (median=0.11, IQR 0.05 to 0.20, signed-rank p<0.001) and significantly negative for the third term (median=−0.20, IQR −0.32 to −0.14, signed-rank p<0.001), implying that participants reacted differently to physically equivalent stimuli in the two noise contexts, consistent with normative estimation of CPP.

Figure S2. Theoretically predicted BOLD time courses for CPP and RU as a function of time after a change point, derived from the approximately Bayesian model. To create this plot we extracted the mean model-derived CPP and RU for sequences of trials aligned to large change points (CPP>0.5) and convolved these values with a canonical HRF.

Figure S3. Behavioral results from the follow-up session. A subset of the original participants (n=13) was re-tested behaviorally with eye-tracking to assess the association between task variables and saccadic eye movements. Behavioral effects were evaluated using the same regression framework described in the main text (see Fig. 2), and results were comparable to the original data set. Participant-wise coefficients significantly exceeded zero for the fixed-learning-rate term (β₁; median=0.50, IQR 0.35 to 0.66, signed-rank p=0.001), and for modulation of learning rate by CPP (β₂; median=0.38, IQR 0.25 to 0.58, signed-rank p<0.001), RU (β₃; median=0.29, IQR 0.15 to 0.59, signed-rank p=0.001), and reward value (β₄; median=0.01, IQR 0 to 0.03, signed-rank p=0.033). As in Fig. 2, estimates of β₄ are scaled by a factor of 5 for visibility. Black markers represent simulated data as in Fig. 2. See Fig. S4 for eye-tracking results.

Figure S4. Given the visuospatial nature of our experimental task, a potential concern is that learning might be associated with increased oculomotor activity, which in turn might provide a more proximate explanation for the observed BOLD effects. To address this issue, we conducted a follow-up eye-tracking session outside of the scanner. Eye position was recorded at 60 Hz using a Tobii T60XL eye tracker (Tobii Technology, Stockholm, Sweden). Blinks and other unreliable signals were identified using a custom algorithm and not analyzed. Trials in which less than 50% of the data were deemed reliable were excluded from analysis. Three participants were removed from analysis due to insufficient reliable data (<120 trials). Saccades were identified using a custom algorithm implemented in Matlab. Saccades were counted for each trial and modeled with two GLMs designed to probe any relationship between learning factors and eye movements. Coefficients for terms in each model were estimated using glmfit in Matlab with a Poisson link function.

The first model looked for a relationship between eye movements and learning factors using regressors analogous to the primary fMRI GLM: (1) the outcome’s left/right position on the screen, (2) model-derived CPP, (3) model-derived RU, (4) reward value, and (5) the difference between the outcome position and the center of the screen. This model also contained two nuisance variables reflecting: (1) the proportion of reliable eye data measured during the outcome phase, and (2) the proportion of reliable eye data measured during the decision phase. Reward value coefficients were slightly negative on average and not significantly different from zero (signed-rank p=0.105). In contrast, coefficients were significantly greater than zero for CPP (signed-rank p=0.002) and RU (signed-rank p=0.037), indicating a potential confound with eye movement.

However, these relationships between eye movements and either CPP or RU were driven by the absolute magnitude of the prediction error, not adaptive learning. We estimated a second GLM that included: (1) absolute prediction error magnitude; and (2) normative learning rates that combined RU and CPP, orthogonalized on absolute prediction-error magnitude. Across participants, the first term tended to be greater than zero (left-hand set of points; signed-rank p=0.002), but the second term, reflecting normative learning, did not differ from zero (right-hand set of points; p=0.492).

Moreover, this relationship between saccadic activity and the absolute magnitude of the prediction error could not by itself explain the relationships between BOLD signals and adaptive learning. We conducted a corresponding fMRI analysis in which the trial-related BOLD response was modulated by: (1) the absolute value of the prediction error; and (2) normative learning rates derived from the approximate Bayesian model, orthogonalized on absolute prediction-error magnitude. Treating the seven common adaptive learning-rate regions as regions of interest (ROIs), each showed significant effects for both terms (all ps<0.01 after Bonferroni correction for 7 comparisons). This result suggests that the observed BOLD effects in these regions were not attributable solely to a simple factor such as increased oculomotor activity for large errors.

Figure S5. Factor-specific regions selectively explain variance in common adaptive learning-rate regions (LR regions). To test whether regions reflecting a specific computational factor might communicate with LR regions according to the extent to which the represented factor is driving learning on a given trial we conducted a psychophysiological interaction (PPI) analysis. In particular, we designed a regression model to examine whether physiological variables reflecting CPP and RU might be more related to LR regions when the reflected variable should be driving more of the learning on a given trial. The psychological variables were trial-by-trial estimates of RU and CPP estimated by our computational model. The physiological variables were trial-wise BOLD amplitudes extracted from the occipital cluster identified as a CPP region and the right aPFC cluster identified as an RU region (Fig. 4). The two physiological and two psychological variables were used to create 4 PPI variables from the interactions of z-scored psychological and physiological terms (CPP×Occipital, CPP×aPFC, RU×Occipital, RU×aPFC). Two of these PPI terms were “matched,” corresponding to the interaction between a learning factor and the area reflecting that factor (CPP×Occipital, RU×aPFC). The other two were “mismatched”, corresponding to the interaction between a learning factor and an area representing the other factor (CPP×aPFC, RU×Occipital). We hypothesized that matched interaction terms would take positive coefficients indicating an increase in shared variance between factor-specific and LR regions when the factor was contributing to learning. We hypothesized that mismatched terms would take smaller or even negative values, which would represent a decrease in shared variance between factor-specific and LR regions when that factor contributed less to the prescribed learning rate.

Psychological, physiological, and PPI variables were included in a regression model that also included an intercept term and several other nuisance variables (outcome value, outcome location, outcome distance from center of screen, signed prediction error). This model was applied to the series of trial-wise BOLD amplitudes extracted from each of the LR regions (Fig. 5).

A: Individual PPI coefficients. PPI coefficients were averaged across the seven LR regions for each participant. The resulting coefficient for each term is plotted on the ordinate (points = across-participant medians, lines = bootstrapped 95% CIs). Terms on the left half of the abscissa (shaded green) are based on matched psychological and physiological variables, and terms on the right half of the abscissa (shaded red) are based on mismatched psychological and physiological variables. The contrast of matched versus mismatched terms was significant (median=0.031, IQR 0.001 to 0.068, signed-rank p=0.002). While all PPI coefficients followed the predicted pattern, the trends were stronger in the aPFC PPI terms (RU×aPFC: median=0.009, IQR −0.010 to 0.031, signed-rank p=0.043; CPP×aPFC: median=−0.011, IQR −0.021 to −0.001, signed-rank p=0.002).

The overall contrast result was not significant in alternative versions of the PPI analysis that substituted other RU-selective regions in place of right aPFC. Results were non-significant for the RU-selective regions in parietal cortex (median=0.018, IQR −0.030 to 0.042; signed-rank p=0.184) and cerebellum (median=0.033, IQR −0.042 to 0.094; signed-rank p=0.067). Comparing the effect across RU-selective regions yielded modest evidence that the effect was greater for aPFC than the parietal region (signed-rank p=0.047) but no evidence of regional specificity in the other two pairwise comparisons.

B: Contrast of matched versus mismatched PPI terms in individual LR regions. Points and lines represent across-participant medians with bootstrapped 95% CIs. Contrast results for individual LR regions are plotted in brown and the aggregate result across LR regions (reported above and in the main text) is plotted in blue. The contrast was significantly greater than zero in the majority of individual regions (signed-rank p<0.05, uncorrected, for all LR regions except DMFC [p=0.197] and PCC [p=0.304]). Only the right parietal region was significant after Bonferroni correction for 7 comparisons (corrected p=0.009).

Table S1, related to Fig. 3. BOLD effects for individual GLM terms.

2. Movie S1.

Animated surface-rendering of change-point-aligned BOLD time courses. Time courses were estimated for each participant using a finite-impulse-response model in the framework of a GLM. The GLM included the same baseline and single-trial nuisance regressors as the primary analysis (see Experimental procedures) plus a total of 26 piecewise linear spline (“tent”) basis functions corresponding to points in the event-related time series. Basis functions were centered every 2.5s from 0 to 30s after change points; a second set of basis functions was placed at the same lags relative to non-change-points. To estimate change-point-related effects we took the difference between each participant’s change-point-aligned and non-change-point-aligned timecourses. The animation displays a simple estimate of across-participant effect size (ES; mean/SD) at each location and time point. Results are shown on an inflated brain and spatiotemporally interpolated for visualization. The animation was created using Freesurfer (http://surfer.nmr.mgh.harvard.edu) and Paraview (http://www.paraview.org).