Factors affecting the repeatability of gamma camera calibration for quantitative imaging applications using a sealed source

Abstract

Several applications in nuclear medicine require absolute activity quantification of single photon emission computed tomography images. Obtaining a repeatable calibration factor that converts voxel values to activity units is essential for these applications. Because source preparation and measurement of the source activity using a radionuclide activity meter are potential sources of variability, this work investigated instrumentation and acquisition factors affecting repeatability using planar acquisition of sealed sources. The calibration factor was calculated for different acquisition and geometry conditions to evaluate the effect of the source size, lateral position of the source in the camera field of-view (FOV), source-to-camera distance (SCD), and variability over time using sealed Ba-133 sources. A small region of interest (ROI) based on the source dimensions and collimator resolution was investigated to decrease the background effect. A statistical analysis with a mixed-effects model was used to evaluate quantitatively the effect of each variable on the global calibration factor variability. A variation of 1 cm in the measurement of the SCD from the assumed distance of 17 cm led to a variation of 1–2% in the calibration factor measurement using a small disc source (0.4 cm diameter) and less than 1% with a larger rod source (2.9 cm diameter). The lateral position of the source in the FOV and the variability over time had small impacts on calibration factor variability. The residual error component was well estimated by Poisson noise. Repeatability of better than 1% in a calibration factor measurement using a planar acquisition of a sealed source can be reasonably achieved. The best reproducibility was obtained with the largest source with a count rate much higher than the average background in the ROI, and when the SCD was positioned within 5 mm of the desired position. In this case, calibration source variability was limited by the quantum noise.

1. Introduction

In a number of nuclear medicine applications, absolute quantification of the administered radiopharmaceutical distribution is essential. These applications include patient and organ specific dosimetry to plan radiopharmaceutical therapies, as well as use of quantitative measures to evaluate disease response to therapy, disease progression and to compare images over time. A precise and accurate calibration factor for the conversion of the voxel value to activity is fundamental for absolute activity quantification, even when images are compensated for image-degrading effects (He and Frey 2006, Zeintl et al 2010, Ritt et al 2011). Accuracies of better than 5% have been achieved in large organs in simulation and phantom studies (He et al 2005, Song et al 2011). Since the accuracy is directly proportional to errors in the calibration factor, variability in the calibration significantly smaller than 5% is desirable in order for the calibration factor not to be a limiting factor in the overall error of activity estimates. Several studies in positron emission tomography imaging have evaluated the effects of the calibration factor on standard uptake value measurement and variability (Kinahan and Fletcher 2010, Lockhart et al 2011), and more reliable measurement methods have been implemented using sealed sources (Zimmerman and Cessna 2010, Zimmerman et al 2014). However, in single photon emission computed tomography (SPECT) there have been few studies of the effects of the calibration factor, and no standardized methods have been established for gamma camera calibration. Indeed, several methods for the calibration factor measurement can be found in the literature including simulation (Dewaraja et al 2005) or experimental measurements with different source sizes, shapes and geometries (Sjögreen et al 2002, He et al 2005, Koral et al 2007, National Electrical Manufacturers Association 2007, Willowson et al 2008) and using SPECT or planar acquisition (Dewaraja et al 2012). In a previous study (Anizan et al 2014), we evaluated factors affecting repeatability of measurement of the system sensitivity using a planar acquisition of an in-air source. That work was based on use of a vial source filled for each patient and showed that preparation and measurement of the activity in the calibration source with the radionuclide activity meter was a major factor affecting the variability of the calibration factor. The background count rate detected in the entire field-of-view (FOV) was also an important component of calibration factor variability for the whole-body acquisition method used.

Because of the simplicity of planar acquisition and to retain continuity with previous work, this study focused on the use of in-air sources and planar acquisitions. To eliminate uncertainty due to the source activity measurement in the radionuclide activity meter and source preparation, we used sealed sources with a long half-life instead of a filled source. The quantification of activity in patients would be more accurate and less variable when using a well-calibrated same sealed source for all calibration factor measurements. In addition, for this investigation it reveals other sources of variability that could be masked by variations in the calibration source preparation and measurement. Because iodine-131 is one of the most commonly used radionuclides for internal radionuclide therapy and quantification is challenging due to its high photopeak energy, we focused on high-energy radionuclides imaging. We thus used a long-life radionuclide, ¹³³Ba, that has similar spectral characteristics as I-131 to evaluate the factors affecting repeatability of calibration factor measurement using a sealed source. The long halflife of Ba-133 allowed repeated measurements over a long period of time for the evaluation of camera stability without concerns about changes in count rate or noise level.

Statistical analyses were performed to estimate quantitatively the effects of various parameters on calibration factor variability. We hypothesized that acquisition geometry could be an important factor affecting variability and thus evaluated the impact of source size, position of the source in the FOV and the distance between the source and the camera. As shown previously, background count rate was an important factor determining variability. We thus compared the use of the counts rates estimated from the entire image FOV to those from a smaller ROI. Finally, variability was investigated for each camera and on multiple SPECT systems.

2. Methods

Different ¹³³Ba source sizes and geometries were used in this study to evaluate by experiment and simulation the variability in the calibration factor and the effect of the different factors described previously. This radionuclide was chosen for its long half-life (T_1/2 = 10.5 years) and because its emission energy is similar to ¹³¹I (Eγ = 356 keV). An energy widow with a full-width of 15% centered on 356 keV was used in all acquisitions for this study. The calibration factor was calculated for each configuration using:

$$\text{CF}=\frac{\text{Calibration}\text{source}\text{count}\text{rate}-\text{Background}\text{count}\text{rate}}{\text{Calibration}\text{source}\text{activity}}.$$ (1)

2.1. Experiments

A disk source consisting of a 0.4 cm diameter compartment containing ¹³³Ba sealed in a plastic cylinder (2.4 cm diameter and 0.5 cm height) and with an activity of 2.8 MBq was imaged on three state-of-the-art SPECT systems whose manufacturer-provided specifications are shown in table 1.

Table 1.

SPECT system specifications.

System	1	2	3
Energy resolution 140 keV	9.8%	9.9%	10%
Intrinsic resolution (cm)	0.39	0.39	0.33
Collimator hole size (cm)	0.4	0.381	0.4
Septal thickness (cm)	0.18	0.173	0.2
Collimator thickness (cm)	6.6	6	5.97
Pixel size (cm)	0.4418	0.4664	0.4795

For each system the source was placed at three different positions in the camera FOV spaced at 2 cm intervals in a plane 17 cm from each of the two cameras to investigate the effect of lateral position. To investigate the effect of the source-to-camera distance (SCD) on the calibration factor measurement, the camera was moved away from the source in 5 mm steps and acquisitions were performed for three different SCDs. At each source and camera position 3 consecutive 5 min planar acquisitions were performed, each giving ~27 kcounts in the entire FOV, to evaluate the variability in consecutive measurements. Finally, three 5 min background acquisitions were performed immediately following the source data acquisitions. These data were used to investigate the impact on variability of using the entire FOV versus a smaller region of interest (ROI) for calculating the counts in equation (1). The use of the full FOV has the advantage that it is simple and a very repeatable ROI. However, the full FOV includes the entire background count rate. While using the full FOV as the ROI for calibration source count rate measurement might seem unwise, it has been used in a number of applications including the dosimetry procedure used as part of the Bexxar^© therapeutic regimen. We included it in this investigation as a frame of reference.

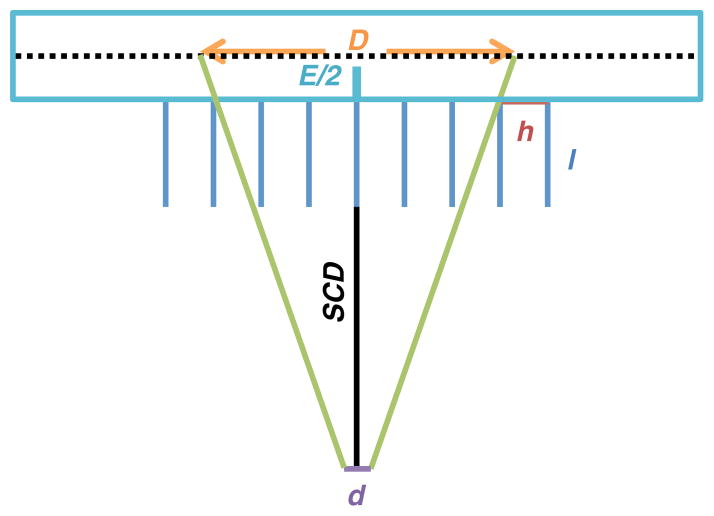
To reduce the effect of ROI definition variability, we used a ROI based on a geometric criterion. The ROI dimensions were defined by projection of the source dimensions to the image plane taking into account the geometric acceptance angle of the collimator holes, as shown in figure 1. The size of the ROI, D, is given by

Figure 1.

ROI size definition in the image plan where D is the source dimensions in the image plan, d the true dimensions of the source, h the collimator hole size, l the collimator thickness, E the crystal thickness and SCD the source-to-camera distance.

$$D=d+2\times \frac{h\times (\text{SCD}+l+E/2)}{l},$$ (2)

where d is the size of the source, h is the diameter of the collimator hole, l is the collimator hole length, E/2 is the distance to the detection plane, typically taken to be half the crystal thickness, and SCD is the source-to-collimator distance. This ROI was designed to include all geometrically collimated photons while limiting the number of photons that penetrated through or scattered in the septa.

The high-energy general-purpose collimators used in this study have a septal thicknesses that is comparable to the intrinsic spatial resolution of the camera. Thus the sensitivity for a small source can vary with lateral position. To investigate, two cylindrical ¹³³Ba sources (Zimmerman et al 2013) with larger dimensions than the disk source were also imaged to evaluate the effect of the source size on the calibration factor repeatability. The active volumes of both rods were 3.8 cm long and consisted of an acrylic shell filled with epoxy containing uniformly distributed Ba-133. The activities and active diameters of the sources were 0.8 cm and 2.9 cm and 0.399 MBq and 1.179 MBq, respectively. The sources were constructed and calibrated by the US National Institute of Standards and Technology. These two sources were positioned with their long axes parallel to the camera face and along the scanner axis. The sources were imaged with system 3 only and, as for the disk source, at three different positions in the FOV and three different SCDs. Then, three consecutive 10 min static acquisitions were performed yielding ~13 kcounts for the smallest rod and ~25 kcounts for the largest rod in the entire FOV. Three 10 min background acquisitions were also performed. Because of their larger dimensions, we were able to repeat the position of the rod sources over 3 consecutive days with a reasonable degree of precision (estimated to be better than 1 mm), and thus evaluated the time variation of the calibration factor measurement. The calibration factor was again calculated using both the counts in a rectangular ROI with dimensions calculated as above and the total counts in the FOV.

The goal of varying the SCD was to investigate how imprecision in source positioning, as might happen in clinical implementation, would affect the precision of the calibration factor measurements. Thus, for the ROI method we calculated the ROI size using an assumed SCD of 17 cm and used this for all the actual SCDs. The center of the ROI was placed over the center of the projected source in the image manually.

The background count rate was computed in the same size region used to calculate the source counts. For the ROI-based calculation the averaged background count rate was calculated over five ROIs placed on the image and over the three acquisitions.

2.2. Simulation

The SIMIND Monte Carlo code was used to evaluate in a precise and controlled manner the effect of variations of single factors on the calibration factor, which was difficult experimentally due to factors such as manual positioning of the ROI that cannot be completely eliminated. Each of the three sources were simulated using models of the three cameras used for the experiment. In the simulations we systematically investigated the effects of lateral source position and SCD variation over a larger range than used in the experiment. We investigated the effects of source position laterally for a SCD of 17 cm by simulating sources with offsets of 0–10 cm in 1 cm increments from the center of the FOV. The ROIs used to calculate the total counts were centered over the center of the source position in the image plane. The SCD was then varied from 14 to 20 cm in 1 cm steps with the source positioned at the center of the FOV. In that case, an ROI size appropriate for a 17 cm SCD was used to calculate the calibration factor for all distances. A long simulation resulting in a low level of noise was first performed. We then generated 20 different noisy planar projections for each source modeling the same activity and acquisition time as in the experiments using a Poisson distributed random number generator.

2.3. Statistical analysis

The effect of each parameter on the calibration factor was assessed using a mixed-effects model. In a mixed-effects model the value of a dependent variable, in this case the calibration factor, is modeled in terms of a set of explanatory variables, which are treated as either fixed and or random effects. A variable treated as a fixed effect is one where there is a systematic association with the dependent variable and assessing the difference in calibration factor associated with different levels of this variable is of interest. For a random effect the values of the variable are considered to be a random sample from an infinite population of values, and there is either no known association between the explanatory and dependent variables or the association is not of interest. We assumed that the random variables were normally distributed with a zero mean and an unknown standard deviation that was estimated during the model fitting procedure.

We performed experiments to examine the impact of three variables including position of the source in the FOV, SCD and the time of acquisition. A mixed-effects model was used to simultaneously estimate the relative contributions of the three explanatory variables on the calibration factor. In the model fixed effects represent the mean calibration factor associated with each value of that variable; random effects are characterized by a variance that affects the overall variance of the calibration factor. Using the mixed-effects model provides information on the fraction of the overall variance contributed by each random effect and the difference in the calibration factor for each value of the fixed effect. We modeled the source-to-collimator distance as a fixed effect, and position and time as random effect for the reasons described below.

• Position of the source in the FOV was considered to be a random effect because we assumed that a displacement of the source laterally would not affect the mean of the calibration factor, in a systematic way, which was confirmed by the simulation results.

• We assumed that the SCD was a fixed effect in the experimental measurements. The simulations showed that the calibration factor varied approximately linearly with the source-to-collimator distance. The experimental measurements were made for a small number of specific distances, and we wished to quantify the impact of the source-to-collimator distance on calibration factor by estimating the mean of the calibration factor associated with each of the three distances where a measurement was obtained.

• The time (including the date) of acquisition was considered to be a random effect because the individual times were random samples of an infinite number of possible acquisition times. The time was only considered for the rod sources because they were positioned consistently on the different days. We did not have confidence that we could reliably reposition the disk source on different days due to the small size of the active portion.

The mixed-effects model used for the disk source for a measurement ijk of the calibration factor is:

$$y_{{\text{CF}}_{\mathit{ijk}}}=\mu +{\beta }_{{\text{distance}}_i}+{\gamma }_{{\text{position}}_j}+{\epsilon }_{\mathit{ijk}}.$$ (3)

In equation (3) y_CFijk denotes the kth observation of the calibration factor at distance i and position j; μ is the overall mean, β_distancei denotes the fixed effect of the source-to-collimator distance for the ith distance and represents the difference between the calibration factor for distance i and the overall mean μ; γ_positionj, is the random effect due to the lateral source position (normally distributed with zero mean and variance ${\sigma }_{{\gamma }_{\text{position}}}^2$, and ε_ijk is the residual error (normally distributed with zero mean and variance ${\sigma }_{\mathrm{E}}^2$ Note that the residual error includes the effects of unknown parameters.

The mixed-effects model for the rod sources was the same as that used for the disk source with the addition of the random component in the CF due to variation over time, η_timel (assumed normally distributed, zero mean with variance ${\sigma }_{{\gamma }_{\text{time}}}^2$). The model is defined by:

$$y_{{\text{CF}}_{\mathit{ijlk}}}=\mu +{\beta }_{{\text{distance}}_i}+{\gamma }_{{\text{position}}_j}+{\eta }_{{\text{time}}_l}+{\epsilon }_{\mathit{ijlk}}.$$ (4)

The parameters in the above models including the mean (μ), fixed effect parameters, variances of random effects and residual error in the above models were estimated using restricted maximum likelihood (REML) (Rao 1997).

3. Results

3.1. Cameras

The correlation between the calibration factors calculated for each of the two cameras for one system was evaluated to determine if the average of the two calibration factors could be used in subsequent analyses. Table 2 shows the Pearson correlation coefficient calculated for the three sources, the three systems and the two methods, ROI versus entire FOV, used to calculate the calibration factor. For all cases, the Pearson coefficient was small, indicating that the correlation in the calibration factor between the two cameras was weak. This indicates that factors unique to the two cameras were more important sources of variation than common factors such as room temperature or electrical voltage variations. Thus in subsequent analysis a separate calibration factor was used for each camera.

Table 2.

Correlation between camera 1 and camera 2.

Source	System	Count rate measurement	Pearson coefficient
Disk source	1	ROI	0.2250
		Entire FOV	0.4718
	2	ROI	0.6581
		Entire FOV	0.5091
	3	ROI	0.4400
		Entire FOV	−0.1330
Small rod	3	ROI	0.1878
		Entire FOV	−0.1473
Large rod	3	ROI	0.0667
		Entire FOV	0.2291

3.2. Background

In a previous study we found that the background count rate had a significant effect on calibration factor repeatability when the counts in the entire FOV were used in the calculation (9% of the total variance of the calibration factor when a ¹³¹I source with an activity of 10 MBq was used). Table 3 shows the ratio of the background count rate to the source count rate when an ROI and the entire FOV were used. In all cases, use of the entire FOV resulted in a very large percentage of the source counts due to background. This was especially true for the small rod because of its low activity compared to the other sources. The use of an ROI decreased substantially the magnitude of the background correction needed in all cases, which would also decrease the effect of background counts on calibration factor variability. For these sources the effect of background was so small that we reasoned that in routine practice a background acquisition would not be needed. Thus, the source count rate was not corrected for the background count rate when the ROI method was used, and the background component was not included in the mixed-effects model. Consequently, only the calibration factor calculated using the ROI was evaluated in subsequent analyses.

Table 3.

Percentage of the source count rate due to background.

Source	System	Count rate measurement	Camera 1 (%)	Camera 2 (%)
Disk source	1	ROI	0.08	0.10
		Entire FOV	14.70	15.77
	2	ROI	0.08	0.07
		Entire FOV	10.26	9.23
	3	ROI	0.10	0.10
		Entire FOV	13.67	8.17
Small rod	3	ROI	1.97	1.44
		Entire FOV	54.27	47.28
Large rod	3	ROI	1.05	0.77
		Entire FOV	28.59	23.17

3.3. Source-to-camera distance

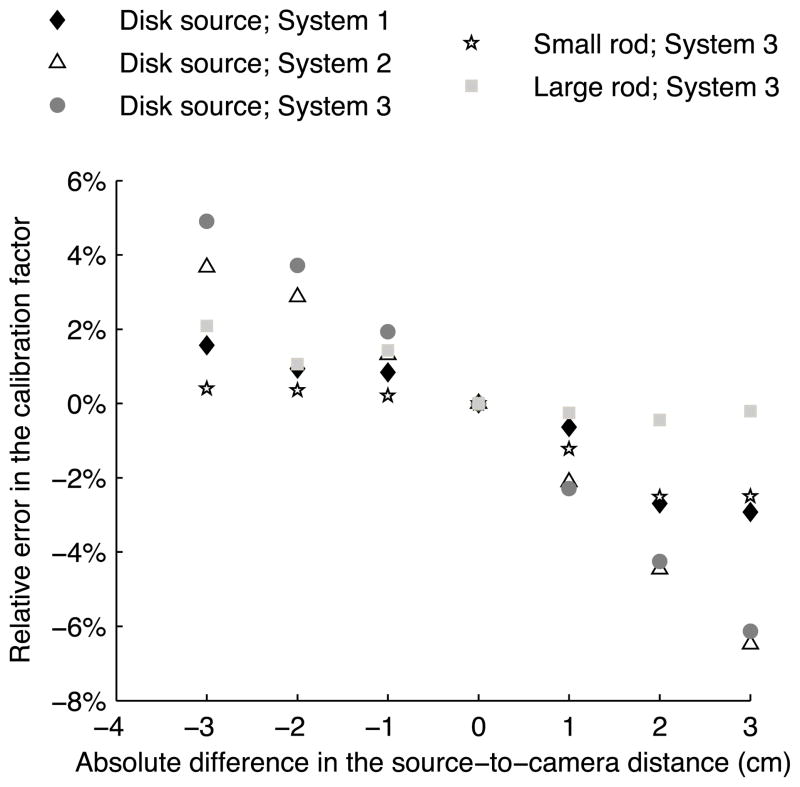
The goal of the following experiment and analyses was to investigate the sensitivity of the calibration factor to exact placement of the source. To this end, we chose the case where the desired SCD, i.e. the distance used to calculate the ROI size, was 17 cm. Figure 2 shows a plot of the error in calibration factor from the Monte Carlo simulations as a function of displacement of the source from the assumed distance of 17 cm from simulated data. Since there were no background counts, the error results from including (for negative displacements) or excluding photons in the calculation. For negative displacements the error represents the inclusion of extra photons that penetrated through or scattered in the septa; for positive displacements the error represents exclusion of some geometrically collimated photons. Linear regression analysis of the five curves showed that, when using the disk source, the SCD displacement led to errors of 0.8% cm⁻¹ (system 1, R² = 0.92514), 1.7% cm⁻¹ (system 2, R² = 0.97933) and 1.9% cm⁻¹ (system 3, R² = 0.99468) in the calibration factor. When the rod sources were used, the errors in the calibration factor were smaller: 0.6% cm⁻¹ (R² = 0.86263) for the small rod and 0.4% cm⁻¹ (R² = 0.8100) for the larger rod.

Figure 2.

Simulated calibration factor variation with the SCD.

The results of the statistical analysis for the experimental data using the mixed-effects model are shown in table 4. In this table, μ_CF1 represents the mean calibration factor estimate for distance number 1 (17 cm); μ_CF1−2 represents an estimate of the difference between the mean calibration factors for distance 1 and distance 2, corresponding to a 5 mm step; and μ_CF1−3 is the same difference for distances 1 and 3, representing a 1 cm step.

Table 4.

SCD effect for system 3.

	Disk source		Small rod		Large rod
	Camera 1	Camera 2	Camera 1	Camera 2	Camera 1	Camera 2
μCF1	19.77 ± 0.15	20.91 ± 0.11	19.85 ± 0.05	19.54 ± 0.06	20.53 ± 0.03	20.18 ± 0.05
μCF1-2	−0.22 ± 0.11	−0.23 ± 0.12	−0.28 ± 0.11a	−0.07 ± 0.12	−0.05 ± 0.07	−0.02 ± 0.08
μCF1-3	−0.30 ± 0.11a	−0.50 ± 0.12a	−0.20 ± 0.11	−0.37 ± 0.12a	−0.06 ± 0.07	−0.23 ± 0.08a

Values are in units of cps MBq⁻¹.

μ_CF1 denotes the mean calibration factor estimate for distance number 1 (17 cm); μ_CF1−2 represents the difference between the mean calibration factors for distance 1 and distance 2, corresponding to a 5 mm step; and μ_CF1−3 is the same difference for distances 1 and 3, representing a 1 cm step.

^aStatistically significant (p < 0.05).

For four out of the six rod source and camera combinations, a variation of 1 cm in the SCD had a statistically significant impact on the calibration factor whereas a 5 mm variation resulted in a statistically significant impact in only one out of six combinations. Based on these experimental data, the errors in the calibration factor averaged over the two system’s cameras from the 1 cm variation were 1.9% cm⁻¹ when the disk source was used, 1.4% cm⁻¹ when the small rod was used and 0.7% cm⁻¹ when the large rod was used and are comparable to the results of 1.9, 0.6, and 0.4% cm⁻¹ from the simulation results.

3.4. Lateral position in the FOV and acquisition time

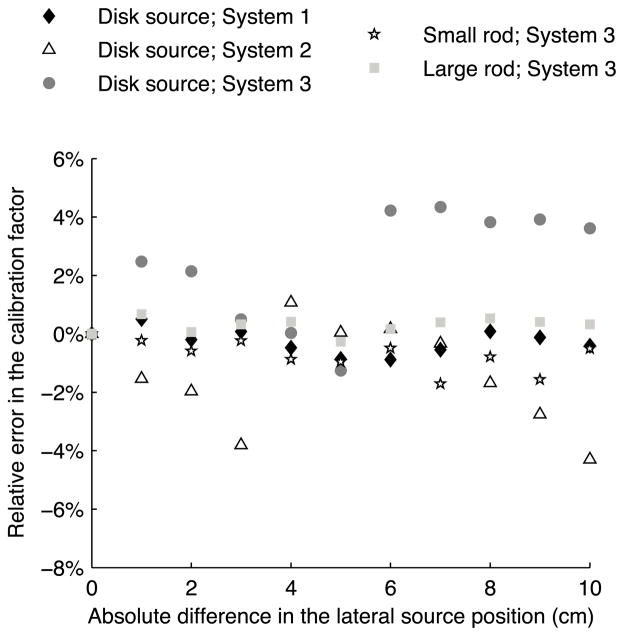
Figure 3 shows simulated results for the variation of the calibration factor when the position of the source was moved laterally in the FOV in 1 cm increments. The variation in the calibration factor with the lateral position in the FOV was on the order of 4% for the disk source and less than 2% for the large rod over the 10 cm range of displacement of the sources. Because no systematic linear association was observed, the simulated results confirmed that lateral positions examined in the experiment could be considered as random samples of a large population of positions and thus treated as a random effect in the mixed-effects model. Note that for increments smaller than collimator hole diameter it is likely that lateral position would be a fixed effect. However, since the position of the sources was unknown with respect to the collimator holes, and given the results for the 1 cm step used in the simulation, treating lateral position as a random effect was justified.

Figure 3.

Variation of the simulated calibration factor with the source position in the FOV.

Table 5 presents the variance component analysis for the two rods. The variance estimates for the position ( ${\sigma }_{{\gamma }_{\text{position}}}^2$) and time ( ${\sigma }_{{\gamma }_{\text{time}}}^2$) effects (treated as random effects) and the residual error ( ${\sigma }_{\epsilon }^2$) are shown in the table. Also shown is the expected variance due to Poisson noise ( ${\sigma }_{\text{Poisson}}^2$) calculated using Var(Count rate)/Source activity². Comparing this to the residual error, ${\sigma }_{\epsilon }^2$, gives an idea of how much of the residual error was due to Poisson noise versus other unmeasured effects.

Table 5.

Variance estimates for the random effects in the rod model.

	Small rod		Large rod
	Camera 1	Camera 2	Camera 1	Camera 2
${\sigma }_{{\gamma }_{\text{time}}}^2$	0.0000	0.0233	0.0007	0.0038
${\sigma }_{{\gamma }_{\text{position}}}^2$	0.0000	0.0005	0.0004	0.0050
${\sigma }_{\epsilon }^2$	0.0794	0.0757	0.0286	0.0290
${\sigma }_{\text{Poisson}}^2$	0.0842	0.0824	0.0293	0.0287

When the rod sources were used to measure the calibration factor, position and time had a small effect on the calibration factor’s variability. The largest component was the residual error, ${\sigma }_{\epsilon }^2$, which was well estimated by the Poisson noise variance estimate. The higher residual value for the small rod is due to its lower activity.

3.5. Source size

Simulation results showed that calibration factor measured using the disk source was more affected by the SCD variation (higher slope in figure 2), which was confirmed by the analysis of experimental data (table 4). Figure 3 also shows there was more variability due to lateral position than for the rod sources. Table 6 gives the coefficients of variation calculated for each source, system and camera using the total variance estimate calculated using the mixed-effects model.

Table 6.

Coefficient of variation of the calibration factor estimate.

Source	System	Camera	COV (%)
Disk source	1	1	0.87
		2	1.40
	2	1	1.24
		2	1.98
	3	1	1.46
		2	1.08
Small rod	3	1	1.43
		2	1.63
Large rod	3	1	0.84
		2	0.97

The lowest variability was for the large rod source, which had a coefficient of variation (COV) of less than 1%. The COVs for the small rod and disk sources were similar and averaged about 1.5%.

4. Discussion

The results of this and previous work (Anizan et al 2014) indicate the importance of the following considerations in order to obtain a reliable calibration factor when using an in-air planar acquisition of a calibration source:

1. It is important to draw a reproducible region around the source to reduce sensitivity to background count rate. The use of an ROI based on the extent of the geometric projection of the object in the image plane substantially reduced the impact of background radioactivity and is not as subjective as a hand-drawn ROI.

2. Variations in the calibration factor for the two cameras in the system were not correlated. This suggests that it is necessary to monitor the quantitative stability of the cameras separately.

3. A source with a size large compared to the voxel and collimator hole size should be used. The data in this study showed greater variability for a source approximately twice the size of the collimator hole than for one approximately seven times as large as the collimator hole size. This indicates that the minimum source extent should be more than twice the collimator hole diameter. The activity of the source should be high enough to provide a count rate much higher than the background rate in the ROI. Thus the activity of the source should increase as the size increases. However, if the activity is too high deadtime effects may result.

4. Positioning of the calibration source should be accurate and reproducible. For the sources used here, an accuracy of 5 mm in the SCD did not result in a statistically significant difference in the calibration factor, and was thus smaller than other sources of imprecision. Consistent positioning allows the use of the same sized ROI for each calibration source measurement and would thus reduce variability of the calibration factor.

5. Lateral position in the FOV had a small effect on calibration factor variability compared to the Poisson noise. Thus, repeatable position in the lateral direction is not essential.

6. When the above are satisfied, the variability of the calibration factor will largely be dominated by Poisson noise. Thus estimates of the counts required in the calibration source image can be made based on the desired level of calibration source variability. Acquisition of 20 000 counts in the ROI would provide a coefficient of variation lower than 1%.

7. There was not a large variation in the calibration factor as a function of time over the time period studied. Previous work (Anizan et al 2014) indicated stability of the calibration factor over periods of months and years. These data indicate that quantitative calibration of the system can be performed relatively infrequently and then only monitored as part of a quality control procedure at an intermediate frequency using a planar measurement such as the one investigated here.

5. Conclusion

A planar acquisition of a source with known activity can be used to measure or monitor the quantitative stability of the calibration factor in quantitative planar or SPECT imaging. In this study, sealed sources and physical and simulation experiments were used to investigate the source and acquisition parameters that affect calibration factor variability. The effect of background radiation on variability can be reduced through the use of an ROI around the source rather than using the entire camera FOV to compute the calibration source count rate. We investigated the use of a manually placed ROI with size and shape based on the extent of the geometric counts from the calibration source. Results showed that use of this ROI substantially reduced the effect of background and was not sensitive to errors of up to 5 mm in the source-to-detector distance used in the calculation of the ROI shape. Further, this provides an objective and consistent method to quantify the source count rate. Results also demonstrated that a larger source size is desirable to reduce the effects of variations in source position on calibration factor precision. Data indicated that a source at least twice the size of the collimator hole diameter should be used. When the above conditions are met, variability in the calibration factor was dominated by Poisson noise, indicating that estimates of the source activity and acquisition time needed to achieve a desired calibration factor precision can be made largely based on considerations of quantum noise. Finally, the calibration factor did not show large variations over time, suggesting that detailed quantitative calibration can be performed relatively infrequently with less detailed monitoring performed more frequently.