Protonation and pK changes in protein-ligand binding

Abstract

Formation of protein-ligand complexes causes various changes in both the receptor and the ligand. This review focuses on changes in pK and protonation states of ionizable groups that accompany protein-ligand binding. Physical origins of these effects are outlined, followed by a brief overview of the computational methods to predict them and the associated corrections to receptor-ligand binding affinities. Statistical prevalence, magnitude, and spatial distribution of the pK and protonation state changes in protein-ligand binding are discussed in detail, based on both experimental and theoretical studies. While there is no doubt that these changes occur, they do not occur all the time; the estimated prevalence varies, both between individual complexes and by method. The changes occur not only in the immediate vicinity of the interface, but sometimes far away. When receptor-ligand binding is associated with protonation state change at particular pH, the binding becomes pH dependent: we review the interplay between sub-cellular characteristic pH and optimum pH of receptor-ligand binding. It is pointed out that there is a tendency for protonation state changes upon binding to be minimal at physiologically relevant pH for each complex (no net proton uptake/release), suggesting that native receptor-ligand interactions evolved to reduce the energy cost associated with ionization changes. As a result, previously reported statistical prevalence of these changes – typically computed at the same pH for all complexes – may be higher than what may be expected at optimum pH specific to each complex. We also discuss whether proper account of protonation state changes appears to improve practical docking and scoring outcomes relevant to structure-based drug design. An overview of some of the existing challenges in the field is provided in conclusion.

1 Introduction

Protein-ligand binding is one of the most ubiquitous and diverse processes in biology. Proteins bind to each other to form vital complexes such as hemoglobin; DNA in higher organisms is found mostly in complex with the histones and other proteins; and when the ligand is a small molecule, it can be the substrate that binds to an enzyme in the course of a biochemical reaction. Binding of small molecules to proteins is of interest for yet another important reason: early stages of structure-based drug discovery^49,60,44 often involve identifying a ligand that binds to the target protein with high affinity.

Regardless of the nature of receptor-ligand binding, understanding the mechanisms involved requires detailed knowledge of the nature and origins of changes in physical states of the participating proteins and ligands. It is well-known that structural complementary plays a critical role in the binding process, and so it is not surprising that structural rearrangements that can accompany protein-ligand binding have been extensively explored,^46,56,16 including variations in ligand binding mode to the same receptor.⁹³ The ”induced fit” mechanism, whereby the protein adjusts its shape to better accommodate the ligand, has long been in textbooks.¹⁴⁶ Structure-energy relationships in the binding process have also been systematically investigated.^{122,38,18,102}

In contrast, relatively little was known until recently about the magnitude, prevalence, and detailed origins of changes in charge states of receptors and ligands upon the binding. These changes are directly related to binding-induced changes in pK ^* values of ionizable groups in proteins and their ligands. In part, the relative underdevelopment of this field compared to its close “relative” – studies of structural changes in protein-ligand binding – can be attributed to the difficulties associated with experimental determination of pK and protonation state changes in a complex formation. Even today, only a handful of relevant data points exist. And even though rigorous physics-based methods able to compute titratable group pK s based on atomic resolution protein structures have existed for at least two decades,^9,159,45,3 no “large scale” studies of pK changes in protein-ligand appeared until recently.

It is important to realize that energetic consequences of binding-induced protonation state changes may be as large as those caused by partial protein unfolding or destabilizing mutations. For example, at pH = 6.5, the cost of changing the ionization state of a single group with pK =4.5 is larger than 2 kcal/mol – a realistic scenario in protein-ligand binding. This relatively large energy should not be surprising if one draws an analogy between ligand binding and protein folding: both processes often involve burial (desolvation) of large parts of the protein. It was well known for a long time that energetic costs of several kcal/mol are often associated with burial of certain ionizable groups inside folded proteins. In fact, it is this effect that leads to the observed pH dependence of protein stability.^136,160 Not surprisingly, the change in the protonation state of the complex relative to that of the separated receptor and its ligand is also a prerequisite for the observed^15,35 pH dependence of receptor-ligand binding.^114,79,55,13 The change of protonation states of titratable groups during particular reaction is the cause of pH -dependence of most enzymatic reactions¹⁴⁶ as well. Since evolution cares about survival and reproduction only, which is related to biological activity and networks on the cellular level, one can ask whether the pH -dependence of activity of biological macromolecules is somehow related to their pH -dependence of stability and interactions.¹³⁵ In addition, how the pH -dependent properties are related to the sub-cellular and tissue pH ?^92,70,39 Is it possible that macromolecular interactions have evolved toward specific pH, and can tolerate small deviations around it. Alternatively, they may have evolved to be strongly pH -dependent to sense or regulate the local pH.⁹² These issues must be considered when discussing protonation state changes in ligand binding and their possible effects on practical computations.

Until recently, many questions related to the magnitude, prevalence, detailed physical origins, and practical implications of changes in the charge state of receptor proteins (and ligands) upon complex formation were not explored on a statistically large scale. Even though earlier case studies suggested that accounting for possible changes in the charge state upon binding may be important for structure-based drug design, practical, automated ligand docking and affinity ordering (scoring) methods¹³⁹ routinely ignored the possibility of ionization state changes upon the binding. Occasional manual intervention, e.g. based on “visual inspection” of polar hydrogens was reported,¹⁵¹ but it is still a common practice to perform a docking calculations with a single protonation state of both the ligand and receptor. Useful prediction of ligand binding affinities is still challenging.^{151,163,44,40,126,113,73,153,147,154}

The situation is now changing rapidly. Reduced computational costs and improved accuracy of practical pK calculations (see recent reviews^3,97), along with availability of such methods as fast web-based tools,^8,36,5 have facilitated large-scale analysis of ionization state changes in protein-ligand binding. Promising methods begin to appear that consistently take variability of receptor/ligand ionization (protonation) states into account.¹⁰⁷ In this brief review we will attempt to summarize what is known, and what challenges lie ahead.

2 Origins of protonation state changes in receptor-ligand binding and related corrections to binding affinity

Any ionizable (titratable) group in a protein is involved in a number of electrostatic interactions, both with the other groups and with the solvent. Ultimately, it is the change of these interactions upon ligand binding that is responsible ^* for the change in the group's pK and charge (protonation) state. The general idea of electrostatic origin of observed pK shifts of ionizable groups in proteins, relative to their values in solution, is behind most methods for pK prediction in proteins, both historic and modern.137,138,9,10,134,159,33,34,121,144,130,6,99,41,94,8,63,124,128,64

As a reasonable first approximation, assume that ionizable groups that change their charge states upon ligand binding do not interact with each other; arguments in favor of the approximation are given in Ref.⁸¹ Within this simplification, the pK change of a given ionizable group in the receptor protein can be decomposed into two distinct contributions,⁹

$$\Delta \mathrm{p}K=\Delta \mathrm{p}{K}^{Born}+\Delta \mathrm{p}{K}^{Back}$$ (1)

where the first term is the so-called “Born” contribution or desolvation penalty, and the second is the “background” contribution. The Born term describes the energetic costs associated with changing the degree of solvation of the group. Typically, these are unfavorable costs of desolvating the group by replacing the solvent – water and ions – in the binding pocket with the ligand, Fig 1 (a). Structural re-arrangements caused in the receptor by the ligand binding, Fig 1 (b), may also contribute to ΔpK ^Born by virtue of changing the solvation pattern of the group. For example, a solvent exposed glutamic acid in the binding pocket may have a pK near its model compound value in solution (about 4.5), thus carrying a net charge of −1 at neutral pH =7.0. Upon complexation, it may find itself buried inside a low dielectric medium (protein + ligand). If it were to stay charged, the energetic penalty would be large. Assuming the proton charge in this case is smeared over a sphere of radius R = 3Å the unfavorable cost of transferring it from water ε_w = 80 to protein interior ε_p = 4, is ΔG ≈ 166[kcal/mol](1/ε_p − 1/ε)e² /R ≈ 12 kcal/mol. On the other hand, if the group picks up a proton from the solvent at this pH, the cost is only 2.3k_BT (pH − pK) ≈ 3.4 kcal/mol, and there is no desolvation penalty to bury the now neutral group. This energetically more favorable scenario is realized, and the group becomes neutralized, Fig. 1 (a). Another way of thinking about the process in this example is that the group's pK is shifted up by (12 kcal/mol)/(2.3 k_BT) ≈ 8.8 pK units upon ligand binding. Its new pK ≈ 13.3 is now larger than the pH of the solvent, and the group picks up a proton.

Figure 1.

Three main mechanisms behind changes in pK (and state of protonation ) of an ionizable group in receptor protein upon ligand binding. a): desolvation of the group upon binding of the ligand, b): direct electrostatic interaction with the ligand, c): structural re-arrangements in the receptor protein caused by the binding.

The ΔpK ^Back term in Eq. 1 sums up the effects of altering electrostatic interactions between the group in question and the “background” charges surrounding it. These interactions can be further broken down into two contributions: interactions of the group with the ligand partial charges, Fig. 1 (b), and altered interactions with partial charges within the receptor protein following conformational rearrangements in the receptor induced by formation of the complex, Fig. 1 (c). These re-arranegemnts may propagate towards a distant ionizable group, altering its local electrostatic iscenarioss (e.g. by changing the hydrogen bonding network) thereby causing the observed pK shift. Note that alterations of hydrogen-bonding networks, interactions with molecular quadrupoles, etc. are included in ΔpK ^Back. For example, a glutamic acid originally partially buried in the binding pocket of the receptor may already have its pK shifted up due to partial desolvation, so that the group is protonated and is net neutral at pH =7.0. Upon complexation, however, the extra cost of interaction of the group's proton with a nearby positive charge on the ligand may become larger than the cost of releasing the proton back to the solvent. The group will release the proton to become negatively charged, Fig. 1, (b).

As we shall see below, all of the three scenarios shown in Fig. 1 are realized in real protein-ligand complexes.

Corrections to the binding affinity

Regardless of the specific mechanism, ionization state changes upon ligand binding cause the binding free energy to become pH -dependent. One of several equivalent expressions⁵⁸ for ΔG(pH) in this case is

$$\Delta G\left(\mathrm{pH}\right)=\Delta G_{ref}-k_{B}Tln\left(\sum _{i=Asp,Glu,His,CT}\frac{1+{10}^{p{K}_i^C-\mathrm{pH}}}{1+{10}^{p{K}_i^F-\mathrm{pH}}}\right)-k_{B}Tln\left(\sum _{i=Arg,Lys,Cys,Tyr,NT}\frac{1+{10}^{\mathrm{pH}-p{K}_i^C}}{1+{10}^{\mathrm{pH}-p{K}_i^F}}\right)$$ (2)

where indices “C” and “F” denote the complexed and the free states of the receptor and ligand, respectively.⁸¹ The first term in the above equation is the binding free energy in the reference state of protonation that corresponds to all Asp, Glu, His (no distinction between tautomers is made), and C-terminal (CT) residues held deprotonated, while all Cys, Tyr, Lys, Arg and N-terminal (NT) residues are protonated. This particular state of protonation is a common, albeit not perfect, assumption in many molecular modeling studies. Note that this state does not necessarily occur naturally at any given pH. The second term in Eq. 2 is the pH -dependent correction to the reference binding free energy. In a way, the correction can be taken as a measure of the (pH - dependent) error associated with the use of the standard protonation state. As we shall see below, both experiment and computation have demonstrated that corrections to the binding free energy that arise from protonation state changes can be as large as the binding free energy estimated without taking the protonation state change into account. Examples of calculations based on Eq. 2 can be found in Refs.^106,81

The mechanisms of binding-induced pK changes shown in Fig. 1 remain qualitatively the same even if the ionizable groups can no longer be approximated as non-interacting, but a more complex formalism than that based on Eq. 1 or 2 is needed for quantitative prediction of pK shifts. Namely, for a receptor and ligand with N and n ionizable groups respectively, all 2^(N+n) possible protonation micro-states of the protein-ligand system needed to be considered,^9,144,91,65 and proper Boltzmann averages computed. To handle the combinatorial complexity of the multiple protonation problem, various approximations are used, e.g. Monte-Carlo based sampling,¹¹ or approaches that single out small clusters of strongly interacting groups.^45,96 These methods are now available in many packages, including web servers.^51,65 Once titration curves of the protein and ligand have been obtained, a general thermodynamic linkage relationship¹³⁶ can be used to estimate the pH -dependent correction to the binding energy:

$$\Delta G\left(\mathrm{pH}\right)=\Delta G\left({\mathrm{pH}}_{ref}\right)+k_{B}T2.3{\int }_{{\mathrm{pH}}_{ref}}^{\mathrm{pH}}\Delta Q\left(\mathrm{pH}\right)d\mathrm{pH}$$ (3)

where ΔQ(pH) is the difference between the net charge of the complex and the corresponding free protein and the ligand at the given pH, ΔQ(pH) = Q_complex(pH)−Q_protein(pH )−Q_ligand(pH). The reference pH _ref can be chosen arbitrarily: often, the choice is dictated by computational convenience. For example, at extreme pH values the protonation states of both the complex and the unbound receptor and ligand are obvious. Note that this type of reference state (definite pH) is different from that used in Eq. 2 (definite state of protonation). It is worth mentioning that the same approach is valid for investigating pH -dependence of protein stability, if one replaces bound and unbound states wi th folded and unfolded states. The approach dates back to Tanford¹³⁶ and Linderstrom-Lang.⁷⁷ Examples of calculations based on Eq. 3 can be found in Refs.^158,91,2,92 An alternative approach not based on Eqs. 3 or 2 was recently developed and explored in the context of protein-ligand docking.¹⁰⁷ Note that in general, protein-ligand binding involves complex interplay between multiple protonation, receptor and ligand conformation states, considered on the same footing, without any assumptions of weak coupling. A Monte-Carlo simulation package developed to handle this very general case is now available.¹⁴⁵ The approach is based on a full microstate description of the receptor and an average description of its surroundings in terms of chemical potentials. The receptor can be modeled in great detail, including conformational flexibility and many binding sites that can bind different ligand types. It should be mentioned that titration curves of strongly interacting groups can sometimes deviate so much from the standard sigmoidal (Henderson - Hasselbalch) shape, that the usual notion of pK as mid-point of the curve may no longer be meaningful.^103,17 Coupling to ligand binding may produce non-trivial cooperative effects,¹⁰⁵ even without any conformational change in the receptor protein.¹²⁹ In fact, the latter possibility was not included in Fig. 1: proton transfer to a distant group can occur via a concerted change of protonation states in a strongly coupled cluster.¹⁰⁴ However, based on available data presented in the following sections, this scenario, if it occurs, is definitely not among the common ones in protein-ligand binding.

3 Magnitude and prevalence of protonation and pK changes in receptor proteins upon igand binding

3.1 What is known from experiment?

Methods that can characterize changes in protonation states of the protein and its ligand upon binding can be divided into two broad classes: “macroscopic” and “atomistic”. Below we briefly outline each of them.

The first (macroscopic) class is represented almost exclusively²⁰ by isothermal titration calorimetry (ITC).^7,108 In this technique, the overall heat of the complex formation is recorded as the ligand is being added to the buffered receptor solution at constant temperature. To detect whether proton transfer from the buffer to the complex has occurred upon binding, the heat of complex formation is measured under different buffer conditions. The stoichiometry of the protonation reaction can also be obtained. Based on thermodynamics, the approach has a clear advantage of being general; it gives direct access to binding affinities. However, by itself, the method can only tell whether a net proton uptake/release has occurred upon binding, but it can not determine which group(s) became protonated or deprotonated. Specific assignments have to be made based on additional information such as computation,¹³¹ mutagenesis,¹¹⁰ ultra-high resolution X-ray structures¹³¹ or NMR data.^20,15 Relatively small number of ITC studies of proton transfer in complex formation have been performed to date, owing to their experimental complexity.²⁹ For small molecule ligands, readily available literature references are limited to very few cases in complexes with enzymes or antibodies.^{29,131,95,50,155} In some of these cases, binding-induced protonation state change in the receptor protein was reported. For example, for serine proteases trypsin and thrombin, binding of a series of small molecule ligands at pH =7.8 was investigated:²⁹ formation of 3 out of 12 complexes was associated with a net proton uptake from the buffer. For protein ligands, a summary of experimental data for 5 different protein-protein complexes involved in electron transfer is given in Ref.:⁶⁷ at near neutral pH, full proton release was observed in one case, and in two cases a partial (~ 50 %) release was reported. The relative error of the measured net proton uptake can be expected to range from 7 to 20%.^29,67 In a separate study, Horn et al.⁵⁷ investigated ovomucoid third domain binding to subtilisin Carlsberg. It was concluded that one residue changes pK appreciably upon binding, from 8.5 to 6.7. At a pH in the middle of the range, a significant deprotonation of the residue occurs. In another work, a very large pK shift, from 4.4 to 8.7, was reported for a Glu residue in Streptomyces griseus proteinase upon complexation with with turkey ovomucoid third domain protein.¹¹⁰ In fact, one can apply the general Eq. 3 to calculate the corresponding net proton uptake/release practically from any experimentally documented pH -dependent binding data. Table 1 provides an example of such experimental data, including the corresponding PDB ID of the structures of the complex, the receptor and the ligand. It should be mentioned that with respect to the proton uptake/release, the collected data set is particularly interesting, since the protonation changes are non integers, and therefore cannot be modeled by manually changing the ionization state (neutral or charged) of any single amino acid. Instead, the modeling would require an ensemble representation where the proton uptake/release may be distributed over several amino acids, and their protonation states may vary within the ensemble. In the simplest case scenario, the ensemble can be represented by a single structure, but different protonation states, or in a more realistic scenario, one should generate an ensemble with both structural and protonation variants. Such ensembles are generated naturally within constant pH Molecular Dynamics.^72,63,94,133 For example, in the approach developed by Mongan et al.,⁹⁴ protonation states are accepted or rejected on the fly, according to a Metropolis criterion, during the course of the simulation.

Table 1.

Cases of receptor-ligand complexes experimentally shown to have pH -dependent binding, which was used to calculate net proton uptake/release (the ΔQ (Eq. 3)) at specific pH. Data is taken from Refs.^{30,100,4,118,119,21} Where the experimental 3D structure is unavailable, the closest homolog is listed.

Name	PDBcomplex	Receptor	Ligand	ΔQ (at pH )
beta-trypsin-BPTI	2PTC	1TGN	6PTI	−0.68(pH = 5.5)
Chymotrypsin-BPTI	1CBW	1YPH	6PTI	−0.48(pH = 5.5)
Salmontrypsin-BPTI	1BZX	1BIT	6PTI	−0.82(pH =5.5)
Barnase-Barstar	1BRS	1A2P	1A19	−0.53(pH = 6.0)
Subtilisin Carlsberg-OMTKY3	1ROR 1YU6	1SBC	1OMU	−0.5(pH =7.0)
Porcine pancreatic elastase-OMTKY3	1PPF	3EST	1OMU	−0.61(pH =5.5)

For nucleic acid ligands, proton uptake by receptor protein upon complexation was reported too.^66,90 In the case of a single-stranded DNA binding to an E-coli protein,⁶⁶ the proton uptake was observed over a wide pH range (5.0 - 10.0). Importantly, most of the calorimetry studies that reported thermodynamic parameters of complex formation, such as ΔH or ΔC_p, also included corrections from protonation-binding linkage. In some cases,⁶⁶ these corrections were as much as half of the total value of the measured parameter.

“Atomistic” techniques such as X-ray crystallography, neutron scattering, and NMR can, principle, pinpoint positions of individual protons in both the bound and unbound states of the complex. In practice, each of the methods has severe limitations when applied to the study of protonation and pK changes upon complex formation – only very few relevant data points exit to-date. The resolution of the absolute majority of currently available X-ray structures is still too low to determine hydrogen positions reliably. While some ultra-high (better than 1 Å) resolution structures are now available, one needs both the complex and the unligated protein structures to tell if a protonation state has indeed occurred upon binding. Our recent¹ search of public databases for pairs of protein-ligand complexes along with their matching unligated proteins identified such pairs only at 1.2Å or lower resolution, which is still not enough for hydrogen assignment from the electron density. While protons are readily available in neutron scattering structures, these are so few that we were not able to find any (complex + unligated protein) pair. NMR thus remains the key source of residue-specific pK in proteins, with a few hundred of experimental data points now available,⁵³ often used to benchmark computational methods^41,130,6 that predict pK. However, only a handful of these data points correspond to pairs of protein-ligand complexes and their matching unligated receptors. Protein-protein complexes continue to present challenge to present day NMR, most likely due to their relatively large size. Several recent computational studies reported relevant compilations from experimental literature,^8,1 see a representative sample in Table 2 from Ref.¹ The only selection criterion used in that compilation was availability of reasonable quality X-ray structures for both the complex and the unligated protein, including the requirement for no missing residues in the middle of the amino-acid sequence. Most of the pK s listed in Table 2 were determined by NMR.

Table 2.

Experimental pK changes in several proteins upon ligand binding. For each group, ΔpK = pK (complex) - pK (unligated receptor). Experimental references are given in (): (a),^127,150 (b),¹⁵⁵ (c),¹⁵⁶ (d),²³ (e),⁶¹ (f)¹³²

Receptor	Ligand	Group	ΔpK	PDB w/o ligand	PDB of complex
HIV-1 protease	pepstatin	ASP25	>+2.2 (a)	3HVP	1HPX
HIV-1 protease	pepstatin	ASP25'	<−1.5 (a)	3HVP	1HPX
Plasmepsin II	pepstatin	ASP34/214	+0.1 (b)	1PFZ	1SME
Plasmepsin II	pepstatin	HIS164	+1.5 (b)	1PFZ	1SME
HIV-1 protease	DMP-32	ASP25/25'	+2.19 (c)	1HHP	1QBS
Chymotrypsin	N-Acetyl-DL-Phe-CF3	HIS57	+3.3 (d)	6GCH	6GCH
Xylanase	2FXb	GLU172	−2.5 (e)	1BVV	1BVV
Hydroxynitrile lyase	thiocyanate	HIS235	+5.5 (f)	2YAS	2YAS

The immediate conclusion from Table 2 is that appreciable, and sometimes very large pK shifts do occur upon binding. We stress that a pK shift, even a large one, does not necessarily entail a protonation state change of the group in question, unless the ambient pH is in-between the group's pK values before and after binding. However, in the case of the groups listed in Table 2, most of their measured pK values fall into the biologically relevant pH range (4-8), which means that a protonation state change can occur upon the complex formation under biologically relevant conditions. For example, HIS235 of hydroxynitrile lyase is unprotonated at pH =7.0 (its pK = 2.5), while complexation with thiocyanate shifts its pK to 8.0, resulting in protonation of the group.¹³² Clearly, the energy cost of mis-assigning the ionization state of just this one group at pH = 7.0 would already be well above the typical error margin of experiments that measure ligand binding affinity.⁴⁴ However, one can immediately notice that the diversity of both the receptor proteins and their ligands in Table 2 is very limited, reducing generality of any conclusion that can be drawn from the data.

To summarize, various experimental techniques point unambiguously to large pK shifts and protonation state changes that can occur in proteins upon protein-ligand binding. The phenomenon is observed for different classes of biologically relevant ligands such as small molecules, other proteins, or nucleic acids. Corrections to thermodynamic parameters of the complex formation associated with these changes were large enough to warrant consideration and inclusion. However, the scarcity of the experimental data makes it hard to estimate the over-all prevalence of these effects within a reasonable statistical margin. For the same reason, it is impossible to extract, from the currently available experimental data alone, trends in how the binding-induced protonation changes may be distributed in the receptor and the ligand. These questions are important both for fundamental understanding of protein-ligand binding process and for the development of computational methods that utilize atomistic protein structures to make predictions.

3.2 What do calculations tell us?

Given the scarcity of the experimental data, computational methods become particularly valuable in studying pK and ionization state changes in protein-ligand binding.

Earlier studies

, see Refs. ^{38,85,19,85,125,91,142} for a representative sample, made progress by detailed analysis of a small number of specific proteins, ligands, and ionizable groups. These works often reported large pK shifts and protonation changes in protein-ligand binding, and pointed to the need to take the associated energetic costs into account for accurate prediction of the binding properties. For example, McDonald et al.,⁸⁵ used continuum electrostatic calculations to investigate the titration behavior of the ionizable residues of the HyHEL-5-hen egg lysozyme complex and its individual components. Several residues of HyHEL-5 had pK values shifted upon binding by more than three pH units. Brandsdal et al.¹⁹ systematically investigated (using free energy calculations) the binding of BPTI with glutamic acid at the primary binding position to trypsin. The predicted pK shift of the key Glu residue upon binding was as large 9.8 units, yielding a pK of 14.3 in the complex. The resulting unusual neutral charge state of the Glu residue was found to be essential to obtain quantitative agreement with the experimental binding data. In another study, Spassov and Bashford¹²⁹ proposed an alternative mechanism for the cooperative binding of charged ligands to proteins based on electrostatic coupling to ionizable groups. The mechanism was investigated on a monomeric protein (calbindin D9k) containing two Ca²⁺-binding sites and 30 ionizable groups. Alexov² investigated the role of individual residues in proton uptake/release experimentally measured for three complexes involving aspartic proteases and pepstatin. It was demonstrated that the conformational changes induced by the binding contribute significantly to the calculated pK changes. In addition, it was pointed out that for correct calculations of the binding energy, one should model ionization and conformational changes within the same algorithm that calculates the energy.

Large scale studies

However, it was not until very recently that computational works based on statistically large sets — thousands of computed pK s — began to appear.^70,81,1 These recent studies have explored and quantified statistical trends in protein-ligand binding in addition to analyzing individual cases in detail. Perhaps the most intriguing finding that has emerged is that changes in pK and ionization states of titratable amino acids occur quite commonly in proteins upon ligand binding. The exact statistics, however, varies appreciably, most likely due to variations in the methodology and data sets used.

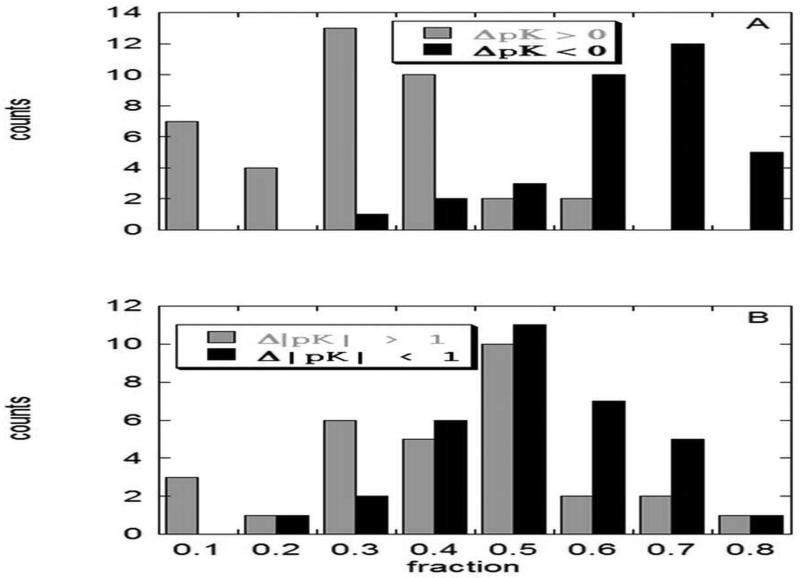
Kundrotas et al.⁷⁰ investigated statistical and electrostatic properties of the interfaces for a set of 37 complexes with diverse functions extracted from a database of protein-protein complexes previously developed by the authors. Multi-conformer, continuum electrostatic pK calculations⁴¹ were performed for all 37 selected complexes for the entire complex and for each of the monomers. The structures of the monomers were kept as they were in the complex, i.e., no conformational changes during the complex formation were considered in this study. It was found that 50 % of interfacial acidic groups have their pK shifted substantially, that is by more than one pH unit relative to the unbound state. The distribution of the pK shifts is presented in Fig. 2; panel A shows that the vast majority (about 80 %) of the interfacial acidic groups have a net stabilizing contribution to the association of the complex (dark bars). However, still about 20% of the groups have a destabilizing contribution (white bars). Panel B of the same figure shows the distribution of the large pK shift, which peaks at 50 %, whereas the distribution of small pK shift results in a broad maximum ranging from 20% to 50%. The finding that 50% of interfacial acidic groups have their pK s shifted by more than one pH unit indicates that individual charged groups, in principle, can contribute noticeably into the protein binding. Interestingly, the acidic groups were predicted to behave differently from histidines (note that pK shifts associated with Arginines and Lysines were not considered to be important for proton uptake/release, because the corresponding pK s are typically outside the experimental/physiological range of pH). It was demonstrated that the complex formation tends to favor acidic pK s by making them lower in the bound state compared with the unbound state. In contrast, histidine pK s tend to be lower in the complex, indicating that the bound state does not provide enough favorable interactions.

Figure 2.

The distribution of pK changes induced by protein-protein binding. A: all pK changes, B: large absolute pK changes versus small absolute pK changes. The horizontal axis shows the fraction of interfacial groups satisfying the corresponding pK shift, while the vertical axis indicates in how many (out of 37) protein complexes this shift occurred. Adopted from Kundrotas et al.⁷⁰

In a separate work, Mason et al.⁸¹ used fast empirical methodology (PROPKA,⁸ web-based) to compute pK values of ionizable residues in 75 protein–protein complexes and their corresponding free forms. Two main types of computations were described. In the first type, the individual (unligated) protein structures were taken directly from the structure of the complex just like in the earlier work by Kundrotas et al.⁷⁰ However, the other set of computations was based on separate X-ray structures determined for the proteins in the absence of the other proteins. This second type of calculation included effects of binding-induced structural rearrangement on the pK values. With the inclusion of these effects, at least one residue per protein was found to completely change its protonation state in 28 % of the complexes. In the computation of the first type (no binding-induced rearrangements), the corresponding number was 12 %. In both types of calculations, protonation state change prevalence increased 2 to 3 fold if partial protonation events (probability 0.5) were also counted. Change in net protonation state of the complex relative to the uncomplexed proteins, that is proton uptake/release from solution, occurred in about 30 % of the cases. The distinction may be important, as protonation state changes in each of the proteins may occur, e.g. through proton transfer between the proteins, without the net proton uptake/release from the buffer solution. Over-all, changes in protonation states upon complex formation were found to be most pronounced for the formation of complexes of large and conformationally flexible proteins; in some of these complexes multiple protonation state changes were observed. In the same work,⁸¹ protonation-conformation coupling was included as a correction to the predicted binding energy for all 75 complexes at pH 7 relative to the standard protonation state, Eq. 2. With binding-induced rearrangements considered, the correction was at least 1.4 kcal/mol (corresponding to one order of magnitude change in the binding constant at room temperature of 298 K) in 45% of the complexes. Without binding-induced rearrangements, the corresponding fraction was 23 % of the complexes. In both cases, some of the corrections were larger than 4.2 kcal/mol by absolute value, affecting the binding constant by more than three orders of magnitude.

In another recent work, Aguilar et all.¹ examined, on an equal footing, pK and protonation state changes in protein-ligand binding for three types of complexes: protein-protein, protein-small molecule, and protein-nucleic acid. Standard continuum electrostatic pK calculations⁹ (H++⁵¹ web-based) were used, followed by a careful examination of the associated uncertainties – the ”noise” level in pK calculations of this type. The study analyzed pK changes upon ligand binding for a total of almost 6,000 ionizable residues in 20 protein-protein, 20 protein-small molecule, and 20 protein-nucleic acid complexes, selected on the basis of reasonably high structure quality. For each protein-ligand complex used in the analysis, the experimentally determined X-ray structure of the corresponding unligated protein was also available.

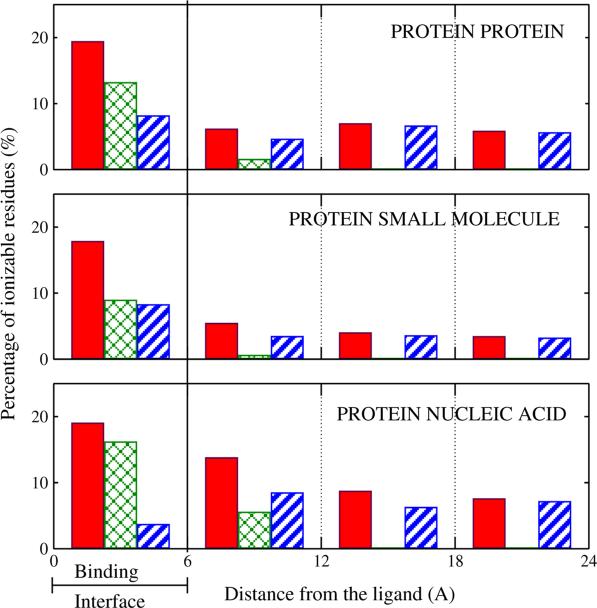
The results of the calculation, which included effects of binding-induced structural rearrangement on the pK values, are as follows. In 60% of all protein-small molecule, 90% of all protein-protein, and 85% of all protein-nucleic acid complexes, at least one ionizable residue was found to completely change its charge state upon ligand binding at neutral pH = 7.0. Over-all, 9% of all ionizable residues (averaged over all complex types) presented a substantial pK change (|ΔpK | >1.0) due to ligand binding in the biologically relevant pH range from 4 to 8. However, averages do not tell the whole story in this case, as the fraction of ionizable sites with substantial pK changes upon binding differs greatly between receptor proteins, Table 3. Overall, substantial pK changes due to binding were found to occur most often in protein-nucleic acid complexes and least often in complexes of proteins with small molecules. Not surprisingly, for all ligand types the effect is the strongest in the immediate binding interface, Fig. 3.

Table 3.

Percentages of ionizable residues in receptor proteins that exhibit substantial pK change (|ΔpK | > 1) upon ligand binding in the biologically relevant pH range from 4 to 8. Adopted from Aguilar et al.¹

Complex type	Minimum	Average	Maximum
Protein-protein (20)	1.5%	8.7%	16.7%
Protein-small molecule (20)	2.1%	5.7%	12.5%
Protein-nucleic acid (20)	5.6%	12.3%	24.4%

Figure 3.

Distance distribution of ionizable residues with substantial pK shifts upon ligand binding in biologically relevant pH range, by the specific mechanism causing the shift. Distance is is to the bound ligand. The three mechanisms, labeled a, b, and c, are described in Fig. 1. Solid red bars: all three mechanisms combined (a+b+c). Cross-hatched green bars: direct electrostatics (a+b). Striped blue bars: binding-induced structural rearrangements in the receptor(c only). The percentage reported for each region is relative to the total number of ionizable residues located in that region. Adopted from Aguilar et al.¹

Relative prevalence of various physical causes of pK shifts in ligand binding

Computationally, one can trace¹ the origins of the pK changes to the three electrostatic mechanisms discussed above, Fig. 1. In the binding interface region, direct electrostatic mechanism – which includes desolvation and direct electrostatic interaction with the ligand – is predominant in effecting pK changes in protein-nucleic acid complexes, Fig. 3. In protein-(small molecule) and protein-protein complexes, both the binding-induced structural rearrangements (“induced-fit”) and direct electrostatic effects play equally important roles in the interface region. The effect of direct electrostatic perturbation is generally “short ranged”, only causing significant pK changes in residues located within ~ 6Å away from the ligand in the majority of protein-protein and protein-small molecule complexes, and weakly extending to 12Å from the ligand in the case of binding of highly charged nucleic acids. At the same time, pK perturbations due to structural re-arrangements propagate well beyond the immediate interface region.^1,8

Long-range coupling between ligand binding and protonation

As seen in Fig. 3, a significant number of substantial pK changes apparently occurs well outside the binding interface, sometimes as far as 24Å away from the ligand, and even further.¹ For protein-(small molecule) complexes a similar observation was also made by Bas et al.,⁸ on roughly the same sample size. A natural question arises if these very distant changes are real, or artifacts of the methodology and inevitable structural imperfections? Note that even though the average systematic error of current pK estimates is probably no larger than the threshold ((|ΔpK | >1.0) typically used to filter meaningful pK changes, there still exists a non-zero probability for any such pK change to be a statistical false positive. This is because the underlying methods are far from perfect: the pK values computed from atomic-resolution input structures are known to be sensitive to structural details.⁹⁸ Uncertainties in the input X-ray structure will be propagated into errors in the computed pK s. To estimate this type of error, Aguilar et al. analyzed the variation in computed pK values that result from structural deviations between several available X-ray structures of the same protein. In an ideal world, these differences should be zero, but in reality they are sometimes larger than 1 pK unit – events that should be counted as ”noise” in distributions such as that in Fig. 3. As it turns out,¹ the ”noise level” in Fig. 3 is lower than the signal everywhere except for protein -small molecule complexes in the region far from the binding interface. A more detailed follow-up statistical analysis could neither confirm nor reject, for the sample size used in Aguilar al., the possibility of statistically substantial pK changes outside the binding interface in protein - small molecule complexes.

One may also wonder if all residues with substantial pK change in regions far from the ligand belong to a small group of complexes that are “unique” in some way. That is not the case:¹ the occurrence of substantial pK changes far from the binding interface appears to be a general property of the ligand binding process. Moreover, there appears to be no single dominant type of ligand-induced structural perturbation that alters local electrostatic interactions ultimately responsible for the “distant” pK changes. Those identified in Aguilar et al. were described previously in different contexts,^42,31,12 and by no means exhaust the list of possible structural perturbations associated with ligand-induced pK changes.^80,8

In summary, the “long-range pK coupling” effect is real in protein-protein and protein-DNA complexes, but the results are still inconclusive for protein-(small molecule) binding where the effect, if it exists, is the weakest. The long-range effect might play a role in allosteric regulation: subtle changes on one site of the receptor protein may affect ligand binding properties on another, distant site. For example, strong long-range site-site interactions were experimentally demonstrated to be important in a family of Ca²⁺-binding proteins.⁸⁰

4 Interplay between sub-cellular pH, pH-optimum of ligand binding, and pH of the corresponding reaction

The concentration of hydrogen ions, typically referred to as pH, is an essential characteristics of the cell and living organisms. At the cell level, different cell compartments (organelles) have different characteristic pH as outlined in Refs.^24,69 A short sample list of characteristic sub-cellular pH values is shown in Table 4.

Table 4.

Sub-cellular compartments and their characteristic pH.

Sub-cellular compartment	Characteristic pH
nucleus	7.7
endoplasmic reticulum,	7.1
Golgi apparatus	6.6
mitochondrion	7.5
vacuole	5.3
cytoplasm	7.3
lysozome	4.8
peroxisome	8.2

In summary, at the cellular level, macromolecules and their complexes can be exposed to pH ranging from value as low as 4.8 and as high as 8.2. Similar wide range of pH can be found at the level of the entire organism, where the pH differs greatly between vital organs and systems. In some organs, the pH is maintained with high precision, while it may vary greatly within others. For example, in human, the normal blood pH is about 7.3; even a small deviation from this optimal value, by as little as fraction of pH unit, can be fatal. For example, if the blood pH drops below 7.0 (acidosis), the effect is depression of the central nervous system resulting in coma. In the opposite case, if the pH increases above 7.8 (alkalosis), the effect is over-excitability of the nervous system that results in convulsions. In contrast, in other parts of the human body, the pH can vary greatly, as for example in the digestive track where it can range from 1.5 up to 7.0.³² Broad range of pH, from 4.5 up to 8.0, occurs in kidney.⁵⁴ All these examples indicate that biological macromolecules and the corresponding complexes function at very different pH conditions, and depending on their function in terms of sub-cellular or tissue localization and trafficking, they should have evolved to either adapt to the corresponding pH or sense it. (see e.g. review by Garcia-Moreno³⁹).

From the evolutionary standpoint, the most important factor is the optimization of biochemical reactions to provide better chances for survival and reproduction. Such evolutionary pressure does not necessary have to be linked with optimized stability of individual macromolecules and affinity of their complexes. However, indirect link may exist since in most cases the optimal biochemical reaction may invoke optimal macromolecular interactions or optimized structural integrity of individual biomolecules. When discussing optimum pH we will follow existing literature and term the pH of optimum of reaction, stability or binding, as the pH -optimum.^{135,92,157,161} In terms of pH -optimum of activity, the pH -optimum varies for different enzymes and biological reactions.^28,43,25 Several examples of various pH -optima of the corresponding reaction are shown in Table 5 to indicate the broad range of pH conditions in biology. These biochemical characteristics were conveniently collected into databases, as for example BRENDA database,^25,117 which makes it possible to address questions about plausible correlations between pH -optimum of binding, activity and stability in a statistical manner.

Table 5.

Examples of various pH -optima of enzyme activity.

Enzyme	pH -optimum
Lipase (pancreas)	8.0
Lipase (stomach)	4.0 - 5.0
Lipase (castor oil)	4.7
Pepsin	1.5 - 1.6
Urease	7.0
Invertase	4.5
Maltase	6.1 - 6.8
Amylase (pancreas)	6.7 - 7.0
Trypsin	7.8-8.7

Many different approaches exist to predict pH -optimum of binding, but arguably the most convenient is to use Eq. 3 introduced above. One can simply calculate the protonation states of the complex and the unbound monomers as a function of pH, and their difference will represent the net pH -dependent proton uptake/release (ΔQ) induced by the binding. Assuming that the optimum (minimum) of the binding free energy occurs at some point within the pH interval where the receptor and the ligand are stable, ∂ΔG(pH)/∂pH = 0 at the pH -optimum^†. The corresponding net proton uptake/release must then equal zero at this pH according to Eq. 3. The above strategy was used in several cases to explore the idea of the similarity of biophysical properties of proteins known to bind to each other.⁷⁰ In order to interact, two proteins must co-occur spatially and temporally. Recently, the possibility of co-evolution of pH -optimum of protein stability and pH -optimum of protein interactions was studied and it was demonstrated that they are indeed correlated.⁹² The idea was used by other researchers to match entries in two databases: the protein-protein interactions and sub-cellular location and substantial overlap was reported.¹²³

These observations suggest that, perhaps, native (or sometimes referred to as physiological) macromolecular interactions should not involve proton uptake/release. Indeed, if the pH -optimum of binding and the pH of the environment where the complex is formed are the same or quite similar, then as discussed above, the net charge difference between the complex and the unbound molecules should be zero at pH -optimum. This does not, however, mean that protonation states are not important for the binding or that they do not change upon it. The only quantity that does not change in physiological (native) interactions is the net charge difference between the complex and unbound monomers. Similar observation was reached in another study which modeled the conformational change observed upon ligand binding and phosphorylation for the cAMP-dependent protein kinase.¹⁴ It was conjectured that the binding of ligands requires the smallest proton release/uptake around pH 7.0 to 8.0. Physiological pH for receptor-ligand binding is therefore the pH value where the energy difference between the bound and unbound states reaches its minimum, that is at the pH -optimum of binding. Moreover, a recent work implied that proton transfer between histidines across the interface of the complex changes the protonation states of the bound monomers, but results in zero net proton uptake/release, and thus no pH -independence of the binding.^148† These suggestions may appear to be at odds with the conclusion from the experimental data and large scale computational studies reviewed above. The latter indicate that net proton uptake/release due to binding is not an uncommon phenomena in protein-ligand binding, while the above discussion seem to suggest that perhaps the receptor-ligand complexes have evolved to avoid proton uptake/release. There is, however, no immediate controversy. The statement about the pH -optimum suggests that each receptor-ligand complex has evolved towards particular pH -optimum, which is related to its function and sub-cellular and tissue localization. However, experiments discussed above are typically either performed at neutral pH, or over a range of pH. Obviously, if the experiment is not done precisely at pH -optimum, binding-induced proton uptake/release may be observed. Similarly, the large-scale computational studies we have discussed are typically done on diverse sets of receptor-ligand complexes (presumably each having its own distinctive pH -optimum), and the protonation state changes are reported at a particular pH, e.g. pH =7. The implication is that had these studies been performed at pH -optimum for each complex, the reported prevalence of protonation states changes may have been lower.

5 Improving docking and scoring outcomes

One of the most recognized approaches to predict 3D structures of receptor-ligand complexes is ab-initio docking (in case of macromolecular binding) or virtual screening/scoring (in case of small molecule binding to a macromolecule). Namely, given the structures of unbound receptor and ligand, one utilizes computational methods to bring them together to predict the 3D structure of the complex. It is outside the scope of this review to mention all docking and screening methods, but some representative examples can be found in Refs.^{22,120,116,101,111} While docking and screening simulations focus on determining the 3D structure of the complex without modeling the binding pathway, the alternative approach known as binding simulations⁸³ reveals all association details including the binding constant of the 3D complex structure.⁴⁸ Further enlargement of the concept of the binding addresses the issue of modeling supramolecular assemblages.⁸⁶ All these approaches differ in their methodology, force fields, and assumptions made. However, despite the differences between the above mentioned docking algorithms, two major problems are common: (a) how to treat conformational changes induced by the binding and (b) how to model protonation changes caused by the complex formation? Obviously, these two issues are coupled and, ideally, have to be modeled within the same numerical protocol. While the importance of conformational changes induced by the complex formation is very well recognized, and significant efforts have been invested to address it, the possibility that binding may cause protonation changes is rarely incorporated into the docking and the screening models. As discussed in the previous sections, it is quite likely that burial of an ionizable group at the binding interface of the complex can cause its protonation/deprotonation, as demonstrated both experimentally and theoretically. If this possibility is not considered, then the most probable candidate complexes causing such ionization changes are likely to be rejected by the scoring function because of unfavorable interactions. The side chain orientations will also be incorrect, even after energy minimization, if the ionization states are not assigned according to the new environment at the interface. However, as detailed in literature,⁴¹ side chain orientation and calculations of the ionizable states should ideally be done simultaneously in the same protocol since they are interdependent. The ionized and neutral from of amino acids differ by a single proton, so from geometric perspective their side chains are almost the same and if the ionization/de-ionization does not cause significant rearrangement, the effect of protonation states on the overall shape can be neglected. However, the charge states affect the scoring function. Typically, the scoring function is derived either from statistical analysis of known receptor-ligand complexes, or it is developed based on some set of empirical rules. Many scoring functions of the first type are based on statistical potentials that depend on amino acid composition of the interfaces and pairing frequencies across the interfaces.^143,59 Such scoring functions can also factor in the significant electrostatic and hydrogen-bonding complementarity observed at the interfaces of hetero complexes.⁸⁴ However, standard protonation states for all ionizable groups are typically assumed. Obviously, the resulting scoring function will not favor unusual protonation states, and wild type receptor-ligand complexes involving non-standard ionization states will be scored unfavorably. Fully empirical scoring functions, on the other hand, should be able to handle cases with unusual protonation states, at least in principle. However, they too will most likely favor ionized states of titratable groups, if they do not properly account for the presence of the solvent, that if no desolvation penalty (Fig. 1) is included.

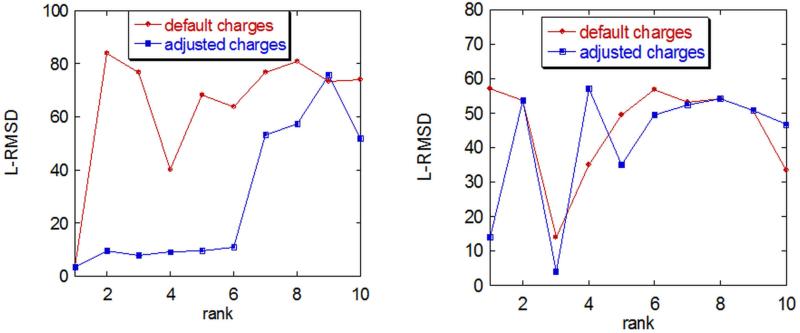
We illustrate the importance of taking into account protonation states for correct prediction of the binding mode using one of the most popular software packages for ab-initio docking, ZDOCK.¹⁰⁹ Two cases are considered: a case of heteroand a case homo-complex, namely PDB codes 1sji and 1xg2, Fig. 4. For 1sji, Lys 49, Glu 117 and Glu 256 were predicted to be neutral at pH =7.0 in the complex according to pK calculations performed with MCCE package.⁴¹ In the case of 1xg2, Asp B 130 was predicted to be neutral, while His A 137 was found to be ionized. The charges of these groups were adjusted accordingly^†, and docking predictions are made, Figure 4. For assessment of the predictions, we use the L-RMSD,⁸⁷ which is the ligand RMSD as defined in the CAPRI experiment.⁷⁴

Figure 4.

L-RMSD of the ten best predictions obtained with ZDOCK with standard (default) protonation states and with adjusted protonation states (see text for details). Left panel: homo-complex, PDB ID 1sji. Right panel: hetero-complex, PDB ID 1gx2

It can be seen that the charge adjustment dramatically changes the quality of the predictions for the homo-complex (1sji), with the adjusted charges (presumably the correct protonation state ) resulting in better predictions compared to the default charges corresponding to the standard protonation state (Fig. 4, left panel). For the hetero-complex, the results are shown in the right panel of Fig. 4. Again, it can be seen that the adjustment of the charges, although they are only two in this case, resulted in different predictions that were slightly better than for the complex with the default charges. The above results were obtained by simply turning on/off the charges of the residues predicted to have unusual charge states in the complex. No extra protons were added or removed. Although this simplification has a negligible effect on the shape of the interface, it has a significant effect on the energy and thus on the quality of the predictions. The effect was found to be very pronounced for the homo-complex, while it was very moderate for the hereto-complex. The reason for this difference could be that more protonation states were adjusted for 1sji (3 titratable groups), while only 2 ionizable groups were adjusted for 1gx2. In addition, the adjustments were made assuming that for both cases the physiological pH is about 7.0, and this may favor 1sji predictions over 1gx2.

While the above example clearly illustrates the importance of correct assignment of protonation states for ab-initio docking, it does not offer a practical solution to real case scenarios where the structure of the corresponding complex is unknown. The other unknown is the relevant pH of the complex formation. As it was discussed in the previous section, some complexes are formed at low physiological pH, while other exist at high physiological pH. The critical question with respect to docking is this: does the ligand binding mode (the binding site and pose of the ligand) changes as ambient pH deviates from the corresponding physiological value? In the vast majority of cases, the answer is ”no”: pH changes are shown to affect the affinity (binding free energy) but not to affect the binding mode (see example cases listed in Table 1). However, opposite examples do exist as well.¹¹⁵ Thus, in cases where pH variations and, therefore, protonation states, do not affect the binding mode, the protonation states are not critical for predicting the binding mode. However, the correct assignment of protonation states will still be crucial for ranking and scoring of the candidate complexes. A wrong assignment of protonation states may cause the native ligand or the best candidate small molecule not to be ranked at the top of the list, and thus not to be predicted. Even more severe consequences of not treating the possibility of protonation state changes may be expected for calculations of the absolute binding energy. One way to deal with this problem is to allow all ionizable groups (or restricted number of groups located at the interface, assuming that the interfaces of both the receptor and the ligand have been identified first) to sample different protonation states during the docking, scoring or energy calculations.¹⁰⁷ Of course, in this approach one should know the relevant physiological pH for the investigated complex(es). In cases for which the binding mode changes with pH, the problem is much more complicated. The receptor-ligand interface and the binding mode/pose is different at different pH, so one should define the relevant pH first, as mentioned above. It is quite unlikely that the predictions of alternative interfaces will be very successful, so one should let all ionizable (or at minimum all surface groups) to sample different protonation states during the docking, scoring or energy calculations. This strategy may not be feasible at present, especially in virtual screening, where one has to screen millions of small molecule candidates. A simple consistency check – whether the assumed, e.g. standard, ionization state stays unchanged upon docking – may be less expensive, and still a better strategy than completely ignoring the possibility.

Individual case studies appear to support the importance of considering the possibility of binding-induced changes in the charge state of the receptor. It was shown both experimentally^27,78 and theoretically⁸² that altering the charge state of the binding interface via specific mutations can affect protein-ligand binding affinity, and can even be used to design complexes with higher affinity.^52,62 Quantum-mechanical calculations have demonstrated that docking accuracy²⁶ and binding affinity prediction³⁷ improve when the energy model accounts for the redistribution of ligand charges upon binding. In another recent study,¹⁵² it was shown that accurate prediction of ionization states is a prerequisite for the accurate prediction of binding affinities between HIV protease and some inhibitors. At the same time, results of “large-scale” docking studies are not uniform with respect to conclusions regarding the value of accounting for protonation state changes in binding, in part because of the use of different scoring and energy function.^{112,75,68,71,89,88} On the one hand, it was shown that proper assignment of the protonation states results in better predictions, especially if the receptor is aspartyl protease.¹¹² This result is consistent with the above discussion, since aspartyl proteases typically function at low pH and therefore some acidic groups are expected to have unusual protonation states. The effect of protonation states on the binding results was also studied on a set of three proteins complexed with ligands having different tautomeric forms.¹⁴¹ It was demonstrated that the majority of the protonation and tautomeric states of the individual groups within the three proteins can be recovered by the docking procedure. However, another recent study¹⁴⁰ reported a similar analysis in which the protonation, tautomeric and stereoisometric states of the ligands were varied; two popular docking programs were employed. It was found that the addition of different ligand protomers sometime improved the docking results and sometime did not. This type of improvement could also be receptor-dependent.¹⁰⁷ One possible explanation for the apparent case-dependence of the docking outcomes that consider protonation state changes is as follows. Perhaps the dependence has the same origin as outlined above, namely that different complexes are formed under different pH conditions. Thus, in some cases, standard protonation/tautomer states are already optimal for docking, while in other cases for which the binding occurs at lower or higher pH, adding alternative protonation states in the docking protocol should offer an advantage. This case dependence illustrates one intrinsic difficulty of the docking and virtual screening approaches – the fact that the true physiological pH is unknown for the candidate complexes. This is particularly important when inhibitors are designed to compete with natural substrates.¹⁶² Recent work showed that the sensitivity of the inhibitor and substrate differ with respect to the protonation states.¹⁶² Case-dependence of the docking outcomes may also stem from variations in the scoring functions used: highly detailed, physics-based scoring functions can be expected to be more sensitive to the proper protonation assignments than knowledge-based functions.

There is little doubt that a truly complete description of protein-ligand binding must consider the possibility of protonation state changes on the same footing with other hard-to-treat effects such conformational changes or water displacement upon binding. Various approaches have recently been developed to account for correct protonation states in ab-initio docking and virtual screening.^{112,75,68,71,89,88} An undeniable advantage of methods accounting for protonation changes upon binding is that they reveal the correct physics and provide the details of the binding reaction. Still, it remains to be seen to what extend today's fast, practical virtual screening methods will benefit from careful treatment of protonation state changes. First, there is the possibility that improving just one approximation out of many that these methods must make to achieve robustness and high computational performance may reduce their accuracy, e.g. by destroying some cancellation of errors that the less detailed descriptions may benefit from. Indeed, many practical scoring functions and docking algorithms do not consider protonation states at all, but perform reasonably well.^47,149 Also, as we have seen, while protonation state changes often occur upon ligand binding, they by no means occur all of the time – neglecting this effect entirely may still be acceptable since the goal of virtual screening is often to find some good drug candidates, not all of them.

6 Outlook

We have presented a review of one aspect of protein-ligand binding process: changes in ionization (protonation, pK) that may occur in the protein when the complex forms. Just like many other binding-related effects, notably conformational changes, changes in the ionization state are complex, and are closely related to other phenomena, such as pH -dependence of binding affinity. Consistent account for these effects is important for both fundamental understanding of one of the most important processes in biology as well as for a very practical reason: early stages of modern drug-discovery often involve computational screening of protein-ligand complexes. Considerable progress has been made, especially recently, in characterizing and understanding binding-induced protonation state changes, as well as incorporating them into computational protocols. At the same time, significant challenges remain.

• (1)Experimental characterization of pK and/or protonation state changes upon complex formation remains challenging; to the best of our knowledge, no “gold standard” set of well-characterized structures is available to serve as a reference and test set for computational studies. Such a gold standard set would have included a good number of very high-resolution complexes along with the corresponding unbound proteins and their ligands. All protonation state changes would have been assigned (experimentally) to specific groups, and binding affinities measured at least at some biologically relevant pH.
• (2)Experimental difficulties are also likely to hinder verification of some of the intriguing computational predictions (and their implications), such as the existence of the “long-range” effect of binding on pK of distant groups.

In the computational arena, the availability of fast and reasonably accurate methods for prediction of pK and protonation states in atomistic protein structures has facilitated dramatically the inclusion of pK and protonation state changes in studies of protein-ligand complexes and their diverse biological properties. Such computational studies are no longer a prerogative of a few expert groups, but are becoming accessible to a much broader class of researchers, especially through web-based tools that have recently come on-line. This, combined with ever growing computational power, facilitates integration of protonation changes into modeling protocols. Yet, many challenges remain as well. Among them, one important class is related to correct modeling of protonation states in studies of protein-ligand binding, which in turn is important to improving docking, scoring, screening and energy calculations. We see the following challenges in this area:

• (3)Accuracy of methods for energy calculations and for scoring, as compared with the magnitude of the binding free energy and the binding free energy difference among competing ligands. Frequently, the binding free energies of different ligands (including small molecules) to the same receptor differ by less than 1kcal/mol. In order to benefit from the inclusion of protonation states into docking, scoring, screening or energy calculation protocols, the accuracy of the computation should be better than the free energy differences between alternative ligands.
• (4)Accuracy of pK predictions. Success of docking, screening and free energy calculations that take into account protonation states of the complex, receptor and ligand, critically depends on the accuracy of the pK predictions (although in some limited cases the necessary experimental data may be available as well). There are many existing methods to compute pK, a large set of them was recently evaluated via pKa-cooperative, an initiative to bring together researchers working in the field of pK calculations (see reviews^97,3). The outcome of the last pKa-cooperative meetings indicates that significant progress still needs to be made to achieve better quality pK predictions, especially for reaching accuracy of 1 pK unit for the pK calculations involving buried groups.
• (5)The nature of the scoring function in docking and virtual screening. To the best of our knowledge, most docking and virtual screening scoring functions are based on calculating or estimating the interaction energy between the receptor and the ligand in the complex. In this case, the protonation states of the unbound receptor and the ligand become irrelevant for the scoring (although they may be physically very important). The only thing that matters are the correct protonation states in the complex. Docking methods that utilize some form of a free energy calculation, by taking the difference between the free energy of the complex and unbound receptor and ligand, are very few, although such an approach clearly represents the right physics. However, to the best of our knowledge, even these advanced approaches do not take into account the pH dependent term. Typically they assume that the default pH is neutral pH, and assign the protonation states according to the pK predictions at such pH.
• (6)The interplay between protonation states and the pH of complex formation. Even in case that the structures of both the bound and unbound receptor and ligand are known, and one can perform pK calculations, the relevant protonation states cannot be assigned if the pH of the corresponding biochemical reaction of the complex formation is unknown. Simply assuming that all receptor-ligand complexes are formed at neutral pH = 7.0 is a great oversimplification. Perhaps the time is ripe for the computational community to add these considerations about the relevant pH when preparing the set of complexes to be instigated, or in the computational protocols that model the docking or binding free energy.
• (7)Treatment of non-integer protonation states. At a particular pH of binding, the given titratable group may be partially ionized, or the net proton uptake may be spread over several titratable group resulting in partial protonation changes (non-integer number of protons). As it was outlined many times in the literature, it is not correct to simply assign partial net charges to the appropriate ionizable groups; instead, the macroscopically calculated partial charge must be properly recovered within an ensemble.^107,2
• (8)A related challenge is consistent treatment of binding-induced protonation state changes on an equal footing with conformational changes. Constant pH Molecular Dynamics is a natural, theoretically well-grounded tool for the job, that also automatically takes care of the partial protonation states issue. However, available implementations are still extremely demanding computationally.