Abstract
Reinforcement learning describes motivated behavior in terms of two abstract signals. The representation of discrepancies between expected and actual rewards/punishments – prediction error – is thought to update the expected value of actions and predictive stimuli. Electrophysiological and lesion studies suggest that mesostriatal prediction error signals control behavior through synaptic modification of cortico-striato-thalamic networks. Signals in the ventromedial prefrontal and orbitofrontal cortex are implicated in representing expected value. To obtain unbiased maps of these representations in the human brain, we performed a meta-analysis of functional magnetic resonance imaging studies that employed algorithmic reinforcement learning models, across a variety of experimental paradigms. We found that the ventral striatum (medial and lateral) and midbrain/thalamus represented reward prediction errors, consistent with animal studies. Prediction error signals were also seen in the frontal operculum/insula, particularly for social rewards. In Pavlovian studies, striatal prediction error signals extended into the amygdala, while instrumental tasks engaged the caudate. Prediction error maps were sensitive to the model-fitting procedure (fixed or individually-estimated) and to the extent of spatial smoothing. A correlate of expected value was found in a posterior region of the ventromedial prefrontal cortex, caudal and medial to the orbitofrontal regions identified in animal studies. These findings highlight a reproducible motif of reinforcement learning in the cortico-striatal loops and identify methodological dimensions that may influence the reproducibility of activation patterns across studies.
Keywords: Prediction Error, Expected Value, Reinforcement Learning, Meta Analysis
1. Introduction
Behavior can be controlled by reward or punishment, and environmental stimuli that predict them. The way animals develop representations of these predictive relationships has been described in terms of mathematical models of reinforcement learning (RL), a restricted set of which dominate experimental and theoretical attention. With the advent of new neurophysiological and imaging methods, insights from these models have advanced our understanding of the role of cortico-striato-thalamic networks, the midbrain, the amygdala, and the monoamine systems in behavioral adaptation. In particular, the activity of dopamine neurons in the mesostriatal pathway has been shown to conform to predictions derived from formal learning rules (Waelti, Dickinson, & Schultz, 2001) and may also distinguish between particular instantiations of RL models (M. R. Roesch, Calu, & Schoenbaum, 2007). Combined with imaging and neurophysiology, they have helped us better understand the types of computations that take place in the reward system and the alterations observed in neurological and psychological disorders including Parkinson’s disease (M. J. Frank, 2005), depression (Kumar et al., 2008), schizophrenia (Gradin et al., 2011), eating disorders (G. K. Frank, Reynolds, Shott, & O’Reilly, 2011), addiction (Chiu, Lohrenz, & Montague, 2008) and suicidal behavior (Dombrovski, Szanto, Clark, Reynolds, & Siegle, 2013). Here, we provide an introduction to the constructs of prediction error, the discrepancy between the expected and obtained outcome, and expected value. We then offer a brief overview of the putative neural substrates of these computations and present a meta-analysis of functional imaging studies that have examined neural correlates of the prediction error and expected value constructs derived from RL models.
1.1. The Rescorla-Wagner model of Pavlovian conditioning
Building on the earlier Bush-Mosteller model (Bush & Mosteller, 1951, 1953), Rescorla and Wagner (RW) developed their influential model of Pavlovian conditioning (Rescorla & Wagner, 1972). The RW model provided an account of animal learning from multiple conditioned stimuli. One challenge here is posed by interactions between the stimuli such as the Kamin blocking effect, or diminished conditioned responding to stimulus X following AX --> US pairing preceded by A --> US (Kamin, 1968). The dependent variable in the Rescorla-Wagner (RW) model was the unobserved, but theoretically plausible associative strength (V) of the CS-US pairing. Associative strength is conceptually close to the expected reward value of a given stimulus (at least when a single appetitive US is presented). Another innovation, which enabled an elegant explanation of the Kamin blocking effect, was to combine the associative strength of all stimuli present on a given trial in order to generate a prediction error. In other words, according to RW, an outcome is surprising only to the extent that it is not predicted by any of the stimuli. Here is how it describes the change in the associative strength of the two stimuli after a trial when the stimulus compound AX is followed by a US:
| Eq. 1 |
where α learning rate for each stimulus, β is the learning rate for the US, λUS is the asymptote of associative strength which the US will support, and VAX=VA+VX. Thus, if stimulus A is pre-trained to the asymptote, subsequent training with the AX compound generates no prediction error for X. Besides blocking and overshadowing, the RW model successfully accounted for a variety of Pavlovian and instrumental phenomena, despite a number of limitations (see Miller, Barnet, & Grahame, 1995).
1.2. Temporal difference models
Temporal difference (TD) models of animal learning, like RW, learn from prediction errors (Sutton & Barto, 1998), and describe an approach modeling prediction and optimal control. TD aims to predict all future rewards, discounting them over time:
| Eq. 2 |
where r is future reward and γ is the temporal discount factor reflecting a preference for immediate over delayed rewards. Instead of waiting until all the outcomes are experienced, TD estimates future rewards by repeating the following algorithm in each learning episode (time step).
| Eq. 3 |
where α[r(t+1) + γV(t+1)−V(t)] is the prediction or temporal difference error, and γV(t+1) takes the place of the remaining terms γr(t+2)+ γ2r(t+3)+…+ γkr(t+k+1).
To deal with the temporal distribution of predictive cues or response options, TD methods introduce the idea of eligibility traces. That is, only closely preceding (eligible) cues or actions are credited for reward or blamed for punishment.
TD provides a real-time account of learning, that RW or other trial-level models do not. A key area of divergence between RW and TD is that TD treats rewards themselves and the cues that predict them as, in principle, equivalent, insofar as they are both stimuli, which can invoke changes in the valuation of future rewards. Both conditioned cues and outcomes can influence value prediction, and can elicit prediction errors. This innovation provides an effective account of the learning of sequences of stimuli, as conditioned cues can come to operate as reinforcers in their own right (Dayan & Walton, 2012). Moreover, reinforcement value is collapsed into a single, common currency across different reinforcers. On the other hand, RW is a model, which describes the extent to which the unconditioned stimulus (US: e.g. reward or punishment) can be predicted by environment stimuli. Thus the major focus of RW is processing of the US, PEs occur only at the US, and conditioned cues are treated as distinct entities, competing to predict the US (Rescorla & Wagner, 1972). At the same time, one can see the parallel between summed associative strength of all presented CSs in RW and value in TD.
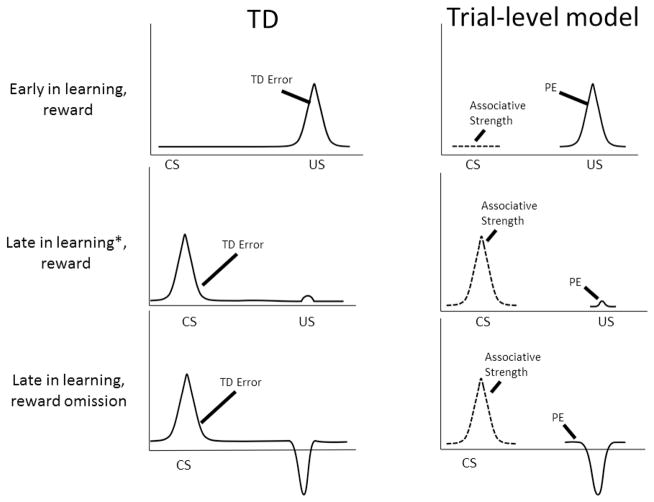
These differences between trial-level models such as RW and TD lead to differential predictions regarding putative neural learning signals, as illustrated in Fig. 1. A trial-level model aligns its associative strength (or expected value) signal with the CS and PE, with the US. One can see that, when signals from a trial-level model such as RW are aligned with stimuli in real time, the time course of TD error approximates the combination of associative strength at the CS and prediction error at the US. On the other hand, in trial-by-trial fMRI learning experiments with short and especially fixed CS-US intervals, predicted BOLD signal corresponding to associative strength or value generated by trial-level models will often approximate those of TD.
Figure 1.
The temporal difference (TD) model describes a real-time course of reward prediction error (PE) signals; PEs transfer from the US to the CS as learning progresses. In contrast, trial-level models such as Rescorla-Wagner describe PE only at the US. Associative strength (conceptually close to value) signals build at the CS. It is easy to see the resemblance between TD error signal and the combination of PE and associative strength signals in trial-level models. * Before the asymptote is reached. At the asymptote, PE at the US disappears.
1.3. Neural Correlates of Prediction Errors: Model based Neuroimaging and Electrophysiology
Prediction error-based learning models have also enabled neuroscientists to interpret neural signals, most prominently from midbrain dopaminergic neurons (Schultz, Dayan, & Montague, 1997). Firing rates in dopaminergic neurons in this region are consistent with the predictions of RW: a blocking experiment revealed that firing rates reflect the contingency between a stimulus and a reward rather than the mere pairing of the two (Waelti et al., 2001). Moreover, specific predictions of the TD model were also corroborated in these neurons: most notably, neural firing within DA neurons in the midbrain gradually becomes coupled to predictive stimuli rather than rewards themselves (Schultz et al., 1997). In addition, a study of conditioned inhibition revealed that an inhibitory cue, predictive of reward omission, could reduce firing rates of sub-populations of these neurons (Tobler, Dickinson, & Schultz, 2003).
A natural development of this work was to apply the same behavioral paradigms and reasoning to human neurophysiological research. While ERP and MEG research has attempted to address analogous questions (Holroyd & Coles, 2008; Krigolson, Hassall, & Handy, 2014), the relatively limited capability of these methods to register unambiguous physiological responses from subcortical or brainstem regions has meant that the majority of progress would depend on functional magnetic resonance imaging (fMRI). Since one of the seminal studies of this field (J. P. O’Doherty, Dayan, Friston, Critchley, & Dolan, 2003), the primary focus of fMRI studies has generally been the ventral striatum, rather than the midbrain itself. A typical explanation (e.g. M. R. Roesch, Calu, Esber, & Schoenbaum, 2010; Tobler, O’Doherty J, Dolan, & Schultz, 2006) is that the fMRI response reflects the phasic input to a structure (Logothetis & Pfeuffer, 2004), rather than the local processing or the region’s output. Thus, given that the dopaminergic neurons of the VTA project to the areas of the striatum (Haber, Fudge, & McFarland, 2000), fMRI-measured VS activation might then be seen as the downstream consequence of VTA firing. This perspective finds considerable support in the literature, although there are two areas of possible complication. First, there is evidence of prediction error-related activation in the VTA itself (e.g. D’Ardenne, McClure, Nystrom, & Cohen, 2008), implying that local processing may also be relevant. Second, the VS also receives input from a wide range of cortical and subcortical regions (Voorn, Vanderschuren, Groenewegen, Robbins, & Pennartz, 2004), any of which could influence its activity and information processing within it. A further advantage of fMRI is that, although focused analysis of prediction error responses in the VTA and VS has been performed with this technique (D’Ardenne et al., 2008), its capability to identify signal across the entire brain has allowed examination of related signals in other parts of the cortex. Integration and analysis of the rich datasets obtained using fMRI methods are the focus of the present work.
1.4. Learned value, economic subjective value and their neural correlates
In economics, subjective value or utility is the theoretical common currency used to compare disparate goods. Economic commodities can be thought of as reinforcers and labor or price paid, as analogues of effort during operant conditioning (Lea, 1978). While economic decision-making has traditionally been studied using stylized description-based prospects, recent research suggests that experience-based experiments resembling animal learning paradigms provide complementary models of real-life economic decision-making (Hertwig & Erev, 2009). Thus, to the degree that economic preferences incorporate one’s reinforcement history, one may hypothesize that revealed preferences and feedback-based animal learning depend on similar neural computations (Fellows, 2011). One of the motivations for the present analysis was to examine whether cortical regions tracking learned reward value coincide with medial prefrontal regions shown to signal economic subjective value on revealed preference tasks (Peters & Buchel, 2010).
In addition, animal electrophysiological studies have found responses which accord well with the what might be expected of learned value signals in regions including the ventral prefrontal cortex (vPFC) and limbic areas such as the cingulate, and the striatum (Samejima, Ueda, Doya, & Kimura, 2005; Simmons, Ravel, Shidara, & Richmond, 2007; Jonathan D. Wallis & Miller, 2003). Here, the vPFC refers to both the orbitofrontal cortex (OFC), the ventromedial prefrontal cortex (vmPFC) as well as more lateral regions of the ventral prefrontal cortex. The vmPFC denotes the mammalian paralimbic agranular/dysgranular prefrontal cortex encompassing monkey areas 14, 25, and rostral 24 and 32 of Petrides and Pandya (Petrides & Pandya, 1994) and human areas 25, and rostral 32 and 24; the orbital aspect of this region is also referred to as the medial orbitofrontal cortex (mOFC). Associative signals represented in the vPFC possess many properties of abstract value: they are sensitive to delays and probability of reward, as well as to the presence of alternatives (Kennerley, Dahmubed, Lara, & Wallis, 2009; Kennerley & Wallis, 2009b; Kobayashi, Pinto de Carvalho, & Schultz, 2010; Padoa-Schioppa & Assad, 2008; M. R. Roesch & Olson, 2005; Tremblay & Schultz, 1999). These signals are “subjective,” integrating internal states such as hunger (Bouret & Richmond, 2010; Critchley & Rolls, 1996). Other decision-related signals have been found in motor prefrontal and parietal cortex (Platt & Glimcher, 1999). However, it appears that these signals may reflect salience (Leathers & Olson, 2012) or motivation (Matthew R. Roesch & Olson, 2004) rather than value.
1.5. The present meta-analysis
The present work provides a quantitative summary of fMRI evidence on prediction error and expected value representations in the human brain using activation likelihood estimation (ALE) meta-analysis. It extends recent meta-analyses of value and prediction error signals (Bartra, McGuire, & Kable, 2013; Clithero & Rangel, 2014; Garrison, Erdeniz, & Done, 2013; Levy & Glimcher, 2012) in two ways. First, to control methodological heterogeneity, our analysis included only studies that used delta-rule reinforcement learning models. This enabled a better-controlled evaluation of the consequences of variations in methodology. We could thus identify core networks that are most reliably detected. Second, to reveal the distributed networks that subserve human reward learning, we jointly mapped the regions responsive to value and prediction error. Based on the animal and human literature reviewed above, we hypothesized that prediction error signals would be observed in the striatum (including putamen, caudate and nucleus accumbens) and midbrain.
In contrast, we hypothesized that expected value signals will be represented in the ventromedial prefrontal cortex. In contrast to previous meta-analyses (Bartra et al., 2013; Garrison et al., 2013; Levy & Glimcher, 2012), we focused only on studies in which signals derived from a reinforcement learning algorithm served as explanatory variables in the analysis of fMRI data. This allowed us to examine if differences in the approach to generating such signals could yield different neural maps. We also examined other methodological variables that could have an impact on the observed coordinate maps derived from reward prediction error (RPE) experiments. Variables of theoretical interest included instrumental or Pavlovian designs, and reinforcer type (monetary, liquid or social). Accounting for the effect of these variables will demonstrate the degree to which the RPE maps are dependent on choices of experimental parameters. To this end, we had several secondary hypotheses.
Pavlovian vs. Instrumental paradigms: Prior studies suggest differential roles for striatal subregions in Pavlovian vs. Instrumental tasks. Pavlovian RPEs recruit the ventral striatum, whereas RPEs on instrumental tasks (most of which include a Pavlovian component) appear to recruit both ventral and dorsal striatum (J. O’Doherty et al., 2004).
Fixed/Individual Learning: All models evaluated in the present work include a parameter which controls the rate at which conditioning occurs. There are three main strategies for determining the learning rate, all three of which are evaluated in a study by Cohen (Cohen, 2007). He compared neural correlates of parameters generated by individual fits of each participant’s responses (‘individual’), with correlates of the group mean of such parameters (‘group fixed’) and an arbitrary fixed estimate of the group response (‘fixed’). Despite somewhat different patterns of activation, the two methods were broadly consistent in indexing similar limbic and prefrontal regions of interest. In general, individually fitted parameters can arguably better accommodate the subject’s behavior (Estes & Maddox, 2005), and thus may provide a more optimal fit of underlying neural signals. Yet, noisy, stochastic behavior, or directed exploration, may deleteriously affect the reliability of estimated parameters. Group fitting (‘group fixed’) parameters provides a form of regularization (N.D. Daw, 2011), leading to more a conservative parameterization which is potentially less susceptible to such misspecification. They may also be well suited to studies of patient groups (e.g. Bernacer et al., 2013). We tested whether each approach biased the discovery of particular brain regions. Alternatively, either approach could simply be a more accurate way of characterizing the neural correlates of individual acquisition curves, and thus be associated with similar, if more finely resolved, patterns of activation.
US-aligned Outcome PE vs. CS- and US-aligned TD error. As noted above, the time course of TD error differs from that of outcome PE generated by trial-level models. It has been suggested, that TD error may be exclusively represented in the ventral striatum, while outcome PE is signaled by a larger network including the caudate (Niv, Edlund, Dayan, & O’Doherty, 2012). Moreover, exclusively outcome-coupled PE regressors may be more susceptible to ongoing activation coupled to the outcome distinct from PE itself, such as the appetitive response to a rewarding outcome (Rohe, Weber, & Fliessbach, 2012). We contrasted TD and outcome PE studies, expecting to see more extensive activation to outcome PE and also anticipating that a conjunction analysis would reveal the ventral striatum as the site of overlap between these studies.
Reward type: Previous meta-analyses have examined patterns of activation in response to various primary and secondary rewards (Sescousse, Caldu, Segura, & Dreher, 2013). However, any differences and commonalities may have been driven by sensory properties of rewarding stimuli. By contrast, our focus on model-estimated PEs allowed us to examine spatial segregation or dissociation of more abstract neural computations triggered by disparate rewards. Based on animal studies reviewed above, we hypothesized that the ventral striatum will be the shared area of activation to all types of rewards.
Smoothing. A variable without theoretical interest that may affect the pattern of data is the smoothing kernel employed by the study. Recently, Sacchet and Knutson have shown that the application of large smoothing kernels can bias the localization of ventral striatal responses to reward anticipation (Sacchet & Knutson, 2013). In addition, it is not easy to detect BOLD activations in subcortical and especially brainstem nuclei because of their small size: only 60 mm3 for the ventral tegmental nucleus (VTA), for example (Paxinos & Huang, 1995). Yet, when preprocessing whole-brain fMRI images, researchers often use spatial filters exceeding the size of potential signal sources in these nuclei. The matched filter principle suggests that such large filters are likely to reduce the signal-to-noise (SNR) ratio in these structures. We tested whether this size mismatch affected the detection of prediction error signal sources in the basal ganglia and midbrain. We contrasted studies that used smaller (<8 mm) filters with those that used larger filters.
2. Methods
2.1. Study Selection Criteria and Definitions
Studies were selected by searching PubMed and Google Scholar to identify fMRI studies that employ computational algorithms to investigate neural correlates of reinforcement learning studies. A combination of keywords was used: [“reinforcement learning” OR “reward learning”], [“prediction error” OR “expected value”], [“rescorla-wagner” OR “temporal-difference” OR “Q-learning”]. We also identified studies using reference tracing and citations within reviews. The search yielded 40 studies. Each article was reviewed by at least two authors to make sure that it fulfilled the following criteria:
Only studies that used a reinforcement learning model (trial-level delta rule models, TD, Back propagating connectionist model) to create regressors for a general linear model (GLM) analysis of BOLD signal were included. The common feature of these studies is a prediction error-based learning rule.
Our prediction error analyses used maps that revealed a positive coupling with appetitive ‘signed’ RPEs, which are positive when the reward is higher than expected or negative when it is lower than expected. Maps reporting aversive prediction errors were excluded, since their number was insufficient for an ALE analysis. Similarly, negative correlations with RPE or expected value (EV) regressors were also not analyzed, as these are not systematically reported.
EV was defined as the extent to which stimuli or actions are predictive of reward.
Studies that used modified delta-rule algorithms were included as long as they involved no additional equations or components that would fundamentally change the representational structure (e.g. an upper layer in a hierarchical model).
Studies in which an RL model, of the sort described above, was refuted or out-performed by a model from a different class (e.g. hidden Markov model, Kalman filter, hierarchical Bayesian models, hybrid models with separate representational systems) were excluded to avoid inclusion of maps derived from potentially disadvantaged models.
Only studies reporting whole brain results were included1. For studies reporting only region of interest or otherwise restricted analyses, we contacted the authors to obtain whole brain coordinates, and included the study if the data were received.
We included only studies of non-clinical adult populations, excluding rare genotypes, subclinical psychopathology and placebo-treated participants.
In total, we included in our ALE analyses 38 studies reporting reward prediction error maps and 16 studies reporting expected value maps with 751 and 337 participants respectively. Of the EV studies, two did not contribute RPE maps. Details of all included studies are listed in Tables 1–3, and proportions of different study designs are displayed in Figure 2.
Table 1.
Studies reporting Reward Prediction Error (RPE) maps, including details of sample size (n) and number of foci, learning rule (US – unconditioned stimulus; TD error – Temporal Difference error), Pavlovian/Instrumental design Learning rate parameter estimation (Fixed = Fixed at group level; Individual = Individually estimated per participant), Reinforcer type
| Study | n | Foci | Learning Rule/PE time course | Pavlovian/Instrumental | Learning Rate Parameter | Reinforcer Type |
|---|---|---|---|---|---|---|
| Bellebaum, Jokisch, Gizewski, Forsting, & Daum, 2012 | 15 | 52 | Outcome PE | Instrumental | Individual | Monetary |
| Bernacer et al., 2013 | 18 | 5 | Outcome PE | Instrumental | Fixed | Monetary |
| Bray & O’Doherty, 2007 | 28 | 6 | Outcome PE | Pavlovian | Individual | Social2 |
| Brovelli, Laksiri, Nazarian, Meunier, & Boussaoud, 2008 | 14 | 2 | Outcome PE | Instrumental | Individual | Cognitive |
| Chowdhury et al., 2013 | 32 | 35 | Outcome PE | Instrumental | Individual | Monetary |
| Dombrovski et al., 2013 | 20 | 16 | Outcome PE | Instrumental | Individual | Cognitive |
| Fareri et al., 2012 | 18 | 6 | Outcome PE | Instrumental | Individual | Monetary & Social / Social only for subgroup analysis |
| Gershman, Pesaran, & Daw, 2009 | 16 | 2 | Outcome PE | Instrumental | Individual | Monetary |
| Glascher, Hampton, & O’Doherty, 2009 | 20 | 10 | Outcome PE | Instrumental | Individual | Monetary |
| Gradin et al., 2011 | 17 | 16 | Outcome PE | Instrumental | Fixed | Liquid |
| Howard-Jones, Bogacz, Yoo, Leonards, & Demetriou, 2010 | 16 | 20 | Outcome PE | Instrumental | Individual | Monetary |
| Jocham, Klein, & Ullsperger, 2011 | 16 | 13 | Outcome PE | Instrumental | Individual | Monetary |
| Jones et al., 2011 | 36 | 12 | Outcome PE | Instrumental | Fixed | Social |
| Kahnt et al., 2009 | 19 | 17 | Outcome PE | Instrumental | Individual | Social |
| Kim, Shimojo, & O’Doherty, 2006 | 16 | 4 | TD error | Instrumental | Individual | Monetary |
| Klein et al., 2007 | 12 | 4 | Outcome PE | Instrumental | Individual | Social |
| Kumar et al., 2008 | 18 | 7 | TD error | Pavlovian | Fixed | Liquid |
| Li, McClure, King-Casas, & Montague, 2006 | 46 | 5 | Outcome PE3 | Instrumental | Individual | Cognitive |
| Madlon-Kay, Pesaran, & Daw, 2013 | 20 | 8 | Outcome PE | Instrumental | Individual | Monetary |
| Metereau & Dreher, 2013 | 20 | 20 | Outcome PE | Pavlovian | Individual | Liquid4 |
| Murray et al., 2008 | 12 | 17 | Outcome PE | Instrumental | Fixed | Monetary |
| Niv et al., 2012 | 16 | 5 | TD error | Instrumental | Individual | Monetary |
| J. P. O’Doherty et al., 2003 | 9 | 17 | TD error5 | Pavlovian | Fixed | Liquid |
| O’Sullivan, Szczepanowski, El-Deredy, Mason, & Bentall, 2011 | 24 | 1 | Outcome PE | Instrumental | Fixed | Monetary |
| Park et al., 2010 | 16 | 33 | Outcome PE | Instrumental | Individual | Social |
| Robinson, Overstreet, Charney, Vytal, & Grillon, 2013 | 24 | 7 | Outcome PE | Pavlovian | Fixed | Social |
| Rodriguez, Aron, & Poldrack, 2006 | 15 | 1 | Outcome PE | Instrumental | Fixed | Cognitive |
| Rodriguez, 2009 | 14 | 5 | Outcome PE | Instrumental | Fixed | Cognitive |
| Schlagenhauf et al., 2012 | 28 | 28 | Outcome PE | Instrumental | Individual | Social |
| Schonberg, Daw, Joel, & O’Doherty, 2007 | 29 | 14 | TD error | Instrumental | Fixed | Monetary |
| Schonberg et al., 2010 | 17 | 22 | TD error | Instrumental | Individual | Monetary |
| Seger, Peterson, Cincotta, Lopez-Paniagua, & Anderson, 2010 | 11 | 16 | Outcome PE | Instrumental | Individual | Cognitive |
| Seymour et al., 2005 | 19 | 2 | TD error | Pavlovian | Fixed | Relief |
| Takemura et al., 2011 | 23 | 8 | Outcome PE6 | Pavlovian | Fixed | Liquid |
| Tanaka et al., 2006 | 18 | 2 | Outcome PE | Instrumental | Individual | Monetary7 |
| Valentin & O’Doherty, 2009 | 17 | 37 | Outcome PE | Instrumental | Fixed | Monetary & Liquid |
| van den Bos, Cohen, Kahnt, & Crone, 2012 | 22 | 65 | Outcome PE | Instrumental | Individual | Cognitive |
| Watanabe, Sakagami, & Haruno, 2013 | 20 | 5 | Outcome PE | Instrumental | Individual | Monetary |
Opposite sex – Unattractive Face
Matching Shoulder -> Rising Optimum; logistic fitting map
Monetary also available
Results are for PE@CS inclusively masked with signed PE@UCS”
‘With’ model selected, including similarity parameter
‘Random’ condition
Table 3.
Overall numbers of participants and foci contributing to each of the contrasts investigated. For the categories included in the subgroup analysis (‘Fixed’ and below), only the studies and accompanying statistics that are included in the final analyses are shown in the table.
| Studies | Participants | Foci | |
|---|---|---|---|
| Reward PE | 38 | 751 | 545 |
| EV | 16 | 337 | 249 |
| Fixed | 14 | 275 | 149 |
| Individual | 24 | 476 | 395 |
| Instrumental | 31 | 610 | 477 |
| Pavlovian | 7 | 141 | 67 |
| RW | 31 | 627 | 473 |
| TD | 7 | 124 | 71 |
| Monetary | 16 | 305 | 215 |
| Liquid | 5 | 87 | 68 |
| Cognitive | 7 | 142 | 110 |
| Social | 7 | 181 | 112 |
Figure 2.
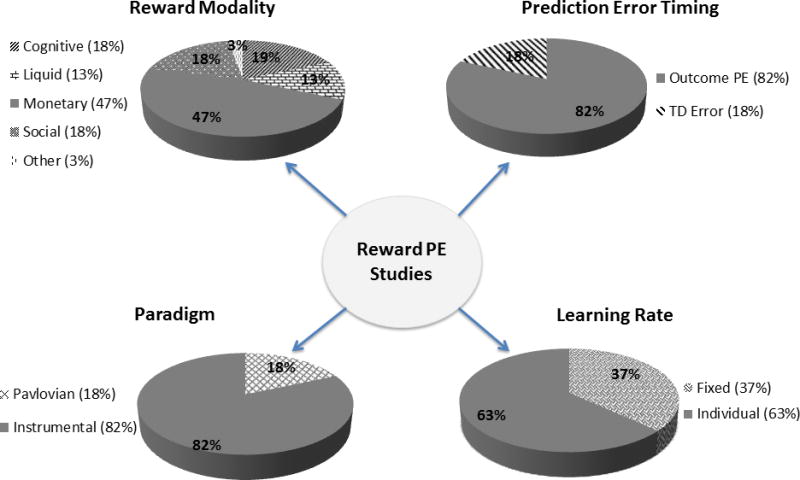
Pie charts show the percentage of studies in each condition that were included in producing the RPE ALE map.
2.2. Subgroup Analyses
Various subgroup analyses investigated heterogeneity across studies. We classified studies into the following categories:
Instrumental/Pavlovian: In ‘Instrumental’ paradigms, outcome is contingent on behavioral response (choice). In ‘Pavlovian’ paradigms, outcome is not contingent on choice, although a response may be made – for example, in order to signal outcome probability.
Fixed/Individual: A ‘fixed’ learning rate is assumed to be equivalent for all participants within the cohort. The learning rate may be estimated at the group level (e.g. (Bernacer et al., 2013)) or by taking a reasonable heuristic (often around 0.2 e.g. (Kumar et al., 2008)). Alternatively, ‘individual’ learning rates are estimated separately for each participant, and prediction error and expected value signals for each participant reflect the individually estimated learning rate.
Outcome PE/TD: Although there were a wide variety of algorithms, we made a broad distinction between Rescorla-Wagner-like trial-level models and temporal difference-like algorithms (‘TD’). Put simply, trial-level models have a single update mechanism at the time of the outcome which forms the basis of the reward PE, whereas reward PEs are computed at both the stimulus/action and outcome phases of the task in TD algorithms.
Monetary/Liquid/Cognitive/Social: ‘Monetary’ and ‘Liquid’ paradigms involved the respective reinforcers; ‘Cognitive’ paradigms employed cognitive reinforcement such as numerical or symbolic feedback; ‘Social’ paradigms involved smiles, frowns, fearful or beautiful faces as reinforcement.
High/Low Smoothing: ‘High’ studies employed a smoothing kernel of 8mm or more; ‘Low’ studies employed a smoothing kernel of 7mm or less.
Where there was a choice of maps to use from a given study which fulfilled our criteria, we selected the one in which the GLM regressor was estimated on the basis of the largest number of trials. For example, we included the overall social and monetary RPE maps reported in the study of Fareri and others (Fareri, Chang, & Delgado, 2012) for the main RPE analysis, but the social RPE map only for all of the subgrouping analyses. Other arbitrary choices included the decision to include the liquid reinforcement map in (Metereau & Dreher, 2013), due to the relatively low number of these studies. Finally, where slightly different models were fitted to the data, the better fitting or otherwise preferred model was selected.
2.3. Activation Likelihood Estimation (ALE)
Statistical analysis of the studies was conducted using the revised activation likelihood estimation (ALE) algorithm (Eickhoff, Bzdok, Laird, Kurth, & Fox, 2012) for coordinate-based analyses (Turkeltaub, Eden, Jones, & Zeffiro, 2002). The method generates meta-analytic maps of consistent brain activation locations from the coordinates derived from neuroimaging studies with similar experimental conditions. The method provides an estimate of the convergence of foci across activation maps, and determines the significance of these estimates via an empirically derived null distribution (Eickhoff et al., 2012). The null hypothesis is that the foci are distributed randomly across the brain, and the test statistic supports a random-effects inference, that the modeled activation (MA) maps reflect an above-chance convergence across studies (Eickhoff et al., 2012; Turkeltaub et al., 2012). A detailed description of the ALE technique can be found elsewhere (Eickhoff et al., 2012; Turkeltaub et al., 2012). In short, activation foci reported for a given experiment are treated as centers of a 3D Gaussian probability distribution, the width of which is empirically derived and reflects an estimate of the spatial uncertainty of the foci of a given map and sample size of each experiment (Eickhoff et al., 2009). Based on the ICBM tissue probability maps, each focus is given a probability value on how likely the activation is located at exactly that position. One modelled activation map (MA) is then created for each experiment by merging the probability distribution of all activation foci. If more than one focus from a single experiment is jointly influencing the MA map, then the maximum probability associated with any one focus reported by the given experiment is used. ALE scores are then calculated by taking the union of these individual MA maps, and these scores reflect the voxel-wise convergence of activation across experiments. The p values of the ALE scores are determined with reference to the null distribution The resulting non-parametric p-values were transformed into Z-scores and thresholded at a cluster-level Family Wise Error (FWE) rate-corrected threshold of p < 0.05 (cluster-forming threshold at voxel-level p<0.001).
Comparison of different subgroups was performed by subtracting voxelwise MA maps from one another, and then comparing this map to an empirically derived null distribution of ALE-differences scores (10,000 permutations). To this end, ALE analyses were performed separately on the experiments associated with either condition and computing the voxel-wise difference between the ensuing ALE maps. All experiments contributing to either analysis were then pooled and randomly divided into two groups of the same size as the two original sets of experiments defined by activation in the first or second cluster (Eickhoff et al., 2011). ALE-scores for these two randomly assembled groups were calculated and the difference between these ALE-scores was recorded for each voxel in the brain. Repeating this process 10,000 times then yielded a null-distribution of differences in ALE-scores between the ALE analyses of the two clusters. The ‘true’ difference in ALE scores was then tested against this null-distribution, yielding a posterior probability that the true difference was not due to random noise in an exchangeable set of labels based on the proportion of lower differences in the random exchange. The resulting probability values were then thresholded at p > 0.95 (95% chance for true difference) and a cluster size (k) of 20.
3. Results
3.1. Reward Prediction Error (RPE)
The activations revealed by the main categories were largely in line with our hypotheses (Table 4; Figures 3 and 4). The ALE meta-analysis of RPE maps revealed clusters encompassing bilateral ventral striatum, bilateral amygdala, midbrain, thalamus, frontal operculum and insula. The largest clusters were seen in the ventral striatum: one activation cluster in each hemisphere which extended from the ventromedial caudate (nucleus accumbens) to the lateral putamen and amygdala (predominantly the superficial subregion: SF). The left frontal operculum cluster impinged both on the pars orbitalis of the inferior frontal gyrus and the anterior insula. RPE-related activation was also observed in the left visual cortex, predominantly located in V3 and V4.
Table 4.
ALE clusters representing Reward Prediction Errors, including peak t statistics, MNI co-ordinates and cluster size. Studies contributing to each cluster, and the extent of their contribution (percent) to the overall cluster are marked. SF=superficial subregion of amygdala.
Figure 3.

Map of significant ALE clusters associated with the RPE contrast, with the activations in the striatum highlighted. Pie charts show the contribution of studies of a particular class to the bilateral striatum activation. Percentages are not corrected for base rate.
Figure 4.

Map of significant ALE clusters associated with the RPE contrast, with the activations in the midbrain and frontal operculum highlighted. Pie charts show the contribution of studies of a particular class to each activation. Percentages are not corrected for base rate.
3.2. RPE: Subgroup analysis
We performed a number of analyses focusing on different subcategories of the RPE studies, in order to identify distinct activations associated with different designs. First, in order to interpret these contrasts appropriately, we examined the extent to which the different categories of experimental design were statistically independent.
3.2.1. Confounding
Fisher’s exact tests (FET) between each of the sub-categories assessed the contingency between design factors. There was a highly significant association between reinforcer type and Pavlovian/Instrumental design (FET=14.67, p<0.001). Monetary reinforcers were more common in instrumental studies and liquid reinforcers were more common in Pavlovian studies. Three other relationships showed trend-level associations (p’s between 0.061 and 0.088): Fixed/Individual vs Pavlovian/Instrumental; Outcome PE/TD error vs Reinforcer type; Outcome PE/TD error vs Pavlovian/Instrumental.
This confounding between Pavlovian designs, liquid reinforcers and TD modeling proved relevant as the activations associated with Pavlovian designs were mostly made up of studies employing liquid reinforcement and had a high contribution from TD studies. There were relatively few TD studies, but these employed either monetary or liquid reinforcers and about half were Pavlovian designs. In general, given the small number of such studies (Pavlovian/TD/Liquid) and the potential for confounding, the findings should be interpreted cautiously from these maps.
Both the individual-related striatal and the fixed-related midbrain activations were predominantly made up of instrumental rather than Pavlovian studies, as would be expected from the higher proportion of instrumental studies. The striatal activations associated with individual studies were about half monetary and half other reinforcers, while the midbrain activation associated with fixed studies was also represented by studies employing a variety of different reinforcers.
3.2.2. Instrumental vs. Pavlovian (Table 5)
Table 5.
ALE clusters representing Instrumental (Instr) and Pavlovian (Pav) activations, including peak t statistics, MNI co-ordinates and cluster size. SF=superficial subregion of amygdala; LB= laterobasal subregion of amygdala; EC= entorhinal cortex
| Region | T statistic | Coordinate | Size |
|---|---|---|---|
| Instrumental | |||
| Left Putamen Left Ventral Caudate Left Dorsal Caudate (Head) |
5.96 5.46 4.64 |
−16 6 −12 −10 8 −6 −12 8 8 |
597 |
| Right Ventral Striatum | 4.78 4.52 3.37 |
14 6 −14 18 16 −6 6 18 −4 |
397 |
| Left Frontal Operculum | 6.32 | −32 24 −8 | 233 |
| Left Fusiform Gyrus (V4), Inferior occipital, lingual gyrus | 4.21 4.17 3.93 |
−22 −82 −18 −34 −84 −8 −24 −88 −16 |
162 |
| Pavlovian | |||
| Left Putamen / Amygdala (SF) | 5.18 4.06 |
−24 4 −10 −20 0 −22 |
194 |
| Right Amygdala (SF) | 5.16 3.71 3.66 |
26 −2 −12 36 0 −10 38 −2 −8 |
136 |
| Pav/Instr conjunction: Left Putamen | 4.77 | −22 6 −12 | 50 |
| Instr > Pav: Left Caudate | 2.98 2.95 2.34 |
−10 8 10 −8 4 10 −10 4 16 |
58 |
| Instr > Pav: Left Pallidum | 1.93 1.86 1.74 |
−12 4 −2 −8 2 −4 −6 4 −2 |
29 |
| Pav > Instr: Right Amygdala (SF/LB) | 2.89 2.49 |
24 −8 −8 34 −2 −12 |
112 |
| Pav > Instr: Left Putamen, Left Amygdala (SF) | 2.69 | −28 2 −10 | 82 |
| Pav > Instr: Left Amygdala (SF/LB), Left Hippocampus (EC) | 2.35 | −22 2 −20 | 50 |
The instrumental RPE map was similar to the overall RPE map, aside from the lack of midbrain activation. Striatal activations were slightly more medial than the overall RPE cluster and did not extend as convincingly into the lateral striatum (putamen) nor further into the amygdala. In addition, the left caudate was activated in this contrast. By contrast, the Pavlovian studies yielded two clusters in the left putamen/amygdala and right amygdala. The amygdala activations were predominantly located in the superficial subregion.
Bilateral amygdala and left lateral putamen were significantly more likely to be activated in Pavlovian than instrumental paradigms. The reverse contrast yielded a significant cluster in the left caudate (anterior and dorsally located), as well as smaller activations in more ventral regions of the medial striatum. A small region reflecting the conjunction of instrumental and Pavlovian tasks was apparent in the left putamen.
3.2.3. Fixed vs. Individual (Table 6)
Table 6.
ALE Clusters representing Individual (Ind) and Fixed activations, including peak t statistics, MNI co-ordinates and cluster size.
| Region | T statistic | Coordinate | Size |
|---|---|---|---|
| Individual | |||
| Left Ventral Striatum | 6.13 5.14 |
−18 4 −12 −10 10 −6 |
441 |
| Right Ventral Striatum | 4.78 4.64 4.25 3.88 3.54 |
18 8 −4 14 6 −16 10 8 −10 24 0 −12 6 18 −4 |
415 |
| Left Fusiform Gyrus (V4), Inferior occipital, lingual gyrus | 4.38 4.06 3.96 3.72 3.47 |
−34 −84 −8 −24 −88 −16 −24 −84 −18 −26 −88 −8 −24 −82 −8 |
217 |
| Left Frontal Operculum | 6.20 | −30 24 −8 | 166 |
| Fixed | |||
| Midbrain / Thalamus | 5.44 3.65 |
−8 −22 −6 6 −16 −10 |
278 |
| Left Putamen (lateral) | 4.57 | −24 6 −8 | 111 |
| Fixed/Individual conjunction: Left Putamen | 4.21 | −24 6 −10 | 51 |
| Ind > Fixed: Left Inferior Occipital, Fusiform Gyrus (V4) | 2.80 2.77 2.60 2.23 |
−34 −80 −8 −36 −80 −12 −24 −80 −6 −28 −88 −8 |
119 |
| Ind > Fixed: Left Ventral Striatum | 2.44 2.35 |
−12 6 −10 −10 10 12 |
113 |
| Ind > Fixed: Right Ventral Striatum | 2.50 | 20 8 −8 | 53 |
| Ind > Fixed: Left Frontal Operculum | 2.09 2.00 |
−26 28 −4 −28 24 −6 |
40 |
| Fixed > Ind: Midbrain/Thalamus | 2.62 2.47 2.46 |
−4 −24 −4 −2 −12 −10 −10 −26 −6 |
151 |
The individual map was also similar to the overall RPE map, without the presence of the midbrain cluster or any activation within the dorsal striatum. The striatal activations were focused within the medial regions of the ventral striatum. By contrast, the fixed map yielded two clusters: one in left putamen and one in the midbrain. Statistical comparison of the contrasts yielded greater activation in the bilateral ventral striatum (medially-focused) for the individual contrast, as well as the left operculum and left visual cortex. The fixed contrast yielded a large midbrain cluster, as well as very small differences in the left lateral putamen. A cluster representing the conjunction of fixed and individual was present in the left putamen.
3.2.4. PE at outcome vs. TD error (Table 7)
Table 7.
ALE clusters representing Temporal Difference (TD) error and PE at outcome activations, including peak t statistics, MNI co-ordinates and cluster size. SF=superficial subregion of amygdala; LB= laterobasal subregion of amygdala; EC= entorhinal cortex
| Region | T statistic | Coordinate | Size |
|---|---|---|---|
| TD error | |||
| Left Putamen, Amygdala (SF/LB), Hippocampus | 5.12 4.31 4.20 3.69 |
−16 6 −14 −24 6 −10 −20 0 −22 −28 −8 30 |
270 |
| PE at outcome | |||
| Left Ventral Striatum | 5.45 5.21 4.62 |
−10 8 −6 −20 6 −12 −12 8 8 |
566 |
| Right Ventral Striatum | 4.59 4.52 4.35 3.44 |
18 8 −4 18 16 −6 10 8 −10 6 18 −4 |
365 |
| Midbrain / Thalamus | 5.10 | −8 −20 −6 | 115 |
| Left Frontal Operculum | 6.28 | −32 24 −8 | 240 |
| PE at outcome only/TD error conjunction: Left Putamen | 4.74 4.31 |
−18 6 −12 −24 6 −10 |
112 |
| TD error > Outcome PE: Left Amygdala (SF, LB), hippocampus (EC) | 3.95 3.26 2.64 |
−18 2 −24 −18 0 −28 −16 −6 −30 |
127 |
| Outcome PE > TD error: Left Caudate | 3.30 2.97 2.95 2.51 1.93 |
−10 10 6 −8 4 10 −10 8 10 −10 8 14 −8 10 0 |
126 |
| Outcome PE > TD error: Left Frontal Operculum, Inferior Frontal Gyrus pars orbitalis | 2.47 2.01 1.98 1.97 1.77 |
−40 34 −10 −34 32 −12 −34 32 −8 −36 36 −12 −38 26 −12 |
64 |
Studies modeling PE at the US only made up a large proportion of the data, and consequently the US PE map was very similar to the overall RPE map. The seven TD error studies yielded a cluster including the left lateral striatum (putamen) and amygdala. A conjunction between the two was again observed within the left putamen. The TD error studies activated the left amygdala/hippocampus more than the US PE studies, while the latter showed greater activation in the left caudate and left frontal operculum
3.2.5. Reinforcer type (Table 8)
Table 8.
ALE clusters representing activations associated with different reinforcers, including peak t statistics, MNI co-ordinates and cluster size. SF=superficial subregion of amygdala; LB= laterobasal subregion of amygdala; CM=centromedial subregion of amygdala; EC= entorhinal cortex
| Region | T statistic | Coordinate | Size |
|---|---|---|---|
| Monetary | |||
| Left Ventral Striatum | 6.07 | −18 6 −14 | 278 |
| Left Inferior Occipital, Lingual gyrus (V4) | 4.87 4.24 3.25 |
−34 −84 −8 −24 −86 −16 −26 −98 −12 |
215 |
| Right Ventral Striatum | 4.35 3.99 3.311 |
10 10 −10 16 6 −14 18 16 −6 |
278 |
| Liquid | |||
| Left Putamen / Amygdala (SF, LB) | 5.76 4.37 |
−24 4 −10 −28 −2 −14 |
260 |
| Right Amygdala (SF, LB, CM) | 5.30 3.71 3.43 |
26 −2 −12 38 −2 −8 32 −14 −14 |
154 |
| Social | |||
| Left Frontal Operculum / IFG | 5.74 | −30 24 −10 | 234 |
| Left Inferior Parietal Lobule (hIP1, Inferior Parietal Cortex (PGa, PFm) | 4.25 3.92 |
−40 −54 42 −50 −56 42 |
123 |
| Cognitive | |||
| No regions |
As with the outcome PE map, monetary reinforcement occurred frequently in the selection of studies. Thus, the monetary sub-analysis revealed a pattern of activations very similar to the overall RPE contrast. The other reinforcer-type sub-analyses were somewhat underpowered, and we did not perform statistical contrasts of these maps. The cognitive sub-analysis did not reveal any significant clusters, but the liquid and social reinforcement maps yielded several distinct clusters. Liquid rewards elicited lateral putamen and amygdala activations, while social rewards produced two left hemispheric activations: one was similar to the frontal opercular/insula cluster in the main reward PE contrast; the second was in the left inferior parietal cortex.
3.2.6. High vs. Low Smoothing (Table 9)
Table 9.
ALE clusters representing activations associated with High and Low Smoothing kernels including peak t statistics, MNI co-ordinates and cluster size. SF=superficial subregion of amygdala.
| Region | T statistic | Coordinate | Size |
|---|---|---|---|
| High Smoothing | |||
| Left Putamen, Amygdala | 6.40 3.61 |
−20 6 −12 −28 −4 −16 |
524 |
| Right Putamen, Amygdala | 4.78 4.66 4.11 3.55 3.11 |
26 −2 −12 14 6 −14 20 10 −4 34 2 −12 6 4 4 |
430 |
| Left Frontal operculum | 5.55 | −30 24 −8 | 137 |
| Low Smoothing | |||
| Thalamus / Midbrain | 4.81 | −8 −18 −2 | 112 |
| Left Inferior Frontal Gyrus (pars orbitalis), Frontal operculum | 4.13 4.07 3.85 |
−34 28 −12 −36 22 −6 −30 28 −14 |
109 |
| High/Low smoothing conjunction: | - | - | - |
| High > Low: Right Amygdala (SF) | 2.44 1.99 1.97 |
24 −2 −14 14 0 −16 16 2 −14 |
57 |
| Low > High: Left Thalamus | 2.09 | −6 −18 −2 | 46 |
High smoothing studies were associated with bilateral putamen and amygdala activation, as well as activation in the left frontal operculum. Low smoothing studies were associated with the thalamus/midbrain and left frontal operculum. The opercular activations were not similar enough to yield a significant conjunction. High smoothing studies were significantly more likely to activate the right amygdala than low smoothing studies. The low smoothing studies were more likely to activate a small cluster of the thalamus, towards the top of the midbrain/thalamus cluster identified in the main RPE contrast.
3.2.7. Overall conjunction
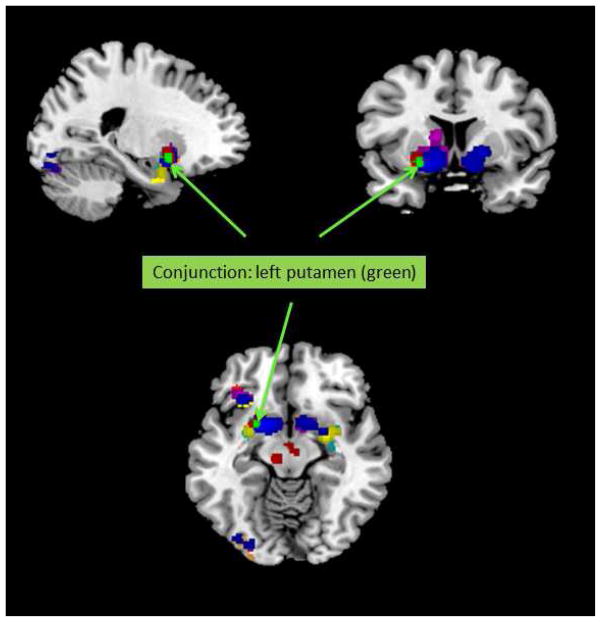
A conjunction analysis was conducted across all of the main contrast types (Instrumental/Pavlovian; Fixed/Individual; RW/TD; High/Low Smoothing) using the minimum statistic across the cluster thresholded contrasts for each of the eight maps (Rottschy et al., 2012). A 30 voxel cluster was revealed in the left putamen (-22, 6, 9) across the first three pairs of contrasts (i.e. excluding smoothing). This cluster thus reflects the strongest convergent evidence for a neural correlate of a signed RPE signal we were able to obtain (see Figure 5). However, when the smoothing-related contrasts were included, no clusters were identified.
Figure 5.
Conjunction map showing the overlap of ALE maps from individual subgroup analyses (Fixed, Individual, Pavlovian, Instrumental, Outcome PE, TD, Monetary, Liquid and Social), with the left putamen cluster (x=-22, y=6, z=9, cluster size = 30) from the conjunction analysis shown in green and marked with arrows.
3.3. Expected Value (Table 10)
Table 10.
ALE cluster representing the activation associated with Expected Value (EV) including peak t statistics, MNI co-ordinates and cluster size. Studies contribution to the cluster, and their percentage contribution are marked
| Region | T statistic | Coordinate | Size | Studies participating (percentage contribution) |
|---|---|---|---|---|
| Subgenual Cingulate |
4.85 3.54 |
4 34 −6 −6 28 −20 |
172 |
FitzGerald et al., 2012 (26.52) Wunderlich et al., 2010 (24.44) Glascher et al., 2009 (21.24) Bernacer et al., 2013 (13.99) Kim et al., 2006 (9.83) Klein et al., 2007 (2.80) Takemura et al., 2011 (0.69) |
The ALE analysis of studies reporting expected value yielded a single activation in the subgenual anterior cingulate cortex (Table 10; Figure 6). To illustrate specificity, RPE and EV maps were contrasted. The subgenual ACC was significantly more likely to be activated in the EV than the RPE condition, while the left striatum and midbrain were significantly more likely to be activated in the RPE than the EV condition. No significant clusters representing the conjunction of EV and RPE were observed.
Figure 6.
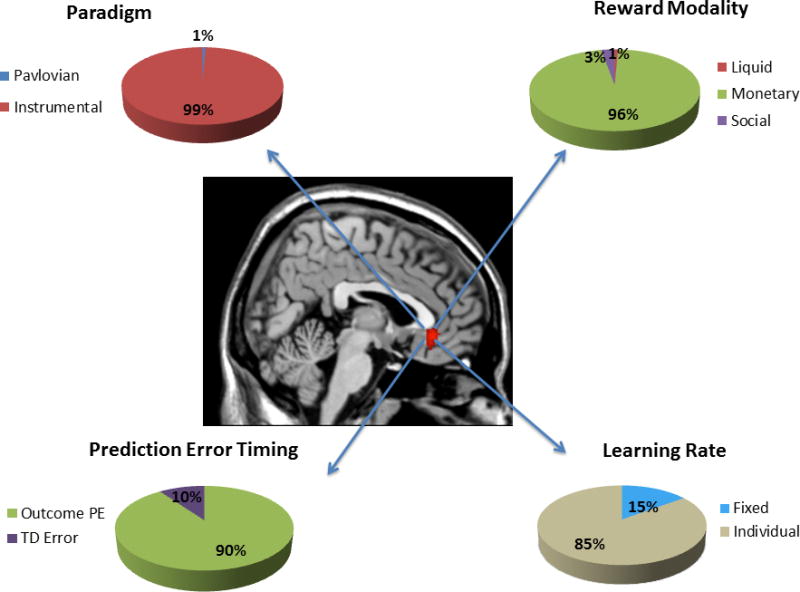
Map of significant ALE clusters associated with the EV contrast. Pie charts show the contribution of studies of a particular class to the subgenual cingulate activation. Percentages are not corrected for base rate.
4. Discussion
In line with previous animal and human studies, the present meta-analysis confirmed our core hypotheses: that the midbrain and striatum represented reward prediction errors, while the subgenual cingulate – a caudal region of the ventromedial prefrontal cortex – represented expected value. In addition, this meta-analysis revealed that the frontal operculum and visual cortices are a part of the reward prediction error network, mainly recruited during social rewards and attentional processing respectively. While largely compatible with previous meta-analyses of the neural bases of prediction errors (Garrison et al., 2013), reward anticipation and receipt (Diekhof, Kaps, Falkai, & Gruber, 2012; Liu, Hairston, Schrier, & Fan, 2011; Sescousse et al., 2013) and value (Bartra et al., 2013; Clithero & Rangel, 2014; Levy & Glimcher, 2012; Peters & Buchel, 2010), the present study extends this work by focusing exclusively on the neural correlates of parametric reward prediction errors and expected value derived from reinforcement learning models. We identified methodological factors that might contribute to divergent findings, including instrumental/Pavlovian designs, reinforcer type and smoothing kernel size.
Core prediction error network
The reproducibility of fMRI BOLD images is often a concern, test-retest reliability of the method being generally modest and very poor in some cases (Bennett & Miller, 2010). Moreover, methodological differences across studies, including differences between scanners, paradigms, participants and analyses software may further conspire to amplify between-study heterogeneity. Nevertheless, a core network of regions associated with prediction errors was readily identified, including the ventral striatum and midbrain as predicted. Indeed, even for two regions that were not predicted – the left frontal operculum and left visual cortex – over 10 studies contributed to each of these clusters. This suggests that this core prediction error network is robust to between-study variability and reflects a level of specificity of the activations. However, each of the activations should be interpreted carefully; it is often difficult to distinguish certain psychological events due to a shared but spurious correlation with the general linear model regressor. The variability of paradigms may act to provide some de-correlation of irrelevant variables from the RPE construct. For example, the lack of prediction error signals in the medial PFC is consistent with the animal electrophysiological studies (M. R. Roesch et al., 2010), although medial OFC activation has been shown to be coupled to RPE in some human fMRI studies. Our findings are consistent with the view that this is likely to be due to the correlation inherent between appetitive properties of the outcome and RPE in many of these designs (Erdeniz, Rohe, Done, & Seidler, 2013; Rohe et al., 2012).
Aside from the reinforcement learning signal hypothetically encoded by dopamine-rich regions such as the midbrain and ventral striatum, associative learning algorithms are often extended to account for salience and attentional phenomena. These constructs may be necessary for interpreting RPE correlates in the visual cortex, amygdala and insula. For example, the Pearce-Hall (PH) model (Pearce & Hall, 1980) emphasizes that cues associated with surprising outcomes command attention: prediction errors not only strengthen associations, but a similar signal, reflecting surprise associated with the outcome, may control the rate at which such associations are strengthened. In the PH model, stimuli which are accompanied by larger prediction errors attract attention, and thus become more readily associated with other stimuli. A recent theme has been to argue that a PH signal might be coupled to the surprising outcome itself, rather than conditioned stimuli. For example, a recent study by Li and colleagues (Li, Schiller, Schoenbaum, Phelps, & Daw, 2011) suggested that, consistent with animal learning studies (Maddux, Kerfoot, Chatterjee, & Holland, 2007), the amygdala codes surprise as predicted by the PH model rather than a signed RPE signal.
In the present study, we found amygdala activation coupled to the RPE contrast. In probabilistic designs that are widely used, it would be difficult to dissociate a PH signal from the basic RPE contrast. It may then be that RPE-coupled amygdala activation reflects some confounding of a PH signal with the RPE signal, particularly as a PH parameter is often not concurrently modelled. However, amygdala activation was particularly associated with studies in which liquid was used as a reinforcer, while larger smoothing kernels were also associated with greater activation in the amygdala. These factors should be independent of the learning rule and contingency under investigation, and should be adequately controlled in future studies of the PH rule.
Other regions that play a well-established role in attention in the fMRI literature were also coupled to the RPE contrast, including the left visual cortex. Although reward-related responses in the visual cortex have been identified, a recent study argued that these signals may reflect attentional processing rather than the appetitive and dopamine-related properties of the reward (Arsenault, Nelissen, Jarraya, & Vanduffel, 2013). We also identified a left frontal operculum/anterior insula region with the RPE contrast, that is activated by a wide range of stimuli and task designs and thus perhaps has a general role in task set representation (Dosenbach et al., 2006). Nevertheless, the activation of this region by reward has been quite well characterized. A study by Rutledge and colleagues (Rutledge, Dean, Caplin, & Glimcher, 2010) parametrically manipulated reward probability of wins and losses, finding that the response of the anterior insula to reward does not follow a pattern that would be expected from a prediction error signal. It was however modulated to some degree by the probability of the outcome, insofar as activation was not observed in the region if the outcome was fully predicted, and showed fairly consistent activation across wins and losses if the outcome was uncertain. Given that the paradigms in the present study generally include a degree of outcome uncertainty, it opens the possibility that anterior insula activation may become coupled with an RPE regressor while not accurately reflecting the predicted RPE signal. Less obvious is the fact that paradigms employing social reinforcement were particularly able to elicit activation in this region. An interpretation of the study of Rutledge might suggest that this is simply related to the kind of contingencies employed in the social paradigms, but equally it is worth considering the possibility that the anterior insula may play a distinct role in the reinforcement process itself.
Pavlovian vs Instrumental
Although the majority of studies were instrumental, requiring the participant to make a choice, we contrasted these studies with a small number of Pavlovian designs. We found differential activation in the left caudate (dorsal striatum), consistent with an influential study of O’Doherty and colleagues (J. O’Doherty et al., 2004), in which the striatum was argued to follow the ‘actor-critic’ model: the anterior, dorsal caudate (‘actor’) was engaged when behavior output was required. By contrast, the ventral striatum (‘critic’) was engaged during errors of value prediction, whether a response was required to obtain reward or not. This distinction is also broadly consistent with animal lesion studies, as the dorsomedial striatum of rodents – a likely homologue of the caudate region identified in the present study and that of O’Doherty et al. (2004) - plays a key role in instrumental, goal directed behavior (Yin, Ostlund, Knowlton, & Balleine, 2005) whereas the ventral striatum is more consistently implicated in Pavlovian behaviors (Corbit & Balleine, 2011; Parkinson, Olmstead, Burns, Robbins, & Everitt, 1999).
Although the notion that the striatum contributes to action selection in a manner predicted by actor-critic model has steadily gathered currency, it was somewhat undermined by a previous meta-analysis by Garrison and colleagues (Garrison et al., 2013). This study found that while both the dorsal and ventral striatum were engaged by instrumental designs, both were significantly more activated by these designs than Pavlovian designs. Our findings contrast from this study, as we did find significant activation in the ventral striatum elicited by Pavlovian designs, although somewhat more lateral than equivalent activations seen in instrumental designs.
Together, the present study and that of Garrison may provoke further debate about the success of the actor-critic model as an account of the striatum’s influence on behavior. However, there are several important reasons as to why providing a definitive contribution to this question might be difficult. First, it has been noted (e.g. Coricelli et al., 2005; Yeung, Holroyd, & Cohen, 2005) that designs in which a (human) participant is required to make a choice, and is reinforced for doing so, are potentially more engaging than Pavlovian designs and consequently can provide more robust neural signals. Given that the MR scanner requires that an individual lie for long periods in a darkened room, performing an often repetitive task, this consideration is not to be taken lightly, and can make it difficult to design an effective Pavlovian paradigm. This may both explain the preponderance of instrumental tasks in the literature, as well as the second key limitation – that Pavlovian designs tend to focus on liquid reinforcers rather than other domains. This is presumably because liquid is a powerful primary reinforcer, particularly when the participant is thirsty (e.g. Kumar et al., 2008), and this may somewhat compensate for a potential lack of engagement described above. A final limitation is the nature of the definition of instrumental and Pavlovian designs. Instrumental behavior can be defined on the basis of the contingency between a particular action and an outcome (Balleine & Dickinson, 1998), and the manner in which a subject can use this information to obtain reinforcement. The presence of stimuli on all of the paradigms we considered in the present work complicates this issue somewhat. Specifically, in any of the instrumental designs included in the present work, it cannot be assumed that this action-outcome contingency is the sole factor which determines choice. Rather, an individual’s responses may also be susceptible to influence by the presented stimuli, and the relationships between the stimuli and reinforcement.
Fixed vs Individual Learning Rates
We investigated whether the strategy of RL model fitting, upon which the pattern of the RPE (and EV) regressors was based, was associated with different patterns of neural activation. Although across most situations, the pattern of RPEs associated with fixed and individual model fitting should be highly similar, it is nevertheless unclear exactly how sensitive the pattern of activations is to the parameterization of the underlying model. Daw has consistently argued that the fixed (or more particularly group fixed) strategy offers advantages over estimating the model parameters per individual (N.D. Daw, 2011). On the other hand, regarding fitting models to behavioral data, Estes and Maddox (Estes & Maddox, 2005) have argued that individual participant fitting avoids certain sources of bias associated with group averaging.
The fixed subgroup shows the strongest corroboration of the classic RPE hypothesis pioneered by Schultz and colleagues (Schultz et al., 1997) as the midbrain was engaged by these studies. In addition, activation in the lateral putamen was also observed, as would be expected on the basis of anatomical connectivity (Haber et al., 2000). However, if the individual method was suboptimal, we would both not expect the method to have obtained traction in the literature, individual studies being more common than fixed, and more importantly, we would not expect a distinct pattern of activations to emerge. It is possible to imagine various scenarios in which the presence of suboptimal acquisition or preprocessing parameters that impair the detection of midbrain activations would sustain the observation of a certain pattern of weaker VS RPE-associated responses beyond the canonical network, but even then, the focus of the activation should not show such a reproducibly medial focus within the striatum. It also does not seem likely that a suboptimal RPE regressor should be better coupled to an experimental confound, such as the response to the reward itself (Rohe et al., 2012). Within the RL framework we have set out, the most likely remaining explanation is that neural responses to RPEs generated by different learning rates are reflected across different regions of the brain (Glascher & Buchel, 2005). For example, a model of Frank et al (M. J. Frank, Moustafa, Haughey, Curran, & Hutchison, 2007) distinguished a rapid but time-dependent learning mechanism, ascribed to the OFC, and a slower, incremental learning mechanism, ascribed to the striatum. Both mechanisms used similar RW-based learning rules, although more recent, comparable models have employed a working memory-based system rather than a rapid RL system (Collins & Frank, 2012). This might therefore provide one interpretation of our data, with the modification that the medial striatum encodes a more variable learning rate (across individuals), perhaps better linked to trial by trial choice performance, while the midbrain and lateral putamen reflect a more homogeneous, slower learning rate that would not be as strongly reflected in behavior.
Conjunction Analyses
A further level of specificity is afforded by the conjunction analysis examining which regions are identified across different designs, and thus relatively invariant. Across several of the subgroup analyses (e.g. fixed/individual; Pavlovian/instrumental; RW/TD), the left putamen was identified. The region was notable insofar as it was positioned at the midpoint between the classic ventromedial striatal region, which may correspond to the nucleus accumbens in humans (Haber & Knutson, 2010), and a more clearly lateralized putamen region. Given that these two regions may be anatomically distinct (Haber et al., 2000), it is important to consider the extent to which smoothing may have played a part in this finding. Smoothing of individual participant images is considered to be an important preprocessing step: though not without drawbacks, the method is thought to enhance statistical power by increasing signal to noise (Yue, Loh, & Lindquist, 2010), and increases the underlying smoothness for Gaussian random field-based (cluster) analyses (Hayasaka & Nichols, 2003). It is intriguing that one subgrouping analysis that did not yield activation in this region was the conjunction of studies which used high and low smoothing kernels. In a recent study, Sacchet and Knutson (2013) demonstrated that larger smoothing kernels can influence the localization of peak activation within the ventral striatum, with larger kernels yielding more posterior activations. In our study, the variability in the magnitude of the smoothing kernel across studies was relatively small, with the large majority of studies choosing an 8mm kernel and no significant differences between the low/high smoothing subgroups were seen. However, it was also notable that studies using a small smoothing kernel were (non-significantly) more capable of revealing midbrain activation. Given that the midbrain is a small structure, matched filter theory (for fMRI see Yue et al., 2010) would predict a smaller filter should therefore be advantageous to identify activation in this region. Overall, as suggested by Sacchet and Knutson, differences in smoothing across studies may provide significant additional heterogeneity, and alternative smoothing methods that honor the geometry and size of these regions may be valuable in future studies.
Core expected value network
Our meta-analysis of RL studies of expected value identified a subregion of the subgenual cingulate cortex, corresponding most closely to areas 25 and 32 of the human and monkey vmPFC. This phylogenetically ancient agranular region is likely homologous to the paralimbic and infralimbic cortex of rodents (J. D. Wallis, 2012).
At the first approximation, our findings converge with primate electrophysiological (Kennerley et al., 2009; Kennerley & Wallis, 2009a, 2009b; Morrison & Salzman, 2009; Padoa-Schioppa & Assad, 2006, 2008; Matthew R. Roesch & Olson, 2004; M. R. Roesch & Olson, 2005; Jonathan D. Wallis & Miller, 2003) and lesion (Izquierdo, Suda, & Murray, 2004; Noonan et al., 2010; P. H. Rudebeck & Murray, 2011) studies as well as rodent lesion studies (Gallagher, McMahan, & Schoenbaum, 1999; McDannald, Lucantonio, Burke, Niv, & Schoenbaum, 2011; Takahashi et al., 2009) implicating the OFC in value computations. Yet, the substantial anatomical heterogeneity between these literatures cannot be ignored. Most primate electrophysiological studies recorded value signals from more rostral, central orbitofrontal regions (BAs 11 and 13). Rodent studies often employed lesions of the more rostral and lateral OFC (Gallagher et al., 1999; McDannald et al., 2011; Takahashi et al., 2009). In contrast, our subgenual cingulate cluster is more medial and caudal and does not extend to the orbital surface. This discrepancy was recently discussed by Wallis (2012), who pointed out a few possible solutions to this puzzle. First, rostromedial OFC BOLD activations in BA 11, medial BA 13 and ventral BA 10 are obscured by the susceptibility artifact. Thus, value signals in the human brain may well extend into the rostral and central OFC areas highlighted by primate physiological studies. However, a recent meta-analysis of fMRI studies of reward value that was not limited to RL studies by Bartra and colleagues reported value-related activations in medial rostral OFC areas most affected by the susceptibility artifact, but not in the more lateral central OFC (Bartra et al., 2013), where signal is often better preserved.
Another set of considerations stems from the medial-lateral organization of the orbitofrontal circuits (Ongur & Price, 2000). The lateral, “orbital” circuit of Carmichael & Price (1996) encompasses central OFC areas, which integrate sensory inputs carrying information about extrinsic food value: taste, olfaction, and vision. It is often argued that this lateral circuit represents not only the value of foods and liquids typically used in animal experiments, but that of external stimuli and outcomes in general (Schoenbaum, Takahashi, Liu, & McDannald, 2011; J. D. Wallis, 2012). Physiologists typically record from this circuit in their studies of the primate and rodent OFC (Kennerley et al., 2009; Kennerley & Wallis, 2009a, 2009b; Morrison & Salzman, 2009; Padoa-Schioppa & Assad, 2006, 2008; Matthew R. Roesch & Olson, 2004; M. R. Roesch & Olson, 2005; Jonathan D. Wallis & Miller, 2003).
An additional reason why fMRI studies do not detect value signals in central OFC is its diametrically opposed value encoding scheme (J. D. Wallis, 2012). Some OFC neurons increase and others decrease their firing rate in response to increasing value (Kennerley & Wallis, 2009a; Morrison & Salzman, 2009; Padoa-Schioppa & Assad, 2006). These opposing responses may cancel each other out at the level of BOLD signal. The medial orbital circuit, encompassing the vmPFC and the subgenual cingulate in particular, has prominent visceral and motor connections (Carmichael & Price, 1996; Ongur & Price, 2000). Its putative functions include sensing internal states, tracking social value, and bridging outcome value and action selection (Bouret & Richmond, 2010; Noonan et al., 2010; Peter H. Rudebeck et al., 2008; P. H. Rudebeck, Buckley, Walton, & Rushworth, 2006). Grabenhorst and Rolls place the vmPFC downstream from the OFC in the processing of reward signals, proposing that the vmPFC receives stimulus value information from the OFC, incorporates other variables such as cost into the decision, and transmits it to the motor areas (Grabenhorst & Rolls, 2011). VmPFC responses often scale with subjective pleasure, which may best correspond to the reward rate or the total value of contingencies that can be exploited.
Not only are the findings of vmPFC value signals consistent in human fMRI studies, but they are also less well established in the primate electrophysiological literature (J. D. Wallis, 2012; but see Strait, Blanchard, & Hayden, 2014). This discrepancy may reflect methodological differences between the human and monkey studies. For example, human studies use mostly secondary reinforcers such as money and correct/incorrect feedback. Only 2/16 value studies in our meta-analysis used primary rewards (liquid). One of them detected value signals in the vmPFC (Takemura, Samejima, Vogels, Sakagami, & Okuda, 2011) and one did not (Gradin et al., 2011), and neither found them in the central OFC. Further, the meta-analysis by Bartra and colleagues reported vmPFC value signals for both primary and monetary rewards (Bartra et al., 2013). A similar explanation focuses on the putative predilection of the vmPFC for social value signals (P. H. Rudebeck et al., 2006). The presence of vmPFC value signals in fMRI studies that used primary, non-social rewards argues against this explanation. That said, demand characteristics may confound in human imaging studies of value signals, and experimenters may thus need to conceal contingency manipulations. In summary, our finding of RL-estimated value signals in the vmPFC/subgenual cingulate is consistent with non-RL-based human imaging studies and diverges somewhat from the primate electrophysiological studies that tend to find value signals in the central OFC.
Given that the EV map was restricted to the vmPFC, a supplementary conjunction analysis of the RPE and EV contrasts did not reveal significant results. Given that the EV maps reflect future expected rewards, it is plausible that a TD-related signal should be observed at this stage, and thus a concurrent striatal or midbrain activation. In fact, significantly different activations were observed between the RPE network (RPE > EV) and the vmPFC EV cluster (EV > RPE). A statistical account of this observation may relate to the combined inclusion of RPE and EV regressors in the general linear model used in the analysis of many of the studies: the presence of each regressor concurrently, combined with a suitable design, may act to orthogonalize these two events and distinguish the resulting maps. Nevertheless, our findings are also consistent with the view that a phasic TD signal might be distinct (in this case, neuroanatomically) from an expected value signal (Ludvig, Sutton, & Kehoe, 2008).
Limitations
Although striking consistency in the pattern of activation was observed across paradigms, there was nevertheless evidence of different classes of paradigm leading to different patterns of findings, as discussed. A limitation of the inferences that can be drawn from analyses of these differences is caused by the presence of confounds between different categories. This was particularly acute for Pavlovian, TD and liquid designs because of their relative infrequency. In particular, amygdala RPE-coupled activations were associated with these classes of design, making it difficult to draw strong conclusions about the amygdala’s engagement by a paradigm class. Overall, our method of contrasting paradigm classes requires that all other dimensions are controlled for strong inferences to be obtained. Although this was not possible, the findings nevertheless point to particular trends of experimental design which may precipitate differences in the pattern of neural activation obtained.
Refutations or refinements of reinforcement learning models are of course a crucial part of their theoretical development within neuroscientific investigation (Gamez, 2012). However, we have restricted our analysis to studies in which the RL model was not refuted or otherwise argued to be an inferior account of the pattern of data, albeit allowing for some modifications of parameterization to the basic RW or TD model. Bayesian models such as the Bayesian learner (Behrens, Woolrich, Walton, & Rushworth, 2007), hidden-Markov models (Hampton, Bossaerts, & O’Doherty, 2006) and Bayesian RL (Mathys, Daunizeau, Friston, & Stephan, 2011), as well as the Kalman filter (N. D. Daw, O’Doherty, Dayan, Seymour, & Dolan, 2006) can all exhibit advantages over many of the models we have examined in the present work. However, the superior performance of the alternative models in the studies we opted to exclude may be a result of peculiarities of the experimental design, which may render these studies more heterogeneous a priori, and thus less suitable for meta-analysis. In addition, the nature of this advantage should be carefully qualified (Myung, 2000): often, these models are representationally more powerful, perhaps reflecting inherent features of the experimental design (e.g. the rule transitions imbedded within reversal learning: (Behrens et al., 2007; Hampton et al., 2006). While pursuing the benefits of these models is likely to be a topic of major ongoing interest, we argue that the incremental increase in complexity and representational capacity of many of these models creates a natural, qualitative distinction with the more traditional RL methods which provide the focus of the present work.
Another limitation of the present study involves the limitation of meta-analysis, over and above the direct pooling of data within a ‘mega’-analysis. Judicious combination of fMRI studies of conditioning could in theory be performed, perhaps along similar lines to an analysis of task-related neural activation by Dosenbach and colleagues (Dosenbach et al., 2006). If possible, this would certainly afford more direct contrast of different modeling strategies (e.g. fixed/individual learning rate; smoothing kernels) and possibly also procedural differences (e.g. reinforcer type, response contingency). Moreover, this approach may afford more detailed investigation of the relationship between individual functional activations and anatomy, providing that adequate structural data is available. The overlap between individually defined regions of interest and brain activations would diminish the necessity of spatial smoothing, and potentially increase specificity in regions of high between-participant anatomical variation.
We have also restricted our study inclusion to healthy adult groups. Individual differences in a variety of demographic factors can influence the pattern of RL-related neural activation and represent possible unmeasured sources of inter-subject variability. Again, a ‘mega’-analysis with suitably recorded data may provide some control of these effects. However, the consistency of some of our findings (e.g. left putamen) across methodological dimensions suggests that these factors may serve to modulate a core pattern of activation rather than yield qualitative differences. Overall, as ALE has been argued to be statistically conservative (Graham et al., 2013), it is likely that, broadly, our findings represent a central, reproducible motif which may provide a useful reference point for future studies of RL and reward-based conditioning studies. Indeed, an increase in the number of available RL studies would allow greater power to address the full diversity of RL-related processes in the human brain. While the number of studies available is adequate, further information would be usefully gleaned by increasing the number of studies (e.g. Rottschy et al., 2012), particularly if these are designs which are not well represented in the current selection (e.g. liquid, TD studies).
Summary
In the present work, we have identified a pattern of human neural correlates of reward prediction error (RPE) and expected value (EV) signals derived from simple reinforcement learning (RL) algorithms. Our findings accord well with existing literature, particularly electrophysiological studies with experimental animals, in our identification of dopamine-rich regions such as the midbrain and striatum in RPE signaling, and the ventromedial prefrontal cortex in EV representation. The main contribution of the present work is to demonstrate that various methodological factors can influence the pattern of findings. These include factors that are possible to control at the analysis stage (e.g. learning rate estimation, smoothing), but also factors that must be examined experimentally (e.g. reinforcer type, behavioral output). Overall, the RL framework has been an empirically successful paradigm for investigating the neurobiology of appetitive behavior, and we anticipate a new generation of studies will seek to develop the implications of these findings further.
Table 2.
Studies reporting Expected Value (EV) maps.
| Study | n | Foci | Pavlovian/Instrumental | Learning Rate Parameter | Reinforcer Type |
|---|---|---|---|---|---|
| Bernacer et al., 2013 | 18 | 2 | Instrumental | Fixed | Monetary |
| Chowdhury et al., 2013 | 32 | 100 | Instrumental | Individual | Monetary |
| Dombrovski et al., 2013 | 20 | 4 | Instrumental | Individual | Cognitive |
| FitzGerald, Friston, & Dolan, 2012 | 26 | 48 | Instrumental | Individual | Monetary |
| Glascher et al., 2009 | 20 | 15 | Instrumental | Individual | Monetary |
| Gradin et al., 2011 | 17 | 8 | Instrumental | Fixed | Liquid |
| Jones et al., 2011 | 36 | 1 | Instrumental | Fixed | Social |
| Kim et al., 2006 | 16 | 2 | Instrumental | Individual | Monetary |
| Klein et al., 2007 | 12 | 8 | Instrumental | Individual | Social |
| Madlon-Kay et al., 2013 | 20 | 6 | Instrumental | Individual | Monetary |
| O’Sullivan et al., 2011 | 24 | 3 | Instrumental | Fixed | Monetary |
| Seger et al., 2010 | 11 | 11 | Instrumental | Individual | Cognitive |
| Tanaka et al., 2006 | 18 | 4 | Instrumental | Individual | Monetary |
| Takemura et al., 2011 | 23 | 24 | Pavlovian | Fixed | Liquid |
| Watanabe et al., 2013 | 20 | 2 | Instrumental | Individual | Monetary |
| Wunderlich, Rangel, & O’Doherty, 2010 | 24 | 11 | Instrumental | Individual | Monetary |
Acknowledgments
We would like to thank the following individuals, and their associated research teams, for contributing data used in the study: Drs Rumana Chowdhury, Jessica Cohen, Thomas Fitzgerald, Gerhard Jocham, Rebecca Jones, Andreas Heinz, Thorsten Kahnt, John O’Doherty, Soyoung Park, Oliver Robinson, Florian Schlagenhauf and Wouter van den Bos. We also thank Drs Masahiko Haruno, Noreen O’Sullivan, Ben Seymour, and Craig Stark for answering our questions.
Footnotes
A study by Wittmann and colleagues (Wittmann, Daw, Seymour, & Dolan, 2008) was not included as the sequence was optimized for ventral structures and regions above the dorsal anterior cingulate were not imaged. However, as this study could potentially have been included given alternative criteria, we compared this RPE map with the other studies. RPE activations reported in this study were highly comparable with similar designs (Fixed, Instrumental, Monetary, TD) studies (e.g. putamen, visual cortex, thalamus, opercular activation)
The authors declare no financial conflicts of interest that may have biased the present work.
References
- Arsenault JT, Nelissen K, Jarraya B, Vanduffel W. Dopaminergic reward signals selectively decrease fMRI activity in primate visual cortex. Neuron. 2013;77(6):1174–1186. doi: 10.1016/j.neuron.2013.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balleine BW, Dickinson A. Goal-directed instrumental action: contingency and incentive learning and their cortical substrates. Neuropharmacology. 1998;37(4–5):407–419. doi: 10.1016/s0028-3908(98)00033-1. [DOI] [PubMed] [Google Scholar]
- Bartra O, McGuire JT, Kable JW. The valuation system: a coordinate-based meta-analysis of BOLD fMRI experiments examining neural correlates of subjective value. Neuroimage. 2013;76:412–427. doi: 10.1016/j.neuroimage.2013.02.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens TEJ, Woolrich MW, Walton ME, Rushworth MFS. Learning the value of information in an uncertain world. Nat Neurosci. 2007;10(9):1214–1221. doi: 10.1038/nn1954. http://www.nature.com/neuro/journal/v10/n9/suppinfo/nn1954_S1.html. [DOI] [PubMed] [Google Scholar]
- Bellebaum C, Jokisch D, Gizewski ER, Forsting M, Daum I. The neural coding of expected and unexpected monetary performance outcomes: dissociations between active and observational learning. Behav Brain Res. 2012;227(1):241–251. doi: 10.1016/j.bbr.2011.10.042. [DOI] [PubMed] [Google Scholar]
- Bennett CM, Miller MB. How reliable are the results from functional magnetic resonance imaging? Ann N Y Acad Sci. 2010;1191:133–155. doi: 10.1111/j.1749-6632.2010.05446.x. [DOI] [PubMed] [Google Scholar]
- Bernacer J, Corlett PR, Ramachandra P, McFarlane B, Turner DC, Clark L, Murray GK. Methamphetamine-induced disruption of frontostriatal reward learning signals: relation to psychotic symptoms. Am J Psychiatry. 2013;170(11):1326–1334. doi: 10.1176/appi.ajp.2013.12070978. [DOI] [PubMed] [Google Scholar]
- Bouret S, Richmond BJ. Ventromedial and orbital prefrontal neurons differentially encode internally and externally driven motivational values in monkeys. J Neurosci. 2010;30(25):8591–8601. doi: 10.1523/JNEUROSCI.0049-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bray S, O’Doherty J. Neural coding of reward-prediction error signals during classical conditioning with attractive faces. J Neurophysiol. 2007;97(4):3036–3045. doi: 10.1152/jn.01211.2006. [DOI] [PubMed] [Google Scholar]
- Brovelli A, Laksiri N, Nazarian B, Meunier M, Boussaoud D. Understanding the neural computations of arbitrary visuomotor learning through fMRI and associative learning theory. Cereb Cortex. 2008;18(7):1485–1495. doi: 10.1093/cercor/bhm198. [DOI] [PubMed] [Google Scholar]
- Bush RR, Mosteller F. A Model for Stimulus Generalization and Discrimination. Psychological review. 1951;58(6):413–423. doi: 10.1037/H0054576. [DOI] [PubMed] [Google Scholar]
- Bush RR, Mosteller F. A Stochastic Model with Applications to Learning. Annals of Mathematical Statistics. 1953;24(4):559–585. doi: 10.1214/aoms/1177728914. [DOI] [Google Scholar]
- Carmichael ST, Price JL. Connectional networks within the orbital and medial prefrontal cortex of macaque monkeys. J Comp Neurol. 1996;371(2):179–207. doi: 10.1002/(SICI)1096-9861(19960722)371:2<179::AID-CNE1>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
- Chiu PH, Lohrenz TM, Montague PR. Smokers’ brains compute, but ignore, a fictive error signal in a sequential investment task. Nat Neurosci. 2008;11(4):514–520. doi: 10.1038/nn2067. [DOI] [PubMed] [Google Scholar]
- Chowdhury R, Guitart-Masip M, Lambert C, Dayan P, Huys Q, Duzel E, Dolan RJ. Dopamine restores reward prediction errors in old age. Nat Neurosci. 2013;16(5):648–653. doi: 10.1038/nn.3364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clithero JA, Rangel A. Informatic parcellation of the network involved in the computation of subjective value. Soc Cogn Affect Neurosci. 2014;9(9):1289–1302. doi: 10.1093/scan/nst106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MX. Individual differences and the neural representations of reward expectation and reward prediction error. Soc Cogn Affect Neurosci. 2007;2(1):20–30. doi: 10.1093/scan/nsl021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins AG, Frank MJ. How much of reinforcement learning is working memory, not reinforcement learning? A behavioral, computational, and neurogenetic analysis. Eur J Neurosci. 2012;35(7):1024–1035. doi: 10.1111/j.1460-9568.2011.07980.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbit LH, Balleine BW. The general and outcome-specific forms of Pavlovian-instrumental transfer are differentially mediated by the nucleus accumbens core and shell. J Neurosci. 2011;31(33):11786–11794. doi: 10.1523/JNEUROSCI.2711-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coricelli G, Critchley HD, Joffily M, O’Doherty JP, Sirigu A, Dolan RJ. Regret and its avoidance: a neuroimaging study of choice behavior. Nat Neurosci. 2005;8(9):1255–1262. doi: 10.1038/nn1514. [DOI] [PubMed] [Google Scholar]
- Critchley HD, Rolls ET. Hunger and satiety modify the responses of olfactory and visual neurons in the primate orbitofrontal cortex. J Neurophysiol. 1996;75(4):1673–1686. doi: 10.1152/jn.1996.75.4.1673. [DOI] [PubMed] [Google Scholar]
- D’Ardenne K, McClure SM, Nystrom LE, Cohen JD. BOLD responses reflecting dopaminergic signals in the human ventral tegmental area. Science. 2008;319(5867):1264–1267. doi: 10.1126/science.1150605. doi:319/5867/1264. [DOI] [PubMed] [Google Scholar]
- Daw ND. Trial-by-trial data analysis using computational models. In: Delgado MR, Phelps EA, Robbins TW, editors. Decision Making, Affect, and Learning: Attention and Performance XXIII. Oxford: Oxford University Press; 2011. [Google Scholar]
- Daw ND, O’Doherty JP, Dayan P, Seymour B, Dolan RJ. Cortical substrates for exploratory decisions in humans. Nature. 2006;441(7095):876–879. doi: 10.1038/nature04766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P, Walton ME. A step-by-step guide to dopamine. Biol Psychiatry. 2012;71(10):842–843. doi: 10.1016/j.biopsych.2012.03.008. [DOI] [PubMed] [Google Scholar]
- Diekhof EK, Kaps L, Falkai P, Gruber O. The role of the human ventral striatum and the medial orbitofrontal cortex in the representation of reward magnitude - an activation likelihood estimation meta-analysis of neuroimaging studies of passive reward expectancy and outcome processing. Neuropsychologia. 2012;50(7):1252–1266. doi: 10.1016/j.neuropsychologia.2012.02.007. [DOI] [PubMed] [Google Scholar]
- Dombrovski AY, Szanto K, Clark L, Reynolds CF, Siegle GJ. Reward Signals, Attempted Suicide, and Impulsivity in Late-Life Depression. JAMA Psychiatry. 2013 doi: 10.1001/jamapsychiatry.2013.75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenbach NU, Visscher KM, Palmer ED, Miezin FM, Wenger KK, Kang HC, Petersen SE. A core system for the implementation of task sets. Neuron. 2006;50(5):799–812. doi: 10.1016/j.neuron.2006.04.031. S0896-6273(06)00349-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff SB, Bzdok D, Laird AR, Kurth F, Fox PT. Activation likelihood estimation meta-analysis revisited. Neuroimage. 2012;59(3):2349–2361. doi: 10.1016/j.neuroimage.2011.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff SB, Bzdok D, Laird AR, Roski C, Caspers S, Zilles K, Fox PT. Co-activation patterns distinguish cortical modules, their connectivity and functional differentiation. Neuroimage. 2011;57(3):938–949. doi: 10.1016/j.neuroimage.2011.05.021S1053-8119(11)00509-X. [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff SB, Laird AR, Grefkes C, Wang LE, Zilles K, Fox PT. Coordinate-based activation likelihood estimation meta-analysis of neuroimaging data: a random-effects approach based on empirical estimates of spatial uncertainty. Hum Brain Mapp. 2009;30(9):2907–2926. doi: 10.1002/hbm.20718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erdeniz B, Rohe T, Done J, Seidler RD. A simple solution for model comparison in bold imaging: the special case of reward prediction error and reward outcomes. Front Neurosci. 2013;7:116. doi: 10.3389/fnins.2013.00116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estes WK, Maddox WT. Risks of drawing inferences about cognitive processes from model fits to individual versus average performance. Psychon Bull Rev. 2005;12(3):403–408. doi: 10.3758/bf03193784. [DOI] [PubMed] [Google Scholar]
- Fareri DS, Chang LJ, Delgado MR. Effects of direct social experience on trust decisions and neural reward circuitry. Front Neurosci. 2012;6:148. doi: 10.3389/fnins.2012.00148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fellows LK. Orbitofrontal contributions to value-based decision making: evidence from humans with frontal lobe damage. Ann N Y Acad Sci. 2011;1239:51–58. doi: 10.1111/j.1749-6632.2011.06229.x. [DOI] [PubMed] [Google Scholar]
- FitzGerald TH, Friston KJ, Dolan RJ. Action-specific value signals in reward-related regions of the human brain. J Neurosci. 2012;32(46):16417–16423a. doi: 10.1523/JNEUROSCI.3254-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank GK, Reynolds JR, Shott ME, O’Reilly RC. Altered temporal difference learning in bulimia nervosa. Biol Psychiatry. 2011;70(8):728–735. doi: 10.1016/j.biopsych.2011.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank MJ. Dynamic dopamine modulation in the basal ganglia: a neurocomputational account of cognitive deficits in medicated and nonmedicated Parkinsonism. J Cogn Neurosci. 2005;17(1):51–72. doi: 10.1162/0898929052880093. [DOI] [PubMed] [Google Scholar]
- Frank MJ, Moustafa AA, Haughey HM, Curran T, Hutchison KE. Genetic triple dissociation reveals multiple roles for dopamine in reinforcement learning. Proc Natl Acad Sci U S A. 2007;104(41):16311–16316. doi: 10.1073/pnas.0706111104. 0706111104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallagher M, McMahan RW, Schoenbaum G. Orbitofrontal Cortex and Representation of Incentive Value in Associative Learning. The Journal of Neuroscience. 1999;19(15):6610–6614. doi: 10.1523/JNEUROSCI.19-15-06610.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gamez D. From baconian to popperian neuroscience. Neural Syst Circuits. 2012;2:2. doi: 10.1186/2042-1001-2-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrison J, Erdeniz B, Done J. Prediction error in reinforcement learning: A meta-analysis of neuroimaging studies. Neurosci Biobehav Rev. 2013;37(7):1297–1310. doi: 10.1016/j.neubiorev.2013.03.023. [DOI] [PubMed] [Google Scholar]
- Gershman SJ, Pesaran B, Daw ND. Human reinforcement learning subdivides structured action spaces by learning effector-specific values. J Neurosci. 2009;29(43):13524–13531. doi: 10.1523/JNEUROSCI.2469-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glascher J, Buchel C. Formal learning theory dissociates brain regions with different temporal integration. Neuron. 2005;47(2):295–306. doi: 10.1016/j.neuron.2005.06.008. [DOI] [PubMed] [Google Scholar]
- Glascher J, Hampton AN, O’Doherty JP. Determining a role for ventromedial prefrontal cortex in encoding action-based value signals during reward-related decision making. Cereb Cortex. 2009;19(2):483–495. doi: 10.1093/cercor/bhn098. bhn098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabenhorst F, Rolls ET. Value, pleasure and choice in the ventral prefrontal cortex. Trends Cogn Sci. 2011;15(2):56–67. doi: 10.1016/j.tics.2010.12.004. [DOI] [PubMed] [Google Scholar]
- Gradin VB, Kumar P, Waiter G, Ahearn T, Stickle C, Milders M, Steele JD. Expected value and prediction error abnormalities in depression and schizophrenia. Brain. 2011;134(Pt 6):1751–1764. doi: 10.1093/brain/awr059. [DOI] [PubMed] [Google Scholar]
- Graham J, Salimi-Khorshidi G, Hagan C, Walsh N, Goodyer I, Lennox B, Suckling J. Meta-analytic evidence for neuroimaging models of depression: state or trait? J Affect Disord. 2013;151(2):423–431. doi: 10.1016/j.jad.2013.07.002. [DOI] [PubMed] [Google Scholar]
- Haber SN, Fudge JL, McFarland NR. Striatonigrostriatal pathways in primates form an ascending spiral from the shell to the dorsolateral striatum. J Neurosci. 2000;20(6):2369–2382. doi: 10.1523/JNEUROSCI.20-06-02369.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haber SN, Knutson B. The reward circuit: linking primate anatomy and human imaging. Neuropsychopharmacology. 2010;35(1):4–26. doi: 10.1038/npp.2009.129. npp2009129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hampton AN, Bossaerts P, O’Doherty JP. The role of the ventromedial prefrontal cortex in abstract state-based inference during decision making in humans. Journal of Neuroscience. 2006;26(32):8360–8367. doi: 10.1523/Jneurosci.1010-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayasaka S, Nichols TE. Validating cluster size inference: random field and permutation methods. Neuroimage. 2003;20(4):2343–2356. doi: 10.1016/j.neuroimage.2003.08.003. [DOI] [PubMed] [Google Scholar]
- Hertwig R, Erev I. The description-experience gap in risky choice. Trends Cogn Sci. 2009;13(12):517–523. doi: 10.1016/j.tics.2009.09.004. [DOI] [PubMed] [Google Scholar]
- Holroyd CB, Coles MG. Dorsal anterior cingulate cortex integrates reinforcement history to guide voluntary behavior. Cortex. 2008;44(5):548–559. doi: 10.1016/j.cortex.2007.08.013. S0010-9452(07)00110-4 [pii] [DOI] [PubMed] [Google Scholar]
- Howard-Jones PA, Bogacz R, Yoo JH, Leonards U, Demetriou S. The neural mechanisms of learning from competitors. Neuroimage. 2010;53(2):790–799. doi: 10.1016/j.neuroimage.2010.06.027. [DOI] [PubMed] [Google Scholar]
- Izquierdo A, Suda RK, Murray EA. Bilateral orbital prefrontal cortex lesions in rhesus monkeys disrupt choices guided by both reward value and reward contingency. J Neurosci. 2004;24(34):7540–7548. doi: 10.1523/JNEUROSCI.1921-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jocham G, Klein TA, Ullsperger M. Dopamine-mediated reinforcement learning signals in the striatum and ventromedial prefrontal cortex underlie value-based choices. J Neurosci. 2011;31(5):1606–1613. doi: 10.1523/JNEUROSCI.3904-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones RM, Somerville LH, Li J, Ruberry EJ, Libby V, Glover G, Casey BJ. Behavioral and neural properties of social reinforcement learning. J Neurosci. 2011;31(37):13039–13045. doi: 10.1523/JNEUROSCI.2972-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahnt T, Park SQ, Cohen MX, Beck A, Heinz A, Wrase J. Dorsal striatal-midbrain connectivity in humans predicts how reinforcements are used to guide decisions. J Cogn Neurosci. 2009;21(7):1332–1345. doi: 10.1162/jocn.2009.21092. [DOI] [PubMed] [Google Scholar]
- Kamin LJ. Predictability, surprise, attention, and conditioning. In: Campbell BA, Church RM, editors. Punishment and aversive behavior. New York: Appleton-Century-Crofts; 1968. pp. 279–296. [Google Scholar]
- Kennerley SW, Dahmubed AF, Lara AH, Wallis JD. Neurons in the frontal lobe encode the value of multiple decision variables. J Cogn Neurosci. 2009;21(6):1162–1178. doi: 10.1162/jocn.2009.21100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennerley SW, Wallis JD. Encoding of reward and space during a working memory task in the orbitofrontal cortex and anterior cingulate sulcus. J Neurophysiol. 2009a;102(6):3352–3364. doi: 10.1152/jn.00273.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennerley SW, Wallis JD. Evaluating choices by single neurons in the frontal lobe: outcome value encoded across multiple decision variables. Eur J Neurosci. 2009b;29(10):2061–2073. doi: 10.1111/j.1460-9568.2009.06743.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim H, Shimojo S, O’Doherty JP. Is avoiding an aversive outcome rewarding? Neural substrates of avoidance learning in the human brain. PLoS Biol. 2006;4(8):e233. doi: 10.1371/journal.pbio.0040233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein TA, Neumann J, Reuter M, Hennig J, von Cramon DY, Ullsperger M. Genetically determined differences in learning from errors. Science. 2007;318(5856):1642–1645. doi: 10.1126/science.1145044. [DOI] [PubMed] [Google Scholar]
- Kobayashi S, Pinto de Carvalho O, Schultz W. Adaptation of reward sensitivity in orbitofrontal neurons. J Neurosci. 2010;30(2):534–544. doi: 10.1523/JNEUROSCI.4009-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krigolson OE, Hassall CD, Handy TC. How we learn to make decisions: rapid propagation of reinforcement learning prediction errors in humans. J Cogn Neurosci. 2014;26(3):635–644. doi: 10.1162/jocn_a_00509. [DOI] [PubMed] [Google Scholar]
- Kumar P, Waiter G, Ahearn T, Milders M, Reid I, Steele JD. Abnormal temporal difference reward-learning signals in major depression. Brain. 2008;131(Pt 8):2084–2093. doi: 10.1093/brain/awn136. awn136. [DOI] [PubMed] [Google Scholar]
- Lea S. The psychology and economics of demand. Psychological Bulletin. 1978;85(3):441. [Google Scholar]
- Leathers ML, Olson CR. In monkeys making value-based decisions, LIP neurons encode cue salience and not action value. Science. 2012;338(6103):132–135. doi: 10.1126/science.1226405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy DJ, Glimcher PW. The root of all value: a neural common currency for choice. Curr Opin Neurobiol. 2012;22(6):1027–1038. doi: 10.1016/j.conb.2012.06.001S0959-4388(12)00100-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, McClure SM, King-Casas B, Montague PR. Policy adjustment in a dynamic economic game. PLoS One. 2006;1:e103. doi: 10.1371/journal.pone.0000103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, Schiller D, Schoenbaum G, Phelps EA, Daw ND. Differential roles of human striatum and amygdala in associative learning. Nat Neurosci. 2011;14(10):1250–1252. doi: 10.1038/nn.2904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Hairston J, Schrier M, Fan J. Common and distinct networks underlying reward valence and processing stages: a meta-analysis of functional neuroimaging studies. Neurosci Biobehav Rev. 2011;35(5):1219–1236. doi: 10.1016/j.neubiorev.2010.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK, Pfeuffer J. On the nature of the BOLD fMRI contrast mechanism. Magn Reson Imaging. 2004;22(10):1517–1531. doi: 10.1016/j.mri.2004.10.018. [DOI] [PubMed] [Google Scholar]
- Ludvig EA, Sutton RS, Kehoe EJ. Stimulus representation and the timing of reward-prediction errors in models of the dopamine system. Neural Comput. 2008;20(12):3034–3054. doi: 10.1162/neco.2008.11-07-654. [DOI] [PubMed] [Google Scholar]
- Maddux JM, Kerfoot EC, Chatterjee S, Holland PC. Dissociation of attention in learning and action: effects of lesions of the amygdala central nucleus, medial prefrontal cortex, and posterior parietal cortex. Behav Neurosci. 2007;121(1):63–79. doi: 10.1037/0735-7044.121.1.63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madlon-Kay S, Pesaran B, Daw ND. Action selection in multi-effector decision making. Neuroimage. 2013;70:66–79. doi: 10.1016/j.neuroimage.2012.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathys C, Daunizeau J, Friston KJ, Stephan KE. A bayesian foundation for individual learning under uncertainty. Front Hum Neurosci. 2011;5:39. doi: 10.3389/fnhum.2011.00039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDannald MA, Lucantonio F, Burke KA, Niv Y, Schoenbaum G. Ventral Striatum and Orbitofrontal Cortex Are Both Required for Model-Based, But Not Model-Free, Reinforcement Learning. The Journal of Neuroscience. 2011;31(7):2700–2705. doi: 10.1523/jneurosci.5499-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metereau E, Dreher JC. Cerebral correlates of salient prediction error for different rewards and punishments. Cereb Cortex. 2013;23(2):477–487. doi: 10.1093/cercor/bhs037. [DOI] [PubMed] [Google Scholar]
- Miller RR, Barnet RC, Grahame NJ. Assessment of the Rescorla-Wagner model. Psychol Bull. 1995;117(3):363–386. doi: 10.1037/0033-2909.117.3.363. [DOI] [PubMed] [Google Scholar]
- Morrison SE, Salzman CD. The Convergence of Information about Rewarding and Aversive Stimuli in Single Neurons. Journal of Neuroscience. 2009;29(37):11471–11483. doi: 10.1523/Jneurosci.1815-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray GK, Corlett PR, Clark L, Pessiglione M, Blackwell AD, Honey G, Fletcher PC. Substantia nigra/ventral tegmental reward prediction error disruption in psychosis. Mol Psychiatry, 13(3) 2008;239:267–276. doi: 10.1038/sj.mp.4002058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myung IJ. The Importance of Complexity in Model Selection. J Math Psychol. 2000;44(1):190–204. doi: 10.1006/jmps.1999.1283. [DOI] [PubMed] [Google Scholar]
- Niv Y, Edlund JA, Dayan P, O’Doherty JP. Neural prediction errors reveal a risk-sensitive reinforcement-learning process in the human brain. J Neurosci. 2012;32(2):551–562. doi: 10.1523/JNEUROSCI.5498-10.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noonan MP, Walton ME, Behrens TE, Sallet J, Buckley MJ, Rushworth MF. Separate value comparison and learning mechanisms in macaque medial and lateral orbitofrontal cortex. Proc Natl Acad Sci U S A. 2010;107(47):20547–20552. doi: 10.1073/pnas.1012246107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Doherty J, Dayan P, Schultz J, Deichmann R, Friston K, Dolan RJ. Dissociable roles of ventral and dorsal striatum in instrumental conditioning. Science. 2004;304(5669):452–454. doi: 10.1126/science.1094285. [DOI] [PubMed] [Google Scholar]
- O’Doherty JP, Dayan P, Friston K, Critchley H, Dolan RJ. Temporal difference models and reward-related learning in the human brain. Neuron. 2003;38(2):329–337. doi: 10.1016/s0896-6273(03)00169-7. [DOI] [PubMed] [Google Scholar]
- O’Sullivan N, Szczepanowski R, El-Deredy W, Mason L, Bentall RP. fMRI evidence of a relationship between hypomania and both increased goal-sensitivity and positive outcome-expectancy bias. Neuropsychologia. 2011;49(10):2825–2835. doi: 10.1016/j.neuropsychologia.2011.06.008. [DOI] [PubMed] [Google Scholar]
- Ongur D, Price JL. The organization of networks within the orbital and medial prefrontal cortex of rats, monkeys and humans. Cereb Cortex. 2000;10(3):206–219. doi: 10.1093/cercor/10.3.206. [DOI] [PubMed] [Google Scholar]
- Padoa-Schioppa C, Assad JA. Neurons in the orbitofrontal cortex encode economic value. Nature. 2006;441(7090):223–226. doi: 10.1038/nature04676. nature04676 [ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Padoa-Schioppa C, Assad JA. The representation of economic value in the orbitofrontal cortex is invariant for changes of menu. Nat Neurosci. 2008;11(1):95–102. doi: 10.1038/nn2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park SQ, Kahnt T, Beck A, Cohen MX, Dolan RJ, Wrase J, Heinz A. Prefrontal cortex fails to learn from reward prediction errors in alcohol dependence. J Neurosci. 2010;30(22):7749–7753. doi: 10.1523/JNEUROSCI.5587-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parkinson JA, Olmstead MC, Burns LH, Robbins TW, Everitt BJ. Dissociation in effects of lesions of the nucleus accumbens core and shell on appetitive pavlovian approach behavior and the potentiation of conditioned reinforcement and locomotor activity by D-amphetamine. J Neurosci. 1999;19(6):2401–2411. doi: 10.1523/JNEUROSCI.19-06-02401.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paxinos G, Huang X-F. Atlas of the human brain stem 1995 [Google Scholar]
- Pearce JM, Hall G. A model for Pavlovian learning: variations in the effectiveness of conditioned but not of unconditioned stimuli. Psychol Rev. 1980;87(6):532–552. [PubMed] [Google Scholar]
- Peters J, Buchel C. Neural representations of subjective reward value. Behav Brain Res. 2010;213(2):135–141. doi: 10.1016/j.bbr.2010.04.031. [DOI] [PubMed] [Google Scholar]
- Petrides M, Pandya D. Comparative architectonic analysis of the human and the macaque frontal cortex. In: Boller F, Grafman J, editors. Handbook of Neuropsychology. Vol. 9. Amsterdam: Elsevier; 1994. pp. 17–58. [Google Scholar]
- Platt ML, Glimcher PW. Neural correlates of decision variables in parietal cortex. Nature. 1999;400(6741):233–238. doi: 10.1038/22268. [DOI] [PubMed] [Google Scholar]
- Rescorla RA, Wagner AR. A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement. In: Black AH, Prokasy WF, editors. Classical Conditioning II: Current Research and Theory. New York: Appleton Century Crofts; 1972. pp. 64–99. [Google Scholar]
- Robinson OJ, Overstreet C, Charney DR, Vytal K, Grillon C. Stress increases aversive prediction error signal in the ventral striatum. Proc Natl Acad Sci U S A. 2013;110(10):4129–4133. doi: 10.1073/pnas.1213923110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez PF. Stimulus-outcome learnability differentially activates anterior cingulate and hippocampus at feedback processing. Learn Mem. 2009;16(5):324–331. doi: 10.1101/lm.1191609. [DOI] [PubMed] [Google Scholar]
- Rodriguez PF, Aron AR, Poldrack RA. Ventral-striatal/nucleus-accumbens sensitivity to prediction errors during classification learning. Hum Brain Mapp. 2006;27(4):306–313. doi: 10.1002/hbm.20186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roesch MR, Calu DJ, Esber GR, Schoenbaum G. All that glitters … dissociating attention and outcome expectancy from prediction errors signals. J Neurophysiol. 2010;104(2):587–595. doi: 10.1152/jn.00173.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roesch MR, Calu DJ, Schoenbaum G. Dopamine neurons encode the better option in rats deciding between differently delayed or sized rewards. Nat Neurosci. 2007;10(12):1615–1624. doi: 10.1038/nn2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roesch MR, Olson CR. Neuronal Activity Related to Reward Value and Motivation in Primate Frontal Cortex. Science. 2004;304(5668):307–310. doi: 10.1126/science.1093223. [DOI] [PubMed] [Google Scholar]
- Roesch MR, Olson CR. Neuronal activity in primate orbitofrontal cortex reflects the value of time. J Neurophysiol. 2005;94(4):2457–2471. doi: 10.1152/jn.00373.2005. [DOI] [PubMed] [Google Scholar]
- Rohe T, Weber B, Fliessbach K. Dissociation of BOLD responses to reward prediction errors and reward receipt by a model comparison. Eur J Neurosci. 2012;36(3):2376–2382. doi: 10.1111/j.1460-9568.2012.08125.x. [DOI] [PubMed] [Google Scholar]
- Rottschy C, Langner R, Dogan I, Reetz K, Laird AR, Schulz JB, Eickhoff SB. Modelling neural correlates of working memory: a coordinate-based meta-analysis. Neuroimage. 2012;60(1):830–846. doi: 10.1016/j.neuroimage.2011.11.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudebeck PH, Behrens TE, Kennerley SW, Baxter MG, Buckley MJ, Walton ME, Rushworth MFS. Frontal Cortex Subregions Play Distinct Roles in Choices between Actions and Stimuli. The Journal of Neuroscience. 2008;28(51):13775–13785. doi: 10.1523/jneurosci.3541-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudebeck PH, Buckley MJ, Walton ME, Rushworth MF. A role for the macaque anterior cingulate gyrus in social valuation. Science. 2006;313(5791):1310–1312. doi: 10.1126/science.1128197. [DOI] [PubMed] [Google Scholar]
- Rudebeck PH, Murray EA. Dissociable Effects of Subtotal Lesions within the Macaque Orbital Prefrontal Cortex on Reward-Guided Behavior. Journal of Neuroscience. 2011;31(29):10569–10578. doi: 10.1523/Jneurosci.0091-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutledge RB, Dean M, Caplin A, Glimcher PW. Testing the reward prediction error hypothesis with an axiomatic model. J Neurosci. 2010;30(40):13525–13536. doi: 10.1523/JNEUROSCI.1747-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sacchet MD, Knutson B. Spatial smoothing systematically biases the localization of reward-related brain activity. Neuroimage. 2013;66(0):270–277. doi: 10.1016/j.neuroimage.2012.10.056. http://dx.doi.org/10.1016/j.neuroimage.2012.10.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samejima K, Ueda Y, Doya K, Kimura M. Representation of action-specific reward values in the striatum. Science. 2005;310(5752):1337–1340. doi: 10.1126/science.1115270. 310/5752/1337. [DOI] [PubMed] [Google Scholar]
- Schlagenhauf F, Rapp MA, Huys QJ, Beck A, Wustenberg T, Deserno L, Heinz A. Ventral striatal prediction error signaling is associated with dopamine synthesis capacity and fluid intelligence. Hum Brain Mapp. 2012 doi: 10.1002/hbm.22000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoenbaum G, Takahashi Y, Liu TL, McDannald MA. Does the orbitofrontal cortex signal value? Critical Contributions of the Orbitofrontal Cortex to Behavior. 2011;1239:87–99. doi: 10.1111/j.1749-6632.2011.06210.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schonberg T, Daw ND, Joel D, O’Doherty JP. Reinforcement learning signals in the human striatum distinguish learners from nonlearners during reward-based decision making. J Neurosci. 2007;27(47):12860–12867. doi: 10.1523/JNEUROSCI.2496-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schonberg T, O’Doherty JP, Joel D, Inzelberg R, Segev Y, Daw ND. Selective impairment of prediction error signaling in human dorsolateral but not ventral striatum in Parkinson’s disease patients: evidence from a model-based fMRI study. Neuroimage. 2010;49(1):772–781. doi: 10.1016/j.neuroimage.2009.08.011. [DOI] [PubMed] [Google Scholar]
- Schultz W, Dayan P, Montague PR. A Neural Substrate of Prediction and Reward. Science. 1997;275(5306):1593–1599. doi: 10.1126/science.275.5306.1593. [DOI] [PubMed] [Google Scholar]
- Seger CA, Peterson EJ, Cincotta CM, Lopez-Paniagua D, Anderson CW. Dissociating the contributions of independent corticostriatal systems to visual categorization learning through the use of reinforcement learning modeling and Granger causality modeling. Neuroimage. 2010;50(2):644–656. doi: 10.1016/j.neuroimage.2009.11.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sescousse G, Caldu X, Segura B, Dreher JC. Processing of primary and secondary rewards: a quantitative meta-analysis and review of human functional neuroimaging studies. Neurosci Biobehav Rev. 2013;37(4):681–696. doi: 10.1016/j.neubiorev.2013.02.002. [DOI] [PubMed] [Google Scholar]
- Seymour B, O’Doherty JP, Koltzenburg M, Wiech K, Frackowiak R, Friston K, Dolan R. Opponent appetitive-aversive neural processes underlie predictive learning of pain relief. Nat Neurosci. 2005;8(9):1234–1240. doi: 10.1038/nn1527. [DOI] [PubMed] [Google Scholar]
- Simmons JM, Ravel S, Shidara M, Richmond BJ. A comparison of reward-contingent neuronal activity in monkey orbitofrontal cortex and ventral striatum: guiding actions toward rewards. Ann N Y Acad Sci. 2007;1121:376–394. doi: 10.1196/annals.1401.028. [DOI] [PubMed] [Google Scholar]
- Strait CE, Blanchard TC, Hayden BY. Reward Value Comparison via Mutual Inhibition in Ventromedial Prefrontal Cortex. Neuron. 2014;82(6):1357–1366. doi: 10.1016/j.neuron.2014.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton RS, Barto AG. Reinforcement learning: An introduction. Cambridge Univ Press; 1998. [Google Scholar]
- Takahashi YK, Roesch MR, Stalnaker TA, Haney RZ, Calu DJ, Taylor AR, Schoenbaum G. The orbitofrontal cortex and ventral tegmental area are necessary for learning from unexpected outcomes. Neuron. 2009;62(2):269–280. doi: 10.1016/j.neuron.2009.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takemura H, Samejima K, Vogels R, Sakagami M, Okuda J. Stimulus-dependent adjustment of reward prediction error in the midbrain. PLoS One. 2011;6(12):e28337. doi: 10.1371/journal.pone.0028337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka SC, Samejima K, Okada G, Ueda K, Okamoto Y, Yamawaki S, Doya K. Brain mechanism of reward prediction under predictable and unpredictable environmental dynamics. Neural Netw. 2006;19(8):1233–1241. doi: 10.1016/j.neunet.2006.05.039. [DOI] [PubMed] [Google Scholar]
- Tobler PN, Dickinson A, Schultz W. Coding of predicted reward omission by dopamine neurons in a conditioned inhibition paradigm. J Neurosci. 2003;23(32):10402–10410. doi: 10.1523/JNEUROSCI.23-32-10402.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tobler PN, O’Doherty JP, Dolan RJ, Schultz W. Human neural learning depends on reward prediction errors in the blocking paradigm. J Neurophysiol. 2006;95(1):301–310. doi: 10.1152/jn.00762.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tremblay L, Schultz W. Relative reward preference in primate orbitofrontal cortex. Nature. 1999;398(6729):704–708. doi: 10.1038/19525. [DOI] [PubMed] [Google Scholar]
- Turkeltaub PE, Eden GF, Jones KM, Zeffiro TA. Meta-analysis of the functional neuroanatomy of single-word reading: method and validation. Neuroimage. 2002;16(3 Pt 1):765–780. doi: 10.1006/nimg.2002.1131. doi:S1053811902911316. [DOI] [PubMed] [Google Scholar]
- Turkeltaub PE, Eickhoff SB, Laird AR, Fox M, Wiener M, Fox P. Minimizing within-experiment and within-group effects in Activation Likelihood Estimation meta-analyses. Hum Brain Mapp. 2012;33(1):1–13. doi: 10.1002/hbm.21186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentin VV, O’Doherty JP. Overlapping prediction errors in dorsal striatum during instrumental learning with juice and money reward in the human brain. J Neurophysiol. 2009;102(6):3384–3391. doi: 10.1152/jn.91195.2008. [DOI] [PubMed] [Google Scholar]
- van den Bos W, Cohen MX, Kahnt T, Crone EA. Striatum-medial prefrontal cortex connectivity predicts developmental changes in reinforcement learning. Cereb Cortex. 2012;22(6):1247–1255. doi: 10.1093/cercor/bhr198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voorn P, Vanderschuren LJ, Groenewegen HJ, Robbins TW, Pennartz CM. Putting a spin on the dorsal-ventral divide of the striatum. Trends Neurosci. 2004;27(8):468–474. doi: 10.1016/j.tins.2004.06.006. [DOI] [PubMed] [Google Scholar]
- Waelti P, Dickinson A, Schultz W. Dopamine responses comply with basic assumptions of formal learning theory. Nature. 2001;412(6842):43–48. doi: 10.1038/35083500. [DOI] [PubMed] [Google Scholar]
- Wallis JD. Cross-species studies of orbitofrontal cortex and value-based decision-making. Nat Neurosci. 2012;15(1):13–19. doi: 10.1038/nn.2956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallis JD, Miller EK. Neuronal activity in primate dorsolateral and orbital prefrontal cortex during performance of a reward preference task. European Journal of Neuroscience. 2003;18(7):2069–2081. doi: 10.1046/j.1460-9568.2003.02922.x. [DOI] [PubMed] [Google Scholar]
- Watanabe N, Sakagami M, Haruno M. Reward prediction error signal enhanced by striatum-amygdala interaction explains the acceleration of probabilistic reward learning by emotion. J Neurosci. 2013;33(10):4487–4493. doi: 10.1523/JNEUROSCI.3400-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wittmann BC, Daw ND, Seymour B, Dolan RJ. Striatal activity underlies novelty-based choice in humans. Neuron. 2008;58(6):967–973. doi: 10.1016/j.neuron.2008.04.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wunderlich K, Rangel A, O’Doherty JP. Economic choices can be made using only stimulus values. Proc Natl Acad Sci U S A. 2010;107(34):15005–15010. doi: 10.1073/pnas.1002258107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeung N, Holroyd CB, Cohen JD. ERP correlates of feedback and reward processing in the presence and absence of response choice. Cereb Cortex. 2005;15(5):535–544. doi: 10.1093/cercor/bhh153. [DOI] [PubMed] [Google Scholar]
- Yin HH, Ostlund SB, Knowlton BJ, Balleine BW. The role of the dorsomedial striatum in instrumental conditioning. Eur J Neurosci. 2005;22(2):513–523. doi: 10.1111/j.1460-9568.2005.04218.x. [DOI] [PubMed] [Google Scholar]
- Yue Y, Loh JM, Lindquist MA. Adaptive spatial smoothing of fMRI images. Statistics and Its Interface. 2010;3(1):3–13. [Google Scholar]