A fast heterogeneous algorithm for light fluence rate for prostate photodynamic therapy

Abstract

To accurately calculate light fluence rate distribution in prostate photodynamic therapy (PDT), optical heterogeneity has to be taken into account. Previous study has shown that a kernel based on analytic solution of the diffusion equation can perform the calculation with accuracy comparable to Finite-element method. An assumption is made that light fluence rate detected at a point in the medium is affected primarily by the optical properties of points (or elements) on the line between the source and the point. The exponential decay term of the light fluence rate is expressed as an integral of effective attenuation coefficient of each point along the line. The kernel method is first developed for a point source and then extended for a linear source. A linear source is considered being composed of multiple point sources and light fluence rate is summation of the fluence rates generated by the point sources. In this study, we have implemented a fast ray-trace algorithm to substantially speed up the calculation. The kernel calculation is compared with FEM calculation and is examined with light fluence rate measurements. The examination with clinical measurement data shows that calculated fluence rates present similar features in distribution as the measurement, with errors of 30%–70% for the peak fluence rates. We concluded that our heterogeneous algorithm is potentially valuable for light fluence rate optimization during interstitial PDT.

1. INTRODUCTION

Accurate dosimetry calculation in photodynamic therapy (PDT) is imperative in quantifying PDT treatment efficacy. In PDT, photosensitizer is administered to the site of the tumor. Illumination of the photosensitizer at a specific wavelength generates the highly toxic singlet oxygen which causes localized cell death and tissue necrosis. Efficacy of PDT therefore depends on the concentration of singlet oxygen, which in turn is determined by light fluence, photosensitizer concentration, and tissue oxygen level. Direct measurement of singlet oxygen concentration is very difficult in vivo with large variability. As a result, to establish the correlation between the macroscopic treatment efficacy of PDT and the microscopic singlet oxygen concentration, one would need to rely on dosimetry calculation based on the in vivo measurements of light fluence, photosensitizer concentration, and tissue oxygen level. Accurate in vivo PDT dosimetry is imperative in understanding the mechanism of singlet oxygen’s toxic effect and how this toxicity translates to tissue necrosis observed with PDT. Ultimately the goal of PDT dosimetry is to enable better PDT treatment planning based on optimized singlet oxygen distribution at the site of the tumor and as a result improve overall PDT treatment efficacy.

In our previous studies, we have used the photosensitizer motexafin lutetium (MLu) for interstitial PDT of the prostate in patients at the University of Pennsylvania ^1–6. Interstitial light delivery, where optical fibers are placed directly into the organs, is chosen because it has been shown to be an efficient illumination scheme for PDT in treating large bulky tumors in solid organs such as prostate ^7–12. A laser at 732 nm is used to excite MLu. Figure 1(a) shows the experimental setup used in the prostate PDT treatment. Cylindrical diffusing fibers (CDFs) with active lengths between 1 and 5 cm are used as light sources. Transparent catheters are inserted in parallel into the prostate with the guidance of a transrectal ultrasound (TRUS) unit through a positioning template. The CDFs were placed in the catheters, with sufficient lengths to cover the prostate geometry. During the treatment, light fluence rates were measured at a few selected locations in the patients’ prostates.

Figure 1.

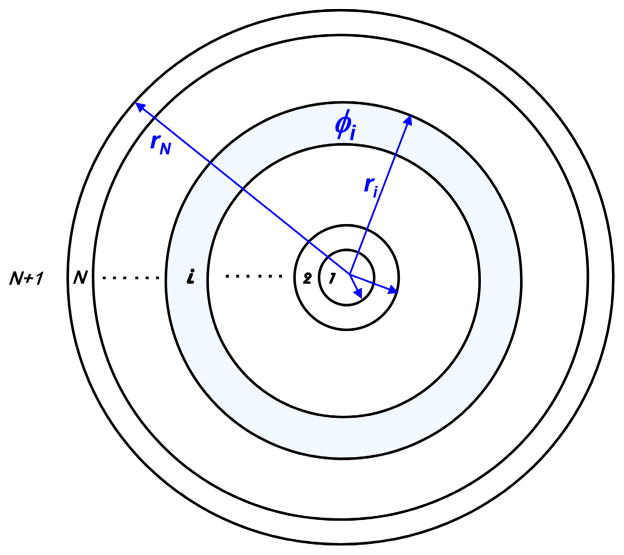
Heterogeneous kernel model. The heterogeneous optical property of a prostate is modeled with spherically symmetric shells with the point source positioned at the center.

This in vivo measurement is limited in that it only measures light fluence rates at limited positions along a set of linear arrays rather than in a full three-dimensional (3D) volume. The ability to accurately calculate 3D light fluence rates is therefore desired as it provides a better prediction of the PDT treatment efficacy. Under the assumptions that 1) light fluence rate detected at a point in the prostate is affected primarily by the optical properties but not the photosensitizer concentrations, and 2) the 3D distribution of the optical properties in a prostate gland is known, e.g. one can determine the optical properties using diffuse optical tomography, an accurate algorithm for 3D light fluence rate calculation can be obtained. In addition, it is desired that the algorithm is fast enough to allow for real-time inverse planning to optimize light fluence rate distribution during treatment. Specifically, we have proposed both a homogeneous ² and a heterogeneous ¹³ kernel model to calculate the light fluence rates in prostate PDT. Calculations obtained from the heterogeneous model have been shown to be in close agreement with in vivo patient measurements ¹³. Indeed, the human study has shown that optical properties are heterogeneous in a prostate, which indicates that to accurately predict light fluence distribution in a prostate, optical heterogeneity needs to be taken into account ³. Note that the finite-element method (FEM) can also deal with heterogeneity and irregular geometries, potentially with greater accuracy. However, FEM calculation requires a lot of computational power and is not fast enough for real-time treatment planning for prostate PDT. In the study, we refined the heterogeneous kernel model developed earlier ¹³, and improved its calculation efficiency when dealing with optical heterogeneity. The calculation accuracy was compared with a FEM model, a phantom experiment and in vivo measurements in patients.

2. METHODS

2.1 Heterogeneous kernel model

The propagation of near-infrared light in tissues can typically be approximated by the diffusion equation ¹⁴,

$$-\nabla ·D\nabla \varphi +{\mu }_a\varphi =S_o$$ (1)

where ϕ is the light fluence rate, $D=1/3{\mu }_s^{\prime }$ is the diffusion coefficient, S_o is the isotropic source distribution and ${\mu }_s^{\prime }$ is the reduced scattering coefficient. In a homogeneous medium, the solution to Eq. (1) can be obtained analytically for a point source ^2,15:

$$\varphi =\frac{3S{\mu }_s^{\prime }}{4\pi r}{\mathrm{e}}^{-{\mu }_{\mathit{eff}}},$$ (2)

where S is the source power, r is the distance between the source and detector, and ${\mu }_{\mathit{eff}}=\sqrt{3{\mu }_a{\mu }_s^{\prime }}$. Extension of this analytic solution to a heterogeneous medium can be achieved for a point source positioned at the center of a spherically symmetric heterogeneous medium. As seen in Fig. 1, the point source is placed at r = 0, surrounded by N layers of spherically symmetric shells, each having different optical properties. Field distribution in the i^th layer is given by

$${\varphi }_i=\frac{C{\mu }_{s,i}^{\prime }}{4\pi r}\left(p_i{e}^{-{\mu }_{\mathit{eff},i}\left(r-r_{i-1}\right)}+q_i{e}^{{\mu }_{\mathit{eff},i}\left(r-r_{i-1}\right)}\right),r_{i-1}<r<r_i,i=1,2,\dots N.$$ (3)

where C as in the case of Eq. (2) is a constant proportional to the source power S. Medium surrounding the N^th shell is denoted the (N + 1)^th layer and its field distribution is

$${\varphi }_{N+1}=\frac{C{\mu }_{s,N+1}^{\prime }}{4\pi r}{p}_{N+1}{e}^{-{\mu }_{\mathit{eff},N+1}\left(r-r_N\right)},r_N<r<\infty .$$ (4)

Boundary conditions between each pair of shells dictate the continuity such that at r = r_i

$${\varphi }_i={\varphi }_{i+1}$$ (5)

$$D_i\frac{\partial {\varphi }_i}{\partial r}=D_{i+1}\frac{\partial {\varphi }_{i+1}}{\partial r},$$ (6)

and the iterative relationship between adjacent fields is given by

$$\left[\begin{array}{c}{p}_i\\ q_i\end{array}\right]=\frac{1}{2}\frac{{\mu }_{\mathit{eff},i+1}}{{\mu }_{\mathit{eff},i}}\left[\begin{array}{rr}{e}^{{\mu }_{\mathit{eff},i}\left(r_i-r_{i-1}\right)}\left(1+\frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}\right)& -e^{{\mu }_{\mathit{eff},i}\left(r_i-r_{i-1}\right)}\left(1-\frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}\right)\\ -e^{-{\mu }_{\mathit{eff},i}\left(r_i-r_{i-1}\right)}\left(1-\frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}\right)& e^{-{\mu }_{\mathit{eff},i}\left(r_i-r_{i-1}\right)}\left(1+\frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}\right)\end{array}\right]\left[\begin{array}{l}{p}_{i+1}\hfill \\ q_{i+1}\hfill \end{array}\right]$$ (7)

To determine the value of C, we note that total power emitted by the point source S equals to the summation of powers deposited in each shell, i.e.

$$\sum _{i=1}^{N+1}{\int }_i{\mu }_{a,i}{\varphi }_i{dv}_i=S.$$ (8)

C is therefore given by

$$C=S{\left(\sum _{i=1}^{N+1}{A}_i\right)}^{-1}$$ (9)

where

$$A_i=\frac{1}{3}\left\{p_i\left[\left(1+r_{i-1}{\mu }_{\mathit{eff},i}\right)-\left(1+r_i{\mu }_{\mathit{eff},i}\right)e^{-{\mu }_{\mathit{eff},i}\left(r_i-r_{i-1}\right)}\right]+q_i\left[\left(1+r_{i-1}{\mu }_{\mathit{eff},i}\right)-\left(1-r_i{\mu }_{\mathit{eff},i}\right)e^{{\mu }_{\mathit{eff},i}\left(r_i-r_{i-1}\right)}\right]\right\}$$ (10)

Note that r_N+1 = ∞ in this case. Assuming that $\left[\begin{array}{c}{p}_{N+1}\\ q_{N+1}\end{array}\right]=\left[\begin{array}{c}1\\ 0\end{array}\right]$, we can now use Eqs. (7) and (9) to determine the field distribution ϕ_i within each shell. An equivalent model derived earlier has been shown to be in good agreement with results obtained from finite element method (FEM) and experimental data ¹³. This current model is formulated in the matrix format in order to improve computational efficiency.

2.2 Approximation to the heterogeneous kernel for improved computational efficiency

Examining Eq. (7) we found that when the optical properties of adjacent layers are identical, i.e. when D_i = D_i+1 and μ_eff,i = μ_eff,i+1, the off-diagonal terms are exactly zero. Indeed, the off-diagonal terms of the transmission matrix tend to zero as the optical properties across adjacent shells become comparable. Therefore, given a stratified medium where variations of its optical constants from one layer to another are small, lower order approximation to Eq. (7) can be employed to further improve the computational efficiency during PDT dose calculation. Here we examine one such approximation and determine its performance in both efficiency and accuracy.

Denote

$${\stackrel{\sim }{p}}_i=p_i{e}^{-{\mu }_{\mathit{eff},i}\left(r_i-r_{i-1}\right)},{\stackrel{\sim }{q}}_i=q_i{e}^{{\mu }_{\mathit{eff},i}\left(r_i-r_{i-1}\right)}$$ (11)

Eq. (7) can now be rewritten as

$$\begin{array}{l}\left[\begin{array}{c}{\stackrel{\sim }{p}}_i\\ {\stackrel{\sim }{q}}_i\end{array}\right]=\frac{1}{2}\frac{{\mu }_{\mathit{eff},i+1}}{{\mu }_{\mathit{eff},i}}\left[\begin{array}{cc}\frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}+1& \frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}-1\\ \frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}-1& \frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}+1\end{array}\right]\left[\begin{array}{cc}{e}^{{\mu }_{\mathit{eff},i+1}\left(r_{i+1}-r_i\right)}& 0\\ 0& e^{-{\mu }_{\mathit{eff},i+1}\left(r_{i+1}-r_i\right)}\end{array}\right]\left[\begin{array}{c}{\stackrel{\sim }{p}}_{i+1}\\ {\stackrel{\sim }{q}}_{i+1}\end{array}\right]\\ =\frac{1}{2}\frac{{\mu }_{\mathit{eff},i+1}}{{\mu }_{\mathit{eff},i}}\left[\begin{array}{ll}\left(\frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}+1\right)e^{{\mu }_{\mathit{eff},i+1}\left(r_{i+1}-r_i\right)}\hfill & \left(\frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}-1\right)e^{-{\mu }_{\mathit{eff},i+1}\left(r_{i+1}-r_i\right)}\hfill \\ \left(\frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}-1\right)e^{{\mu }_{\mathit{eff},i+1}\left(r_{i+1}-r_i\right)}\hfill & \left(\frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}+1\right)e^{-{\mu }_{\mathit{eff},i+1}\left(r_{i+1}-r_i\right)}\hfill \end{array}\right]\left[\begin{array}{c}{\stackrel{\sim }{p}}_{i+1}\\ {\stackrel{\sim }{q}}_{i+1}\end{array}\right]\end{array}$$ (12)

Separating the diagonal and off-diagonal terms of the transition matrix and denote,

$$a_i={\mu }_{\mathit{eff},i+1}\left(r_{i+1}-r_i\right)$$ (13)

$$b_i=\frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}+1$$ (14)

$$c_i=\frac{D_i{\mu }_{\mathit{eff},i}}{D_{i+1}{\mu }_{\mathit{eff},i+1}}-1$$ (15)

from Eq. (12) we have

$$\left[\begin{array}{c}{\stackrel{\sim }{p}}_i\\ {\stackrel{\sim }{q}}_i\end{array}\right]=\frac{1}{2}\frac{{\mu }_{\mathit{eff},i+1}}{{\mu }_{\mathit{eff},i}}\left\{\left[\begin{array}{cc}{b}_i{e}^{a_i}& 0\\ 0& b_i{e}^{-a_i}\end{array}\right]+\left[\begin{array}{cc}0& c_i{e}^{-a_i}\\ c_i{e}^{a_i}& 0\end{array}\right]\right\}\left[\begin{array}{c}{\stackrel{\sim }{p}}_{i+1}\\ {\stackrel{\sim }{q}}_{i+1}\end{array}\right]$$ (16)

where the diagonal matrix $\left[\begin{array}{cc}{b}_i{e}^{a_i}& 0\\ 0& b_i{e}^{-a_i}\end{array}\right]$ is designated as the “transmission” term and the off-diagonal matrix $\left[\begin{array}{cc}0& c_i{e}^{-a_i}\\ c_i{e}^{a_i}& 0\end{array}\right]$ “reflection” term of the transition matrix. Again the off-diagonal matrix tends to zero as the difference in optical property diminishes between the i^th and (i + 1)^th layers. As a result, we can now isolate the effects of transmission and reflection terms, and examine the transition matrix for a layered medium with slowly varying optical properties. Again assuming $\left[\begin{array}{c}{\stackrel{\sim }{p}}_{N+1}\\ {\stackrel{\sim }{q}}_{N+1}\end{array}\right]=\left[\begin{array}{c}1\\ 0\end{array}\right]$, for the zeroth order contribution from reflection terms are ignored and we have,

$${\stackrel{\sim }{p}}_i^{(0)}=C_i\prod _{k=i}^N{b}_k{e}^{a_k}=C_i{e}^{\sum _{k=i}^N{a}_k}\prod _{k=i}^N{b}_k$$ (17)

$${\stackrel{\sim }{q}}_i^{(0)}=C_i\prod _{k=i}^N{b}_k{e}^{-a_k}=C_i{e}^{-\sum _{k=i}^N{a}_k}\prod _{k=i}^N{b}_k$$ (18)

where

$$C_i=\prod _{k=i}^N\frac{1}{2}\frac{{\mu }_{\mathit{eff},k+1}}{{\mu }_{\mathit{eff},k}}.$$ (19)

First order approximation takes into account one of the reflections within the layers where

$$\mathrm{\Delta }{\stackrel{\sim }{p}}_i^{(1)}=0$$ (20)

$$\mathrm{\Delta }{\stackrel{\sim }{q}}_i^{(1)}=C_i\sum _{l=i}^N\left(b_i\cdots b_{l-1}{c}_l{b}_{l+1}\cdots b_N·e^{-\left(a_i+\cdots +a_{l-1}\right)}{e}^{-a_l}{e}^{\left(a_{l+1}+\cdots +a_N\right)}\right).$$ (21)

Similarly, second order terms are given by

$$\mathrm{\Delta }{\stackrel{\sim }{p}}_i^{(2)}=C_i\sum _{l=i}^N\sum _{l<m\le N}\left(b_i\cdots b_{l-1}{c}_l{b}_{l+1}\cdots b_{m-1}{c}_m{b}_{m+1}\cdots b_N·e^{\left(a_i+\cdots +a_{l-1}\right)}{e}^{-a_l}{e}^{-\left(a_{l+1}+\cdots a_{m-1}\right)}{e}^{a_m}{e}^{\left(a_{m+1}+\cdots +a_N\right)}\right).$$ (22)

$$\mathrm{\Delta }{\stackrel{\sim }{q}}_i^{(2)}=0$$ (23)

where the double summation consists of $\left(\begin{array}{c}N-i+1\\ 2\end{array}\right)=\frac{\left(N-i+1\right)\left(N-i\right)}{2}$ terms. Higher order perturbations can also be obtained following this procedure and the overall field quantity can therefore be approximated by

$${\stackrel{\sim }{p}}_i={\stackrel{\sim }{p}}_i^{(0)}+\mathrm{\Delta }{\stackrel{\sim }{p}}_i^{(2)}+\mathrm{\Delta }{\stackrel{\sim }{p}}_i^{(4)}+\cdots$$ (24)

$${\stackrel{\sim }{q}}_i={\stackrel{\sim }{q}}_i^{(0)}+\mathrm{\Delta }{\stackrel{\sim }{q}}_i^{(1)}+\mathrm{\Delta }{\stackrel{\sim }{q}}_i^{(3)}+\cdots$$ (25)

The exact solution of the heterogeneous kernel Eq. (7), i.e. the field distribution within each shell, can now be approximated by Eqs. (11), (17) and (18) for improved computational efficiency. The coefficient C associated with the power of the point source can still be determined by Eqs. (9) and (10) although it is now an approximation.

3. SIMULATION RESULTS

Validity of the kernel method is verified against the finite element method (FEM) using a spherically symmetric model. Following this verification, patient geometry and measurement data are used in the calculation and the difference between the kernel and the FEM methods is examined.

3.1 Spherically symmetric model

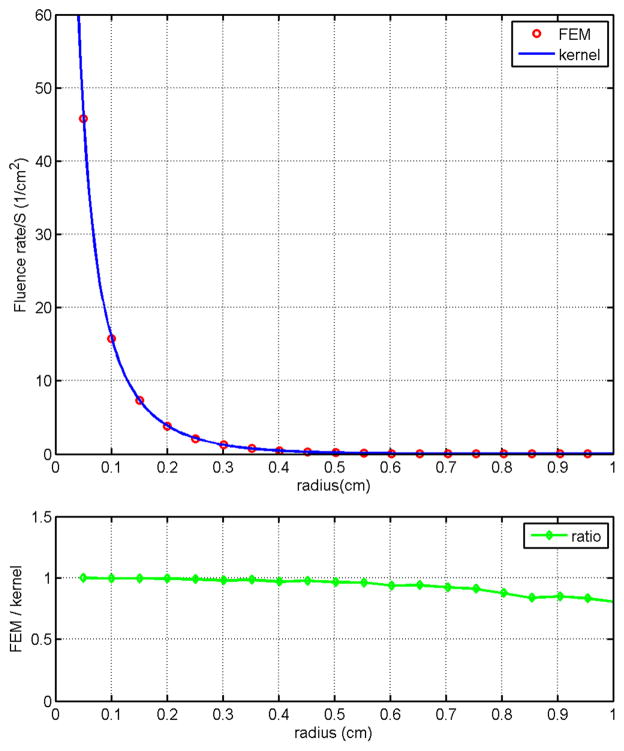
The spherically symmetric geometry used for this simulation has four layers. A matched boundary condition is assumed for the outermost layer. The absorption coefficients for the layers are μ_a = 1.3 cm⁻¹, 1.2 cm⁻¹, 0.8 cm⁻¹, and 0.3 cm⁻¹, respectively, from the center of the sphere toward the outermost layer. The reduced scattering coefficients μ_s′ are 14 cm⁻¹ for all layers. The radii for the layers are 0.2 cm, 0.6 cm, 0.9 cm, and 5.0 cm, respectively. Results obtained using the kernel method and the FEM are shown in Fig. 2(a) for comparison. Agreement between these two methods is observed clearly. The ratio of the fluence rate obtained using the kernel method to that of the FEM is shown in Fig. 2(b) and again it is clearly observed that these two methods are in good agreement. The discrepancy in regions close to the point source is expected due to the limitation of the diffusion equation. Computation time for the kernel method on a Pentium 3.4 GHz PC is less than 1 sec while the time required for the FEM is about 110 sec. This significant improvement in computational efficiency makes the heterogeneous kernel model an ideal candidate for the development of real-time PDT dosimetry.

Figure 2.

Spherically symmetric geometry. Both the heterogeneous kernel model and FEM are used to solved the diffusion equation in a spherically symmetric geometry. Optical properties resemble that of a prostate is used with the point source positioned at the center of the sphere. Agreement between these two methods is clearly observed as the ratio of the fluence rate obtained using these two methods being approximately 1.

3.2 Comparison with patient measurement data

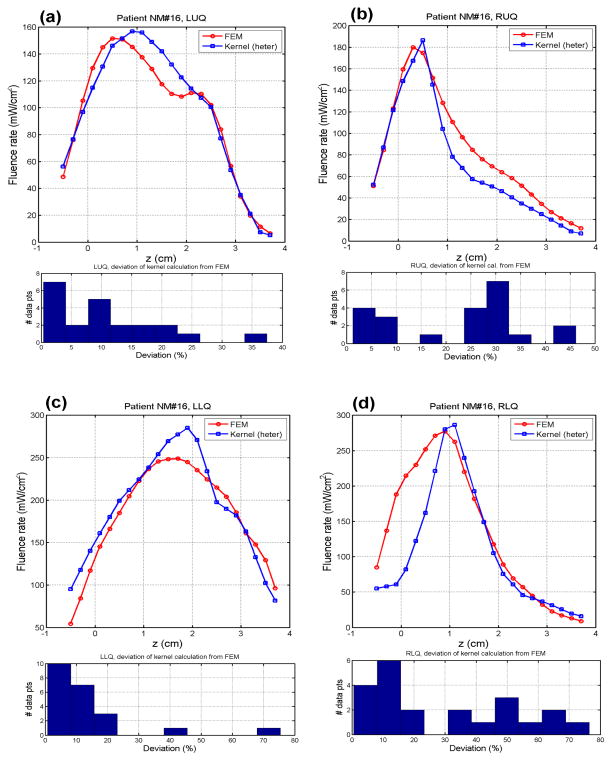
Following the successful validation shown above, we applied this heterogeneous kernel model to a patient geometry and compare the results obtained used FEM. Figure 3 shows the fluence rate calculation using these two methods. Reasonable agreement is attained between the results obtained from the heterogeneous kernel and the FEM. Agreement between the kernel method and FEM can be seen clearly in all quadrants, demonstrating the capability of this heterogeneous kernel model.

Figure 3.

Calculation using patient geometry. Actual patient geometry and optical properties are used to calculate the spatial fluence rate distribution in a patient geometry. Both heterogeneous kernel model and FEM are used for comparison. The computation time for the kernel model is about 16 sec while that for the FEM is about 5 minutes. Results in the fluence rate distribution are in good agreement between these two methods.

The time required for the heterogeneous kernel to calculate the fluence rate is about 16 sec while that for FEM is about 5 minutes. The kernel method provides conspicuous computational advantage over FEM and at the same time maintains the same level of accuracy. Study is therefore currently underway to further improve the computational efficiency and quantify the accuracy of the proposed kernel algorithm for real-time prostate PDT dosimetry.