Maximizing overall liking results in a superior product to minimizing deviations from ideal ratings: an optimization case study with coffee-flavored milk

Abstract

In just-about-right (JAR) scaling and ideal scaling, attribute delta (i.e., “Too Little” or “Too Much”) reflects a subject’s dissatisfaction level for an attribute relative to their hypothetical ideal. Dissatisfaction (attribute delta) is a different construct from consumer acceptability, operationalized as liking. Therefore, we hypothesized minimizing dissatisfaction and maximizing liking would yield different optimal formulations. The objective of this research was to compare product optimization strategies, i.e. maximizing liking vis-à-vis minimizing dissatisfaction.

Coffee-flavored dairy beverages (n = 20) were formulated using a fractional mixture design that constrained the proportions of coffee extract, milk, sucrose, and water. Participants (n = 388) were randomly assigned to one of three research conditions, where they evaluated 4 of the 20 samples using an incomplete block design. Samples were rated for overall liking and for intensity of the attributes sweetness, milk flavor, thickness and coffee flavor. Where appropriate, measures of overall product quality (Ideal_Delta and JAR_Delta) were calculated as the sum of the absolute values of the four attribute deltas. Optimal formulations were estimated by: a) maximizing liking; b) minimizing Ideal_Delta; or c) minimizing JAR_Delta. A validation study was conducted to evaluate product optimization models.

Participants indicated a preference for a coffee-flavored dairy beverage with more coffee extract and less milk and sucrose in the dissatisfaction model compared to the formula obtained by maximizing liking. That is, when liking was optimized, participants generally liked a weaker, milkier and sweeter coffee-flavored dairy beverage. Predicted liking scores were validated in a subsequent experiment, and the optimal product formulated to maximize liking was significantly preferred to that formulated to minimize dissatisfaction by a paired preference test. These findings are consistent with the view that JAR and ideal scaling methods both suffer from attitudinal biases that are not present when liking is assessed. That is, consumers sincerely believe they want ‘dark, rich, hearty’ coffee when they do not. This paper also demonstrates the utility and efficiency of a lean experimental approach.

1. Introduction

Cold coffee flavored beverages continue to grow in popularity; between 2009 and Q1 2013, the share of cold-served coffee beverages of all coffee on food service menus in the US increased from 19% to 24% (Mintel, 2013s). Notably, millenials are heavy consumers of these beverages compared to boomers: as 38% of those 18 to 24 drink iced coffee versus 11% of individuals aged 55 to 64 (Mintel, 2013). These beverages can be formulated with either water or milk as base (e.g, Petit & Sieffermann, 2007). For most Americans, consumption of dairy products falls well below recommendations in The Dietary Guidelines for Americans (Hayden, Dong, & Carlson, 2013). This is consistent with data showing fluid milk consumption among children and adolescents in the United States has been declining since 1977–1978 (Hayden et al., 2013; Sebastian, Goldman, Enns, & LaComb, 2010). As flavored milks are very popular in both children and adults (Kim, Lopetcharat, & Drake, 2013), the introduction of new flavored milks may help individuals reach recommended intake of nutrients like calcium and vitamin D (Kim et al., 2013; Nicklas, O'Neil, & Fulgoni, 2013).

Coffee flavor can be a positive factor for consumer acceptance of a coffee beverage (Li, Hayes, & Ziegler, 2014a). However, increasing coffee flavor by adding more coffee extract also increases bitterness, and excessive bitterness typically reduces consumer acceptance (Harwood, Ziegler, & Hayes, 2012; Hayes, Sullivan & Duffy, 2010; Lanier, Hayes & Duffy, 2005; Moskowitz & Gofman, 2007). The amount of milk in a coffee beverage influences not only the appearance and the amount of milk flavor, but other attributes via physicochemical interactions. For example, the casein found in milk reduces the bitterness of coffee (Parat-Wilhelms et al., 2005). Therefore, a trade-off decision has to be made to reach an optimal formulation, which can be assisted using optimization techniques. Here, we optimized coffee flavored fluid milk (coffee milk) using two distinct approaches, and we describe the insights gained in the process.

Optimization is an important practice for product developers and sensory specialists (Ares, Varela, Rado, & Giménez, 2011; Dutcosky, Grossmann, Silva, & Welsch, 2006; Villegas, Tarrega, Carbonell, & Costell, 2010). Given intense competition in the market, the food industry is perpetually interested in optimization tools that are both rapid and cost effective. According, just-about-right (JAR) scales have gained popularity as an optimization technique because they are quick and easily executed by sensory analysts (Popper & Gibes, 2004; Rothman & Parker, 2009; Xiong & Meullenet, 2006). Operationally, optimization can be approached in two distinct ways: by maximizing overall acceptability (e.g., Deshpande, Chinnan, & McWatters, 2008; Youn & Chung, 2012) or by minimizing dissatisfaction.

Using JAR scaling, an attribute is evaluated for its appropriateness relative to some ideal (Rothman & Parker, 2009; Worch, Dooley, Meullenet, & Punter, 2010). This hypothetical ideal is designated “Just About Right” or “Just Right.” Accordingly, a participant may indicate an attribute is “Too Little”, “Too Much” or “Just About Right.” Generally, when an attribute is “Too Little” or “Too Much”, the product developer increases or decreases the amount of the ingredient that corresponds to the attribute. Thus, JAR scales are said to give directional guidance. This technique may be useful when developers have only a limited number of prototypes to evaluate (versus a designed experiment with a large number of prototypes covering a wide product space), but there has been little validation of this (Moskowitz, 2001), and textbooks (Stone & Sidel, 2004) recommended against replacing designed experiments with JAR scaling for product optimization. JAR scaling has been criticized for conflating the measurements of attribute intensity and consumer acceptability into one measurement scale (Moskowitz, Muñoz, & Gacula, 2003). Additionally, JAR scales may suffer from other flaws that interfere with optimization, such as attitudinal biases unrelated to sensory properties, or a lack of attribute independence (Rothman & Parker, 2009).

As an alternative to JAR scaling, ideal scaling measures the perceived intensity of an attribute and the intensity of a hypothetical ideal separately (Gilbert, Young, Ball, & Murray, 1996; Rothman & Parker, 2009; van Trijp, Punter, Mickartz, & Kruithof, 2007; Worch, Le, Punter, & Pages, 2012). Unlike JAR scaling, where the ideal level (i.e., “Just About Right” or “Just Right”) is fixed at the middle of the scale, ideal scaling allows a participant to place his or her hypothetical ideal anywhere along the line. The magnitude of “Too Little” or “Too Much” can then be estimated by the deviation (delta) between the perceived intensity and ideal intensity.

Using either ideal scaling or JAR scaling, the deviation from ideal (or delta), is a measure of dissatisfaction in regard to that specific attribute. The farther the attribute intensity deviates from the ideal level (i.e., the larger the delta), presumably the lower the product quality would be, and the more a consumer would be dissatisfied.

We believe it is important to distinguish between minimizing dissatisfaction, as is done when directional information from JAR or ideal scales are used to reformulate products, and maximizing liking, via designed experiments, as different a route to product optimization. Notably, in the Kano model, consumer dissatisfaction is not simply the opposite of satisfaction (Berger et al., 1993; Kano, Seraku, Takahashi, & Tsuji, 1984). Further, disparities in optimal levels for a single attribute obtained from JAR scaling and hedonic scores have been widely reported (Bower & Boyd, 2003; Daillant & Issanchou, 1991; Epler, Chambers IV, & Kemp, 1998; Shepherd, Smith, & Farleigh, 1989; van Trijp et al., 2007; Vickers, 1988). These differences may be greater when health-related attributes are rated.

Lovely and Meullenet (2009) compared four approaches to the optimization of a strawberry yogurt – external preference mapping (EPM), Euclidian distance ideal point mapping (EDIPM), landscape segment analysis (LSA), and JAR – and concluded that EPM, EDIPM and JAR produced equivalent results. They further concluded that JAR optimization was an acceptable alternative to more complicated preference mapping methods, and that LSA did not yield a superior product (greater liking). However, these techniques were not compared to a product formulated by simply maximizing liking, but only to the original product with the highest liking. They recommended further research in which direct comparisons of optimization strategies are made, and concluded that validation studies were a logical means to compare the efficacy of methods.

It is not certain that directional ratings (JAR or ideal) truly reflect a consumer’s ability to know the ideal point and judge the magnitude of deviation from that ideal point (Moskowitz, 2001). Consumer data showing that maximal liking corresponds to minimal deviation from the ideal (“just right”) would provide evidence for the validity of directional scales. Moskowitz (2001) addressed this question using a ½ replicate central composite design requiring 48 prototypes to optimize the visual appearance of pizza topping formulations, and concluded that creating a product for which the directionals are all simultaneously “on target” produced a highly acceptable, but not necessarily maximally acceptable product. Moskowitz (2001) suggested that the generalizability of these results should be tested with other food products and attributes, especially flavor.

Here we test the validity of directional ratings by comparing optimal formulations obtained by maximizing liking as compared to minimizing attribute deltas (dissatisfaction) for taste and texture of coffee-flavored dairy beverages. Furthermore, we take a lean experimental approach using a fractional, constrained mixture design for formulation with an incomplete block design for sensory analysis.

2. Materials and methods

This project comprised two studies, i.e., study I: product optimization, and study II: optimization validation. In study I, product optimization was conducted under three research conditions that differed in research ballot design (designated as Liking, Ideal and JAR). In study II, consumer overall liking and preference for two selected optimal formulations were evaluated separately. The method of product preparation was identical for both studies.

Informed consent was provided by the participants, and data were collected with the approval of the Penn State Office of Research Protections as exempt from IRB review under the wholesome foods exemption in 45 CFR 46.101(b)(6). Participants were compensated for their time.

2.1 Sample formulation and preparation

In study I, twenty coffee-flavored dairy beverages were formulated (Table 1) using eChip® software (Wilmington, DE) to create a fractional, mixture design with four constrained variables: coffee extract (3.0 – 5.0 wt %; Autocrat Sumatra 1397, Autocrat Natural Ingredients, Lincoln, RI), sucrose (5.0 – 8.0 wt %), milk (35 – 55 wt %, 2 % fat), and water (35 – 55 wt %). In study II, only two samples were tested either for liking or preference. These two samples were formulated using optimal formulations (Table 2) obtained from the JAR_liking and JAR_Delta models developed in study I (i.e. contrasting optimization strategies within the same individuals). For both studies, formulation variables accounted for 99.8 % of the individual formulations. A constant amount of pectin (0.2 wt %; Grinsted® SY, Dupont Danisco) was added to all the samples. Pectin was mixed with sucrose before blending them with water, milk, and coffee extract to make sample batches, which were then heated to 72 °C and held 15 seconds to assure that the sucrose was completely dissolved, the pectin dispersed, and the product safe for human testing. The finished samples were kept at refrigeration temperature (∼4.0 °C) for at least 24 h before serving. Two ounces of coffee milk were served in 4-oz Solo transparent plastic cups (Solo Cup Company, Urbana, IL).

Table 1.

Sample formulations (in weight percentage) in study I

Product1	Milk	Water	Coffee extract	Sucrose	Solids content2
1	35.93	54.89	3.99	4.99	10.02
2	45.24	45.24	4.32	4.99	11.11
3, 19	36.93	54.89	2.99	4.99	9.90
4,9	53.89	34.93	2.99	7.98	14.75
5	34.93	51.90	4.99	7.98	13.14
6, 18	34.93	54.89	4.99	4.99	10.15
7	44.91	43.41	4.99	6.49	12.73
8	35.93	54.39	2.99	6.49	11.29
10	54.89	34.93	4.99	4.99	12.32
11	44.41	44.41	2.99	7.98	13.71
12, 16	54.39	34.93	3.99	6.49	13.53
13	54.89	36.93	2.99	4.99	11.86
14, 17	34.93	53.89	2.99	7.98	12.68
15	51.90	34.93	4.99	7.98	14.99
20	34.93	52.89	3.99	7.98	12.91

¹Samples in the same row share the same formulation.

²Calculated from the solids content of the ingredients.

Table 2.

Two “optimal” formulations (in weight percentage) in study II

Samples1	Description2	Milk	Water	Coffee extract	Sucrose
3% Coffee	JAR_liking	54.3	35.8	3.0	6.7
5% Coffee	JAR_Delta	44.9	43.4	5.0	6.5

¹For convenience, the sample created using the optimal formulation obtained by JAR_liking model was identified as “3% coffee”; the sample created using the optimal formulation obtained from JAR_Delta model was identified as “5% coffee.”

²Refers to optimization models that determined corresponding formulations.

2.2 Participants

Participants were recruited via email using an existing participant database maintained by the Sensory Evaluation Center at Penn State or via staff intercepts in public spaces in and around the Food Science Department at Penn State. To qualify for participation, individuals had to be regular drinkers of coffee or coffee-flavored beverages, and free of food allergies.

In study I, participants (n = 388, 110 men) were randomly assigned to one of three research conditions. The majority of participants (155) were between 18 −27 years old, 72 were 28 – 37, 56 were 38 – 47, 75 were 48 – 57, 26 were 58 – 67, and only 4 were over 67 years old. The majority were White (n = 298, ∼77%), 59 identified themselves as Asian or Pacific Islander, 9 as African or African American, 11 as Hispanic or Latino and 11 did not report their ethnicity. About 60% of the participants indicated they drank coffee with milk, cream, and/or sugar for all methods (Table 3).

Table 3.

Frequency (%) of regularly consumed coffee-flavored beverages for participants in optimization study I.

Product	Method	Liking (n=127)	Ideal (n=129)	JAR (n=132)
Cappuccino		19.7	20.9	30.3
Latte		32.3	24.0	37.9
Black Coffee		21.3	27.9	25.8
Iced Coffee		33.9	25.6	37.9
Coffee with milk, cream, and/or sugar		60.6	61.2	58.3

Note: This is a “check all that apply” question. So the sums of percentage in a column may exceed 100%.

In study II, participants (n = 122) were recruited and randomly assigned into either a liking test or preference test. Gender distribution in the two research conditions was similar: 72 % women (liking) and 69 % women (preference). In the liking test (n = 61), about 65 % were either 18 – 27 years old (n = 15) or 28 – 37 years old (n = 25), 6 were 38 – 47, 13 were 48 – 57, 2 were 58 – 67; the majority were White (n = 51, ∼83%), 5 identified themselves as Asian or Pacific Islander, 1 as African or African American, 3 as Hispanic/Latino, and 1 as Other. In the preference test (n = 61), just under 60 % were between 18 – 27 years old (n = 21) or 28 – 37 years old (n = 14), 12 were 38 – 47, 13 were 48 – 57,1 was 58 – 67. Similarly, the majority were White (n = 53, ∼87 %), 2 identified themselves as Asian or Pacific Islander, 1 as African or African American, 3 as Hispanic/Latino, and 2 as Other. Compared to Study I (Table 3), fewer participants (∼35 %) indicated they consume coffee with milk, cream, and/or sugar (Table 4).

Table 4.

Frequency (%) of regularly consumed coffee-flavored beverages for participants in validation study II.

Products	Comparison test	Liking (n=61)	Preference (n=61)
Cappuccino		78.6	72.1
Latte		65.5	72.1
Black coffee		65.5	73.8
Iced coffee		59.0	70.4
Coffee with milk, cream, and/or sugar		32.8	37.7

Note: This is a “check all that apply” question. So the sums of percentage in a column may exceed 100%.

2.3 Product testing

Data collection was conducted using Compusense five® software (Compusense Inc., Ontario, Canada). The protocols differed between study I and II.

2.3.1 Study I: Product optimization

Participants were randomized to 1 of 3 test conditions as they entered individual sensory booths. In the “Liking” method (n = 127), only overall liking and attribute intensities were collected. In the “Ideal” method (n = 129), participants rated overall liking, attribute intensities, and their ideal attribute intensities on separate, appropriately-worded line scales. In the “JAR” method (n = 132), overall liking was collected, and attribute appropriateness was assessed with just-about-right (JAR) line scales.

Liking was assessed first using a standard 9-point hedonic scale (1= “Dislike Extremely”, 5 = “Neither Like Nor Dislike”, and 9=“Like Extremely”) (Peryam & Pilgrim, 1957). Attribute intensities, both perceived and ideal, were measured using continuous line scales (0–100); two descriptive anchors were placed at 10% and 90% of these scales, representing low intensity (e.g., “Not At All Sweet”) and high intensity (e.g., “Extremely Sweet”). Just-about-right (JAR) scales were designed as continuous line scales with three descriptive anchors, low intensity (i.e., “Much Too Weak”) on the left end, “Just About Right” at the middle, and high intensity (i.e., “Much Too Strong”) on the right end. Although many practitioners choose to use category scales to collect JAR data, continuous JAR scales are described in common references (Lawless & Heymann, 2010; Rothman & Parker, 2009) and seminal papers in the literature use continuous scales to collect JAR data (e.g. Booth, Thompson, & Shahedian, 1983). We used continuous JAR scales here both to facilitate a more direct comparison with data from the ideal scaling condition, and to avoid the classic flaws with category scales (e.g., range-frequency bias, end use avoidance, etc). After all samples had been evaluated, demographics and consumption behavior for coffee-flavored beverages were collected.

To minimize sensory fatigue, participants received 4 formulas out of 20 using an incomplete block design. Given the total number of participants (n=388), this ensured that each sample was rated by at least 19 individuals. The samples were served in a monadic sequential order, with a two-minute mandatory break between samples. During the break, participants were asked to rinse with room temperature (22 °C) filtered water to reduce potential carry-over effects.

2.3.2 Study II: Optimization validation

In the liking test, all participants rated both samples served in a balanced, sequential monadic order. In the preference test, the two samples were served in pairs, with a counterbalanced order of presentation. Participants were asked to rinse with room temperature (22°C) filtered water between samples to reduce potential carry-over effects.

Liking was assessed using a standard 9-point hedonic scale (1 = “Dislike Extremely”, 5 = “Neither Like Nor Dislike”, and 9 = “Like Extremely”) (Peryam & Pilgrim, 1957). Preference was measured using a two-alternative forced choice test (i.e., “no preference” was not allowed). Demographics and consumption behavior for coffee-flavored beverages were collected after the samples had been evaluated.

2.4 Data processing and statistical analyses

In study I, mean liking was not significantly influenced by research method (Li et al., 2014a), so liking data were aggregated and mean liking (Overall_Liking) for each sample (n = 20) was calculated across all methods and panelists. Overall_Liking was regressed on formulation variables (coffee, milk, sucrose, and water) to yield an optimal formulation using eChip® software (Wilmington, DE). Similarly, to calculate optimal formulae for each of the individual methods, mean liking scores were calculated for each coffee sample across all of the participants within a research method (LikingOnly, Ideal, and JAR). For convenience, these mean liking scores within each condition were identified as Liking Only_liking, Ideal_liking, and JAR_liking, respectively.

For each participant in the Ideal and JAR conditions, deltas for each of the four attributes were calculated as the absolute value of the deviation of rated intensity from ideal (for ideal scaling), or the distance from “just about right” level (for JAR scaling). Because participants in the ideal scaling condition had 4 different “ideal” ratings (one from each sample they tasted), we used the mean of their ideal ratings as the ideal point for that individual when calculating the delta for that sample and attribute. Using the individual attribute deltas for each person, we created summary variables called Ideal_Delta and JAR_Delta to estimate the total deviation of each product from ideal (i.e., dissatisfaction), within each method. These summary variables consisted of the sum of the individual deltas for each attribute (sweetness, milk flavor, thickness, and coffee flavor) across participants within each scaling method, as follows:

• Ideal_Delta, = Σ(|delta_sweetness| + |delta_{coffee flavor}| + |delta_{milk flavor}| + |delta_thickness|)

• JAR_Delta = Σ(|delta_sweetness| + |delta_{coffee flavor}| + |delta_{milk flavor}| + |delta_thickness|)

We note here that this approach does not attempt to weight the attributes for their relative influence on dissatisfaction the consequences of which are discussed later.

The five outcome variables – Overall_liking, Liking Only_liking, Ideal_liking, JAR_liking, Ideal_Delta and JAR_Delta – were fitted as a function of formulation variables (coffee extract, sucrose, milk, and water) in eCHIP®. To achieve optimal formulations, response variables Overall_liking, Liking Only_liking, Ideal_liking, and JAR_liking were maximized or Ideal_Delta and JAR_Delta were minimized.

In study II, data were analyzed using JMP® version 9.02 (SAS Institute Inc.). Mean liking for the two samples were compared using an analysis of variance, where participant was treated as a random effect and sample was a fixed effect (a paired two-sample t-test resulted in the same conclusions). Mean liking for each sample was also compared to the corresponding predicted optimal liking values to test the predictive ability of optimization models. Preference data were analyzed using a binomial test to see if one sample was significantly preferred over the other.

3. Results

3.1.1 Study I: Product optimization using Overall_Liking (n = 388)

The regression model explained 75.8 % (Adj. R² = 0.540) of the variation in Overall_Liking (p = 0.033, with no lack-of-fit). Only the variables water (p = 0.019), sucrose (p = 0.006), milk*sucrose (p = 0.029), and sucrose² (p = 0.025) were significant in the final model (Table 5). Interestingly, no coffee-related variables were significant. Figure 1 is the response trace plot for Overall_Liking, where the centroid (i.e. Component Range = 0) represents the reference mixture. The trace plot illustrates the influence of each component on Overall_Liking as the amount of that component either increases or decreases while the proportions of the other components remain the same. A horizontal trace indicates an “inactive” component (Myers & Montgomery, 2002). Though nearly horizontal, Overall_Liking does increase as the trace for coffee extract approaches its lower bound. The other components show the classic “inverted-U” response of liking to changes in ingredient concentration (Moskowitz & Gofman, 2007).

Table 5.

Overall_Liking optimization model (n=388)

Predictor variables	Coefficients	p-value
Intercept	7.06	--
Milk	−0.43	0.3036
Water	−0.84	0.0185
Coffee	−3.21	0.4993
Sucrose	10.62	0.0061
Milk*water	−0.61	0.3452
Milk*coffee	−2.62	0.6723
Milk*sucrose	10.28	0.0285
Water*coffee	3.27	0.5340
Water*sucrose	7.36	0.0848
Coffee*sucrose	5.37	0.8610
Milk*Milk	−0.73	0.2922
Water*Water	−0.82	0.1447
Coffee*Coffee	−22.15	0.8162
Sucrose*Sucrose	−116.07	0.0246

Note: p-values in bold indicate terms are significant in the model at α=0.05. Italicized p-values are significant at α=0.10.

Figure 1.

Trace plots for Overall_Liking as a function of milk, water, sucrose and coffee extract concentrations.

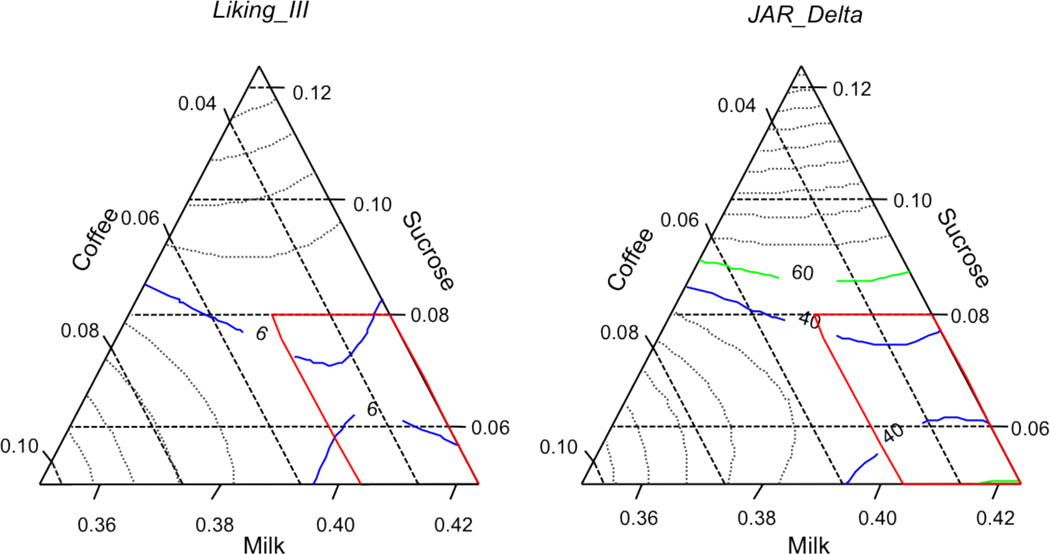
Using this prediction model, the optimal formulation (in weight percentage) for a coffee-flavored dairy beverage was determined as milk = 54.2, water = 35.6, coffee extract = 3.0, and sucrose = 7.0 (Figure 2). This optimal beverage is predicted to have a mean liking of 6.9 (95 % CI of 6.0 – 7.9), which is close to 7.0 (i.e., “Like Moderately” on a 9-point hedonic scale).

Figure 2.

Contour plot for product optimization using Overall_Liking

Notes: 1. Solid lines in the contour plot indicate that predicted responses were significantly different from each other (a = 0.05). 2. Dashed lines refer to predicted responses outside of the observed range of liking. 3. Contour lines are placed at the least significant difference between liking values. 4. The parallelogram defines the experimental space. Added water = 0.496.

3.1.2 Study I: Product optimization using LikingOnly_liking (n = 127)

The regression model explained 77.6% (Adj. R² = 0.574) of the variation in Liking Only_liking (p = 0.024, with no lack-of-fit). Only the variables water (p = 0.004) and sucrose (p = 0.022) were significant in the final model (Table 6). An optimal formulation for coffee milk was determined as milk = 49.2, water = 38.7, coffee extract = 4.2, and sucrose = 7.7 weight % (Figure 3). This optimized coffee milk is predicted to have an average liking of 7.2 (95 % CI of 5.9 – 8.5), which is close to 7.0 (“Like Moderately”) on a 9-point hedonic scale.

Table 6.

Liking_liking optimization model (n=127)

Predictor variables	Coefficients	p-value
Intercept	7.45	--
Milk	−0.24	0.6670
Water	−1.52	0.0035
Coffee	1.96	0.7573
Sucrose	11.21	0.0220
Milk*water	0.49	0.5671
Milk*coffee	−3.91	0.6411
Milk*sucrose	8.73	0.1383
Water*coffee	2.53	0.7196
Water*sucrose	−0.19	0.9718
Coffee*sucrose	66.95	0.1276
Milk*Milk	−1.71	0.0811
Water*Water	−0.58	0.4218
Coffee*Coffee	−98.79	0.4482
Sucrose*Sucrose	−91.47	0.1533

Note: p-values in bold indicate terms are significant in the model at α=0.05. Italicized p-values are significant at a=0.10.

Figure 3.

Contour plots for product optimization using Liking_liking (n=127)

Notes: 1. Solid lines in the contour plot indicate that predicted responses were significantly different from each other (a = 0.05). 2. Dashed lines refer to predicted responses outside of the observed range of liking. 3. Contour lines are placed at the least significant difference between liking values. 4. The parallelogram defines the experimental space. Added water = 0.496.

3.1.3 Study I: Product optimization using Ideal_liking and Ideal_Delta (n = 129)

The regression model explained 62.5 % (Adj. R² = 0.287) of the variation in Ideal_liking (p = 0.175, with no lack-of-fit). None of the terms were significant, although water, sucrose, milk*sucrose, and sucrose² terms were all marginal (Table 7). An optimal formulation for coffee milk was estimated as milk = 48.3, water = 41.5 coffee extract = 3.4, and sucrose = 6.6 weight % (Figure 4, left). This coffee milk formula is predicted to have a mean liking of 6.9 (95 % CI of 5.8 – 8.0), which is also close to 7.0 (“Like Moderately”) on the 9-point hedonic scale.

Table 7.

Ideal_liking and Ideal_Delta optimization model (n=129)

	Ideal_liking model		Ideal_Delta model
Predictor variables	Coefficients	p-value	Coefficients	p-value
Intercept	7.31	--	50.12	--
Milk	−0.26	0.5768	14.87	0.2651
Water	−0.73	0.0529	15.74	0.1261
Coffee	0.63	0.9042	−101.45	0.5001
Sucrose	6.42	0.0919	−135.57	0.1934
Milk*water	−0.33	0.6418	12.93	0.5212
Milk*coffee	0.09	0.9893	−76.58	0.6965
Milk*sucrose	7.92	0.1094	−42.12	0.7475
Water*coffee	6.49	0.2808	−11.55	0.9441
Water*sucrose	4.35	0.3371	−84.41	0.5041
Coffee*sucrose	16.83	0.6265	−343.93	0.7238
Milk*Milk	−0.97	0.2147	−0.57	0.9784
Water*Water	−0.91	0.1489	2.39	0.8865
Coffee*Coffee	−101.52	0.3525	1363.34	0.6527
Sucrose*Sucrose	−87.95	0.1044	1075.83	0.4568

Note: p-values in bold indicate terms are significant in the model at α=0.05. Italicized p-values are significant at a=0.10.

Figure 4.

Contour plots for product optimization using Ideal_liking and Ideal_Delta (n = 129)

Notes: 1. Solid lines in the contour plot indicate that predicted responses were significantly different from each other (a = 0.05). 2. Dashed lines refer to predicted responses outside of the observed range of Ideal_liking or Ideal_Delta. 3. Contour lines are placed at the least significant difference between Ideal_liking or Ideal_Delta values. 4. The parallelogram defines the experimental space. Added water = 0.496.

The regression model explained 38.0 % (Adj. R² = 0.000) of the variation in Ideal_Delta, and was not significant (p = 0.711, with no lack-of-fit) (Table 7). An optimal formulation (in weight percentage) minimizing Ideal_Delta for coffee milk was estimated as milk = 44.9, water = 43.4, coffee extract = 5.0, and sucrose = 6.5 (Figure 4, right).

3.1.4 Study I: Product optimization using JAR_liking and JAR_Delta (n = 132)

The regression model explained 72.1 % (Adj. R² = 0.470) of the variation in JAR_liking (p = 0.058, with no lack-of-fit). Sucrose, milk*water, milk*sucrose, water*sucrose and sucrose² significantly contributed to variation in JAR_liking (Table 8). An optimal formulation (in weight percentage) for coffee milk was determined as milk = 54.3, water = 35.8, coffee extract = 3.0, and sucrose = 6.7 (Figure 5, left). This optimized coffee milk is predicted to have a mean liking of 7.1(95%CI of 5.8–8.5).

Table 8.

JAR_liking and JAR_Delta optimization model (n=132)

	JAR_liking model		JAR_Delta model
Predictor variables	Coefficients	p-value	Coefficients	p-value
Intercept	6.39	--	30.34	--
Milk	−0.72	0.2113	22.14	0.0330
Water	−0.31	0.4638	15.25	0.0464
Coffee	−12.04	0.0820	62.41	0.5585
Sucrose	14.07	0.0071	−278.06	0.0024
Milk*water	−1.91	0.0461	35.39	0.0285
Milk*coffee	−4.14	0.6244	61.66	0.6591
Milk*sucrose	13.98	0.0286	−271.11	0.0135
Water*coffee	−0.18	0.9796	−23.56	0.8409
Water*sucrose	17.12	0.0084	−282.25	0.0086
Coffee*sucrose	−62.94	0.1525	628.07	0.3726
Milk*Milk	0.44	0.6333	−4.49	0.7658
Water*Water	−0.83	0.2626	12.88	0.2932
Coffee*Coffee	138.26	0.2992	−1273.33	0.5560
Sucrose*Sucrose	−164.88	0.0201	3213.47	0.0087

Note: p-values in bold indicate terms are significant in the model at α=0.05. Italicized p-values are significant at a=0.10.

Figure 5.

Contour plots for product optimization using JAR_liking and JAR_Delta (n = 132)

Notes: 1. Solid lines in the contour plot indicate that predicted responses were significantly different from each other (a = 0.05). 2. Dashed lines refer to predicted responses outside of the observed range of JAR_liking or JAR_Delta. 3. Contour lines are placed at the least significant difference between JAR_liking or JAR_Delta values. 4. The parallelogram defines the experimental space. Added water = 0.496.

For JAR_Delta, the regression model explained 71.5 % (Adj. R² = 0.458) of the variation (p = 0.063, with no lack-of-fit). The terms milk, water, sucrose, milk*water, milk*sucrose, water*sucrose, and sucrose² contributed significantly to variation in JAR_Delta (Table 8). An optimal formulation (in weight percentage) minimizing JAR_Delta for coffee milk was determined as milk = 44.9, water = 43.4, coffee extract = 5.0, and sucrose = 6.5 (Figure 5, right). Notably, this optimal formulation is identical to the one obtained from the Ideal_Delta model.

3.2 Study II: Optimization validation

Two optimal formulations (Table 2) obtained from the JAR_liking and JAR_Delta models (i.e. two optimization approaches within the same participants) were compared in a subsequent validation study. In the acceptance test (rated liking), the 3% coffee formula had a mean liking of 7.2, that was significantly higher than the mean liking for the 5% coffee formula (6.4) (F_1,60 = 10.93, P = 0.002). Likewise, in the preference test (n = 61), the 3% coffee formula was also significantly preferred over the 5% coffee formula (40 vs 21) (p = 0.010). This result was in agreement with the study by Epler et al. (1998), where the participants preferred “the most liked” sweetness level over the “just right” level in a lemonade beverage.

Strikingly, observed liking (7.2) for the 3% coffee formula in Study II was not significantly different (t = 0.231, p = 0.818) from the predicted optimal liking (7.1) obtained using the JAR_liking model in Study I. Observed mean liking (6.4) for the 5% coffee formula was also not significantly different (t=0.0539, P=0.957) from the predicted liking (6.4) for this formula. (Because it is not possible to directly predict liking in a model that minimizes delta, the value for predicted liking was obtained by inserting the optimal formulation levels from JAR_Delta model into the equation from the Overall_Liking model.)

4. Discussion

4.1 Design space

Response surfaces are created using a mixture design when the factors are ingredients of a mixture that sum to unity, meaning the level of these factors cannot be chosen independently. Consequently, the coefficients in the fitted polynomial model obtained from mixtures are not unique. This is often dealt with using non-redundant canonical or Scheffé models without a constant term. Quadratic models of this form often delete the squared terms. Cox (1971) provided an alternative to canonical polynomials for mixture experiments that retains individual parameters with an interpretation closer to ordinary response functions and which included the squared terms. This approach is employed by eChip®, with the overall centroid as the reference mixture (Wheeler, 1993).

In the present case, there are constraints on the ingredient compositions, which lead to an experimental space that is not a simplex. In such cases, Myers & Montgomery (2002) suggested using some kind of computer-generated design. Mixture designs using trace variables, i.e. those with small concentration ranges (e.g. coffee extract here), are easily influenced by rounding errors. To avoid this and other problems, eChip® stretches the experimental region (Wheeler, 1993) using pseudocomponent transformations (Myers & Montgomery, 2002).

Extreme vertices designs, like the design used here, employ combinations of the upper- and lower-bound constraints as the basis of the design along with a subset of points at the centers of the edges, faces and the overall centroid of the region. For a four component system (e.g., milk, water, sucrose and coffee extract) there are 8 extreme vertices, 12 edge midpoints, 6 face centroids and 1 overall centroid, for a possible 27 unique points that could form the basis of the design; a full replication would then require 54 samples. Myers & Montgomery (2002) recommend 8–10 samples beyond the minimum required to fit a model with half of these being replicates. Therefore, the quadratic models fit here (with 15 terms) would require a minimum of 20 unique points with 5 replicates (Table 1).

A full replication of the experiment using a complete block design with replication for the sensory analysis would have required 108 evaluations per participant, or a total of 41,904 evaluations for our 388 participants. The fractional design (20 of 27 unique points), if replicated, would still require 80 evaluations per participant for a total of 31,040 evaluations. Therefore, in addition to the fractional factorial design, we employed an incomplete block analysis with only 4 of 20 samples evaluated by each participant, requiring a total of 1,552 separate evaluations. As designed, this provided 20 observations per formula, which we felt to be the minimal number required to provide a reasonable estimate of descriptors.

An optimal formulation coincides with the maxima in the Overall_Liking model. Ideally this optimum should not occur at the boundary of the experimental range as it did in this case for coffee extract (i.e., 3.0 %). In hindsight, the range in concentration of coffee extract we selected was too narrow, and probably should have extended to 2 %. Though none of the coffee-related variables were significant in any of the regression the models, as a coffee-flavored dairy beverage, coffee extract was obviously an important ingredient in these formulations. This result was similar to that of Lovely & Meullenet (2009) wherein the “strawberry impression intensity” of a strawberry yogurt was not influenced by the amount of flavor added, nor was the amount of strawberry flavor a driver of hedonic scores. Previously, we found coffee extract concentration had a significant effect on perceived coffee flavor (Li et al., 2014a). Thus, the absence of a significant effect for coffee extract in the optimization model for acceptability here likely reflects an overly narrow range of concentrations (3.0 % to 5.0 %) that were very close to the optimum. Presumably, a broader range of concentration (e.g. 2 to 6 %), or greater deviation from the optimum would have revealed a significant effect of coffee extract on liking.

The interaction between milk and sucrose indicated that the optimal level of sucrose varied as a function of the amount of milk in the beverage. This result was comparable to a previous finding that optimal sucrose levels differed across low and high milk concentration in coffee milk drinks (Moskowitz, 1985). Milky flavor was also affected by sucrose levels in an instant coffee drink (Varela, Beltrán, & Fiszman, 2014), as it was for these coffee-flavored dairy beverages (Li et al., 2014a).

4.2 Comparisons of optimization models

With the same set of participants, the variance explained in the Ideal_Delta model (38%) was much lower than in the Ideal_liking model (63%). The low R-squared in the Ideal_Delta model might be due to additional noise introduced by the multiple rating steps required in ideal scaling (rating of intensity, followed by rating of ideal) (Li et al., 2014b). In contrast, the variance explained by JAR_Delta model (72%) was similar to the JAR_liking model (72%).

The resulting optimal formulations and predicted liking from the different models are summarized in Table 9. In the dissatisfaction models (Ideal_Delta and JAR_Delta), participants indicated that they desired a coffee-flavored dairy beverage with a higher concentration of coffee extract (5.0 %) and lower concentrations of milk (45.0 %) and slightly less sucrose (6.5 %) compared to the optimal formulations determined by the models based on liking. This finding empirically illustrates a disparity between what consumers indicated they want and what they liked most, which is reportedly a frequent occurrence (Moskowitz, 2001). Using the model of Table 5, a liking of 6.4 was predicted for the optimal formulation resulting from the Ideal_Delta and JAR_Delta models, which was lower than that predicted from all other models based on liking. Optimal formulations obtained from directional models (Ideal_Delta and JAR_Delta) differed substantially from those from liking models. These differences may be due to the distinct measurements of product acceptability defined by two parameters (i.e., Ideal_Delta/JAR_Delta and liking), and also to biases inherent to ideal scaling and JAR scaling.

Table 9.

“Optimal” formulations and predicted likings

	Overall (n=388)	Liking (n=127)	Ideal (n=129)		JAR (n=132)
Model	Overall_Liking	Liking_liking	Ideal_liking	Ideal_Delta	JAR_liking	JAR_Delta
Milk (%)	54.2	49.2	48.3	44.9	54.3	44.9
Water (%)	35.6	38.7	41.5	43.4	35.8	43.4
Coffee
extract	3.0	4.2	3.4	5.0	3.0	5.0
(%)
Sucrose (%)	7.0	7.7	6.6	6.5	6.7	6.5
Predicted liking	6.9	7.2	6.9	6.4*	7.1	6.4*

Note: Predicted likings for both Ideal_Delta and JAR_Delta were estimated using the Overall_Liking optimization model including all terms (Table 5).

In this study Ideal_Delta and JAR_Delta measured participant dissatisfaction in overall product quality in terms of the performance of four attributes. In contrast, overall liking is a holistic measurement of consumer satisfaction. In the Kano model, consumer satisfaction and dissatisfaction are two different constructs related to consumer acceptance of a product (Berger et al., 1993; Kano et al., 1984). Consequently, factors driving satisfaction might differ from those driving dissatisfaction (Bi, 2012; Li, 2011). Factors affecting liking of an instant coffee drink are not the same as those affecting disliking (Varela et al., 2014). Accordingly, it is not entirely surprising that optimal formulations resulting from the Ideal_Delta and JAR_Delta models are different from the formulations obtained from the liking models, even within the same individuals.

In both ideal scaling and JAR scaling, attribute deltas were measured in reference to one’s “ideal” that incorporates his/her beliefs or desires. In contrast, liking is a holistic parameter that presumably measures the enjoyment derived from a product or service in the moment. The difference between attribute delta and liking reflects a dissociation between attitudinal and behavioral factors (e.g. Drewnowski & Moskowitz, 1985). This suggests that what a consumer states he/she would like is not always the same as what he/she actually likes.

Some evidence suggests the difference between attribute delta and liking models might be greater when attributes are related to health concerns, such as salt and sucrose levels (Drewnowski & Moskowitz, 1985; Epler et al., 1998). For example, an individual on a diet might be more likely to rate “sweetness” in a beverage as “too much”. Indeed, Epler and colleagues found the optimal sucrose level for a lemonade beverage was 9.3 % using a JAR scale but 10.3 % using a liking scale, and participants significantly preferred the beverage with 10.3 % sucrose (Epler et al., 1998). Likewise, optimal sweetness intensity (6.43) for a yogurt obtained by a liking model was much higher than those optimal intensities obtained from the methods of self-reported (4.20), JAR-derived (4.33) and variant-derived (4.40) methods (van Trijp et al., 2007). For a salted snack, Drewnowski and Moskowitz observed the self-reported ideal NaCl level (1.5) was much lower than the one predicted by a liking model (5.1). In contrast, optimal levels for spice obtained by the two methods (4.0 vs 4.0) were similar; the authors suggested that, in contrast to salt, spice is presumably a relatively neutral attribute as far as health is concerned (Drewnowski & Moskowitz, 1985).

Similar biases might also occur when attributes have positive or negative associations that are independent of their actual influence on liking. Americans believe they want a “rich, hardy, roast” coffee, thus participants might tend to rate coffee flavor as “not strong enough”. However, on the basis of liking, a lower optimal level of coffee extract was predicted. In contrast to dissatisfaction-based models, liking models might have detected the negative impact of bitterness that resulted from adding more coffee extract into the beverage. The bitterness in coffee is generally regarded as negatively affecting consumer acceptance (even though some appropriate amount of bitterness might drive liking). As a result, a product with all “just right” attributes still might not be the most liked formulation (Moskowitz, 2004; Moskowitz, Munoz, & Gacula, 2003 ).

4.3 Validation study

While the literature is replete with optimization studies, very few follow up with validation of predicted results (a notable exception being Epler et al., 1998). Here we demonstrate that models developed for predicting liking using a lean fractional formulation design with an incomplete block sensory analysis can accurately predict liking in a different set of consumers separated by more than a year in time.

Interestingly, the “5% coffee” sample, formulated using the dissatisfaction models (Ideal_Delta and JAR_Delta) where participants stated they would like a coffee-flavored dairy beverage with less sucrose and milk, and more coffee extract (i.e., a product that was less sweet and milky, and stronger coffee flavor) was not preferred by the participants. In the dissatisfaction models, participants provided directional guidance on what they thought they wanted, but formulating a product to their ideal point (or to “Just-about-right”) did not result in a product that was preferred over the product obtained by maximizing liking; this result is wholly consistent with the work of Epler and colleagues (Epler et al., 1998). Participants did not know what they wanted; that is, what they ask for is not what is maximally liked (Moskowitz & Gofman, 2007).

4.4 Limitations of optimization models derived from directional data

In addition to the low R² for some models, which presumably could be improved with a greater number of observations, there were some inherent limitations to the approach we took. It should be kept in mind that Ideal_Delta and JAR_Delta were created to reflect overall product quality using the ratings of only four attributes (sweetness, milk flavor, coffee flavor, and thickness) that were assumed to be drivers of product performance. When a participant is asked holistically for his/her degree of liking for a product, he or she may assess attributes beyond the four considered here. Neglected attributes (e.g. mouth coating) may potentially be important for consumer acceptability. In particular, the absence of a rating of bitterness, often perceived as a negative attribute that would contribute to dissatisfaction, was a shortcoming. As a result, Ideal_Delta and JAR_Delta as defined here may be incomplete measurements for overall product quality compared to holistic ratings of overall liking for a product.

In addition, the logic behind the creation of Ideal_Delta and JAR_Delta could be questioned. In creating Ideal_Delta and JAR_Delta, “Too Little” and “Too Much” were weighted equally, as were each of the four attributes. However, prior work shows that too little or too much of an attribute can influence liking differently (Li et al., 2014b; Xiong & Meullenet, 2006). In a previous paper we demonstrated that the influence of the four attributes assessed herein on liking were not the same (Li et al., 2014b). Given Figure 1, one could also surmise that the Ideal_Delta and JAR_Delta should be calculated as the sum of the squared deltas, but this resulted in exactly the same prediction for the optimal formulation (data not shown). The correlation between Ideal_liking and Ideal_Delta (r = −0.51) was weak, and while that between JAR_liking and JAR_Delta was stronger (r = −0.87), the model for JAR_Delta still failed to predict an optimum with the highest liking. More importantly, if a significant amount of work to accurately model the relationship of JAR_Delta to liking is required, this would undermine the raison d’etre for using JAR scales in the first place, i.e., simplicity.

5. Conclusions

Minimizing dissatisfaction as measured by the deviation of intensity ratings from either one’s ideal or “just-about-right” does not result in a product with the highest overall acceptance. In fact, the use of JAR ratings may even mislead, resulting in a decrease in liking. For example, if we had tested a single prototype comprising 50 % milk, 40 % water, 6 % sucrose and 4 % coffee extract (roughly the midpoint between the optimums predicted for JAR_liking and JAR_Delta), the use of JAR scaling would have taken us in a direction away from the maximum liking. This implies that what consumers indicate they would like may not be a reliable way to determine an optimal formulation, suggesting maximizing liking is a more reliable tool for determining an optimal formulation. Liking is a main factor driving consumption (Tuorila et al., 2008), and compared to attribute deltas (Ideal_Delta and JAR_Delta), liking is a more holistic parameter for measuring overall product quality.

Highlights.

1. Optimizing liking and attributes qualities yield distinct product optimal formulations.

2. Consumers may not know what they want but know what they like.

3. Asking a consumer panel to design a product using JAR or ideal scales may be misleading.

4. Optimizing liking is a reliable tool to create a preferable product.

5. Both JAR and ideal scaling commit similar biases.