Practical Steps for Applying a New Dynamic Model to Near-Infrared Spectroscopy Measurements of Hemodynamic Oscillations and Transient Changes

Abstract

Rationale and Objectives

Perturbations in cerebral blood volume (CBV), blood flow (CBF), and metabolic rate of oxygen (CMRO₂) lead to associated changes in tissue concentrations of oxy- and deoxy-hemoglobin (ΔO and ΔD), which can be measured by near-infrared spectroscopy (NIRS). A novel hemodynamic model has been introduced to relate physiological perturbations and measured quantities. We seek to use this model to determine functional traces of cbv(t) and cbf(t) − cmro₂(t) from time-varying NIRS data, and cerebrovascular physiological parameters from oscillatory NIRS data (lowercase letters denote the relative changes in CBV, CBF, and CMRO₂ with respect to baseline). Such a practical implementation of a quantitative hemodynamic model is an important step toward the clinical translation of NIRS.

Materials and Methods

In the time domain, we have simulated O(t) and D(t) traces induced by cerebral activation. In the frequency domain, we have performed a new analysis of frequency-resolved measurements of cerebral hemodynamic oscillations during a paced breathing paradigm.

Results

We have demonstrated that cbv(t) and cbf(t) − cmro₂(t) can be reliably obtained from O(t) and D(t) using the model, and that the functional NIRS signals are delayed with respect to cbf(t) − cmro₂(t) as a result of the blood transit time in the microvasculature. In the frequency domain, we have identified physiological parameters (e.g., blood transit time, cutoff frequency of autoregulation) that can be measured by frequency-resolved measurements of hemodynamic oscillations.

Conclusions

The ability to perform noninvasive measurements of cerebrovascular parameters has far-reaching clinical implications. Functional brain studies rely on measurements of CBV, CBF, and CMRO₂, whereas the diagnosis and assessment of neurovascular disorders, traumatic brain injury, and stroke would benefit from measurements of local cerebral hemodynamics and autoregulation.

Near-infrared spectroscopy (NIRS) can assess noninvasively cerebral hemodynamics and brain function by being sensitive to cerebral concentrations of deoxyhemoglobin (D) and oxy-hemoglobin (O). Noninvasive measurements of task-related functional activity with NIRS, or fNIRS, have been reported (1–3). These hemodynamic changes result from changes in the cerebral blood volume (CBV), cerebral blood flow (CBF), and metabolic rate of oxygen (CMRO₂) as a result of brain activation and neurovascular coupling. Understanding the interplay between these physiological/functional/metabolic processes and the measured signals with functional neuroimaging techniques such as fNIRS and functional magnetic resonance imaging is the major objective of hemodynamic models (for a review, see Buxton, 2012 (4)).

A novel hemodynamic model has been recently introduced to provide an analytical tool for the study of oscillatory (frequency domain) and time varying (time domain) hemodynamics that are measurable with NIRS (5). The model relates normalized perturbations in CBV, CBF, and CMRO₂ to the dynamics of O and D concentrations in tissue. In particular, this model treats the cerebral microvasculature in terms of three compartments (arterial, capillary, venous) and describes the effects of changes in blood volume in all three compartments (even though the capillary contribution to blood volume changes may be negligible), and the effects of changes in blood flow and metabolic rate of oxygen in the capillary compartment (direct effects) and the venous compartment (indirect effects). This novel model can be applied to measurements in the time domain (O(t), D(t)), where hemodynamic changes are induced over time, and in the frequency domain (via the phasors O(ω), D(ω)), where induced hemodynamic oscillations are measured as a function of the frequency of oscillation. Hemodynamic oscillations at a specific frequency can be induced by a number of protocols including paced breathing (6), head-up-tilting (7), squat-stand maneuvers (8), and pneumatic thigh-cuff inflation (9), leading to a technique that we have recently proposed, coherent hemodynamics spectroscopy (CHS) (5,10).

In this article, we use a new formulation of this hemodynamic model by Fantini (11) to develop its practical implementation for NIRS and fNIRS measurements. In the time domain, we show how the model can be used to translate time traces of O(t) and D(t) into time-varying measures

$$O(t)=\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}[S^{(a)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}(1+\mathrm{c}\mathrm{b}{\mathrm{v}}^{(a)}(t))+<S^{(c)}>{\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}+S^{(v)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}(1+\mathrm{c}\mathrm{b}{\mathrm{v}}^{(v)}(t))]++\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}[\frac{<S^{(c)}>}{S^{(v)}}(<S^{(c)}>-S^{(v)}){\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}{h}_{RC-LP}^c(t)+(S^{(a)}-S^{(v)})\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}{h}_{G-LP}^{(v)}(t)]*[\mathrm{c}\mathrm{b}\mathrm{f}(t)-\mathrm{c}\mathrm{m}\mathrm{r}{\mathrm{o}}_2(t)],$$ (1)

$$D(t)=\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}[(1-S^{(a)})\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}(1+\mathrm{c}\mathrm{b}{\mathrm{v}}^{(a)}(t))+(1-<S^{(c)}>){\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}+(1-S^{(v)})\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}(1+\mathrm{c}\mathrm{b}{\mathrm{v}}^{(v)}(t))]+-\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}[\frac{<S^{(c)}>}{S^{(v)}}(<S^{(c)}>-S^{(v)}){\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}{h}_{RC-LP}^c(t)+(S^{(a)}-S^{(v)})\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}{h}_{G-LP}^{(v)}(t)]*[\mathrm{c}\mathrm{b}\mathrm{f}(t)-\mathrm{c}\mathrm{m}\mathrm{r}{\mathrm{o}}_2(t)],$$ (2)

of cbv(t) and the difference cbf(t) − cmro₂(t)^⋆. In the frequency domain, we demonstrate how the model can be used to measure a number of physiologically relevant parameters such as the blood transit time in the microvasculature and the cutoff frequency for cerebral autoregulation. The work presented here demonstrates, in practical terms, that the new hemodynamic model is a workable model for translation of NIRS measurements into functional and physiological parameters. The feasibility of a practical implementation of this mathematical model, in combination with noninvasive NIRS and fNIRS measurements, is a critical element for its translation toward functional and clinical studies.

HEMODYNAMIC MODEL

In the time domain, all of the time-dependent quantities are represented by time varying real functions. In the frequency domain, all of the oscillatory quantities are represented by phasors (5). In the following sections, we discuss how the model equations can be implemented in practice to measure (1) the time dependence of the CBV, and a combination of CBF and CMRO₂ associated with brain activation (functional neuroimaging) or (2) a set of physiological parameters on the basis of frequency-resolved measurements of the amplitude and phase of hemodynamic oscillations (CHS).

Time domain equations

We denote with lowercase letters the relative changes in CBV, CBF, and CMRO₂ with respect to baseline (cbv(t) = ΔCBV(t)/CBV₀, cbf (t) = ΔCBF(t)/CBF₀, cmro₂(t) = ΔCMRO₂(t)/CMRO₂|₀), where ΔCBV(t) = CBV(t) − CBV₀, ΔCBF = CBF(t) − CBF₀, and ΔCMRO₂ = CMRO₂(t) − CMRO_2|0. The time-dependent expressions for the absolute tissue concentrations of O(t), D(t), and total hemoglobin (T(t)) are given by (11):

$$T(t)=\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}\mathrm{C}\mathrm{B}{\mathrm{V}}_0[1+\mathrm{c}\mathrm{b}\mathrm{v}(t)].$$ (3)

Note that the right sides of Equations (1)–(3) are given by the sum of time-independent terms (which correspond to the baseline values O₀ in Eq. (1), D₀ in Eq. (2), and T₀ in Eq. (3)) and time-dependent terms associated with cbv^(a)(t), cbv^(v)(t), cbv(t), cbf (t), and cmro₂(t). Explicitly, the time-independent, baseline concentrations of O, D, and T are given by:

$$O_0=\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}[S^{(a)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}+<S^{(c)}>{\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}+S^{(v)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}],$$ (4)

$$D_0=\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}[(1-S^{(a)})\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}+(1-<S^{(c)}>){\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}+(1-S^{(v)})\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}],$$ (5)

$$T_0=\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}\mathrm{C}\mathrm{B}{\mathrm{V}}_0.$$ (6)

In these equations, ctHb is the hemoglobin concentration in blood; Ƒ^(c) is the Fåhraeus factor (ratio of capillary-to-large vessel hematocrit); and the superscripts (a), (c), and (v) for CBV and cbv indicate partial contributions from the arterial, capillary, and venous compartments, respectively, with $\mathrm{C}\mathrm{B}{\mathrm{V}}_0=\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}+{\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}+\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}$ . The dynamic model takes into account that the arterial, capillary, and venous compartments provide individual contributions to the overall concentrations of O and D. The weights of such contributions are expressed in terms of S^(a), <S^(c)>, S^(v), $\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)},{\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}$ , and $\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}$ as specified by Equations (1) and (2). Also, in Equations (1) and (2), we have set the capillary volume perturbation cbv^(c)(t) = 0 because capillary recruitment and capillary dilation in the brain has been found to be negligible (12–17). Subscript “0” indicates baseline values, and S^(a), <S^(c)>, and S^(v) are the arterial, mean capillary, and venous saturation, respectively. The mean capillary and venous saturations are given by <S^(c)> = S^(a)(1 − e^−αt(c))/(αt^(c)) and S^(v) = S^(a)e−^αt(c) (18), in which α is the rate constant of oxygen diffusion and t^(c) is the mean transit time of blood in the capillaries. The impulse response functions associated with the blood transit time in the capillary bed— $\text{bed}—h_{RC-LP}^{(c)}(t)$ —and in the venous compartment— $h_{G-LP}^{(v)}(t)$ —are given by the following resistance-capacitance (RC) and Gaussian low-pass filters (5):

$$h_{RC-LP}^{(c)}(t)=H(t)\frac{e}{t^{(c)}}{e}^{-et/t^{(c)}},$$ (7)

$$h_{G-LP}^{(v)}(t)=\frac{1}{0.6(t^{(c)}+t^{(v)})}{e}^{-\pi {[t-0.5(t^{(c)}+t^{(v)})]}^2/{[0.6(t^{(c)}+t^{(v)})]}^2},$$ (8)

in which H(t) is the Heaviside unit step function—H(t) = 0 for t < 0; H(t) = 1 for t ≥ 0.We note that both impulse responses are convolved with cbf (t) − cmro₂(t) in Equations (1) and (2), as indicated by the convolution operator*.

Measuring the Time Course of cbv and the Difference cbf-cmro₂

In a practical implementation of this hemodynamic model in the time domain, one would like to derive the temporal dynamics of CBV, CBF, and CMRO₂ from the measured time traces of the concentrations of O and D. Equation (3) provides a direct measurement of cbv(t) in terms of the relative change in T with respect to the baseline value T₀ = ctHbCBV₀:

$$\mathrm{c}\mathrm{b}\mathrm{v}(t)=\frac{\mathbf{\Delta }T}{T_0}.$$ (9)

The convolution operator in Equations (1) and (2) introduces a computational complication that can be addressed by Fourier transformation, which converts convolution products into regular products. By denoting the Fourier transforms with tildes and introducing the angular frequency ω, the difference of the Fourier transformed Equations (1) and (2), after normalization by dividing both equations by T₀ = ctHbCBV₀, leads to the following expression for $\widetilde{\mathrm{c}\mathrm{b}\mathrm{f}}(\omega )-{\widetilde{\mathrm{c}\mathrm{m}\mathrm{r}\mathrm{o}}}_2(\omega )$ :

$$\widetilde{\mathrm{c}\mathrm{b}\mathrm{f}}(\omega )-{\widetilde{\mathrm{c}\mathrm{m}\mathrm{r}\mathrm{o}}}_2(\omega )=\frac{\frac{\widetilde{\mathbf{\Delta }O}(\omega )-\widetilde{\mathbf{\Delta }D}(\omega )}{T_0}-(2S^{(a)}-1)\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}{\widetilde{\mathrm{c}\mathrm{b}\mathrm{v}}}^{(a)}(\omega )-(2S^{(v)}-1)\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}{\widetilde{\mathrm{c}\mathrm{b}\mathrm{v}}}^{(v)}(\omega )}{2[\frac{<S^{(c)}>}{S^{(v)}}(<S^{(c)}>-S^{(v)}){\mathrm{Ƒ}}^{(c)}\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}{\mathrm{H}}_{RC-LP}^{(c)}(\omega )+(S^{(a)}-S^{(v)})\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}{\mathrm{H}}_{G-LP}^{(v)}(\omega )]},$$ (10)

in which the complex transfer functions ${\mathrm{H}}_{RC-LP}^{(c)}(\omega )$ and ${\mathrm{H}}_{G-LP}^{(v)}(\omega )$ (which are the Fourier transforms of the corresponding impulse response functions in Eqs. (1) and (2)) are given by (5):

$${\mathrm{H}}_{RC-LP}^{(c)}(\omega )=\frac{1}{\sqrt{1+{\left(\frac{\omega t^{(c)}}{e}\right)}^2}}{e}^{-i{\text{tan}}^{-1}\left(\frac{\omega t^{(c)}}{e}\right)}$$ (11)

$${\mathrm{H}}_{G-LP}^{(v)}(\omega )=e^{-\frac{\text{ln}2}{2}{[\omega 0.281(t^{(c)}+t^{(v)})]}^2}{e}^{-i\omega 0.5(t^{(c)}+t^{(v)})}.$$ (12)

To apply Equation (10) to translate NIRS measurements of ΔO(t) and ΔD(t) (ie, the changes with respect to the corresponding baseline values O₀ and D₀ [once they are Fourier-transformed as $\widetilde{\mathbf{\Delta }O}(\omega )$ and $\widetilde{\mathbf{\Delta }D}(\omega )$ ] into the difference cbf (t) − cmro₂(t) [by inverse Fourier transforming cbf $\widetilde{\mathrm{c}\mathrm{b}\mathrm{f}}(\omega )-{\widetilde{\mathrm{c}\mathrm{m}\mathrm{r}\mathrm{o}}}_2(\omega )$ )]), one needs to:

1. Normalize the measured changes ΔO(t) and ΔD(t) by the baseline total hemoglobin concentration T₀, which is also required to obtain a measure of cbv(t) via Equation (9)

2. Assume the values of the following baseline parameters: S^(a), α, t^(c) (these three parameters also determine <S^(c)> and S^(v)), t^(v), and the blood volume ratios $\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}/\mathrm{C}\mathrm{B}{\mathrm{V}}_0,{\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}/\mathrm{C}\mathrm{B}{\mathrm{V}}_0$ , and $\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}/\mathrm{C}\mathrm{B}{\mathrm{V}}_0$

3. Estimate the dynamic relative changes in the arterial and venous blood volumes $({\widetilde{\mathrm{c}\mathrm{b}\mathrm{v}}}^{(a)},{\widetilde{\mathrm{c}\mathrm{b}\mathrm{v}}}^{(v)})$ in relation to the overall blood volume changes obtained from Equation (9). Because we have set cbv^(c)(t) = 0, the overall blood volume change can be written as follows:

   $$\mathrm{c}\mathrm{b}\mathrm{v}(t)=\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(a)}(t)+\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(v)}(t)$$ (13)

because it can be directly derived by the definition given at the beginning of the Time Domain Equations section: cbv(t) = ΔCBV(t)/CBV₀. If we proceed on the assumption that the time dependence of cbv^(a)(t) and cbv^(v)(t) is the same, then the time dependence of cbv(t) is also the same, they are all proportional to each other and one can write:

$$\mathrm{c}\mathrm{b}{\mathrm{v}}^{(a)}(t)=\sigma \frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}}\mathrm{c}\mathrm{b}\mathrm{v}(t),$$ (14)

$$\mathrm{c}\mathrm{b}{\mathrm{v}}^{(v)}(t)=(1-\sigma )\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}\mathrm{c}\mathrm{b}\mathrm{v}(t),$$ (15)

where σ is a constant such that 0≤σ≤1. If one assumes that cbv^(a)(t) = cbv^(v)(t), then $\sigma =\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}/(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}+\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)})$ .

This analysis shows that it is not possible to disentangle the contributions of the arterial and venous compartments to the dynamics of the overall cbv(t) because, according to Equations (9) and (13), the change in total hemoglobin concentration (which is measured) is related to a weighted average of the blood volume perturbations in the individual compartments. Furthermore, the model shows that only the difference, cbf(t) − cmro₂(t), can be measured by NIRS. We observe that these restrictions are not specific to the model used, but are intrinsic to any technique that measures the cerebral concentrations of O and D.

Frequency Domain Equations

In the frequency domain, the model describes sinusoidal oscillations at a given angular frequency ω. Following the convention of Fantini’swork (5), oscillatory quantities are represented by phasors that are indicated in bold type. The model expressions for O(ω), D(ω), T(ω) (i.e., the phasors that describe the oscillations of O, D, and T concentrations) as a function of cbv(ω), cbf(ω), and cmro₂(ω) (i.e., the phasors that describe the oscillations of CBV, CBF, and CMRO₂) are as follows (11):

$$\mathbf{O}(\omega )=\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}[S^{(a)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(a)}(\omega )+S^{(v)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(v)}(\omega )]++\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}[\frac{<S^{(c)}>}{S^{(v)}}(<S^{(c)}>-S^{(v)}){\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}{\mathrm{H}}_{RC-LP}^{(c)}(\omega )+(S^{(a)}-S^{(v)})\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}{\mathrm{H}}_{G-LP}^{(v)}(\omega )][\mathbf{c}\mathbf{b}\mathbf{f}(\omega )-\mathbf{c}\mathbf{m}\mathbf{r}{\mathbf{o}}_2(\omega )],$$ (16)

$$\mathbf{D}(\omega )=\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}[(1-S^{(a)})\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(a)}(\omega )+(1-S^{(v)})\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(v)}(\omega )]+-\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}[\frac{<S^{(c)}>}{S^{(v)}}(<S^{(c)}>-S^{(v)}){\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}{\mathrm{H}}_{RC-LP}^{(c)}(\omega )+(S^{(a)}-S^{(v)})\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}{\mathrm{H}}_{G-LP}^{(v)}(\omega )][\mathbf{c}\mathbf{b}\mathbf{f}(\omega )-\mathbf{c}\mathbf{m}\mathbf{r}{\mathbf{o}}_2(\omega )],$$ (17)

$$\mathbf{T}(\omega )=\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}[\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(a)}(\omega )+\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(v)}(\omega )],$$ (18)

in which ${\mathrm{H}}_{RC-LP}^{(c)}(\omega )$ and ${\mathrm{H}}_{G-LP}^{(v)}(\omega )$ are the complex transfer function given in Equations (11) and (12), and we have set cbv^(c)(ω) = 0 because of the negligible dynamic dilation and recruitment of capillaries in brain tissue (12–17). The notation in Equations (16)–(18) matches that in Equations (1)–(3), and we stress that the cbv, cbf, and cmro₂ phasors are all dimensionless, with their magnitude indicating the amplitude of oscillations normalized to the average, or baseline, values. Because of the high-pass nature of the cerebral autoregulation process that regulates CBF in response to blood pressure changes (19–21), we consider the following relationship between cbf and cbv (5):

$$\mathbf{c}\mathbf{b}\mathbf{f}(\omega )=k{\mathrm{H}}_{RC-HP}^{(\text{AutoReg})}(\omega )\mathbf{c}\mathbf{b}\mathbf{v}(\omega )=k{\mathrm{H}}_{RC-HP}^{(\text{AutoReg})}(\omega )[\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(a)}(\omega )+\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(v)}(\omega )],$$ (19)

in which k is the inverse of the modified Grubb exponent, ${\mathrm{H}}_{RC-HP}^{(\text{AutoReg})}$ is the RC high-pass transfer function with cutoff frequency ${\omega }_c^{(\text{AutoReg})}$ that describes the effect of autoregulation, and the second equalities follows from Equation (13). More precisely, the expression of the RC high-pass transfer function is:

$${\mathrm{H}}_{RC-HP}^{(\text{AutoReg})}(\omega )=\frac{1}{\sqrt{1+{\left(\frac{{\omega }_c^{(\text{AutoReg})}}{\omega }\right)}^2}}{e}^{i{\text{tan}}^{-1}\left(\frac{{\omega }_c^{(\text{AutoReg})}}{\omega }\right)}$$ (20)

We observe that, while O(t), D(t), and T(t) in the time domain (Eqs. (1)–(3)) represent the absolute concentrations of O, D, and T, the frequency-domain phasors O(ω), D(ω), and T(ω) of Equations (16)–(18) represent oscillations about baseline values.

Measuring Physiological Parameters with CHS

Fourteen physiological parameters appear in the expressions for O(ω), D(ω), and T(ω) (Eqs. (16)–(18)), namely: ctHb, S^(a), α, t^(c), t^(v), $\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)},{\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)},\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}$ , cbv^(a)(ω), cbv^(c)(ω), cbv^(v)(ω), cmro₂(ω), ${\omega }_c^{(\text{AutoReg})}$ , and k. A new method for the assessment of cerebral hemodynamics, CHS, is based on the frequency-resolved measurement of induced hemodynamic oscillations (5) and potentially allows for the measurements of these parameters. Because it is impractical, and in some cases impossible, to control the amplitude and the phase of induced hemodynamic oscillations at different frequencies, we consider the following phasor ratios, thereby canceling unknown common amplitude or phase factors:

$$\frac{\mathbf{D}(\omega )}{\mathbf{O}(\omega )}=\frac{|\mathbf{D}(\omega )|}{|\mathbf{O}(\omega )|}{e}^{i\{\text{Arg}[\mathbf{D}(\omega )]-\text{Arg}[\mathbf{O}(\omega )]\}},$$ (21)

$$\frac{\mathbf{O}(\omega )}{\mathbf{T}(\omega )}=\frac{|\mathbf{O}(\omega )|}{|\mathbf{T}(\omega )|}{e}^{i\{\text{Arg}[\mathbf{O}(\omega )]-\text{Arg}[\mathbf{T}(\omega )]\}},$$ (22)

Furthermore, if the induced hemodynamic oscillations do not involve modulation of the cerebral metabolic rate of oxygen, one can assume cmro₂(ω) = 0, so that the model Equations (16)–(18), in conjunction with Equation (19), yield the following expressions for the phasor ratios of Equations (21) and (22):

$$\frac{\mathbf{D}(\omega )}{\mathbf{O}(\omega )}=\frac{\begin{array}{c}(1-S^{(a)})\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(a)}(\omega )}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(v)}(\omega )}+(1-S^{(v)})\hfill \\ -[\frac{<S^{(c)}>}{S^{(v)}}(<S^{(c)}>-S^{(v)})\frac{{\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{H}}_{RC-LP}^{(c)}(\omega )\hfill \\ +(S^{(a)}-S^{(v)}){\mathrm{H}}_{G-LP}^{(v)}(\omega )]k\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}{\mathrm{H}}_{RC-HP}^{(\text{AutoReg})}(\omega )[\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(a)}(\omega )}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(v)}(\omega )}+1]\hfill \end{array}}{\begin{array}{c}{S}^{(a)}\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(a)}(\omega )}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(v)}(\omega )}+S^{(v)}\hfill \\ +[\frac{<S^{(c)}>}{S^{(v)}}(<S^{(c)}>-S^{(v)})\frac{{\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{H}}_{RC-LP}^{(c)}(\omega )\hfill \\ +(S^{(a)}-S^{(v)}){\mathrm{H}}_{G-LP}^{(v)}(\omega )]k\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}{\mathrm{H}}_{RC-HP}^{(\text{AutoReg})}(\omega )[\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(a)}(\omega )}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(v)}(\omega )}+1]\hfill \end{array}}$$ (23)

$$\frac{\mathbf{O}(\omega )}{\mathbf{T}(\omega )}=\frac{\begin{array}{c}{S}^{(a)}\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(\alpha )}(\omega )}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(v)}(\omega )}+S^{(v)}\hfill \\ +[\frac{<S^{(c)}>}{S^{(v)}}(<S^{(c)}>-S^{(v)})\frac{F^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{H}}_{RC-LP}^{(c)}(\omega )\hfill \\ +(S^{(\alpha )}-S^{(v)}){\mathrm{H}}_{G-LP}^{(v)}(\omega )]k\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}{\mathrm{H}}_{RC-HP}^{(\text{AutoReg})}(\omega )[\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(\alpha )}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(\alpha )}(\omega )}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathbf{c}\mathbf{b}{\mathbf{v}}^v(\omega )}+1]\hfill \end{array}}{\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(\alpha )}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(\alpha )}(\omega )}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathbf{c}\mathbf{b}{\mathbf{v}}^{(v)}(\omega )}+1}$$ (24)

A first observation is that, contrary to the time domain case, by taking the phasor ratios D/O and O/T, we do not have access to cbv(ω). In fact, the blood volume phasor cbv(ω) contains an unknown frequency-dependent term related to the variability of the amplitude of the induced hemodynamic oscillations as a function of frequency, which cancels out in the ratios cbv^(a)(ω)=cbv^(v)(ω) that appear in Equations (23) and (24). Similar to the time domain case, we assume that the blood volume of the arterial and venous compartments have the same frequency dependence, and we take the phase of blood volume oscillations as the phase reference. In other words, we set cbv^(a)(ω) = cbv^(a)(ω) ∠ 0° and cbv^(v)(ω) = cbv^(v)(ω)∠0°, with cbv^(a)(ω) ∝ cbv^(v)(ω), so that the phasor ratio cbv^(a)(ω)/cbv^(v)(ω) is replaced by the real constant cbv^(a)/cbv^(v) in Equations (23) and (24).

A second observation is that of the 14 model parameters, one (ctHb) has canceled out in Equations (23) and (24), and the remaining 13 are combined in Equations (23) and (24) in a way that reduces the number of independent parameters to eight: S^(a), α, t^(c), t^(v), ${\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}/\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)},(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(a)})/(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(v)}),{\omega }_c^{(\text{AutoReg})}$ , and $k\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}/\mathrm{C}\mathrm{B}{\mathrm{V}}_0$ . S^(a), the arterial saturation, typically assumes values greater than 0.95 in healthy adults, and we will set it to 0.98. The two parameters α and t^(c) are always coupled in the product αt^(c) in the expressions for <S^(c)> and S^(v), but t^(c) also appears independently in ${\mathrm{H}}_{RC-LP}^{(c)}(\omega )$ and ${\mathrm{H}}_{G-LP}^{(v)}(\omega )$ . We will assume a value of α = 0.8 seconds⁻¹ on the basis of literature results (22), and we will show how this assumption influences the results presented here. The venous blood transit time t^(v) only appears in ${\mathrm{H}}_{G-LP}^{(v)}(\omega )$ . ${\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}/\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}$ provides a measure of the baseline capillary to venous blood volume ratio, whereas $(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(a)})/(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(v)})=\mathbf{\Delta }\mathrm{C}\mathrm{B}{\mathrm{V}}^{(a)}/\mathbf{\Delta }\mathrm{C}\mathrm{B}{\mathrm{V}}^{(v)}$ is the ratio of the arterial to venous blood volume oscillations. The autoregulation cutoff frequency $({\omega }_c^{(\text{AutoReg})}/(2\pi ))$ , which appears in ${\mathrm{H}}_{RC-HP}^{(\text{AutoReg})}(\omega )$ , provides a measure of the efficiency of cerebral autoregulation (with higher values of the autoregulation cutoff frequency indicating a broader frequency range over which autoregulation is effective). Finally, the high-frequency flow-to-volume amplitude ratio (k) does not appear independently, but rather is coupled with the base-line venous-to-total blood volume through the product $k\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}/\mathrm{C}\mathrm{B}{\mathrm{V}}_0$ .

METHODS

Time Domain

The goal of this work for the time domain is to demonstrate in practical terms how the novel hemodynamic model introduced by Fantini (5,11) can be applied to time-varying hemodynamic signals measured with fNIRS to obtain measures of cbv(t), cbf(t), cmro₂(t). We point out that Equations (9) and (10) show that fNIRS can lead to measures of blood volume, cbv(t), and the difference, cbf (t) − cmro₂(t), not cbf (t) and cmro₂(t) separately. To this aim, we have used simulated data for O(t) and D(t). There are several mathematical functions that have been proposed to describe hemodynamic changes during functional brain activation (23–27). Often used for describing the functional magnetic resonance imaging blood oxygen level–dependent signal as a hemodynamic response function consisting of one or two gamma functions (26). Here we have chosen the following expression for simulating the temporal traces of ΔO(t) and ΔD(t):

$$\gamma (t)=A\left(\frac{{(t-t_0)}^{\delta -1}{\beta }^{\delta }{e}^{-\beta (t-t_0)}}{\mathrm{\Gamma }(\delta )}\right),$$ (25)

in which γ(t) stands for either ΔO(t) or ΔD(t), t is time, and t₀ is the time at which brain activation starts. Γ represents the gamma function, which acts as a normalizing parameter, and δ and β are constants for which we set values of δ = 8 and β = 0.6 seconds⁻¹. The amplitude A was set to 3 µMs for ΔO(t) and − 1 µMs for ΔD(t). These parameters were chosen to best represent typical hemodynamic signals during activation (2,28–30), as seen in Figure 1a, where the ΔO(t) and ΔD(t) traces peak simultaneously at t − t₀ = 11.7s.We set the baseline total hemoglobin concentration T₀ = 55 µM and the baseline tissue saturation S₀ = 65%. These values fall within typical values reported in the literature for the human brain, which range between 42 and 79 µM for T₀, and between 55 and 75% for S₀ (31–36). Because the hemodynamic model depends on several parameters (as described previously), we have studied the sensitivity of cbf (t) − cmro₂(t) on the values assigned to these parameters. We further compared the model output with a steady-state approach that has been used extensively in the literature (37–41). In comparison to the dynamic model (5,11), a steady-state model does not consider any temporal shifts between cbf(t)—or cmro₂(t)—and ΔO(t) or ΔD(t). Mayhew et al. expressed the venous contributions to the tissue concentrations of D and T (D^(v), T^(v)) in terms of the measurable overall tissue concentrations of D and T as follows (41,42):

$$\frac{\mathbf{\Delta }{D}^{(v)}}{D^{(v)}{|}_0}-\frac{\mathbf{\Delta }{T}^{(v)}}{T^{(v)}{|}_0}={\gamma }_r\frac{\mathbf{\Delta }D}{D_0}-{\gamma }_t\frac{\mathbf{\Delta }T}{T_0}=-(\mathrm{c}\mathrm{b}\mathrm{f}(t)-\mathrm{c}\mathrm{m}\mathrm{r}{\mathrm{o}}_2(t)).$$ (26)

in which γ_r and γ_t have been assumed to be constants within the range 0.2 to 5 (41) and D^(v)|₀ and T^(v)|₀ are the baseline deoxy hemoglobin concentration and total hemoglobin concentration in the venous compartment, respectively. Equation (26) fits in the definition of steady-state models because it introduces no temporal shift between the changes in the D and T hemoglobin concentrations (D^(v), T^(v)), and the blood flow and oxygen consumption perturbations (cbf(t), cmro₂(t)) that cause them. Recently, Fantini (11) derived the following explicit expressions for the coefficients γ_r and γ_t, under the approximation (1 − S^(a)) ≅ 0:

$${\gamma }_r=\frac{(1-<S^{(c)}>)\frac{{\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}+(1-S^{(v)})}{\frac{<S^{(c)}>}{S^{(v)}}(<S^{(c)}>-S^{(v)})\frac{{\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}+(S^{(a)}-S^{(v)})},$$ (27)

$${\gamma }_t=\frac{1-S^{(v)}}{\frac{<S^{(c)}>}{S^{(v)}}(<S^{(c)}>-S^{(v)})\frac{{\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}+(S^{(a)}-S^{(v)})\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}}\frac{\mathbf{\Delta }\mathrm{C}\mathrm{B}{\mathrm{V}}^{(v)}}{\mathbf{\Delta }\mathrm{C}\mathrm{B}\mathrm{V}}.$$ (28)

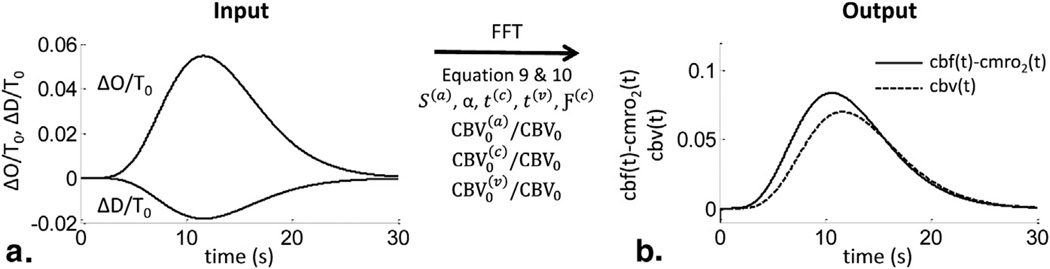
Figure 1.

Workflow of determining (cbv(t)) and cbf(t)−cmro₂ (t) with the new hemodynamic model. (a) Normalized total oxy- and deoxy-hemoglobin (ΔO(t) and ΔD(t)) are the input quantities, measured with functional near-infrared spectroscopy, for the model. By assuming specific values for the physiological model parameters, the optical measurements can be converted into cbv (t) and cbf (t) − cmro 2(t) traces (b). The traces in (b) were obtained by using Eqs. (9) and (10). cbf, relative changes in cerebral blood flow with respect to baseline; CBV, cerebral blood volume; cbv, relative changes in CBV with respect to baseline; crmo₂, relative changes in metabolic rate of oxygen with respect to baseline; FFT, fast Fourier transform; S^(a), arterial saturation; t^(c), capillary blood transit time; Ƒ^(c), Fåhraeus factor in capillaries; blood transit time in capillaries; t, time; t^(v), venous blood transit time.

Using Equations (26)–(28), one can determine the cbf (t) − cmro₂(t) traces derived using the steady-state approach and compare them to those derived using the hemodynamic model of Fantini.

Frequency Domain

The goal of this work for the frequency domain is to demonstrate in practical terms how the novel hemodynamic model introduced by Fantini (5) can be applied to frequency-resolved measurements of induced hemodynamic oscillations to determine the following independent combinations of model parameters: t^(c), t^(v), ${Ƒ}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}/\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)},(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(a)}/\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(v)}),{\omega }_c^{(\text{AutoReg})}$ and $k\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}/\mathrm{C}\mathrm{B}{\mathrm{V}}_0$ , after having assumed specific values for S^(a) = 0.98 (the arterial saturation) and α = 0.8 seconds⁻¹ (the rate constant for oxygen diffusion from the capillary bed to tissue). The methods of obtaining such frequency resolved spectra (CHS) has been described previously (5,10). Here we perform a new analysis of previously collected paced breathing data, which we are analyzing with the novel description of the model in terms of cbf(ω) and cbv(ω) (Eqs. (23) and (24)). Details about the data acquisition methods have been reported previously (10) and are described only briefly here. NIRS measurements were performed with a commercial tissue oximeter (OxiplexTS, ISS, Inc., Champaign, IL) on 11 healthy subjects. The optical probe was placed on the right side of the subject’s forehead. Subjects were asked to perform paced breathing, guided by a metronome. Five subjects performed paced breathing at 11 frequencies (0.071, 0.077, 0.083, 0.091, 0.100, 0.111, 0.125, 0.143, 0.167, 0.200, and 0.250 Hz). Six subjects performed paced breathing at four frequencies (0.071, 0.100, 0.167, and 0.250 Hz). After slow temporal drifts were removed from the data, band-pass filtering was performed around each paced breathing frequency. Based on phasor analysis and using this band-pass filtered data, we could obtain |D|/|O|, |O|/|T|, arg(D) − arg(O), and arg(O) − arg(T) for each paced breathing frequency (with arg describing the angle). For the purpose of this work, we have calculated the average and standard error of the data collected on all 11 subjects. The experimental protocol was approved by the institutional review board, and written informed consent was obtained from all participants before the study.

After setting S^(a) = 0.98 and α = 0.8 seconds⁻¹, we are left with six unknown parameters t^(c), t^(v), $\frac{{Ƒ}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}},\frac{(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(a)})}{(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(v)})},{\omega }_c^{(\text{AutoReg})}/(2\pi )$ , and $\frac{k\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}$ . Those parameters can be determined by fitting experimental data with the model (Eqs. (23) and (24)). We have used a built-in fitting procedure in MATLAB (function “lsqcurvefit”) with the default reconstruction algorithm, which is a trust region reflective algorithm. This algorithm allows one to carry out a reconstruction of the six unknowns by searching within a bounded region of the six parameters’ space. The fitting procedure considers as known or input values the four parameters |D|/|O|, |O|/|T|, arg(D) − arg(O), and arg(O) − arg(T) (measured at multiple frequencies) and finds the optimal set of the six unknown parameters by minimizing a cost function (χ²) that is the sum of the residuals squared. The phase differences were expressed in radians, so that the four different input quantities were of the same order of magnitude. For the fitting procedure, we have set upper and lower limits on the parameters as summarized in Table 1. The lower and upper limits were based on physiological ranges for these parameters. The limits for t^(c) (0.4–1.4 seconds) were set by requiring that the venous saturation be bound between 32 and 71%. The limits for t^(v) correspond to a range of venule lengths of 1 to 3 mm assuming a typical speed of blood flow in venules of 1 mm/s (43). The limits of (0.8–2.4) for the capillary to venous blood volume times the Fåhraeus factor (set to 0.8) correspond to the reported range of ~(0.3–0.65) for the capillary to total blood volume over cortical depths of 0–2.5 mm (44) after assuming that overall arteriole and venule blood volumes are the same. This latter assumption also results in the limits for $\frac{(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(a)})}{(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(v)})}$ (0.2–5) by allowing for a range of scenarios between the extreme cases of arterial-dominated (value of 5) and venous-dominated (value of 0.2) blood volume changes. The limits for the autoregulation cutoff frequency $({\omega }_c^{(\text{AutoReg})}/(2\pi ))$ reflect the full range between a lack of autoregulation (0 Hz) and normal autoregulation (0.15 Hz) (19). Finally, the limits for $k\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}/\mathrm{C}\mathrm{B}{\mathrm{V}}_0$ result from a reported range for k (the inverse of the Grubb’s exponent) of 2 to 5 (45–48) and from the range of venous-to-total blood volume ratio (0.2–0.35) obtained from the capillary to total blood volume ratio (0.3–0.65) in the human brain cortex (44) under the assumption that $\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}=\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}$ . We have used 54 different sets of initial guesses for the six unknown parameters, which were evenly spread out throughout the range of upper and lower bounds of the parameters. For each initial guess, the solution of the six parameters and the corresponding χ² value was stored for further analysis of the obtained solutions.

TABLE 1.

Upper and Lower Limits for the Six Fitting Parameters of the Model

	t(c) (s)	t(v) (s)	$\frac{{Ƒ}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}$	$\frac{(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(a)})}{(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(v)})}$	$\frac{{\omega }_c^{(\text{AutoReg})}}{2\pi }$ (Hz)	$\frac{k\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}$
Lower limit	0.4	1	0.8	0.2	0	0.4
Upper limit	1.4	3	2.4	5	0.15	1.6

(a), contributions from arterial compartments;

(c), contributions from capillary compartments; CBV, cerebral blood volume; cbv, relative change in CBV with respect to baseline; k, inverse of the modified Grubb exponent;

t^(c), capillary blood transit time in seconds (s); t, time;

(v), contributions from venous compartments;

ω_c, cutoff frequency of autoregulation.

RESULTS

Time Domain Results for cbv(t) and cbf(t) − cmro₂ (t)

To obtain the cbv(t) traces, Equation (9) was applied and ΔT(t) was obtained from the sum of ΔO(t) and ΔD(t) (Figure 1a). The corresponding time traces can be seen in Figure 1b (dashed line). To obtain the cbf (t) − cmro₂(t) traces, ΔO(t) and ΔD(t) were first normalized to the baseline total hemoglobin T₀ = 55 µM (Figure 1a). Then, we set the model parameters to typical values obtained from the literature (5). Those values are S^(a) = 0.98, α = 0.8 seconds⁻¹, t^(v) = 2s, Ƒ^(c) = 0.8, $\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}=1$ , and $\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}=0.65$ . Because the baseline tissue saturation was set to S₀ = 65%and the relative arterial, capillary, and venous blood volumes were set to the values reported previously, the transit time in the capillaries could be calculated as t^(c) = 1.23s from the following equation that expresses the tissue saturation as a weighted average of the arterial, capillary, and venous saturation:

$$S_0=\frac{S^{(a)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}+S^{(a)}\frac{1-\text{exp}(-\alpha t^{(c)})}{\alpha t^{(c)}}{\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}+S^{(a)}\text{exp}(-\alpha t^{(c)})\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}.$$ (29)

Furthermore, we assumed the arterial and venous volume perturbations to have the same magnitude and time dependence (ie, cbv^(a)(t) = cbv^(v)(t) or $\sigma =\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}/(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}+\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)})$ using the notation of Equations (14) and (15)). Taking the fast Fourier transform (FFT) of ΔO(t) and ΔD(t), we found $\widetilde{\mathrm{c}\mathrm{b}\mathrm{f}}(\omega )-{\widetilde{\mathrm{c}\mathrm{m}\mathrm{r}\mathrm{o}}}_2(\omega )$ from Equation (10), and by applying an inverse FFT (FFT⁻¹), we found cbf (t) − cmro₂(t) as shown in Figure 1b.

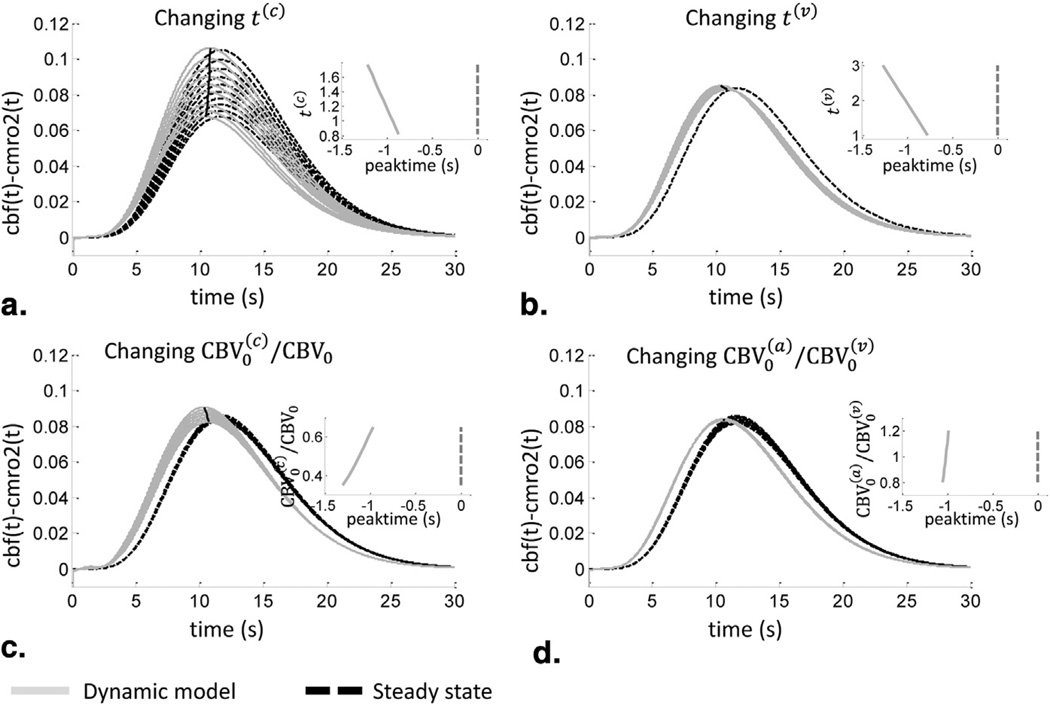
The determination of cbv(t) is model-independent and only depends on ΔT(t) and T₀ as shown by Equation (9). To determine the sensitivity of the derived trace of cbf (t) − cmro₂(t) on the assumed values for the model parameters, we have considered multiple values of the input parameters. First, the sensitivity to the capillary transit time, t^(c), was evaluated (Figure 2a). Keeping all other parameters fixed to the values used to generate Figure 1, we assumed a range of the tissue saturation S₀ from 75 to 55%, which correspond, according to Equation (29), to a range for t^(c) of 0.8 to 1.8 seconds. The associated variability in the derived traces of cbf (t) − cmro₂(t) can be seen in Figure 2a (solid light gray lines). The magnitude of cbf (t) − cmro₂(t) ranges from 0.07 for t^(c) = 1.8s to 0.11 for t^(c) = 0.8s. The steady-state solution of cbf (t) − cmro₂(t) was also determined by using Equations (26)–(28) with the traces of ΔO(t) and ΔD(t). In comparison to the dynamic model, the steady-state solutions (dashed black lines) show the same magnitude change, with γ_r varying between 0.86 and 0.99 and γ_t varying between 0.86 and 1.04. In addition, the peak time for cbf (t) − cmro₂(t) differs between the dynamic model prediction and the steady-state solutions as seen in the inset of Figure 2a. By definition, the steady-state prediction shows a peak time coincident with the peak times of ΔO(t) and ΔD(t). The dynamic model, however, predicts an earlier rising of cbf (t) − cmro₂(t) in comparison to ΔO(t) and ΔD(t), with peak times preceding the hemoglobin signals by 0.9 seconds for t^(c) = 0.8s and 1.2 seconds for t^(c) = 1.8s. This temporal lead of the physiological changes (cbf (t) − cmro₂(t)) with respect to the measured signals ΔO(t) and ΔD(t) is the result of the blood transit time in the microvasculature.

Figure 2.

Sensitivity of cbf(t)−cmro₂(t) on the model parameters and comparison to the steady-state predictions, with cmro₂ indicating metabolic rate of oxygen. (a) The dependence on the capillary blood transit time (t^(c)), (b) the venous blood transit time (t^(v)), (c) the relative capillary blood volume, and (d) on the arterial to venous blood volume ratio. Dynamic model results (solid light gray lines); steady-state results (dashed dark black lines). Insets show the peak time of cbf(t)−cmro₂(t) (on the x axis) calculated with the dynamic model with respect to the peak time of O(t) (broken line at 0) as a function of the parameters considered in each panel. See Figure 1 for additional definitions.

We have set α = 0.8 seconds⁻¹. The rate constant of oxygen diffusion can be estimated by α = D/d², where D is the diffusion coefficient of oxygen in tissue and d is the intercapillary distance. For the oxygen diffusion coefficient D, literature values of 1.7 × 10⁻⁵ to 2 × 10⁻⁵ cm²/s have been reported for brain tissue (22,49,50). Values of ~40–60 µm have been reported for the intercapillary distance d in the rat brain and human gray matter (51–53). These reported measured ranges for D and d lead to a range of possible oxygen diffusion rate constants α of 0.4 to 1.2 seconds⁻¹. We have evaluated the influence of α by keeping the baseline tissue saturation S₀ constant at 65%. Based on Equation (29), the capillary transit time for a given α was calculated and the corresponding cbf (t) − cmro₂(t) traces were obtained (data not shown). We found that the magnitude of cbf (t) − cmro₂(t) was independent of the value of α, provided that the product αt^(c) is kept constant. However, the peak time of cbf (t) − cmro₂(t) varied by 400 ms because of the variability in t^(c).

The effect of changing the venous transit time t^(v) between 1 and 3 seconds can be seen in Figure 2b, where again we kept constant all other model parameters and the baseline tissue saturation, which was set to S₀ = 65%. A change in magnitude as well as in peak time of cbf (t) − cmro₂(t) can be seen. However, the effect of changing t^(v) is negligible in comparison to the effect of t^(c). For the steady-state solutions, we found γ_r = 0.93 and γ_t = 0.96. According to the dynamic model, changing the capillary-to-total blood volume ratio, $\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}$ , between 0.3 and 0.65, we observe a magnitude change between 0.08 and 0.09 and a change in peak time that precedes by 0.9 to 1.3 s the peak time of ΔO(t) and ΔD(t) as seen in Figure 2c. Again, the steady-state solutions show comparable magnitudes, with γ_r within the range 0.93–0.97 and γ_t within the range 0.96–0.99. Last, changing the arterial-to-venous blood volume ratio, $\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}$ , between 0.8 and 1.2 did not result in a magnitude change in the dynamic model determination of cbf (t) − cmro₂(t), as seen in Figure 2d. The peak times were only slightly affected, ranging from 0.97 to 1.05 seconds. Also in this case, the steady-state solutions show a comparable magnitude, with γ_r within the range 0.93–0.94 and γ_t within the range 0.91–1.02.

Frequency Domain Results

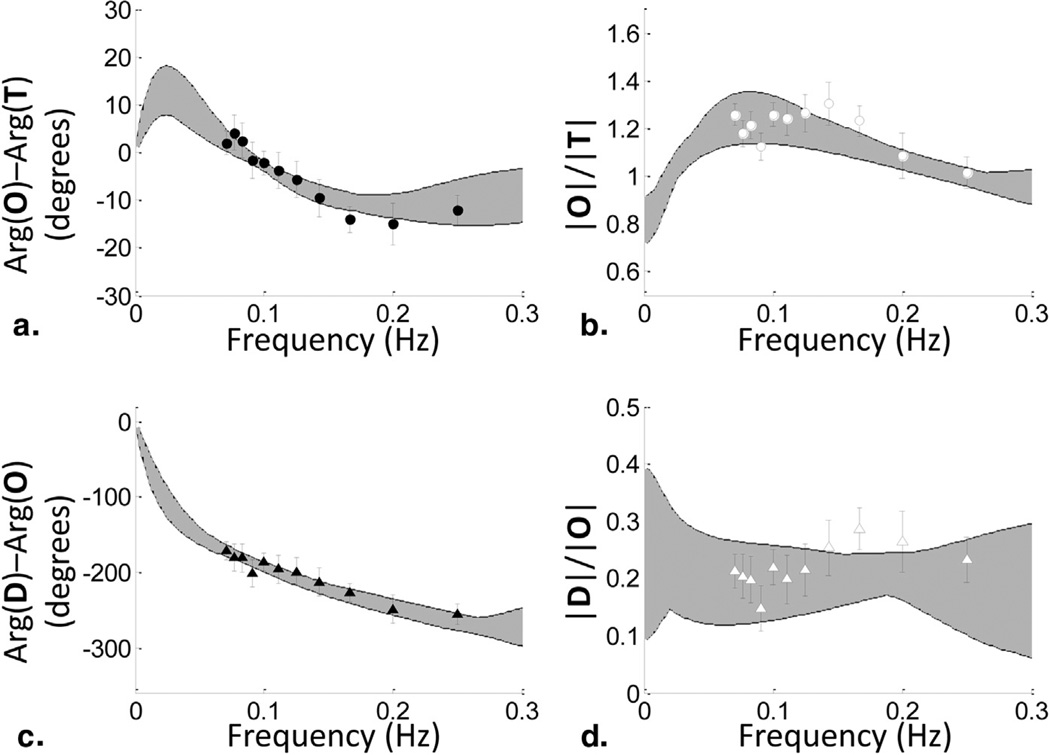
Figure 3 shows the experimental results of the average data set from 11 paced breathing subjects, with the data points being the mean values of the data collected on the 11 subjects and the error bars showing the standard error. Launching 54 initial guesses for the six parameters of the fitting procedure, we found 54 times the same final values with the same minimum χ² value. Those parameter values were: t^(c) = 1.19 seconds, t^(v) = 1 s, $\frac{{Ƒ}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}=1,\frac{(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(a)})}{(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(v)})}=4.14,{\omega }_c^{(\text{AutoReg})}/2\pi =0.04\text{Hz}$ , and $\frac{k\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}=0.47$ . However, although the solution with the smallest χ² value is a robust solution in terms of independence of the initial guess, there are other solutions with marginally larger χ² values that also result in good fits to the data. Because the fitting procedure used did not provide errors of the solutions and did not take the standard error of the experimental data into account, we included a number of solutions for each parameter corresponding to a range of χ² values, with the criteria being that the fit for |D|/|O|, |O|/|T|, arg(D) − arg(O), and arg(O) − arg(T) goes through all the experimental data points and their error bars.

Figure 3.

Experimental results of frequency-resolved measurements of cerebral hemodynamic oscillations during a paced breathing protocol in human subjects. (a) Phase difference between phasors O and T, arg(O) − arg(T); (b) amplitude ratio |O|/|T|; (c) phase difference between D and O, arg(D) − arg(O); and (d) amplitude ratio |D|/|O|. The symbols and error bars were obtained by averaging the data over the 11 subjects and taking the standard errors. A set of spectra corresponding to a range of χ² values corresponding to model results that fall within the data error bars is shown (shaded areas).

The shaded area in Figure 3 contains all the spectra for |D|/|O|, |O|/|T|, arg(D) − arg(O), and arg(O) − arg(T) for a set of solutions for the six parameters that results in χ² values that are within a range of 0.02 (the minimum χ²) to 0.15. The solutions for the data set shown in Figure 3 are summarized in Table 2, where we report the mean value and standard deviation of the set of acceptable values for each parameter. The cutoff frequency, ${\omega }_c^{(\text{AutoReg})}/(2\pi )$ , which provides a measure of the efficiency of cerebral autoregulation, shows the smallest relative standard deviation (5.7%) of all six parameters.

TABLE 2.

Results of the Fitting Procedure for the Six Parameters of the Model, Reported in Terms of Their Mean Value and Standard Deviation

	t(c) (s)	t(v) (s)	$\frac{{Ƒ}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}$	$\frac{(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(a)})}{(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(v)})}$	$\frac{{\omega }_c^{(\text{AutoReg})}}{2\pi }$ (Hz)	$\frac{k\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}$
Mean ± SD	0.92 ± 0.18	1.29 ± 0.26	1.08 ± 0.27	2.95 ± 0.85	0.035 ± 0.002	0.59 ± 0.10

(a), contributions from arterial compartments;

(c), contributions from capillary compartments; CBV, cerebral blood volume; cbv, relative change in CBV with respect to baseline; k, inverse of the modified Grubb exponent;

t(c), capillary blood transit time in seconds (s); t, time;

(v), contributions from venous compartments;

ω_c, cutoff frequency of autoregulation.

As in the time domain, we kept α = 0.8 s⁻¹. However, as discussed previously, a may vary between ~0.4 and 1.2 s⁻¹. We evaluated the dependence of the frequency domain results on α by making it an independent parameter in the fit (data not shown). It was found that the mean values of the six parameters stay within one standard deviation of the mean values reported in Table 2, further validating the assumption of keeping α constant.

DISCUSSION

In the time domain, we have used simulated data for ΔO(t) and ΔD(t) and shown how the novel hemodynamic model by Fantini (5,11) can be used to obtain traces of cbf (t) − cmro₂(t), in addition to the cbv(t) trace directly derived from ΔT(t). The temporal traces of cbv(t) and cbf (t) − cmro₂(t) are descriptive of the underlying physiology of cerebral activation, so that they can be used to investigate the processes associated with brain activity or to detect and assess neurovascular deficits. We have shown that the obtained traces are robust in terms of magnitude and temporal shift for varying t^(v), $\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}}$ , and $\frac{\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}}{\mathrm{C}\mathrm{B}{\mathrm{V}}_0}$ , with the magnitude change being between 0.08 and 0.09, which is a variability of 10%. For those three parameters of the model, we have found that the time of the peak was also shifted with a variability of ~500 ms. The one parameter of the model that resulted in a large variability of cbf (t) − cmro₂(t) magnitude was the capillary transit time t^(c), in which the magnitude showed a variability of 50%. However, the t^(c) range considered here corresponds to a wide range in the tissue saturation S₀ of 55 to 75%. A measurement of S₀, as opposed to an assumption based on literature values, can provide a more precise estimate and a smaller uncertainty in the magnitude of cbf (t) − cmro₂(t). For example, a range of 62 to 68% for S₀ corresponds to a magnitude variability for cbf (t) − cmro₂(t) of 15%. As a result, by assuming typical values for the model parameters and by refining these assumptions by appropriate baseline measurements, the model yields reliable traces for the temporal evolutions of cbv(t) and cbf (t) − cmro₂(t).

We have assumed the baseline total hemoglobin concentration, T₀, to be known. From this, we were able to derive time-dependent traces for volume changes, cbv(t), as seen in Figure 1b. If however, T₀ is not known while assuming the other model parameters to be known, and we allow a range of values of T₀ from 42 to 79 µM, the magnitude of cbv(t) will vary between 0.05 and 0.09. The corresponding magnitude change in cbf (t) − cmro₂(t) would show a variability from 0.06 to 0.11. As pointed out for S₀, this variability can be drastically reduced if absolute values of T₀ are known.

We have further evaluated the dependence on α, where we found that the magnitude of cbf (t) − cmro₂(t) is only dependent on the product αt^(c), which is fixed when keeping the baseline tissue saturation constant at S₀ = 65%. However, as seen in Equation (29), S₀ depends on the relative volumes of the three vascular compartments, which are typically not known. Alternatively, instead of setting the constrain on S₀, one could set a constrain on the venous saturation, which does not depend on the blood volume fractions being given by S^(v) = S^(a)e^−at(c) (18).

Because of the dynamic nature of the novel hemodynamic model, we were able to report cbf (t) − cmro₂(t) time traces, which showed an earlier rising and peak time than the steady-state version reported in the literature (41,42). Also, Fantini (11) reported analytical expressions for the empirical constants γ_r and γ_t, which we have used here, allowing us to have access to those values. We found both γ_r and γ_t to be ~1, which falls within typical literature values, with 0.75 to 1.25 being reported to be a plausible physiological range (42).

For the frequency domain part of the model, we have used experimental data from a paced breathing paradigm designed to induce hemodynamic oscillations, described by phasors O and D, at multiple frequencies. Using a fitting procedure, the new hemodynamic model yielded the values of six physiological parameters that are related to the cerebral hemodynamics in the microvasculature. The first two parameters—t^(c) and t^(v)—provide a measure of the blood transit time in the capillary bed and in the venous compartment that lies within the optically probed volume. These are the two parameters that determine, according to this new model, the delay (in the time domain) or the phase lag (in the frequency domain) between the hemoglobin concentration changes measured with NIRS and the underlying CBF and CMRO₂ changes. The model does not allow for a complete determination of the relative arterial, capillary, and venous blood volume, but it yields the ratio of the capillary to venous blood volume (where the capillary blood volume contains the Fåhraeus factor: ${\mathrm{Ƒ}}^{(c)}\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(c)}/\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}$ . The ratio between the magnitudes of the arterial and venous blood volume oscillations— $\frac{(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(a)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(a)})}{(\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}\mathrm{c}\mathrm{b}{\mathrm{v}}^{(v)})}$ —contains the ratio of arterial to venous blood volume, which is expected to be close to 1 in the microvasculature (because of the symmetrical architecture of the arteriolar and venular branches) but may deviate from 1 in the presence of larger arterial or venous vessels within the tissue volume probed by NIRS. The autoregulation cutoff frequency $({\omega }_c^{(\text{AutoReg})}/(2\pi ))$ was found to be robustly determined by fitting the measured CHS spectra with the new model. However, it is important to point out that it is not defined in terms of systemic arterial blood pressure and global cerebral blood flow as typically done in the literature (19,54). By contrast, cerebral autoregulation is defined here in terms of the local cerebral blood flow and the microvascular blood volume as described by Equation (19). This accounts for a specific physiological meaning of the autoregulation cutoff frequency as defined here, and more work is needed to fully characterize its information content and its meaning in relation to the conventional definition of cerebral autoregulation. The asymptotic blood flow to volume ratio (k) (i.e., the ratio between changes in blood flow and changes in blood volume in the absence of autoregulation) cannot be measured by the approach presented here, unless an assumption is made on the venous to total blood volume ratio because it appears in the parameter $k\mathrm{C}\mathrm{B}{\mathrm{V}}_0^{(v)}/\mathrm{C}\mathrm{B}{\mathrm{V}}_0$ . These six physiological parameters have a diagnostic potential for any neurovascular disorder or brain damage that impact the cerebral hemodynamics and microvascular integrity. Recently, we have demonstrated the clinical applicability of CHS to patients in the hemodialysis unit, for whom we found a significantly slower cerebral microvascular blood flow with respect to a group of healthy controls (55).

Similar to the time domain case, we have set α = 0.8 s⁻¹. We have found that by considering α as a variable parameter and fitting for α does not change the results for the other six parameters, confirming that the reported solutions are insensitive to α. This insensitivity results from the fact that only the ratios of the hemodynamic signals are considered. Because, as shown in the time domain, a together with t^(c) determine a magnitude change in the data, the effect is canceled out by taking the ratios of |D|/|O|, |O|/|T|. This lack of sensitivity to absolute changes in D and O makes the fitting procedure robust for determining the other six parameters of the model.

CONCLUSIONS

We have demonstrated how the novel dynamic hemodynamic model by Fantini (11) can be applied to analyze NIRS measurements of time-varying hemodynamics (time domain) and frequency-dependent hemodynamic oscillations (frequency domain). In the time domain, the model can be used to convert measured O(t) and D(t) traces into cbf (t) − cmro₂(t) traces. We have shown that the magnitude of cbf (t) − cmro₂(t) is relatively insensitive to the model parameters if the absolute values of baseline total hemoglobin concentration (T₀) and tissue saturation (S₀) are known. It is inherent to fNIRS data that cbf (t) and cmro₂(t) cannot be accessed independently. If, however, an independent measurement of cbf (t) is available, a decoupling of cbf (t) and cmro₂(t) is, of course, possible. In the frequency domain, the model has led to the novel CHS method, which is based on measurements of induced hemodynamic oscillations at multiple frequencies as described by phasors O(ω) and D(ω). Here, the model can be used to derive the blood transit time in capillaries and venules, the cutoff frequency for cerebral autoregulation, and measures of capillary-to-venous blood volume ratio and arterial-to-venous blood volume changes.

This formulation of the new hemodynamic model results in a practical analytical tool that can find broad applicability in the study of functional brain activation and cerebral hemodynamic assessment with NIRS. In particular, measurements of cerebral blood volume, blood flow, and metabolic rate of oxygen are of paramount importance in studies of brain activation and neurovascular coupling. The quantitative assessment of brain microvascular hemodynamics, cerebral autoregulation, and cerebrovascular reactivity can have farreaching implications in the diagnosis and assessment of a variety of neurovascular disorders, traumatic brain injury, and stroke.