On the use of coupled shape priors for segmentation of magnetic resonance images of the knee

Abstract

Active contour techniques have been widely employed for medical image segmentation. Significant effort has been focused on the use of training data to build prior statistical models applicable specifically to problems where the objects of interest are embedded in cluttered background. Usually the training data consists of whole shapes of certain organs or structures obtained manually by clinical experts. The resulting prior models enforce segmentation accuracy uniformly over the entire structure or structures to be identified. In this paper, we consider a new coupled prior shape model which is demonstrated to provide high accuracy, specifically in the region of the interest where precision is most needed for the application of the segmentation of the femur and tibia in magnetic resonance (MR) images. Experimental results for the segmentation of MR images of human knees demonstrate that the combination of the new coupled prior shape and a directional edge force provides the improved segmentation performance. Moreover, the new approach allows for equivalent accurate identification of bone marrow lesions (BMLs), a promising biomarker related to osteoarthritis (OA), to the current state of the art but requires significantly less manual interaction.

I. Introduction

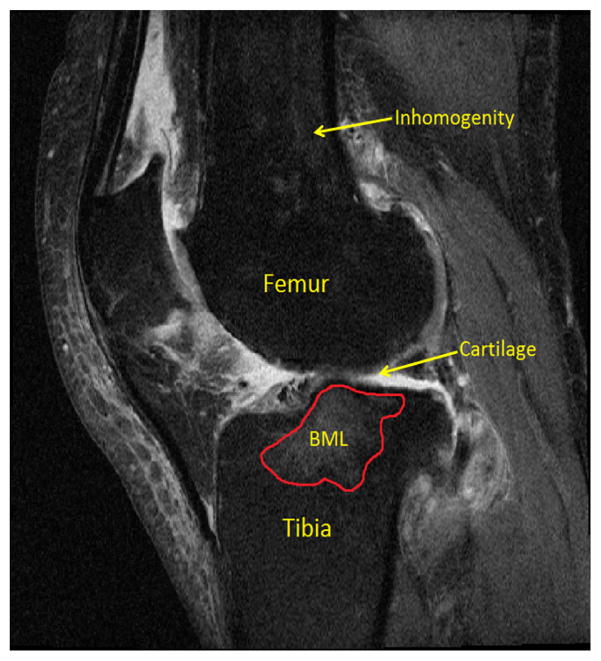
Osteoarthritis (OA) is a common debilitating disease afflicting over 71 million people globally. Due to its large social and economical burden, significant resources have been directed to understanding the pathophysiology of OA. Cartilage degeneration is an important index of OA progression, thus a large number of image processing-based quantitative measurement methods for cartilage measurement [1]–[6] have been developed to aid clinical researchers. In addition to cartilage, bone marrow lesions (BMLs) also represent a common OA-related MRI finding associated with structural degeneration and pain [7]–[11]. From an image processing perspective, characterization of cartilage and BMLs tend to follow a two-step approach: locate the bones, then locate the cartilage or BMLs. This strategy is necessitated by the challenges associated with identifying cartilage or BMLs directly. As shown in Fig. 1, knee cartilage is quite thin relative to the femur and tibia, may be affected with poor contrast in the image and cartilage defects may well indeed comprise multiple cartilage components depending on the state of OA in the knee and the image slice being segmented. In the case of BMLs, it is difficult to extract and quantify these structures directly due to the uncertain shapes, numbers and locations of BMLs [12]. Thus most researchers [10], [13]–[15] also prefer to segment bone first to either define a region of interest (ROI) in which BMLs may be located or to serve as reference for healthy bone.

Fig. 1.

An MRI knee image with femur, tibia, cartilage, BML denoted.

Although characterizations of cartilage and BMLs follow the same two-step approach, the MR sequences for imaging cartilage and BMLs are very different [16]. The MR sequences for cartilage evaluation suppress the inhomogeneity (mainly BMLs) [1]–[6] while in the MR sequences for BMLs segmentation, the heterogeneity in the bone regions is more prominent [7]–[11]. State of the art bone segmentation methods [1]–[6] have been designed and validated for the former type of data. Unfortunately, as we demonstrate in Section III-A, the application of these methods to the data of interest here results in degraded performance specifically for those cases where there is significant structure within the bones such as BMLs.

Motivated by these results, in this article, we present an active contour algorithm based on the level set framework [17], [18]. It is designed to segment femur and tibia on data collected using a BML protocol. Active contours have been widely used in medical image segmentation problems [19], [20] and can be divided into two classes: region-based and edge-based. In the case of the region-based approach, a number of statistically-driven curve evolution techniques have been developed. For example, the well-known Chan-Vese model [21] implicitly assumes that the intensity distribution of object and background are Gaussian with the same variance, and as a consequence seeks a segmentation which minimizes, in part, a mean square error-type of objective function. For cases where such a parametric model is not appropriate, a variety of nonparametric techniques have been developed most often based on the estimation of pixel-intensity probability distribution functions (PDFs) constructed using the kernel density estimation (KDE) method [22]. These approaches employ training data to construct prior distributions for the object and background pixels. From these estimated PDFs, objects are identified using curve evolution algorithms designed to maximize the match between the PDFs constructed for an estimated object and background relative to these priors. Here we point to a range of metrics that have been developed to measure quality of the match including the Kullback-Leibler (KL) distance [23], the Bhattacharyya distance [24] etc. However the size, location and the intensity histogram of the inhomogeneous area and the BMLs within the bone area (see Fig. 1 and other figures in Section III) are uncertain in our knee bone segmentation problem making the intensity distributions of bones very difficult to model. Thus as we demonstrate in Section III-A, region-based active contours have a difficult time performing well for our problem.

In contrast to region-based active contour, edge-based active contour [25] tends to suffer from limited capture range and sensitivity to initialization. Thus many active contour methods based on the use of image gradient information have been developed to address this challenge. Xu and Prince [26] developed the Gradient Vector Flow (GVF) method which not only increases the capture range for edge-based contours but also is bidirectional which means initial curves are not necessary to be either inside or outside true boundaries as required in [25] etc. Later, Li and Acton [27] proposed Vector Field Convolution (VFC). The VFC field is generated simply by convolving the image edge map with a suitably designed vector field kernel. Although certain anatomical structures of the knee bone exists in our problem, noise, clutter, BMLs and degeneration in the boundaries yield rather poor performance for purely edge-based active contour methods.

Due to noise, artifacts, and other inconsistencies encountered when dealing with real data, active contour techniques typically require some form of regularization to achieve suitable results in practice. While generic curvature based methods were initially considered [17], in recent years, there has been considerable effort directed toward the use of prior instances of segmented shapes for purposes of regularization [28]–[35]. Generally, there are two ways to encode prior shape information into a level set-base active contour segmentation scheme. The first one is to represent the level set function ϕ as a linear combination of basis functions obtained via principal component analysis (PCA) applied to the signed distance functions in the training set [33], [35]. Modifications to the methods in [33], [35] include the use of binary prior shapes in [31], [36], Kernel PCA of binary prior shapes in [36] and the addition of constraints on the evolution of the PCA coefficients in [31]. The second way to incorporate prior shape is to use a penalty term to ensue that the evolving curve does not move “far” from the reference shapes. In [28], [29], the authors consider the use of a single such reference shape. Extensions to libraries of prior observed shapes include the work in [30], [32], [37] based on kernel density estimation (KDE) techniques to estimate the similarities between a shape and a set of training shapes as well as [30], [32] where the metrics to evaluate the similarities between two shapes are also mentioned and briefly discussed. The introduction of KDE into the prior shape model as in [30] and [32] employed the shape information for each image in the training set and thus improved the capability to capture large shape variances when segmenting test data.

All the prior shape methods mentioned above are for single object problems. For the case of segmenting multiple components, not only the shape of each object or component but also the relative positions among objects could be used as prior information for segmentation. Tsai et al. [38] directly extended their PCA prior shape model of single object [33], [35] for multiple objects. In addition to the shape information, Han et al. [39] proposed an algorithm to maintain the number of initial disconnected components during the evolution of multiple curves while Sundaramoorthi and Yezzi [40] designed a coupling repulsive force to realize the same functionality. In addition, Zimmer et al. [41] used a penalty term to prevent two curves from overlapping each other. Moreover [42], [43] designed specific coupling forces to take into account more information about the relative position or topology of the object structure. In addition, Ma et al. proposed a shape influence term [44] to incorporate relative distance information and used the region competition scheme [45] for the segmentation of female pelvic organs [46]–[48]. Moreover, the Coupled Nonparametric Shape (CNS) [49] model used the KDE [22] to incorporate the prior shape information and extended the single prior shape model in [32] to multiple components situation for the segmentation of basal and ganglia structures.

In the case of BMLs within the knee, clinicians are especially concerned with accuracy in the vicinity of the joint. The key contribution of the work in this paper is the adaptation of shape prior methods to account for this type of region-specific accuracy requirement in the context of a multi-part segmentation problem in [7] to the curve evolution process. More specifically, of primary concern in this paper is the segmentation in the vicinity of the joint where we seek a method that can identify the individual bones reliably even when provided with imagery containing BMLs corrupting the bones themselves. In our coupled shape model, this prior places strong constraints on the segmentation in the region near the joint (i.e. areas within the two horizontal lines as show in Fig. 2(a)) where the separate components (femur and tibia segments) must be kept from either merging or moving too far from one another even in the presence of significant clutter from BMLs, cartilage etc. Moreover, the model provides less of a constraint in those areas further from the joint in our case where either accuracy is not required (e.g. inhomogeneous area in Fig. 1). Here we want to point that the idea of [49] is similar to ours but still like other prior shape methods, [49] also evaluates the match uniformly over the whole image domain which is not what we seek for the knee segmentation problem and, as we show empirically in Section III-A, does not perform quite as well as the approach we suggest for the problem of interest here.

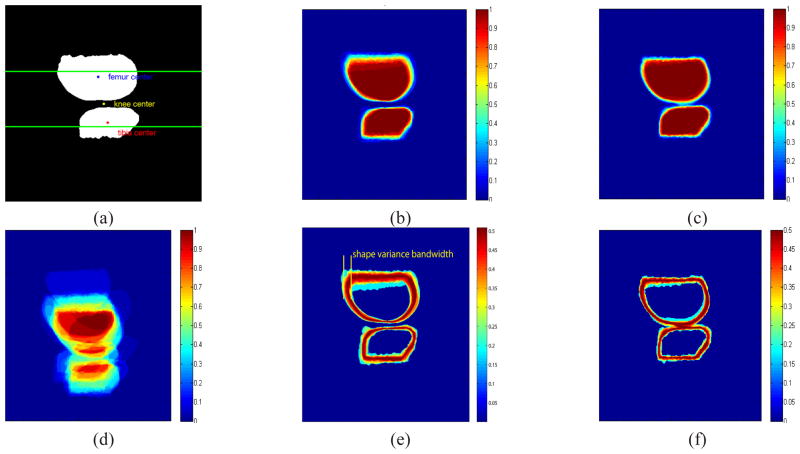
Fig. 2.

(a) The reference image for alignment and our primary concern is the area near the joint which is between the two horizontal lines. (b) Aligned shape stack with respect to the newly defined knee centers u_ϕ. (c) Aligned femur with respect to the femur center u_ϕ1 and tibia center u_ϕ2 individually (CNS model in [49]). (d) Unaligned shape stack. (e)(f) Standard deviation of aligned shape stacks with respect to (b)(c) respectively.

In addition to the coupled prior shape model, active contours can be driven by image based forces (region-based or edge-based). As mentioned before, it is very challenging to build region-based forces due to the uncertain size, location and intensity histogram of BMLs within the bone region. Moreover, the femur and tibia are separated by the cartilage which is very thin as shown in Fig. 1. Thus edge force fields generated by the femur/cartilage interface and tibia/cartilage interface using e.g., GVF and VFC methods can overwhelm with each other as illustrated in Figure 4. To overcome this difficulty, we adapt the directional edge information idea [50], [51], adjust and apply it to our knee segmentation problem. By combining the coupled prior shape model and the directional force field, we demonstrate that our active contour model is robust to initializations and can segment the femur and tibia accurately even in highly cluttered situations. Another major contribution of this paper is the development and validation of our active contour model for knee bone segmentation and sequently BML segmentation and quantification which yields comparable results but requires far less human interaction with the data than competing methods.

Fig. 4.

(a) A MRI knee image with region of interest (red box), the femur-cartilage and tibia-cartilage interfaces within region of interest are denoted by the blue and green lines respectively. (b) Original VFC field. (c) Directional VFC field based on $f_d^1(x,y)$. (d) Directional VFC based on $f_d^2(x,y)$. In (b) neither of the interfaces are preserved. In (c)(d), the femur-cartilage and tibia-cartilage are well preserved respectively.

Before moving on, we note that the work in this paper is concerned primarily with the processing of two dimensional (2D) images with relatively large slice thickness and inter-slice gap. The fact that state of the art in cartilage segmentation does consider the full three dimensional (3D) problems such as [3], [4] is due at least in part to the availability of MRI data sets characterized by small slice thickness and usually no interslice gaps. As illustrated in Section III-A, the 3D methods have similar results as our 2D method when bone regions are homogeneous and with few BMLs but their performance does degrade when large BMLs and other inhomogeneities are present. This fact indicates the advantages of our method in cases of great relevance to BML analysis. Based on our validated 2D method in this paper, we feel that extension to 3D is best left to the future.

The remainder of this paper is organized as follows. In Section II, we present the level set framework of knee segmentation and our coupled prior shape model as well as the directional edge based force. Then experimental results are presented and discussed in Section III. Finally, we draw our conclusion and discuss our future work in Section IV.

II. Segmentation based on Coupled Prior Shape and Directional Edge Force

In this section, we first set up the framework of curve evolution for our knee segmentation problem in Section II-A. In Section II-B and Section II-C, our coupled prior shape model and the directional Vector Field Convolution (DVFC) are illustrated respectively. The implementation details are presented in II-D.

A. Framework of curve evolution

The essential idea of level set methods for segmentation is to represent a curve C⃗(t) as the zero slice of an auxiliary level set function ϕ(x, t) where t is an artificial time parameter; i.e., C⃗(t) = {x|ϕ(x, t) = 0)}. Active contour techniques using level set functions “evolve” ϕ as a function of time such that, as t → ∞, C⃗(t) approaches the the contour of interest in the image. Since we are going to handle two curves simultaneously, we use two level set functions to model the shapes of both femur and tibia¹. Thus, we seek to identify two closed curves C⃗₁ and C⃗₂ which we define as the zero level sets of functions ϕ₁ and ϕ₂ respectively

$${\overrightarrow{C}}_k=\{\mathbf{x}\in {\mathrm{\Omega }}_k\mid {\varphi }_k(\mathbf{x})=0\},k=1,2,$$

where Ω₁ and Ω₂ represent the femur and tibia respectively. By using the chain rule, an evolution equation of ϕ_k is

$$\frac{\partial {\varphi }_k}{\partial t}=-\nabla {\varphi }_k·\mathbf{F}(\mathbf{x}),$$ (1)

where F(x) = x_t is known as the speed function. If F(x) is in the normal direction of C⃗(t), then (1) becomes

$$\frac{\partial {\varphi }_k}{\partial t}=\mid \nabla {\varphi }_k\mid F(\mathbf{x}),$$ (2)

where F(x) = |F(x)| is the magnitude of F(x).

The essential work of various active contour methods [21], [24], [26], [27], [30], [32], [37] is to design the speed function F(x) or F(x). From the variational perspective, some of these forces are conservative vector fields which means they equal the gradient of a scalar functional. Those conservative vector fields are always oriented towards the normal direction of C⃗_k(t) [52] and result in evolution processes of the form in (2). Usually energy functionals based on image fitting [21], [24], [53], [54] and prior shape modeling [28]–[30], [32] are constructed and the corresponding forces are derived. From a force balance perspective [26], [27], [52], F(x) could also be designed directly without constructing the associate energy functional [26], [27], [43], [55].

In this paper, we present two novel force fields denoted by ${\mathbf{F}}_{cs}^k$ and ${\mathbf{F}}_{\mathit{dvfc}}^k$ which act upon the curve C⃗_k(k = 1, 2). Since ${\mathbf{F}}_{cs}^k$ is derived from a Coupled Shape prior based energy functional and its direction is toward the normal direction of C⃗_k, we only focus on its magnitude $F_{cs}^k$. In addition, ${\mathbf{F}}_{\mathit{dvfc}}^k$ is constructed directly by incorporating Directional information to the existing Vector Field Convolution method [27]. By combining those two forces, we have the following evolution equation

$$\frac{\partial {\varphi }_k}{\partial t}=\lambda \mid \nabla {\varphi }_k\mid F_{cs}^k(\mathbf{x})-\nabla {\varphi }_k·{\mathbf{F}}_{\mathit{dvfc}}^k(\mathbf{x}),k=1,2,$$ (3)

where λ is a positive coefficient to balance these two force fields, $F_{cs}^k$ is derived from a shape prior while ${\mathbf{F}}_{\mathit{dvfc}}^k$ from the edge information. In the following two sections, we illustrate how to build $F_{cs}^k$ and ${\mathbf{F}}_{\mathit{dvfc}}^k$ respectively.

B. Coupled Prior Shape Force

Similar to [30], [32], [37], we employ the KDE method [22] to capture our prior shape information. Instead of modeling p(ϕ₁) and p(ϕ₂) separately, we model the joint probability density function p(ϕ₁, ϕ₂) as follows

$$p({\varphi }_1,{\varphi }_2)\propto \frac{1}{N}\sum _{i=1}^{N}exp\left\{-\frac{D_i({\varphi }_1,{\varphi }_2)}{2{\sigma }_{\varphi }^2}\right\}$$ (4)

resulting in the corresponding Coupled Shape energy

$$E_{cs}=-logp({\varphi }_1,{\varphi }_2),$$

where D_i(ϕ₁, ϕ₂) is a shape dissimilarity metric between ϕ₁, ϕ₂ and the corresponding shapes in the ith training sample and N is the number of training samples. In addition, σ_ϕ is the kernel width. One contribution in this paper is that our design of a novel D_i(ϕ₁, ϕ₂) discussed below. We set ${\sigma }_{\varphi }^2$ the mean squared nearest-neighbor distance following [30].

By using the calculus of variation, we have

$$\frac{\partial E_{cs}}{\partial {\varphi }_k}=\frac{{\sum }_{i=1}^N{D}_{i}exp\{-\frac{D_i}{{2\sigma }_{\varphi }^2}\}\frac{\partial D_i}{\partial {\varphi }_k}}{2{\sigma }_{\varphi }^2{\sum }_{i=1}^{N}exp\{-\frac{D_i}{2{\sigma }_{\varphi }^2}\}}$$ (5)

where k = 1, 2 and thus the force derived from the prior shape driving curve evolution can be defined by

$$F_{cs}^k=-\frac{\partial E_{cs}}{\partial {\varphi }_k},k=1,2.$$ (6)

Next, we introduce a new coupled prior shape model to describe the knee shape for both femur and tibia as well as their relative positions simultaneously by defining a new D_i(ϕ₁, ϕ₂). For the ith training image i = 1, 2, ···, N, we obtain the shape of the femur and tibia and denote their corresponding level set functions as ${\psi }_1^i$ and ${\psi }_2^i$ respectively. For all i, we pre-process the data to ensure that, ${\psi }_1^i$ and ${\psi }_2^i$ are aligned via only translation (i.e., no rotation or scaling) with respect to the “center” of the two objects structure as illustrated in Fig. 2(a) and defined rigorously below. The aligned shapes of knees are displayed in Fig. 2(b).

For arbitrary level set functions ϕ₁ and ϕ₂ (for femur and tibia respectively in our knee problem), the dissimilarity between the pair of ϕ₁ and ϕ₂ and the pair ${\psi }_1^i$ and ${\psi }_2^i$ is defined by

$$D_i({\varphi }_1,{\varphi }_2,{\psi }_1^i,{\psi }_2^i)={\int }_{\mathrm{\Omega }}{[H_{2,\epsilon }({\varphi }_1(\mathbf{x}+{\mathbf{u}}_{\varphi }))+H_{2,\epsilon }({\varphi }_2(\mathbf{x}+{\mathbf{u}}_{\varphi }))-H_{2,\epsilon }({\psi }_1^i)-H_{2,\epsilon }({\psi }_2^i)]}^{2}d\mathbf{x}.$$ (7)

The approximate Heaviside function H_2,ε(·) is defined in [21] as

$$H_{2,\epsilon }(z)=\frac{1}{2}\left(1+\frac{2}{\pi }arctan(\frac{z}{\epsilon })\right).$$ (8)

For simplicity, we use H(·) to represent H_2,ε(·) through the paper. In addition, the knee center u_ϕ is defined as follows (see Fig. 2(a)). First, the centroids of the femur and tibia are computed. We define u_ϕ as a point that lies on the line crossing the femur and tibia centroids with the same distance to both bones. Formally u_ϕ is given by

$${\mathbf{u}}_{\varphi }=s{\mathbf{u}}_{{\varphi }_1}+(1-s){\mathbf{u}}_{{\varphi }_2},$$ (9)

where

$${\mathbf{u}}_{{\varphi }_i}=\frac{\int \mathbf{x}H({\varphi }_i)d\mathbf{x}}{\int H({\varphi }_i)d\mathbf{x}},i=1,2$$

and s ∈ (0, 1) such that

$$d({\mathbf{u}}_{\varphi },{\mathrm{\Omega }}_1)=d({\mathbf{u}}_{\varphi },{\mathrm{\Omega }}_2).$$

Here d(u_ϕ, Ω_k), k = 1, 2 denotes the distance from u_ϕ to the region Ω_k.

Eqn. (7) is inspired by the intrinsic alignment shape model proposed by [30]. The major difference between our coupled prior shape model and [30] is the definition of u_ϕ. In [30], u_ϕ is defined as the center of gravity of a single shape. In our situation, since the clinical researchers are mostly interested in the femur and the tibia near the joint, people usually do not segment the parts of the femur and the tibia far from the joint in a consistent way (see Fig. 2), meaning that the center of gravity for both the femur and tibia are not consistently defined. However the newly defined u_ϕ in (9) takes into account this factor by linking itself to the geometry of the gap between the bones where we do have significant information and where accuracy is most required. Moreover, our method is also different from [49] in two aspects. Firstly, for each component, the aligned center is still defined as the center of gravity of that component which means the prior shape constraint is still imposed uniformly around the shape rather than in a specific region. In addition, [49] use the summation of KDE of the shape of each component to build the energy functional and establish the coupling relationships among components.

As an example, we show in Fig. 2, the results of aligning 30 femur and tibia support functions from the data set used to validate our approach in Section III. The reference image within the training set for alignment is displayed in Fig. 2(a). In Fig. 2(c) the centroids of the individual bones are used to aligned the tibia and femurs as in [49]. In Fig. 2(b), we display the result of jointly aligning both bones with respect to u_ϕ defined in (9). As can be seen both from the overlay of the individual images in the training sets (Figures 2(b) and (c)) as well as from the maps of the variance in each pixel of the aligned training sets (Figures 2(e) and (f)), the coupled shape approach provides greater stability and thus a stronger geometric constraint precisely in the region of most interest for this problem; i.e., in the vicinity of the joint. As mentioned, due to the inconsistency of shape far from the joint in the training set, the alignment with respect to the centroids of femur and tibia individually causes large variance near the joint region as shown in Fig. 2(f) indicating week constraint there [34].

$$\begin{array}{c}\frac{\partial D_i}{\partial {\varphi }_1}=2\delta ({\varphi }_1(\mathbf{x}))\{[H({\varphi }_1(\mathbf{x}))+H({\varphi }_2(\mathbf{x}))-H({\psi }_1^i(\mathbf{x}-{\mathbf{u}}_{\varphi }))-H({\psi }_2^i(\mathbf{x}-{\mathbf{u}}_{\varphi }))]\\ +s\frac{{(\mathbf{x}-{\mathbf{u}}_{{\varphi }_1})}^T}{\int H({\varphi }_1)d\mathbf{x}}\int [H({\varphi }_1({\mathbf{x}}^{\prime }))+H({\varphi }_2({\mathbf{x}}^{\prime }))-H({\psi }_1^i({\mathbf{x}}^{\prime }-{\mathbf{u}}_{\varphi }))-H({\psi }_2^i({\mathbf{x}}^{\prime }-{\mathbf{u}}_{\varphi }))]\delta ({\varphi }_1({\mathbf{x}}^{\prime }))\nabla {\varphi }_1({\mathbf{x}}^{\prime })d{\mathbf{x}}^{\prime }\},\\ \frac{\partial D}{\partial {\varphi }_2}=2\delta ({\varphi }_2(\mathbf{x}))\{[H({\varphi }_1(\mathbf{x}))+H({\varphi }_2(\mathbf{x}))-H({\psi }_1^i(\mathbf{x}-{\mathbf{u}}_{\varphi }))-H({\psi }_2^i(\mathbf{x}-{\mathbf{u}}_{\varphi }))]\\ +(1-s)\frac{{(\mathbf{x}-{\mathbf{u}}_{{\varphi }_2})}^T}{\int H({\varphi }_2)d\mathbf{x}}\int [H({\varphi }_1({\mathbf{x}}^{\prime }))+H({\varphi }_2({\mathbf{x}}^{\prime }))-H({\psi }_1^i({\mathbf{x}}^{\prime }-{\mathbf{u}}_{\varphi }))-H({\psi }_2^i({\mathbf{x}}^{\prime }-{\mathbf{u}}_{\varphi }))]\delta ({\varphi }_2({\mathbf{x}}^{\prime }))\nabla {\varphi }_2({\mathbf{x}}^{\prime })d{\mathbf{x}}^{\prime }\}\end{array}$$ (10)

By using calculus of variation, we obtain the gradient flow of (7) as (10) where the delta function δ(·) in (10) is defined as the derivative of H_2,ε. Details concerning the derivation of (10) are provided in the Appendix.

C. Directional vector field convolution force

The force $F_{cs}^k$ stems from prior shape information discussed above is the gradient of an associated energy functional. However, forces can be also designed directly without constructing the corresponding energy functionals from a force balance perspective. One drawback of the VFC and GVF method is that weak edges might be overwhelmed by the strong edges especially for our knee segmentation problem in the cartilage region [27], [55]. Inspired by the works of [43], [50], [51], we constructed a directional VFC force field which incorporates direction information into the VFC method.

A VFC field F(x) = F(x, y) is usually obtained by convolving a feature map f(x, y) with a kernel ker(x, y) = [ker_x(x, y), ker_y(x, y)],

$$\mathbf{F}(x,y)=[f(x,y)\ast {\mathit{ker}}_x(x,y),f(x,y)\ast {\mathit{ker}}_y(x,y)],$$

where f(x, y) is usually taken as the edge map which usually is a single plane image of edge magnitudes. The kernel ker(x, y) is

$$\mathbf{ker}(x,y)=m(x,y){\mathbf{n}}^{\prime }(x,y),$$

where m(x, y) is the magnitude of the ker(x, y) at location (x, y). We adapt the power form definition of m(x, y) as defined in [27]

$$m(x,y)={(r+{\epsilon }^{\prime })}^{-\gamma }$$ (11)

and

$${\mathbf{n}}^{\prime }(x,y)=[-x/r,-y/r]$$ (12)

except n′(0, 0) = [0, 0] and $r=\sqrt{x^2+y^2}$, ε′ is a small number to prevent division by zero and γ is a positive number to control the decrease. The continuous ker(x, y) is discretized over a region {(x, y)|x, y = −R, · · ·, −1, 0, 1, · · · R} for implementation and R denotes the kernel radius. More information about the edge map f(x, y) and the kernel ker(x, y) can be found in [27].

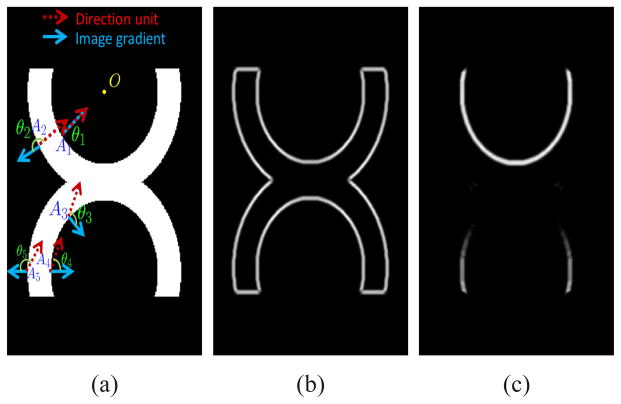
From the MRI knee imagery in e.g., Figure 1, we see that the healthy femur and tibia are the dark regions separated by the cartilage and surrounded by tissue. Because both cartilage and tissue are brighter than the femur and tibia, there exists some directional information about femur and tibia edges that can be incorporated into the VFC model. Here we draw on the ideas in [51] using the synthetic image Fig. 3 to help illustrate the concepts.

Fig. 3.

(a) Original image. O represents a reference point. Red dash arrow represents direction unit. Blue solid arrow denotes image gradient. Five typical points are represented by A₁–A₅. (b) Conventional image edges. (c) Directional image edges.

Assume the reference point O in Fig. 3 has the coordinate (x₀, y₀), then the directional edge map is

$$f_d(x,y)=\{\begin{array}{cc}\nabla I(x,y)·\mathbf{n},& 0\le \theta <\pi /2\\ 0,& \mathit{else}.\end{array}$$ (13)

where $\mathbf{n}=(x-x_0,y-y_0)/\sqrt{{(x-x_0)}^2+{(y-y_0)}^2}$ and θ is the angle between n and ∇I which is the gradient of the image. From Fig. 3, we can see that the outer edge is omitted in the directional edge map. For example, A₂, A₅ are typical points in the outer edges and we can see that θ₂, θ₅ > π/2. In addition, the inner edge in the center part such as A₃ is also omitted which will prove quite useful for the knee problem.

In our knee problem, we let (x_k, y_k) be a point within the femur (k=1) and the tibia (k=2) and denote the angle between the vector (x − x_k, y − y_k) and the image gradient, ∇I, as θ_k(x, y). We now note that only the edges with 0 ≤ θ_k(x, y) < π/2 are the valid edges for the femur Ω₁ and the tibia Ω₂ and thus we have the directional edge map for this structure as follow

$$f_d^k(x,y)=\{\begin{array}{cc}\nabla I(x,y)·{\mathbf{n}}_{\mathbf{k}},& 0\le {\theta }_k<\pi /2\\ 0,& \mathit{else}.\end{array}$$ (14)

where ${\mathbf{n}}_{\mathbf{k}}=(x-x_k,y-y_k)/\sqrt{{(x-x_k)}^2+{(y-y_k)}^2}$ and θ_k is the angle between ∇I and n_k.

Thus the directional VFC force can be defined by

$$\begin{array}{c}{\mathbf{F}}_{\mathit{dvfc}}^k=[f_d^k(x,y)\ast {\mathit{ker}}_x(x,y),f_d^k(x,y)\ast {\mathit{ker}}_y(x,y)],\\ k=1,2.\end{array}$$ (15)

To illustrate the utility of this new force, consider the knee data shown in Fig. 4(a) with the smaller region of interest provided along with a number of VFC-based force fields. From Fig. 4(b), we observe that the traditional VFC force field “leaks” into the inter-bone region which will degrade the resulting segmentation. For example the tibia edges in the middle and the femur edges in left up are overwhelmed in Fig. 4(b). Alternatively, Fig. 4(c) and (d) show that the edges of femur and tibia are well preserved by incorporating direction information respectively.

D. Implementation

By combining the shape prior force $F_{cs}^k$ and the directional VFC based force ${\mathbf{F}}_{\mathit{dvfc}}^k$ and according to (3), we get the curve evolution equation for our knee segmentation problem as

$$\frac{\partial {\varphi }_k}{\partial t}=\lambda F_{cs}^k-{\mathbf{F}}_{\mathit{dvfc}}^k·\nabla {\varphi }_k,k=1,2$$ (16)

where the λ is a positive coefficient to balance these two forces, $F_{cs}^k$ and ${\mathbf{F}}_{\mathit{dvfc}}^k$ are defined in (6) and (15) respectively. In addition, ϕ₁ and ϕ₂ are regularized as Signed Distance Functions [17], [18] and for each iteration, ϕ₁ and ϕ₂ are updated, then the centroid u_ϕ is updated according to (9). For the Heaviside function H(·) and the delta function defined in (8) and its derivative d(·), we use ε = 1.5.

For the directional VFC force, we set the location reference points (x₁, y₁) and (x₂, y₂) as the centroids for the initial curves for the femur and tibia respectively. The kernel radius R is set to 15 in all of our experiments which is at the same scale of the shape variance bandwidth as displayed in Fig. 2(e). In addition, we set γ = 1.5 and ε′ = 0.002. We also scale $F_{cs}^k$ to have maximum value equal to one at each iteration leaving λ to determine the relative impact of the two forces. In all experiments presented in this paper λ = 0.5 so that the force due to the prior is generally a bit smaller than that of the edges. With this weighting, in the early stages of the evolution we see two effects. First, ${\mathbf{F}}_{\mathit{dvfc}}^k$ allows the curves to quickly converge to those portions of the bones characterized by well defined edges. At the same time, for those areas where the edges are less well defined or where there is clutter, the prior shape term keeps the curve from straying too far from ground truth. At the later stages of the algorithm after the clear edges are identified, in some of the more ambiguous regions, ${\mathbf{F}}_{\mathit{dvfc}}^k$ will then move the curve to better find the true edges than would have been the case were only the shape prior used.

The convergence criterion for the curve evolution process is that if the region size change of ϕ₁ ≥ 0 and ϕ₂ ≥ 0 is less than 2 pixels between two adjacent iterations and we assume that the force balance is achieved.

III. Experiment and discussion

To evaluate the validity of our new knee bone segmentation method, we conducted two experiments based on the Osteoarthritis Initiative (OAI) databases, which are available for public access at http://oai.epi-ucsf.org. All images were obtained using the Siemens Trio 3T MR systems and a USA instruments quadrature transmit-receive knee coil at one of four OAI clinical sites. The MR sequences were acquired using sagittal intermediate weighted, turbo spin echo, fat-suppressed MR sequences (field of view = 160 mm, slice thickness = 3 mm, skip = 0 mm, flip angle = 180 degrees, echo time = 30 ms, recovery time = 3200 ms, 313 × 448 matrix [interpolated to 512 × 512, phase encode superior/inferior. x resolution = 0.357 mm, and y resolution = 0.511 mm). The first experiment aims to illustrate the type of scenario where our prior model provides improved performance relative to a number of state-of-the-art, comparable segmentation techniques such as [3], [4], [30].

In the second experiment, we explore the performance of the bone segmentation approach developed in this paper in the context of BML identification. As shown in Fig. 5, in [10] we developed and validated a BML segmentation scheme that was based on a two-step process involving first the segmentation of the bones and then the identification of BMLs using a modified Chan-Vese [21] curve evolution technique which accounted for the bones structures. Unlike the approach in this paper, the bone segmentation strategy in [10] uses a combination of edge and local region information [55] to overcome the challenges associated with the bone inhomogeneities. Since both edge and local region information based forces are sensitive to initial curves, for the method in [55] the user needs to initialize two polygons close to the femur and tibia boundaries for each MR slice, a process requiring significant manual interaction with the data. In Section III-B, we compare BML localization performance when using the method in [10] to that obtained when bone segmentation is accomplished via the approach in this paper with the second step being identical to that of [10]. We demonstrate that despite a factor of 30 drop in the time required for human interaction with the data, ultimate accuracy in identification of BMLs is impacted relatively little.

Fig. 5.

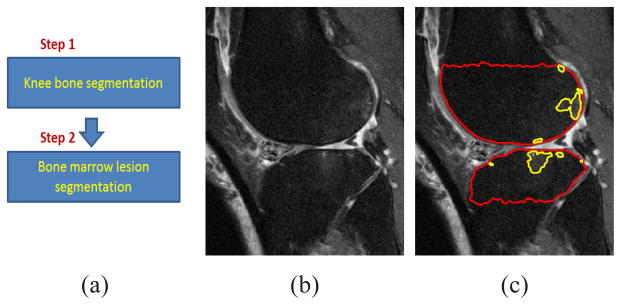
(a) Scheme for knee bone and BML segmentation. (b) Original MR image. (c) Knee bone and BML segmentation results. Red and yellow lines denote the knee bone and BML segmentation respectively.

A. Segmentation results on MRI slice with typical BMLs

We begin by comparing the method of interest in this paper to a number of comparable techniques for the segmentation of the femur and tibia from the data sets described at the beginning of Section III. Of specific interest are robustness to two issues: intensity inhomogeneities (mainly BMLs, see Fig. 1) within the bone regions and curve initialization. Because many BMLs are located close to the edges of bones, robustness to intensity inhomogeneities is needed to ensure that BML regions are not excluded from the bone areas. Moreover, robustness to curve initialization means that our method requires less effort to initialize which is essential to reduce user interaction thereby facilitating the analysis of large data sets.

We build two coupled prior shape models for the lateral and medial knee respectively. For each model, thirty training slices are used. The initial curves are two blue circles inside the femur and the tibia respectively as displayed in Figure 6. In Figures 6 and 7, we provide a collection of segmentation results comparing the method proposed in this paper to a number of alternative techniques. To be clear, in all cases the results are obtained using images that are not in the associated training sets. In both Figures 6 and 7, the ground truth knee bone segmentations are as displayed as red lines. The ground truth knee bone segmentation were obtained by well trained researchers at Tufts Medical Center using Matlab Graphic User Interface (GUI) tools as described in [10]. In addition, an expert looked over all of the segmentation results and adjusted them as necessary.

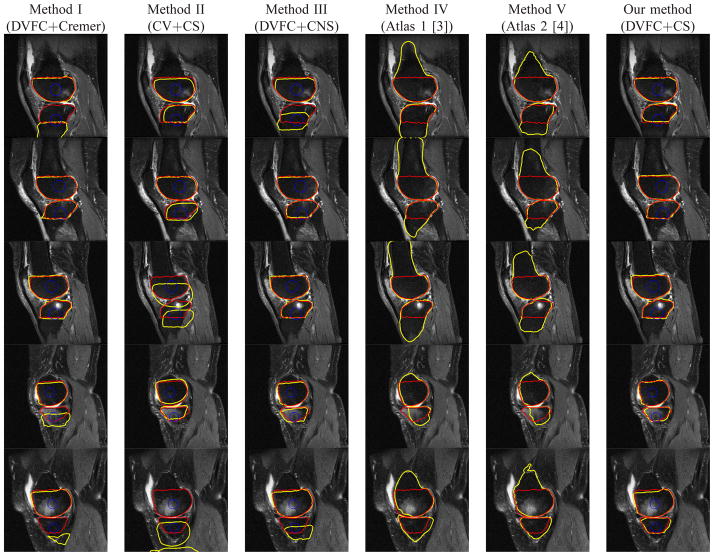
Fig. 6.

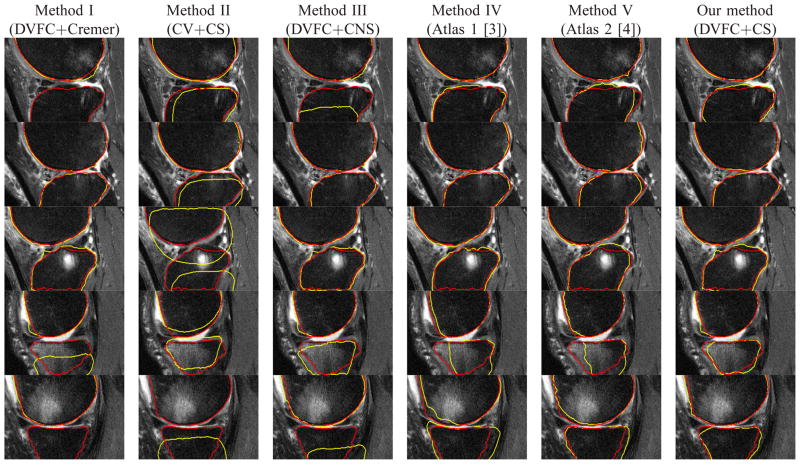
Example segmentation results for a number of images from data set discussed in Section III-A. The red line denotes the ground truth for the femur and tibia, the blue line represents initial curves and the yellow line represents the segmentation results. Rows: individual cases. Columns 1 to 6: results using Methods I (DVFC+Cremer), II (CV+CS), III (DVFC+CNS), IV [3], V [4] and our method (DVFC+CS) respectively. Methods IV and V are 3D atlas based method and no initial curve is used.

Fig. 7.

Corresponding zoomed - in images for the areas near the joint in Fig. 6.

Method I (DVFC+Cremer) uses two separate prior shapes (Cremer’s model) for femur and tibia plus the directional VFC force. Method II (CV+CS) uses our coupled prior shape plus the Chan-Vese’s image term. Method III (DVFC+CNS) uses the directional VFC force and the coupled nonparametric shape model [49]. Our proposed method (DVFC+CS) is the combination of the directional VFC force and our coupled prior shape model. In addition to these four curve evolution based methods, we also present results from two 3D atlas based methods [3], [4] which are considered as state of the art 3D knee bone segmentation techniques for cartilage imaging based MR sequences. These 3D methods [3], [4] are applied to the entire MR slice stack for each knee but here only results for slices are displayed for direct comparison with the 2D methods. Figure 6 provides representative results for the methods described previously. From Figure 6, we can see that Method I (DVFC+Cremer) provided strong results in some cases (the second and the third rows), but we observe in the results in the first, the fourth and the fifth rows that the tibia contours are trapped in local minima. Method II (CV+CS), preserves the relative position between the segmented femur and tibia as well as the bone shapes but the inhomogeneous pixels distributions in both bones due to the BMLs prevent the curve evolve to the desired position especially in the third and the fifth rows. Method III (DVFC+CNS) does have some improvements over Method I (DVFC+Cremer) in the first, fourth and the fifth rows, but it seems that the inter components constraint of the CNS model [49] is not strong enough to draw curves into the right position. In general, Method IV (Atlas 1) [3] and V (Atlas 2) [4] do a good job in most cases except in cases that very large BML exists such as in the fourth and fifth rows where some degradation can be seen. In particular, the BMLs volumes for the knees in the fourth and fifth rows of Figure 6 are 1.53cm³ and 14.1cm³ for the femur and 8.4cm³ and 0.8cm³ for the tibia while the BMLs volumes for the knees in the first to the third rows are 3.2cm³, 1.2cm³ and 2.7cm³ for the femur, 1.9cm³, 1.3cm³ and 2.2cm³ for the tibia. Our method (DVFC+CPS) outperforms the other methods in those knee images, because the directional edge-based force could push the contours into the right position and the coupled prior shape force preserves both the femur and tibia shape and as well as the relative positioning information.

Figure 7 displays the magnified areas near the joints of the images in Figure 6. Here we see that an added complication associated with the processing of the BMLs data set is that the articular cartilage may have a lower signal intensity than normal (e.g., closer to the signal intensity of bone) due to anatomical features and/or the composition of articular cartilage. Some examples can be found in parts of the tibial cartilage in the first and the third rows of Fig. 7. Essentially two things could cause cartilage to look darker - the structural composition of cartilage could be different (e.g., a different amount of water in the tissue) or certain areas of the knee or certain knee shapes may be predisposed to having abnormal signal intensity in the cartilage. In such kind of challenging cases, our method does degrade a bit, but still is no worse than other methods as shown in Fig. 7.

For more quantitative analysis, we compare the accuracy of our approach to Methods I (DVFC+Cremer), III (DVFC+CNS), IV (Atlas 1) [3] and V (Atlas 2) [4] as the poor performance of Method II (CV+CS) in Figs. 6 and 7 was generally the case for a wider range of knees thereby precluding this approach from further consideration. As the basis for the quantitative analysis, we consider the average symmetric surface distance (AvgD) as defined in [56] but here adapted to the 2D problem. In a bit more detail, we start by extracting the boundary pixels in our segmentation results as well as in the ground truth. For each pixel on the boundary of the segmentation, the nearest pixel in the reference is determined and the Euclidean distance between them is calculated and saved. Then for each boundary pixel in the ground truth, the closest pixel in the segmentation boundary is found and the Euclidean distance between them is computed and stored. Finally the average distance of all the stored values is the AvgD. In addition, to better quantify the segmentation error near the knee joint region, we also calculated the AvgD for boundaries in region between the two horizonal lines as shown in Fig. 2(a) as well as Figs 8. The distance between these lines is 120 pixels and the distances from the centroids of knee bones for each image to the upper and bottom lines are 70 and 50 pixels respectively.

Fig. 8.

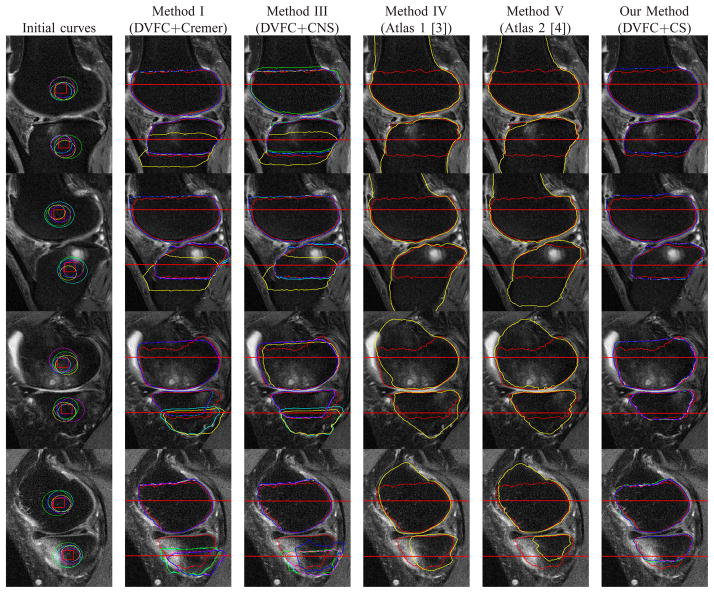
Example segmentation results for a number of images from data set discussed in Section III-A. Rows: individual cases. Column 1: Randomly generated initialing curves (circles). The centers of these circles uniformly distribute within the red squares and their radii uniformly distribute within 15 to 30. Columns 2, 3 and 6: the results based on Methods I (DVFC+Cremer), III (DVFC+CNS) and our method (DVFC+CS). Columns 4 and 5: red line denotes the ground truth, yellow line denotes the segmentation results based on Method IV and V. Different colors (yellow, blue, cyan, green and magenta) represent the results based on the corresponding initial curves in column 1 and the red line denotes the ground truth. The area near the joint where the AvgD is evaluated is denoted by red horizontal lines.

We pick 20 MRI slices with BMLs. These 20 MRI slices are from 10 patients with age 61 ± 8. Most of these patients have BLOKS [57] BML score 2 or 3 (0 means healthy and 3 means the worst). In addition, about 2 MR slices were chosen manually by identifying the slices of the largest BMLs per patient. Then we use randomly generated circles as initial curves and apply our method (DVFC+CS) and Methods I (DVFC+Cremer) and III (DVFC+CNS) to these 20 MRI slices. The centroids of these circles are uniformly distributed within the red squares (20 × 20 pixels) in the first column of Fig. 8, the radii of these circles are uniformly distributed between 15 and 30 pixels. Some of the segmentation results are displayed in Fig. 8. For each initialization, we compute the AvgD values near the joint between knee bone segmentation and the ground truth and then we calculate the mean and standard deviation of the AvgD values regard to different initializations for each slice. Since Methods IV (Atlas 1) [3] and V (Atlas 2) [4] do not use initial curves, the AvgD near the joint is computed only once. Detailed information including the mean and standard deviation for AvgD values near the joint of various methods is displayed in Fig. 9. The curve evolution methods (Method I, Method III, our method) work well for the femur but Methods I (DVFC+Cremer) and III (DVFC+CNS) are very sensitive to the initial curves in slices 1, 2, 4, 6, 12, 14, 19 and 20 (8 out of 20) for the tibia. In Table I, both the mean and the standard deviation of the AvgD statistic for our method are substantially smaller than those of Methods I (DVFC+Cremer) and Method III (DVFC+CNS) which means that our method not only better captures the true boundary of the tibia but also is more robust to different initializations.

Fig. 9.

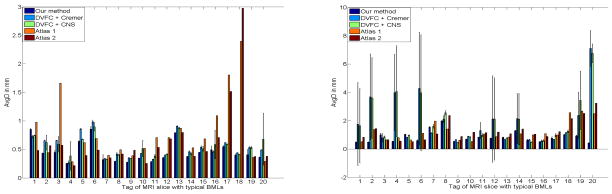
The error bar figures of the AvgD values regarding different initializations. Left and right figures represent the AvgD values for the femur and the tibia respectively. The MR slices are tagged from 1 to 20 in ascending order to their knee BMLs volumes in the femur for the left figure and in the tibia for the right figure.

TABLE I.

AvgD values near the joint of different methods to the ground truth (unit: mm)

Structure	Our Method	Method I	Method III	Method IV	Method V
Femur	0.459 ± 0.187	0.543 ± 0.201	0.545 ± 0.167	0.795± 0	0.651 ± 0
Tibia	0.845 ± 0.392	1.944 ± 1.675	2.000 ± 0.629	1.216± 0	1.301 ± 0

The 3D atlas methods (Methods IV and V) work well except Method IV [3] for slices 3, 16, 17 and 18 (4 out of 20) and Method V [4] for slices 17 and 18 (2 out of 20) mainly due to very large BMLs in the femur. Here we assume slices with AvgD values for the femur larger than 1mm are failures. For the tibia, Methods IV [3] and V [4] perform well except slices 18 to 20 (3 out of 20) for Method IV and slices 8, 18 to 20 (4 out of 20) for Method V again mainly caused by large BMLs. We assume slices with AvgD values for the tibia larger than 2mm are failures, since the mean AvgD value for tibia is much larger than that of femur.

The AvgD values (excluding failure slices) near the joint of various methods are displayed in Table II. We can see that after excluding the failure slices, the AvgD values near the joint for our method and the 3D atlas methods are almost the same for the femur while for the tibia, the 3D atlas methods are slightly larger (about 0.14mm). Therefore our method performs slightly better than state of the art 3D Methods IV [3] and V [4] for cases where there are no or few BMLs. However we do significantly better when inhomogeneity areas such as BMLs within the knee bones are apparent. This is exactly the case for which our method is designed.

TABLE II.

AvgD values near the joint (excluding failure slices) of different methods to the ground truth (unit: mm)

Structure	Our Method	Method I	Method III	Method IV	Method V
Femur	0.459 ± 0.187	0.543 ± 0.201	0.545 ± 0.167	0.560 ± 0	0.474 ± 0
Tibia	0.845 ± 0.392	0.953 ± 0.432	1.032 ± 0.575	0.976 ± 0	0.986 ± 0

B. Application on the BML segmentation

In this section, we show that our method could provide comparable accuracy to the BML related clinical research while requires only about one thirtieth manual operation than our previous method [10]. The method in [10] is considered state of the art for bone marrow lesion segmentation because it could segment BMLs without the reader needing to manually segment each BML. In addition, to the best of our knowledge, [10] is the first semi-automated method to evaluate BMLs volume size quantitatively rather than some semi-quantitative rating scores such as [57]. Since the method in [10] is well validated and already used for clinical research focusing on BMLs volume changes [58], [59], we use the BML volumes and the knee bone segmentations obtained by two raters using method in [10] as the ground truth for evaluation in this experiment. The method we are going to validate in this experiment and that of [10] have the same framework displayed in Figure 5. Given the knee bones are identified, the Chan-Vese method [21] are used to obtain the BMLs within the segmented bone region. The difference is how Step 1 - knee bone segmentation as shown in Figure 5(a) is performed.

For each knee, both the baseline and 24-month follow-up were tested and two raters segmented those 15 knees using the approach in [10] in which clinical researchers have to initialize two polygons near the knee bones for every MRI slice which costs about 30 seconds for each slice. For our new approach, we only initialize two slices for each knee data set, one for the lateral part and one for the medial part of each knee data set, for these two slices, we only need to draw two circles as displayed in Figs. 6, 7 and 8 which costs about 3–5 seconds. Due to the robustness to initial curves as shown in Section III-A, the segmentation result of a MRI slice could be used as initial curves for the next slice. Instead of directly using the segmentation result of the current slice as the initial curves for the next slice, we applied the erosion morphological operation [60] to keep the initial curves inside the femur and the tibia. Thus in general the manual interaction time for each data set could be reduced from 6 minutes (for 12 slices as discussed below) to about 10 seconds.

Following [10], there were about 37 slices and we omitted the central slices from the analysis (i.e., the middle 9 slices) to focus on BMLs adjacent to the chondral surface and to improve reliability for each knee. For analyses with pain, it is likely to underestimate the association between BMLs and pain due to the exclusion of the central lesion. For analyses with structure, omitting these slices would unlikely influence our results. It is reported that central BMLs were not associated with cartilage loss unless they extended into the subchondral region of the index compartment [61], which we measured. We acknowledge that it would be ideal if we could include this region down the road but this is particularly challenging based on the noise on these slices as well as the challenges in identifying the border of the bone.

We applied our algorithms to 15 knee data sets. The goal of that study was to validate the accuracy and consistency of our semi-automated processing approach across multiple users. Quantitatively, there we used intraclass correlation (ICC) analysis [62] to measure this consistency. Within the context of that analysis, fifteen participants was deemed sufficient to detect a significant ICC if the coefficient was greater than 0.65 (with an alpha level < 0.05 and power > 0.90). Hence we choose to use these same 15 data sets for our analysis here. As the primary objective of this work is to demonstrate the utility of the modeling ideas in Section II especially in Section II-B, we consider a slice-by-slice approach to the processing of these MRI images. In addition, we also omitted the beginning and ending slices for each knee which have no or little bone structure. Over the entirety of the data set, there were 363 MRI slices processed in total with 12.1 ± 1.92 MRI slices per data set.

Slices in a single knee data set were divided into six groups from a lateral to medial order. As a group, these images have similar bone geometries near the joint region. Hence, six prior shape models were generated respectively. Given a new knee, each slice was assigned to one of these six groups based on the order within the knee and processed using the corresponding prior shape model. For each of these six groups, we used 30 training images to construct the coupled prior shape and none of the training slices was part of the test slices. These training slices were generated by Rater 1.

The parameters stated in Section II-D work well for 347 out of the 363 slices. For the other 16 slices, good segmentation results could be obtained by tuning the kernel radius R from 10 to 20. As in section III-A, we also used the AvgD and the partial AvgD values near the joint area to evaluate our femur and tibia segmentation results as displayed in Tables. III, and IV respectively. Comparing Tables. III, and IV, we can see that significant variability arises from regions that are far from the joint area. This is to be expected, because the boundaries of the knee bones near the joint are real anatomical structures and they could be consistently segmented for the training set while on the contrast the boundaries for the knee bones far from the joint are “virtual” boundaries to define region of interest and they could hardly be defined in a consistent way (see Fig. 2). Thus the region near the joint could be more accurately segmented due to both more edge information and stronger geometric prior shape constraint.

TABLE III.

AvgD values between our method and manual results (unit: mm)

Structure	our method and Rater 1	our method and Rater 2	Rater 1 and Rater 2
Femur	0.950 ± 0.452	1.128 ± 0.346	0.742 ± 0.166
Tibia	1.241 ± 0.363	1.423 ± 0.379	0.923 ± 0.155

TABLE IV.

AvgD values between our method and manual results near the joint(unit: mm)

Structure	our method and Rater 1	our method and Rater 2	Rater 1 and Rater 2
Femur	0.532 ± 0.293	0.524 ± 0.264	0.310 ± 0.095
Tibia	0.795 ± 0.191	0.852 ± 0.200	0.489 ± 0.093

From Table. IV, we can see that the AvgD values near the joint area for two raters are 0.310 mm and 0.489 mm for the femur and tibia respectively. The AvgD values for our method between the two raters for the femur part are 0.532 mm and 0.524 mm which are slightly bigger (less than one pixel) than that of the two raters. The AvgD values for our method between the two raters for the tibia part are 0.795 mm and 0.852 mm which are also less than or about one pixel larger than that of the two raters. In summary, the approach considered here provides accuracy in terms of segmenting the femur and tibia that is within about a pixel of that obtained by two human raters but requires about one thirtieth (10s vs 6 minutes) the time in terms of human interaction with the image data for each knee as in [10].

To determine if our method generated similar BML volumes as the manual bone segmentation, we performed the BMLs segmentation within the segmented knee bones obtained by our method (n = 15 knees). Given the segmented bone structures, the BMLs segmentation method is based on the Chan-Vese’s method [21] with details provided in [10]. We tested the inter-method reliability based on intra-class correlation coefficients (ICC) [2,1 model] [62] which is commonly used in the OA research [7], [10], [63]. For each knee data set, we obtained four BMLs volumes (V_i, i = 1, 2, 3, 4), which corresponded to BMLs in lateral femur (V₁), lateral tibia (V₂), medial femur (V₃), and medial tibia (V₄) for both the baseline and 24-month follow-up. Then we calculated the ICCs of V_i, for baseline, follow-up, as well as the V_i change from baseline to follow-up among two raters and our method. Usually the criterion for validating a BML segmentation method is that the ICC of the volume V_i for baseline and follow-up between two raters are larger than 0.8 and the volume changes correlation are larger than 0.7 [64]. The results are presented in Table V². From Table V, we can see that our automated method achieved this criterion except that the ICC of the follow-up V₄ between Rater 2 is slightly less than 0.8. Thus our approach is consistent with manual segmentation for the application on BML segmentation.

TABLE V.

Inter-tester reliability for BML volume change given the knee bone segmented by our method

		Rater 1 and our method	Rater 2 and our method	Rater 1 and 2
V1	Baseline	0.99	0.92	0.93
	Followup	0.92	0.90	0.89
	Change	0.99	0.93	0.93
V2	Baseline	0.99	0.91	0.95
	Followup	0.99	0.96	0.99
	Change	0.91	0.95	0.98
V3	Baseline	0.99	0.97	0.97
	Followup	0.99	0.95	0.95
	Change	0.98	0.93	0.90
V4	Baseline	0.96	0.85	0.86
	Followup	0.88	0.79	0.87
	Change	0.95	0.87	0.86

As some have suggested bone marrow lesion volume could be an outcome measure in clinical trials [63], [65], [66]. Methods like ours which could measure BMLs efficiently and reproducibly would help to obtain BML volume in a big data set and thus facilitate the investigation of the outcome measure for OA patient.

IV. Conclusions and future work

In this paper, we presented a new coupled prior shape model which implicitly incorporates prior shape and also the relative position information for multiple objects. In addition, our new shape model also implicitly puts on more constraint in areas with less shape difference compared to the conventional shape models which constrain informally on the whole shape. Moreover, an edge based force incorporating directional information was also introduced in this paper. Segmentation results on the real MRI knee images demonstrate the feasibility of our new coupled prior shape modal and also the directional edge-based force. Based on the combination of our coupled prior shape model and the directional edge-based force, we could reduce the processing time for BML segmentation without sacrifice of accuracy.

The current methods exclude the patella to focus on the tibiofemoral joint. It would be ideal to eventually include the patella and this is a future goal for our projects but at this time we focused on the tibia and femur. This is also advantageous for us since our group often focuses on measures of tibiofemoral OA progression using measures of tibiofemoral joint space width or joint space narrowing and peri-articular bone measures in the tibia. The patella indeed has BMLs but can represent unique segmentation challenges because of the size, shape, and occasionally the lack of adequate fat suppression. An accurate analysis of patella BML might also require an axial scan. After confirming that the method is functional in the two main bones, our goal will be to explore segmenting the patella as well as extend our method from the current 2D form to its 3D version.

Appendix: Proof of Equation (10)

Due to similar formulation of $\frac{\partial D_i}{\partial {\varphi }_1}$ and $\frac{\partial D_i}{\partial {\varphi }_2}$ as in (10), we only deduce $\frac{\partial D_i}{\partial {\varphi }_1}$ here.

From (9), we have

$${\mathbf{u}}_{{\varphi }_1+{\epsilon }_1{\stackrel{\sim }{\varphi }}_1}=\frac{\int \mathbf{x}H({\varphi }_1+{\epsilon }_1{\stackrel{\sim }{\varphi }}_1)d\mathbf{x}}{\int H({\varphi }_1+{\epsilon }_1{\stackrel{\sim }{\varphi }}_1)d\mathbf{x}}.$$

Here ϕ̃₁ is a small perturbation of ϕ₁ and ε₁ is a scalar.

By using Taylor expansion, we have

$$H({\varphi }_1+\epsilon {\stackrel{\sim }{\varphi }}_1)\approx H({\varphi }_1)+{\epsilon }_1{\stackrel{\sim }{\varphi }}_1\delta ({\varphi }_1).$$ (17)

Thus

$$\begin{array}{l}{\mathbf{u}}_{{\varphi }_1+{\epsilon }_1{\stackrel{\sim }{\varphi }}_1}\approx \frac{\int \mathbf{x}[H({\varphi }_1)+{\epsilon }_1{\stackrel{\sim }{\varphi }}_1\delta ({\varphi }_1)]d\mathbf{x}·\int H({\varphi }_1)d\mathbf{x}}{\int H({\varphi }_1)d\mathbf{x}·\int H({\varphi }_1)+{\epsilon }_1{\stackrel{\sim }{\varphi }}_1\delta ({\varphi }_1)d\mathbf{x}}\\ =\left({\mathbf{u}}_{{\varphi }_1}+\frac{{\epsilon }_1\int \mathbf{x}{\stackrel{\sim }{\varphi }}_1\delta ({\varphi }_1)d\mathbf{x}}{\int H({\varphi }_1)d\mathbf{x}}\right)\left(\frac{1}{1+\frac{{\epsilon }_1\int {\stackrel{\sim }{\varphi }}_1\delta ({\varphi }_1)d\mathbf{x}}{\int H({\varphi }_1)d\mathbf{x}}}\right)\\ \approx \left({\mathbf{u}}_{{\varphi }_1}+\frac{{\epsilon }_1\int \mathbf{x}{\stackrel{\sim }{\varphi }}_1\delta ({\varphi }_1)d\mathbf{x}}{\int H({\varphi }_1)d\mathbf{x}}\right)\left(1-\frac{{\epsilon }_1\int {\stackrel{\sim }{\varphi }}_1\delta ({\varphi }_1)d\mathbf{x}}{\int H({\varphi }_1)d\mathbf{x}}\right)\\ ={\mathbf{u}}_{{\varphi }_1}+\frac{{\epsilon }_1\int (\mathbf{x}-{\mathbf{u}}_{{\varphi }_1}){\stackrel{\sim }{\varphi }}_1\delta ({\varphi }_1)d\mathbf{x}}{\int H({\varphi }_1)d\mathbf{x}}+O({\epsilon }_{\mathit{1}}^{\mathit{2}})\\ \approx {\mathbf{u}}_{{\varphi }_1}+\frac{{\epsilon }_1\int (\mathbf{x}-{\mathbf{u}}_{{\varphi }_1}){\stackrel{\sim }{\varphi }}_1\delta ({\varphi }_1)d\mathbf{x}}{\int H({\varphi }_1)d\mathbf{x}}.\end{array}$$

Thus we have

$$\begin{array}{l}{\mathbf{u}}_{\varphi +{\epsilon }_1{\stackrel{\sim }{\varphi }}_1}=s{\mathbf{u}}_{{\varphi }_1+{\epsilon }_1{\stackrel{\sim }{\varphi }}_1}+(1-s){\mathbf{u}}_{{\varphi }_2}\\ =s\left({\mathbf{u}}_{{\varphi }_1}+\frac{{\epsilon }_1\int (\mathbf{x}-{\mathbf{u}}_{{\varphi }_1}){\stackrel{\sim }{\varphi }}_1\delta ({\varphi }_1)d\mathbf{x}}{\int H({\varphi }_1)d\mathbf{x}}\right)+(1-s){\mathbf{u}}_{{\varphi }_2}\\ ={\mathbf{u}}_{\varphi }+s\frac{{\epsilon }_1\int (\mathbf{x}-{\mathbf{u}}_{{\varphi }_1}){\stackrel{\sim }{\varphi }}_1\delta ({\varphi }_1)d\mathbf{x}}{\int H({\varphi }_1)d\mathbf{x}}.\end{array}$$ (18)

Let define the coupling prior shape energy as

$$D_i({\varphi }_1,{\varphi }_2)={\int }_{\mathrm{\Omega }}{[H({\varphi }_1(\mathbf{x}+{\mathbf{u}}_{\varphi }))+H({\varphi }_2(\mathbf{x}+{\mathbf{u}}_{\varphi }))-H({\psi }_1^i)-H({\psi }_2^i)]}^{2}dx$$

then we want to obtain

$$\frac{d}{d\epsilon }\int D({\varphi }_1+\epsilon {\stackrel{\sim }{\varphi }}_1,{\varphi }_2){\mid }_{\epsilon =0}.$$

For simplicity, we use D_i(ϕ₁ + εϕ̃₁) to denote D_i(ϕ₁ +εϕ̃₁, ϕ₂). Then

$$\begin{array}{l}\frac{d}{d\epsilon }\int D_i({\varphi }_1+\epsilon {\stackrel{\sim }{\varphi }}_1){\mid }_{\epsilon =0}\\ =\int 2[H({\varphi }_1+\epsilon {\stackrel{\sim }{\varphi }}_1)(\mathbf{x}+{\mathbf{u}}_{\varphi +\epsilon {\stackrel{\sim }{\varphi }}_1})+H({\varphi }_2(\mathbf{x}+{\mathbf{u}}_{\varphi +\epsilon {\stackrel{\sim }{\varphi }}_1}))\\ -H({\psi }_1^i)-H({\psi }_2^i)]·[d\frac{H({\varphi }_1+\epsilon {\stackrel{\sim }{\varphi }}_1)(\mathbf{x}+{\mathbf{u}}_{\varphi +\epsilon {\stackrel{\sim }{\varphi }}_1})}{d\epsilon }\\ +d\frac{H({\varphi }_2(\mathbf{x}+{\mathbf{u}}_{\varphi +\epsilon {\stackrel{\sim }{\varphi }}_1}))}{d\epsilon }]{\mid }_{\epsilon =0}.\end{array}$$ (19)

Substituting (17)(18) into (19), we obtain

$$\begin{array}{l}\frac{d}{d\epsilon }\int D({\varphi }_1+\epsilon {\stackrel{\sim }{\varphi }}_1){\mid }_{\epsilon =0}\\ =2\int [H({\varphi }_1(\mathbf{x}+{\mathbf{u}}_{\varphi }))+H({\varphi }_2(\mathbf{x}+{\mathbf{u}}_{\varphi }))\\ -H({\psi }_1^i(\mathbf{x}))-H({\psi }_2^i(\mathbf{x}))]\\ ·[s\delta ({\varphi }_1(\mathbf{x}+{\mathbf{u}}_{\varphi }))\nabla ({\varphi }_1(\mathbf{x}+{\mathbf{u}}_{\varphi }))\\ ·\frac{\int {({\mathbf{x}}^{\prime }-{\mathbf{u}}_{{\varphi }_1})}^T{\stackrel{\sim }{\varphi }}_1({\mathbf{x}}^{\prime })\delta ({\varphi }_1({\mathbf{x}}^{\prime }))d{\mathbf{x}}^{\prime }}{\int H({\varphi }_1({\mathbf{x}}^{\prime }))d{\mathbf{x}}^{\prime }}+{\stackrel{\sim }{\varphi }}_1(\mathbf{x}\\ +{\mathbf{u}}_{\varphi })\delta ({\varphi }_1(\mathbf{x}+{\mathbf{u}}_{\varphi }))]d\mathbf{x}\\ =2\int [H({\varphi }_1(\mathbf{x}))+H({\varphi }_2(\mathbf{x}))\\ -H({\psi }_1^i(\mathbf{x}-{\mathbf{u}}_{\varphi }))-H({\psi }_2^i(\mathbf{x}-{\mathbf{u}}_{\varphi }))]\\ ·[s\delta ({\varphi }_1(\mathbf{x}))\nabla ({\varphi }_1(\mathbf{x}))\\ ·\frac{\int {({\mathbf{x}}^{\prime }-{\mathbf{u}}_{{\varphi }_1})}^T{\stackrel{\sim }{\varphi }}_1({\mathbf{x}}^{\prime })\delta ({\varphi }_1({\mathbf{x}}^{\prime }))d{\mathbf{x}}^{\prime }}{\int H({\varphi }_1({\mathbf{x}}^{\prime }))d{\mathbf{x}}^{\prime }}\\ +{\stackrel{\sim }{\varphi }}_1(\mathbf{x})\delta ({\varphi }_1(\mathbf{x}))]d\mathbf{x}\\ =2\int [H({\varphi }_1(\mathbf{x}))+H({\varphi }_2(\mathbf{x}))\\ -H({\psi }_1^i(\mathbf{x}-{\mathbf{u}}_{\varphi }))-H({\psi }_2^i(\mathbf{x}-{\mathbf{u}}_{\varphi }))]\\ ·{\stackrel{\sim }{\varphi }}_1(\mathbf{x})\delta ({\varphi }_1(\mathbf{x}))d\mathbf{x}\\ +2\int [H({\varphi }_1({\mathbf{x}}^{\prime }))+H({\varphi }_2({\mathbf{x}}^{\prime }))\\ -H({\psi }_1^i({\mathbf{x}}^{\prime }-{\mathbf{u}}_{\varphi }))-H({\psi }_2^i({\mathbf{x}}^{\prime }-{\mathbf{u}}_{\varphi }))]\\ ·s\delta ({\varphi }_1({\mathbf{x}}^{\prime }))\nabla ({\varphi }_1({\mathbf{x}}^{\prime }))d{\mathbf{x}}^{\prime }\frac{\int {(\mathbf{x}-{\mathbf{u}}_{{\varphi }_1})}^T{\stackrel{\sim }{\varphi }}_1(\mathbf{x})\delta ({\varphi }_1(\mathbf{x}))d\mathbf{x}}{\int H({\varphi }_1(\mathbf{x}))d\mathbf{x}}.\end{array}$$

Therefore $\frac{\partial D_i}{\partial {\varphi }_1}$ in (10) holds. Similarly, we can also obtain $\frac{\partial D_i}{\partial {\varphi }_2}$.