Joint optimization of collimator and reconstruction parameters in SPECT imaging for lesion quantification

Abstract

Obtaining the best possible task performance using reconstructed SPECT images requires optimization of both the collimator and reconstruction parameters. The goal of this study is to determine how to perform this optimization, namely whether the collimator parameters can be optimized solely from projection data, or whether reconstruction parameters should also be considered. In order to answer this question, and to determine the optimal collimation, a digital phantom representing a human torso with 16-mm-diameter hot lesions (activity ratio 8:1) was generated and used to simulate clinical SPECT studies with parallel-hole collimation. Two approaches to optimizing the SPECT system were then compared in a lesion quantification task: sequential-optimization, where collimation was optimized on projection data using the Cramer-Rao bound, and joint-optimization, which simultaneously optimized collimator and reconstruction parameters. For every condition, quantification performance in reconstructed images was evaluated using the root-mean-squared-error of 400 estimates of lesion activity. Compared to the joint-optimization approach, the sequential-optimization approach favoured a poorer resolution collimator, which, under some conditions, resulted in sub-optimal estimation performance. This implies that inclusion of the reconstruction parameters in the optimization procedure is important in obtaining the best possible task performance; in this study, this was achieved with a collimator resolution similar to that of a general-purpose (LEGP) collimator. This collimator was found to outperform the more commonly used high-resolution (LEHR) collimator, in agreement with other task-based studies, using both quantification and detection tasks.

1. Introduction

The optimal parameters of a parallel-hole collimator (hole size, septal length and septal thickness) in SPECT imaging depend on the task to be performed, e.g., whether it is a detection or estimation task, and on the lesion size and the characteristics of the surrounding background. A number of studies have previously been undertaken to determine the optimal collimation for various tasks, such as detection (Tsui et al 1978, Moore et al 1995, Zeng and Gullberg 2002, Moore et al 2005, Zhou et al 2009, Zhou and Gindi 2009) and quantification (Kamphuis et al 1999, Kamphuis et al 2000, Lau et al 2001, Moore et al 2005, Larsson et al 2010), for both planar (Tsui et al 1978, Tsui et al 1983, Moore et al 1995, Moore et al 2005) and SPECT imaging (Kamphuis et al 1999, Kamphuis et al 2000, Lau et al 2001, Zeng and Gullberg 2002, Zhou et al 2009, Zhou and Gindi 2009, Zhang and Zeng 2010, Larsson et al 2010).

Although the techniques for selecting collimator parameters for a given geometric resolution are well established (Keller et al 1968, Beck and Gunter 1985, Moore et al 2005), questions remain regarding how best to optimize the resolution-sensitivity trade-off for a given task. In particular, for estimation tasks involving reconstructed data, it has not been determined whether optimization of the collimator can be performed on the projection data alone, or whether the reconstruction algorithm also needs to be considered. If the former is true, then the optimal collimator parameters are independent of the reconstruction and can, therefore, be determined solely from projection data, as for planar imaging or projection-based tasks in tomographic imaging. The imaging system as a whole could then be optimized using a sequential approach, whereby the collimator is optimized using projection data and, subsequently, the reconstruction parameters are optimized for the chosen collimator. However, if the reconstruction affects the optimal collimation, a joint optimization strategy, by which the collimator and reconstruction parameters are simultaneously optimized, is required in order to obtain the overall best performance. It should be noted that estimation tasks should be performed using the raw data if possible (Huesman 1984, Muzic et al 1998, Muüller et al 1990, Whitaker et al 2008). Because estimation performance from projection data alone depends solely on the choice of collimator parameters, reconstruction parameters are irrelevant in this case and do not need to be considered. In clinical practice, however, most tasks (for example, the calculation of the standardized uptake value (SUV)) are performed using reconstructed images and, hence, determining how best to optimize the SPECT system for such tasks is an important consideration.

An investigation of optimization strategies has previously been undertaken by Zhou et al (2009) for a detection task. Hot lesions of known activity were placed in a digital torso phantom and sequential- and joint-optimization strategies were compared. Using an ideal observer (Barrett and Myers 2004) to assess lesion detection performance on projection data and a channelized Hotelling observer (CHO) (Barrett and Myers 2004) to assess performance on reconstructed images, they found that the different optimization approaches resulted in the selection of different collimators, where the sequential approach favoured a poorer resolution, higher sensitivity collimator, compared with the joint-optimization. In that paper, the jointly-optimized collimator outperformed the sequentially-optimized collimator, implying that the reconstruction is an important consideration in the optimization of the collimator.

The aim here was to compare sequential- and joint-optimization approaches for an estimation task, to ascertain whether or not the findings of Zhou et al (2009) for detection would hold true for lesion activity estimation. For this investigation, a digital phantom was constructed and forward-projected with using an analytical projector. Assessments of activity estimation performance were carried out on both projection and reconstructed data for a range of collimator resolution values, for phantoms with both uniform and non-uniform ‘lumpy’ backgrounds, and for two different estimation metrics. This allowed not only a comparison between the optimization strategies but also an assessment of the effects of the background type and the method of estimating the lesion activity.

The results found in this paper can be used to guide selection of SPECT imaging parameters, and also reveal whether such choices are influenced by factors such as estimation-metric type and the form of the background surrounding the lesion of interest.

2. Methods

2.1 Phantom

For this investigation, we generated projections of a digital phantom using an analytical projector. The phantom was designed to represent hot lesions within a human-sized torso; 20 hot spheres of diameter 16 mm were placed at 4 different radial locations (0, 64, 88 and 128 mm from the central axis) within an elliptical cylinder (of diameters 350 and 270 mm in the horizontal and vertical directions, respectively). The phantom was generated in a 128 × 128 × 128 volume, with a voxel size of 4 mm; however, the spheres were created initially with voxels of 0.4 mm before being down-sampled, to allow a better representation of the spheres in the larger voxel size. The background around the spheres was then modified accordingly. While this is not a perfect representation of the continuous function simulated, it allowed for a very good approximation of the desired activity map. The sphere size was selected so as to provide a challenging estimation task, close to the limit of what can be reliably visualized above the noisy background, once collimator blurring has been applied. The lesion-to-background activity ratio was 8:1 for all spheres. Spheres were placed so that adjacent spheres were always separated by at least 5 sphere diameters, so that analysis performed on reconstructed images would not be adversely affected by nearby lesions. The phantom is shown in figure 1, for both uniform and non-uniform backgrounds.

Figure 1.

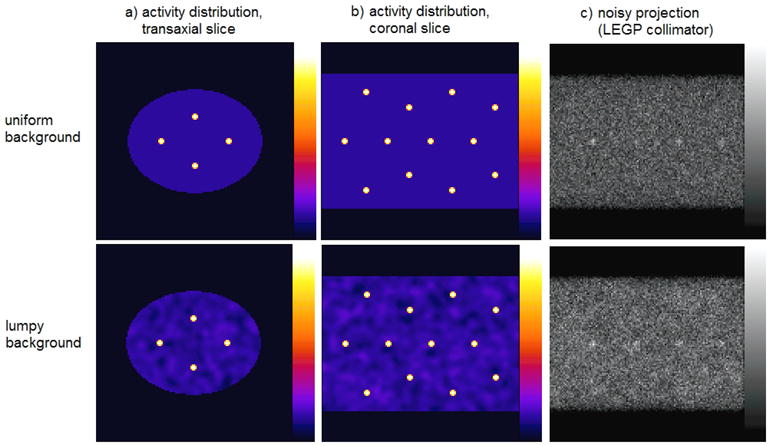
a) Transaxial and b) coronal slices through the digital phantom used in simulations with a uniform background (top row) and a lumpy background (bottom row). c) A sample projection from the uniform- and lumpy-background phantoms, produced using the LEGP collimator.

The non-uniform background was generated using Gaussian-shaped ‘lumps’, using an approach described by Rolland (1990) to represent physiological variations in uptake, which may be present in patient studies; this approach provided more clinical realism than using uniform backgrounds. The non-uniform backgrounds were created by convolving a Gaussian-distributed white noise field (with a mean pixel value of zero and standard deviation of 80) with a three-dimensional Gaussian function with a FWHM of 20 mm. Values outside the elliptical cylinder were zeroed, and those inside were added to a flat background and scaled to ensure positivity of all voxel values and to achieve the desired sphere-to-background activity ratio (8:1). Twenty different realizations of volumes containing Gaussian lumps were generated, using a pseudo-random number generator, thereby creating a total of 400 unique sphere/background combinations. One such lumpy-background volume is shown in figure 1.

2.2 Collimator Designs

Simulations were performed using 10 parallel-hole collimator designs, each with a different resolution-sensitivity trade-off. The collimator parameters (septal length, hole size and septal thickness) were chosen to maximize sensitivity for each selected resolution, while fixing the single-septal penetration probability of Tc-99m at 1.4% to match that of the Siemens LEHR collimator for the e.cam system. These conditions meant that all 3 parameters could be specified for a given collimator resolution, using the equations given in Keller (1968), Beck and Gunter (1985) and Moore et al (2005). The resulting collimators follow the resolution–sensitivity curve shown in figure 2, with the collimators selected for simulation marked as points on this curve. Additionally, the parameters of each collimator are listed in Table 1.

Figure 2.

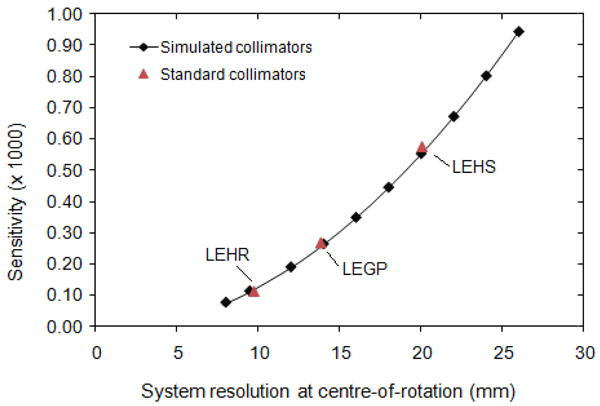
The family of collimators simulated, in terms of their resolution at the centre-of-rotation (165 mm from the collimator surface) and sensitivity. For comparison, typical low-energy high-resolution (LEHR), low-energy general-purpose (LEGP) and low-energy high-sensitivity (LEHS) collimators are also plotted.

Table 1.

The parameters of the collimators simulated. The hole length was 25.1 mm for all collimators.

System resolution at centre-of-rotation (mm)	Collimator sensitivity (×100)	Hole size (mm)	Septal thickness (mm)
8 mm	0.076	0.920	0.127
9.5 mm (chosen to match the Siemens LEHR collimator)	0.113	1.117	0.154
12 mm	0.190	1.451	0.200
14 mm	0.264	1.710	0.235
16 mm	0.349	1.966	0.271
18 mm	0.445	2.222	0.306
20 mm	0.553	2.476	0.341
22 mm	0.672	2.730	0.376
24 mm	0.803	2.984	0.411
26 mm	0.944	3.237	0.466

2.3 Projection of Phantom Data

Projections were created using an analytical projector at 3° intervals over 360°. Attenuation and distance-dependent blurring were incorporated into the simulation, but scatter was not. Scatter would not be expected to affect the determination of the optimal collimator parameters, as it contributes a low-frequency distribution of counts arising predominantly from the patient. A Gaussian function was used to model distance-dependent blurring, taking into account the collimator blurring and the intrinsic resolution of the camera. Each projection was acquired in a 128 × 128 matrix, with a pixel size of 4 mm × 4 mm. A non-circular orbit was simulated, whereby the detectors maintained a constant distance (12 mm) from the phantom surface. Therefore, the radial distance of the cameras from the centre-of-rotation varied between 147 and 187 mm as the cameras moved around the elliptical cylinder. The projection data were scaled to a 10-million count acquisition with a low-energy, high-resolution (LEHR) collimator, taking into account the various collimator sensitivities relative to LEHR. Collimators with a better resolution and lower sensitivity than the LEHR collimator consequently yielded acquisitions with fewer than 10-million counts, and vice versa for poorer resolution collimators. Twenty noise realizations were generated for each condition, for both uniform and lumpy background phantom projections, giving rise to 400 spheres in each case. Poisson-distributed random deviates were generated using a pseudo-random number generator. In addition to having different Poisson noise realizations, each lumpy-background phantom also had a different Gaussian lump realization.

2.4 Overview of Optimization Strategies

The flowchart in figure 3 outlines the methods used in both the sequential and joint optimizations.

Figure 3.

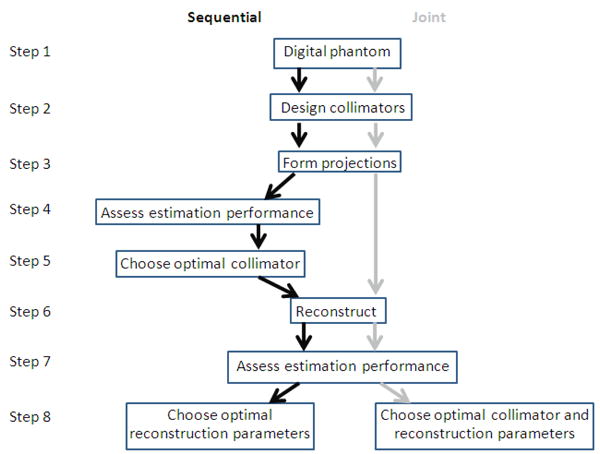
The stages involved in the sequential- and joint-optimization methods. The black arrows on the left indicate the steps involved in sequential optimization and the grey arrows on the right are those involved in the joint optimization. Both methods were evaluated for digital phantoms with uniform and lumpy backgrounds.

The sequential optimization approach firstly involved selecting the optimal collimator based on the projection data alone (steps 4 and 5 in figure 3), prior to reconstructing. The Cramer-Rao Bound (CRB) was used as the assessment metric for the projection data, as described in 2.5.1. Subsequently, the projection data for the optimal collimator were reconstructed in order to obtain a measure of activity estimation performance (steps 6 to 8 in figure 3). We used standard iterative OSEM for reconstructing all data, with 10 subsets of 12 projections per subset. As described below in section 2.5.2, we optimized two different parameters for the two different metrics we considered; for an SUV metric, we optimized the Gaussian post-smoothing filter width applied after 80 OSEM iterations, whereas for a partial-volume correction approach, we optimized the number of iterations. In this manner, the collimator and reconstruction parameters were optimized separately, one after the other. It should be noted that the CRB analysis must be performed on noise-free projection data (Poisson statistics are assumed in its calculation), as it is based on expected values, but the subsequent reconstructions in the second stage of the optimization are carried out on conventional, noisy projection data. The joint optimization was implemented by assessing collimator performance using reconstructed projection data from all collimators, allowing the globally optimal combination of collimator and reconstruction parameters to be determined. This was evaluated over all 400 spheres (20 spheres per phantom and 20 phantom volumes with different Poisson noise realizations, as well as different Gaussian lump realizations in the non-uniform background case).

2.5 Assessment Metrics

2.5.1 Projection-Based Assessment using the Cramer-Rao Bound

For unbiased estimators, the Cramer-Rao bound (CRB) can be used to evaluate performance, as it represents the best possible precision and, hence, the best performance that can be achieved for the given task. This metric was used to compare collimators on the basis of performance in estimating sphere activity from projection data, which was used as part of the sequential optimization approach (steps 4 and 5 in figure 3).

For uniform backgrounds, in the absence of Poisson noise, the projection data in pixel i(λ_i) can be described by:

$${\lambda }_i=A{f}_i+B{g}_i$$ (1)

where f_i is the projection of the sphere with unit activity, g_i is the projection of the background with unit activity, and A and B are scalars describing the activity concentrations of the sphere and background, respectively. To avoid the influence of overlapping activity from different spheres, one sphere was considered at a time, within a local background, such that 20 separate sets of projection data were created, corresponding with the 20 sphere locations within the phantom. This was performed for the uniform background phantom and each of the 20 lumpy background phantoms.

For this linear estimation problem, it can be shown that the CRB on the estimate of A (CRB (Â)) is equal to the variance of A (var (Â)) when estimated simultaneously with B (Van Trees 1968). Using the formulation given in (1), and the definition of the CRB, then it is straightforward to show that var (Â) is given by:

$$\text{var}(\widehat{A})=\text{CRB}(\widehat{A})=\frac{{\sum }_i\left[\frac{g_i\cdot g_i}{{\sigma }_i^2}\right]}{{\sum }_i\left[\frac{f_i\cdot f_i}{{\sigma }_i^2}\right]\times {\sum }_i\left[\frac{g_i\cdot g_i}{{\sigma }_i^2}\right]-{\left({\sum }_i\right[\frac{f_i\cdot g_i}{{\sigma }_i^2}\left]\right)}^2}$$ (2)

where ${\sigma }_i^2$ is the expected noise variance in pixel i. Since Poisson statistics have been assumed, in this case, ${\sigma }_i^2$ is equal to the value of pixel i. This is calculated separately for each of n spheres.

Rather than performing the calculation over the entire projection array, a local circular mask of 48-mm-diameter (3 sphere diameters) was applied to the projection dataset, such that only those pixels in the vicinity of the projected sphere were included in the CRB calculation. All other pixels, outside of the 48 mm diameter region, were set to zero and excluded from the calculation. This was applied in every projection angle, so that the non-zero circular region was centred on the sphere in every view. Zeroing data distant to the sphere was done in order to avoid the unrealistic scenario in which the entire background volume is used in the estimation; this leads to optimal estimation of sphere activity at excessively poor resolution. The local mask, as used by Moore et al (2005), for example, ensured clinical realism. Its size was chosen to ensure that the projected sphere and some background were included within the non-zero region for all collimators. The influence of the mask size on the optimal collimator resolution is discussed in section 4.

For each collimator, the overall measure of precision obtainable for sphere-activity estimation in phantoms with a uniform background was calculated from the CRB(Â) values over the 20 spheres, as follows:

$$\%\text{precision}=\frac{\sqrt{\frac{1}{20}{\sum }_{k=1}^{20}{\text{CRB}}_k(\widehat{A})}\times 100}{A}$$ (3)

where k is the sphere number in the phantom. Similarly for lumpy background phantoms, the precision was calculated as follows:

$$\%\text{precision}=\frac{\sqrt{\frac{1}{400}{\sum }_{k=1}^{20}{\sum }_{m=1}^{20}{\mathit{\text{CRB}}}_{km}(\widehat{A})}\times 100}{A}$$ (4)

where m is the background lump realization. Although all spheres were the same size, location-dependent differences in attenuation and collimator blurring led to different CRB values. The optimal collimator for this optimization strategy was deemed to be that with the lowest percent precision, using a polynomial fit to determine the minimum.

2.5.2 Metrics for Activity Estimation in Reconstructed Images

Two different metrics were used to estimate sphere-activity concentration using reconstructed images. Firstly, a metric similar to the commonly used maximum standardized uptake value (SUV_max) was calculated for every sphere and, secondly, a two-parameter estimation of sphere and background activity incorporating correction for partial-volume effects was used. Both metrics were calculated from the uniform- and lumpy-background datasets, with the root-mean-squared-error (rMSE) over the 400 spheres used to assess performance under each condition.

For evaluation using a SUV type metric, each dataset was reconstructed using ordered-subsets expectation-maximization (OSEM) (Hudson and Larkin 1994), with 80 iterations and 10 subsets, in order to attain a good level of convergence for spheres at all radial locations. The OSEM algorithm incorporated the same model as the analytical projector, allowing compensation of both attenuation and distance-dependent blurring. The reconstructed images were then smoothed with a 3-dimensional Gaussian kernel, to reduce the high levels of noise which would otherwise be present. The full-width at half-maximum (FWHM) of the Gaussian kernel was varied between 2 and 16 mm (0.5 - 4 pixels) so that the optimum smoothing width could be ascertained for each collimator. Therefore, the reconstruction parameter being optimized in this case was the level of post-reconstruction smoothing, while the number of OSEM iterations was kept fixed for all collimators. It is also possible to optimize the number of OSEM iterations instead of applying post-reconstruction smoothing, but it was expected that more reliable results would be obtained by performing the analysis on images that had reached a good level of convergence, and hence a large number of OSEM iterations and variable smoothing were used.

The mean value in an 8-voxel (2 × 2 × 2) region, centred on each sphere, was then calculated, producing an estimate of sphere activity concentration, which will be referred to here as SUV_peak. Because the sphere was 4 pixels in diameter, these 8 central voxels were fully encompassed within the sphere and not near the edges; therefore, the influence of partial volume effects was diminished. From the set of 400 measures of SUV_peak, the rMSE for each collimator/smoothing width combination was calculated by comparing the 400 estimated SUV_peak values with the known true sphere-activity concentration.

A novel method of activity estimation, which corrects for partial-volume effects (Moore et al 2010), was also used to determine the optimal collimator/reconstruction combination. This metric is a projection-based method, but requires the reprojection of a reconstructed image and hence is dependent on both collimator and reconstruction parameters. It has been shown to yield better quantification performance than SUV_peak, because prior information about the lesion size and shape is included in the Moore estimation procedure to overcome partial-volume effects. This comparison between the two metrics was, therefore, undertaken both to test the assertion that the partial-volume corrected method would outperform the SUV_peak metric and to ascertain whether or not this would influence the choice of collimator deemed to be optimal.

The partial-volume correction method involves estimating activity concentrations within a volume-of-interest (VOI), which is defined in a reconstructed image. The VOI fully encompasses the lesion and includes some local background and possibly other nearby structures. The estimation is then performed in projection space, by obtaining unit projections of each structure within the VOI and reprojecting the reconstructed data outside the VOI to account for all remaining data. This approach therefore requires that structures with different values of activity concentration can be identified, e.g., by a high resolution imaging modality, such as a registered CT image. For our experiments, the VOI contained only the lesion and some of the background, the shapes of which were identified in the original phantom, thereby mimicking a registered CT.

Using an analogous formulation to (1), the projection data can be described as follows:

$${\lambda }_i=A{f}_i+B{g}_i+{\text{G}}_i^{(k)}$$ (5)

where G_i^(k) is the reprojection of the reconstructed data outside of the VOI, where the data have been reconstructed with k iterations. A is the true sphere activity concentration, as in (1), and B now represents the true concentration in the local background (within the VOI). f_i and g_i have the same meaning as previously; they are obtained by projecting unit activity maps of the sphere and local background, respectively. In this way, data outside of the local VOI are accounted for in the reprojection (third) term, and only the structures within the VOI need to be segmented and corrected for resolution blurring. The quantities λ_i, f_i, gi and G_i^(k) are known and, hence, the 2-parameter estimation of activity concentration (A and B) can be performed as in the sequential optimization approach for the calculation of the CRBs. We start with the log of the Poisson likelihood of detecting n_i counts in detector pixel i, given an expected value of λ_i from the projection-data model of equation (5):

$$ln(L)={\sum }_{i\in \mathit{\text{VOI}}}{n}_{i}ln({\lambda }_i)-{\lambda }_i-ln(n_i!)$$ (6)

Next we set the derivatives of this expression with respect to A and B to zero; this provides two equations which are then easily solved simultaneously for unknowns, A and B. Because the resulting values depend on the term G_i^(k), which, in turn, depend (weakly) on iteration number k, A and B can be calculated after each of a few iterations to determine the number of iterations providing the best estimates using the minimum mean-squared error condition. Although both the sphere (A) and background (B) activity concentrations are estimated simultaneously, only the sphere result was used in subsequent analysis, because this is the parameter of clinical interest.

Unlike SUV_peak, where the post-reconstruction smoothing parameter needed to be optimized, here, the iteration number from which the reprojected data (G_i^(k)) is generated needs to be optimized. This estimation method was performed for up to 30 OSEM iterations (each with 10 subsets) for every collimator, which, as before, included corrections for distance-dependent collimator blurring and attenuation. The size of the cubic region used for the VOI was 16 pixels. As with the SUV-type metric, the sphere activity concentration, A, was calculated for all 400 spheres, from which the rMSE of the estimated sphere activity concentration was calculated by comparison with the known, true value. This metric was calculated separately for both uniform- and lumpy-background phantoms.

3. Results

3.1 Projection-Based Collimator Optimization

Performance in estimating the variance of the sphere activity estimation from projection data is summarized in figure 4. Precision values were calculated from the CRB for 20 spheres throughout the phantom volume, using equation (3) for the uniform-background phantom and equation (4) for lumpy-background phantoms.

Figure 4.

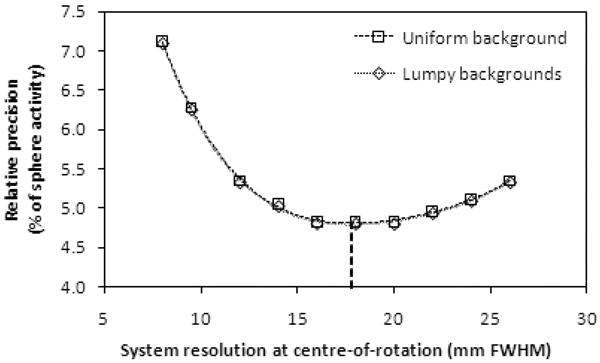
The relative precision of sphere activity estimates as a function of system resolution, for projection-based optimization, for uniform- and lumpy-background phantoms. The dotted line indicates the minimum precision obtained by polynomial curve fitting, which, for both background types, occurs at a system resolution of 17.8 ± 0.3 mm at the centre-of-rotation.

The curves in this graph exhibit a clear minimum, which, for both background types, was found to lie at a system resolution of 17.8 ± 0.3 mm. To obtain this value, the minima of 4th-order polynomial fits (shown in figure 4) were evaluated and the errors were obtained by propagation of the errors in the fit parameters. This result shows that for estimation from projection data, the collimator that produced a system resolution of approximately 18 mm at the centre-of-rotation yielded the best precision and, therefore, the best performance in estimation of sphere activity concentration, for both uniform- and lumpy-background phantoms. Of the standard collimators shown in figure 2, this resolution is most similar to (but slightly better than) the LEHS collimator. The resulting precision at the optimum resolution for both backgrounds was 4.8 ± 0.1 % of the true sphere activity concentration.

The effect of varying the mask size when performing the CRB calculations was assessed by repeating the optimization with the 48-mm diameter (12-pixel) mask decreased to a 32-mm-diameter (8-pixel) mask. It was found that for both background types, the smaller mask resulted in an optimal system resolution of 14.2 ± 0.3 mm, which produced a precision of 6.3 ± 0.1 % of the true sphere activity concentration. The impact of this finding is discussed in section 4.

The optimal collimator's performance in sphere-activity estimation was subsequently assessed using both the SUV and the partial-volume correction metrics; these results are discussed in the following section.

3.2 Activity Estimation in Reconstructed Images

Figure 5 shows the relative rMSE for estimation using SUV_peak as a function of post-reconstruction smoothing, for the uniform- and lumpy-background phantoms, for collimators with system resolution up to 20 mm. (Results for collimators with poorer resolution have not been plotted, as these were clearly suboptimal.) By looking at the minimum rMSE for each collimator, it can be seen that the collimators vary both in terms of the degree of smoothing found to be optimal and in the minimum rMSE achieved.

Figure 5.

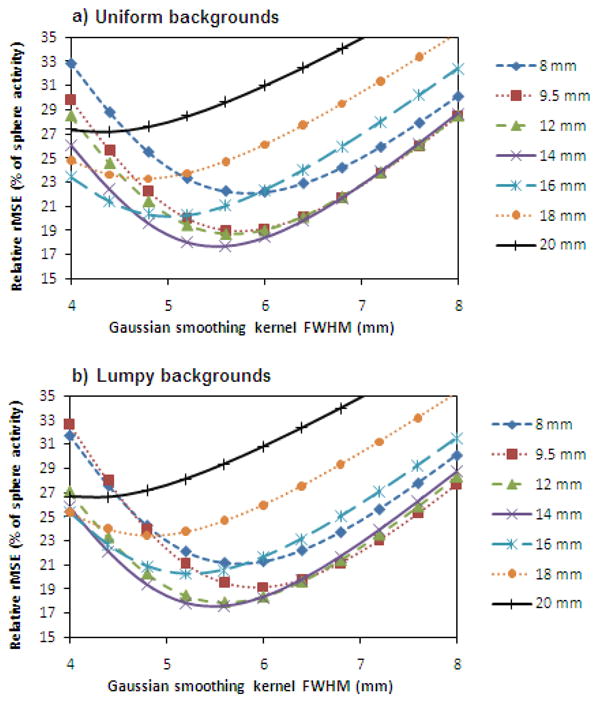
Relative rMSE for estimation using SUV_peak as a function of post-reconstruction smoothing for phantoms with a) uniform backgrounds and b) lumpy backgrounds. Each collimator's curve is labelled with the system resolution it yields at the centre-of-rotation.

The minimum rMSE for each collimator is plotted in figure 6 for both the uniform- and lumpy-background phantoms. The global minima in rMSE represent the jointly optimized results (over all collimators and smoothing levels), found to be at a system resolution (at the centre-of-rotation) of 12.6 ± 0.3 mm for uniform backgrounds and 12.4 ± 0.3 mm for lumpy backgrounds. These were determined by fitting 2nd order polynomials to the data and the errors in the optimal system resolution values represent the uncertainties in the fitting parameters. The minimum rMSE was 18.0 ± 0.8 % for the uniform-background phantom and 17.8 ± 0.6 % for the lumpy-background phantoms. The error bars shown were obtained by calculating the standard deviation of the minimum rMSEs over all spheres for each noise realization.

Figure 6.

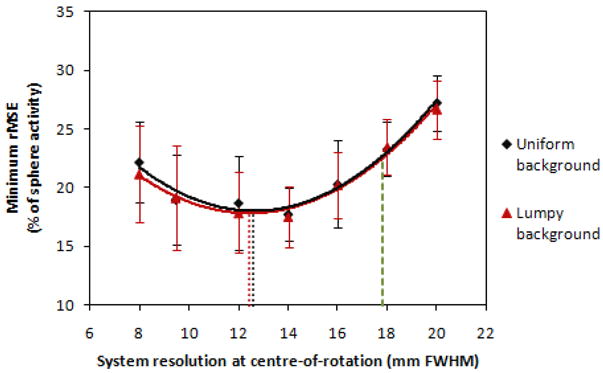
The minimum rMSE (after selecting the optimal post-reconstruction smoothing for each collimator) for sphere activity concentration estimation as a function of system resolution at the centre-of-rotation, using an SUV-type metric. Both curves are 2nd order polynomial fits, the minima of which are shown as dotted lines. The best result obtainable using the sequentially optimized collimator is indicated by a dashed line at a system resolution of 17.8 mm.

It can be seen in figure 6 that the collimator selected from the sequential optimization approach (yielding a system resolution of 17.8 mm at the COR) would have resulted in a sub-optimal estimate of sphere activity; the minimum rMSE for this collimator was approximately 23 % for both background types. The minimum rMSE achieved for both optimization approaches are summarized in Table 2. The difference in the minimum rMSE achieved for the two collimators shows that for this task and estimation metric, the joint-optimization approach was required to obtain the globally optimal results. This, in turn, implies that optimization of the collimator parameters should not be based solely on projection data, but that the reconstruction parameters should also be considered.

Table 2.

The rMSE for the collimators found to be optimal from both the sequential and joint optimization approaches, for the different background types and estimation metrics. The figures quoted for the sequential optimization results were obtained using a 17.8 mm collimator (considered optimal from analysis of projection data) and the joint optimization results are given for the collimators listed. For comparison, the CRB analysis on both uniform and lumpy background phantoms produced a minimum rMSE of 4.8 ± 0.1%.

Metric	Background type	Sequential Optimization	Joint Optimization
		Minimum rMSE for a 17.8 mm collimator (% of sphere activity)	Optimal collimator (system resolution at COR (mm))	Minimum rMSE for optimal collimator (% of sphere activity)
SUV	Uniform	22.7 ± 0.7 %	12.6 ± 0.3 mm	18.0 ± 0.8%
SUV	Lumpy	22.5 ± 0.6 %	12.4 ±0.3 mm	17.8 ± 0.6 %
Local partial-volume corrected estimation method	Uniform	5.4 ± 0.2 %	14.9 ± 1.2 mm	5.3 ± 0.2%
Local partial-volume corrected estimation method	Lumpy	9.1 ± 0.4 %	13.2 ± 1.1 mm	8.5 ± 0.4%

The results obtained using the local partial-volume correction method for sphere-activity estimation are shown in figures 7 and 8. Figure 7 shows the rMSE as a function of OSEM iteration number for the uniform background phantom, and the minimum rMSE achieved for every collimator for both background types is shown in figure 8. The errors shown in figure 8 were calculated using the same method as for figure 6. It can be seen that the partial-volume correction approach converges very quickly, with a stable value being reached within only a few OSEM iterations. This is because the method requires only the estimation of a small number of model parameters that characterize a few tissue types within a small volume-of-interest. Individual voxel values in the remainder of the image are not needed; the procedure requires only their integrals along the projection rays, which are much less noisy. For these reasons, the estimation procedure converges much faster than the individual voxel values of a reconstructed image, especially those within the spheres.

Figure 7.

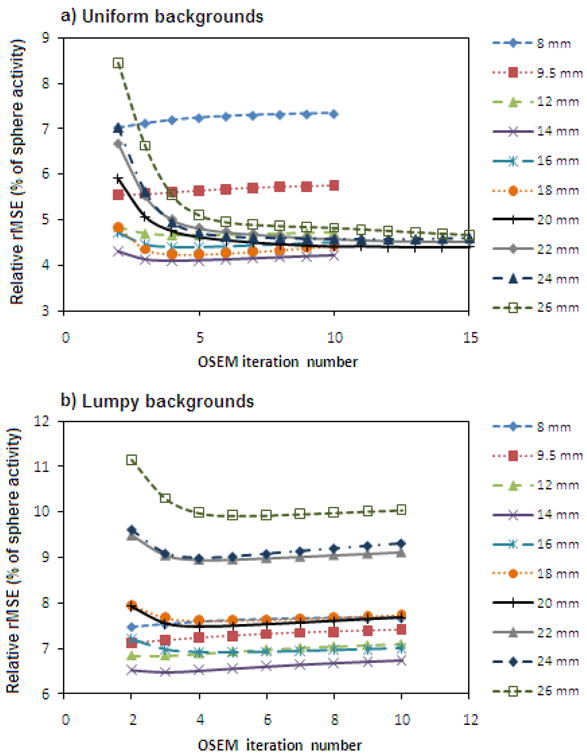
Relative rMSE of estimates obtained using the local partial volume correction method as a function of OSEM iteration number, for phantoms with a) uniform backgrounds and b) lumpy backgrounds. Each collimator's curve is labelled with the system resolution it provides at the centre-of-rotation. Reconstructed images with up to 30 OSEM iterations were included in this analysis, but for clarity only the results from the first 10 or 15 iterations are plotted here.

Figure 8.

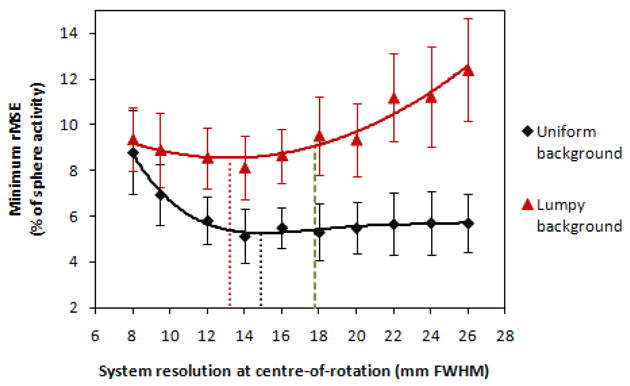
The minimum rMSE for estimating sphere activity concentration from reconstructed images using a local partial-volume correction method, as a function of system resolution at the centre-of-rotation. The curves are 4th and 2nd order polynomial fits to the uniform- and lumpy-background data, respectively, with the minimum in each curve indicated by the dotted lines. The best result achievable by the sequentially optimized collimator is indicated by a dashed line at a system resolution of 17.8 mm.

As in the SUV_peak results, the optimal value of the reconstructed parameter and the best performance achievable varies among collimators. High resolution, low sensitivity collimators are seen to reach their optimal performance in fewer iterations compared with those of poorer resolution. However, unlike the SUV_peak results, the curves for the partial-volume corrected estimation metric for phantoms with uniform- and lumpy-backgrounds differ in shape. They reach a minimum at 14.9 ± 1.2 mm and 13.2 ± 1.1 mm respectively. As for the SUV_peak analysis, the errors are calculated from uncertainties in the fit parameters. The optimum resolution for both background types is approximately equivalent to that of a LEGP collimator (14 mm system resolution at the centre-of-rotation).

The minimum rMSE observed was 5.3 ± 0.2 % for uniform-background phantoms and 8.5 ± 0.4 % for lumpy-background phantoms. The performance of the partial-volume corrected method is worse for lumpy backgrounds, due to violation of the assumption of uniform activity concentration within both the sphere and the local background (within the VOI). Non-uniformities in either of these regions would therefore be expected to result in some degradation of the technique's performance, as seen in the lumpy background phantom results. Additionally, a more pronounced degradation in estimation performance was observed with the lumpy background phantoms with increasing (worsening) resolution, making the choice of collimator more important in non-uniform conditions.

Repeating the uniform-background calculations with a different VOI cube size showed that the system resolution of the optimal collimator had a small dependence on the size of the VOI. Reducing it from 16 pixels in each dimension to 12 (a 58 % reduction in the VOI volume) resulted in only a 4 % reduction in the optimal resolution. Therefore it can be seen that the system resolution of the optimal collimation is fairly robust to VOI size in the range that would be most useful in the clinical setting, i.e. large enough to fully contain the lesion and adequate background, but not too large as to contain distant structures that are not of interest.

If a sequential optimization approach were taken, resulting in the selection of a 17.8 mm collimator, the minimum rMSE achievable would be equal to 5.4 ± 0.2 % for uniform backgrounds and 9.1 ± 0.4 % for lumpy backgrounds. The minimum rMSE figures are summarized in Table 2. The estimation performance with partial volume correction appears to be more robust to worsening collimator resolution compared with SUV_peak, particularly for the uniform background phantoms. In changing from the globally optimum collimation obtained by the joint optimization to the sequentially optimized collimator at 17.8 mm, there is only a small degradation in performance for the lumpy background phantoms and no appreciable degradation for those with uniform backgrounds.

4. Discussion

The results obtained here allow an assessment of the optimal SPECT imaging parameters for estimating the activity concentration of a hot lesion and also enable a comparison between the different methods of optimizing the system. It was found that although the collimation found to be optimal varied slightly with background type and estimation metric, the joint-optimization method consistently favoured a better resolution collimator than the sequential approach. The system resolution at the centre-of-rotation was approximately 12 - 15 mm for the joint optimization (75 – 94 % of the sphere diameter), compared with ∼18 mm for sequential optimization (113 % of the sphere diameter); these values correspond most closely to the LEGP and LEHS collimators, respectively.

When the CRB calculations used for sequential optimization were repeated using a 32-mm (8-pixel) diameter mask, instead of a 48-mm (12-pixel) diameter mask, the optimal system resolution (both for lumpy and uniform backgrounds) improved from 17.8 mm to 14.2 mm; thus, the smaller mask moved the optimal collimator resolution to the poorer end of the range of resolution values found to be optimal with the joint optimization tasks. However, since the mask size was then only somewhat bigger than the blurred lesion size, such a mask would be very challenging to use in practice for any realizable 2-parameter (lesion and background) estimation procedure. In fact, the precision of lesion activity estimates for the optimal collimator using an 8-pixel mask was significantly (∼30%) worse than that determined using our original 12-pixel mask, indicating that the 8-pixel mask provided inferior task performance.

On the other hand, when the mask size was increased, the percent variance improved, but the optimal resolution worsened, moving even further away from the resolution seen to be optimal for the joint optimization tasks. For practical reasons, any clinically straightforward estimation procedure would have to be restricted to a fairly compact region surrounding each lesion of interest, e.g., to avoid other nearby anatomic structures (on clinical images) characterized by significantly different activity concentration. The mask size was chosen to be approximately three times the lesion size because such a mask is small enough to ensure a local estimation procedure, yet large enough to provide very precise estimates of background-activity concentration that do not seriously limit the sphere activity estimates.

Comparisons of estimation performance between optimization strategies were therefore carried out using the 48-mm-diameter mask as part of the sequential optimization. It was found that the better resolution, jointly-optimized collimator matched or outperformed that obtained using the sequential approach, for both background types and estimation metrics considered. This indicates that for SPECT imaging, collimator choice should not be made based on projection data alone, but that consideration of the reconstruction parameters is also beneficial. This finding agrees with that of Zhou et al (2009), who studied optimization strategies for the detection of a 19 mm square hot lesion in reconstructed images. They also found that a sequential optimization resulted in a collimator of poorer resolution, which yielded inferior detection ability than a jointly-optimized collimator. For their task, the jointly-optimized collimator was approximately equivalent to a LEGP collimator.

Although in this study the joint-optimization was found to be preferable overall, the difference in performance with the two optimization strategies was found to depend on the estimation metric used, with smaller differences observed when using the local partial-volume corrected estimation method, compared to an SUV-type metric. The reason is that the former method is more robust to worsening collimator resolution; this was particularly noticeable in the results for the uniform background phantoms (see figure 8), where the assumption of uniform activity concentration in each tissue-type within the VOI was met. Even though there was no appreciable difference in performance between the optimization strategies in this case, a joint-optimization approach still appears to be the most appropriate method to use, since some degradation was seen in the more clinically realistic lumpy-background case, where the partial-volume correction method was not fully able to describe the background activity with a single parameter. In clinical practice, it is likely that the model will not be able to fully describe the acquired data, and hence an increased dependence on collimator resolution, similar to that of the lumpy-background phantoms, might be expected.

Despite the increased sensitivity of the partial-volume correction method to these non-uniformities, it was still found to outperform the SUV_peak metric in every case. In other words, the rMSE of the activity estimation was found to be lower for every condition using this estimation metric and, hence, a better estimation of sphere activity was achieved. This is not surprising, since the partial-volume correction method incorporates additional prior knowledge regarding lesion size and shape into the estimation procedure and thereby improves quantitative accuracy. This indicates that such a metric could be of benefit in clinical scenarios where quantification is important.

It was found that both optimization strategies and estimation metrics favoured a collimator of poorer resolution than that of the LEHR collimator, which would most commonly be selected for an imaging task such as this. This suggests that clinical studies involving estimation could benefit from the use of a higher sensitivity collimator than that commonly used, provided that compensation for distance-dependent blurring is incorporated into the reconstruction algorithm. Other authors have found that the resolution requirements of the collimator are lessened when resolution modelling is used (LEGP favoured with resolution modelling and ultra-high resolution or high-resolution favoured without, as found by Kamphuis et al (2000) and Lau et al (2001) respectively) and hence our findings should be compared with those that also incorporate resolution modelling. It should be noted that if a larger scan orbit were used than that simulated here (which averaged 16.5 cm), a better resolution collimator would be required to obtain the desired spatial resolution at the centre-of-rotation. However, the phantom dimensions used in this study were chosen to be representative of a typical patient size and, hence, the results obtained here should be appropriate in most cases. Additionally, our findings are in agreement with other studies, which have also noted that optimal performance requires a higher sensitivity collimator than the LEHR collimator, for quantification tasks (Kamphuis et al 1999, Kamphuis et al 2000, Larsson et al 2010), detection tasks (Zeng and Gullberg 2002, Zhou et al 2009, Zhou and Gindi 2009) and studies of image noise levels (Lau et al 2001, Zhang and Zeng 2010). Although there is some variation in the specific findings of these investigations with regards to what degree of sensitivity is optimal, they consistently favour a higher sensitivity, poorer resolution collimator than LEHR when resolution modelling is used, with many instead recommending LEGP (Kamphuis et al 2000, Lau et al 2001, Zhou et al 2009, Larsson et al 2010) and hence support the conclusions drawn here.

It was previously observed in a similar estimation task that optimal collimation was not affected by the activity ratio of the lesion to background, when it was varied between 4:1 and 10:1 (Moore et al 2008), suggesting that our results (obtained with a ratio of 8:1) would hold true for a wide range of clinically relevant activity ratios. The effect of varying the lesion size has also previously been investigated (Tsui et al 1978, Tsui et al 1983, Moore et al 2005), where it has been seen that the ratio of optimal resolution to lesion size is approximately constant. Consequently, the results obtained here pertain to the specific lesion size investigated, which is not known prior to imaging, although it should also be noted that some researchers have advocated the use of adaptive collimation (Barrett et al 2008). While this approach has been tested with pinhole collimation, we are not aware of any fully adaptive parallel-hole collimation system. Even with fixed (non-adaptive) collimation, however, our results still have general applicability in SPECT imaging, since optimization should be performed for challenging cases, where parameter selection will have the biggest impact in the performance of the system. For example, the uptake of a large, high contrast lesion would be relatively easy to quantify, regardless of collimator selection and hence the system should not be optimized for this scenario. Selecting imaging parameters for a more difficult case, however, will result in the optimal performance of the system overall and is, therefore, the strategy for optimization that should be adopted. The task chosen here has been constructed to meet this requirement and, consequently, to produce clinically relevant results.

5. Conclusions

It has previously been unclear whether the reconstruction parameters need to be taken into consideration when optimizing collimation for quantitative SPECT imaging, or whether it can be optimized based solely on projection data. This question was assessed for a lesion quantification task, where the activity of 16 mm diameter lesions distributed throughout a human torso sized digital phantom was estimated under a variety of conditions.

It was found that for two estimation metrics and two phantom background types (uniform and lumpy), a joint-optimization of collimator and reconstruction parameters resulted in matched or better estimates of lesion activity (lower rMSEs) than a sequential optimization where the collimator was selected based on analysis of only projection data. The sequential approach was seen to result in the selection of a poorer resolution collimator, which agrees with other findings for a detection task. These results indicate that it is important to consider the reconstruction when determining the optimal parallel-hole collimator, in order to achieve the best possible performance.

The overall best estimate of lesion activity was achieved with a collimator resolution comparable to that of the LEGP collimator (obtained via joint-optimization) and with the use of a local estimation method that corrects for partial-volume effects. Although the LEHR collimator is typically favoured in the clinical setting, these results suggest that studies performed under comparable conditions would benefit from the use of a somewhat poorer resolution collimator. This observation is consistent with the findings from several other task-based studies.