Comparison of Fitting Methods and b-Value Sampling Strategies for Intravoxel Incoherent Motion in Breast Cancer

Abstract

Purpose

To compare fitting methods and sampling strategies, including the implementation of an optimized b-value selection for improved estimation of intravoxel incoherent motion (IVIM) parameters in breast cancer.

Methods

Fourteen patients (age, 48.4 ± 14.27 years) with cancerous lesions underwent 3 Tesla breast MRI examination for a HIPAA-compliant, institutional review board approved diffusion MR study. IVIM biomarkers were calculated using “free” versus “segmented” fitting for conventional or optimized (repetitions of key b-values) b-value selection. Monte Carlo simulations were performed over a range of IVIM parameters to evaluate methods of analysis. Relative bias values, relative error, and coefficients of variation (CV) were obtained for assessment of methods. Statistical paired t-tests were used for comparison of experimental mean values and errors from each fitting and sampling method.

Results

Comparison of the different analysis/sampling methods in simulations and experiments showed that the “segmented” analysis and the optimized method have higher precision and accuracy, in general, compared with “free” fitting of conventional sampling when considering all parameters. Regarding relative bias, IVIM parameters f_p and D_t differed significantly between “segmented” and “free” fitting methods. Conclusion: IVIM analysis may improve using optimized selection and “segmented” analysis, potentially enabling better differentiation of breast cancer subtypes and monitoring of treatment.

INTRODUCTION

Diffusion-weighted imaging (DWI), which is sensitive to the mobility of water molecules in the tissue environment, is a noninvasive, endogenous-contrast imaging tool that provides imaging biomarkers for cancer diagnosis and characterization (1). Extensive literature has shown DWI to be useful when characterizing features such as tumor cellularity and tissue organization (1–3). In aggressive tumors, the proliferating cellularity tends to increase restriction by decreasing the extracellular space, and consequently, decrease the apparent diffusion coefficient (ADC). Therefore, ADC has become a widely accepted marker of cellularity (4–9). Recently, use of intravoxel incoherent motion (IVIM) (10) in DWI has gained attention for its sensitivity to both cellularity and microvascular flow (11–19). In the IVIM model, tissue diffusion and pseudo-diffusion coefficients are separated through biexponential analysis. Presently, there is a growing need to optimize the precision of these IVIM metrics, comprehend their impact, and identify their relationships with cancer physiology. A better understanding of these IVIM coefficients can result in clinically useful biomarkers.

Many different approaches to DWI analysis have been proposed over the years, motivated by empirical data representation, biophysical modeling, or a hybrid of both. Ideally, use of these approaches should be guided by awareness of the underlying tissue physiology. For example, oncological studies apply the IVIM model to distinguish hypervascularity and hypercellularity components in malignant neoplasms (20–28) including breast cancer (15–17), particularly in comparison with the weakly perfused and much less structurally dense fibro-glandular tissue.

Various approaches have also been used in the selection of diffusion gradients or b-values. Currently, many DWI protocols for breast cancer subjects calculate ADC values using b-values between 500 and 800 s/mm² (4,9,15,29–31). Previous literature has shown that different ranges of b-value selections sensitize the signal to different components of diffusion and can affect the calculation of the diffusion coefficients in different systems for a variety of reasons (32–34). Questions remain as to whether b-values should be adjusted based on conditions such as tumor type or location. Better estimation of vascular diffusion effects can be made when sampling includes lower b-values (0 <b <200 s/mm²). Non-Gaussian diffusion effects at higher b-values (b > 1000 s/mm²) can affect quantification even with the simple ADC model (28,35–37).

Consequently, quantification of DWI data with the biexponential IVIM fitting model can be numerically nontrivial, and a variety of methods have been developed to address this challenging quantification including optimal sampling (38,39), Bayesian fitting (18,40,41), maximum likelihood estimation (MLE) (33,42), or fusion bootstrap moves (FBM) (43). Importantly, it has been shown that an evenly distributed sampling of b-values is not necessarily optimal for the biexponential model (38,39). Quantitative optimization for b-value sampling, based on the minimization of analytical error propagation factors, has been explored for mono-exponential analysis in the brain (34) and for biexponential IVIM analysis in the kidney (38,39), liver (44,45), and prostate (46).

In this study, we used an optimized b-value selection for biexponential IVIM analysis of breast lesions. We also conducted computer simulations to obtain the IVIM parameter values for calculation of accuracy and precision of the optimized b-value selection approach. We hypothesized that this approach can increase precision of the biexponential fitting of IVIM analysis in breast lesions. Guided by analytical and simulation results from a renal IVIM study as mean values of breast lesions are comparable to values found in renal lesions (38), we implemented a similar optimized b-value selection pattern of repeated acquisitions at key b-values rather than conventionally distributed sampling. Also, the sampled dataset was analyzed with both an unconstrained least squares fit (“free”), and a two-step constrained analysis (“segmented”) approach, which is an alternative route for reducing measurement error. Both fitting methods were also used for the simulation results. This fitting strategy has been used in a range of in vivo IVIM studies (11,14,47–52), with the goal of providing increased precision while making stronger assumptions about the estimated parameters’ values. Relative bias, relative error, and coefficient of variation (CV) estimates for each parameter were compared for each method of fitting for the entire group of lesions studied and in simulations conducted at several signal-to-noise ratio (SNR) levels. The primary motivation for these alternative techniques is to increase measurement precision, thereby increasing diagnostic differentiation between cancerous subtypes and potentially allowing more careful monitoring of response to treatment.

METHODS

Patients

Fourteen patients (mean age, 48.4 ± 14.27 years; range, 28–77 years) with known diagnosed breast lesions [14 malignant lesions with 12 invasive malignant lesions—11 invasive ductal carcinoma (IDC), 1 invasive lobular carcinoma (ILC), and 2 ductal carcinoma in situ (DCIS)] underwent routine 3T breast MRI examination along with a HIPAA-compliant, local institutional review board approved DWI research study between July 11, 2012 and February 27, 2013. All patients were diagnosed either through stereotactic core biopsy, US-guided fine needle aspirations (FNA), or MRI guided core biopsy.

MRI Protocols

Patients underwent a bilateral MRI breast examination in a full body Siemens 3 Tesla (T) MRI scanner (Siemens Medical Solutions, Erlangen, Germany) using a seven-element breast coil array (Invivo Corp., Gainsville, FL). Anatomical imaging was performed with fat saturated and non–fat-saturated T1-weighted volume interpolated breath hold examinations (VIBE) (TR/TE = 3.66 / 1.1 ms, matrix 384 × 384, 288 slices, resolution 1.2 × 0.9 × 1.5 mm³ and scan time 1:10 each). Total scan time for precontrast T1 VIBE images was 2.3 min.

The diffusion weighted imaging (DWI) protocol was carried out using a twice refocused, bipolar gradient single-shot turbo-spin echo (TSE) sequence (repetition time/echo time (TR/TE) 2000 / 103 ms, matrix 108 × 128, bandwidth 797 Hz/px, echo train duration 110 × 4.5 ms = 495 ms, 18 axial slices, voxel 2.7 × 2.7 × 4 mm voxel, GRAPPA (iPAT) parallel imaging acceleration factor = 2) (15). Axial TSE-DWI images with bilateral breast coverage were collected with frequency-selective fat suppression and diffusion sensitization in the anterior–posterior direction applied with 2 different sets of weighting factors (b-values) of (conventional) 0, 30, 70, 100, 150, 200, 300, 400, 500, 800 s/mm² and (optimized) 0 s/mm² plus 3 repetitions of 70, 300, 800 s/mm². These b-values are close to the values optimized by our proposed approach (38). A TSE DWI sequence was used instead of echo planar imaging (EPI) to avoid susceptibility artifacts and distortion (53,54). Total scan time for the TSE-DWI scan was 8 min. The imaging slices were centered on the lesion of interest as identified in the contrast-enhanced scan. A fat saturated axial T2-weighted TSE scan (TR/TE = 3.66 / 1.1 ms, matrix 384 × 384, 288 slices, iPat factor = 2, resolution 1 × 1 × 5 mm³) was performed postcontrast for a total scan time of 4.5 min. A high-resolution (TR/TE = 4.23 / 1.55 ms, matrix 384 × 384, 224 slices, iPat factor = 2, 1.3 × 1.1 × 1.5 mm³) axial 3D postcontrast VIBE scan was performed to guide DWI image region of interest (ROI) analysis with a total scan time of 2.5 min.

Image Analysis

Apparent diffusion coefficient and IVIM biomarkers were calculated from DWI ROI signal decays using two fitting methods (“free” versus “segmented” fit). DWI analysis was performed with custom-written routines within Igor Pro (Wavemetrics, Inc., Portland, OR).

DWI images of all b-values were first fitted voxel-by-voxel using a monoexponential decay model to produce ADC maps for all slices:

$$\mathrm{M}/{\mathrm{M}}_0={\mathrm{e}}^{-\mathrm{b}·\text{ADC}}$$ [1]

A combination of ADC maps, unweighted (b = 0 s/ mm²) diffusion images, and contrast-enhanced images guided lesion sampling during quantitative IVIM analysis. A ROI was drawn on the largest tumor area enclosing the whole lesion and analyzed for both conventional and optimized b-value selections. Average ROI size was 2.57 (1.49) cm².

A biexponential analysis was used to quantify both microvascular and diffusion properties from DWI data. Images were processed using a ROI-based signal analysis method whereby one set of IVIM parameters was calculated from the signal intensities integrated over each ROI. The signal decay curve is fitted to the following biexponential expression:

$$\mathrm{M}={\mathrm{M}}_0·({\mathrm{f}}_{\mathrm{p}}·{\mathrm{e}}^{-\mathrm{b}·{\mathrm{D}}_{\mathrm{p}}}+(1-{\mathrm{f}}_{\mathrm{p}})·{\mathrm{e}}^{-\mathrm{b}·{\mathrm{D}}_{\mathrm{t}}})$$ [2]

where M₀ is total reference magnetization, f_p is perfusion fraction, D_p is pseudo-diffusivity, and D_t is tissue diffusivity. The initial values used as inputs for the “free” fitting were f_p = 30%, D_p = 3 μm²/ms, and D_t = 1 μm²/ms. In unconstrained “free” fitting, all variables in Eq. [2] were varied in the optimization to minimize the difference between the fitted signals and the measured ones. However, fitting the data to a biexponential model without constraints can be numerically challenging; thus, a constrained two-step analysis (or “segmented” analysis) was also evaluated. The first step was to fit data with b-value higher than 150 s/mm² with a monoexponential model to obtain D_t. Here, we assume the fast decay component is negligible in this regime. We then extrapolated the mono- exponential fit back to b = 0 to estimate f_p. In the second step, with D_t and f_p fixed at their estimates from the first step, D_p was determined in a constrained biexponential fit (Eq. [2]). Both the unconstrained “free” fit and the constrained or “segmented” approach were used in this study for both conventional and optimal b-value selection. We also computed ADC values from monoexponential fits of the experimental data. For some patients, the fitting method failed to properly fit the optimized b-value data when using the “segmented” approach, producing unphysical f_p values (<0) or indeterminate D_p values (>1000 μm²/ms). In these cases, another representative adjacent slice was used for IVIM analysis. Residual values from the curve fitting were calculated as root-mean-square deviations of the measured signals from the fitted function and averaged for each sampling method. For the “segmented” fitting, the residual values were obtained from the second step of the fitting process.

SNR in each lesion was also estimated based on the “subtraction of two signal-containing images” method (55), because our optimized diffusion weighting protocol provides repetitions of equivalent protocols. Image noise was defined as an average of the standard deviations from the same lesion ROI applied to the subtraction image. There were three subtraction images for each repeated b-value (70, 300, 800 s/mm²), resulting in a total of nine subtraction images for a given patient case. No systematic bias of the standard deviation from the ROIs of subtracted images was evident either as a function of subtraction pair or b-value; therefore, the nine standard deviation values were averaged for each patient case for the final noise estimate. This average standard deviation or image noise measurement was then corrected by dividing by square root of 2 to obtain the correct image noise (55). Finally, to obtain SNR, the mean lesion ROI signal intensity at b = 0 was divided by the noise standard deviation. Average SNR over all b-values for both the conventional and the optimized b-value set was also determined on a per patient basis, and group averages were determined.

Experimental results were summarized as follows for quality assessment and comparison with simulations (described below). Mean and standard deviation values over the group were derived for each sampling / analysis approach. Relative error for each case was determined as the ratio of parameter uncertainty, determined by Levenberg-Marquardt least-squares fitting analysis as the ratio of the square root of the diagonal element of the covariance matrix for that parameter to the parameter value (56). The mean and standard deviation of relative error were computed for each parameter and analysis method.

Simulations

Computer simulations were conducted to compare accuracy and precision of the different b-value sampling and fitting methods. To obtain the IVIM parameter values for calculation of accuracy and precision, Monte Carlo simulation trials were run using MATLAB (Mathworks, Natick, MA). For each of the trials, parameter values were randomly chosen 1000 times within the following ranges for each IVIM parameter: f_p (0.1015 ± 0.05), D_t (1.38 ± 0.65 μm²/ms), and D_p (15.9 ± 10.0 μm²/ms). Signal curves were built using the biexponential model (10), and sampled using either the full conventional b-value set or the optimized b-value set. Gaussian noise was added to the sampled signal curves at four different levels of SNR (10, 20, 39.2, 80), defined by the ratio of maximal signal intensity to standard deviation of noise intensity. Finally, for each signal result, magnitude data was fit using Eq. [2] with both “free” and “segmented” fitting methods. At each point, parameters were initialized with their true values; this approach focuses the analysis on SNR dependence of precision and accuracy rather than sensitivity to local minima in the parameter space. Residuals (root-mean-square deviations of the simulated data from the model fits) were computed for each parameter, SNR level, and analysis method. From this protocol, we obtained the values of the IVIM parameters to compare for precision, accuracy, and group variance analysis.

Relative Bias / Relative Error / Coefficient of Variation Calculations

Relative bias for the simulations was computed as a difference between the true input IVIM parameter values and the obtained IVIM parameter values from the fitting methods, normalized to the true value and represented as a percentage. Bias values were only reported for simulations because it is only in that context that the true input parameter values are well-defined. The reported bias values are the average of this calculation over all 1000 Monte Carlo trials.

For relative error measurements, the average relative error was calculated by dividing the standard error from estimates of nonlinear least-squares fitting analysis for each parameter by the estimated parameter value. This was done for both simulation and experimental data and represented as a percentage.

Coefficient of variation (CV) for each parameter and method was computed as a percentage based on the ratio of the standard deviation of the mean IVIM parameter values of the group to the group mean IVIM parameter value. Using CV, one can observe the impact of analysis method on group differentiation as a measure of group precision.

Statistical Analysis

Statistical analysis was completed for the results from the clinical experiments. Comparisons between parameters derived from patient data by different sampling / analysis were based on paired t-tests. Statistical significance was indicated when P <0.05 and all analyses were conducted using SPSS 2.0 (IBM, New York).

RESULTS

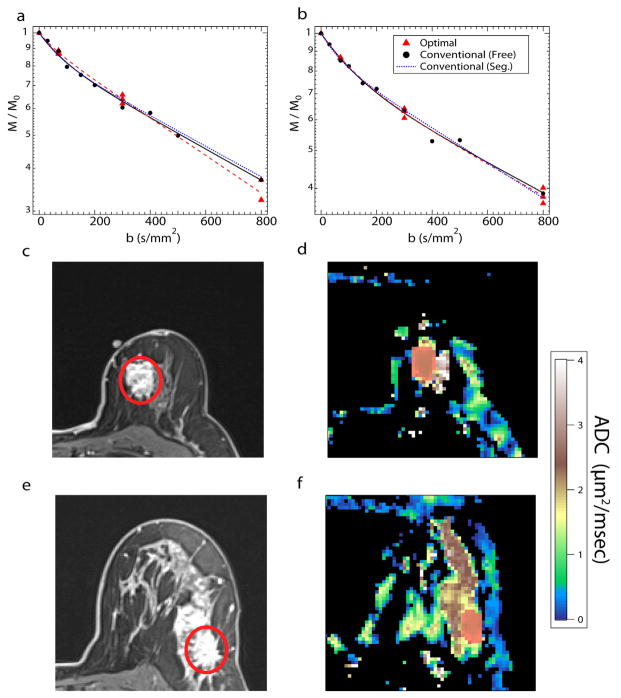
Table 1 shows the mean IVIM metrics obtained from the simulation analysis and patient experiments. Average ADC values of the lesion from the patient experiments were 1.691 ± 0.480 μm²/ms and 1.552 ± 0.523 μm²/ms for conventional and optimized b-value selection, respectively. The standard deviation of the estimated IVIM parameters at four different SNR levels for the simulations show reduction in variance as SNR increases. Differences were noticeable between the f_p mean values as the “free” fitting resulted in higher values than “segmented” fitting. Conversely, D_t and D_p values were lower using the “free” fitting when compared with the “segmented” fitting methods. For simulations, small differences were observed for each individual IVIM parameter value at the same SNR between different b-value selection methods. This same pattern held true within the standard deviation values, which showed that “segmented” standard deviation values were smaller than their “free” counterparts. As simulated SNR increased, the estimated values of f_p decreased while D_t and D_p increased. Paralleling the simulations, the estimated f_p values in the experimental lesions were significantly lower (P <0.05) for “segmented” fitting than “free” fitting with either conventional b-values or optimized b-values. While the f_p values for the “segmented” fitting for the optimized sampling were also lower than the “free” fitting for either b-value selection, this was not significant. Figure 1 shows signal decays, contrast-enhanced images, and ADC maps of two different patient lesion examples (IDC and ILC) with the three different fit methods used.

Table 1.

Simulation and Patient Experimental Results^a

	SNR	Conventional						Optimized
		Dt (μm2/ms)	SD	fp (%)	SD	Dp (μm2/ms)	SD	Dt (μm2/ms)	SD	fp (%)	SD	Dp (μm2/ms)	SD
Free	10	1.106	0.569	21.41	17.31	15.132	11.102	1.162	0.524	20.39	17.30	15.005	11.694
	20	1.187	0.482	17.84	14.65	16.203	11.150	1.227	0.441	16.93	13.17	15.900	11.207
	39.2	1.239	0.415	15.34	10.84	16.463	10.406	1.278	0.404	13.62	8.64	16.530	10.040
	80	1.296	0.387	12.27	6.30	16.957	8.716	1.314	0.391	11.43	5.30	16.949	8.315
	Exp.	1.01	0.397	28.40†	15.99	8.67	4.258	1.088	0.390	24.89*	11.39	11.028	7.981
Segmented	10	1.365	0.610	7.89	16.81	17.700	8.865	1.377	0.615	6.00	20.59	15.583	8.822
	20	1.375	0.459	8.13	8.92	19.041	8.883	1.353	0.454	8.61	10.24	16.734	8.924
	39.2	1.360	0.406	8.58	5.14	19.723	8.239	1.339	0.410	9.44	5.99	17.840	8.527
	80	1.362	0.394	8.61	3.55	20.569	6.546	1.339	0.391	9.56	3.80	18.159	7.267
	Exp.	1.323	0.472	13.31*†	5.05	15.31	9.634	1.195	0.471	16.83	9.06	13.183	6.529

^aAverage values and standard deviation results from the different b-value selection and fitting methods at four levels of SNR and from patient experiments. Daggers represent significant differences between fitting methods free and segmented, while asterisks represent significant (P <0.05) differences between the different b-value selection.

FIG. 1.

a–f: Signal decay curves, contrast enhancement, and ADC maps of breast cancer from two different patients, Patient 1 (a,c,d) is diagnosed with ILC, while Patient 2 (b,e,f) is diagnosed with IDC. Red circle and highlighted regions show the ROI selection.

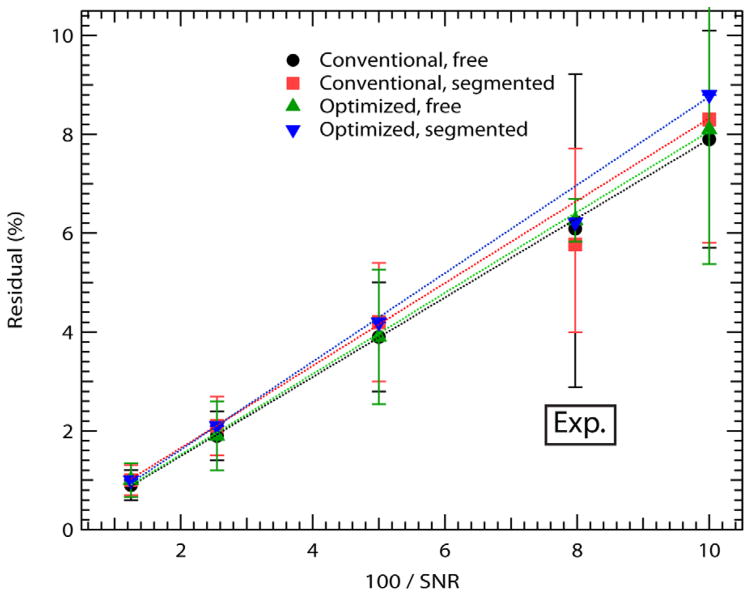
Fit residuals from the simulations (Fig. 2) increased linearly with the inverse SNR as expected; the residual value differences were small between the different IVIM fitting methods and b-value selections, though residuals for optimized b-values and “segmented” approaches were slightly higher than for conventional b-values with “free” fitting. Average signal to noise ratios (SNR) for the experimental lesions considered in this study were 12.71 ± 6.51, range 5.52 to 25.72. Average SNR over all b-values within this group was 8.74 ± 4.55 for the conventional b-value set and 7.97 ± 4.25 for the optimized b-value set. Experimental residuals are also indicated on Figure 2 at this SNR level, and are consistent with the trend observed in simulations. The experimental residual value differences between methods were also small, ranging from 5.4 % to 6.3% for the experimental fits with the conventional “segmented” method (5.4%) having the lowest average residuals, while the highest residual was 6.3% from the optimized “free” fitting method.

FIG. 2.

Fit residuals. Residual values from the different IVIM fitting methods of the simulations and patient experimental (Exp.) data.

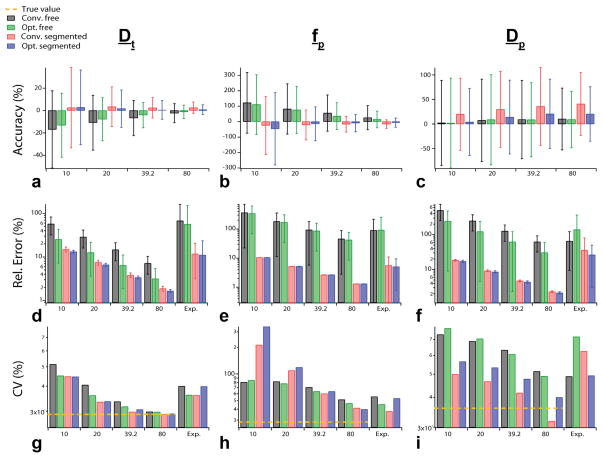
The three quality metrics considered in this study (bias, relative error, and group coefficient of variation) from both simulations and experiments are illustrated in Figure 3. Figures 3a–c show relative bias values from the simulations. The relative bias between the input IVIM parameters and the obtained IVIM parameters from simulation show both the optimized b-value selection and the “segmented” fitting methods generally improved the accuracy of the measurements with the exception of D_p, which showed better accuracy for the “free” fitting and at lower SNR. In addition, the “free” fitting methods led to overestimation (positive values) of the f_p values, while D_t values were slightly overestimated by the “segmented” approach. D_p values were overestimated by all methods. Regarding accuracy, the IVIM parameter, f_p, differed most significantly between analysis methods.

FIG. 3.

Bar graphs of the relative error and coefficient of variation results from simulations, patient experiments (Exp.). Relative bias results from simulation for IVIM parameters errors (a–c), relative error of simulation and patient experiments (d–f), and CV results (g–i).

Figures 3d–f show relative error results from simulations, as well as values derived from the experimental cohort. Simulated relative error values for any given parameter (D_t, f_p, or D_p) or SNR level were highest using “free” fitting with conventional b-values compared with other approaches. The “segmented” analysis presented lower relative error values especially as SNR increases, particularly for f_p and D_p, whereas the optimized b-value selection method showed less improvement over conventional b-value selection. The lowest relative error values were found in the optimized b-value selection using “segmented” analysis for simulations. D_p values had the highest relative error values of the IVIM parameters for all methods.

Experimentally, for each IVIM parameter, the highest relative error was found for “free” fitting of conventional b-values, followed by “free” fitting of optimized b-values, with the lowest values found for “segmented” fitting of conventional b-values, except for D_p which showed lower relative error values for the “segmented” fitting of optimized b-values. This trend, in general, mirrored that of simulations at any given SNR level. Quantitatively, the average relative experimental error was similar to the simulations at SNR level of 20, although this depended on the parameter and method used.

Figures 3g–i show results of group coefficient of variation (CV) for the simulation data and experimental cohort. The simulated data were compared with a “true” CV (i.e., the standard deviation of input IVIM metrics over all trials without noise). Differences in simulated CV values between methods were less pronounced and universal than those among relative precision. Estimated D_t values approached the true value at the highest SNR and show reductions in CV from optimized sampling and “segmented” fitting at low SNR. In addition, f_p values showed a similar improvement at high SNR, but at low SNR the “segmented” methods showed very high CV. Finally, D_p values showed CV reduction with “segmented” fitting. Experimentally, “segmented” fitting showed improved group precision with reduced CV values, except for D_t. Considering the total CV of all parameters, it is evident that optimized sampling or “segmented” fitting reduces CV at high SNR. Finally, the experimental metrics of CV and relative error for the “free” fit were also computed from results obtained when parameters were initialized to their values from segmented fitting. Average CV values over all parameters were reduced by 1.8% / 3.0% of their values, and relative error by 8.2% / 2.3% of their values, by parameter initialization for conventional / optimized b-value sampling.

DISCUSSION

The goal of this study was to improve the precision and accuracy of IVIM biexponential analysis while faced with scan time restrictions in the clinical setting. Comparison of the different analysis methods showed that both the “segmented” analysis and the optimized b-value selection method had higher precision and accuracy than conventional b-value sampling and “free” fitting when considering all IVIM parameters for both simulation and patient data. Relative bias values showed similar trends in the simulation results especially in the f_p and D_t values though some exceptions did exist, particularly involving D_p. Experimentally, the “segmented” approach estimated a lower f_p value compared with the other two approaches (12). This is further corroborated by the simulation results, which showed that the “segmented” f_p values were in general underestimated (negative values) compared with the true value (Fig. 3b). However, the “segmented” approach provided dramatic reduction in relative error and some reduction in CV for sufficiently high SNR. Individualized parameter initialization before free fitting provided slight improvement in group CV and relative error in our experimental results, though not uniformly for all parameters

D_p values were, in general, the least precise of the IVIM parameters for all of the different methods, and showed the largest bias particularly for the segmented approach. This bias may have arisen because the “segmented” approach uses a global b-value threshold in its first step that may not be an equally accurate approximation for all points within the simulated IVIM parameter range. Pseudo diffusion reflects the decay rate of the smallest fractional signal component and is correspondingly the most difficult to estimate even in the “segmented” approach. However, D_p values showed acceptable precision and accuracy, indicating the feasibility of characterizing pseudodiffusion in the tumor microenvironment. In general, while accuracy, precision, and group variance are all relevant measures of bio-marker robustness, the latter two typically command a higher priority as they determine whether diagnostic groups or multiple individual assessments are clinically differentiable. In that sense, the tradeoffs inherent to the “segmented” analysis and optimized sampling procedures are acceptable when properly understood.

The precision results suggest that the “segmented” approach generally outperformed the optimized b-value selection. This may be due in part to the heuristic selection of b-values guided by prior simulations from renal cancer rather than a dedicated breast cancer simulation, although the relevant IVIM ranges are similar in both types of lesions. In fact, a potentially more optimal b-value selection for breast patients may exist. Furthermore, it should be stressed that the optimized b-value sampling pattern was adopted based on simulations of a “free” fitting approach. A different b-value sampling scheme may be more favorable when using the “segmented” fitting approach. However, while the accuracy of selection of the b-value component is important, the concept of repetition of key b-values was the main inspiration of this study. Finally, the reduction in the experimental and simulated group variance (CV) was less than the reduction in individual variance reflected in the average relative error. This is understandable as random noise is only part of the group variance in the actual biomarkers collected in a cohort of breast cancer lesions; some inter-subject heterogeneity will be present by any analysis method. Simulations also indicated that the “segmented” analysis algorithm provides larger benefits for individual patient tracking (reproducibility, treatment monitoring) than it does for group differentiation (such as demonstrating differences between diagnostic groups), though both applications benefit.

For some patients, the fitting method failed to properly fit the optimized b-value data when using the “segmented” approach. Because the “segmented” fitting uses b-values >150 s/mm² for the monoexponential fitting of the tissue diffusivity, only the last 2 b-values fall under this limit. The variance between the scans within these 2 b-values (i.e., due to motion or other artifacts) results in a less robust monoexponential fit, i.e., in some cases, unphysical or indeterminate IVIM parameter estimates resulted. In these cases, another slice that was adjacent to the first slice was selected to obtain more robust IVIM values.

Analysis was more robust for simulated data because the variance between the repeated b-values was not as great, possibly due to the absence of image artifacts and motion. These results suggest that any IVIM workflow, either for integrated signals or voxelwise analysis, should include some outlier rejection criteria (12,57,58). In addition, as stated above, a different b-value sampling scheme may be more favorable when combined with the “segmented” approach.

Similarly, the residual results for the experimental data, while fairly low (~6%) indicating good fits, showed large variation within the patient group. They were also most similar to the simulation residual results from SNR of 10 or 20, which was similar to the experimental SNR calculation (SNR ~12.7). In addition, the quality metrics (bias, relative error, CV) for the experimental data were often similar to those found at the lower simulated SNR levels. The small discrepancies that do exist between the measured SNR and the corresponding fit residuals may originate from several factors. It should be noted that the image difference method for SNR calculation, while more accurate than estimation of noise from a single image, remains an approximation. Also, both the experimental residuals and the noise estimated from the difference method may have exceeded that expected from thermal noise alone, due to measurement noise from motion, physiological noise, or other imaging artifacts unique to the experimental platform; the consistency between experiment and simulations in Figure 2 indicates the difference method to be a fair measure of effective SNR in this context. Moreover, the general trends in the experimental quality metrics (bias, relative error, CV) as function of fitting and sampling algorithms mirror those seen in simulations, and correspondingly, the experimental sources of error do not prohibit measurement of the IVIM parameters.

Several other limitations to this study should be noted. First, we used a small number of subjects. Also, we were unable to observe accuracy in patients due to the inaccessibility of “true” values, nor was the entire exam repeated on the same patient for an assessment of reproducibility. Rician noise was also not considered in the simulations; although for the lowest SNR considered (~10), its influence is expected to be small. Experimental IVIM fits for either algorithm used uniform parameter initialization rather than patient-specific values. Similarly, the average SNR of the two sampling schemes was slightly different, which may have contributed to their differential residuals and competed with the improved fit precision afforded by repeated sampling. The combination of “segmented” fitting and optimal b-value sampling, while providing some advantages in parameter estimation, was not universally robust in the experimental data in this cohort; further analysis of the best combination of these algorithms is warranted. Finally, though outside the specific scope of this study, general caveats regarding IVIM should be noted. As with any higher order approach, more scan time is required to collect sufficient diffusion weightings for model parameter estimation. The approach is more useful in hypervascular breast lesions than in the weakly perfused fibroglandular tissue, and the pseudodiffusion D_p is measurable only when f_p is nonnegligible. Finally, the biexponential model assumes both the vascular and tissue compartments display Gaussian diffusion behavior, which is an approximation that may not hold for all vascular architectures or b-value ranges (59). However, when executed with appropriate sampling, analysis, and acknowledgment of underlying assumptions, the IVIM approach provides a practical multi-parametric assessment of cancerous tissue.

This study shows that improvements can be made in the precision of breast IVIM analysis using different methods of analysis (“free” and “segmented”) and optimized b-value selection. Time constraints and efficiency are key factors that motivate implementation of optimized gradient selection. Previous literature has shown effectiveness of such optimization in several abdominal organs (38,39,44–46). Improvements to the precision of IVIM analysis using optimized b-values may allow for improved discrimination between benign and malignant lesions especially when there are restrictions to scan time in a clinical setting. Furthermore, when combined with other techniques for robust IVIM parameter estimation, i.e., Bayesian (18,40,41), MLE (33,42), or bootstrapping (43), better precision may potentially be obtained during analysis of IVIM parameters. Future studies may explore a hybridization of both fit algorithms and b-value selections to better delineate the vascular and cellular biomarkers of the IVIM model for breast cancer assessment.