An Evolutionary Perspective on Learning Disability in Mathematics

Abstract

A distinction between potentially evolved, or biologically-primary forms of cognition, and the culturally-specific, or biologically-secondary forms of cognition that are built from primary systems is used to explore mathematical learning disability (MLD). Using this model, MLD could result from deficits in the brain and cognitive systems that support biologically-primary mathematical competencies, or from the brain and cognitive systems that support the modification of primary systems for the creation of secondary knowledge and secondary cognitive competencies. The former include visuospatial long-term and working memory and the intraparietal sulcus, whereas the latter include the central executive component of working memory and the anterior cingulate cortex and lateral prefrontal cortex. Different forms of MLD are discussed as related to each of the cognitive and brain systems.

When viewed from the lens of evolution and human cultural history, it is not a coincidence that public schools are a recent phenomenon and emerge only in societies in which technological, scientific, commercial (e.g., banking, interest) and other evolutionarily-novel advances influence one’s ability to function in the society (Geary, 2002, 2007). From this perspective, one goal of academic learning is to acquire knowledge that is important for social or occupational functioning in the culture in which schools are situated, and learning disabilities (LD) represent impediments to the learning of one or several aspects of this culturally-important knowledge. It terms of understanding the brain and cognitive systems that support academic learning and contribute to learning disabilities, evolutionary and historical perspectives may not be necessary, but may nonetheless provide a means to approach these issues from different levels of analysis. I illustrate this approach for MLD. I begin in the first section with an organizing frame for approaching the task of decomposing the relation between evolved brain and cognitive systems and school-based learning and learning disability (LD). In the second section, I present a distinction between potentially evolved biologically-primary cognitive abilities and biologically-secondary abilities that emerge largely as a result of schooling (Geary, 1995), including an overview of primary mathematics. In the third section, I outline some of the cognitive and brain mechanisms that may be involved in modifying primary systems to create secondary abilities, and in the fourth section I provide examples of potential the sources of MLD based on the framework presented in the first section.

COGNITIVE EVOLUTION AND LEARNING IN SCHOOL

Evolution and learning are about modification and adaptation of traits in response to ecological or social change, but on different time scales; specifically, across generations and within life spans, respectively. The former occur when individual differences in a trait or phenotype are partly heritable and influence survival or reproductive prospects in the same way across generations (Darwin & Wallace, 1858). These same traits may also evolve such that they can be modified, within constraints, during the life span (West-Eberhard, 2003). Trait plasticity can evolve if some features of the ecology or social environment that drove the evolution of the trait fluctuate during lifetimes. If the ability to adapt to these fluctuations influences survival or reproductive prospects, then conditions are set for the evolution of trait plasticity. The conditions that create such fluctuations can be climatic or result from biological arms races. The latter are common among organisms with competing interests, as in predator-prey and host-parasite relationships (Darwin, 1859; Dawkins & Krebs, 1979). They are also common in species that live in complex social groups, which results in ever changing patterns of cooperation and competition for control of resources associated with survival or reproductive prospects.

The evolutionary result of cross-generational consistency in selection pressures is a core set of physical (e.g., bipedal), developmental (e.g., length of juvenile period), cognitive (e.g., attentional control), and behavioral (e.g., facial expressions) traits that define the species. The evolutionary result of within-lifetime fluctuations in the specifics of some of these pressures is a subset of traits that are modifiable in response to experience, especially during the developmental period. The advantage of modifiable phenotypes is of course developmental adaptation to change in ecological or social conditions and thus the ability to occupy many niches, but at cost of increased risk of poor developmental outcomes if conditions deviate from the species-typical range (Scarr, 1993). The potential costs of plasticity thus place limits on the extent to which the traits can be modified and often limits on the points in the life span when modifications can occur (West-Eberhard, 2003).

Although many traits may be modified during the life span and as a result of developmental experiences, the traits cannot be modified in anticipation of novel ecological or social conditions, with the exception of some aspects of human behavior and cognition. Indeed, among the many traits that make humans a unique species is the ability to create a range of evolutionarily novel behavioral and cognitive solutions to anticipated problems; specifically, potential solutions can be mentally constructed and rehearsed before a social or ecological demand has been encountered (Alexander, 1989). The selection pressures that resulted in the evolution of the associated brain and cognitive systems are debated, and include variation and novelty that result from climate fluctuation (Potts, 1998; Vrba, 1995), hunting and foraging opportunity (Kaplan, Hill, Lancaster, & Hurtado, 2000), and the dynamics of social cooperation and competition (Alexander, 1989; Dunbar, 1998; Flinn, Geary, & Ward, 2005; Geary, 2005; Humphrey, 1976). Many species, of course, are able to cope with variation in social and ecological conditions but these behavioral changes are in response to—not in anticipation of—this variation and are often highly ritualized and not sufficient for coping with evolutionarily novel situations (Parker, 2004; Suddendorf & Busby, 2003; Suddendorf & Corballis, 1997).

In other words, for nonhuman species modification of evolved traits automatically occurs in response to specific developmental and sometimes later experiences, and this is likely to be true for most human traits as well. The one exception appears to be some features of the human brain that are modifiable in response to experiences and in response to mental simulations of experiences. In other words, there are many evolved, biologically-primary systems (described below) that define core features of human cognition—reflecting cross-generational consistency in corresponding selection pressures—that are modifiable in response to experience (Geary & Huffman, 2002). Much of the time, these cognitive traits are modified automatically and implicitly, that is, without our awareness. Human evolution has also resulted in brain and cognitive systems that enable the top-down, conscious modification of these same biologically-primary systems—these are the mechanisms that enable humans to anticipate and mentally generation solutions to problems that may arise in the future (Flinn et al., 2005; Geary, 2005). One important result has been the evolution of a cultural species, that is, a species that has the ability to not only create novel solutions but to organize these solutions as a knowledge base that is passed from one generation to the next in the form of books, morals, and so forth (Baumeister, 2005; Richerson & Boyd, 2005). The cross-generational accumulation of this information (e.g., base-10 arithmetic) has resulted in the creation of a vast amount of biologically secondary knowledge, a culture that is increasingly reliant on this knowledge, and the corresponding need for longer periods of formal schooling (Geary, 2002).

In this view, the ability to learn evolutionarily novel information, such as the base-10 system, results from two types of brain and cognitive plasticity. The first is a base of biologically-primary modular systems, some of which are modifiable during the developmental period, but within constraints. The second type of plasticity results from our ability to mentally represent and manipulate information in working memory, which in turn creates mental experiences, so to speak, that can modify primary systems (Damasio, 1989; Dehaene & Naccache, 2001; Geary, 2005). From this perspective, individual differences in secondary learning, including LD, may result from multiple sources, including the degree of plasticity in primary systems, the ability to link primary systems in novel ways, and from the ability to engage working memory in ways that support second learning (Garlick, 2002; Geary, 2007; Sporns, Tononi, & Edelman, 2000).

PRIMARY AND SECONDARY ABILITIES

Biologically primary abilities represent the core modular, though plastic, systems that define the human mind, and secondary abilities are built from these based on cultural need and practices, such as schooling. In the first section, a brief introduction to a taxonomy of primary abilities is provided as a means to orient later discussion. In the second section, an overview of primary mathematical abilities and a contrast with several secondary mathematical abilities is provided.

Taxonomy of Primary Abilities

For humans, primary abilities appear to be organized around the domains of folk psychology (people), folk biology (other living beings), and folk physics (the physical world). The extent to which these information-processing biases are inherently modular or become increasingly modular as a result of developmental experiences is not fully understood and vigorously debated (Hauser, Chomsky, & Fitch, 2002; Heyes, 2003; Pinker & Jackendoff, 2005; Quartz & Sejnowski, 1997); the details of the debate are provided elsewhere (Geary, 2005). In either case, modularity means the systems are restricted in the forms of information, such as visual contours or phonemes, that it responds to and processes (Fodor, 1983), but these systems may still be modifiable within limits (Geary & Huffman, 2002). Moreover, lower-level perceptual systems (e.g., line orientation) may be used in multiple higher-level cognitive representations (e.g., recognition of faces and objects; Marcus, 2004), which also provides a mechanism for linking primary systems in the creation of secondary abilities (Garlick, 2002).

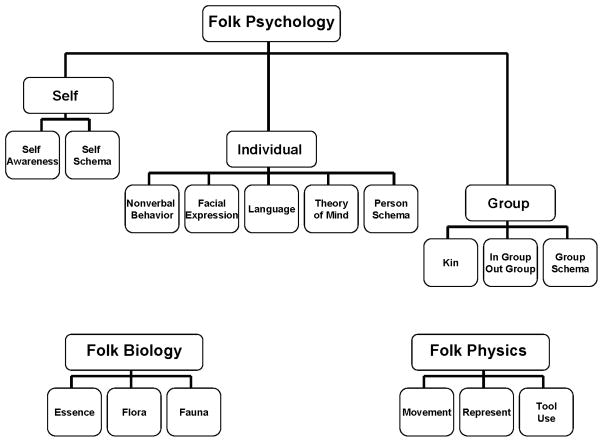
Whatever the extent of inherent modularity, the primary folk-psychological systems appear to be organized around information related to the self, relationships and interactions with other people, and group-level relationships and interactions. These dynamics are supported by the respective modular systems corresponding to self, individual, and group shown in the top section of Figure 1 (see also Geary, 2005). People living in traditional societies use the local ecology to support their survival and reproductive needs. The associated activities include hunting and foraging and are supported by the folk biological and folk physical modules shown in the bottom section of Figure 1. The folk biological modules support the categorizing of flora and fauna in the local ecology, especially species used as food, medicines, or in social rituals (Berlin, Breedlove, & Raven, 1973; Caramazza & Shelton, 1998). Folk biology also includes systems that support an understanding of the essence of these species (Atran, 1998). Essence is knowledge about growth patterns and behavior that facilitates hunting and other activities involved in securing and using these species as food and medicine. Physical modules are for guiding movement in physical space, mentally representing this space (e.g., demarcating the in-group’s territory), and for using physical materials (e.g., stones, metals) for making tools (Pinker, 1997; Shepard, 1994).

FIGURE 1.

Evolved cognitive modules that compose the domains of folk psychology, folk biology, and folk physics.

Across domains, many of these primary abilities are fleshed out during development and in the context of species-typical parent-child interactions, peer relationships, and children’s self-initiated exploration of the environment (Bjorklund, 2006; Bouchard, Lykken, Tellegen, & McGue, 1996; Greenough, Black, & Wallace, 1987; Scarr, 1993). The emergence of primary abilities through an interaction between experience and inherent constraints ensures that all people develop the same core systems of abilities and, at the same time, allows these systems to be fined tuned to the nuances of the local social group, and the biological and physical ecologies in which they are situated (Geary, 2005). In other words, children are biologically biased to engage in the types of activities and seek the types of experiences that adapt their primary systems to information that tends to fluctuate across social groups and ecologies; for instance, there are primary systems that orient infants to the shape of the human face and conjoined systems that are modified based on experiences, such that individual faces are recognized.

Mathematics

Primary Mathematics

Many species of animal are able to discriminate smaller from larger amounts, and some are able to make finer discriminations (e.g., two items vs. three items) and order a series of relative quantities (e.g., two to four items). Still other species may have a rudimentary ability to count and engage in simple addition and subtraction (Beran & Beran, 2004; Boysen & Berntson, 1989; Brannon & Terrace, 1998; Hauser, Carey, & Hauser, 2000; Nieder, Diester, & Tudusciuc, 2006). Most of these competencies have been studied in mammals, but evidence for similar competencies has also been found in several species of bird (Lyon, 2003; Pepperberg, 1987). In some traditional cultures, number words are only found for “one,” “two,” sometimes “three,” and for estimates of relatively larger amounts (e.g., “more than two”; Chagnon, 1997; Gordon, 2004; Pica, Lemer, Izard, & Dehaene, 2006). More sophisticated enumeration systems are found in some traditional cultures, but these appear to be less common and still limited to quantities less than 30 (De Cruz, 2006; Saxe, 1981). These and related studies as well as studies of human infants and preschool children are consistent with the evolution of a core system of quantitative abilities in many species, although the details of these systems may vary from one species to the next. The core set of primary mathematical abilities found in humans is shown in Table 1.

TABLE 1.

Core Primary Mathematical Competencies

Numerosity: The ability to accurately determine the quantity of sets of up to three to four items, or events, without counting (Sharon & Wynn, 1998; Starkey & Cooper, 1980: Strauss & Curtis, 1984; Wynn, Bloom, & Chiang, 2002).

Ordinality: An implicit understanding of more than and less than for comparison of sets of three to four items (Brannon, 2002; Cooper, 1984; Feigenson, Carey, & Hauser, 2002; Strauss & Curtis, 1984).

Counting: A nonverbal system for enumeration of small sets of items (Gallistel & Gelman, 1992; Hauser et al., 2000; Starkey, 1992), and implicit knowledge of counting principles (e.g., one to one correspondence; Gelman & Gallistel, 1978).

Simple arithmetic: Sensitivity to increases (addition) and decreases (subtraction) in the quantity of small sets of items (Boysen & Berntson, 1989; Kobayashi, Hiraki, Mugitani, & Hasegawa, 2004; Wynn, 1992).

Estimation: Inexact estimation of relative quantity, magnitude, or size (Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999; Feigenson, Dehaene, & Spelke, 2004; Pica et al., 2004).

Geometry: Implicit understanding of shape and spatial relations (Dehaene, Izard, Pica, & Spelke, 2006; Geary, 1995).

The cross-cultural and cross-species evidence for rudimentary quantitative abilities is not surprising given the usefulness of these competencies in many contexts and thus the potential for the evolution of supporting brain and cognitive systems. However, it does not necessarily follow that the initial evolved function of all of these abilities is mathematical. Numerosity or the ability to quickly apprehend the quantity of small sets without counting may have initially evolved as object identification mechanisms in the visual system (Simon, 1997; Trick, 1992), and may emerge developmentally as a numerical ability because of quantitative demands in the early environment, because of an evolved number mechanism that operates using information from the object identification mechanisms, or some combination. Although the evolutionary and epigenetic mechanisms that contribute to the core mathematical areas shown in Table 1 are not fully understood, these represent measurable quantitative competencies during infancy and the pre-school years and provide the foundation for learning many features of secondary mathematics in school (Geary, 2006; Spelke, 2000).

Unlike, for instance, mechanisms for processing facial expressions which have a clearly social function, the functional advantages for processing primary quantitative information, or folk mathematics, cannot be as easily categorized into the folk domains shown in Figure 1. Nonetheless, brain imaging studies consistently indicate engagement of areas of the parietal cortex, and in particular the horizontal intraparietal sulcus, when children and adults engage in many primary as well as secondary mathematics tasks (Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999; Eger, Sterzer, Russ, Giraud, & Kleinschmidt, 2003; Pinel, Piazza, Le Bihan, & Dehaene, 2004; Qin, et al., 2004; Qin, et al., 2003; Rivera, Reiss, Eckert, & Menon, 2005; Temple & Posner, 1998; Zorzi, Priftis, & Umiltá, 2002). This pattern of brain activation while processing quantitative information indicates an empirical link with aspects of folk physics.

The extent of activity-driven fleshing out of primary mathematical abilities is not fully understood. Some features of primary mathematics—such as a sensitivity to differences in the quantity of small sets (e.g., 2 vs. 3)—are evident during infancy (Antell & Keating, 1983), and do not show developmental change either in terms of functional skills (Mandler & Shebo, 1982) or the brain systems that are engaged during this task (Temple & Posner, 1998). Other features of primary mathematics—such as understanding cardinal value (i.e., that the last number word stated represents the number of items in a counted set)—emerge slowly during the preschool years and only after other features of primary mathematics are in place (Bermejo, 1996; Gelman & Gallistel, 1978). These slowly developing competencies likely emerge epigenetically: Foundational abilities are defined by attentional and perceptual biases that orient infants to quantitative features of their environment and provide the skeletal structure for slower maturing abilities (Gelman, 1990). The fleshing out of the skeletal structure likely occurs as attentional and activity biases (e.g., counting) create experiences that feedback onto the developing brain and cognitive systems to create more mature procedural skills (e.g., counting behavior), conceptual knowledge (e.g., cardinality), and declarative facts (e.g., number words) organized around the areas shown in Table 1 (e.g., Gelman & Gallistel, 1978).

The more slowly developing aspects of primary mathematical abilities may be open to early parental influences. For example, the fundamentals of the numerosity and estimation systems shown in Table 1 emerge with or without parental fostering of quantitative competencies (Dehaene et al., 2006; Pica et al., 2004), but the coordination of these systems with the culture’s number words may require more explicit, though informal instruction. The learning of specific quantities beyond three or four and associating number words with corresponding amounts (e.g., “five” = |||||) appears to involve mapping words onto the primary estimation system. The latter represents general amounts, not specific quantities (Gallistel & Gelman, 1992), and thus children’s conception of the quantities represented by larger number words is dependent to an important degree on their learning of the standard counting sequence (i.e., “one,” “two,” “three”…), properties of this sequence—that successive number words represent an increase of exactly “one”—and integrating them with the primary estimation system. The extent to which integration of the counting and estimation systems will emerge naturally from children’s self-initiated activities or from the informal parental instruction that is found in many middle class families is not known (Saxe, Guberman, & Gearhart, 1987).

In any event, by the end of the preschool years, most children have in place an integrated and functional core of skills and knowledge that allow them to engage in and understand some quantitative activities, including counting, simple measurements, and basic addition and subtraction (Geary, 1995). Although impressive in many respects, this system of primary abilities is restricted in comparison to the mathematics that children are expected to learn in modern societies.

Secondary Mathematics

Much of modern day mathematics is biologically secondary in the sense that this knowledge is of recent historical origin and does not emerge without formal schooling, sometimes many years of schooling. A foundational part of junior high school and high school algebra includes, as an example, an understanding of the x-axis/y-axis coordinate system and procedures for plotting lines in this two-dimensional space; for instance, the slope-intercept form, y = mx + b, where b is the y-intercept and m is the slope defining change in y as a function of change in x. This is rudimentary knowledge for anyone wishing to pursue a career that involves even moderately complex mathematics, as in understanding regression analyses in statistics, but is far removed from the core primary abilities shown in Table 1. To understand individual differences in ease of learning secondary concepts (e.g., coordinate plane) and procedures (e.g., graphing functions in this plane), it would be useful to know the primary systems from which this knowledge is built and the pattern, quantity, and quality of instructional and other experiences that lead to the more basic skills (e.g., number line) that support ease of learning these concepts and procedures when they are introduced in school. We are not yet at the point where we can decompose these complex secondary mathematical abilities but we can begin to explore the relation between primary abilities and more elementary secondary abilities.

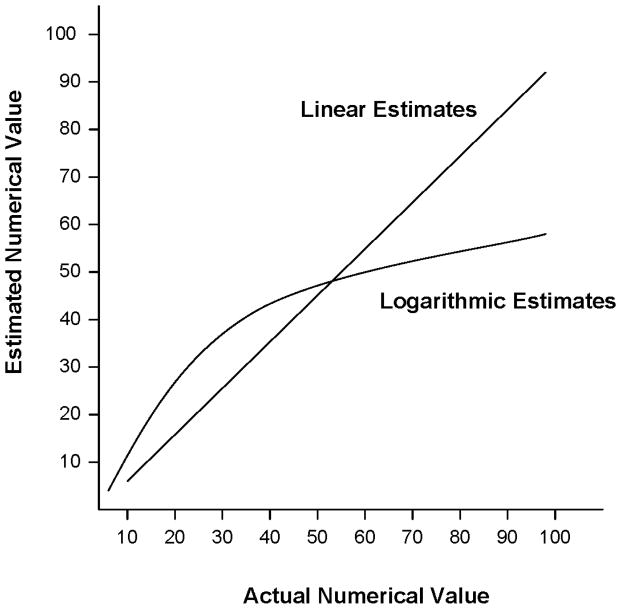
As an example of the potential relation between primary and secondary mathematical abilities, consider the number line: Number lines are used in many areas of mathematics from representing quantity in arithmetic to the x-axis/y-axis coordinate plane in algebra. From an evolutionary perspective, children’s initial representations of the number line are predicted to be based on the inherent estimation system (Dehaene et al., 1999; Gallistel & Gelman, 1992). If children are initially dependent on this primary system for understanding and creating number lines, then their placement of values along a number line should conform to the natural logarithm (ln) of the number, that is, the placement should be compressed for larger magnitudes such that the perceived distance between 2 and 3 is larger than the perceived distance between 20 and 21, which in turn is larger than the perceived distance between 80 and 81. The logarithmic pattern is found in many species when responding to relative magnitudes, such that three items of food vs. two items is more salient than ten items vs. nine items (Gallistel & Gelman, 1992). Figure 2 illustrates the pattern of logarithmic-based placements that are dependent on the estimation system and the linear placements that emerge with formal schooling (Siegler & Booth, 2004; Siegler & Opfer, 2003). For the latter, the distance between any two successive numbers is always “one” regardless of position on the number line.

FIGURE 2.

Predicted number line placements when children use the estimation and magnitude representation system (Logarithmic estimates) and when they use the school-taught, formal mathematical system (Linear estimates).

The ability to estimate and form representations of magnitude are dependent on visuospatial systems situated in regions of the parietal cortex (Dehaene et al., 1999; Pinel et al., 2004; Zorzi et al., 2002) and that may have evolved as a component of primary folk-physical systems. Pinel et al. found the brain regions that represent numerical magnitude also represent spatial magnitude (i.e., relative size of objects), and Zorzi et al. found that individuals with injury to the right-parietal cortex showed deficits in spatial orientation and number line estimation. Individual differences in ease of spatially representing the log-scale number lines and presumably ease of creating linear representations of these number lines are predicted to be related to the integrity and fidelity of these visuospatial, parietal systems. In other words, anatomical or functional deficits in the ability to represent visuospatial information in working memory or to form associations of these representations in long-term memory are predicted to disrupt procedural and conceptual learning in some areas of mathematics, including the number line and related areas (e.g., coordinate plane). In this situation, any associated learning disability would be related to deficits in the primary brain and cognitive systems that support this aspect of secondary learning, as contrasted with the attentional and inhibitory control systems of the central executive described in the next section.

Another example of the relation between primary systems and secondary knowledge is provided by the base-10 system. A conceptual understanding of this system is an essential component of learning modern arithmetic and is facilitated by an understanding of the mathematical number line and an ability to decompose the number line into sets of ten and then to organize these sets into clusters of 100 (i.e., 10, 20, 30…), 1000, and so forth. Infants and young children implicitly organize collections of objects into sets and this may provide an early foundation for understanding sets at a more abstract level, but the creation of sets around 10 and the superordinate organization of these sets does not emerge naturally from this primary knowledge. The explicit organization of the number system around 10 must also be systematically mapped onto the number word system (McCloskey, Sokol, & Goodman, 1986), and integrated with school-taught procedures for solving complex arithmetic problems (Fuson & Kwon, 1992; Geary, 1994). The development of base-10 knowledge thus requires the extension of primary number knowledge to very large numbers; the organization of these number representations in ways that differ conceptually from primary knowledge; and, the learning of procedural rules for applying this new knowledge to the secondary domain of complex, mathematical arithmetic (e.g., to solve 234 + 697).

In other words, there are multiple potential sources of individual differences in children’s conceptual understanding of the base-10 system and to skilled use of associated procedures. These sources can range from poor primary systems (e.g., estimation system that supports number line development) to poor instruction in the context of intact primary systems to poor working memory needed to execute procedures (next section) to some combination. The more complex the secondary mathematics—the more primary systems it draws upon and the more it is dependent on previous secondary learning—the more potential sources of variation in learning and MLD. The framework presented in the final section will outline an approach that might be useful for decomposing this variation.

BRAIN AND COGNITIVE MECHANISMS FOR SECONDARY LEARNING

Empirical studies have revealed that performance on measures of intelligence is one of the best predictors of ease of learning in school and in other evolutionarily-novel contexts (Gottfredson, 1997; Lubinski, 2000; Walberg, 1983). An evolutionary model of secondary learning must then accommodate this empirical finding and corresponding research on the mechanisms that underlie individual differences in intelligence. I provide a brief review of the empirical literature on intelligence in the first section, and provide an integration of this research with a model of brain and cognitive evolution in the second section; a more thorough integration is provided elsewhere (Geary, 2005, 2007).

Fluid Intelligence

In 1904, Spearman (1904) empirically demonstrated that above average performance in one academic area is associated with above average performance in all other academic areas, with performance on many sensory and perceptual tasks, and with teacher and peer ratings of in-school intelligence and out-of-school common sense. On the basis of these findings, Spearman (p. 285) concluded “that all branches of intellectual activity have in common one fundamental function (or group of functions),” which he termed general intelligence or g. Cattell and Horn (Cattell, 1963; Horn, 1968; Horn & Cattell, 1966) argued that the single general ability proposed by Spearman should be subdivided into two equally important but distinct abilities. The first ability is called crystallized intelligence (gC) and is manifested as the result of experience, schooling, and acculturation and is referenced by over-learned skills and knowledge, such as vocabulary. The second ability is called fluid intelligence (gF), and represents a biologically-based ability to acquire skills and knowledge during the life span. In the original study, Cattell (1963, p. 3) proposed, “Fluid general ability … shows more in tests requiring adaptation to new situations, where crystallized skills are of no particular advantage”. The implication is that gF should predict learning in evolutionarily novel contexts, such as school and the modern workplace, and this is the case (Carroll, 1993; Gottfredson, 1997; Walberg, 1984).

Cognitive Systems

Theoretical and empirical work in recent decades indicate that working memory is a core mechanism underlying individual differences in gF (Carpenter, Just, & Shell, 1990; Conway, Cowan, Bunting, Therriault, & Minkoff, 2002; Engle, Tuholski, Laughlin, & Conway, 1999; Fry & Hale, 1996; Mackintosh & Bennett, 2003); the strength of the relation between performance on working memory tasks and gF range from moderate (rs ~ 0.5; Ackerman, Beier, & Boyle, 2005; Mackintosh & Bennett, 2003) to very high (rs > 0.8; Conway et al., 2002). The core cognitive mechanisms that compose working memory have been narrowed to a fundamental speed of information processing (Jensen, 1998), attentional control (Engle, Kane, & Tuholski, 1999), or some combination. These mechanisms are necessary but not sufficient, because the creation and learning of secondary abilities also require the systematic manipulation of and reasoning about the information represented in working memory (Stanovich & West, 2000). Overall, strategic problem solving and abstract reasoning define gF, and the primary cognitive system underlying problem solving, reasoning, and thus gF is working memory (Carpenter et al., 1990; Horn, 1968; Stanovich, 1999).

Speed of Processing

Several patterns have emerged from studies of the relation between speed of processing (e.g., speed of retrieving a letter name from long-term memory) and performance on measures of g (Hunt, 1978); the associated measures often assess a combination of gC and gF. First, faster speed of processing is related to higher scores on measures of g (Jensen & Munro, 1979) but the strength of the relation is moderate (rs ~ 0.3 to 0.4). Second, variability in speed of processing is also related to scores on measures of g (rs ~ 0.4; Jensen, 1992), and especially gF (Larson & Saccuzzo, 1989). The variability measure provides an assessment of the consistency in speed of executing the same process multiple times. Individuals who are consistently fast in executing these processes have higher scores on measures of gF than do their less consistent peers (Deary, 2000). Third, the speed with which individuals can identify information (e.g., whether “>” is pointed left or right) that is presented very briefly (e.g., 50 msec) is moderately correlated with g (rs ~ 0.4 to 0.5; Deary & Stough, 1996).

These studies suggest that intelligence is related, in part, to the speed, accuracy, and consistency with which information is identified and processed by the associated brain and perceptual systems. The benefits are likely manifest at two levels. First, the processing of this information is often implicit and results in fast and automatic responses to over-learned information typically associated with gC (e.g., a written word) and presumably fast and automatic responses to the forms of information (e.g., a facial expression) represented by the taxonomy in Figure 1. The fast and automatic processing of information in folk domains and of over-learned secondary information allows individuals to navigate evolutionarily-significant contexts (e.g., automatic processing of facial features) and contexts frequently encountered in the culture without effortful engagement of working memory resources (Gigerenzer, Todd, and ABC Research Group, 1999; Gigerenzer & Selten, 2001; Kanwisher, McDermott, & Chun, 1997; H. Simon, 1956). The second benefit is faster speed of processing may enable larger amounts of information to be simultaneously represented in working memory and thus more information that can be considered when explicit problem solving becomes necessary, that is, when conditions are variant or novel.

Attentional and Inhibitory Control

From an evolutionary perspective, the explicit or conscious representation of information in working memory is only necessary when the automatic and implicitly operating folk mechanisms or learned heuristics are not sufficient for coping with current social or ecological conditions. In this situation, there is an automatic shift in attention to this information (Botvinick, Braver, Barch, Carter, & Cohen, 2001). The focusing of attention results in an explicit representation of the information in working memory (Cowan, 1995), and simultaneous inhibition of irrelevant information or previously used behavioral responses (Engle, Conway, Tuholski, & Shisler, 1995). The ability to inhibit evolved or learned behavioral responses and to represent associated behavioral scripts in working memory enables the conscious evaluation of the source of the variation or conflict. Inhibition is also a necessary first step in the use of problem solving to reconfigure behavioral scripts to cope with these conditions or to simply to make an explicit decision regarding whether to use a previously learned or evolve heuristic or to switch to a novel solution (e.g., Daw, O’Doherty, Dayan, Seymour, & Dolan, 2006).

The attentional system that controls the explicit manipulation of information during problem solving is Baddeley and Hitch’s (1974) central executive component of working memory. The central executive operates on information represented in three slave systems; specifically, the phonological loop (auditory), visuospatial sketch pad, and episodic buffer (Baddeley, 1986, 2000a, 2000b). Baddeley and Hitch’s model can be situated into a broader evolutionary framework in which information can be processed and represented in any of the six broad sensory and perceptual systems shown in Figure 3 (Geary, 2005). The focus of cognitive psychologists on auditory, spatial, and visual information follows from the fact that humans are a diurnal (awake during the day) species of primate—visuospatial systems are elaborated in these species (Barton, 1996)—that is heavily dependent on language for social communication. The evolution of most of the primary systems shown in Figure 1 and associated with folk mathematics is predicted to be have been the result of the differentiation and modification of these broad auditory, visual, and spatial systems.

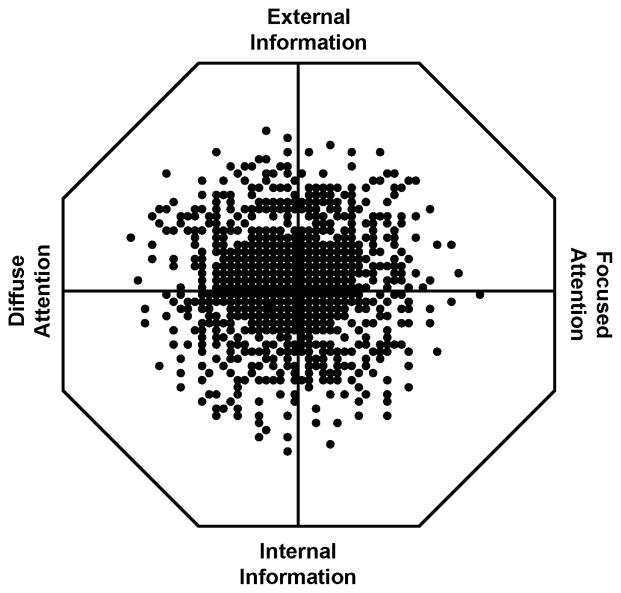
FIGURE 3.

Auditory, spatial, visual, gustatory, kinesthetic, and olfactory in the outer section of the oval represent neural, sensory, perceptual, and cognitive modules that process external information patterns in these domains. The central executive is composed of the mechanisms that direct attention to one of these domains and result in a conscious, explicit awareness and representation of the corresponding information. Adapted from The origin of mind: Evolution of brain, cognition, and general intelligence, by D. C. Geary, p. 206. Copyright 2005 by the American Psychological Association. Reprinted with permission.

The slave systems in turn can be decomposed into brain and cognitive subsystems that process finer-grained pieces of information, such as facial features (Kanwisher et al., 1997; Schyns, Bonnar, & Gosselin, 2002), language sounds (Price, 2000), body shape (Downing, Jiang, Shuman, & Kanwisher, 2001), and so on. Constellations of these subsystems comprise the primary folk modules shown in Figure 1 (Geary, 2005). The estimation of magnitudes described in Table 1 and represented by the log number line in Figure 2 is constructed from subsystems that are part of Baddeley’s visuospatial sketch pad (Baddeley & Logie, 1999; Pinel et al., 2004). The episodic buffer, in contrast, does not process phonetic or visuospatial information per se, but rather results in the conscious awareness of experiences that require an integration of information—potentially including that represented in the phonological buffer and visuospatial sketch pad—across space and sometimes across time. The buffer is very similar to Tulving’s (2002) model of mental time travel and Suddendorf and Corballis’ (1997) self awareness, and almost certainly represents core brain and cognitive systems that enable humans to anticipate ecological or social change and to mentally reconstruct past representations of similar conditions as a means to generate potential behavioral solutions, as described in Evolutionary Model.

Explicit Problem Solving and Reasoning

Working memory does not explain all of the individual variation in gF (Stanovich, 1999). In fact, many measures of gF required explicit, stepwise reasoning and the drawing of inductive or deductive inferences, but the different contributions of working memory and reasoning are not always separated in these studies (Kyllonen & Christal, 1990). Embretson (1995) conducted one of the few studies that did separate working memory capacity and the processes involved in making controlled, explicit inferences. The combination of working memory capacity and the ability to explicitly make inferences using information represented in working memory explained almost all of the individual differences in gF across a group of 577 air force (U.S.) recruits. Skill at making inferences explained about 2/3 of the individual differences in gF and working memory capacity explained the remaining variation. This study suggests gF involves the ability to hold and manipulate information in working memory, draw inferences about relations among these pieces of information, and then apply these inferences during the act of controlled problem solving. These findings are also in keeping with the research of Stanovich and West (2000; Stanovich, 1999), and their proposal that the ability to reason explicitly and logically is a competency in and of itself.

Brain Systems

Brain regions that become activated or inhibited while individuals solve items on measures of gF have been assessed in numerous studies (Duncan et al., 2000; Gray, Chabris, & Braver, 2003; Haier et al. 1988; Prabhakaran, Smith, Desmond, Glover, & Gabrieli, 1997). Most of the studies reveal a pattern of activation and deactivation in a variety of brain regions, much of which is likely due to task-specific content of the reasoning measures (e.g., verbal vs. visual information; Stephan et al., 2003). Consistent across-task activation has nonetheless been found in the same system of brain regions that the support the attentional control and inhibitory control components of the central executive (Esposito, Kirkby, van Horn, Ellmore, & Berman, 1999; Kane & Engle, 2002), and the ability to explicitly reason and problem solve (Fugelsang & Dunbar, 2005; Stavy, Goel, Critchley, & Dolan, 2006). These areas include the lateral prefrontal cortex, anterior cingulate cortex, and regions of the parietal cortex associated with attentional focus (Duncan et al., 2000), although size and white matter organization in other brain regions may also contribute to individual differences in gF.

Other studies suggest that some areas of the anterior cingulate cortex are heavily involved in achieving goals that are not readily achieved by means of implicitly operating heuristics and behavioral scripts (Miller & Cohen, 2001; Ranganath & Rainer, 2003). The anterior cingulate cortex in particular is activated when goal achievement requires dealing with some degree of novelty, or conflict (e.g., choosing between two alternatives), although the anterior cingulate cortex is complex and involved in many other functions as well (Bush, Luu, & Posner, 2000). The result appears to be an automatic attentional shift to the novel or conflicted information and activation of the dorsolateral and ventrolateral prefrontal areas (Botvinick et al., 2001). These areas in turn enable inhibition of evolved or over-learned responses and the explicit, controlled problem solving needed to cope with the novel situation or to resolve the conflict (Kerns, Cohen, MacDonald, Cho, Stenger, & Carter, 2004; Stavy et al., 2006). Botvinick and colleagues’ proposal that novelty and conflict result in automatic attentional shifts and activation of executive functions is important, as it addresses the homunculus question. The central executive does not activate itself, but rather is automatically activated when implicitly operating folk processes or over learned responses are not sufficient for dealing with current social or ecological information patterns or tasks.

The repeated activation of these systems and associated problem solving enable individuals to learn semantic information and to develop behavioral heuristics for coping with these and similar situations. In addition to the prefrontal cortex and anterior cingulate cortex, the learning of semantic information engages areas of the medial temporal cortex, specifically the hippocampus and adjacent areas (Squire & Alvarez, 1995; Squire & Bayley, 2003), whereas learning of heuristics engages nuclei of the basal ganglia (Graybiel & Saka, 2003; Jog, Kubota, Connolly, Hillegaart, & Graybiel, 1999). After a period of consolidation, the long-term memories for these contexts and the behavioral heuristics for coping with them appear to be represented in distributed areas of the cortex involved in processing the original information (e.g., Damasio, 1989).

Empirical Integration

Individuals who score well on measures of gF process information such that it is activated in short-term memory more quickly and with greater accuracy than it is for their lower scoring peers. Once active in short-term memory, the information is available for conscious, explicit representation and reasoned manipulation in working memory, but this only happens for the subset of information that becomes the focus of attention. Explicit representation of information in working memory appears to result from a synchronization of the prefrontal brain regions that subserve the central executive and the brain regions that process the specific forms of information that are the foci of attention, such as a voice, face, or object (Damasio, 1989; Dehaene & Naccache, 2001; Posner, 1994). An attention-driven synchronization of the activity of dorsolateral prefrontal cortex and the brain regions involved in the processing of external information or internal mental simulations would be facilitated by faster speed of processing and rich interconnections among these brain regions; the latter are associated with larger brain size and especially a greater volume of white matter. Synchronization appears to be dependent on the white matter connections that communicate back and forth between different brain regions, creating feedback cycles. Faster speed of processing would enable more accurate adjustments in synchronization per feedback cycle. With repeated synchronized activity, the result appears to be the formation of a neural network that automatically links the processing of these information patterns (Sporns et al., 2000).

Once attention is focused, intelligent people are able represent more information in working memory than are other people and more easily manipulate this information. The manipulation in turn is guided and constrained by reasoning and inference making mechanisms (Johnson-Laird, 1983; Newell & Simon, 1972; Stanovich, 1999), which also appear to be dependent on regions of the prefrontal cortex (Fugelsang & Dunbar, 2005; Green, Fugelsang, Kraemer, Shamosh, & Dunbar, 2006; Stavy et al., 2006). Repeated attentional focus and synchronization of associated brain regions results in the creation of secondary knowledge and eventually this information is processed automatically and implicitly, as in word recognition for skilled readers (Sereno & Rayner, 2003).

Evolutionary Model

Elaborating on Alexander’s proposal (1989; see also Flinn et al., 2005) and building on Tulving’s (1992; Wheeler, Stuss, & Tulving, 1997) model of self awareness and Suddendorf’s model of mental time travel (Suddendorf & Busby, 2003; Suddendorf & Corballis, 1997), I argued the core cognitive system underlying the human ability to cope with novelty and change during the life span is the autonoetic mental model (Geary, 2005). The autonoetic mental model is a component of a more general motivation to control theory. The motivation to control represents a shorthand for the function of evolved traits, that is, to enable attempts to gain access to and control of the social (e.g., mates), biological (e.g., food), and physical (e.g., nesting spots) resources that covaried with survival or reproductive prospects during the species’ evolutionary history. The shape of a finch’s beak and associated foraging behaviors, for instance, allow the bird to gain access to seeds and other forms of food. Presumably, there is no conscious motivation to control these resources, but the evolved function is all about resource control. The folk domains represented in Figure 1 are part of the motivation to control and correspond to the three general forms of resource around which control related behaviors and cognitions are organized, that is, social (folk psychology), biological (folk biology), and physical (folk physics). As noted, these folk modules process restricted forms of information (e.g., facial features) and guide heuristic-based decision making.

The autonoetic mental model is a self centered recreation of past experiences, simulations of potential future states, or of the “ideal” world in working memory. In this simulated world, other people behave in ways consistent with one’s self interest and biological, physical, and symbolic (e.g., money) resources are under one’s control. The ideal world serves as a goal to be achieved and is compared against a mental representation of current circumstances. Working memory and attentional mechanisms serve as the platform for mentally simulating social and other current circumstances and then using problem solving and reasoning to devise behavioral strategies that will reduce the difference between the current state and the ideal state. These problem solving activities are ultimately directed toward the goal of attempting to achieve control of social and other resources. Social dynamics are the most likely key to understanding the evolution of these abilities (Alexander, 1989; Humphrey, 1976). The ability to mentally project the self into the future, to generate and rehearse social strategies, and to anticipate and generate counter moves to others’ social strategies provides a distinct advantage over individuals who can only respond to social situations with evolved heuristics or simple variants of these heuristics, as appears to be the case with other species of primate (Parker, 2004).

Once the ability to generate autonoetic mental models emerged, the stage was set for an evolutionary arms race, whereby within-species social competition drove brain and cognitive evolution and resulted in the emergence of a suite of unique human traits, including self awareness and the working memory system and attentional/inhibitory control mechanisms that compose gF. The same mechanisms appear to allow people to pass this new knowledge to other people (Geary, 2007). If this proposal is correct, then the brain and cognitive systems that underlie gF are the mechanisms that provide the theoretical link between primary abilities and secondary learning, that is, these are the systems involved in the modification of primary systems to create secondary competencies. The latter is the creation of gC and typically includes the learning of declarative or semantic knowledge, such as an explicit understanding negative numbers or addition facts, and procedural abilities, as in being able to execute the trading procedure in complex addition.

EVOLUTION AND INDIVIDUAL DIFFERENCES IN LEARNING

The consideration of school-taught knowledge and abilities from an evolutionary perspective may provide a useful means of conceptualizing the potential sources of LD. A full discussion of the nuances of this perspective would require detailed evaluation of the relation between folk abilities (e.g., inferential biases; Gelman, 2003; Wellman & Gelman, 1992) and the ways in which these abilities influence secondary learning in specific domains (Geary, 2007), as well as consideration of how patterns of brain maturation and variation in these patterns influence ease of modifying primary systems in the creation of secondary competencies (Gieddet al., 1999; Shaw et al., 2006; Sowell, Peterson, Thompson, Welcome, Henkenius, & Togo, 2003; Sowell, Thompson, Holmes, Batth, Jernigan, & Toga, 1999). Our current state of knowledge does not allow firm conclusions to be drawn, but, nonetheless, enough is known to explore the potential utility of this approach. In the first section, I define a primary system deficit and provide an example of how these might influence secondary learning and LD. In the second section, I provide an evolutionary analysis of core components of the executive system and illustrate how such an analysis can add to our understanding of individual differences in secondary learning.

Primary System Deficits

Primary systems are those that compose the folk psychology, folk biology, and folk physics domains shown in Figure 1 and the folk mathematics described in Table 1. Primary system deficits affect one or several of these systems, in the context of normal or near normal functioning of other primary systems. From an evolutionary perspective, intraindividual variation and interindividual differences in primary systems can result from the cost-benefit trade offs that emerge with the proximate development and maintenance of these traits such that the enhancement of one trait can often result in costs to the development of another trait (Williams, 1957; West-Eberhard, 2003). As an example, prenatal exposure to male hormones may enhance the early organization of folk physical systems, but at a cost to the early development of folk psychological systems (Baron-Cohen, 2003; Geary, 1998).

Intraindividual and interindividual variation in primary systems is also predicted to emerge for species in which different individuals may occupy different ecological and social niches, and especially in the human species that appears to have evolved to create complex social-cultural organizations (Baumeister, 2005). In these social contexts, people vary in interests and activity patterns along two fundamental dimensions, people-things and concrete-abstract (Prediger, 1982; Roe & Klos, 1969). These dimensions, in turn, are related to patterns of cognitive strengths and weaknesses and influence occupational choices (Ackerman & Heggestad, 1997; D. Campbell & Holland, 1972; Lubinski & Benbow, 2000). The specific occupations are of course culturally relative and historically recent, but the underlying interest dimensions and the tendency of people to organize activities along these dimensions is consistent with evolution in complex social groups and benefits to variation in niche construction (Geary, 2007). In other words, the benefits of cooperation and a division of labor within a group context create a situation in which different patterns of interests, across individuals, and cognitive strengths and weaknesses, across and within individuals, in primary systems could evolve.

An example of a primary system deficit is provided by individuals with Asperger syndrome, many of whom have specific deficits associated with attending to, processing, and interpreting folk psychological information, such as facial features (Baron-Cohen, 1995), but may excel in the processing and comprehension of folk physical information (Baron-Cohen, 2003; Baron-Cohen, Wheelwright, Stone, & Rutherford, 1999). The deficits associated with the processing of facial features, in turn, may be related to abnormalities in the fusiform gyrus of the temporal cortex (Schultz et al., 2000), whereas the processing of many aspects of folk physics appears to engage areas of the parietal cortex (Johnson-Frey, 2003; Vanduffel et al., 2002). Baron-Cohen and colleagues have suggested the cognitive strengths and weaknesses of high functioning individuals with Asperger syndrome are the result of prenatal exposure to male hormones. Although they conceptualize these strengths and weaknesses somewhat differently, the hypothesis is consistent with expected cost-benefit trade offs; in this case enhanced folk physical competencies at a cost to folk psychological competencies.

Primary system deficits may also influence the ability to learn in secondary domains. A well studied example of the building of secondary abilities from primary systems is provided by the relation between early reading acquisition and language systems (Bradley & Bryant, 1983; Hindson, Byrne, Shankweiler, Fielding-Barnsley, Newman, & Hine, 2005; Mann, 1984; Rozin, 1976). Crucial components in early reading acquisition include an explicit awareness of distinct language sounds, that is, phonemic awareness, and the ability to decode unfamiliar written words into these basic sounds. Decoding requires an explicit representation of the sound (e.g., ba, da, ka) in phonemic working memory and the association of this sound, as well as blends of sounds, with corresponding visual patterns, specifically letters (e.g., b, d, k) and letter combinations (Bradley & Bryant, 1983; Wagner, Torgesen, & Rashotte, 1994). Phonetic working memory has also been proposed as the mechanism that supports vocabulary acquisition during natural language learning (Baddeley et al., 1998; Mann, 1984), but this form of word learning occurs implicitly and much more quickly (sometimes with one exposure) than does the achievement of automatic word recognition during reading acquisition (Pinker, 1994; Sereno & Rayner, 2003).

Functional or structural abnormalities in the brain and cognitive systems that support the processing of language sounds and the ability to associate these sounds with objects contribute to difficulties in learning to decode written words and in fluent word reading, and thus can result in a reading disability (RD; Bruck, 1992; Eden & Moats, 2002; Gaillard et al., 2006; Turkeltaub, Gareau, Flowers, Zeffiro, & Eden, 2003). For individuals with RD, it is commonly found that areas of the temporal cortex (e.g., superior temporal gyrus) that support the processing of phonetic sounds and areas involved in forming associations between written words and sounds (e.g., angular gyrus) are structurally abnormal and/or show hypo-activation during word reading (Eden & Zeffiro, 1998; Hynd & Semrud-Clikeman, 1989; Paulesu et al., 2001; Shaywitz et al., 1998); there may also be mild cytoarchitectonic abnormalities other brain regions (Hynd & Semrud-Clikeman, 1989), as well as variation in the pattern of functional brain activation during word reading across individuals with RD (Eden & Zeffiro, 1998).

At the same time, there is often hyperactivation in areas of the frontal cortex—indicating these individuals are exerting more effort than normal readers when attempting to read—and activation of areas of the right hemisphere that are analogous to the reading-related areas of the left hemisphere (Shaywitz & Shaywitz, 2005). The latter suggests that brain regions not typically involved in reading may be engaged in a compensatory manner when individuals with RD read. With early and explicit teaching of phonemic decoding and practice of word reading, many but not all, children with RD eventually show engagement of the normal reading-related areas of the left hemisphere although subtle reading deficits often remain (Shaywitz et al., 2004). Many adults with RD continue to have difficulties with the decoding of unfamiliar words (Bruck, 1992), and may continue to recruit areas of the right hemisphere to compensate for poor engagement of reading-related regions of the left hemisphere (Eden et al., 2004).

Executive System Deficits

The points of the proceeding section are that there can be specific cognitive and neural deficits in evolved, biologically-primary systems and that these can sometimes affect the ease of learning specific secondary abilities that are built from these primary systems. Deficits in the executive system, that is, components of gF, are sometimes used as exclusionary criteria in the diagnosis of LD, but the utility of this practice has been questioned (Stuebing, Fletcher, LeDoux, Lyon, Shaywitz, & Shaywitz, 2002). Indeed, the importance of these systems for understanding individual differences in secondary learning means that variation in executive system functioning should be considered in any analysis of difficulties in secondary learning. In the following sections, I illustrate how an evolutionary perspective might add to our understanding of the empirical relation between executive functions and secondary learning and how this might contribute to our understanding of LD.

Attentional and Inhibitory Control

Information associated with primary domains, such as that conveyed by the human face (Schyns et al., 2002), will automatically capture the attention of the corresponding brain and perceptual systems and guide the execution of behavioral heuristics (Gelman, 1990; Gigerenzer et al., 1999; Simon, 1956). Much of this information processing occurs implicitly and results in behavioral biases that may recreate the dynamics associated with the evolution of these systems (Caporael, 1997). The recreation involves the automatic execution of the behavioral heuristics that evolved to cope with this information. The pattern of automatic heuristic response to situations that parallel those that resulted in the evolution of the heuristic is common across species and likely influences much of human behavior (Gigerenzer et al., 1999). As noted earlier, the ability to control attention in ways that facilitate the modification of primary systems is predicted to evolve in species that experience rapidly changing ecological or social conditions that affect survival or reproductive prospects during the lifespan, and when preexisting primary-system behavioral heuristics are insufficient for coping with this variation (Geary, 2005).

From this perspective, the brain and cognitive mechanisms that support attentional and inhibitory control are evolved systems in and of themselves and are assumed to be subject to the same cost-benefit trade offs and individual variation noted for primary systems. Potential anatomical correlates of individual variation in attentional and inhibitory control, as related to adaptation to variation and change in social or ecological conditions, include the anterior cingulate cortex, the lateral prefrontal cortex, the attention areas of the parietal cortex, and white matter connections among these brain regions and the brain regions that process the primary information mentioned earlier. Engagement of the basal ganglia (Graybiel & Saka, 2003; Jog et al., 1999), as related to the acquisition of procedural skills, and the hippocampus and other areas of the medial temporal lobe (Squire & Alvarez, 1995; Squire & Bayley, 2003), as related to the initial learning of facts and other declarative knowledge, are also important components of the brain systems that have evolved for learning during the life span. A full evolutionary analysis of each of these areas as related to academic learning is beyond the scope of this article, but brief consideration of the anterior cingulate cortex and lateral prefrontal cortex illustrates the potential utility of such an analysis.

Evolutionary Analysis

Areas of the anterior cingulate cortex are engaged in situations that involve cognitive conflict, that is, when a decision regarding alternative choices must be made or when current behavioral or cognitive heuristics are not sufficient for achieving the desired goal (Miller & Cohen, 2001). These cognitive areas of the anterior cingulate cortex (see Bush et al., 2000) may be components of an alerting-attention shifting mechanism that engages the lateral prefrontal cortex (Botvinick et al., 2001; Kerns et al., 2004). The lateral prefrontal cortex includes the ventral area which is involved in the inhibition of evolved or over-learned responses, among other functions, and the dorsal area which is involved in the explicit representation of the attended information in working memory. Once in working memory, effortful problem solving can be employed to attempt to resolve the conflict or make the decision. If the cognitive areas of the anterior cingulate cortex along with the lateral prefrontal cortex are core components of a wider system of brain regions that support humans’ ability inhibit evolved and over-learned responses and thus use working memory and problem solving to cope with variation and change within the life span, then evolutionary modification in the size and architecture of these brain regions should have occurred and should show functional relations to the ability to cope with change (Geary, 2005).

In addition to a 3-fold increase in overall brain size during the past 4 million years of human evolution (Holloway, 1973; Tobias, 1987), comparative studies support the prediction of anatomical modification of these brain regions. The anterior cingulate cortex is larger in primates than in other mammals (Vogt, 1987), and there is a form of neuron that is found only in the anterior cingulate cortex of great apes and humans (Nimchinsky, Gilissen, Allman, Perl, Erwin, & Hof, 1999). These cells are more tightly organized (i.e., clustered in groups) and considerably larger in humans than in great apes, and appear to be involved in connecting the anterior cingulate cortex with the prefrontal cortex and with other brain regions. Evolutionary change in cranial shape suggests substantive modification of the architecture of the prefrontal cortex (Holloway, Broadfield, & Yuan, 2004), and comparative and neuroimaging evidence suggests the changes involved, at least in part, greater differentiation of functional abilities within the prefrontal cortex and greater white matter integration among these areas (Koechlin, Ody, & Kouneiher, 2003; Preuss, 2004; Semendeferi, Armstrong, Schleicher, Zilles, & van Hoesen, 2001). These patterns are consistent with the proposal that in comparison to related species, humans may have a lower threshold for detecting subtle variation and change in ecological, social, or other forms of information associated with folk modules (Figure 1), a greater capacity for inhibiting evolved responses to this information, and greater capacity for using working memory resources for devising solutions to cope with changing ecological or social conditions.

In addition to palaeontological and comparative patterns, examination of behavioral and cognitive biases associated with the extremes of attentional and inhibitory control, as may be manifested as behavioral or psychiatric disorders, provides a means to decompose the predicted trade offs associated with the evolved function of the executive system. Figure 4 provides an example of the trade offs across two core cognitive dimensions, diffuse to focused attention and internal to external focus of attention. Diffuse focus provides the benefit of simultaneous monitoring of multiple aspects of social and ecological conditions or shifting from one internal representation to another, but at a cost to the ability to maintain attentional focus on subtle details. A focus on external conditions allows for monitoring of social and ecological conditions, but at a cost to the ability to create mental models of these conditions as potentially related to future behavioral strategy (Geary, 2005). Of course, the best outcome is when individuals can shift from diffuse to focused attention and from a focus on external or internal information, as conditions change. Indeed, the advantages of the ability to shift attention across these dimensions is predicted to result in evolved traits such that most individuals will cluster at the center of the figure. The cost to this flexibility may be that exceptional ability is not achieved on either dimension. Nonetheless, some individuals are predicted to be at the extremes of one or both dimensions and it is these individuals that afford the opportunity to identify and decompose the predicted evolved functional systems. For instance, individuals at the extreme in the top right quadrant of the figure are predicted to be highly sensitive to change in external conditions and manifest a corresponding focus on detailed features of this information. Moreover, the focus is predicted to be on forms of information that were of evolutionary significance, such as social or predatory threats, risk of contamination, sexual opportunity, and so forth.

FIGURE 4.

The Cost-benefit trade offs result in variation in evolved traits. Here, the costs and benefits along dimensions of focused to diffuse attention and focus on external to internal information results in most individuals clustering toward the center of the figure. In this area, individuals can shift attentional resources along these dimensions, as circumstances change. Individuals in the upper left quadrant are predicted to show symptoms of ADHD, whereas those in the lower right quadrant are predicted to show obsessions associated with OCD.

If there are evolved mechanisms associated with the dimensions shown in Figure 4, then there should be syndromes that capture behavioral and cognitive features of the extremes in the four quadrants of the figure and differential patterns of activation of the same brain systems should underlie these different behavioral and cognitive biases. Attention deficit/hyperactivity disorder (ADHD) and obsessive-compulsive disorder (OCD) may provide an example. There is considerable heterogeneity within these diagnostic categories which may, in part, be due to variation in the underlying brain systems that contribute to the behavioral and cognitive features of these disorders (e.g., Halperin & Schulz, 2006). With this caveat in mind, hypoactivation of the anterior cingulate cortex and ventrolateral prefrontal cortex is often found with individuals with ADHD (Bush, Valera, & Seidman, 2005; Fassbender & Schweitzer, 2006), whereas hyperactivation of these areas is common with individuals with OCD (Aouizerate et al. 2004; Evans, Lewis, & Iobst, 2004; Maltby, Tolin, Worhunsky, O’Keefe, & Kiehl, 2005). It is likely that subcortical areas, such as the basal ganglia and substantia nigra, involved in vigilance and the modulation of arousal are also part of this system of brain regions and contribute to individual differences in attentional and inhibitory control (Halperin & Schulz, 2006).

In theory, hypoactivation of the anterior cingulate cortex and any integrated subcortical systems will result in a high threshold for triggering the attentional focus and inhibitory control mechanisms of the lateral prefrontal cortex. The results would include poor engagement of the systems that enable inhibition of evolved or over-learned heuristics, and thus frequent attentional shifts and “impulsive” behaviors or an inability to focus on the mental construction of strategies for coping with change (e.g., excessive wandering thoughts); Fassbender and Schweitzer (2006, p. 445) recently concluded, “individuals with ADHD may be less able to engage higher order executive systems to flexibly recruit brain regions to match given task demands.” This cost is balanced against the benefit of rapid response to changes in the environment, albeit with evolved or over-learned behavioral heuristics.

Hyperactivation of the anterior cingulate cortex is associated with OCD, which in theory will result in a low threshold for triggering attentional focus and inhibitory control mechanisms (Aouizerate et al., 2004; Maltby et al., 2005). One predicted result is automatic alerting and attentional focus on very subtle variation in details that differ from previous experiences or previous organization of social relationships or ecological context. The benefits include automatic alerting by and the shifting of attention to details that vary from the routine and the inhibition of impulsive behavioral responses. The latter, in theory, creates the potential to adjust evolved or previously learned heuristics to cope with this change. The potential costs include being alerted by and an unnecessary attentional focus on unimportant details or change, potential difficulties in disengaging attentional focus, or a compulsion to behaviorally or cognitively respond to this detail if it provokes anxiety (American Psychiatric Association, 1996). If one component of OCD is hypersensitivity to change, then one coping strategy is to reduce the triggering of this system by arranging the environment or one’s thoughts in ways that reduce introduction of change.

My point is that existence of ADHD and OCD is consistent with the cost-benefit trade offs—intraindividual and interindividual variation in the corresponding brain and cognitive systems—that are predicted to be associated with the evolution of an executive system that functions to direct attention toward variation and change in the environment, inhibit evolved or over-learned responses, and mentally construct novel approaches to coping with this variation (Geary, 2005). In short, these disorders represent extremes of presumably normally distributed brain and cognitive systems that compose an alerting-attentional control and behavioral inhibition system. The evolved function of these systems is for tracking and responding to dynamic change in ecological or social contexts. Because individuals with ADHD and OCD are at the extreme on more or more components, the systems do not function in ways that allow for adaptive attentional and inhibitory control.

In any event, the implication is that construction of evolutionarily novel solutions to changing dynamics requires the coordinated functioning of at least three component systems. The first is associated with the anterior cingulate cortex and functions to shift attention to aspects of the ecology or social environment that differ from past memories or that are currently changing. The second is associated with the ventrolateral prefrontal cortex and contributes to the ability to inhibit evolved or over-learned responses, such that the third system can operate. This latter system is associated with the dorsolateral prefrontal cortex and functions to create an explicit mental representation of details of the context that are novel and enables the use of reasoning and problem solving to construct novel solutions. Given that schools and much of academic learning is evolutionarily novel, frequent engagement of these areas is expected and thus each of these systems and their interactions represent a potential source of individual differences in ease of secondary learning and in LD.

MATHEMATICAL LEARNING DISABILITY

Neuropsychological measures of number and arithmetic deficits associated with dyscalculia, that is, math-related deficits that result from overt brain injury (e.g., McCloskey, Caramazza, & Basili, 1985; Shalev, Manor, & Gross-Tsur, 1993), have been administered to large samples of school children in the United States (Badian, 1983), Europe (Kosc, 1974; Ostad, 1998), and Israel (Gross-Tsur, Manor, & Shalev, 1996; Shalevet al., 2001). In these studies, performance that deviates from age-related norms and is similar to that associated with dyscalculia is used as a diagnostic criterion for MLD. The result have consistently indicated that 5% to 8% of school-age children exhibit some form of MLD, at least with respect to basic number and arithmetic learning; the prevalence of MLD as related to other forms of mathematics, such as algebra or geometry, is not known. Many of these children have comorbid disorders, including RD and ADHD (Gross-Tsur et al., 1996), but many of the core number and arithmetic deficits are similar—though of varying severity—in children with or without comorbid disorders (Geary, Hamson, & Hoard, 2000; Jordan & Montani, 1997).

In cognitive studies, the diagnosis of MLD is typically based on performance on standard mathematics achievement tests, with cutoff criteria ranging from less the 10^th to the 35^th national percentile, some times higher (Murphy, Mazzocco, Hanich, & Early, 2007). Even with variation in rigor of the cutoff criterion, the deficits in number, counting, and arithmetic that have been identified in these studies tend to be the same as those identified in the neuropsychological assessments (e.g., Garnett & Fleischner, 1983; Geary, 1993; Geary & Brown, 1991; Jordan, Hanich, & Kaplan, 2003a; Jordan & Montani, 1997; Ostad, 1997; Russell & Ginsburg, 1984); recent reviews are provided elsewhere (Berch & Mazzocco, 2007; Geary, 2004). However, recent studies suggest that children with math achievement scores < 10th percentile and with IQ scores in the average range may have more pervasive deficits across working memory systems (e.g., central executive, visuospatial sketch pad) and math cognition tasks than do children identified with lenient criteria (Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Murphy et al., 2007). The latter group of children might still have a learning disability but it appears to be restricted to one or a few mathematical areas, such as arithmetic fact retrieval. In the following sections, I integrate some of these findings into the primary and executive system deficits outlined in the preceding section. My goal in doing so is to illustrate how an evolutionary perspective can help to guide the search for and the understanding of MLD.

Primary System Deficits

Deficits in mathematical learning could be evident in any one or several of the primary mathematical areas listed in Table 1. There have been no studies of the ability of young children with MLD to make basic ordinality judgments, but there are studies that have focused on the remaining primary mathematical abilities. As described in Primary Mathematics, brain imaging and comparative studies provide consistent evidence for areas of the parietal cortex, especially the intraparietal sulcus, as being the seat of many if not all of the competencies listed in Table 1. A recent study of neural activity in the intraparietal sulcus of two macaques (Macaca mulatta) revealed distinct areas of this brain region are involved in numerosity judgements, nonverbal counting, and for maintaining an abstract representation of quantities of 1 to 3 (Nieder et al., 2006). The implications are that neuro-developmental disorders that affect a large portion of the intraparietal sulcus will impair many if not all of the primary mathematical abilities, and that neuro-developmental disorders that affect a smaller portion of this sulcus may impair only one or a few of these abilities.

Numerosity

Koontz and Berch (1996) conducted the only study of numerosity judgments, or subitizing, in children with MLD. In this study, 3rd and 4th grade children with MLD and normal peers were administered a variant of Posner, Boies, Eichelman, and Taylor’s (1969) physical identity and name identity task. For instance, children were asked to determine if combinations of Arabic numerals (e.g., 3–2), number sets (e.g., ||-||), or numerals and sets were the same (e.g., 2-||) or different (e.g. 3-||). In keeping with previous studies (Mandler & Shebo, 1982), reaction time patterns for the normal children indicated fast access to numerosity representations for quantities of two and three, regardless of whether the code was an Arabic numerical or number set. The children with MLD showed fast access to numerosity representations for the quantity of two, but appeared to rely on counting to determine quantities of three. Although in need of replication, the results are intriguing and suggest that some children with MLD might not have an inherent representation for numerosities of three or the representational system for three does not reliably discriminate two from three.

Using a newly developed Number Sets Test, Geary et al. (2007) found potential corroborating evidence. Here, children are asked to combine pairs or triplets of Arabic numerals (e.g., 3–4) or sets of objects (e.g., ♣ ♣ ◆ ◆ ◆) and quickly determine if they match a target number (e.g., 5). One strategy for combining small sets of objects is subitizing, that is, determining the numerosity of small sets and then adding the associate quantities (e.g., ♣ ♣ ◆ ◆ ◆ = 5; Geary & Lin, 1998). The task was administered to groups of MLD, low achieving (LA), and typically achieving (TA) 1st graders matched or equated on IQ. Children with MLD performed more poorly on this task than did children in the two other groups. More important, the difference for number of hits (i.e., correct matches) comparing the MLD and LA groups was partially mediated by a group difference in visuospatial working memory. Other patterns suggested that the children with MLD may have had difficulty subitizing and thus had to resort to counting more often than did LA children.

Counting

The nonverbal counting system, as assessed in studies of preschool children (Starkey, 1992), has not been examined for children with MLD. Nonetheless, Gelman and Gallistel’s (1978) implicit principles that appear to guide preschool children’s emergent use of verbal counting behaviors have been assessed (Geary, Bow-Thomas, & Yao, 1992; Geary et al., 2000; Geary, Hoard, & Hamson, 1999). Children with MLD understand most of the counting principles proposed by Gelman and Gallistel, but often make errors on items that involve double-counting (e.g., tagging one object “one,” “two”), which violate the one-one correspondence principle (one and only one word tag is assigned to each counted object). Children with MLD often fail to detect these errors when the first item is double counted, but detect them when the last item is double counted. The pattern suggests children with MLD understand one-one correspondence, but have difficulty retaining a notation of the counting error in working memory when they have to monitor additional counts (Geary et al., 2007; Hoard, Geary, & Hamson, 1999). Thus, even if these children understand the biologically-primary features of verbal counting, their ability to use these during problem solving (e.g., using counting to solve 3 + 5) may be compromised by poor working memory (described below).

Simple Arithmetic

There have been many studies of the basic arithmetic competencies of children with MLD (Garnett & Fleischner, 1983; Geary & Brown, 1991; Jordan et al., 2003a; Ostad, 1997; Russell & Ginsburg, 1984), but most of these have focused on school-taught, secondary arithmetic. A nonverbal addition and subtraction task developed by Levine, Jordan, and Huttenlocher (1992) provides a potential means to assess the primary arithmetic knowledge of children with MLD. In this task, the child watches as an experimenter places, for instance, a set of 5 disks under a mat and then removes 2 disks, one at a time. The child’s task is to indicate the number of disks remaining under the mat by placing a corresponding number of disks on a mat of their own. The original study indicated that preschool children can perform simple additions and subtractions using this format and subsequent studies have revealed performance on this task is correlated with other numerical and arithmetical competencies in kindergarten. Children with cognitive delays do not perform as well as other children, that is, they can only solve smaller valued manipulations (e.g., 3–2; Jordan, Levine, & Huttenlocher, 1995).

Jordan and colleagues found that children at risk for MLD—children entering kindergarten with low math skills and showing little gain across the school year—may enter kindergarten with a lower capacity for solving these nonverbal calculations (Jordan, Kaplan, Oláh, & Locuniak, 2006). However, longer-term follow up studies of these same children will be needed to determine if children with this lower capacity are in fact MLD and if so whether any nonverbal deficits contribute to difficulties in learning secondary arithmetic.

Estimation and Geometry

Jordan and colleagues presented simple addition and subtraction problems with two potential answers (e.g., 4 + 5 = 10 20) to 2nd and 3rd graders and asked them to quickly estimate which answer was closest to the correct answer; both potential answers were wrong but one was close to the actual answer and one was more distant (Hanich, Jordan, Kaplan, & Dick, 2001; Jordan, Hanich, & Kaplan, 2003b). The children with MLD chose the more distant answer more frequently than did their peers, indicating poor estimation skills in the former group. However, this task involved some amount of secondary learning (e.g., formal format for addition with Arabic numerals) and thus it is not clear to what extent the performance of the MLD children was influenced by a potential deficit in the inherent magnitude estimation system, poorly developed secondary arithmetic skills (Dowker, 2003), or some combination.

The number line task and the pattern of natural log (ln) or linear estimates described earlier and shown in Figure 1 may provide a more direct measure of the inherent estimation system, although the task involves some secondary learning (e.g., knowledge Arabic numerals). Geary et al. (2007) administered this task to the groups of MLD, LA, and TA 1st graders noted above. Although not presented in Geary et al., group-level medians were fitted to log and linear curves, as shown in Figure 5. In theory, representations based on the inherent magnitude and secondary mathematical systems should conform to the log and linear models, respectively. As can be seen in the figure, the log model better fitted the estimates for the MLD and LA groups, whereas the TA group’s estimates where linear. The log equation for the LA group (Y = 18.98 ln(x) – 15.21, where x = child’s estimate) was remarkably similar to that found for another sample of 1st graders (Y = 19.29ln(x) – 14.98) by Siegler and Booth (2004). The similarity across studies is consistent with the proposal that many 1st graders are relying on the inherent magnitude estimation system when making number line estimates (Siegler & Opfer, 2003), and that the curve shown for LA children provides a good psychological representation of the degree of discrimination of adjacent numbers.

FIGURE 5.

Logarithmic and linear fits to median number line estimates for children with MLD, low achieving children (LA), and typically achieving children (TA).

The curve for the children with MLD was also better fitted by the log than the linear equation, but differed from that of the LA group and even from that found for kindergarten children by Siegler and Booth (2004). For all comparisons, the ln coefficient is smaller for the MLD group, suggesting that their estimates become compressed, that is, less differentiated, at lower numerical values than those of other 1st graders and even kindergarteners. Although not conclusive, the pattern suggests that children with MLD may have a deficit in the primary visuospatial system that supports inherent magnitude estimations.

Integration and Future Directions

Although all of the just described results are preliminary, they suggest many children with MLD may have a primary mathematical deficit in one or several areas: A more thorough assessment of the primary mathematical abilities listed in Table 1 for samples of MLD children is needed. Koontz and Berch’s (1996) findings for numerosity judgments and Geary et al.’s (2007) findings for number line estimation implicate potential deficits in the intraparietal sulcus. This is clearly a region of interest in brain imaging studies of children with MLD. This same region may support nonverbal counting (Nieder et al., 2006) and magnitude estimates in nonmathematical domains (e.g., relative size; Pinal et al., 2004). Thus, if this brain region is broadly impaired in some children with MLD, then they are predicted to show deficits in nonverbal counting—using behavioral procedures similar to those described by Nieder et al.—and show poor magnitude estimates in nonmathematical domains. The involvement of the intraparietal sulcus in simple nonverbal arithmetic remains to be demonstrated, but is a strong possibility. In any event, learning difficulties and disabilities are predicted for secondary mathematical domains that are heavily dependent on these primary systems. For instance, impairment of the intraparietal sulcus and thus difficulty in making visuospatial estimates is predicted to make the learning of many aspects of geometry and some aspects of algebra (e.g., graphing functions in coordinate space) difficult.

Executive System Deficits

It has been consistently found that, as a group, children with MLD do not perform as well as their same-age peers on working memory tasks (Bull & Johnston, 1997; Bull, Johnston, & Roy, 1999; Geary, Hoard, Byrd-Craven, & Desoto, 2004; Geary et al., 2007; Hitch & McAuley, 1991; McLean & Hitch, 1999; Siegel & Ryan, 1989; Swanson, 1993; Swanson & Sachse-Lee, 2001; Wilson & Swanson, 2001). Across most of these studies, a compromised central executive has been implicated in many of the math cognition deficits of these children, although a compromised phonological loop or visuospatial sketch pad may also contribute to deficits in specific areas. In the following sections, I attempt to further decompose the potential relation between the central executive and MLD using the above described evolutionary analysis. I do so by organizing the discussion around the anterior cingulate cortex and the lateral prefrontal cortex, that is, the core brain systems that underlie executive functions.

Attentional Focus, Error Detection, and the Anterior Cingulate Cortex

The relation between the functioning of the anterior cingulate cortex and secondary learning in general and learning disabilities in particular has not been systematically explored. As described earlier, individual differences in sensitivity of the anterior cingulate cortex, and perhaps subcortical regions associated with vigilance and modulation of attention, can be represented as variation in a threshold for alerting individuals to features of situations in which evolved or previously learned responses might not be sufficient for coping with associated demands, and for triggering the attentional focus and inhibitory mechanisms of the lateral prefrontal cortex needed to support explicit problem solving or decision making. The alerting mechanisms may be particularly sensitive to changes in social dynamics, such as group composition or the details of dyadic interactions, which is functional in many settings. The issue here is the sensitivity of the alerting-attention shifting mechanisms to variation in biologically-secondary material, which will likely compete with more evolutionarily salient social information for attentional focus.

If these areas are functioning (e.g., hypoactivation of the anterior cingulate cortex) such that children with ADHD, for instance, have a high threshold for activation of the mechanisms that support attentional focus and inhibitory control, then automatic attentional shifts to changing social or environmental conditions are predicted. In school settings, difficulties attending to academic lessons and the details of secondary material is predicted and well documented (Biederman et al. 2006). Even variation in attentional focus within the normal range is associated with individual differences in on-task behavior in the classroom and to individual differences in learning secondary mathematics (Fuchs et al. 2006). In contrast, socially and behaviorally inhibited children who also have preclinical levels of OCD may show an acute sensitivity to the details of secondary material and a tendency toward repetitive use of any associated procedures (Evans et al., 2004).

A point more relevant to the current treatment is with respect to the potential role of the anterior cingulate cortex in error detection and for detecting subtle variation in secondary mathematical procedures and concepts. With mathematics, seemingly minor changes in an equation can result in a substantive change in the result. For instance, the basic equation for an ellipse is x²/a² + y²/b² = 1 (a and b = length of the major and minor axes, respectively), whereas that for a hyperbola is x²/a² − y²/b² = 1 (2a and 2b = length of the axes used in the plotting of the asymptotes). The only difference is the presence of a “+” or a “−” sign, but inclusion of one operation versus the other results in a completely different result. In theory, variations in basal activation levels of the anterior cingulate cortex will result in variation in children’s sensitivity to these details and through this contribute to individual differences in ease of learning the associated materials.

If some forms of MLD are associated with low basal levels of anterior cingulate activation and thus low sensitivity to subtle variation in external information and a poor ability to maintain attentional focus on the details they do detect, then these children are predicted to show frequent failures to detect subtle, yet very important, distinctions across related mathematical procedures and concepts. Equally important, these children are also predicted to show difficulties in detecting subtle variation in general. If so, then performance on simple perceptual same/different (e.g., -– tasks, for instance, will be predictive of failures to detect detail in mathematics tasks. If this is confirmed and linked to activation levels of the anterior cingulate cortex, then these types of perceptual tasks may prove useful for assessing risk for later MLD.

I noted earlier that children with MLD appear to detect double counting errors but often fail to retain a notation of the error in working memory, if the error occurs early in the count. In theory, poor skill at detecting counting-procedure errors may compromise the ability to correct these errors (Ohlsson & Rees, 1991), and thus result in more errors when counting is used to solve secondary arithmetic problems (e.g., use of counting to solve 3 + 5). At this point, it is not known which aspect of working memory is involved in the failure to retain the error notation, but the anterior cingulate cortex is a candidate. In this context, the dynamics of cingulate activation may differ for children with MLD and their peers. Specifically, if the anterior cingulate cortex is activated on the conflict trial, that is, when the counting violates the one-one correspondence principle, then activation of the lateral pre-frontal cortex should follow and enable explicit determination that the count was incorrect (e.g., Kerns et al., 2004). However, when the response is delayed, as it is when the double count occurs on the first item, then the spike in activation of the anterior cingulate cortex may need to be maintained until a response can be made. If these activation levels decay more rapidly in children with MLD than their peers, then the observed pattern of more failures to retain notations of counting errors—an implicit “sense” that something is wrong—would occur (Geary et al., 2007). Of course, the same behavioral pattern could emerge due to failure of dorsolateral activity, as noted below.

Attentional and Inhibitory Control and the Lateral Prefrontal Cortex

Ventrolateral

The interrelationships between numbers, arithmetical operations, mathematical procedures, and so forth are multifold and make the ability to inhibit information not relevant to the problem at hand especially complex. For instance, the similarities between the equations for ellipses and hyperbolas and similarities in related procedures almost certainly increase the likelihood of retrieving an incorrect procedure when graphing these equations. In fact, inhibition of irrelevant information is an important component of mathematical learning and a potential source of MLD even with simple arithmetic. When first learning to solve simple addition problems, children often retrieve the counting string associate of the addends. When asked to solve 3 + 4, children sometimes retrieve an answer of “5” (Siegler & Robinson, 1982). The retrieval of “5” is correct when the children are counting, but incorrect for this addition problem. When first learning basic multiplication facts, children will often confuse addition and multiplication (J. Camp-bell, 1995; K. Miller & Parades, 1990); they might retrieve an answer of “12” for the problem 3 + 4.

These forms of confusion are common among academically normal children, but these children are eventually able inhibit irrelevant associations. Many children with MLD, in contrast, do not develop these inhibitory capacities to the same degree (Barrouillet, Fayol, & Lathuliére, 1997; Geary et al., 2000). In the Geary et al. study, one of the arithmetic tasks required children to only use retrieval—the children were instructed not to use counting strategies—to solve simple addition problems (see also Jordan & Montani, 1997). Children with MLD, as well as children with RD, committed more retrieval errors than did their academically normal peers, even after controlling for IQ. The most common of these errors was a counting-string associate of one of the addends. For instance, common retrieval errors for the problem 6 + 2 were 7 and 3, the numbers following 6 and 2, respectively, in the counting sequence. Hanich et al. (2001) found a similar pattern, although the proportion of retrieval errors that were counting-string associates was lower than that found by Geary et al. (2000).

These intrusions of task-irrelevant information not only increase the frequency of wrong answers, but also the overall functional capacity of working memory is reduced (Engle et al., 1995). Reduction in working memory capacity in turn will hamper the solving of more complex mathematics problems (Geary & Widaman, 1992). Given the role of the ventrolateral prefrontal cortex in the inhibition of context irrelevant behaviors and cognitions, this brain region is a prime candidate for studies of intrusion errors in children with MLD.

Dorsolateral

This area of the prefrontal cortex is crucial for maintaining attentional focus and for the explicit representation and maintenance of information in working memory during problem solving (e.g., Kane & Engle, 2002; Smith & Jonides, 1999), and is an important source of individual differences in gF (Duncan et al., 2000). This brain region will be critical for the explicit, abstract, and logical problem solving that becomes increasingly important in mathematics, as in the use of geometric postulates to build theorems. A compromised dorsolateral prefrontal cortex is thus predicted to interfere with many aspects of mathematical learning, but in ways that might differ from a compromised anterior cingulate cortex or ventrolateral prefrontal cortex. The dorsolateral region is predicted to be particularly involved in mathematical learning that involves the explicit manipulation, integration, and use of mathematical knowledge and procedures during problem solving. In a pair of brain imaging studies, Qin and colleagues (Qin et al., 2003; Qin et al., 2004) found this brain region was indeed involved when adolescents and adults manipulated simple algebraic equations, such as 4y – 3 = 12.

As noted, a compromised ventrolateral prefrontal cortex will often result in the intrusion of irrelevant associations into working memory, that is, these intrusions will increase the amount of information being maintained by the dorsolateral prefrontal cortex and thus reduce its functional capacity. Even in the absence of ventrolateral deficits, it is almost certain that there are individual differences in the attentional capacity of the dorsolateral prefrontal cortex and thus potential for learning deficits specific to this region. The analysis of potential deficits associated specifically with the dorsolateral prefrontal cortex is complicated by findings that suggest the left- and right- cortices may be biased toward the manipulation of verbal information and visuospatial information, respectively (Stephan et al., 2003), and that the left dorsolateral prefrontal cortex is involved in the logical reasoning needed to solve many mathematical problems (Fugelsang & Dunbar, 2005). Although both the left- and right- parietal cortices are engaged in many mathematical tasks (e.g., Dehaene et al., 1999; Qin et al., 2003), a compromised right dorsolateral prefrontal cortex may disproportionately compromise the ability to engage these posterior regions for mathematical tasks dependent on visuospatial representations. A compromised left dorsolateral prefrontal cortex would also likely degrade the ability to engage the parietal cortex and visuospatial representations, along with difficulties in the logical reasoning needed in complex problem solving.

As noted earlier, synchronization of dorsolateral prefrontal cortex with the posterior brain systems representing mathematical information may be necessary for explicit representation of this information in working memory (Geary, 2005). Fewer white matter connections, for instance, between the dorsolateral prefrontal cortex and the intraparietal sulcus would in theory result in less fidelity in the synchronization process and less stable access to implicit primary mathematical knowledge. In this situation, the dorsolateral prefrontal cortex and intraparietal sulcus may be structurally and functionally intact but unstable synchronization of these regions may manifest in the same way as the potential primary deficits, such as poor access to primary numerosity representations (Koontz & Berch, 1996), resulting from a compromised intraparietal sulcus. Fewer white matter connections between the dorsolateral prefrontal cortex and posterior brain regions might also explain the finding that children with MLD tend to be slower on reaction time measures which sometimes contributes to their poor math performance (e.g., Bull & Johnston, 1997).

Other Brain Systems

Although I have focused on components of the central executive as potential sources of the learning difficulties experienced by children with MLD, these are not the only possibilities. Errors in retrieving arithmetic facts—a cardinal feature of MLD in elementary school (Geary, 1993)—could be related to a compromised ventrolateral prefrontal cortex, as mentioned. In theory, a compromised hippocampus could also interfere with fact learning (Squire & Bayley, 2003); specifically, committing the facts to memory. Indeed, Geary et al. (2000) suggested two forms fact-retrieval deficit, one associated with poor inhibition of irrelevant information and the other associated with difficulty in forming or accessing long-term memory representations of these facts. Whether these two respective forms of retrieval deficit are related to the ventrolateral prefrontal cortex and the hippocampus remains to be determined.

Another cardinal feature of an early MLD is delayed learning of arithmetical procedures (Geary, 1993). Empirically, delayed procedural development appears to be related to a poor understanding of associated concepts and to difficulties effectively using working memory to execute the procedures (Geary et al., 2004). In addition to working memory, delayed procedural learning might also be related to a comprised or immature basal ganglia (Graybiel & Saka, 2003). In this case, procedural deficits may emerge even with individuals with an intact prefrontal cortex and normal working memory capacity.

DISCUSSION

Humans are clearly a species that has evolved to create culture, that is, a system of rules and shared information that facilitates large-scale cooperative efforts, a division of labor, and so forth (Baumeister, 2005). The emergence of humans as a cultural species is dependent on the ability to create evolutionarily-novel information and to pass this information from one generation to the next by means of morals, stories, and more recently in written form (Richerson & Boyd, 2005; Geary, 2005). Written records of evolutionarily-novel, or biologically-secondary knowledge, such as Euclid’s (1956) geometry, have been accumulating during the past several millennia and accelerating over the past several centuries. When much of the population was agrarian, learning secondary knowledge was not important for the day-to-day living of most people. With industrialization and the emergence of an information-based economy, successful living in modern society requires considerable secondary knowledge. It is not a coincidence that schools emerged in societies in which a growing base of knowledge created a gap between biologically-primary folk knowledge and the competencies needed for living in the society. One function of schools is to organize the activities of children such that they acquire the secondary competencies that close the gap between their folk knowledge and the secondary knowledge needed to navigate the occupational and social demands of the society (Geary, 2002).

From this perspective, there are brain and cognitive systems that have evolved to operate on and modify primary folk systems to create the secondary knowledge that enables the generation of culture (Geary, 2007). The brain systems include the prefrontal cortex and anterior cingulate cortex, and the cognitive systems include the central executive components of working memory, specifically, attentional and inhibitory control and the ability to explicitly use reasoning and problem solving to cope with novel conditions or information. Individual differences in the ease of learning secondary knowledge, including LD, is then predicted to emerge from an interaction between these brain and cognitive systems and the primary folk systems most closely related to the secondary task. Examples of the latter include use of the primary language systems to support word decoding and word retrieval during the learning of and act of reading (Mann, 1984; Rozin, 1976).

With respect to MLD, there is preliminary evidence for potential deficits in at least some of the primary mathematical domains listed in Table 1 (Geary et al., 2007; Koontz & Berch, 1996), which in turn makes the intraparietal sulcus a strong candidate for brain imaging studies of this form of LD, given the involvement of this brain region on many primary and some secondary mathematical tasks (Dehaene et al., 1999; Pinal et al., 2004). In theory, MLD can also result from deficits in the brain and cognitive systems that evolved to create secondary knowledge from primary systems, that is, the prefrontal cortex, anterior cingulate cortex, and the executive components of working memory. This prediction is by no means novel, nor does it necessarily require an evolutionary explanation. Nonetheless, approaching these potential relations from an evolutionary perspective may enable the generation more detailed predictions regarding the deficits that underlie MLD, and a more nuanced understanding of the classroom and academic functioning of these children; for instance, if the anterior cingulate cortex is involved in detecting subtle detail, which will be important for math learning, then simple perceptual discrimination tasks might provide a means to assess early risk for MLD. These are admittedly conjectures, but they do point to testable hypotheses and provide a broader lens from which to approach academic learning and difficulties with this learning.