Abstract
Objective:
The objective was to investigate the effect of silver nanoparticles (AgNPs) incorporation on viscoelastic properties of acrylic resin denture base material.
Materials and Methods:
A total of 20 specimens (60 × 10 × 2 mm) of heat cured acrylic resin were constructed and divided into four groups (five for each), according to the concentration of AgNPs (1%, 2%, and 5% vol.) which incorporated into the liquid of acrylic resin material and one group without additives (control group). The dynamic viscoelastic test for the test specimens was performed using the computerized material testing system. The resulting deflection curves were analyzed by material testing software NEXYGEN MT.
Results:
The 5% nanoparticles of silver (NAg) had significantly highest mean storage modulus E’ and loss tangent Tan δ values followed by 2% NAg (P < 0.05). For 1% nanosilver incorporation (group B), there were no statistically significant differences in storage modulus E’, lost modulus E” or loss tangent Tan δ with other groups (P > 0.05).
Conclusion:
The AgNPs incorporation within the acrylic denture base material can improve its viscoelastic properties.
Keywords: Acrylic resin denture, nanoparticles, viscoelastic
INTRODUCTION
An ideal denture base material is that possesses biocompatibility with the oral tissues, excellent esthetics, superior mechanical properties especially modulus of elasticity, impact strength, flexural strength, hardness, sufficient bond strength with artificial teeth and lining materials, ability to repair or alter the contours, and dimensional accuracy.[1,2]
Clinical failures of complete or partial denture prosthesis caused from polymethyl methacrylate (PMMA) are most likely in the form of fracture either due to fatigue or impact forces of mastication.[3,4]
Moreover, flexural fatigue of dentures as evidenced by midline fracture is due to the stress concentration around the microcracks formed in the material due to continuous applications of small forces. Similarly, repetitive nature of masticatory load results in the propagation of cracks which weakens the denture base and finally results in the fracture.[1,5]
Fracture of dentures in clinical service has been concerned, and several attempts have been made to improve flexural and impact strength of PMMA. Researches in these areas aimed to modifying the composition or reinforcing the PMMA with another stronger materials for developing a new materials with better properties.[6]
Several researchers have been demonstrated that the PMMA can be showing improved physical and mechanical properties such as thermal conductivity, polymerization shrinkage, water sorption, fatigue behavior, impact strength and flexural modulus when it is reinforced by carbon, Aramid, ultra-high molecular weight polyethylene, glass, silver, copper, and/or aluminum fibers.[7,8,9]
Noort[10] stated that the tensile strength of acrylic resins is typically no more than 50 mega Pascal (MPa), but the elastic modulus is low, and the flexural modulus is in the region of 2200–2500 MPa. Therefore, the lack of strength and toughness of acrylic resin dentures is a serious problem and can result in fractures of up to 10% of dentures within 3 years of use.
Another problem with acrylic resins is the creep, particularly with the chemical cured resins as they are the viscoelastic materials. Therefore, by addition of cross-linking agent, the creep of acrylic resins can reduce but it cannot eliminate.[11,12]
Recently, more attention has directed toward the incorporation of nanoparticles into PMMA to improve its properties. Elsewhere, the properties of polymer nanocomposites depend on the type of incorporated nanoparticles, their size, and shape as well as the concentration and interaction with the polymer matrix.[13]
Therefore, a method of incorporating silver nanoparticles (AgNPs) into acrylic resin denture base materials to enhance physicomechanical properties was developed. The purpose of this study was to evaluate the effect of nanosilver incorporation on viscoelastic properties of acrylic resin denture base material.
MATERIALS AND METHODS
A total of 20 specimens (60 × 10 × 2 mm) of heat cured acrylic resin were constructed and divided into four groups (five for each), according to the concentration of AgNPs (1%, 2% and 5%) which incorporated into the liquid of acrylic resin material and one group without additives (control group) as the following:
Group A: Heat-cured acrylic resin without additives (control group)
Group B: Heat-cured acrylic resin with 1% nanoparticles of silver (NAg)
Group C: Heat-cured acrylic resin with 2% NAg
Group D: Heat-cured acrylic resin with 5% NAg.
Specimens’ preparation
Three copper metal plates were milled into rectangular forms with 60 mm lengths, 10 mm width and thicknesses of 2 mm. To produce standardized specimens of dimensions complying with the ADA specifications No. 12 for heat cured denture base acrylic resin.[14] Metal handles were prepared in the top surface of the metal plates to facilitate their removal (key). Separating medium applied to plates and flasked, after complete setting of plaster the top half of the denture flask with the copper metal plates removed leaving spaces in plaster of the bottom half of denture flask with the same dimensions, the mold then painted with a separating medium for the application of denture base materials.
Heat-cured acrylic resin was used in this study (Acrostone (A), Anglo-Egyptian Company. Hegaz, Cairo, Egypt, Batch No. 505/04) supplied in powder and liquid forms. According to Monteiro et al.,[15] NAg in the form of colloidal solution added to the monomer of acrylic resin by volume proportion with concentration of (1%, 2%, and 5%) to form a mixture.
Then, the powder and liquid with nanoparticles solution were proportioned and mixed according to manufacture recommendation. The heat cured acrylic resin was packed in spaces in the preformed plaster mold at the dough stage then the flask was closed and pressed under pressure device. After polymerization, the acrylic blocks removed, finished and polished. The acrylic block specimens in a layer of 2 mm thickness were immersed in distilled water and stored at 37°C for 1-week.
After the immersion period, the specimens were removed from the distilled water and the acrylic blocks were tested by dynamic viscoelastic test.
Measurement and analysis
The dynamic viscoelastic test was done for the test specimens using the computerized material test system. The resulting deflection curves were analyzed by material testing software NEXYGEN MT (AMETEK Lloyd instruments limited. England. Part No: 40/0658 Version: 4.5). A special design specimen holder with tightened screw was prepared and used to hold the specimens during the test.
In the designed part of the testing machine, the specimens were mounted and adjusted symmetrically over 50 mm distance from both ends. Deflection cycles to each specimen were repeatedly carried out for 1-min with a crosshead speed of 6.0 mm/min.
The cyclic load was applied on the center of the specimen and adjusted at 1 Hz, 1 cycle/s. The software connected to the testing machine was adjusted to draw and record load (stress)-time scale and extension (strain)-time scale within 10 s or more, automatically.
From both scales, the viscoelastic behavior of the materials can be understood, as for perfectly elastic solid, the strain (extension) is in exact period (time) with the applied stress (load) by means both curves exactly corresponding (0 degree out of phase). Otherwise, for a perfectly viscous liquid, the strain is 90 degree out of phase. Therefore, in the situation of a viscoelastic material, the strain is somewhere in between elastic and viscous degree.
Mathematical analysis method
The mathematic method conducted by Murata et al.,[16] and Lombardo et al.,[17] was used in this study. The dynamic measurements for all group specimens were made at the same standardized conditions.
From the load-time scale, the amplitude of the stress response was calculated by the equation of bending as:
δ =3ΔPL°/wh2MPa [1]
Where: δ: Is the amplitude of the stress response of the specimen (flexural or transverse strength) by Newton. ΔP: Is the change of the maximum load applied on the scale by Newten. L°: Is the measured length of the specimen in the test machine (constant 50 mm). w: Is the width of the specimen (constant 10 mm). h: Is the height (thickness) of the specimen by millimeters.
From the extension-time scale, the actual strain was calculated by the equation:
ε = ΔL/L° mm [2]
Where: ε: Is the amplitude of the applied strain by mm. ΔL: Is the change in length on the scale by mm (change in length as the experiment progresses). L°: Is the measured length on the test machine (length at the onset of the experiment), constant 50 mm.
From scales, extension-time, and load-time, the shift angle (phase angle between stress and strain) was calculated by the equation:
δ = ώ Δt rad/s [3]
ώ =2 πƒ
Where: δ: is the phase angle between stress and strain, termed loss tangent or damping factor, it is a measure of the viscous response of the material to dynamic strain. ώ: Is the angular frequency of oscillation (unites of radians per second, rad/s). The angular frequency is related to the frequency, f, measured in cycles per second (Hz), as ώ =2 πƒ. Δt: Is the angular shift between stress-time and strain-time scale by mm. ƒ: Is the frequency per second (constant = 1 Hz).
From equation (1), (2) and (3); the dynamic modulus was resolved into two components, one that is in phase (E’) and one that is out of phase (E”) with the applied strain:
E′ = (б/ε) cos δ
E″ = (б/ε) sin δ
Where: E艂: Is the storage modulus equivalent to the modulus of elasticity or Young's modulus, measure of the stored energy (the elastic part). E″: Is the loss modulus, measure of the energy lost as heat (viscous part). δ: Is loss tangent = energy loss E”/energy stored E’.
Calculation of tan δ
Tan δ = sin δ/cos δ = E艃/E艂
The storage and loss moduli represent the elastic and viscous components, respectively. Tan δ is a measure of the ratio of energy lost to energy stored during cyclic deformation and gives an indication of the relative contributions of the elastic and viscous components of material behavior.[16,18]
Statistical analysis
Data were collected and statistically analyzed using one-way ANOVA followed by Tukey's post-hoc test for pair-wise comparisons. The significance level was set at α = 5%.
RESULTS
The mean values and standard deviations of the storage modulus E’ of the heat cured acrylic resin specimens for different groups (A, B, C, and D) were (136.33 ± 18.17, 118.32 ± 8.25, 193.31 ± 1.02, 193.50 ± 8.18), respectively. The mean values and standard deviations of the lost modulus E” of the heat cured acrylic resin specimens for different groups (A, B, C, and D) were (110.41 ± 18.63, 88.36 ± 13.04, 137.53 ± 0.48, 110.31 ± 19.98), respectively [Figure 1]. The mean values and standard deviations of the loss tangent (Tan δ) of the heat cured acrylic resin specimens for different groups (A, B, C, and D) were (0.81 ± 0.07, 0.75 ± 0.09, 0.71 ± 0.0, 0.57 ± 0.08), respectively [Figure 2].
Figure 1.
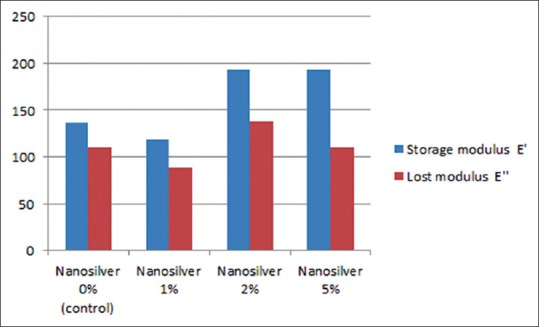
The mean values of the storage modulus and lost modulus of the acrylic resin specimens of different groups
Figure 2.
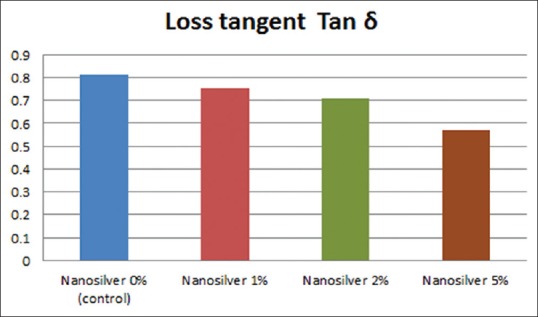
The mean values and standard deviations of the loss tangent (Tan δ) of the heat cured acrylic resin specimens of different groups
For 1% nanosilver incorporation (group B), there were no statistically significant differences in storage modulus E’, lost modulus E” or loss tangent Tan δ with the other groups (P < 0.05). For 2% nanosilver incorporation (group C), there was a statistically significant difference in storage modulus E’ with groups A and B and for lost modulus E” with group B (P < 0.05), but no significant difference was observed for loss tangent Tan δ with other groups (P > 0.05) [Table 1].
Table 1.
The mean values of storage modulus E’, lost modulus E” and loss tangent Tan δ of tested groups A, B and C

For 5% nanosilver incorporation (group D), there were statistically significant differences for storage modulus E’ and loss tangent Tan δ with groups A, B, and C (P < 0.05). However, no statistically significant difference was observed for lost modulus E” with the other groups (P > 0.05) [Table 1].
DISCUSSION
Heat curing is the most popular method of processing denture base acrylics. The heat curing system was selected due to its adequate accuracy, good resistance to attack by solvents, and the laboratory cost is substantially less. Furthermore, the heat curing procedures resulting in dentures containing less significantly unreacted methyl methacrylate monomer.[19,20]
In this study, the method for adding nanoparticles into acrylic resin material was in the form of liquid added to the monomer of acrylic resin. This method can be explained, as the distribution of particles is more equal than if placed in the powder form into acrylic powder. This is disagreement with the method of Hamedi-Rad et al.,[14] as they showing that the proportional amounts of acrylic resin powder and nanosilver determined by weighting with a digital scale were mixed in an amalgamator to achieve a homogenous mixture of PMMA and nanosilver powder.
The acrylic resin test specimens were prepared according to the ADA specification No. 12 for heat cured denture base acrylic resin in order to standardize the dimension for all the specimens during testing procedures. The acrylic resins specimens used in this study were prepared in thickness (2 mm) as the actual average thickness of denture base.
For 1-week, the modified processed acrylic specimens were immersed in distilled water at 37°C; this may explain the similar environment of denture base as in clinical use in the oral cavity. This method is in coincidence with the similar methods of Murata et al., and Rached et al.[16,21]
The testing machine (computerized material testing system model LRX plus) was chosen due to its technical specifications. The technical specifications of LRX plus are the load measuring system exceeds the requirements of BSEN ISO 7500-1:1999 Class 0.5 ASTM E4, DIN 1221. The load and strain measuring accuracy is better than 0.5%, and the crosshead speed accuracy is ± 0.2%/100 mm/min. The resultant curves (load/time and strain/time curves) were analyzed by material testing software (NEXYGEN MT).
The mathematical methods suggested by Murata et al.,[16] and Lombardo et al.,[17] were chosen in this study to calculate the dynamic viscoelastic properties of the different test groups specimens. The dynamic measurements for all groups’ specimens were made at the same standardized conditions and from the load-time scales and the extension-time scales the dynamic viscoelastic responses were calculated by mathematical equations.
Abe et al.,[22] interpreted that the complex modulus E* (MPa) was calculated by the expression; E* = (storage modulus [E’]2 + loss modulus [E”]2)1/2 and loss tangent (tan δ) was calculated by the equation tan δ = E”/E’. where E’ is the elastic stiffness of the material and E” describes its viscous behavior. High E* generally indicates the characteristic of being to deform. The scale of energy loss is indicated by tan δ; materials that absorb energy as a result of deformation show high tan δ value.
The result of this study showed that 1% nanosilver incorporation had no significance differences in storage modulus E’, lost modulus E” or loss tangent Tan δ. For 2% nanosilver incorporation had a significance of storage modulus E’ and lost modulus E”, but for loss tangent Tan δ had no significance. For 5% nanosilver incorporation had a significance differences for storage modulus E’ and loss tangent Tan δ but for lost modulus E” had no significance with the other groups. These results support the finding of the study conducted by Sun et al.[23] They reported that the increase in impact strength at 5% due to the interfacial shear strength between nanofiller and matrix is high due to formation of cross-links or supramolecular bonding which cover or shield the nanofillers which in turn prevent propagation of crack. In addition, good bonding between nanofiller and resin matrix can change the crack propagation.
Furthermore, the findings of this study are in agreement with the opinion suggested that the increase in transverse strength that occur with addition of nanoparticles due to good distribution of the very fine size of nanoparticles which enable them to enter between linear macro-molecular chains of the polymer and segmental motions of the macro-molecular chains are restricted lead to improve transverse strength.[24]
Hamedi-Rad et al.,[14] showed that the mean thermal conductivity and compressive strength of PMMA reinforced with nanosilver were significantly higher than the unmodified PMMA while the tensile strength decreased significantly after the incorporation of nanosilver. These results come with the agreement of this study.
CONCLUSION
The AgNPs incorporation within the acrylic denture base material can improve its viscoelastic properties. Heat-cured acrylic resin with the addition of NAg showed higher values of storage modulus E’, lost modulus E” and loss tangent Tan δ than that of the control group. With the considerations from the study, there is no ideal denture base material but some modifications can improve its properties. In the future, nanotechnology will be introduced into all dental field either materials, instruments or health.
Footnotes
Source of Support: Nil.
Conflict of Interest: None declared.
REFERENCES
- 1.Meng TR, Jr, Latta MA. Physical properties of four acrylic denture base resins. J Contemp Dent Pract. 2005;6:93–100. [PubMed] [Google Scholar]
- 2.Tuna SH, Keyf F, Gumus HO, Uzun C. The evaluation of water sorption/solubility on various acrylic resins. Eur J Dent. 2008;2:191–7. [PMC free article] [PubMed] [Google Scholar]
- 3.Alla R, Sajjan S, Alluri V, Ginjupalli K, Upadhya N. Influence of fiber reinforcement on the properties of denture base resins. J Biomater Nanobiotechnol. 2013;4:91–7. [Google Scholar]
- 4.Arikan A, Ozkan YK, Arda T, Akalin B. Effect of 180 days of water storage on the transverse strength of acetal resin denture base material. J Prosthodont. 2010;19:47–51. doi: 10.1111/j.1532-849X.2009.00495.x. [DOI] [PubMed] [Google Scholar]
- 5.Hirajima Y, Takahashi H, Minakuchi S. Influence of a denture strengthener on the deformation of a maxillary complete denture. Dent Mater J. 2009;28:507–12. doi: 10.4012/dmj.28.507. [DOI] [PubMed] [Google Scholar]
- 6.Jagger DC, Harrison A, Jandt KD. The reinforcement of dentures. J Oral Rehabil. 1999;26:185–94. doi: 10.1046/j.1365-2842.1999.00375.x. [DOI] [PubMed] [Google Scholar]
- 7.Bulbul M, Kesim B. The effect of primers on shear bond strength of acrylic resins to different types of metals. J Prosthet Dent. 2010;103:303–8. doi: 10.1016/S0022-3913(10)60063-7. [DOI] [PubMed] [Google Scholar]
- 8.Bertassoni LE, Marshall GW, de Souza EM, Rached RN. Effect of pre- and postpolymerization on flexural strength and elastic modulus of impregnated, fiber-reinforced denture base acrylic resins. J Prosthet Dent. 2008;100:449–57. doi: 10.1016/S0022-3913(08)60263-2. [DOI] [PubMed] [Google Scholar]
- 9.Nakamura M, Takahashi H, Hayakawa I. Reinforcement of denture base resin with short-rod glass fiber. Dent Mater J. 2007;26:733–8. doi: 10.4012/dmj.26.733. [DOI] [PubMed] [Google Scholar]
- 10.Noort RV. 2nd ed. Edinburgh, London, New York, Philadelphia, London, New York, Philadelphia: St Louis, Sydney and Toronto: Mosby; 2002. Introduction to Dental Materials; p. 212. 213. [Google Scholar]
- 11.Faot F, Panza LH, Garcia RC, Cury AA. Impact and flexural strength, and fracture morphology of acrylic resins with impact modifiers. Open Dent J. 2009;3:137–43. doi: 10.2174/1874210600903010137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ajaj-Alkordy NM, Alsaadi MH. Elastic modulus and flexural strength comparisons of high-impact and traditional denture base acrylic resins. Saudi Dent J. 2014;26:15–8. doi: 10.1016/j.sdentj.2013.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jordan J, Jacob KL, Shart MA. Experimental trends in polymer Nano-composites – A review. Mater Sci Eng. 2005;393:1–11. [Google Scholar]
- 14.Hamedi-Rad F, Ghaffari T, Rezaii F, Ramazani A. Effect of nanosilver on thermal and mechanical properties of acrylic base complete dentures. J Dent (Tehran) 2014;11:495–505. [PMC free article] [PubMed] [Google Scholar]
- 15.Monteiro DR, Gorup LF, Takamiya AS, de Camargo ER, Filho AC, Barbosa DB. Silver distribution and release from an antimicrobial denture base resin containing silver colloidal nanoparticles. J Prosthodont. 2012;21:7–15. doi: 10.1111/j.1532-849X.2011.00772.x. [DOI] [PubMed] [Google Scholar]
- 16.Murata H, Toki K, Hong G, Hamada T. Effect of tissue conditioners on the dynamic viscoelastic properties of a heat-polymerized denture base. J Prosthet Dent. 2002;88:409–14. doi: 10.1067/mpr.2002.128101. [DOI] [PubMed] [Google Scholar]
- 17.Lombardo CE, Canevarolo SV, Reis JM, Machado AL, Pavarina AC, Giampaolo ET, et al. Effect of microwave irradiation and water storage on the viscoelastic properties of denture base and reline acrylic resins. J Mech Behav Biomed Mater. 2012;5:53–61. doi: 10.1016/j.jmbbm.2011.09.011. [DOI] [PubMed] [Google Scholar]
- 18.Wagner WC, Kawano F, Dootz ER, Koran A., 3rd Dynamic viscoelastic properties of processed soft denture liners: Part I – Initial properties. J Prosthet Dent. 1995;73:471–7. doi: 10.1016/s0022-3913(05)80077-0. [DOI] [PubMed] [Google Scholar]
- 19.Hashem M, Alsaleem SO, Assery MK, Abdeslam EB, Vellappally S, Anil S. A comparative study of the mechanical properties of the light-cure and conventional denture base resins. Oral Health Dent Manag. 2014;13:311–5. [PubMed] [Google Scholar]
- 20.Dalkiz M, Arslan D, Tuncdemir AR, Bilgin MS, Aykul H. Effect of different palatal vault shapes on the dimensional stability of glass fiber-reinforced heat-polymerized acrylic resin denture base material. Eur J Dent. 2012;6:70–8. [PMC free article] [PubMed] [Google Scholar]
- 21.Rached RN, Powers JM, Del Bel Cury AA. Repair strength of autopolymerizing, microwave, and conventional heat-polymerized acrylic resins. J Prosthet Dent. 2004;92:79–82. doi: 10.1016/j.prosdent.2004.04.005. [DOI] [PubMed] [Google Scholar]
- 22.Abe Y, Taji T, Hiasa K, Tsuga K, Akagawa Y. Dynamic viscoelastic properties of vinyl polysiloxane denture soft lining materials. J Oral Rehabil. 2009;36:887–93. doi: 10.1111/j.1365-2842.2009.02015.x. [DOI] [PubMed] [Google Scholar]
- 23.Sun L, Ronald FG, Suhr J. Energy absorption capability of Nano-composites: A review. Compos Sci Technol. 2009;69:2392–409. [Google Scholar]
- 24.Katsikis N, Franz Z, Anne H, Helmut M. Thermal stability of PMMA/Silica nano-and micro composites as investigated by dynamic mechanical experiments. Polym Degrad Stab. 2007;22:1966–76. [Google Scholar]


