Abstract
Objective:
Most studies of adolescent drinking focus on single alcohol use behaviors (e.g., high-volume drinking, drunkenness) and ignore the patterning of adolescents’ involvement across multiple alcohol behaviors. The present latent class analyses (LCAs) examined a procedure for empirically determining multiple cut points on the alcohol use behaviors in order to establish a typology of adolescent alcohol involvement.
Method:
LCA was carried out on six alcohol use behavior indicators collected from 6,504 7th through 12th graders who participated in Wave I of the National Longitudinal Study of Adolescent Health (AddHealth). To move beyond dichotomous indicators, a “progressive elaboration” strategy was used, starting with six dichotomous indicators and then evaluating a series of models testing additional cut points on the ordinal indicators at progressively higher points for one indicator at a time. Analyses were performed on one random half-sample, and confirmatory LCAs were performed on the second random half-sample and in the Wave II data.
Results:
The final model consisted of four latent classes (never or non–current drinkers, low-intake drinkers, non–problem drinkers, and problem drinkers). Confirmatory LCAs in the second random half-sample from Wave I and in Wave II support this four-class solution. The means on the four latent classes were also generally ordered on an array of measures reflecting psychosocial risk for problem behavior.
Conclusions:
These analyses suggest that there may be four different classes or types of alcohol involvement among adolescents, and, more importantly, they illustrate the utility of the progressive elaboration strategy for moving beyond dichotomous indicators in latent class models.
An area of continuing interest over the past 40 years has been research focused on typologies of alcohol involvement among adolescents. Typological research is an example of “person-centered” research (Bergman, 2000) that focuses on description of individuals who exhibit similar profiles across a number of variables—in this case, different alcohol use behaviors. This type of research is in contrast to “variable-centered” research that focuses on issues such as the correlations among variables or the factors underlying involvement with alcohol.
Historically, two kinds of typologies have been used to characterize patterns of alcohol use among adolescents. The first classified adolescents into types based on both their drinking frequency and usual intake per occasion, resulting in types labeled abstainers, infrequent drinkers, light drinkers, moderate drinkers, moderate-heavy drinkers, heavy drinkers (Barnes & Welte, 1986; Rachal et al., 1976; Zucker & Harford, 1983) and problem drinkers (Windle, 1996). The second divided adolescents into regular drinkers versus not (e.g., Reifman et al., 1998) or heavy episodic drinkers versus not (Cranford et al., 2006; D’Amico et al., 2001) based on single alcohol use behaviors.
A more recent, comprehensive method is the use of latent class analysis (LCA), a form of cluster analysis that takes into account measurement error (see Auerbach & Collins, 2006; Collins & Lanza, 2010; Dauber et al., 2009; Fergusson et al., 1995; Lanza et al., 2007; Lee et al., 2013; Reboussin et al., 2006; Wells et al., 2004). This method identifies groups of adolescents (classes) that differ in their patterns of involvement in a larger array of alcohol behaviors (ever use, frequency, usual intake, high-volume drinking, drunkenness, etc.) and assigns individuals probabilistically to groups or classes.
Most LCAs of alcohol use, however, have relied on dichotomous indicators of each alcohol behavior, even when the questions used categorical (ordinal) responses. There is, however, no mathematical necessity for using dichotomous indicators in LCA (Lanza et al., 2003). Where studies have used trichotomous splits on manifest indicators (Auerbach & Collins, 2006; Dauber et al., 2009; Fergusson et al., 1995; Percy & Iwaniec, 2007), investigators have decided where to split the ordinal responses before performing the LCA.
The present research advances the notions that manifest ordinal variables should be split at multiple locations to better reflect the diversity among adolescents in their alcohol use patterns, and that the location of cut points along the alcohol behavior responses should be determined empirically.
The present study therefore had three aims: (a) to perform a “progressive elaboration” LCA (described below) to better characterize the diversity of patterns of alcohol involvement, (b) to perform confirmatory LCAs (Finch & Bronk, 2011) of the resulting classes, and (c) to further examine the validity of the resulting latent classes of adolescent alcohol involvement by comparing them on an array of psychosocial risk factors for problem behavior.
Method
This study was based on secondary analyses of the Public Use Data Set (Harris & Udry, 2014) of the in-home interviews collected in Waves I and II of the National Longitudinal Study of Adolescent to Adult Health (AddHealth).
Procedures
The AddHealth project was a nationally representative probability survey of adolescents in grades 7–12 that involved an in-school questionnaire, a Wave-I in-home interview, a Wave-II in-home interview a year later, and two data collections in young adulthood.
The in-school survey used a multistage stratified cluster design to sample public and private high schools in the United States. Of the 26,666 eligible high schools, 80 high schools and 52 middle (feeder) schools were randomly selected proportional to enrollment size, school type, and percentage of White students. Between September 1994 and April 1995, 90,118 students with parental consent completed an in-school questionnaire.
Within each school, approximately 17 students were randomly selected by gender within grade to complete computer-assisted personal interviews. Alcohol and other drug questions were asked using audio computer-assisted personal interviews. Between April and December 1995, 80% of selected students (n = 20,745) were interviewed (including the core sample and the supplementary samples of disabled students, ethnic minorities, and samples of students for genetic and social network analyses). In addition, 85% had a parent or caretaker (usually the biological mother) complete a parental questionnaire. One year later, participants were recontacted, and 14,738 completed Wave II home interviews (Harris, 2013).
Participants
The age distribution for the 12,105 adolescents in the Wave I core sample was as follows: age 12 (2.5%), 13 (10.9%), 14 (13.2%), 15 (17.6%), 16 (19.6%), 17 (19.3%), and age 18 or older (17.0%). In this sample, 49.1% were boys and 50.9% girls. With respect to father’s education, 25.2% had not finished high school, 14.2% had graduated, 16.3% had some college or other postsecondary education, 9% were college graduates, and 35.2% had some postgraduate education. The ethnic/racial distribution was White (52.8%), African American (21.4%), Hispanic (17.0%), and other (8.8%).
The Public Use Data Set (Harris & Udry, 2014) contains Wave I data for 6,504 students randomly selected from the core sample and Wave II data for 4,834 students.
Measurement of alcohol use behaviors
The measures of alcohol behavior used in the AddHealth in-home interviews were generally modifications of questions previously developed for testing Problem Behavior Theory (Jessor & Jessor, 1977; Jessor et al., 1992). Alcohol behavior questions included the following:
“Have you had a drink of beer, wine, or liquor—not just a sip or a taste of someone else’s drink—more than two or three times in your life?” (no, yes)
“During the past 12 months, on how many days did you drink alcohol?” (every day; 3–5 days a week; 1 or 2 days a week; 2 or 3 days a month; 3–12 times in past 12 months; 1 or 2 days in past 12 months; did not have a drink in the past 12 months)
“Think of all the times you have had a drink during the past 12 months. How many drinks did you usually have each time? (A “drink” is a glass of wine, a can of beer, a wine cooler, a shot glass of liquor, or a mixed drink.)” (1–90 drinks; did not drink in past 12 months)
“Over the past 12 months, on how many days did you drink five or more drinks in a row?” (every day; 3–5 days a week; 1 or 2 days a week; 2 or 3 days a month; 3–12 times in past 12 months; 1 or 2 days in past 12 months; did not have a drink in the past 12 months)
“In the past 12 months, on how many days have you gotten drunk or ‘very, very high’ on alcohol?” (every day; 3–5 days a week; 1 or 2 days a week; 2 or 3 days a month; 3–12 times in past 12 months; 1 or 2 days in past 12 months; did not have a drink in the past 12 months)
“Over the past 12 months, how many times has each of the following happened? You got into trouble with your parents because you had been drinking? You’ve had problems at school or with school work because you had been drinking? You had problems with your friends because you had been drinking? You had problems with someone you were dating because you had been drinking? You did something you later regretted because you had been drinking?” (For each: never; once; twice; 3–4 times; 5 or more times)
All were categorical indicators except for the question on ever alcohol use, which was dichotomous. Responses were recoded so that higher scores reflected more frequent behavior, with abstainers and non–current drinkers receiving the lowest code. Negative consequences experienced in the past 12 months were summed across the five component questions.
Measurement of validation variables
The resulting latent classes of adolescent alcohol involvement from Wave I were validated by comparing them on concurrent personality, social environment, and behaviour variables previously identified as risk factors for alcohol involvement (Donovan, 2004; Resnick et al., 1997). Parental Drinking Frequency was the average of mother and father reports from the Wave I Parent Interview. Emotional Distress was a 15-item measure of depression and negative affectivity (α = .86). Self-Esteem was a six-item scale assessing agreement with statements of good personal qualities (α = .85). Religiosity was a two-item measure of the personal importance of religion and the frequency of prayer (α = .86). Relation with Parents was the average of a six-item measure of closeness to mother and satisfaction with relationship with mother (α = .84) and a five-item measure of closeness to father and satisfaction with relationship with father (α = .88). School Bonding was a four-item measure of connection to school, teachers, and other students (α = .75). Friend Models for Drinking asked how many (of three) best friends drank alcohol at least once a month. Friend Models for Smoking asked how many best friends smoked at least one cigarette a day. Friend Models for Drug Use asked how many best friends used marijuana at least once a month. Delinquent Behavior was a 15-item scale assessing marking and damaging property, theft, shoplifting, running away, school suspension, and lying to parents (α = .83). Cigarette Smoking asked about ever trying cigarettes, even 1–2 puffs. Frequency of Marijuana Use asked about lifetime frequency of use. Number of Other Drugs Used assessed ever use of cocaine, inhalants, or other illegal drugs (α = .62). Religious Behavior asked about the frequency of attendance at religious services and church youth group activities in the past year (α = .91). School Grades averaged most recent grades in English, mathematics, history or social studies, and science (α = .75).
Latent classes having greater involvement with alcohol should exhibit greater psychosocial risk for problem behaviour than classes showing less involvement. Greater risk is indicated by more frequent parental drinking; greater emotional distress; lower self-esteem; lower bonding to school; lower religiosity; less satisfying relations with parents; more friends who drink, smoke, and use marijuana; more frequent delinquent behavior; greater personal smoking and other drug use; less religious behavior; and lower school grades.
Analytic procedures
For the LCAs, the Wave I sample was split into random halves (n1 = 3,217 and n2 = 3,287) using the Select Cases procedure in IBM SPSS Version 21 (IBM Corp., Armonk, NY). The half-samples did not differ significantly on gender, ethnic/racial background, grade in school, or any of the six alcohol use behavior items.
LCAs were carried out in the first half-sample (3,148 subjects with complete data on the alcohol items) using Latent Gold 4.0 (Vermunt & Magidson, 2005). To move beyond dichotomous indicators, the following “progressive elaboration” strategy was used. It began with six dichotomous indicators and then evaluated a series of models testing additional cut points at progressively higher points for one indicator at a time (after fixing the cut points for previously evaluated indicators). The strategy started with the indicator reflecting the lowest intensity of involvement with alcohol (frequency of use) and progressed through the indicators reflecting increasingly greater intensity of involvement (usual intake, times drunk, frequency of heavy episodic drinking, and negative consequences of drinking; see Donovan & Molina, 2013).
For example, when determining where a second cut point should be added (resulting in a trichotomous indicator) for the frequency of drinking, cuts were made in turn at “1–2 times/year” (the binary cut point) and at “3–12 times in past 12 months,” at “2 or 3 days/month,” and at “1 or 2 days/week.” The second cut point that resulted in the lowest Bayesian Information Criterion (BIC) statistic (based on the log likelihood) was chosen, and this trichotomy figured in subsequent analyses examining potential second cut points for each remaining indicator.
In addition to having the lowest BIC, two additional criteria were used. Most importantly, any model accepted also had to exhibit a sizable conditional probability for each of the indicator’s categories on one or more of the latent classes. That is, every category of a trichotomy, for example, was required to have a high conditional probability (e.g., > .50) for at least one of the latent classes, thus demonstrating that all three categories were useful in classifying the adolescents. Second, acceptable models at each step generally had to exhibit a similar or higher entropy R2 than the preceding model in which the indicator of interest had one fewer cut points. Entropy R2 is a measure of the uncertainty in individuals’ assignments to the latent classes discovered, basically a weighted average posterior probability (the higher the measure, the lower the degree of uncertainty). This process was repeated where possible to determine whether third cut points (to constitute a four-category indicator) were needed. Latent Gold 4.0 was used for the progressive elaboration because it could access SPSS data files directly. Because of the exploratory nature of these analyses, the national sample clustering and sample weights were not applied.
For comparison purposes, an LCA was also performed based on the original categorical responses to the six alcohol use questions.
Confirmatory and validation analyses.
Confirmatory LCAs (Finch & Bronk, 2011) were performed using Mplus Version 7.1 (Muthén & Muthén, 2012) in the second random half-sample of Wave I and in the Wave II data. Class means and indicator thresholds derived from the first half-sample were fixed in the LCA of the second half-sample. Similarly, class means and indicator thresholds from Wave I were fixed in the LCA of the Wave II data. Nonsignificant likelihood ratio tests indicated acceptable fit.
Wald tests for equality across the latent classes of means on the psychosocial variables were run on the full Wave I sample using 20 pseudo-class-based multiple imputations employing the Auxiliary command in Mplus Version 7.1 (Asparouhov, 2010; Asparouhov & Muthén, 2014). The demographic variables of sex, grade, and ethnic/racial background were also examined. In the confirmatory LCAs and the examination of the psychosocial covariates of the classes, the clustering and sample weights for the national sample were taken into account.
Results
The initial LCAs used dichotomous indicators to constitute latent classes in the Wave I first half-sample. This was followed by progressive elaboration of each of the five categorical variables in turn, resulting in a final model of latent classes of adolescents.
Latent class analyses using dichotomous indicators
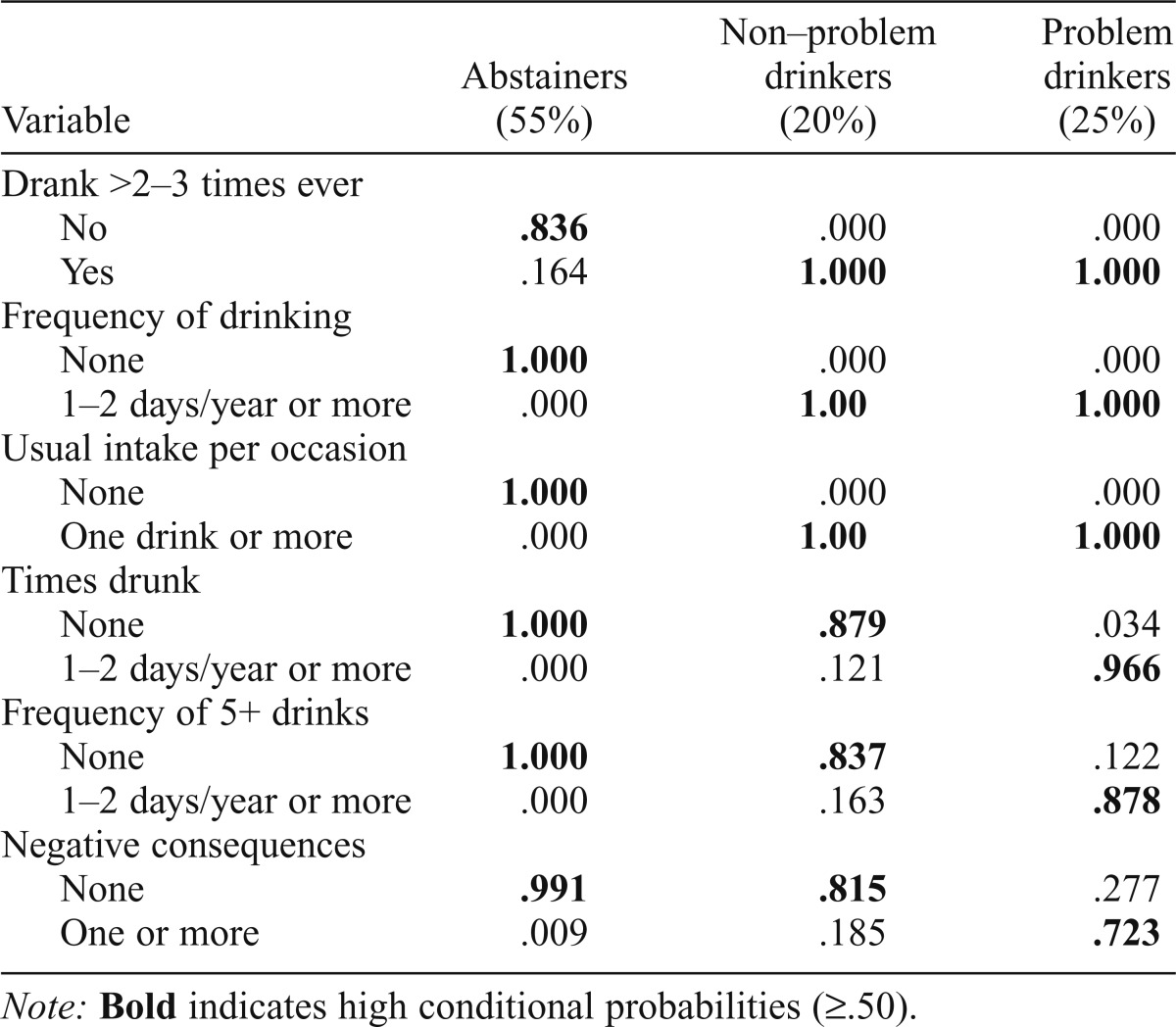
This strategy started with dichotomous splits (no/never/none vs. yes/ever/some) on all six indicators and evaluated the relative fit of one-class to five-class models. The BIC and the likelihood ratio chi-squared statistic (L2) and its associated probability level (see Vermunt & Magidson, 2004) were used to compare the models. The three-class model fit the data best, BIC = 11,117.7, L2(43) = 3.82, p = 1.00, significantly better than the two-class model (p = .000) according to the Bootstrap Likelihood Ratio Test (BLRT). The conditional probabilities for each response to the dichotomous indicators (given class membership) are presented in Table 1 for the three latent classes, characterized as never or non–current drinkers (55%), non–problem drinkers (20%), and problem drinkers (25%). The entropy R2 for this three-class solution was .937.
Table 1.
Conditional probabilities describing the three latent classes from latent class analysis using dichotomous indicators (Wave I first half-sample)
| Variable | Abstainers (55%) | Non–problem drinkers (20%) | Problem drinkers (25%) |
| Drank >2–3 times ever | |||
| No | .836 | .000 | .000 |
| Yes | .164 | 1.000 | 1.000 |
| Frequency of drinking | |||
| None | 1.000 | .000 | .000 |
| 1–2 days/year or more | .000 | 1.00 | 1.000 |
| Usual intake per occasion | |||
| None | 1.000 | .000 | .000 |
| One drink or more | .000 | 1.00 | 1.000 |
| Times drunk | |||
| None | 1.000 | .879 | .034 |
| 1–2 days/year or more | .000 | .121 | .966 |
| Frequency of 5+ drinks | |||
| None | 1.000 | .837 | .122 |
| 1–2 days/year or more | .000 | .163 | .878 |
| Negative consequences | |||
| None | .991 | .815 | .277 |
| One or more | .009 | .185 | .723 |
Note: Bold indicates high conditional probabilities (≥.50).
Progressive elaboration of the categorical indicators (trichotomies)
LCAs were performed to evaluate whether a second cut point (comprising a trichotomous indicator) at progressively higher points on each of the five categorical indicators in turn (ever use was dichotomous) improved the fit of the latent class model.
Frequency of drinking in past 12 months.
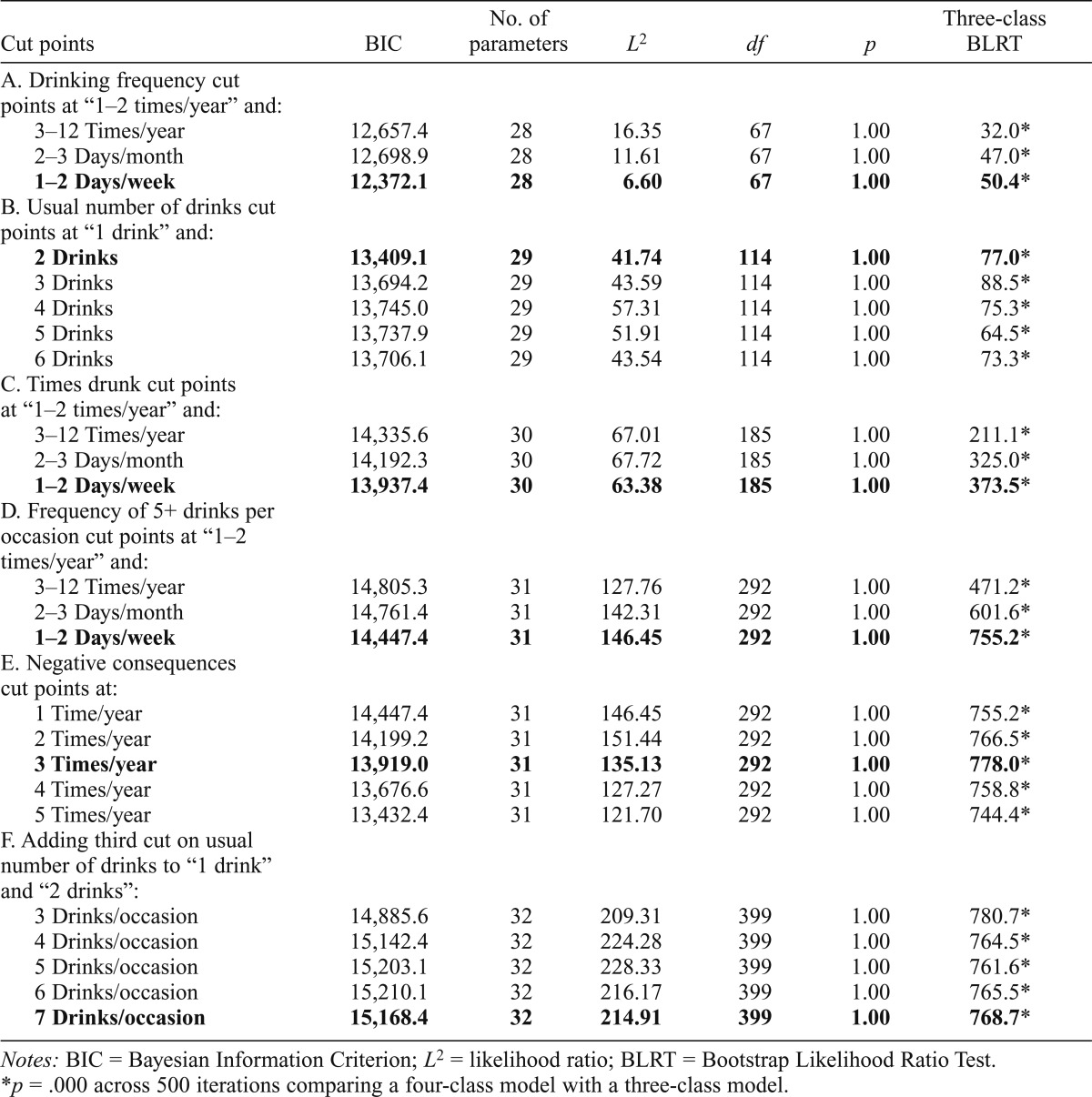
Three models were evaluated that cut frequency of drinking at “1–2 times” (the binary cut point) and at “3–12 times in past 12 months,” “2 or 3 days a month,” and “1 or 2 days a week,” respectively (higher cuts had <100 subjects). For each potential cut point, LCAs compared the fit of 3–5 classes (since the dichotomous-split model found three classes). In all cases, the four-class model fit better than the three-class model (by BLRT). Table 2 shows that the lowest BIC was for the model that trichotomized frequency at “1–2 times” and “1–2 days/week.” For this solution, each response category exhibited a high conditional probability for one or more of the four latent classes. The entropy R2 was .866, which cannot be compared directly to the three-class dichotomous-split solution.
Table 2.
Goodness-of-fit statistics for latent class analyses with different cut points on the categorical indicators, all for the best-fitting four-class solutions in Wave I first half-sample (model selected as best fit on all criteria, not just BIC, in bold)
| Cut points | BIC | No. of parameters | L2 | df | p | Three-class BLRT |
| A. Drinking frequency cut points at “1–2 times/year” and: | ||||||
| 3–12 Times/year | 12,657.4 | 28 | 16.35 | 67 | 1.00 | 32.0* |
| 2–3 Days/month | 12,698.9 | 28 | 11.61 | 67 | 1.00 | 47.0* |
| 1–2 Days/week | 12,372.1 | 28 | 6.60 | 67 | 1.00 | 50.4* |
| B. Usual number of drinks cut points at “1 drink” and: | ||||||
| 2 Drinks | 13,409.1 | 29 | 41.74 | 114 | 1.00 | 77.0* |
| 3 Drinks | 13,694.2 | 29 | 43.59 | 114 | 1.00 | 88.5* |
| 4 Drinks | 13,745.0 | 29 | 57.31 | 114 | 1.00 | 75.3* |
| 5 Drinks | 13,737.9 | 29 | 51.91 | 114 | 1.00 | 64.5* |
| 6 Drinks | 13,706.1 | 29 | 43.54 | 114 | 1.00 | 73.3* |
| C. Times drunk cut points at “1–2 times/year” and: | ||||||
| 3–12 Times/year | 14,335.6 | 30 | 67.01 | 185 | 1.00 | 211.1* |
| 2–3 Days/month | 14,192.3 | 30 | 67.72 | 185 | 1.00 | 325.0* |
| 1–2 Days/week | 13,937.4 | 30 | 63.38 | 185 | 1.00 | 373.5* |
| D. Frequency of 5+ drinks per occasion cut points at “1–2 times/year” and: | ||||||
| 3–12 Times/year | 14,805.3 | 31 | 127.76 | 292 | 1.00 | 471.2* |
| 2–3 Days/month | 14,761.4 | 31 | 142.31 | 292 | 1.00 | 601.6* |
| 1–2 Days/week | 14,447.4 | 31 | 146.45 | 292 | 1.00 | 755.2* |
| E. Negative consequences cut points at: | ||||||
| 1 Time/year | 14,447.4 | 31 | 146.45 | 292 | 1.00 | 755.2* |
| 2 Times/year | 14,199.2 | 31 | 151.44 | 292 | 1.00 | 766.5* |
| 3 Times/year | 13,919.0 | 31 | 135.13 | 292 | 1.00 | 778.0* |
| 4 Times/year | 13,676.6 | 31 | 127.27 | 292 | 1.00 | 758.8* |
| 5 Times/year | 13,432.4 | 31 | 121.70 | 292 | 1.00 | 744.4* |
| F. Adding third cut on usual number of drinks to “1 drink” and “2 drinks”: | ||||||
| 3 Drinks/occasion | 14,885.6 | 32 | 209.31 | 399 | 1.00 | 780.7* |
| 4 Drinks/occasion | 15,142.4 | 32 | 224.28 | 399 | 1.00 | 764.5* |
| 5 Drinks/occasion | 15,203.1 | 32 | 228.33 | 399 | 1.00 | 761.6* |
| 6 Drinks/occasion | 15,210.1 | 32 | 216.17 | 399 | 1.00 | 765.5* |
| 7 Drinks/occasion | 15,168.4 | 32 | 214.91 | 399 | 1.00 | 768.7* |
Notes: BIC = Bayesian Information Criterion; L2 = likelihood ratio; BLRT = Bootstrap Likelihood Ratio Test.
p = .000 across 500 iterations comparing a four-class model with a three-class model.
Usual intake per occasion.
The next trichotomy evaluated was usual intake per occasion. Five potential cut points above “1 drink per occasion” were examined for 3–5 latent classes. As above, four-class models fit best. The best second cut point was at “2 or more drinks” (Table 2). All response categories for this and previously evaluated indicators had high conditional probabilities for one or more latent classes. With this cut point added, the entropy R2 was .854 (lower than the previous model, suggesting that additional cut points were necessary; see below).
Times drunk in past 12 months.
Repeating the same procedure for times drunk, the best fitting model was a fourclass model with cut points for a trichotomy at “1–2 times/year” and “1–2 days/week” (Table 2). All categories for this and previous indicators had high conditional probabilities on one or more latent classes. With this cut point, the entropy R2 was .922, higher than the preceding model.
Frequency of five or more drinks per occasion.
Three models were evaluated to determine the best second cut point (beyond “1–2 times”) on five or more drinks per occasion for 3–5 latent classes. All four-class models fit best. The best-fitting four-class model trichotomized at “1–2 times/year” and “1–2 days/week” (Table 2). All response categories for this and previously evaluated indicators had high conditional probabilities for one or more latent classes. The entropy R2 was .939, higher than the preceding model and equivalent to the dichotomous-split model.
Negative consequences of drinking.
Four models compared alternative second cut points at 2–5 negative consequences of drinking in the past 12 months for 3–5 classes. Although four-class models fit best, in no case were there high conditional probabilities for all three categories on this indicator (0, 1, 2–5+). An alternative strategy evaluated models using four different first cut points of 2–5 times/year, in contrast to the preceding model (cut at 1 time/year). Although the lowest BICs were for models with cuts at 4 or 5 times/year (Table 2), the conditional probabilities were too low for the higher category in all four classes. The next lowest BIC used a cut at 3 times/year and fit better than the cut at 1 time/year. Both resulting categories (0–2 and 3+) had high conditional probabilities in one or more latent classes. The entropy R2 (.938) was equivalent to the preceding model and the dichotomous-split model.
Evaluating a third cut point for usual intake
After fixing all of the manifest indicators at the cut points identified above, additional models examined whether a further (third) cut point on usual intake improved the fit of the latent class solution. Given the low second cut point for this indicator (at 2 drinks), five potential third cut points (at 3–7 drinks) were evaluated (Table 2). The two models with the lowest BICs added cut points at 3 and 4 drinks, respectively, but one category failed to have a high conditional probability for any class. The model with the next lowest BIC used cut points at 1, 2–6, and 7+ drinks, and each category had a high conditional probability for at least one class. The entropy R2 was .937, equivalent to both the dichotomous-split solution and the preceding model.
Description of the final classes
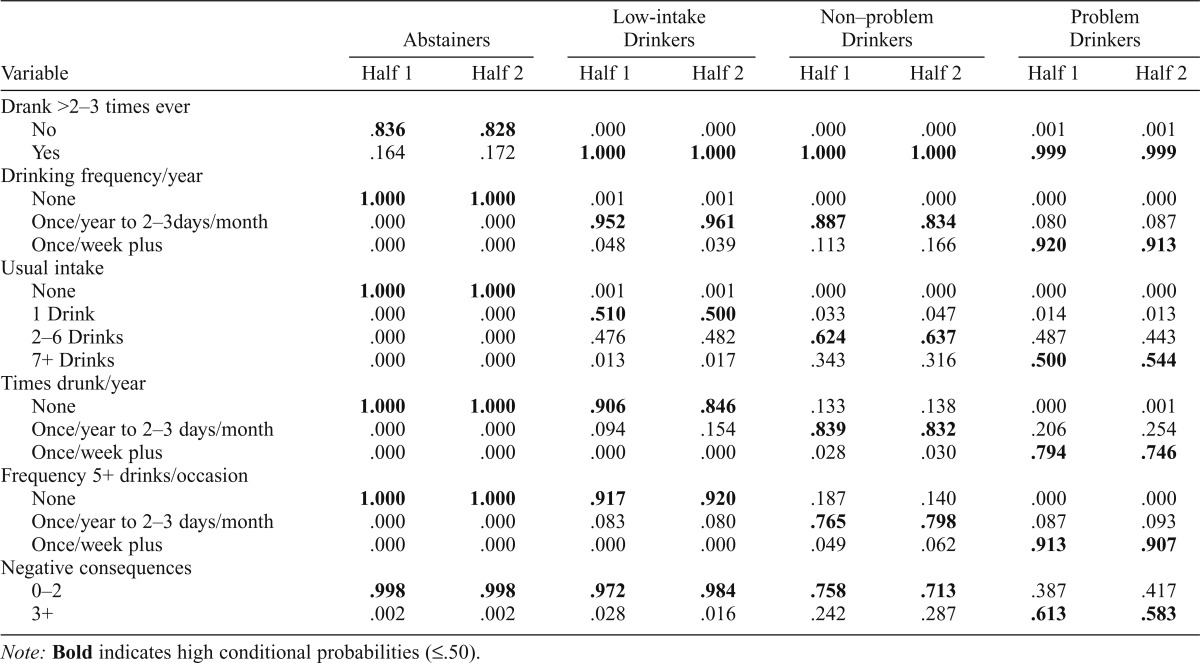
Table 3 presents the conditional probabilities for each response on the dichotomous, trichotomous, and fourcategory indicators, given membership in each of the four final classes. In the first random half-sample, never or non–current drinkers comprised 55.2% (most of whom had never consumed alcohol). Low-intake drinkers, who drank less than weekly and half of whom drank only one drink per occasion, comprised 17.1%. Non–problem drinkers—who also drank less than weekly, usually drank 2–6 drinks per occasion, and reported less-than-weekly drunkenness and episodic heavy drinking—comprised 21.7%. Problem drinkers comprised 6.1% and were most likely to report weekly or more frequent drinking, drunkenness, and episodic heavy drinking and to report three or more negative consequences of drinking in the past year. It is clear that the resulting classes exhibit both homogeneity (shown by high conditional probabilities within classes) and latent class separation (shown by differing patterns of high conditional probabilities). Wald tests showed that all six indicators contributed significantly (p < .0001) to the latent classifications.
Table 3.
Results of latent class analysis in the two Wave I random half-samples [Conditional probabilities given class membership, from Latent Gold 4.0]
| Variable | Abstainers |
Low-intake Drinkers |
Non–problem Drinkers |
Problem Drinkers |
||||
| Half 1 | Half 2 | Half 1 | Half 2 | Half 1 | Half 2 | Half 1 | Half 2 | |
| Drank >2–3 times ever | ||||||||
| No | .836 | .828 | .000 | .000 | .000 | .000 | .001 | .001 |
| Yes | .164 | .172 | 1.000 | 1.000 | 1.000 | 1.000 | .999 | .999 |
| Drinking frequency/year | ||||||||
| None | 1.000 | 1.000 | .001 | .001 | .000 | .000 | .000 | .000 |
| Once/year to 2–3days/month | .000 | .000 | .952 | .961 | .887 | .834 | .080 | .087 |
| Once/week plus | .000 | .000 | .048 | .039 | .113 | .166 | .920 | .913 |
| Usual intake | ||||||||
| None | 1.000 | 1.000 | .001 | .001 | .000 | .000 | .000 | .000 |
| 1 Drink | .000 | .000 | .510 | .500 | .033 | .047 | .014 | .013 |
| 2–6 Drinks | .000 | .000 | .476 | .482 | .624 | .637 | .487 | .443 |
| 7+ Drinks | .000 | .000 | .013 | .017 | .343 | .316 | .500 | .544 |
| Times drunk/year | ||||||||
| None | 1.000 | 1.000 | .906 | .846 | .133 | .138 | .000 | .001 |
| Once/year to 2–3 days/month | .000 | .000 | .094 | .154 | .839 | .832 | .206 | .254 |
| Once/week plus | .000 | .000 | .000 | .000 | .028 | .030 | .794 | .746 |
| Frequency 5+ drinks/occasion | ||||||||
| None | 1.000 | 1.000 | .917 | .920 | .187 | .140 | .000 | .000 |
| Once/year to 2–3 days/month | .000 | .000 | .083 | .080 | .765 | .798 | .087 | .093 |
| Once/week plus | .000 | .000 | .000 | .000 | .049 | .062 | .913 | .907 |
| Negative consequences | ||||||||
| 0–2 | .998 | .998 | .972 | .984 | .758 | .713 | .387 | .417 |
| 3+ | .002 | .002 | .028 | .016 | .242 | .287 | .613 | .583 |
Note: Bold indicates high conditional probabilities (≤.50).
Comparison latent class analyses using original ordinal variables
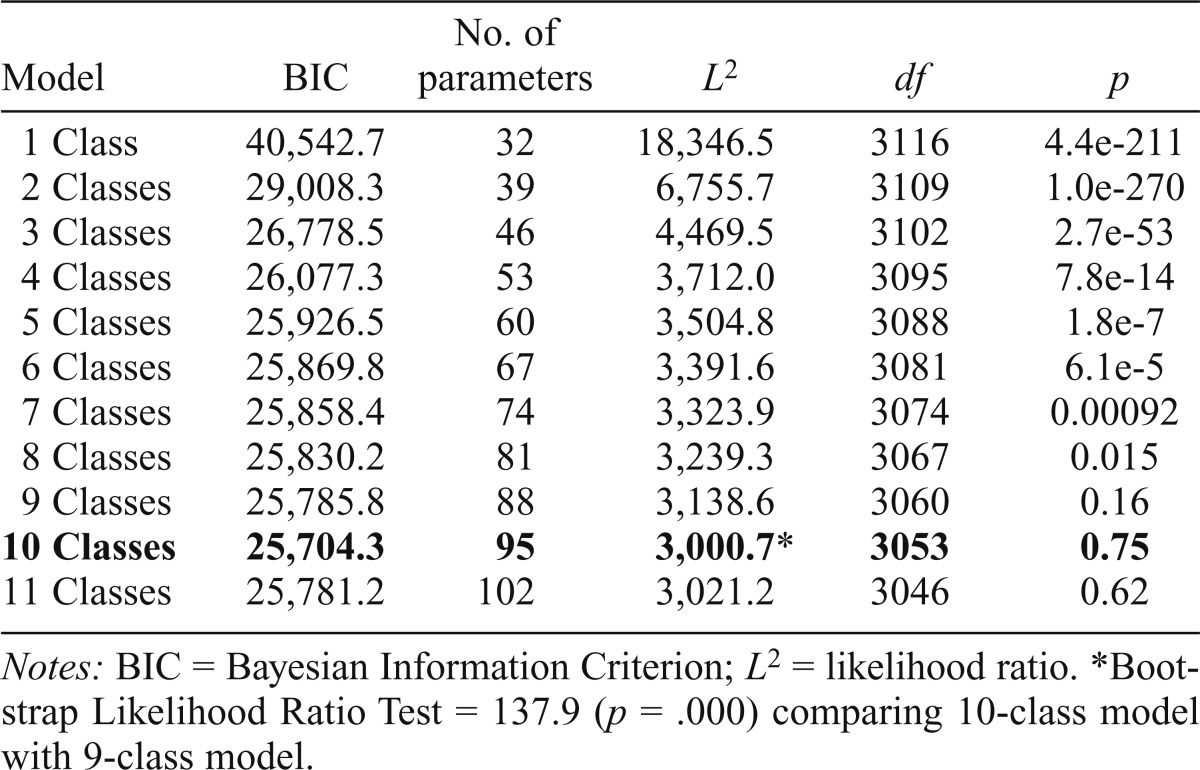
A comparison of the final four-class model with LCAs based on the original responses to the alcohol behaviour questions (also in the Wave I first half-sample) shows that the former results are much more parsimonious and exhibit a higher entropy R2 (.938 vs. .910). Although a 10-class solution fit the original questions best (Table 4), six classes comprised less than 4% of the sample each. Table 5 also shows that many of the indicator response categories do not have high conditional probabilities in any of the classes. Class 1 (55.2%), Class 2 (12.8%), and Class 5 (3.8%), however, are similar to the never or non–current drinkers, low-intake drinkers, and problem drinkers, respectively, found in the elaboration analyses.
Table 4.
Goodness-of-fit statistics for latent class analyses in Wave I first half-sample using original ordinal responses to the alcohol use questions (best-fitting model in bold)
| Model | BIC | No. of parameters | L2 | df | p |
| 1 Class | 40,542.7 | 32 | 18,346.5 | 3116 | 4.4e-211 |
| 2 Classes | 29,008.3 | 39 | 6,755.7 | 3109 | 1.0e-270 |
| 3 Classes | 26,778.5 | 46 | 4,469.5 | 3102 | 2.7e-53 |
| 4 Classes | 26,077.3 | 53 | 3,712.0 | 3095 | 7.8e-14 |
| 5 Classes | 25,926.5 | 60 | 3,504.8 | 3088 | 1.8e-7 |
| 6 Classes | 25,869.8 | 67 | 3,391.6 | 3081 | 6.1e-5 |
| 7 Classes | 25,858.4 | 74 | 3,323.9 | 3074 | 0.00092 |
| 8 Classes | 25,830.2 | 81 | 3,239.3 | 3067 | 0.015 |
| 9 Classes | 25,785.8 | 88 | 3,138.6 | 3060 | 0.16 |
| 10 Classes | 25,704.3 | 95 | 3,000.7* | 3053 | 0.75 |
| 11 Classes | 25,781.2 | 102 | 3,021.2 | 3046 | 0.62 |
Notes: BIC = Bayesian Information Criterion; L2 = likelihood ratio.
Bootstrap Likelihood Ratio Test = 137.9 (p = .000) comparing 10-class model with 9-class model.
Table 5.
Conditional probabilities describing 10 latent classes from latent class analysis using all responses on the ordinal indicators in Wave I first half-sample (high conditional probabilities in bold)
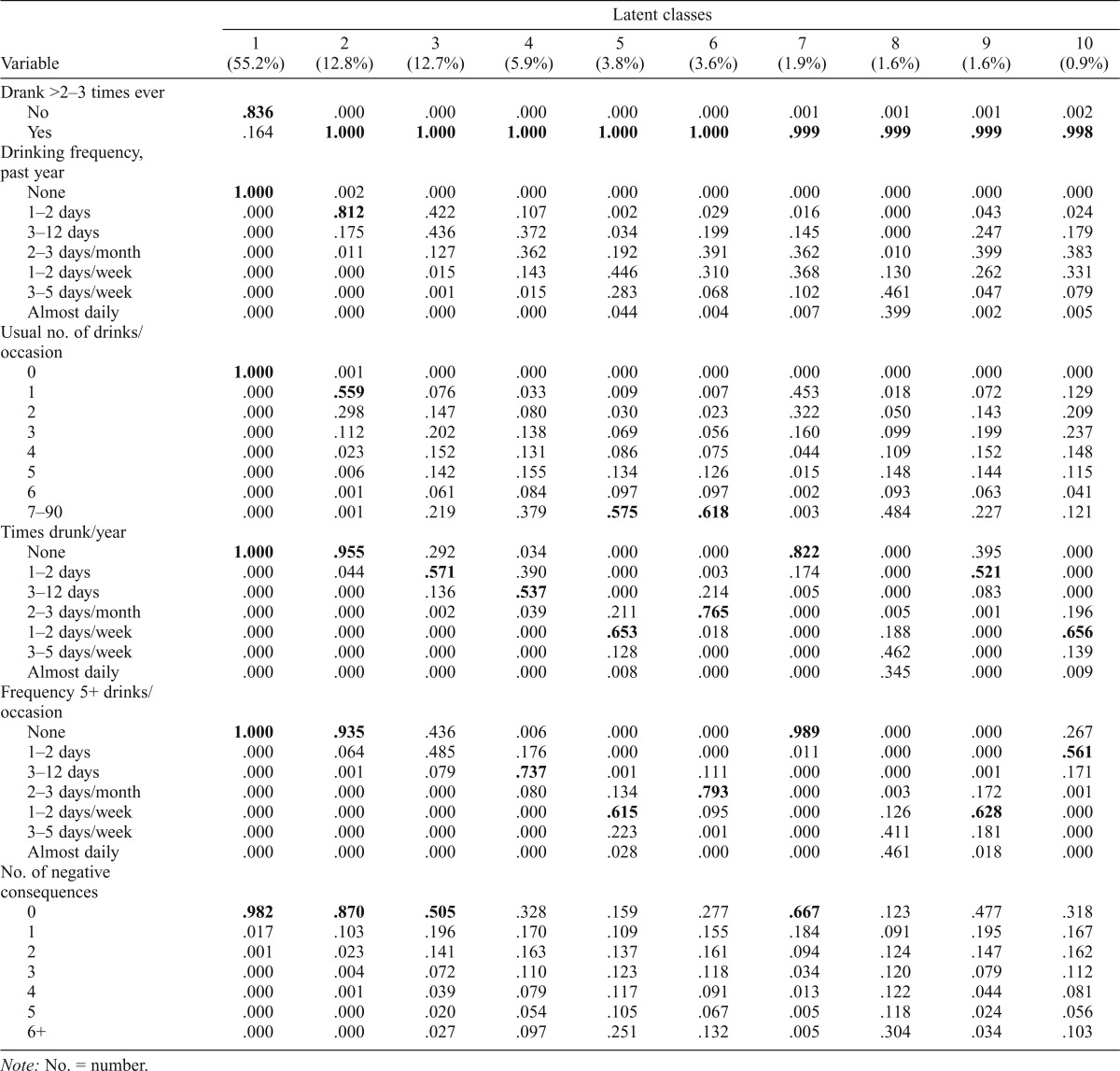
| Variable | Latent classes |
|||||||||
| 1 (55.2%) | 2 (12.8%) | 3 (12.7%) | 4 (5.9%) | 5 (3.8%) | 6 (3.6%) | 7 (1.9%) | 8 (1.6%) | 9 (1.6%) | 10 (0.9%) | |
| Drank >2–3 times | ||||||||||
| No | .836 | .000 | .000 | .000 | .000 | .000 | .001 | .001 | .001 | .002 |
| Yes | .164 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | .999 | .999 | .999 | .998 |
| Drinking frequency, past year | ||||||||||
| None | 1.000 | .002 | .000 | .000 | .000 | .000 | .000 | .000 | .000 | .000 |
| 1–2 days | .000 | .812 | .422 | .107 | .002 | .029 | .016 | .000 | .043 | .024 |
| 3–12 days | .000 | .175 | .436 | .372 | .034 | .199 | .145 | .000 | .247 | .179 |
| 2–3 days/month | .000 | .011 | .127 | .362 | .192 | .391 | .362 | .010 | .399 | .383 |
| 1–2 days/week | .000 | .000 | .015 | .143 | .446 | .310 | .368 | .130 | .262 | .331 |
| 3–5 days/week | .000 | .000 | .001 | .015 | .283 | .068 | .102 | .461 | .047 | .079 |
| Almost daily | .000 | .000 | .000 | .000 | .044 | .004 | .007 | .399 | .002 | .005 |
| Usual no. of drinks/occasion | ||||||||||
| 0 | 1.000 | .001 | .000 | .000 | .000 | .000 | .000 | .000 | .000 | .000 |
| 1 | .000 | .559 | .076 | .033 | .009 | .007 | .453 | .018 | .072 | .129 |
| 2 | .000 | .298 | .147 | .080 | .030 | .023 | .322 | .050 | .143 | .209 |
| 3 | .000 | .112 | .202 | .138 | .069 | .056 | .160 | .099 | .199 | .237 |
| 4 | .000 | .023 | .152 | .131 | .086 | .075 | .044 | .109 | .152 | .148 |
| 5 | .000 | .006 | .142 | .155 | .134 | .126 | .015 | .148 | .144 | .115 |
| 6 | .000 | .001 | .061 | .084 | .097 | .097 | .002 | .093 | .063 | .041 |
| 7–90 | .000 | .001 | .219 | .379 | .575 | .618 | .003 | .484 | .227 | .121 |
| Times drunk/year | ||||||||||
| None | 1.000 | .955 | .292 | .034 | .000 | .000 | .822 | .000 | .395 | .000 |
| 1–2 days | .000 | .044 | .571 | .390 | .000 | .003 | .174 | .000 | .521 | .000 |
| 3–12 days | .000 | .000 | .136 | .537 | .000 | .214 | .005 | .000 | .083 | .000 |
| 2–3 days/month | .000 | .000 | .002 | .039 | .211 | .765 | .000 | .005 | .001 | .196 |
| 1–2 days/week | .000 | .000 | .000 | .000 | .653 | .018 | .000 | .188 | .000 | .656 |
| 3–5 days/week | .000 | .000 | .000 | .000 | .128 | .000 | .000 | .462 | .000 | .139 |
| Almost daily | .000 | .000 | .000 | .000 | .008 | .000 | .000 | .345 | .000 | .009 |
| Frequency 5+ drinks/occasion | ||||||||||
| None | 1.000 | .935 | .436 | .006 | .000 | .000 | .989 | .000 | .000 | .267 |
| 1–2 days | .000 | .064 | .485 | .176 | .000 | .000 | .011 | .000 | .000 | .561 |
| 3–12 days | .000 | .001 | .079 | .737 | .001 | .111 | .000 | .000 | .001 | .171 |
| 2–3 days/month | .000 | .000 | .000 | .080 | .134 | .793 | .000 | .003 | .172 | .001 |
| 1–2 days/week | .000 | .000 | .000 | .000 | .615 | .095 | .000 | .126 | .628 | .000 |
| 3–5 days/week | .000 | .000 | .000 | .000 | .223 | .001 | .000 | .411 | .181 | .000 |
| Almost daily | .000 | .000 | .000 | .000 | .028 | .000 | .000 | .461 | .018 | .000 |
| No. of negative consequences | ||||||||||
| 0 | .982 | .870 | .505 | .328 | .159 | .277 | .667 | .123 | .477 | .318 |
| 1 | .017 | .103 | .196 | .170 | .109 | .155 | .184 | .091 | .195 | .167 |
| 2 | .001 | .023 | .141 | .163 | .137 | .161 | .094 | .124 | .147 | .162 |
| 3 | .000 | .004 | .072 | .110 | .123 | .118 | .034 | .120 | .079 | .112 |
| 4 | .000 | .001 | .039 | .079 | .117 | .091 | .013 | .122 | .044 | .081 |
| 5 | .000 | .000 | .020 | .054 | .105 | .067 | .005 | .118 | .024 | .056 |
| 6+ | .000 | .000 | .027 | .097 | .251 | .132 | .005 | .304 | .034 | .103 |
Note: No. = number.
Confirmatory latent class analysis in the second half-sample
The robustness of these results was first tested in the second half-sample from Wave I using Latent Gold 4.0. All of the categorical thresholds (or cut points) were fixed to be the same as those found in the first half-sample, and a four-class solution was specified. A highly similar fit was obtained, BIC = 16,041.9, L2(399) = 211.60, p = 1.00, with similar percentages in each class (53.6%, 18.1%, 22.7%, and 5.6%, respectively) and an entropy R2 of .928. Table 3 illustrates the high similarity between the two half-samples in their conditional probabilities on the indicators, given class membership.
A stronger test of the robustness of the first half-sample results used a confirmatory LCA. For this, the final fourclass LCA on the first half-sample was rerun using Mplus 7.1 (also taking into account the clustering and sample weights) to obtain the class means and indicator threshold values to be fixed in the confirmatory LCA on the second half-sample, Pearson χ2(384) = 147.5, p = 1.00; likelihood ratio χ2(384) = 145.9, p = 1.00; entropy R2 = .950. The four-class solution from the first half-sample fit the second half-sample data well, Pearson χ2(431) = 305.6, p = 1.00; likelihood ratio χ2(431) = 213.6, p = 1.00; entropy R2 = .943.
Confirmatory latent class analysis in the Wave II data
The four-class LCA was rerun including just the 8th–12th graders in Wave I to generate the class means and indicator thresholds to be fixed in the confirmatory LCA in Wave II (when the adolescents were a year older). With all 47 parameters fixed, the model did not fit (p = .000), but it did fit when a single parameter (the threshold for ever drinking) was freed in the least involved class, Pearson χ2(430) = 379.0, p = .963; likelihood ratio χ2(430) = 380.2, p = .959; entropy R2 = .944. Freeing this threshold resulted in better fit because adolescents in this class in Wave II were less likely to be non–current drinkers (more likely to be never drinkers) than in Wave I.
Validation analyses of the final latent classes in Wave I
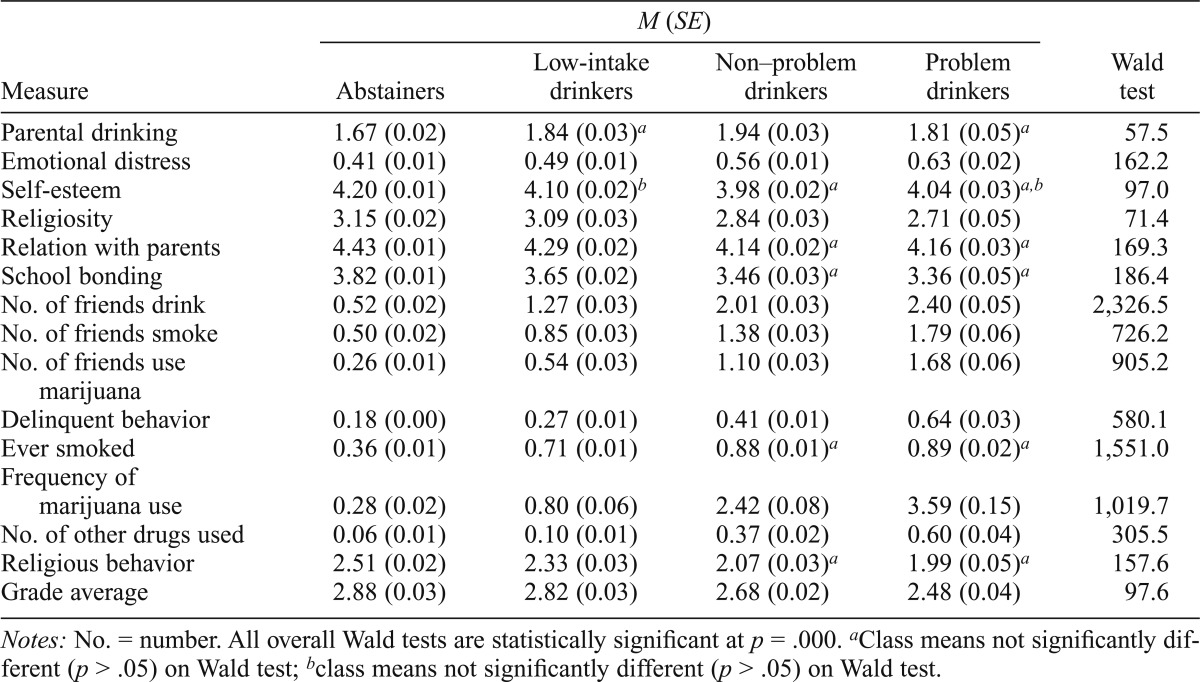
Table 6 presents the results of Wald tests in the full Wave I sample examining the equality of the means assessing psychosocial risk for problem behavior across the latent classes. All 15 variables differed significantly (p < .001) across the latent classes. The class means ordered monotonically in the directions expected for 12 of 15 measures (with problem drinkers exhibiting the greatest risk), and significant Wald tests between all four classes (six comparisons) were found for nine measures. The means for the non–problem drinkers and problem drinkers did not differ significantly on just five measures (see superscripts).
Table 6.
Wald tests of the equality of means on the Wave I measures of psychosocial risk across the four latent classes of adolescent alcohol involvement (full Wave I sample)
| Measure |
M (SE) |
||||
| Abstainers | Low-intake drinkers | Non–problem drinkers | Problem drinkers | Wald test | |
| Parental drinking | 1.67 (0.02) | 1.84 (0.03)a | 1.94 (0.03) | 1.81 (0.05)a | 57.5 |
| Emotional distress | 0.41 (0.01) | 0.49 (0.01) | 0.56 (0.01) | 0.63 (0.02) | 162.2 |
| Self-esteem | 4.20 (0.01) | 4.10 (0.02)b | 3.98 (0.02)a | 4.04 (0.03)a,b | 97.0 |
| Religiosity | 3.15 (0.02) | 3.09 (0.03) | 2.84 (0.03) | 2.71 (0.05) | 71.4 |
| Relation with parents | 4.43 (0.01) | 4.29 (0.02) | 4.14 (0.02)a | 4.16 (0.03)a | 169.3 |
| School bonding | 3.82 (0.01) | 3.65 (0.02) | 3.46 (0.03)a | 3.36 (0.05)a | 186.4 |
| No. of friends drink | 0.52 (0.02) | 1.27 (0.03) | 2.01 (0.03) | 2.40 (0.05) | 2,326.5 |
| No. of friends smoke | 0.50 (0.02) | 0.85 (0.03) | 1.38 (0.03) | 1.79 (0.06) | 726.2 |
| No. of friends use marijuana | 0.26 (0.01) | 0.54 (0.03) | 1.10 (0.03) | 1.68 (0.06) | 905.2 |
| Delinquent behavior | 0.18 (0.00) | 0.27 (0.01) | 0.41 (0.01) | 0.64 (0.03) | 580.1 |
| Ever smoked | 0.36 (0.01) | 0.71 (0.01) | 0.88 (0.01)a | 0.89 (0.02)a | 1,551.0 |
| Frequency of marijuana use | 0.28 (0.02) | 0.80 (0.06) | 2.42 (0.08) | 3.59 (0.15) | 1,019.7 |
| No. of other drugs used | 0.06 (0.01) | 0.10 (0.01) | 0.37 (0.02) | 0.60 (0.04) | 305.5 |
| Religious behavior | 2.51 (0.02) | 2.33 (0.03) | 2.07 (0.03)a | 1.99 (0.05)a | 157.6 |
| Grade average | 2.88 (0.03) | 2.82 (0.03) | 2.68 (0.02) | 2.48 (0.04) | 97.6 |
Notes: No. = number. All overall Wald tests are statistically significant at p = .000.
Class means not significantly different (p > .05) on Wald test;
class means not significantly different (p > .05) on Wald test.
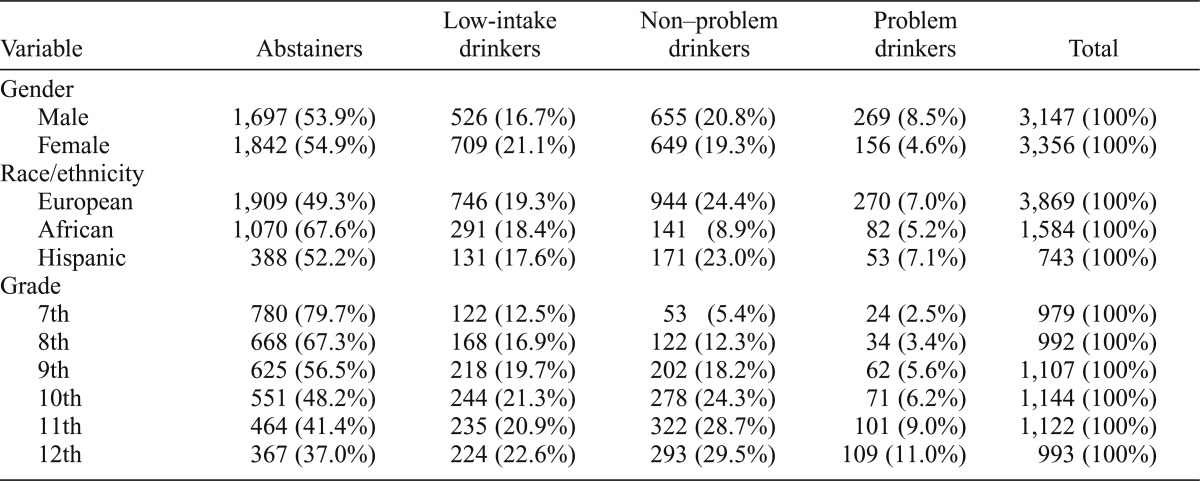
In addition to these psychosocial differences, the alcohol involvement latent classes differed as expected on the demographic variables examined (Table 7). Cross-tabulations were statistically significant between class membership and gender, χ2(3) = 56.5, p < .001; ethnic/racial background, χ2(6) = 212.8, p < .001; and grade in school, χ2(15) = 597.6, p < .001. Younger adolescents and African Americans were more likely to be abstainers, whereas male adolescents, older adolescents, and European American and Hispanic American adolescents were more likely to be problem drinkers (consistent with contemporaneous results from the 1995 Monitoring the Future survey; Johnston et al., 1996).
Table 7.
Differences among the alcohol involvement latent classes on the sociodemographic variables in the full Wave I sample (adolescents assigned to most probable class)
| Variable | Abstainers | Low-intake drinkers | Non–problem drinkers | Problem drinkers | Total |
| Gender | |||||
| Male | 1,697 (53.9%) | 526 (16.7%) | 655 (20.8%) | 269 (8.5%) | 3,147 (100%) |
| Female | 1,842 (54.9%) | 709 (21.1%) | 649 (19.3%) | 156 (4.6%) | 3,356 (100%) |
| Race/ethnicity | |||||
| European | 1,909 (49.3%) | 746 (19.3%) | 944 (24.4%) | 270 (7.0%) | 3,869 (100%) |
| African | 1,070 (67.6%) | 291 (18.4%) | 141 (8.9%) | 82 (5.2%) | 1,584 (100%) |
| Hispanic | 388 (52.2%) | 131 (17.6%) | 171 (23.0%) | 53 (7.1%) | 743 (100%) |
| Grade | |||||
| 7th | 780 (79.7%) | 122 (12.5%) | 53 (5.4%) | 24 (2.5%) | 979 (100%) |
| 8th | 668 (67.3%) | 168 (16.9%) | 122 (12.3%) | 34 (3.4%) | 992 (100%) |
| 9th | 625 (56.5%) | 218 (19.7%) | 202 (18.2%) | 62 (5.6%) | 1,107 (100%) |
| 10th | 551 (48.2%) | 244 (21.3%) | 278 (24.3%) | 71 (6.2%) | 1,144 (100%) |
| 11th | 464 (41.4%) | 235 (20.9%) | 322 (28.7%) | 101 (9.0%) | 1,122 (100%) |
| 12th | 367 (37.0%) | 224 (22.6%) | 293 (29.5%) | 109 (11.0%) | 993 (100%) |
Discussion
These results support the use of a progressive elaboration approach for the discovery of latent classes based on categorical indicator measures. The analyses suggest that adolescents may be classified into four latent classes or types based on their patterns of involvement in different alcohol use behaviors. These classes include never or non–current drinkers, low-intake drinkers, non–problem drinkers who occasionally drank 5 or more drinks and/or got drunk, and problem drinkers who engaged weekly or more often in high-volume drinking and becoming intoxicated and who got into trouble because of their drinking. These classes of adolescents display the full gamut of alcohol involvement and exhibit both homogeneity (within-group similarity) and latent class separation (differing profiles between classes), the hallmarks of a successful typology.
The four-class solution from the progressive elaboration was not only more parsimonious than the LCA based on the original ordinal responses to the alcohol behaviors (which found 10 classes), but it also demonstrated a higher entropy R2. Although the four-class model and the initial dichotomous LCA achieved similar entropy R2s, there were important qualitative differences. Both solutions identified never or non–current drinkers, non–problem drinkers, and problem drinkers. However, the progressive elaboration strategy split the non–problem drinker class into drinkers who drank less per occasion and did not get drunk or experience negative consequences (low-intake drinkers) and drinkers whose usual intake per occasion was greater and who occasionally got drunk and consumed five or more drinks but were unlikely to experience negative consequences. The characteristic alcohol involvement of the problem-drinker class was also much more intense in the four-class model.
In addition to cross-validating the latent classes of adolescent drinking in the second half of the sample and in the Wave II data, the present analyses validated the classes by showing that adolescents in the classes differed systematically on measures of psychosocial risk for problem behavior. As the types exhibited greater involvement with alcohol, their means on the personality, social, and behavior variables increased or decreased as predicted. These results demonstrated the construct validity of the latent classes uncovered here.
The major differences between the present results and the earlier typology created by Rachal et al. (1976) and later used by Zucker and Harford (1983) and by Barnes and Welte (1986) are that the present latent class solution is not only more parsimonious, with four latent classes instead of six types, but it also includes high-volume drinking, drunkenness, and alcohol problems, which were not within the compass of the earlier typology.
Previous LCAs of national samples of adolescents (e.g., Dauber et al., 2009; Lanza et al., 2007; Percy & Iwaniec, 2007) similarly discovered four or five latent classes of adolescent alcohol involvement. Despite their use of somewhat different alcohol use questions, a priori cut points, and LCA software, there is some similarity among the resulting latent classes, with the exception being that the present empirical cut points captured more extreme patterns of use among problem drinkers.
Alcohol involvement typologies such as the one described here should be useful for longitudinal monitoring of trends in different patterns of adolescent alcohol use over time, particularly those patterns predictive of problematic use, rather than focusing on trends in single alcohol use behaviors such as high-volume drinking or drunkenness. Such a typology of classes of adolescent alcohol involvement is particularly useful for longitudinal analyses focused on the identification of the antecedent risk factors for transitions in involvement from one class or pattern of alcohol use to another. This approach has been illustrated in the earlier research using latent transition analysis by Guo et al. (2000) and Lanza and Collins (2008).
It would be important in future research to determine the extent to which the present typology of adolescent drinking needs to be modified for the description of alcohol involvement in younger populations, such as children and preadolescents. It is possible that additional classes would need to be added on the lower end to capture the large number of children whose only alcohol exposure is in the form of sips or tastes of alcohol (see Donovan & Molina, 2013), and that there would be few problem drinkers. It would similarly be important to determine whether late adolescents and young adults display the same patterns of alcohol use and problems, possibly using AddHealth data from Waves III and IV.
The present findings should be considered in light of the following limitations. First, the proportion of adolescents in each of the latent classes may not reflect the current prevalence of these classes because these national sample data were collected in 1994–1995. It should be realized, however, that the major emphasis in this study was not on the prevalence of each type but rather on their number and composition. Second, the alcohol use behaviors included as indicators for the LCA did not assess symptoms of impairment, interference in role performance, or physical withdrawal, and therefore could not identify latent classes reflecting alcohol abuse or alcohol dependence as defined by Diagnostic and Statistical Manual of Mental Disorders, Fifth Edition (American Psychiatric Association, 2013), criteria. Adolescents exhibiting such alcohol use disorders, however, were likely assigned to the latent class of problem drinkers identified here.
Third, the present analyses used the BIC statistic to help identify which of several cut points on the indicator measures performed better in classifying the adolescents. This is a nonstandard use of the statistic that is most often used to determine the appropriate number of latent classes in a data set (Nylund et al., 2007). Use of the BIC statistic in conjunction with the requirement for a high conditional probability for each category of the indicator in one or more of the classes, however, may offset this limitation. Further exploration is needed to determine the best index for use in deciding empirically where to insert multiple cut points on categorical indicators in latent class modeling.
These limitations are mitigated to some extent by the fact that the analyses were based on a large representative national sample of adolescents and confirmed in the second wave of that national survey. Future analyses are planned to determine whether the latent classes of adolescent alcohol involvement found here replicate in other community and national data sets that used similar alcohol behavior questions (Costa et al., 1995; Donovan & Molina, 2013; Donovan et al., 1999; Jessor & Jessor, 1977).
Despite the limitations mentioned above, the results suggest that the variety of patterns of adolescent involvement in alcohol use behaviors can be described by just four latent classes and illustrate the utility of the progressive elaboration strategy for moving beyond dichotomous indicators in latent class models of adolescent alcohol involvement.
Footnotes
This research was supported by National Institute on Alcohol Abuse and Alcoholism Grant No. AA-015575. This research is based on data from the AddHealth project, a program designed by J. Richard Udry (principal investigator) and Peter Bearman and funded by Grant P01-HD31921 from the National Institute of Child Health and Human Development to the Carolina Population Center, University of North Carolina at Chapel Hill, with cooperative funding participation by the National Cancer Institute; the National Institute on Alcohol Abuse and Alcoholism; the National Institute on Deafness and Other Communication Disorders; the National Institute on Drug Abuse; the National Institute of General Medical Sciences; the National Institute of Mental Health; the National Institute of Nursing Research; the Office of AIDS Research, National Institutes of Health (NIH); the Office of Behavior and Social Science Research, NIH; the Office of the Director, NIH; the Office of Research on Women’s Health, NIH; the Office of Population Affairs, Department of Health and Human Services (DHHS); the National Center for Health Statistics, Centers for Disease Control and Prevention, DHHS; the Office of Minority Health, Office of Public Health and Science, DHHS; the Office of the Assistant Secretary for Planning and Evaluation, DHHS; and the National Science Foundation. The public use data files for the study are distributed by the Inter-University Consortium for Political and Social Research of the University of Michigan: http://www.icpsr.umich.edu/icpsrweb/ICPSR/studies/21600?archive=ICPSR&q=21600.
References
- American Psychiatric Association. Diagnostic and statistical manual of mental disorders. 5th ed. Arlington, VA: Author; 2013. [Google Scholar]
- Asparouhov T. Wald test of mean equality for potential latent class predictors in mixture modeling. Los Angeles, CA: Muthén & Muthén; 2010. Retrieved from http://www.statmodel.com/download/meantest2.pdf. [Google Scholar]
- Asparouhov T., Muthén B. Auxiliary variables in mixture modeling: Three-step approaches using Mplus. Structural Equation Modeling: A Multidisciplinary Journal. 2014;21:329–341. [Google Scholar]
- Auerbach K. J., Collins L. M. A multidimensional developmental model of alcohol use during emerging adulthood. Journal of Studies on Alcohol. 2006;67:917–925. doi: 10.15288/jsa.2006.67.917. [DOI] [PubMed] [Google Scholar]
- Barnes G. M., Welte J. W. Patterns and predictors of alcohol use among 7–12th grade students in New York State. Journal of Studies on Alcohol. 1986;47:53–61. doi: 10.15288/jsa.1986.47.53. [DOI] [PubMed] [Google Scholar]
- Bergman L. R. The application of a person-oriented approach: Types and clusters. In: Bergman L. R., Cairns R. B., Nysted L., editors. Developmental science and the holistic approach. Mahwah, NJ: Erlbaum; 2000. pp. 137–154. [Google Scholar]
- Collins L. M., Lanza S. T. Latent class and latent transition analysis with applications in the social, behavioral and health sciences. Hoboken, NJ: Wiley; 2010. [Google Scholar]
- Costa F. M., Jessor R., Donovan J. E., Fortenberry J. D. Early initiation of sexual intercourse: The influence of psychosocial unconventionality. Journal of Research on Adolescence. 1995;5:93–121. [Google Scholar]
- Cranford J. A., McCabe S. E., Boyd C. J. A new measure of binge drinking: Prevalence and correlates in a probability sample of undergraduates. Alcoholism: Clinical and Experimental Research. 2006;30:1896–1905. doi: 10.1111/j.1530-0277.2006.00234.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Amico E. J., Metrik J., McCarthy D. M., Frissell K. C., Appelbaum M., Brown S. A. Progression into and out of binge drinking among high school students. Psychology of Addictive Behaviors. 2001;15:341–349. [PubMed] [Google Scholar]
- Dauber S., Hogue A., Paulson J. F., Leiferman J. A. Typologies of alcohol use in White and African American adolescent girls. Substance Use & Misuse. 2009;44:1121–1141. doi: 10.1080/10826080802494727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donovan J. E.2004Adolescent alcohol initiation: A review of psychosocial risk factors Journal of Adolescent Health 35529e7–529.e18 [DOI] [PubMed] [Google Scholar]
- Donovan J. E., Jessor R., Costa F. M. Adolescent problem drinking: Stability of psychosocial and behavioral correlates across a generation. Journal of Studies on Alcohol. 1999;60:352–361. doi: 10.15288/jsa.1999.60.352. [DOI] [PubMed] [Google Scholar]
- Donovan J. E., Molina B. S. G. Types of alcohol use experience from childhood through adolescence. Journal of Adolescent Health. 2013;53:453–459. doi: 10.1016/j.jadohealth.2013.03.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fergusson D. M., Horwood L. J., Lynskey M. T. The prevalence and risk factors associated with abusive or hazardous alcohol consumption in 16-year-olds. Addiction. 1995;90:935–946. doi: 10.1046/j.1360-0443.1995.9079356.x. [DOI] [PubMed] [Google Scholar]
- Finch W. H., Bronk K. C. Conducting confirmatory latent class analysis using Mplus. Structural Equation Modeling: A Multidisciplinary Journal. 2011;18:132–151. [Google Scholar]
- Guo J., Collins L. M., Hill K. G., Hawkins J. D. Developmental pathways to alcohol abuse and dependence in young adulthood. Journal of Studies on Alcohol. 2000;61:799–808. doi: 10.15288/jsa.2000.61.799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris K. M. The Add Health Study: Design and accomplishments. 2013 Retrieved from http://www.cpc.unc.edu/projects/addhealth/data/guides/
- Harris K. M., Udry J. R. National Longitudinal Study of Adolescent to Adult Health (Add Health), 1994-2008 [Public Use] (ICPSR21600) Chapel Hill, NC: Carolina Population Center, University of North Carolina-Chapel Hill/Ann Arbor, MI: Inter-University Consortium for Political and Social Research [distributors]; 2014. Retrieved from http://doi.org/10.3886/ICPSR21600.v15. [Google Scholar]
- Jessor R., Donovan J. E., Costa F. M. Health Behavior Questionnaire. Boulder, CO: Institute of Behavioral Science; 1992. University of Colorado. Retrieved from http://www.colorado.edu/ibs/jessor/questionnaires. [Google Scholar]
- Jessor R., Jessor S. L. Problem behavior and psychosocial development: A longitudinal study of youth. New York, NY: Academic Press; 1977. [Google Scholar]
- Johnston L. D., O’Malley P. M., Bachman J. G. National survey results on drug use from the Monitoring The Future Study, 1975-1995: Volume 1, Secondary School Students (NIH Publication No. 96-4139) Rockville, MD: National Institute on Drug Abuse; 1996. [Google Scholar]
- Lanza S. T., Collins L. M. A new SAS procedure for latent transition analysis: Transitions in dating and sexual risk behavior. Developmental Psychology. 2008;44:446–456. doi: 10.1037/0012-1649.44.2.446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanza S. T., Collins L. M., Lemmon D. R., Schafer J. L. PROC LCA: A SAS procedure for latent class analysis. Structural Equation Modeling: A Multidisciplinary Journal. 2007;14:671–694. doi: 10.1080/10705510701575602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanza S. T., Flaherty B. P., Collins L. M. Latent class and latent transition analysis. In: Schinka J. A., Velicer W. F., editors. Handbook of psychology: Vol. 2. Research Methods in Psychology. Hoboken, NJ: Wiley; 2003. pp. 663–685. [Google Scholar]
- Lee M. R., Chassin L., Villalta I. K. Maturing out of alcohol involvement: Transitions in latent drinking statuses from late adolescence to adulthood. Development and Psychopathology. 2013;25:1137–1153. doi: 10.1017/S0954579413000424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthén L. K., Muthén B. O. Mplus user’s guide: Statistical analysis with latent variables. 7th ed. Los Angeles, CA: Authors; 2012. [Google Scholar]
- Nylund K. L., Asparouhov T., Muthén B. O. Deciding on the number of classes in latent class analysis and growth mixture modeling: A Monte Carlo simulation study. Structural Equation Modeling: A Multidisciplinary Journal. 2007;14:535–569. [Google Scholar]
- Percy A., Iwaniec D. The validity of a latent class typology of adolescent drinking patterns. Irish Journal of Psychological Medicine. 2007;24:13–18. doi: 10.1017/S0790966700010089. [DOI] [PubMed] [Google Scholar]
- Rachal J. V., Hubbard R. L., Williams J. R., Tuchfeld B. S. Drinking levels and problem drinking among junior and senior highschool students. Journal of Studies on Alcohol. 1976;37:1751–1761. doi: 10.15288/jsa.1976.37.1751. [DOI] [PubMed] [Google Scholar]
- Reboussin B. A., Song E.-Y., Shrestha A., Lohman K. K., Wolfson M. A latent class analysis of underage problem drinking: Evidence from a community sample of 16-20 year olds. Drug and Alcohol Dependence. 2006;83:199–209. doi: 10.1016/j.drugalcdep.2005.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reifman A., Barnes G. M., Dintcheff B. A., Farrell M. P., Uhteg L. Parental and peer influences on the onset of heavier drinking among adolescents. Journal of Studies on Alcohol. 1998;59:311–317. doi: 10.15288/jsa.1998.59.311. [DOI] [PubMed] [Google Scholar]
- Resnick M. D., Bearman P. S., Blum R. W., Bauman K. E., Harris K. M., Jones J., Udry J. R. Protecting adolescents from harm: Findings from the National Longitudinal Study on Adolescent Health. Journal of the American Medical Association. 1997;278:823–832. doi: 10.1001/jama.278.10.823. [DOI] [PubMed] [Google Scholar]
- Vermunt J. K., Magidson J. Latent GOLD 4.0 user’s guide. Belmont, MA: Statistical Innovations, Inc; 2005. [Google Scholar]
- Wells J. E., Horwood L. J., Fergusson D. M. Drinking patterns in mid-adolescence and psychosocial outcomes in late adolescence and early adulthood. Addiction. 2004;99:1529–1541. doi: 10.1111/j.1360-0443.2004.00918.x. [DOI] [PubMed] [Google Scholar]
- Windle M. An alcohol involvement typology for adolescents: Convergent validity and longitudinal stability. Journal of Studies on Alcohol. 1996;57:627–637. doi: 10.15288/jsa.1996.57.627. [DOI] [PubMed] [Google Scholar]
- Zucker R. A., Harford T. C. National study of the demography of adolescent drinking practices in 1980. Journal of Studies on Alcohol. 1983;44:974–985. doi: 10.15288/jsa.1983.44.974. [DOI] [PubMed] [Google Scholar]


