Stochastic dynamic causal modeling of working memory connections in cocaine dependence

Abstract

Although reduced working memory brain activation has been reported in several brain regions of cocaine‐dependent subjects compared with controls, very little is known about whether there is altered connectivity of working memory pathways in cocaine dependence. This study addresses this issue by using functional magnetic resonance imaging‐based stochastic dynamic causal modeling (DCM) analysis to study the effective connectivity of 19 cocaine‐dependent subjects and 14 healthy controls while performing a working memory task. Stochastic DCM is an advanced method that has recently been implemented in SPM8 that can obtain improved estimates, relative to deterministic DCM, of hidden neuronal causes before convolution with the hemodynamic response. Thus, stochastic DCM may be less influenced by the confounding effects of variations in blood oxygen level‐dependent response caused by disease or drugs. Based on the significant regional activation common to both groups and consistent with previous working memory activation studies, seven regions of interest were chosen as nodes for DCM analyses. Bayesian family level inference, Bayesian model selection analyses, and Bayesian model averaging (BMA) were conducted. BMA showed that the cocaine‐dependent subjects had large differences compared with the control subjects in the strengths of prefrontal–striatal modulatory (B matrix) DCM parameters. These findings are consistent with altered cortical–striatal networks that may be related to reduced dopamine function in cocaine dependence. As far as we are aware, this is the first between‐group DCM study using stochastic methodology. Hum Brain Mapp 35:760–778, 2014. © 2012 Wiley Periodicals, Inc.

INTRODUCTION

Functional magnetic resonance imaging (fMRI) univariate analysis of regional activation is valuable for understanding the regional neural substrates associated with cognitive functions. However, this method has a potential inherent disadvantage when it is used for studying disease, i.e., difficulty in interpreting the results because of significant variations in blood oxygen level‐dependent (BOLD) response caused by the disease [Buxton, 2009]. Changes in the BOLD signal could be confounded by the possible disruption by disease or drugs on neurovascular coupling and/or hemodynamic response [Iannetti and Wise, 2007]. Correspondingly, a previous study [Choi et al., 2006] has shown that the direct effects of dopamine on the vasculature need to be considered when measuring the hemodynamic coupling associated with dopaminergic drugs. This is especially relevant in cocaine dependence, for which studies have suggested is a disorder associated with reduced dopamine neurotransmission in the brain [Volkow et al., 2007, 2009].

Interregional connectivity is generally quantified by using functional connectivity or effective connectivity analysis techniques [Friston, 1995a]. Functional connectivity refers to the correlations between spatially remote neurophysiological events [Friston, 1995a]. Unlike functional connectivity, effective connectivity measures the causal effect that one region's activity has on that of another region [Friston, 1995a]. Dynamic causal modeling [DCM; Friston et al., 2003; Li et al., 2011a) can explicitly evaluate the directional modulation effects of contextual experimental conditions on effective connectivity [Stephan et al., 2007a]. Furthermore, effective connectivity in DCM is modeled at the underlying neuronal level rather than the observed hemodynamic level [Friston et al., 2003; Stephan et al., 2007a]. In addition, DCM may reduce the potential hemodynamic confounding effects on effective connectivity through jointly optimizing the underlying neuronal parameters of the effective connectivity and the regionally specific hemodynamic response functions [Stephan et al., 2007b]. DCM has been successfully used to study the effective connectivity of several diseases [see Seghier et al., 2010 for review].

An advance in DCM technique that has recently been implemented in SPM8, stochastic DCM [Daunizeau et al., 2009; Li et al., 2011a), is an extension of deterministic DCM, which seeks to improve model estimation by modeling random fluctuations (or noise variance) and hidden neuronal causes in the differential equations of the neuronal states [Li et al., 2011a]. Stochastic DCM can obtain improved estimates, relative to deterministic DCM, of hidden neuronal causes before convolution with the hemodynamic response [Li et al., 2011a]. Therefore, the effective connectivity estimated by stochastic DCM may be less influenced by the confounding effects of significant variations in BOLD response caused by disease or drugs.

Cocaine dependence is associated with several cognitive deficits, including working memory [Ardila et al., 1991; Beveridge et al., 2008; George et al., 2008; Jovanovski et al., 2005; Sofuoglu, 2010]. Current functional neuroimaging research on cognitive deficits in substance dependence has focused on identifying regional neural substrates mediating the impaired cognitive functions [see Aron and Paulus, 2007; Lundqvist, 2010 for review). Several research groups have used fMRI to study regional brain activation, finding differences in BOLD activation between cocaine‐dependent subjects and controls while performing a working memory task. For example, using an n‐back working memory task, Tomasi et al. 2011 found lower working memory load‐dependent activation in the prefrontal and parietal cortices in cocaine abusers compared with controls. Another study using an n‐back task reported that, relative to controls, cocaine‐dependent subjects showed reduced activation in the right inferior parietal cortex [Bustamante et al., 2011]. Using a working memory task with variable load, Moeller et al. 2010 found that cocaine‐dependent subjects showed significantly lower working memory load‐dependent activation in several cortical and subcortical regions compared with normal control subjects, including caudate nucleus, middle, superior, and inferior frontal gyri, and thalamus.

Accumulated findings from human and animal studies have led to models for interpreting the neural basis of cognitive functions as interactions between functionally related brain regions [Collette and Van der Linden, 2002; D'Esposito, 2007; Funahashi, 2006; Fuster, 2006; Vuilleumier and Driver, 2007]. Recent studies have shown that interregional connectivity methods are more sensitive to the presence or severity of diseases and/or treatment effects than the traditional univariate analysis of regional activations [reviewed by Rowe, 2010].

Several studies [Camchong et al., 2011; Gu et al., 2010; Hanlon et al., 2011; Kelly et al., 2011; Li et al., 2011b; Tomasi et al., 2010; Wilcox et al., 2011] have used functional connectivity to study cocaine dependence. For example, Tomasi et al. 2004 used a drug‐word fMRI paradigm and found that, relative to controls, cocaine abusers had lower functional connectivity of midbrain with thalamus, cerebellum, and rostral cingulate. In addition, the lower functional connectivity was associated with less activation in thalamus and cerebellum and greater deactivation in rostral cingulate [Tomasi et al., 2010]. These studies demonstrated abnormal functional connectivity in cocaine users during tasks [Hanlon et al., 2011; Li et al., 2011b; Tomasi et al., 2010] or during resting state [Camchong et al., 2011; Gu et al., 2010; Kelly et al., 2011; Li et al., 2011b; Wilcox et al., 2011]. In addition, other studies using diffusion tensor imaging found reduced white matter integrity in the anterior and posterior corpus callosum in cocaine‐dependent subjects compared with controls [Ma et al., 2009; Moeller et al., 2005, 2010]. The findings of these studies suggested that transcallosal connections, including those that are important for working memory, may be compromised in cocaine‐dependent subjects.

Based on these findings in the context of interregional connectivity models for working memory [e.g., Fuster, 2006, 2008, 2010; Ma et al., 2012], and the findings that cocaine dependence is associated with reduced dopamine neurotransmission in the brain [Volkow et al., 2007, 2009], we hypothesized that the effective connectivity of brain regions involved in working memory is altered in cocaine‐dependent subjects. To test this hypothesis, we used stochastic DCM to measure the differences in fMRI‐based effective connectivity of the working memory system between nineteen cocaine‐dependent subjects and fourteen normal control subjects while they performed a working memory task with variable loads. As far as we are aware, this is the first between‐group DCM study using stochastic methodology.

MATERIALS AND METHODS

Subjects

This study was approved by the institutional review board at the University of Texas Health Science Center at Houston and was performed in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki). Subjects with current cocaine dependence and nondrug‐using normal controls were recruited through advertisements for research volunteers. Informed consent was obtained from all subjects.

All subjects were screened for psychiatric disorders using the Structured Clinical Interview for Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition [DSM‐IV; First et al., 1996]. All subjects underwent physical examination, and their medical history was obtained. Subjects also underwent the Addiction Severity Index [McLellan et al., 1992] to document possible lifetime drug and alcohol use. All female subjects underwent a urine pregnancy test immediately before MRI scanning. Each subject's urine was screened for tetrahydrocannabinol, opiates, cocaine (benzoylecgonine), amphetamines, and benzodiazepines using an immunochromatographic assay (Syva Company, Dearfield, IL), and each subject was screened for alcohol using an Intoximeter Alcosensor III breathalyzer (Intoximeters, St. Louis, MO) immediately before MRI scanning.

After meeting the inclusion and exclusion criteria, a total of 19 cocaine‐dependent subjects (cocaine group) and 14 control subjects (control group) were included in this study, out of 71 subjects (28 controls and 43 cocaine subjects) who were initially screened. Among the 33 subjects in this study, eight cocaine subjects and six controls had been previously studied in Moeller et al. 2010, which was purely an fMRI activation study that did not perform any DCM or other connectivity analysis. Among the 14 control subjects in this study, 13 of them had been used in the DCM study by Ma et al. 2010, which examined effective connectivity in normals only and did not involve any group comparisons. None of the cocaine subjects in this study had ever been studied previously using DCM or any other functional or effective connectivity analysis. This study is the first time that our group has compared fMRI‐based connectivity in cocaine users with normal controls. See Supporting Information for the inclusion and exclusion criteria, and the details regarding the subjects who were excluded.

IMT/DMT fMRI Protocol

The immediate memory task (IMT) and delayed memory task (DMT) working memory protocol has been described in detail in Moeller et al. 2010 and the references therein. In DMT, the target and probe stimuli are separated by distracter stimuli, consisting of strings of zeros, and the memory delay between the end of the target stimulus and beginning of the probe stimulus is 3.5 s. In IMT, there are no distracter stimuli, and thus the memory delay is 0.5 s. The A′ score [Donaldson, 1992] is used as an accuracy measure. The IMT/DMT fMRI protocol is a block design, and the duration of each block is 42.5 s. There are 12 blocks alternating between IMT and DMT within each run. Each stimulus string can be three, five, or seven digits in length, which is held constant within a block. In detail, the blocks during each run were: three‐digit‐IMT, three‐digit‐DMT, five‐digit‐IMT, five‐digit‐DMT, seven‐digit‐IMT, and seven‐digit‐DMT; which were then repeated during the same run, in which the order of the three, five, and seven digits was counterbalanced across runs and subjects. In addition there was a 20‐s rest period at the beginning of the run, and a 10‐s rest period between each of the above blocks.

Data Acquisition

MRI data, including three‐dimensional spoiled gradient recalled echo (3D‐SPGR), fMRI, and fluid‐attenuated inversion recovery sequences were acquired on a Philips 3.0 T Intera system with an eight‐channel receive head coil (Philips Medical Systems, Best, Netherlands). Single shot spin‐echo echo planar imaging (EPI) was used for acquiring the fMRI data. The spin echo EPI sequence eliminates signal losses caused by through‐slice dephasing in medial orbitofrontal cortex [Kruger et al., 2001; Norris et al., 2002; Wang et al., 2004]. The fMRI acquisition parameters were: SENSE factor = 2.0, repetition time = 2212 ms, echo time = 75 ms, flip angle = 90°, number of axial slices = 22, field‐of‐view = 240 mm × 240 mm, in‐plane resolution 3.75 mm × 3.75 mm, slice thickness = 3.75 mm, gap = 1.25 mm, repetitions = 294 after 10 dummy acquisitions, and total scan duration = 10 min 47 s. Each subject had two runs of fMRI scans.

Stimulus presentation and recording of behavioral IMT/DMT performance data during fMRI scanning were managed through the Integrated Functional Imaging System‐Stand Alone (IFIS‐SA, Invivo Corporation, Orlando, FL) fMRI system or the Eloquence (an update of IFIS‐SA) fMRI System (Invivo Corporation, Orlando, FL). The software controlling the task was exactly the same in both systems. Using the two systems, we ascertained that each subject could see the visual stimuli adequately on the screen before the start of the fMRI scan. Fourteen IFIS subjects and 19 Eloquence subjects were included for final analysis.

fMRI Preprocessing

Preprocessing of the fMRI data was performed using AFNI software [Cox, 1996] (http://afni.nimh.nih.gov/afni/) and Statistical Parametric Mapping 8 (SPM8) software (http://www.fil.ion.ucl.ac.uk/spm/) from the Wellcome Department of Cognitive Neurology, London, UK, implemented in MATLAB 7.1 (MathWorks, Sherborn, MA). Preprocessing consisted of examination for artifacts using AFNI, and slice‐timing correction, realignment, coregistration, normalization, and smoothing using standard SPM8 modules. See Supporting Information for details of the fMRI preprocessing.

Univariate fMRI Statistical Parametric Mapping Analysis

First‐level univariate statistical analysis of the fMRI data was conducted using SPM8. The IMT and DMT blocks for each digit condition were modeled by boxcar functions convolved with the SPM8 canonical hemodynamic response function. The parameters for each condition were estimated using the General Linear Model [Friston, 1995b] at each voxel without global normalization. The fMRI time series was high‐pass filtered with an optimized cut‐off period of 330 s determined by the Fourier transformation of each condition's time model. Activation for each digit condition was defined as the contrast of DMT minus IMT parameter estimates (“DI”) for that digit condition (i.e., DI3, DI5, and DI7 for three digits, five digits, and seven digit conditions, respectively). In addition, the following contrast images were defined to determine the interaction effects between the memory delay (IMT and DMT) and the digit load (three digits, five digits, and seven digits): DI5 minus DI3, DI3 minus DI5, DI7 minus DI3, DI3 minus DI7, DI7 minus DI5, and DI5 minus DI7. The following contrast image was defined to determine the main effects of memory delay (pooled across three digits, five digits, and seven digits): combined DI3, DI5, and DI7. The summary contrast images were output for each subject for entry into the second‐level analysis.

Because DCM in patients focuses on the characterization of abnormal connectivity in a common network of regions in which the models must have identical nodes, Seghier et al. 1995 recommended that only commonly activated regions in patients and controls should be included as nodes in DCM [Seghier et al., 2010]. According to the practical steps in a typical DCM analysis suggested by Seghier et al. [1995; Fig. 1], random effects group analysis can be used to determine the DCM nodes. Consistent with Seghier et al.'s recommendation and previous DCM studies [e.g., Bitan et al., 2005; Deserno et al., 2012; Dima et al., 2009; DiQuattro and Geng, 2011; Wang et al., 2011], we used random effects [Holmes and Friston, 1998] group analysis to determine the regions that significantly activated across both groups in this study, along with conservative correction for multiple voxelwise comparisons, to provide a valid generalization of the results to the populations from which the subjects were sampled. In a relatively large cognitive fMRI‐based DCM study such as this (14 controls and 19 patients), there is no guarantee that each individual subject activates exactly the same region in common with all the other subjects, unless extremely low thresholds are used ad hoc in some subjects without adequate protection against Type I statistical error due to multiple voxelwise comparisons. In our preliminary analysis we found this to be the case even when using SPM8 Small Volume Correction (data available on request). In addition (see Stochastic DCM section), the principal eigenvariate was extracted from the volume of interest and used as a summary of the time series. This procedure does not assume homogenous responses within the volume of interest, and uses the temporal covariance of voxels in the volume of interest to find coherent spatial modes of activation [Friston et al., 2006]. Furthermore (see Stochastic DCM section), individual differences between subjects in DCM parameters can be captured by the Bayesian model averaging (BMA) procedure which was conducted in this study. For each type of summary contrast image, the group difference and the main effects across the means for both groups were determined with the default nonsphericity correction for unequal variance between groups.

Figure 1.

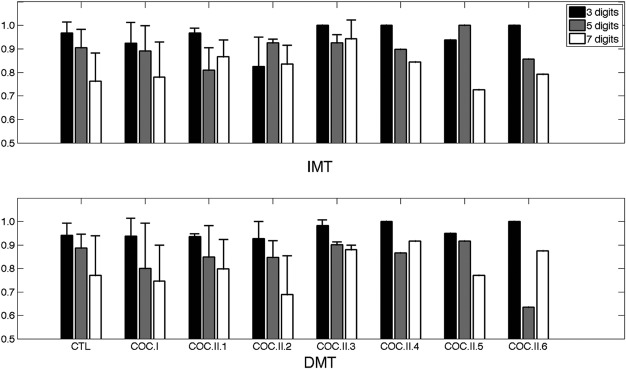
Plots showing the values of the mean (bar) and standard deviation (error bar) of the A′ accuracy scores for the control group, Cocaine Groups I and II and each of the subgroups within Cocaine Group II. Error bars are not shown for Cocaine subgroups II.4, II.5, and II.6 because there was only one subject in each of those subgroups. The top panel is for the IMT (shorter memory delay) condition, and the bottom panel is for the DMT (longer memory delay) condition. CTL = control and COC = cocaine.

Statistical significance of the univariate fMRI analysis was defined to be false discovery rate (FDR) corrected cluster P less than 0.05. The cluster‐defining threshold was voxel t = 2.4. Approximate anatomical labels for regions of activation were determined using the Anatomical Automatic Labeling [Tzourio‐Mazoyer et al., 2002] toolbox for SPM.

Stochastic DCM

Stochastic DCM [Daunizeau et al., 2009; Li et al., 2011a], as implemented in DCM10 (SPM8 revision 4010), was used for effective connectivity analysis. Stochastic DCM is an extension of deterministic DCM, which seeks to improve model estimation by modeling random fluctuations (or noise variance) and hidden neuronal causes in the differential equations of the neuronal states [Li et al., 2011a]. In stochastic DCM for fMRI, the dynamics of the neural states underlying the BOLD response are modeled by a differential state equation that describes how the neural states change based on the current neural states and the exogenous inputs [Friston et al., 2003]. In addition, random fluctuations [Li et al., 2011a] are modeled in stochastic DCM, which are not modeled in deterministic DCM. In this differential equation, the interactions between the neural states are termed as endogenous connections and quantified by A matrix parameters. The contextual experimental conditions can bilinearly modulate the connections as quantified by B matrix parameters, or affect the nodes of DCM as driving inputs as quantified by C matrix parameters [Friston et al., 2003; Stephan et al., 2007a]. If there are connections that are gated by some regions in the system, the gating effects (nonlinear) can be modeled by D matrix parameters [Stephan et al., 2008]. The random differential equation treats the driving inputs as priors on the hidden neuronal causes because the fluctuations induce uncertainty about the way that the driving inputs affect neuronal activity [Li et al., 2011a]. Li et al. 2003 have demonstrated that stochastic DCM can show improvement in parameter estimation over deterministic DCM. More recently, Daunizeau et al. 2012 have validated stochastic DCM and shown that stochastic DCM is superior over deterministic DCM in both model structure inference and model parameter inference. We used bilinear stochastic DCM in this study (the nonlinear D‐matrix option was not applied).

Regions of interest

The regions of interest (ROIs) were chosen based on the following criteria: (1) these regions showed significant activation in the univariate SPM second‐level analysis of the main effect of memory delay for the combined groups (see Results section); (2) previous meta‐analyses of neuroimaging studies have shown that these regions activate consistently during verbal working memory tasks [Owen et al., 2005; Wager and Smith, 2003]; (3) these regions have been implicated in working memory processes, e.g., encoding [Woodward et al., 2006], storage [Hartley and Speer, 2000], maintenance [Hartley and Speer, 2000; Wager and Smith, 2003; Woodward et al., 2006], and executive control [Hartley and Speer, 2000]. Based on these criteria, the ROIs for the DCM analyses in this study were: (1) left (L) inferior frontal cortex (IFC), (2) L middle frontal gyrus (MFG) (i.e., representing left dorsolateral prefrontal cortex), (3) L posterior parietal cortex (PPC), (4) right (R) PPC, (5) combined left and right (LR) supplementary motor area (SMA), (6) L striatum (STR), and (7) R STR. The LR SMA was treated as a single ROI because the detected activation in SMA contiguously spanned both L and R sides combined.

Volumes of interest and time series extraction

We followed the method of constructing the volumes of interest that was described in Ma et al. 2010. The significant group level activation clusters formed the volumes of interest, which were further constrained [Stephan and Friston, 2010] to be within the boundaries of the aforementioned seven ROIs, as defined by anatomical atlases. The atlas‐derived binary masks of the regions were obtained from the Anatomical Automatic Labeling atlas [Tzourio‐Mazoyer et al., 2002] as implemented in the WFU (Wake Forest University) PickAtlas SPM toolbox [Maldjian et al., 2003, 2002]. The binary mask of IFC was the set‐theoretic union of the atlas‐based binary masks of inferior frontal gyrus pars opercularis and inferior frontal gyrus pars triangularis. The binary mask of PPC was the union of the atlas‐based binary masks of superior parietal lobule and inferior parietal lobule. The binary mask of STR was the union of the atlas‐based binary masks of caudate, putamen, and nucleus accumbens. The atlas‐derived binary mask of the nucleus accumbens was obtained from the Harvard‐Oxford Subcortical Structural atlas (http://www.cma.mgh.harvard.edu/) as provided in the FSL software [Smith et al., 2004; Woolrich et al., 2009]. Each volume of interest was obtained by the intersection of the atlas‐based binary masks with the significant activation clusters in common for both groups, as determined by the SPM second‐level random effects univariate analysis. After the volumes of interest have been determined, it is necessary to obtain a summary of their activity. The principal eigenvariate of the volume of interest (the first principal component of the local multivariate time series over all voxels in the volume of interest) is usually used as such a summary for fMRI‐based DCM analysis [Stephan and Friston, 2010]. Different from the mean, the principal eigenvariate does not assume homogenous responses within the volume of interest and uses the temporal covariance of voxels in the volume of interest to find coherent spatial modes of activation [Friston et al., 2006]. Thus the principal eigenvariate avoids the cancellation of positive and negative responses in extracting a summary time series across voxels [Friston et al., 2006; Stephan and Friston, 2010]. For each subject, the principal eigenvariates were obtained from all volumes of interest. Each principal eigenvariate was adjusted for the F‐contrast of effects of interest before it was input into DCM for model estimation [Stephan and Friston, 2010]. In SPM, the F‐contrast of effects of interest includes each parameter corresponding to each condition (except for the constant representing the mean). The same volumes of interest were used for all subjects.

Endogenous connections

Full endogenous connections (the DCM “A” matrix) were specified between all the ROIs (Supporting Information Fig. 1). In other words, each ROI connected all other ROIs. Thus, there were 42 endogenous connections, and they were used in all subsequent DCM analyses.

DCM structure inference at group level

In the studies comparing DCMs between groups that were reviewed by Seghier et al. 1995, one study [Rocca et al., 2009] located the optimal DCM in controls and used this DCM in comparison to patients. The majority of studies in that review conducted model inference independently in patients and controls, based on the same set of alternative models [e.g., Allen et al., 2010; Almeida et al., 2009; Rowe et al., 2010; Schlosser et al., 2008, 2007b; Sonty et al., 2007]. In addition, Seghier et al. 1995 suggested that Bayesian model comparison can be conducted separately on patients and controls to identify the best family of models in patients and controls. In this study, consistent with Seghier et al.'s recommendation, inference on DCM structure was conducted separately in both controls and cocaine subjects. If group differences in DCM structure were not found, group differences were then inferred at the DCM parameter level.

We used a heuristic strategy for finding the group‐level optimal DCMs (or DCM families), which has been described in Ma et al. 2010. In brief, we used random effects Bayesian family level inference [Penny et al., 2010] and Bayesian model selection [BMS; Stephan et al., 2009] to consider increasingly complex models, based on the model with the highest evidence at each level of complexity as reflected by the Bayesian exceedance probability [Stephan et al., 2009]. The exceedance probability (ϕ) for a given model denotes the probability that this model was more likely to have generated the observed data than any other model considered [Stephan et al., 2009]. According to Stephan et al. 2007, random effects BMS derives the so‐called “exceedance probability”, which is the probability that a particular model is more frequent than any other model tested, given the group data. Note that the exceedance probability of a model differs in a subtle but important way from the conventional posterior probability of a model in Bayesian model comparison at the subject level. This is because when considering a group of subjects, the frequency of models in the population is itself treated as a random (unknown) variable. In this context, the exceedance probability is a statement of belief about the frequency of models within the population. So, for example, when we say that the exceedance probability is 98%, we mean that we can be 98% confident that the favored model is more frequent than any other model tested. In addition to BMS, exceedance probabilities are useful in reporting the results of Bayesian family level inference [Penny et al., 2010]. For the Bayesian family level inference and BMS procedures in this article, we used the criterion that exceedance probability ϕ = 0.95, as the threshold to determine an optimal DCM (or family), to reduce model selection risk (i.e. the probability of picking a wrong model).

Based on our design, we tested three putative modulation types (B‐matrix) based on the three available types of contextual experimental conditions. Modulation Type 1: a putative all‐visual‐stimulus modulation includes all 12 experimental blocks (but not the rest periods). Modulation Type 2: the putative memory‐delay modulations consist, respectively, of the IMT blocks that represent the relatively shorter memory delay period of 0.5 s (two blocks of three‐digit‐IMT, two blocks of five‐digit‐IMT, and two blocks of seven‐digit‐IMT), but not including the rest periods; and the DMT blocks that represent the relatively longer memory delay period of 3.5 s (two blocks of three‐digit‐DMT, two blocks of five‐digit‐DMT, and two blocks of seven‐digit‐DMT), but not including the rest periods. In the DCM analysis of B matrix modulations, a parameter is estimated for the IMT condition and a parameter is estimated for the DMT condition. The IMT and DMT parameters can vary independently from each other with respect to the mean because the mean also takes into account the rest periods. Modulation Type 3: the putative digit‐length modulations consist, respectively, of the three‐digit blocks (two blocks of three‐digit‐IMT, and two blocks of three‐digit‐DMT); the five‐digit blocks (two blocks of five‐digit‐IMT, and two blocks of five‐digit‐DMT); and the seven‐digit blocks (two blocks of seven‐digit‐IMT, and two blocks of seven‐digit‐DMT), but not including the rest periods. In the DCM analysis of B matrix modulations, a parameter is estimated for each putative digit‐length condition. The digit‐length parameters can vary independently from each other with respect to the mean because the mean also takes into account the rest periods. We used Bayesian family level inference and BMS to determine which of these three modulation types is the optimal modulation type, and also used Bayesian family level inference and BMS to determine which connection(s) is (are) the optimal location(s) for the modulation.

Similarly, we tested three putative driving input types (C‐matrix) based the three types of contextual experimental conditions. Driving Input Type 1 consists of the same experimental conditions as Modulation Type 1 above, Driving Input Type 2 consists of the same experimental conditions as Modulation Type 2 above, and Driving Input Type 3 consists of the same experimental conditions as Modulation Type 3 above. We use Bayesian family level inference and BMS to determine which of these three driving input types is the optimal driving input (C‐matrix), and also used Bayesian family level inference and BMS to determine which ROI(s) is (are) the optimal driving input location(s).

Group differences in DCM parameters

To conduct inference on DCM parameters [Stephan and Friston, 2010], we used BMA [Penny et al., 2010; Stephan and Friston, 2010]. BMA is a Bayesian approach that averages each parameter across subjects and across models such that the contribution of each model (of each subject) for that parameter is weighted by each model's posterior probability for that subject. When multiple competing DCMs are averaged for each group, BMA avoids the rigid assumption of an identical single DCM for all subjects in both groups that is required in classical “Frequentist” analysis of model parameters. In this study, the parameter strengths for each group were determined by conducting a separate BMA analysis within each group.

During the BMA analysis, a software bug was found that some values exceeded the machine limits resulting in MATLAB infinity or divide by zero errors. All BMA results in this article were determined after the bug was fixed by regularizing extreme values to be within the MATLAB range for finite numbers.

Statistical Analyses

Student's t‐test and Fisher's exact test were used to evaluate group differences on continuous and categorical demographic variables, respectively. Linear mixed models analysis, as implemented in SPSS Version 19 (SPSS, Chicago, IL) for Windows (Microsoft Corp., Redmond, WA), was used to analyze the main effects of the three factors and their interaction effects on the behavioral accuracy scores (A′). The between‐subjects factor in this analysis was group (cocaine and control groups), a within‐subjects factor was memory delay (IMT and DMT), and another within‐subject factor was digit load (three digits, five digits, and seven digits). If main effects or interactions were statistically significant, then post hoc analyses were conducted with the Bonferroni correction for multiple comparisons.

RESULTS

Demographics

There were 6 females and 13 males in the cocaine group, and five females and nine males in the control group. The ages were: cocaine group 37.2 ± 6.0 (mean ± standard deviation) years (range 23.1 – 47.7); and control group 37.2 ± 8.2 years (range 19.7 – 48.8). The education durations were 13.0 ± 1.6 years (range 10.0 – 16.0) for the cocaine group; and 13.6 ± 2.5 years (range 11.0 – 19.0) for the control group.

Student t‐tests showed that there were no significant differences in age (t = 0.010, P = 0.992, degrees of freedom [df] = 31) and education duration (t = 0.871, P = 0.391, and df = 31) between groups. Fisher's exact tests revealed that there were no significant differences in proportion of female and male subjects (P > 0.999, two tails) and proportion of IFIS and Eloquence subjects (P > 0.999, two tails) between groups.

DSM‐IV Diagnosis

None of the control subjects had a DSM‐IV diagnosis of any drug abuse or dependence. All the cocaine subjects had a DSM‐IV diagnosis of current cocaine dependence. Among the 19 cocaine‐dependent subjects, 11 of them were treatment‐seeking subjects, and eight of them were nontreatment‐seeking subjects; 10 of them had cannabis abuse and/or cannabis dependence diagnoses, and nine of them did not have any of these cannabis diagnoses; and eight of them had alcohol abuse and/or past alcohol dependence, and 10 of them did not have any of these alcohol diagnoses. See Supporting Information for any additional DSM‐IV diagnoses for the cocaine‐dependent subjects.

Behavior During fMRI Scanning

The mean and standard deviation of the subjects' performance accuracy (A′) in each group during memory delays and different digit loads are shown in Table 1. The SPSS linear mixed model analysis revealed statistically significant main effects of digit load (F = 43.08; df = 2, 93.17; P < 0.001). The main effects of subject group (F = 0.035; df = 1, 129.621; P = 0.853) and memory delay (F = 2.010; df = 1, 129.621; P = 0.159) were not statistically significant. The interactions of subject group × memory delay (F = 0.360; df = 1, 129.621; P = 0.550), subject group × digit load (F = 1.790; df = 2, 93.173; P = 0.173), and memory delay × digit load (F = 0.149; df = 2, 93.173; P = 0.861) were not statistically significant. The three‐way interaction of subject group × memory delay × digit load also was not significant (F = 1.096; df = 2, 93.173; P = 0.338). Post hoc comparisons showed that A′ during seven digits was significantly lower than A′ during five digits (P < 0.001, corrected) and significantly lower than A′ during three digits (P < 0.001, corrected). In addition, A′ during five digits was significantly lower than A′ during three digits (P < 0.001, corrected).

Table 1.

Mean and standard deviation of the performance accuracy (A′) in each subject group during different digit loads and memory delays

	IMT			DMT
	Three digits	Five digits	Seven digits	Three digits	Five digits	Seven digits
Cocaine	0.941 ± 0.088	0.883 ± 0.092	0.843 ± 0.114	0.945 ± 0.056	0.853 ± 0.143	0.782 ± 0.137
Control	0.967 ± 0.047	0.904 ± 0.078	0.762 ± 0.121	0.941 ± 0.051	0.887 ± 0.059	0.771 ± 0.169

To test whether there were group differences in behavior that could have been obscured because of the heterogeneous treatment and diversity of substance abuse, we partitioned the cocaine‐dependent subjects into the following subgroups: (1) treatment‐seeking (11 subjects) and nontreatment‐seeking (eight subjects) cocaine groups, (2) cannabis (with cannabis abuse and/or cannabis dependence, 10 subjects) and noncannabis (without cannabis abuse and without cannabis dependence, nine subjects) cocaine groups, and (3) alcohol (with alcohol abuse and/or past alcohol dependence, eight subjects) and nonalcohol (without alcohol abuse and without alcohol dependence, 11 subjects) cocaine groups. We did not conduct other subgroup partitions because there were only sporadically other DMS‐IV diagnoses. Three separate SPSS linear mixed models analyses were conducted to test whether there were group differences in behavior between any of the cocaine groups and control group or between the cocaine groups.

Treatment‐seeking cocaine group, and nontreatment‐seeking cocaine group, versus control group: The SPSS linear mixed model analysis revealed statistically significant main effects of digit load across all groups (F = 36.971; df = 2, 92.649; P < 0.001). The main effects of subject group (F = 0.401; df = 2, 130.652; P = 0.670) and memory delay (F = 2.283; df = 1, 130.652; P = 0.133) were not statistically significant. The interactions of subject group × memory delay (F = 0.278; df = 2, 130.652; P = 0.758), subject group × digit load (F = 1.533; df = 4, 92.649; P = 0.199), and memory delay × digit load (F = 1.023; df = 2, 92.649; P = 0.364) were not statistically significant. The three‐way interaction of subject group × memory delay × digit load also was not significant (F = 0.802; df = 4, 92.649; P = 0.527). Post hoc comparisons showed that A′ during seven digits was significantly lower than A′ during five digits (P < 0.001, corrected) and significantly lower than A′ during three digits (P < 0.001, corrected) across all groups. In addition, A′ during five digits was significantly lower than A′ during three digits (P < 0.001, corrected) across all groups.

Cannabis cocaine group, and noncannabis cocaine group, versus control group: The SPSS linear mixed model analysis revealed statistically significant main effects of digit load (F = 38.856; df = 2, 93.419; P < 0.001) across all groups. The main effects of subject group (F = 1.508; df = 2, 131.944; P = 0.225) and memory delay (F = 2.523; df = 1, 131.944; P = 0.115) were not statistically significant. The interactions of subject group × memory delay (F = 0.196; df = 2, 131.944; P = 0.822), subject group × digit load (F = 1.069; df = 4, 93.419; P = 0.376), and memory delay × digit load (F = 1.176; df = 2, 93.419; P = 0.313) were not statistically significant. The three‐way interaction of subject group × memory delay × digit load also was not significant (F = 0.802; df = 4, 93.419; P = 0.527). Post hoc comparisons showed that A′ during seven digits was significantly lower than A′ during five digits (P = 0.001, corrected) and significantly lower than A′ during three digits (P < 0.001, corrected) across all groups. In addition, A′ during five digits was significantly lower than A′ during three digits (P < 0.001, corrected) across all groups.

Alcohol cocaine group, and nonalcohol cocaine group, versus control group: The SPSS linear mixed model analysis revealed statistically significant main effects of digit load (F = 37.005; df = 2, 93.631; P < 0.001) across all groups. The main effects of subject group (F = 0.067; df = 2, 132.227; P = 0.935) and memory delay (F = 2.373; df = 1, 132.227; P = 0.126) were not statistically significant. The interactions of subject group × memory delay (F = 0.204; df = 2, 132.227; P = 0.815), subject group × digit load (F = 0.857; df = 4, 93.631; P = 0.493), and memory delay × digit load (F = 1.360; df = 2, 93.631; P = 0.262) were not statistically significant. The three‐way interaction of subject group × memory delay × digit load also was not significant (F = 1.286; df = 4, 93.631; P = 0.281). Post hoc comparisons showed that A′ during seven digits was significantly lower than A′ during five digits (P = 0.001, corrected) and significantly lower than A′ during three digits (P < 0.001, corrected) across all groups. In addition, A′ during five digits was significantly lower than A′ during three digits (P < 0.001, corrected) across all groups.

Cocaine groups partitioned based on individual DCM results versus control group: To test whether there were group differences in behavior that could have been obscured because of the heterogeneity in individual optimal DCMs among the cocaine‐dependent subjects (see DCM analysis section and Supporting Information), we partitioned the cocaine group into: Cocaine Group I (seven subjects), in which the subjects had an optimal DCM that was the same as the optimal DCM of the control group (the memory delay modulated the connection from L MFG to L IFC), and Cocaine Group II (12 subjects), in which the subjects had optimal DCMs that were different from the optimal DCM of the control group. Within Cocaine Group II, four subjects (Cocaine subgroup II.1) had optimal DCM in which the memory delay modulated the connection from L IFC to L MFG; three subjects (Cocaine subgroup II.2) had optimal DCM in which the memory delay modulated the connection from L IFC to L PPC; two subjects (Cocaine subgroup II.3) had optimal DCM in which the memory delay modulated the connection from L PPC to L IFC; one subject (Cocaine subgroup II.4) had optimal DCM in which the memory delay modulated the connection from R PPC to L IFC; one subject (Cocaine subgroup II.5) had optimal DCM in which the memory delay modulated the connection from L IFC to LR SMA; and 1 subject (Cocaine subgroup II.6) had optimal DCM in which the memory delay modulated the connection from LR SMA to L IFC.

An SPSS linear mixed models analysis was conducted to test whether there were statistically significant group differences in A′ accuracy score between the control group and Cocaine Groups I and II. Because of the small number of subjects within each of the Cocaine II subgroups, the Cocaine II subgroups were not statistically analyzed individually. This SPSS linear mixed model analysis revealed statistically significant main effects of digit load (F = 38.146; df = 2, 93.500; P < 0.001) across all groups. The main effects of subject group (F = 1.340; df = 2, 132.008; P = 0.265) and memory delay (F = 2.586; df = 1, 132.008; P = 0.110) were not statistically significant. The interactions of subject group × memory delay (F = 0.232; df = 2, 132.008; P = 0.793), subject group × digit load (F = 0.976; df = 4, 93.500; P = 0.424), and memory delay × digit load (F = 1.280; df = 2, 93.500; P = 0.283) were not statistically significant. The three‐way interaction of subject group × memory delay × digit load also was not significant (F = 0.829; df = 4, 93.500; P = 0.510). Post hoc comparisons showed that A′ during seven digits was significantly lower than A′ during five digits (P = 0.001, corrected) and significantly lower than A′ during three digits (P < 0.001, corrected) across all groups. In addition, A′ during five digits was significantly lower than A′ during three digits (P < 0.001, corrected) across all groups.

A separate SPSS linear mixed models analysis was conducted to test whether there were group differences in A′ accuracy score between the control group and Cocaine Group II, in which the cocaine subjects had optimal DCMs that were different from the optimal DCM of the control group. This SPSS linear mixed model analysis revealed statistically significant main effects of digit load (F = 34.186; df = 2, 69.850; P < 0.001) across both groups. The main effects of subject group (F = 0.211; df = 1, 94.478; P = 0.647) and memory delay (F = 1.465; df = 1, 94.478; P = 0.229) were not statistically significant. The interactions of subject group × memory delay (F = 0.212; df = 1, 94.478; P = 0.646), subject group × digit load (F = 2.120; df = 2, 69.850; P = 0.128), and memory delay × digit load (F = 0.285; df = 2, 69.850; P = 0.753) were not statistically significant. The three‐way interaction of subject group × memory delay × digit load also was not significant (F = 1.106; df = 2, 69.850; P = 0.337). Post hoc comparisons showed that A′ during seven digits was significantly lower than A′ during five digits (P = 0.001, corrected) and significantly lower than A′ during three digits (P < 0.001, corrected) across both groups. In addition, A′ during five digits was significantly lower than A′ during three digits (P < 0.001, corrected) across both groups.

The values of the A′ accuracy scores (mean and standard deviation) for the control group, Cocaine Groups I and II, and each of the subgroups within Cocaine Group II are displayed graphically in Fig. 1, which shows that there are no marked differences in A′ among any of the groups or subgroups.

SPM Univariate Analysis of fMRI

The SPM univariate second‐level GLM analysis of the fMRI data revealed four FDR corrected significant clusters for the main effects of the delayed minus immediate memory conditions pooled across three digits, five digits, and seven digits per stimulus and across both groups combined (Fig. 2 and Table 2). In addition, the univariate SPM second‐level analysis found a cluster with trend of significance (P = 0.095, FDR‐corrected) showing a group difference in activation (control greater than cocaine) at the seven‐digit condition (DI7). No significant clusters were found for the other SPM second‐level analyses. For each of the clusters (Clusters 1–4), the cluster‐level FDR corrected P value, number of voxels, mean difference in activation across all voxels in cluster, and the Montreal Neurological Institute (MNI) coordinates of the voxel with relative maximal t value are listed in Table 2.

Figure 2.

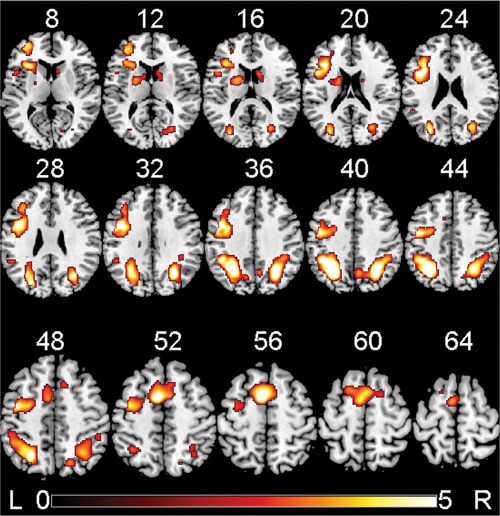
False discovery rate corrected significant clusters for the main effect of the delayed minus immediate memory conditions pooled across three digits, five digits, and seven digits per stimulus and across both groups combined, detected by the univariate SPM8 second‐level GLM analysis. Brain activations are overlaid in color on axial slices of the MNI template brain. The number above each slice indicates slice location (mm) of the MNI z coordinate. Scale on color bar represents voxel t values. The viewer's left (L) side of each slice is left hemisphere of the brain, and right (R) side of each slice is right hemisphere of brain.

Table 2.

Univariate SPM second‐level general linear model analysis (random effects) of regional activation for the main effect of the delayed minus immediate memory conditions pooled across three digits, five digits, and seven digits per stimulus and across both groups combined

Contrast	Cluster label	Cluster P [FDR‐ corrected]	Number of voxels	Mean activation across all voxels in cluster [percent of whole brain activation] (±CI)	Maximal voxel t value (31 df)	Maximal voxel t MNI coordinates [x, y, z]	Maximal voxel t location
Main effects of memory delay (pooled across three digits, five digits, and seven digits, and across both groups combined)	1	<0.001	2396	1.04 (0.21)	7.61	−28, −56, 40	L inferior parietal lobule
	2	<0.001	2104	0.79 (0.19)	6.73	28, −64, 34	L parietal lobe white matter
	3	0.006	979	0.94 (0.23)	6.60	−6, 4, 54	L supplementary motor area
	4	<0.001	4265	0.81 (0.34)	6.18	−42, 10, 24	L precentral g

Within each significant cluster, the voxel with relative maximal t value and its approximate anatomical location are listed. CI = 90% confidence interval. x, y, and z = MNI standard space coordinates (mm). Negative x = left hemisphere. Smoothness of residual field (FWHM) = [13.2 12.8 11.1] mm. Search volume = 125,395 voxels = 495.0 resolution elements (resels). FDR, false discovery rate corrected probability; L, left; R, right; g, gyrus; df, degrees of freedom.

For the main effects of memory delay, Cluster 1 was found in portions of L inferior parietal lobule, L superior parietal lobule, and other posterior regions (see Supporting Information for details). Cluster 2 was found in portions of R inferior parietal lobule, R superior parietal lobule, and other posterior regions (see Supporting Information for details). Cluster 3 was found in portions of L SMA, R SMA, L MFG, and other frontal regions (see Supporting Information for details). Cluster 4 was found in portions of L MFG, L inferior frontal gyrus pars triangularis, L inferior frontal gyrus pars opercularis, L caudate, R caudate, L putamen, and other frontal and subcortical regions (see Supporting Information for details). Another cluster which had trend of significance (FDR corrected cluster P = 0.095, number of voxels = 650) for the group difference (control greater than cocaine) at the seven‐digit condition, was found in portions of R superior frontal gyrus, R MFG, R anterior cingulate cortex, R superior medial frontal gyrus, and R middle cingulate cortex.

DCM Analysis

The number of voxels, volume, and center of mass of the seven volumes of interest are listed in Supporting Information Table 1.

Inference on DCM structure

Optimal driving input type (C matrix) established at family level

A random effects Bayesian family level inference analysis in the control group established that Driving Input Type 1 (all‐visual‐stimulus) was the optimal driving input (C matrix) type (ϕ = 0.984, relative to the other five model families), and this Bayesian family level inference analysis also established that the optimal number of regions receiving the driving input was one region (L IFC) for the control group.

A separate Bayesian family level inference analysis conducted independently in the cocaine group established that, same as the control group, Driving Input Type 1 (all‐visual‐stimulus) was the optimal driving input (C matrix) type (ϕ = 0. 999, relative to the other five model families), and this Bayesian family level inference analysis also established that, same as the control group, the optimal number of regions receiving the driving input was one region (L IFC) for the cocaine group.

See Supporting Information for detailed description of above Bayesian family level inference analyses.

Optimal modulation type (B matrix) established at family level

Based on the above findings, a third random effects Bayesian family level inference conducted independently within the control group showed that Modulation Type 2 (memory delay) was the optimal bilinear modulation type (B matrix) for the control group (ϕ = 0.991, relative to the other five modulation families). This optimal DCM family for the control group consisted of 42 DCMs, and the only difference among these DCMs was which connection was modulated by the memory delay. In each of these 42 DCMs, the optimum driving input (C‐matrix) entered the model through L IFC, as established in the previous step for the control group.

Similarly, Bayesian family level inference conducted independently within the cocaine group showed that Modulation Type 2 (memory delay) was also the optimal bilinear modulation type (B matrix) for the cocaine group (ϕ = 0.989, relative to the other five model families). This optimal DCM family for the cocaine group consisted of 42 DCMs, and the only difference among these DCMs was which connection was modulated by the memory delay. In each of these 42 DCMs, the optimum driving input (C‐matrix) entered the model through L IFC, as established in the previous step for the cocaine group.

See Supporting Information for detailed description of above Bayesian family level inference analyses and the optimal DCM family.

Inference on DCM structure at model level

Within the optimal DCM family (Modulation Type 2) described above for the control group, random effects BMS analysis conducted independently for the control group (Fig. 3, left panels) revealed that the DCM with the location of the bilinear memory‐delay modulation on the connection from L MFG to L IFC had the highest exceedance probability (ϕ = 0.901, relative to the other 41 DCMs).

Figure 3.

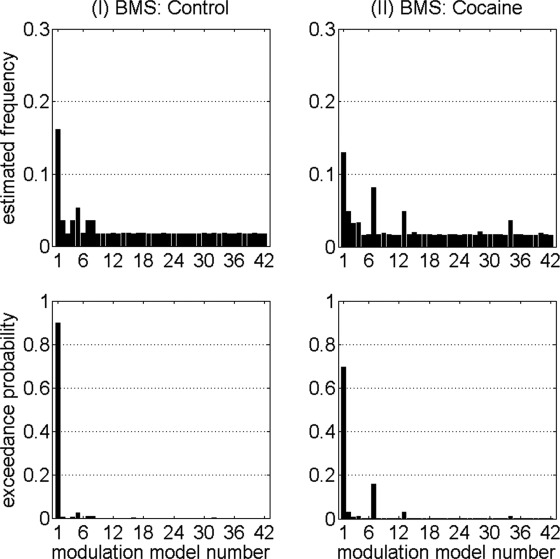
Random effects BMS results (left panels for control group, and right panels for cocaine group) of the connections modulated by the optimal bilinear modulator (memory delay). For the control group, two single‐modulation DCMs (corresponding to connections L MFG to L IFC, and L STR to L IFC, respectively) had exceedance probabilities that were at least five times greater than the mean exceedance probability of the other 40 DCMs. For the cocaine group, six single‐modulation DCMs (corresponding to connections L MFG to L IFC, L IFC to L MFG, L PPC to L IFC, L IFC to L PPC, LR SMA to L IFC, and R PPC to L STR, respectively) had exceedance probabilities that were at least five times greater than the mean exceedance probability of the other 36 DCMs. See Supporting Information Table 2 for the 42 endogenous connections that correspond to the 42 modulation model numbers.

Within the optimal DCM family (Modulation Type 2) described above for the cocaine group, random effects BMS analysis conducted independently for the cocaine group (Fig. 3, right panels) likewise revealed that the DCM with the location of the bilinear memory‐delay modulation on the connection from L MFG to L IFC had the highest exceedance probability (ϕ = 0.698, relative to the other 41 DCMs).

The preliminary BMS results showed that, in the cocaine group, six of the single‐modulation models had higher exceedence probabilities than the other 36 (Fig. 3, right panels); the exceedence probability of each of these six DCMs was at least five times the mean exceedence probability of the other 36 DCMs. However, there was no obvious clear‐cut “winner” among these six models because of the finding that these six single‐modulation models had exceedance probabilities that were not markedly different from each other (Fig. 3, right panel), but which were clearly superior to the other 36 single‐modulation DCMs. A possible explanation for this finding would be that all six of these “winning” connections may have been modulated by the memory delay in the cocaine group. Here we used a heuristic strategy that was based on the analysis strategy in a previous DCM study by our group [Ma et al., 2012] by constructing a putative multiple‐modulation DCM, consisting collectively together in the same model all six modulated connections (L MFG to L IFC, L IFC to L MFG, L PPC to L IFC, L IFC to L PPC, LR SMA to L IFC, and R PPC to L STR) that had the highest exceedence probability in the previous preliminary BMS step. An additional BMS analysis showed that this multiple‐modulation DCM was “better” (ϕ = 0.940) than the single‐modulation DCM that had shown the largest exceedance probability in the previous preliminary BMS analysis (in spite of the penalty for model complexity inherent in the BMS procedure [Stephan et al., 2009]), but the exceedance probability did not reach the threshold ϕ = 0.95.

Applying the same reasoning and criteria to the control group as in the cocaine group, we constructed a multiple‐modulation DCM with two modulated connections (L MFG to L IFC, and L STR to L IFC) in the control group, based on the finding that in the control group there were two “winning” models that each had exceedence probabilities that were at least five times of the mean of those of the other DCMs (Fig. 3, left panels). Another BMS analysis showed that this multiple‐modulation DCM was “better” (ϕ = 0.687) than the single‐modulation DCM that had shown the largest exceedance probability in the previous preliminary BMS analysis.

Because neither the single‐ nor multiple‐modulation DCMs within each group had exceedance probabilities that were greater than the threshold ϕ = 0.95, group difference in DCM structure could not clearly be established. However, in each group, the multiple‐modulation DCM had exceedance probability greater than the single‐modulation DCM that had shown the largest exceedance probability in the previous preliminary BMS analysis, suggesting that these putative multiple‐modulation DCMs are plausible and appropriate to be included along with the putative single‐modulation DCMs in the model space of the subsequent BMA analysis (see next section).

Group differences on DCM parameters

Because of the fact that group difference in DCM structure could not be clearly established stemming from Bayesian family level inference and BMS conducted independently within each group, we used BMA to identify quantitative differences in memory modulation parameters between patients and controls. The relatively low exceedance probabilities (less than 0.95 for both groups) of the “winning” DCM in each group suggest high model selection risk [i.e., the probability of picking a wrong model; Daunizeau et al., 2011]. Therefore, the inference on DCM parameters was conducted at the family level rather than the model level. Family inference helps to increase statistical power by pooling evidence across models belonging to the same family [Penny et al., 2010].

We constructed the model space for the BMA analysis for each group to consist of both of the two aforementioned putative multiple‐modulation DCMs (i.e., the six‐modulation DCM from the cocaine group and the two‐modulation DCM from the control group) in addition to all 42 putative single modulation DCMs. Thus, the same, identical model space was used in both BMA analyses that were conducted independently for each group.

For each endogenous connection, the posterior mean (or group difference), standard deviation, and the probability that a Bayesian posterior mean (or group difference between posterior means) is different from zero are listed separately for the cocaine group, the control group, and the group‐difference in Supporting Information Table 2. The corresponding measures are also listed for the modulation effects exerted by IMT and DMT in Supporting Information Table III and Supporting Information Table IV, respectively.

Twenty‐eight of the 42 connections showed probabilities of at least 0.999 that the group difference between posterior means was different from zero for the bilinear modulation effects exerted by the IMT condition, and 27 of the 42 connections showed probabilities of at least 0.999 that the group difference between posterior means was different from zero for the bilinear modulation effects exerted by the DMT condition. For IMT condition, the connection showing largest difference between groups was L IFC to L STR (Fig. 4, left panels): the IMT condition exerted more negative bilinear modulation strength in the cocaine group (−0.026 ± 0.044 Hz) compared with the control group (−0.007 ± 0.041 Hz) on this connection. For DMT condition, the connection showing largest difference between groups was L MFG to L STR (Fig. 4, right panels): the DMT condition exerted a negative bilinear modulation effect on this connection in the cocaine group (−0.005 ± 0.028 Hz) and a positive modulation effect on this connection in the control group (0.015 ± 0.033 Hz).

Figure 4.

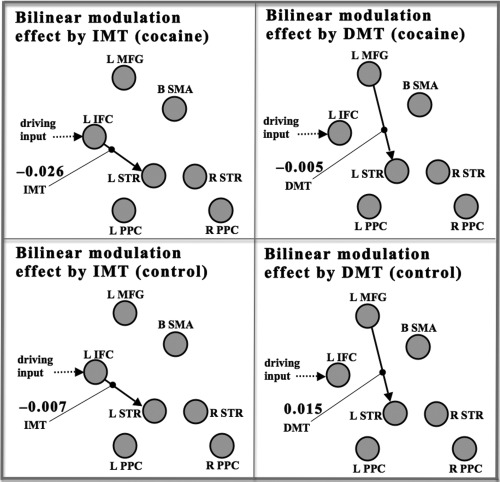
The results of BMA analysis showing the largest group differences in posterior mean values of the DCM bilinear modulation (B‐matrix) parameters. The endogenous connections (that were bilinearly modulated) are denoted by solid line with arrow. The driving input (Type 1, all visual stimuli) is depicted by dotted line with arrow. The bilinear modulation effects exerted separately by IMT (shorter working memory delay) and DMT (longer working memory delay) are depicted by thin lines ending with solid dot. The mean strengths (in units of Hz) of the bilinear modulation effects exerted by the IMT condition (left panels), and the bilinear modulation effects exerted by the DMT condition (right panels) are separately shown for the cocaine group (top panels), and the control group (lower panels). The ROIs of the DCM analysis are depicted by gray circles. The abbreviations for the ROI labels are defined in Regions of interest section.

The driving input (C‐matrix) exerted by the all‐visual‐stimulus (Driving Input Type 1) on the L IFC showed a probability of 0.999 that the group difference was different from zero. The driving input in the cocaine group (0.076 ± 0.024 Hz) was greater than that in the control group (0.059 ± 0.028 Hz).

Because of the heterogeneity within the cocaine group, BMS analysis was conducted for each individual cocaine subject to test whether this heterogeneity can be captured. The detailed results of this analysis are shown in Supporting Information.

DISCUSSION

To the best of our knowledge, this is the first published between‐group study using stochastic DCM, which takes into account random fluctuations in neuronal and vascular responses that may have profound effects on the measurement of effective connectivity [Li et al., 2011a]. Group differences were first evaluated at the DCM structure level. The random effects Bayesian family level inference procedures showed strong evidence (ϕ > 0.95) that the cocaine group and the control group had the same type of bilinear modulation (i.e., memory delay) at the family level. But further random effects BMS procedures did not provide strong evidence showing whether or not the cocaine group and the control group had the same DCM structure in terms of which connections were modulated by the memory delay. These DCM structure inference results warranted DCM parameter inference to be conducted. To avoid picking a wrong model, group differences in DCM parameters were evaluated at the DCM family level using BMA. The BMA analyses revealed that the cocaine‐dependent subjects had marked differences in bilinear modulation effective connectivity strengths in prefrontal–striatal connections compared with the control group. Cocaine subjects differed from controls in terms of the connection from L IFC to L STR being less affected by the IMT (shorter memory delay) in the cocaine group compared with the control group, and the connection from L MFG to L STR being less affected by the DMT (longer memory delay) in the cocaine group compared with the control group. Consistent with previous studies comparing cocaine users and controls using PET or fMRI [Moeller et al., 2010; Tomasi et al., 2007; Volkow et al., 2007], prefrontal regions and STR were involved in this altered effective connectivity.

The altered prefrontal–striatal effective connectivity observed in cocaine‐dependent subjects is in the associative loop of cortical–striatal connections that may be related to cognitive functions [Leh et al., 2007, 2003], and is consistent with findings [e.g., Hanlon et al., 2011; Wilcox et al., 2011] and theories [e.g., Volkow et al., 2011] regarding altered cortical–striatal function in cocaine dependence. As discussed in Volkow et al. 2011, several brain circuits related to reward, motivation, conditioning, and inhibitory or executive control are thought to be critical for the development of addiction. Although there may be alternative interpretations, e.g., brain perfusion [Tucker et al., 2004], white matter integrity [Moeller et al., 2005; Romero et al., 2010], or gray matter structure [Barros‐Loscertales et al., 2011], the result that dopaminergic target regions (prefrontal regions and STR) were involved in the connections showing the largest and most reliable group differences lead us to speculate that the changes in dopamine function in cocaine users could be an underlying factor for the altered effective connectivity. Evidence to support a role for dopamine function in the observed altered effective connectivity comes from a previous study showing that dopamine synthesis capacity as measured by 6‐[18F]‐fluoro‐l‐m‐tyrosine PET was correlated with frontal–caudate functional connectivity during a working memory task [Klostermann et al., 2012]. Other evidence comes from a study showing that dopamineric augmentation increased frontal–striatal functional connectivity and behavioral performance in low working‐memory capacity individuals [Wallace et al., 2011]. In addition, studies on human subjects other than cocaine users have shown that brain connectivity can be tuned by dopaminergic medications [Honey et al., 2003; Jahanshahi et al., 2010; Kelly et al., 2009; Palmer et al., 2009; Wallace et al., 2011].

Consistent with the above interpretation was the negative modulation effect between prefrontal cortical regions and STR that was observed in the cocaine‐dependent subjects which differed from the modulation effect in controls. Previous studies by Volkow and associates have shown significant correlations between reduction in dopamine D2 receptor function and glucose metabolism in orbitofrontal cortex, anterior cingulate, and dorsolateral prefrontal cortex in subjects with cocaine dependence and other drug abuse disorders [Volkow et al., 2007, 2009]. A prefrontal–striatal glutamatergic pathway may regulate striatal dopamine function through glutamatergic efferents from prefrontal regions, involving both direct and indirect projections to brainstem and STR [Carlsson et al., 2001; Meyer‐Lindenberg et al., 2002; Kalivas, 2004]. Evidence from animal studies shows that stimulation of the prefrontal regions elevates dopamine release in the nucleus accumbens and burst firing of midbrain dopamine neurons [Karreman and Moghaddam, 1996; Murase et al., 1993; Taber and Fibiger, 1995; Tong et al., 1996]. This is consistent with a study in humans showing that administration of the N‐methyl‐d‐aspartate receptor antagonist ketamine resulted in increased amphetamine‐induced dopamine release in the STR [Kegeles et al., 2000]. The prefrontal–striatal glutaminergic pathway has been hypothesized to be critical for addictions [Koob and Volkow, 2010]. Evidence for a direct link between prefrontal cortical glutamate and striatal function includes a study showing that prefrontal glutamate release into the nucleus accumbens mediates cocaine‐induced reinstatement of drug‐seeking behavior [McFarland et al., 2003]. Glutamate perfused into the STR increases dopamine release [Shimizu et al., 1990]. We speculate that altered prefrontal–striatal effective connectivity in cocaine users could be related to a reduction in prefrontal cortical glutamatergic input to the STR, resulting in reduction in striatal dopamine function. Further studies are needed to examine this issue, including further studies on effective connectivity between prefrontal cortex and STR in cocaine dependence.

We have found a significant group difference in effective connectivity. However, we did not find a significant group difference in behavioral performance, and the nonsignificance remained after the heterogeneous treatment, the diversity of substance abuse, and the heterogeneity in optimal DCMs in the cocaine‐dependent subjects were considered statistically. These results are consistent with the opinion that altered effective connectivity may not necessarily produce altered behavior between groups [Seghier et al., 2010]. Behavioral and brain activation measures are often jointly used in neuroimaging experiments to infer group differences between patients and controls. It is a common observation that these two measures generate divergent results [Wilkinson and Halligan, 2004]. For example, using fMRI and an n‐back working memory task, Tomasi et al. 2011 found widespread group differences in brain activation between cocaine abusers and controls but did not find a significant group difference in behavior. The combination of significant group difference in neural activity and insignificant group difference in behavioral measures is a possible outcome in neuroimaging experiments and may not be evidence of a weak hypothesis [Wilkinson and Halligan, 2004]. In fact, the absence of a between‐group difference in behavioral performance may be helpful in interpreting the neuroimaging results as a difference between groups at the neuronal level because it reduces the confounding effects due to difference in behavioral performance between groups [Price and Friston, 2002]. For example, decreased performance compared with normals may cause (rather than be a consequence of) decreased neuronal activation because of decreased engagement of unimpaired processes [Price and Friston, 2002]. On the other hand, abnormal neuronal responses in the context of normal performance can indicate alternative neuronal mechanisms for supporting the same level of task performance [Price and Friston, 2002]. Our findings reflect that the effective connectivity as measured by DCM may be a more sensitive indicator of altered neural pathways between groups than the behavioral measures. This interpretation may not be very surprising, because it is possible that fairly subtle neural processes can be detected using DCM analysis [Rowe, 2010; Stephan and Friston, 2010].

Given the relatively large number of regions, it is almost impossible to evaluate all possible DCMs given the current computation technique. Therefore, a relevant model space should include a set of plausible DCMs, based on previous knowledge of the system [Stephan and Friston, 2010]. In our DCM analysis, when constructing the putative modulation model space, we used a two‐step heuristic strategy to reduce the number of models examined to a manageable level. Other strategies could have been used to reduce the model space to a manageable level, but the heuristic strategy that we used was a plausible and principled approach that was based on the analysis strategy in a previous DCM study by our group [Ma et al., 2012]. We believe that the procedure for constructing putative multiple‐modulation DCMs was reasonable, given that the modulated connections in each multiple‐modulation model, respectively, corresponded to the DCMs with highest exceedance probabilities in the BMS analysis within each group in the first preliminary BMS step. We would like to emphasize that that these putative multiple‐modulation models were not arbitrarily selected for use in the subsequent BMA comparison of model parameters between groups. Instead, the multiple‐modulation models were tested against the corresponding single‐modulation models in a second BMS step, and the multiple‐modulation models were included in the BMA model search space only if the multiple‐modulation had greater exceedence probability than the corresponding single‐modulation models.

We have chosen to use stochastic DCM rather than deterministic DCM. Unlike deterministic DCM, stochastic DCM takes into account random fluctuations in physiological noise that may contribute to the system connectivity input [Li et al., 2011a] due to stochastic fluctuations in neuronal and vascular responses [Kruger and Glover, 2001; Li et al., 2011a]. Li et al. 2003 have demonstrated that stochastic DCM can show improvement in parameter estimation over deterministic DCM. More recently, Daunizeau et al. 2012 have validated stochastic DCM and shown that the stochastic DCM is superior over deterministic DCM in both model structure inference and model parameter inference. In this study, we studied cocaine dependence, which is a disorder associated with altered dopaminergic (and perhaps other) neurotransmission in the brain [Volkow et al., 2007, 2009]. In disease populations, changes in the BOLD signal could be confounded by the possible disruption by disease or drugs on neurovascular coupling and/or hemodynamic response [Iannetti and Wise, 2007]. In addition, Choi et al. 2002 has shown that the direct effects of dopamine on the vasculature need to be considered when measuring the hemodynamic coupling associated with dopaminergic drugs. Because stochastic DCM can account for these confounding effects better than deterministic DCM, we believe that stochastic DCM can detect the altered effective connectivity in cocaine‐dependent subjects more accurately than deterministic DCM.

See Supporting Information for additional discussion on the regional activation in left prefrontal regions, the between‐study comparison of regional activations, and the between‐study comparison of DCM inference on model structure.

Several limitations regarding the application of DCM and the IMT/DMT protocol in working memory studies have been discussed in Ma et al. 2010. Additional limitations specifically for this study include the heterogeneous sample in the cocaine group, which consisted of treatment‐seeking and nontreatment‐seeking patients. The inclusion of more than half (11) of the total sample of cocaine‐dependent subjects who had other types of substance abuse in addition to cocaine dependence also may limit interpretation of the findings of this study. Further studies with more homogeneous groups are necessary to clarify these issues.

In summary, stochastic DCM analysis showed that compared with normal controls, cocaine‐dependent subjects had markedly altered working‐memory related prefrontal–striatal effective connectivity that may reflect altered cortical–striatal networks in cocaine‐dependent subjects. Reduced dopamine function in cocaine users may be an underlying factor for the altered effective connectivity observed in this study. Future studies are needed to test this hypothesis.

Supporting information

Supporting Information