Linking molecular models with ion mobility experiments. Illustration with a rigid nucleic acid structure

Abstract

Ion mobility spectrometry experiments allow the mass spectrometrist to determine an ion's rotationally averaged collision cross section Ω_EXP. Molecular modelling is used to visualize what ion three-dimensional structure(s) is(are) compatible with the experiment. The collision cross sections of candidate molecular models have to be calculated, and the resulting Ω_CALC are compared with the experimental data. Researchers who want to apply this strategy to a new type of molecule face many questions: (1) What experimental error is associated with Ω_EXP determination, and how to estimate it (in particular when using a calibration for traveling wave ion guides)? (2) How to generate plausible 3D models in the gas phase? (3) Different collision cross section calculation models exist, which have been developed for other analytes than mine. Which one(s) can I apply to my systems? To apply ion mobility spectrometry to nucleic acid structural characterization, we explored each of these questions using a rigid structure which we know is preserved in the gas phase: the tetramolecular G-quadruplex [dTGGGGT]₄, and we will present these detailed investigation in this tutorial. © 2015 The Authors. Journal of Mass Spectrometry published by John Wiley & Sons Ltd.

Introduction

Electrospray mass spectrometry (ESI-MS) in native conditions can preserve the structures of biomolecules and separate them according to their mass-to-charge ratios.[1,2] Ion mobility spectrometry (IMS) separates ions according to their size-to-charge ratios in the gas-phase.[3–6] Size is related to the mass (or number of atoms) and to the three-dimensional shape of a molecule. Therefore, by hyphenating IMS to mass spectrometry (IM-MS), one can sort ions according to both mass and shape. The challenge is to decipher structural information from ion mobility experiments.[7–9]

The physical quantity characterizing the shape is the collision cross section (CCS),[10] which will be introduced in more detail in the Section on Ion mobility and collision cross sections. The present tutorial clarifies how to interpret CCS measurements in terms of three-dimensional structure for ions larger than 100 atoms extracted from the solution by electrospray ionization (ESI). The gold standard is to match CCSs experimentally obtained from IMS with CCSs calculated for modelling three-dimensional structures of the ion of interest. We will discuss the factors that can affect the precision (reproducibility) and accuracy in both the measurements and the calculations. Understanding each of these factors is crucial to interpret quantitative matches confidently and assess the meaningfulness of structural assignments.

On the experimental side, we will describe the determination of CCS from traveling wave ion mobility spectrometers and from drift tube ion mobility spectrometers, with example data recorded on commercially available instruments of each type. For structural interpretation, CCS experimental data are compared with CCS calculated data generated independently. We will therefore discuss how to estimate the error and provide recommendations on how experimental data should be documented.

On the calculation side, we will discuss the choice of the starting model(s), the methods for three-dimensional structure calculation in the gas phase, the sampling of structures in the gas phase and the different methods available to calculate CCSs. To assess the errors and biases pertaining to modelling, we needed a system with limited conformational diversity in the gas phase. We chose the parallel-stranded [dTGGGGT]₄ G-quadruplex DNA structure (Fig.1) because (1) starting atomic coordinates of [dTGGGGT]₄ are available from X-ray crystallography,[11–14] (2) the same molecular assembly was studied by nuclear magnetic resonance (NMR) as well and presents the same G-quadruplex core arrangement, although the thymine placement differs, with evidence for T–T interactions,[15–17] and (3) the central guanine-rich core remains very rigid in the gas phase, [18–21] thanks to the preservation of the G-quartet hydrogen bonds and to the coordination of three ammonium cations in-between the four guanine G-quartets. Only the position of thymines in the gas phase is less certain.

Figure 1.

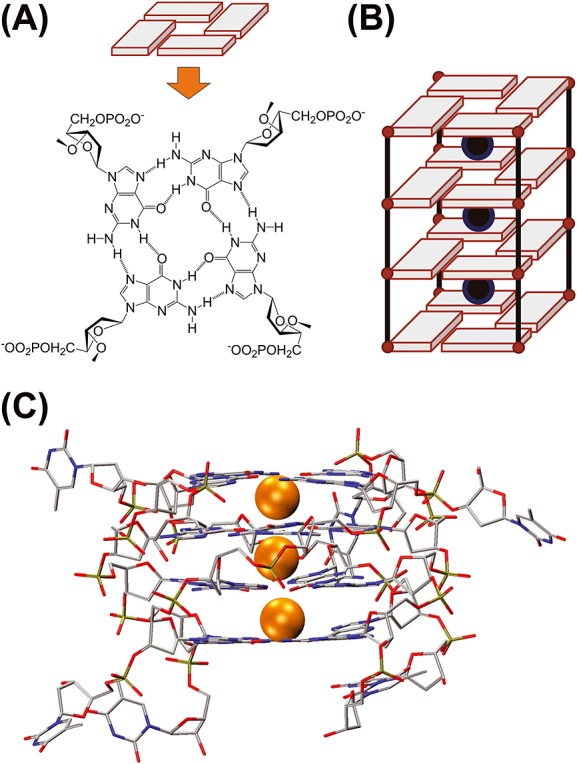
What is a G-quadruplex? (A) Four guanines forming a G-quartet via Hoogsteen H-bonds, involving N1-O6 and N2-N7 atoms. (B) Sequences containing consecutive guanines form G-quartets core stabilized by the coordination of monovalent cations in-between G-quartets. (C) 3-D crystal structure of the DNA G-quadruplex [dTGGGGT]₄; cations shown as orange spheres; PDB reference 352D.[11]

This ammonium-bound, 24-nucleobase structure (795 atoms and 7504 Da) therefore constitutes a rigid model system in which to assess the structure determination from CCS matching. Two important questions for using IMS-MS in the field of nucleic acid structural biophysics are (1) which model and parameterization of CCS calculation work for nucleic acids of this size, although none of the models was parameterized for nucleic acids specifically, and (2) if ion mobility approaches linked to molecular modelling methodologies are able to detect minor structural changes such as the different positioning of one or two nucleobases from a 24-nucleotide structure.

Ion mobility and collision cross sections

Ions moving in a chamber filled with gas under the influence of an external electric field (E) will reach an apparent steady state drift velocity (v_d) if the collisions are frequent enough to reach a regime where friction forces compensate the electric drag forces. The drift velocity is linearly proportional to the electric field (E), and the proportionality factor is termed the mobility (K):

(1)

Because the velocities (v_d) of the ions are influenced by the collisions with the drift gas molecules, K depends on the number density of the drift gas (N). The reported value is the reduced mobility (K₀), normalized to standard pressure and temperature (p₀ = 760 Torr and T₀ = 273.16 K):

(2)

In the low field limit (E/N ratio ≤ 2 × 10⁻²¹ V m², or 2 Td), K₀ is independent on the electric field and, based on the gas kinetic theory, can be expressed as follows: [22]

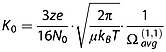(3)

where z is the nominal ion charge, e is the absolute charge of an electron, N₀ is the gas number density at p₀ and at T₀ (N₀ = 2.687 × 10²⁵ m⁻³), μ is the reduced mass of the collision partners (1/μ = 1/M + 1/m, where M is the ion mass and m is the mass of the collision gas), k_B is the Boltzmann's constant, T is the temperature of the gas and 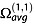is the orientationally averaged momentum transfer collision integral. 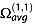is also commonly called the ‘collision cross section’ and noted Ω or ‘CCS’ for brevity.

The CCS influences the ion mobility because it represents the effective area for the interaction between the ions and the gas responsible for slowing down the ions by friction.

Section on experimental collision cross section determination explains how to deduce K₀ and therefore the experimental CCS (Ω_EXP) from measured drift times. The section also clarifies how measurements are done directly in drift tube IMS cells and how to obtain a Ω_EXP,He from measurements carried out in a nitrogen-filled travelling wave ion guide IMS cell, following proper calibration. On the theoretical side, to determine theoretically CCS (Ω_CALC) values, the most representative gas-phase conformations of the ion have to be generated first by molecular modelling (we will discuss this procedure in Section on relating ion mobility spectrometry measurements to molecular structure), and then some approximate methods can be applied on these potential geometries, with the ultimate goal to fit at the best within the Ω_EXP values. Most of the approximate methods have been parameterized using helium as collision gas because helium is most likely to behave as a hard sphere upon collision with an ion, but efforts are now made to predict CCS in other gases. A good knowledge of the theory behind the calculation methods guides the proper method choice and is crucial for the interpretation of the matching between Ω_EXP and Ω_CALC values, as will be discussed in Section on how to obtain theoretical collision cross section from atomistic models.

Experimental collision cross section determination

Introduction: hardware considerations, electric field regimes and collision gas

Knowledge of the instrument hardware is essential to obtain best quality results or to assess the quality of published results. Although we will focus here on the IMS cell, other parts of the mass spectrometer are also important. In particular, all parameters affecting the ion transfer from the solution to the IMS cell can potentially affect the ion structure and the overall result (Ω_EXP). For structural biology applications in which the goal is to trace back the solution structure from the gas-phase measurement, soft ionization from native solutions (usually by electrospray) is usually preferred. Besides the experiment, the conception of the modelling workflow also benefits from deeper knowledge of the ionization mechanism[23–25] and of ion activation prior to entrance in the IMS cell (effective temperature of the ions and possible ensuing rearrangements).[26,27] Here, with the aim of assessing the determination of experimental and theoretical CCS, we chose a conformationally rigid molecule that is little affected by instrument tuning. However, the reader should beware that the conformations of floppy molecules can be affected in the gas phase by parameters such as desolvation gas temperature, direct current (DC) and radio frequency (RF) voltages and even molecular charge states.

Ion mobility separation hardware can be of three types:

1. In tubes filled with static gas, the ions move under the influence of electric fields, and the ions transit time in the tube is related to their mobility. IMS tubes are the mobility spectrometry analogues of time-of-flight (TOF) mass spectrometers. We will distinguish constant and low-field drift tube ion mobility spectrometry (DTIMS, Fig.2A) from travelling-wave ion mobility spectrometry (TWIMS, Fig.2B). In the latter case, the field is not constant and the regime is not in the low field limit at all times [26,28] and, therefore, calibration with ions of known collision cross section is always required.

2. Filters are filled with gas, and only ions with a given mobility can reach the exit slit of the filter. They are the mobility analogues of quadrupole or sector-type mass analyzers. Filters can operate in the low field limit (like differential mobility analyzers or ‘DMA’) or involve high fields (like field asymmetric waveform ion mobility spectrometry or ‘FAIMS’). In the low field limit, DMA can potentially provide collision cross sections as defined in Eqn (3), [29,30] whereas high-field phenomena in FAIMS are much more complicated.[31]

3. In trapping IMS devices (TIMS), ions face a counter-current gas flow and are trapped, depending on the electric field. Scanning the electric field provides a mobility-selective instability scan, the IMS analogue of mass-selective instability scans in quadrupole ion trap mass spectrometers.[32]

Figure 2.

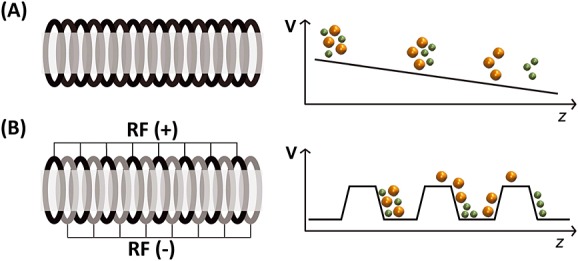
Main difference between (A) drift tube ion mobility spectrometry (DTIMS) and (B) traveling wave IMS (TWIMS). High mobility ions are in green and low mobility ions are in orange. (A) In DTIMS, a constant and homogeneous potential gradient is applied along the tube. (B) In TWIMS, the ions are confined by a radio frequency (RF) applied to a stacked ring ion guide. In addition, a direct current voltage wave is traveling to the exit (T-wave). Ions of higher mobility are picked up more easily by the waves, whereas larger ions are subjected to larger friction with the gas and slip more often behind the waves and therefore take longer to exit the mobility cell.

Any configuration in the low field limit can provide collision cross sections from first principles (without calibration), provided that the gas flows, pressure and purity are carefully controlled and accurately known and that the electric field is known exactly in all parts of the IMS device. If not, calibration with compounds of known collision cross section remains possible. Here, we describe the two tube-type IMS cells (DTIMS and TWIMS) that are the most commonly encountered in the literature and are commercially available, coupled with high resolution TOF mass analyzers. Commercial instruments are usually specified to work best with nitrogen in the mobility cells, whereas collision cross sections obtained in helium are preferable for matching with calculations. We will therefore also discuss the adaptation of the commercial DTIMS hardware to enable measurements in helium and calibration of TWIMS measurements performed in nitrogen using ions of known collision cross sections in helium.

Drift tube ion mobility spectrometry

Principle of drift tube ion mobility spectrometry

In DTIMS, a static uniform electric field propels the ions in the drift tube (Fig.2a), and there is (usually) no RF confinement. The electric field is E = V/L (V is the voltage applied across the cell length L). The drift tube is filled with gas, typically helium or nitrogen, kept at constant and known pressure. The drift velocity (v_d) of the ions is determined from the drift time, knowing that v_d = L/t_drift, where L is the drift cell length, and t_drift is the time spent inside the tube. The ions exiting the drift tube are detected as a function of time, yielding an arrival time distribution. All previous equations can be combined with Eqns (1) and (2) to express the arrival time t_A,

(4)

which is the sum of t_drift (the time spent in the tube) and t₀ (the time spent outside the drift cell and before detection). t₀ is also ion-dependent and must be determined in each experiment through voltage-dependent experiments: a graph of measured t_A as a function of 1/V (or of p/V if the pressure changes significantly for each voltage) is linear and the slope is proportional to 1/K₀. The accuracy of the determined K₀ depends directly on the accuracy with which the cell length L, voltage V, pressure p and temperature T are known. The pressure determination is the most delicate, for several reasons. (1) The pressure gauge can not be placed directly inside the tube, but as close as possible to it so as to reflect the inner pressure. (2) Capacitance diaphragm gauges must be used instead of Pirani gauges for all gases except nitrogen. This is because Pirani gauges are based on a thermal conductivity measurement, which conversion to pressure is calibrated for nitrogen and air. The calibration with other gases greatly diverges above 1 mbar. Capacitance diaphragm gauges measure the pressure on a membrane, and the reading is gas-independent. (3) The gas must be static on average and homogeneously distributed throughout the tube, and care must be given to the design of flow controllers and pumping system for gas regulation inside the tube.

The experimental CCS is then determined from K₀ using Eqn (3). For known analytes, the mass and charge are known accurately. The temperature is determined using a thermocouple plunged in the tube exit. An isolating blanket around the whole tube helps in homogenizing the temperature and minimizing temporal fluctuations. Our instrument is placed in a room with robust air conditioning and the inner temperatures fluctuate by <0.5 °C day-to-day, <0.1 °C during a CCS measurement. We however draw the attention on the gas purity. Operating drift tubes in 100% nitrogen is not particularly difficult with ambient sources (for electrospray, the source nebulizing gas is nitrogen, and most commercial instrument operate with counter-current nitrogen flows in their electrospray interface to reduce contamination). However, achieving 100% helium purity in the tube (even if using high purity helium as a supply), while having nitrogen up front, is more difficult and requires some precautions. If helium is contaminated with nitrogen, the ions would be slowed down more than with pure helium and the Ω_EXP would be biased and too high.

Materials and methods

Sample preparation

Lyophilized dTGGGGT and dT₆ oligodeoxynucleotides were purchased from Eurogentec (Belgium) with RP-cartridge-Gold purification grade. Ammonium acetate (BioUltra ∼ 5M) was from Fluka (Sigma-Aldrich, Saint-Quentin Fallavier, France), and nuclease-free water from Ambion (Fisher Scientific, Illkirch, France). Single strand stock solutions were prepared at 1 mM in water. dTGGGGT was annealed at 200 μM single strand (50 μM tetramolecular G-quadruplex [dTGGGGT]₄ when fully formed; beware the formation rates are slow)[33] in 100 mM aqueous NH₄OAc. Before injection, the samples were prepared at room temperature and injected at a final concentration of ∼5 μM quadruplex [dTGGGGT]₄ and 5 μM single strand dT₆ (added as internal standard).

Drift tube ion mobility spectrometry

Experiments were performed on an Agilent 6560 DTIMS-Q-TOF instrument (Agilent Technologies, Santa Clara, CA), with the dual-ESI source operated in the negative ion mode. The syringe pump flow rate was 180 µl/h. The source and Q-TOF parts were optimized, so as to minimize the fragmentation of a reference oligonucleotide complex [(dG₄T₄G₄)₂(NH₄⁺)₃]⁵⁻.[27] The drying gas was 100 °C or 200 °C (the CCS results were not affected by this temperature). There is no ion injection in this instrument, but a relatively low field (∼17 V/cm) between the trap funnel exit and the drift tube entrance. The trap funnel is the region where ion fragmentation is most prominent because of RF heating, and diminishing the trapping funnel RF amplitude from 180 to 90 V improves softness. Fortunately, the abundance and collision cross section of our ion [(dTGGGGT)₄(NH₄⁺)₃-8H]⁵⁻is insensitive over that tuning range, and it is another reason why we chose this G-quadruplex nucleic acid as a test system.

Experiments were first carried out using the standard configuration of the Agilent 6560 IMS-Q-TOF (Agilent Technologies). The drift tube length is 78.1 cm. For nitrogen experiments, the collision gas pressure was around 4.2 Torr and monitored throughout the experiment with the pirani gauge. The drift tube pressure was 0.14 Torr higher than the trapping funnel pressure. The drift cell exit voltage was 210 V, and the drift cell entrance voltage was ramped from 1000 to 1700 V. For helium experiments, the pumping system was modified by connecting an E2M80 oil pump (Edwards SAS, Gennevilliers, France) to the source region, whereas the original pump was connected to the Q-TOF region. Helium (Alphagaz 1 grade from Air Liquide, H₂O <3 ppm, C_nH_m <0.5 ppm, O₂ <2 ppm) was introduced in the drift tube through the same tubings as in the standard configuration. The pressures in the drift tube and in the front funnel were monitored using capacitance diaphragm gauges (CDG-500, Agilent Technologies). The drift tube pressure was set around 3.70 Torr (measured accurately by the CDG), and 0.23 Torr higher than the trapping funnel pressure, to ensure no nitrogen enters the drift tube. Lower pressure differential resulted in higher collision cross sections, indicating nitrogen contamination.

Experiments were also repeated with the ‘Alternate Gas Option’ added to the standard configuration. Here, CDGs are connected to the trapping funnel and to the drift tube for all measurements. An additional flow controller admits gas in the trapping funnel, and the flow controller is regulated by a feedback reading of the pressure in the drift tube. We connected a second Tri-scroll 800 pump (Agilent Technologies) to the source region (with an Edwards SP16K connected to the front pumping line), while the original Tri-scroll 800 pump is connected to the Q-TOF region. This configuration stabilizes the drift tube pressure. For nitrogen and helium measurements, the pressure in the drift tube was 3.95 ± 0.01 Torr for helium and 3.65 ± 0.01 Torr for nitrogen. The actual pressure can vary and the results would not change, but the pressure differential between the drift tube and the trapping funnel must always be at least 0.18 Torr.

The data were analysed using the IM-MS Browser software version B.06.01 (Agilent Technologies), which measures the centroid arrival time of a selected peak as a function of the drift voltage and performs all calculations described in Eqns (1–4). The automatic calculations were checked by manually integrating the peaks using PeakFit v4.11 (Systat Softwares, San Jose, CA). The CCS obtained in the two different instrument configurations were the same, but the second configuration makes it easier to reach the same pressure differential every day.

Results

Figure3A shows the mass spectrum of [dTGGGGT]₄, acquired in negative ESI and ion mobility mode, with helium drift gas. The m/z confirms that the tetramolecular complex contains three ammonium ions at all charge states. The most abundant is 5− (m/z = 1499.8), meaning that eight negative charges sit presumably on phosphate groups and three positive charges on the inner cations specifically trapped in-between G-quartets. Figure3B shows the arrival time distribution of [d(TGGGGT)₄ + 3NH₄]^5- at a drift cell entrance voltage of 800 V. Figure3C shows the linear regression of the average arrival time t_A as a function of 1/V, which was used to determine Ω_EXP and t₀. The error from a single regression is on the order of 1 A², and manual peak fitting to obtain the average t_A was helpful in reducing this source of error. CCS distributions can be reconstructed from the arrival time distributions, after determining t₀, using Eqn (5), with t_A and t₀ in seconds, L in centimeter, μ in Daltons:

Figure 3.

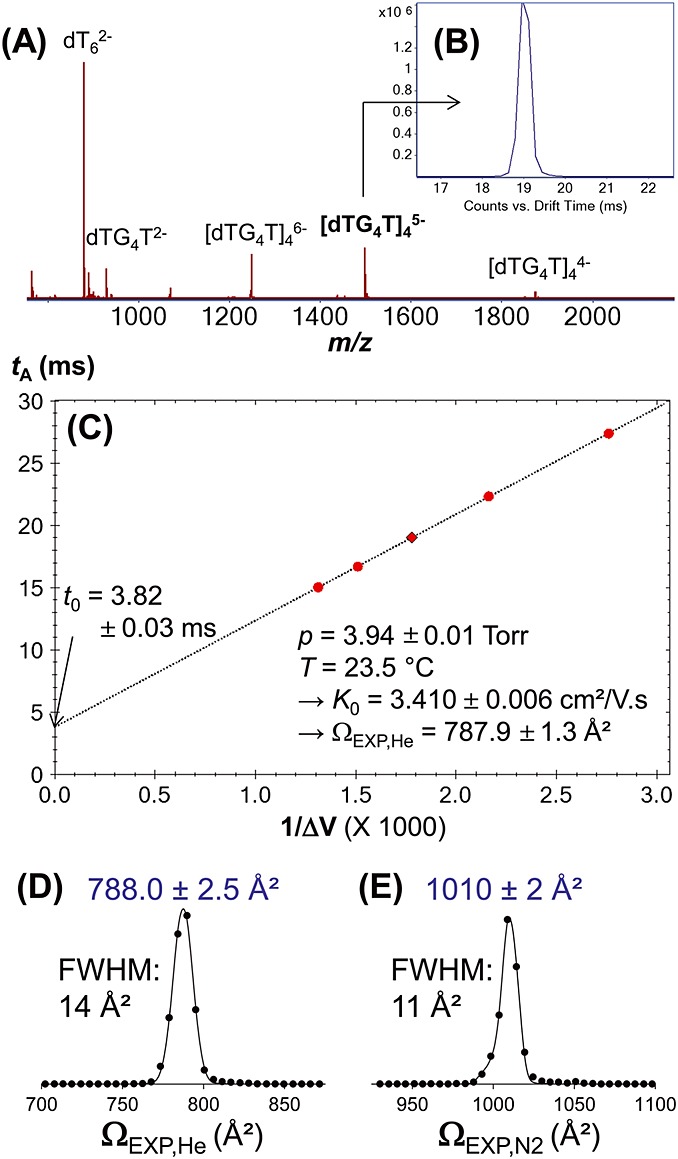
(A) Electrospray ionization mass spectrum of d(TGGGGT) quadruplex in ammonium acetate, sprayed in negative ion mode. dT₆ was an internal standard. (B) Arrival time distribution of [d(TGGGGT)₄ + 3NH₄]⁵⁻ in helium, with a drift cell entrance of 800 V (drift cell exit = 210 V, hence ΔV = 590 V). (C) Linear regression of the average arrival time t_A as a function of 1/ΔV to determine the reduced mobility K₀ and the collision cross section Ω from the slope. (D) Reconstructed collision cross section distributions in helium. (E) Reconstructed collision cross section distributions in nitrogen.

(5)

In helium, we measured Ω_EXP,He = 787 ± 3 Ų (average value ± standard deviation on 10 measurements) without the alternate gas option, and Ω_EXP,He = 789.1 ± 1.6 Ų (7) with the alternate gas option. Overall average is 788.0 ± 2.5 Ų, and a typical CCS distribution is shown in Fig.5D. The CCS peak resolution in helium is ∼55. For the same nucleic acid complex, Gidden et al. had reported an experimental CCS of 775 ± 15 Ų, [20] measured with a home-made, 5-cm-long drift tube.[34] The average helium experimental values differ by 1.5%. In nitrogen, we obtain Ω_EXP,N2 = 1010 ± 2 Ų (six experiments, see Fig.5E for a typical distribution) on both instrument configurations, and the CCS peak resolution is ∼90.

Figure 5.

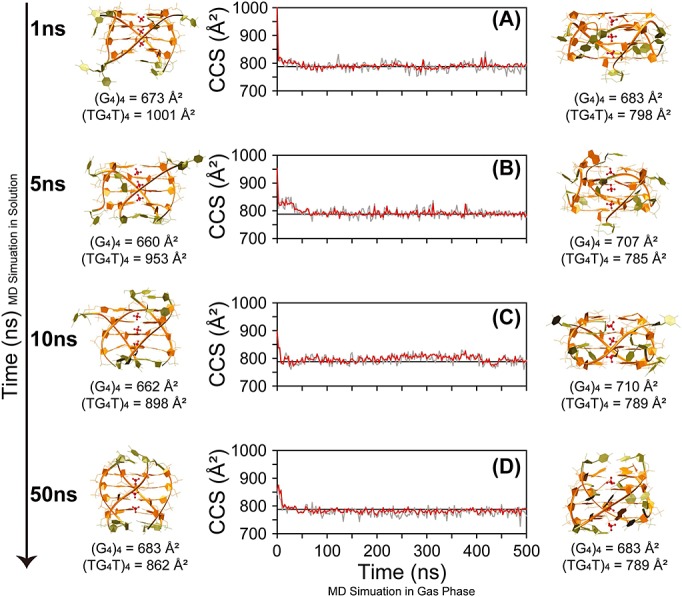
Monitoring of Ω_CALC of [(dTGGGGT)₄ + 3 NH₄]^5- for four gas phase 500 ns MD replicas started from different time points of the solution molecular dynamics (MD): after (A) 1 ns, (B) 5 ns, (C) 10 ns, and (D) 50 ns of MD in solution. Red and grey line are to Ω_CALC obtained by using EHSSrot-Siu and mobcal-He25, respectively. The black horizontal line indicates the average experimental value. The starting structures taken from the solution MD and the final structures of the MD simulations in gas phase are shown on the left and on the right, respectively. Furthermore, the Ω_CALC of the starting structures and the final structures of the MD simulations in gas phase are indicated below each structure. (G₄)₄ refers to the Ω_CALC calculated for the sole G-core (in orange on the molecular models), while (TG₄T)₄ refers to the Ω_CALC calculated for the whole structure.

Travelling-wave ion mobility spectrometry

Principle of travelling wave ion mobility spectrometry

Travelling wave ion guides are stacked ring ion guides (SRIG) enabling RF confinement, and DC potentials are applied on some of the rings (Fig.2B). The DC potentials travel towards the exit of the SRIG. The experimental variables are the wave height and the wave speed, the nature of the gas and its pressure. If the pressure in the SRIG is low (few or no collisions), the device functions as an ion guide. However, if the pressure is sufficiently high that the ions undergo numerous collisions and therefore undergo friction, the time spent in the traveling wave ion guide depends on the ion mobility. Ions are separated according to the transit time in the TWIMS cell because of the fact that collisions slow the larger ions more than the smaller ions, causing them to exit later in time than the smaller ions as the waves sweep them through the cell.[35,36]

Like in DTIMS, ions with higher mobility exit the TWIMS earlier than ions with lower mobility. However, unlike the DTIMS, analytical equations describing ion movement are complicated to derive because the field is not linear and varies both in time and space. Schvartsburg et al.[28] approximated the ion motion using triangular or half-sinusoidal waves and demonstrated that the drift time is related to approximately the Ω². In practice, this exponent and the proportionality constant have to be determined by calibration using molecules of known CCS. Eqn (6) is expressed here in a way it can be compared with Eqn (5).

(6)

Factors A and B include the effect of all instrumental conditions (wave height, velocity and profile, cell length, gas pressure and temperature). The manufacturer provides information to calculate t₀ for each ion mass and charge as a function of the instrumental parameters,[37] and there is no mobility-dependent contribution to t₀ by instrumental design (low pressure outside the TWIMS). The calibration involves prior knowledge of CCSs of a range of ions, which cover the transit time range of the ions of interest. The calibration curve to find A and B is usually represented as Ω′ (Ω corrected for ion reduced mass and charge) as a function of 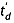(the time spent in the TWIMS):

(7)

If the literature values were obtained in helium, the calibration will provide predicted Ω_EXP in helium, even if other gases (typically nitrogen) may have been used in the TWIMS. However, the relationship between nitrogen and helium CCS depends on the molecule size, charge and chemical nature.[38,39] Therefore, calibrating a TWIMS operated in nitrogen using helium CCSs is more reliable using molecules of similar size, charge and chemical nature as the analytes.

Materials and methods

Experiments were carried out both on a first-generation Synapt HDMS (commonly called ‘Synapt G1’) and a Synapt G2 HDMS. The source and desolvation gas temperatures were 40 °C and 60 °C, respectively. The instruments differ in their TWIMS cell length, pressure, wave profile and optimal heights and velocities. On the Synapt G1, the TWIMS gas was nitrogen at pressure p = 0.532 ± 0.002 mbar, and we used 8-V waves traveling at 300 m/s. Soft ion injection conditions correspond to a bias voltage of 10 V and harsher conditions to a bias voltage up to 30 V. On the Synapt G2, the TWIMS cell is longer, has a helium cell in front (inlet flow maintained at 180 ml/min) and is filled with nitrogen flow regulated so as to read a pressure of 2.760 ± 0.005 mbar on a capacitance gauge (CERAVAC CTR 90, Oerlikon Leybold Vacuum, London, UK) linked to a vacuum controller (Center two, Oerlikon). Soft ion injection conditions were obtained using a bias voltage of 30 V and harsher conditions using a bias voltage of 45 V. The wave profile also differs from the Synapt G1. Optimal separation was obtained using 40 V wave height, travelling at 1000 m/s.

The quadruplex [dTGGGGT]₄ was prepared as described in the Section on Materials and methods. Nucleic acid calibrants included dT₁₀, injected at 2 μM in 50:50 (v:v) water/methanol (Ω_literature = 446 Ų (3−), 537 Ų (4−), 627 Ų (5−) and 641 Ų (6−),[40] and several G-quadruplexes injected at 5 μM strand annealed in 100 mM NH₄OAc, and injected in 20% methanol: d(TTAGGG)₆ (Ω_literature = 989 Ų (5−), 1010 Ų (6−), 1074 Ų (7−, peak favored at low injection energy and with ammonium ions preserved), 1232 Ų (7−, peak favored at high injection energy and without ammonium ion adducts) and 1405 Ų (8−, always denatured),[41] d(TTAGGG)₄ (Ω_literature = 789 Ų (5−, to record only on the species with no ammonium adducts obtained in relatively harsh injection conditions) and 805 Ų (6−),[41] dGGG(TTAGGG)₃ (Ω_literature = 688 Ų (4−), 718 Ų (5−),[42] dGAGGGTGGGGAGGGTGGGGAAG (Ω_literature = 701 Ų (4−), 757 Ų (5−, to record on the complex with two ammonium ions and only in soft injection conditions), 696 (5−, to record on the complex without ammonium adduct and in harsh injection conditions) and 900 Ų (6−, denatured),[42] and the dimer of the latter sequence Ω_literature = 1098 Ų (7−) and 1113 Ų (8−).[43] All literature values are in helium. The calibration curves were generated using Sigmaplot 12.5 (Systat software).

Results and discussion

Figure4A shows the calibration for the Synapt G2 mass spectrometer (the calibration for the Synapt G1 can be found in the supplementary material of reference[44]). The black line shows the curve fitting using Eqn (7). The blue lines delimit the 95% confidence band: the interval in which there is 95% confidence that the true value lies, assuming that the calibrants literature measurements were not biased. Here, we used calibrant literature data coming from two different labs, and all data fit the same trend, increasing our confidence that no bias is introduced. The red lines delimit the 95% prediction band: the interval in which there is 95% chance to make one or more future observations if the measurement is repeated in a similar way as the given data were sampled (here, with a drift tube similar to those used for measuring the calibrants).

Figure 4.

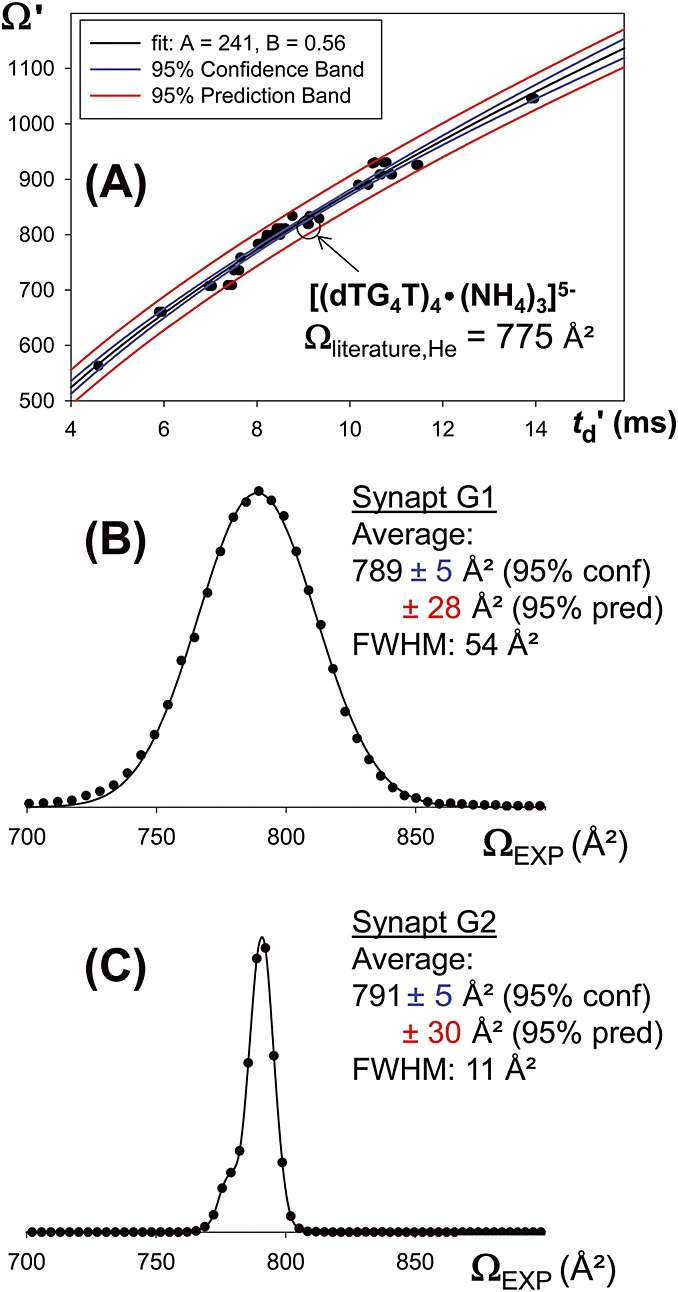
(A): Oligonucleotide-based calibration curve for the Synapt G2 HDMS The datapoint of the structure of interest is circled: it falls outside the 95% confidence band and inside the 95% prediction band. Ω_literature refers to data of reference [20] (B): Reconstructed collision cross section distributions for the ion [(dTG₄T)₄•(NH₄)₃]⁵⁻ on the Synapt G1 and (C) Reconstructed collision cross section distributions for the ion [(dTG₄T)₄•(NH₄)₃]⁵⁻ on the Synapt G2. Summary collision cross section data of the main peak.

Figure4B and 4C shows the CCS distributions reconstructed from the arrival time distributions obtained on the Synapt G1 and Synapt G2, using their respective calibration factors. The position of the peak average, obtained by Gaussian peak fitting is virtually the same (within the 95% confidence interval of 5 Ų), although the experiments were completely independent. This peak position also matches with the DTIMS measurements.

The prediction interval of the TWIMS calibration curve is particularly useful to assess the comparison between TWIMS measurements and measurements carried out on other instruments in other laboratories: measurements carried out independently have 95% chance to fall in this prediction interval. With the current set of calibrants for oligonucleotides, the best prediction interval (in the middle of the curve where there is least extrapolation) is 3% of the average CCS. The previously published literature value (775 ± 15 Ų) [20] falls in this interval.

The accuracy of CCS data obtained from TWIMS crucially depends on the accuracy of the calibrant data. For oligonucleotides, the number of calibrants selected for calibration is limited. CCS data on other oligonucleotides exist in the literature, and we tried to include them all. However, we could not always reproduce the literature data and in many cases, obtained calibration points that were clear outliers. The reader may have noticed the level of detail in which the peak attribution is described in the Section on Materials and methods. The non-trivial point when calibrating using literature data is that the gas-phase structure and hence the CCS depends on gas-phase activation and possible rearrangements. Some of the calibrant structures used here undergo such rearrangement. Prior experience in the drift tube measurement with some structures that served for calibration made it easier to assign the peaks in the TWIMS experiments. Peak assignment is also more secure if exactly the same instrument source and ion transfer geometries are used for the calibration and the experiment. For this reason, a modified Waters Synapt in which the SRIG is operated in a drift tube mode (without travelling waves)[38,45–47] was built and calibration data were recorded. In the future, an inter-laboratory calibration would be useful to identify the most reliable and robust calibrants.

Relating ion mobility spectrometry measurements to molecular structure: how to choose the simulation strategy?

Introduction

The measured CCS distributions reflect the conformational space that molecules explore in the gas phase under the experimental conditions, but IMS data alone do not offer structural interpretation. IMS data can however be interpreted using molecular modelling techniques. The gold standard for structural biology interpretation of IMS data is a satisfactory match between the experimental CCSs and those calculated on a pool of candidate structures generated via computational chemistry techniques. This section explains how to choose or develop a proper simulation strategy to generate structures, and the comparison between calculated and experimental data will be discussed in Section on how to obtain theoretical collision cross section from atomistic models.

Computational approaches

Protein Data Bank (PDB) entries of biomolecules resolved at atomistic level, coming from either X-ray crystallography or NMR techniques, represent a valuable starting point. They can be used either as initial coordinates for the conformational sampling or for first guess of structural assignment after a gas phase energy minimization, or quantum optimization if size-wise applicable. If no atomic-level structure is available, software to manually build initial atom coordinates include, but are not limited to Hyperchem,[48] Discovery Studio,[49] Maestro,[50] NAB[51] and Avogadro.[52]

Computational chemistry methods include quantum mechanical (QM) methods and classical methods. QM methods are capable of describing the electronic structure, thus, they achieve a high level of accuracy, but are typically viable only for small systems. QM methods include ab initio geometry optimization methods, such as Hartree-Fock (HF), post-HF like coupled cluster (CC) and perturbation theory methods, density functional theory (DFT) and semi-empirical methods (useful for systems ranging from hundreds up to thousands of atoms in size).[53] Then, ab initio molecular dynamics (MD) methods, such as Car–Parrinello MD and Born–Oppenheimer MD, are to be implemented in case one is interested into electrons quantum effects on nuclei classical motion.

Conversely, classical methods describe large biosystems properties by a parameterized potential energy surface, and they include the molecular mechanics for optimization procedures, Monte Carlo (MC) and MD techniques for sampling. There are pros and cons in applying MD or MC, and one technique is not better than the other, as both work out ensemble properties. The pro of MD, a deterministic method, is that time-dependent properties can be studied (indeed, the time variable is absent in MC), whereas the pro of MC, a stochastic method, lies in its higher flexibility in sampling regions of the configuration space and, hence, the user can in principle ‘decide’ to explore certain conformational areas of interest.[54]

A first method selection criterion is the size of the molecular system under investigation. MD using classical methods are preferred for biomolecules, such as proteins, protein/protein complexes and large oligonucleotides, where a satisfactory conformational sampling is more desirable than accounting for electronic structure effects.[41,55,56] MD simulations can however be hampered by multiple local energy minima, where the biomolecule can be trapped. Several enhanced sampling techniques allow the species to overcome energetic barriers and explore other conformational basins, for example simulated annealing molecular dynamics,[57–60] replica-exchange molecular dynamics [61–63] and adaptively biased molecular dynamics. [64,65] On the other hand, when the molecular system taken into account is too big, as for instance large multiprotein complexes (>500 kDa), all the aforementioned atomistic methods are still too computationally expensive, but some qualitative models can be built instead, such as (bead-type) coarse grained models.[37,66–69]

Force fields

A possible pitfall intrinsic in classical MD simulations in gas phase is related to the use of force fields (FFs) that are presently parameterized based on high-level quantum calculations, but eventually tested and tuned in aqueous phase (with either explicit or implicit water models). For example, in the development of FFs, such as AMBER[70] and CHARMM[71] (two of the most popular in simulations of biosystems), the charges are derived and/or optimized to be compatible with interactions with the highly polarizing water molecules, and then all the parameters of the remaining contributions (stretching, bending, torsion, etc.) to the FF are generated subsequently. In principle, to run simulations of biomolecules in solvent-free environments, one should recalculate the charges in the gas phase and re-optimize all the FFs parameters, but unfortunately, structural biology experimental data in gas phase against which the comparison should be performed are not available. Therefore, the sampling in gas phase using the available FFs has to always be considered with caution.

Notwithstanding that, Orozco et al. have carried out control gas phase MD simulations for DNAs in which they scaled all the AMBER charges by a factor of 0.8 (so that to take into account the depolarization that all the bonds would undergo during the dehydration process), showing that no major differences arise in the final average properties.[30]

Charge location

To generate the charge states detected from the IM-MS spectra, the neutralization of the titrable groups of the macromolecule under investigation is commonly accepted. In the case of proteins, the basic and acidic side chains plus the N- and C-terminus represent the titrable groups that can be neutralized by protons to achieve the desirable net charge state. Therefore, many ways of distributing the charges among these titrable groups are compatible with a specific net charge shown in the ESI spectra. To tackle this issue, different methodologies have been developed, which either take into account how the acidic strength (the pK_a) of the (conjugated) acid (e.g.−COOH and−NH₃⁺), varies depending on the surrounding environment, going from residues deeply buried in the protein (very low pK_a) up to residues surrounded nearly by only water (with a pK_a practically equal to that of the lone residue in bulk water),[55,72] or consider energy states resulting from different protonation schemes. [73,74]

In the case of nucleic acids, assuming that all the phosphates can be equally titrable, a different strategy must be used to obtain the net charge state, and two main methods are available in literature: the distributed charge (DC) and the localized charge (LC) method.[75] With the former, the partial charges of all the phosphate groups present in the oligonucleotide are scaled by a proper factor in order to achieve the aimed net charge; with the latter, one neutralizes as many phosphate groups as sufficient to reach the needed total charge by adding one proton to the available oxygen atom. The LC method requires firstly the generation of all the possible substates (equal in number to 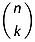, where n is the number of phosphate groups and k is the number of protons to be added), and then the selection of the most representative one according to a chosen criterion (usually the lowest in energy). Both DC and LC methodologies applied on DNA double helix [75] and G-quadruplex cores[76] did not give remarkable different results in terms of structures and energetics; thus, in presence of relatively large systems, if the explicit presence of protons is not needed, the DC model is preferred because it is more easily implemented than the LC method. Nevertheless, the LC method is imperative if one is interested in the investigation of possible intramolecular proton transfer reactions.[77]

Materials and methods for [dTGGGGT]₄ molecular dynamics simulations

The [dTGGGGT]₄ G-quadruplex DNA structure represents a suitable system to assess the structure determination by matching experimental and theoretical CCS. Even though the stability of the G-core was already assessed in the gas phase,[76] we chose to investigate the robustness of the MD trajectories of this system by using diverse starting conformations, differing for the initial positioning of thymine residues. We wanted (i) to define the possible convergence of the simulations to a common ensemble, despite the inclusion of the thymine residues in the MD simulation runs; and (ii) to better evaluate the experimental results, we wanted to appreciate whether and how the positioning of the thymines influences or not the theoretical CCS calculations. To avoid subjective (user-dependent) definition of the starting points, we used an MD simulation trajectory in solution to generate different structures with various thymine positions.

All simulations have been carried out using the AMBER12 suite of programs [78] and applying the parmbsc0 force field.[79] The parmbsc0 force field is the improved version of Cornell et al. force field [80] and, together with the CHARMM force fields,[81] is the best and most popular force field for nucleic acids.[82] Moreover, parmbsc0 was already successfully used by Orozco et al. for computational studies of diverse nucleic acids structural motifs in gas phase;[44,75–77] therefore, we opted to make use of this force field, which can be readily utilized within the Amber12 suite of programs.

The crystal structure of the parallel [dTGGGGT]₄ G-quadruplex (PDB entry 352D)[11] was relaxed performing a 50 ns MD run in explicit water. The module pmemd, which uses the Particle Mesh Ewald (PME)[83] method to compute electrostatic interactions, was used and the radial cut-off for the non-bonded interactions was set to 8 Å. This is a crucial step to be applied when dealing with MD simulations in explicit water and periodic boundary conditions: PME method implemented to calculate the pair-wise electrostatic forces increases both computation speed and accuracy with respect to the direct Coulomb summation and, as we shall discuss in the succeeding section, the approach is totally different when the same electrostatic interactions are to be computed in gas phase.

Four snapshots (specifically those at 1, 5, 10 and 50 ns) of this solution simulation were selected to create the starting structures needed for four independent gas phase MD runs, the detailed procedure of which is given in the Supporting Information. Water molecules and counter ions external to the core were removed; then, the charge state of the models was adapted with the predominant observed in ESI-MS experiments (corresponding to−5) by applying the DC model.[76]

Gas phase MD simulations were run with the sander module of Amber12, in canonical ensemble (at T = 298 K) using a weak coupling thermostat,[84] implementing a direct Coulomb summation for evaluating the electrostatic interactions, using an integration time-step of 1 fs and no radial cut-off for the non-bonded forces. Because the screening effect of the solvent is missing in vacuo, (1) we set no radial cut-off for both Coulomb and van der Waals interactions and (2) the PME algorithm can not be applied. In order to calculate the Ω_CALC from the four gas phase MD simulations, snapshots were collected at each 2.5 ns, for a total of 800 candidate geometries (see the last paragraph of the section on how to obtain theoretical collision cross section from atomistic models for the results).

For all the simulations (solution and gas phase), frames were collected every 2 ps and the resulting trajectories analysed with cpptraj module [85] in Ambertools13.[86] Pictures were created with VMD software.[87]

Results and discussion

Solution molecular dynamics simulation

The MD simulation in solution yields a stable trajectory, as demonstrated from the low variation of the structural descriptors of the system (Fig S1). The radius of gyration (R_g) accounts for an initial compaction of the structure, which take takes place in the first few nanosecond of the simulation, then remains constant at a value of ∼10 Å for the rest of the dynamics (Fig S1, panel a). The average backbone root mean square deviation (RMSd) of the G-tetrads (1.2 ± 0.2 Å) is significantly lower than that of all the backbone atoms (4.6 ± 0.4 Å), denoting the great stability of the stacked G-quartets core. Wobbling effects are experienced by the terminal thymines with an average RMSd of 2.9 ± 0.1 Å (Fig S1, panel b). The rigidity of the G-quadruplex core is also highlighted by the root mean square fluctuations (RMSF) calculation: none of the guanines is subjected to fluctuations exceeding 1.2 Å, while thymines are more mobile, with fluctuations ranging from 1.5 to 5.5 Å (Fig S1, panel c). To further ascertain the maintenance of the Hoogsteen H-bonding geometry, we also analysed the interatomic distances between guanine N1-O6 and N2-N7 atoms (directly involved in the characteristic G-quartets H-bonds set), which are maintained throughout all the simulation run, (Fig S1d). All results suggest that only one major conformational transition occurs during the simulation run: the rearrangement of the thymines nucleobases, which fold above the rigid quadruplex core, in agreement with solution NMR measurements.

The snapshot structures obtained after 1, 5, 10 and 50 ns simulation in solution are shown on the left hand side of Fig.5. The G-quartet core is basically unchanged, whereas the thymines, located on the outside in the starting point (X-ray crystal structure) close on the top and bottom tetrads within 50 ns. Interaction between thymines agrees with NMR data. This illustrates that relaxing crystal structures (that could be hampered by lattice effects) in water prior the running of the MD simulations in gas phase is recommended, particularly when the question is whether the solution phase structure is preserved in the gas phase.

Gas phase molecular dynamics simulation

The four snapshots mentioned earlier were selected as starting structures for gas phase simulations. We will refer to the four ensuing gas phase MDs as replicas 1 to 4. Each [d(TGGGGT)₄ + 3NH₄]⁵⁻replica was simulated for 0.5 µs.

The results, summarized in Figs S2–S5, show that all the performed simulations lead to stable trajectories, sharing a common compaction that occurs during the first nanoseconds of the MD simulations, as depicted from the variation of the R_gs (Figs S2–S5, panels a). In agreement with the experiments, all the G-quadruplex-ammonium ions complexes are retained; in particular, their positions in the central channel of the structures do not experience fluctuations exceeding 0.7 Å for replicas 1 to 3, and reaching the 1.4 Å for replica 4 (Figs S2–S5, panels c, depicted in grey). The four replicas of the gas phase MD simulation show that (i) memory of the G-tetrads geometry from the starting conformations, as shown from the average RMSDs of the guanines that quickly plateaus at ca. 1.4 Å, and (ii) rearrangements of the thymine residues that occur in the first few nanoseconds of the simulations and are maintained during the entire trajectories, as shown from the average RMSDs of the thymines plateau at ca. 4 Å for replicas 1 to 3, and ca. 6 Å for replica 4 (Figs S2–S5, panels b). Thymine bases interact mostly with the grooves of the quadruplex.

Representative gas-phase structures for each replica are shown on the right hand side of Fig.5. The [dTGGGGT]₄ G-quadruplex DNA structure is clearly able to maintain its G-core structuring in the gas phase, even though the flipping of the terminal thymines can lead to slightly diverse final conformers.

How to obtain theoretical collision cross section from atomistic models?

Introduction to the different collision cross section calculation models

The experimental CCS measured by IM-MS is the momentum transfer collision integral 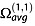averaged over all possible ion collision geometries defined by the angles θ, ϕ and γ. 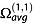reflects the effect of the collisions on slowing down the ion and therefore depends also on the scattering angle χ (the angle through which the gas is deflected after the collision with the ion). 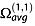is obtained by integrating the momentum transfer cross section over the impact parameter b and relative velocities g:

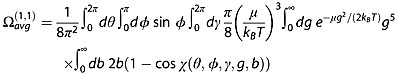(8)

Several computational models (schematized in Fig.6) have been developed to approximate , and those computed values will be denoted Ω_CALC. The most widely used CCS calculation methods are the trajectory method (TM),[88,89] the exact hard sphere scattering (EHSS)[90] and the projection approximation (PA).[88,90] All were initially parameterized to evaluate Ω_CALC with helium collision gas. Several optimizations either of the calculation algorithm or of the parameterization,[45,91,92] including for nitrogen collision gas,[93,94] have been proposed. This section aims at clarifying these variations. Besides, new computational methods are still being developed to provide Ω_CALC in a faster and/or more accurate way and in different gases. Among these methods are the projection superposition approximation (PSA) described below,[95–98] the diffuse hard spheres scattering and diffuse trajectory models [99] and the scattering on electron density isosurfaces.[100]

Figure 6.

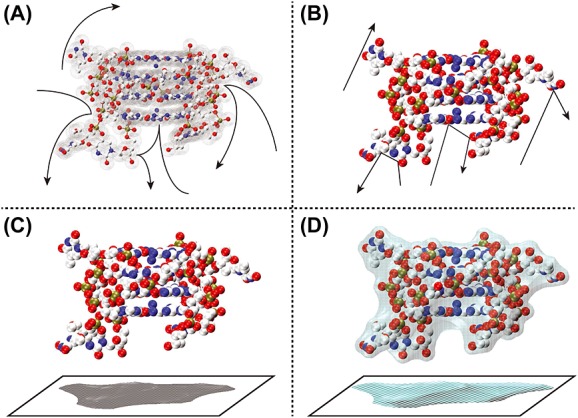
Schematic representation of how the different models calculate Ω_CALC. (A): Trajectory model: the long-range interactions between the drift gas and the polyatomic ion are taken into account to determine gas deflection trajectories (shown as arrows) and the scattering angle. (B): Exact hard sphere scattering model: the ion's atoms are considered as hard spheres and the scattering angles between the incoming and departing collision gas atom trajectories (shown as arrows) resulting from the collision with the polyatomic ion are calculated. (C): Projection approximation (PA): the ion's atoms are considered as hard spheres and the average Ω_CALC is defined by calculating the projected ‘shadow’ of the polyatomic ion, averaged over all possible orientations. (D): Projection superimposition approximation: similar to PA, but the ion's atoms are considered as ‘soft’ spheres, accounting for the collective size effect by superimposition of all atomic contributions, and the resulting value is scaled by a shape factor ρ, which takes into account the shape effects by assessing the molecule's concavities.

Trajectory model

The TM simulates the trajectories in a realistic potential that accounts for the long-range interactions between the drift gas and the polyatomic ion by evaluating the effective potential of the ion (using Lennard-Jones potentials):

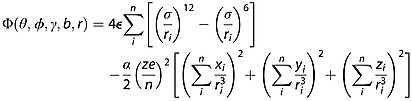(9)

The first term is a sum of Lennard-Jones two-body 6–12 short-range van der Waals interactions between the collision gas and individual atom i in the polyatomic ion. The second term is the charge-induced dipole interaction. ε and σ are the Lennard-Jones parameters (ε is the well depth and σ is the distance where the potential become positive), α is the polarizability of the IM collision gas and n represents the number of atoms in the polyatomic ion. This potential is then used to determine the scattering angle of the incoming and departing collision gas atom trajectories.

The evaluation of the Ω_CALC with TM is not only the most physically appealing but also the most computationally expensive type of calculation, especially if applied to large polyatomic ions (>1000 atoms). It requires information about the intermolecular potential that should be obtained by fitting measured mobilities as a function of temperature. A TM algorithm is available in the mobcal program,[101] and the original parameters were obtained based on ion mobility measurements of carbon clusters in helium collision gas.[88,89]

In 2008, Kim et al. proposed a modified TM algorithm and parameterization to calculate the Ω_CALC with nitrogen collision gas.[94] They modified the potential of Eqn (9) by taking the Lennard-Jones parameters described in the universal force field [102] and setting the polarizability of neutral gas for N₂, without neglecting the ion–quadrupole interaction and molecular orientation due to the linear geometry of N₂. Based on Kim's modified TM, Campuzano and Bush parameterized both the N₂-based and the He-based trajectory method algorithms by applying a scaling factor to the Lennard-Jones parameters, based on IM measurements on drug-like molecules. The optimized N₂ and He trajectory method source codes, mobcal_He and mobcal_N2, are provided upon request to the corresponding authors .[45]

Exact hard spheres scattering

The EHSS model assumes that both the individual atoms of the polyatomic ion and the collision gas behave as hard spheres.[10] EHSS computations determine the scattering angles from the trajectories resulting from the gas collision with the polyatomic ion. Therefore, Eqn (8) is approximated by the orientationally averaged hard-sphere CCS Ω,

(10)

where φ, and γ are the spatial angles defining the ion orientation and Ω_dir is the corresponding directional cross section, which depends on how the interaction between the ion and the collision gas is evaluated. In EHSS, the scattering angle χ of the collision gas is taken into account as follows:

(11)

An EHSS algorithm is available in the original mobcal program,[101] where original atom size parameters are provided again based on IMS measurements on carbon clusters. In 2007, A. A. Shvartsburg proposed EHSSrot, a more computationally effective algorithm in which the EHSS calculations are accelerated by reducing the number of ion rotation steps through evaluation of multiple ion/gas collisions per orientation. The EHSSrot source code is provided for academic use upon request to the corresponding author. [92] Regarding the atom size parameterization, Siu et al. optimized the EHSS parameters by varying the collision radii of He-H and He–X atoms (where X is C, N or O) in order to match IM experiments from several peptide ions, which structures could be computed with high accuracy DFT calculations.[91] Siu's atom parameters can be included either in the mobcal algorithm or in the EHSSrot algorithm.

Projection approximation

The PA approach calculates Ω_CALC by finding the average ‘shadow’ of the polyatomic ion (onto a defined plane) by rotating the structure through all possible orientations. The projection of the polyatomic ion onto the yz -plane is computed as follows:

(12)

where M is unity when a collision occurs for the configuration defined by φ, γ, y and z, and null otherwise. PA algorithms are the most simple and computationally effective and can be found in the sigma program by Bower et al. [103] and in mobcal.[101] It is now known that the PA greatly underestimates 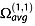because the gas slow-down effect is greater in cavities than on convex surfaces, and the projection masks the cavities effect. Consequently, PA correctly estimates 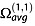only for small convex molecules (10–200 atoms).

Projection superposition approximation

The computational speed of the PA method inspired further refinements to render the method more accurate for very large molecules, including those containing cavities. Bower et al. developed the PSA model.[95–98] PSA is based on the PA concept, improved by taking into account (1) the cooperative size effect by superposition of diffuse atomic contributions and (2) the presence of cavities using a shape factor ρ. This algorithm, whose atomic parameters were obtained for H, C, N, O, Na and K based on experimental cross section measurements, is made available to the community as a web service[104] to compute Ω_CALC in both He and N₂.

Materials and methods

The calculations with all the listed algorithms (except for PSA that is available as web server) were carried out on an Intel Xeon Processor E5-2650 v2 server, equipped with two CPUs consisting of 16 hyper-threading cores each. One thread per computation was used, because none of the previous listed codes is parallelized.

For TM, the following programs have been tested: mobcal,[88] mobcal-He,[45] mobcal-N2[45] and their related optimizations. In mobcal and mobcal-He source codes, atom masses and sizes are defined starting on lines 586 and 2616. We added there parameters for phosphorus, by setting the atomic energy and the van der Waals distance parameters (the variables eolj and rolj in the source codes) equal to those of silicon. Furthermore, we also tested a slightly modified version of mobcal-He and mobcal-N2, in which we decreased the impact parameter (reported as imp in the source codes and representing the number of points in the Monte Carlo integration of the impact factor and orientation) from 1000 to 25, to check the influence of this parameter on the balance between calculation speed and accuracy. We will refer to these modified versions as mobcal-He25 and mobcal-N25. Besides, because of the size of our system (795 atoms), the mobcal-N2 and mobcal-N25 algorithms were not able to compute the CCS in a reasonable computer time. We therefore tested modified input files excluding the partial atomic charges (keyword ‘none’ in line 5 of the input file). These modified algorithms are referred to as mobcal-N2-mod and mobcal-N25-mod.

For EHSS, we used all mobcal programs (which are equivalent for the EHSS part) and EHSSrot. In the latter, the collision radii of the atoms in He as collision gas are defined starting on line 52; here, we added the optimized parameters proposed by Siu et al.,[91] and we will refer to this optimized version of the algorithm as EHSSrot-Siu. For PA, we used mobcal with the original parameters, with the addition of phosphorus parameters. For PSA, theoretical CCS data were obtained by participating to the beta-testing of WebPSA, the web interface provided by the University of California, Santa Barbara.[101]

Results and discussion: matching between theoretical and experimental collision cross section for the [dTGGGGT]₄ quadruplex nucleic acid

The Ω_CALC values were calculated on 200 structures collected along the gas-phase MD simulation of replica 1. After discarding those coming from the first 25 ns of the MD simulation in the gas phase, the CCS values vary by no more than 1.5% (Fig.5A). The averages and standard deviation are listed in Table 1, together with the percentage differences between experimental and theoretical values (<%diff> = <[(Ω_CALC–Ω_EXP)/Ω_EXP] × 100%>) and the computer time required per structure calculation.

Table 1.

Summary of theoretical collision cross section of [(dTGGGGT)₄ + 3NH₄]⁵⁻ replica 1: average values with standard deviations (Ω_CALC, reported in Ų); average percent difference between experimental and theoretical CCS (<%diff> = <[(Ω_CALC- Ω_EXP) /Ω_EXP]x100%>); and computer time required per structure calculation (time, expressed in minutes); n. a. stands for not acquired

Method	Algorithm	ΩCALC	<%diff>	Time (min)
Trajectory method	mobcal	810 ± 12	2.8%	∼10
	Mobcal-He	788 ± 7	0%	∼1080
	Mobcal-He25	788 ± 14	0%	∼35
	Mobcal-N2	n. a.	n. a.	∼40320
	Mobcal-N25	n. a.	n. a.	∼25920
	Mobcal-N2-mod	n. a.	n. a.	∼11520
	Mobcal-N25-mod	1004 ± 15	−0.6%	∼360
Exact hard sphere scattering	mobcal	813 ± 8	3.2%	∼10
	Mobcal-He	813 ± 8	3.2%	∼1080
	Mobcal-He25	813 ± 8	3.2%	∼35
	EHSSrot	816 ± 8	3.5%	∼1
	EHSSrot-Siu	789 ± 7	0.1%	∼1
Projection approximation	mobcal	687 ± 6	−12.8%	∼10
	Mobcal-He	687 ± 6	−12.8%	∼1080
	Mobcal-He25	687 ± 6	−12.8%	∼35
Projection superposition approximation	He	781 ± 14	−0.9%	∼15
	N2	941 ± 17	−6.8%	∼15

In helium, Ω_CALC and Ω_EXP match within 4%, except for the PA method that underestimates the CCS by 12.8%. This underestimation was expected because our molecule is much larger (795 atoms) than typically appropriate for PA (10–200 atoms). The PSA method has correctly taken into account the effect of the cavities. Both for TM and EHSS, the original atom parameterizations give rise to a Ω_CALC about 3–4% higher than Ω_EXP (with TM calculations converged with a precision within 1.4%), and more recent parameters (implemented in mobcal-He for TM and Siu's parameters for EHSS) lead to a very good match (within 1%, with TM calculations converged with a precision within 1.4%). The EHSSrot-Siu calculations were 1000 times faster than using mobcal-He. Reducing the impact parameter from 1000 to 25 in mobcal-He reduced the computation time by a factor of 30 (from 18 h to 35 min per structure) and led to the same average value and twice the standard deviation (with calculations converged with a precision within 7.2%).

The perfect match (within 1%) may have been obtained just by luck with one single MD trajectory. To test the robustness of our conclusion on the best matching computational method in helium, the same procedure was followed for EHSSrot-Siu and mobcal-He25 on the three other replica, that is, with different starting structures coming from different points of the solution MD. The results are summarized in Fig.5 and Table 2. The data show that the solution phase structures experience a significant decrease of the CCSs while in the gas phase. By measuring the CCS of the starting and final conformations of the four replicas with and without the thymine residues, we find that the CCS of the G-quadruplex core is not undergoing significant changes, denoting that the decrease of the CCS is mainly due to the rearrangements of the thymine residues, as anticipated from the variations of the structural descriptors of the replicas during the MD simulations in gas phase (see also Figs S2–S5).

Table 2.

Summary of Ω_CALC obtained for each [(dTGGGGT)₄ + 3NH₄]^5- replica through EHSSrot-Siu and mobcal-He25 algorithms: average values with standard deviations reported in Ų

Replica	ΩEHSSrot-Siu	Ωmobcal-He25
1	789 ± 7	788 ± 14
2	791 ± 9	793 ± 13
3	798 ± 10	795 ± 15
4	782 ± 6	778 ± 13
Av.	790 ± 10	788 ± 15

Although the structures differ with respect to the thymines positions relative to the G-quadruplex core, the average Ω_CALC of each trajectory matches remarkably well with Ω_EXP. This gives us confidence to ascertain that the modified atom parameters, although optimized on molecules of a different chemical nature, are transferrable to nucleic acids (at least in the size range around 24 bases). The results also underline, however, that several different structures (in the present case with different thymine positions) can give the same Ω_CALC. It is also possible that all structures with all the different thymine placements are contributing to the observed population. Note also that a narrow Ω_EXP distribution indicates either that all structures present in the population have a narrow distribution of 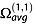or that structures that could have a broader distribution of 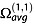interconvert rapidly compared with the time scale of the experiment.

In nitrogen, the only TM calculation that can be carried out within affordable computational time (yet still 6 h per structure) is using mobcal-N25-mod, with a decreased number of impact trajectories and without considering partial charges. The agreement between the calculation and the experiment is again notable (within 1%, with calculations converged with a precision within 7.7%). The PSA calculations in N₂ are 25 times faster than with this modified TM, but unfortunately, PSA in N₂ underestimates the CCS by 6.8%. It is important to note that, contrary to helium parameters, nitrogen parameters for PSA are still preliminary.

The quest for a universally applicable and computationally affordable method to compute CCSs is however far from finished, particularly for other gases than helium. The [dTGGGGT]₄ quadruplex structure is a good candidate to benchmark the applicability of novel methods to negatively charged nucleic acids. Meanwhile, for structural interpretation applications, it is advisable to keep to helium CCS measurements and calculations. Based on our results, for future high throughput nucleic acid CCS determination during MD trajectories, we will choose the EHSSrot-Siu combination, which is the most convenient because it is the fastest. For rigorous confirmation, the Ω_CALC of representative structures will also be checked with TM and PSA.

Conclusions and perspectives

In summary, relative CCS values for a system of given size inform us on whether the ion is more compact or more extended. Molecular modelling's added value is to provide a spatial representation of ion structures that are compatible with the experiment. Quantum mechanics or molecular dynamics simulations describe structures with atomistic detail. However, the information from the CCS measurement of each separated species comes only from the average value (entailed with error) and from the peak width (if larger than the instrumental function). Even for the particular rigid DNA molecule presented here, it is important to realize that several structurally and energetically realistic structures are compatible with a given experiment. In other words, the solution is not unique, although often a single representative image is chosen to illustrate the discussion of IMS results. These images should be interpreted as representative structure(s) from an ensemble compatible with the experiment. Extensive modelling and computational resources are required to ascertain how large this ensemble can be.

One criterion for delimiting the ensemble of compatible molecular models is matching values of Ω_EXP and Ω_CALC. This tutorial has highlighted the different sources of error pertaining to the three key steps: the CCS measurement, the generation of the molecular models, and the calculation of the CCS from the models.

The CCS measurements are subject to experimental errors. The prediction intervals of the Synapt calibrations tell us that for nucleic acids, there is a 95% chance that any repeated measurement by any lab would fall within 3% of the average value. The reproducibility of CCS measurements with current commercial instruments is actually much better (standard deviation between average values is less than 1%). Improvement must therefore come from reducing systematic biases. An inter-laboratory study of CCS measurements, with different instruments (commercial and non-commercial) would be needed to approach true values for a set of compounds that could be then used by the community for quality control, calibration or internal standard correction of the CCS. Such an incentive is currently under way in Europe.

On the molecular modelling side, the biggest challenge for biomolecules larger than 100 atoms is to properly explore realistic conformational ensembles. In the particular case where large systems were measured using soft ion desolvation and transfer in order to preserve as many structural features as possible from the solution to the gas phase, the phase space exploration can be biased voluntarily. This approach was chosen here: a plausible structure is modelled first in solution, then solvent and counter-ions not observed in the mass spectra are removed, charges are modified to mimic the experimental charge state and the structure is left to evolve in the gas phase. The confrontation of these modelling results with the experiments can teach us what structural features are maintained from the solution to the gas phase (and for how long, depending on the temperature). They can also potentially teach us something on the ionization mechanism and specifically what happens to ion structure upon transfer to the gas phase. Modelling the ESI process to generate solvent-free polyatomic ions and the subsequent ion structural changes in the gas phase however encounters three major challenges to be addressed in the future as follows: (1) realistic description of solvent evaporation effects on the species conformation, (2) partial charges location for a given charge state, and (3) the time scale (milliseconds for an IMS experiment). The first two issues have not yet been clarified for all biological molecules, although several attempts been made in this direction, [55,72,74,75,105–107] whereas the latter point would require a rather nowadays unaffordable computer time, above all for large systems like biopolymers (to the best of our knowledge, the sub-milliseconds time scale in a MD simulation in gas phase has been achieved only for a 7-mer oligonucleotide).[77]

Finally, although there is still room for improvement in CCS calculation approaches, algorithms and parameterization (especially for gases other than helium), we were pleased to find out that several of the currently available methods, although developed and parameterized for totally different molecules, transpose well to the 24-nucleotide nucleic acid structure studied here. This is an important stepping stone for future studies of other nucleic acid structures, for which IMS-MS can bring important insight on the populations coexisting in solution. It will be important for future work to further how robust each CCS calculation method can be when applied to ions of diverse chemical nature and different sizes, shapes and degrees of flexibility. For that, reference molecules for which the gas-phase structure is predicted robustly, in a similar way to the (dTGGGGT)₄ quadruplex nucleic acid, should be preferred. Ideally, calibrants envisaged for an inter-laboratory experimental calibration study should also ideally have robust predicted gas-phase structure. Meanwhile, for all readers interested in using IMS-MS to investigate ion structures in the gas phase, all three steps of this tutorial will have to be carried out carefully for the system of interest.

Supporting Information

Additional supporting information may be found in the online version of this article at the publisher's web site.

Supporting info item