Genetic linkage analysis in the age of whole-genome sequencing

Abstract

For many years, linkage analysis was the primary tool used for the genetic mapping of Mendelian and complex traits with familial aggregation. Linkage analysis was largely supplanted by the wide adoption of genome-wide association studies (GWASs). However, with the recent increased use of whole-genome sequencing (WGS), linkage analysis is again emerging as an important and powerful analysis method for the identification of genes involved in disease aetiology, often in conjunction with WGS filtering approaches. Here, we review the principles of linkage analysis and provide practical guidelines for carrying out linkage studies using WGS data.

Linkage analysis was the predominant statistical genetic mapping approach used in the latter half of the twentieth century. More recently, the focus shifted to association studies of complex traits that analyse common variants, which have a modest effect. For such variants, association analyses are more powerful than linkage analyses, and genome-wide association studies (GWASs) using single-nucleotide polymorphism (SNP) marker loci became the preferred association mapping tool. However, an emerging view is that rare variants, which are not well interrogated by GWASs, could be responsible for a substantial proportion of complex human disease¹. Importantly, the increased availability of exome and whole-genome sequence data has brought linkage analysis once again to the forefront owing to the development of powerful methods to detect rare variants involved in disease aetiology using family-based data; such an approach has many advantages over simply using filter methods to identify causal variants. Several reviews^2–5 and books^6–8 have been written on genetic linkage analysis, but none, to our knowledge, covers linkage analysis coupled with whole-genome sequencing (WGS).

Several recent studies have generated genome-wide association data for families. For example, the T2D-GENES (Type 2 Diabetes Genetic Exploration by Next-generation sequencing in Ethnic Samples) consortium has generated WGS data on 1,043 individuals from 20 Mexican families and reported analysis of risk variants for type 2 diabetes. However, for cost reasons, most studies currently only obtain WGS data for a small number of family members.

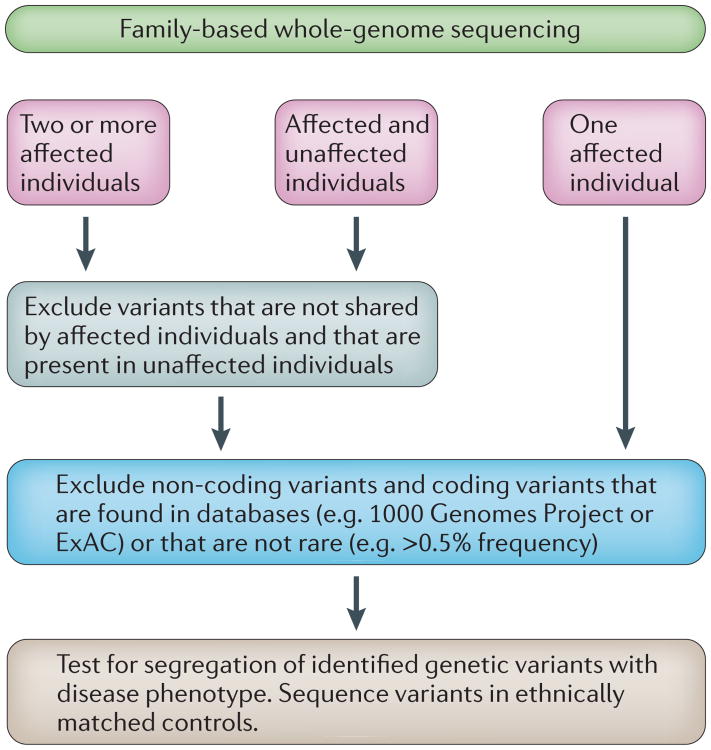
To date, most family-based WGS studies have therefore been analysed using filtering approaches, and only a few family members are prioritized for sequencing (Fig. 1). However, filtering approaches do not offer statistical evidence of a variant's involvement in disease susceptibility, whereas linkage analysis does provide this statistical support. With the decreasing cost of sequencing, it will become more common-place to have WGS data available for every informative pedigree member.

Figure 1. Workflow for the whole-genome sequencing filtering approach in human family data.

Usually, one, two or more affected individuals, or affected and unaffected individuals, in a family have their genomes or exomes sequenced. Variants that are not predicted to be nonsense, missense or splice-site variants are usually excluded from further analyses because it is unlikely that they are causal. When the mode of inheritance of a disease is known, this information can be used to aid the selection of variants. For example, for an autosomal dominant disease, the affected pedigree member's sequence data should display a heterozygous causal variant. Sequence data on additional pedigree members can help to reduce the number of variants that could potentially be disease causing. A final filtering step is performed in which those variants that are present in the databases dbSNP, 1000 Genomes, ExAC and Exome Variant Server are excluded. Additionally, bioinformatic tools, such as Polyphen-2 (Ref. 102), and measures of conservation, for example, PhyloP¹⁰³, are often used to predict whether a variant is deleterious and therefore likely to be disease causing. Even after filtering steps, there may be many variants that need to be followed up in the remaining family members to elucidate whether the variant (or variants) segregate with the disease phenotype. If the family is from a population that is not represented in databases, then ethnically matched controls need to be sequenced to evaluate the frequency of the variant (or variants).

This Review provides the reader with a practical guide for performing linkage analysis to identify variants that are responsible for Mendelian⁹ trait aetiology. After briefly mentioning the relative merits of linkage and association analysis, we discuss linkage algorithms and their implementations in computer programs, with a special emphasis on the use of sequence data. We then outline a step-by-step approach to successful linkage analysis using WGS data.

Genome-wide linkage analysis

For all informative family members, genotypes can be generated using SNP arrays and analysed using genome-wide linkage analysis. This approach is beneficial in that it evaluates DNA sample quality; elucidates whether specified familial relationships are correct; allows the detection of mis-specification of affection status and locus heterogeneity; aids the selection of an individual (or individuals) to undergo WGS; and facilitates the mapping of the disease locus to a region (or regions) of the genome, thus reducing the number of variants that need to be followed up. Linkage analysis can also provide statistical evidence of the involvement of a variant or gene in disease aetiology and can be performed either directly using WGS data or after filtering using data on variants that have been followed up by sequencing¹⁰ across entire families. However, it should be noted that although linkage analysis provides statistical evidence that a variant is involved in disease aetiology, false positives can occur when the variant that is tested is only in linkage disequilibrium with the causal variant. When filter approaches are used, phenocopies^11,12 and reduced penetrance can inhibit the ability to elucidate the causal variant but, because parametric linkage analysis incorporates a penetrance model, even under these circumstances the causal variant can usually be mapped.

Association analysis versus linkage analysis

Pertinent reviews of family-based association analysis have previously been published^13–15, and only highlights are therefore presented here. Genetic linkage and association between two loci are both related to recombination — in the former, recombination events are scored over a limited number of observed generations, whereas the latter relies on large numbers of unobserved recombination events in past generations. As generations go by after an initial disease mutation has occurred, recombination events ( crossing over) with surrounding markers tend to occur closer and closer to the disease locus so that measurable association between disease and marker loci extends only over short distances of up to 100 kb^16,17, corresponding approximately to a recombination fraction (represented by θ) of 0.001, given 1 Mb ≈ 1 cM. Most differences between association and linkage analysis are due to this difference in the number of generations.

Association analysis using common variants generally allows for finer mapping than linkage analysis using SNP loci, but one potentially problematic aspect of association analysis is population stratification, which can lead to an increased number of false-positive results if not properly accounted for¹⁸. This is not a problem in linkage analysis because children's genotypes depend on those of their parents and not on population genotype frequencies. However, if some parental genotype data are missing, using incorrect marker allele frequencies can increase type I and II errors. It has thus been tempting to combine positive aspects of linkage and association analysis, which may be achieved by using family-based rather than population-based control individuals. Consider an affected individual and his or her parents. At a given marker locus, the alleles inherited by the child may be contrasted with the alleles that are not inherited^19,20, where the latter can be shown to be representative of the alleles in the population²¹. The most well-known use of such family-based controls is probably the transmission disequilibrium test (TDT)²². For this to apply to multiple offspring, the null hypothesis of the TDT must include absence of linkage (θ = 0.5), so the TDT is a test for linkage that is only powerful when there is both linkage and association²¹. The TDT has been extended (the rare variant-TDT (RV-TDT))²³ for use with WGS data incorporating several rare variant association tests and has been implemented in the Family-Based Association Test Toolkit (FBAT) suite of programs²⁴. Some rare variant association tests²⁵ analyse variants in aggregate (usually across a genomic region such as a gene) instead of analysing individual rare variants. It has been shown that analysing rare variants in aggregate is much more powerful than the individual analysis of rare variants^25,26.

Approaches for linkage analysis

LOD scores

Linkage analysis can be carried out between a putative disease locus and a single marker locus (two-point linkage) or across a set of markers (multipoint analysis) consisting of a small number of markers or even all markers on a given chromosome. For multipoint analysis, the LOD score, Z(x) = log₁₀[L(x)/L(∞)], is computed as the logarithm of the likelihood ratio, with the numerator specifying a position, x, of the putative disease locus on the marker map. For the denominator, one assumes the disease locus to be off the map — that is, infinitely far away from the markers (Fig. 2). The multipoint LOD score can furnish a curve over all markers on a chromosome (Fig. 3); the maximum of this curve, over all chromosomes, then represents the estimated position of the disease locus on the human gene map provided that the maximum LOD score is at least equal to 3.3 (Ref. 101). Evidence for linkage can be obtained from a single pedigree or multiple pedigrees with LOD scores summed at the same θ or map position. When linkage analysis was previously performed with marker loci and the individual genes within a region had to be sequenced using, for example, Sanger sequencing, false-positive regions would not be followed up owing to reasons of time and cost, so it was important for a pedigree or a group of pedigrees to meet the genome-wide significance level. There is less concern now with meeting this criterion because it is quick and relatively inexpensive to follow by WGS of associated regions. Smaller pedigrees with suggestive LOD scores can still be followed up with WGS, although there may be multiple linkage regions that could potentially harbour the causative variant. If a putative causal variant is identified in a small pedigree, it is imperative that additional families are identified that segregate either the same variant or another putatively causal variant within the same gene. If a variant is identified that segregates with a phenotype in a large pedigree and produces a LOD score >3.3, it is also desirable to have additional pedigrees that segregate the same variant or different variants within the same gene. Even with a significant LOD score, the finding could be a false positive or the variant that was identified may only be in linkage disequilibrium with the causal variant, which may not have been observed in the sequence data; for example, the variant might not have been captured or there might have been insufficient read depth. Additionally, performing functional studies can be important on two levels: to provide additional evidence for gene causality and to better understand the role of the gene in disease aetiology²⁷.

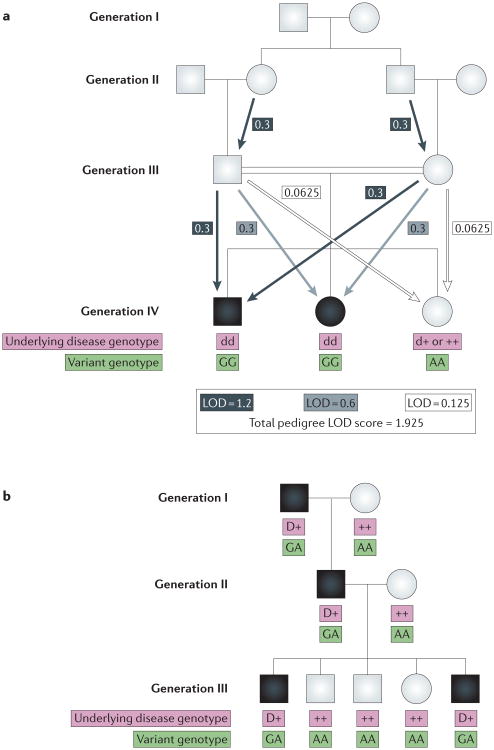
Figure 2. Linkage information for a first-cousin mating for an autosomal recessive trait and a phase-known autosomal dominant trait.

The disease is fully penetrant without phenocopies and has a minor allele frequency of 0.0001. Circles represent females and squares males. Individuals represented by solid black symbols are affected, and individuals represented by white symbols are unaffected. Shown below each individual in generation IV are the possible underlying disease genotypes. a| An autosomal recessive trait pedigree in which the affected children are offspring of first-cousin parents is shown. Consanguinity is indicated by the double horizontal line. The affected individuals are homozygous for a variant that is either causal or in perfect linkage disequilibrium with the causal variant. The unaffected sibling is homozygous wild type. The arrows show each informative meiosis and the contribution to the LOD score. For this pedigree configuration, the rare variant must have entered the pedigree through one of the great-grandparents. The meiosis events from the great-grandparents to their children do not contribute to the LOD score; however, the meiosis events from the affected children's grandparents to their parents and from the parents to the first affected child each contribute 0.3 to the LOD score, yielding a total LOD score of 1.2. The second affected child only adds 0.6 to the LOD score for the family because only the meioses from her parents yield new linkage information. Each additional unaffected child only yields an additional LOD score of 0.125 because for unaffected children it is not possible to elucidate whether they are homozygous wild type or causal-variant carriers; each of these possibilities have a probability of 1/3 and 2/3, respectively. These two probabilities are incorporated into the calculation of the LOD score, and linkage information is therefore lost. b| A phase-known autosomal dominant pedigree with five children is shown. This pedigree with five offspring for which there are no recombination events will lead to a maximum LOD score of 1.5 at θ = 0, where Z(θ) = log₁₀[(1 – θ)⁵/(½)⁵]. However, if no genotype information is available for the grandparents (shown in generation I), making the pedigree phase-unknown, the pedigree will yield a maximum LOD score of 1.2 at θ = 0, where Z(θ) = log₁₀[((1 – θ)⁵ + θ⁵)/((½)⁵ + (½)⁵)].

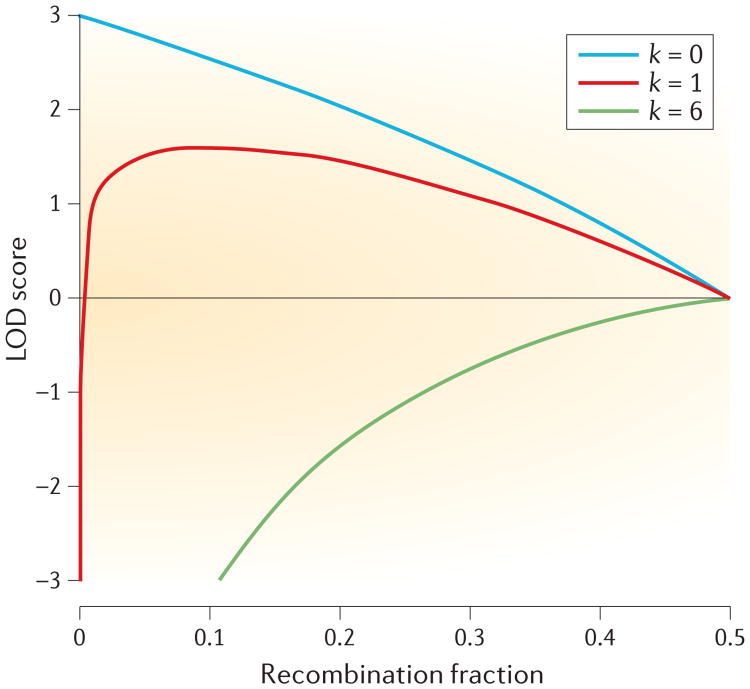
Figure 3. LOD score curves for a phase-known autosomal dominant pedigree with ten children in the third generation.

The LOD score curve is displayed for k recombination events (k = 0, 1 and 6) out of 10 meioses. The disease phenotype segregating in this pedigree is fully penetrant and has no phenocopies. Phenotype and genotype information are available for all pedigree members. The marker locus that is analysed is fully informative. The maximum LOD scores are 3.0 at a recombination fraction of 0 (θ = 0), 1.6 at θ = 0.1 and 0 at θ = 0.5, respectively, for k = 0, 1 and 6. When multiple pedigrees are analysed, the resulting LOD scores can be summed across families at either the same θ value or the same map position.

A parent must be heterozygous at each of two loci to be ‘informative for linkage’; otherwise, there is insufficient information to distinguish recombinant from non-recombinant events in offspring. When grandparents are unavailable (that is, in ‘phase-unknown pedigrees’), there must be at least two children in the third generation for linkage to be potentially informative. In some instances, such as for autosomal recessive and X-linked recessive traits, grandparents do not help to set the phase because they are usually unaffected and disease allele carriers cannot be distinguished from non-carriers. Pedigrees in which the grandparents provide phase information are known as ‘phase-known pedigrees’. In suitable situations, the number of recombinant events (k) and of non-recombinant events (n – k) can be counted directly. The estimate of the recombination fraction is then simply θ = k/n. Generally, however, the recombination fraction is estimated by the maximum likelihood (LOD score) method.

The recombination fraction tends to be different in males and females. It may also depend on age²⁸, but human studies have provided varied results^29–32.

Penetrance

For many traits, penetrance is incomplete. For example, in torsion dystonia, penetrance has been estimated as 29%³³; that is, fewer than one-third of disease-gene carriers express the trait. Penetrance can be age and sex dependent. For example, in Huntington disease, penetrance is zero at birth and gradually increases to 100% later in life^34,35. Multiple penetrance classes in linkage analysis can have functions similar to those of predictor variables in logistic regression for case–control association studies^6,36. If the penetrance for a disease is unknown or not well established, an ‘affected-only’ analysis can be performed, in which individuals who are unaffected are given an unknown affection status.

We distinguish between two penetrances: g for genetic cases and f for phenocopies, with g > f. In many linkage studies, f is taken to be a small number, such as 0.01 or smaller. The penetrance ratio, g/f, is analogous to the risk ratio in epidemiology³⁷ and indicates how well the disease phenotype (or any phenotype, for that matter) can discriminate between underlying genotypes.

Initial SNP genotyping

Performing linkage analysis with a SNP genotyping array can be beneficial in the identification of concerns about the data set. SNP genotyping can elucidate potential problems with the quality of the DNA samples, detect whether samples have been swapped and indicate instances in which a relationship has not been correctly specified. Additionally, if the pedigree produces a much lower LOD score than that expected for the number of informative meioses, this might indicate problems with phenotypic information that need to be rectified before additional analysis can be performed, or it might indicate that locus heterogeneity is present in the pedigree. The resulting linkage results and haplotype reconstruction can also aid in the selection of individuals for WGS: selection could be based on the smallest haplotype or on a haplotype that overlaps across affected individuals. Additionally, haplotype information can elucidate whether there are individuals within a pedigree who are phenocopies and therefore should not be selected for WGS. After performing WGS, fewer variants need to be followed up than when performing filtering alone because the causal variant is likely to be in the linked regions. For a family that can establish linkage, this strategy usually only yields 1–3 variants that have to be followed up in additional pedigree members and ethnically matched controls.

Linkage algorithms

With few exceptions³⁸, the calculation of pedigree likelihoods is done recursively by starting with a portion of the data and then working through the rest of the data. Two main algorithms are in general use. The Elston–Stewart algorithm^39–42 recursion takes place over individuals in a pedigree so that computing effort is linear with pedigree size but increases exponentially with the number of loci considered simultaneously. Conversely, the Lander–Green algorithm⁴³ recursion takes place over loci so that computing effort increases linearly with the number of loci but exponentially with family size. For multipoint analysis, the marker map is generally limited to 6–8 markers in the Elston–Stewart algorithm, whereas thousands of markers on any chromosome can be accommodated by the Lander–Green algorithm. However, the Lander–Green algorithm can only handle small- to medium-sized families, whereas the Elston–Stewart algorithm is applicable to very large pedigrees. Many programs have been developed that implement the Elston–Stewart algorithm (for example, LINKAGE⁴⁴ and FASTLINK⁴⁵) and the Lander–Green algorithm (for example, GeneHunter⁴⁶ and MERLIN⁴⁷). Although these programs were not developed for analysing WGS data, analysis of sequence data can easily be performed by converting Variant Cell Format (VCF) files into the linkage file format (also known as the PLINK⁴⁸ file format). These conversions can readily be made with PLINK version 1.9, VCFtools⁴⁹, Variant Association Tools (VAT)⁵⁰ or SEQLinkage⁵¹. If the conversion is performed using either VCFtools or VAT, the user will have to create a file that contains parameter information. However, SEQLinkage will create both the pedigree and parameter files for direct use in linkage analysis. Additionally, SEQLinkage can be used to directly perform linkage analysis using VCF files. However, the analysis of individual rare variants can be poorly powered when using SEQLinkage, so the software authors, motivated by rare-variant association tests, developed the collapsed haplotype pattern (CHP) method, which aggregates rare variants within regions (usually a gene) to create a ‘super locus’ (Ref. 51). The CHP method is more powerful than analysing rare variants individually, particularly in the presence of allelic heterogeneity.

There is no exact algorithm that can realistically accommodate large families and large numbers of loci, but computer-based methods have been developed to approximate linkage likelihoods for these situations. They are generally based on Markov-chain Monte Carlo (MCMC) methods⁵² and can allow for multiple disease loci, large family pedigrees and large numbers of marker loci. Two examples of linkage analysis programs that use MCMC approaches are Loki⁵³ and SimWalk2 (Ref. 54).

Multipoint analysis is useful when analysing SNP genotyping arrays for which the genotypes for the causal variant are unavailable because analysing multiple markers is usually more informative than analysing an individual SNP marker locus. However, for sequence data, there is no advantage in performing multipoint analysis if genotype data are available for the causal variant because no additional linkage information will be obtained.

Parameter-free methods

So-called parameter-based (‘parametric’) methods require specification of an inheritance model for the trait locus, unlike allele sharing (parameter-free) methods, which do not require specification of a disease model. Parameter-free methods are sometimes referred to as ‘non-parametric’, but this term should be avoided because it means, in the statistics literature, that analysis is carried out on ranks rather than the original data, which is not the case for these methods. The simplest type of allele-sharing analysis is based on affected sibpairs (ASPs)^55,56, but more-sophisticated approaches have been developed^57,58. However, many of these methods do imply a specific Mendelian inheritance model. For example, analysis of identity-by-descent (IBD) sharing in affected siblings has been shown to be equivalent to an analysis under a fully penetrant recessive mode of inheritance⁵⁹. Newer parameter-free approaches make use of large pedigrees and both affected and unaffected individuals⁵⁸. Allele-sharing linkage methods are based on the principle that if two relatives with a similar phenotype (for example, both affected) inherit the same marker allele from a common ancestor more often than expected by chance, then this indicates that a disease locus is linked with the marker locus. Various sharing statistics have been developed⁵⁷, but the subject of parameter-free linkage analysis is beyond the scope of this Review.

Extended approaches

Methods have also been developed to allow for two trait loci^56,60,61, often referred to as digenic inheritance⁶², but it is not entirely clear what LOD score threshold for significance should be applied to such bivariate analyses⁶³, and their power gain over single-locus analyses has been questioned⁶⁴.

For children who are affected with an autosomal recessive trait and whose parents are cousins or similarly close relations, marker loci linked with the trait locus tend to be homozygous⁶⁵. These runs of homozygosity can be quickly detected for either SNP genotype array or WGS data using, for example, Homozygosity Mapper⁶⁶. Linkage analysis can be used to obtain LOD scores for the variants within the region (or regions) of homozygosity through multipoint analysis (for SNP genotyping array data) or two-point linkage (for WGS data). It should be noted that in the very rare circumstance that the disease trait in a consanguineous pedigree is due to compound heterozygous variants⁶⁷, homozygosity mapping will not lead to detection of the region harbouring the causal variants, although linkage analysis results will not be influenced by the variants being compound heterozygotes instead of being homozygous.

Steps for a successful linkage study

Phenotyping

Two classes of phenotypes can be distinguished: qualitative and quantitative traits. Qualitative traits consist of a discrete number of classes, such as ‘affected’ and ‘unaffected’, whereas quantitative traits occur with a continuous distribution. In this Review, we focus on qualitative (disease) traits.

For many traits there is little question as to who is affected and who is not. Even when disease definition might be ambiguious, there are usually medical rules to determine disease status — for example, the conditions that need to be satisfied for someone to be diagnosed as schizophrenic. Whether these rules are genetically relevant is generally unclear, and researchers sometimes choose to rely on ‘endophenotypes’; that is, phenotypes correlated with disease that might be closer to gene action than the overall disease definition. It can also be more powerful to analyse separate underlying quantitative phenotypes instead of an overall clinical phenotype (for example, hypertension) that might be based on several quantitative traits. For example, rather than applying the medical diagnosis of hypertension, researchers working with the Lyon hypertensive rat carried out linkage analysis with each of three components of blood pressure (systolic, diastolic and pulse pressure, with pulse pressure being the difference between systolic and diastolic blood pressure); they found significant results for two different loci that each control a different blood pressure component⁶⁸. Such clear results might have been difficult to obtain if hypertension was considered as a single phenotype.

Various approaches can be taken to accommodate multiple phenotypes involved in a disease. For example, two different lipid levels have been analysed jointly in a bivariate analysis relating to diabetes⁶⁹. Most often, however, multiple phenotypes are suitably combined as a weighted sum^70–73, which is then used as a single quantitative trait in linkage analysis, or tests on single phenotypes are combined to show their joint effect⁷⁴. It is best to avoid dichotomizing a quantitative trait because substantial linkage information can be lost. A number of programs, including FASTLINK and MERLIN, can perform quantitative trait linkage analysis.

Selecting family members for sequencing

If only a fraction of all family members can be sequenced owing to reasons of cost, scientists are faced with the dilemma of which pedigree members to select for WGS. SNP genotyping data can aid selection, but such data are not always available. Some general guidelines are given below, but more advanced approaches rely on computer simulation, which emulates a linkage study by generating marker data and analysing it with the same parameter that will be used in the linkage study. For example, SLINK could be used to generate marker data, and MSIM could be used to perform the analysis. A sophisticated statistical framework for prioritizing individuals for sequencing has recently been developed and implemented in a computer program called GIGI-Pick⁴² (Table 1).

Table 1. Computer implementations.

Software	Description and purpose	URL	Refs
easyLINKAGE	Integrated suite that generates the necessary files and performs analysis using several programs, including GeneHunter	http://sourceforge.net/projects/easylinkage/	92
Genome Analysis Toolkit (GATK)	Toolkit for call variants from WGS data	https://www.broadinstitute.org/gatk/	81
GeneHunter	Lander–Green algorithm Can be applied to small- to medium-sized families and large numbers of marker loci Features parametric and non-parametric multipoint linkage analysis for qualitative and quantitative traits	http://www.broadinstitute.org/ftp/distribution/software/genehunter/	46
GIGI-Check	MCMC algorithm Detects Mendelian-consistent genotyping errors	https://faculty.washington.edu/wijsman/progdists/gigi/software/GIGI-Check/GIGI-Check.html	86
GIGI-Pick	Can be used to prioritize individuals for WGS	https://faculty.washington.edu/wijsman/progdists/gigi/software/GIGI-Pick/GIGI-Pick.html	42
LINKAGE and FASTLINK	Elston–Stewart algorithm Can be applied to large families but only to a limited number of marker loci for multipoint, parametric two-point and parametric multipoint linkage analysis for qualitative and quantitative traits Can be used to detect Mendelian-consistent genotyping errors	http://www.jurgott.org/linkage/LinkagePC.html; http://www.ncbi.nlm.nih.gov/CBBresearch/Schaffer/fastlink.html	44, 93
Loki	MCMC algorithm Can be used to perform multipoint linkage and segregation analysis of quantitative traits on large pedigrees	http://www.stat.washington.edu/thompson/Genepi/Loki.shtml	94
Mendel	Elston–Stewart and Lander–Green algorithms Can be applied to the analysis of qualitative or quantitative traits in pedigree- or population-based data Can combine multiple (rare) variants into superloci	http://www.genetics.ucla.edu/software/mendel	95, 96
MERLIN	Lander–Green algorithm Can be applied to small- to medium-sized pedigrees Handles closely spaced SNPs by combining them into superloci	http://www.sph.umich.edu/csg/abecasis/Merlin/	47
MSIM	Elston–Stewart algorithm Can be used to analyse simulated pedigree data to evaluate power, maximum LOD scores and expected LOD scores Useful for simulation studies to evaluate the most-informative pedigree members to select for WGS	http://watson.hgen.pitt.edu/docs/SLink.html	97
PedCheck	Detects genotype incompatibilities in pedigree data	http://watson.hgen.pitt.edu/register/docs/pedcheck.html	98
PLINK	Whole-genome association tool set for genotype data Can be used to estimate IBD sharing between two individuals	http://pngu.mgh.harvard. edu/∼purcell/plink/	48
Pseudomarker	Family-based association testing (joint linkage and linkage analysis) for qualitative traits using cases and controls, trios, sibpairs, sibships and extended families	http://www.helsinki.fi/∼tsjuntun/pseudomarker/	99
SEQLinkage	Elston–Stewart algorithm Can be used for parametric linkage analysis of WGS data using the collapsed haplotype pattern method Generates linkage files from VCF files for use with any linkage program that performs parametric linkage analysis	http://bioinformatics.org/seqlink	51
SimWalk2	MCMC algorithm Can handle large pedigrees and an intermediate number of marker loci for parametric and non-parametric multipoint linkage analysis of qualitative and quantitative traits	http://www.genetics.ucla.edu/software/	54
SLINK and FastSLINK	Simulates pedigree data that are conditional and unconditional on qualitative and quantitative phenotypes Limited in size of pedigree and number of marker loci MSIM can be used to analyse the simulated pedigrees	http://watson.hgen.pitt.edu/docs/SLink.html	97
Superlink	Bayesian networks Can handle large, complex pedigrees with multiple inbreeding loops segregating dichotomous traits Performs two-point and multipoint (with a limited number of markers) linkage analysis	http://bioinfo.cs.technion.ac.il/superlink/	100
TLINKAGE	Elston–Stewart algorithm Can handle large pedigrees Performs parametric two-locus linkage analysis	http://www.jurgott.org/linkage/tlinkage.htm	63
Variant Association Tools (VAT)	Pipeline for quality control and analysis of WGS and genotype data Can be used to generate linkage files for VCF files and to estimate IBD sharing between a pair of individuals	http://varianttools.sourceforge.net/VAT	50
VCFtools	Program to manipulate VCF files	http://vcftools.sourceforge.net/	49

IBD, identity-by-descent; MCMC, Markov-chain Monte Carlo; SNP, single-nucleotide polymorphism; VCF, Variant Cell Format; WGS, whole-genome sequencing.

Consider an autosomal recessive trait that is carried by two unaffected parents, who are cousins, and by their two children, who are affected with the trait. At least one of the affected offspring should be sequenced because, in this family, this child can yield a LOD score of 1.20 when both the trait and the linked variant alleles are rare. If an additional individual is to be sequenced, should this be a parent or the other affected child? A parent with an unknown genotype is likely to be heterozygous for a rare variant, and the affected child will have one variant in common with the parent, so each additional affected child can produce an LOD score increment of 0.60. Thus, it is less important to sequence the parents than to sequence the affected siblings in this situation. However, sequencing parents is necessary for identifying compound heterozygotes and de novo events.

For dominant traits, it is generally best to sequence distantly related individuals, a principle established some 20 years ago⁷⁵. The same rare allele occurring in two relatives is likely to represent two copies of an ancestral allele rather than two alleles independently acquired by the two individuals, which translates into an LOD score that increases with increasing distance of relationship. For rare variants for a disease without phenocopies, even only two distantly related individuals can yield sufficient linkage information. For example, consider two second cousins affected with an autosomal dominant trait for which the causal variant has a minor allele frequency of 0.0001; all other relatives are of unknown disease and marker status. The resulting LOD score is equal to 1.20, and more-distant relationships can yield even higher LOD scores.

For WGS studies, one or two unaffected individuals in a family should also be sequenced as controls, but in linkage analysis a negative LOD score is a sufficient indication that a given variant is not linked with the trait gene. For traits with reduced penetrance, unaffected pedigree members can be carriers of causal variants and therefore do not make ideal controls. Usually, there is no need to obtain variant frequencies in unaffected controls because this same information can readily be obtained from databases such as dbSNP⁷⁶, Exome Variant Server⁷⁷, ExAC and 1000 Genomes⁷⁸. Variants that occur at higher frequencies in these databases — for example, >0.5% — are unlikely to be causal¹. It should be noted that even fully penetrant disease variants may be present in variant databases for several reasons: these are not databases of disease-free individuals, and for autosomal recessive traits disease-free carriers may be included.

SNPs from sequence data

After individuals in a family have been sequenced, variants are extracted from the sequence data⁷⁹. If a given variant is not observed in available databases, it can be assumed to be rare and given a low allele frequency: for example, 0.0001. When performing linkage analysis, it is necessary to have VCF files that contain genotype information for every family member for which there is a variant site in at least one of the pedigree members. If this information is not available, it is impossible to distinguish between missing data and an individual who is a homozygous non-carrier. Additionally, if a sufficient number of family members are being subjected to WGS, a family-aware variant caller⁸⁰, such as that implemented in the Genome Analysis Toolkit (GATK)⁸¹, should be used to increase the accuracy of the variant calls.

Quality control

For WGS data, quality control can be performed as previously described⁵⁰; however, these procedures will not completely eliminate genotyping errors from WGS data. In contrast to association studies⁸², in families genotyping errors have traditionally been detected as Mendelian inconsistencies^83–85. However, particularly in small families, and given the biallelic nature of most variants, all sequencing errors will not be detected as Mendelian inconsistencies, and the fraction of such undetected errors can be high. MERLIN (double recombination events over short distances) and GIGI-Check (MCMC approach) are able to detect Mendelian-consistent errors⁸⁶.

Mendelian inconsistencies may be due to sequencing error or pedigree inconsistency (adoption, non-paternity⁸⁷ or swapped samples). In the case of pedigree inconsistency, large numbers of variants are expected to exhibit inconsistencies. To identify a specific individual causing these errors, it is useful to estimate the proportion of alleles shared IBD 0, 1 and 2 for pairs of individuals (implemented, for example, in the VAT or the PLINK programs). For example, for siblings, these proportions are expected to be 0.25, 0.5 and 0.25, respectively; if IBD proportions deviate from these values, then the two individuals are unlikely to be full siblings.

Computing LOD scores

To compute parameter-based LOD scores for linkage between a hypothesized disease locus and a given DNA variant, one needs to specify Mendelian model parameters such as allele frequencies and penetrances. Some handy rules are as follows. For example, consider a recessive trait so that the (homozygous) susceptibility genotype has frequency p², where p is the disease allele frequency under Hardy–Weinberg equilibrium. Trait population frequency (K) is then predicted to be K = gp² + f(1 – p²), where g and f are the respective penetrances for genetic cases and phenocopies. Fixing, for example, f = 0.01 and g = 0.90, allows the disease allele frequency to be determined as p = √[(K – f)/(g – f)]. In large families, penetrances may be estimated by maximum likelihood in suitable computer programs, but this is rarely done. Rather, one may determine the fraction of obligate disease-gene carriers who are unaffected, which should be approximately equal to 1 – g. For age-dependent penetrance, it is generally sufficient to find two time points, a₁ and a₂, where a₁ is the youngest age at which anyone has been diagnosed with the disease and a₂ is the oldest age at which the disease has manifested. Then, in a coordinate system with age as the x axis and penetrance as the y axis, the age-of-onset curve is approximated by a straight line rising from a penetrance of 0 at a₁ to the maximum penetrance at a₂ (Ref. 7).

Heterogeneity

Two types of heterogeneity may be distinguished: locus heterogeneity and allelic heterogeneity. Allelic heterogeneity refers to different alleles at the same locus (gene) conferring disease risk on different families or individuals, whereas in locus heterogeneity, different genes, possibly on different chromosomes, are disease causing. In linkage analysis, in contrast to association analysis performed with SNP marker loci, allelic heterogeneity does not generally represent a problem because linkage refers to a relationship between loci, not alleles. With WGS data, variants at different sites in the same gene may lead to disease; when such rare variants are being analysed using rare-variant association methods, allelic heterogeneity does not present a problem because rare variants within a gene region are analysed in aggregate. When allelic heterogeneity is present within a causal gene and individual variants are analysed, there can be a great loss of power because different pedigrees will not be informative for the same variant for pedigrees in which disease aetiology is due to the same gene but not the same variant; therefore, when LOD scores are summed across pedigrees, most pedigrees will not be informative and the power to detect linkage will be low. However, this problem can be avoided by using the CHP method described above, which analyses rare variants within a gene region in aggregate.

When analysing SNP marker loci, locus heterogeneity generally leads to a mixture of families that do and do not exhibit linkage to a given variant. Thus, in addition to estimating the recombination fraction θ in families with linkage, at the same time one also estimates the proportion (α) of linked families. The likelihood is maximized over α and θ, and the resulting LOD scores are known as heterogeneity LOD scores (HLODs)⁸⁸. When analysing rare variants, locus heterogeneity does not usually have a great impact because families that are not linked to the causal gene generally do not have an informative variant within the causal gene region; therefore, instead of producing negative LOD scores, they are uninformative for linkage.

Conclusion

Linkage analysis is again emerging as an extremely useful method in genomic analysis, particularly for the identification of rare variants associated with a complex trait with high penetrance. Linkage analysis has many advantages over filtering approaches in terms of limiting the number of genes that have to be analysed; namely, it takes account of phenocopies and reduced penetrance, which are often features of Mendelian traits, and in addition it provides statistical evidence of the involvement of a variant in disease aetiology. Many new disease susceptibility genes have been successfully identified using linkage analysis coupled with WGS, and this strategy has been successfully used to identify the association of rare variants to phenotypic traits such as hearing impairment^10,89, familial goitres⁹⁰ and familial hypertension⁹¹. In the future, with the reduction in cost of WGS, linkage analysis of WGS data will be widely used.

Glossary

Genetic mapping

The ordering of loci on a chromosome and the determination of the distances between two adjacent loci. For short distances, the recombination fraction can serve as a measure of genetic distance, with the unit of measurement being the centimorgan (cM); 1 cM = 1% recombination fraction

Genetic linkage

A phenomenon whereby two alleles, one each at two different loci, are transmitted together from parents to offspring more often than expected by chance. It leads to a recombination fraction smaller than 0.5

Phenocopies

Individuals that exhibit the phenotype of a Mendelian trait but that are not carriers of a susceptible genotype. Phenocopies were thought to result from non-genetic factors, but genes at locations other than those under current consideration can also lead to (genetic) phenocopies

Penetrance

The conditional probability of being affected given one of the genotypes at the disease locus, ‘+ +’, ‘+d’ or ‘dd’, where ‘d’ is the disease allele and ‘+’ the non-disease (wild-type) allele. More generally, penetrance is the conditional probability of a phenotype given a genotype

Recombination

Two alleles, one from each of two loci, can be inherited from one parent but originate from two different grandparents. If the two marker loci are on the same chromosome, a recombination is the result of an odd number of crossovers between the markers

Crossing over

A cytogenetic phenomenon that occurs during the formation of human gametes (egg or sperm cells). The salient feature of crossing over is that it occurs semi-randomly along chromosomes, with at least one crossover occurring on each chromosome in meiosis

Recombination fraction (θ)

The expected proportion of recombinant children divided by the total number of recombinant and non-recombinant children. For two loci in close proximity to each other, θ is small owing to the randomness of crossing over, but it increases to 0.5 for loci that are far apart

LOD score

Z(x) = log₁₀[L(x)/L(∞)] is the logarithm of the likelihood ratio, with the numerator being calculated under the assumption of linkage and the denominator under no linkage. A LOD score of 3.3 or higher has been shown to correspond to a genome-wide significance level of 0.05

Mendelian inheritance model

The Mendelian laws of inheritance, when applied to variants, stipulate that an individual carries two copies (alleles) of a given nucleotide and passes one of them at random to each of their offspring. Disease may be the result of a single copy of the allele (dominant inheritance) or of two copies (recessive inheritance) in an individual