Assessment of white matter microstructure in stroke patients using NODDI

Abstract

Diffusion weighted imaging (DWI) is widely used to study changes in white matter following stroke. In various studies employing diffusion tensor imaging (DTI) and high angular resolution diffusion imaging (HARDI) modalities, it has been shown that fractional anisotropy (FA), mean diffusivity (MD), and generalized FA (GFA) can be used as measures of white matter tract integrity in stroke patients. However, these measures may be non-specific, as they do not directly delineate changes in tissue microstructure. Multi-compartment models overcome this limitation by modeling DWI data using a set of indices that are directly related to white matter microstructure. One of these models which is gaining popularity, is neurite orientation dispersion and density imaging (NODDI). This model uses conventional single or multi-shell HARDI data to describe fiber orientation dispersion as well as densities of different tissue types in the imaging voxel. In this paper, we apply for the first time the NODDI model to 4-shell HARDI stroke data. By computing NODDI indices over the entire brain in two stroke patients, and comparing tissue regions in ipsilesional and contralesional hemispheres, we demonstrate that NODDI modeling provides specific information on tissue microstructural changes. We also introduce an information theoretic analysis framework to investigate the non-local effects of stroke in the white matter. Our initial results suggest that the NODDI indices might be more specific markers of white matter reorganization following stroke than other measures previously used in studies of stroke recovery.

I. Introduction

DWI is a non-invasive technique that measures the diffusion of water molecules in tissue. Particularly, in white matter, water diffusion is anisotropic - it is faster along axon bundles than through myelin. This physical property allows diffusion MRI to map white matter architecture and possibly to assess its integrity. In a few recent studies, DTI was employed to study motor impairment after stroke [1], [2]. In these works, FA was used as a biomarker of motor tract integrity, and was correlated with motor impairment to predict stroke's outcome. However DTI is limited in modeling brain regions of complex white matter architecture and hence, FA may not be a reliable measure of tract integrity. For example, low FA values may indicate regions of crossing fibers rather than low integrity. To enable modeling of regions of complex white matter architecture, new techniques such as q-ball imaging (QBI) and diffusion spectrum imaging (DSI) have emerged [3]. These techniques enable derivation of new measures of white matter integrity such as GFA, which uses the orientation distribution function (ODF) geometry as an indicator of diffusion anisotropy. To enable a more accurate study of white matter reorganization after stroke, GFA was used in several studies as a white matter integrity measure instead of FA [4], [5], [6]. However, despite the sensitivity of FA and GFA to cellular architecture, they are inherently non-specific, as a reduction in their value can be associated with different types of microstructural changes, such as demyelination or reduction in axonal density. On the other hand, parametric models such as [7], [8] enable differentiation of white matter tissue into microstructures with different diffusion patterns characterized by a set of parameters. By estimating these parameters from multi-shell DWI data, a new set of biomarkers that are specific to microstructural changes can be generated. In this paper, we adopt the NODDI parametric model [7] and apply it for the first time to DWI data from stroke patients. In order to be able to accurately estimate the model parameters, we acquired four-shell HARDI data. Using pre-defined regions of interest (ROIs) located in both ipsilesional and contralesional regions of the white matter, we compare NODDI indices in the damaged tissue to the normal tissue. Our preliminary findings suggest that NODDI indices can be used as specific surrogate markers of white matter integrity in stroke patients.

II. Methods

A. Brain tissue modelling using NODDI

NODDI is a multi-compartment model, which enables brain tissue differentiation into three different environments [7]. Each environment is characterized by a unique diffusion pattern, and is modeled by a separate compartment. The model differentiates between intracellular (IC) diffusion, extracellular (EC) diffusion, and isotropic diffusion (ISO). Axons and dendrites are modeled in NODDI as zero radius cylinders (sticks), where the IC diffusion compartment describes a diffusion process, which is restricted perpendicular to the cylinder, and unhindered along the cylinder. The IC diffusion compartment has a volume fraction W_ic that corresponds to neurite density (ND). The IC diffusion signal, S_ic also encodes the orientation dispersion of neurites via the Watson distribution $f(\mathbf{x}\mid \mu ,k)=M{(\frac{1}{2},\frac{3}{2},k)}^{-1}{e}^{k{\left({\mu }^T\mathbf{x}\right)}^2}$, where M is the hypergeometric function, and k is the concentration parameter measuring the extent of orientation dispersion about the mean orientation, μ. The extracellular compartment, denoted by S_ec, corresponds to the glial cells or the cell bodies in gray matter. Diffusion of molecules in this compartment is hindered by the presence of neurites, and is thus modelled by Gaussian anisotropic diffusion, i.e. a cylindrically symmetric tensor. The final compartment S_iso, isotropic Gaussian diffusion, models the cerebrospinal fluid (CSF). The full normalized signal in a NODDI model is a mixture of these three different diffusion environments, and is given by

$$S=w_{\mathrm{iso}}{S}_{\mathrm{iso}}+(1-w_{\mathrm{iso}})(w_{\mathrm{ic}}{S}_{\mathrm{ic}}+(1-w_{\mathrm{ic}})S_{\mathrm{ec}}).$$ (1)

As defined in [7], the intra-cellular diffusion compartment is composed of the probability to find a stick (e.g., an axon) in direction x given by f (x|μ,k)dx, and the exponential signal decay due to unhindered diffusion along a stick aligned with x resulting in the following signal model

$$S_{\mathrm{ic}}={\int }_{S^2}f(\mathbf{x}\mid \mu ,k)e^{-b{d}_{\parallel }(\mathbf{q}\cdot \mathbf{x})},$$ (2)

where d_∥ is the diffusivity along the stick, q is the gradient direction, and b corresponds to the measurement b-value.

The extra-cellular signal model is given by

$$S_{\mathrm{ec}}=e^{-b{\mathbf{q}}^T\left({\int }_{S^2}f(\mathbf{x}\mid \mu ,k)D\left(\mathbf{x}\right)d\mathbf{x}\right)\mathbf{q}},$$ (3)

where D(x) is a cylindrically symmetric tensor aligned with x, with diffusivities $d_{\parallel }^{\mathrm{ec}}$ and $d_{\perp }^{\mathrm{ec}}$. Finally, the CSF isotropic compartment is given by S_iso = e^−bd_iso, with free water diffusion coefficient d_iso. In this paper, the free model parameters are w_iso, w_ic, and the concentration parameter k. The diffusivities are set based on known values in the human brain and different assumptions: d_iso = 3 · 10⁻³mm²·s⁻¹, d_∥ = 2 · 10⁻³mm²·s⁻¹, $d_{\parallel }^{\mathrm{ec}}=d_{\parallel }$ and $d_{\perp }^{\mathrm{ec}}=(1-w_{\mathrm{ic}})d_{\parallel }^{\mathrm{ec}}$. The w_iso parameter reflects the CSF volume fraction. The orientation dispersion index (ODI) is defined with respect to k as follows

$$\mathrm{ODI}=\frac{2}{\pi }\arctan \left(k\right),$$ (4)

where it ranges from 0, for coherently oriented structures, to 1 for isotropic structures.

B. Data acquisition

Diffusion MRI data in two stroke patients was acquired with a standard EPI sequence using a 32-channel head coil. One subject was scanned on a Siemens 3T Verio scanner, and the other subject on a Siemens 3T IMRIS scanner. Patient 1 was male, age 43, 9 days post-stroke at imaging and had a Fugl-Meyer upper extremity score of 54/66. The 2^nd patient was male, age 73, 7 days post-stroke, Fugl-Meyer 23/66. Data was acquired in four shells as follows: b=500 (20 directions), b=1000 (30 directions), b=2000 (64 directions), and b=5000 (64 directions). All shells were acquired with identical echo time (TE) and repetition time (TR). One b=0 image was acquired separately for each shell. Other scan parameters were TR=264 ms, TE=138 ms, FOV= 230 mm², matrix size=108 × 108 and 36 slices were acquired with a slice thickness of 3 mm. All data was acquired in accordance with the University of Utah Institutional Review Board (IRB) guidelines.

C. Processing

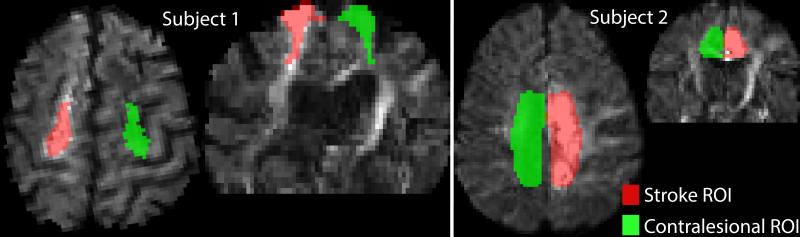
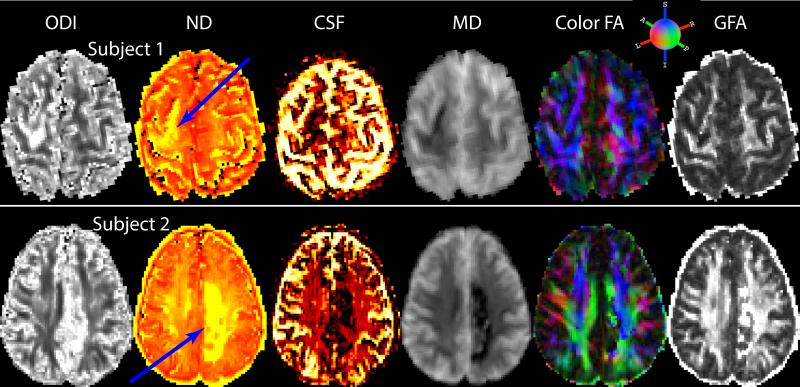
For both subjects, eddy current related distortion and head motion of each data set were corrected using the eddy_correct command in the FSL¹. The b-vectors were rotated using the rotation component of the transformation matrices obtained from the correction process. Brain regions were extracted using the b = 0 image as input to the brain extraction tool, also part of FSL. The diffusion tensor elements were calculated using non-linear estimation in CAMINO² with data from all shells and then, FA and MD were estimated. The NODDI compartment model (Eq. (1)) was then fit to the data using NODDI Matlab toolbox³. In addition, we used Dipy⁴ to fit the data with the constant solid angle (CSA) model [9] with fourth-order spherical harmonics, and generated GFA maps from estimated ODFs. We identified the entire stroke region and the corresponding contralesional region. Regions of interest (ROIs) encompassing the stroke area in each axial slice were manually drawn on a b=2000 raw diffusion image. Contralesional ROIs were obtained by reflecting stroke ROIs about the central line bisecting the brain hemi-spheres in each slice. Fig. 1 shows lesion and contralesional ROIs in one slice. We first examine the differences between the stroke and contralesional regions using the six different microstructural measures obtained from the three different diffusion models - NODDI, DTI and HARDI. Fig. 2 shows the axial slices of different NODDI measures as well as MD (mm²·s⁻¹), FA obtained from the DTI model, and GFA maps obtained from the HARDI model. Qualitatively we can observe an increase in ODI and ND values (pointed by blue arrows) and a decrease in CSF fractions in stroke regions. In order to quantify these differences, we use Kullback-Liebler divergence (KLD) to compute the distance between the distributions of the micro-structural and diffusion measures in both the regions. The KLD between two distributions F₁ and F₂ is defined as in [10], [11]:

$$\mathrm{KLD}(F_1,F_2)={\int }_R\ln \left(\frac{F_1\left(x\right)}{F_2\left(x\right)}\right)F_1\left(x\right)dx.$$ (5)

KLD in Eq. (5) is the expected value of the log-ratio of the probability distributions under F₁. The log-ratio intuitively captures the differences in representational complexities of the two distributions. As the KLD in Eq. (5) is not symmetric i.e. KLD(F₁,F₂)≠KLD(F₂,F₁), we use the following naturally symmetrized version,

$$\mathrm{sKLD}(F_1,F_2)=\frac{\mathrm{KLD}(F_1,F_2)+\mathrm{KLD}(F_2,F_1)}{2}.$$ (6)

To obtain the distributions necessary to compute the sKLD we use shrinkage estimator for the frequencies [11] after discretizing the measure values into 10 bins for each measure. Since the range of the measures is 0 to 1 we are thus able to capture differences at the 0.1 level.

Fig. 1.

Manually drawn ROIs encompassing stroke region overlaid on a diffusion weighted image at b=2000 s·mm⁻² in one axial slice. Corresponding contralesional ROIs are also shown. Red for ipsilesional hemisphere and green for contralesional hemisphere. Axial and coronal views are shown in two subjects.

Fig. 2.

Microstructural and diffusion measures in two subjects. The blue arrows point to stroke regions in both subjects.

In order to examine the non-local effects of the stroke on other white matter regions of the brain, we extract the microstructural measures from a set of 21 tracts defined bilaterally. White matter labels from the JH-ICBM atlas [12] were transferred to individual subjects using ANTS⁵ deformations derived from registering the individual FA maps to the ICBM template FA. ROIs on the template and those warped onto the individual spaces of the two subjects are shown in Fig. 3. The non-local effects of the stroke are computed as shifts in the sKLDs for the tract measures in the ipsilesional hemisphere from the baseline sKLDs obtained from the corresponding tracts in contralesional hemisphere.

Fig. 3.

JH-ICBM white matter labels warped into the individual subject spaces using ANTS are shown on their respective FA maps.

Formally, for each tract T_i in the ipsilesional hemisphere the non-local effect on it is captured by

$$\Delta \mathrm{sKLD}\left(T_i\right)=\mid \mathrm{sKLD}(F_{T_i},F_{\mathrm{Stroke}})-\mathrm{sKLD}(F_{T_i^{\prime }},F_{\mathrm{Contralesion}})\mid ,$$ (7)

where F_Ti is the distribution of a measure in the tract i while F_Stroke,F_Contralesion are the distributions of the measure in the stroke and the contralesional ROIs. $T_i^{\prime }$ is the tract in the contralesional hemisphere corresponding to T_i.

III. Results

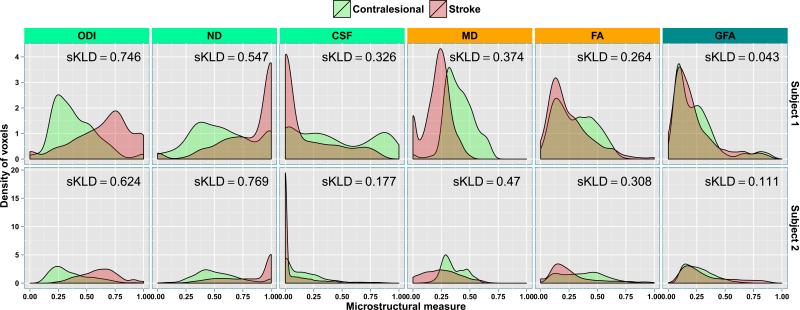
The quantitative differences between the stroke and the contralesional ROIs of the six diffusion measures (Fig. 2) are shown in Fig. 4. The measures show varying degree of differences between the two regions. While ODI and ND measures are higher in stroke ROIs as compared to those measures in contralesional ROIs, CSF seems to be strikingly lower in stroke ROIs as compared to the values in contralesional ROIs. MD also captures the differences significantly. The distinction between the stroke and contralesional ROIs using FA and GFA on the other hand is not as stark compared to NODDI measures indicating potentially improved sensitivity using the NODDI model, although in the stroke environment the interpretation of NODDI parameters such as neurite density may need to be reconsidered.

Fig. 4.

The density estimates of the microstructural measure distributions for ODI, ND, CSF as well as MD, FA and GFA obtained from stroke and contralesional ROIs in the two subjects. The symmetrized KLD (sKLD) values are shown in each facet. The range for all the measures is 0 to 1. MD values are in mm²·s⁻¹ while the other indices are in arbitrary units (a.u.).

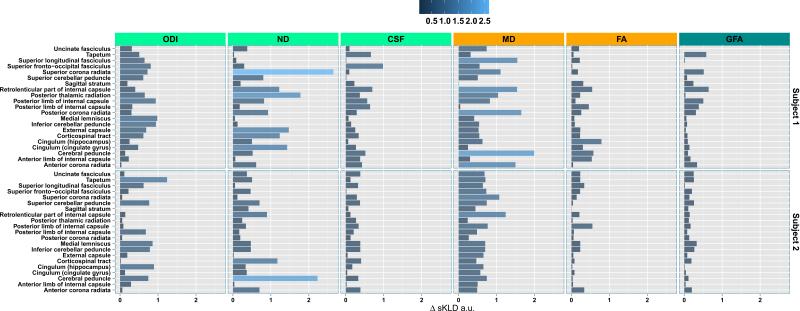
The non-local effects measure (Eq. (7)) on the 21 tracts in ipsilesional hemisphere are shown in Fig. 5 (top half for Subject 1 and bottom half for Subject 2). In Subject 1 some of the largest non-local effects, as seen in ODI, ND, CSF, and MD, seem to be felt by superior corona radiata, posterior limb of the internal capsule, corticospinal tract and the cingulate hippocampal gyrus. The superior longitudinal fasciculus, external capsule, anterior corona radiata, anterior limb of the internal capsule, and the cerebral peduncle, seem to be affected moderately. In Subject 2 we can observe the largest effects on retrolenticular part of the internal capsule, cerebral peduncle, superior cerebellar peduncle, and the anterior corona radiata.

Fig. 5.

The non-local effects of stroke on the 21 tracts obtained from the JH-ICBM template. The tract names are ordered in reverse alphabetical order.

IV. Conclusions

In this paper, we used four-shell HARDI data to explore for the first time the application of the NODDI model to study white matter microstructural changes in stroke patients. We found an increase in the fiber orientation dispersion index, as well as clear changes in densities of intra-cellular and free water diffusion compartments in the stroke regions. This preliminary study suggests that the NODDI indices could complement FA and GFA as specific surrogate markers of white matter integrity in stroke patients, and may lead to more insight on white matter reorganization following stroke. In addition, we presented an information theoretic analysis framework for identifying non-local effects of stroke on white matter tracts. This framework can be extended to measure the effects of stroke on the rest of the brain voxelwise by replacing sKLD with a simple difference of any two scalar measures. As future work we plan to include additional voxelwise analyses and include patients scanned at different time points. This would allow us to explore longitudinal changes in the NODDI indices and correlate the changes with white matter reorganization and degree of motor impairment after stroke.