Abstract
We report the seeded synthesis of gold nanoparticles (GNPs) via the reduction of HAuCl4 by (L31 and F68) triblock copolymer (TBP) mixtures. In the present study, we focused on [TBP]/[Au(III)] ratios of 1–5 (≈ 1 mM HAuCl4) and seed sizes ~ 20 nm. Under these conditions, the GNP growth rate is dominated by both the TBP and seed concentrations. With seeding, the final GNP size distributions are bimodal. Increasing the seed concentration (up to ~ 0.1 nM) decreases the mean particle sizes 10-fold, from ~1000 to 100 nm. The particles in the bimodal distribution are formed by the competitive direct growth in solution and the aggregative growth on the seeds. By monitoring kinetics of GNP growth, we propose that (1) the surface of the GNP seeds embedded in the TBP cavities form catalytic centers for GNP growth and; (2) large GNPs are formed by the aggregation of GNP seeds in an autocatalytic growth process.
Keywords: metal nanoparticles, colloidal gold, size-controlled synthesis, aggregative growth, triblock copolymers
INTRODUCTION
There is considerable interest in synthetic methods for gold nanostructures, with particular emphasis on the manipulation of size and shape. Gold nanoparticles (GNPs) are intensively studied because properties that depend on their size and shape lead to useful applications in photonics, catalysis and biomedicine.1 One area of active research is GNP formation by the reduction of tetrachloroauric acid (HAuCl4) using the triblock copolymers (TBPs) of poly(ethylene oxide) (PEO) and poly(propylene oxide) (PPO) to function both as reducing and capping agents.2 The use of TBPs in the HAuCl4 reduction process is desirable because the synthesis is water based and TBP coated GNPs are nontoxic.2-3 Our previous work showed that varying the reaction conditions and the PO:EO ratio of the TBP influences the size and shape of the resulting GNPs.4
The size of the gold nanocolloids can be controlled on the basis of the phase behavior and amphiphilic structures of these copolymers.5 Alexandridis and coworkers5a, 5b proposed a GNP growth model that incorporates Au(III) reduction from crown ether-like PEO complexes. This is followed by primary nanocrystalline formation. The TBPs adsorbed on the surface of these primary nanocrystallites then act as nucleation centers for layered Ostwald type growth. Khullar and coworkers5d, 6 further refined this picture by assuming that reduction occurs on the surface cavities of the PEO blocks within the micellar corona. They proposed that there is a positive correlation of greater mean GNP sizes with an increasing cavity size.5d, 6
An alternative way to control particle size is to use seeding methodologies, where preformed GNP seeds are included in the precursor solution before the full reduction of precursor gold cations. Natan and co-workers7 pioneered the seeded growth of GNPs using mild reducing agents such as sodium citrate or hydroxylamine to obtain GNPs of ~ 100 nm in diameter. Murphy8 and Liz-Marzan9 were able to improve GNP monodispersity by using ascorbic acid as a reducing agent and cetyltrimethylammonium bromide (CTAB) as a cationic surfactant. Using the CTAB seed approach, Eguchi and co-workers10 were able to produce monodisperse polyhedral gold nanoparticles with various shapes. Although CTAB-based methods allow the control of GNP morphology, CTAB binds strongly to the surface and restricts subsequent functionalization. Njoki and co-workers11 synthesized GNPs with high monodispersity (2% relative standard deviation) using sodium acrylate as the reducing agent. Bastús and co-workers12 were able to synthesize monodisperse citrate-stabilized gold nanoparticles using the seeding approach with uniform quasi-spherical shapes of up to ~200 nm. Zielger and Eychmüller13 described a similar protocol using ascorbic acid as the reductant and sodium citrate as the stabilizer. Thus the seeding methodology represents an attractive approach to narrow the particle size distribution.
Although the synthesis of GNPs using TBPs is known to be a facile process, the polydisperse nature of the resulting GNPs has limited its usefulness in practical applications. Achieving monodisperse GNP size distributions from TBP mediated reduction requires a mechanistic understanding of the nucleation and growth processes. By using seeding methodology as reported in this work an attractive approach leading to reducing the polydispersity of TBP coated GNPs is described. In the following sections, we postulate a GNP growth mechanism that incorporates GNP seeding. We measure the growth kinetics and particle size distributions as a function of the concentration of the GNP seeds.
EXPERIMENTAL SECTION
Materials
The Pluronics® L31 (EO2-PO16-EO2 MW ≈ 1100; Batch #: 01631MH), and F68 (EO78-PO30-EO78 MW ≈ 8400; Batch #: 018K0029); hydrogen tetrachloroaurate (III) trihydrate (HAuCl4.3H2O); trisodium citrate (HOC(COONa)(CH2COONa)2·2H2O); 11-mercaptoundecanoic acid (MUA); and 3-aminopropyltriethoxysilane (APTS) were used as received (Sigma Aldrich, Milwaukee, WI, USA). Milli-Q water (Millipore) was used.
Instrumentation
Field emission scanning electron microscopy (FESEM) analysis was carried out on a Zeiss Gemini FIB/FESEM instrument with scanning transmission electron microscopy (STEM) capabilities (at an operating voltage of 20 kV). Digital TEM images were obtained using a Philips Tecnai 12 instrument operating at 80 kV and fitted with a Gatan camera. Atomic force microscopy (AFM) images were generated with a Multimode 8 scanning probe microscope (Bruker, Santa Barbara CA) in the Tapping™ (k = 42 Nm−1, f = 285 kHz) and peakforce™ tapping (k = 0.4 Nm−1, f = 70 kHz) modes.
The reduction of HAuCl4 and the formation of gold nanoparticles were monitored by observing the changes in the absorption spectrum using a UV-vis spectrometer (Varian Cary 300 and 500) fitted with temperature control at 25 ± 1 °C. Dynamic light scattering (DLS) measurements were made with a model NICOMP 370 submicron particle sizer (Particle Sizing Systems, Santa Barbara CA, USA) using a 632 nm Helium-Neon laser at 60 mW. Data was collected at a scattering angle of 90° and fitted with a proprietary autocorrelation function to calculate the distribution of the diffusion coefficient by the inverse Laplace transformation method. The apparent spherical hydrodynamic diameters were estimated assuming the Stokes-Einstein equation. Volume- and number-weighted distributions are obtained from the intensity-weighted plot by dividing each diameter bin value by its volume and volume squared, respectively. Prior to UV-vis and DLS measurements, TBP coated GNP samples were washed by centrifugation (17,900 g; 5 min) to remove excess surfactant and suspended in water.
All static light scattering (SLS) spectra were recorded on a Model T PTI spectrofluorometer (Photon Technology International, Birmingham, NJ, USA), equipped with a magnetic microstirrer and Peltier temperature regulation. Static light scattering experiments were done at λex = λem = 450 nm, bandwidth ≈ 1 nm, at a 90° scattering angle, with stirring. An inner filter correction, , was applied to the measured fluorescence intensities.14 Synchronous scans at Δλ = 0 nm were performed between 300–700 nm.
Scattering coefficient calculations of colloidal GNPs of different diameters were obtained using MiePlot software15 considering gold spheres embedded in water at 25 °C based on the Mie theory as presented by Bohren and Huffmann.16 In all cases, mean sizes and volume weighted particle size distributions measured by DLS were used for the calculations. The volume weighted DLS analyses were performed to appropriately represent the amount of material present.
Synthesis of TBP Coated Gold Nanoparticles
The synthesis protocol12 and characterization for citrated GNP seeds of ~23 nm is described in the supplemental information. A typical stock TBP solution was prepared by adding 10 mL of 50% w/v F68 and 10 mL L31 to 100 mL water (8 mM/4 mM; L31/F68). Total volumes of 1, 5, 3 mL (8 mM/4 mM) L31/F68 solutions were used for UV-vis/DLS, microscopy, and static light scattering/synchronous scan experiments, respectively. To these volumes, citrated GNP seeds were added. For the results presented here, on the 1 mL scale, 0–100 μL (0, 5, 10, 20, 50, 100 μL) citrated GNP seeds (≈1 nM) were added and incubated at 25 °C for ~15 min before adding 10μL 100 mM HAuCl4 to give a final Au(III) concentration of 1 mM.
Sample Preparation for AFM and STEM
It was necessary to pretreat both the mica (15 mm radius) and carbon coated Cu grids (Ted Pella 200 mesh) with freshly made aqueous APTS (0.1% v/v) solution to produce a positively charged surface to which the GNPs would adhere (Supplemental for details).
Analysis of Growth Kinetics
The growth kinetics was monitored using the 535 nm plasmon resonance peak with a UV-vis spectrometer. As proposed by Buhro17 and coworkers and described previously,4 a modified form of the Kolmogorov–Johnson–Mehl–Avrami (KJMA) equation was used to analyze the data.
Static light-scattering and plasmon resonance light-scattering (PRLS) were used to monitor nanoparticle aggregation. The PRLS peak intensity increases when aggregation of GNPs occurs.18 Irreversible particle aggregation can be classified as either diffusion-limited colloid aggregation (DLCA) or reaction limited colloid aggregation (RLCA).19 Compared to DLCA, there is a substantial activation energy barrier for RLCA.19 For RLCA the light scattering intensity scales with time t as ~ e−Kt−2.1, where K is a proportionality constant.20 For DLCA the intensity scales as ~ tn, where the exponent n is an arbitrary value. This power dependence has the same functional form as reaction controlled Ostwald ripening (OR) making it impossible to distinguish between them. However, aggregative growth can be readily distinguished from OR mechanisms by the direct observation of polycrystallinity in the nanostructures.20
RESULTS
Seeding Effects on Particle Morphology
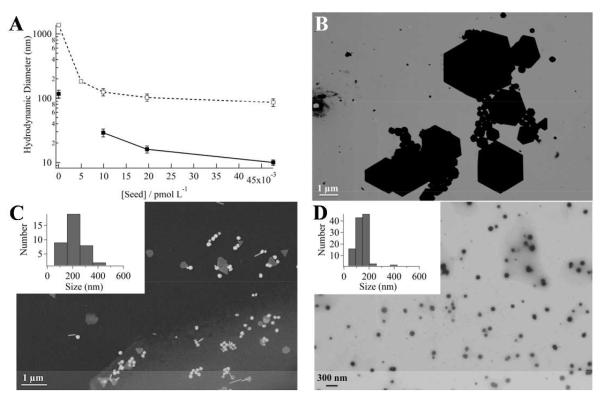
Figure 1 shows the effects of GNP seeding on particle size in (8 mM/4 mM) L31/F68 solutions after incubation for 7 days at room temperature. DLS results show that the GNP size distributions are bimodal (Figure 1A; Figure S2). Without seeding, the GNPs formed are heterogeneous in shape and size (Figure 1B). An examination of the volume weighted DLS particle size distribution shows that increasing the seed concentration decreases the mean hydrodynamic diameters from (1370 ± 290) to (86 ± 12) nm in the larger GNP population. Similarly, the mean hydrodynamic diameters decrease from (117 ± 37) to (10 ± 1) nm in the smaller GNP population. It is clear that low concentration seeding (0 – 5 pM) has the most significant effects in reducing particle sizes (Figure 1A). With seed concentrations above 20 pM, the seeding concentration has minimal effects on the final larger GNP diameters, while the size of the smaller GNPs continuously decreases. The width of the size distribution for the larger particles is reduced with the increase of the seed concentration (insert of Figure 1C and D). Comparable bimodal size distributions were also obtained for ≈ 4 mM F68 aqueous solutions (Figure S2). In the 50 pM seed concentration limit, the DLS volume weighted distribution indicates that the smaller GNPs account for the majority (≈ 80% by mass) of the particles (Table 1). Electron microscopy images confirm that the larger size GNP populations decrease in mean size with seeding (Figure 1C and D; Figure S3). Furthermore, the GNP size distributions become narrower with increasing seed concentration, indicating less heterogeneity in shape and size.
Figure 1.
The presence of citrated gold nanoparticle (GNP) seeds in aqueous precursor solutions containing L31(8 mM)/F68(4 mM) mixtures reduces the formed GNP sizes, when ≈ 1 mM Au(III) is added, followed by incubation for 7 days at room temperature. (A) Mean hydrodynamic diameters of the formed GNPs against seed concentrations. Data represent the smaller (closed squares) and the larger (open squares) GNPs size populations. Panels (B)-(D) are representative electron micrographs of the larger size population GNPs produced at seed concentrations of (B) 0, (C) 5 (168 ± 123 nm), and (D) 50 pM (110 ± 41 nm).
Table 1.
Particle size distributions determined by dynamic light scattering along with calculated and experimental surface plasmon resonance (SPR) values.
| Seed Concentration/pM |
Pop 1 Diam./nm |
bWeight/% | Pop 2 Diam./nm |
b Weight/% | SPR (calc)/nm |
SPRc nm |
||
|---|---|---|---|---|---|---|---|---|
| Pop 1 | Pop 2 | |||||||
| 0 | 1370 ± 290 | 87 | 117 ± 37 | 13 | ||||
| 5 | 183 ± 25 | 100 | 550,670 | 558(556) | 700 | |||
| 10 | 125 ± 16 | 56 | 29 ± 4 | 44 | 590 | 522 | 578(583) | |
| 20 | 103 ± 14 | 38 | 16 ± 2 | 62 | 569 | 521 | 562(558) | |
| 50 | 86 ± 12 | 21 | 10 ± 1 | 79 | 553 | 521 | 545(542) | |
Values Mean ± SD.
Integrated DLS volume weighted intensities.
The wavelengths of the composite SPR spectral maxima, experimental(calculated) in nm.
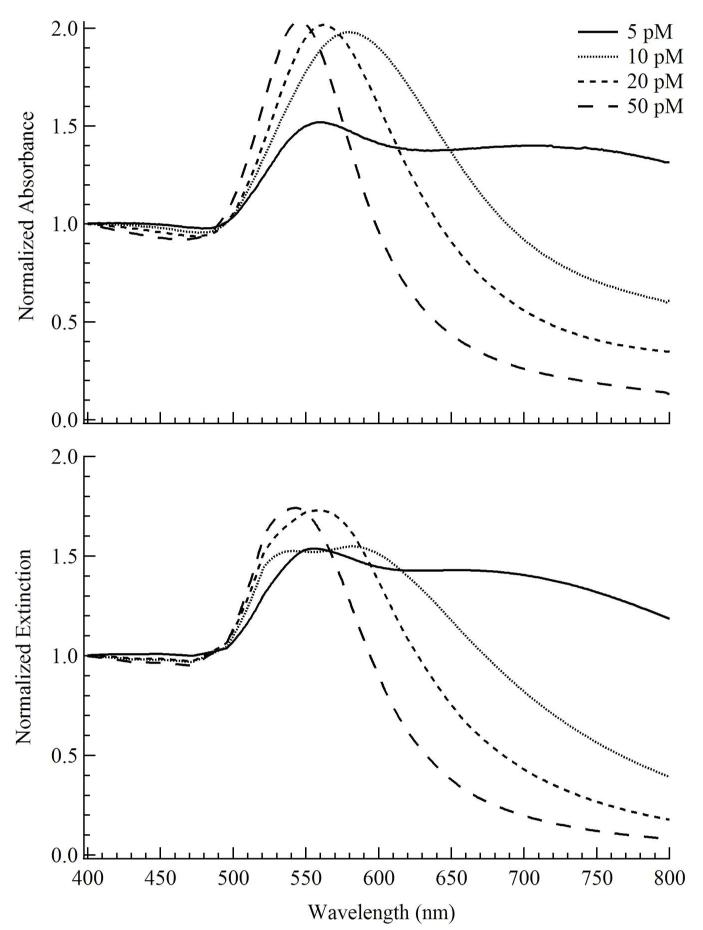
The dipolar localized surface plasmon resonance (LSPR) peaks were monitored by UV-vis. With increasing seed concentration the LSPR peak blue-shifts from ~560 nm to 545 nm along with decreasing peak width (Figure 2A). To evaluate the relative contributions of the GNP populations to the extinction spectrum, UV-vis spectra were compared to Mie scattering simulations (Figure 2B). These simulations assume only spherical GNPs in the solution ignoring the anisotropic GNPs. Experimentally, the anisotropic GNPs accounted for less than 20% of the total GNPs produced (Figure 3A). The simulated spectra are summations of individual extinction components of the GNP populations and are weighted by their relative volume weighted DLS populations (Table 1) accounting for the GNP measured standard deviation. At 5 pM seed concentration, the peaks at ≈ 558 and 700 nm are assigned to quadrupolar and dipolar plasmon resonance bands, respectively.9 For 10 to 50 pM seed concentrations, the assignments were based on the two GNP populations (Table 1). The UV-vis peak for 10 pM seed concentration at ≈ 578 nm is assigned to the superposition of ~522 nm (30 nm GNPs) and ~590 nm (~125 nm GNPs) dipolar plasmon resonances. Similarly, for 20 pM seed concentration the UV-vis peak ~ 562 nm is assigned to the superposition of ~522 nm (16 nm GNPs) and ~590 nm (~103 nm GNPs) dipolar plasmon resonances. The 50 pM seeded GNP solution UV-vis peak at ≈ 545 nm is assigned to the superposition of ~522 nm (10 nm GNPs) and ~590 nm (~ 86 nm GNPs) dipolar plasmon resonances. Thus, the simulated spectra reproduce qualitatively the observations indicating that the spectral changes are dominated by the narrowing of the particle size distributions.
Figure 2.
This figure compares the normalized (400 nm) (A) measured absorbance (after 7 days incubation at room temperature) of TBP coated GNPs produced using 50 pM citrated Au seeds (~ 23 nm diameter) in aqueous precursor solutions containing L31(8 mM)/F68(4 mM) and ≈ 1 mM Au(III) after 7 days incubation at room temperature. (B) Calculated extinction spectra at 5, 10, 20, 50 pM seed concentrations. For the calculated spectra, the lines are sums of the extinction spectra using the sizes of the two populations determined from dynamic light scattering, weighted by the volume distribution.
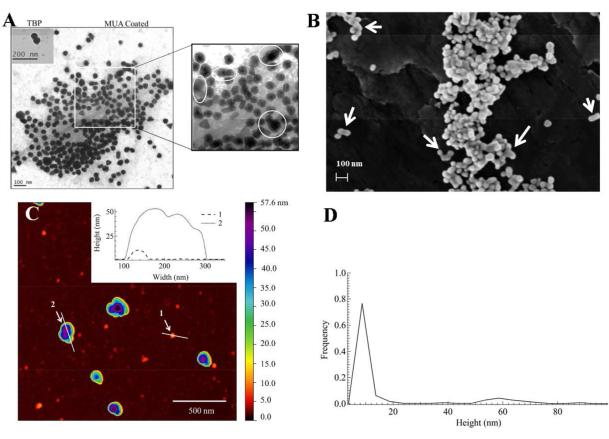
Figure 3.
Electron and atomic force microscopy characterization of TBP coated GNPs produced using 50 pM citrated ~ 23 nm seeds in aqueous precursor solutions containing L31(8 mM)/F68(4 mM) and ≈ 1 mM Au(III) after 7 days incubation at room temperature. (A) Transmission EM of TBP coated (inset) and 11-mercaptoundecanoic acid (MUA) coated GNPs. (B) Scanning EM image of TBP coated GNPs, where the white arrows show the compact aggregates. (C) Representative AFM (512 × 512 pixels) 2 × 2 μm2 image of TBP coated GNPs. (D) Particle height distribution (N = 401), from AFM analyses, with two main population means at (9.3 ± 1.9) nm and (59 ± 8) nm, respectively.
The detailed GNP morphologies were further examined by electron microscopy and AFM (Figure 3). Thiolation by MUA alters the surface properties of GNPs so that the TBP coating is removed and surface features are more easily observed (Figure S4; Supplemental for protocol). The inset and main TEM images show the TBP coated GNPs (~ 50 nm diameter) and thiolated GNPs, respectively (Figure 3A). From these electron micrographs, we estimate that the TBP coating is ~ 5 nm in thickness. Approximately 15% of these particles have anisotropic morphologies (rods and prisms). Similarly, using 5% w/v F68, Chen and co-workers21 achieved particle sizes ~ 40 nm along with larger anisotropic aggregates with lengths between 50 to 80 nm as well as rod-like structures. The polyhedral GNP sub-population mean size (d) is 44 ± 5 nm, in which , where A is the average projected area. Some of the nanostructures represent combinations of crystallographically variously orientated GNPs (Figure 3A, circles). This type of observation has precedent in the crystal growth of ZnS nanoparticles, and was explained via an orientated attachment (OA) growth mechanism.22 Previous TEM studies of TBP facilitated GNP synthesis also show evidence of polycrystallinity.4, 5d, 6 Additionally, there is evidence for inter-particle aggregation in the FESEM images (Figure 3B).
AFM measurements (Figure 3C) of TBP coated GNPs provide evidence for the formation of compact aggregates. Interspersed between the larger GNPs the AFM was able to resolve some finer nanostructures below 10 nm. Although the resolution capabilities of AFM in the x and y directions are compromised by the probe surface interactions, this is not the case for the z-axis where atomic resolution (~ 0.05 nm) is possible.23 Figure 3D shows a representative AFM height distribution of 50 pM seeded GNPs. A bimodal distribution can be clearly identified with mean heights of ≈ (9 ± 2) and ≈ (59 ± 8) nm, respectively. The examples of typical heights of both large and small particles are shown in the insert of Figure 3C. Some ultra-small nanocrystallites with heights between 2-5 nm were also observed. The observation of sub-10 nm GNPs has precedent. For example, F127 (EO99-PO65-EO99) mediated Au(III) reduction nanostructures of ~ 6 nm were detected by Polte and co-workers24 using quantitative small-angle X-ray scattering (SAXS) and X-ray absorption spectroscopy (XAS). We assume that such primary nanocrystallites are formed during the “burst” nucleation process.
Kinetic Modeling of GNP growth
Gold nanostructures lie in the intermediate size regime between single molecule and macroscopic crystallite. Thus, GNP growth follows a stochastic process subject to Brownian motion. To understand the relationship between seed concentration and final NP size we conducted kinetic Monte Carlo (KMC) simulations using the direct method algorithm from Gillespie25 to model the competitive GNP growth pathways. Initially, Au(III) is reduced by TBP in a sequence of Au(III) → Au(I) → Au(0),5b, 26 as established previously (Supplemental for discussion). Two competitive growth pathways are expected in our seeded model: (1) GNP direct growth in solution by the coalescence of reduced gold atoms and (2) the reduced gold atoms adsorbed on the surface of the seeding particles. GNP growth can occur in the solution where the terms Au(0) and Au(0)n represent gold atoms and higher order aggregates, respectively: (2 Au(0) → Au(0)2) and (Au(0) + Au(0)2 → Au(0)3…) followed by (Au(0) + Au(0)n → Au(0)n+1). For seeded growth of each cluster, the adsorption and growth processes occur sequentially with gold atom adsorption on the seed surface at seed adsorption site, Ns, followed by further gold atom attachment to this first adsorbed gold atom. In the presence of GNP seeds, the adsorption and growth steps are represented by (Au(0) + Ns → Au(0)ads) and (Au(0) + Au(0)ads → Au(0)ads+1).
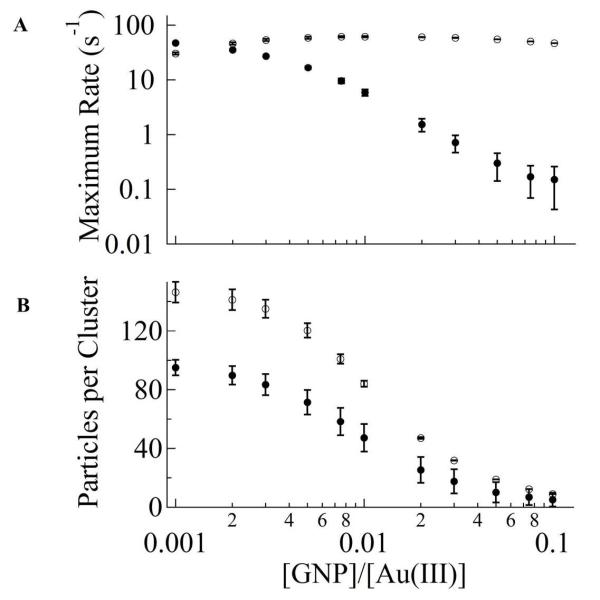
The results of the simulations show that seeding the solution suppresses the growth in the solution (Figure 4A, B). This is due to the fast consumption of Au(0) by the seeds making the chain growth of GNPs in solution kinetically insignificant. With our chosen kinetic parameters, as the seed concentration approaches 1% of Au(III) concentration the growth rate of GNPs from solution becomes negligible compared to that on the seed surface. Optimal growth rate occurs in the [GNP seed]/[Au(III)] ratio between 0.5% and 5%. Below this range the GNP growth is limited by the seed availability, while above this range it is limited by the Au(III) concentration in solution. We note that from the KMC simulation (Figure 4B), as the GNP seed concentration is increased the final cluster size is decreased. This is in good agreement with our experimental observation (Figure 1A). Such consistency indicates that the competitive growth pathway proposed in our KMC simulation model and the used kinetic parameters are qualitatively justified.
Figure 4.
This figure shows the kinetic Monte Carlo simulation of GNP growth. (A) Representative plot of maximum GNP growth rate on the seed (open circles) and in the solution (closed circles). The simulation represents an average of 100 runs with an initial particle number 104. (B) A plot of cluster size in solution (closed circles) and on the seed (open circles) against [GNP seed]/[Au(III)] concentrations.
Temporal Evolution in GNP growth
Both citrated GNP seeded and unseeded GNP growths were monitored by visible spectroscopy (535 nm) and light scattering (Figure 5A, B). The UV-vis absorption shows that aggregative and Ostwald growth regimes may be recognized by their exponential and linear growth behaviors, respectively (Figure 5A).4, 17a The effective growth rate, k, was found in both cases (seeded and unseeded) to be comparable (~ 0.2 min−1). Static light scattering was followed in the early time period (< 20 min of growth), when the GNPs are sufficiently small to be in the Rayleigh scattering regime (Figure 5B). For small size GNPs (< 40 nm) the exact shape of the scattering centers can be ignored and may be treated as spheres of equivalent volume. The measured static light scattering data points curves were fitted with a combined (RLCA + DLCA) model giving growth rates (45 ± 0.2 min2.1) and (34 ± 1 min2.1) for unseeded and seeded GNPs, respectively. Therefore, we expect that the initial growth kinetics is dominated by the reduction of Au(III). Adding GNP seeds slightly reduces the initial growth rate due to the adhesion of Au(0) on the seed surfaces, Ns.
Figure 5.
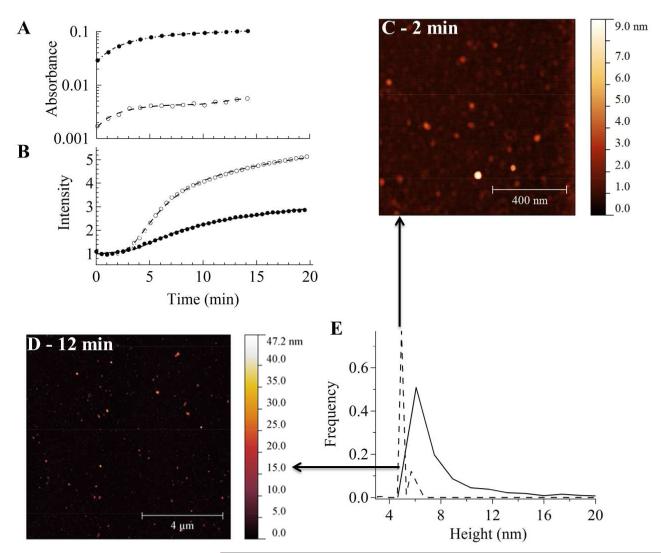
This figure shows the early-time evolution of GNP growth measured by UV-vis, static light scattering, and AFM using 50 pM citrated ~ 23 nm seeds in aqueous precursor solutions containing L31(8 mM)/F68(4 mM) and ≈ 1 mM Au(III). (A) Absorbance (535 nm) and (B) scattering intensities (450 nm) for 0 (open circles) and 50 pM (closed circles) citrated seeded precursor solutions. The absorbance curves in (A) are fitted with an aggregative model: . For unseeded conditions the fits are: n = 1, k = (3.11 ± 0.60) × 10−1 min−1, tOR = (10.4 ± 0.8) min, A = (4.6 ± 0.2) × 10−3, B = (3.0 ± 0.2) × 10−3, C = (2.9 ± 0.8) × 10−4 min−1, w = 1 min−1. For seeded conditions (50 pM seeds) the fits are: n = 1, k = (2.10 ± 0.09) × 10−1 min−1, tOR = (11.5 ± 1.5) min, w = 1 min−1, A = (1.04 ± 0.02) × 10−1, B = (7.74 ± 0.12) × 10−2, C = (9.7 ± 6.5) × 10−4 min−1. For light scattering in (B), the curves are fitted with a combined RLCA and DLCA model: I(t) = y0 + y1e−y2t−2.1 + y3t , where y0 is constrained to unity. For unseeded conditions the fits are: y1 = 1.17 ± 0.06, y2 = 45 ± 0.2 min2.1, y3 = (4.3 ± 0.3) × 10−2 min−1. For seeded conditions (50 pM seeds) the fits are: y1 = 3.56 ± 0.57, y2 = 34 ± 1 min2.1, y3 = (3.8 ± 0.3) × 10−2 min−1. Representative AFM images (C) (512 × 512 pixels − 5 × 5 μ>m2) and (D) (1024 × 1024 pixels − 10 × 10 μ>m2) with height distributions (E) at 2 (dashed line; N = 265) and 12 (solid line; N = 912) minutes, respectively.
AFM measurements were also used to characterize the relative particle size distributions of seeded growth (≈ 23 nm citrated GNP seeds) in 1 mM Au(III) solutions within the first 15 minutes (Figure 5C, D). The observed small GNPs were assumed to be spherical, with the heights used to construct the size distributions. Suitable sampling statistics were achieved by taking multiple AFM images on several different regions of the mica surface. Representative AFM images at ≈ 50 pM citrated GNP seeding show that the modal height increases from ~ 3 to 6 nm at growth time of 2 (sampled from 265 GNPs) and 12 (sampled from 912 GNPs) minutes (Figure 5C, D). Meanwhile, the width of the size distribution also increases from ~0.5 to 3 nm. Such behavior also suggests that the initial growth is controlled by the reduction of the Au(III).
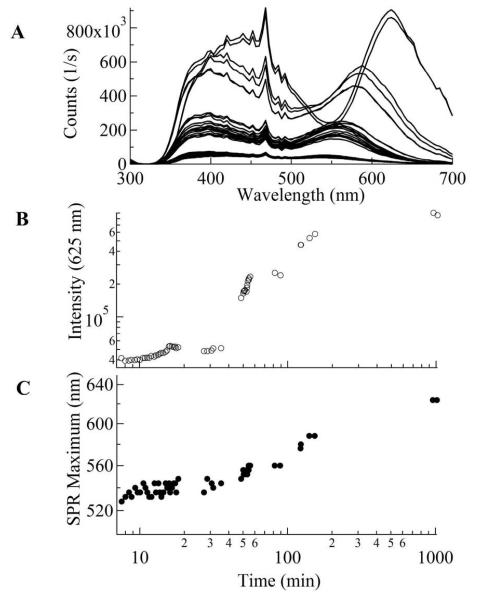
The time-evolution of the GNP sizes within 24 hours was monitored by resonant light scattering (Figure 6). These TBP solutions were seeded with 150 μL (3 mL TBP solution) of ≈ 23 nm GNPs (≈ 1 nM) with the addition of 1 mM Au(III). The PRLS intensity is very sensitive to GNP aggregation. If loose aggregation occurred, the PRLS intensity would increase, but the peak position of the plasmon resonance would not. In contrast, both intensity and peak wavelength increase as a function of growth time. Within 60 min of growth, the intensity increases rapidly, by at least a factor of 10 (Figure 6B), while the peak position only red-shifted slightly, from 525 to 555 nm (Figure 6C). This behavior suggests that initially, the particles are aggregated loosely. With growth time longer than 60 min the growth rate is reduced. Meanwhile the peak position shifts towards longer wavelength much faster than at earlier time. The observation of spectral changes, i.e., red-shifting from 540 to 625 nm and the concomitant step-wise intensity changes, are consistent with the formation of compact aggregates after 60 min of growth (Figure 6B, C).
Figure 6.
The evolution of GNP growth measured by plasmon resonance light scattering (PRLS) using 50 pM citrated ~ 23 nm seeds in aqueous precursor solutions containing L31(8 mM)/F68(4 mM) and ≈ 1 mM Au(III). (A) Time-evolution PRLS spectra upon GNP growth. (B) The time-evolution of the PRLS intensity at 625 nm (position of aggregate maximum). (C) Red-shifting of the surface plasmon resonance (SPR) intensity maximum wavelength during GNP growth.
DISCUSSION
GNP Growth Models
In classical growth models, it is assumed that when preformed nanoparticle seeds are introduced into the reaction mixture the atomic clusters precipitate on the surface of these particles. This heterogeneous nucleation process suppresses the formation of additional nuclei in the solution (homogeneous nucleation). When the ratio of the diffusion rate to the precipitation rate is small, the overall growth rate is governed by the rate of mass transfer, which is diffusion limited, and the particle size-distribution is narrowed.27 In contrast, when this ratio is high, this condition becomes reaction limited. Then the smaller particles dissolve more quickly than bigger ones, broadening the particle size distribution through OR processes. However, Park et al.28 noted that diffusion controlled OR models are limited to crystallization as a solid-solute conversion. In reality, (1) reduction of Au(III) to Au(0) may occur as a multiple step process; (2) dissolution and precipitation may not be entirely reversible; and (3) this classical description does not incorporate any aggregative growth processes.
In our experiments, the TBP concentration (5 mM of F68 or 8 mM/4 mM L31/F68) is far below the critical micelle concentration (CMC) of F68. For aqueous F68 the critical micelle concentration at 25 °C is ≈ 320 mM.29 Under these conditions, the TBPs exist predominantly as unimers and weakly associated aggregates. This will lead to a higher mass transfer rate for the gold particles and a slower reduction rate of Au(III) by TBPs, resulting in broad GNP size distributions. This broad distribution is demonstrated by the growth of GNPs in TBP solution without GNP seeds in Figure 1B. With low TBP concentrations, the mobility of large GNPs will also be higher and aggregative growth will become more significant than the Oswald ripening, which is less dependent on the particle mobility.
Kinetic Mechanism of Seeded GNP Growth
By adding GNP seeds, a bimodal particle size distribution is observed with much narrower size distributions compared to unseeded solutions. This seeding suppresses GNP self-aggregative growth. Moreover, we propose that the GNP seeds in the precursor solution provide a platform on which the TBP unimers and Au(III) can adsorb and react. The adsorbed TBP blocks act as catalytic sites for the reduction and the self-aggregation of primary nanocrystallites. The UV-vis and static light scattering studies at the early stage of the growth indicate the formation of such primary nanocrystallites, which grow by both aggregation and Oswald ripening mechanisms. The aggregation is responsible for the formation of large size GNPs following the competitive pathways of self-aggregation and coalescence on GNP seeds. We note that observations of silver and gold nanoparticle coarsening by aggregative processes have precedent.17, 11b, 30
Without seeding, the self-aggregation is dominated by stochastic processes subject to Brownian motion and crystal face orientation and is also influenced by the TBP phase behavior. This coalescence on GNP seeds is an energetically favored process. Theoretical studies by Zukoski and co-workers31 indicate that small nanocrystals are unstable. Moreover, Alivisatos and coworkers32 using TEM directly observed nanoparticle aggregation and coalescence during the early stages of growth.
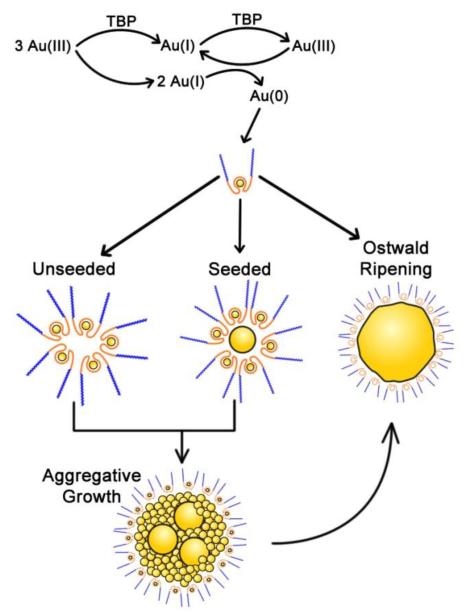
By adding GNP seeds, the growth is dominated by the coalescence of primary nanocrystallites to the seeds, and self-aggregation is suppressed. This will reduce the effective concentration of the primary particles in the solution for self-aggregation. With increasing seed concentration, the concentration of primary crystallites will be reduced, and the final size of the GNPs will also decrease. In such a process the self-aggregation is not completely eliminated, which will then contribute to the bimodal distribution of the nanocrystallites. The expected rate of coalescent growth on GNP seeds, Rgnp, is defined by k1[Au(0)]2 + k3[Au(0)]Ns (derivation in Supplemental), where Ns is autocatalytic site concentration of the adsorbed TBP blocks on the GNP seed surfaces. This rate of aggregative growth is dependent upon the concentrations of both Au(0) and GNP seeds. At higher [TBP]/[Au(III)] ratios (10-50), the rapid depletion in Au(III) concentration limits the growth of GNPs. In contrast at lower [TBP]/[Au(III)] ratios (1–5), the higher concentration of Au(0) will form more primary nanocrystallites in which Ostwald type growth will dominate after initial aggregative events. The second term k3[Au(0)]Ns accounts for the coalescence on the GNP seeds. At later reaction times, GNP growth becomes self-limited by the depletion in Au(0) and Ns. The Monte-Carlo simulations (Figure 4) based on the proposed mechanism produce bimodal GNP populations, in agreement with the experimental results. The proposed competitive growth mechanism is illustrated in Scheme 1.
Scheme 1.
The proposed model of seeded GNP growth. In this model, GNP growth occurs via (1) nanocrystallite formation (≈2 nm), followed by (2) autocatalytic aggregation on seed surfaces or in the solution; and (3) Ostwald type growth by the molecular addition of Au(0) atoms.
Taken together, there are design considerations that can be used to optimize TBP coated GNP sizes. First, larger anisotropic GNPs are formed when [TBP]/[Au(III)] ratios are small ~ 1–5.4 Second, The TBP phase-behavior determines the GNP particle size distributions. Indeed for F127, where the CMC at 25 °C is ~ 1 mM,33 single population GNP size distributions were obtained at the onset of aggregation (0.4 mM) and at the ordered (5 mM) micellar phase regimes.5b In the same study, the narrowest size distributions were obtained also at TBP concentrations close to the CMC for the more hydrophobic TBPs P103 and P105. Third, the seeding methodology is effective in producing monodisperse NPs when it catalyzes the “burst” nucleation rather than aggregative growth processes. This is the case for citrated GNP growth,12-13 where there is heterogeneous Au(III) reduction on the GNP seeds followed by Ostwald growth. GNP monodispersity can be achieved via altering the equilibrium of Au(I) disproportionation 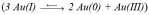 by using weak reducing agents that reduce Au(III) to Au(I) in the TBP precursor solution. Consequently, a high concentration of seeds is produced in-situ.
by using weak reducing agents that reduce Au(III) to Au(I) in the TBP precursor solution. Consequently, a high concentration of seeds is produced in-situ.
In summary, the mechanism of GNP growth is complex, with possible simultaneous processes of nucleation, aggregation and Ostwald growth. We propose that the mechanism of seeded GNP growth include the following steps (Scheme 1): (1) Au(III) reduction to produce primary nanocrystallites in the PEO-PPO-PEO cavities, (2) the formed crystals are less stable and bind preferentially to the surface of GNP seeds and (3) adsorbed nanocrystallites will eventually coalescence with the GNP seeds and form large crystallized particles, as confirmed by the red-shift of peak positions in PRLS spectra.
CONCLUSIONS
In the ≈ 1 mM Au(III) concentration range, the mean GNP size is reduced 10-fold in the presence of citrated GNP seeds. Furthermore, the resulting GNP size distribution is bimodal consisting of two populations, one at ~ 10 nm and another at ~ 100 nm. The underlying mechanism of GNP growth is thought to be dominated by aggregation. Several experiments were presented suggesting GNP coarsening via the coalescence of GNPs (Figures 1, 3 and 6) during the growth process. First, static light scattering confirms fractal RLCA growth behavior (Figure 5). Second, DLS and AFM imaging show the polydisperse nature of the particle size distributions (Figures 1, 3, and 5). Third, the spectral changes in the plasmon resonance light scattering (Figure 6) implicate the processes of collision-coalescence followed by crystallization.
Our results have shown that optimizing size and shape of GNPs formed in the presence of TBPs remains a challenging problem. However, there are lessons for further research: the combinations of low (< 2000) and high (> 6000) molecular weight TBPs produce an additional level of control over the GNP size distribution. Seeding catalyzes the aggregation of the primary nanocrystallites and the growth rate is strongly dependent on seed concentration rather than seed size.
Supplementary Material
ACKNOWLEDGEMENTS
This work was supported by the Loma Linda University. Access to the FESEM was provided by the Center for Nanoscale Science and Engineering (CNSE) at the University of California Riverside (UCR) and access to the Cary 50 UV/Vis/NIR spectrometer by the Analytical Chemistry Instrumentation facility (UCR) (NSF CHE-9974924).
Footnotes
Supporting Information Available: 1) Details of citrated GNP synthesis and characterization; 2) TBP coated GNP size distributions by DLS and STEM; 3) Details of GNP functionalization by MUA; 4) description of the KMC simulations; and 5) derivation of rate equation; this material is available free of charge via the Internet at http://pubs.acs.org
REFERENCES
- 1.(a West JL, Halas NJ. ENGINEERED NANOMATERIALS FOR BIOPHOTONICS APPLICATIONS: Improving Sensing, Imaging, and Therapeutics. Annu. Rev. Biomed. Eng. 2003;5(1):285–292. doi: 10.1146/annurev.bioeng.5.011303.120723. [DOI] [PubMed] [Google Scholar]; (b) Ozbay E. Plasmonics: Merging Photonics and Electronics at Nanoscale Dimensions. Science. 2006;311(5758):189–193. doi: 10.1126/science.1114849. [DOI] [PubMed] [Google Scholar]; (c) Halas NJ, Lal S, Chang W-S, Link S, Nordlander P. Plasmons in Strongly Coupled Metallic Nanostructures. Chem. Rev. 2011;111(6):3913–3961. doi: 10.1021/cr200061k. [DOI] [PubMed] [Google Scholar]
- 2.Alexandridis P. Gold Nanoparticle Synthesis, Morphology Control, and Stabilization Facilitated by Functional Polymers. Chem. Eng. Technol. 2011;34(1):15–28. [Google Scholar]
- 3.(a) Kabanov AV. Polymer genomics: An insight into pharmacology and toxicology of nanomedicines. Adv. Drug Deliv. Rev. 2006;58(15):1597–1621. doi: 10.1016/j.addr.2006.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Batrakova EV, Kabanov AV. Pluronic block copolymers: Evolution of drug delivery concept from inert nanocarriers to biological response modifiers. J. Controlled Rel. 2008;130(2):98–106. doi: 10.1016/j.jconrel.2008.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sabir TS, Yan D, Milligan JR, Aruni AW, Nick KE, Ramon RH, Hughes JA, Chen Q, Kurti RS, Perry CC. Kinetics of Gold Nanoparticle Formation Facilitated by Triblock Copolymers. J. Phys. Chem. C. 2012;116(7):4431–4441. [Google Scholar]
- 5.(a) Sakai T, Alexandridis P. Single-Step Synthesis and Stabilization of Metal Nanoparticles in Aqueous Pluronic Block Copolymer Solutions at Ambient Temperature. Langmuir. 2004;20(20):8426–8430. doi: 10.1021/la049514s. [DOI] [PubMed] [Google Scholar]; (b) Sakai T, Alexandridis P. Mechanism of metal ion reduction, nanoparticle growth and size control in aqueous amphiphilic block copolymer solutions at ambient conditions. J. Phys. Chem. B. 2005;109(16):7766–7777. doi: 10.1021/jp046221z. [DOI] [PubMed] [Google Scholar]; (c) Sakai T, Alexandridis P. Size- and shape-controlled synthesis of colloidal gold through autoreduction of the auric cation by poly(ethylene oxide)–poly(propylene oxide) block copolymers in aqueous solutions at ambient conditions. Nanotechnology. 2005;16(7):S344. doi: 10.1088/0957-4484/16/7/006. [DOI] [PubMed] [Google Scholar]; (d) Khullar P, Singh V, Mahal A, Kaur H, Singh V, Banipal TS, Kaur G, Bakshi MS. Tuning the Shape and Size of Gold Nanoparticles with Triblock Polymer Micelle Structure Transitions and Environments. J. Phys. Chem. C. 2011;115(21):10442–10454. [Google Scholar]
- 6.Khullar P, Mahal A, Singh V, Banipal TS, Kaur G, Bakshi MS. How PEO-PPO-PEO Triblock Polymer Micelles Control the Synthesis of Gold Nanoparticles: Temperature and Hydrophobic Effects. Langmuir. 2010;26(13):11363–11371. doi: 10.1021/la100734p. [DOI] [PubMed] [Google Scholar]
- 7.Brown KR, Walter DG, Natan MJ. Seeding of Colloidal Au Nanoparticle Solutions. 2. Improved Control of Particle Size and Shape. Chem. Mater. 1999;12(2):306–313. [Google Scholar]
- 8.Jana NR, Gearheart L, Murphy CJ. Seeding Growth for Size Control of 5–40 nm Diameter Gold Nanoparticles. Langmuir. 2001;17(22):6782–6786. [Google Scholar]
- 9.Rodríguez-Fernández J, Pérez-Juste J, García de Abajo FJ, Liz-Marzán LM. Seeded Growth of Submicron Au Colloids with Quadrupole Plasmon Resonance Modes. Langmuir. 2006;22(16):7007–7010. doi: 10.1021/la060990n. [DOI] [PubMed] [Google Scholar]
- 10.Eguchi M, Mitsui D, Wu H-L, Sato R, Teranishi T. Simple Reductant Concentration-Dependent Shape Control of Polyhedral Gold Nanoparticles and Their Plasmonic Properties. Langmuir. 2012;28(24):9021–9026. doi: 10.1021/la3002114. [DOI] [PubMed] [Google Scholar]
- 11.(a) Njoki PN, Lim IIS, Mott D, Park H-Y, Khan B, Mishra S, Sujakumar R, Luo J, Zhong C-J. Size Correlation of Optical and Spectroscopic Properties for Gold Nanoparticles. J. Phys. Chem. C. 2007;111(40):14664–14669. [Google Scholar]; (b) Njoki PN, Luo J, Kamundi MM, Lim S, Zhong C-J. Aggregative Growth in the Size-Controlled Growth of Monodispersed Gold Nanoparticles. Langmuir. 2010;26(16):13622–13629. doi: 10.1021/la1019058. [DOI] [PubMed] [Google Scholar]
- 12.Bastús NG, Comenge J, Puntes V. c. Kinetically Controlled Seeded Growth Synthesis of Citrate-Stabilized Gold Nanoparticles of up to 200 nm: Size Focusing versus Ostwald Ripening. Langmuir. 2011;27(17):11098–11105. doi: 10.1021/la201938u. [DOI] [PubMed] [Google Scholar]
- 13.Ziegler C, Eychmüller A. Seeded Growth Synthesis of Uniform Gold Nanoparticles with Diameters of 15–300 nm. J. Phys. Chem. C. 2011;115(11):4502–4506. [Google Scholar]
- 14.Gu Q, Kenny JE. Improvement of Inner Filter Effect Correction Based on Determination of Effective Geometric Parameters Using a Conventional Fluorimeter. Anal. Chem. 2008;81(1):420–426. doi: 10.1021/ac801676j. [DOI] [PubMed] [Google Scholar]
- 15.Laven P. MiePlot. 2012:4.3. [Google Scholar]
- 16.Bohren C, Huffman D. Absorption and Scattering of Light by Small Particles (Wiley science paperback series) Wiley-VCH; 1998. [Google Scholar]
- 17.(a) Richards VN, Rath NP, Buhro WE. Pathway from a Molecular Precursor to Silver Nanoparticles: The Prominent Role of Aggregative Growth. Chem. Mater. 2010;22(11):3556–3567. [Google Scholar]; (b) Shields SP, Richards VN, Buhro WE. Nucleation Control of Size and Dispersity in Aggregative Nanoparticle Growth. A Study of the Coarsening Kinetics of Thiolate-Capped Gold Nanocrystals. Chem. Mater. 2010;22(10):3212–3225. [Google Scholar]
- 18.(a) Xiang M, Xu X, Liu F, Li N, Li K-A. Gold Nanoparticle Based Plasmon Resonance Light-Scattering Method as a New Approach for Glycogen–Biomacromolecule Interactions. J. Phys. Chem. B. 2009;113(9):2734–2738. doi: 10.1021/jp8065822. [DOI] [PubMed] [Google Scholar]; (b) Wang X, Xu Y, Chen Y, Li L, Liu F, Li N. The gold-nanoparticle-based surface plasmon resonance light scattering and visual DNA aptasensor for lysozyme. Anal. Bioanal. Chem. 2011;400(7):2085–2091. doi: 10.1007/s00216-011-4943-1. [DOI] [PubMed] [Google Scholar]
- 19.Lin MY, Lindsay HM, Weitz DA, Ball RC, Klein R, Meakin P. Universality in colloid aggregation. Nature. 1989;339(6223):360–362. [Google Scholar]
- 20.Skrdla PJ. Roles of Nucleation, Denucleation, Coarsening, and Aggregation Kinetics in Nanoparticle Preparations and Neurological Disease. Langmuir. 2012;28(10):4842–4857. doi: 10.1021/la205034u. [DOI] [PubMed] [Google Scholar]
- 21.Chen S, Guo C, Hu G-H, Wang J, Ma J-H, Liang X-F, Zheng L, Liu H-Z. Effect of Hydrophobicity inside PEO–PPO–PEO lock Copolymer Micelles on the Stabilization of Gold Nanoparticles: Experiments. Langmuir. 2006;22(23):9704–9711. doi: 10.1021/la061093m. [DOI] [PubMed] [Google Scholar]
- 22.(a) Zhang J, Lin Z, Lan Y, Ren G, Chen D, Huang F, Hong M. A Multistep Oriented Attachment Kinetics: Coarsening of ZnS Nanoparticle in Concentrated NaOH. J. Am. Chem. Soc. 2006;128(39):12981–12987. doi: 10.1021/ja062572a. [DOI] [PubMed] [Google Scholar]; (b) Huang F, Zhang H, Banfield JF. Two-Stage Crystal-Growth Kinetics Observed during Hydrothermal Coarsening of Nanocrystalline ZnS. Nano Lett. 2003;3(3):373–378. [Google Scholar]
- 23.(a) Boyd R, Cuenat A. New analysis procedure for fast and reliable size measurement of nanoparticles from atomic force microscopy images. J. Nanopart. Res. 2011;13(1):105–113. [Google Scholar]; (b) Wong C, West PE, Olson KS, Mecartney ML, Starostina N. Tip dilation and AFM capabilities in the characterization of nanoparticles. JOM. 2007;59(1):12–16. [Google Scholar]
- 24.Polte J. r., Emmerling F, Radtke M, Reinholz U, Riesemeier H, Thünemann AF. Real-Time Monitoring of Copolymer Stabilized Growing Gold Nanoparticles. Langmuir. 2010;26(8):5889–5894. doi: 10.1021/la903829q. [DOI] [PubMed] [Google Scholar]
- 25.(a) Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81(25):2340–2361. [Google Scholar]; (b) Gillespie DT. Deterministic Limit of Stochastic Chemical Kinetics. J. Phys. Chem. B. 2009;113(6):1640–1644. doi: 10.1021/jp806431b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Longenberger L, Mills G. Formation of Metal Particles in Aqueous Solutions by Reactions of Metal Complexes with Polymers. J. Phys. Chem. 1995;99(2):475–478. [Google Scholar]
- 27.Talapin DV, Rogach AL, Haase M, Weller H. Evolution of an Ensemble of Nanoparticles in a Colloidal Solution: Theoretical Study. J. Phys. Chem. B. 2001;105(49):12278–12285. [Google Scholar]
- 28.Park J, Joo J, Kwon SG, Jang Y, Hyeon T. Synthesis of Monodisperse Spherical Nanocrystals. Angew. Chem., Int. Ed. 2007;46(25):4630–4660. doi: 10.1002/anie.200603148. [DOI] [PubMed] [Google Scholar]
- 29.Alexandridis P, Holzwarth JF, Hatton TA. Micellization of Poly(ethylene oxide)-Poly(propylene oxide)-Poly(ethylene oxide) Triblock Copolymers in Aqueous Solutions: Thermodynamics of Copolymer Association. Macromolecules. 1994;27(9):2414–2425. [Google Scholar]
- 30.(a) Ji X, Song X, Li J, Bai Y, Yang W, Peng X. Size Control of Gold Nanocrystals in Citrate Reduction: The Third Role of Citrate. J. Am. Chem. Soc. 2007;129(45):13939–13948. doi: 10.1021/ja074447k. [DOI] [PubMed] [Google Scholar]; (b) Polte J. r., Ahner TT, Delissen F, Sokolov S, Emmerling F, Thünemann AF, Kraehnert R. Mechanism of Gold Nanoparticle Formation in the Classical Citrate Synthesis Method Derived from Coupled In Situ XANES and SAXS Evaluation. J. Am. Chem. Soc. 2010;132(4):1296–1301. doi: 10.1021/ja906506j. [DOI] [PubMed] [Google Scholar]
- 31.Bogush GH, Zukoski Iv CF. Uniform silica particle precipitation: An aggregative growth model. J. Colloid Interface Sci. 1991;142(1):19–34. [Google Scholar]
- 32.Zheng H, Smith RK, Jun Y.-w., Kisielowski C, Dahmen U, Alivisatos AP. Observation of Single Colloidal Platinum Nanocrystal Growth Trajectories. Science. 2009;324(5932):1309–1312. doi: 10.1126/science.1172104. [DOI] [PubMed] [Google Scholar]
- 33.Perry CC, Sabir TS, Livingston WJ, Milligan JR, Chen Q, Maskiewicz V, Boskovic DS. Fluorescence of commercial Pluronic F127 samples: Temperature-dependent micellization. J. Colloid Interface Sci. 2011;354(2):662–669. doi: 10.1016/j.jcis.2010.10.028. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.