An assessment technique for computer-socket manufacturing

Abstract

An assessment strategy is presented for testing the quality of carving and forming of individual computer aided manufacturing facilities. The strategy is potentially useful to facilities making sockets and companies marketing manufacturing equipment. To execute the strategy, an evaluator fabricates a collection of test models and sockets using the manufacturing suite under evaluation, and then measures their shapes using scanning equipment. Overall socket quality is assessed by comparing socket shapes with electronic file shapes. Then model shapes are compared with electronic file shapes to characterize carving performance. Socket shapes are compared with model shapes to characterize forming performance. The mean radial error (MRE), which is the average difference in radii between the two shapes being compared, provides insight into sizing quality. Inter-quartile range (IQR), the range of radial error for the best matched half of the points on the surfaces being compared, provides insight into shape quality. By determining MRE and IQR for carving and forming separately, the source(s) of socket shape error may be pinpointed. The developed strategy may provide a useful tool to the prosthetics community and industry to help identify problems and limitations in computer aided manufacturing and insight into appropriate modifications to overcome them.

Introduction

Computer-socket manufacturing has the potential to reduce the time and cost of making prostheses for people with limb amputation. Unlike traditional socket fabrication methods, with computer-socket manufacturing the mold making and socket forming processes are automated. This automation reduces the amount of manual technical work, potentially saving time and money and allowing the practitioner to spend more time with patients. Additional benefits may include lower operating expenses and less required lab space thus lower overhead, as well as lower equipment, supply, and maintenance costs.

Despite its potential benefits, computer-socket manufacturing is estimated used by only 24% of practitioners regularly ¹. Inconsistent or poor performance is believed to be part of the reason for low use. This is likely due to computer manufacturing facilities not making the shape designed by the practitioner on the computer ². There is a wide range of quality in the industry. Clinical evaluations have shown that the mean number of computer sockets required to properly fit subjects to range from 1.5 to 5.0 ^3,4,5,6,7,8 depending on the investigation. At least part of the reason for needing so many sockets may have been poor manufacturing quality. If many fabrication runs are required to achieve a socket of acceptable fit then the advantages of computer manufacturing are lost, and traditional methods might as well be used.

Facilities implementing computer manufacturing to fabricate practitioner-designed model or socket shapes as well as manufacturers of fabrication equipment face an important challenge. There is no practical means for assessment of carving and forming performance. Nor are there testing standards in the industry. If facilities could regularly assess the shape quality of their models and sockets with a widely-accepted protocol then they could identify and correct errors, resulting in higher quality products delivered to the practitioner and patient. Documentation demonstrating good manufacturing practices could be disseminated, building clinician confidence in these facilities. This would likely result in the increased acceptance and use of CAD as a clinic tool.

The purpose of this paper is to present a testing strategy for computer-socket manufacturing. The strategy is designed to help facilities to test the quality of their models and sockets, to identify fabrication problems and limitations, and to provide insight into needed modifications to their equipment to overcome them.

Assessment Strategy

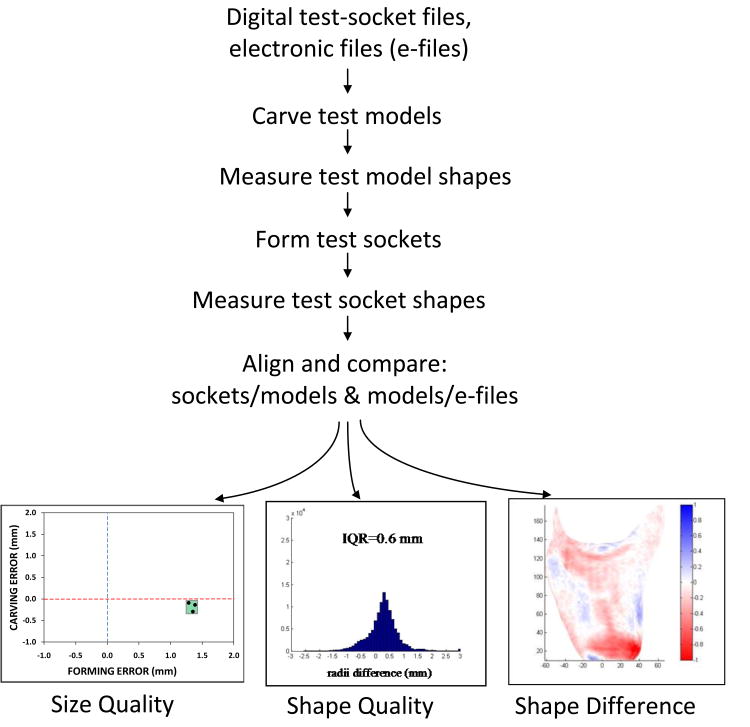
The assessment strategy is to fabricate a collection of test models and sockets using the computer manufacturing equipment under evaluation. The shapes of the fabricated models and sockets are measured and then compared with each other and with the electronic file shapes from which they were fabricated (FIGURE 1). Quantitative analyses as described below provide insight into the severity of error and the likely source(s).

Figure 1. Assessment strategy.

A diagram summarizing the assessment strategy is shown. In the Size Quality plot (left panel), carving error is the mean radial error (MRE) of the model compared with the electronic file shape; forming error is the MRE of the socket compared with the model. In the Shape Quality plot (center panel), the vertical axis is number of points on the surface, and IQR is inter-quartile range. In the Shape Difference plot (right panel), radial error (in mm) between a socket and model is illustrated.

The test shapes are selected to represent a range of socket shapes encountered in clinical practice in amputee prosthetics. Three trans-tibial amputee socket shapes are used in the example presented here, though additional socket shapes or other types of prostheses could also be tested. The examples used here are from a commercial software package for prosthetic socket design (ShapeMaker™, Sheck and Siress, Chicago, Illinois). The first model was of a patellar tendon bearing socket design that was for a person with a short and conical residual limb with a prominent fibular head. The second model was of a total surface bearing socket design that was for a person with a fleshy cylindrical residual limb with minimal bony prominences. The third model was of a patellar tendon bearing socket design for an individual with a bony and cylindrically shaped residual limb. Model lengths from the mid-patellar tendon to the distal end were 12.8, 14.2, and 15.7 cm for three models, respectively. These models were chosen because they represent a range of shapes, contours, and lengths which is important when evaluating carving and vacuum forming performance.

Collecting the Data

Carve test models

A model is carved for each of the three shapes using the facility's computer carving equipment. The settings used (e.g. bit size, carving speed) are selected based on the analysis of interest to the evaluator. For example, if a facility seeks to evaluate the quality of carves and sockets that they send out to customers regularly then they should use their usual carver settings. If a facility is interested in evaluating the influence of carving speed on their product then they should carve one set of test models at a slow speed and another set at a fast speed, and then from the quantitative analyses described below see how the results differ.

Measure test model shapes

The shapes of the models are then measured using an accurate scanning instrument. The scanning instrument should not contact the model so as to ensure the model shape is not distorted during measurement. If a laser scanner is used, measurement error is lower if the plane of laser light is projected perpendicular to the model surface rather than at an acute or obtuse angle. There is less distortion to the line that the laser light makes on the model surface.

There are different emerging technologies that may satisfy the measurement need. We have found that a high quality 3D laser scanner (3D Scanner HD, NextEngine Inc., Santa Monica, California) has acceptable performance for this application. The manufacturer states an accuracy of approximately 0.1 mm. The scanner uses multiple laser stripes to cross-validate the geometry data it collects, which helps to minimize error. We used a high-definition setting of 2000 points per square inch, and it took approximately 40 min to scan each model.

Form test sockets

Sockets are then formed over each of the three carved models, using the facility's regular forming practices. The socket material is selected based on the analysis of interest to the evaluator. If test socket fabrication is be evaluated then test socket materials should be used. If definitive socket fabrication is of interest then definite socket materials should be used. It might also be of interest to compare the influence of material selection on socket shape quality. In that case one set of models should be made with one material and another set of models made with the other material, then differences in the results compared.

Measure test socket shapes

The shapes of the sockets are then measured using an accurate scanning instrument. Unlike model shape assessment, the scanning instrument must measure within a confined space, i.e. within the prosthetic socket. We are not aware of any currently available commercial products that are small enough and meet the required accuracy threshold. The contact scanner we developed had an accuracy of approximately 0.1 mm for a wide range of socket shapes tested, and sampled at 800 points per slice ² with a 0.8 mm slice spacing. These performance qualities are important not necessarily because this level of accuracy is needed in socket manufacturing, but because current algorithms to properly align socket shapes with model shapes require such accuracy. In other words, poor socket shape measurement may introduce socket-to-model alignment errors that substantially distort the results of interest in the evaluation. Potentially, new alternative alignment algorithms could be created to overcome this restriction, but we are unaware of any such technologies available currently.

Align and compare shapes

The shapes of the sockets are then compared to the shapes of the models so that the error in forming can be determined. Since the model shape data and the socket shape data are acquired in different reference frames and with different sampling densities, they need to be aligned to each other first before comparisons between them can be made. An optimization procedure is used to do this. The optimization procedure minimizes a quantitative measure of clinical relevance. For example, commercially available software packages in the prosthetics industry typically implement an optimization procedure that minimizes the volume difference between the two shapes of interest. In other words, the shapes are moved relative to each other until the volume within them is as nearly equal as possible. This procedure performs well if the radii differences between the shapes are relatively even over the surface ⁹. It does not perform well if there are highly localized regions of shape difference. In these cases, research has shown that an optimization procedure that minimizes volume difference while maximizing shape similarity performs better ⁹. Maximizing shape similarity means that regions on the two surfaces that are very similar in shape are given higher priority (weighting) than regions that are highly dissimilar in shape. Computationally, using the inverse hyperbolic tangent of the surface normals as an optimization variable the highest weighting is given to surface normals that are close together, while the lowest weighting is give to surface normals that are far apart. Thus if for example the fibular head region of the socket is shaped poorly and oversized but everywhere else the socket is shaped correctly, the algorithm would produce an image that is highlighted blue at the fibular head, indicating a need for reduction, with little to no color elsewhere on the surface.

In addition to comparing the sockets to the models, the models also need to be compared to the electronic file shapes. This comparison is necessary because it will identify how much carving contributed to fabrication error, as opposed to forming. An algorithm similar to that described above for aligning sockets to models is executed to align models to electronic file shapes. In the example below, the algorithm that uses both volume difference minimization and shape similarity maximization ⁹ is implemented.

Analysis to Identify Sources of Error

Size quality

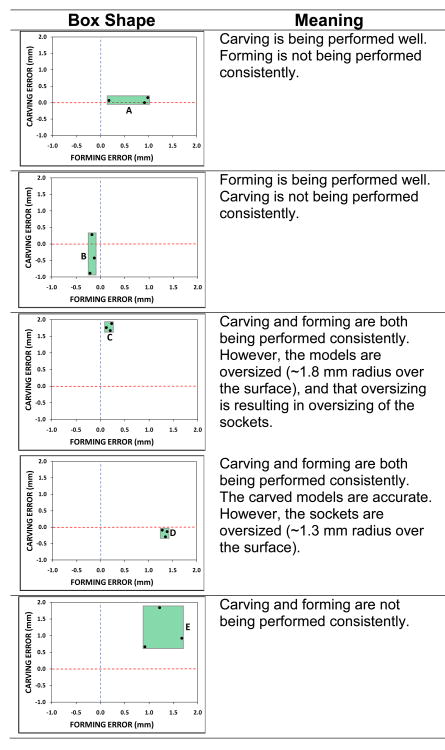
To quantify to what degree carving and forming are sources of error, the mean radial error (MRE) for all model-socket and all model-electronic file shape pairs is plotted (FIGURE 2). MRE is the average difference in radii between two surfaces. A box around the three points, one point for each socket-model and model-file shape pair, provides an indication of the consistency of error. If the box is small then both carving and forming are being performed consistently. If the box is large then there is an inconsistency problem.

Figure 2. Size Quality Graph: Interpreting the shape of the box.

The shape of the box indicates if there are sizing problems in carving and forming. Carving Error is mean radial error of the models, and Forming Error is the mean radial error of the sockets.

Examples ‘A’ to ‘E’ in FIGURE 2 illustrate how the Size Quality graph is interpreted. If the box is long and narrow and close to the ‘x’-axis (example ‘A’) then the carving is being performed well but forming is not being performed consistently. Possibly there is an inconsistent shrinkage problem using the polymer. If the box is tall and thin (example ‘B’) then forming is being performed well but carving is not being performed consistently. Possibly the facility is changing bit size from one carve to the next, and the bit is not being inserted to a consistent depth each time in its holder. If the box is small but far from the ‘x’-axis (example ‘C’) then carving and forming are both being performed consistently. However, the models are oversized (∼1.8 mm radius over the surface in this example) and that oversizing is resulting in oversizing of the sockets. Possibly there is a calibration offset error in the carver. If the box is small but far from the ‘y’-axis (example ‘D’) then carving and forming are both being performed consistently. The carved models are accurate. However, the sockets are oversized (∼1.3 mm radius over the surface in this example). Possibly a thick sock is being put over the model before forming. If the box is large and away from both axes (example ‘E’) then carving and forming are not being performed consistently. To identify the source(s) of error further testing is needed.

Shape quality

While presentation of the Size Quality data provides insight into sizing errors and the degree of inconsistency, a different chart is needed to characterize shape quality. Shape quality has to do with how well the manufactured shape matches that designed by the practitioner. A means for illustrating shape error is a histogram as shown in FIGURE 3a,b. A histogram shows the distribution of radial error. If the histogram is tall and narrow (FIGURE 3a) then the shape error is low, meaning that the radial error is relatively even over the surface. If the histogram is short and wide, however, (FIGURE 3b) then the radial error is high at some locations and low at other locations. In other words, the shape is distorted. The inter-quartile range (IQR) may be used to characterize the degree of distortion. The inter-quartile range is the range of radial error for the best-matched half of points on the surface, the central 50% of the points in the histogram.

Figure 3. Example histograms.

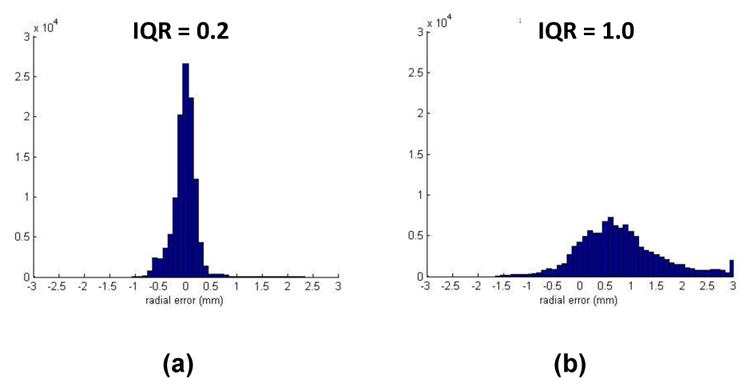
The distribution of radial error is narrow in (a) thus there is little distortion. The distribution of error is broad in (b) indicating substantial distortion.

Shape difference

While the histogram and IQR quantify distortion, they do not indicate where the distortions are located on the surface. A visual image of shape differences (FIGURE 4) shows locations of undersizing in red and locations of oversizing in blue. With this image, the evaluator can visually inspect if shape errors are localized to certain locations, for example at the fibular head and anterior distal end where there is much curvature (FIGURE 4a). The error might be more uniformly distributed over the surface, indicating uniform undersizing or oversizing (FIGURE 4b). For cases where both a volume error and a shape error are present, quantifying and displaying the closeness of surface normals might facilitate presentation. This presentation would distinguish shape error from volume error. With the three charts (Size Quality; Shape Quality; and Shape Difference) the evaluator is provided with an informative summary about fabrication performance, from which likely sources of error can be deduced.

Figure 4. Shape Difference Plots.

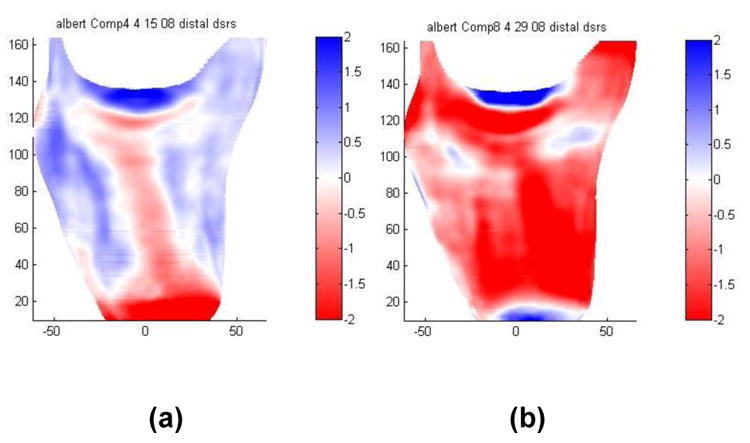
(a) This socket shows undersizing over the tibial crest and the fibular head. (b) This socket is uniformly undersized except at the medial and lateral tibial plateau.

Example Case

The example case presented below illustrates how this assessment strategy is implemented (FIGURE 5). The example is from a central fabrication facility, labeled here as Company XXX, that requested an analysis of their model and socket forming processes.

Figure 5. Example assessment report.

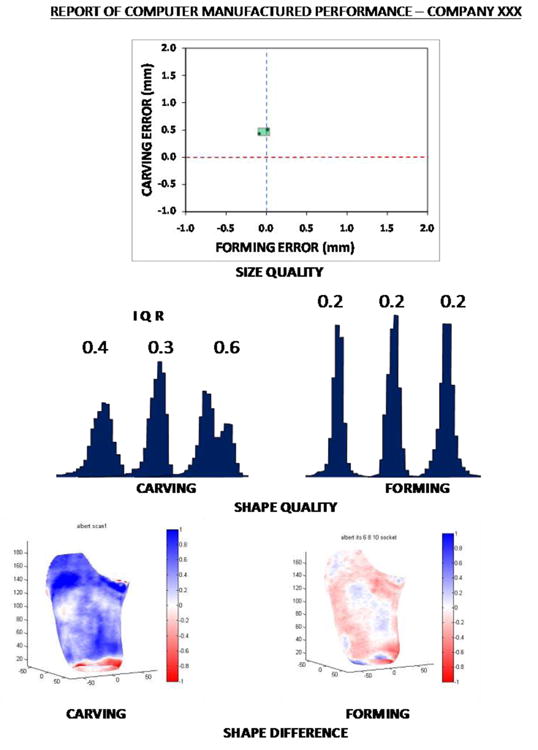
A sample report evaluating Company XXX's carving and forming procedures is shown.

Results from this analysis show that this company has very consistent carving and forming processes. The box in the Size Quality chart is very small, meaning that the range of MRE for both carving and forming is small. However, because the box is offset relative to the ‘x’-axis, the models are consistently oversized. There is an error in the company's carver that is causing a 0.5 mm radial (1.0 mm diameter) oversizing of all models, which is equivalent to an approximately 1.7% volume error. This oversizing remains after forming (in the Size Quality image (upper right) the green box is on the ‘y’-axis, meaning that errors during carving are propagated through forming). From the Carving Shape Difference plot, it is clear that the radial error is relatively uniform over the surface.

Thus we suspect that there is a calibration error. The location of the tip of the bit may not be correctly programmed into the carver. Calibration error may be corrected by recalibrating the carver using the manufacturer's recommended calibration procedures.

This company's socket forming practices are remarkably accurate. The narrow tall histograms (FIGURE 5, Shape Quality plots) show that their sockets are almost exactly the same shapes as their models. The very light colors in the Shape difference images further support that their socket forming practices are exceptionally good.

Presentation of shape differences between the socket and electronic file shapes might also be helpful for presentation in that it shows the combined error of carving and forming. We chose not to present those data here because it made the presentation overwhelming and confusing.

Discussion

From previous reports in the literature ^2,10, it is clear that there is variability in quality and consistency among different central fabrication facilities making prosthetic models and sockets for people with limb amputation. It would therefore seem reasonable for facilities to assess their manufacturing equipment as part of their regular practice. Manufacturers of computer-socket fabrication equipment seeking to improve their products could facilitate these efforts by including a means for assessment as part of the technology they sell. Regular evaluation would tell a fabrication facility quickly if something in their process needed correction. Such efforts might reduce down-time, enhance quality, and lower operating cost in the prosthetic socket fabrication industry. The ultimate goal is for practitioners to receive a socket shape well-matched to the shape they created on the computer, and for amputee patients to consistently receive a high quality product.

It is important to recognize that there are two issues in fabrication quality: (1) consistency; and (2) accuracy. Both can be assessed through the evaluation strategy described here. However, the ease with which the test results are interpreted is strongly influence by presence of the former, i.e. consistency. In the case demonstrated here, the source of fabrication error was easily identified because it was present in each model-socket pair made by the facility. Inconsistent errors are more difficult to interpret but, in general, point to a human technician issue. One example of a human technician issue would be differences in the amount of material removed during model sanding (most facilities sand their models by hand before forming). If assessment technology was implemented, fabrication facilities would be provided with the information necessary to find and correct error and improve their model and socket products. If many technicians are making models and sockets then this assessment methodology could help identify which technician's procedures are different from others.

Evaluation technology potentially provides a base for standards or certification of computer-socket fabrication centers and equipment. One approach to certification could be to rate facilities on a scale, for example 1 to 5 based on product consistency and accuracy, with 1 meaning highly consistent and highly accurate and 5 meaning highly inconsistent and highly inaccurate.

From our experience comparing socket manufacturing accuracy and practitioner-rated socket fit ¹¹, some subjects are more tolerant to shape error than are others. We expect that there is a threshold error that most patients using prosthetic limbs and practitioners would deem acceptable. In other words, there is no need to expend the time and funds to make sockets more accurate than this threshold level because there is no difference in clinical fit or in the patient's functional outcome. Prosthetics research has yet to identify this threshold, but it is likely it exists, and is just a matter of time before it is determined. While we expect there is a threshold that holds for most patients, we do not expect that it holds for all patients. There are likely select patients that require a special more accurate socket shape. An analogy to this concept is in the podiatry field. Some patients require custom orthotic inserts for their shoes while many others do fine with off-the-shelf orthosis products. In prosthetics, some patients might require a special more accurate socket shape than others might do fine with the normal quality shape. Presumably the cost of fabricating a very accurately shaped socket is higher, particularly if the latest technology, i.e. additive fabrication techniques ^{13,14,15,16,17}, is used. One possible means for managing these differences in patient adaptability is to distinguish the minimally adaptable patient via a special rating, for example P1. A patient with a P1 rating is highly unusual and does not easily adapt and is intolerant to even small shape errors. An example might be a severely diseased patient with thin skin over bony prominences and minimal limb soft tissue. A patient with a normal rating, a person who adapts to a normal shape quality socket, might be termed a P2 patient. A facility with a 1 rating would be capable of fabricating sockets accurately for both patients. A facility with a rating of 4 could only manufacture acceptable sockets for the normal P2 individuals, patients who adapt to shape errors. Selection of the facility with a 1 rating is thus imperative and justified for patients with P1 ratings while both facilities are appropriate for patients with either P1 or P2 ratings.

An important challenge towards this evaluation strategy is that currently we do not know how much socket fabrication error is acceptable nor what determines to which group a patient should be assigned. Data presented in the literature on the influence of patient volume change on fit provide a starting point for establishing socket and model volume accuracies and radial accuracies needed for computer manufactured sockets. Fernie and Holliday ¹² state that a patient using a sock ply that is 10% or more of his or her residual limb volume should be fit with a new smaller socket. When the sock ply is between 5% and 10% of the limb volume, the socket is “acceptable,” and when the sock ply is between 0% to 5% of the limb volume, the socket is “good.” These ranges were developed by Fernie and Holliday in 1982 based on their experience using a water displacement method in the clinic to measure limb volume change on amputee subjects at various stages post-amputation. Perhaps the clinical community would benefit from a revised and updated set of standards created using current methodology. Using sockets in the present investigation, 5% and 10% volume errors correspond to mean radial errors of approximately 1.8 mm and 3.4 mm, respectively.

Studies on amputee subjects are needed to quantify the clinical impact of socket shape error on patient discomfort, performance, function, and duration the socket fit is acceptable. For example, do computer-manufactured sockets with much MRE and IQR error need to be replaced sooner, and thus actually increase health care costs over other methods that do not have these errors? Obtaining meaningful results from clinical studies will be challenging because there are confounding factors simultaneously influencing fit. The patient's health status, tissue tolerance, disease, and other characteristics might influence tolerance to socket shape error. Patient weight changes over time are considered influential to limb volume and thus fit ¹². Further, some patients can adapt easily to accommodate socket shape errors while others cannot. The degree of acceptable error is likely patient dependent, and a challenge to prosthetics researchers will be to determine which patient characteristics correlate with low threshold to socket shape error and which do not.

Overcoming Error

One means for overcoming manufacturing error in prosthetics is to use a different modality. Direct socket fabrication approaches have been pursued in research investigations ^{13,14,15,16,17,18} and potentially have less error than current computer socket manufacturing techniques. While moving to one of these technologies is a means of potentially overcoming shape fabrication error, these technologies are not yet commercially available for prosthetics. High cost, licensing, and mechanical strength issues are part of the limitation. Further, it is not clear if from a socket quality standpoint as discussed above, such technologies are necessary. There may, however, be other advantages to these technologies outside of just fabrication accuracy.

Another approach to correcting for socket shape error for individual fabrication facilities is to characterize the nature of the error and then correct for it in the carving process. In a recent investigation ², most of the time (seven of ten companies tested) all three models tested for a company had relatively consistent error, meaning that the error should be capable of being well characterized using a modeling approach. The model can then be used to correct the fabrication process by altering the electronic file shape sent to the manufacturing equipment. Using models to correct fabrication processes like this is a technique pursued in other fields, for example the automotive industry ¹⁹. In engineering, this effort is known as “solving the inverse problem.” Such algorithms proceed as an optimization procedure where the manufacturing file shape is locally altered until the shape predicted by the model is within a specified tolerance for the application at hand. These sorts of correction algorithms do not currently exist in prosthetic socket manufacturing. However, they could potentially improve socket fabrication by automating correction.

An issue related to shape error has to do with the point density specified in electronic file shapes used to make models and sockets. Too fine a density can detrimentally affect computing speed and disk storage space as well as slow down manufacturing speed. Too low a density potentially introduces shape error that may make the socket fit unacceptable. Once the accuracy needs of models and sockets are better determined via clinical outcomes assessment then it should be clear if prosthetic computer manufacturing point densities need adjustment from their current levels. Quantification of the spatial frequency content of a population of well-fit traditionally made sockets would be another approach to gaining insight into an appropriate point density. Spatial frequency analysis has been investigated by Hastings et al. as related to digitizer performance ²⁰, but not for model or socket fabrication.

Tools for Assessment

With recent enhancements in imaging systems, such as the laser scanner used to assess models in this study, characterizing the shapes of positive models is simplified over custom techniques described previously ¹⁰. Small scanners that fit within a prosthetic socket are starting to emerge and should soon be able to replace custom socket scanning instruments. Once commercially available technology is demonstrated to have sufficiently low error to meet the need then central fabrication facilities will have viable means to conduct in-house assessment using a methodology similar to that described here and to determine if they have manufacturing errors.

It is important to recognize that when engineering an evaluation technology for socket shape that there is an important harmony between the measurement technique and the means for aligning measured shapes (e.g. models, sockets, and electronic file shapes). The optimization algorithm described in this investigation used a combination of maximization of shape similarity and minimization of shape difference ⁹. In the literature, researchers have described other methods for alignment, including minimization of volume difference ²¹, anatomical landmarks ^22,23,24, and top and bottom slice centroids ²⁵. We developed the new method because our investigations demonstrated that alignment of residual limb shapes using a mean absolute difference (volume minimization) algorithm alone or a surface normal optimization algorithm alone depended upon the nature of the shape difference, which was not acceptable ⁹. Use of a combination of minimization of mean error and alignment of surface normals did not depend upon the nature of shape difference, and thus produced better results. If socket and model shapes are to be compared to each other or to electronic file shapes then care must be taken to ensure that the alignment algorithm is not sensitive to the nature of the shape difference. An additional goal is to create an alignment optimization algorithm that is minimally sensitive to measurement errors in the scanning instrument with which it is coupled.

Potentially the assessment methods described in this paper can be applied to other aspects of computer socket manufacturing, namely the limb shape measurement phase. Geil ²⁶ showed that manual, optical, and electromagnetic shape-capture systems produced anthropometric measurements similar to each other, thus suggesting minimal advantage to using electronic measurement systems for shape assessment. McGarry et al. ²⁷ showed that an electromagnetic contact sensor system did not perform as well on trans-tibial models as on cylindrical models. Geil's and McGarry et al.'s evaluations were very helpful towards telling us where the technology currently stands, but it still remains to be determined how accurate scanning technologies need to be for effectively implementing computer manufacturing methods.

Conclusion

An assessment method to evaluate the quality of computer manufactured models and sockets is presented. The prosthetics computer-socket fabrication industry may benefit from creating and implementing model and socket assessment standards so as to enhance quality and consistency across the industry. Such an effort might improve practitioner confidence in computer socket manufacturing, serve as a basis for enhancement, reduce patient care costs, and serve as a means for documenting performance.

Further research is needed to establish a relationship between computer socket fabrication error and patient functional outcome, prosthesis performance, and the duration of time the socket is usable by the person with limb amputation.