Brain pressure responses in translational head impact: a dimensional analysis and a further computational study

Abstract

Brain pressure responses resulting from translational head impact are typically related to focal injuries at the coup and contrecoup sites. Despite significant efforts characterizing brain pressure responses using experimental and modeling approaches, a thorough investigation of the key controlling parameters appears lacking. In this study, we attempted to identify three parameters specific and important for brain pressure responses induced by isolated linear acceleration (a_lin) via a dimensional analysis: a_lin itself (magnitude and directionality), brain size and shape. These findings were verified using our recently developed Dartmouth Head Injury Model (DHIM). Applying a_lin to the rigid skull, we found that the temporal profile of the given a_lin directly determined that of pressure. Brain pressure was also found to be linearly proportional to brain size and dependent on impact direction. In addition, we investigated perturbations to brain pressure responses as a result of non-rigid skull deformation. Finally, DHIM pressure responses were quantitatively validated against two representative cadaveric head impacts (categorized as “good” to “excellent” in performance). These results suggest that both the magnitude and directionality of a_lin as well as brain size and shape should be considered when interpreting brain pressure responses. Further, a model validated against pressure responses alone is not sufficient to ensure its fidelity in strain-related responses. These findings provide important insights into brain pressure responses in translational head impact and the resulting risk of pressure-induced injury. In addition, they establish the feasibility of creating a pre-computed atlas for real-time tissue-level pressure responses without a direct simulation in the future.

1 Introduction

Traumatic brain injury (TBI) continues to be a major public health problem in the United States (Centers for Disease Control and Prevention 2003). Understanding the biomechanical mechanisms of TBI is critical for establishing injury tolerance criterion and for designing better protective devices to prevent or reduce the incidence and severity of the injury. Despite substantial efforts, the underlying biomechanical mechanisms of TBI remain elusive. Kinematics-based injury metrics such as linear (a_lin) and rotational (a_rot) acceleration peak magnitudes as well as their variants have been historically employed to characterize the potential injury tolerance criteria. However, no consensus has been reached on a tolerance threshold or even on which injury metric is the most appropriate. Because HIC only considers resultant a_lin while many believe a_rot is responsible for initiating diffuse axonal injury (King et al. 2003), its applicability in assessing the risk of mild traumatic brain injury (mTBI) has been criticized. More recent injury metrics typically include rotational accelerations, including the generalized acceleration model for brain injury threshold (GAMBIT; Newman 1986), head impact power (HIP; Newman et al. 2000), and the HIT severity profile (HITsp; Greenwald et al. 2008). Notably, injury metrics such as the brain injury criterion (BrIC; Takhounts et al. 2013), the rotational injury criterion (RIC) and power rotational head injury criterion (PRHIC) based on the HIC and HIP counterparts, respectively (Kimpara and Iwamoto 2012), are solely composed of rotational components from the six degrees-of-freedom (DOFs) head impact. While these efforts focus on the significance of rotational accelerations on brain injury, combining both linear and rotational accelerations was found to significantly improve concussion prediction based on peak acceleration magnitudes (Rowson and Duma 2013).

Regardless, both a_lin and a_rot contribute to head impact kinematics in real-world injury events. Using random sampling and statistical linear regression, Ji et al. (2014c) identified that brain strain-related responses (strain, strain rate and von Mises stress) are significantly correlated to both the magnitude and duration of a_rot but are insensitive to a_lin due to brain’s near incompressibility, confirming previous observations (Zhang et al. 2004; Kleiven 2007; Takhounts et al. 2008). Although the significant correlation between pressure and a_lin magnitude is also well known (Nahum et al. 1977; Zhang et al. 2004; Hardy et al. 2007; Kleiven 2007; Ji et al. 2014a), influences from other parameters such as a_lin directionality, geometrical features of the head itself, are less clear.

Gurdjian et al. (1961) first measured brain pressure responses and a_lin in human cadaveric head impact in an automobile crash setting and found that brain temporal pressure increased with the increase of a_lin magnitude. Nahum et al. (1977) and Hardy et al. (2007) further observed a linear relationship between brain pressure and a_lin magnitude in experiments, which was confirmed by a number of computational studies using finite element (FE) models of the human head (Zhang et al. 2004; Kleiven 2007; Ji et al. 2014a). Ward et al. (1980) later proposed a brain injury criterion based on head resultant time-varying a_lin according to brain pressure tolerance. Trosseille et al. (1992) also measured brain pressure responses in cadaveric head impacts to develop a validation protocol for head FE models. Using a computational model, only Kleiven and von Holst (2002) related brain pressure responses to different head sizes with an identical frontal impact a_lin applied to the rigid skull. They found that the coup and contrecoup pressures (i.e., positive and negative pressures characterizing the compressive and tensile forces at the impact and opposite site of the head, respectively) increased with the increase in head size nearly linearly, and suggested that HIC may not be sufficiently accurate because no size-dependency was considered. More recently, Yoganandan et al. (2014) reviewed normalization and scaling techniques for a range of physical variables as a result of sample size difference in order to transform findings from cadaveric tests to derive human response corridors in a reference or a targeted population. The dependency of brain pressure responses on head impact location was also observed (Ruan et al. 1994; Zhang et al. 2001a), which was attributed to local geometrical curvature of the head. Findings on the influence of skull thickness on pressure responses suggest that coup (contrecoup) pressure decreased (increased) with the decrease of skull thickness (Ruan and Prasad (2001)). Generally, it is believed that brain bulk but not shear modulus plays an important role on pressure responses (Meaney et al. 2014) as observed in Kleiven and Hardy (2002) and Ruan and Prasad (2006), despite finding from Horgan and Gilchrist (2003) indicating otherwise.

Regardless of all these efforts, a thorough investigation of the fundamental parameters specific and important for brain pressure responses appears lacking. In this study, we attempted to identify critical controlling parameters important for brain pressure responses via a dimensional analysis, which is a valuable tool to contract the functional form of physical relationships (Sonin 2001). Interestingly, an analogous approach has already been applied to relate difference in brain size to explain the ability of woodpeckers to withstand much higher a_lin magnitudes than the human brain tolerance during drilling without suffering from apparent brain injury (albeit the validity of their scaling relationship depended on the near incompressibility of the brain, which was only implicitly utilized; Gibson 2006). In our study, we significantly extended the previous investigations by identifying both input kinematic and head model geometrical parameters that are specific and important to brain pressure responses and further verified the derived results via a computational approach using the recently developed Dartmouth Head Injury Model (DHIM). Perturbations due to dimensional analysis simplifications as well as sensitivities of brain material properties (dilatational and deviatoric) were also investigated. Finally, the DHIM pressure responses were quantitatively validated against two representative cadaveric head impact experiments. Findings from this study may provide important insights into brain pressure responses in translational/direct head impact in general, the resulting risk of pressure-induced injury (e.g., contusion (King et al. 1995) or head injuries resulting from falls or vehicular crashes where linear accelerations induced by contact forces typically dominate (King et al. 1995; Yoganandan et al. 2009)), and towards ensuring the biofidelity of computational head models especially in terms of pressure responses. Further, an important purpose of the dimensional analysis in this study is to expose the underlying independent variables required to establish a pre-computed brain pressure response atlas analogous to that for brain strain responses (Ji and Zhao 2014) in order to substantially improve the efficiency in head impact simulation. Combining these atlases for (near) real-time tissue-level estimates of pressure and strain responses may provide the computational tools necessary and critical to accelerate the exploration of the biomechanical mechanisms of traumatic brain injury in the future.

2 Methods

2.1 A dimensional analysis of brain pressure responses due to isolated linear acceleration

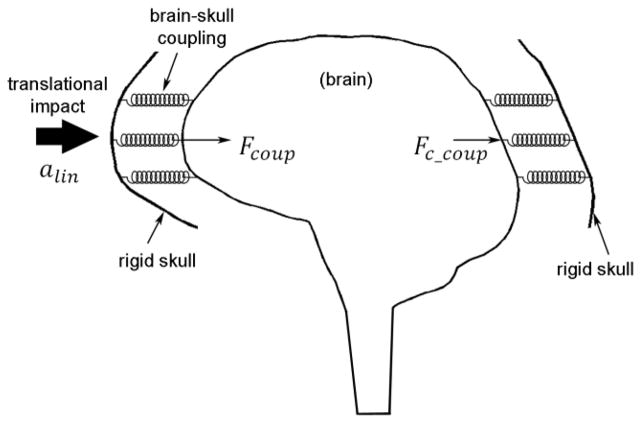
To facilitate the dimensional analysis, the cerebrospinal fluid (CSF) and pia/arachnoid mater were simplified as an elastic coupling between the brain and skull. When the brain is subjected to isolated a_lin, little strain is produced as a result of the brain’s high bulk modulus (K) leading to its near incompressibility (Ji et al. 2014c). Consequently, the brain translates along with the skull similarly to a rigid-body. The brain-skull interface, therefore, can be conceptually approximated as a simple spring-mass system (Fig. 1), leading to the following force (F) expressions:

$$F_{\mathit{coup}}=k_{\mathit{coup}}{x}_{\mathit{coup}},\text{and}{F}_{c\_\mathit{coup}}=k_{c\_\mathit{coup}}{x}_{c\_\mathit{coup}},$$ (1)

where k symbolizes the brain-skull coupling, x refers to the relative brain-skull displacement at the interface, and the subscripts are self-explanatory (not repeated hereafter). Because the brain moves as a rigid-body along with the separate rigid skull, non-zero x_coup and x_{c_coup} are identical in magnitude. When using a tied or sliding-only boundary condition without brain-skull separation (Kleiven and von Holst 2002; Kimpara et al. 2006; Kleiven 2007) or sharing nodes at the interface such as SIMon (Takhounts et al. 2008) and DHIM (Ji et al. 2014b), k_coup and k_{c_coup} will be identical, leading to an equal magnitude between contact forces F_coup and F_{c_coup}. When combined, the following relationship is obtained to determine brain acceleration according to the Newton’s law:

$$m_{\mathit{brain}}{a}_{\mathit{lin}}=F_{\mathit{coup}}+F_{c\_\mathit{coup}},$$ (2)

where m_brain is the brain mass. Because the forces are essentially generated by distributed pressure, P, the following relationships ensue:

$$F_{\mathit{coup}}=P_{\mathit{coup}}{A}_{\mathit{coup}},\text{and}{F}_{c\_\mathit{coup}}=P_{c\_\mathit{coup}}{A}_{c\_\mathit{coup}},$$ (3)

where A is the effective brain-skull contact area. Because the proportionality between A_coup and A_{c_coup} is constant for a given head model and a given a_lin directionality, the equality between F_coup and F_{c_coup} is translated into a linear proportionality between P_coup and P_{c_coup}. Combining with Eqn. 2, therefore, the following dimensional relationship is derived (subscripts are dropped to indicate its applicability to both P_coup and P_{c_coup}):

$$P\propto \frac{m_{\mathit{brain}}\times a_{\mathit{lin}}}{A},$$ (4)

suggesting that brain pressure responses are linearly related to a_lin magnitude, brain mass, and effective brain-skull contact area. Because of the scaling relationship between brain mass and effective contact area (i.e., proportional to the 3^rd and 2^nd order of brain characteristic length, respectively), P is linearly proportional to brain size. In addition, pressure P is also inversely proportional to the effective brain-skull contact area, which is essentially determined by brain shape or local curvature of the brain-skull interface. In sum, therefore, brain pressure responses are uniquely determined by a_lin (magnitude and directionality), brain size and shape (a_lin directionality, contact area and brain shape are uniquely related for a given head model).

Fig. 1.

Schematic of the brain-skull coupling system. See text for details.

In the following sections, we verify these relationships derived from the dimensional analysis via model simulation using our recently developed DHIM, which was previously validated in terms of brain-skull relative displacement and strain responses (Ji et al. 2014b) and is further validated in this study in terms of pressure responses. Because these relationships depend on the brain’s near incompressibility assumption only that leads to an essentially rigid-body motion of the brain along with the skull, we further varied the brain’s bulk modulus and shear stiffness properties (model and stiffness values) in order to investigate their significance and insignificance on P, respectively.

2.2 The Dartmouth Head Injury Model (DHIM)

All model simulations in this study were conducted using the recently developed Dartmouth Head Injury Model (DHIM; Fig. 2) previously validated for relative brain-skull displacements and brain strain responses (Ji et al. 2014b; Ji et al. 2014c). The DHIM is composed of solid hexahedral and surface quadrilateral elements with a total of 101.4 k nodes and 115.2 k elements (56.6 k nodes and 55.1 k elements) with a combined mass of 4.562 kg for the whole head. The brain has a mass of 1.579 kg or 1.558 kg with or without the spinal cord. The average element size for the whole head and the brain is 3.2±0.94 mm and 3.3±0.79 mm, respectively. An isotropic Ogden hyperelastic model identical to the “average” model in Kleiven 2007 was used to simulate the brain mechanical behavior. A combined pia-arachnoid complex CSF layer existed between the brain surface and all of its surrounding structures (similar to (Takhounts et al. 2008)) to allow brain interfacial sliding through CSF deformation (nodes between all anatomical interfaces were shared). A “good” to nearly “excellent” performance was achieved when validating the DHIM against relative brain-skull displacements in cadaveric head impacts and strain responses in a live human according to a biofidelity rating (de Lange et al. 2005). The baseline material properties for the skull and brain are summarized in Table 1 (along the “compliant” and “stiff” properties for the brain, see Section 2.3 for details).

Fig. 2.

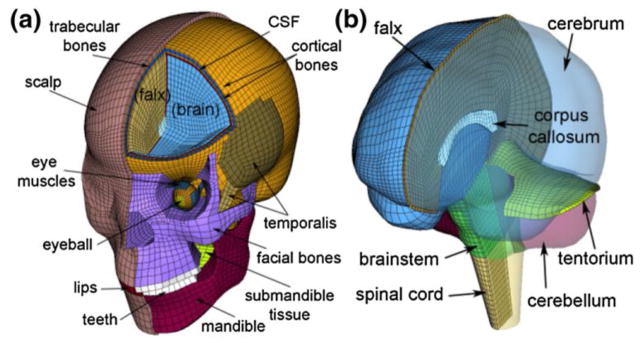
The DHIM showing color-coded regions including the head exterior (a) and intracranial components (b), as well as part of the spinal cord to improve its biofidelity in the inferior region.

Table 1.

Baseline skull and brain material properties for the DHIM, along with the “compliant” and “stiff” property for the brain used in this study. All property values have been converted into the Abaqus convention (Abaqus 2012).

	ρ (kg/m3)	E (MPa)	υ
brain	1040	K = 0.219 GPa	(depends on specific property used)
cortical bone	3000	15000	0.22
diploe	1750	5660	0.22
other properties of DHIM		see (Ji et al. 2014b)

		μ1(Pa)	α1	μ2(Pa)	α2
Ogden hyperelastic material properties for the brain (Kleiven 2007)	compliant	135.8	10.1	388.3	−12.9
	average (baseline)	271.7	10.1	776.6	−12.9
	stiff	543.7	10.1	1553.2	−12.9

	i = 1	i = 2	i = 3	i = 4	i = 5	i = 6
gi	7.69E-1	1.86E-1	1.48E-2	1.90E-2	2.56E-3	7.04E-3
τi	1.0E-6	1.0E-5	1.0E-4	1.0E-3	1.0E-2	1.0E-1

2.3 Correlation between pressure and a_lin

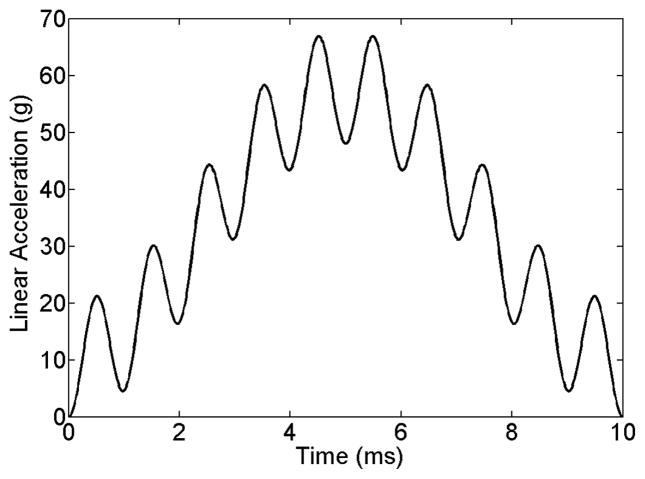
Because the dimensional analysis suggests that pressure, P, is uniquely determined by a_lin for a given head model and a_lin direction (so that m_brain and A remain identical; Eqn. 4), the temporal profile of P is anticipated to follow that of a_lin. To challenge this prediction, we arbitrarily generated a temporal profile of a_lin of a sinusoidal waveform with its peak magnitude chosen to be the 95^th percentile peak a_lin value in ice-hockey (i.e., 49 g, where g is 9.8 m/s²; Ji et al. 2014a) with an additional oscillation according to the following function (Fig. 3; time, t, in seconds):

$$a_{\mathit{lin}}(t)=49\times {\mathit{sin}}^2(100\times \pi t)+20\times {\mathit{sin}}^2(1000\times \pi t).$$ (5)

Fig. 3.

An arbitrarily generated temporal profile of a_lin based on a sinusoidal function with an additional higher frequency oscillation to challenge DHIM-estimated brain pressure responses.

The acceleration was then applied to the rigid skull in the anterior-posterior direction, representing a frontal impact. To investigate the significance of brain’s near incompressibility property on pressure responses, the brain bulk modulus, K, was varied by 5 orders of magnitude (1E−3 to 1E+2 relative to the baseline value of 219 MPa; Ji et al. 2014b) while maintaining the brain’s shear stiffness values (i.e., using the “average” model in (Kleiven 2007)). To investigate the significance of brain’s shear stiffness property, the “compliant” and “stiff” models in (Kleiven 2007; Table 1) and other commonly used material models (e.g., viscoelastic and Mooney-Rivlin hyperelastic models) found in the literature (Zhang et al. 2001b; Kleiven and Hardy 2002; Takhounts et al. 2008; Mao et al. 2013, see Table 2) were adopted while maintaining the same baseline K value. For each simulation, pressure responses were extracted with a temporal resolution of 0.1 ms for each element. The locations of the largest pressure magnitudes were identified at the coup and contrecoup sites, and the corresponding pressure values were further averaged by those from their eight neighboring surface elements, respectively, to determine the coup (P_coup) and contrecoup (P_{c_coup}) pressures at each time point.

Table 2.

Additional brain material properties evaluated in this study. All property values are in the Abaqus convention (Abaqus 2012). The Young’s modulus, E, for each viscoelastic material was obtained based on K and the long-term shear modulus, G_∞.

Mooney-Rivlin hyperelastic material properties for the brain – “average” in (Kleiven and Hardy 2002)
C10 (Pa)	C01 (Pa)	g1	g2	τ1 (s)	τ2 (s)
62	69	0.678	0.437	0.008	0.149

Viscoelastic material properties for the brain
	E (Pa)	G∞ (Pa)	G0 (Pa)	K (MPa)	g1	τ1 (s)
Zhang et al. (2001b)	6000	2000	10000		0.800	0.0125
Takhounts et al. (2008)	2784	928	1660	219	0.441	0.0590
Mao et al. (2013)	3600	1200	6000		0.800	0.0125

2.4 Correlation between pressure and brain size for a given a_lin

To verify that P is linearly proportional to brain size for a given a_lin according to the dimensional analysis, five head models were created by scaling the DHIM brain mass 0.5 – 1.5 times relative to the baseline equally in all three axes with a linear scaling factor range of 0.794 – 1.145. The resulting brain mass ranged 0.779 – 2.337 kg (without spinal cord), approximately corresponding to a head mass range of 2.841 – 6.268 kg, encompassing the 5^th percentile female and 95^th percentile male head sizes (Kleiven and von Holst (2002)). A triangulated impulse with a peak a_lin magnitude of 49 g (95^th percentile in ice-hockey, Ji et al. 2014a) and a duration of 10 ms was applied to the rigid skull in the anterior-posterior, left-right, and posterior-anterior directions that represented a frontal, a lateral, and an occipital impact, respectively. The peak coup ( $P_{\mathit{coup}}^p$) and peak contrecoup ( $P_{c\_\mathit{coup}}^p$) pressures were determined from the time-varying P_coup and P_{c_coup}, respectively.

2.5 Significance of non-rigid skull deformation on pressure

The dimensional analysis assumed a rigid-body skull. While this is likely true for mild rate head impacts, it is important to understand the significance of non-rigid skull deformation on brain pressure responses especially when a_lin is high. A uniformly distributed impact force with a peak magnitude of 15 kN (approximately equal to that in experiment 41 conducted in Nahum et al. (1977) in order to induce sufficient skull deflection) and a duration of 3 ms was used as model input, analogous to that in (Ruan et al. 1994). An explicit impactor was not included in the parametric study here in order to simplify the iterative process for adjusting the impact force (see below). The DHIM was rotated forward by 45° to ensure that the impact force passed through the head center of gravity (CG). A free boundary condition was used in the inferior region of the spinal cord, which was considered appropriate in a rather short duration (Ruan et al. 1994).

Altering either the skull’s stiffness (i.e., Young’s modulus), E, or its thickness would induce varied non-rigid skull deformation. To maintain the same baseline DHIM geometrical model for simplicity in this study, only E was scaled by a range of factors (0.2 – 10) relative to the baseline value (Table 1) while skull thickness and all other model material properties remained unchanged. When the head was subjected to an identical impact force, the magnitude of a_lin would decrease with the increase in non-rigid skull deformation due to energy absorption as compared to that with an otherwise rigid skull. To compare pressure at the same a_lin level with a rigid skull, the magnitude of the impact force was iteratively adjusted to maintain an identical peak a_lin magnitude, which was determined as the average acceleration value of all skull nodes (excluding those near the impact site; 3423.8 m/s² as determined from the baseline model).

To compute the non-rigid skull deflection at the impact site, all DHIM mesh nodes corresponding to the skull (excluding those within a radius of 5 cm relative to the impact site) at each time point in simulation were first rigidly co-registered with their initial undeformed counterparts via a singular value decomposition method (Arun et al. 1987). Skull deflection was then calculated by subtracting the corresponding nodal positions between the deformed and undeformed profiles and the maximum deflection in the region and across the entire impact simulation was obtained. For each E value, $P_{\mathit{coup}}^p$ and $P_{c\_\mathit{coup}}^p$ were computed and compared with those obtained from the rigid skull.

2.6 Validation of DHIM-estimated pressure against cadaveric head impacts

DHIM-estimated pressure responses were compared with those from a short-(Nahum et al. 1977) and a long-duration (Trosseille et al. 1992) cadaveric head impact. For the short-duration impact with negligible rotation, experiment 37 in Nahum et al. 1977 was selected for comparison, similarly to many other head FE models (Kleiven and von Holst 2002; Takhounts et al. 2008; Mao et al. 2013). Because brain pressure responses are proportional to brain size according to the dimensional analysis, the DHIM was scaled to match the dimension of the corresponding cadaveric head as in Horgan and Gilchrist (2003). The scaled DHIM was then rotated forward so that the Frankfurt anatomical plane was inclined 45° to the horizontal plane. A rigid cylindrical impactor with a mass of 5.59 kg was launched to induce a resultant acceleration at the head CG at the same level of that measured. Because the property of the padding material between the impactor and head was not reported, a rubber-like padding was used with its stiffness property iteratively adjusted until the impact duration matched with that from the experiment. Pressure time-history curves at four locations (frontal lobe adjacent to the impact contact area, parietal, occipital lobe as well as posterior fossa) were obtained and compared with the measurements. Such a strategy for model validation was similar to other studies previously reported (Kang et al. 1997; Kleiven and von Holst 2002; Horgan and Gilchrist 2003; Takhounts et al. 2008)).

A long-duration head impact with a high level of rotation, MS 428–2 in (Trosseille et al. 1992), was also utilized that measured brain pressure responses when a seated cadaver was impacted in an anterior-posterior direction. Because only the full 6 DOFs a_lin and a_rot relative to the head CG were available, the baseline DHIM with a rigid skull was employed. The resulting pressure responses in the frontal and occipital lobes as well as in the lateral and 3rd ventricles were compared with measurements.

The performance of both pressure validations was evaluated using correlation score (CS) to assess the agreement between model-estimated pressure responses and the measurement counterpart time histories in terms of phase (N-phase), amplitude (N-amp) and shape (N-shape). The technical details have been previously published to validate the THUMS (Total HUman Model for Safety; (Kimpara et al. 2006)). In addition, we also reported correlation coefficients between model-estimated and measured pressures analogously to that in (Kleiven 2006).

3. Data analysis

All simulations were conducted using Abaqus/Explicit (version 6.12; Dassault Systèmes, France) on a multi-core Linux cluster (Intel Xeon X5560, 2.80 GHz, 126 GB memory). To quantify the variation in pressure as a result of the change in bulk modulus or shear stiffness properties, the Root Mean Squared Error (RMSE) based on the differences in pressure magnitudes relative to that from the baseline DHIM at every time point was calculated. DHIM pressure validation performances were quantified using CS and correlation coefficients. The change in pressure as a result of skull deflection due to the change in skull Young’s modulus was also reported. Statistical significance was reached when the p-value was less than 0.05. All data analyses were conducted in MATLAB (R2013a; MathWorks, Natick, MA).

4. Results

4.1 Significance of brain bulk modulus and shear stiffness

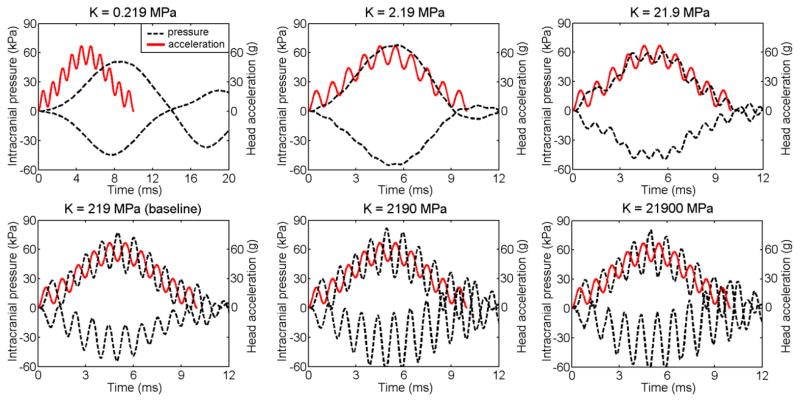
For each brain bulk modulus value, coup and contrecoup pressure (P_coup and P_{c_coup}) temporal profiles were compared with that of the linear acceleration, a_lin (Fig. 4). Evidently, when the bulk modulus, K, was equal to or above the baseline value of 219 MPa, P_coup temporal profile correlated well in shape with that of a_lin, with a slight delay of approximately 0.5 ms and more pronounced variation in relative magnitudes. However, such similarity faded and eventually disappeared when the bulk moduli were lower, as also confirmed by the RMSE relative to the baseline (Table 3). Little change in P_coup was evident when further increasing K above the baseline (Fig. 4 and Table 3), although changes in P_{c_coup} was more significant (Fig. 4). For the baseline K, the Pearson correlation coefficient between P_{c_coup} and P_coup was −0. 953 (p<0.0001), suggesting their linear but inverse proportionality.

Fig. 4.

Correlation between P_coup/P_{c_coup} and the given a_lin over time for a range of brain bulk moduli. When the bulk modulus was sufficiently high (e.g., ≥ 219 MPa), the P_coup temporal profile maintained a similar shape of a_lin, although a slight delay of ~0.5 ms was evident.

Table 3.

RMSE of P_coup and P_{c_coup} for different bulk moduli of the brain.

K (MPa)	0.219	2.19	21.9	219 (baseline)	2190	21900
RMSEcoup (kPa)	25.09	12.40	10.47	0	4.25	4.74
RMSEc_coup (kPa)	20.63	14.40	10.94	0	10.27	11.06

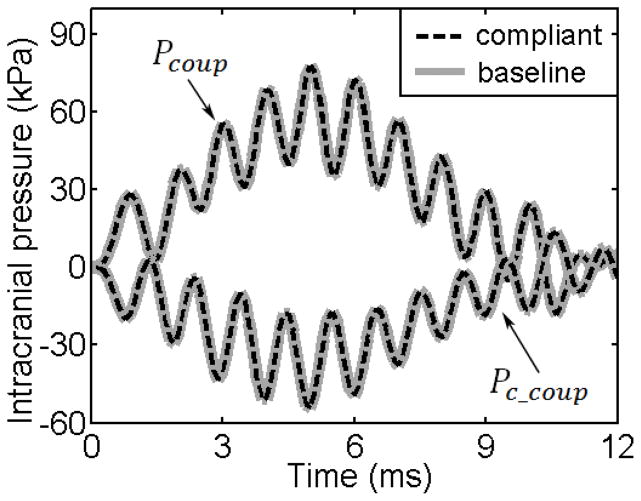
Regardless of the brain shear stiffness property (material models or parameter values), P_coup and P_{c_coup} were nearly identical to those from the baseline DHIM (Fig. 5; only showing results using the “compliant” model in (Kleiven 2007) for illustration), as further confirmed by the rather small RMSE (Table 4).

Fig. 5.

P_coup and P_{c_coup} obtained from the “compliant” model in Kleiven (2007) compared with the baseline. Similarly, pressure responses from all other shear stiffness properties were virtually identical and are not shown here.

Table 4.

RMSE of P_coup and P_{c_coup} for different shear stiffness properties of the brain.

	Ogden (Kleiven 2007)			Mooney-Rivlin	Viscoelastic
shear stiffness	average (baseline)	compl.	stiff	(Kleiven and Hardy 2002) – average	Zhang et al. (2001b)	Takhounts et al. (2008)	Mao et al. (2013)
RMSEcoup (kPa)	0	0.035	0.046	0.022	0.158	0.046	0.098
RMSEc_coup (kPa)	0	0.028	0.040	0.020	0.116	0.031	0.069

4.2 Significance of brain size

The linearly proportional relationship between peak coup/contrecoup pressure ( $P_{\mathit{coup}}^p/P_{\mathit{coup}}^p$) and brain size is clearly illustrated in Fig. 6 for all of the impact directions evaluated. Interestingly, for the lateral impact, $P_{\mathit{coup}}^p$ and $P_{c\_\mathit{coup}}^p$ were nearly indistinguishable in magnitude as indicated by the line fitting parameters, confirming the previous assertion that the contact forces were (approximately) equal at the coup and contrecoup sites in the dimensional analysis (brain-skull contact areas at the two locations were identical in this case). In contrast, $P_{\mathit{coup}}^p$ and $P_{c\_\mathit{coup}}^p$ from the frontal or occipital impacts were simply inverted in sign when the a_lin direction was reversed, again, as indicated by the fitted lines. In both cases (frontal or occipital impact), the pressure magnitude in the frontal region was larger than that in the occipital region due to the larger curvature or smaller brain-skull contact area in the frontal region, as previously observed (Ruan et al. 1994; Zhang et al. 2001a).

Fig. 6.

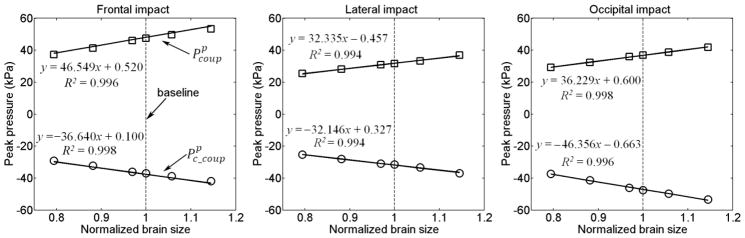
The linearly proportional relationship between the peak pressure magnitudes and brain size in three impact directions, with fitted lines shown.

4.3 Significance of non-rigid skull deformation

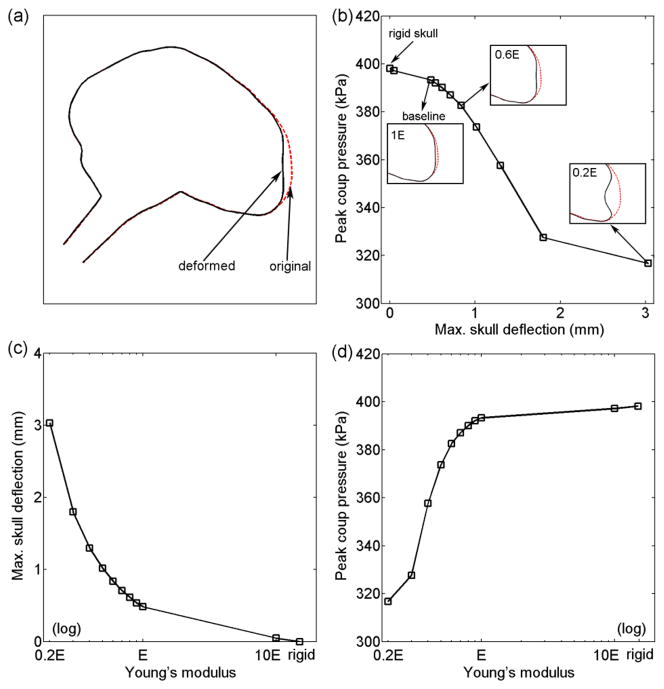
Non-rigid skull deformation reduced $P_{\mathit{coup}}^p$ relative to that from the rigid skull when a_lin magnitude was maintained (Fig. 7). Using the baseline skull Young’s modulus, a 0.483 mm skull deflection and 1.2% decrease in pressure were observed. As expected, with much stiffer Young’s modulus (i.e., 10 times the baseline) that resulted in negligible skull deflection (0.048 mm; Fig. 7c), the brain pressure response was nearly identical to that from the rigid skull (difference of 0.23%; Fig. 7b). For the spectrum of skull Young’s modulus analyzed, $P_{\mathit{coup}}^p$ varied by 20.40% relative to the baseline, while $P_{c\_\mathit{coup}}^p$ only varied by 4.15%. When the Young’s modulus was reduced to a certain level (e.g., <0.2 times the baseline), however, the skull started to buckle, resulting in a much higher (as opposed to lower) pressure response at the impact site (not shown).

Fig. 7.

(a) Illustration of rigidly co-registered profiles of the deformed and undeformed skull in the mid-sagittal plane. (b) $P_{\mathit{coup}}^p$ as a function of maximum skull deflection at the impact site. (c) Maximum skull deflection as a function of the relative skull Young’s modulus. (d) $P_{\mathit{coup}}^p$ as a function of skull Young’s modulus. The deformed and undeformed skull profiles are compared for selected simulations in (b). For all deformed skull, deformation was magnified by 10 times to improve visualization.

4.4. DHIM pressure validation

The pressure responses from the scaled DHIM for the short-duration impact correlated well with P_coup and P_{c_coup} measurements (Fig. 8a), showing the typical pattern of pressure gradients as observed in other head FE models (e.g., Kang et al. 1997; Kleiven and von Holst 2002; Mao et al. 2013). The correlation scores and correlation coefficients between the simulated and experimental findings are summarized in Table 5.

Fig. 8.

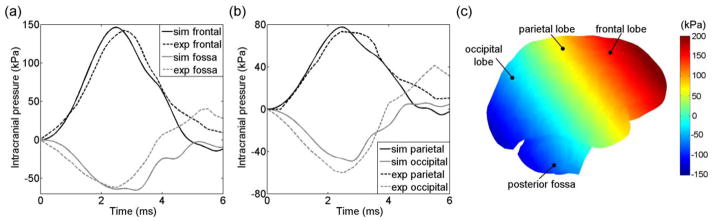
Comparison of simulated pressures with measurements in (Nahum et al. 1977) in the frontal and posterior fossa regions (a) as well as in the parietal and occipital regions (b) along with the distribution and measurement locations (c).

Table 5.

Summary of DHIM pressure validation performances against measurements from cadaveric experiments. (CS: correlation score; R: correlation coefficient)

	Location	CSN-phase	CSN-amp	CSN-shape	average	R	p-value
Nahum et al. (1977)	Frontal	94.99	100.00	97.19	97.39	0.97	<0.0001
	Parietal	98.61	99.97	99.22	99.27	0.96	<0.0001
	Occipital	95.02	94.92	95.44	95.13	0.94	<0.0001
	Posterior fossa	81.93	99.94	94.76	92.21	0.81	<0.0001
Trosseille et al. (1992)	Frontal	96.85	93.71	89.10	93.22	0.77	<0.0001
	Occipital	94.67	80.04	79.20	84.64	0.91	<0.0001
	Lateral ventricle	96.44	92.96	77.86	89.08	0.05	0.63
	3rd ventricle	63.18	75.88	90.73	76.60	0.40	<0.0001

For the long-duration head impact with rigid skull, the simulated pressures were similar in temporal profile shape compared to the measurements, and the corresponding correlation scores and correlation coefficients are summarized in Table 5. Except for $P_{\mathit{coup}}^p$ at the occipital lobe with an overestimation of 28.20 kPa (~252%), pressure magnitudes were generally underestimated (e.g., by 16.13 kPa (~18%), 10.33 kPa (~34.58%) and 7.64 kPa (~18.83%) at the frontal lobe, lateral ventricle and the 3^rd ventricle, respectively). These simulation results were, nevertheless, similar to previous reports (Horgan and Gilchrist 2004; Kleiven 2006; Tse et al. 2013; Mao et al. 2013).

Regardless, based on the correlation scores, both the short-and long-duration validations achieved a “good” to “excellent” performance overall according to a fidelity rating (de Lange et al. 2005). Nearly all pressure responses yielded high and statistically significant correlation coefficients (Table 5).

5. Discussion

Understanding the causal relationships between brain tissue-level mechanical responses and head impact kinematic variables as well as model parameters of the head itself is critical to ultimately help elucidate the underlying biomechanical mechanisms of traumatic brain injury (TBI) in general. Using a dimensional analysis based on the brain’s near incompressibility property and rigid-body skull assumption, we have successfully identified three controlling parameters specific and important for brain pressure responses in translational/direct impact: the magnitude and directionality of the linear acceleration (a_lin) itself, brain mass and effective brain-skull contact area, or alternatively, brain size and shape. In essence, such a pressure response mechanism is analogous to the well-established hydrostatic pressure distribution (e.g., Thomas et al. 1966; see Fig. 8c). Using an arbitrarily generated a_lin as model input in a frontal impact to challenge the induced pressure responses, we found that the temporal profile of the coup pressure (P_coup) closely followed that of a_lin (with an approximately 0.5 ms phase shift and variation in magnitude) when the bulk modulus (K) was sufficiently high (i.e., ≥ 219 MPa), as expected. When K was lower, however, such similarity faded and eventually disappeared (Fig. 4); thus, invalidating results from the dimensional analysis (again, suggesting the importance of brain’s near incompressibility property in the analysis in (Gibson 2006), which was unrecognized). Pressure was anticipated to be linearly proportional to brain size for a given a_lin (magnitude and direction), which was successfully confirmed (Fig. 6). In addition, the virtually linear but inverse proportionality between P_coup and P_{c_coup} agreed well with the dimensional analysis predictions. The asserted (approximately) equal contact forces at the coup and contrecoup sites (compression and tension, respectively) from the dimensional analysis were further verified from the computational results (as clearly shown by the line fitting parameters in Fig. 6). The contact forces can be directly determined from Eqn. 2; however, determination of the contact areas (i.e., P_coup and P_{c_coup}) will likely require a more in-depth analysis of the FE simulation results to account for the relative orientations of individual brain surface elements with respect to the impact direction, which was not performed in this study.

While these causal relationships depend on brain’s dilatational property (i.e., near incompressibility), they do not depend on brain’s deviatoric material properties (i.e., shear stiffness), which was well recognized (Meaney et al. 2014) and successfully verified in this study (Fig. 5; although seemingly contradictory to reports in Horgan and Gilchrist (2003), which may be attributed to their much larger long-term shear moduli of the brain (e.g., 20–500 kPa, vs. 0.26–2.09 kPa in Kleiven and Hardy 2002 and Kleiven 2007)). An important implication of this finding is that brain deformation response can substantially vary over a range of shear stiffness properties that would not significantly affect pressure distributions during translational/direct impact. Therefore, models validated against brain pressure responses alone cannot be used to estimate brain deformation responses (i.e., relative brain-skull displacements and strain-related responses (Kraft et al. 2012; Wright et al. 2013; Morse et al. 2014)).

Because brain pressure depended on brain size (Fig. 6, similar to that in (Kleiven and von Holst 2002)), the DHIM was scaled to match the reported cadaveric head dimension (albeit not “brain” dimension which was not reported in (Nahum et al. 1977)) prior to validation, where an “excellent” performance was achieved (average correlation score and correlation coefficient of 94.8 and 0.89, respectively). No scaling was performed when validating against the long-duration impact (average correlation score and correlation coefficient of 85.89 and 0.53, respectively) because the head/brain size was not reported in Trosseille’s study. Interestingly, the brain size dependency in pressure responses appears to have been largely ignored in the research community because no “brain” size was reported in the experimental studies ((Nahum et al. 1977) and (Hardy et al. 2007) only reported head sizes) and no brain size scaling was performed or discussed in the context of pressure responses in most previous computational studies of the human head either (except for (Kleiven and von Holst 2002; Horgan and Gilchrist 2003)). Regardless, the overall pressure validation was categorized as “good” to “excellent” according to a fidelity rating (de Lange et al. 2005). These performances are important additions to the previous reports of validations against relative brain-skull displacements and strain responses (also categorized as “good” to “excellent”; (Ji et al. 2014b; Ji et al. 2014c)), and are essential to ensure sufficient fidelity of DHIM in brain response simulations in the future.

Results from the dimensional analysis could provide important insights into the fundamental mechanisms of brain pressure responses in translational/direct impact. Because of the unique head shape where a larger curvature of the skull occurs in the forehead that results in a smaller brain-skull contact area in this location, the brain frontal region always sustains a larger pressure for a given a_lin irrespective of whether the impact is frontal or occipital (Fig. 6), as observed in (Ruan et al. 1994). This finding suggests that the brain frontal region is likely more vulnerable to (pressure-induced) injury, which appears to agree well with many clinical observations (e.g., Sano and Norio 1967; Levin and Kraus 1994).

More importantly, because brain pressure is linearly proportional to a_lin, only a baseline response along each given translational axis is necessary to directly determine P_coup and P_{c_coup} without the need to re-compute. Therefore, only two independent variables characterizing the directionality of the translational axis (the azimuth and elevation angles) are necessary to establish a pre-computed pressure response atlas subject to isolated a_lin, or more realistically, a_lin-dominated head impact, as opposed to four independent variables for the brain strain response atlas (Ji and Zhao 2014). Such a pre-computed atlas is essentially a profile of element-wise distribution of pressure values for each discrete translational axis to allow an instantaneous estimation of brain pressure responses at the tissue level (i.e., interpolated at every element throughout the brain) without a time-consuming direct simulation that typically requires hours or more on a high-end computer or even a super computer (Zhang et al. 2001b; Takhounts et al. 2008; Chen and Ostoja-Starzewski 2010; Ji et al. 2014a). Although debate still exists whether a_lin-induced brain pressures could also contribute to mild injuries such as sports-related concussion on the field (Rowson and Duma 2013) because many believe a_rot as opposed to a_lin causes diffuse axonal injury (King et al. 2003), at the minimum, the pressure response atlas appears directly functional whenever the classical injury metric HIC is applicable. Together with the pre-computed brain strain response atlas (Ji and Zhao 2014), these tools may have the potential to substantially increase the throughput in head impact simulation, and therefore, accelerate the exploration of the biomechanical mechanisms of TBI in general.

It is important, however, to recognize that the dimensional analysis and the resulting predictions in this study were based on isolated a_lin only while both a_lin and a_rot contribute to head impact kinematics in real-world injury events. Similarly to the a_lin–induced perturbations to strain, a_rot is likely to impose perturbations to pressure relative to the baseline responses generated from isolated a_lin as well. Although the insignificance of a_lin on brain strain-related responses has been previously observed (Zhang et al. 2004; Kleiven 2007) and further systematically quantified (Ji et al. 2014c), an analogous investigation into the significance of a_rot on brain pressure responses has not been performed yet and warrants further study.

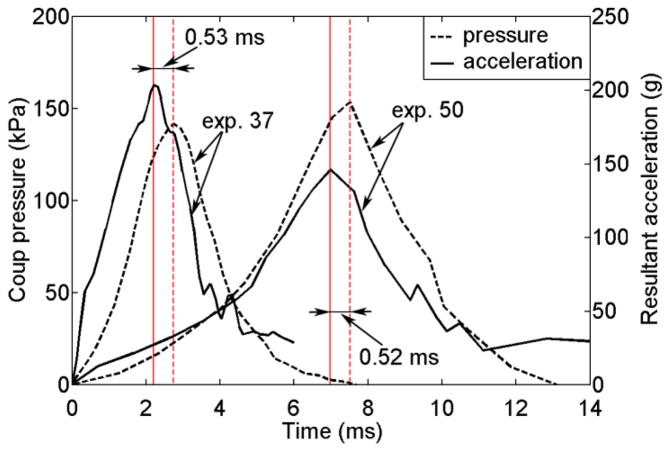
Perturbation to brain responses relative to that predicted from the dimensional analysis was anticipated because of the simplifications and assumptions necessary in order to capture the main fundamental relationship between output response variables and kinematic input/model parameters. For example, the phase shift (~0.5 ms) between P_coup relative to the given a_lin temporal profile as well as the seemingly amplified difference in amplitude variation (when K ≥ 219 MPa) was likely a perturbation in part resulting from the omission of CSF and pia/arachnoid mater between the brain and skull in the dimensional analysis. The different CSF modeling strategies will likely result in different response perturbations (Ruan et al. 1994; Chafi et al. 2009), which were not investigated in this study. On the other hand, it is interesting to note that the same phase shift was already observed in the original experiments of (Nahum et al. 1977). Fig. 10 shows the response histories of a_lin and the resulting P_coup for two representative cadaveric head impact tests (Nahum et al. 1977), where a similar ~0.5 ms time delay was evident. The similar shapes of a_lin and P from the actual measurements further confirm the near incompressibility property of the brain (otherwise the shapes would not agree as shown in Fig. 4).

Fig. 10.

Resultant head a_lin and the resulting P_coup measured for two representative cadaveric head impacts in Nahum et al. 1977. Their similar shapes in temporal profile confirm brain’s near incompressibility. Note that the two experiments were conducted on two different cadaveric samples with different impact conditions; thus, they had inconsistent relative magnitudes of pressure and a_lin.

The brain’s near incompressibility was also recently verified using digital image correlation (Libertiaux et al. 2011). However, a “ground-truth” bulk modulus value (K) is nevertheless unavailable. Although a K value between 21.9 MPa and 219 MPa was recommended (Ruan et al. 1994), many head FE models adopt a higher K value of 2.19 GPa for the brain (e.g., Zhang et al. (2001b); Horgan and Gilchrist (2003); Zhang et al. (2004); Horgan and Gilchrist (2004); Kimpara et al. (2006); Chafi et al. (2009); Mao et al. (2013)), despite that a lower value produced very similar pressure results (Ruan et al. 1994; Kang et al. 1997; Takhounts et al. 2008; Tse et al. 2013). The K value is directly related to the stable time increment in an explicit simulation that determines the overall computational cost. Increasing K an order of magnitude would in theory lead to $\sqrt{10}$ or 3.16 times increase in simulation time (Abaqus manual). For example, a 50 min is required to simulate a typical 40 ms head impact using DHIM with K of 219 MPa and it would be increased to ~160 min with K of 2.19 GPa but with negligible difference in results. Surprisingly, the significance of using a somewhat lower K value to minimize the computation cost without appreciable alteration in results seems under-recognized in the research community, especially when no “ground-truth” K value is available. Based on the brain pressure responses in this study and our previous successful model validation in terms of relative brain-skull displacement in cadavers and strain responses in a live human (Ji et al. 2014c), it appears that a K value of 219 MPa, i.e., the upper bound of the recommended range in Ruan et al. (1994), would be an optimal balance between fidelity in results and economy in computation. The resulting significant increase in computational efficiency (as compared to using a higher K value of 2.19 GPa) would be important for large-scale impact simulations particularly for on-field head impacts.

Nevertheless, perturbation to brain pressure responses due to skull non-rigid deformation was also investigated. By maintaining an identical a_lin magnitude while adjusting the skull Young’s modulus and impact force, we found that increasing skull deflection reduced $P_{\mathit{coup}}^p$, likely due to the increase in local contact area (before skull started to buckle; Fig. 7). The magnitude of skull deflection in our study (up to 3 mm) was much lower than that in Zhang et al. (2001a) (up to 7.1 mm, surpassing the skull fracture tolerance of 5.8 mm proposed in Yoganandan et al. (1995)) because we are more interested in the mild spectrum of head impact. On the other hand, it must be recognized that we have iteratively adjusted the force magnitude in order to maintain an identical level of resultant a_lin, which was significantly different from previous investigations that either adopted a constant impact force with the same skull thickness while varying skull’s Young’s modulus (Ruan et al. 1994) or applied an identical impactor (mass and velocity) with the same skull’s Young’s modulus while varying its thickness (Ruan and Prasad 2001). In both Ruan et al. (1994) and Ruan and Prasad (2001), only brain mass (m_brain) was kept constant while both a_lin magnitude and effective brain-skull contact area (A) were altered in different head impacts due to non-rigid skull deformation and in Ruan and Prasad (2001), the change in head mass as well. Therefore, these studies effectively investigated the combined effects of a_lin and A (Eqn. 4) on brain pressure responses while our study attempted to isolate the effect of changes in local brain-skull contact area only by maintaining the same a_lin magnitude. When head impact kinematics is only known in terms of a_lin rather than impact force, our perturbation study investigating the significance of local skull non-rigid deflection will likely be more relevant. Nevertheless, because of the likely much more distributed impact force in a helmet-to-helmet impact as opposed to the rather localized impact here to induced skull deflection, caution must be exercised when interpreting these non-rigid skull perturbation results to helmeted head impacts on the sports field.

Finally, our finding that brain pressure responses are linearly proportional to a_lin magnitude but depend on its directionality and brain geometry (size and shape) merits further discussion. Presumably, tissue-level regional pressure responses are directly responsible for pressure-induced focal injuries (when skull deformation is negligible). The head injury criterion (HIC) defined based on the temporal profile of the resultant magnitude of a_lin appears capable of capturing the temporal shapes of brain pressure responses (see Fig. 4). However, because it does not account for a_lin directionality or brain geometry, HIC may not be sufficiently accurate to represent tissue-level pressure response magnitude, as indicated in a previous study that explored the significance of “head size” (albeit, perhaps more accurately, “brain” size irrespective of skull/scalp thickness; Kleiven and von Holst (2002)). For a typical frontal impact (Fig. 6), $P_{\mathit{coup}}^p$ sustained by the largest brain simulated in this study was 43.4% higher than that for the smallest. While it may be possible to simply scale the magnitude of a_lin or pressure directly to account for the difference in brain size (Fig. 6), compensating for a_lin directionality (effectively, differences in brain-skull contact area) may require a pre-computed pressure response atlas. Such a unique capability readily achievable from a pre-computed pressure atlas, however, is not available from HIC. On the other hand, it must be recognized, again, that HIC does not account for a_rot or its resulting strain or deformation. When a_rot becomes increasingly substantial, strain-induced brain injury such as diffuse axonal injury may become more dominant, thereby invalidating the use of HIC for injury risk assessment in these situations. These observations highlight the complex nature of the biomechanical mechanisms of traumatic brain injury.

6 Conclusions

Using a dimensional analysis, we have successfully identified three controlling parameters specific and important to brain pressure responses: linear acceleration (magnitude and directionality), brain mass and effective brain-skull contact area or alternatively, brain size and shape. These results were further successfully verified using the recently developed Dartmouth Head Injury Model (DHIM). Because brain pressure responses are linearly proportional to the magnitude of linear acceleration and brain size while dependent on the impact direction or head geometry, it may be possible to establish a pre-computed atlas to provide an instantaneous estimate of pressure responses without a time-consuming direct simulation when the head is subjected to impact dominated by linear acceleration. Dilatational pressure responses of the DHIM were also successfully and quantitatively validated against two representative cadaveric experiments with a “good” to “excellent” fidelity rating. These validation performances are important additions to the previous deviatoric behavior validations of the DHIM to ensure its sufficient fidelity in impact simulation. Further, perturbations due to dimensional analysis simplifications (omission of CSF and pia/arachnoid mater as well as non-rigid skull deflection) and sensitivities of brain material properties (dilatational and deviatoric) were also investigated. Results from this study suggest that the magnitude and directionality of linear acceleration as well as brain size and shape should be considered when validating brain pressure responses against experiments (i.e., scaling the model first to match sample size whenever possible) or designing pressure-based injury criteria. Further, a model validated against pressure responses alone is not sufficient to ensure its fidelity in strain-related responses. These findings provide important insights into brain pressure responses in translational head impact and the resulting risk of pressure-induced injury. In addition, they establish a solid foundation to allow creating a pre-computed atlas for real-time tissue-level pressure responses without a time-consuming direct simulation. In conjunction with a precomputed strain response atlas, these tools could substantially improve the throughput in head impact simulation, and therefore, to accelerate the exploration of the biomechanical mechanisms of traumatic brain injury.

Fig. 9.

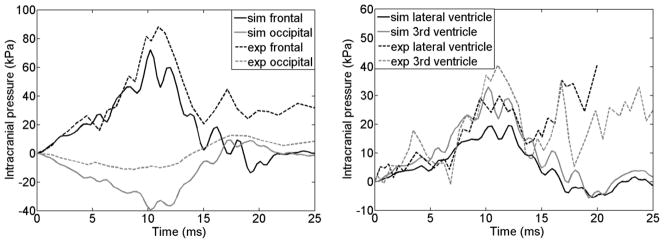
Comparison of simulated pressures with measurements in Trosseille et al.’s study.