Abstract
We consider statistical inference for potentially heterogeneous patterns of association characterizing the expression of bio-molecular pathways across different biologic conditions. We discuss a modeling approach based on Gaussian-directed acyclic graphs and provide computational and methodological details needed for posterior inference. Our application finds motivation in reverse phase protein array data from a study on acute myeloid leukemia, where interest centers on contrasting refractory versus relapsed patients. We illustrate the proposed method through both synthetic and case study data.
Keywords: Conditional independence, Directed acyclic graphs, Gaussian Markov models, Reversible jumps MCMC
1. Introduction
In “omics” studies, data often manifests as an 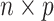 matrix
matrix  , which forms the empirical basis for the exploration of scientific hypotheses relating a set of
, which forms the empirical basis for the exploration of scientific hypotheses relating a set of  genes, metabolites, proteins, etc., to an underlying biological process. When inference focuses on molecular interactions, bio-melecular pathways are often interpreted as describing marginal or conditional independence restrictions, compatible with a data generating mechanism for
genes, metabolites, proteins, etc., to an underlying biological process. When inference focuses on molecular interactions, bio-melecular pathways are often interpreted as describing marginal or conditional independence restrictions, compatible with a data generating mechanism for 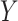 (see, e.g., Dobra and others, 2004 or Telesca and others, 2012). More precisely, the joint sampling distribution of
(see, e.g., Dobra and others, 2004 or Telesca and others, 2012). More precisely, the joint sampling distribution of 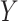 is assumed to factor according to stochastic restrictions encoded in a graphical model
is assumed to factor according to stochastic restrictions encoded in a graphical model 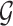 (Lauritzen, 1996) and inference about molecular pathways is interpreted as inference about a graph
(Lauritzen, 1996) and inference about molecular pathways is interpreted as inference about a graph 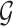 supporting the observed data
supporting the observed data 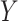 .
.
These biomedical studies are often designed to contrast characteristics of population subgroups. In this manuscript, we consider the problem of contrasting differential association structures characterizing labeled subsets of a data matrix 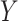 . Our application finds motivation in a proteomics study of acute myeloid leukemia (AML) patients (Tibes and others, 2006). This study targets a specific proteomic pathway, thought to be associated with disease progression. Interest centers on understanding what components of this pathway behave differently when one compares refractory patients to patients experiencing relapse after standard treatment. Figure 1 shows the targeted protein expression level for AML patients, measured using a high-throughput proteomic technology called reverse-phase protein array (RPPA) (Tibes and others, 2006), along with the sample partial correlation matrix of the expression levels for both refectory and relapsed patients in the upper and lower triangle, respectively. The two sample partial correlation mostly agree with each other, yet there are clear discrepancies that may signify differing interactions mechanism (Table 1).
. Our application finds motivation in a proteomics study of acute myeloid leukemia (AML) patients (Tibes and others, 2006). This study targets a specific proteomic pathway, thought to be associated with disease progression. Interest centers on understanding what components of this pathway behave differently when one compares refractory patients to patients experiencing relapse after standard treatment. Figure 1 shows the targeted protein expression level for AML patients, measured using a high-throughput proteomic technology called reverse-phase protein array (RPPA) (Tibes and others, 2006), along with the sample partial correlation matrix of the expression levels for both refectory and relapsed patients in the upper and lower triangle, respectively. The two sample partial correlation mostly agree with each other, yet there are clear discrepancies that may signify differing interactions mechanism (Table 1).
Fig. 1.

The observed expression levels of targeted proteins for AML patients quantified using RPPA (left) and a image plot of the sample partial correlation coefficients for refractory patients in the upper triangle and relapsed patients in the lower triangle (right).
Table 1.
The list of differential edges
| Extra edges |
CASP9  YAP, STAT3 YAP, STAT3  YAP, SRC YAP, SRC 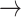 YAP, P38 YAP, P38 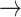 YAP, FOXO3A YAP, FOXO3A 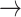 YAP, RB YAP, RB 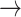 YAP, YAP, |
GSK3 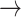 AKT, PTEN AKT, PTEN 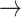 GSK3, CASP9 GSK3, CASP9 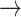 GSK3, BAX GSK3, BAX 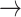 GSK3, BCL2 GSK3, BCL2  BAD BAD |
| Canceled edges |
NF2 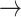 EGFR, PDK1 EGFR, PDK1 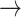 P53, PDK1 P53, PDK1 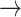 STAT3, BCL2 STAT3, BCL2 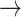 PDK1, BCL2 PDK1, BCL2 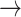 HER2, HER2, |
GAB2 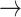 HER2, PDK1 HER2, PDK1 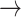 HER2, P38 HER2, P38 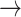 BAD, PRC BAD, PRC  BAX, FOXO3A BAX, FOXO3A  GAB2 GAB2 |
There is a large body of literature focused on the estimation of a single graphical model. However, limited attention has been given to the estimation of a collection of graphs accounting for data heterogeneity. Flexible models for heterogeneous association have been introduced by Ickstadt and others (2010) and Rodriguez and others (2011). These models focus on relaxing the assumption of multivariate Gaussianity, rather then testing specific contrasts in biological pathways. More in line with our inferential goals are the procedures introduced by Guo and others (2011) and Danaher and others (2011). Both manuscripts consider regularized estimation of inverse covariance matrices, using hierarchical extensions of the graphical lasso, originally proposed by Friedman and others (2008). The proposed procedures are shown to be scalable to large undirected graphs, with estimators that enjoy asymptotic consistency.
Beyond statistical exploration of structured dependence, proteomics studies, like the one motivating this manuscript, is inherently designed to test statistical hypotheses that go beyond simpler hypothesis generation exercises. This need finds available statistical techniques to be wanting in several directions. First, substantive understanding of biomolecular interactions is often based on directed graphs. Therefore, statistical inference should consider more general classes of graphical models that go beyond the estimation of structural zeros in inverse covariances. Secondly, even in the simplified setting of undirected graphs, the use of lasso-based estimation techniques, beyond exploratory analyses, does raise methodological and theoretical concerns regarding multiplicity correction and error estimation (Kyung and others, 2010). Third, gene and protein interactions have been studied for decades, with comprehensive databases providing the opportunity for informed priors on model spaces (The Gene Ontology Consortium, 2000, http://geneontology.org; The Kyoto Encyclopedia of Genes and Genomes http://genome.jp/kegg/; the BioCarta pathways, http://biocarta.com/genes/index/asp; etc.).
This manuscript addresses these issues considering a model of differential interaction based on directed acyclic graphs (DAGs). A DAG is a directed graph with no directed cycles, encoding Markov properties by d-separation (Pearl, 1986, 2000). We discuss how scientific knowledge about pathways known a priori can be incorporated in the inference through different classes of prior probabilities. Finally, we propose inference based on Bayesian model determination through decision theoretic principles aimed at controlling false discoveries.
This paper is structured as follows. In Section 2, we propose a Gaussian differential DAG model followed by computational detail in Section 3. We illustrate the application of the proposed method with a simulated example and an application to the RPPA data. We conclude the manuscript with a critical discussion in Section 5.
2. A model for differential interactions
We consider data in the form of an 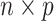 matrix
matrix 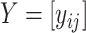 , where the rows of
, where the rows of 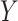 are assumed to be indexed by two known sample subgroups and are labelled by
are assumed to be indexed by two known sample subgroups and are labelled by 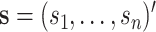 , with
, with 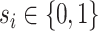 . We refer to the group indexed with
. We refer to the group indexed with 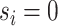 as the baseline group and the ones indexed with
as the baseline group and the ones indexed with 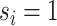 as the differential group. Within each group, we assume that the joint sampling distribution factors according to a DAG
as the differential group. Within each group, we assume that the joint sampling distribution factors according to a DAG 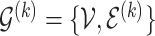 ,
, 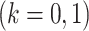 ; where
; where 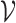 indexes the set of
indexes the set of 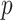 genes or proteins and
genes or proteins and 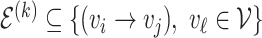 is the set of edges characterizing
is the set of edges characterizing 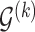 . Finally, the strength of conditional dependence is indexed by two parameter vectors
. Finally, the strength of conditional dependence is indexed by two parameter vectors 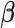 and
and 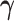 .
.
Let 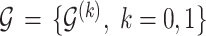 denote the collection of graphs associated with
denote the collection of graphs associated with 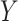 , the proposed joint probability model is constructed as follows:
, the proposed joint probability model is constructed as follows:
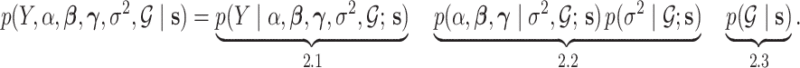 |
(2.1) |
The model includes two separate graphs, 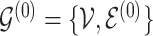 for the baseline sample (
for the baseline sample (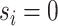 ) and
) and 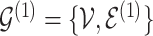 for the differential sample (
for the differential sample (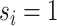 ). Our inference will focus on identifying a set of differential interactions partially indexed by the set
). Our inference will focus on identifying a set of differential interactions partially indexed by the set 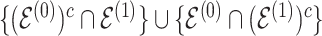 . Each sub model is discussed in individual sections, as indicated by the under-braces.
. Each sub model is discussed in individual sections, as indicated by the under-braces.
2.1. Sampling model: 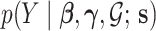
We assume that 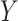 can be subdivided into two groups
can be subdivided into two groups 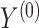 and
and 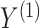 each of size
each of size 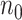 and
and 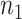 , where
, where 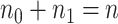 . Given the graphical structures
. Given the graphical structures 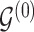 and
and 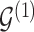 , let
, let 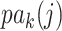 denote the parent nodes of vertex
denote the parent nodes of vertex 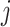 , induced by graph
, induced by graph 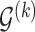 , (
, (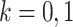 ), and
), and 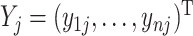 , denote the
, denote the 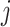 th column of
th column of 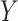 ,
, 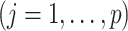 . The joint likelihood is defined as
. The joint likelihood is defined as
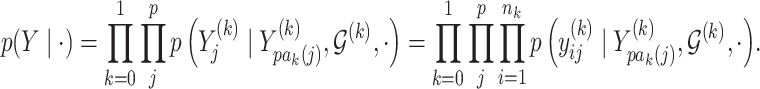 |
In the multivariate Gaussian framework, we can express each of 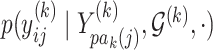 as a conditional linear model of the form
as a conditional linear model of the form
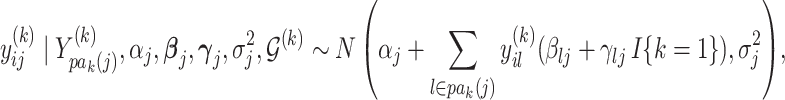 |
(2.2) |
for 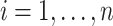 ,
, 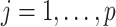 , and
, and 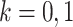 . Here,
. Here, 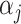 parametrizes a conditional mean value and
parametrizes a conditional mean value and 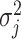 is a conditional variance. In the foregoing formulation,
is a conditional variance. In the foregoing formulation, 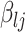 indexes the strength of association between
indexes the strength of association between 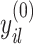 and
and 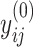 , with the convention
, with the convention 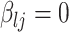 when
when 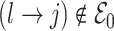 . The strength of association between
. The strength of association between 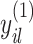 and
and 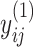 is defined by
is defined by 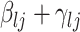 , with
, with 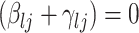 whenever
whenever 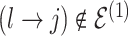 . In this setting, the parameter
. In this setting, the parameter  becomes the main quantity of interest as it directly informs the differences in association between subgroup random quantities.
becomes the main quantity of interest as it directly informs the differences in association between subgroup random quantities.
Throughout the manuscript we will refer to  and
and 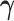 to index full sets of interaction coefficients and a will use a subscript to denote their column subsets. Details about how
to index full sets of interaction coefficients and a will use a subscript to denote their column subsets. Details about how 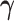 is used to index the differences between
is used to index the differences between 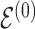 and
and 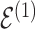 and final inference about differential interactions are discussed in Section 2.2.
and final inference about differential interactions are discussed in Section 2.2.
2.2. Priors on continuous parameters 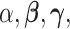 and
and 
The strength of association between random quantities in the baseline group is parametrized through the 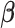 coefficients. Differential parameters
coefficients. Differential parameters 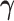 distinguish the strength of association between the baseline and differential groups. We explicitly address two inferential questions. First, are there differences in patterns of conditional dependence between baseline and differential groups? This question relates to the identification of the set
distinguish the strength of association between the baseline and differential groups. We explicitly address two inferential questions. First, are there differences in patterns of conditional dependence between baseline and differential groups? This question relates to the identification of the set 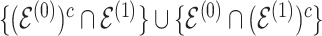 . Secondly, when considering edges that are shared between both baseline and differential groups, are there significant differences in the way these edges define conditional dependence patters? Here, we consider the set
. Secondly, when considering edges that are shared between both baseline and differential groups, are there significant differences in the way these edges define conditional dependence patters? Here, we consider the set 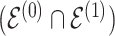 , but we are specifically interested in the size of
, but we are specifically interested in the size of 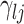 .
.
We encode these inferential goals directly in the prior. In particular, it is convenient to define latent trinary indicators 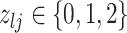 distinguishing between three cases: (1)
distinguishing between three cases: (1) 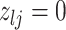 , whenever the association implied by the edge
, whenever the association implied by the edge 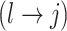 is invariant with group label; (2)
is invariant with group label; (2) 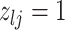 , whenever
, whenever 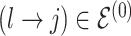 , but
, but 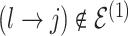 ; and (3)
; and (3) 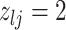 , whenever the strength of association implied by
, whenever the strength of association implied by 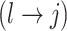 varies with group label, beyond the scenario of case (2). Note that
varies with group label, beyond the scenario of case (2). Note that 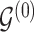 and
and 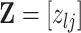 together deterministically determine
together deterministically determine 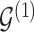 . However,
. However, 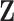 codes information beyond topological differences between
codes information beyond topological differences between 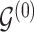 and
and 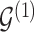 by also indicating common edges with varying strength across conditions.
by also indicating common edges with varying strength across conditions.
For any configuration of 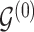 and
and 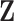 (implying also a configuration of
(implying also a configuration of 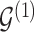 ), and for all
), and for all 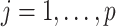 ; let
; let 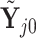 denote the matrix including all parents of
denote the matrix including all parents of 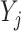 in
in  . Similarly, let
. Similarly, let 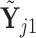 denote the matrix including all parents of
denote the matrix including all parents of 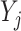 in
in 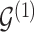 , for which
, for which 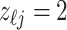 . We define a differential autoregression matrix
. We define a differential autoregression matrix 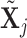 s.t.
s.t.
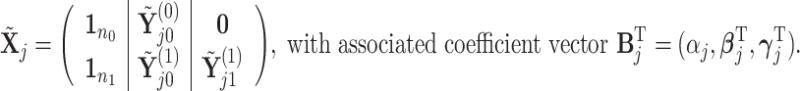 |
Using this notation, the conditional likelihood in (2.2) is represented as
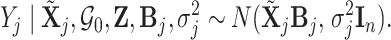 |
A conditional Zellner g-prior (Zellner, 1986) is then defined as
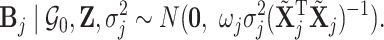 |
Different choices of 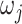 have been proposed in the model selection literature (Celeux and others, 2012). We consider the benchmark prior
have been proposed in the model selection literature (Celeux and others, 2012). We consider the benchmark prior 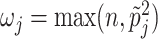 (Fernandez and others, 2001), where
(Fernandez and others, 2001), where 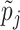 is the number of columns in
is the number of columns in  . Alternatively, data-dependent choices have been discussed in Consonni and La Rocca (2012).
. Alternatively, data-dependent choices have been discussed in Consonni and La Rocca (2012).
Given this parametrization, posterior inference over differential patterns of interaction focuses on 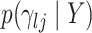 , as this quantity is directly informative about the size of differences in partial correlation and about the significance of such differences, as measured by
, as this quantity is directly informative about the size of differences in partial correlation and about the significance of such differences, as measured by 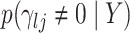 . Finally, dispersions
. Finally, dispersions 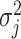 ,
, 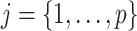 are modeled independently as a conjugate inverse gamma priors with hyper parameters
are modeled independently as a conjugate inverse gamma priors with hyper parameters 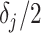 and
and 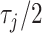 , so that
, so that 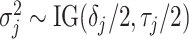 .
.
2.3. Model space priors
Let 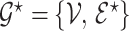 be a prior graph derived through direct expert opinion or constructed using public databases (e.g., a DAG-derived through Gene Ontology, http://genontology.org). In order to define a prior centered on
be a prior graph derived through direct expert opinion or constructed using public databases (e.g., a DAG-derived through Gene Ontology, http://genontology.org). In order to define a prior centered on 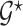 , we follow Telesca and others (2012) and define an exponentially decaying function centered around the prior graph
, we follow Telesca and others (2012) and define an exponentially decaying function centered around the prior graph 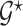 , so that
, so that 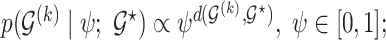 where the graph distance function is defined as
where the graph distance function is defined as 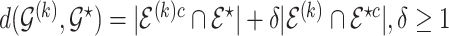 . This prior depends on inclusion probabilities
. This prior depends on inclusion probabilities 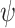 , on which we place a hierarchical beta
, on which we place a hierarchical beta
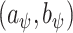 prior, as suggests in Scott and Berger (2006) to control for error control in the multiple comparison problem. Marginalizing over
prior, as suggests in Scott and Berger (2006) to control for error control in the multiple comparison problem. Marginalizing over 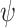 the model space prior becomes
the model space prior becomes  which is strictly decaying function with respect to
which is strictly decaying function with respect to 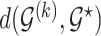 . Given the prior graph
. Given the prior graph 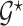 , we model
, we model 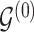 and
and 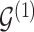 as partially exchangeable, thus we define the overall model space prior as
as partially exchangeable, thus we define the overall model space prior as 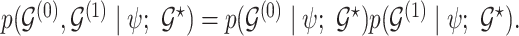 We note that this prior becomes a simple sparsity prior when
We note that this prior becomes a simple sparsity prior when 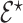 is empty, making it useful for de-novo analyses. Our simulation (see supplementary material available at Biostatistics online) do however outline the advantage of partially informative model space priors, even in the context of partial misspecification.
is empty, making it useful for de-novo analyses. Our simulation (see supplementary material available at Biostatistics online) do however outline the advantage of partially informative model space priors, even in the context of partial misspecification.
3. Posterior simulation
To obtain draws from the posterior distribution 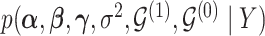 , we use a Gibbs sampling algorithm similar to Smith and Kohn (1996), with slight modification in the proposal strategy. The conditionally conjugate structure of priors and likelihood allows for the computation of models marginal likelihood (see Appendix D of supplementary material available at Biostatistics online for details) and efficient transitions in the model space (Eklund and Karlsson, 2007).
, we use a Gibbs sampling algorithm similar to Smith and Kohn (1996), with slight modification in the proposal strategy. The conditionally conjugate structure of priors and likelihood allows for the computation of models marginal likelihood (see Appendix D of supplementary material available at Biostatistics online for details) and efficient transitions in the model space (Eklund and Karlsson, 2007).
The proposed transition sequence extends the method proposed by Fronk and Giudici (2004). to allow for transitions over the additional structure 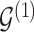 . We note that, in our formulation,
. We note that, in our formulation, 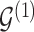 is fully determined by
is fully determined by 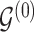 and latent components
and latent components 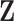 . It follows that systematic or random scans through the following transition sequence define an ergodic Markov chain that we can use to sample from posterior quantities of interest. In particular, we consider the following transition sequence
. It follows that systematic or random scans through the following transition sequence define an ergodic Markov chain that we can use to sample from posterior quantities of interest. In particular, we consider the following transition sequence
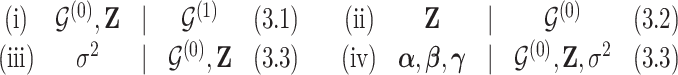 |
Details about each transition are explained in the corresponding sections.
3.1. Updating the baseline DAG 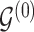
To update 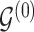 , we select an edge
, we select an edge 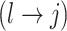 at random, that is, using a uniform distribution over all possible edges. If
at random, that is, using a uniform distribution over all possible edges. If 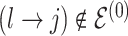 we propose its addition to
we propose its addition to 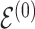 (birth); if
(birth); if 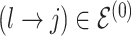 we propose removal (death); if
we propose removal (death); if 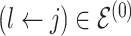 but
but 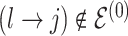 then propose to remove
then propose to remove 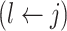 and add
and add 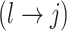 (switch). This transition can be represented through changes in the differential autoregressive matrix
(switch). This transition can be represented through changes in the differential autoregressive matrix 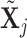 consistent with the proposed
consistent with the proposed 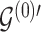 and
and 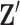 . Acceptance of a move is defined as
. Acceptance of a move is defined as
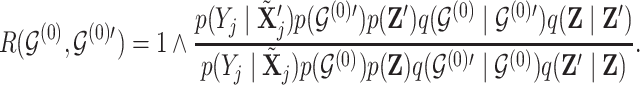 |
The moves are deterministic except for the case when 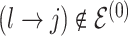 but
but 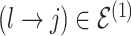 where we propose
where we propose 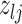 as 0 or 2 with equal probability. For the list of all possible moves, see Table 3 of supplementary material available at Biostatistics online. Computational efficiency can be gained by pre-computing
as 0 or 2 with equal probability. For the list of all possible moves, see Table 3 of supplementary material available at Biostatistics online. Computational efficiency can be gained by pre-computing 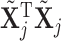 and
and 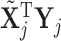 for saturated models. Details are discussed in Eklund and Karlsson (2007).
for saturated models. Details are discussed in Eklund and Karlsson (2007).
3.2. Updating the differential model space through latent indicators 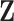
Given the baseline graph 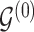 , we propose to move over the differential model space updating the latent variables
, we propose to move over the differential model space updating the latent variables 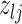 . Updates in the state of
. Updates in the state of 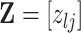 will also define changes in
will also define changes in 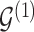 . We select an edge
. We select an edge 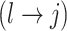 at random. Depending on the current state of
at random. Depending on the current state of 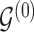 and
and 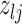 , we consider the proposal transitions summarized in Table 2. The proposed extension on simple birth, death, and switch moves allows for transitions that do not alter the structure of
, we consider the proposal transitions summarized in Table 2. The proposed extension on simple birth, death, and switch moves allows for transitions that do not alter the structure of 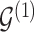 but change the magnitude of association (move
but change the magnitude of association (move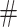 4,7). As before, all moves define a new differential autoregression matrix
4,7). As before, all moves define a new differential autoregression matrix 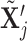 . The acceptance ratio is defined as
. The acceptance ratio is defined as
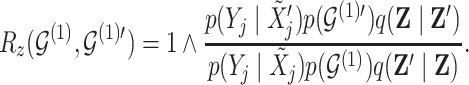 |
Table 2.
Proposal transition scheme for exploration of the differential model space to update 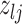
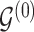 |
Current 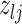
|
Proposed 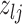
|
Probability | Move # | Type |
|---|---|---|---|---|---|
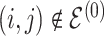 |
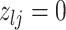 |
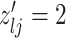 |
1 | 1 | Birth |
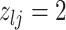 |
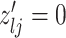 |
1 | 2 | Death | |
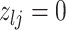 |
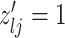 |
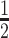 |
3 | Death | |
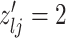 |
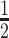 |
4 | Differential | ||
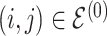 |
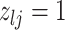 |
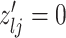 |
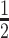 |
5 | Birth |
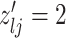 |
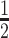 |
6 | Birth | ||
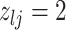 |
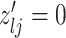 |
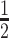 |
7 | Differential | |
 |
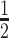 |
8 | Death |
The transition probabilities 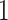 through
through 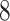 include four pairs of moves that are each other's inverse:
include four pairs of moves that are each other's inverse: 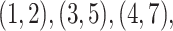 and
and 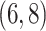 .
.
3.3. Updating 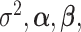 and
and 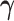
Given 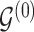 and
and 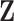 , sampling
, sampling 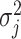 from their marginal posterior distributions and
from their marginal posterior distributions and 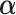 ,
, 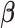 , and
, and 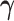 given
given 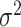 from their conditional posterior distributions is achieved through direct simulation. Detailed calculations are reported in Appendix of supplementary material available at Biostatistics online.
from their conditional posterior distributions is achieved through direct simulation. Detailed calculations are reported in Appendix of supplementary material available at Biostatistics online.
3.4. Posterior summaries
Posterior probabilities 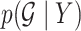 ,
, 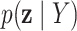 and corresponding MCMC samples characterize our knowledge about baseline and differential interactions in light of the data. Based on these quantities, the main inferential goal is to select representative baseline and differential graphs, say
and corresponding MCMC samples characterize our knowledge about baseline and differential interactions in light of the data. Based on these quantities, the main inferential goal is to select representative baseline and differential graphs, say 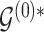 and
and 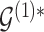 . While posterior probabilities do summarize evidence about interaction structures, selecting a point estimate in these model spaces requires further consideration.
. While posterior probabilities do summarize evidence about interaction structures, selecting a point estimate in these model spaces requires further consideration.
Given a joint model on edge and parameter inclusion probabilities, in the Bayesian framework, selection of point estimators for interaction structures 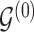 and
and 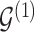 usually translates into the appropriate definition of a cutoff value for posterior inclusion probabilities (Scott and Berger, 2006; Müller and others, 2006). A cutoff threshold is often determined in order to ensure optimization of a chosen loss function.
usually translates into the appropriate definition of a cutoff value for posterior inclusion probabilities (Scott and Berger, 2006; Müller and others, 2006). A cutoff threshold is often determined in order to ensure optimization of a chosen loss function.
An alternative operational strategy is to select a point estimator, on the basis of multiple comparison arguments. An often used error rate is the false discovery rate (FDR) (Benjamini and Hochberg, 1995). Rules as discussed in Benjamini and Hochberg (1995) control the frequentist expectation of the error rate across repeat experimentation. Several authors chose instead to control the posterior expectation of the same error rate (see, e.g., Newton, 2004). From a Bayesian perspective, Müller and others (2006) illustrate a decision-theoretic procedure aimed at minimizing the posterior expected false negative rate (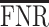 ), while controlling for the posterior expected
), while controlling for the posterior expected 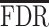 at a level
at a level 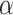 . The rest of this article is based on results obtained under Bayesian FDR control proposed by Müller and others (2006). Details, along with simulations, can be found in supplementary material available at Biostatistics online. Our studies show that the procedure controls for empirical FDR and FNR at the specified error rate.
. The rest of this article is based on results obtained under Bayesian FDR control proposed by Müller and others (2006). Details, along with simulations, can be found in supplementary material available at Biostatistics online. Our studies show that the procedure controls for empirical FDR and FNR at the specified error rate.
4. Case study: acute myeloid leukemia
We apply our model to the data from a study of acute myeloid leukemia (AML) obtained using the RPPA (Tibes and others, 2006). RPPA is a high-throughput proteomic technology that provides a quantification of the expression for specifically targeted proteins selected from molecular pathways. Our study is based on RPPA of bone marrow specimens collected from 435 newly diagnosed AML patients; 332 primary refractory patients and 103 relapsed patients. We will call the refractory patients the baseline group and the relapsed patients the differential group.
Scientific interest centers on the identification of differential signal transduction pathways (STPs), which are suspected to contribute to leukemogenesis by perturbing the rates of proliferation, differentiation, and apoptosis (Kornblau and others, 2006). The objective of this study is to investigate the difference in interactions of important protein markers related to AML for the refractory patients and the relapsed patients. We selected 29 proteins in signal transduction, apoptosis, and cell cycle regulatory pathways and studied their expression profiles in all 435 samples. An attractive feature of the AML data under study is that the number of samples 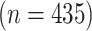 is much greater than the number of proteins
is much greater than the number of proteins  , which provides an opportunity for principled inference about differential interaction structures on the basis of a highly structured stochastic system.
, which provides an opportunity for principled inference about differential interaction structures on the basis of a highly structured stochastic system.
The prior signaling network was developed based on published articles from PubMed searches as well as from the connections map in Signal Transduction Knowledge Environment (http://www.stke.org). Other prior distributions on the parameters were selected as vague as possible to show that it is suitable for initial studies since the likelihood will dominate the posterior when the sample size is large. The two parameters of the dispersion parameter  where set to 0.5 and 0.5. The prior on
where set to 0.5 and 0.5. The prior on 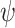 is set to beta
is set to beta
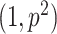 . We ran our algorithm for 2 million iteration saving every 100th sample while discarding the initial 1 million samples.
. We ran our algorithm for 2 million iteration saving every 100th sample while discarding the initial 1 million samples.
For the decision rule, we employed the criteria of Bayesian FDR control method proposed by Müller and others (2006) that simultaneously controls for the expected posterior FDRs and FNRs. We control the expected posterior FDR at 1% for both baseline and differential associations separately.
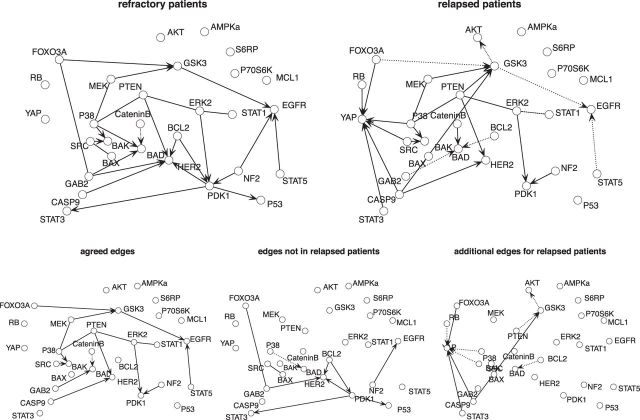
Figure 2 is a network representation of the estimated graph in the form of essential graph (Chickering, 2002) for the refractory and relapsed patients. The bottom three figures show edges that patients in two conditions agree on, that exists only in the refractory patients and that exists only in the relapsed patients. A solid line indicates a positive coefficient estimate and a dotted line indicates a negative coefficient.
Fig. 2.
Network representation of the estimated protein network for refectory patients and relapsed patients for associations chosen at 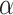 level of 0.01 using the decision criteria of Müller and others (2006). The positive associations are shown as a solid line and negative associations are shown as a dotted line. The bottom three plots classify the edges into three categories: the edges that two groups agree on, the edges that do not exist in the differential graph, and edges that only exist in the differential graph.
level of 0.01 using the decision criteria of Müller and others (2006). The positive associations are shown as a solid line and negative associations are shown as a dotted line. The bottom three plots classify the edges into three categories: the edges that two groups agree on, the edges that do not exist in the differential graph, and edges that only exist in the differential graph.
While we maintain that our findings are exploratory, we have observed that selected differential interaction patterns have been confirmed in the literature as potential indicators of more aggressive forms of AML. For example, we find a the striking differential role of the YAP protein (Yes-associated protein) as a hub node in the relapse sample. This protein plays a key role in the Hippo pathway, usually associated with the regulation of proliferation and apoptosis. While the role of Hippo has been established in solid tumors, only recent reports (Kornblau and others, 2013) associate YAP with differential prognostics in AML.
Figure 3 is the estimated posterior inclusion probability. The figures for the estimated mixing proportion and the posterior density plot of the coefficients can also be found in supplementary material available at Biostatistics online. A comprehensive bio-medical interpretation of our findings is perhaps out of the scope or this paper, but it is our hope that our illustration shows the potential and practical relevance of the proposed method.
Fig. 3.
Barplot of the estimated edge inclusion probability for the refractory patients (left) and the relapsed patients (right) for each edge. Rows/columns correspond to the 29 proteins AKT(1), AMPKa(2), BAD(3), BAK(4), BAX(5), BCL2(6), EGFR(7), FOXO3A(8), CASP9(9), CateninB(10), GAB2(11), GSK3(12), ERK2(13), HER2(14), MEK(15), MCL1(16), NF2(17), P38(18), P53(19), P70S6K(20), PDK1(21), PTEN(22), RB(23), S6RP(24), SRC(25), STAT1(26), STAT3(27), STAT5(28), YAP(29).
To validate our modeling approach, we compared our proposal with a model ignoring sample labeling and fitting a Gaussian DAG model without differential interactions. The result showed that the difference in average log marginal likelihood was 325.19 and the difference in log conditional predictive ordinate was 75.04, both suggesting strong evidence for the differential association.
5. Discussion
We proposed a probability model for inference on differential interaction in Gaussian DAGs. The proposed framework is likely to be particularly useful when primary interest focuses on potential contrasts characterizing the association structure between known subgroups of a given sample. Although we worked on a case where there are only two subgroups, the method is directly generalizable to the case of 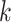 subgroups. Monte Carlo studies (supplementary material available at Biostatistics online) show the model to be robust against prior graph misspecification. Inference yields well-calibrated empirical FDR and FNR scaling to larger graphs and sample sizes. We evaluated our method analyzing data generated from a synthetic experiment and showed that our inferences have desirable operative characteristics (see supplementary material available at Biostatistics online for details). The application of the proposed model to the analysis of RPPA data in AML identified interesting differential regulation patterns, distinguishing refractory from relapsed patients. While we are well aware that our model belongs to the class of hypothesis generation tools, we remark that the proposed methodology avoids the use of step-wise analyses and ad hoc penalization choices, providing a principled tool for inference on differential networks.
subgroups. Monte Carlo studies (supplementary material available at Biostatistics online) show the model to be robust against prior graph misspecification. Inference yields well-calibrated empirical FDR and FNR scaling to larger graphs and sample sizes. We evaluated our method analyzing data generated from a synthetic experiment and showed that our inferences have desirable operative characteristics (see supplementary material available at Biostatistics online for details). The application of the proposed model to the analysis of RPPA data in AML identified interesting differential regulation patterns, distinguishing refractory from relapsed patients. While we are well aware that our model belongs to the class of hypothesis generation tools, we remark that the proposed methodology avoids the use of step-wise analyses and ad hoc penalization choices, providing a principled tool for inference on differential networks.
Although we avoided all the costly matrix inversion steps in our computation, when dealing with large and dense graphs, the sheer size of the space to explore could make the computation challenging. Alternative strategies may be necessary for these large problems.
The proposed framework of differential network inference could be extended beyond the multivariate Gaussian distribution. Models space and interaction parameters could, for example, be applied to the approach of Telesca and others (2012), who show how to incorporate heavy tails in the observations by the use of a mixture model. As for the case of discrete and mixed data, the copula Gaussian graphical model framework proposed by Dobra and Lenkoski (2011) could be easily expanded using a modeling strategy similar to the one proposed in this paper.
Extension beyond DAGs may be desirable in many applied settings. For example, in the setting of Reciprocal Graphs (Koster, 1996), used in Telesca and others (2011) one may allow baseline and differential models, to be defined in terms of undirected edges as well as the directed ones, with the possibility of including cycles and reciprocal relations. We should also point out that the same idea could of course be applied to undirected graphical models. While these extension are conceptually trivial, coherent multivariate representation and computational constraints may require extensive additional work.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
Yuan Ji's research is in part supported by NIH R01 CA132897. Peter Mueller's research is in part supported by NIH R01 CA132897 and NIH/NCI R01CA075981. Donatello Telesca's research was in part supported by NIH grant R01 CA158113-01.
Supplementary Material
Acknowledgement
The authors acknowledge two anonymous referees for their important feedback on the original manuscript. Conflict of Interest: None declared.
References
- Benjamini Y., Hochberg Y. (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological) 57(1), 289–300. [Google Scholar]
- Celeux G., El Anbari M., Marin J. M., Robert C. P. (2012). Regularization in regression: comparing Bayesian and frequentist methods in a poorly informative situation. Bayesian Analysis 7(2), 477–502. [Google Scholar]
- Chickering D. M. (2002). Learning equivalence classes of Bayesian-network structures. The Journal of Machine Learning Research 2, 445–498. [Google Scholar]
- Consonni G., La Rocca L. (2012). Objective Bayes factors for Gaussian directed acyclic graphical models. Scandinavian Journal of Statistics 39(4), 743–756. [Google Scholar]
- Danaher P., Wang P., Witten D. M. (2011). The joint graphical lasso for inverse covariance estimation across multiple classes. arXiv preprint arXiv:1111.0324. [DOI] [PMC free article] [PubMed]
- Dobra A., Hans C., Jones B., Nevins J. R., Yao G., West M. (2004). Sparse graphical models for exploring gene expression data. Journal of Multivariate Analysis 90(1), 196–212. [Google Scholar]
- Dobra A., Lenkoski A. (2011). Copula Gaussian graphical models and their application to modeling functional disability data. The Annals of Applied Statistics 5(2A), 969–993. [Google Scholar]
- Eklund J., Karlsson S. (2007). Computational Efficiency in Bayesian Model and Variable Selection. Central Bank of Iceland, Economics Department. [Google Scholar]
- Fernandez C., Ley E., Steel M. F. J. (2001). Benchmark priors for Bayesian model averaging. Journal of Econometrics 100(2), 381–427. [Google Scholar]
- Friedman J. H., Hastie T. J., Tibshirani R. (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9, 432–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fronk E.-M., Giudici P. (2004). Markov Chain Monte Carlo model selection for DAG models. Statistical Methods & Applications 13, 259–273. [Google Scholar]
- Guo J., Levina E., Michailidis G., Zhu J. (2011). Joint estimation of multiple graphical models. Biometrika 98(1), 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ickstadt K., Bornkamp B., Grzegorczyk M., Wieczorek J., Sheriff M., Grecco H., Zamir E. (2010). Nonparametric Bayesian networks. Bayesian Statistics 9, 283–316. [Google Scholar]
- Kornblau S. M., Hu C. W., Qiu Y. H., Yoo S. Y., Zhang N., Kadia T. M., Ferrajoli A., Coombes K. R., Qutub A. A. (2013). Hippo pathway (hp) activity in acute myelogenous leukemia (aml): Different prognostic implications of taz versus yap inactivation by phosphorylation. Blood 15(21), 1337. [Google Scholar]
- Kornblau S. M., Womble M., Qiu Y. H., Jackson C. E., Chen W., Konopleva M., Estey E. H., Andreeff M. (2006). Simultaneous activation of multiple signal transduction pathways confers poor prognosis in acute myelogenous leukemia. Blood 108(7), 2358–2365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koster J. T. A. (1996). Markov properties of nonrecursive causal models. The Annals of Statistics 24(5), 2148–2177. [Google Scholar]
- Kyung M., Gill J., Ghosh M., Casella G. (2010). Penalized regression, standard errors, and Bayesian lassos. Bayesian Analysis 5(2), 369–411. [Google Scholar]
- Lauritzen S. L. (1996). Graphical Models, Volume 17 USA: Oxford University Press. [Google Scholar]
- Müller P., Parmigiani G., Rice K. (2006) FDR and Bayesian multiple comparisons rules. Johns Hopkins University, Department of Biostatistics; Working Papers, 115. [Google Scholar]
- Newton M. A. (2004). Detecting differential gene expression with a semiparametric hierarchical mixture method. Biostatistics (Oxford) 5(2), 155–176. [DOI] [PubMed] [Google Scholar]
- Pearl J. (1986). Fusion, propagation, and structuring in belief networks. Artificial Intelligence 29(3), 241–288. [Google Scholar]
- Pearl J. (2000). Causality: Models, Reasoning and Inference. The Edinburgh Building, Cambridge CB2 2RU, UK: Cambridge University Press. [Google Scholar]
- Rodriguez A., Lenkoski A., Dobra A. (2011). Sparse covariance estimation in heterogeneous samples. Electronic Journal of Statistics 5, 981–1014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott J. G., Berger J. O. (2006). An exploration of aspects of Bayesian multiple testing. Journal of Statistical Planning and Inference 136(7), 2144–2162. [Google Scholar]
- Smith M., Kohn R. (1996). Nonparametric regression using bayesian variable selection. Journal of Econometrics 75(2), 317–343. [Google Scholar]
- Telesca D., Muller P., Kornblau S., Suchard M., Ji Y. (2011). Modeling protein expression and protein signaling pathways. COBRA Preprint Series, 87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Telesca D., Müller P., Parmigiani G., Freedman R. S. (2012). Modeling dependent gene expression. The Annals of Applied Statistics 6(2), 542–560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibes R., Qiu Y., Lu Y., Hennessy B., Andreeff M., Mills G. B., Kornblau S. M. (2006). Reverse phase protein array: Validation of a novel proteomic technology and utility for analysis of primary leukemia specimens and hematopoietic stem cells. Molecular Cancer Therapeutics 5(10), 2512–2521. [DOI] [PubMed] [Google Scholar]
- Zellner A. (1986). On assessing prior distributions and Bayesian regression analysis with g-prior distributions. Bayesian Inference and Decision Techniques: Essays in Honor of Bruno de Finetti. Amsterdam: North-Holland, pp. 233–243. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.