Abstract
Outbreaks of infectious disease can pose a significant threat to human health. Thus, detecting and characterizing outbreaks quickly and accurately remains an important problem. This paper describes a Bayesian framework that links clinical diagnosis of individuals in a population to epidemiological modeling of disease outbreaks in the population. Computer-based diagnosis of individuals who seek healthcare is used to guide the search for epidemiological models of population disease that explain the pattern of diagnoses well. We applied this framework to develop a system that detects influenza outbreaks from emergency department (ED) reports. The system diagnoses influenza in individuals probabilistically from evidence in ED reports that are extracted using natural language processing. These diagnoses guide the search for epidemiological models of influenza that explain the pattern of diagnoses well. Those epidemiological models with a high posterior probability determine the most likely outbreaks of specific diseases; the models are also used to characterize properties of an outbreak, such as its expected peak day and estimated size. We evaluated the method using both simulated data and data from a real influenza outbreak. The results provide support that the approach can detect and characterize outbreaks early and well enough to be valuable. We describe several extensions to the approach that appear promising.
Keywords: infectious disease, outbreak detection, outbreak characterization, clinical reports, Bayesian modeling
1. Introduction
There remains a significant need for computational methods that can rapidly and accurately detect and characterize new outbreaks of disease. In a cover letter for the July 2012 “National Strategy for Biosurveillance” report, President Obama wrote: As we saw during the H1N1 influenza pandemic of 2009, decision makers — from the president to local officials — need accurate and timely information in order to develop the effective responses that save lives [1]. The report itself calls for “situational awareness that informs decision making” and innovative methods to “’forecast that which we cannot yet prove so that timely decisions can be made to save lives and reduce impact.” The report echoes a call made by Ferguson in 2006 in Nature for similar forecasting capabilities [2].
The current paper describes a Bayesian method for detecting and characterizing infectious disease outbreaks. The method is part of an overall framework for probabilistic disease surveillance that we have developed [3], which seeks to improve situational awareness and forecasting of the future course of epidemics. As depicted in Figure 1, the framework supports disease surveillance end-to-end, from patient data to outbreak detection and characterization. Moreover, since detection and characterization are probabilistic, they can serve as input to a decision-theoretic decision-support system that aids public-health decision making about disease-control interventions, as we describe in [3].
Fig. 1. Schematic of the probabilistic disease surveillance system.
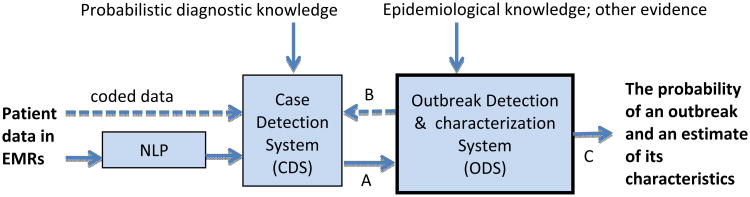
CDS transmits to ODS the likelihoods of each patient's findings, given the diseases being monitored (see arc A). ODS computes the probabilities of the epidemic models that were found during its model search. From these models, ODS can compute the probability of an outbreak, as well as estimate outbreak characteristics, such the outbreak size. For each of the monitored diseases, ODS also computes the prior probability that the next patient has that disease; it passes this information to CDS to use in deriving the posterior probability distribution over the diseases for that patient (see arc B). Thus, in an iterative, back-and-forth fashion, diagnostic information on past patients supports outbreak detection, and outbreak detection supports diagnosis of the next patient. This paper focuses on ODS and arcs A and C in the figure.
In the approach, a case detection system (CDS) obtains patient data (evidence) from electronic medical records (EMRs) [4]. The patient data include symptoms and signs extracted by a natural language processing (NLP) system from text reports. CDS uses data about the patient and probabilistic diagnostic knowledge in the form of Bayesian networks [5] to infer a probability distribution over the diseases that a patient may have. For a given patient-case j, the result of this inference is expressed as likelihoods of the patient's data Ej, both with and without an outbreak disease dx. In a recently reported study, CDS achieved an area under the ROC curve of 0.75 (95% CI: 0.69 to 0.82) in identifying influenza cases from findings in ED reports [6].
A second component of the system, which is the focus of this paper, is the outbreak detection and characterization system (ODS). ODS receives from CDS the likelihoods of monitored diseases for all patients over time. ODS searches a space of possible epidemic models that fit the likelihoods well, and it computes the probability of each model, denoted as P(epidemic modeli | dataall). The distribution over these epidemic models can be used to detect, characterize, and predict the future course of disease outbreaks. The output of ODS may be used to inform decisions about disease control interventions.
For each day, ODS also computes a prior probability that a patient seen on that day will have disease dx. To do so, ODS uses its estimate of (1) the extent of dx in the population, and (2) the fraction of people in the population with dx who will seek medical care. These ODS-derived patient priors can be used by CDS to compute the posterior probability that patient j has disease dx, that is, P(dx | dataj). The probability that a patient has a disease can inform clinical decisions about treatment and testing for that patient, public health case finding, and public health disease reporting.
We previously described the overall disease surveillance system architecture shown in Figure 1, including a high-level description of ODS [3]. The purpose of the current paper is to provide a detailed mathematical description of the current ODS model and inference methodology, as well as an initial evaluation of it using data from a real outbreak and from simulated disease outbreaks. The paper focuses on epidemiologic applications of ODS, which includes all the information flowing from left to right that are shown with solid arrows in Figure 1.
2. Background
Outbreak detection and characterization (OD&C) is a process that detects the existence of an outbreak and estimates the number of cases and other characteristics, which can guide the application of control measures to prevent additional cases [7]. In this section, we review representative prior work on OD&C algorithms, and we describe the novel characteristics of our approach.
Non-Bayesian OD&C algorithms can be classified as temporal [8-15], spatial [16-22], or spatio-temporal [23]. Almost all of these approaches follow a frequentist paradigm and share a key limitation: they only compute a p value (or something related to it) of a monitored signal; given the signal, they do not derive the posterior probability that there is an outbreak of disease dx, which is what decision makers typically need. It is also difficult for frequentist approaches to incorporate many types of prior epidemiological knowledge about disease outbreaks.
Bayesian algorithms have been developed for outbreak detection [24-39]. These algorithms can derive the posterior probabilities of disease outbreaks, which are needed in setting alerting thresholds and performing decision analyses to inform public-health decision-making. Bayesian algorithms have also been developed to perform some types of outbreak characterization [31, 38, 40, 41]. However, all of these algorithms have a major limitation: the evidence they receive as input is constrained to be counts, such as the daily number of patients presenting to outpatient clinics with symptoms of cough and fever. Although such counts are informative about outbreaks, they cannot feasibly express many rich sources of information, such as that found in a patient's emergency department (ED) report, which includes a mix of history, symptoms, signs, and lab information.
In the current paper, we describe a more flexible and general approach that models probabilistically the available evidence using data likelihoods, such as the probability of the findings in a patient's ED report conditioned on the patient having influenza (or alternatively some other disease). This approach can use counts as evidence, but it is not limited to doing so. It leverages the intrinsic synergy between individual patient diagnosis and population OD&C. In particular, in this approach OD&C is derived based on probabilistic patient diagnostic assessments, expressed as likelihoods. In general, the more informative is available patient evidence about the diseases being monitored, the more informative are the resulting probabilities of those diseases. For example, evidence that a patient has a fever, cough, and several other symptoms consistent with influenza will generally increase the probability of influenza in that patient, relative to having evidence regarding only one symptom, such as cough. The higher those probabilities (if well calibrated), the more informed the OD&C method will be about which patients have the outbreak disease, which in turn supports the detection and characterization of the outbreak in the population. In general, it is desirable to be able to incorporate whatever evidence happens to be available for each individual patient (including symptoms, signs, and laboratory tests) as early as possible in order to support outbreak detection and characterization. The method described in this paper provides such flexibility and generality.
In addition, the diagnosis of a newly arriving patient is influenced by prior probabilities that are derived from probabilistic inference over current OD&C models. To our knowledge, no prior research (either Bayesian or non-Bayesian) has (1) used a rich set of clinical information in EMR records as evidence in performing disease outbreak detection and characterization, nor (2) taken an integrated approach to patient diagnosis and population OD&C. While the power of this synergy is intuitive, the contribution of this paper is in describing a concrete approach for how to realize it computationally. In addition, we evaluate the approach.
Beyond being able to use a variety of evidence, the approach we propose can be applied with many different types of disease outbreak models. In the current paper we investigate the use of SEIR (Susceptible, Exposed, Infectious, and Recovered) compartmental models that use difference equations to capture the dynamics of contagious disease outbreaks, which is a highly relevant and important class of outbreak diseases in public health [42]. SEIR models have been extensively developed and applied to model contagious disease outbreaks [42]. In particular, this paper focuses on modeling influenza using a SEIR model, which is an important class of pathogens that cause disease outbreaks and pandemics.
3. Computational Methods
This section first describes the general approach we have developed for deriving the posterior probabilities of epidemic models for use in detecting and characterizing a disease outbreak. It then gives a general description of a method for searching over models.
3.1. Model Scoring
Our goal is to take clinical evidence in the form of EMR data, such as real-time ED reports, and to then automatically infer whether a disease outbreak is occurring in the population at large, and if so, its characteristics. Let dataall represent all of the available patient data and let modeli denote a specific model (epidemiological hypothesis) of the disease outbreak in the population. By Bayes' theorem we obtain the following:
| (1) |
where the sum is taken over all the models in set S that we assume have a non-zero prior probability (i.e, P(modeli) > 0).
In Equation 1, P(modeli) is the prior probability of modeli, which is assessed based on domain knowledge about possible types of outbreaks and their characteristics. For example, if we are using SEIR models [42, 43], then the basic reproduction number R0 is one such characteristic of population disease. By convention, we consider model0 to be a model that represents the absence of a disease outbreak.
We derive P(dataall | modeli) in Equation 1 as follows. Given a model, we assume that the evidence over all patients on each given day1, which we denote as E(day), is conditionally independent of evidence on other days, given a model:
| (2) |
where the product is over all the days that we are monitoring for an outbreak, from an initial StartDay to a final EndDay, which typically would be the most recent day for which we have data, such as EMR data. We emphasize that in general modeli is a temporal, disease transmission model, which represents that the evidence on one day is related to the evidence of another day; so, the evidence from one day to the next is not unconditionally independent; rather, in Equation 2 the evidence is only assumed to be independent given modeli.
Let r be the number of patients (e.g., ED patients) on a given day who have the outbreak disease dx (e.g., influenza) that is being monitored.2 As we will see below, it is convenient to average over all values of r to derive the term in the product of Equation 2 as follows:
| (3) |
where #Pts(day) is a function that returns the total number of patients who visited the health facilities being monitored on a given day.
We derive the first term in the sum of Equation 3 as follows. The evidence for each day consists of the evidence over all of the patients seen on that day. We denote the evidence for an arbitrary patient j as Ej(day | r, modeli); for example, it might consist of all the findings for the patient on that day that are recorded in an EMR by a physician. We assume that the evidence of one patient is conditionally independent of the evidence of another patient, given a model and a value for r. Thus, we have the following:
| (4) |
Let dx = 1 represent that patient j has the outbreak disease dx, and let dx = 0 represent that he or she does not. Conditioned on knowing the disease status of a patient, we assume that the evidence about that patient's disease status is independent of r and modeli. Under this assumption, the term in the product of Equation 4 is as follows:
| (5) |
Recall that modeli is a model of the outbreak disease dx in the population at large, r is the number of presenting patients on a given day that have disease dx, and P(dx = 1 | r, modeli) is the prior probability that a given patient will have dx given r and modeli. Clearly this probability is influenced by the value of r; however, given r, knowing modeli would generally provide no additional information about the chance that the patient has disease dx. Based on this line of reasoning, we obtain the following:
| (6a) |
| (6b) |
Substituting Equations 6a and 6b into Equation 5, we obtain the following:
| (7) |
For a given value of r, we derive the prior probability that a patient has disease dx as follows:
where recall that #Pts(day) is the total number of patients on that day who sought care, which is a known quantity. We also have that P(dx = 0 | r) = 1 – P(dx = 1 | r).
The likelihood terms P(Ej(day)|dx = 1) and P(Ej(day)|dx = 0) in Equation 7 are provided by CDS, which is described in detail in [4]. In this way, CDS passes patient-centric information to ODS for it to use in performing disease detection and characterization. An important point to emphasize is that Ej can represent an arbitrarily rich and diverse set of patient information; in the limit, it could represent everything that is known about the patient at the time that care is sought. This point highlights the generality of the approach being described here in terms of linking the clinical care of individual patients to the epidemiological assessment of disease in the population.
We now return to Equation 3 to derive P(r | modeli), which will complete the analysis. Let n represent the number of individuals who according to modeli are infected with a given pathogen that is causing dx in the population on a particular day and are subject to visiting the ED because of their infection. Let θ denote the probability that a person in the population with dx will seek care and thereby become a patient who is seen on the given day. Assuming these patients seek care independently of each other, we obtain the following:
| (8) |
where Binomial(r ; n, θ) denotes a binomial distribution over r, given values of n and θ. If r > n, then Binomial(r ; n, θ) = 0.
Equation 8 assumes that n and θ are known with certainty; however, in general they are not. By considering the distribution of the values of n, we generalize Equation 8 to be the following:
| (9) |
where Npop is the size of the population of interest, which we assume is constant from StartDay to EndDay; if we wish to model that it varies, we can use Npop(day), which is a function that returns the size of the population of interest on each day.
We also can integrate over the distribution of the values of θ. Although we do not know θ, we will assume that its value — whatever it may be — persists over the course of a given disease outbreak. Thus, we modify Equation 2 to become the following:
| (10) |
where the prior probability density function f(θ) must be specified, and the term in the product is given by Equations 3 through 9, as before.
The combination of the above equations leads to the following overall solution to Equation 2:
| (11) |
where P(E(day) | r) is defined as follows:
Note that the term P(E(day) | r) in Equation 11 is independent of modeli; thus, it can be computed once, cached, and then used in efficiently scoring many different models.
In Equation 11, the key modeling components are P(Ej(day)|dx) and P(n|modeli). The first component is a clinical inference and the second is an epidemiological one. Equation 11 provides a principled way of combining these two components in deriving (dataall | model i), from which we derive P(model i | dataall) in Equation 1, which serves as a score of modeli.
3.2. Model Search
Fig. 2 provides as pseudocode a general method for searching the space of epidemiological models, using the model-score calculations described in the previous section.
Fig. 2.
Pseudocode of a general method for searching the space of epidemiological models in ODS.
ModelSearch creates a set of models that are stored in array V, along with the posterior probability of each model. The function GenerateModel in ModelSearch is left general, because there are many ways to implement it. In the next section, we discuss an implementation that randomly samples the epidemiological parameters of a SEIR model over specified value ranges.
Relative to the models generated, we can estimate numerous quantities of interest. For example, the probability that an outbreak has occurred during the period being monitored is one minus the probability that no outbreak has occurred, which is 1 - P(model0 | dataall), where model0 is the non-outbreak model. Recall that P(model0 | dataall) is stored in V[0].
Assuming the presence of an outbreak, we can estimate its characteristics using the most probable outbreak model in array V, including the outbreak's estimated start time and epidemic curve, as well as model parameters, such as R0. Alternatively, we can estimate these characteristics by model averaging over all the models in V, weighted by the posterior probability of each model, which is also stored in V.
4. An Implementation for Influenza Monitoring
This section describes details of applying the general approach described in the previous section to monitor for influenza outbreaks among humans in a given region.
4.1. SEIR Model
We used a standard SEIR model to model the dynamics of an influenza outbreak in a population using difference equations [42, 43]. The model contains a compartment called Susceptible which represents the number of individuals in the population who are susceptible to being infected by a given strain of influenza. The model also represents that other individuals may be in an Exposed and Infected compartment, in an Infectious compartment, and finally in a Recovered compartment, which includes those individuals who are immune due to prior infection or immunization. Since the compartments are mutually exclusive and complete, the sum of the counts taken over the four compartments equals the population size. We set the initial Exposed and Infected count to zero for all models. We set the initial Recovered count to be the population size minus the initial Susceptible. We initialized the Susceptible and Infectious counts as described below, which we consider as parameters of a SEIR model.
Movement of individuals from one such compartment to the next over time is specified by a set of differential or difference equations. We used a difference equation implementation. These equations include three parameters that also define an instance of the class. The basic reproduction number (R0) is the expected number of secondary cases of infection arising from a primary case. The latent period is the expected time from when an individual is infected to when he or she becomes infectious. The infectious period is the expected time an individual is infectious. Given a specification of these parameters, a SEIR model derives the number of individuals in each of the four compartments at each unit of time (e.g., each day).
Thus, in our implementation for the disease Influenza a given set of values for the parameters in a SEIR model defines a modeli in Equation 1. In the GenerateModel function of the ModelSearch procedure in Fig. 2, ODS samples over a range of values of these SEIR parameters in seeking models that score highly. The prior probability of a modeli, P(modeli), is equal to the probability of the SEIR parameter values; we discuss this prior probability in more detail below.
We use the SEIR model to determine the probability distribution P(n | modeli), as shown in Equation 9, where n is the number of individuals with influenza who are infectious on a given day. Since a SEIR model is deterministic, the probability simplifies to P(n | modeli) = 1 when n is the value given by the SEIR model on that day; P(n | modeli) = 0 for other values of n. However, on a given day the number of patients in the population with influenza who visit the ED remains a binomial probability distribution, as shown in Equation 9.
4.2. Prior Probabilities
ODS contains three types of prior probability distributions. One type involves the distribution over the six parameters shown in Table 1. The table shows the bounds over which we sampled each parameter independently and uniformly in performing model search. We chose the bounds for R0, the latent period, and the infectious period because they correspond to plausible ranges, based on past influenza outbreaks [42]. The initial susceptible parameter range corresponds to an estimate of the population size of Allegheny County, Pennsylvania, where we are monitoring for influenza outbreaks; the upper bound is the estimated population size, based on 2009 estimates [44], and the lower bound is 90% of the population size, corresponding to an estimate that as many as 10% of the population may have been exposed to the influenza outbreak strain previously. The number of infectious individuals on the first day of the outbreak is assumed to be between 1 and 100.
Table 1.
The ranges over which the model parameters were sampled.
| parameter | lower bound | upper bound |
|---|---|---|
| R0 | 1.1 | 1.9 |
| latent period (days) | 1 | 3 |
| infectious period (days) | 1 | 8 |
| initial susceptible | 1,096,645 | 1,218,494 |
| initial infectious | 1 | 100 |
| outbreak start day | 1 | day of analysis |
The second type of prior probability involves the distribution over θ, as shown in Equation 10. We used a uniform discrete distribution over the following values for θ: 0.0090, 0.0095, 0.01, 0.0105, 0.011, which correspond to a range of values with 0.01 as the median. Appendix A describes how 0.01 was derived. The other values from 0.0090 to 0.011 correspond to a range that is +/- %10 around 0.01. For computational efficiency in this initial implementation, in Equation 10 we used a maximum a posteriori (MAP) assignment of θ in place of the integral shown there.
The third type of prior probability is the probability of an influenza outbreak occurring during a yearlong period. We estimate this probability to be 0.9 and distribute it evenly over the year. A more refined prior would be non-uniform; we discuss this issue in the Discussion section.
4.3. Filtering Sampled Models
ODS uses the previously listed parameter ranges to generate models which can describe the disease dynamics in the population. However, not all models generated using these ranges can be considered realistic. For example, it is possible to construct a SEIR model from the listed ranges so that the peak date is over 600 days after the start of an outbreak. We would not consider such a model realistic since there is no evidence to support that a single influenza outbreak can last that long.
To avoid including such models in its sample set, ODS can check the dynamics of a sampled model, and if it does not satisfy some basic criteria for a realistic outbreak, the model is discarded and replaced with a new sample, which is checked in the same way. For real data, we assumed that a model is valid if its peak occurs within a 1-year period from the earliest possible start date of the outbreak. For simulated data, we assumed a model is valid if it predicts an outbreak to last no more than 240 days; the predicted outbreak is defined to be over when the number of people predicted to be infected is less than 1.
4.4. Modeling Non-influenza Influenza-like Illness
An important task when monitoring for an influenza outbreak is to model patients who present to an ED showing symptoms consistent with influenza, but which do not actually have influenza. Such patients are described as exhibiting a non-influenza influenza-like illness (NI-ILI). Cases of NI-ILI are frequent enough during both outbreak and non-outbreak periods to form a baseline of influenza-like disease. This baseline should be incorporated when applying the modeling approach described in Section 3 to detect and characterize influenza outbreaks.
Recall the term P(Ej(day) | dx = 0)· P(dx = 0| r) from Equation 7. For the disease influenza, dx = 0 indicates that patient j does not have influenza. This could mean that patient j has NI-ILI, or neither NI-ILI nor influenza, which we will denote by the term other. Thus, we can compose this term into the following parts:
| (12) |
CDS is applied to derive P(Ej(day) | dx= other) in Equation 12. In this paper, the evidence Ej(day) that we used consisted only of patient symptoms and signs. In terms of symptoms and signs, influenza and NI-ILI may appear very similar. Therefore, as a first-order approximation, we assumed that the likelihood of NI-ILI evidence is the same as that of influenza evidence. This assumption allows the use of the influenza model to derive the likelihoods for the NI-ILI model:
| (13) |
where dx = 1 signifies influenza being present, as above. In light of Equation 13, CDS uses the influenza Bayesian network model to derive likelihoods for NI-ILI patient cases.
We now return to Equation 12. Since we are modeling an NI-ILI baseline, we assume the probability that a patient has NI-ILI is independent of the number of patients with influenza, and thus:
| (14) |
Using Equations 12, 13, and 14, Equation 7 becomes the following:
| (15) |
where P(dx = other | r) = 1- P(dx = 1| r)- P(dx = NI-ILI) such that only values of r are considered that render non-negative values of P(dx = other | r).
Appendix B contains a derivation of the term P(dx = NI-ILI) immediately above. As explained there, we model this probability as being time varying from day to day.
5. Experimental Methods
We performed an evaluation of ODS using both a real influenza outbreak as well as simulated outbreaks. We applied ODS to real clinical data recorded by EDs in Allegheny County, PA in the time surrounding an H1N1 influenza outbreak in the fall of 2009. These results provide a realistic case study of how ODS might perform during a real outbreak in the future. On the other hand, simulated outbreaks allow the evaluation of ODS over a wide range of possible outbreak scenarios and have the advantage that the complete and correct course of the outbreak is available for analyzing the ability of ODS to detect and characterize outbreaks of influenza. Since simulations are always simplifications of reality, however, these results should be interpreted with appropriate caution.
ODS was implemented using Java. The timing results reported here were generated when using a PC with a 64-bit Intel Xeon E5506 processor with a 2.13GHz clock rate and access to 4 GB of RAM, which was running Windows 7.
5.1. A real influenza outbreak
We analyzed the performance of ODS on real data from the 2009 H1N1 influenza outbreak in Allegheny County (AC). The real data were provided to ODS by CDS in the form of disease likelihoods generated for ED patients from seven hospitals in AC for each day from June 1, 2009 through December 31, 2009. We selected four analysis dates during the outbreak and ran ODS on each of those dates. In running ODS, we started the monitoring for an influenza outbreak on June 1, 2009. We applied ODS in the same way as described in Section 5.2.2 below, with uniform sampling over the ranges just as they appear in Table 1.
As a measure of outbreak detection, we report the posterior probability of an outbreak at each of the four analysis dates. As a measure of outbreak characterization, we compared the peak dates predicted by ODS with the peak dates of retail sales of thermometers in AC. Previously, we showed that retail thermometer sales have a strong positive correlation with ED cases that are symptomatic of influenza [45].
5.2. Simulated outbreaks
5.2.1. Generating simulated outbreak data sets
We used a SEIR model to generate 100 influenza outbreaks. The epidemiological parameters defining the generated outbreaks were obtained by uniformly sampling over the ranges defined in Table 1, with the following exceptions. First, we assumed that the initial number of infectious individuals was 50, which corresponds to a moderate initial number. Second, we assumed that the outbreak start day was day 32, relative to the beginning of the simulation. For each day of an outbreak, the SEIR model determined the number of patient cases with influenza. For an individual with influenza, we assumed that the probability of him/her seeking care at an ED on a given day was 1/100, for the reasons given in Appendix A. We assumed individuals with influenza sought care independently of each other. For a simulated ED patient with influenza, we sampled with replacement his/her ED report from a pool of real ED reports of patients who were PCR positive for influenza. We combined this time series of simulated influenza cases with a time series of patient cases that did not exhibit influenza, which is described next.
We considered two types of patient cases that did not exhibit influenza. One type had non-influenza influenzalike illness (NI-ILI). The other type had neither influenza nor NI-ILI, and we labeled these as Other cases. We determined the number of NI-ILI cases on a given day by sampling from a Poisson distribution. The mean μNI-ILI of the distribution was determined as follows. Let μED denote the average number of total cases presenting to the monitored EDs; based on data from the summer months of 2009, 2010, and 2011 for the EDs we are monitoring in Allegheny County, we estimated μED to be 590 cases per day. We used summer months, because an influenza outbreak is unlikely to have occurred during those periods. We used μNI-ILI = 0.1 × μED, where the fraction of 0.1 is based on an estimate of the fraction of NI-ILI cases during the summer months (see Appendix B for details). If n NI-ILI cases were simulated as presenting to the ED on a given day, we sampled with replacement n ED reports from the set of real influenza cases described above. Since in this evaluation CDS used only symptoms and signs in the ED reports to diagnosis influenza, we used influenza cases to represent the presentation of other types of influenza-like illness.
We determined the number of Other cases on a given day by sampling from a Poisson distribution with a mean fraction of 0.9 × μED. For each of these cases, we sampled an ED report from a pool of real ED reports of patients who (1) were negative for influenza according to a PCR test, or who did not have a PCR test ordered, and (2) did not have symptoms consistent with influenza-like illness.
All cases were provided to CDS, which processed them and provided likelihoods to ODS. For each day of a simulation, the simulated influenza patients who visited the ED were combined with the simulated non-influenza patient cases who visited the ED (NI-ILI and Other cases) to create the set of all patients who visited the ED on that day. One hundred such simulated datasets were generated.
5.2.2. Applying ODS to the simulated outbreaks
We applied a version of ODS that implements the ModelSearch algorithm in Fig. 2. ModelSearch sampled 10,000 SEIR models; that is, once 10,000 SEIR models were sampled, the stopping condition in the repeat statement of ModelSearch was satisfied. The GenerateModel function generated these SEIR models according to the methods described in Section 4.1, 4.2 and 4.3. In particular, in generating a SEIR model the parameters in Table 1 were uniformly randomly sampled over the ranges shown there and then filtered to retain realistic models.
We performed Bayesian model averaging over the 10,000 SEIR models to predict the total size of the outbreak for each of the 100 simulated outbreaks. Thus, the prediction of outbreak size from each model was weighed by the posterior probability of that model, which was normalized so that the sum of the posterior probabilities over all 10,000 models summed to 1. To predict the peak date, we derived a model averaged daily influenza incidence curve, by Bayesian model averaging over the 10,000 influenza incidence curves. We then identified the peak date in the model averaged curve and used it as the predicted peak date.
5.1.3. Analyzing ODS performance on simulated outbreaks
We quantified outbreak progression as being the fraction at some point of the total number of outbreak cases that occurred over the entire course of the outbreak. For example, 0.5 corresponds to half of the total cases having had occurred. We also derived the corresponding number of days into the outbreak.
We analyzed the ability of ODS to detect and characterize outbreaks. We analyzed the posterior probability that an outbreak is occurring on a given date, as computed by ODS, in order to assess the timeliness of detection. An outbreak probability is only useful if it is high when an outbreak is occurring and low when an outbreak is not occurring. Thus, for a given outbreak posterior probability P, we also report an estimate of the fraction of days during a non-outbreak period when ODS would predict an outbreak probability as being greater than or equal to P. We assume that outbreak probabilities from ODS are being generated on a daily basis.
We used two measures of population-wide outbreak characterization performance. First, we measured how well ODS estimated the total number of outbreak cases (including future cases) as the outbreak progressed. As a quantitative measure, we used |actual_number - estimated_number| /actual_number, which is the relative error (RE). Second, we measured how well ODS estimated the peak day of an outbreak, using |actual_peak_date - estimated_peak_date|, which is the absolute error that is measured in days.
6. Experimental Results
6.1. Results using real data
On August 15, 2009 the posterior probability of an influenza outbreak according to ODS was about 26%, which is moderate, but certainly not definitive. By September 8 the probability had risen to about 97%, which is 41 days before the October 19 peak date of the outbreak, as discussed below. Table 2 shows the posterior probabilities on September 8 and three subsequent dates in 2009. The table also shows the predicted peak date of the outbreak according to ODS and the peak date according to thermometer sales.
Table 2.
Results of the application of ODS to real data from EDs in Allegheny County Pennsylvania at four dates in the fall of 2009.
| ODS analysis date | probability outbreak is occurring | peak date of thermometer sales | ODS predicted peak date | thermometer peak minus ODS peak |
|---|---|---|---|---|
| September 8 | 0.973 | October 19 | October 19 | 0 |
| October 12 | > 0.999 | October 19 | November 10 | -22 |
| October 26 | > 0.999 | October 19 | October 26 | -7 |
| November 29 | > 0.999 | October 19 | October 17 | 2 |
For each target date, ODS estimated the past, present, and future daily incidence of newly infectious individuals in the population. The solid plot line in Figure 3 shows those results for predictions made on September 8. The gray area in the figure indicates dates beyond September 8, and thus these are predictions of future cases. The dotted line shows the number of thermometer sales in AC on each day, as an independent indicator of the number of new influenza cases on that day. The peak number of thermometer sales occurred on October 19 (see small circle on the dotted line in Fig. 3), which we will use as the presumptive true peak date. Figures 4-6 show the results for the other three target dates.
Fig. 3.
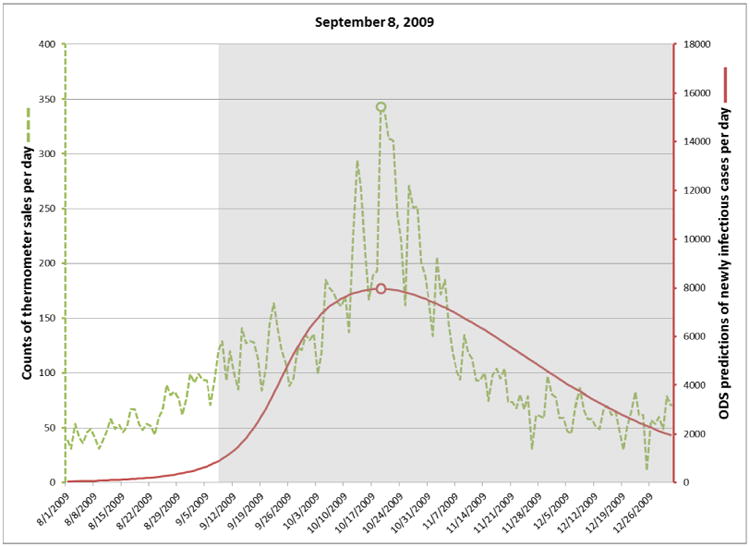
Incidence of newly infectious influenza cases calculated by ODS on September 8, 2009 (solid line). Daily thermometer sales are shown as an independent indicator of the peak date of the influenza outbreak (dotted line).
Fig. 4.
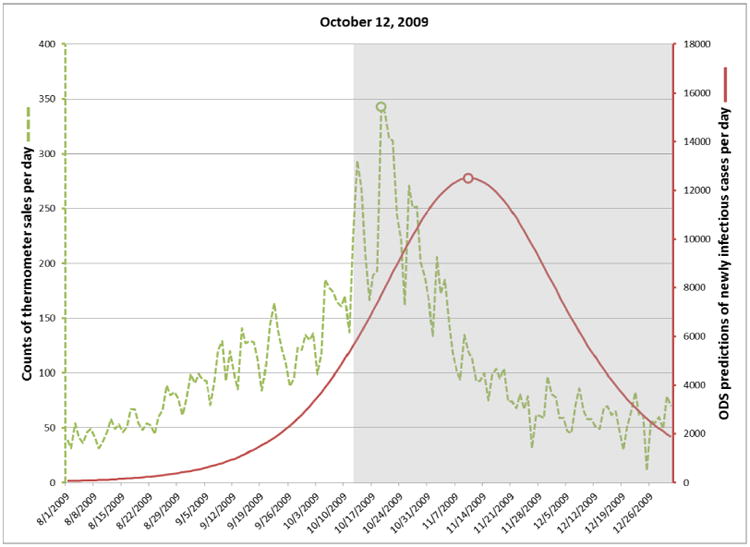
Incidence of newly infectious influenza cases calculated by ODS on October 12, 2009.
Fig. 6.
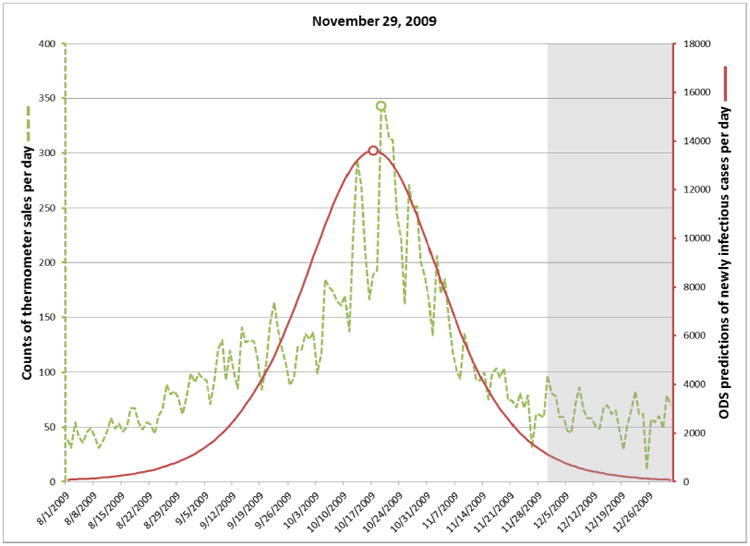
Incidence of newly infectious influenza cases calculated by ODS on November 29, 2009.
The computational run time for the analyses shown in Table 2 ranged from 11 minutes for the September 8 analysis to 29 minutes for November 29 analysis. Later dates required more computer time, due to there being more days over which to consider that an outbreak could have begun.
6.2. Results using simulated data
Table 3 shows the results for the simulated outbreaks. As an example, consider row 3 in which the mean fraction of outbreak cases is 0.064, corresponding to about 52 days into the outbreak on average. The ODS posterior probability of the outbreak is about 97% on average. The mean error in estimating the total number of outbreak cases at that point is approximately 11%. The error in estimating the peak day at that point is about 4 days. Only in about 1 in 200 days (= 0.005) will there be a false-positive prediction of an outbreak, relative to a posterior probability of 97%.
Table 3.
The results of an evaluation involving 100 simulated influenza outbreaks. Each cell contains a mean value followed in parenthesis by the 95% confidence interval around that mean.
| mean fraction of outbreak cases | mean number of days into the outbreak | mean posterior probability P that an outbreak is occurring | mean relative error in estimating the total number of outbreak cases | mean absolute error of estimating the peak day | mean false positive rate relative to P |
|---|---|---|---|---|---|
| 0.001 | 17.6 (17.0, 18.3) | 0.125 (0.118, 0.132) | 0.874 (0.867, 0.881) | 13.4 (11.8, 15.0) | 0.695 (0.665, 0.726) |
| 0.01 | 35.8 (34.5, 37.2) | 0.363 (0.316, 0.410) | 0.649 (0.606, 0.692) | 9.3 (8.2, 10.4) | 0.283 (0.235, 0.331) |
| 0.064 | 51.9 (50.0, 53.9) | 0.972 (0.947, 0.996) | 0.106 (0.084, 0.128) | 4.1 (3.4, 4.9) | 0.005 (0.00, 0.01) |
| 0.1 | 56.0 (53.9, 58.1) | 0.981 (0.962, >0.999) | 0.086 (0.068, 0.104) | 3.2 (2.6, 3.9) | 0.003 (0.000, 0.009) |
| 0.2 | 62.8 (60.4, 65.2) | 0.996 (0.995, 0.997) | 0.069 (0.051, 0.087) | 3.6 (2.9, 4.3) | 0.00 (0.00, 0.00) |
| 0.5 | 74.2 (71.3, 77.1) | 0.997 (0.996, 0.999) | 0.063 (0.051, 0.074) | 2.5 (1.9, 3.0) | 0.00 (0.00, 0.00) |
7. Discussion
The plots in Figures 3 through 6 show how well ODS was able to predict the peak day of a real outbreak that occurred in 2009. On September 8 (Fig. 3), ODS predicted that a peak incidence of infectious influenza cases would occur on October 19, which is the presumptive true peak date, based on counts of thermometer sales. On October 12 (Fig. 4), the ODS prediction of the peak date is 22 days beyond the true peak date. Thus, the peak prediction worsened from September 8 to October 12. We conjecture that this result may be influenced by the actual outbreak being asymmetric, as indicated by the thermometer counts, where there is a more gradual slope before the peak day than after it. The asymmetry could result from vaccinations, a change in the frequency and extent to which people are in physical contact with each other, and other factors, which potentially could be modeled in ODS. In contrast, SEIR models are largely symmetric, which biases ODS toward fitting epidemiological curves that are also symmetric. Alternatively, it is possible that the peak count of thermometer sales in the region does not correspond the peak day of incidence of influenza cases in the region; however, the results in the next paragraph suggest it is a good estimate. Other reasons for the peak prediction results are possible as well, and it is an open problem to investigate such possibilities.
On October 26 (Fig. 5) ODS predicts that the peak has occurred at that point. On November 29 (Fig. 6), which is late into the outbreak, ODS predicts that the peak occurred on October 17, which is two days earlier than the peak predicted by thermometer sales. Since these two peak dates were derived by entirely different data sources and methods, it provides support that the peak date was close to October 19.
Fig. 5.
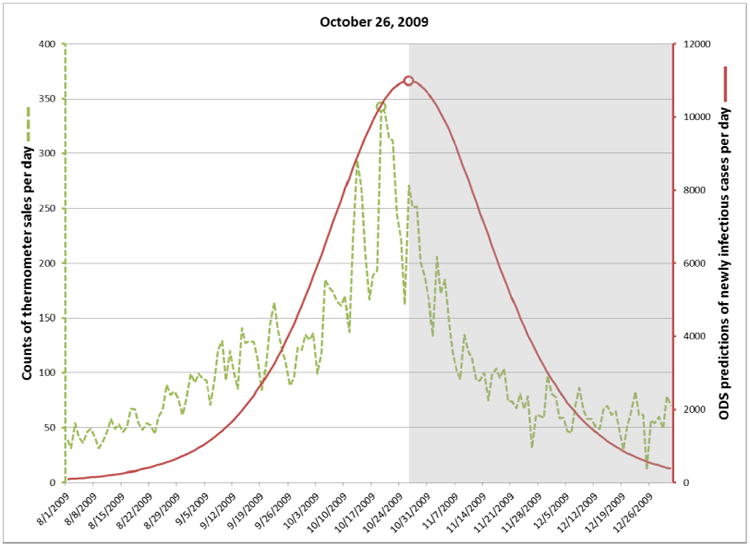
Incidence of newly infectious influenza cases calculated by ODS on October 26, 2009.
The simulation results in row 3 of Table 3 indicate that an outbreak is typically detected as highly likely at 52 days after it started, at which point about 6% of the outbreak cases have occurred. At 56 days into the outbreak, which corresponds to the first 10% of outbreak cases, the total number of cases (past, present, and future) are estimated with an error rate of about 9%, and the peak is estimated within an error of about 3 days. Since the peak day occurred on average at 74 days into the outbreak, these results provide support that influenza outbreaks can be detected and characterized well before the peak day is reached. Such information could help inform public-health decision making.
ODS makes use of epidemiological knowledge about influenza disease transmission in the form of prior distributions over its model parameters, which include parameters for influenza in a SEIR model and other parameters. When coupled with probabilistic case detection based on ED reports, this knowledge appears sufficient to achieve outbreak detection and characterization that are early enough to be relevant to disease-control decision making.
Extensions
We have applied the ODS framework in ways that go beyond those described above. We have used it to predict a posterior distribution over outbreak model parameters, such as R0 and the length of the infectious period, as well as outbreak characteristics, such as the estimated length of an outbreak. We have also applied ODS to predict the prior probability that the next patient in the ED will have influenza, which can be used in a patient diagnostic system. Patient data allow ODS to infer outbreaks in the population, which in turn allow ODS to infer the prior probability of patient disease. Thus, ODS provides a principled way of linking population-health assessment and patient diagnosis [3, 4]. The predictions of ODS can also be used in support of decision analytic systems that help public health decision makers decide how to respond to disease outbreaks [3], a functionality we have demonstrated in a decision-support tool called BioEcon, which can compute a Monte Carlo sensitivity analysis of disease control strategies over a set of ODS-scored models.3
Limitations
A limitation of the current implementation of ODS is its use of SEIR models. While these models provide useful approximations to many real outbreaks, which can be computed quickly, they may not adequately capture the complexities of some outbreaks. The results reported above for a real outbreak in 2009 suggest that the apparent asymmetry of the outbreak may have contributed to the error in predicting the peak date by ODS. It is an interesting open problem to investigate models with more complex behavior than the standard SEIR modeling framework. Such extensions could include, for example, SEIR models in which the parameters (e.g., R0) are modeled as changing over time in specific ways, in order to capture changes in the dynamics of person to person contact. As another example, the SEIR model could be augmented by a model of how ongoing vaccinations in the population for the outbreak disease are affecting the number of people who are susceptible to infection by that disease. As a third example, we could replace or augment the use of SEIR models with agent-based models, which can capture many details of a disease outbreak.
Within the SEIR-model framework reported here, we assumed that a single influenza outbreak would occur with a probability of 0.9 per year; its start date was evenly distributed over all 365 days of the year. As mentioned in Section 4.2, a more refined prior probability distribution over the start date would be non-uniform, which might well improve the performance of ODS on real influenza outbreak data. We note that the distribution over the start date of an outbreak is not the same as the distribution over the date the outbreak will be detected by public health. On the start date, there may be only a few cases of the disease in the population, and the start date can precede the detection date by many months. Quantifying the prior probability distribution over the start date for an influenza (or other type) outbreak is an interesting and challenging problem for future research.
There are also limitations in the experiments reported here. The experiments that used simulated data were useful in evaluating a range of outbreak scenarios. The overall performance of ODS appears good, which provides some support for its utility. However, evaluations based on simulated data are subject to bias. In particular, we used the same class of models (SEIR) for both outbreak simulation and outbreak detection. Moreover, we generated outbreaks using a range of model parameters that defined the uniform priors for those parameters in ODS. Thus, it seems reasonable to view the simulation results reported here as an upper bound on the performance we would expect from ODS in detecting and characterizing a real influenza outbreak. In future work, it will be useful to evaluate the performance of ODS using many more simulations, including those in which the assumptions of the simulator are at odds with the assumptions of ODS. It would also be interesting to measure the performance of ODS, as the amount of clinical data per patient is attenuated from (for example) all the findings in a full ED report, to a smaller set of selected findings, to just the chief complaint finding(s).
The evaluation using real data focused on an influenza outbreak in 2009 that was particularly interesting because Influenza A(H1N1)pdm was a new viral clade that caused a large and concerning pandemic that year. The ability to detect such pandemics is one of the primary reasons for developing systems such as ODS. Thus, the results of that evaluation are of special interest. Nonetheless, it will be important in future work to evaluate the performance of ODS on a larger set of real outbreaks.
It will also be important to compare the performance of ODS to other methods of outbreak detection and characterization, including some of the methods reviewed in Section 2. As mentioned in that section, to our knowledge there are currently no other methods that can use a rich set of patient findings as evidence in performing outbreak detection and characterization. Thus, comparisons to ODS will need to provide each method with the type of evidence it can use, while maintaining case consistency across the different types of evidence being used by each method.
Future Research
The ODS framework supports multiple directions for future research which appear promising. The framework is very flexible in terms of the type of data that are used as clinical evidence for given individuals, such as ED patients. The data could be derived from free text using NLP, as reported here, as well as coded data, such as laboratory results. Moreover, the type of evidence available for one individual can be different from that available for another. For example, for some patients we may only know their chief complaint and basic demographic information. For others, we may have a rich set of clinical information for the EMR. The use of heterogeneous data in outbreak detection and characterization is an open problem for future investigation.
The ODS framework is also flexible in supporting different types of epidemiological models. For concreteness, in this paper we focus on using SEIR models; however, other epidemiological models can be readily substituted. This paper also focuses on influenza as an example of an outbreak disease. Nevertheless, influenza is not “hard coded” into ODS. Rather, ODS allows other disease models to be used. It is possible for different types of outbreak diseases to be modeled using different types of epidemiological models. For example, we could use a SEIR model for modeling influenza and a SIS (Susceptible-Infectious-Susceptible) model for modeling gonorrhea.
ODS currently assumes at most one disease outbreak is influencing the data (during the interval from StartDay to EndDay. However, the general framework can accommodate the detection of multiple outbreaks that are concurrent or sequential. An example is the detection of an RSV outbreak that begins and ends in the middle of an influenza outbreak. Developing efficient computational methods for detecting and characterizing multiple, overlapping outbreaks is an interesting area for future research.
An important problem is to detect and characterize outbreak diseases that are an atypical variant of a known disease or an unmodeled disease, perhaps due to it being novel. There are two main patterns of evidence that can suggest the presence of such events. One occurs at the patient diagnosis level when modeled diseases match patient findings relatively poorly for some patients. Another occurs at the epidemiological modeling level when the estimates of the epidemiological parameters for an ongoing outbreak do not match well the parameter distributions of any of the currently modeled disease outbreaks. It is an interesting open problem to develop a Bayesian method for combining these two sources of evidence to derive both (1) a posterior probability of an outbreak being an atypical variant of some known disease and (2) a posterior probability that an outbreak is unmodeled, and thus, possibly novel.
Currently, ODS detects and characterizes outbreaks in a specific region of interest, such as a county. It will be useful to extend it to detect and characterize outbreaks within subregions of a given region. Each subregion may have a different epidemiological behavior (e.g., a different epidemiological curve in the case of an outbreak of influenza) than the other subregions. Being able to characterize the individual and joint behavior of these subregions could help support public health decision making.
As the capabilities of ODS are extended, it will be important to further improve its computational efficiency. One direction is to use more sophisticated methods to sample the model parameters, rather than use simple uniform sampling over a range of values. We could, for example, apply dynamic importance sampling [46], which tends to sample the parameters in the regions of the model space that appear to contain the most probable models. We might also assess more informative prior probability distributions over the parameters.
8. Conclusions
This paper describes a novel Bayesian method called ODS for linking epidemiological modeling and patient diagnosis to perform disease outbreak detection and characterization. The method was applied to develop a system for detecting and characterizing influenza in a population from ED free-text reports. A SEIR model was used to model influenza. A Bayesian belief network was used to develop an influenza diagnostic system, which takes as evidence findings that are extracted from ED reports using NLP methods. An evaluation was reported using simulated influenza data and a real outbreak of influenza in the Pittsburgh region in 2009. The results support the approach as promising in being able to detect outbreaks well before the peak outbreak date, characterize when the peak will occur, and estimate the total size of the outbreak in the case of simulated outbreaks. The general ODS framework is flexible and supports many directions for future extensions.
Highlights.
We describe a Bayesian method for detecting and characterizing infectious disease outbreaks.
The method takes as input clinical reports from an electronic medical record system.
The method outputs the probability of an outbreak and estimates of the outbreak's characteristics.
We applied the method to the detection of influenza outbreaks from emergency department reports.
Results from simulated and real influenza outbreaks support that the method is promising.
Acknowledgments
This research was supported by grant funding from the National Library of Medicine (R01-LM011370 and R01-LM009132), from the Center for Disease Control and Prevention (P01-HK000086), and from the National Science Foundation (IIS-0911032).
Appendix A
This appendix describes the derivation of 1/100 as an estimate of the probability that an individual who is infectious with influenza on a given day of the outbreak will visit the ED on that day due to the influenza. This posterior probability appears in Section 4.2 of the paper. We factor it into the following four component probabilities:
| (A1) |
| (A2) |
| (A3) |
| (A4) |
In the events appearing in the probabilities above, the word “ever” refers to any time during a given individual's infection with a given case of influenza. Equation A1 is definitional. Equation A2 is based on assuming that only about 67% of individuals who become infected with influenza exhibit symptoms of influenza [47]. Equation A3 is based on a telephone survey performed in New York City in 2003, which found that about 9% of people who had symptoms of influenza said they visited an ED because of that episode of illness [48, Table 2]. Equation A4 assumes that if an individual will visit the ED due to symptoms of influenza, then (1) the symptoms persist for an estimated six days [47], and (2) the individual is equally likely to visit the ED on any one of those six days.
The probability of interest is taken to be the product of the above four probabilities:
| (A4) |
Appendix B
This appendix describes the method we applied to derive the prior probability of non-influenza influenza-like-illness (NI-ILI) on a given day. This quantity appears as P(dx= NI -ILI) in Equation 15. A new value of this prior probability is derived for each day that is being monitored for an outbreak.
Let d denote the variable day that appears in Equation 15. It might, for example, denote the current day in a system that is monitoring for outbreaks of disease. We would like to estimate the fraction Q of patient cases on day d that present for care due to having NI-ILI. We will then use fraction Q as our estimate of P(dx = NI-ILI) on day d. Let Qd be an estimate of Q on day d. Our goal is to estimate Qd well.
We first estimated values for Q during a period when we presume there is no outbreak of influenza. Since influenza outbreaks are unlikely in the summer, we used the summer months for this purpose. For each day during the summer period, we found the value for the prior P(dx = NI-ILI) that maximized Equation 3, assuming that each patient case had either a NI-ILI or an Other disease. Let MLPd denote this maximum likelihood prior for day d. We then derived the mean μ and standard deviation σ of these MLPd values over a period of summer days. Assuming a normal distribution, we used μ and σ to derive a threshold T such that only about 2.5% of MLPd values are expected to be higher.
When monitoring for an outbreak on day d, we derived Qd as follows. If MLPd-1 < T, then Qd := MLPd-1. The rationale is that an MLP value yesterday (d-1) that is below T is consistent with ILI today (d) being due to non-influenza. However, if MLPd-1 ≥ T then an influenza outbreak is suspected, because it is unlikely that NI-ILI in the population could account for such a high extent of ILI. In that case, we estimate Qd as the mean value of recent, previous values of Q. In particular, we estimate Qd as being equal to the mean value of Q over the previous 21 days prior to d; if fewer than 21 days are available, we use the number that is available; when d = 1, no previous values are available, so we use Q1 = μ The rationale for using this method is that the current rate of NI-ILI is likely to be similar to its rate in the recent past.
Footnotes
The unit of time need not be days, but rather could be hours, for example.
For simplicity of presentation we assume here that only one disease is being monitored for an outbreak.
BioEcon and its user manual can be downloaded from http://research.rods.pitt.edu/bioecon; the use of BioEcon with ODS is described in Chapter 8 of that manual.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Obama B. National Strategy for Biosurveillance, Office of the President of the United States. Washington, DC: 2012. http://www.whitehouse.gov/sites/default/files/National_Strategy_for_Biosurveillance_July_2012.pdf. [Google Scholar]
- 2.Ferguson NM, Cummings DA, Fraser C, Cajka JC, Cooley PC, Burke DS. Strategies for mitigating an influenza pandemic. Nature. 2006;442(7101):448–452. doi: 10.1038/nature04795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wagner MM, Tsui F, Cooper G, Espino JU, Levander J, Villamarin R, Voorhees R, Millett N, Keane C, Dey A, Manik R, Hu Y, Tsai M, Brown S, Lee B, Gallagher A, Potter M. Probabilistic, decision-theoretic disease surveillance and control. Online Journal of Public Health. 2011;3(3) doi: 10.5210/ojphi.v3i3.3798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tsui F, Wagner MM, Cooper G, Que J, Harkema H, Dowling J, Sriburadej T, Espino JU, Voorhees R. Probabilistic case detection for disease surveillance using data in electronic medical records. Online Journal of Public Health. 2011;3(3) doi: 10.5210/ojphi.v3i3.3793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Darwiche A. Modeling and Reasoning with Bayesian Networks. Cambridge University Press; 2009. [Google Scholar]
- 6.Ye Y, Tsui F, Wagner M, Espino JU, Li Q. Influenza detection from emergency department reports using natural language processing and Bayesian network classifiers. Journal of the American Medical Informatics Association. 2014 doi: 10.1136/amiajnl-2013-001934. Published Online First. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wagner M. Chapter 1 Introduction. In: Wagner M, Moore A, Aryel R, editors. Handbook of Biosurveillance. New York: Elsevier; 2006. [Google Scholar]
- 8.Page ES. Continuous inspection schemes. Biometrika. 1954;41(1):100–115. [Google Scholar]
- 9.Serfling RE. Methods for current statistical analysis of excess pneumonia-influenza deaths. Public Health Reports. 1963;78(6):494–506. [PMC free article] [PubMed] [Google Scholar]
- 10.Grant I. Recursive least squares. Teaching Statistics. 1987;9(1):15–18. [Google Scholar]
- 11.Box GEP, Jenkins GM. Time Series Analysis: Forecasting and Control. Prentice Hall; 1994. [Google Scholar]
- 12.Neubauer AS. The EWMA control chart: Properties and comparison with other quality-control procedures by computer simulation. Clinical Chemistry. 1997;43(4):594–601. [PubMed] [Google Scholar]
- 13.Zhang J, Tsui FC, Wagner MM, Hogan WR. Detection of outbreaks from time series data using a wavelet transform. Proceedings of the Annual Fall Symposium of the American Medical Informatics Association. 2003 [PMC free article] [PubMed] [Google Scholar]
- 14.Ginsberg J, Mohebbi M, Patel R, Brammer L, Smolinski M, Brilliant L. Detecting influenza epidemics using search engine query data. Nature. 2009;457(7232):1012–1014. doi: 10.1038/nature07634. [DOI] [PubMed] [Google Scholar]
- 15.Villamarin R, Cooper G, Tsui FC, Wagner M, Espino J. Estimating the incidence of influenza cases that present to emergency departments. Proceedings of the Conference of the International Society for Disease Surveillance. 2010 [Google Scholar]
- 16.Kulldorff M. Spatial scan statistics: Models, calculations, and applications. Scan Statistics and Applications. 1999:303–322. [Google Scholar]
- 17.Kulldorff M. Prospective time periodic geographical disease surveillance using a scan statistic. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2001;164(1):61–72. [Google Scholar]
- 18.Kleinman K, Lazarus R, Platt R. A generalized linear mixed models approach for detecting incident clusters of disease in small areas, with an application to biological terrorism. American Journal of Epidemiology. 2004;159(3):217–224. doi: 10.1093/aje/kwh029. [DOI] [PubMed] [Google Scholar]
- 19.Zeng D, Chang W, Chen H. Proceedings of the International IEEE Conference on Intelligent Transportation Systems. IEEE; 2004. A comparative study of spatio-temporal hotspot analysis techniques in security informatics; pp. 106–111. [Google Scholar]
- 20.Bradley CA, Rolka H, Walker D, Loonsk J. BioSense: Implementation of a national early event detection and situational awareness system. Morbidity and Mortality Weekly Report (MMWR) 2005;54(Suppl):11–19. [PubMed] [Google Scholar]
- 21.Duczmal L, Buckeridge D. Using modified spatial scan statistic to improve detection of disease outbreak when exposure occurs in workplace --Virginia, 2004. Morbidity and Mortality Weekly Report. 2005;54(Supplement 187) [Google Scholar]
- 22.Chang W, Zeng D, Chen H. Proceedings of the IEEE Conference on Intelligent Transportation Systems. IEEE; 2005. Prospective spatio-temporal data analysis for security informatics; pp. 1120–1124. [Google Scholar]
- 23.Kulldorff M, Heffernan R, Hartman J, Assuncao R, Mostashari F. A space-time permutation scan statistic for disease outbreak detection. PLoS Med. 2005;2(3):e59. doi: 10.1371/journal.pmed.0020059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Shiryaev AN. Optimal Stopping Rules. Springer; 1978. [Google Scholar]
- 25.Harvey AC. The Kalman filter and its applications in econometrics and time series analysis. Methods of Operations Research. 1982;44(1):3–18. [Google Scholar]
- 26.Rabiner LR. A tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of the IEEE. 1989;77(2):257–286. [Google Scholar]
- 27.Stroup DF, Thacker SB. A Bayesian approach to the detection of aberrations in public health surveillance data. Epidemiology. 1993;4(5):435–443. doi: 10.1097/00001648-199309000-00009. [DOI] [PubMed] [Google Scholar]
- 28.Le Strat Y, Carrat F. Monitoring epidemiologic surveillance data using hidden Markov models. Statistics in Medicine. 1999;18(24):3463–3478. doi: 10.1002/(sici)1097-0258(19991230)18:24<3463::aid-sim409>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
- 29.Nobre FF, Monteiro ABS, Telles PR, Williamson GD. Dynamic linear model and SARIMA: A comparison of their forecasting performance in epidemiology. Statistics in Medicine. 2001;20(20):3051–3069. doi: 10.1002/sim.963. [DOI] [PubMed] [Google Scholar]
- 30.Rath TM, Carreras M, Sebastiani P. Automated detection of influenza epidemics with hidden Markov models. Proceedings of the International Symposium on Intelligent Data Analysis. 2003 [Google Scholar]
- 31.Jiang X, Wallstrom GL. A Bayesian network for outbreak detection and prediction. Proceedings of the Conference of the American Association for Artificial Intelligence. 2006:1155–1160. [Google Scholar]
- 32.Neill DB, Moore AW, Cooper GF. A Bayesian spatial scan statistic. Advances in Neural Information Processing Systems. 2006;18:1003–1010. [Google Scholar]
- 33.Sebastiani P, Mandl KD, Szolovits P, Kohane IS, Ramoni MF. A Bayesian dynamic model for influenza surveillance. Statistics in Medicine. 2006;25(11):1803–1816. doi: 10.1002/sim.2566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mnatsakanyan ZR, Burkom HS, Coberly JS, Lombardo JS. Bayesian information fusion networks for biosurveillance applications. Journal of the American Medical Informatics Association. 2009;16(6):855–863. doi: 10.1197/jamia.M2647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Watkins R, Eagleson S, Veenendaal B, Wright G, Plant A. Disease surveillance using a hidden Markov model. BMC Medical Informatics and Decision Making. 2009;9(1):39. doi: 10.1186/1472-6947-9-39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chan TC, King CC, Yen MY, Chiang PH, Huang CS, Hsiao CK. Probabilistic daily ILI syndromic surveillance with a spatio-temporal Bayesian hierarchical model. PLoS ONE. 2010;5(7):e11626. doi: 10.1371/journal.pone.0011626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Neill DB, Cooper GF. A multivariate Bayesian scan statistic for early event detection and characterization. Machine Learning. 2010;79(3):261–282. [Google Scholar]
- 38.Ong JBS, Chen MIC, Cook AR, Lee HC, Lee VJ, Lin RTP, Tambyah PA, Goh LG. Real-time epidemic monitoring and forecasting of H1N1-2009 using influenza-like illness from general practice and family doctor clinics in Singapore. PLoS ONE. 2010;5(4):e10036. doi: 10.1371/journal.pone.0010036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Burkom HS, Ramac-Thomas L, Babin S, Holtry R, Mnatsakanyan Z, Yund C. An integrated approach for fusion of environmental and human health data for disease surveillance. Statistics in Medicine. 2011;30(5):470–479. doi: 10.1002/sim.3976. [DOI] [PubMed] [Google Scholar]
- 40.Skvortsov A, Ristic B, Woodruff C. Predicting an epidemic based on syndromic surveillance. Proceedings of the Conference on Information Fusion (FUSION) 2010:1–8. [Google Scholar]
- 41.Que J, Tsui FC. Spatial and temporal algorithm evaluation for detecting over-the-counter thermometer sales increasing during the 2009 H1N1 pandemic. Online Journal of Public Health Informatics. 2012;4(1) doi: 10.5210/ojphi.v4i1.3915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Vynnycky E, White R. An introduction to infectious disease modelling. Oxford University Press; 2010. [Google Scholar]
- 43.Diekmann O, Heesterbeek JAP. Mathematical epidemiology of infectious diseases: Model building, analysis, and interpretation. Wiley; Chichester: 2000. [Google Scholar]
- 44.Census US. Annual Estimates of the Resident Population for Counties of Pennsylvania. 2009 http://www.census.gov/popest/data/counties/totals/2009/tables/CO-EST2009-01-42.csv.
- 45.Villamarin R, Cooper G, Wagner M, Tsui FC, Espino J. A method for estimating from thermometer sales the incidence of diseases that are symptomatically similar to influenza. Journal of Biomedical Informatics. 2013;46:444–457. doi: 10.1016/j.jbi.2013.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Owen AB, Zhou Y. Safe and effective importance sampling. Journal of the American Statistical Association. 2000;95:135–143. [Google Scholar]
- 47.Carrat F, Vergu E, Ferguson NM, Lemaitre M, Cauchemez S, Leach S, Valleron AJ. Time lines of infection and disease in human influenza: A review of volunteer challenge studies. American Journal of Epidemiology. 2008;167:775–785. doi: 10.1093/aje/kwm375. [DOI] [PubMed] [Google Scholar]
- 48.Metzger KB, Hajat A, Crawford M, Mostashari F. How many illnesses does one emergency department visit represent? Using a population-based telephone survey to estimate the syndromic multiplier. Morbidity and Mortality Weekly Report (MMWR) 2004;53(Syndromic Surveillance Supplement):106–111. [PubMed] [Google Scholar]



