Application of Improved Homogeneity Similarity-Based Denoising in Optical Coherence Tomography Retinal Images

Abstract

Image denoising is a fundamental preprocessing step of image processing in many applications developed for optical coherence tomography (OCT) retinal imaging—a high-resolution modality for evaluating disease in the eye. To make a homogeneity similarity-based image denoising method more suitable for OCT image removal, we improve it by considering the noise and retinal characteristics of OCT images in two respects: (1) median filtering preprocessing is used to make the noise distribution of OCT images more suitable for patch-based methods; (2) a rectangle neighborhood and region restriction are adopted to accommodate the horizontal stretching of retinal structures when observed in OCT images. As a performance measurement of the proposed technique, we tested the method on real and synthetic noisy retinal OCT images and compared the results with other well-known spatial denoising methods, including bilateral filtering, five partial differential equation (PDE)-based methods, and three patch-based methods. Our results indicate that our proposed method seems suitable for retinal OCT imaging denoising, and that, in general, patch-based methods can achieve better visual denoising results than point-based methods in this type of imaging, because the image patch can better represent the structured information in the images than a single pixel. However, the time complexity of the patch-based methods is substantially higher than that of the others.

Introduction

Optical coherence tomography (OCT) is an emerging optical imaging technology that performs high-resolution, cross-sectional tomographic imaging of internal structures in biological systems and materials [1]. Currently, OCT systems are employed in diverse applications, such as diagnostic medicine and interventional cardiology [2], especially in ophthalmology where it is effective to generate detailed images from within the retina. Since OCT is based on interferometric detection of coherent optical beams, OCT images contain speckle noise [3]. Speckle in OCT tomograms is dependent on both the wavelength of the imaging beam and the structural details of the imaged object [4]. Speckle is an inherent characteristic of images acquired with any imaging technique that is based on detection of coherent waves, for example ultrasound and coherent optical imaging. Speckle carries information about both the structure of the imaged object as well as a noise component, which causes grainy appearance of the images. In addition to speckle noise, shot noise also exists in OCT images, which is additive in nature and can be adequately described by the Additive White Gaussian Noise (AWGN) process [5].

OCT image denoising techniques can be categorized into two types: hardware-based techniques and digital image post-processing methods. In Schmitt’s paper [3], three hardware-based speckle-reduction techniques (polarization diversity [6], spatial compounding [7, 8], and frequency compounding [9]) were described. In the compounding technique, a series of images of one target are sampled at different times, with different frequencies, or in different scan directions. They are then merged to form a composite image. However, these hardware-based techniques suffer from a decrease in spatial resolution. In addition, they require hardware modifications that can be expensive and can be costly to implement. Therefore, the development of digital image post-processing methods is an important strategy for OCT image denoising. Numerous denoising methods have been adopted for speckle noise reduction in OCT images, such as median filtering [10, 11]. Rogowska and Brezinski [4] adopted the rotating kernel transformation technique to the speckle reduction and enhancement of OCT images, which was based on sequential application of directional masks and the selection of the maximum of all outputs. I-divergence regularization [12] was used to despeckle and retain the detail of the original data. This method produced a synthesized complex amplitude image that constrained the complex data to be consistent with the measured data in a least-squares sense, but also manipulated the magnitudes of the complex data to the degree allowed by measurement error. Wong et al. [13] proposed a Bayesian estimation for speckle noise reduction. This method projected the imaging data into the logarithmic space and a general Bayesian least-squares estimate of the noise-free data was found using a conditional posterior sampling approach.

A good image denoising algorithm should have the following properties: noise removal; preservation of the image information (edge, corner, texture, and contrast), and no artifacts [14]. However, the presence of the speckle noise naturally reduces imaging contrast and makes boundaries between highly scattering structures in tissue difficult to differentiate [3]. Due to the limited dynamic range of display monitors, the OCT signal is normally log-compressed to fit in the display range. Such compression of the OCT signal changes the characteristics of its probability density function [3, 15]. Prior to the logarithm compression stage for the envelope signal, speckle noise can be approximated as multiplicative noise. The logarithmic operation transforms this multiplicative noise into additive form. Therefore, the speckle pattern becomes additive white noise after the log-transformation, and the denoising goal transforms into removing this additive speckle noise. Salinas and Fernandez [16] compared the Perona-Malik (PM) model [17] with the complex diffusion filter [18]. Their approach leads to efficient denoising with well-preserved image details for better diagnosis. One of the advantages of the complex diffusion filter is that it avoids the staircase effect that is characteristic of gradient-controlled nonlinear processes such as the PM model. Recently, Fang et al. [19] presented a multiscale sparsity-based tomographic denoising (MSBTD) method for OCT images using the sparse representation technique.

In this paper, we present the application of a recently introduced homogeneity similarity-based method [14]—a patch-based method—in OCT image denoising. To make the homogeneity similarity-based method more suitable for retinal OCT images, two modifications are presented by considering the OCT image characteristics. To test the performance of the proposed method, we also provide a comparison both in terms of visual quality of the results and in quantitative measurements such as peak signal-to-noise ratio and mean structure similarity with other well-known denoising methods: the classic bilateral filtering [20], five PDE-based methods [17, 18, 21–23], and three patch-based methods [14, 24, 25].

Materials and Methods

Improved Homogeneity Similarity-Based Method

In traditional patch-based methods, such as the NL-means method, block matching mainly depends on structure similarity. The homogeneity similarity (HS)-based method [14] is defined in adaptive-weighted neighborhoods. The weight of the matching neighborhood depends on intensity similarity. The method is defined by the formula:

$$h\left(x,y\right)=\frac{{\displaystyle {\int }_{\Omega }u\left(p,q\right)w_H\left(x,y,p,q\right)}\mathit{dpdq}}{{\displaystyle {\int }_{\Omega }{w}_H\left(x,y,p,q\right)\mathit{dpdq}}}$$ 1

where u(p, q) is the pixel value of the input image at location (p, q). h(x, y) is the pixel value of the output image at location (x, y), where 1 ≤ x ≤ Ih and 1 ≤ y ≤ Iw. Ih and Iw represent the image height and width, respectively. The weight function w_H(x, y, p, q) depends on the range similarity between corresponding patches centered at points (x, y) and (p, q). In practical implementation, the spatial neighborhood is often restricted in a small search window for computational purpose, instead of the entire image domain Ω.

The common definition of a patch is that Ρ^u_(x,y) located at (x, y) ∈ Ω on the image u is the set of all image values belonging to a spatially discretized local d × d (square) neighborhood of u centered at (x, y). The size d is considered as odd, i.e., (r ∈ Ν). Then, the definition of the weight function is

$$w_H\left(x,y,p,q\right)=e^{-\frac{{\left|H_{\left(x,y\right)}\circ \left({{\rm P}}_{\left(x,y\right)}^u-{{\rm P}}_{\left(p,q\right)}^u\right)\right|}^2}{t^2}}$$ 2

where t is the range filtering parameter . The range similarity H_(x,y) is weighted by homogeneity similarity defined as $H_{\left(x,y\right)}\left(i,j\right)=\frac{e^{-k\cdot {\left(u\left(x,y\right)-u\left(i,j\right)\right)}^2}}{{\displaystyle \sum _{i=1}^d{\displaystyle \sum _{j=1}^d{e}^{-k\cdot {\left(u\left(x,y\right)-u\left(i,j\right)\right)}^2}}}}$, where the parameter k is a positive constant. ‘∘’ represents the element-wise multiplication operator, namely the multiplications of the corresponding elements of H_(x,y) and (P^u_(x,y) − P^u_(p,q)).

The HS-based method was originally proposed for general imaging purposes [14], similar with other patch-based methods. It was not optimized for OCT retinal image denoising. In the following, we introduce two modifications to achieve better image denoising results. The modifications we explored were a preprocessing median filtering step and consideration of neighborhood shape in retinal OCT imaging.

Preprocessing for Patch-Based Methods

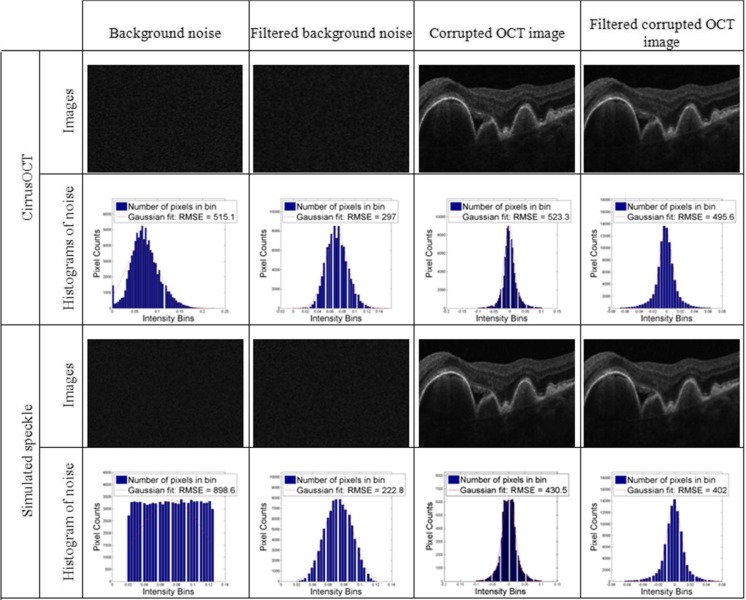
It has been shown that speckle noise is the most predominant noise source in OCT imaging [3–9]. Apart from other system-specific noise like electric or shot noise, speckle is common to all OCT commercial systems [26]. The signal-dependency property of speckle noise makes it difficult to remove without losing important image information, like edges or texture. In theory, patch-based methods can produce an optimal denoising result for Gaussian noise [27], but they are probably not the most suitable methods for reducing the speckle noise present in OCT imaging. In our proposed method, we investigated adopting a median filtering step in order to make the noise present in OCT images closer to a Gaussian distribution, and reducing its signal-dependency before the HS-based method is applied. To do so, we collected background noise images from one commercial system—CirrusOCT (Carl Zeiss Meditec)—as well as simulated speckle noise background image that was generated using “imnoise”, a function integrated in MATLAB (The Mathworks, Inc.). The background level and variance for the simulated speckle noise was set equal to the mean value and variance observed in the CirrusOCT background image, respectively. The properties of each noise signal were also investigated to computationally corrupt an averaged virtually noise-free in vivo OCT of the retina were noise is minimum [28] (high-dimensional CirrusHDOCT image, Carl Zeiss Meditec), considering the signal-dependency of this type of noise. We assumed that the acquired background images were formed by a constant value corrupted by multiplicative noise. We then computed the noise used to corrupt the retina original images by adding the logarithm of background noise signal minus this constant value (mean) to the logarithm of the original image, and later taking the exponential of the result. The sign of the exponential was also considered to either increase or decrease the pixel values in the original image. Figure 1 shows the comparison of the noise distribution of the background and signal-present corrupted images before and after a median filtering preprocessing step. We have computed the histograms for each noise image (background and signal present), both before and after median filtering, and fitted a Gaussian function to each of the results.

Fig. 1.

Example images and histograms of background signal in OCT (first to columns on the left) and a retina sample (two columns on the right), before and after median filtering. The first and third rows display the OCT B-scan images and their respective histograms are displayed under them (second and third rows)

For the images of background noise collected from the commercial systems and the simulated speckle, we can observe how their histograms more closely resemble a Gaussian distribution after the median filtering preprocessing step than before this step (examples shown in Fig. 1), also indicated by a lower root mean square error (RMSE) in their Gaussian fitting. Therefore, although limited to the images used in our analysis, this median filtering step seems to help transforming the background noise in OCT images to resemble a Gaussian distribution, making it more adequate for patch-based denoising methods. This preprocessing step was employed in our proposed denoising method.

For the corrupted retina images, the distribution of noise values after the median filtering was also closer to a Gaussian distribution after the median filtering, although the results were less dramatic than with background noise, most probably due to the presence of foreground signal in the images. Nevertheless, their value distribution was satisfactory and experiments showed that this median filtering preprocessing step improved the denoising method producing results with higher signal-to-noise ratio (Fig. 8).

Fig. 8.

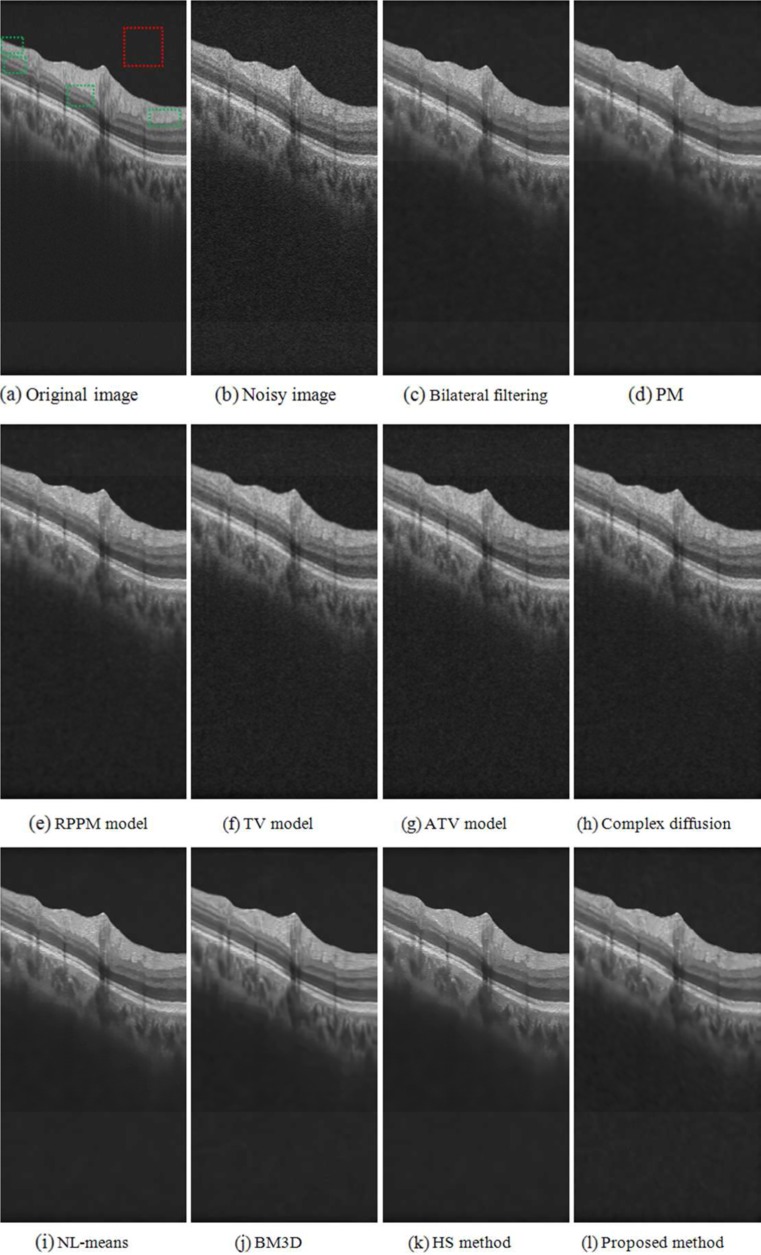
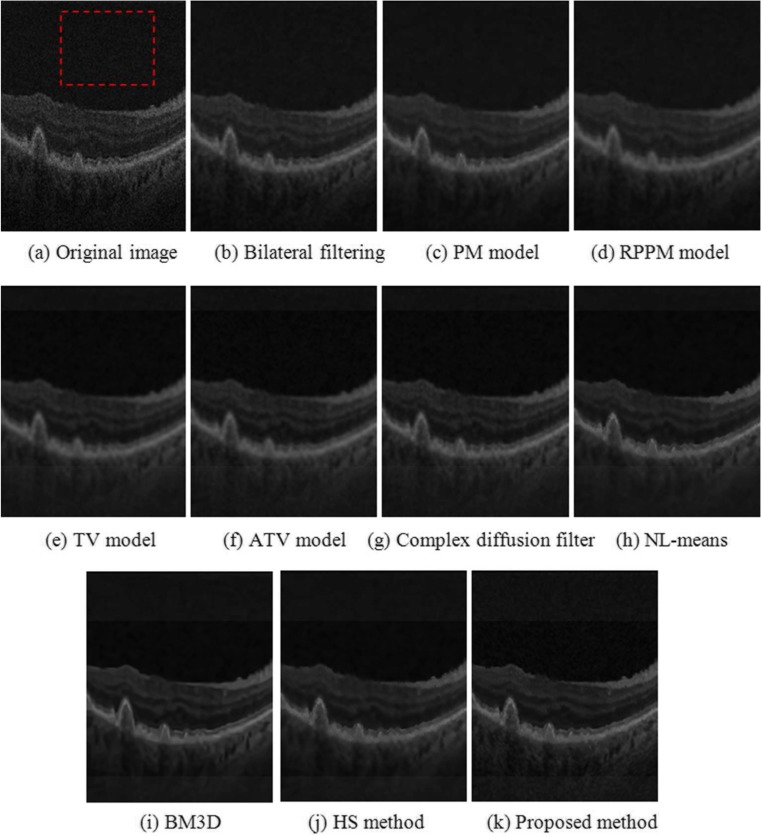
Image denoising of a synthetic noisy OCT retinal image. a Original “noise-free” B-scan. The red square indicates an example location identified as background region, the green rectangles indicate example locations considered as foreground regions. b B-scan corrupted by synthetic noise. c to i Results obtained from the different denoised methods investigated

Neighborhood Shape

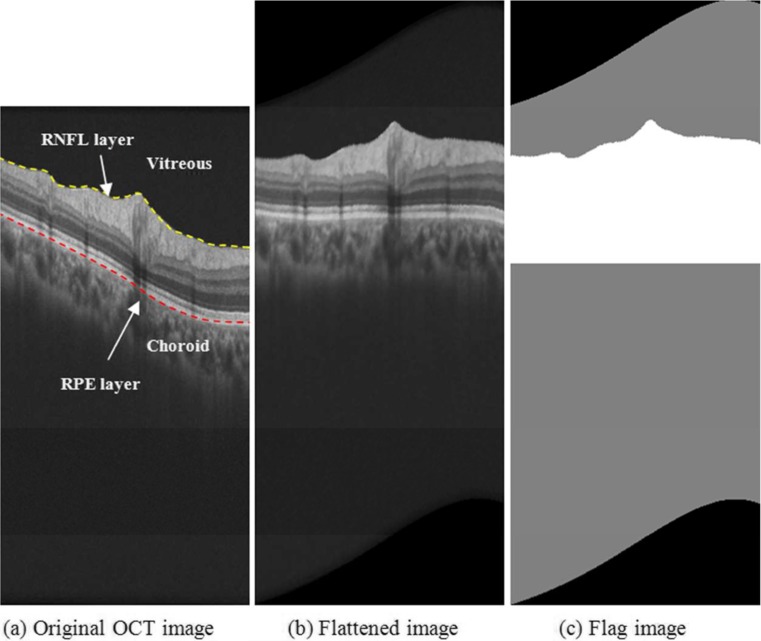
The basic idea of most image denoising methods (such as bilateral filtering and HS-based method) is to find similar pixels in each pixel neighborhood and compute their weighted average. If a larger number of similar pixels are located within the neighborhood definition, the denoised result will be better. Since each layer of the retina in OCT images tends to be shaped like a curved surface extending in the horizontal plane, it would seem preferable to change the traditional square neighborhood into a horizontally stretched rectangular neighborhood for the purpose of denoising retinal OCT images. A previous flattening of the OCT B-scans based on the retinal curvature observed in the boundaries of retinal layers, such as the retinal pigment epithelium (RPE) layer (marked with the dashed red curve in Fig. 2a)—namely shifting the pixels up or down according to an estimated RPE boundary [29]—makes this rectangle neighborhood more adequate.

Fig. 2.

Optimization of neighborhood shape for RPE layer. a Identifies the RNFL boundary, RPE layer, and vitreous and choroid regions in an original B-scan. b Displays the same example B-scan after the flattening step according to the location of the RPE layer. c Shows the identified regions of the B-scan where whether homogeneity similarity denoising (white region) or bilateral filtering (gray region) was employed

The location of the RPE boundary was automatically detected using a segmentation tool developed by our group that analyzes individual B-scan pixel statistics [30, 31]. Figure 2b is the flattened image version of the original B-scan displayed in Fig. 2a according to the RPE layer. Retinal layers present more tendencies to extend in the horizontal plane in the flattened image than in the original image. Patch-based denoising methods are usually very computational time and memory demanding. However, since most of the effective information related to retinal diseases are located between the retinal nerve fiber layer (RNFL, which inner boundary is marked with the dashed yellow curve in Fig. 2a) and the choroid region, we adopted different denoising methods for different regions in order to decrease the computing complexity. For the retinal layer region between the inner RNFL layer and the upper choroid layer (white region in Fig. 2c), we used the improved homogeneity similarity-based method so as to preserve effective information well. For the background region, namely the vitreous region and the lower choroid region (the gray region in Fig. 2c), a simple bilateral filtering can be used to remove noise. Since the effective region (white region in Fig. 2c) is a small part of the whole B-scan, and the bilateral filtering is less demanding than the homogeneity similarity-based method, the computing complexity was greatly reduced.

Data Collection

We compiled a set of 10 clinical SD-OCT images from 10 patients to qualitatively assess the denoising performance of our proposed homogeneity similarity-based method. Our clinical OCT images were obtained from our institution’s ophthalmology department, acquired in patients diagnosed with acute macular degeneration of the retina. This study was approved by our institution’s Institutional Review Board (IRB). Each SD-OCT image was acquired over a 6 × 6 mm area (corresponding to 512 × 128 pixels) and a 1024-pixel axial resolution using a CirrusOCT (Carl Zeiss Meditec, Inc., Dublin, CA) device.

For the same set of patients, we also had available high-definition (HD) scans acquired from the same system but using a different setting, in which only four HD B-scans (1024 × 1024 lateral and axial resolution) were acquired from each eye, presenting a much higher signal-to-noise ratio than regular SD-OCT scans [28, 32]. We also created a set of synthetic noise OCT images in which known noise was added to high-density OCT images collected in the clinic, in order to perform a detailed quantitative comparison of denoising results. Ten of these HD B-scans were randomly selected to construct a quantitative evaluation of the denoising methods. This particular setting produces high-density cross-sectional images of the retina with very high signal-to-noise ratio [26, 28, 32], where the noise component is minimal when compared to regular SD-OCT imaging B-scans, at the expense of only acquiring 4 B-scans per cube instead of the 512 B-scans typically acquired across the macula. In order to further reduce the inherent noise component in the HD images, they were downsampled from their original 1024 × 1024 resolution to 512 × 256 by bicubic interpolation. Our goal was to evaluate the performance of the proposed denoising method with the presence of general speckle noise and also in system-specific noise produced by typical retina SD-OCT devices. For the purposes of this study, we performed our evaluation with the characteristic noise produced by Cirrus OCT systems, which are one of the most broadly used and successful clinical systems [26, 28, 32]. A background noise signal generated from this system was collected and employed to computationally corrupt the original HD images, forming noisy images in which the noise component was known. The original images were corrupted such that the noise component was signal-dependent, following the behavior of speckle noise, and the added noise component was measured to produce synthetic noise images with a peak signal-to-noise ratio (PSNR) close to 30 dB. The averaged HD images were selected as virtually “noise-free” images in our experiments since they were very high quality and their inherent noise component was reduced by the interpolation operation, and virtually non-existent when compared to the 30 dB of PSNR recorded in the synthetic noise cases. We also repeated the process in the same set of original images using a more general speckle noise component, this time corrupting the images with simulated speckle noise using “imnoise”, an integrated function for this purpose available in Matlab (The Mathworks Inc.), tuning it to produce the same 30 dB PSNR level in the synthetic images.

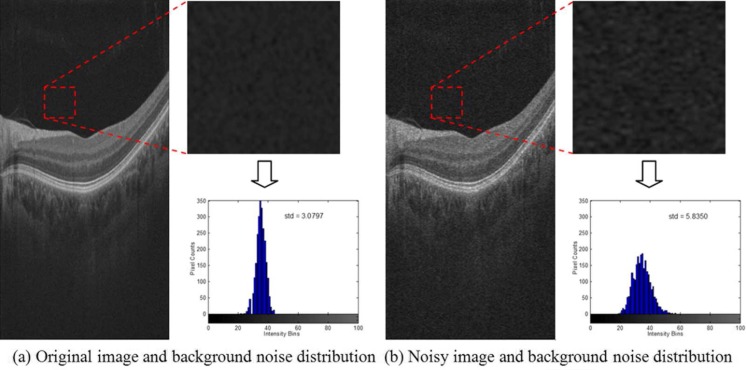
Figure 3 demonstrates the generation of the synthetic noise OCT images using the noise signal acquired from the Cirrus OCT system, where Fig. 3a shows a downsampled high-resolution OCT retinal image (left) taken as the virtually “noise-free” image, and a detail and histogram (right) of the background region indicated by the dashed red square. Figure 3b is the synthetic noisy image generated by computationally adding the signal-dependent background noise from the Cirrus OCT hardware into the noise-free image. The standard deviation (std) of the background noise in the noisy image is obviously higher than that in the original image.

Fig. 3.

Generation of a synthetic noisy OCT image. a Displays a downsampled high-resolution image. The dashed red square indicates an area identified as mainly background and the histogram of such area is also displayed. b Result of adding synthetic noise obtained from Cirrus OCT hardware to the image displayed in (a)

Experimental Studies to Evaluate Methods

The experiments were performed on a 2.83-GHz Pentium 4 PC with 3.37 GB memory. Each denoising method was implemented in Matlab and run on the same machine. The time required to run each algorithm was recorded.

For a qualitative evaluation, ten images were rated qualitatively by one of the authors, who is an ophthalmologist with more than 10 years’ experiences on ophthalmic image analysis, evaluating the clarity and sharpness of the retinal layers. The images were rated by assigning grades from 1 to 3, with lower grades indicating higher denoising performance. We also computed the method noise (the image difference between the original image and the denoised image [22]) for each denoising method as to evaluate the impact of the method on the preservation of the image structure information. An optimal denoising method should produce a method noise containing as little structure information as possible, such as shape edges.

Since a gradient of the OCT images is commonly generated from a large number of OCT image processing applications (like retinal layer segmentation techniques), we also evaluated the impact of the different denoising methods on the image gradient. The gradient images of the denoised results from each method were evaluated by the expert qualitatively in terms of regularity. The common qualitative rule is that the more dominant the gradient information in image boundaries is over the homogeneous regions (such as background), the better a denoised method can effectively remove noise and preserve edges.

In order to quantitatively measure the denoising performance with full reference metrics, synthetic noise OCT images were generated by computationally corrupting virtually noiseless clinical images using a known amount of noise. We obtained images of background noise from a commercial SD-OCT device (i.e., CirrusOCT) in order to characterize the expected noise, which was later employed to computationally alter averaged HD clinical B-scans in a signal-dependent manner (as expected with noise in SD-OCT systems [3–9]). The effect of corrupting the averaged HD clinical images with a more general simulated speckle noise was also investigated. Four metrics: peak signal-to-noise ratio (PSNR), mean structural similarity (MSSIM) [33], mean-to-standard deviation ratio (MSR) [34] and contrast-to-noise ratio (CNR) [35], were adopted to quantitatively evaluate the results.

The PSNR is a popular quantitative measurement for image denoising performance, which is computed according to the standard formula

$$\mathrm{PSNR}=10{log}_{10}\frac{max{\left(u_0\left(x,y\right)\right)}^2}{\mathrm{M}\mathrm{S}\mathrm{E}}$$ 3

where $\mathrm{M}\mathrm{S}\mathrm{E}=\frac{{\displaystyle {\sum }_{\left(x,y\right)\in \Omega }{\left(u_0\left(x,y\right)-u\left(x,y\right)\right)}^2}}{\left|\Omega \right|}$, u₀(x, y) is the noise-free original image at location (x, y),“max” indicates its maximum value and u(x, y) is the noise-present image at location (x, y).

The MSSIM is effective to evaluate the structure similarity, and is defined as

$$\mathrm{MSSIM}\left(u_0,u\right)=\frac{1}{M}{\displaystyle \sum _{j=1}^M\mathrm{SSIM}\left(u_0^j,u^j\right)}$$ 4

where u^j₀ and u^j are the image contents at the jth local window, and M is the number of local windows of the image. The structural similarity (SSIM) is defined by SSIM(u₀, u) = $\frac{\left(2{\mu }_{u_0}{\mu }_u+C_1\right)\left(2{\sigma }_{u_{0}u}+C_2\right)}{\left({\mu }_{u_0}^2+{\mu }_u^2+C_1\right)\left({\sigma }_{u_0}^2+{\sigma }_u^2+C_2\right)}$, where ${\mu }_{u_0}$ and μ_u are the mean intensity of u₀ and u, respectively; ${\sigma }_{u_0}$ and σ_u are the standard deviation; the correlation coefficient ${\sigma }_{u_{0}u}$ corresponds to the cosine of the angle between the vectors $u_0-{\mu }_{u_0}$ and u − μ_u; C₁ and C₂ are two constants. For the detailed interpretation of SSIM, the reader can refer to [33].

The MSR and CNR are defined as follows:

$$\mathrm{M}\mathrm{S}\mathrm{R}=\frac{{\mu }_f}{{\sigma }_f}$$ 5

$$\mathrm{C}\mathrm{N}\mathrm{R}=\frac{\left|{\mu }_f-{\mu }_b\right|}{\sqrt{0.5\cdot \left({\sigma }_f^2+{\sigma }_b^2\right)}}$$ 6

where μ_b and σ_b are the mean and the standard deviation of the background region (e.g., red box in Fig. 8a), while μ_f and σ_f are the mean and the standard deviation of the foreground regions (e.g., green boxes in Fig. 8a).

Results

Our proposed denoising method was compared with nine existing spatial image denoising methods representative of those used for processing OCT images (Table 1), including one classic method, five PDE-based methods and three patch-based methods. The basic idea of the point-based methods is to construct similarity weight based on point intensity and position. PDE-based methods construct diffusion coefficients of PDE functions based on image gradient and texture. Patch-based methods construct similarity weight based on structure or homogeneity similarity of image patches. Although recent work on the MSBTD method has shown some of its advantages [19], due to its high time demands and complicated parameter tuning, it was not included in the evaluation. MSBTD is listed in Table 1 so as to present a more comprehensive list.

Table 1.

Representative spatial denoising methods

Category	Point-based methods	PDE-based methods	Patch-based methods
Representative methods	Bilateral filtering [19]	PM model [16], complex diffusion filter [17], Ramp preserving Perona-Malik (RPPM) model [21], Rudin-Osher-Fatemi (ROF) model [22], and Adaptive total variation (ATV) model [20]	Non local means (NL-means) method [23], HS based method [13], and block matching and 3D filtering (BM3Da) [24]
Approach	Point similarity weight construction	Diffusion coefficient construction	Patch similarity weight construction

^a http://www.cs.tut.fi/~foi/GCF-BM3D/

Each of these methods produces different denoising results depending on the values of various parameters. Identifying the most suitable method for a particular application in OCT imaging (e.g., image segmentation) would require extensive tuning of each of the parameters to obtain the best achievable performance from each denoising method. Rather, our goal was to assess the performance of our proposed homogeneity similarity method based on qualitative measurements that result comparable to the other methods. Specifically, we adjusted the denoising parameters of each method such that the homogeneity of the background in the resulting images was similar. We assumed that the background in noise-free images should be completely homogeneous, so a similar standard deviation in the resulting denoised background, such as the red dashed region in Fig. 4a, was used to adjust the parameters of each method so as to produce a similar degree of denoising. This common point of the same standard deviation of the background pixels was not intended to optimize each particular denoising technique, but rather to establish a common point for a qualitative comparison of the resulting images.

Fig. 4.

Denoising results obtained from different methods in a sample B-scan of a real OCT retinal image. a Original B-scan. The dashed red square indicates an example location identified as background and used to adjust the denoising methods to produce similar results in terms of standard deviation measured in background pixels. b to k Results obtained from the different denoised methods investigated

Qualitative Evaluation

Table 2 is the summary of the qualitative results of ten clinical images, where the grades are assigned from 1 to 3 based on the quality and sharpness of the retinal layers, with lower grades indicating higher performance of the denoising method. Table 2 indicates that the HS method, BM3D, and the proposed method consistently have the highest qualitative grade in all the images tested.

Table 2.

Grades of ten clinical images

Method	Bilateral filtering	PM model	RPPM model	TV model	ATV model	Complex diffusion	NL-means	HS method	BM3D	Proposed method
Image 1	2	3	3	3	3	3	2	1	1	1
Image 2	2	3	3	3	3	3	2	1	1	1
Image 3	2	3	3	3	3	3	2	1	1	1
Image 4	2	3	3	3	3	3	2	1	1	1
Image 5	2	3	3	3	3	3	2	1	1	1
Image 6	2	3	3	3	3	3	2	1	1	1
Image 7	2	3	3	3	3	3	2	1	1	1
Image 8	2	3	3	3	3	3	2	1	1	1
Image 9	2	3	3	3	3	3	2	1	1	1
Image 10	2	3	3	3	3	3	2	1	1	1

1 excellent; 2 ok, but not perfect; 3 blurry

Figure 4 shows an example of the denoising results. Figure 4a is the original OCT retinal image, where the red dashed region represents the part of the background region used to establish a common standard deviation of the resulting image pixel values as to adjust the parameters of each denoising method. Qualitatively, the patch-based image denoising methods, NL-means (Fig. 4h), BM3D (Fig. 4i), HS method (Fig. 4j), and the proposed method (Fig. 4k), yielded better results based on the expert quality ratings in terms of edge and detail preservation.

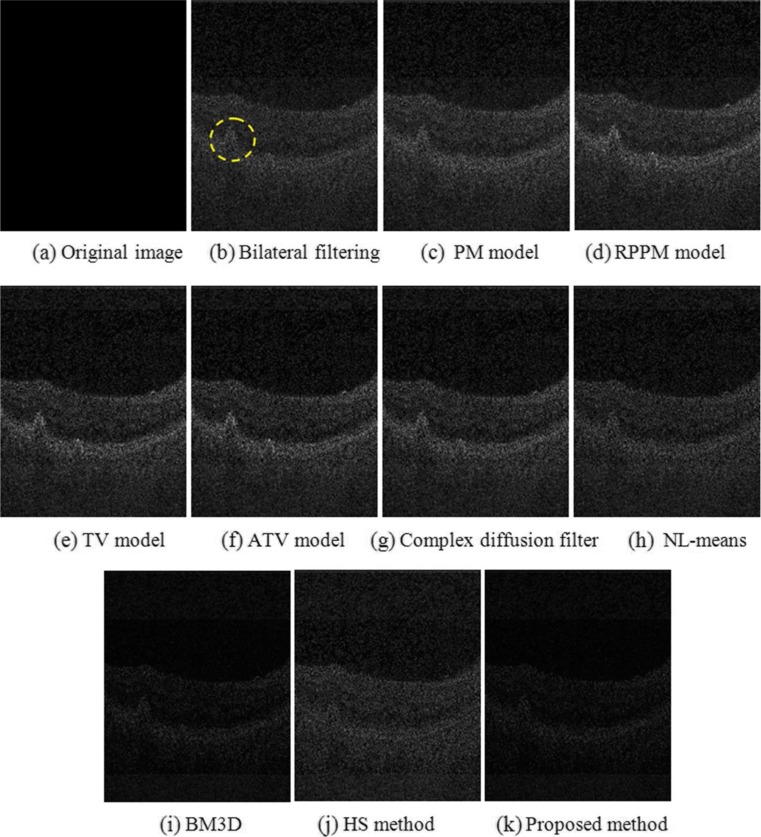
Figure 5 shows the method noise of each of the denoising results from Fig. 4. The structure signal in Fig. 5h to k seems weaker than that in Fig. 5b to g, such as the edges in the large drusen marked with the yellow dashed circle in Fig. 5b.

Fig. 5.

Method noise (magnified ×2) obtained from the denoising of the same example B-scan as in Fig. 4. a Computed from original B-scan (appears blank since there is no noise removal). b to k Results obtained from the different denoised methods investigated. The dashed yellow ellipse in b indicates an extructure of interest in the retina

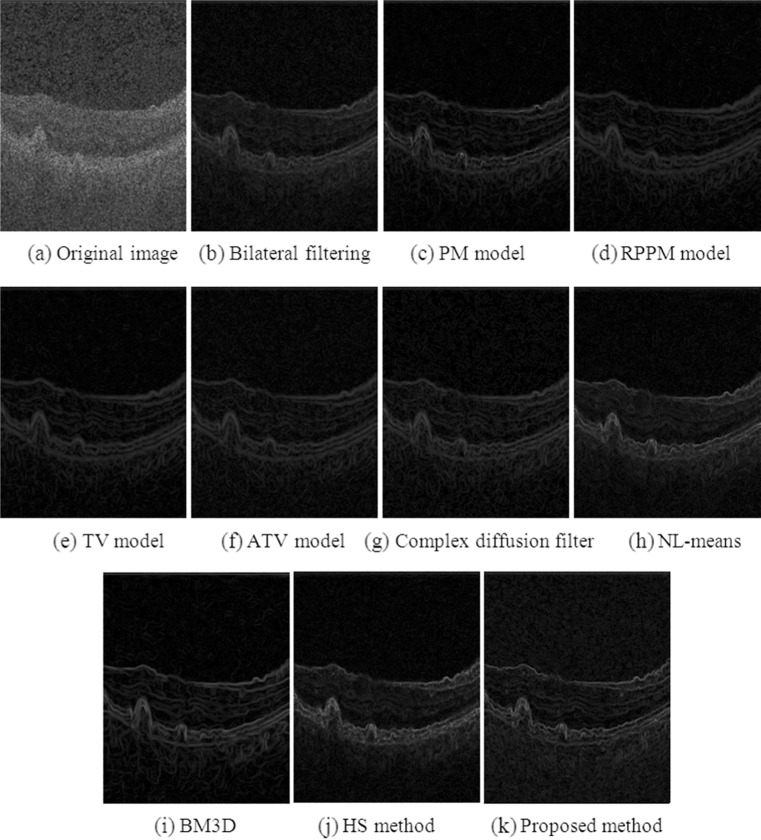
Figure 6 shows the gradient images of Fig. 4. The gradient strength of objects in Fig. 6h to k was observed to be higher than that in Fig. 6b to g, which indicates that patch-based methods are better for edge preservation in retinal OCT imaging.

Fig. 6.

Gradient (magnified ×4) computed from the denoising of the same example B-scan as in Fig. 4. a Computed from original B-scan. b to k Results obtained from the different denoised methods investigated

Quantitative Evaluation in Synthetic Noise OCT Images

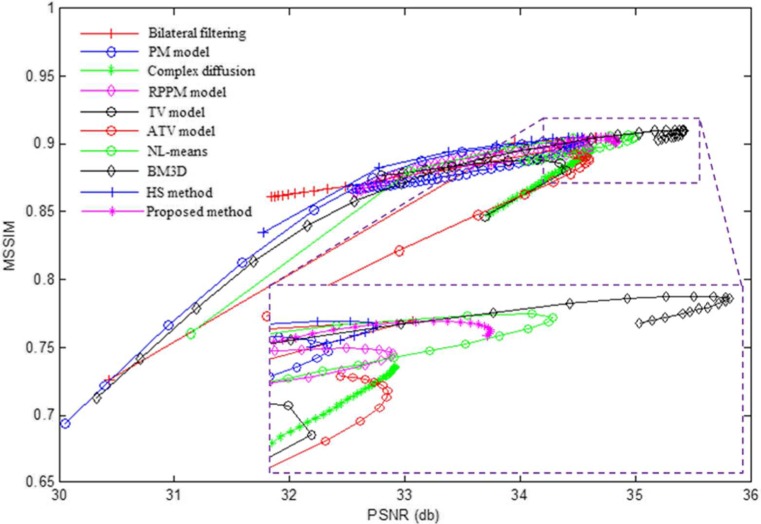
We compared the performance of each denoising method using the PSNR, MSSIM, MSR, and CNR as quantitative measurements. Each particular method produces different results as we vary their global parameters. Parameters producing results with higher PSNR may indicate better overall noise reduction but this may also be accompanied with loss of edge intensity and structure information, and a lower MSSIM. We tuned each of the investigated denoising methods by varying their global parameters and measured the resulting mean PSNR and MSSIM for each set of parameters. The results obtained from this tuning process for the images corrupted by noise from the Cirrus OCT system are shown in Fig. 7. The resulting values of PSNR and MSSIM for each input parameter set are plotted for each method, producing a curve characterizing each method performance at different input settings. Higher values of both PSNR and MSSIM indicate increased denoising performance so a curve with values closer to the top right corner of the graph indicates better results. Table 3 summarizes the parameters of these methods corresponding to maximum PSNR values.

Fig. 7.

PSNR and MSSIM results obtained from tuning the global parameters for each denoising method. A detail of the peak in PSNR is shown in the box

Table 3.

Parameters for denoising methods

Method	Bilateral filtering [20]	PM model [17]	RPPM model [21]	TV model [23]	ATV model [14]
Parameters	σ s = 3, σ i = 0.06	k = 0.023	τ = 19, λ = 1	λ = 0	k = 0.1
Method	Complex diffusion [18]	NL-means [24]	HS method [22]	BM3D [25]	Proposed method
Parameters	k = 0.0136	h = 0.0021	t = 0.002	k = 17	t = 0.00071

Remark: σ _s and σ _i represent the standard deviations of the spatial-domain and the intensity-domain, respectively. The parameter h in NL-means denotes the degree of filtering. For a detailed explanation of the parameters employed in each method we refer to their indicated references

The turning point of maximum PSNR was chosen to quantitatively compare the performance of each of the denoising methods. That is, the global control parameters of each method were tuned to maximize the resulting PSNR value. We observe that the patch-based methods (BM3D, NL-means, the proposed method, and HS method) acquire the better results in terms of PSNR and MSSIM than the point-based methods, and our proposed method seems to produce a substantial improvement over the HS method. Tables 4 and 5 show the average and variance of PSNR and MSSIM of the ten test images when the methods are tuned to produce maximum PSNR for the set of images corrupted by noise for the Cirrus system and a system-independent simulated speckle, respectively.

Table 4.

Average and variance of peak signal-to-noise ratio (PSNR) (unit: db) and mean structural similarity (MSSIM) of ten test images corrupted by Cirrus system noise. The MSSIM is between 0 and 1 with a score of 1 being given only if the denoised image is exactly equivalent to the original image

Method		Noisy image	Bilateral filtering	PM model	RPPM model	TV model	ATV model
PSNR	Average	30.43	33.73	33.54	33.67	33.72	33.93
	Variance	0.13	0.34	0.82	0.87	0.83	0.61
MSSIM	Average	0.73	0.86	0.83	0.84	0.84	0.85
	Variance (×10−4)	4.3	8.7	26.7	23.4	10.8	7.0
Method		Complex diffusion	NL-means	HS method	BM3D	Proposed method
PSNR	Average	33.90	33.95	33.70	34.27	33.72
	Variance	0.70	0.79	0.63	1.29	1.32
MSSIM	average	0.85	0.84	0.84	0.84	0.83
	Variance (×10−4)	10.7	22.8	22.4	29.7	31.0

Table 5.

Average and variance of peak signal-to-noise ratio (PSNR) (unit: db) and mean structural similarity (MSSIM) of ten test images corrupted by simulated speckle. The MSSIM is between 0 and 1 with a score of 1 being given only if the denoised image is exactly equivalent to the original image

Method		Noisy image	Bilateral filtering	PM model	RPPM model	TV model	ATV model
PSNR	Average	30.43	34.13	34.49	34.84	35.05	35.28
	Variance	0.13	0.35	0.96	1.0	1.41	0.65
MSSIM	average	0.71	0.87	0.85	0.86	0.86	0.87
	Variance (×10−4)	5.0	7.9	23.7	20.1	11.6	4.0
Method		Complex diffusion	NL-means	HS method	BM3D	Proposed method
PSNR	Average	35.11	35.18	34.56	35.44	34.20
	Variance	1.24	1.04	0.82	1.61	1.67
MSSIM	average	0.87	0.87	0.85	0.86	0.83
	Variance (×10−4)	12.3	17.3	19.3	26.3	31.0

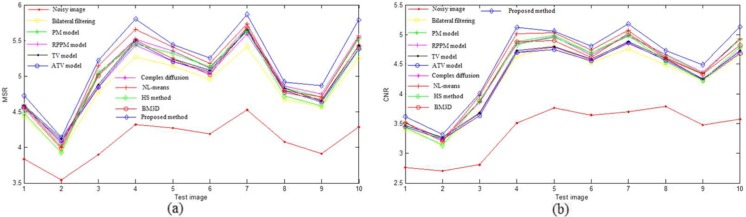
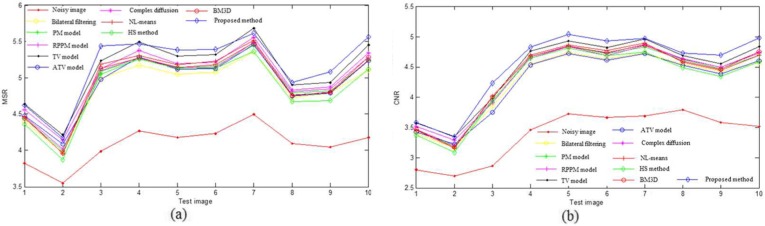
In the PSNR and MSSIM metrics, the original image should be a noise-free image, while there still exists slight noise in the downsampled high-resolution B-scans. In addition, for the proposed method, the improved homogeneity similarity-based method is only used in the retinal layer region from the RNFL layer to the upper choroid layer. Thus, two regions of interest (ROI)-based metrics, MSR and CNR, were also used to quantitatively evaluate the denoising performance. Figure 8 shows one example of a synthetic noisy OCT retinal image, where the background and foreground regions are selected randomly and marked with the dashed red and green boxes, respectively. Tables 6 and 7 show the average and variance of MSR and CNR of the ten test images for the set of images corrupted by noise for the Cirrus system and a system-independent simulated speckle, respectively. Figures 9 and 10 are the MSR and CNR comparison for ten test images corrupted by Cirrus system noise and simulated speckle, respectively. Table 8 shows the average denoising time.

Table 6.

Average and variance of the MSR and CNR results for ten test images corrupted by Cirrus system noise

Method		Noisy image	Bilateral filtering	PM model	RPPM model	TV model	ATV model
MSR	Average	4.13	4.91	5.10	5.12	5.06	5.03
	Variance	0.29	0.46	0.51	0.51	0.48	0.47
CNR	Average	3.37	4.23	4.41	4.40	4.30	4.26
	Variance	0.44	0.60	0.64	0.64	0.60	0.60
Method		Complex diffusion	NL-means	HS method	BM3D	Proposed method
MSR	Average	5.02	5.14	5.03	5.05	5.27
	Variance	0.47	0.55	0.53	0.51	0.55
CNR	average	4.28	4.44	4.35	4.38	4.54
	Variance	0.60	0.67	0.66	0.64	0.67

Table 7.

Average and variance of the MSR and CNR results for ten test images corrupted by simulated speckle

Method		Noisy image	Bilateral filtering	PM model	RPPM model	TV model	ATV model
MSR	Average	4.09	4.84	5.03	5.05	5.00	4.97
	Variance	0.26	0.41	0.44	0.44	0.44	0.41
CNR	average	3.38	4.26	4.34	4.35	4.44	4.25
	Variance	0.42	0.58	0.60	0.60	0.59	0.56
Method		Complex diffusion	NL-means	HS method	BM3D	Proposed method
MSR	Average	4.95	5.07	4.97	4.98	5.20
	Variance	0.43	0.47	0.47	0.46	0.47
CNR	average	4.37	4.35	4.27	4.35	4.53
	Variance	0.58	0.61	0.61	0.60	0.61

Fig. 9.

MSR (a) and CNR (b) comparison of different denoising methods for ten test images corrupted by Cirrus system noise

Fig. 10.

MSR (a) and CNR (b) comparison of different denoising methods for ten test images corrupted by simulated speckle

Table 8.

Average denoising time of ten test images

Method (number of iteration)	Bilateral filtering (1)	PM model (20)	RPPM model (8)	TV model (2)	ATV model (6)	Complex diffusion (5)	NL- means (1)	HS method (1)	Proposed method (1)
Time (s)	2.75	0.63	0.28	0.06	0.25	0.19	134.26	138.45	41.10

Discussion

Based on the OCT imaging characteristics and the clinical diagnosis importance, two improvements of the proposed method are given: (1) median filtering preprocessing is used to make the noise distribution of OCT images more suitable for patch-based methods; (2) rectangle neighborhood and region restricted denoising methods are adopted to accommodate the horizontal stretching of retinal structures when observed in OCT images, and given the fact that most of the effective information related to retinal diseases is located in retina and choroid regions.

The object edges in Fig. 4b to g are blurred because they are based on intensity similarity (such as bilateral filtering) or gradient information (such as the PM model) of each pixel, which cannot effectively preserve weak edges. Using a local region can better represent structure information than using a single pixel, so the patch-based methods can preserve the weak edges of the retinal layers better. From Fig. 5, it can be seen that the patch-based methods (Fig. 5h to k) appear better qualitatively than point similarity-based methods (Fig. 5b to g) in terms of structure preservation. The retinal layers in the gradient images after each denoising technique (Fig. 6b to k) appear more regular than that in the original image, which facilitates subsequent image processing, such as layer segmentation and drusen detection. Although the patch-based methods can achieve more effective denoising results than the point-based methods, their processing time required is much higher (Table 8). For example, the time required to process the image shown in Fig. 4 was in the order of hundreds of seconds with the patch-based methods, while it was in the order of seconds with the other methods.

Figure 4j to k indicates that the proposed modified HS method results are better qualitatively for noise removal and structure information preservation in retinal OCT imaging than the original HS method. From Fig. 6j to k, we can observe that the gradient of the retinal layers are more regular in our result than in the result with the HS method.

Tables 4 and 5 demonstrate that the BM3D, ATV model, and NL-means have a relatively higher PSNR and MSSIM than other methods. From Fig. 8, it can be seen that the patch-based methods (i-l) can obtain a better visual performance. Tables 6 and 7 and Figs. 9 and 10 indicate that the proposed method has the highest average MSR and CNR for the images corrupted by Cirrus system noise and simulated speckle, and can achieve the highest MSR and CNR for most noisy images.

The times of patch-based methods were longer than those of the others. Compared with the homogeneity similarity-based method, the time of the proposed method was reduced obviously. Therefore, the proposed method has a relatively good performance by considering the denoising effect and time.

Conclusions

This paper presents the application of a modified homogeneity similarity-based image denoising technique in retinal OCT images. The original homogeneity similarity method was modified in the following two respects for a better adaptation to the imaging technique: (1) median filtering is used as a preprocessing step to make the noise closer to Gaussian distribution; (2) after the retinal OCT B-scans are flattened based on RPE layers, the neighborhood shape of the search window is changed from a square to a rectangular region to find more similar pixels following the shape of the retinal layers. In addition, a combination of methods (HS method and bilateral filtering) is adopted in the flattened images to reduce the denoising time. Nine spatial denoising methods (bilateral filtering, five PDE-based methods, and three patch-based methods) were qualitatively and quantitatively compared with the proposed method for OCT retinal image denoising in order to assess the performance of the proposed technique. Experimental results demonstrate that the proposed method produced results with quality on par with the best results from the other methods, and that in general, patch-based methods are better in terms of image information preservation than point-based methods for OCT retinal imaging applications. However, patch-based methods are more time-consuming computationally than that for the other methods.