DTI template-based estimation of cardiac fiber orientations from 3D ultrasound

Abstract

Purpose:

Cardiac muscle fibers directly affect the mechanical, physiological, and pathological properties of the heart. Patient-specific quantification of cardiac fiber orientations is an important but difficult problem in cardiac imaging research. In this study, the authors proposed a cardiac fiber orientation estimation method based on three-dimensional (3D) ultrasound images and a cardiac fiber template that was obtained from magnetic resonance diffusion tensor imaging (DTI).

Methods:

A DTI template-based framework was developed to estimate cardiac fiber orientations from 3D ultrasound images using an animal model. It estimated the cardiac fiber orientations of the target heart by deforming the fiber orientations of the template heart, based on the deformation field of the registration between the ultrasound geometry of the target heart and the MRI geometry of the template heart. In the experiments, the animal hearts were imaged by high-frequency ultrasound, T1-weighted MRI, and high-resolution DTI.

Results:

The proposed method was evaluated by four different parameters: Dice similarity coefficient (DSC), target errors, acute angle error (AAE), and inclination angle error (IAE). Its ability of estimating cardiac fiber orientations was first validated by a public database. Then, the performance of the proposed method on 3D ultrasound data was evaluated by an acquired database. Their average values were 95.4% ± 2.0% for the DSC of geometric registrations, 21.0° ± 0.76° for AAE, and 19.4° ± 1.2° for IAE of fiber orientation estimations. Furthermore, the feasibility of this framework was also performed on 3D ultrasound images of a beating heart.

Conclusions:

The proposed framework demonstrated the feasibility of using 3D ultrasound imaging to estimate cardiac fiber orientation of in vivo beating hearts and its further improvements could contribute to understanding the dynamic mechanism of the beating heart and has the potential to help diagnosis and therapy of heart disease.

1. INTRODUCTION

Heart disease is the leading cause of death in the United States.¹ During the heart beating period, the cardiac fiber orientation plays an important role in determining both electrical propagation and stress distribution within the cardiac walls.² Abnormal cardiac fiber orientations directly affect the heart functions such as ejection fraction, or even cause sudden death in arrhythmia.^3,4 Therefore, estimating the patient’s personalized cardiac fiber orientations can help not only in understanding the cardiac pathology but also in the diagnosis and treatment of cardiovascular diseases, especially those with cardiac remodeling such as cardiac ischemia, ventricular hypertrophies, and heart failures.

Although cardiac fiber orientations are important in understanding heart physiology and pathology, the determination of cardiac fiber orientations is still difficult. It is a challenging task to image and quantify fiber orientations in the heart.⁵

Early efforts were made to directly measure the fiber orientations from histology slices of ex vivo hearts.^6,7 Manual operation and significant time were required for the process. Furthermore, the accuracy could not be guaranteed because of tissue deformations. Meanwhile, magnetic resonance diffusion tensor imaging (DTI) was introduced to estimate the fiber orientations of hearts because of its ability to measure the anisotropic diffusion of water in biological tissues.^8–12 The main advantage of DTI is that it can image three-dimensional (3D) fiber orientations at high resolutions. Unfortunately, DTI can be time consuming and can have severe motion artifacts during in vivo cardiac imaging. Consequently, these problems limit its application in the clinic. Recently, Lee et al. applied an ultrasound shear wave imaging method to this area. Their estimated fiber orientations were correlated with histological findings and with DTI results.^13,14 This procedure still needs to be improved in order to map accurate 3D orientations to the whole heart.

Comparing with those direct imaging methods, rule-based methods were proposed by estimating personalized cardiac fiber orientations from cardiac models,^12,15–17 but highly accurate models still need to be developed. Recently, a new procedure was proposed to estimate the whole cardiac fiber architecture by shape-based transformations from sparsely acquired in vivo DTI images.¹⁸ Meanwhile, another pipeline based on geometry registrations was developed to estimate the patient-specific cardiac fiber orientations from ex vivo DTI cardiac fiber template¹⁹ and was applied to ischemic simulations.²⁰ The approach was based on the hypothesis that fiber orientation similarities between two hearts could be estimated from their geometric similarities. Helm et al. utilized the large deformation diffeomorphic metric mapping (LDDMM) algorithm to register the cardiac fiber orientation and geometry from DTI data and the method was validated by histological findings.²¹ Later, Sundar et al. proposed the idea of mapping the diffusion tensor of the template onto patient-specific cardiac geometry using an elastic registration.²² Zhang et al. provided an atlas-based geometry pipeline that could deform diffusion tensor data to patient geometries using the Demons registration method and that could also reconstruct the cardiac Hermite model.²³ Lately, Vadakkumpadan et al. applied this hypothesis to estimate the patient-specific ventricular fiber orientations from in vivo CT images.¹⁹ They also found that the errors of this method slightly impacted the electricity simulations.

The main focus to date has been on estimating personalized cardiac fiber orientations from MRI and CT modalities; less attention has been paid to ultrasound imaging. Only a few efforts were made on investigating the relationships between the myocardium anisotropy and ultrasound characteristics of heart tissue.^24–27 However, cardiac ultrasound has become one of the most widely utilized modality in cardiac imaging, because it is a noninvasive, cost-effective, versatile imaging modality without ionizing radiation while providing real-time imaging and comprehensive clinical information.²⁸ Moreover, when compared with MR or CT, the superior temporal resolution of ultrasound could be advantageous to patients with arrhythmias or respiratory difficulties. Estimating fiber orientation from cardiac ultrasound, especially from 3D image volumes, will not only extend the ultrasound applications but also benefit cardiac diagnosis and therapies. Previously, we mapped cardiac fiber orientations from DTI to 3D ultrasound volume, but the DTI data were still acquired from the same target heart rather than from an existed template and only registration errors were evaluated.²⁹

Therefore, this paper provided a DTI template-based framework to estimate the personalized cardiac fiber orientations from 3D ultrasound. It estimated the cardiac fiber orientations of the target heart by deforming the fiber orientations of the template heart, based on the deformation field of the registration between the ultrasound geometry of the target heart and the MRI geometry of the template heart. Its accuracies of performed registrations and fiber orientations were evaluated by high-resolution ultrasound, T1-weighted MRI, and DTI images of animal hearts ex vivo. Moreover, its feasibility was also tested using the 3D ultrasound data of a rat heart in vivo.

This paper is organized as following: Sec. 2 describes the method for data acquisitions, fiber orientation estimation and its evaluations; Sec. 3 describes the validation results; discussions and conclusions are described in Secs. 4 and 5, respectively.

2. METHODS

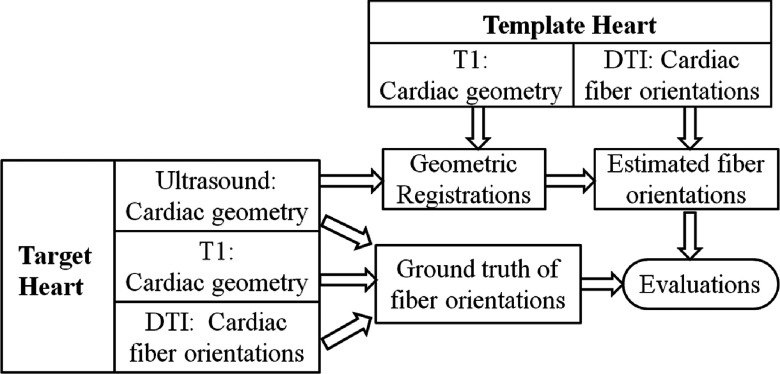
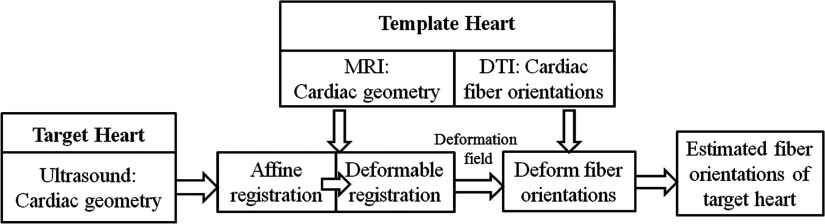
In this framework, the geometry of the target heart is from ultrasound images, and the fiber orientations and geometry of the template heart are from DTI and T1-weighted MR images, respectively. The target and template hearts are from different subjects. The whole flowchart including fiber orientation estimations and its validations is illustrated in Fig. 1. First, the geometry of the template heart from the T1 MR images is registered to the geometry of the target heart from ultrasound images, and a deformation field between both geometries is generated. Then, based on this deformation field, the DTI fiber orientations of the template heart are relocated and reoriented as the estimated fiber orientations of the target heart. Finally, the estimated fiber orientations are evaluated by the ground truth of the target heart, which comes from fiber orientation as measured by the DTI images of the target heart.

FIG. 1.

Illustration of validating the cardiac fiber orientations estimated from ultrasound geometry.

2.A. Data acquisition

The hearts of three male Sprague Dawley rats were excised and then quickly perfused by 4 °C 1 × PBS to achieve diastolic arrest and also to clean the residual blood in the heart pools and vessels. The hearts (20 mm in length and 15 mm in maximum diameter) were then fixed using 4% phosphate buffered paraformaldehyde (PFA) solution for 14 h and were then embedded in 2% agar with cubic shapes for the following imaging procedures.

First, the heart phantoms were imaged by ultrasound. They were settled on the imaging platform and were imaged by the Vevo 2100 ultrasound system (FUJIFILM VisualSonics, Inc., Toronto, Canada) with a 30 MHz transducer. B-mode ultrasound images of the hearts in the short-axis view were acquired from apex to base, slice by slice, at a 0.2 mm thickness interval in a FOV of 15.4 × 18 × 20 mm³.

After ultrasound imaging, the heart phantoms including the fixed hearts were kept in glass tubes and immediately placed in a high-field Biospec 7 T MRI system (Bruker Corporation, MA). A RF coil with an inner diameter of 30 mm was used to transmit/receive the signals. Before DTI, T1-weighted anatomical images were acquired at a voxel resolution of 0.078 × 0.078 × 0.156 mm³. Then, the cardiac fiber orientations were imaged in 30 directions by the spin echo sequences at a 0.234 mm isotropic resolution in a FOV of 30 × 30 × 20 mm³. Each slice was also imaged in the short-axis view from the ventricular apex to the base. Then, each heart was imaged three times for DTI; total MR imaging time was 50 h. After DTI data acquisitions, corresponding diffusion tensors from the three DTI volumes were motion corrected and averaged as one volume for the following analysis.

For in vivo 3D ultrasound imaging experiment, a rat was settled on an imaging platform and its beating heart was imaged in vivo using the same ultrasound imaging system with a 21 MHz transducer. B-mode ultrasound images of the hearts in the short-axis view were acquired slice by slice from base to apex at a 0.2 mm thickness. Each slice position was dynamically imaged as a serial of beating cycles and the pixel size in the B-mode image was 0.06 mm. During the image acquisition, both ECG and respiration signals were recorded. The 3D ultrasound images in the diastole phase were selected based on both ECG and respiration signals. After in vivo ultrasound imaging, the animal was scarified and the fiber orientations of the heart were also imaged by high-resolution DTI.

2.B. Data processing

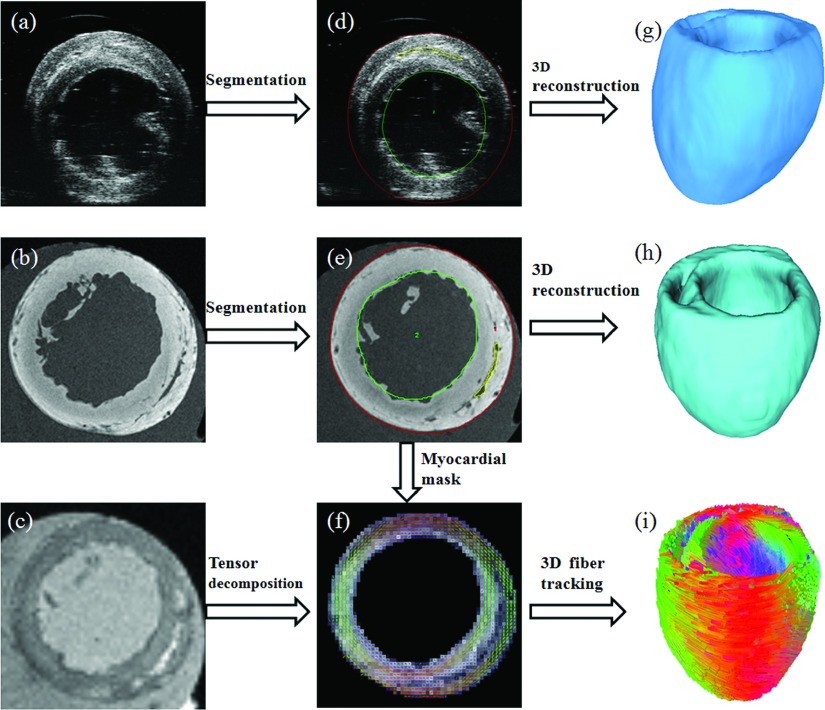
According to the cardiac fiber estimation procedure, the accuracy of the geometry and fiber orientation reconstructions will directly affect the results. Thus, highly accurate geometric segmentation and fiber orientation reconstruction are required, shown in Fig. 2.

FIG. 2.

Processing of cardiac imaging data. (a) 3D ultrasound image. (b) T1-weighted MR image. (c) DTI data. [(d) and (e)] Geometric segmentation results. (f) Tensor decomposition of DTI data based on the segmentation mask from T1-weighted MRI. [(g) and (h)] Reconstructed 3D geometric volumes. (i) Tracked 3D cardiac fibers.

In order to improve accuracy, the myocardium in both T1-weighted MRI and ultrasound images was segmented slice by slice using the Analyze software (AnalyzeDirect, Inc., Overland Park). In each short-axis slice, the myocardium was segmented by the closed splines interpolated from the landmark points, which were semiautomatically placed along both endocardium and epicardium. Then, the 3D binary geometric volume of each heart was reconstructed from MRI and ultrasound images, respectively. Based on the segmented cardiac masks from T1-weighted MRI, the myocardium regions in DTI data were also segmented by mapping the segmented masks from T1-weighted MR images, because the hearts were kept stable during both DTI and T1-weighted MR imaging. After that, the cardiac fiber orientations were reconstructed from DTI data using principle eigenvectors as the fiber directions, which corresponded to each voxel in geometric volumes. Finally, these cardiac fibers were tracked using a determinative method of fractional anisotropy³⁰ and were then visualized in 3D using the DSI studio.³¹

2.C. Cardiac fiber orientation estimation from ultrasound geometry

There are two steps to estimate cardiac fiber orientations from ultrasound geometries: the first is to generate the deformation field between the ultrasound geometry of the target heart and the geometry of the template heart from T1-weighted MRI; the second is to relocate and reorient DTI fiber orientations of the template heart to the target heart as the final results based on the deformation field. Figure 3 illustrates this procedure.

FIG. 3.

Flowchart of deforming cardiac fiber orientations based on the geometric registrations between ultrasound and MRI.

2.C.1. Template geometric registration

During the geometry registration step, the template geometry is first registered to target geometry by supervised affine transformations (translation, rotation, shear, and scaling) using the Analyze software. After that, a deformable registration is utilized to acquire the final results. For this step, diffeomorphic transformation is one of the requirements to deform cardiac geometries. Moreover, the invertible transformation is also needed for the registration of DTI, because the tensor reorientations are usually derived from the corresponding spatial transformations.³² Due to these requirements, LDDMM was proposed and applied in nonrigid registrations of cardiac geometrics and DTI mapping.³³ In order to register different hearts as one statistical template, Peyrat et al. used a hybrid intensity based registration method by combining thin-plate splines and a diffeomorphic registration algorithm.³⁴ Here, we prefer to utilize the diffeomorphic Demons (DD),³² which is not only diffeomorphic for deformable registration but also computationally efficient. Moreover, Demons was tested to be suitable for binary image registrations.³⁵

In order to match two images I₀ and I₁ by a transformation s, the typical Demons registration requires a similarity criterion Sim(I₀, I₁, S) to measure the similarity between both images and also a regularization energy Reg(s) to evaluate their transformation likelihood. They are defined as follows:

$${\displaystyle E\left(s\right)=\frac{1}{{\sigma }_i^2}\text{Sim}\left(I_0,I_1,S\right)+\frac{1}{{\sigma }_T^2}\text{Reg}\left(S\right),}$$ (1)

where σ_i relates to the noise of the image and σ_T weighs the regularization effect. However, traditional Demons usually cannot supply the diffeomorphic transformations which are necessary for maintaining the topology of the cardiac anatomical structures and the invertible deformation field for fiber reorientations of DTI data. Thus, Vercauteren et al. adapted the Demons as an optimization procedure on the entire space of displacement fields to a space of diffeomorphic transformations through the exponential. The modified energy function is described as follows:

$${\displaystyle E_{\text{diffeo}}\left(I_o,I_1,s,u\right)=\text{Sim}\left(I_o,I_1,s\circ exp\left(u\right)\right)+{‖u‖}^2,}$$ (2)

where u is the velocity field and $‖u‖$ is its norm. Its exponential $exp\left(u\right)$ is a time stationary ordinary differential equation (ODE): $\partial p\left(t\right)/\partial t=u\left(t\right)$ and p is the image position. Then, the transformation s is updated by $exp\left(u\right)$ as the form of $s°exp\left(u\right)$. Based on this improvement, the registration method can provide both efficient computations and invertible transformations between two geometries.

2.C.2. Template fiber orientation deformation

After that, based on the deformation fields generated by the geometric registrations, the fibers from DTI are first relocated to the corresponding geometric locations and then reoriented as the estimated fiber orientations of the target heart. Each voxel containing fiber orientation of the template heart is first relocated to the geometry of the target heart from 3D ultrasound following the deformation. Then, based on the same deformation fields, each fiber orientation is reoriented by the strategy of preservation of principal directions (PPD),³⁶ which has been utilized in the similar cardiac fiber orientation estimations.¹⁹

2.D. Evaluations

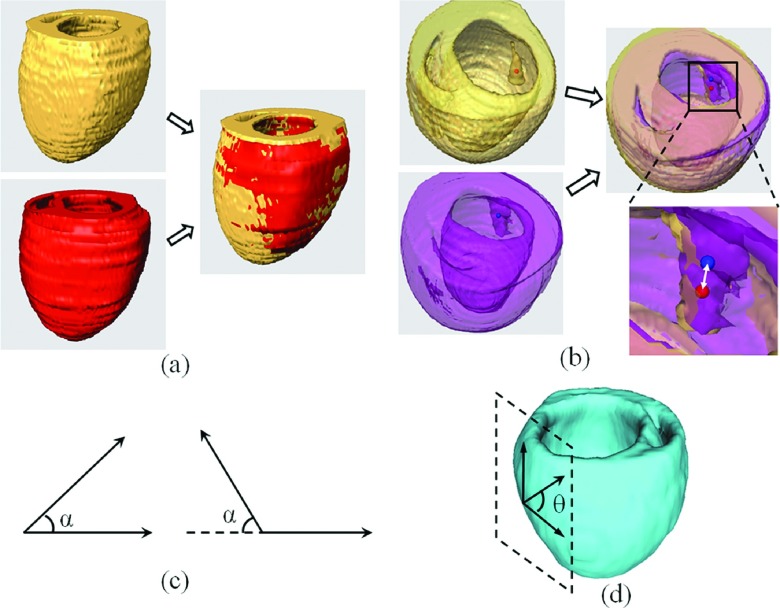
For the purpose of evaluating the performance of our proposed framework, four different evaluation parameters as illustrated in Fig. 4, and four different evaluation approaches as listed in Table I, are utilized for the assessments.

FIG. 4.

Evaluation methods for validating the accuracy of both geometry and fiber orientation deformation. (a) 3D geometric overlap ratio between the target (red) and template (yellow) hearts, calculated as DSC. (b) Distance between the corresponding papillary muscle centers of the template (red dot) and target (blue dot) hearts, calculated as the target registration error (the distance of the white double-head arrow in the amplified image). (c) Acute angle α between both imaged and estimated fiber directions. (d) Angle θ between the tangential directions of the epicardial contour in the short-axis plane and the fiber direction projected in the epicardial tangential surface, as calculated as the inclination angle.

TABLE I.

Different evaluation approaches to assess the performance of the proposed estimation framework.

Evaluation			Evaluation
steps	Target	Template	parameters
1	MRI geometry of canine hearts with HF	Geometry and fiber of healthy canine atlas	DSC, AAE, IAE
2	Ultrasound geometry of rat hearts	Geometry and fiber of the same rat hearts	DSC, TRE
3	Ultrasound geometry of rat hearts	Geometry and fiber of different rat hearts	DSC, AAE, IAE
4	MRI geometry of rat hearts	Geometry and fiber of different rat hearts	DSC, AAE, IAE

Note: HF = heart failure; DSC = Dice similarity coefficient; TRE = target registration error; AAE = acute angle error; IAE = inclination angle error.

2.D.1. Evaluation parameters

The first quantitative evaluation of the volume registrations is conducted by comparing the registered volume with the corresponding target volume. The Dice similarity coefficient (DSC) is used as the performance assessment score of the similarity between both volumes. It is computed as follows:

$${\displaystyle \text{DSC}(R,S)=\frac{2\hspace{0.17em}\text{Volum}(R\cap S)}{\text{Volum}\left(R\right)\hspace{0.17em}+\hspace{0.17em}\text{Volum}\left(S\right)},}$$ (3)

where R and S represent the voxel sets in the volumes of both registered volume and the corresponding target volume, respectively.

The other evaluation method for the geometry registrations is the target registration error (TRE), which calculates the distance between corresponding markers in both volumes. We use the papillary muscles in the hearts as the anatomic markers. Then, the distance between the mass centers in both markers is calculated as the target error.

In order to evaluate the estimated cardiac fiber orientations, the acute angle error (AAE) is utilized to measure the angular separation between both estimated and ground-truth orientations of the same fiber by inverting the absolute of their dot product in 3D into an angle, which is between 0° and 90°.^22,36 But this angle is insufficient because the cardiac fibers are strictly arranged along the laminar sheets in myocardium.

Thus, the inclination angle error (IAE) was introduced in this calculation.³⁷ First, each fiber orientation is projected onto its nearest epicardial tangential plane. Then, the angle between the projected vector and the tangential vector of the epicardial contour in the short-axis view is measured as the inclination angle of each voxel. Finally, the inclination angle error for each voxel is calculated by taking the absolute difference between both inclination angles of estimated and ground-truth fiber orientations. These inclination angle errors are arranged from 0° to 180°.

2.D.2. Evaluation steps

As shown in Table I, four different evaluation steps were performed in order to rigorously assess the accuracy and performance of the proposed framework for the estimation of cardiac fiber orientations.

Evaluation Step 1: Assessing the proposed framework using public canine data. The performance of both geometric registration and fiber orientation deformation of our method is first evaluated by a public canine dataset shared by the researchers at Johns Hopkins University, Baltimore, MD,³⁸ which has been tested by others.^19,22 In the canine data, we utilize a statistical atlas of nine healthy hearts as the template to estimate the cardiac fiber orientations of the hearts with heart failures.³⁴

Evaluation Step 2: Assessing registration errors between T1-weighted MRI and 3D ultrasound of the same rat hearts. In order to evaluate our framework, the fiber orientations from DTI serve as the ground truth. Although the rat hearts were fixed before ultrasound and DTI data acquisitions, there were still difference in orientations and slight geometric deformation between ultrasound and DTI. Thus, the fiber orientations from DTI are deformed based on the registration between the geometries from 3D ultrasound and T1-weighted MRI of the same heart and then serve as the gold standard for evaluation.

Evaluation Step 3: Assessing the accuracy of the fiber orientations that are estimated from the ultrasound geometry when the fiber template of a different heart is used for the estimation. Cardiac fiber orientations of each rat heart, which are estimated from the ultrasound geometry based on the fiber template of a different heart, are evaluated using the corresponding DTI data of the same heart.

Evaluation Step 4: Assessing the accuracy of the fiber orientation that is estimated from the geometry of T1-weighted MRI when the fiber template of a different heart is used for the estimation. The cardiac fiber orientations of each rat heart, which are estimated from the geometry obtained from T1-weighted MRI and are based on the fiber template of a different heart, are evaluated by the corresponding DTI data. As the MR geometry based fiber orientation estimation has been verified, we utilize this approach to compare our ultrasound geometry based estimation method.

3. RESULTS

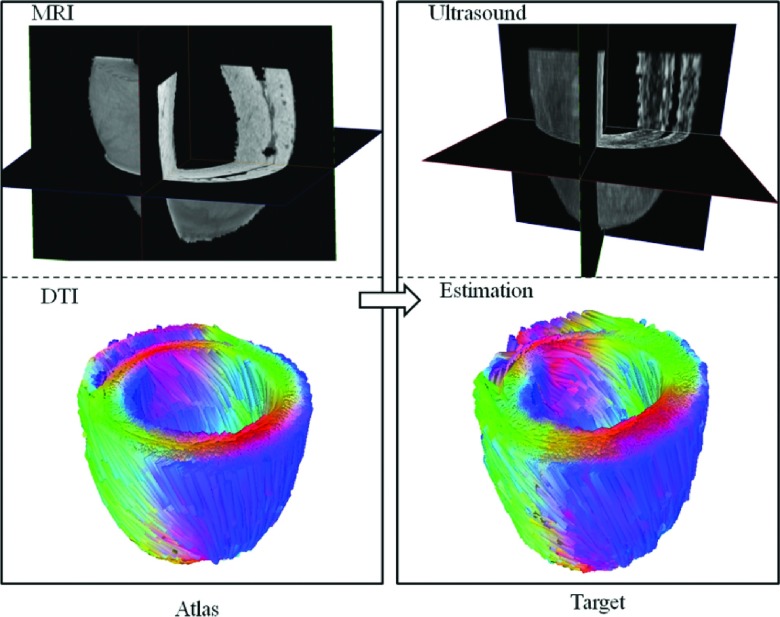
The feasibility of the proposed method for estimating cardiac fiber orientations from 3D ultrasound was demonstrated by three rat hearts, which were scanned by 3D ultrasound, T1-weighted MRI, and DTI. During the evaluations, each heart was separately utilized as the template heart or the target heart one time. Figure 5 illustrates the visualizations of the estimated results: the 3D geometry imaged by T1-weighted MRI and the fiber orientations imaged by DTI of the template heart, and the 3D geometry imaged by 3D ultrasound and the estimated fiber orientations of the target heart. The quantitative evaluations are presented in the following sections.

FIG. 5.

Results of the cardiac fiber orientations estimated from 3D ultrasound of a rat heart, based on the template of MRI and DTI. Left column is the MRI geometry and DTI fiber orientations of the template heart; right column is the ultrasound geometry and the estimated cardiac fiber orientations of the target heart.

3.A. Validation using public data (Evaluation Step 1)

We first tested the effectiveness of both geometric registration and fiber orientation deformation of our proposed method using the public canine database.³⁸ The concept of estimating cardiac fiber orientations from geometries using MRI has been tested in these canine hearts.^19,21,22 Their angle errors or ECG simulations concluded that there were insignificant differences between estimated and real data using their methods. Hence, we applied these canine heart data to test our procedure. In the canine data, we evaluated the cardiac fiber orientations of four hearts with heart failure, which were estimated from a statistical template of nine healthy hearts.³⁴ Figure 6 shows the estimated results of a target heart, the estimated one from the template, and the corresponding errors. The main errors between geometries are around the epicardium and endocardium, which is the same to the inclination angle errors between both fiber orientations. The total estimation results are listed in Table II, including DSC, acute angle errors, and inclination angle errors. From the table, the mean and standard deviation of the DSCs are 82.7% ± 2.3% and 95.9% ± 0.9% for both affine and diffeomorphic Demons registrations, respectively. The AAE is 19.2° ± 1.5° and the IAE is 17.6 ± 0.9. The results from the canine data are similar to those as previously reported,^19,20,22 indicating that our proposed method works well in these canine heart data.

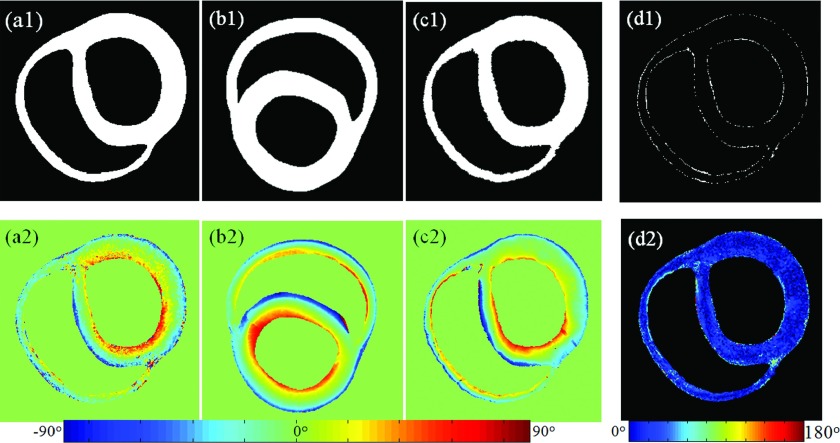
FIG. 6.

Results of both geometry and fiber orientation deformation of one slice from the canine heart data, including their estimation errors. Upper row is the geometric results and the lower row is the fiber orientation results. [(a1) and (a2)] Geometry and inclination angles of the target heart. [(b1) and (b2)] Geometry and inclination angles of the template heart. [(c1) and (c2)] Estimated geometry and inclination angles of the target heart. [(d1) and (d2)] Corresponding errors between the target and its estimation.

TABLE II.

Geometry and fiber reorientation errors using public canine data.

		DSC (%)
Target	Template	Affine	DD	AAE (deg)	IAE (deg)
HF 1	Healthy	83.7	96.8	17.9	16.5
HF 2	Healthy	84.1	95.5	19.1	17.9
HF 3	Healthy	79.8	94.3	21.3	18.6
HF 4	Healthy	82.3	96.5	18.5	17.2

Note: HF are the canine hearts with heart failure from Ref. 38; Healthy is the healthy hearts as the template from Ref. 34; DSC = Dice similarity coefficient; AA = acute angle error; IAE = inclination angle error; DD = diffeomorphic Demons.

3.B. Evaluation of the registration between T1-weighted MRI and 3D ultrasound of the same heart (Evaluation Step 2)

The accuracy of this step was estimated using the DSC and TRE for both rigid and DD registration. The estimated accuracies for the registration were listed in Table III. Although both ultrasound and T1-weighted MRI data are from the same fixed heart, it can be seen that there are still more than 10% errors in DSC, and 0.5 mm in TRE between both ultrasound and MRI geometries after rigid transformation. Therefore, further registration was needed here. Then, the DD deformable registration increased the final accuracy with more than 96% in DSC and less than 0.2 mm in TRE.

TABLE III.

Evaluations of setting ground truth for each heart.

	DSC (%)		TRE (mm)
Dataset	Rigid	DD	Rigid	DD
Rat 1	86.6	96.6	0.53	0.19
Rat 2	84.8	97.3	0.42	0.17
Rat 3	82.5	96.5	0.55	0.21

Note: DSC = Dice similarity coefficient; TRE = target registration error; DD = diffeomorphic Demons.

3.C. Evaluation of fiber orientation estimation when a different rat heart is used as the template (Evaluation Steps 3 and 4)

We evaluated the cardiac fiber orientations estimated from the ultrasound geometries of three rats as described in Evaluation Step 3. During the estimation process, the utilized template heart for each target rat heart is listed in Table IV. Then, both the estimated cardiac geometry and fiber orientations for each heart were compared with its corresponding ground truth of Evaluation Approach 2 for evaluation. The mean DSC of the geometric registrations was 95.4% for the three hearts. The average angle errors were 21.0° in AAE and 19.4° in IAE, respectively.

TABLE IV.

Geometry and fiber orientation errors of rat hearts based on Evaluation Steps 3 and 4.

Target			DSC (%)
Geometry	Rat number	Template (rat number)	Affine	DD	AAE (deg)	IAE (deg)
US	1	3	85.3	96.2	20.2	18.4
US	2	1	82.4	96.9	21.7	20.7
US	3	2	80.1	93.2	21.1	19.2
T1-MRI	1	3	86.5	96.9	17.3	16.7
T1-MRI	2	1	80.9	95.9	20.2	19.1
T1-MRI	3	2	81.5	95.4	19.4	18.5

Note: US = ultrasound; DD = diffeomorphic Demons; DSC = Dice similarity coefficient; AA = acute angle error; IAE = inclination angle error.

After that, Evaluation Approach 4 estimated the cardiac fiber orientations of the three rats from the T1 geometries. The comparison between Evaluation Steps 3 and 4 indicated that the estimation errors of the ultrasound-based fiber estimation method were comparable to those of the MRI-based method: the average AAE of Approach 3 was 1.5° higher and the average IAE was 1.3° higher than those of Approach 4. Moreover, although there were estimation errors in the DTI based estimation methods, a previous study of ventricular electrophysiological simulations indicated that the IAE of less than 20° between both estimated and acquired fiber orientations led no significant differences at a clinically observable level.¹⁹

3.D. Estimated fiber orientations from 3D ultrasound images in vivo

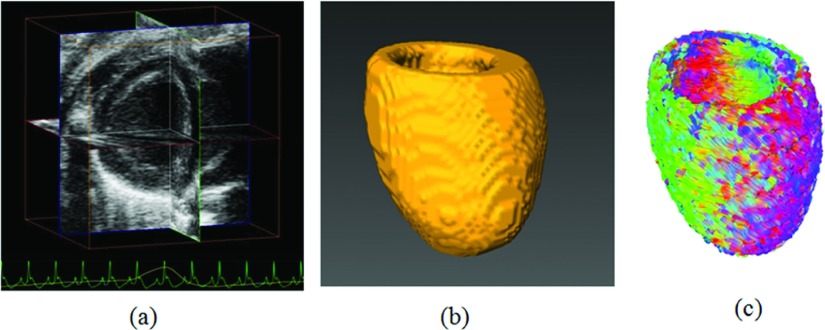
The feasibility of the proposed framework was tested on the in vivo 3D ultrasound images of the rat heart, as shown in Fig. 7. The cardiac geometry in the diastole phase was segmented and reconstructed from the ultrasound volume. The fiber orientations were estimated by this proposed method, which used another ex vivo heart as the template. These results demonstrated the feasibility of utilizing our proposed method to estimate cardiac fiber orientations from a rat heart in vivo.

FIG. 7.

Cardiac fiber orientation estimation of an in vivo beating heart. (a) 3D ultrasound volume in vivo. (b) Reconstructed cardiac geometry. (c) Estimated cardiac fiber orientations from the geometry.

4. DISCUSSION

In this project, we proposed an estimation method to estimate cardiac fiber orientations from 3D ultrasound volumes and also evaluated the accuracies with corresponding ground truth. Both the fiber template and the ground truth were built on the high-resolution DTI data. The fundamental idea was based on the hypothesis that the cardiac fiber orientations are related to the corresponding geometry, which means the possibility of directly estimating cardiac fiber orientations from its geometry,³⁸ because cardiac fibers are helically and regularly arranged in the heart.³⁹ This arrangement matches the requirements of the systolic and diastolic motions of myocardium as the heart beats, which must be efficient and avoid tangling. Furthermore, simulations of a mathematical model indicated that myofiber bundles were arranged in special minimal surfaces to close the gap between individual myofibers and their general layers. Therefore, the cardiac fiber orientations could be estimated from its geometry based on another heart template including cardiac fiber orientations and geometry.

The accuracy of the proposed cardiac fiber orientation estimation method relates to the cardiac geometries. There are artifacts in the cardiac ultrasound images even in ex vivo imaging, such as scattering speckles, contrast inhomogeneity, and data dropout in the image. Moreover, the papillary muscles can blur the endocardial boundary or add extra regions. Considering imaging quality, accurate segmentations become important, especially for the purpose of image-guided computational modeling.⁴⁰ Current automatic segmentation methods, such as those for the right ventricle segmentation,⁴¹ still need improvement for cardiac ultrasound segmentation. Alternatively, the data in our project were manually segmented by an experienced scientist to ensure the accuracy and robustness. Besides the errors derived from ultrasound artifacts, the estimation errors could also come from the geometry registration and fiber reorientation. Thus, we utilized the public canine dataset and the rat heart data to verify our framework based on different evaluation approaches. Comparing with the current geometry based registration, further improvement of an intensity based registration method may be able to improve the accuracy of the fiber estimations.

In this study, the quantitative evaluation was mainly performed on the normal hearts. We plan to improve the accuracy of the current estimation and then extend its application to potential disease models, such as ventricular remodeling, in the future. The proposed method has the potential to be extended to clinical applications. Based on the cardiac template of human beings,¹¹ it could estimate cardiac fiber orientations from 3D ultrasound images of each patient’s heart. In this study, high-frequency ultrasound images allow us to see the four chambers of the rat heart that has a small size because the images have a relatively high spatial resolution. For a human heart, cardiac ultrasound imaging uses a relatively lower frequency, e.g., 3.5 MHz, because of a relatively large field of view for a human heart and because of a relatively deep tissue penetration of low-frequency ultrasound. As far as the ultrasound images can provide the geometric information of the human heart, as it is true for human cardiac ultrasound imaging, our method can be used to estimate the cardiac fiber orientation. Our estimation method was validated by the canine hearts that had a similar scale as the human heart. When we apply this method to the ultrasound images of human hearts, the template data from an ex vivo human heart can have a high resolution of 0.43 × 0.43 × 1 mm³. The major concern will focus on whether we can acquire accurate myocardial geometry from 3D cardiac ultrasound of a human patient. Most of these geometric and fiber orientation errors will occur in the boundary regions of the myocardium. However, these errors can be decreased by the improvement of 3D echocardiographic segmentations.^42,43 For transesophageal echocardiography (TEE), which has a frequency of up to 10 MHz, it is anticipated that the accuracy of the fiber estimated can be further improved. In these applications, the estimated fiber orientations can be valuable for clinical cardiac diagnosis when the fiber information is combined with electrophysiological models.^44–46 It might also play a role in both surgical plans and ablation guidance, especially for the ventricular tachycardia and ventricular arrhythmia.^28,47–49

5. CONCLUSION

In this study, we proposed and evaluated a template-based ultrasound method for cardiac fiber imaging. The method estimates the cardiac fiber orientations of the target heart by deforming the DTI data of a template heart, which is based on the deformations between the ultrasound geometry of the target heart and the geometry of the template heart. The accuracy of this method was evaluated in both rat and canine hearts.

It is important to visualize and quantify cardiac fiber orientations for cardiac research and clinical applications because cardiac fiber orientations decide both cardiac electrophysiological and mechanical properties of the beating heart. As ultrasound imaging has been widely used in cardiac examinations, the proposed method and its further improvements might contribute to better understanding of cardiac physiology and may provide a tool for diagnosis of heart diseases.