Abstract
The measurement of reaction rate as a function of pH provides essential information about mechanism. These rates are sensitive to the pKa values of amino acids directly involved in catalysis that are often shifted by the enzyme active site environment. Experimentally observed pH-rate profiles are usually interpreted using simple kinetic models that allow estimation of “apparent pKa” values of presumed general acid and base catalysts. One of the underlying assumptions in these models is that the protonation states are uncorrelated. In the present work, we introduce the use of constant pH molecular dynamics simulations in explicit solvent (CpHMD) with replica exchange in the pH-dimension (pH-REMD) as a tool to aid in the interpretation of pH-activity data of enzymes, and test the validity of different kinetic models. We apply the methods to RNase A, a prototype acid/base catalyst, to predict the macroscopic and microscopic pKa values, as well as the shape of the pH-rate profile. Results for apo and cCMP-bound RNase A agree well with available experimental data, and suggest that deprotonation of the general acid and protonation of the general base are not strongly coupled in transphosphorylation and hydrolysis steps. Stronger coupling, however, is predicted for the Lys41 and His119 protonation states in apo RNase A, leading to the requirement for a microscopic kinetic model. This type of analysis may be important for other catalytic systems where the active forms of implicated general acid and base are oppositely charged and more highly correlated. These results suggest a new way for CpHMD/pH-REMD simulations to bridge the gap with experiments to provide a molecular-level interpretation of pH-activity data in studies of enzyme mechanisms.
Acid-base catalysis is a common catalytic strategy in protein and RNA enzymes,1 and is employed in the cleavage of the RNA phosphodiester backbone by RNase A2,3 as well as small nucleolytic RNA enzymes.4 General base and acid catalysts facilitate nucleophile activation through proton abstraction, and promote leaving group departure through proton donation, respectively. The observed reaction rate is assumed to be proportional to the probability of finding the enzyme in a “catalytically active” state with the acid protonated (i.e., able to donate a proton), and the base deprotonated (i.e., able to receive a proton). This conditional probability will thus be a function of the pH, and the pH-rate curves will be sensitive to the pKa values of the general acid and base.5,6
The measurement of reaction kinetics as a function of pH provides vital information about mechanism; however, the interpretation of this data is not always straightforward.6 Experimentally determined pH-rate curves are commonly fit to a simple equilibrium model where the apparent pKa values of the general acid and base appear as independent parameters. When protonation states are strongly coupled as they often are in enzyme active sites, irregular titration behavior occurs, requiring a more detailed theoretical analysis.5,7,8 Recently, computational methods have emerged that allow molecular simulations in explicit solvent to be performed under constant pH conditions (CpHMD), and the conditional probabilities of correlated protonation events to be directly determined.9–16 CpHMD can be used in conjunction with replica exchange molecular dynamics in the pH dimension (pH-REMD) in order to enhance sampling of important states while at the same time providing information over a range of pH values that can be used to predict complex titration curves.9,17 The present work reports the first application of the CpHMD/pH-REMD method to the prediction of the pH-rate curves for the apo and the 2′,3′-cyclic phosphate (2′O-transphosphorylation product) bound RNase A, a prototype acid-base catalyst.
RNase A catalyzes a 2′O-transphosphorylation of a bound RNA substrate that involves cleavage of the phosphodiester backbone to form a 2′,3′-cyclic phosphate and 5′-hydroxyl termini.2,3 In a subsequent reaction RNase A catalyzes the hydrolysis of the cyclic phosphate to form a 3′ phosphate. Both transphosphorylation and hydrolysis involve general acid-base catalysis, and thus are strongly pH-dependent. The kinetics of RNase A have been extensively studied,18,19 including analysis of the roles of His12 and His11920 and the pH-dependence of substrate association.21 In the present work, we examine the effect of pH on the acid-base catalytic step in RNase A 2′O-transphosphorylation and hydrolysis. We do not consider here the effect of pH on substrate association and binding, which is known to be important.21 Extension of the theoretical framework to take into account the added dimension of substrate binding is possible, but this requires technical details that are beyond the scope of this first application. Nonetheless, we note that very recent progress in this area has been reported.22
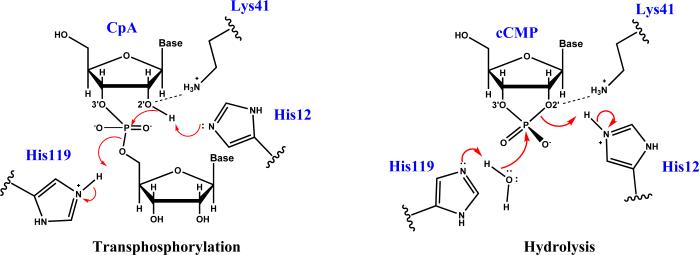
Scheme 1 illustrates the putative mechanism of RNA cleavage via transphosphorylation and hydrolysis of cytidyl-3′-5′adenosine (CpA) and 2′,3′-cyclic phosphate by RNase A.2,3 The His119/His12 pair is generally accepted general acid/base pair in transphosphorylation (although other mechanisms have been proposed and discussed3). His12 abstracts the proton from O2′ to facilitate the nucleophilic attack on the adjacent phosphorus atom. His119 act as the general acid to donate a proton to the O5′ leaving group, resulting in a 2′,3′-cyclic phosphate. Subsequent hydrolysis occurs by the action of His119 as the general base to abstract the proton from a water molecule in order to facilitate nucleophilic attack. The His12 residue acts as the general acid to donate a proton to O2′ and leads to the 3′-phosphomonoester final product. Note that some reports in the literature23,24 have suggested that Lys41, rather than His12, may play the role of the general base in transphosphorylation. Although this mechanism is not widely accepted, we nonetheless consider it for comparison.
Scheme 1.
The putative mechanism of transphosphorylation (left) and hydrolysis (right) by RNase A. The generally accepted view is that H119/H12 acts as the general acid/base pair in transphosphorylation, and their roles are reversed in hydrolysis. However, there has been some debate in the literature that alternatively, K41 might act as general base in transphosphorylation, although this is less widely accepted.
Methods
Interpretation of pH-rate data for general acid-base catalysis
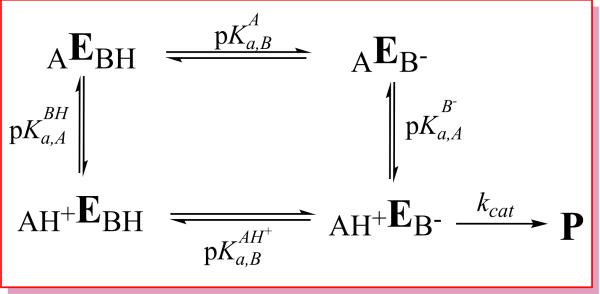
Scheme 2 illustrates a microscopic kinetic model for general acid-base catalysis used to interpret pH-activity data. The underlying kinetic assumption is that the catalytic rate is proportional to the active species, AH+EB−, which has the general base deprotonated (B−) so as to be able to accept a proton and activate the nucleophile, while the general acid (AH+) is protonated so as to be able to donate a proton to the leaving group.
Scheme 2.
Microscopic general acid-base protonation state model used to interpret pH-activity data: AH+EB–, AH+EBH, AEBH, AEB– are four microstates. E stands for “enzyme” and subscripts A and B indicate the acid and base, respectively. The pKa shifts discussed in the text are defines as , and . Note the constraint of the thermodynamic cycle ensures ΔpKa,A,+ΔpKa,B=0, and a positive value for ΔpKa,B indicates anticooperative coupling of protonation states (i.e., protonation of the acid site disfavors protonation of the base), whereas a negative value of ΔpKa,B indicates cooperative coupling (i.e., protonation of the acid site favors protonation of the base). The “apparent pKa” model discussed in the text involves fitting of pH-rate data under the constraint that ΔpKa,A=−ΔpKa,B=0 (see text). This scheme does not consider the pH-dependence of substrate binding, which is also important for a complete kinetic characterization.
The pH-dependent probabilities for each of the four micro-states illustrated in Scheme 2 can be described by the partition function Q
| (1) |
from which the probabilities (fractions) for each state can be determined as:
| (2) |
| (3) |
| (4) |
| (5) |
Note that the reference energy in the partition function is taken as that of the active state AH+EB− (set to zero energy). The microscopic pKa values can be determined from fitting to these four fractions simultaneously under the constraint that their related free energy values sum to zero in accord with the thermodynamic cycle shown in Scheme 2. The plots of the data used in deriving microscopic pKa values can be found in supporting information.
A common assumption in the interpretation of pH-rate profiles is that the protonation/deprotonation events are uncorrelated; i.e., an equivalence is assumed between microscopic pKa values and , or equivalently that , where and (for more complete discussion, see reference 6). Fitting of the pH-rate data under these constraints leads to apparent pKa values for the general acid and base, and we will henceforth refer to this model as the “apparent pKa model” to distinguish it from the “microscopic pKa model” which allows this coupling parameter to be optimized. Alternatively, direct determination of the macroscopic pKa values of the individual acid and base sites involves fitting to each of the corresponding independent acid and base fractions
| (6) |
| (7) |
using the Hill equation
| (8) |
where f(d) is the deprotonated fraction of the residue of interest (either f(AH) or f(B−)) and n is the Hill coefficient.
Molecular dynamics simulations at constant pH
The starting structures for the simulations were prepared by modifying the crystallographic structure of apo RNase A (PDB ID:1KF5)25 and RNase A complexed with deoxycytidyl-3′,5′-deoxyadenosine [(d(CpA))] (PDB ID:1RPG)26 solved at 1.15 Å and 1.4 Å resolution, respectively. Two separate sets of explicit solvent constant pH replica exchange molecular dynamics (CpHMD/pH-REMD)9 simulations were performed using developmental version of Amber 1227 molecular dynamics package on apo RNase A and the product state, 2′,3′-cyclic phosphate (cCMP) bound RNase A. The apo and complexed RNase A structures were each placed in a cubic box of TIP4PEw28 water molecules having a buffer of at least 10 Å on each side, and neutralized by chloride counterions for the expected charge of the systems (standard amino acid protonation states) at pH 7 with the exception of His12 and His119 treated as fully protonated. Note that the net number of explicit ions are constant in all the simulations, so the net charge of the system does vary as titratable residues change protonation state. This point was addressed specifically with regards to the titration process in Swails et al.9 and shown not to affect the titration since the sampling of protonation states occurs using an implicit solvent model based on the conformations generated with explicit solvent simulation. After initial minimization and equilibration with molecular dynamics, pH-REMD simulations in explicit solvent9 were performed at 300K and 1 bar using a total of 24 replicas corresponding to different pH values between 2 and 13. During these simulations, His12, Lys41 and His119 were treated as titratable. Long range electrostatics were computed using the smooth particle-mesh Ewald (PME) method.29,30 Note that the PME method implicitly introduces a background term that neutralizes the system (sometimes referred to as a “neutralizing plasma”) that is further corrected for finite size effects31 with a volume-dependent term. Other corrections can be made to remove pressure and free energy artifacts for charged periodic systems,32 but in previous studies9 these were not found to be necessary and were not used here. Simulations were performed using a 2 fs integration step, with exchanges between adjacent replicas attempted every 200 fs, and carried out to 74 and 104 ns for each replica of apo and cCMP-bond RNase A. The 60 ns of production simulation was analyzed and reported for both systems. A full description of the simulation protocol, pH-activity curves, convergence tests on the sampled protonation states, and details about the side-chain conformations, hydrogen bonding networks in the active site and binding of cCMP at different pH values can be found in the supporting information.
Results and Discussion
Simulations accurately predict the macroscopic pKas for apo and cCMP-bound RNase A
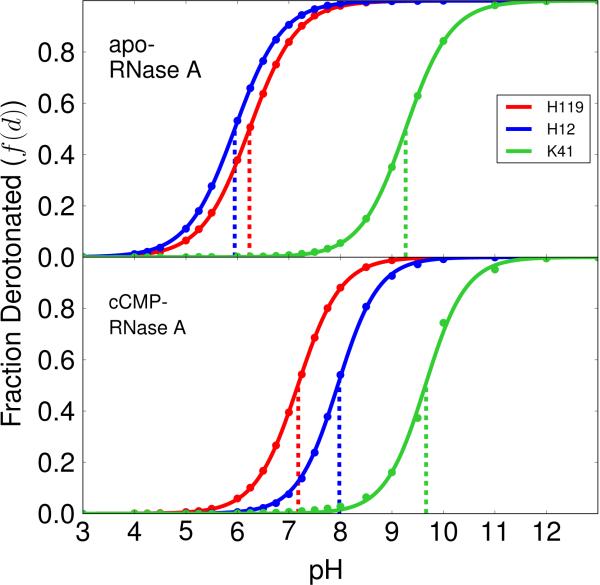
Analysis of the pH-REMD simulations provides values for the fractions f(AH+/B−), f(AH++/BH), f(A/BH), and f(A/B−) described in Eq. (2)-Eq. (5), and hence via Eq. (6) and Eq. (7) the overall acid and base fractions, f(AH+) and f(B−). The titration curves for His12, His119 and Lys41 for both apo and cCMP-complexed RNase A can be found in Figure 1. Each fraction is observed to exhibit near-ideal Henderson-Hasselbalch behavior. Fitting the acid and base fractions to the Hill equation (Eq. (8)), allows direct evaluation of the simulated macroscopic pKas. Comparison of the simulated and experimental pKa values are listed in Table 1 for both apo and cCMP-complexed RNase A. In the case of apo RNase A, the simulated pKa values for His12, His119 and Lys41 (5.95, 6.23 and 9.26) are within approximately 0.3 units of the corresponding experimental values.33,34 The simulations of RNase A complexed with cCMP predict shifted pKa values for His12, His119 and Lys41 to 7.95, 7.17 and 9.65, respectively and are in reasonable agreement with the experimentally estimated values 8.0,7.4 and 9.11, respectively.34,35 In the course of the simulations over the pH range 2-8, the integrity of the active site is maintained. Beyond pH 8, the interaction between Asp121 and His119 that form the His-Asp catalytic dyad begins to become displaced.36 At high pH values, the cCMP becomes more loosely bound37 in the binding pocket, leading to larger fluctuations and greater difficulty sampling. Details about the key structural features of the simulations at each pH are provided in the supporting information.
Figure 1.
Titration curves (lines) fitted to simulation data (points) with the Hill equation [Eq. (8)]. The upper panel represents the apo enzyme and the lower panel represents the cCMP-bound enzyme. The Hill coefficients for His119, His12 and Lys41 are 0.94, 0.94, 0.98 for the apo enzyme and 1.04, 1.09, 1.10 for the cCMP-bound enzyme, respectively.
Table 1.
Comparison of experimental and simulated macroscopic pKas for apo and cCMP-RNase A using the Hill equation and the “apparent pKa” model.
| His12 | His119 | Lys41 | |
|---|---|---|---|
| Apo RNase A | |||
| Expt. | 5.8a | 6.2a | 9.0b |
| Hill Eq. | 5.95 (0.14) | 6.23 (0.07) | 9.27 (0.07) |
| Expt. (“Apparent” pKa estimate)c | 4.9-5.2 | 6.3-6.9 | - |
| “Apparent” pKa model with H12(B)/H119(A) | 5.88 (0.14) | 6.27 (0.08) | - |
| “Apparent” pKa model with K41(B)/H119(A) | - | 6.17 (0.21) | 8.81 (0.21) |
| cCMP-RNaseA | |||
| Expt. (3′-CMP) | 8.0d | 7.4d | 9.11e |
| Hill Eq. | 7.95 (0.15) | 7.17 (0.12) | 9.65 (0.16) |
| Expt. (cCMP “Apparent” pKa)f | 8.10 | 6.30 | - |
| Expt. (cCMP “Apparent” pKa)g | 9.0 | 6.25 | - |
| “Apparent” pKa model with H119(B)/H12(A) | 7.92 (0.16) | 7.16 (0.12) | - |
| “Apparent” pKa model with H119(B)/K41(A) | - | 7.18 (0.13) | 9.64(0.16) |
The calculated macroscopic pKa values using the Hill equation [Eq. (8)] and the “apparent pKa” model for the apo and cCMP-bound RNase A were compared with the experimental macroscopic and kinetic pKa (Expt.) values from the literature. Statistical error estimates, shown in parentheses, were obtained as standard deviations derived from values computed from data in 5 ns intervals over the 60 ns of production.
Taken from Ref. 33
Taken from Ref. 34
Taken from Ref. 35
Taken from Ref. 34
Taken from Ref. 38
Taken from Ref. 19;
3′-CMP, cCMP are the substrates: 3′-cytidine monophosphate, 2′,3′-cyclic phosphate
Simulated protonation states can be interpreted using a microscopic pKa model
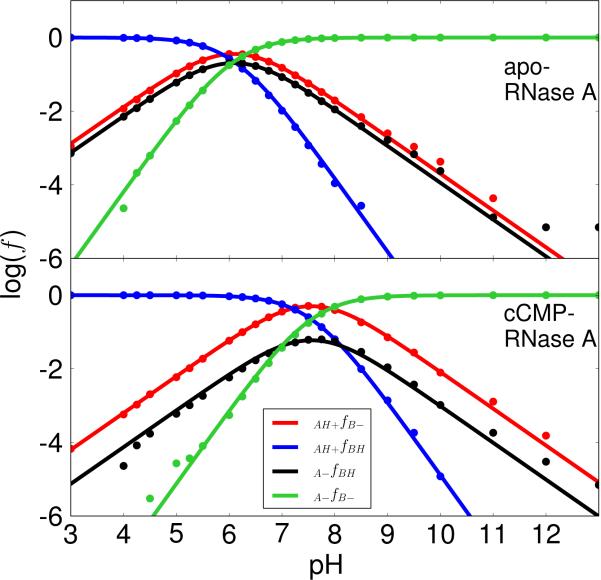
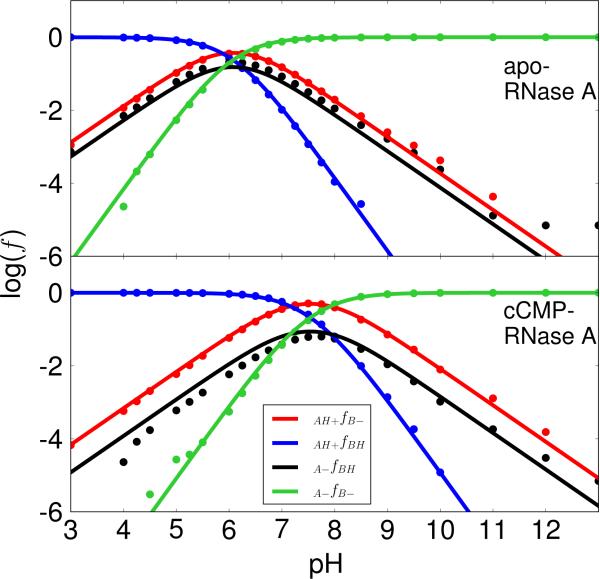
The microscopic model illustrated in Scheme 2 was fit to the simulated fractions of His12 as the general base/acid and His119 as the general acid/base for apo/cCMP-RNase A (Figure 2). The model, which has three independent parameters, fits the simulation data extremely well. This general trend is that the curves for the cCMP-complex shift to higher pH values relative to those for the apo enzyme. This trend is primarily due to the existence of the negatively charged cyclic phosphate on cCMP that is in fairly close proximity to the titratable residues in the active site. Further, the microscopic pKa values derived from the fitting are in very good agreement with those measured from NMR experiments36 for the apo enzyme (Table 2). For the cCMP-bound complex, to our knowledge, there currently does not exist experimental microscopic pKa values that would allow a direct comparison. Nonetheless, there are microscopic pKa values reported for a 3′-UMP inhibitor.36 The microscopic pKa values for His12 and His119 in the 3′-UMP bound RNase A indicate a different trend than the experimental pKa values for 3′-CMP and cCMP- bound RNase A complexes19,35,38 and the simulated values reported here (Table 1); nonetheless, we can compare the magnitude of the coupling (ΔpKa values in Table 2) between protonation states.
Figure 2. Microscopic pKa model results with H12/H119 acting as the general acid and base.
The plots of the logarithm of protonated fractions, log(f), versus pH of each microstate for apo (top) and cCMP-bound RNase A (bottom) were obtained by fitting the simulation data for all fractions to the equations derived from the microscopic model (Scheme 2) with His12/His119 acting as the general base/acid for apo RNase A (transphosphorylation model) and the general acid/base for cCMP-bound RNase A (hydrolysis model), respectively, as depicted in Scheme 1. The simulation data fits well with RMS errors of 0.22 (apo) and 0.17 (cCMP) for the log(f) values. The log(f) maximums (−0.45 and −0.30) for the curve of the active fraction, f(AH+/B–), are at 6.1 (apo) and at 7.5 (cCMP), respectively.
Table 2.
Comparison of experimental and simulated microscopic pKas using the microscopic model illustrated in Scheme 2 for apo and cCMP-bound RNase A.
| ΔpKa,B | ΔpKa,A | |||||
|---|---|---|---|---|---|---|
| Apo-RNase A with His12(B )/His119(A) | ||||||
| Expt.a | 5.87 | 6.18 | 0.31 | 6.03 | 6.34 | −0.31 |
| Microscopic model | 5.88 (0.14) | 6.05 (0.15) | 0.17 | 6.13 (0.05) | 6.30 (0.10) | −0.17 |
| Apo-RNase A with Lys41(B )/His119(A) | ||||||
| Microscopic model | 8.29 (0.14) | 9.26 (0.07) | 0.97 | 6.23 (0.07) | 7.21 (0.21) | −0.97 |
| cCMP-RNase A with His119(B )/His12(A) | ||||||
| Expt. (3′-UMP)a | 7.95 | 7.85 | −0.1 | 6.45 | 6.35 | 0.1 |
| Microscopic model | 7.20 (0.12) | 6.99 (0.20) | −0.21 | 8.12 (0.17) | 7.92 (0.16) | 0.21 |
| cCMP-RNase A with His119(B )/Lys41(A) | ||||||
| Microscopic model | 7.17 (0.12) | 7.41 (0.40) | 0.24 | 9.40 (0.18) | 9.64 (0.16) | −0.24 |
The calculated microscopic pKa values are derived from the thermodynamic cycle illustrated in Scheme 2, which contains three free parameters that were fit to the acid/base fractions f(AH+/B-), f(AH+/BH), f(A/BH), and f(A/B-). The pKa shifts are defines as , and . Note the constraint of the thermodynamic cycle in Scheme 2 ensures ΔpKa,A+ΔpKa,B=0, and a positive value for ΔpKa,B indicates anticooperative coupling of protonation states (i.e., protonation of the acid site disfavors protonation of the base), whereas a negative value of ΔpKa,B indicates cooperative coupling (i.e., protonation of the acid site favors protonation of the base). Statistical error estimates, shown in parentheses, were obtained as standard deviations derived from values computed from data in 5 ns intervals over the 60 ns of production. Results were compared with the experimental (Expt.) values obtained from NMR
Taken from Ref. 36 in order to validate the model. In order to explore the degree to which this weak coupling persists with other plausible general base and acid pairs, the general base was replaced by Lys41 for each case and the resulting microscopic pKa values were determined.
The experimental microscopic pKa values suggest that the His12 and His119 protonation states are weakly coupled in both the apo enzyme and the 3′-UMP bound RNase A (ΔpKa,B values of 0.31 and −0.1 pKa units, respectively). The calculated microscopic pKa values are in reasonable agreement, and predict the apo and cCMP-bound RNase A have ΔpKa,B values of 0.17 and −0.21 pKa units, respectively. Overall, the experimental and calculated coupling between His12 and His119 protonation states is fairly weak. The observed weak coupling can be explained by the fact that the acid and base protonation sites are fairly far apart in the active site, and in the catalytically active state, involve interactions between a neutral and a positively charged residue (as opposed to oppositely charged residues). A fairly striking result is that the experimental ΔpKa,B value for the 3′-UMP bound RNase A is negative, suggesting that protonation of one of the active-site histidine residues favors protonation of the other. This observation has been made experimentally36 and has been explained as a result of enhanced interactions with the phosphate when both sites are protonated. The simulation results reported here are completely consistent with this interpretation (see SI for additional details), and as indicated in Table 2, suggest that only in the phosphate-bound systems does such cooperative coupling occur. The fact that the simulation results (both for the apo and cCMP-complex enzymes) can be precisely fit to all four fractions by the 3-parameter microscopic kinetic model lends credence to its validity.
“Apparent” (uncorrelated) pKa model for His12/His119 is justified for the catalytic steps in RNase A
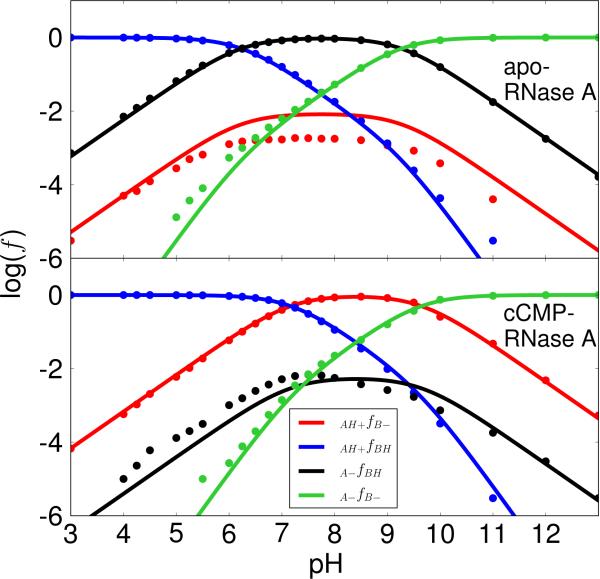
The experimental analysis of pH-rate data involves fitting the observed rate curve to a simple kinetic model with apparent pKa values for the presumed general acid and base. The correspondence of directly measured macroscopic pKa values of presumed general acid and base residues with the apparent pKa values is often interpreted as indirect evidence supportive of their catalytic roles. The computational analog of this procedure would be to fit only the active fraction, f(AH+/B–), to the thermodynamic cycle shown in Scheme 2, but with only two free parameters, pKa,A and pKa,B (or alternatively, under constraints that and ). The fitted apparent pKa curve for His12 and His119 as the general acid and base, respectively, is shown in Figure 3, and the values for the apparent pKas are shown in Table 1. Note that although the apparent pKa values only consider the active fraction in the fitting, as would be the procedure used to fit experimental curves, these parameters also determine the fractions of the other protonation states in accord with the partition function in Eq. (1). Unlike experiment, these non-active fractions are available from the simulations, and thus available for comparison. The fit to the active fraction (red line in Figure 3) is excellent; however, model curves for the other fractions, particularly f(A−/BH), are somewhat worse than for the curves shown in Figure 2 that involved fitting the microscopic model to all of the fractions simultaneously. Nonetheless, the apparent pKa values fitted to the active fraction are in remarkably close agreement (within 0.07 pKa units) to the macroscopic pKa values that were derived from fitting the protonation fractions to the Hill equation (Table 1). This is a direct consequence of the very weak coupling between the His12 and His119 protonation states. Under these conditions, the assumptions of independent protonation events and the interpretation of the apparent pKa values used to gain insight into general acid-base mechanism is a valid one. Note, however, the present discussion assumes that the only protonation events that are affecting the catalytic activity are those of the general acid and base, and in many cases this may not be true.
Figure 3. Apparent pKa model results with H12/H119 acting as the general acid and base.
The plots of the protonated fractions, log(f), versus pH of each microstate for apo (top) and cCMP-bound RNase A (bottom) were obtained by fitting the simulation data to ONLY the ACTIVE FRACTION (f(AH+/B–), shown in red) with His12/His119 acting as the general base/acid for apo RNase A (transphosphorylation model) and the general acid/base for cCMP-bound RNase A (hydrolysis model), respectively, as depicted in Scheme 1. The model assumes no coupling of the microstates, and although only the active fraction is considered in the fitting (as would be the case experimentally), the parameters nonetheless are able to determine the other fractions which can be compared with the simulation data. The upper panel represents the apo RNase A and the lower panel represents the cCMP bound RNase A. The RMS errors for the log(f) values are 0.25 (apo) and 0.18 (cCMP) respectively. The log(f) maximums (−0.43 and −0.30) for the curve of the active fraction, f(AH+/B–), are at 6.1 (apo) and at 7.5 (cCMP), respectively.
Coupling of protonation states for His119 and Lys41 is significant
The above example of general acid-base catalysis in apo RNase A, with His12 and His119 as the presumed general acid and base, respectively, indicates that treatment of the protonation states as uncorrelated within the framework of the “apparent pKa” model is justified. However, it should not be assumed that this is a general phenomena. In order to demonstrate this point, we consider the scenario whereby the role of general base is replaced by Lys41 in the kinetic model for the apo RNase A enzyme. Evidence suggests this is likely not the biological role of Lys41 in catalysis by RNase A, but for the purposes of demonstration, it is still instructive to examine.
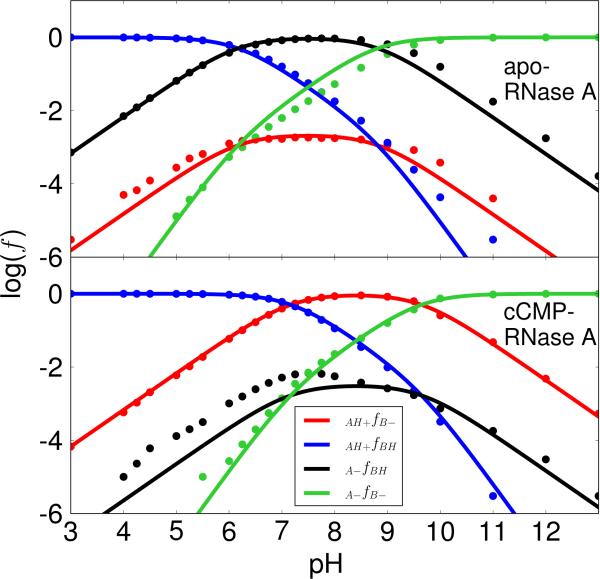
The microscopic model is able to fit the simulation data very well for all fractions (Figure 4). However, considerably stronger protonation state coupling (ΔpKa,A=ΔpKa,B=0.97) is observed between Lys41 and His119 relative to that of His12 and His119 (Table 2). The apparent pKa values for Lys41 and His119 are 8.81 and 6.17, which differ somewhat from the macroscopic pKa values obtained from the Hill equation (9.27 and 6.23, respectively). Moreover, the “apparent pKa model” does not closely reproduce the protonation state fractions (Figure 5), including the active fraction that was used in the fitting. Although the slopes of the higher and lower pH-regimes of the pH-rate curve is not influenced by the interactions between the residues, the maximum probability is observed to be approximately 3 times larger. However, the predicted pKa from the microscopic model illustrates that the “apparent pKa model” has limitations with regard to mechanistic interpretation in the regime where key protonation states are more strongly coupled. This may be particularly relevant for some RNA enzymes where the active form of the general acid and base are oppositely charged species that can be expected to exhibit stronger electrostatic interactions.
Figure 4. Microscopic pKa model results with K41/H119 acting as the general acid and base.
The plots of the logarithm of protonated fractions, log(f), versus pH of each microstate for apo (top) and cCMP-bound RNase A (bottom) were obtained by fitting the simulation data for all fractions to the equations derived from the microscopic model (Scheme 2) with Lys41/His119 acting as the general base/acid for apo RNase A (transphosphorylation model) and the general acid/base for cCMP-bound RNase A (hydrolysis model), respectively. This is not the generally accepted mechanism depicted in Scheme 1, but has nonetheless received some support in the literature24,40 and so is considered here for comparison. The RMS errors for the log(f) values are 0.31 (apo) and 0.44 (cCMP) respectively. The log(f) maximums (−2.09 and −0.05) for the curve of the active fraction, f(AH+/B–), are at 7.7 (apo) and at 8.4 (cCMP), respectively.
Figure 5. Apparent pKa model results with K41/H119 acting as the general acid and base.
The plots of logarithm of protonated fractions, log(f), versus pH of each microstate for apo (top) and cCMP-bound RNase A (bottom) were obtained by fitting the simulation data to ONLY the ACTIVE FRACTION (f(AH+/B–), shown in red) with Lys41/His119 acting as the general base/acid for apo RNase A (transphosphorylation model) and the general acid/base for cCMP-bound RNase A (hydrolysis model), respectively. This is not the generally accepted mechanism depicted in Scheme 1, but has nonetheless received some support in the literature24,40 and so is considered here for comparison. The model assumes no coupling of the microstates, and although only the active fraction is considered in the fitting (as would be the case experimentally), the parameters nonetheless are able to determine the other fractions which can be compared with the simulation data. The upper panel represents the apo RNase A and the lower panel represents the cCMP bound RNase A. The RMS errors for the log(f) values are 0.33 (apo) and 0.48 (cCMP) respectively. The log(f) maximums (−2.69 and −0.11) for the curve of the active fraction, f(AH+/B–), are at 7.5 (apo) and at 8.4 (cCMP), respectively.
Summary and Perspective
Recently, advances in computational methods have allowed simulations of biological molecules to be performed in explicit solvent under constant pH conditions. These simulations allow conformations and protonation states to be sampled together across a range of pH conditions. This enables the prediction of pH-rate curves from molecular simulation, as well as tools to provide atomic-level interpretation of pH-activity data. More importantly, this method allows one to quantify the probability of finding an enzyme system in a catalytically active protonation state from which it is capable to go on to react with a pseudo first-order rate constant in the catalytic chemical step. Together with other methods, such as combined quantum mechanical/molecular mechanical simulations that can be used to map the free energy landscape for the catalytic chemical steps of the reaction, a complete description of catalysis can be obtained and compared directly with experimental data. The results described here demonstrate promise for theory and experiment to work together to understand enzyme mechanisms.
Supplementary Material
Acknowledgments
Special thanks to Timothy Giese, Ming Huang and Maria Panteva for their for useful suggestions on the manuscript.
Funding
This work was financially supported by the National Institute of Health (NIH) grant number GM062248 to D.M.Y., NIH grant GM096000 to M.E.H. and National Science Foundation (NSF) grant numbers ACI-1147910 and ACI-1036208 to A.E.R. The simulations were carried out with the Blue Waters supercomputer, supported by the NSF grant numbers ACI-0725070 and ACI-1238993, and the Extreme Science and Engineering Discovery Environment (XSEDE), supported by NSF grant number OCI-1053575.
Footnotes
Supporting Information Available
A full description of the simulation protocol, pH-activity curves, convergence tests on the sampled protonation states, and details about the side-chain conformations, hydrogen bonding networks in the active site and binding of cCMP at different pH values can be found in the supporting information. This material is available free of charge via the Internet at http://pubs.acs.org/.
References
- 1.Kirby AJ. Encyclopedia of Life Sciences (ELS) John Wiley & Sons, Ltd; Chichester: 2010. Chapter Acid-Base Catalayis by Enzymes. [Google Scholar]
- 2.Raines RT. Ribonuclease A. Chem. Rev. 1998;98:1045–1065. doi: 10.1021/cr960427h. [DOI] [PubMed] [Google Scholar]
- 3.Cuchillo CM, Nogués MV, Raines RT. Bovine pancreatic ribonuclease: Fifty years of the first enzymatic reaction mechanism. Biochemistry. 2011;50:7835–7841. doi: 10.1021/bi201075b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Doudna JA, Cech TR. The chemical repertoire of natural ribozymes. Nature. 2002;418:222–228. doi: 10.1038/418222a. [DOI] [PubMed] [Google Scholar]
- 5.Onufriev A, Case DA, Ullmann GM. A novel view of pH titration in biomolecules. Biochemistry. 2001;40:3413–3419. doi: 10.1021/bi002740q. [DOI] [PubMed] [Google Scholar]
- 6.Bevilacqua PC. Mechanistic considerations for general acid-base catalysis by RNA: Revisiting the mechanism of the hairpin ribozyme. Biochemistry. 2003;42:2259–2265. doi: 10.1021/bi027273m. [DOI] [PubMed] [Google Scholar]
- 7.Ullmann GM. Relations between protonation constants and titration curves in polyprotic acids: A critical view. J. Phys. Chem. B. 2003;107:1263–1271. [Google Scholar]
- 8.Klingen AR, Bombarda E, Ullmann GM. Theoretical investigation of the behavior of titratable groups in proteins. Photochem. Photobiol. Sci. 2006;5:588–596. doi: 10.1039/b515479k. [DOI] [PubMed] [Google Scholar]
- 9.Swails JM, York DM, Roitberg AE. Constant pH replica exchange molecular dynamics in explicit solvent using discrete protonation states: Implementation, testing, and validation. J. Chem. Theory Comput. 2014;10:1341–1352. doi: 10.1021/ct401042b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wallace JA, Shen JK. Continuous constant pH molecular dynamics in explicit solvent with pH-based replica exchange. J. Chem. Theory Comput. 2011;7:2617–2629. doi: 10.1021/ct200146j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wallace JA, Shen JK. Charge-leveling and proper treatment of long-range electrostatics in all-atom molecular dynamics at constant pH. J. Chem. Phys. 2012;137:184105. doi: 10.1063/1.4766352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Goh GB, Knight JL, Brooks CL. Constant pH molecular dynamics simulations of nucleic acids in explicit solvent. J. Chem. Theory Comput. 2012;8:36–46. doi: 10.1021/ct2006314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Goh GB, Knight JL, III CLB. pH-dependent dynamics of complex RNA macromolecules. J. Chem. Theory Comput. 2013;9:935–943. doi: 10.1021/ct300942z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Baptista AM, Teixeira VH, Soares CM. Constant-pH molecular dynamics using stochastic titration. J. Chem. Phys. 2002;117:4184–4200. [Google Scholar]
- 15.Donnini S, Tegeler F, Groenhof G, Grubmüller H. Constant pH molecular dynamics in explicit solvent with λ-dynamics. J. Chem. Theory Comput. 2011;7:1962–1978. doi: 10.1021/ct200061r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Börjesson U, Hünenberger PH. Explicit-solvent molecular dynamics simulation at constant pH: Methodology and application to small amines. J. Chem. Phys. 2001;114:9706–9719. [Google Scholar]
- 17.Itoh SG, Damjanović A, Brooks BR. pH replica-exchange method based on discrete protonation states. Proteins. 2011;79:3420–3436. doi: 10.1002/prot.23176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Findlay D, Mathias AP, Rabin BR. The active site and mechanism of action of bovine pancreatic ribonuclease. 4. The activity in inert organic solvents and alcohols. Biochem. J. 1962;85:134–138. doi: 10.1042/bj0850134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Eftink MR, Biltonen RL. Energetics of ribonuclease A catalysis. 1. pH, ionic strength, and solvent isotope dependence of the hydrolysis of cytidine cyclic 2′,3′-phosphate. Biochemistry. 1983;22:5123–5134. doi: 10.1021/bi00291a011. [DOI] [PubMed] [Google Scholar]
- 20.Park C, Schultz LW, Raines RT. Contribution of the active site histidine residues of ribonuclease A to nucleic acid binding. Biochemistry. 2001;40:4949–4956. doi: 10.1021/bi0100182. [DOI] [PubMed] [Google Scholar]
- 21.Park C, Raines RT. Catalysis by ribonuclease A is limited by the rate of substrate association. Biochemistry. 2003;42:3509–3518. doi: 10.1021/bi026076k. [DOI] [PubMed] [Google Scholar]
- 22.Kim MO, Blachly PG, Kaus JW, McCammon JA. Protocols utilizing constant pH molecular dynamics to compute pH-dependent binding free energies. J Phys Chem B. 2014 doi: 10.1021/jp505777n. DOI:10.1021/jp505777n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wladkowski BD, Krauss M, Stevens WJ. Ribonuclease A catalyzed transphosphorylation: An ab Initio theoretical study. J. Phys. Chem. 1995;99:6273–6276. [Google Scholar]
- 24.Wladkowski BD, Ostazeski P, Chenoweth S, Broadwater SJ, Krauss M. Hydrolysis of cyclic phosphates by ribonuclease A: A computational study using a simplified ab initio quantum model. J. Comput. Chem. 2003;24:1803–1811. doi: 10.1002/jcc.10331. [DOI] [PubMed] [Google Scholar]
- 25.Berisio R, Sica F, Lamzin VS, Wilson KS, Zagari A, Mazzarella L. Atomic resolution structures of ribonuclease A at six pH values. Acta Crystallogr. D. 2002;58:441–450. doi: 10.1107/s0907444901021758. [DOI] [PubMed] [Google Scholar]
- 26.Zegers I, Maes D, Dao-Thi M-H, Poortmans F, Palmer R, Wyns L. The structures of RNase A complexed with 3’-CMP and d(CpA): Active site conformation and conserved water molecules. Protein Sci. 1994;3:2322–2339. doi: 10.1002/pro.5560031217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Case DA, et al. AMBER 12. University of California, San Francisco; San Francisco, CA: 2012. [Google Scholar]
- 28.Horn HW, Swope WC, Pitera JW, Madura JD, Dick TJ, Hura GL, Head-Gordon T. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004;120:9665–9678. doi: 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
- 29.Darden T, York D, Pedersen L. Particle mesh Ewald: An N log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 30.Essmann U, Perera L, Berkowitz ML, Darden T, Hsing L, Pedersen LG. A smooth particle mesh Ewald method. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- 31.Figueirido F, Del Buono GS, Levy RM. On finite-size effects in computer simulations using the Ewald potential. J. Chem. Phys. 1995;103:6133–6142. [Google Scholar]
- 32.Bogusz S, Cheatham TE, III, Brooks BR. Removal of pressure and free energy artifacts in charged periodic systems via net charge corrections to the Ewald potential. J. Chem. Phys. 1998;108:7070–7084. [Google Scholar]
- 33.Markley JL. Correlation proton magnetic resonance studies at 250 MHz of bovine pancreatic ribonuclease. I. Reinvestigation of the histidine peak assignments. Biochemistry. 1975;14:3546–3554. doi: 10.1021/bi00687a006. [DOI] [PubMed] [Google Scholar]
- 34.Jentoft J, Gerken T, Jentoft N, Dearborn D. [13C]Methylated Ribonuclease A, 13C NMR studies of the interaction of lysine 41 with active site ligands. J. Biol. Chem. 1981;256:231–236. [PubMed] [Google Scholar]
- 35.Meadows DH, Jardetzky O. Nuclear magnetic resonance studies of the structure and binding sites of enzymes. IV. Cytidine 3’-monophosphate binding to ribonuclease. Proc. Natl. Acad. Sci. USA. 1968;13:406–413. doi: 10.1073/pnas.61.2.406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Quirk DJ, Raines RT. His . . . Asp catalytic dyad of ribonuclease A: Histidine pKa values in the wild-type, D121N, and D121A enzymes. Biophys. J. 1999;76:1571–1579. doi: 10.1016/S0006-3495(99)77316-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Neuberger A, Brocklehurst K, editors. Hydrolytic Enzymes; New Comprehensive Biochemistry. Elsevier; Amsterdam, The Netherlands: 1987. [Google Scholar]
- 38.Herries D, Mathias AP, Rabin BR. The active site and mechanism of action of bovine pancreatic ribonuclease. 3. The pH-dependence of the kinetic parameters for the hydrolysis of cytidine 2′,3′-phosphate. Biochem.J. 1962;85:127–134. doi: 10.1042/bj0850127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gu H, Zhang S, Wong K-Y, Radak BK, Dissanayake T, Kellerman DL, Dai Q, Miyagi M, Anderson VE, York DM, Piccirilli JA, Harris ME. Experimental and computational analysis of the transition state for ribonuclease A-catalyzed RNA 2’-O-transphosphorylation. Proc. Natl. Acad. Sci. USA. 2013;110:13002–13007. doi: 10.1073/pnas.1215086110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wladkowski BD, Krauss M, Stevens WJ. Transphosphorylation catalyzed by ribonuclease A: Computational study using ab Initio effective fragment potentials. J. Am. Chem. Soc. 1995;117:10537–10545. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.