Solid-state dynamic nuclear polarization at 263 GHz: spectrometer design and experimental results

Abstract

Dynamic Nuclear Polarization (DNP) experiments transfer polarization from electron spins to nuclear spins with microwave irradiation of the electron spins for enhanced sensitivity in nuclear magnetic resonance (NMR) spectroscopy. Design and testing of a spectrometer for magic angle spinning (MAS) DNP experiments at 263 GHz microwave frequency, 400 MHz ¹H frequency is described. Microwaves are generated by a novel continuous-wave gyrotron, transmitted to the NMR probe via a transmission line, and irradiated on a 3.2 mm rotor for MAS DNP experiments. DNP signal enhancements of up to 80 have been measured at 95 K on urea and proline in water–glycerol with the biradical polarizing agent TOTAPOL. We characterize the experimental parameters affecting the DNP efficiency: the magnetic field dependence, temperature dependence and polarization build-up times, microwave power dependence, sample heating effects, and spinning frequency dependence of the DNP signal enhancement. Stable system operation, including DNP performance, is also demonstrated over a 36 h period.

1. Introduction

Solid-state NMR has been demonstrated as a powerful technique for structure determination of biological solids, in particular amyloid and membrane proteins.^1–5 However, the experiments often suffer from low sensitivity or long acquisition times due to the small polarization of nuclear spins at thermal equilibrium. DNP experiments can provide substantial enhancements in NMR sensitivity by transferring the higher Boltzmann polarization of electron spins to nuclear spins.^6–9 This polarization transfer is driven by microwave irradiation at or near the electron paramagnetic resonance (EPR) frequency. The potential gain in sensitivity can be on the order of the ratio of the electron and nuclear gyromagnetic ratios, ~660 for transfer from electron to ¹H spins and ~2600 for transfer to ¹³C spins. It is difficult to reach these limits experimentally, except at very low temperature and with long polarization times such as for polarized target work and magnetic ordering.^10,11 For solid-state NMR applications including multi-dimensional experiments significantly shorter polarization times are required.

Early solid-state NMR DNP work was performed at low field of 1.4 T or less and primarily focused on materials, such as polymers or carbonaceous materials.^12–16 Applications to high field NMR were pioneered by Griffin and coauthors (MIT), using gyrotrons as a microwave source.^17–22 DNP signal enhancements of 100–300 are routinely achieved at 5–9 T (140–250 GHz EPR frequency), 90 K sample temperature, and with reasonable polarization times.^23,24 In addition, a wide range of biological solids have been successfully polarized²⁵ and the mechanism of the proton pump membrane protein, bacteriorhodopsin, has been elucidated.^26,27

A paramagnetic center, unpaired electron, is required for DNP experiments. Most of the high field DNP experiments from MIT utilize the cross effect (CE) polarization mechanism with nitroxide radicals¹⁸ or biradicals, two nitroxide radicals tethered together for stronger electron–electron coupling.^28,29 The CE mechanism relies on three-spin flip processes where two electrons that differ in energy by the nuclear Larmor frequency, ω_n, flip flop and the energy difference is used to flip a nuclear spin. Hence, the EPR spectrum must be wider than ω_n or two narrow lines separated by ω_n.^30–32 Nitroxide-based radicals or biradicals are well suited for DNP experiments to ¹H spins. In typical experiments, the sample of interest is dissolved in or mixed with a cryoprotectant solvent doped with paramagnetic centers and then frozen for DNP experiments at cryogenic temperatures. Continuous irradiation of the EPR line and ¹H spin diffusion facilitate distribution of the enhanced polarization throughout the solvent and solute.^25,33 The enhanced polarization is then transferred from the abundant ¹H spins to a low-gamma nucleus, such as ¹³C or ¹⁵N via cross-polarization (CP),³⁴ prior to detection or any other solid-state NMR pulse sequence.

The CE efficiency increases with the microwave field at the sample, B₁, up to a saturation level, increases with decreasing sample temperature, and is inversely proportional to the external magnetic field, B₀.²⁹ For experiments at very low temperature or with very efficient microwave delivery to a static sample, a low power microwave source may be sufficient.^33,35 High resolution solid-state NMR experiments with MAS, have more geometrical constraints on the sample shape and surrounding components such as the MAS stator and NMR coil. The microwave irradiation of the sample may not be as efficient and higher microwave power is important. Additionally, for MAS with cold nitrogen gas (> 77 K), higher microwave power is again critical compared to DNP measurements at lower temperature. Gyrotrons can provide the necessary microwave power with stable continuous-wave (CW) operation.

Most gyrotrons are designed for military, radar, and plasma fusion applications typically with output frequency of up to 170 GHz and high output power, kW to MW. They are often operated with pulses of several seconds or tens of seconds with low duty cycles; and minimal stability requirements. For DNP experiments, true CW operation for days with high frequency and power stability is required. This is especially important for structural studies where the DNP-enhanced NMR signal intensity must be stable over extended periods of time. Gyrotrons have been successfully developed and utilized by MIT for DNP applications at 140 and 250 GHz^22,36–38 and a 460 GHz gyrotron has been experimentally demonstrated.^39,40 More recently, a 394 GHz DNP gyrotron was designed and tested by the University of Fukui⁴¹ and a 260 GHz gyrotron by IAP/GYCOM, N, Novgorod, Russia.⁴²

In this paper, we describe a DNP spectrometer with a 263 GHz gyrotron microwave source for MAS experiments at 400 MHz ¹H frequency and 100 K sample temperature. The gyrotron frequency was selected as a reasonable compromise between demonstrated DNP gyrotrons at 140 and 250 GHz and the high magnetic fields typically used in solid-state NMR experiments. The gyrotron was designed specifically for extended DNP applications requiring CW operation with stable frequency and output power. Details of the gyrotron design, including electron tube, magnet, and control system, are described and tuning curves are presented. The microwave beam is transmitted to the NMR probe via a corrugated transmission line and mode pattern images were taken for evaluation of the microwave beam at the sample area. DNP signal enhancements were measured on urea and proline in water–glycerol doped with TOTAPOL biradical^28,43 at 95 K. The DNP efficiency depends on a multitude of experimental parameters including the NMR magnetic field position, sample temperature, microwave power, and spinning frequency. These effects were examined experimentally and are reported in this publication. Polarization build-up times and sample heating from microwave irradiation are also discussed. Finally, high stability of the gyrotron and DNP-enhanced signal intensity are demonstrated over a 36 h period.

2. Experimental

2.1 263 GHz gyrotron design

Gyrotrons are cyclotron resonance masers and a special form of vacuum electronic device (VED) relying on the interaction between an electron beam and a resonant cavity condition to generate microwaves.^44,45 All VED's share the following basic components. First, an electron gun contains a cathode and heater for electron emission, with initial electron beam acceleration when a high voltage (cathode voltage) is applied across the cathode to ground or an anode. The electron beam is further accelerated and focused through the electron tube by a magnetic field. Electron beam energy is then converted into radiation in the interaction circuit or cavity. After the cavity, the electron beam continues to the collector while the microwave beam exits the VED through the output window. Gyrotron cavities are cylindrical and can be overmoded. Therefore, the cavity dimensions are not limited by the wavelength and gyrotrons can produce high output power even at frequencies above 30 GHz where the performance of other types of VEDs declines rapidly. More detailed information on gyrotron components and operating principles can be found in several recently published books and articles.^22,44–50

Gyrotron tube

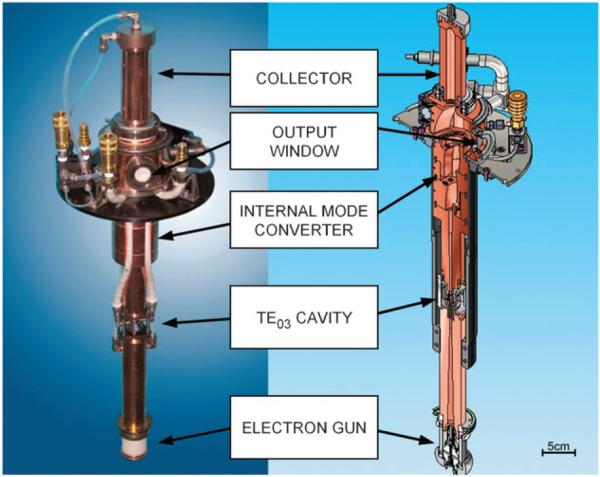
A solid model and photograph of the 263 GHz gyrotron tube are shown in Fig. 1. It is a hard-sealed gyrotron tube, with welded and brazed vacuum joints. After assembly, the tube is processed at high temperature for several days to reduce gas pressure and improve operability. Details of the gyrotron tube key elements, electron gun, interaction cavity, internal mode converter, output window, and collector are described below.

Fig. 1.

Photograph and solid model cross section of 263 GHz gyrotron tube.

Electron gun

A single-anode, or diode, magnetron-injection gun (MIG) was designed to operate at a nominal accelerating voltage, cathode voltage, of 11–15 kV and electron beam currents in the range of 20–100 mA. The average cathode radius is 0.5 cm and the average cathode loading, at 50 mA beam current, is less than 1 A cm^–2. The cathode angle and the electrode shapes were optimized to minimize the electron perpendicular velocity spread, which is predicted to be less than 1% at the nominal velocity pitch factor, α, the ratio of transverse to axial electron velocity. The cathode includes a filament heater for electron emission. The magnetic field is generated by a 9.7 T superconducting magnet and the ratio of the magnetic field at the cathode to the magnetic field in the interaction cavity is 26.5. The distance from the cathode to the cavity is approximately 25 cm and the region between the electron gun and the cavity, the beam compression region, includes alternating copper and lossy-ceramic rings to prevent oscillations.

Interaction cavity

The interaction cavity was designed to support the transverse electric TE_0,3,1 mode at 263 GHz. The cavity, which consists of an input taper, a straight section, and an output taper, is predicted to have a cold quality factor, Q, of 6000 and an output mode purity of 99.7%. The measured Q factor ranged from 4000 to 5000 for 4 gyrotron tubes. The calculated peak power density in the cavity, including the non-ideal effects of copper, is 47 W cm^–2 for a nominal output power of 40 W. Because the diffractive cavity Q is nearly equal to the ohmic cavity Q, approximately half of the power generated in the cavity is lost in the cavity walls.

Multi-mode efficiency calculations were carried out with a self-consistent, time-dependent code.⁵¹ Potential competing modes, including the TE_2,3,1, the TE_5,2,1, and TE_0,2,3 modes, were evaluated and found to have higher starting currents than the desired TE_0,3,1 mode for the nominal beam, cavity, and magnetic field parameters. Single-mode operation in the TE_0,3,1 mode was also predicted to cover a wide range of operating parameters. Large signal modeling indicated that, for a cathode voltage of 15 kV, a beam current of 30 mA, and a velocity pitch factor of 2.0, more than 100 W of power would be generated in the TE_0,3,1 mode of the cavity, resulting in more than 50 W of power at the cavity exit. Key design parameters of the interaction cavity are shown in Table 1.

Table 1.

Design parameters for the interaction cavity

Parameter	Design value
Operating mode	TE0,3,1
Cold Q	6000
Frequency/GHz	263.58
Cathode voltage/kV	15
Beam current/mA	30
Output power/W	50
Efficiency	11%

The cavity was designed to be thermally isolated from the gun and internal converter regions of the gyrotron to allow for frequency tuning with varying inlet temperatures of the cavity coolant water at a rate of approximately 4 MHz °C^–1.

Internal mode converter

The internal mode converter was designed to transform the annular TE_0,3,1 mode produced in the cavity to a Gaussian beam that exits the gyrotron through the output window perpendicular to the beam axis. The converter consists of a simple helically cut Vlasov launcher⁵² and five focusing and steering mirrors, designed to direct the beam out of the region of the gyrotron in the magnet bore and to focus the Gaussian beam waist to the correct size and position to exit through the window and couple to 19.3 mm ID corrugated waveguide. Because of the non-optimized launcher, the limited space afforded by the magnet bore, and the extended axial distance traveled by the microwave beam from the cavity to the window, the calculated diffraction losses for the internal converter system were as high as 7% and the output mode purity was expected to be no greater than 90%. Cold tests (low power) were performed to align the mirrors and verify the properties of the output beam.

Output window, matching unit and gap filter

The output window consists of a single 0.093-cm thick disk of Al₂O₃ with a clear aperture of 2.54 cm. Since the incident power and subsequent losses in the window disk are low, the predicted temperature rise with no direct cooling is less than 5 °C, which offers a large margin of safety for mechanical stresses. A matching unit at the gyrotron window provides a DC electrical break and supports and centers a segment of 19.3 mm ID corrugated waveguide. This first segment is followed by a gap filter with water-cooled Teflon tubing and adjustable horizontal gap length, which absorbs unwanted stray radiation.

Collector

The collector consists of a 2-cm diameter cooled copper section designed to dissipate the spent electron beam, which follows the natural trajectories dictated by the magnetic field of the superconducting magnet. The predicted peak power loading is 250 W cm^–2 resulting in a predicted temperature on the vacuum wall of the collector of about 100 °C.

Gyrotron magnet

A magnet is required for electron beam acceleration, beam compression to the cavity and decompression to the collector, and electron cyclotron resonance in the cavity region. The magnet designed for the 263 GHz gyrotron is shown in Fig. 2. It is a persistent superconducting magnet with two independent magnetic centers, one in the cavity region and one in the electron gun region. The nominal field for the cavity coil is approximately 9.7 T while the gun coil can be independently adjusted for gyrotron testing and optimization. The magnet configuration provides a good compromise between short gyrotron tube length and reasonable magnet length for a cryogenically-cooled magnet. The magnet is actively shielded with 1 meter radial 5 Gauss line. The microwave beam exits the gyrotron tube transverse to the bore axis above the magnet top plate.

Fig. 2.

Photograph of 263 GHz gyrotron showing from left to right: microwave transmission line, gyrotron magnet with tube installed, gyrotron control system console, and two chiller units.

Gyrotron control system

The control system monitors and controls a set of components and parameters for safe and stable operation of the 263 GHz gyrotron. It was designed on a PXI platform from National Instruments using LabWindows/CVI to develop the software, and is contained in a single-bay cabinet plus two water chillers. A wide range of operating parameters, such as the electron beam voltage and current, body current, tube vacuum, water flow and temperature, gun cooling gas flow, gyrotron magnet and waveguide connection, are continuously monitored and compared to threshold fault values. Two layers of automatic shutdown conditions are built into the system to protect from potential personal injury or instrumentation damage. Critical faults are handled directly through hardware with fast shutdown time while non-critical errors are handled through the software.

The gyrotron microwave power and frequency depend on the cathode voltage, electron beam current, cavity temperature, and magnetic field, all of which must be stable for constant output power and frequency. The high voltage power supply is a modified 4 kW Spellman X-ray power supply (DF series) with filament heater and high stability on the cathode voltage. The electron beam current is stabilized via a proportional-integrative (PI) controller which adjusts the filament current. There are two separate water circuits with PI controllers, one for the cavity with low heat load but high stability requirement, and one for the collector and tube body with higher heat load but lower stability requirements (chillers from Optitemp). Cooling and heating elements are included in the cavity circuit to cover a temperature range of 12 to 35 °C for frequency tuning. The control system also contains a power supply for the gyrotron tube 21 s^–1 VacIon pump and pressure regulator for gas cooling of the electron gun.

2.2 263 GHz transmission line and instrumentation for power and frequency measurement

The microwave beam output of the gyrotron matching unit and gap filter couples into a 19.3 mm ID corrugated transmission line. The transmission line is precision machined in 25 cm long aluminium segments that are joined together by coupling clamps and held on an extruded aluminium support rail. Individual corrugations are cut with a period of 1/3 wavelength and 1/4 wavelength depth and length.⁵³ Three flat-mirror 90° miter bends are included in the transmission line as the microwave beam travels across the gyrotron magnet top plate, down to a horizontal support rail, across to the NMR magnet, and up to the NMR probe base. The first horizontal segment above the gyrotron magnet, vertical rail, and start of long horizontal rail can be seen in Fig. 2. The distance between the two magnet bores is 2.9 metres. After the third miter bend, at the probe base, a Lucite sleeve provides a DC break between the 19.3 mm transmission line and probe waveguide, followed by a corrugated taper to 7.6 mm ID. The 7.6 mm ID probe waveguide is machined from phosphor bronze and helically tapped. The probe waveguide ends with two closely-spaced miter bends, 54.7° followed by 90°, for microwave irradiation transverse to the NMR sample rotation and coil axis. The microwave beam is launched directly to the NMR sample from the 7.6 mm ID waveguide after the 90 degree miter bend. A 7 mm diameter hole is cut through the bottom of the MAS stator and the center turns of the NMR coil are spaced out for improved microwave penetration. Compared to a regular NMR coil, a 25–30% increase in DNP efficiency is observed with the wider coil spacings.

A directional coupler, consisting of a 0.96 mm thick quartz plate at a 45 degree angle, is included in the transmission line for frequency and power measurements.⁵⁴ Microwave power is monitored on the forward port with frequency measurement or an absorbing load placed on the reflected port. A Scientech laser calorimeter (AC2500 and S310D display) is used for power measurement with black paint coating on the calorimeter surface to increase absorption at 263 GHz. Alternatively, a WR-3.4ZBD zero-bias detector diode from Virginia Diodes can be utilized with additional attenuation after the directional coupler. Microwave power can also be measured directly in line with a water load (calorimetric measurements), consisting of fully absorbing water-filled Teflon tubing in an aluminium housing with temperature sensors for measuring the input and output water temperatures and a flow meter. The water load is used for calibration of the directional coupler and laser calorimeter and power measurements on transmission line components. Frequency measurements are performed with a frequency locked tunable 24 GHz local oscillator source with better than 2 ppm frequency accuracy from Bruker BioSpin and a WR-3.4 harmonic mixer from Virginia Diodes. The resulting intermediate frequency from 11th harmonic mixing is detected on an oscilloscope after amplification and filtering.

During the initial gyrotron tests, power and frequency were measured directly at the gyrotron window using a calorimetric water load for power measurement and a spectrum analyzer (Tektronix 2784) with a 175–325 GHz harmonic mixer (Tektronix WM782J) for frequency measurement. The water load has typical error bars of ±3% and can measure powers as low as 0.4 W. Beam images were recorded with an infrared camera (FLIR ThermaCam SC640), burn paper, and liquid crystal paper.

2.3 NMR Spectrometer and DNP measurements

DNP experiments were performed on a Bruker BioSpin Avance III 400 Wide Bore NMR spectrometer equipped with a 3.2 mm quadruple resonance ¹H/¹³C/¹⁵N/electron low temperature magic angle spinning (LTMAS) probe and cooling cabinet. Three independent gas channels—bearing, drive, and variable temperature (VT)—are cooled through a liquid nitrogen heat exchanger enabling MAS experiments at 95–100 K and up to 14 kHz spinning frequency with ±2 Hz stability.⁵⁵ The heat exchanger was designed specifically for low temperature MAS applications to provide sample rotation stability at the lowest temperature possible. The temperatures of all three gas channels are monitored and regulated by a BVT3000 LTMAS temperature control unit. The LTMAS probe has sample insert and eject capabilities at low temperature and samples were inserted into the pre-cooled probe, spun up and allowed to thermally equilibrate for approximately 10 min before any measurements were performed. The LTMAS probe includes the 263 GHz probe waveguide detailed in section 2.2.

Typical NMR acquisition parameters are 100 kHz field on ¹H channel with TPPM⁵⁶ or SPINAL 64⁵⁷ decoupling, 55–60 kHz on ¹³C CP, 40–45 kHz on ¹⁵N CP, 10% ramp on ¹H during CP, 0.5–3 ms CP contact time, 20–50 ms acquisition time, 2–10 s recycle delay depending on relaxation time and signal intensity. The magic angle was set at low temperature using potassium bromide, KBr, and shimming on KBr and N-acetylvaline.

All reported DNP measurements were performed using gyrotron tube serial number one which operates at 15 kV cathode voltage, 60 mA beam current, 27.5 °C cavity temperature, and 263.343 GHz microwave frequency. The NMR field is set to 399.90 MHz ¹H frequency. DNP experiments were performed with the gyrotron on continuously and with cross polarization from ¹H to ¹³C or ¹⁵N. Therefore, the reported DNP signal enhancements are from the enhanced ¹H spins. The DNP signal enhancement is calculated by comparison of the NMR signal intensities or integrals with and without microwave irradiation. The microwave power at the end of the probe waveguide was approximately 6 W unless otherwise specified. Error bars in the DNP signal enhancement measurements, typically 1–2%, arise from the higher noise level of the spectrum without microwave irradiation. Spin lattice relaxation times, T₁, and DNP build-up times, T_pol, were recorded with saturation recovery pulse sequences.

2.4 Sample preparation and EPR measurements

All DNP samples were prepared with TOTAPOL biradical⁴³ in glycerol-d₈–D₂O–H₂O solution with a 60 : 30 : 10 volume ratio, unless otherwise specified. Liquid samples were transferred by pipette into 3.2 mm OD, 2.2 mm ID sapphire or zirconia rotors with 30 μl active sample volume. Only 22–25 μl sample volume was actually utilized to leave sufficient space for soft silicone sealing plugs that are inserted above the liquid to prevent any sample leakage before freezing. Zirconia drive caps are used for low temperature experiments. Unused filled rotors are stored in the freezer with the sealing plug still in place.

The actual nitroxide radical concentration was measured by EPR spectroscopy at 9.8 GHz using a Bruker BioSpin EMX-Plus spectrometer. Packed and sealed 3.2 mm rotors fit in a 4 mm ID EPR tube. The nitroxide concentration was calculated using the Bruker BioSpin EPR acquisition and processing software package Xenon for spin quantification. The spin count measures the nitroxide spin concentration independent of its form, mono radical or biradical. The TOTAPOL concentration was calculated by dividing the nitroxide concentration from the spin count by two, assuming that all the measured nitroxide spins are in biradical form. EPR measurements produced 20–50% lower TOTAPOL concentration than expected from calculated concentrations.

2.5 Temperature calibration

The spin lattice relaxation time, T₁, of ⁷⁹Br in KBr was used as a thermometer following the methods detailed in Thurber et al. for temperature calibration.⁵⁸ KBr was tightly packed into 3.2 mm zirconia and sapphire rotors and sealed with PTFE spacers. The spin–lattice relaxation times were recorded with a saturation recovery pulse sequence comprising 11 data points corresponding to delays from 10 ms to 15 s. Spectra for the zirconia rotor sample were collected at MAS frequencies of 12.5 kHz, 8.5 kHz and static conditions, from 100 K to 205 K. For the sapphire rotor, T₁ was recorded from 6 KHz to 14 kHz MAS frequency in increments of 2 kHz and for a static sample, all at 100 K. The actual sample temperature was calculated from the T₁ value of the ⁷⁹Br nuclei in KBr using previously described methods⁵⁸ and used for calibration of two thermocouples in the probe, the stator exhaust temperature and the thermocouple in the variable temperature line. The sample temperatures reported in this paper correspond to the calibrated values with no microwave irradiation on.

The KBr T₁s were measured with the gyrotron on and off for the zirconia and sapphire rotor to measure the sample heating due to microwave irradiation. Additionally, to measure the temperature rise in an actual frozen DNP sample a quartz capillary, 0.5 mm ID, 0.7 mm OD, approximately 5 mm in length was packed with KBr and sealed with an epoxy resin. The capillary was mounted into a PTFE spacer so that only the epoxy seal was in the spacer. The capillary and spacer were then placed into a 3.2 mm sapphire rotor filled with glycerol-d₈–D₂O–H₂O (60 : 30 : 10 volume ratio) stock solution with 10 mM TOTAPOL and closed with a zirconia drive cap. This was done in a manner so that the KBr in the capillary was surrounded by the DNP stock solution. The T₁ values of the capillary samples were recorded under static and 1.2 kHz spinning frequency at 100 K.

3. Results and discussion

3.1 263 GHz gyrotron test

Four nominally identical gyrotron tubes were fabricated and demonstrated. A summary of the typical test sequence and measured data for gyrotron tube serial number 4 follows.

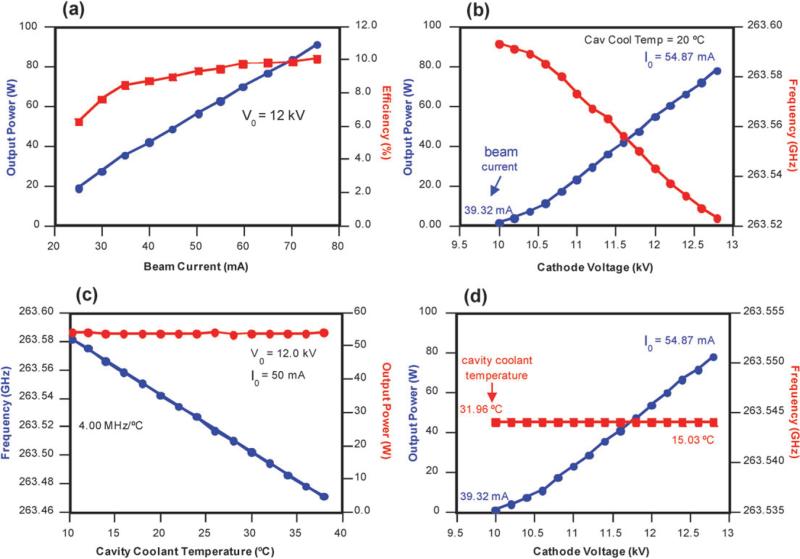
During the initial tests, beam voltage, beam current, magnetic field in the cavity region, and magnetic field in the electron gun region were systematically varied to determine the parametric limits and to select a nominal operating point. After initial testing, the gyrotron magnet was placed in persistent mode and no measurable effect on gyrotron performance was noticed from possible magnet drift. Fig. 3a shows the measured output power and efficiency as a function of beam current for a cathode voltage of 12 kV and a fixed magnetic field. Output powers of 20 W to 90 W and efficiencies up to 10% were measured for beam currents from 25 mA to 75 mA. To obtain lower output power, the cathode voltage can also be adjusted as shown in Fig. 3b, where the output power varies smoothly from 90 W to less than 2 W by varying the cathode voltage from 12.8 kV to 10 kV while holding the magnetic field and filament power fixed and allowing the beam current to fall naturally as the voltage is reduced. For the measurement, the cavity coolant temperature was held constant at 20 °C and the frequency varied from 263.59 GHz to 263.52 GHz as the power was tuned.

Fig. 3.

263 GHz gyrotron tuning curves: (a) output power (blue circles) and efficiency (red squares) as function of electron beam current at 12 kV cathode voltage, V₀. (b) Output power (blue circles) and frequency (red circles) versus beam voltage for fixed cavity inlet coolant temperature (20 °C), magnetic field, and filament power. The beam current, I₀, varied as indicated on the plot. (c) Frequency (blue circles) and output power (red circles) as a function of inlet cavity coolant temperature with all other parameters fixed. (d) Output power (blue circles) and frequency (red squares) versus beam voltage for fixed magnetic field and filament power. The cavity inlet coolant temperature is adjusted to maintain a constant frequency, 263.544 GHz.

To achieve smooth power tuning with cathode voltage while maintaining a constant frequency, the inlet temperature of the cavity cooling water can be varied. Fig. 3c shows the measured change in output frequency as a function of cavity coolant temperature with the beam voltage and beam current held fixed at 12 kV and 50 mA, respectively, and all other parameters kept constant. As shown in the Figure, the output power does not vary as a function of cavity coolant temperature and the frequency varies with the coolant temperature at a rate of 4 MHz °C^–1 from 10 °C to 38 °C. The ability to tune the frequency by varying the cavity coolant temperature was exploited to maintain a constant frequency while output power is varied, as shown in Fig. 3d.

At the nominal operating points, the output frequency of the four gyrotron tubes ranged from 263.39 GHz to 263.73 GHz and maximum efficiencies ranged from 4% to 10%. For the initial experimental demonstration, each gyrotron was routinely operated continuously for days without fault. Additionally, no time limitations have been observed during continuous gyrotron operation for DNP experiments. Further, it was demonstrated that the gyrotron could operate without fault with 100% of the microwave power reflected back into the device through the output window. Slightly elevated gas levels indicated some additional heating in the gyrotron tube due to the reflected power, but the gyrotron operated without fault at parameters that would have yielded 40 W output power with no reflection present.

3.2 Mode pattern measurements at the sample

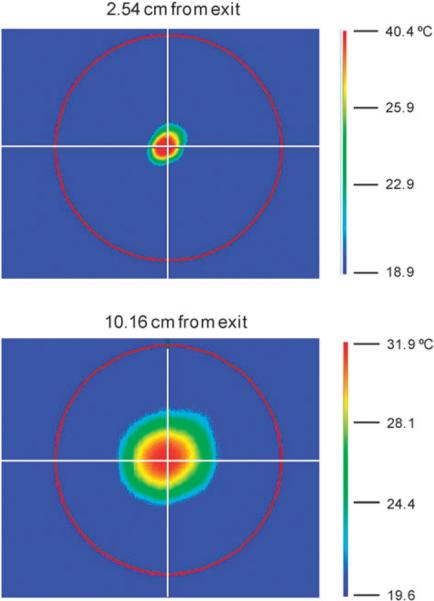
The gyrotron output microwave beam is transmitted to the sample through a metallic corrugated waveguide transmission line. The microwaves are launched from the end of the probe waveguide and form a Gaussian-like beam in free space directed at the sample. Infrared images of the microwave beam were obtained to verify the beam pattern at the DNP sample area. A paper target was positioned perpendicular to the waveguide exit and IR images in planes at varying distances of 2.5 cm to 20.3 cm from the waveguide were made. Fig. 4 shows the images at 2.54 cm (1 inch) and 10.16 cm (4 inches) from the probe waveguide exit. As is evident in the Figure, the microwave power exits the waveguide as a high quality Gaussian beam that is centered and directed at the sample. The distance from the end of the waveguide to the center of the sample is 13.4 mm and the beam waist (radius at which the amplitude is 1/e of the peak value) is estimated at 3.4 mm based on images closest to the waveguide and the expansion out. This beam waist matches well to the NMR sample size, a cylinder with 2.2 mm diameter (rotor ID) and 5 mm length.

Fig. 4.

Infrared images of microwave beam exiting the 7.6-mm diameter probe waveguide after the final miter bend. The target was positioned perpendicular to the waveguide exit. The cross hairs indicate the center of the waveguide and the red circles denote a 7.6 cm diameter.

3.3 DNP measurements on standard samples and characterization of experimental parameters

DNP signal enhancement of urea and proline standard samples

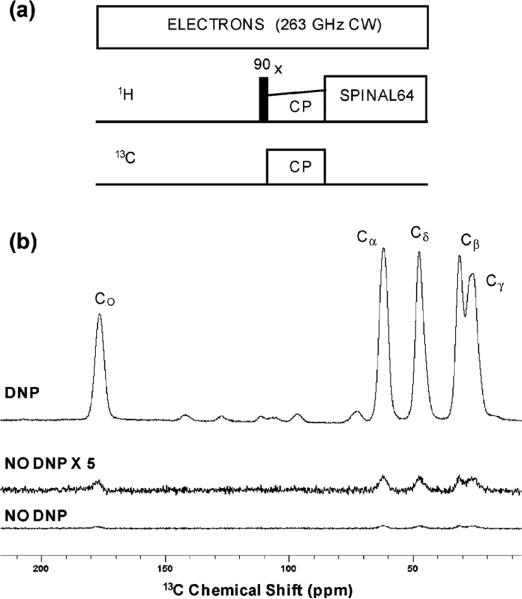
Initial DNP experiments were performed on ¹³C-urea and uniformly labeled ¹³C, ¹⁵N-proline samples dissolved in glycerol–water with 15 mM TOTAPOL. A typical DNP pulse sequence for a CPMAS experiment is shown in Fig. 5a. The microwaves are on continuously and any solid-state NMR pulse sequence can be performed. DNP signal enhancements of a factor of 80 were measured on urea at spinning frequency, ω_r/2π, of 5 kHz, and of 70 on proline at ω_r/2π = 8 kHz, both at 95 K sample temperature, and 6 W of microwave power at the end of the probe waveguide. The ¹³C CPMAS spectra of the proline sample with and without DNP are shown in Fig. 5b and excellent sensitivity can be seen in the DNP-enhanced spectrum with just 8 s of data acquisition. These results are consistent with previously published DNP signal enhancement factor of 100–115 at 250 GHz and slightly lower temperature.^59,60

Fig. 5.

(a) DNP CPMAS pulse sequence; (b) spectra of 0.5 M U- ¹³C, ¹⁵N-proline in glycerol-d₈–D₂O–H₂O (60 : 30 : 10 volume ratio) and 15 mM TOTAPOL biradical, 25 μl sample volume, with DNP (top trace) and without DNP (bottom traces). Spectra acquired at ω_r/2π = 8 kHz MAS, 95 K sample temperature, 4 scans, 2 s recycle delay, and one dummy scan. Higher numbers of scans were also acquired with microwaves off for more accurate DNP signal enhancement calculation.

Field dependence curve

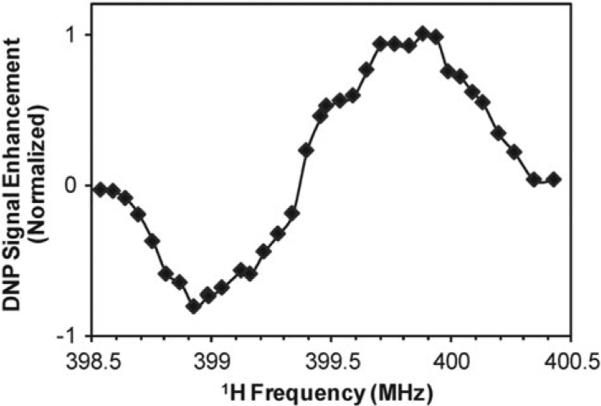
The DNP signal enhancement varies as a function of irradiation position within the EPR line. Since the gyrotron frequency has a limited tuning range compared to the width of the TOTAPOL EPR line, the NMR magnetic field was swept while the gyrotron frequency remained constant. The resulting field dependence curve plotting DNP signal enhancement as a function of NMR ¹H frequency is shown in Fig. 6. The curve has a base-to-base width of 410 Gauss (1.15 GHz) and follows the expected profile for nitroxide biradicals via the cross effect DNP for ¹H spins.²⁹ The gyrotron frequency tuning range of 100 MHz (35 Gauss) with the cavity temperature allows for local tuning about the maximum position of the field dependence curve. Following the field sweep, the NMR field position was set to the positive maximum of the curve.

Fig. 6.

Field dependence curve on 2 M ¹³C urea in glycerol-d₈–D₂O–H₂O (60 : 30 : 10 volume ratio) with 15 mM TOTAPOL biradical. The NMR field was swept while the gyrotron remained at fixed frequency, 263.343 GHz. Each field position was measured with ¹³C CPMAS experiment with microwaves on and off for calculating the DNP signal enhancement. 4 scans, 10 s recycle delay, and 2 dummy scans per experiment, ω_r/2π = 5.1 kHz, 105 K sample temperature. The transmitter frequency of the ¹H and ¹³C channel was adjusted for each field point. Error bars on the DNP signal enhancement measurements are ±2%.

Temperature dependence and polarization build-up times

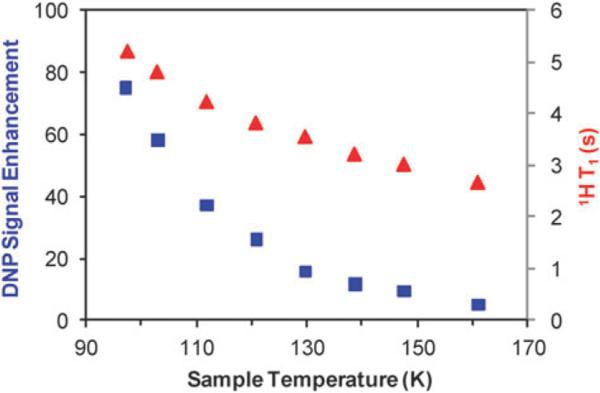
The cross effect polarization transfer is more favorable at low temperature due to longer electron and proton relaxation times²³ and the first high field DNP experiments using nitroxide radicals were performed at 140 GHz with static sample at ~20 K and with MAS at 60 K.^18,19 The helium temperature experiments were followed by nitrogen temperature experiments at 140 and 250 GHz.^20–21,26 Fig. 7 shows the temperature dependence of the ¹H DNP signal enhancement from 97 K to 160 K at 263 GHz with TOTAPOL biradical as polarizing agent. The DNP efficiency increases steeply as the temperature approaches 95 K and larger DNP signal enhancements should be observed at lower temperatures using helium-temperature probes.^19,61,62 Reasonable DNP efficiency can still be observed at higher temperature, with a factor of 10 signal enhancement measured at 150 K on the urea sample, expanding high-field CE DNP experiments to a higher temperature range than previously reported. Additionally, it is clear that the sample temperature must be stable for constant DNP signal enhancement during long experiments.

Fig. 7.

Temperature dependence of the ¹H DNP signal enhancement (blue squares) and ¹H spin lattice relaxation times, T₁, (red triangles) measured on 2 M ¹³C urea in glycerol-d₈–D₂O–H₂O (60 : 30 : 10 volume ratio) with 15 mM TOTAPOL biradical. ¹³C CPMAS experiments with 4 scans, 10 s recycle delay, 2 dummy scans, ω_r/2π = 6.2 kHz. Each temperature point was measured with microwaves on and off for calculation of the DNP signal enhancement. ¹H T₁ was measured with ¹H saturation recovery with CP detection, 11 points and 2 scans per point. Standard deviation was less 1 × 10^–2 on the calculated T₁ values. Error bars on the DNP signal enhancements are ±2%. The sample temperature corresponds to calibrated temperature with the microwaves off.

The ¹H spin lattice relaxation times, T₁, were also measured as a function of temperature using a saturation recovery CPMAS experiment and are plotted in Fig. 7. For both the urea and proline samples, the ¹H T₁s measured in the glycerol solvent and the urea or proline solute are identical and also similar to the polarization build-up time (saturation recovery experiment with the microwaves on). The time constants can differ between solvent and solute in the case of macroscopic samples, for example in amyloidal nanocrystals.²⁵ For NMR experiments requiring signal averaging with multiple scans, both the DNP signal enhancement and the polarization time must be considered, as excessive polarization times can offset the gains from DNP signal enhancement. In the temperature range of 97–160 K, net gains in sensitivity-per-unit-time are still obtained by going to lower temperature. Higher radical concentration can also be utilized to shorten T₁.^60,62

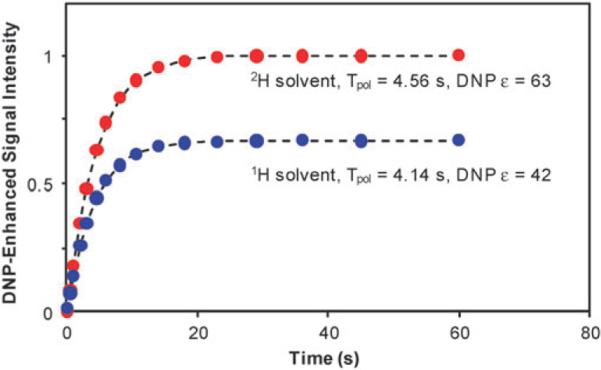
Deuterated solvents have been used to further enhance sensitivity for ¹H DNP experiments followed by CP to low abundance nuclei.^28–29,63 Fig. 8 shows the polarization build-up for 0.1 M proline in two different frozen solutions, glycerol-d₈–D₂O–H₂O (60 : 30 : 10 volume ratio) and fully protonated glycerol–H₂O (60 : 40 volume ratio), both with 10 mM TOTAPOL. The 90% deuterated solvent has a DNP signal enhancement of 63 while the protonated sample measures a factor of 42. The higher DNP signal enhancement is due to the reduced number of bulk ¹H spins and more ¹Hs are polarized with respect to total number of ¹H spins. The polarization build-up time constant is slightly longer with deuterated solvent, 4.56 s versus 4.14 s. Still, a net gain in sensitivity is obtained with solvent deuteration. The CP match condition can become much sharper with highly deuterated solvents, so a balance must be achieved between the DNP and CP efficiency.

Fig. 8.

DNP polarization build-up and signal enhancement, ε, for 0.1 M U-¹³C-¹⁵N-proline in glycerol-d₈–D₂O–H₂O (60 : 30 : 10 volume ratio), red circles, and in glycerol–H₂O (60 : 40 volume ratios), blue circles, both with 10 mM TOTAPOL. Polarization build-up measured with ¹H saturation recovery with ¹³C CP detection and normalized for maximum value of ²H solvent. 4 scans per point, ω_r/2π = 8 kHz, 97 K sample temperature, microwaves on continuously. The dashed lines through the data points show the fit to a single exponential function.

Power dependence, sample heating, and magic angle spinning

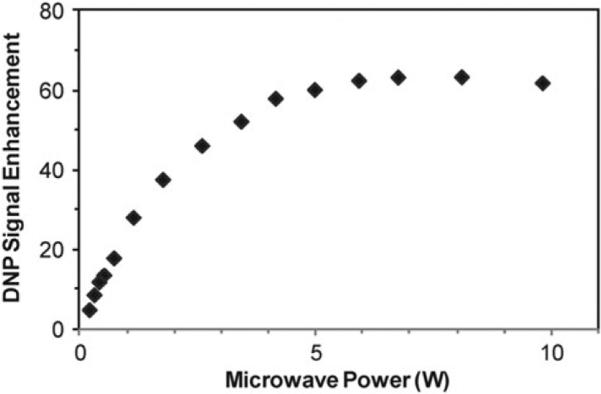
The DNP signal enhancement as a function of microwave power at the end of the probe waveguide is shown in Fig. 9. The DNP signal enhancement increases with microwave power up to a saturation level. This saturation level does not correspond to an intrinsic maximum DNP efficiency, but rather a contribution from a range of experimental parameters, such as the rotor material, beam pattern, coil design, sample temperature, etc. For example, during initial testing of different NMR coils for optimization of microwave penetration, the power curves showed the same pattern but reached a plateau at a lower maximum DNP signal enhancement. Similarly, different rotor materials lower the maximum DNP signal enhancement achieved. For zirconia rotors, the maximum DNP signal enhancement was 18–20% lower than for sapphire rotors filled with the same DNP stock solution and sample volume. The high output power of the 263 GHz gyrotron allows for DNP saturation studies, whereas experiments with the MIT 250 GHz gyrotron were often power limited.

Fig. 9.

¹H DNP signal enhancement as a function of microwave power at the end of the probe waveguide measured on 0.1 M U-¹³C-¹⁵N-proline in glycerol-d₈–D₂O–H₂O (60 : 30 : 10 volume ratio). ¹³C CPMAS experiment with 8 scans, 10 s recycle delay, 1 dummy scan, ω_r/2π = 8 kHz, 97 K sample temperature, microwaves on continuously. 64 scans were acquired for the microwave off measurement and the error bar on the DNP signal enhancement is ±1%. The gyrotron electron beam current, cathode voltage, and cavity temperature were varied to cover the full power range with constant frequency. The microwave power was measured with the transmission line directional coupler and calorimeter, calibrated with the water load at the end of the probe waveguide.

The sample temperature rise due to microwave irradiation was measured using a sealed KBr quartz capillary (0.7 mm OD) in a sapphire rotor (2.2 mm ID) filled with glycerol-d₈–D₂O–H₂O and 10 mM TOTAPOL. The temperature of the capillary sample was calculated from KBr T₁ measurements.⁵⁸ For a static sample, the sample temperature increased by more than 15 K upon microwave irradiation. At ω_r/2π = 1.2 kHz, the sample temperature increased by 8–9 K. The temperature rise due to microwave irradiation was also measured in sapphire and zirconia rotors fully packed with just KBr. For the sapphire rotor packed with KBr powder, a 4 K temperature rise with microwave irradiation was measured for static experiments, 1–2 K for ω_r/2π = 1.5 kHz, and <1 K for ω_r/2π = 8 kHz. The zirconia rotor filled with KBr experienced 11–12 K sample heating in static experiment and 4 K heating at ω_r/2π = 12.5 kHz. All measurements were performed with 6 W of microwave power at the end of the probe waveguide.

Sample spinning reduces microwave heating since the microwave irradiation is transverse to the sample rotation axis and different parts of the sample are heated during a rotation period. It is also beneficial for more uniform microwave irradiation of the sample. Additionally, for DNP experiments using a polarizing agent with an EPR line broadened by g-anisotropy in a static configuration only a subset of electron spins are on-resonance with microwave irradiation and take part in the DNP process. Since the nitroxide electron g-anisotropy, ~1 GHz, is 3 orders of magnitude larger than the spinning frequency, it is not averaged during MAS. Instead, during a rotor period, different electron spins become on resonance with the microwave frequency and effectively more electron spins are irradiated than during a static experiment.⁶⁴

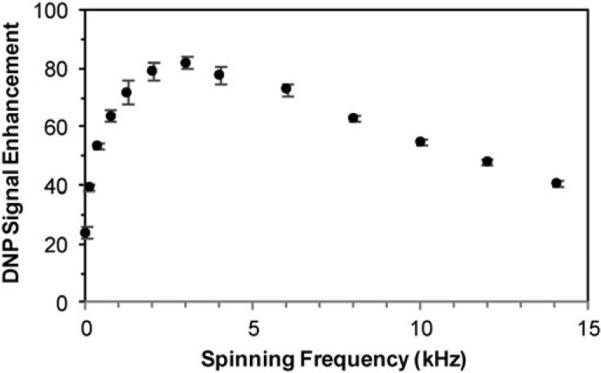
These factors contribute to the observed dependence of the DNP signal enhancement on the MAS frequency, shown in Fig. 10. The DNP signal enhancement increases quickly from static experiment to ω_r/2π = 3 kHz, reaches a maximum efficiency around 3 kHz, and then decreases as the spinning frequency is further increased.

Fig. 10.

Spinning frequency dependence of the ¹H DNP signal enhancement of 0.1 M U-¹³C-¹⁵N-proline in glycerol-d₈–D₂O–H₂O (60 : 30 : 10 volume ratio), measured with ¹³C CPMAS experiment at 97 K. Spectra were measured with and without microwave irradiation at each spinning frequency for calculation of the DNP signal enhancement. 10 s recycle delay, 1 dummy scan, 16 to 64 scans per experiment depending on the spinning frequency. Error bars are indicated on the plot.

We have observed from the KBr temperature measurements that for constant bearing, drive, and VT gas temperatures entering the MAS stator, the actual sample temperature in the sapphire rotor increases by 4 K from static to 8 kHz MAS spinning frequency and an additional 5 K from 8 to 12 kHz. Recalling the temperature dependence in Fig. 7 it is clear that increased sample temperature due to MAS would have an adverse effect on the DNP efficiency and comparison of the two data sets indicates that the decrease in DNP efficiency from 8 to 12 kHz spinning frequency is in qualitative agreement with the expected sample temperature rise due to sample spinning. For example, there is a 22% drop in DNP efficiency from ω_r/2π = 8 kHz to 12 kHz and 23% drop in DNP efficiency from 97.3 K to 103.0 K.

3.4 System stability for extended experiments

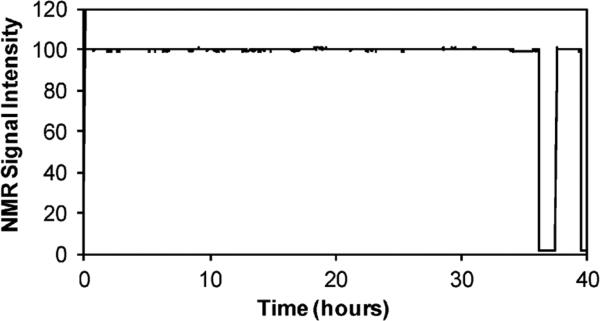
NMR measurements with hours or days of signal averaging time require stable experimental conditions. Gyrotron parameters that provided the frequency and power tuning capabilities described in Section 3.1 must now be held constant. Stable gyrotron and DNP operation was demonstrated during a 36 h run. The NMR signal intensity of the ¹³C_δ resonance of proline in water–glycerol with TOTAPOL is shown in Fig. 11 recorded as a series of ¹³C CPMAS experiments. The spinning frequency was regulated by the MAS controller at 8 kHz ± 2 Hz and the temperature by the BVT3000 LTMAS to within ±0.1 degree of set value on all three gas channels. The DNP-enhanced signal intensity variation is less than ±1% for the largest observed deviations (0.31% standard deviation). Measurements of DNP signal enhancements on similar samples and at similar experimental conditions, such as sample temperature, microwave power, and spinning frequency, are also highly reproducible between different experiments.

Fig. 11.

NMR signal intensity for ¹³C_δ resonance of 0.1 M ¹³C-¹⁵N proline in glycerol-d₈–D₂O–H₂O (60 : 30 : 10 volume ratio) with 10 mM TOTAPOL during extended experiment run consisting of 36 h gyrotron-on, followed by 80 min gyrotron-off, 2 h gyrotron back on and off again. ¹³C CPMAS experiment with 1.5 ms 55 kHz CP, 33 ms acquisition time with 100 kHz SPINAL64 decoupling, ω_r/2π = 8 kHz, 97 K sample temperature, 16 scans, 1 dummy scan, 6 s recycle delay for each point.

The 36 h gyrotron-on period was followed by 80 min with the gyrotron off and a 2 h back on period before final off, with the NMR acquisition continuing during all time periods. During the gyrotron-off segment, the cathode voltage is set to zero while the filament current remains at its last value before the gyrotron was turned off. When the gyrotron is turned back on, the cathode voltage increases gradually to 15 kV over approximately 30 s. The electron beam current briefly overshoots the target value and is then within 4 min regulated back down. The NMR signal intensity also takes a few minutes to stabilize, due to the cathode voltage ramp, electron beam current overshoot, and the equilibration time for the increase in sample temperature from microwave irradiation. Nevertheless, 5 min from when the gyrotron was turned back on, the NMR signal intensity had returned to within ±1% of its average value during the 36 h run. Significantly slower stabilization times after turning on the gyrotron were observed with previous designs at 140 and 250 GHz.^22,36–38 Detailed information including stability plots on the gyrotron parameters, cathode voltage, electron beam current, microwave power measurement, gyrotron cavity temperature, and tube vacuum, can be found in the ESI.†

4. Conclusion

A 263 GHz DNP spectrometer has been designed, built, and utilized for MAS NMR experiments at ~100 K with enhanced sensitivity. The measured dependence of the DNP signal enhancement on sample temperature, microwave power, and sample spinning frequency provide an insight into the possible parameter space for DNP experiments and highlight the requirements for stable and reproducible DNP signal enhancements. The spectrometer has been shown to have the high stability that is required for multi-dimensional experiments including correlation spectroscopy, and distance and torsion angle measurements. Examples of applications on amyloid fibrils and nanocrystals can be found in the publication by Debelouchina et al.⁶⁵ also submitted to this special issue of Physical Chemistry Chemical Physics on high frequency DNP. The water–glycerol solvent doped with TOTAPOL nitroxide biradical used in the experiments is compatible with a wide range of biological solids. The enhanced sensitivity from DNP experiments and the demonstrated stability should expand possible applications of solid-state NMR to samples that are otherwise unattainable due to small sample amount or dilute concentration, such as large membrane proteins or integral biological systems.