Conspectus
In any physicochemical process in liquids, the dynamical response of the solvent to the solutes out of equilibrium plays a crucial role in the rates and products: the solvent molecules react to the changes in volume and electron density of the solutes to minimize the free energy of the solution, thus modulating the activation barriers and stabilizing (or destabilizing) intermediate states. In charge transfer (CT) processes in polar solvents, the response of the solvent always assists the formation of charge separation states by stabilizing the energy of the localized charges. A deep understanding of the solvation mechanisms and time scales is therefore essential for a correct description of any photochemical process in dense phase and for designing molecular devices based on photosensitizers with CT excited states.
In the last two decades, with the advent of ultrafast time-resolved spectroscopies, microscopic models describing the relevant case of polar solvation (where both the solvent and the solute molecules have a permanent electric dipole and the mutual interaction is mainly dipole–dipole) have dramatically progressed. Regardless of the details of each model, they all assume that the effect of the electrostatic fields of the solvent molecules on the internal electronic dynamics of the solute are perturbative and that the solvent–solute coupling is mainly an electrostatic interaction between the constant permanent dipoles of the solute and the solvent molecules. This well-established picture has proven to quantitatively rationalize spectroscopic effects of environmental and electric dynamics (time-resolved Stokes shifts, inhomogeneous broadening, etc.). However, recent computational and experimental studies, including ours, have shown that further improvement is required.
Indeed, in the last years we investigated several molecular complexes exhibiting photoexcited CT states, and we found that the current description of the formation and stabilization of CT states in an important group of molecules such as transition metal complexes is inaccurate. In particular, we proved that the solvent molecules are not just spectators of intramolecular electron density redistribution but significantly modulate it.
Our results solicit further development of quantum mechanics computational methods to treat the solute and (at least) the closest solvent molecules including the nonperturbative treatment of the effects of local electrostatics and direct solvent–solute interactions to describe the dynamical changes of the solute excited states during the solvent response.
Introduction
Most chemical and biological processes occur in liquids. The dense and dynamic nature of the liquid phase provides a favorable environment for energy exchange and thus for chemical reactions.1−3 When we study photochemical reactions, the dynamical response of the solvent (the so-called solvation response function1,4,5) to solutes brought out of equilibrium by photoexcitation plays a crucial role in defining rates and products. Indeed the solvent molecules react to changes in the volume and electron density of the solutes to minimize the free energy of the solution, thus modulating the activation barriers and stabilizing (or destabilizing) intermediate states.1−4 An important case is polar solvation of photoexcited polar solutes in polar solvents, where the solvent–solute interaction is mainly dipole–dipole.
The first attempts to understand this time evolution were based on the extension to the time-dependent regime of the equilibrium solvation models of Born and Onsager.4 These treatments, however, do not take into account specific solvent–solute interactions, because they describe solvation as an effect of the bulk solvent dynamics. The advent of ultrafast spectroscopies in the 1990s brought new insights, by giving access to all relevant time scales of solvation relaxation (i.e., from tens of femtoseconds to tens of picoseconds)5 and allowing researchers to show the inadequacy of that approach.5,6 These studies triggered the development of microscopic models that include the specificity of rotational and translational motions of the solvent molecules closest to the solute.4 The application of these models to computer simulation studies has allowed great advances in the understanding of solvation dynamics at the molecular scale.2,3,5−7
With regard to solvation of metal complexes, ultrafast studies are surprisingly few. All the more so since this wide class of complexes is at the base of schemes for artificial photosynthesis, photocatalysis, and molecular based photovoltaic and optoelectronic devices.8−10 These complexes can indeed exhibit optically accessible metal-to-ligand or ligand-to-ligand charge transfer states (MLCT and LL′CT states, respectively), which make them versatile photosensitizers for light-energy conversion, molecular electronics, or photonic devices.11,12 They are also excellent ultrafast probes for fundamental studies on electron capture and transfer in biological molecules.13−15
In the last years, several research groups have worked on these topics,16−22 and our understanding has greatly advanced. These studies, mostly dealing with pyridine metal complexes, describe the photoexcited electron localization on the ligands as a convoluted process of electron-density redistribution, intersystem crossing, and intramolecular vibrational energy redistribution, which is completed within the first 100 fs after excitation.11,23,24
Nevertheless, slower picosecond kinetics, usually accompanied by a strengthening of the optical and vibrational transitions, were also reported.20,21,23,25−27 They were tentatively assigned to intramolecular mechanisms, such as interligand electron hopping, or to structural effects of intramolecular vibrational relaxations mediated by strong anharmonicities,20,21,23,25,26 but these explanations were not conclusive and other mechanisms could be invoked.26 In addition, such dynamics were also observed in complexes containing only one pyridine, thus questioning the explanation in terms of interligand electron hopping.17,21,26
All this evidence17−27 strongly suggests that the solvent can significantly affect the CT dynamics by shaping the electron density distribution and imposing the time scales, in contradiction to the aforesaid solvation models. These models assume that the solvent–solute interaction has a perturbative effect on the electronic properties of the complex. This implies that upon excitation the electron density distribution is fully defined by the excited electronic state, and the permanent dipole of the excited complex is immediately defined after the excitation. If this seems a reasonable assumption in the case of chromophores that do not undergo a direct CT process upon excitation, it is less straightforward with transition metal complexes exhibiting MLCT or LL′CT states. Indeed upon optical excitation of such transitions, very large changes in the dipole moment and thus of the reaction field (easily more than 10 D28 and 10 MV/cm,29 respectively) can be triggered, and in this case a perturbative approach could be insufficient.17,18 In this respect, a more complex picture of solvation dynamics in pyridine complexes was recently proposed, which invoked novel effects such as solute intercalation and clustering.29,30
Because of the relevance of the topic and the need to improve the present models, we investigated different metal complexes to understand how and under what conditions solvents and more generally local electrostatics can control electron density redistribution around a molecule and CT dynamics.
Among the several aforesaid evidence, we discuss in this Account two representative key cases that illustrate this behavior: solvent intercalation and clustering in pyridine complexes and unconstrained solvation in hyperpolarizable dithiolene complexes (Figure 1).
Figure 1.
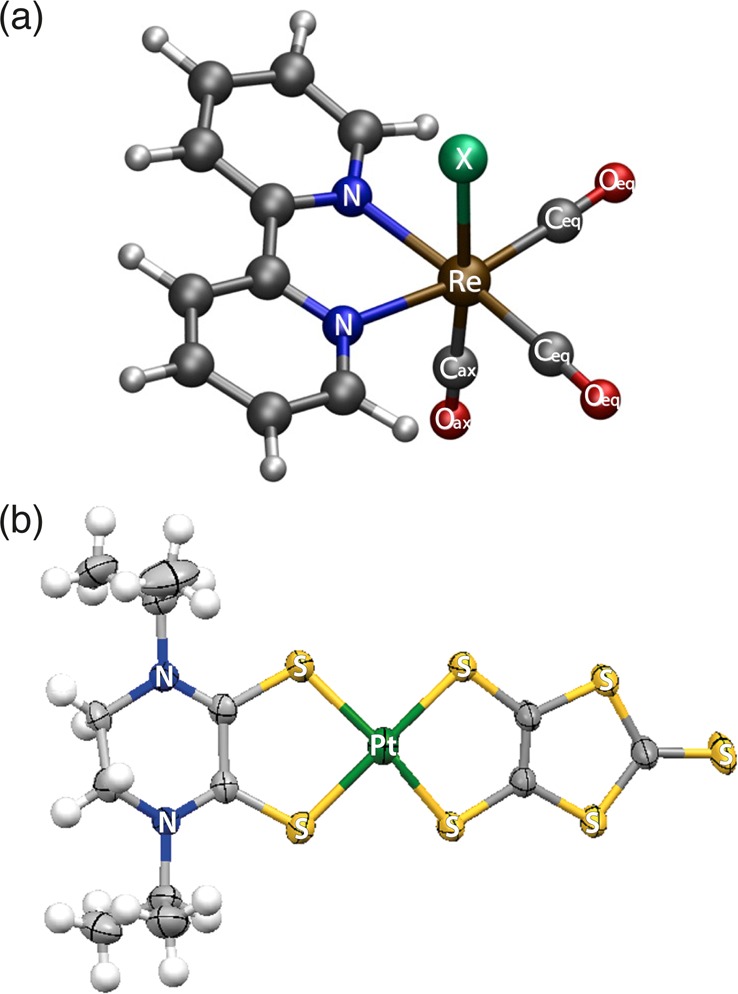
Structure of the investigated complexes: (a) rhenium carbonyl-diimine complexes [Re(X)(CO)3(bpy)]n (X = Cl, Br, I, n = 0; X = 4-ethyl-pyridine, n = 1+). Adapted with permission from ref (16). Copyright 2008 American Chemical Society. (b) A planar Pt dithione-dithiolato complex [Pt(iPr2pipdt)(dmit)]. Adapted with permission from ref (18). Copyright 2014 Royal Society of Chemistry.
Constrained Solvation-Driven Charge Transfer Process: Intercalation and Clustering Makes Solvent–Solute Interaction Stronger and Slower
Following the pioneering work by Vleck and co-workers,21,26 we investigated a series of rhenium carbonyl-diimine complexes (Figure 1) in acetonitrile (MeCN) and dimethylformamide (DMF),13,16 which are well suited for fundamental studies of photophysics of pyridine metal complexes, since they contain a single electron-accepting bipyridine ligand, thus avoiding the problem of excited-electron localization that is ubiquitous in Ru(II) polypyridine photophysics. Moreover, their carbonyl ligands can serve as IR markers of electron density redistribution around the central metal atom upon excitation.26,31 It was indeed observed that ν(CO) vibrations undergo detectable blue shifts proportional to the decrease of the electron density on the metal, which causes a decrease of Re → CO π back-donation and an increase of OC → Re σ donation.26,31 They can therefore serve as an instantaneous molecular electrometer to monitor electron density redistribution around the metal atom.
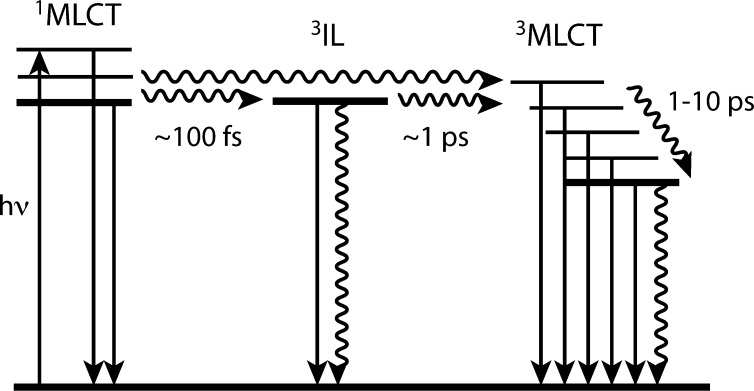
Although our main interest was to observe the changes in the electron density, the first mandatory step was the characterization by ultrafast time-gated emission of the photocycle to understand the nature of the excited states at any time after excitation and to disentangle intramolecular electronic relaxations from solvation related processes.16 The first singlet 1MLCT state, populated upon excitation at 400 nm, decays in ∼100 fs toward two triplet states: an intraligand (3IL) and a “hot” 3MLCT state. The intermediate 3IL state undergoes conversion to the 3MLCT on ∼1 ps, from which a long-lived phosphorescence stems. After the subsequent cooling of the 3MLCT in ∼10 ps, the electronic state appears equilibrated with no indication of further dynamics (Figure 2). Hence, when this study was complemented by femtosecond UV–vis transient absorption (TA) measurements,17,22 it was surprising to observe that more than 20% of TA signal kept increasing over 50 ps.
Figure 2.
Photocycle of [Re(L)(CO)3(N,N)]n complexes after ref (16) (see text for details). Adapted with permission from ref (16). Copyright 2008 American Chemical Society.
Figure 3 shows representative TA spectra (a) and kinetics (b) of [Re(Br)(CO)3(bpy)] in DMF at different time delays and wavelengths, respectively. To rule out any contribution due to rotational reorientation of the transition dipole, the measurements were carried out at the magic angle. The intensity of the dominant 373 nm band increases by more than 20% up to 20–40 ps with a rise time of 16 ps. The visible absorption (400–600 nm) rise is completed within ∼5 ps, in agreement with the relaxation of the 3IL to the 3MLCT state. The slower increase of the UV line was surprising in two respects: (1) no further changes in the population of the excited electronic state occur, in agreement with time-gated emission studies16 and with the evolution of the visible band; (2) it is slower than the slowest relevant component of the DMF solvation response function (1.7 ps).5
Figure 3.
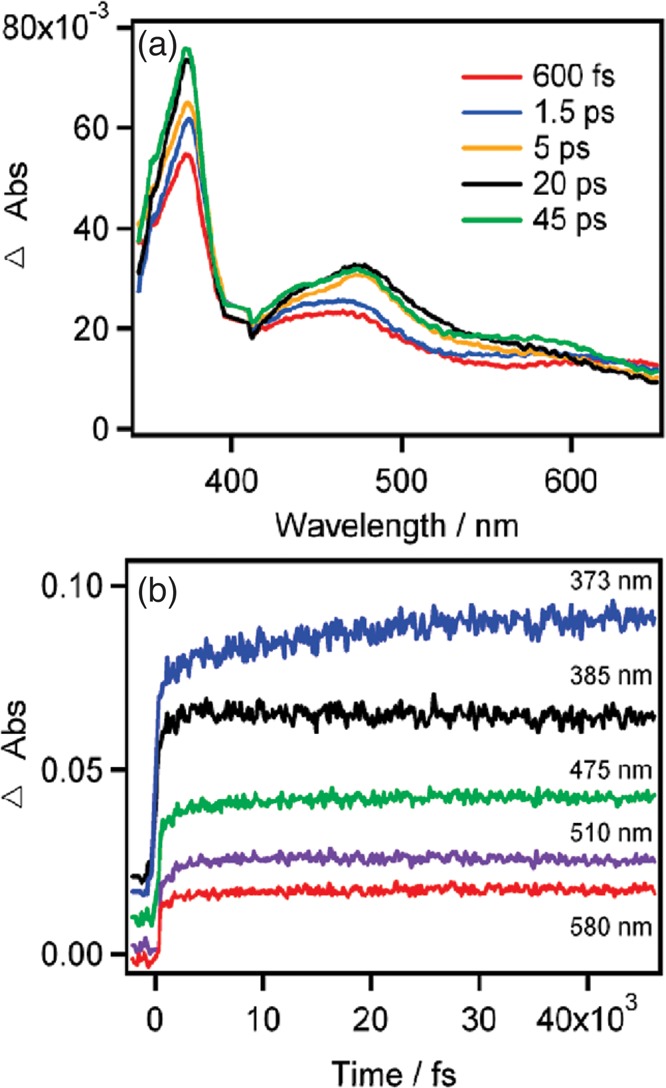
A representative selection of TA spectra at different time delays (a) and kinetic traces at different wavelengths (b) of [Re(Br)(CO)3(bpy)] in DMF after excitation (400 nm,1 kHz, 1 μJ/pulse, 100 μm spot, 150 fs time resolution) at magic angle.17 In panel b, traces are displaced vertically for clarity. Reproduced with permission from ref (17). Copyright 2010 American Chemical Society.
To clarify the role of the solvent, DMF was replaced by an ionic liquid with a very slow dielectric relaxation rate (0.1 to 1 ns depending on temperature).21 The effect is colossal: the intensity of the excited-state UV band (now at 360 nm) increases by more than 25% with a characteristic time of 710 ps (Figure 4). A matching behavior of the ν(CO) shifts was observed by Vlcek and co-workers, both in terms of time scales and dependence on the solvent (Figure 4b shows the case of slowly relaxing ionic liquids).
Figure 4.
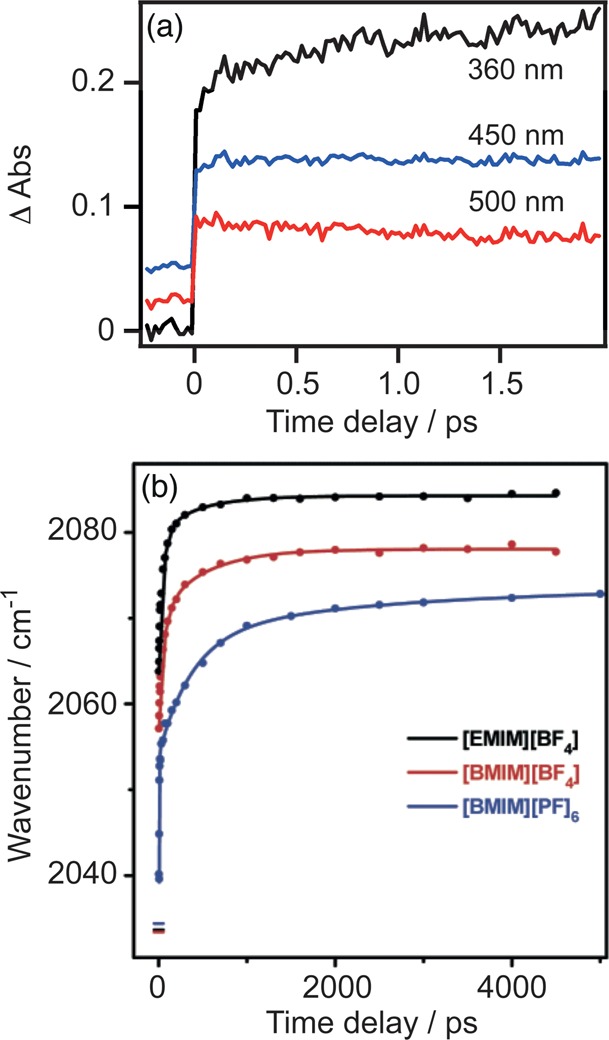
(a) Kinetic traces of [Re(Etpy)(CO)3(bpy)]+ in 1-ethyl-3-methylimidazolium tetrafluoroborate ([EMIM]BF4) at selected wavelengths at magic angle. Traces are displaced vertically for clarity.16,17 The excitation conditions are the same as those in Figure 3. Reproduced with permission from ref (17). Copyright 2010 American Chemical Society. (b) Time dependences of the A′(1) IR ν(CO) band peak in different ionic liquids. The horizontal lines at zero time delay show the ground-state positions of the A′(1) band. Reproduced with permission from ref (21). Copyright 2008 American Chemical Society.
To give a robust interpretation of these dynamics and infer a more conclusive picture, Zalis et al. carried out open-shell TD-DFT calculations to assign these UV–vis TA spectra.32 The origin of the intense band in the UV region is largely due to an IL ππ* transition of the reduced bpy moiety (Figure 5) and the excited states can be approximately formulated as *[ReII(Cl)(CO)3(bpy•–)]. Hence, the strength of this transition serves as an optical mark of the amount of charge effectively transferred from the metal. Conversely, the excited-state visible spectral pattern arises from predominantly LMCT transitions, which report mainly on the nature of the populated excited states but not on the reduction of the bpy.
Figure 5.
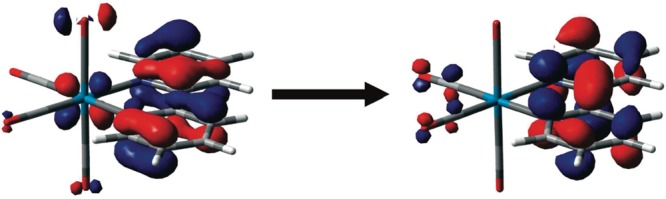
Spin orbitals involved in the transition responsible for the 373 nm excited-state absorption band of [Re(Br)(CO)3(bpy)] (the Br ligand points up). Reproduced with permission from ref (17). Copyright 2010 American Chemical Society.
The increase of the ππ*(bpy•–) band on a ∼15 ps time scale, while the LMCT bands in the visible remain essentially constant, is the most striking feature of this study. These kinetics in dipolar solvents are much slower than the longest significant component of solvation dynamics. Both the bpy•– absorbance rise and the ν(CO) dynamic shift become much slower (∼1000 ns and ∼330 ps, respectively) in the ionic liquid [EMIM]BF4 (Figure 4). The latter has a very different solvation mechanism and slow dielectric relaxation times of 130 ps and 1.29 ns. These observations indicate the following: (i) these kinetics describe the relaxation of the lowest triplet 3MLCT state but not the population changes; (ii) the process involves changes in the 3MLCT electronic wave function, whereby the electron density shifts from the Re(X)(CO)3 moiety to bpy; and (iii) the solvent is involved but neither through dielectric reorientation, nor as a simple heat-bath acceptor of vibrational energy, since the accompanying 9–15 ps ν(CO) dynamic shift is independent of solvent thermal diffusivity.26
A similar time scale of 5–15 ps was reported at magic angle and anisotropic TA of the bpy•– band of [Ru(bpy)3]2+ in MeCN and was assigned to interligand electron hopping.20 Recently Moret et al. demonstrated by QM/MM simulations of aqueous [Ru(bpy)3]2+ that the first hydration shell consists of ca. 15 water molecules intercalated between the bpy ligands.29,30 A water residence time in the first solvation shell of 12 ps was computed, three times longer than that of bulk water. Other confirmations of solvent intercalation in metal complexes come from soft X-ray fluorescence yield spectra of aqueous [Fe(CN)6]3+ and [Fe(bpy)3]2+.33
This picture was later confirmed and extended to [Ru(bpy)3]2+ in MeCN by Hoff et al.34 Similar calculations on Re carbonyl complexes are currently not available, but the open 3D structure of these complexes and their strong electric field gradients pointing toward the central-atom make the solvent restructuring and intercalation of polar solvents such as DMF and planar cations of ionic liquids21,35,36 a conceivable picture. It is worth mentioning that nanostructural organization in ionic liquids and its effect on inter- and intramolecular electron transfers were already reported.35,36
This evidence, together with our observations, points strongly to a slow solvent relaxation due to reorganization within a supramolecular cluster consisting of the [Re(X)(CO)3(bpy)]n chromophore and several strongly interacting local solvent molecules, probably lying between the ligands. Amazingly, the solvent reaction field turns out to be strong enough to prevent >20% of the transferred charge to be promptly localized on the ligand. The subsequent local-solvent restructuring changes the reaction field, allowing the Re(X)(CO)3 → bpy charge separation (CS) to evolve further, as befits the equilibrated 3MLCT state. The system undergoes a prompt and a slow CT process, as confirmed by the evolution of the area under the UV peak and the shift of the ν(CO) peaks, which consists of an “instantaneous” change within the instrumental time resolution (ITR) and a picosecond rise due to the increase of electron density on bpy•– and the concomitant electronic depopulation of the Re(CO)3. This interpretation of the <15 ps relaxation kinetics is applicable to the rise of the bpy•– UV band20 and resonance Raman bands of RuII–bipyridine complexes.37 The electron redistribution is solvent-driven but slower than the orientational dielectric relaxation of the solvent because the 3D structure of pseudo-octahedral Re and Ru complexes allows for solvent clustering around the molecule and solvation relaxation requiring more extensive restructuring of the solvent shell.29,30
In conclusion, the synergic use of UV–vis TA and time-resolved IR (TRIR) spectroscopies and computational methods have revealed a picture of the solvent–solute interaction in pyridine metal complexes much more complex than previously assumed: the two processes of solvent intercalation and distortion of the electron density distribution by local reaction field are revealed to be dominant in the CT formation, making the process solvent-driven. The derived picture provides a unifying explanation to several experimental results and corroborates recent computational simulations.
From a methodological point of view, this study shows the unique complementarity of UV pump–probe spectroscopy on pyridine38 and of TRIR on carbonyl ligand, which provide independent time-resolved information on the charge density of the accepting ligand and the Re(CO)3 unit, respectively. It is worth noticing that this approach is not limited to pyridine complexes, since similar UV bands were identified, which can serve as markers in other ligands, for example, in phenanthroline and dimethyl-phenanthroline.22 On the other hand, TRIR spectroscopy of carbonyl-diimine complexes is emerging as a new way to investigate various aspects of solvation dynamics and the role of interface fluctuation in electron injection.13,14
Solvent-Driven Charge Transfer in Hyperpolarizable Metal Complexes: Making a General Effect Detectable
The results discussed in the previous section might suggest that the dominant role of the solvent in shaping the electron density distribution originates from the particular condition of solvent intercalation, raising the question whether this could also happen with unconstrained solvents. To address this question, we investigated the ultrafast excited-state dynamics of planar Pt, Pd, and Ni dithione-dithiolato complexes in MeCN and DMF with TA18 and transient grating (TG) techniques.39 The interest was manifold but presently we will focus only on the solvent–solute interaction.
These complexes experience a strong metal–ligand electronic delocalization, because the metal and the ligand orbitals occur in the same energy range, giving origin to unique properties, among these exceptional polarizability and second-order nonlinear optical properties.40,41 They show an intense solvatochromic NIR absorption band in the 750–900 nm range that originates from the HOMO → LUMO transition of a predominantly dithiolato → dithione LL′CT character.40 Such a transition results in a large electron density redistribution in the complex and a large change of the molecular dipole moment, up to 11 D.28 They are planar and, except in the case of specific interactions with the solvent, the solute–solvent interactions that lead both to solvatochromism28,41 and femtosecond solvation dynamics are primarily electrostatic in nature. Last, as discussed hereafter, the optically populated LL′CT state typically survives several picoseconds. The coexistence of these properties makes metal dithiolene complexes prime candidates to investigate solvation-induced changes in the electronic structure of the solute. All the samples show the same photoinduced behavior:18 the lowest singlet excited state (a dmit → iPt2pipdt 1LL′CT state) is optically populated by 800 nm radiation and relaxes in 3.4 ps toward the lowest triplet state 3LL′CT after solvent reorganization (760 and 300 fs in DMF and MeCN, respectively) and cooling in 1–3 ps. In the 3LL′CT state, the system undergoes a multiphasic decay toward the ground state. In the following, we will show in detail only the representative case of [Pt(iPr2pipdt)(dmit)] (Figure 1).
Figure 6a shows a selection of TA spectra of [Pt(iPr2pipdt)(dmit)] in DMF at different pump–probe time delays. The earliest dynamics are also displayed in Figure 6b, where kinetic traces at selected probe wavelengths are plotted over the first 5 ps. A strong excited-state absorption (ESA) develops within the ITR (180 fs, fwhm), characterized by a broad band around 630 nm and an absorption below 440 nm that increases into the UV region. After the first few hundreds of femtoseconds, during which the signal stays nearly constant, most of the ESA decays in less than 10 ps, leaving a weak long-lasting (≫500 ps) component assigned to the 3LL′CT. The negative bands at 480 nm and ≥700 nm closely match the inverted steady-state absorption spectrum and are therefore attributed to the bleached ground-state absorption (GSB). Because we monitor at higher frequencies than the excitation, no emission signals are expected.
Figure 6.
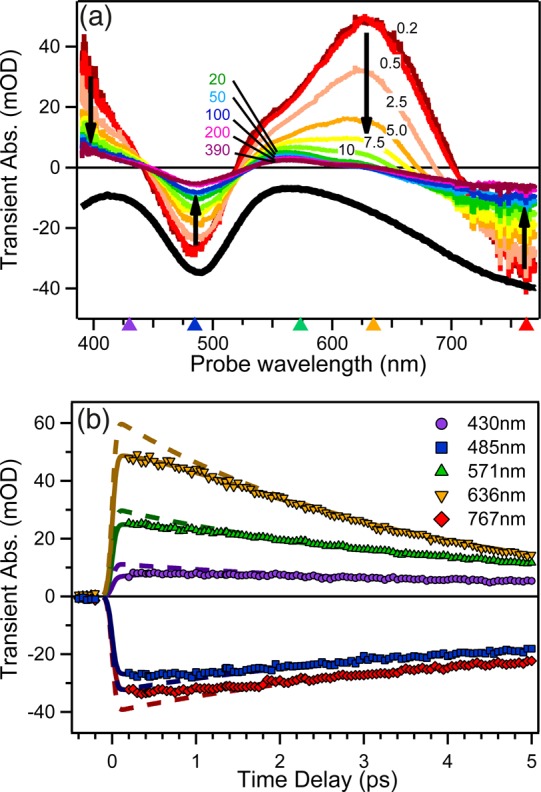
Representative selection of (a) TA spectra at different time delays and (b) kinetic traces of [Pt(iPr2pipdt)(dmit)] in DMF upon 800 nm excitation. (a) The black curve shows an inverted ground-state absorption spectrum. Black arrows indicate the evolution of the different bands with time. Triangles on the horizontal axis denote the wavelengths of the kinetic traces in panel b. (b) Solid and dashed lines are best fitting curves according to eq 1 and related discussion. Adapted with permission from ref (18). Copyright 2014 The Royal Society of Chemistry.
The most arresting result of these measurements is the lack of decay in the first hundreds of femtoseconds at any wavelength and regardless of the nature of the signal (ESA or GSB), as revealed by comparing the spectra at 200 and 500 fs and by the kinetics in panels a and b of Figure 6, respectively. Such kinetic behavior can be rationalized only assuming a sub-picosecond rise in the signal with its sign, which competes with the 3.4 ps depopulation mechanism. This is illustrated in Figure 6b where the experimental time traces ΔA(λ,t) are fitted according to a kinetic model with a rise component for the optically populated excited state (solid lines in Figure 6b):
| 1 |
u(t) is the Heaviside function, irf(t) is the response function, τj and τrise are the time constants of the relaxation processes relevant to the photocycle. In particular, we found τ1 = 3.4 ± 0.09 ps and τrise = 760 ± 60 fs for the exited state population decay and the rise, respectively.18 Another four constants were necessary to properly fit the traces corresponding to the 1LL′CT cooling in 1–3 ps and the 3LL′CT relaxations (cooling in 10 ps, rotational diffusion in 100s of ps, GS recovery).18 In the fitting procedure, they were considered as global parameters, while the amplitude Aλ,j and Rλ were wavelength dependent parameters. Rλ (= Aλ,rise/Aλ,j) is a number between 0 and 1 that represents the fraction of the total signal (Aλ,1) that evolves within τrise and is not instantaneously (within our ITR) generated upon excitation. The equation describes a sequential process where only the 1LL′CT is initially populated by the optical excitation and all the other vibrational and electronic states involved in the relaxation are populated from it. To point out the need for a rise component, the same functions with Rλ set to zero are plotted in Figure 6b (dashed lines). The comparison in Figure 6b shows that the observed kinetics speak unambiguously for a sub-picosecond rising component, which accounts for 20% of the total signal.
We also calculated Aλ,j and Aλ,rise as a function of wavelength (in this case Aλ,j are also called decay associated spectra, or DAS) and Figure 7 shows Aλ,1, Aλ,rise, and (Aλ,1 – Aλ,rise). The rise component, Aλ,rise, shows nearly the same shape as the singlet state ESA spectrum, Aλ,1, but with an inverted sign, indicating a rise of the whole signal at any wavelength occurring with a 760 fs lifetime. Most of Aλ,1 decays with 3.4 ps (see Figure 3) due to the depopulation of the 1LL′CT state, and a combination of this decay with the 760 fs rise kinetics explains the lack of spectral evolution in the sub-picosecond range. It is noteworthy that in (Aλ,1 – Aλ,rise), the component of the singlet state ESA spectrum Aλ,1 is instantaneously populated upon excitation.
Figure 7.
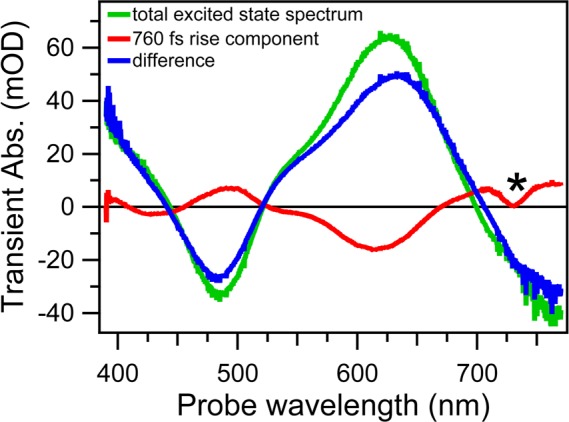
Decay associated spectra obtained by analysis of TA spectra of [Pt(iPr2pipdt)(dmit)] in DMF representing Aλ,1, the total signal from all the excited molecules after the solvation relaxation (green line); Aλ,rise, the 760 fs rise (red line); and their difference (blue line), which is the signal prior to any solvation. The * indicates an analysis artifact.
Given that the TA signal rise also concerns the GSB signal, we looked for further evidence of the sub-picosecond dynamics by carrying-out TG measurements resonant with the NIR transitions. In this experiment, two resonant pulses at 800 nm, arriving at the same time, create a spatial population grating in the sample, on which a delayed third pulse is diffracted. By monitoring the intensity of the diffracted light (the so-called TG signal), we were able to measure directly the GSB dynamics as TA but with twice better ITR (typically 80 fs fwhm). The technique and the setup are described in detail elsewhere.38,39
Typical TG traces are shown in Figure 8, where the data are compared with the respective TA traces at 800 nm. Similar results were found in all the other samples investigated (as an example, traces of [Ni(iPr2pipdt)(dmit)] in DMF are also shown). The improved time resolution definitively proves the presence of the initial strengthening of TA signals. Furthermore, TG data suggest that the rising component is multiphasic and even more pronounced than what was derived from the TA experiment. However, further investigation is required for a more conclusive statement.
Figure 8.
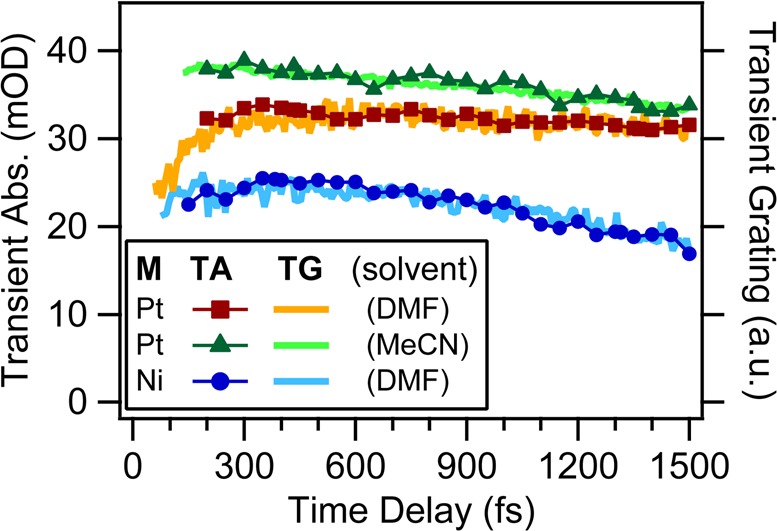
Comparison of TA (connected symbols) and TG (solid lines) measurements at 800 nm from [Pt(iPr2pipdt)(dmit)] in DMF and MeCN and [Ni(iPr2pipdt)(dmit)] in DMF. TA traces are inverted for comparison.
To clarify which steps are affected by solvation dynamics, we compared the behavior in DMF (Figure 6) and MeCN (Figure 9). These two solvents have comparable permanent dipole moments and static dielectric constants, while MeCN shows faster solvation response (150 fs) than DMF (670 fs).5 Static (not shown) as well as TA spectra show very similar spectral patterns in the two solvents, indicating the same characters of electronic transitions and excited states. The same analysis yielded a similar dependence of τrise on the solvent response time: the rise of the ESA signal and GSB deepening is twice faster in MeCN (300 ± 80 fs) than in DMF. TG and TA kinetics in Figure 8 show indeed a shorter initial plateau in MeCN than DMF, speaking for a faster rise time.
Figure 9.
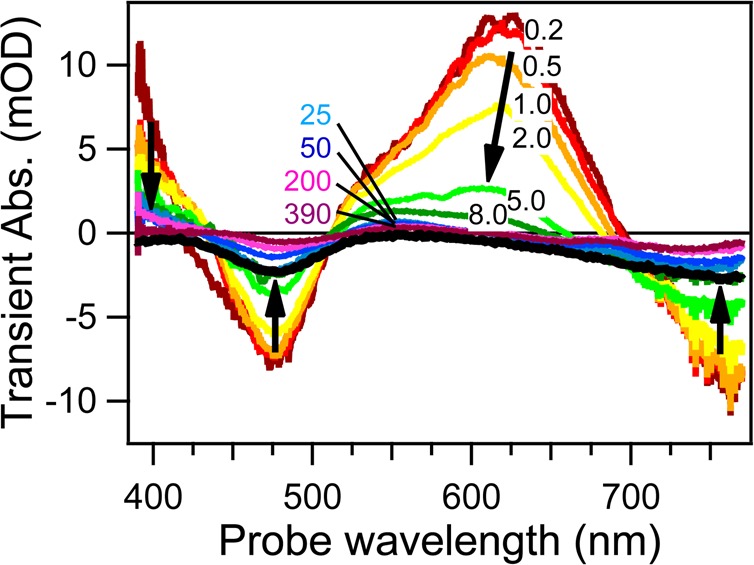
Representative selection of TA spectra at different time delays of [Pt(iPr2pipdt)(dmit)] in acetonitrile upon 800 nm excitation. The black curve shows an inverted ground-state absorption spectrum. Black arrows indicate the evolution of the different bands with time. Adapted with permission from ref (18). Copyright 2014 The Royal Society of Chemistry.
As in the case of metal pyridine complexes, the assignment of the ESA is a compulsory step to rationalize the origin of the femtosecond kinetics component. Based on the strong similarities between our TA spectra and the spectrum of the electrochemically monoreduced [Pt(Bz2pipdt)(dmit)]−,32 we can safely state that the excited electron is mainly localized at iPt2pipdt in the 1,3LL′CT states. This is expected, because of the prevalent HOMO → LUMO character of the LL′CT transition and the predominant LUMO localization on the iPt2pipdt dithione ligand.28,40 Moreover, solvent-dependent DFT and TD-DFT calculations revealed that the interaction with the solvent increases the HOMO and LUMO localization at the dithiolato and dithione ligands, respectively.40,41 On the other hand, the time constant τrise, measured in MeCN (300 fs) and DMF (760 fs), scales with the characteristic solvent relaxation time, 150 and 670 fs, respectively.5 Hence, we can attribute the femtosecond dynamics to solvation-driven charge redistribution in the excited molecule triggered by the large change in the molecular dipole moment (11 D for the investigated complexes).28 The derived picture is similar to the one of pyridine metal complexes: immediately after excitation, the solvent reaction field corresponds to the ground state dipole of the complex and this hinders the excitation-induced CT from dmit to iPt2pipdt. The subsequent solvent reorientation (which minimizes the total free energy corresponding to the new molecular charge distribution) drives the CS in the excited molecule to completion by changing the excited-state wave function. Experimentally, this is manifested in the rise of the ESA bands, since they originate from transitions localized at the ligand reduced by excitation. It can thus be argued that the LL′CT excited-state character (formally *1[M(II)(Rpipdt•–)(dmit•–)]) of the 1CT state is fully developed only after this ultrafast solvent relaxation step. This conclusion is supported by the mirrored match between the femtosecond rise DAS with the DAS corresponding to the LL′CT state depopulation (Figure 7).
Metal dithione-dithiolato complexes are planar, apparently not undergoing any specific solvation with MeCN or DMF; thus the solute–solvent interactions are primarily electrostatic in nature. In this respect, these complexes resemble the Coumarin 153 dye that was originally used to determine dynamics of nonspecific solvation dynamics.5 The common nonspecific, electrostatic nature of solvation explains the match between the solvation dynamics determined with Coumarin 1535 and metal dithione-dithiolato complexes. The strengthening of the GSB signal indicates that the excited state before the full development of the CS possesses weak ground-state-like absorption bands whose intensities decrease in the course of the CS, itself manifested in a deepening of the GSB signal.
Two concluding remarks are noteworthy. First, similar to the 3MLCT states of Re(I) and Ru(II) diimine complexes, the 1LL′CT excited states of dithione-dithiolato complexes present another example of solvation-driven CS. Thus, this process and the modulation of ESA bands originating from transitions localized on the photoreduced ligand suggest a very general scenario, which takes place in different excited states and coordination geometries. Second, we identified dithione-dithiolato complexes as a new prime family of probes to investigate solvation-induced changes in the solute electronic structure thanks to their large change in permanent dipole, the intramolecular dynamics of the LL′CT state being slower than the solvation response, an unusual polarizability and a pure electrostatic interaction with the solvent.
Final Comments and Perspective
Several studies in the last years have clearly pointed to unexpected solvent effects on the earliest ultrafast dynamics of CT states of several coordination complexes. Our study proves that the solvent can drive, rather than just affect, the excited-state dynamics of the solute, in particular by changing the electron density distribution around the latter. We found indeed that 20–25% (or even more, according to TG measurements) of the total transferred charge relaxes from the donor toward the acceptor following the solvent reorganization to the new equilibrium configuration. We strongly believe that this effect is general, but particularly relevant in chromophores with optically accessible CT states, as discussed in the Introduction.
In a broader perspective, we found that the current description of the formation and stabilization of CT states in the important transition metal complexes is certainly inaccurate. A more realistic picture of the electron density distribution and its evolution requires including the nonperturbative treatment of local electrostatics and direct solvent–solute interactions (as indeed intercalation and clustering). Our results solicit further development of quantum mechanics computational methods to treat the solute and (at least) the closest solvent molecules including the nonperturbative treatment of the effects of local electrostatics and direct solvent–solute interactions to describe the dynamical changes of the solute excited states during the solvent response. These methodological improvements and their extension to other solvents besides water and to intramolecular electrostatic environments is a challenge for future research.
These results have implications for the design of artificial photocatalyzers based on coordination complexes, since picosecond to 100s of picoseconds are time scales long enough to be relevant for photochemistry. It follows that many important ultrafast photochemical processes of metal pyridine complexes, such as electron injection into semiconductors or electron shuttling through macromolecules, actually occur from these unequilibrated states. Thus, understanding the nature of the distortion and controlling its lifetime could be relevant for supramolecular photochemistry. In this respect, generation of intramolecular or external intense (MV/cm to GV/cm) electric fields synchronized with the CT process is nowadays possible. It is for instance conceivable to use photoexcited retinals to generate intramolecular fields with tens of MV/cm strength in less than 100 fs, as it occurs in photoactivated proteins.38 Considering external fields, the technology to generate intense picosecond, even single-cycle terahertz, pulses is nowadays mature, and it has recently been proposed to use them in electric or magnetic switching applications.42
In conclusion, it is worth stating that the requirement of a nonperturbative approach to the photophysics of solvated molecules is very likely not limited only to transition metal complexes but also to nonmetal acceptor–donor complexes.
Acknowledgments
Financial support by European Union (ERC Starting Grant 279599), Swiss NSF through the NCCR MUST, and European programme COST (Action CM1202) is gratefully acknowledged. Authors are indebted to professors A. Vlcek, P. Deplano, and M. Chergui for their invaluable support and discussion. Investigation on pyridine complexes was carried out by A.C. while he was a research fellow in M. Chergui’s laboratories.
Biographies
Ariana Rondi (Ph.D. Physics, 2011, University of Geneva) is a Postdoctoral Fellow in the group of Professor Cannizzo at the University of Bern. Her research interests include quantum control, UV pulse-shaping, and nonlinear molecular spectroscopy.
Yuseff Rodriguez (M.S. Nuclear Physics, 2009, Higher Institute of Technologies and Applied Sciences of Havana) is a Ph.D. student at the University of Bern, supervised by Professors Feurer and Cannizzo. His research interests include nonlinear phenomena, pulse-shaping, and multidimensional spectroscopy.
Thomas Feurer (Ph.D., 1994, University of Wuerzburg) received his Habilitation in 2001 from the University of Jena. He continued his career as a research associate at MIT until 2004 when he became Professor at the University of Bern.
Andrea Cannizzo (Ph.D. Physics, 2005, University of Palermo) spent six years as a Postdoctoral Fellow at the Ecole Polytechnique Fédérale de Lausanne and is currently an Assistant Professor of Physics at the University of Bern since 2011. His research group focuses on functional dynamics in biomolecules, molecular devices, and supramolecular structures.
The authors declare no competing financial interest.
Special Issue
Published as part of the Accounts of Chemical Research special issue “Ultrafast Excited-State Processes in Inorganic Systems”.
References
- Pal S. K.; Zewail A. H. Dynamics of water in biological recognition. Chem. Rev. 2004, 104, 2099–2123. [DOI] [PubMed] [Google Scholar]
- Barbara P. F.; Meyer T. J.; Ratner M. A. Contemporary issues in electron transfer research. J. Phys. Chem. 1996, 100, 13148–13168. [Google Scholar]
- Heitele H. Dynamic solvent effects on electron-transfer reactions. Angew. Chem., Int. Ed. 1993, 32, 359–377. [Google Scholar]
- Bagchi B.; Jana B. Solvation dynamics in dipolar liquids. Chem. Soc. Rev. 2010, 39, 1936–1954. [DOI] [PubMed] [Google Scholar]
- Horng M. L.; Gardecki J. A.; Papazyan A.; Maroncelli M. Subpicosecond measurements of polar solvation dynamics: Coumarin-153 revisited. J. Phys. Chem. 1995, 99, 17311–17337. [Google Scholar]
- Jimenez R.; Fleming G. R.; Kumar P. V.; Maroncelli M. Femtosecond solvation dynamics of water. Nature 1994, 369, 471–473. [Google Scholar]
- Maroncelli M.; Fleming G. R. Comparison of time-resolved fluorescence Stokes shift measurements to a molecular theory of solvation dynamics. J. Chem. Phys. 1988, 89, 875–881. [Google Scholar]
- Kalyanasundaram K.; Graetzel M. Artificial photosynthesis: Biomimetic approaches to solar energy conversion and storage. Curr. Opin. Biotechnol. 2010, 21, 298–310. [DOI] [PubMed] [Google Scholar]
- Concepcion J. J.; Jurss J. W.; Brennaman M. K.; Hoertz P. G.; Patrocinio A. O. T.; Iha N. Y. M.; Templeton J. L.; Meyer T. J. Making oxygen with ruthenium complexes. Acc. Chem. Res. 2009, 42, 1954–1965. [DOI] [PubMed] [Google Scholar]
- Balzani V.; Credi A.; Venturi M. Photochemical conversion of solar energy. ChemSusChem 2008, 1, 26–58. [DOI] [PubMed] [Google Scholar]
- Kallioinen J.; Benko G.; Sundstrom V.; Korppi-Tommola J. E. I.; Yartsev A. P. Electron transfer from the singlet and triplet excited states of Ru(dcbpy)2(NCS)2 into nanocrystalline TiO2 thin films. J. Phys. Chem. B 2002, 106, 4396–4404. [Google Scholar]
- Campagna S.; Puntoriero F.; Nastasi F.; Bergamini G.; Balzani V. Photochemistry and photophysics of coordination compounds: Ruthenium. Top Curr. Chem. 2007, 280, 117–214. [Google Scholar]
- Blanco-Rodriguez A. M.; Di Bilio A. J.; Shih C.; Museth A. K.; Clark I. P.; Towrie M.; Cannizzo A.; Sudhamsu J.; Crane B. R.; Sykora J.; Winkler J. R.; Gray H. B.; Zalis S.; Vlcek A. Phototriggering electron flow through Re(I)-modified Pseudomonas aeruginosa azurins. Chem.—Eur. J. 2011, 17, 5349–5360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shih C.; Museth A. K.; Abrahamsson M.; Blanco-Rodriguez A. M.; Di Bilio A. J.; Sudhamsu J.; Crane B. R.; Ronayne K. L.; Towrie M.; Vlcek A.; Richards J. H.; Winkler J. R.; Gray H. B. Tryptophan-accelerated electron flow through proteins. Science 2008, 320, 1760–1762. [DOI] [PubMed] [Google Scholar]
- Arkin M. R.; Stemp E. D. A.; Holmlin R. E.; Barton J. K.; Hormann A.; Olson E. J. C.; Barbara P. F. Rates of DNA-mediated electron transfer between metallointercalators. Science 1996, 273, 475–480. [DOI] [PubMed] [Google Scholar]
- Cannizzo A.; Blanco-Rodriguez A. M.; El Nahhas A.; Sebera J.; Zalis S.; Vlcek A.; Chergui M. Femtosecond fluorescence and intersystem crossing in rhenium(I) carbonyl-bipyridine complexes. J. Am. Chem. Soc. 2008, 130, 8967–8974. [DOI] [PubMed] [Google Scholar]
- El Nahhas A.; Cannizzo A.; van Mourik F.; Blanco-Rodriguez A. M.; Zalis S.; Vlcek A.; Chergui M. Ultrafast excited-state dynamics of [Re(L)(CO)3(bpy)]n complexes: Involvement of the Solvent. J. Phys. Chem. A 2010, 114, 6361–6369. [DOI] [PubMed] [Google Scholar]
- Frei F.; Rondi A.; Espa D.; Mercuri M. L.; Pilia L.; Serpe A.; Odeh A.; Van Mourik F.; Chergui M.; Feurer T.; Deplano P.; Vlcek A.; Cannizzo A. Ultrafast electronic and vibrational relaxations in mixed-ligand dithione-dithiolato Ni, Pd, and Pt complexes. Dalton Trans. 2014, 17666–17676. [DOI] [PubMed] [Google Scholar]
- McCusker J. K. Femtosecond absorption spectroscopy of transition metal charge-transfer complexes. Acc. Chem. Res. 2003, 36, 876–887. [DOI] [PubMed] [Google Scholar]
- Wallin S.; Davidsson J.; Modin J.; Hammarstrom L. Femtosecond transient absorption anisotropy study on [Ru(bpy)3]2+ and [Ru(bpy)(py)4]2+. Ultrafast interligand randomization of the MLCT state. J. Phys. Chem. A 2005, 109, 4697–4704. [DOI] [PubMed] [Google Scholar]
- Blanco-Rodriguez A. M.; Ronayne K. L.; Zalis S.; Sykora J.; Hof M.; Vlcek A. Solvation-driven excited-state dynamics of [Re(4-Et-pyridine)(CO)3(2,2′-bipyridine)]+ in imidazolium ionic liquids. A time-resolved infrared and phosphorescence study. J. Phys. Chem. A 2008, 112, 3506–3514. [DOI] [PubMed] [Google Scholar]
- El Nahhas A.; Consani C.; Blanco-Rodriguez A. M.; Lancaster K. M.; Braem O.; Cannizzo A.; Towrie M.; Clark I. P.; Zalis S.; Chergui M.; Vlcek A. Ultrafast excited-state dynamics of rhenium(I) photosensitizers [Re(Cl)(CO)3(N,N)] and [Re(imidazole)(CO)3(N,N)]+: Diimine effects. Inorg. Chem. 2011, 50, 2932–2943. [DOI] [PubMed] [Google Scholar]
- Yeh A. T.; Shank C. V.; McCusker J. K. Ultrafast electron localization dynamics following photo-induced charge transfer. Science 2000, 289, 935–938. [DOI] [PubMed] [Google Scholar]
- Bhasikuttan A. C.; Suzuki M.; Nakashima S.; Okada T. Ultrafast fluorescence detection in tris(2,2′-bipyridine)ruthenium(II) complex in solution: Relaxation dynamics involving higher excited states. J. Am. Chem. Soc. 2002, 124, 8398–8405. [DOI] [PubMed] [Google Scholar]
- Damrauer N. H.; McCusker J. K. Ultrafast dynamics in the metal-to-ligand charge transfer excited-state evolution of [Ru(4,4′-diphenyl-2,2′-bipyridine)3]2+. J. Phys. Chem. A 1999, 103, 8440–8446. [Google Scholar]
- Liard D. J.; Busby M.; Matousek P.; Towrie M.; Vlcek A. Picosecond relaxation of 3MLCT excited states of [Re(Etpy)(CO)3(dmb)]+ and [Re(Cl)(CO)3(bpy)] as revealed by time-resolved resonance Raman, UV-vis, and IR absorption spectroscopy. J. Phys. Chem. A 2004, 108, 2363–2369. [Google Scholar]
- Onfelt B.; Lincoln P.; Norden B.; Baskin J. S.; Zewail A. H. Femtosecond linear dichroism of DNA-intercalating chromophores: Solvation and charge separation dynamics of [Ru(phen)2dppz]2+ systems. Proc. Natl. Acad. Sci. U. S. A. 2000, 97, 5708–5713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deplano P.; Pilia L.; Espa D.; Mercuri M. L.; Serpe A. Square-planar d8 metal mixed-ligand dithiolene complexes as second order nonlinear optical chromophores: Structure/property relationship. Coord. Chem. Rev. 2010, 254, 1434–1447. [Google Scholar]
- Moret M. E.; Tavernelli I.; Chergui M.; Rothlisberger U. Electron localization dynamics in the triplet excited state of [Ru(bpy)3]2+ in aqueous solution. Chem.—Eur. J. 2010, 16, 5889–5894. [DOI] [PubMed] [Google Scholar]
- Moret M. E.; Tavernelli I.; Rothlisberger U. Combined QM/MM and classical molecular dynamics study of [Ru(bpy)3]2+ in water. J. Phys. Chem. B 2009, 113, 7737–7744. [DOI] [PubMed] [Google Scholar]
- Dattelbaum D. M.; Omberg K. M.; Schoonover J. R.; Martin R. L.; Meyer T. J. Application of time-resolved infrared spectroscopy to electronic structure in metal-to-ligand charge-transfer excited states. Inorg. Chem. 2002, 41, 6071–6079. [DOI] [PubMed] [Google Scholar]
- Zalis S.; Consani C.; El Nahhas A.; Cannizzo A.; Chergui M.; Hartl F.; Vlcek A. Origin of electronic absorption spectra of MLCT-excited and one-electron reduced 2,2′-bipyridine and 1,10-phenanthroline complexes. Inorg. Chim. Acta 2011, 374, 578–585. [Google Scholar]
- Aziz E. F.; Rittmann-Frank M. H.; Lange K. M.; Bonhommeau S.; Chergui M. Charge transfer to solvent identified using dark channel fluorescence-yield L-edge spectroscopy. Nat. Chem. 2010, 2, 853–857. [DOI] [PubMed] [Google Scholar]
- Hoff D. A.; Silva R.; Rego L. G. C. Subpicosecond dynamics of metal-to-ligand charge-transfer excited states in solvated [Ru(bpy)3]2+ complexes. J. Phys. Chem. C 2011, 115, 15617–15626. [Google Scholar]
- Castner E. W.; Margulis C. J.; Maroncelli M.; Wishart J. F. Ionic liquids: Structure and photochemical reactions. Annu. Rev. Phys. Chem. 2011, 62, 85–105. [DOI] [PubMed] [Google Scholar]
- Nagasawa Y.; Miyasaka H. Ultrafast solvation dynamics and charge transfer reactions in room temperature ionic liquids. Phys. Chem. Chem. Phys. 2014, 16, 13008–13026. [DOI] [PubMed] [Google Scholar]
- Henry W.; Coates C. G.; Brady C.; Ronayne K. L.; Matousek P.; Towrie M.; Botchway S. W.; Parker A. W.; Vos J. G.; Browne W. R.; McGarvey J. J. The early picosecond photophysics of Ru(II) polypyridyl complexes: A tale of two timescales (vol 112A, pg 4537, 2008). J. Phys. Chem. A 2008, 112, 10703–10704. [DOI] [PubMed] [Google Scholar]
- Cannizzo A. Ultrafast UV spectroscopy: From a local to a global view of dynamical processes in macromolecules. Phys. Chem. Chem. Phys. 2012, 14, 11205–11223. [DOI] [PubMed] [Google Scholar]
- Frei F.Automated two-dimensional pulse shaping and spectroscopy. Ph.D. Thesis, Universität Bern, 2011. [Google Scholar]
- Espa D.; Pilia L.; Marchio L.; Artizzu F.; Serpe A.; Mercuri M. L.; Simao D.; Almeida M.; Pizzotti M.; Tessore F.; Deplano P. Mixed-ligand Pt(II) dithione-dithiolato complexes: Influence of the dicyanobenzodithiolato ligand on the second-order NLO properties. Dalton Trans. 2012, 41, 3485–3493. [DOI] [PubMed] [Google Scholar]
- Pilia L.; Espa D.; Barsella A.; Fort A.; Makedonas C.; Marchio L.; Mercuri M. L.; Serpe A.; Mitsopoulou C. A.; Deplano P. Combined experimental and theoretical study on redox-active d8 metal dithione-dithiolato complexes showing molecular second-order nonlinear optical activity. Inorg. Chem. 2011, 50, 10015–10027. [DOI] [PubMed] [Google Scholar]
- Merbold H.; Brunner F.; Cannizzo A.; Feurer T. Near field enhancement for THz switching and THz nonlinear spectroscopy applications. Chimia 2011, 65, 316–319. [DOI] [PubMed] [Google Scholar]