Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2015 Apr 23;119(20):6190–6197. doi: 10.1021/acs.jpcb.5b02348

Enhanced Ligand Sampling for Relative Protein–Ligand Binding Free Energy Calculations

Joseph W Kaus †, J Andrew McCammon †,‡,¶,§,*
PMCID: PMC4442669  PMID: 25906170

Abstract

graphic file with name jp-2015-023488_0008.jpg

Free energy calculations are used to study how strongly potential drug molecules interact with their target receptors. The accuracy of these calculations depends on the accuracy of the molecular dynamics (MD) force field as well as proper sampling of the major conformations of each molecule. However, proper sampling of ligand conformations can be difficult when there are large barriers separating the major ligand conformations. An example of this is for ligands with an asymmetrically substituted phenyl ring, where the presence of protein loops hinders the proper sampling of the different ring conformations. These ring conformations become more difficult to sample when the size of the functional groups attached to the ring increases. The Adaptive Integration Method (AIM) has been developed, which adaptively changes the alchemical coupling parameter λ during the MD simulation so that conformations sampled at one λ can aid sampling at the other λ values. The Accelerated Adaptive Integration Method (AcclAIM) builds on AIM by lowering potential barriers for specific degrees of freedom at intermediate λ values. However, these methods may not work when there are very large barriers separating the major ligand conformations. In this work, we describe a modification to AIM that improves sampling of the different ring conformations, even when there is a very large barrier between them. This method combines AIM with conformational Monte Carlo sampling, giving improved convergence of ring populations and the resulting free energy. This method, called AIM/MC, is applied to study the relative binding free energy for a pair of ligands that bind to thrombin and a different pair of ligands that bind to aspartyl protease β-APP cleaving enzyme 1 (BACE1). These protein–ligand binding free energy calculations illustrate the improvements in conformational sampling and the convergence of the free energy compared to both AIM and AcclAIM.

Introduction

Protein–ligand interactions are important to study during the development of new pharmaceuticals. One way to study these interactions is by using relative binding free energy (RBFE) calculations. These calculations combine alchemical perturbations of the ligand with molecular dynamics (MD) to predict the binding free energy for two ligands to a common receptor. The accuracy of the resulting free energy depends on both an accurate force field and adequate conformational sampling.1−5 Adequate conformational sampling may occur on time scales longer than can be explored with conventional MD. A lack of proper conformational sampling can cause the system to become stuck in a metastable state, which makes the resulting free energy dependent on the initial conformation of the ligand. Each ligand conformation has a different affinity for the protein; therefore, the lack of proper sampling can prevent convergence of the calculated free energy.

A number of methods have been developed to improve conformational sampling in free energy calculations, including the Adaptive Integration Method (AIM).1 AIM changes the alchemical coupling parameter, λ, during the course of a single simulation, so that conformations sampled at one λ can help sampling at other λ values. This is similar to λ-hopping replica exchange methods,6 but only a single simulation is run rather than a series of replicas run in parallel with different λ values.

Many of the methods that have been developed to enhance conformational sampling modify the potential energy surface to decrease the barriers separating the major conformations. These methods include accelerated MD (aMD),7−9 replica exchange with solute tempering (REST),10−13 and the accelerated adaptive integration method (AcclAIM).2 These methods alter the potential energy to lower the barrier between conformations, making it more likely for these conformations to be adequately sampled. However, for systems with very large barriers, these methods may not be able to lower the barrier enough for proper sampling to take place. An example of this is a ligand that binds to aspartyl protease β-APP cleaving enzyme 1 (BACE1), which has a pyridine ring with a propynyl group attached. The interaction between the substituted ring and the protein causes the barrier separating the ring conformations to be very large. In this case, even applying enhanced sampling methods is not sufficient to adequately sample the different ring conformations, making the resulting free energy dependent on the initial conformation of the ring.

Monte Carlo (MC) simulations have been used as an alternative to MD for conformational sampling. In principle, using MC for sampling has the advantage that the system can move directly from one potential well to another, without needing to climb over it. However, with biomolecular systems, it may be difficult to determine which changes in the coordinates will adequately sample both protein and ligand conformations.14 This method of sampling has been used for free energy calculations15 including with a modified form of REST.16

In this work, we describe a method called AIM/MC which alters conformational MC moves to overcome large conformational barriers, with MD, to sample smaller motions. Incorporating conformational MC into AIM improves conformational sampling for ligands with conformations separated by large potential barriers. We examined ligands with asymmetric substitutions of a six-membered conjugated ring, either pyridine or phenyl. These rings have two possible orientations with respect to the protein, and properly sampling these two ring conformations is difficult due to the large potential barrier separating them.

AIM/MC is applied to two protein–ligand relative binding free energy calculations. The first transformation involves calculating the relative binding free energy of two ligands to thrombin, a system which has been studied previously with REST13 and AcclAIM.2 We show that AIM/MC is able to rapidly sample the different ring conformations of the ligand, resulting in quick convergence of the free energy, with less uncertainty compared to AcclAIM. Then, AIM/MC was applied to calculate the relative binding free energy of two ligands to BACE1. In this system, one ligand has a large propynyl functional group attached to the pyridine ring, making it difficult for AcclAIM to properly sample both conformations. However, AIM/MC is able to properly sample both ring conformations, resulting in a converged free energy. In both transformations, AIM was not able to properly sample the ring conformations, causing the free energy to depend on the initial ring conformation.

Theory and Methods

Adaptive Integration Method

A brief description of AIM and AcclAIM is presented here; see Fasnacht et al.1 and Kaus et al.2 for a more thorough description. AIM is used to calculate the free energy of alchemically transforming a molecule from an initial state to a final state. These states are represented by the alchemical coupling parameter λ, which varies from λ = 0 representing the initial state to λ = 1 representing the final state. AIM uses biased MC to dynamically alter the λ value during the simulation, allowing conformations sampled at one λ to aid sampling at other λ values.1,2 The biasing factor helps improve the probability of accepting a move between adjacent λ values, with the acceptance criterion

graphic file with name jp-2015-023488_m001.jpg 1

Pacc,AIM is the probability of accepting the transitions between λ values, ΔU is the difference in the potential energy between adjacent λ values for a given conformation, and ΔF is the biasing factor. In this work, the biasing factor denoted as MC2,2 was used for all simulations. In principle, a number of methods could be used to calculate the free energy, including thermodynamic integration (TI),17 Bennett acceptance ratio (BAR),18 and multistate Bennett acceptance ratio (MBAR).19,20 In this work, the free energies were calculated using TI with cubic spline interpolation for the method of numerical integration. This has been shown to give better results compared to trapezoidal integration.21,22

AcclAIM builds on AIM by modifying the potential energy at intermediate λ values in a way that decreases the size of potential barriers, making it easier for the system to overcome the barrier and sample alternate conformations. The modified potential is given by2

graphic file with name jp-2015-023488_m002.jpg 2

where α determines how much the potential energy is scaled at intermediate λ values. At λ = 0 or λ = 1, the original potential energy is recovered, so that the resulting free energy is not biased by the modifications to the potential energy.2 Usually, only part of the potential energy is modified, so that the acceptance ratio for moves between adjacent λ values remains reasonably high.2

While AcclAIM has been shown to improve conformational sampling for free energy calculations,2 there are cases where the barrier separating the conformations is very high, preventing proper sampling even using AcclAIM. To overcome this challenge, we examined the combination of a conformational MC step with AIM, developing a method called AIM/MC. This MC step helps improve sampling, by rotating part of the molecule a certain number of degrees and then accepting the change in conformation with the probability

graphic file with name jp-2015-023488_m003.jpg 3

where ΔUconf is the difference in the potential energy between the initial and final conformations. The probability of accepting the move is higher when the potential energy for the final conformation is lower than the potential energy for the initial conformation. In the context of free energy calculations, if part of the molecule is modeled using softcore potentials23−27 and this part is fully interacting at the final state where λ = 1, then it will not contribute to the nonbonded potential at λ = 0 and is said to be decoupled. This decoupling increases the acceptance probability because moves that would have been rejected due to steric clashes can now be accepted for this step. Correct sampling is maintained because changes between adjacent λ values are still accepted with the probability given by eq 1.

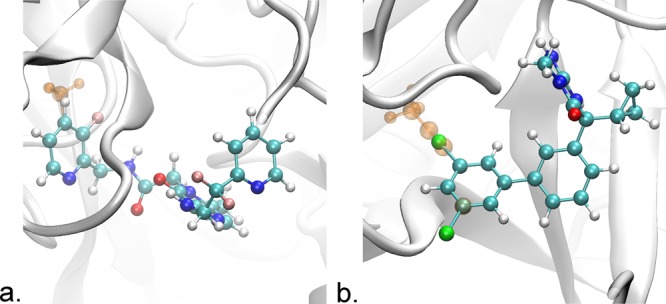
While this method could be applied to any part of the molecule that is decoupled at either the initial or final state, the focus of this work was demonstrating this method on ligands containing planar six-membered rings. These rings have bulky functional groups attached, making proper sampling of the different ring conformations difficult. An example is shown in Figure 1 for two ligands that bind to BACE1. The one ligand, 17a, has a 2,5-dichlorophenyl group and the other ligand, 24, has a propynyl group attached. Figure 1a shows the initial state, where the Chlorine atoms fully interact with the rest of the system and the propynyl group is decoupled. Rotations of the ring by 180° will be accepted with a higher probability, because the 2,5-dichlorophenyl group is symmetric about the axis of rotation. In practice, small differences in the positions of the corresponding atoms will reduce the acceptance probability, but it will still be sufficiently high to improve conformational sampling. Figure 1b shows the final state, where the chlorine atoms are decoupled and the propynyl group fully interacts with the rest of the system. Attempts to rotate the ring will have a low acceptance probability because the propynyl atoms are likely to sterically clash with protein or water atoms.

Figure 1.

Figure 1

Open in a new tab

Two ligands bound to BACE1 (gray ribbon) in (a) the initial state at λ = 0 and (b) the final state at λ = 1. Ligand 17a has a 2,5-dichlorophenyl group, while ligand 24 has a propynyl group attached to a pyridine ring. In the initial state, ligand 17a fully interacts with the rest of the system (opaque spheres), while the propynyl group of ligand 24 is decoupled (transparent spheres) and does not interact with the rest of the system. In the final state, the chlorine atoms of ligand 17a are decoupled (transparent spheres), while the propynyl group fully interacts (opaque spheres). The acceptance probability after a rotation when the molecule is in the initial state will be high, because of the symmetry of 2,5-dichlorophenyl. In this state, the propynyl atoms are decoupled and do not have charge or vdW interactions with the protein or water molecules, preventing steric clashes. The acceptance probability after rotation in the final state will be much lower, due to a higher chance of steric clashes between the propynyl group and other molecules in the system. Tachyon28 in visual molecular dynamics29 was used for rendering.

Using AIM, the conformations sampled in the initial state will still improve sampling of the ring in the final state. Thus, AIM/MC is most effective when the rotation is made while this part of the molecule is in the decoupled state, so the acceptance probability is reasonably high. This is also an important limitation of this method; unlike AcclAIM which is general to any degree of freedom,2 this MC step requires knowledge about the slow degrees of freedom. These slow degrees of freedom must also have a decoupled state which is sufficiently symmetric such that rotation between the major possible conformations has a reasonable acceptance probability. This method is also applicable to ligands containing multiple rings. If the rings are not coupled, that is rotation of one ring does not affect the rotation of the other, then the method can be applied independently to each ring. However, if the rings are coupled, as with the BACE1 ligands, then the outer ring would need to be decoupled, so that the acceptance probability would remain reasonably high.

Simulation Details

The simulations in this work used a modified version of the pmemd module in the Amber 12 package.30 These modifications allow alchemical transformations to be run using pmemd,31 and include AIM and AcclAIM.2 Additional changes were then made to run the conformational MC procedure.

System Parametrization

The system was parametrized using Amber 99SB-ILDN32,33 for the protein, the generalized Amber force field (GAFF)34 for the ligands, and TIP3P for the solvent.35 The partial charges for the ligands were derived using Gaussian 0936 by fitting the electrostatic potentials determined using Hartree–Fock/6-31G* to atomic centers with RESP.37 The simulations used a truncated octahedral box, which was large enough so that the solute atoms were at least 10 Å away. Short-range nonbonded interactions used an 8 Å cutoff, and long-range electrostatics used particle mesh Ewald (PME).38 Bonds to hydrogen atoms were constrained with SHAKE39 and SETTLE40 so that a 2 fs time step could be used. LEaP was used to add missing atoms.30

System Equilibration

To start, a 20000-step steepest descent minimization was run. This was followed by heating the system to 300 K over 500 ps using the Langevin thermostat41,42 with a 2 ps–1 collision frequency. Then, a 500 ps NPT simulation was run using the Berendsen barostat,43 with the pressure at 1 bar and a 2 ps coupling constant. Finally, a 500 ps NVT simulation was run as equilibration.

Distribution of λ Values

The procedure used to determine the number of λ values is the same as described previously.2 Briefly, a short 110 ps simulation was run starting with 11 λ values, equally spaced between λ = 0 and λ = 1. The term ΔU – ΔF, which is described in eq 1, was recorded every 50 steps. Then every 5 ps, the λ value changed, increasing until λ = 1 and then going back to λ = 0.

The average value for the term ΔU – ΔF was determined at each λ window. If this value was greater than 2 kcal/mol for a pair of adjacent λ values, N additional windows were added as given by ref (2)

graphic file with name jp-2015-023488_m004.jpg 4

The number of λ values obtained using this procedure for the production simulations are summarized in Table S5 in the Supporting Information.

Production Simulations

Production simulations were run for 55 ns. Changes in λ were attempted every 500 steps, with the acceptance probability given by eq 1. For the AIM/MC simulations, conformational changes were attempted every 100 steps when λ < 0.5, with the acceptance criterion given by eq 3. At higher λ values, the asymmetry of the ligand was expected to make the acceptance ratio very low, so conformational MC moves were not attempted. Energies and coordinates were recorded every 500 steps for later analysis. System specific simulation details are discussed below.

Protein–Ligand Complexes

Thrombin Ligand Transformation

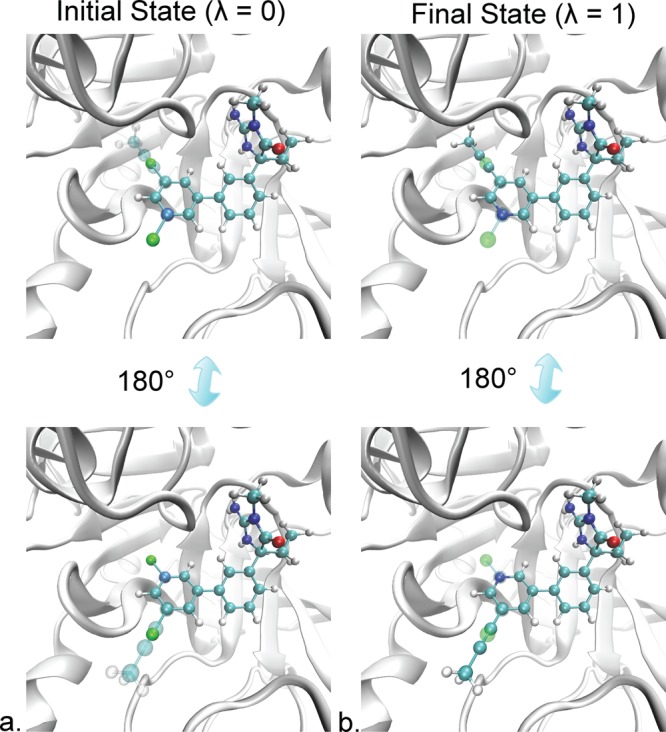
The first transformation studied was the relative binding free energy of the ligands CDA and CDB to thrombin. This transformation has been studied previously using REST,13 AIM, and AcclAIM.2 The preparation for this system is the same as in the AIM and AcclAIM study;2 for ease of reference, the procedure for preparing this system will be recapitulated here. Compared to CDA, CDB has an additional methyl group attached to the P1 pyridine ring (see Figure 2a). Separate simulations were started with the P1 pyridine ring in the In and Out conformations to assess convergence. The fluorine atom attached to the P1 pyridine ring was set to be softcore, as was done in both the REST13 and the AcclAIM2 studies. AIM/MC was applied to enhance sampling of the transition between the two possible ring conformations. The 180° rotations of the P1 pyridine ring about the axis defined by the CDA ligand atoms C15 and C16 were attempted, using the acceptance probability defined by eq 3. The structure of these ligands with the atoms numbers listed is given in Figure S1 in the Supporting Information. The initial structure of thrombin bound to CDA came from PDB 1MU6, with the structure of CDB from PDB 1MU8.44 Residues 146 to 150 were modeled using the structure from PDB 4MLF.45 The histidine residues were set to the epsilon form.

Figure 2.

Figure 2

Open in a new tab

Structures of the systems studied in this work. (a) Thrombin (gray ribbon) bound to the ligands CDA and CDB. The ligands differ in that CDB has a methyl group, represented here in orange, attached to the P1 pyridine ring. This ring has two possible conformations, one where the methyl group points In toward the protein as shown here and the other where the ring has flipped out. (b) BACE1 (gray ribbon) bound to the ligands 17a and 24. Ligand 17a has a 2,5-dichlorophenyl group, while ligand 24 has a 5-(Prop-1-yn-1-yl)pyridin-3-yl group. The atoms unique to ligand 24 are shown as transparent orange. This ring has two possible conformations, either In as shown or Out where it is flipped 180°. Tachyon28 in visual molecular dynamics29 was used for rendering.

BACE1 Ligand Transformation

The second transformation studied was the relative binding free energy of the ligands 17a and 24 to BACE1. Ligand 17a has a 2,5-dichlorophenyl group, while ligand 24 has a 5-(Prop-1-yn-1-yl)pyridin-3-yl group as shown in Figure 2b. The binding affinity for these ligands is known experimentally, and ligand 24 also has a crystal structure (PDB 4DJY).46 The chlorine atoms of ligand 17a and the propynyl atoms of ligand 24 were set to be softcore. The AcclAIM simulations scaled the potential for all of the atoms in the perturbed ring. For these simulations, the acceleration parameter α was set to 0.05. AIM/MC simulations were run, with 180° rotations attempted about the axis defined by the atoms C13 and C14. The structure of these ligands with the atoms numbers listed is given in Figure S2 in the Supporting Information. As with the thrombin transformation, separate simulations were run with the ring starting with the In and Out conformations. The initial structure of BACE1 bound to ligand 24 came from PDB 4DJY.46 The structure for ligand 17a was modeled using ligand 24, with the appropriate changes made to the structure. The Histidine residues were set to the epsilon form. All acidic residues, including those in the ligand binding site, were deprotonated.

Analysis and Error

Four trials were run for each simulation. Free energies were calculated using TI17,47 with cubic spline interpolation and subsampling as implemented in pyMBAR (https://simtk.org/home/pymbar).19,21 Free energy results were computed as a function of total simulation time by averaging over the four simulations and propagating the error according to

graphic file with name jp-2015-023488_m005.jpg 5

The probability of finding the ring in either the In or Out conformation was calculated as a function of simulation time. The dihedral connecting the ring of interest to the rest of the molecule was used to determine the ring conformation. For thrombin, this dihedral is defined by the CDA atoms N5, C15, C16, and C17 (see Figure S1a in the Supporting Information). For BACE1, this dihedral is defined by the ligand 17a atoms C15, C14, C13, and C11 (see Figure S2a in the Supporting Information). The probabilities were averaged over the four trials, with the error given by the standard deviation.

Results and Discussion

Free Energy Results

Thrombin

Sampling of the P1 pyridine ring conformations for the thrombin ligands was determined by examining the fraction of time that the ring spends in the In conformation as a function of simulation time. Figure 3a shows the fraction In at λ = 0, which corresponds to CDA, and Figure 3b shows the fraction In at λ = 1, which corresponds to CDB. The results for AIM and AcclAIM with α = 0.05 come from the AcclAIM study2 and are reproduced here for comparison.

Figure 3.

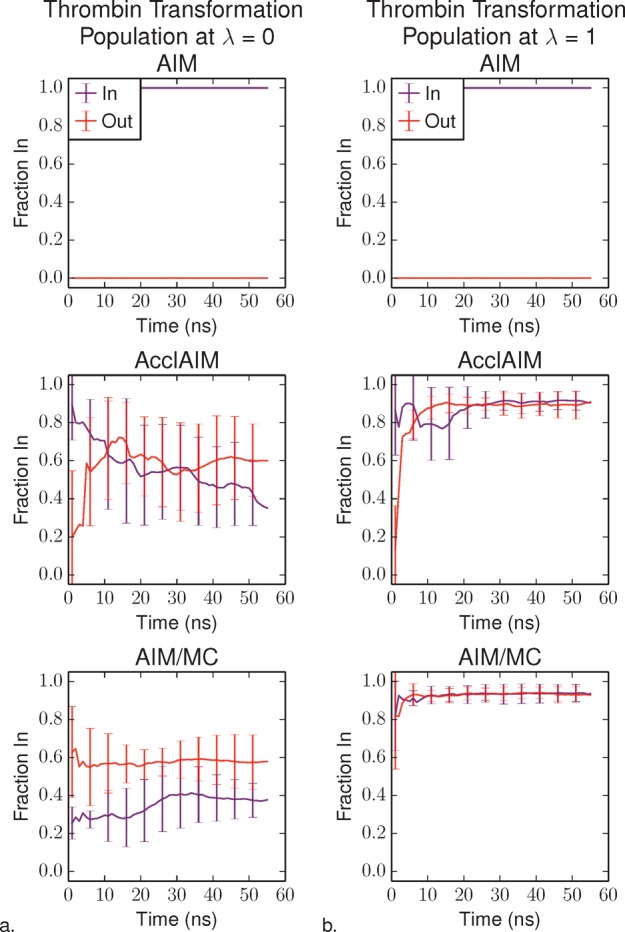
Figure 3

Open in a new tab

Fraction of the thrombin ligand P1 pyridine ring in the In conformation as a function of simulation time at (a) λ = 0, corresponding to CDA and (b) λ = 1, corresponding to CDB. The purple series shows the results for the simulations starting with the In conformation, and the red series shows the results for the simulations starting with the Out conformation. The AIM and AcclAIM results have been reported previously2 and are reproduced here for comparison. Error bars represent the standard deviation over four independent trials.

AIM was not able to sample the different P1 pyridine ring conformations; the ring only sampled the initial conformation for the entire simulation. AcclAIM was able to sample both P1 pyridine ring conformations, regardless of the initial conformation of the ring.2 AIM/MC compares favorably with AcclAIM, where both ring conformations are sampled. The average fraction In is the same within uncertainty for both of these methods. However, even the AcclAIM simulations with the strong scaling factor of α = 0.05 did not converge as rapidly as AIM/MC, especially at λ = 1. The ability for AIM/MC to rapidly sample the different P1 pyridine ring conformations is expected to improve the rate of convergence for the free energy.

The free energy results are shown in Figure 4. Because of the lack of proper sampling, the AIM simulations show a difference of 2 kcal/mol between the simulations starting with the ring In conformation and the simulations starting with the ring Out conformation. AcclAIM is able to sample both ring conformations, so the free energy converges regardless of the initial conformation of the ring.2 The free energy values calculated using AIM/MC rapidly converge, with a smaller uncertainty compared to AcclAIM. This is due to the improved sampling of the ring conformations, especially at λ = 1. The calculated relative binding free energy for AcclAIM and AIM/MC is close to the experimental value. These results show that AIM/MC is able improve upon the results from AcclAIM for this pair of ligands.

Figure 4.

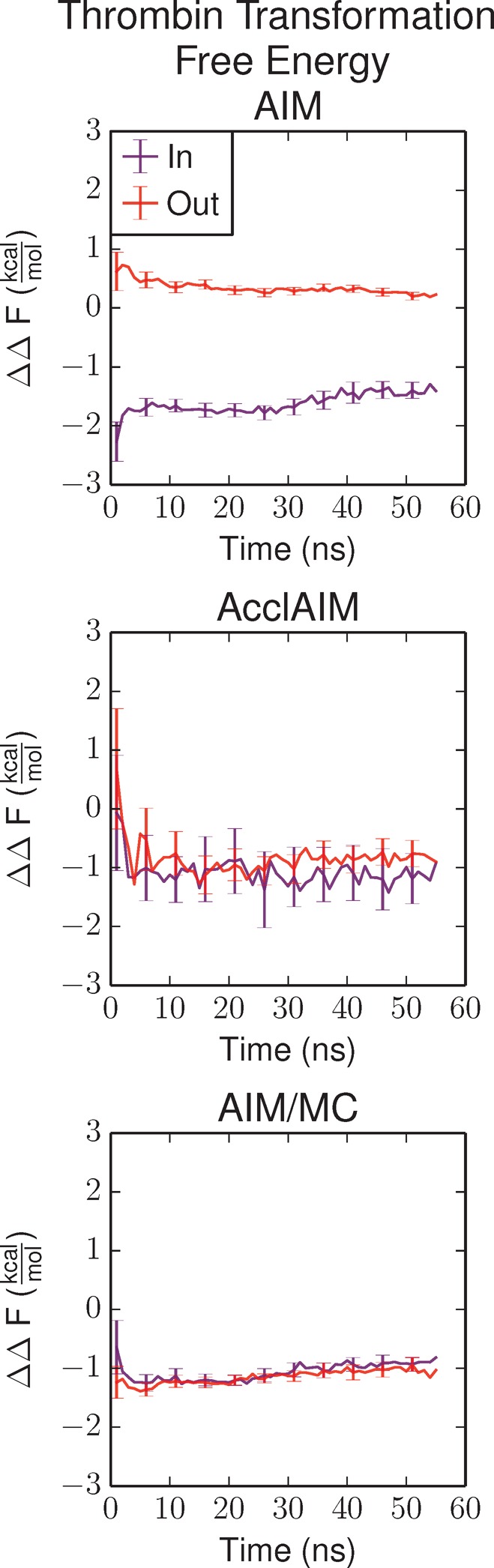
Figure 4

Open in a new tab

Relative binding free energy for the transformation of thrombin ligand CDA to CDB as a function of simulation time. The purple series shows the results for the simulations starting with the In conformation, and the red series shows the results starting with the Out conformation. The AIM and AcclAIM results have been reported previously2 and are reproduced here for comparison. Error bars represent the propagation of the error according to eq 5.

BACE1

As with thrombin, sampling of the ring conformations was examined using the fraction of time that the ring is in the In conformation as a function of simulation time. Figure 5a shows the fraction In at λ = 0, which corresponds to ligand 17a and Figure 5b shows the fraction In at λ = 1, which corresponds to ligand 24. For the AIM simulations, the ring conformation sampled is just that of the initial conformation. For the AcclAIM simulations, a few of the trials starting with the ring in the In conformation were able to flip Out, causing the fraction In to be lower than one. The simulations starting with the Out conformation were not able to flip to sample the In state. Even with lower barriers between the two ring conformations, AcclAIM was not able to adequately sample both possible ring conformations, causing the fraction In to be biased based on the initial ring conformation. However, AIM/MC was able to adequately sample both ring conformations at λ = 0 and λ = 1 as indicated by the overlap between the fraction In for the simulations starting with either ring conformation.

Figure 5.

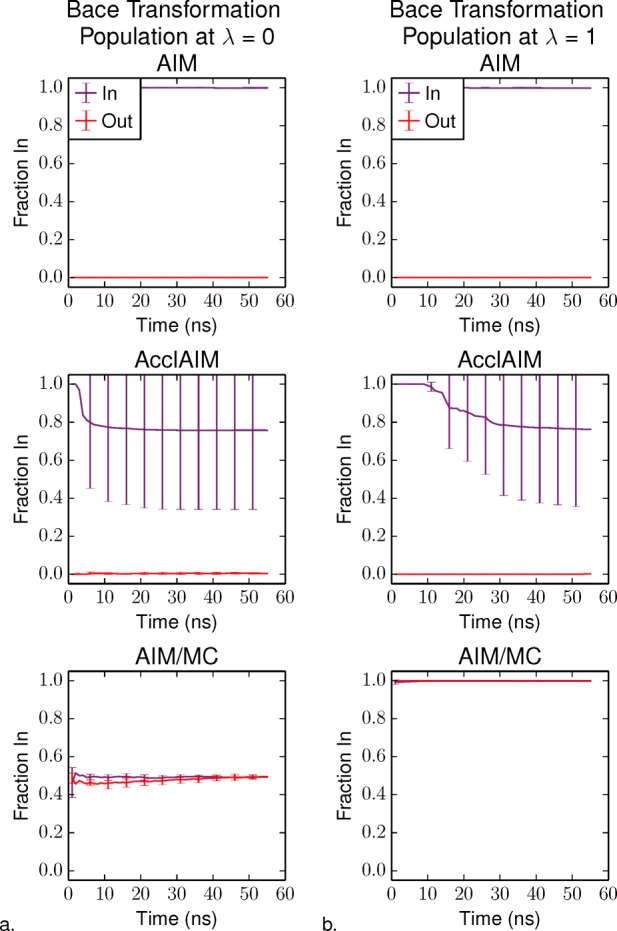
Figure 5

Open in a new tab

Fraction of the BACE1 ligand ring in the In conformation as a function of simulation time at (a) λ = 0, corresponding to ligand 17a and (b) λ = 1, corresponding to ligand 24. The purple series shows the results for the simulations starting with the In conformation, and the red series shows the results starting with the Out conformation. Error bars represent the standard deviation over four independent trials.

Ligand 17a has a 2,5-dichlorophenyl group, which is symmetric about the attachment point to the rest of the ligand. Thus, the fraction In at λ = 0 should be 0.5 because the molecule has two degenerate ring conformations. However, because of the presence of the large chlorine atoms at λ = 0 and the propynyl functional group at λ = 1, AcclAIM is not able to sample both ring conformations, even with the scaling factor set to α = 0.05. AIM/MC is able to sample both ring conformations, the fraction In quickly converges to the expected value of 0.5 (Figure 5a). The crystal structure for ligand 24 bound to BACE1 shows the In conformation is favored. While AcclAIM is not able to correctly sample the In conformation, AIM/MC properly samples this conformation for both the In and Out starting states, as indicated by the fraction In close to 1.0 (Figure 5b).

The free energy as a function of time is shown in Figure 6. The lack of proper sampling of the ligand ring conformations causes the free energy calculated using both the AIM and AcclAIM methods to depend on the initial conformation. The difference in the predicted free energy is on the order of 3–4 kcal/mol. AIM/MC improves sampling of the ligand ring conformations, resulting in the quick convergence of the calculated free energy. Compared to the experimental result, the predicted free energy is 1 kcal/mol more favorable, possibly caused by a small inaccuracy in the force field. Thus, AIM/MC is an effective method for improving the precision of relative binding free energy calculations for protein–ligand systems by improving the conformational sampling of the ligand.

Figure 6.

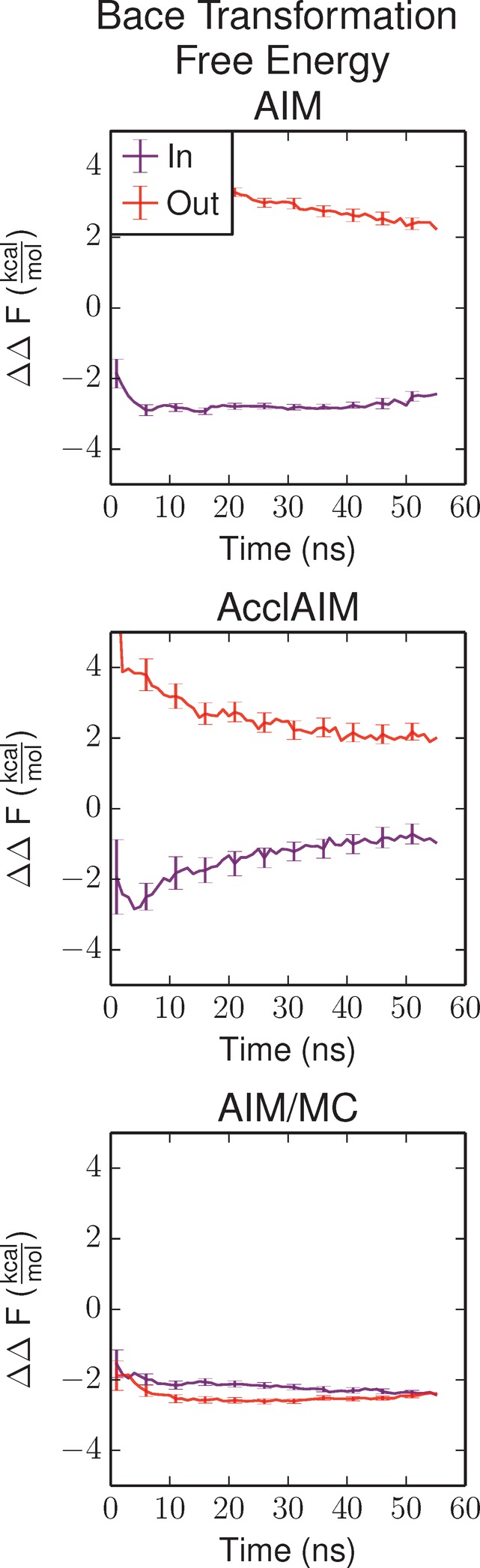
Figure 6

Open in a new tab

Relative binding free energy for the transformation of BACE1 ligand 17a to 24 as a function of simulation time. The purple series shows the results for the simulations starting with the In conformation, and the red series shows the results starting with the Out conformation. Error bars represent the propagation of the error according to eq 5.

Generality of AIM/MC

A requirement for applying the AIM/MC method is the presence of a sufficiently symmetric state where the rotation has a reasonable acceptance probability according to eq 3. The acceptance probability at λ = 0 for the systems studied in this work is given in Table 1. For the thrombin transformation, the acceptance probability is low, close to 1%. This is caused by the asymmetry of the CDA ring undergoing the rotation at λ = 0. On one side of the axis of rotation is a nitrogen atom, and on the other side is a carbon atom bonded to a fluorine atom (see Figure 2a). After a trial rotation, there is a higher chance that the fluorine atom will sterically clash with a water or protein atom, because there is nothing attached to the nitrogen to create space for the fluorine atom. This is the cause of the lower acceptance probability.

Table 1. Percent Acceptance Probability, Pacc,rot, at λ = 0 for the Rotation of the Ring in Each System, Calculated Using Equation 3a.
Pacc,rot   in out
thrombin complex free 1.1 ± 0.4% 1.6 ± 0.2%
1.3 ± 0.1% 1.2 ± 0.1%
BACE1 complex free 12.8 ± 1.1% 13.2 ± 1.1%
22.9 ± 0.8% 22.6 ± 0.1%
Open in a new tab
a

Values represent averages over the four independent trials, and error bars represent the standard deviation.

The acceptance probability for the BACE1 transformation is higher, at 13% for the complex simulation and 23% for the simulation free in water. Looking at the structure of the molecule before and after an attempted rotation (Figure S3 in the Supporting Information), there are slight differences in the bond angles for the chlorine atoms, reducing the overlap after rotation and therefore the acceptance probability. An alternative would be to transform each ligand to a symmetric intermediate, such as a planar six-membered ring without hydrogen atoms. Then, transform this intermediate molecule into the second ligand. This two step procedure would improve the acceptance probability but requires the use of two separate simulations. However, even with a lower acceptance probability, AIM/MC is able to significantly improve conformational sampling for these transformations, resulting in the convergence of the free energy.

Conclusions

The AIM/MC method was developed and applied to two challenging alchemical transformations, involving ligands with substituted six-membered rings, improving the conformational sampling in these systems. The first transformation was between CDA and CDB bound to thrombin. The results demonstrate using AIM/MC improved conformational sampling compared to AIM and reduced the uncertainty of the calculated free energy compared to AcclAIM.

Then, this method was applied to calculate the relative binding free energy between the BACE1 ligands 17a and 24. This is a challenging system because of the large size of the propynyl group in ligand 24. Both AIM and AcclAIM were not able to properly sample the ring conformations, causing the final free energy to depend on the initial conformation of the ring. However, AIM/MC was able to rapidly sample the ring conformations, resulting in convergence of the free energy.

AIM/MC can be applied to any system where the molecule has a high degree of symmetry at certain λ values. In cases where this is not true, a two-step procedure can be used, where a transformation goes through a symmetric intermediate. The resulting free energies can then be added together. Also, this method could be combined with AcclAIM to improve the sampling of the functional groups attached to the ring. Future work may explore ways to apply this method when the ligand of interest does not have a high degree of symmetry and combination with AcclAIM for functional group sampling.

Acknowledgments

The authors thank Lingle Wang for useful discussions. Support is provided by the NIH (NIH Grant GM031749), the NIH Molecular Biophysics Training Program from the National Institute of General Medical Sciences (T32 Grant GM08326), the NSF (MCB Grant 1020765), the Howard Hughes Medical Institute, Achievement Rewards for College Scientists, the National Biomedical Computation Resource, and the NSF Supercomputer Centers.

Supporting Information Available

Ligand parameters, the number of λ windows used for each simulation, and a comparison of the structure for the BACE1 ligand before and after an attempted rotation. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.5b02348.

The authors declare no competing financial interest.

Supplementary Material

jp5b02348_si_001.pdf (741.7KB, pdf)

References

  1. Fasnacht M.; Swendsen R.; Rosenberg J. Adaptive Integration Method for Monte Carlo Simulations. Phys. Rev. E 2004, 69, 056704. [DOI] [PubMed] [Google Scholar]
  2. Kaus J.; Arrar M.; McCammon J. A. Accelerated Adaptive Integration Method. J. Phys. Chem. B 2014, 118, 5109–5118. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Chodera J. D.; Mobley D. L.; Shirts M. R.; Dixon R. W.; Branson K.; Pande V. S. Alchemical Free Energy Methods for Drug Discovery: Progress and Challenges. Curr. Opin. Struct. Biol. 2011, 21, 150–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Beauchamp K. A.; Lin Y.-S.; Das R.; Pande V. S. Are Protein Force Fields Getting Better? A Systematic Benchmark on 524 Diverse NMR Measurements. J. Chem. Theory Comput. 2012, 8, 1409–1414. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Zuckerman D. M. Equilibrium Sampling in Biomolecular Simulations. Annu. Rev. Biophys. 2011, 40, 41–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Woods C. J.; Essex J. W.; King M. A. The Development of Replica-Exchange-Based Free-Energy Methods. J. Phys. Chem. B 2003, 107, 13703–13710. [Google Scholar]
  7. Hamelberg D.; Mongan J.; McCammon J. A. Accelerated Molecular Dynamics: A Promising and Efficient Simulation Method for Biomolecules. J. Chem. Phys. 2004, 120, 11919. [DOI] [PubMed] [Google Scholar]
  8. de Oliveira C.; Hamelberg D.; McCammon J. A. Coupling Accelerated Molecular Dynamics Methods with Thermodynamic Integration Simulations. J. Chem. Theory Comput. 2008, 4, 1516–1525. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Arrar M.; de Oliveira C. A. F.; Fajer M.; Sinko W.; McCammon J. A. w-REXAMD: A Hamiltonian Replica Exchange Approach to Improve Free Energy Calculations for Systems with Kinetically Trapped Conformations. J. Chem. Theory Comput. 2013, 9, 18–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Liu P.; Kim B.; Friesner R. A.; Berne B. J. Replica Exchange with Solute Tempering. A Method for Sampling Biological Systems in Explicit Water. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 13749–13754. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Wang L.; Friesner R. A.; Berne B. J. Replica Exchange with Solute Scaling: A More Efficient Version of Replica Exchange with Solute Tempering (REST2). J. Phys. Chem. B 2011, 115, 9431–9438. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Moors S. L. C.; Michielssens S.; Ceulemans A. Improved Replica Exchange Method for Native-State Protein Sampling. J. Chem. Theory Comput. 2011, 7, 231–237. [DOI] [PubMed] [Google Scholar]
  13. Wang L.; Berne B. J.; Friesner R. A. On Achieving High Accuracy and Reliability in the Calculation of Relative Protein-Ligand Binding Affinities. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 1937–1942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Vitalis A.; Pappu R. V. Methods for Monte Carlo Simulations of Biomacromolecules. Annu. Rep. Comput. Chem. 2009, 5, 49–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Jorgensen W. L. Efficient Drug Lead Discovery and Optimization. Acc. Chem. Res. 2009, 42, 724–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Cole D. J.; Tirado-Rives J.; Jorgensen W. L. Enhanced Monte Carlo Sampling through Replica Exchange with Solute Tempering. J. Chem. Theory Comput. 2014, 10, 565–571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kirkwood J. G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar]
  18. Bennett C. H. Efficient Estimation of Free Energy Differences from Monte Carlo Data. J. Comput. Phys. 1976, 22, 245–268. [Google Scholar]
  19. Shirts M. R.; Chodera J. D. Statistically Optimal Analysis of Samples from Multiple Equilibrium States. J. Chem. Phys. 2008, 129, 124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Tan Z.; Gallicchio E.; Lapelosa M.; Levy R. M. Theory of Binless Multi-State Free Energy Estimation with Applications to Protein-Ligand Binding. J. Chem. Phys. 2012, 136, 144102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Paliwal H.; Shirts M. R. A Benchmark Test Set for Alchemical Free Energy Transformations and Its Use to Quantify Error in Common Free Energy Methods. J. Chem. Theory Comput. 2011, 7, 4115–4134. [DOI] [PubMed] [Google Scholar]
  22. Bruckner S.; Boresch S. Efficiency of Alchemical Free Energy Simulations. II. Improvements for Thermodynamic Integration. J. Comput. Chem. 2011, 32, 1320–1333. [DOI] [PubMed] [Google Scholar]
  23. Zacharias M.; Straatsma T. P.; McCammon J. A. Separation-Shifted Scaling, A New Scaling Method for Lennard-Jones Interactions in Thermodynamic Integration. J. Chem. Phys. 1994, 100, 9025–9031. [Google Scholar]
  24. Beutler T. C.; Mark A. E.; van Schaik R. C.; Gerber P. R.; van Gunsteren W. F. Avoiding Singularities and Numerical Instabilities in Free Energy Calculations Based on Molecular Simulations. Chem. Phys. Lett. 1994, 222, 529–539. [Google Scholar]
  25. Shirts M. R.; Pande V. S. Solvation Free Energies of Amino Acid Side Chain Analogs for Common Molecular Mechanics Water Models. J. Chem. Phys. 2005, 122, 134508. [DOI] [PubMed] [Google Scholar]
  26. Steinbrecher T.; Joung I.; Case D. A. Soft-Core Potentials in Thermodynamic Integration: Comparing One- and Two-Step Transformations. J. Comput. Chem. 2011, 32, 3253–3263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Steinbrecher T.; Mobley D. L.; Case D. A. Nonlinear Scaling Schemes for Lennard-Jones Interactions in Free Energy Calculations. J. Chem. Phys. 2007, 127, 214108. [DOI] [PubMed] [Google Scholar]
  28. Stone J.An Efficient Library for Parallel Ray Tracing and Animation. M.Sc. Thesis, University of Missouri-Rolla, Rolla, MO, 1998. [Google Scholar]
  29. Humphrey W.; Dalke A.; Schulten K. VMD-Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]
  30. Case D. A.; Darden T. A.; Cheatham T. E. III; Simmerling C. L.; Wang J.; Duke R. E.; Luo R.; Walker R. C.; Zhang W.; Merz K. M.. et al. AMBER 12; University of California: San Francisco, CA, 2012.
  31. Kaus J. W.; Pierce L. T.; Walker R. C.; McCammon J. A. Improving the Efficiency of Free Energy Calculations in the Amber Molecular Dynamics Package. J. Chem. Theory Comput. 2013, 9, 4131–4139. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Hornak V.; Abel R.; Okur A.; Strockbine B.; Roitberg A.; Simmerling C. Comparison of Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters. Proteins 2006, 65, 712–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Lindorff-Larsen K.; Piana S.; Palmo K.; Maragakis P.; Klepeis J. L.; Dror R. O.; Shaw D. E. Improved Side-Chain Torsion Potentials for the Amber ff99SB Protein Force Field. Proteins 2010, 78, 1950–1958. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
  35. Jorgensen W. L.; Chandrasekhar J.; Madura1 J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926. [Google Scholar]
  36. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.. et al. Gaussian 09, revision D.01; Gaussian, Inc.: Wallingford, CT, 2009.
  37. Cornell W. D.; Cieplak P.; Bayly C. I.; Gould I. R.; Merz K. M.; Ferguson D. M.; Spellmeyer D. C.; Fox T.; Caldwell J. W.; Kollman P. A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar]
  38. Darden T.; York D.; Pedersen L. Particle mesh Ewald: An Nlog(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar]
  39. Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. C. Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar]
  40. Miyamoto S.; Kollman P. A. SETTLE: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar]
  41. Pastor R. W.; Brooks B. R.; Szaboc A. An Analysis of the Accuracy of Langevin and Molecular Dynamics Algorithms. Mol. Phys. 1988, 65, 1409–1419. [Google Scholar]
  42. Loncharich R. J.; Brooks B. R.; Pastor R. W. Langevin Dynamics of Peptides: The Frictional Dependence of Isomerization Rates of N-Acetylalanyl-N′-Methylamide. Biopolymers 1992, 32, 523–535. [DOI] [PubMed] [Google Scholar]
  43. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar]
  44. Burgey C. S.; Robinson K. A.; Lyle T. A.; Sanderson P. E. J.; Lewis S. D.; Lucas B. J.; Krueger J. A.; Singh R.; Miller-Stein C.; White R. B.; et al. Metabolism-Directed Optimization of 3-Aminopyrazinone Acetamide Thrombin Inhibitors. Development of an Orally Bioavailable Series Containing P1 and P3 Pyridines. J. Med. Chem. 2003, 46, 461–473. [DOI] [PubMed] [Google Scholar]
  45. Vogt A. D.; Pozzi N.; Chen Z.; Cera E. D. Essential Role of Conformational Selection in Ligand Binding. Biophys. Chem. 2014, 186, 13–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Cumming J. N.; Smith E. M.; Wang L.; Misiaszek J.; Durkin J.; Pan J.; Iserloh U.; Wu Y.; Zhu Z.; Strickland C.; et al. Structure Based Design of Iminohydantoin BACE1 Inhibitors: Identification of an Orally Available, Centrally Active BACE1 Inhibitor. Bioorg. Med. Chem. Lett. 2012, 22, 2444–2449. [DOI] [PubMed] [Google Scholar]
  47. Straatsma T. P.; McCammon J. A. Multiconfiguration Thermodynamic Integration. J. Chem. Phys. 1991, 95, 1175–1188. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp5b02348_si_001.pdf (741.7KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES