Differentiating between apparent and actual rates of H₂O₂ metabolism by isolated rat muscle mitochondria to test a simple model of mitochondria as regulators of H₂O₂ concentration

Abstract

Mitochondria are often regarded as a major source of reactive oxygen species (ROS) in animal cells, with H₂O₂ being the predominant ROS released from mitochondria; however, it has been recently demonstrated that energized brain mitochondria may act as stabilizers of H₂O₂ concentration (Starkov et al. [1]) based on the balance between production and the consumption of H₂O₂, the later of which is a function of [H₂O₂] and follows first order kinetics. Here we test the hypothesis that isolated skeletal muscle mitochondria, from the rat, are able to modulate [H₂O₂] based upon the interaction between the production of ROS, as superoxide/H₂O₂, and the H₂O₂ decomposition capacity. The compartmentalization of detection systems for H₂O₂ and the intramitochondrial metabolism of H₂O₂ leads to spacial separation between these two components of the assay system. This results in an underestimation of rates when relying solely on extramitochondrial H₂O₂ detection. We find that differentiating between these apparent rates found when using extramitochondrial H₂O₂ detection and the actual rates of metabolism is important to determining the rate constant for H₂O₂ consumption by mitochondria in kinetic experiments. Using the high rate of ROS production by mitochondria respiring on succinate, we demonstrate that net H₂O₂ metabolism by mitochondria can approach a stable steady-state of extramitochondrial [H₂O₂]. Importantly, the rate constant determined by extrapolation of kinetic experiments is similar to the rate constant determined as the [H₂O₂] approaches a steady state.

Graphical abstract

Highlights

• •Compartmentalization of mitochondrial H₂O₂ metabolism is important to interpreting in vitro results, leading to underestimation of rates.
• •Accounting for apparent rates of H₂O₂ metabolism indicates support for integrated [H₂O₂]-dependent respiration-driven H₂O₂ consumption.
• •Mitochondria may be able to regulate steady state [H₂O₂] based on substrate availability.

Introduction

Hydrogen peroxide is well recognized as an important intracellular signaling molecule but if present at high levels this reactive oxygen species (ROS) may cause substantial oxidative stress to cells. The capacity of mitochondria, and submitochondrial particles, to produce H₂O₂ has been known for about half a century [2–5]; however, the exact role(s) of mitochondria in cellular H₂O₂ metabolism continues to be debated. For example, while mammalian mitochondria are often ascribed a role as net producers of H₂O₂, this notion has been challenged [6]. Nonetheless, mitochondria as a net source of ROS, or as a cause of cell-level oxidative stress, have been widely implicated in many metabolic disease states as well as aging related disease and declines in cellular function (for a few of the many examples see [7–13]).

The production of H₂O₂ by mitochondria is understood to some degree, with the majority of the H₂O₂ initially coming from superoxide production by mitochondrial enzyme complexes, although H₂O₂ may be formed directly in some cases [14,15]. Superoxide is mainly released to the matrix and cannot readily cross the mitochondrial inner membrane; the accumulation of the superoxide radical in the matrix is prevented by Mn-superoxide dismutase, which forms membrane permeable H₂O₂. When mitochondria are oxidizing respiratory substrates, superoxide/H₂O₂ is produced from at least 10 sites within the matrix and mitochondrial inner membrane [16]; however, the sites and their relative contributions to the total superoxide/H₂O₂ formed varies widely by metabolic condition, bioenergetic state, substrate choice and concentration [14,17–23]. The rate of superoxide/H₂O₂ production by intact mitochondria is frequently measured by fluorometric assays coupled to horseradish peroxidase. Using this fluorometric assay, the rate of production of superoxide/H₂O₂ can be demonstrated to be quite low with poorly oxidized substrates like malate but can be 1–2 orders of magnitude higher when succinate alone is oxidized [22,24]. For simplicity, we will from here on refer solely to H₂O₂ production; however, unless otherwise stated we use this to describe the combined production of superoxide that is dismuted to H₂O₂ and the direct H₂O₂ production by mitochondrial enzyme complexes.

Mitochondria also have substantial capacity to consume H₂O₂, but this aspect receives less focus than their capacity to produce H₂O₂. The capacity of mitochondria to consume H₂O₂ added to the surrounding medium is several fold higher than H₂O₂ efflux under similar conditions of substrate supply in brain, heart and skeletal muscle mitochondria [24–29]. More importantly, in brain, heart and skeletal muscle mitochondria this high capacity to consume H₂O₂ is predominantly linked to respiratory substrate oxidation. This dependency on the supply of electrons is consistent with NADPH-dependent glutathione and thioredoxin-dependent peroxidases being the major mitochondrial H₂O₂ consumers in many tissues [24,27,28], with the exception of liver where catalase is a major H₂O₂ consumer [28].

As has been noted previously [6], the discrepancy between maximal capacity to consume H₂O₂ and the apparent rate of H₂O₂ production by mitochondria is counterintuitive to the notion of mitochondria as net producers of H₂O₂. Some authors have concluded that energized mitochondria may act as H₂O₂ sinks [25]. More recently, Starkov and colleagues presented data supporting a profoundly different perspective where mitochondria would be stabilizers of cellular H₂O₂, acting as a net sink when the concentration is above a certain level and as source when below [1]. The authors propose that the relationship between production and consumption leads to this stabilizing role, which is summarized by the following elegantly simple equation:

V^P/k=[H₂O₂]_ss (1)

where V^P is the rate of H₂O₂ production, k is the first order rate constant of all H₂O₂ consuming processes integrated into a single ‘consumption’ rate and [H₂O₂]_ss is the steady-state concentration established under any particular condition of V^P. In this case, mitochondria are neither net producers nor consumers. Instead, mitochondria oxidizing respiratory substrates can be viewed as regulators of extramitochondrial [H₂O₂] dependent on the balance between production, which changes with the substrate(s) present, and consumption which is assumed to be relatively independent of substrate selection. The data used to derive and support the concepts that led to Eq. (1) were based on isolated rat brain mitochondria [1]; however, if the concept is applicable to mitochondria in general then this would present a powerful new tool for understanding the role of mitochondria in cellular oxidant metabolism and signaling.

In the current study we expand on this general concept and develop means to test the hypothesis that mitochondrial H₂O₂ metabolism may be summarized or approximated into the simple relationship in Eq. (1) or derivatives thereof. To do this we use rat skeletal muscle mitochondria where, similar to brain [1], catalase is a minor influence on mitochondrial H₂O₂ consumption [29,30]. In the process we develop experiments to allow for the important distinction between actual and apparent rates of production and consumption with intact mitochondria. To appreciate the differences between apparent and actual rates some consideration of how the compartmentalization of the processes involved is necessary.

The importance of compartmentalization, diffusion gradients and apparent rates

One challenge of working on mitochondrial ROS metabolism, especially ROS balance, is that the compartmentalization of mitochondria is important to maintain and produce adequate gradients (i.e. protonmotive force). The generation of these gradients is vital because they can lead to feedback at the level of enzyme and electron carrier reduction, which is central to the production of ROS from the various sites within the mitochondrion [21–23]. This means that assays, such as measuring H₂O₂ efflux or the consumption of extramitochondrial H₂O₂, are diffusion-dependent systems that rely on H₂O₂ moving between the intramitochondrial compartment and the extramitochondrial medium (Fig. 1A). The compartmentalization also results in partitioning ‘sources’ and ‘sinks’ for H₂O₂, which may complicate interpretation because these sources and sinks can be working in directions competing or conflicting with the assay being conducted. We use three different experimental series to differentiate H₂O₂ metabolism into its consistent parts and test if, as a system, muscle mitochondrial H₂O₂ metabolism is approximated by Eq. (1) or derivatives thereof.

Fig. 1.

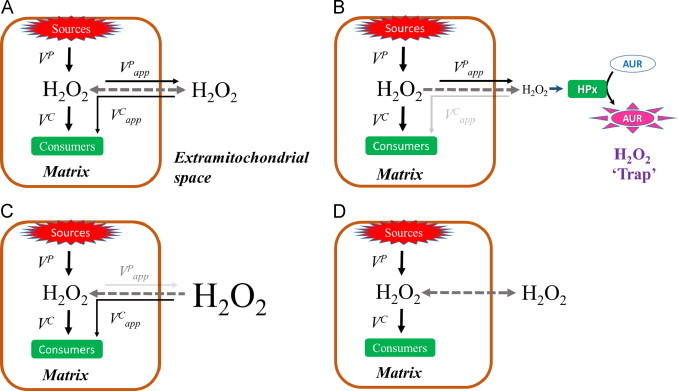
Generalized models differentiating between actual and apparent rates related to H₂O₂ metabolism in mitochondria. (A) The general model and B–D illustrate the specific conditions used in the experiments of this study. The dashed arrow indicates the direction of net H₂O₂ flux between the medium (extramitochondrial space) and the matrix. (B) Experiments in Series 1 where the H₂O₂ efflux is measured via the H₂O₂ consuming horseradish peroxidase linked assay. (C) Conditions for Series 1 and 2 experiments where the disappearance of exogenously added H₂O₂ is monitored by an electrochemical sensor. Note, the apparent rate of efflux is shown to illustrate the contribution of H₂O₂ production to the underestimate of apparent H₂O₂ consumption. The discrepancy between actual and apparent rates of disappearance may also be due to partial collapse of the inward directed diffusion gradient rather than true efflux. (D) Experiments from Series 3 where the mitochondrial system is allowed to approach steady-state [H₂O₂] in the medium.

First, consider H₂O₂ efflux, an extremely common approach to measure mitochondrial superoxide/H₂O₂ production. Generally the enzyme linked detection assay is extramitochondrial (e.g. using horseradish peroxidase linked assays) and only detects H₂O₂ that has diffused out of the mitochondrion. These assays rely on maintaining extramitochondrial [H₂O₂] as close to zero as possible, thus creating as strong a diffusion gradient as possible from the intramitochondrial source(s) of superoxide/H₂O₂ to the extramitochondrial detection system.

In these assays the influence of the intramitochondrial H₂O₂ consuming pathways is often ignored or overlooked; however, the supply of respiratory substrate will result in both the accumulation of electrons in ROS producing enzyme complexes as well as prime the NADPH-dependent peroxidase systems. Because production and consumption of H₂O₂ are linked by the bioenergetics driven by substrate oxidation it is reasonable to anticipate that some of the produced H₂O₂ is consumed before it can escape the mitochondrion. Thus there should be an actual net rate of H₂O₂ production (V^P), which will include the combined sources of superoxide and H₂O₂ under any defined condition, and an apparent rate of production ($V_{app}^P$) which can be measured with intact mitochondria as H₂O₂ efflux (Fig. 1B).

A similar issue arises when determining the kinetics of H₂O₂ consumption based on the disappearance of H₂O₂ from the medium. While there will be a true substrate-dependent rate of H₂O₂ consumption within the matrix (V^C), the disappearance of H₂O₂ from the medium relies on the concentration gradient into the matrix, which will be influenced to some degree by the mitochondrial production of H₂O₂. Thus, although net flux into the mitochondrion will show disappearance of H₂O₂ from the medium ($V_{app}^C$), this value should also be an underestimate of the actual maximal consumption rate (Fig. 1C). The degree of underestimation of V^C should be inversely related to V^P and vice versa.

Finally, experiments can be designed to allow energized mitochondria to build up H₂O₂ and approach equilibrium where the [H₂O₂] is at a steady state ([H₂O₂]_ss), presumably approaching equal concentrations within the matrix and medium, and V^P=V^C (Fig. 1D). In the current study we test if H₂O₂ metabolism by isolated rat skeletal muscle mitochondria can be approximated by a simple relationship based on the integration of production and consumption, the latter of which follows, or is reasonably estimated by, first order rate kinetics that can ultimately reach a steady state [H₂O₂].

Materials and methods

Animals and mitochondrial isolation

Sprague–Dawley rats, of mixed sex, from approximately 200–350 g were used for all experiments. Animals were housed at 22 °C, with a 12:12 h light cycle, in standard cages with ad libitum access to chow and water. Rats were killed by asphyxiation with CO₂ followed by pneumothorax and laceration of the heart with scissors. All animal procedures have been approved by the University of Manitoba Animal Care Committee. Hind limb and back skeletal muscle was dissected away and transferred to ice-cold isolation medium and mitochondria were isolated as previously described [31]. Mitochondrial protein content was measured using the biuret assay with 0.2% (w/v) sodium deoxycholate as detergent and bovine serum albumin as a protein standard. All biochemical assays were conducted at 37 °C.

Fluorometric H₂O₂ detection

The efflux of H₂O₂ was based on the fluorescent Amplex UltraRed (AUR) assay described elsewhere [31] using wavelengths of 560 nm and 590 nm as excitation and emission respectively; however, we used a phosphate containing respiration medium (pH 7.2) for all experiments [29]. For experiments where the accumulation of H₂O₂ in the medium was measured all fluorometric assay components were added with the exception of AUR, which was added as indicated in the relevant figures. The increase in fluorescence upon addition of AUR was taken as a measure of the accumulated H₂O₂ in the medium. In all cases fluorescence was converted to nmol of H₂O₂ based upon calibration curves using H₂O₂ added to cuvettes that contained mitochondria suspended in the respiration medium but no respiratory substrates. It is important to note that both BSA (0.3%) and the amount of mitochondria used in the current studies (0.2–0.3 mg mitochondrial protein ml⁻¹) quench the fluorescent signal and thus must be accounted for in the H₂O₂ calibration.

Electrochemical H₂O₂ detection

The disappearance of extramitochondrial H₂O₂ was measured using an Innovative Instruments HP-250 Hydrogen Peroxide Electrochemical Sensor as described and demonstrated previously [29]. Auranofin, an inhibitor of thioredoxin reductase, was included at the start of the assay (when present) along with mitochondria, and a 3–5 min preincubation was allowed before addition of H₂O₂ or substrates. The addition of H₂O₂ (2500 or 3000 nM) was done prior to the addition of respiratory substrates and acted as both a calibration as well as peroxidase substrate. To calculate rates of consumption ($V_{app}^{Cmax}$ in nmol min⁻¹ mg mitochondrial protein⁻¹) the initial, approximately linear, rate of disappearance shortly after addition of respiratory substrate was used. The apparent rate constant for H₂O₂ consumers were determined by fitting a first order decay curve (see Series 2 and Eq. (4)) to the data for <2000 nM H₂O₂. In some experimental conditions the mitochondria consumed H₂O₂ to an apparent stable and very low [H₂O₂]. With our current apparatus we cannot distinguish this very low level of H₂O₂ from simple electrode drift and conclude that in these cases the extramitochondrial [H₂O₂] is below limits of detection.

A low rate of H₂O₂ consumption occurs in the absence of added respiratory substrate. It is unclear what this may be from [28,29] but since this rate is far lower than the respiration-dependent H₂O₂ consumption we have not explored it in detail. It is assumed this low rate will also be a small part of the integrated pool of mitochondrial H₂O₂ consumers.

Enzyme assays

Nicotinamide nucleotide transhydrogenase (NNT) activity was measured spectrophotometrically by following the reduction of 3-acetylpyridine adenine dinucleotide (APAD) by NADPH in the presence of previously frozen mitochondria. The assay medium is described elsewhere [32,33] and NNT activity was determined based on the rate of absorbance change in cuvettes maintained at 37 °C (pH 8.0) assuming a millimolar extinction coefficient for APAD of 5.1 at 375 nm.

NADP⁺-dependent malic enzyme (ME) was measured spectrophotometrically based on the reduction of NADP⁺ to NADPH by freeze–thawed muscle mitochondria. The assay used is based on [34,35] using an assay medium consisting of 50 mM Tris (pH 7.8 at 25 °C), 1 mM MnCl₂, 0.1 mM dithiothreitol, 1.0 mM NADP⁺ and 0.1% (v/v) triton-X 100. Assays were maintained at 37 °C and the rate of absorbance change at 340 nm due to the reduction of NADP⁺ in the presence of 15 mM malate was used to determine ME activity assuming a millimolar extinction coefficient of 6.2 for NADPH.

Regression analysis and statistics

Regressions: all regression analysis, both linear and nonlinear, were done using SigmaPlot 13.0. The equation initially used to fit the disappearance of H₂O₂ from the medium (Experimental Series 2) differed from a simple first order decline [1] in that it included a constant allowing for the data to approach a [H₂O₂]_ss above zero; however, in all cases except one experiment with succinate (not shown) this constant was not significantly different from 0 nM H₂O₂. Therefore this constant was removed and data were fitted to Eq. (4) as shown and explained below ([H₂O₂]_t = [H₂O₂]₀×e^{−k_app·pr·t}).

For the experiments in Series 3 the values for V^P, k and [H₂O₂]_ss were determined for each individual experiment based on the constants found by the nonlinear fitting of the data points. Note, there is a modest delay in the stabilization of the $V_{app}^P$, approximately 30 s, and all time based data points were shifted by 30 s to accommodate this lag.

Statistical analysis: all means were compared based on one-way ANOVA with the exception of non-independent data, which were compared using a paired t-test. In all cases p<0.05 was considered significant.

Results and discussion

Assumptions and predictions

To test the simple V^P/k=[H₂O₂]_ss model some assumptions must be made. First, it is assumed that all H₂O₂ consumers can be combined and described by a simple single first order reaction. This is likely untrue in an absolute sense because there are at least two candidate enzyme systems involved that require NADPH (thioredoxin and glutathione dependent pathways) and these may have different affinities for substrates and cofactors; however, even if the first order fit is imperfect, as long as it approximates the observations reasonably closely then it is still a valuable new approach to the study of mitochondrial H₂O₂ metabolism. We have already reported that the consumption of H₂O₂ by energized rat skeletal muscle mitochondria is not linear as H₂O₂ is consumed, consistent with some degree of [H₂O₂] dependency [29]. Similar nonlinear results have also been found using brain mitochondria [1,28,36].

The second assumption is that the only factor affecting H₂O₂ production is the respiratory substrate(s) added to the assay. In other words, we assume changing the [H₂O₂] does not alter or feedback directly on the pathways leading to H₂O₂ production. This assumption allows comparison of assays that use the same respiratory substrates but differ in the net H₂O₂ diffusion direction. A third assumption is that apparent rates are reasonable proxies of the actual rates. As such, the ranking or relative differences in rates found across respiratory substrates are assumed to reflect the relative ranking of actual rates. The fourth assumption we make is that production and consumption are inversely related, which is a reasonable inference from Eq. (1). Combining these assumptions allows us to extrapolate trends seen across a range of apparent rates to estimate consumption dynamics when production is approximately zero.

Several criteria of the model can also be predicted a priori. For example, because the matrix consumers have preferential initial access to H₂O₂, the actual production of H₂O₂ in the matrix (V^P) should be greater than the apparent production when measured as H₂O₂ efflux ($V_{app}^P$). We can manipulate V^P by adding different respiratory substrates and $V_{app}^P$ should change in accordance; however, the degree of underestimation of H₂O₂ production, that is the absolute difference between V^P and $V_{app}^P$, should be a function of [H₂O₂]_matrix as long as the matrix consumers are not saturated. Thus, the net underestimation should be a function of V^P, or $V_{app}^P$ by proxy. Second, if consumption capacity is inhibited, estimates of k must decrease, reflecting this change. It should be possible to estimate k based on the disappearance of H₂O₂ from the medium as well as based on the dynamics seen as mitochondria approach [H₂O₂]_ss. These estimates of k should be similar regardless if determined from H₂O₂ disappearance or based on [H₂O₂]_ss. Finally, estimates of V^P based on [H₂O₂]_ss should be greater than the measured $V_{app}^P$ under the same conditions. We examine the above through three experimental series.

Series 1: Inhibiting consumption increases H₂O₂ efflux consistent with a [H₂O₂]_matrix-dependent consumer

If the consumption of H₂O₂ in the matrix influences $V_{app}^P$ then inhibition of V^C should increase $V_{app}^P$. The following equation describes the relationship:

V^P_app=V^P−V^C where V^C=k[H₂O₂] (2)

(i.e. assumed first order kinetics for consumers)

The thioredoxin reductase inhibitor auranofin strongly impairs respiration-dependent H₂O₂ consumption in brain mitochondria [28] and micromolar or lower concentrations of auranofin have been shown to increase H₂O₂ efflux from isolated mitochondria [37,38]. We assume that auranofin does not have any off-target effects on bioenergetics, which could then alter H₂O₂ efflux; however, if auranofin was to compromise mitochondrial inner membrane barrier function we would expect this uncoupling effect would decrease H₂O₂ efflux. Moreover, auranofin does not alter oxygen consumption from NADH or succinate oxidation with submitochondrial particles [27], indicating that auranofin is unlikely to inhibit electron transport chain flux, which might also increase H₂O₂ efflux. Rat skeletal muscle mitochondria display a marked increase in the rate of H₂O₂ efflux ($V_{app}^P$) in the presence of auranofin (Fig. 2A). Using several different substrates we can generate apparent rates of H₂O₂ production that span an order of magnitude from <0.1 to >1.0 nmol min⁻¹ mg mitochondrial protein⁻¹. Since $V_{app}^P$ will be some function of the actual product (V^P) it is reasonable to assume that V^P also varied by a similar magnitude in these experiments.

Fig. 2.

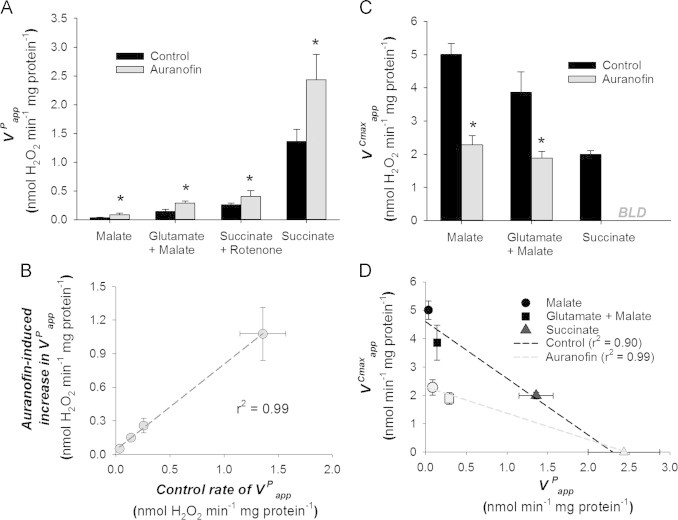
The effect of auranofin on the apparent kinetics of H₂O₂ metabolism by rat skeletal muscle mitochondria. (A) Auranofin (2 µM) increases $V_{app}^P$ across several substrate conditions. Data are mean±SEM (n=4–5), ^⁎ significant increase due to auranofin (p<0.05). (B) The auranofin dependent increase in H₂O₂ efflux is strongly proportional to the apparent rate of H₂O₂ efflux in control mitochondria, consistent with a [H₂O₂]_matrix dependent consumer. Data mean±SEM (n=4–5) with auranofin-induced increase calculated as the difference in H₂O₂ efflux between the same mitochondria in the presence or absence of 2 µM auranofin to inhibit thioredoxin dependent peroxidase capacity. (C) The rate of extramitochondrial H₂O₂ disappearance (V ^Cmax_app) is substrate dependent and inhibited by auranofin (2 µM) in all cases. Data are mean±SEM (n=3–5), ^⁎ significant decrease due to auranofin (p <0.05). BLD=below limit of detection (i.e. not different from zero). (D) Comparison between $V_{app}^P$ and $V_{app}^{Cmax}$ in muscle mitochondria respiring on different substrates. Control (black) or auranofin (grey) values are taken from Fig. 2A and C with each substrate condition indicated by a different symbol. Linear regressions are shown to illustrate the relationship between apparent rates of production and consumption.

Based on Eq. (2), if the consuming pathways behave like a first order reaction we can predict that the underestimation of V^P, when measured as $V_{app}^P$, should be a function of matrix H₂O₂ levels ([H₂O₂]_matrix). As explained above, our measure of mitochondrial H₂O₂ efflux clamps the [H₂O₂] in the medium ([H₂O₂]_medium) to levels approaching 0 nM. Therefore the $V_{app}^P$ will be a function of the diffusion gradient, which will be set by the [H₂O₂]_matrix. In other words, for there to be an increased rate of efflux, there must be an increase in the diffusion gradient for H₂O₂ across the mitochondrial membranes. Since V^C and the diffusion gradient should be a function of [H₂O₂]_matrix the absolute underestimate of V^P should increase as a function of increasing V^P, or by proxy $V_{app}^P$. Across a range of V^P, the increase in H₂O₂ efflux in response to auranofin shows a strong positive relationship between $V_{app}^P$ in control mitochondria and the absolute $V_{app}^P$ increase in response to auranofin (Fig. 2B), consistent with a [H₂O₂]_matrix-dependent consumer.

With H₂O₂ efflux behaving in a manner consistent with the presence of a [H₂O₂]_matrix-dependent consumer, we then turned to the consumption of extramitochondrial H₂O₂. For simplicity we are assuming that V^C is not affected by the substrate(s) used, an assumption that requires an adequate and sustained supply of electrons to the NADPH-dependent peroxidase systems. This could be facilitated by either transhydrogenation or NADP-dependent dehydrogenases. Consistent with this requirement the activity of nicotinamide-nucleotide transhydrogenase (NNT) and NADP-dependent malic enzyme (ME) are high relative to rates of H₂O₂ production or consumption in our rat skeletal muscle mitochondria preparations (91±15 nmol min⁻¹ mg mitochondrial protein⁻¹ (n=4) for NNT, 40±4.7 nmol min⁻¹ mg mitochondrial protein⁻¹ (n=3) for ME). As such, we feel it is reasonable to assert that NADPH supply to the matrix peroxidase systems is likely sufficient in energized mitochondria under all substrate conditions tested.

Similar to measurements of H₂O₂ efflux, when measuring the disappearance of H₂O₂ from the medium there is expected to be an actual matrix level consumption (V^C) and an apparent rate of consumption by the mitochondria ($V_{app}^C$). The difference between these should be due to matrix H₂O₂ production (Fig. 1C). The overall relationship can be described by

V^C_app=V^C −V^P where V^C=k[H₂O₂] (3)

(i.e. first order)

Although it is clear the decay of H₂O₂ from the medium is non-linear over the range of [H₂O₂] used (see representative trace from [29] and Fig. 3A of the current work), it is initially more straightforward to compare rates rather than rate constants versus $V_{app}^P$. As such, we use the initial rate of H₂O₂ disappearance as a measure of $V_{app}^{Cmax}$ when the [H₂O₂] is high; we designate this approximately linear initial phase of disappearance $V_{app}^{Cmax}$ to allow for direct initial comparisons of rates. This allows for estimates of extramitochondrial H₂O₂ clearance with the exception of succinate plus auranofin where we found no consistent time-dependent consumption of H₂O₂ (Fig. 2C). For simplicity we have deemed the rate with succinate+auranofin as below limits of detection and enter it as such or as zero in figures. Similar to H₂O₂ efflux, there is a range of respiration-dependent values for $V_{app}^{Cmax}$ depending on the substrate condition used. Malate has the highest value and succinate the lowest $V_{app}^{Cmax}$ (Fig. 2C). For all substrates the addition of auranofin to the assay markedly inhibited $V_{app}^{Cmax}$ (Fig. 2C), confirming that the auranofin-induced increase in $V_{app}^P$ (Fig. 2A) is likely due to impaired consumption of H₂O₂ within the matrix.

Fig. 3.

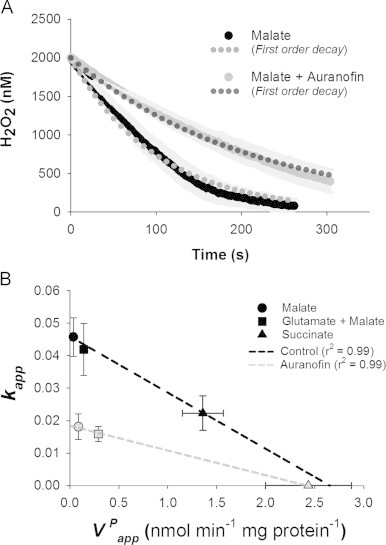
(A) The fit of a first order rate equation to the disappearance of H₂O₂ from the medium by respiring mitochondria. Note, although only 5 mM malate or 5 mM malate plus 2 µM auranofin are illustrated, similar fits and variation were found for all other conditions. Solid lines are the mean for each condition with SEM indicated by light grey (n=4 for each condition). Dotted lines (r²=0.98 for mean malate and 0.99 for mean malate+auranofin values) represent regressions fitting [H₂O₂]_t=[H₂O₂]₀×e−k_app·pr·t to the mean data values. (B) Extrapolating the inverse relationship between $V_{app}^P$ and k_app to determine k. Data are mean±SEM (n=4–6) based on H₂O₂ efflux (Fig. 2A) and calculated first order rate constant using the consumption of H₂O₂ based on [H₂O₂]_t = [H₂O₂]₀⋅e^{−k_app·pr·t} and [H₂O₂]₀ set at 2000 nM. Black is control, grey is with 2 µM auranofin present. Estimates for k when $V_{app}^P$ is zero are 0.045 and 0.018 under control and auranofin inhibited conditions respectively.

Experiments with the extramitochondrial horseradish peroxidase-linked H₂O₂ detection system (Fig. 2A and B) are not necessarily a direct quantitative comparison to those that monitor the decomposition of extramitochondrial H₂O₂ (Fig. 2C); but, if one accepts the models set out in Fig. 1 then it should be possible to compare mitochondria oxidizing the same substrate to examine the pattern between proxies of production and consumption. Doing so indicates a strong negative relationship between H₂O₂ efflux, a proxy of V^P, and the $V_{app}^{Cmax}$ (Fig. 2D). This is consistent with the expectations that arise from Eq. (3) assuming V^C is relatively independent of the respiratory substrate added. Thus, the substrate dependency of $V_{app}^{Cmax}$ can be explained entirely by a change in production (V^P), or more precisely by a varying degree of collapse in the inward directed H₂O₂ diffusion gradient as V^P increases from the low rates with malate alone to the high rates with succinate. Note, because glutamate+malate gave rates of H₂O₂ efflux similar to those found with succinate+rotenone we omitted the latter condition from the consumption experiments. The inverse relationship between $V_{app}^{Cmax}$ and $V_{app}^P$ (Fig. 2D) is altered by inhibiting consumption with auranofin but remains strong despite having a much lower slope when V^C is impaired.

Overall, the results from Series 1 experiments demonstrate the importance of compartmentalization in explaining the apparent and actual rates of H₂O₂ metabolism; the difference between these rates is consistent with diffusion driven H₂O₂ movement between the intra- and extramitochondrial compartments and [H₂O₂]_matrix-dependent consumption.

Series 2: Estimating k by extrapolation of apparent kinetics for H₂O₂ disappearance

The consumption of extramitochondrial H₂O₂ behaves as described in Fig. 1C, consistent with an underestimation of the actual rate. As such, estimating the rate constant (k) of H₂O₂ consumers (V^C) using the apparent kinetics of H₂O₂ disappearance ($V_{app}^C$) requires correcting for the difference between apparent and actual rates.

Assuming relative consistency of V^C across different respiratory substrate conditions, the apparent consumption kinetic constant (k_app) should decrease as a function of increasing V^P. We have already demonstrated that V^P, or proxies thereof, can be manipulated by substrate selection (Fig. 2). Therefore, as V^P (or by proxy $V_{app}^P$) increases, k_app should decrease in a linear fashion because in the simple model (Eq. (1)) V^P and k are inversely, but directly, related.

The consumption of H₂O₂ from the medium by energized mitochondria was fitted by nonlinear regression to the following equation:

[H₂O₂]_t=[H₂O₂]₀×e^{−k_app·pr·t} (4)

where t is the time (s), pr is the mitochondrial protein concentration in g l⁻¹ and k_app is the first order rate constant in s⁻¹ g⁻¹ l. Starkov et al. [1] find only an approximately proportional relationship between estimates of k and the amount of protein added in the assay; however, there is no obvious reason why k, or proxies thereof, should be dependent on protein concentration per se. We also find that estimates of $V_{app}^{Cmax}$, as the initial rate of disappearance, are linear with mitochondrial protein in the range used in this study. Thus, we have added a protein term to our model to make k independent of the quantity of mitochondrial H₂O₂ consumers added to the cuvette, thereby accounting for the dependency of $V_{app}^C$ on the amount of mitochondria present in the assay.

Overall the fits are reasonable (r²>0.94 for all individual experiments across all conditions) but clearly there is some deviation from the observed data (Fig. 3A). Table 1 gives the values for k_app and range of r² values for different substrate conditions in the absence or presence of auranofin. An additional challenge arose with succinate+auranofin, which could not be estimated because for this condition the [H₂O₂]_medium did not decrease to 2000 nM, which was used as the [H₂O₂]₀ common for all other experiments. Indeed, in some cases there was some net appearance of H₂O₂ in the medium. Since succinate+auranofin did not fit within the constraints used for all other experimental conditions we use zero as the approximation of k_app as a compromise value for this condition.

Table 1.

Regression parameters for estimation of k_app for muscle mitochondria respiring on different substrates.

Substrate	Control		Auranofina
	kapp (mean ± SEM)	r2 (range)	kapp (mean ± SEM)	r2 (range)
Malate	0.046±0.006	0.96–0.98	0.018 ± 0.004	0.99–1.0
Glutamate+malate	0.042±0.008	0.95–0.99	0.016 ± 0.002	0.99–1.0
Succinate	0.022±0.015	0.95–0.99	N/A	−

Values are for n=4–6. N/A=not analysed (see text for explanation).

^a2 µM auranofin added.

Combining the values for k_app (Table 1) and the $V_{app}^P$ (Fig. 2A) for the same respiratory substrate conditions demonstrates that, as the capacity to produce H₂O₂ increases, k_app decreases in a linear fashion (Fig. 3B). The slope of this relationship is, as expected, lower with auranofin (Fig. 3B). This relationship allows the prediction of k, because as V^P, or V^P_app, approaches zero, k_app will approximate k. Using this extrapolation method, k in control mitochondria is 0.045 (95% confidence interval of 0.031–0.059), and auranofin decreases k to 0.018 (95% confidence interval of 0.014–0.023).

Series 3: Estimating k based on establishing steady-state [H₂O₂]

Having determined k based on extrapolation of the k_app to zero $V_{app}^P$, we can advance the new premise; if the V/k=[H₂O₂]_ss model is a reasonable approximation of H₂O₂ balance, then the same value of k should be calculated based on the [H₂O₂]_ss. This cannot be done using an extramitochondrial detection system that destroys H₂O₂. However, by withholding a component of the extramitochondrial H₂O₂ detection system (AUR) for varying amounts of time it should be possible to determine H₂O₂ accumulation in the medium.

When glutamate and malate are used as the respiratory substrates we find that there is no appreciable accumulation of H₂O₂ in the medium (Fig. 4A). This indicates that if V^P is low there is limited accumulation of H₂O₂ in the medium, which is below detection in this case. However, if V^C is impaired by the addition of auranofin then there is a net accumulation of H₂O₂ in the medium over time (Fig. 4B). Unfortunately, we find that $V_{app}^P$ is not strictly linear over time if the assay is extended beyond 10 min after the addition of substrates, with rates noticeably declining between 10 and 20 min (data not shown). As such, we could not simply extend the assay duration to determine the [H₂O₂]_ss using substrates that will have a low rate of H₂O₂ production relative to the capacity for consumption (i.e. glutamate+malate, succinate+rotenone, malate). Nevertheless, these experiments do confirm the importance of H₂O₂ consumption capacity in the role mitochondria may play in regulating cellular H₂O₂ levels. Moreover, under conditions were V^P is low, uninhibited muscle mitochondria may only appear to ‘produce’ significant H₂O₂ because of the presence of an extramitochondrial H₂O₂ trapping system like the fluorescent detection systems typically used to measure H₂O₂ efflux. Presumably this is because the consumption pathways maintain low [H₂O₂]_ss unless V^P is high, such as with succinate (see next paragraph), or if the endogenous consumption pathways are inhibited.

Fig. 4.

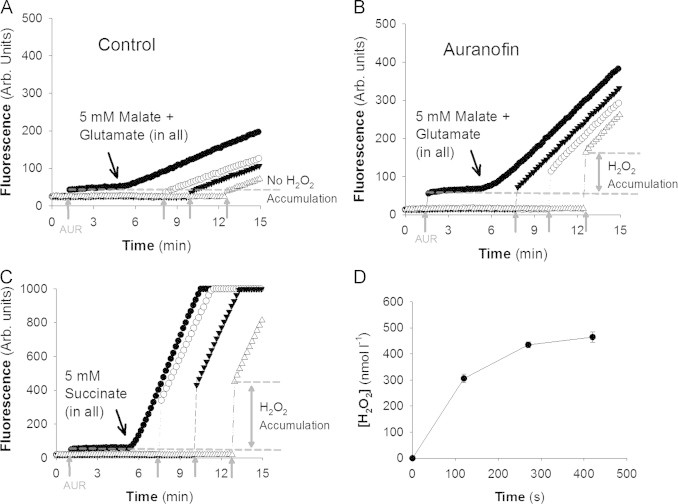
Testing for the accumulation of H₂O₂ in the medium over time with muscle mitochondria. For A–C all assay components were added before beginning the assay, with the exception of Amplex Ultrared (AUR) which was added as indicated by vertical grey arrows (↑). Fluorescence is in arbitrary (rb.) units. Note, for A–C there is some initial fluorescent product due to the quality and age of the AUR that must be subtracted from all other values. (A) Negligible accumulation of H₂O₂ in medium with mitochondria respiring on 5 mM glutamate and malate. (B) Addition of 2 µM auranofin to mitochondria respiring on 5 mM glutamate and malate results in H₂O₂ accumulation. (C) Mitochondria respiring on 5 mM succinate accumulate H₂O₂ in the medium in a time dependent manner. Note, where the traces reach 1000 Arb. units the detector has reached its maximum for the sensitivity settings used. (D) Accumulation of H₂O₂ in the medium by mitochondria respiring on 5 mM succinate approaches a stable steady-state concentration. Data are mean±SEM (n=3).

When we use succinate as the respiratory substrate in the absence of rotenone there is accumulation of H₂O₂ in the medium (Fig. 4C and D) presumably because of higher V^P. Another important aspect is that, following the addition of AUR, the $V_{app}^P$ is comparable over the entire duration of the experiment. This later point is vital for the experimental design because it shows that H₂O₂ production is roughly stable (no more than 10% change) for the entire duration, and thus the system appears to be stable over time.

Using this experimental design, with succinate as the substrate, we can fit the accumulation of H₂O₂ in the medium (Fig. 4C and D) to the following equation and solve V^P and k for each individual experiment:

[H₂O₂]_t = V^P/k (1−e^−k.pr.t) (5)

Since V^P/k=[H₂O₂]_ss as t→∞ we can also calculate [H₂O₂]_ss for each individual experiment (Table 2). Note Eq. (5) is the same as that derived by Starkov et al. [1]; however, we have incorporated a protein term into the model (as described above). It is important to stress that the values derived from these experiments (Table 2), where the system is allowed to approach equilibrium (i.e. approach where V^P=V^C), allows for direct determination of V^P and k (Fig. 1D) instead of the apparent values measured in the previous section. We also calculate $V_{app}^P$ based on the rate of fluorescence increase following the addition of AUR.

Table 2.

Summary of results and comparisons of nonlinear regression based determinations of H₂O₂ metabolism by muscle mitochondria respiring on 5 mM succinate.

Parameter
VP (nmol H2O2 g protein−1 s−1)	17.4±1.8a
k (s−1 g protein −1 l)	0.037±0.003b
[H2O2]ss (nmol l−1)	484±28

^ap<0.05 for paired t-test compared to measured $V_{app}^P$ of 12.7±1.48 nmol H₂O₂ g protein⁻¹ s⁻¹.

^bWithin 95% confidence interval (0.031–0.059) for k based on regression of k_app as $V_{app}^P$ approaches zero for uninhibited mitochondria (Fig. 3B).

As predicted from the diffusion based models of H₂O₂ exchange we found that V^P is greater than $V_{app}^P$ for the same mitochondria respiring on succinate (Table 2). Moreover, the estimate of k from experiments where [H₂O₂]_ss is approached is within the 95% confidence interval for k based on the extrapolation of k_app used in the previous section (Fig. 3). Thus, estimates of k from experiments designed to extrapolate from apparent values or as [H₂O₂]_ss is approached are in reasonable agreement. This is a central requirement for the simple model expressed in Eq. (1) to be a reasonable approximation of the integrated metabolism of H₂O₂ by mitochondria.

Summary

We find support for both (i) the assumed diffusion driven system between the mitochondrial and extramitochondrial compartments that complicates interpretation based on apparent rates and (ii) the simple V^P/k=[H₂O₂]_ss model, although our results indicate that this simple model is an approximation. Nonetheless, this simple approach presents a valuable new tool in the study of the mitochondrial H₂O₂ metabolism. This approach may well extend to mitochondria in general, although it has only been examined in rat skeletal muscle and brain mitochondria [1].

In particular, we urge caution in interpreting values obtained using a H₂O₂ trap system such as AUR since they do not represent actual rates of production (V^P). Indeed, these experiments demonstrate that rates of superoxide/H₂O₂ production, when measured as H₂O₂ efflux, are not only an underestimation; these rates do not reflect a true H₂O₂ burden a cell may have to detoxify. This is because the rate of appearance is largely due to the trapping of extramitochondrial H₂O₂. Left without the complete extramitochondrial trapping mechanism, mitochondria appear to maintain extramitochondrial H₂O₂ as a function of the balance between the potential to produce ROS and the capacity to consume H₂O_2. Overall, these data support the contention that the role of mitochondria in cellular H₂O₂ metabolism is a function of the interaction between the production and consumption capacity and not a simple function of production or consumption individually. Future studies determining how the balance between mitochondrial H₂O₂ production and consumption may vary between different physiological/pathological conditions are warranted.

However, even if mitochondria may act as stabilizer of H₂O₂ in vitro this does not definitely answer if they are a net sink or source of H₂O₂ in vivo. Extramitochondrial compartments also possess ROS generating sites capable of producing superoxide/H₂O₂ [6]. There are also comparable GSH and Trx-dependent antioxidant pathways outside of the mitochondria which may behave in a manner similar to our findings with isolated mitochondria, for instance following a [H₂O₂]-dependent decay. Within this context, experiments to differentiate between how mitochondria may be acting to stabilize H₂O₂in vivo at a particular target level, set by their bioenergetic state, also need to consider how that level of H₂O₂ may compare to that of the cytosol and the influences on non-mitochondrial sources and consumers.