Space-Time Data fusion Under Error in Computer Model Output: An Application to Modeling Air Quality

Summary

We provide methods that can be used to obtain more accurate environmental exposure assessment. In particular, we propose two modeling approaches to combine monitoring data at point level with numerical model output at grid cell level, yielding improved prediction of ambient exposure at point level. Extending our earlier downscaler model (Berrocal, V. J., Gelfand, A. E., and Holland, D. M. (2010b). A spatio-temporal downscaler for outputs from numerical models. Journal of Agricultural, Biological and Environmental Statistics 15, 176–197), these new models are intended to address two potential concerns with the model output. One recognizes that there may be useful information in the outputs for grid cells that are neighbors of the one in which the location lies. The second acknowledges potential spatial misalignment between a station and its putatively associated grid cell.

The first model is a Gaussian Markov random field smoothed downscaler that relates monitoring station data and computer model output via the introduction of a latent Gaussian Markov random field linked to both sources of data. The second model is a smoothed downscaler with spatially varying random weights defined through a latent Gaussian process and an exponential kernel function, that yields, at each site, a new variable on which the monitoring station data is regressed with a spatial linear model. We applied both methods to daily ozone concentration data for the Eastern US during the summer months of June, July and August 2001, obtaining, respectively, a 5% and a 15% predictive gain in overall predictive mean square error over our earlier downscaler model (Berrocal et al., 2010b). Perhaps more importantly, the predictive gain is greater at hold-out sites that are far from monitoring sites.

1. Introduction

The need for accurate assessment of exposure to air pollutants arises to effectively investigate the linkage between ambient exposure and health effects. It also arises with regard to compliance with legislated regulatory standards to control levels of environmental exposure. As a result, the US Environmental Protection Agency (EPA) monitors pollutant levels using information from monitoring networks as well as estimates generated by deterministic numerical models. The former measure pollutant concentrations using instruments at a sparse set of stations, while the latter yield estimates of the average concentration in grid cells of prespecified dimensions by numerically solving complex systems of differential equations capturing various diffusion, chemical, and atmospheric processes. The computer model output spans large spatial domains with no missingness.

Fusing these information sources can improve exposure assessment at high, in fact, point-level resolution. Combining data from multiple sources, so-called data assimilation, is well-known in the atmospheric sciences (Kalnay, 2003). There, the goal is to combine observational data on the current state of the atmosphere with a short-range forecast in order to obtain initial conditions for a numerical atmospheric model. Most methods proposed in atmospheric data assimilation are algorithmic, ad hoc and do not address the “change of support” problem (Cressie 1993; Gotway and Young 2002; Banerjee, Carlin, and Gelfand 2004, chapter 6).

The statistics literature on “data fusion” can be grouped into two paths. One is Bayesian melding (Fuentes and Raftery 2005) where observational data is combined with computer model output by introducing a latent point-level process driving both sources of data. The numerical model output is then expressed as a linearly calibrated integral over a grid cell (scaled by the area of the cell) of the latent point-level process while the monitoring data is related to the latent process via a measurement error model. A spatio-temporal extension of Bayesian melding has been presented by McMillan et al. (2010). This approach offers a solution to the problem through upscaling to grid cells.

The second approach uses a two-stage regression, dating to Guillas et al. (2008) and subsequently Liu, Le, and Zidek (2008), with an ad hoc method to allow the coefficients of the linear regression to be spatially interpolated. Berrocal, Gelfand, and Holland (2010a, 2010b) propose univariate and bivariate hierarchical downscaler models that relate the monitoring station data and the computer model output using a spatial linear model with spatially varying coefficients in turn modeled as Gaussian processes (GPs). These models offer the advantage of local calibration of the numerical model output without incurring in problems due to the dimensionality of the computer model output, as for example in Bayesian melding, since they are only fitted at the numerical model grid cells where the monitoring stations reside.

The contribution of this article is to provide two useful neighbor-based extensions of our earlier downscaler modeling work. That is, there may be useful information in the output at neighboring grid cells to the one where the location lies and there may be misalignment between stations and putatively associated grid cells. These extensions do not seek directly to remedy other forms of error that may be built into the numerical model (errors reflecting uncertainty in model input, uncertainty in the partial differential equations for the dynamics of pollution transport, and uncertainty introduced by the numerical approximation methods used to solve the resulting system of partial differential equations). In particular, these new models provide adaptive smoothing to the computer model output which achieves stronger association with the observed station data. Improved spatial interpolation of the ambient exposures results; using hold out data, we achieve gains of 5% and 15%, respectively, in predictive mean square error over our original downscaler. One extension introduces a Gaussian Markov random field (GMRF) to smooth the computer model. The other introduces spatially varying weights driven by a latent GP to accomplish the smoothing. This last model falls in the realm of recent work to render conditionally autoregressive models (CAR; Besag 1974; Banerjee et al. 2004) more flexible by allowing adaptive adjacency structure (e.g. Lu and Carlin 2005; Kyung and Ghosh 2010).

We apply our approach to interpolate ozone levels in space and time for the summer of 2001 using station data and the Community Multiscale Air Quality model (CMAQ; Byun and Schere 2006) output. However, the strategy is applicable to other environmental contaminants and to other data fusion settings.

The format of the article is as follows. In Section 2, we present the motivating data. In Section 3, we review the elementary downscaler model (Berrocal et al., 2010b) and introduce two extensions. In Section 4, we discuss computation details relative to the fitting of these downscaler models, while in Section 5, we present results on the predictive performance of these models. We conclude with Section 6 where we briefly discuss future extensions of the smoothed downscaler with spatially varying random weights. Supplementary material including additional figures and results is available online at the Biometrics website (http://www.biometrics.tibs.org).

2. Data

Ground-level ozone is one of the six “criteria pollutants” that the US EPA is required to monitor by the Clean Air Act. To keep track of ozone concentration, the EPA utilizes monitoring devices sparsely located across the United States along with estimates of ground-level ozone concentration produced by the deterministic numerical air quality model, Models-3/ Community Mesoscale Air Quality model, CMAQ (Byun and Schere 2006; http://epa.gov/asmdnerl/CMAQ). We illustrate our fully model based fusion approach using these two sources. In both cases, the data refer to the daily 8-hour maxima ozone concentration (henceforth daily concentration) for the Eastern United States during the summer months of June, July, and August 2001, when the elevated temperatures and solar radiation exacerbate the production of ozone.

Figure 1 displays the locations of the 800 monitoring sites belonging to the National Air Monitoring Stations/State and Local Air Monitoring Stations (NAMS/SLAMS) network that we employed for our analysis. Of the 800 sites, we selected 700 at random as a fitting dataset (percentage of missing data during the 92 summer days of 2001 = 2.8%), while we used the remaining 100 (percentage of missing data = 2.2%) to assess the out-of-sample predictive performance of four approaches: (i) a kriging model using only the station data, (ii) the spatio-temporal downscaler model discussed above (Berrocal et al., 2010b), (iii) a downscaler model with GMRF smoothing, and (iv) a downscaler model with smoothing obtained using spatially varying random weights.

Figure 1.

Training and validation sites used to fit and assess the out-of-sample predictive performance of the ordinary kriging model, the downscaler, the GMRF smoothed downscaler and the smoothed downscaler using spatially varying random weights.

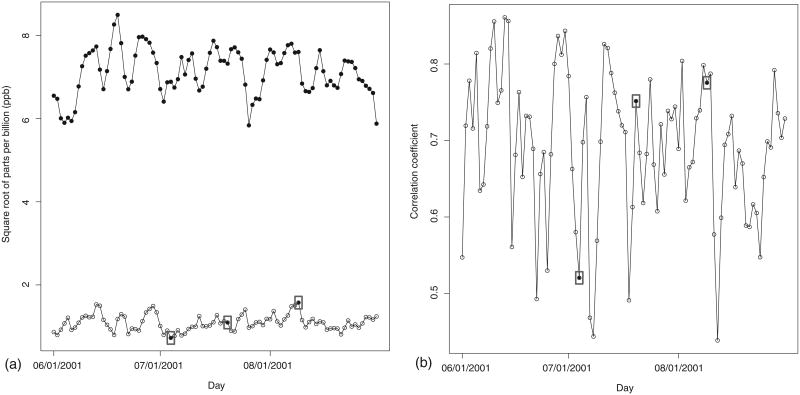
Following Berrocal et al. (2010b), Sahu, Gelfand, and Holland (2007) and references therein, we have modeled ozone concentration on the square root scale to achieve approximate normality and stabilize the variance. The observed ozone concentration data display a fair degree of variability during the summer months of 2001: the daily mean of the daily ozone concentration over the 800 monitoring sites, ranges from 5.8 to 8.5 √ppb (parts per billion), while the daily standard deviation varies from 0.7 to 1.6 √ppb (Figure 2a).

Figure 2.

(a) Daily mean (filled circles) and standard deviation (empty circles) of square root of observed ozone concentration at all the 800 monitoring sites. (b) Daily correlation betweeen square root of observed ozone concentration and square root of CMAQ output of ozone concentration. In both plots, the three days for which we will present results in Section 5 are surrounded by a box. They are, respectively, July 4, July 20, and August 9, 2001.

CMAQ produces estimates of ozone concentration over the United States at predetermined spatial and temporal scales. We used CMAQ for the eastern United States at 12-km resolution yielding 40,044 daily grid cell values. Although at areal scale rather than at point level, the CMAQ output has the advantage of complete spatial coverage and no missingness. In addition, it is moderately to fairly strongly correlated with the observed ozone concentration data, suggesting its potential for improved spatial interpolation. In particular, Figure 2(b) displays the daily correlation between the square root of observed ozone concentration at site s and the square root of the CMAQ output at the grid cell B that contains s.

3. Modeling

We briefly review the downscaler model of Berrocal et al. (2010b) and then we present the two promising specifications that extend the downscaler model to improve the fusion in light of concerns mentioned in the Introduction. For each model, we first present its static version and then its spatio-temporal formulation.

3.1 Static Setting

3.1.1 The univariate downscaler

Let Y(s) denote the square root of the daily ozone concentration observed at site s, and let x(B) indicate the square root of the daily ozone concentration predicted by CMAQ over grid cell B.

In the downscaler model, the change of support problem is addressed by relating Y(s) to the CMAQ output, x(B), at the grid cell B that contains s, via the model

$$Y(\mathbf{s})={\stackrel{\sim }{\beta }}_0(\mathbf{s})+{\stackrel{\sim }{\beta }}_1(\mathbf{s})x(B)+\epsilon (\mathbf{s}),\epsilon (\mathbf{s})\stackrel{\mathit{\text{ind}}}{~}\mathrm{N}(0,{\tau }^2),$$ (1)

where ε(s) is a white noise process with nugget variance τ², and β̃₀(s) and β̃₁(s) are spatially varying coefficients that can be decomposed as

$$\begin{array}{c}{\tilde{\beta }}_0(\mathbf{s})={\beta }_0+{\beta }_0(\mathbf{s})\\ {\tilde{\beta }}_1(\mathbf{s})={\beta }_1+{\beta }_1(\mathbf{s}),\end{array}$$ (2)

with β₀ and β₁, respectively, the overall intercept and slope in calibrating the CMAQ model output and β₀(s) and β₁(s), respectively, the local adjustments to these terms. Anticipating association between β₀(s) and β₁(s), the two spatially varying coefficients are in turn modeled as correlated mean-zero Gaussian spatial processes using the method of coregionalization (Wackernagel 2003; Gelfand et al. 2004). Thus, we assume two mean-zero unit-variance independent GPs v₀(s) and v₁(s) each, for convenience, equipped with an exponential covariance structure having decay parameters, respectively, ϕ₀ and ϕ₁, such that

$$\left(\begin{array}{c}{\beta }_0(\mathbf{s})\\ {\beta }_1(\mathbf{s})\end{array}\right)=\mathbf{A}\left(\begin{array}{c}{v}_0(\mathbf{s})\\ v_1(\mathbf{s})\end{array}\right),$$ (3)

where the unknown A matrix in (3) can be assumed, without loss of generality, to be lower-triangular. To complete the hierarchical specification, we need to provide prior distributions for the overall bias terms, β₀ and β₁, the nugget variance, τ², the three nonnull elements of the coregionalization matrix A, and the decay parameters ϕ₀ and ϕ₁.

The downscaler model “fuses” the two sources of data while avoiding problems due to the large number of grid cells (>40,000) associated with the CMAQ model output since only numerical model grid cells with monitoring station observations are used in fitting. As a result, we can address the change of support problem while avoiding introduction of stochastic integrals, needed in the scaling up associated with Bayesian melding. Such integrals render the latter models computationally challenging to fit for a large number of grid cells and hopeless when we introduce measurements over time.

Comparison with ordinary kriging has shown that the downscaler model yields better in and out-of-sample predictive performance. Lower predictive mean square and absolute value errors along with predictive intervals having coverage close to the nominal value result.

3.1.2 A GMRF smoothed downscaler

In (1) the CMAQ model output enters as a covariate. Here, we introduce a smoothed version of the {x(B)} surface arising from a latent Gaussian Markov random field (GMRF), i.e., let

$$x(B)=\mu +V(B)+\eta (B)\eta (B)\stackrel{\mathit{\text{ind}}}{~}N(0,{\sigma }^2)$$ (4)

with μ an overall mean and V(B) a mean-zero Gaussian Markov random field equipped with a conditionally autoregressive structure (CAR; Besag 1974; Banerjee et al. 2004). In other words, if g is the number of numerical model grid cells, then we assume that

$$V(B_i)|\{V(B_j):j\ne i\}\sim N(\sum _{j\in \delta B_i}\frac{V(B_j)}{m_i},\frac{{\xi }^2}{m_i})i=1,\dots ,g$$ (5)

where δB_i denotes the set of grid cells that are neighbors to B_i. Although the joint distribution of the {V(B_i)} is improper, the joint distribution for the {x(B_i)} given the V's is proper and so we have a valid model for the data {x(B_i)}. Also, the GMRF specification makes it clear that {Ṽ(B): Ṽ(B) = μ + V(B)} is a smoothed version of {x(B)}. Hence, for s ∈ B, we revise (1) to

$$Y(\mathbf{s})={\stackrel{\sim }{\beta }}_0(\mathbf{s})+{\beta }_1\stackrel{\sim }{V}(B)+\epsilon (\mathbf{s})\epsilon (\mathbf{s})\sim N(0,{\tau }^2)$$ (6)

where, again, β̃₀(s) = β₀ + β₀(s) with β₀(s) modeled as a mean-zero GP with exponential covariance structure, decay parameter ϕ₀ and marginal variance ${\sigma }_{{\beta }_0}^2$.¹

Differently from the downscaler model, with the GMRF smoothed downscaler model we sacrifice dimension reduction. Though (6) is still fitted only at those grid cells B with observations, (4) with (5) requires the entire latent field V(B). Fortunately, the computation associated with a GMRF is local so we can still fit this model efficiently. Also, (6) through (4) and (5) clarifies that we are implicitly relating the Y(s) with the CMAQ model output at all the grid cells that are neighbors of the grid cell B containing s.

3.1.3 A smoothed downscaler using spatially varying random weights

Here, we introduce smoothing using weights that are random and spatially varying. Now, we regress the observation at site s, Y(s), on a point-level regressor, x̃(s), obtained by creating, at each site s, a weighted average of all the numerical model output with weights that are site-specific.

We replace (6) with

$$Y(\mathbf{s})={\stackrel{\sim }{\beta }}_0(\mathbf{s})+{\beta }_1\stackrel{\sim }{x}(\mathbf{s})+\epsilon (\mathbf{s})\epsilon (\mathbf{s})\sim N(0,{\tau }^2)$$ (7)

where β̃₀(s) is as in (6) and

$$\stackrel{\sim }{x}(\mathbf{s})=\sum _{k=1}^g{w}_k(\mathbf{s})x(B_k).$$ (8)

The weights w_k(s) are in turn defined as follows: let r_k, k = 1,…, g be the centroids of the g numerical model grid cells, and let Q(r) be a mean-zero GP having exponential covariance function with decay parameter ϕ_Q and marginal variance ${\sigma }_Q^2$. Then, given {Q(r_k)}, the g-dimensional random vector of weights {w_k(s)}_{k=1,…, g} at s is given by

$$w_k(\mathbf{s}):=\frac{\mathcal{K}(\mathbf{s}-{\mathbf{r}}_k;\psi )\cdot exp(Q[{\mathbf{r}}_k])}{{\sum }_{l=1}^g\mathcal{K}(\mathbf{s}-{\mathbf{r}}_l;\psi )\cdot exp(Q[{\mathbf{r}}_l])}$$ (9)

where 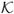(s − r_k; ψ) is an exponential kernel with decay parameter ψ.

Expression (9) is reminiscent of the discretized version of process convolution introduced by Higdon (1998). However, that work developed a stochastic process model with covariance function induced by the kernel 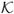. Here, we are only interested in creating a spatially varying set of weights that are spatially dependent, positive and sum to 1. If we define the weights w_k(s) without introducing the latent GPQ(r) they would not be directional and would have the same circular contour when moving from site to site. From (9), the Q(·) process is not identified; its center is arbitrary. So, we impose a “sum to 0” constraint, implementing it on the fly in the model fitting. Further discussion regarding the effect on the weights due to ψ, ϕ_Q, and ${\sigma }_Q^2$ is provided in Section 4.

Evidently, we allow calibration in the association between the observational data at s, Y(s), and the revised numerical model output at the grid cell B that contains s. Also, we clearly relate Y(s) to CMAQ levels at neighbors of the grid cell s belongs to. Moreover, as in the GMRF smoothed downscaler model, the collection {x̃(r_k)}_{k=1,…, g} can be interpreted as a smoothed version of the CMAQ model output, analogous to the collection {Ṽ(B_k)}_{k=1,…, g}.

3.2 Spatio-Temporal Modeling

We now extend these downscaler models to handle data collected over space and time.

3.2.1 The univariate downscaler

Let t denote time with t = 1,…, T, and let Y(s, t) denote the square root of the daily ozone concentration observed at site s and time t. Following Section 3.1.1, x(B, t) is the square root of the CMAQ predicted daily average ozone concentration over grid cell B at time t. As in the static setting, we associate to each point s the CMAQ grid cell B in which it lies, and extend (1) to

$$Y(\mathbf{s},t)={\stackrel{\sim }{\beta }}_0(\mathbf{s},t)+{\stackrel{\sim }{\beta }}_1(\mathbf{s},t)x(B,t)+\epsilon (\mathbf{s},t),$$ (10)

where $\epsilon (\mathbf{s},t)\stackrel{\mathit{\text{ind}}}{\sim }N(0,{\tau }^2)$. For each t = 1,…, T, we decompose β̃_i(s, t), i = 0, 1 as the sum of an overall coefficient and a local adjustment to it, that is: β̃_i(s, t) = β_{i, t} + β_i(s, t), i = 0, 1.

We consider two ways to introduce temporal dependence in the time varying parameters β_{0, t}, β_{1, t}, β₀(s, t), and β₁(s, t). The first is to assume that they are nested, i.e. they are independent across time; the second is to assume that they evolve dynamically in time (West and Harrison 1999). For the former, we would adopt ${\beta }_{i,t}\stackrel{\mathit{\text{ind}}}{\sim }N({\mu }_i,{\sigma }_i^2),i=0,1$ while if they are dynamic, we would assume

$${\beta }_{i,t}={\rho }_i{\beta }_{i,t-1}+{\varsigma }_{i,t}{\varsigma }_{i,t}\stackrel{\mathit{\text{ind}}}{\sim }N(0,{\varsigma }_i^2)i=0,1.$$ (11)

If the β₀(s, t) and β₁(s, t) are assumed nested within time, then for each t = 1,…, T, they are expressed as a linear combination of uncorrelated latent mean-zero unit-variance GPs v₀(s, t) and v₁(s, t) having exponential covariance functions with decay parameters, respectively ϕ_{0, t} and ϕ_{1, t}, i.e. similar to (3),

$$\left(\begin{array}{c}{\beta }_0(\mathbf{s},t)\\ {\beta }_1(\mathbf{s},t)\end{array}\right)=\mathbf{A}\left(\begin{array}{c}{v}_0(\mathbf{s},t)\\ v_1(\mathbf{s},t)\end{array}\right)$$ (12)

with A coregionalization matrix and v₀(s, t) and v₁(s, t) independent replicates of two GPs. Conversely, if β₀(s, t) and β₁(s, t) evolve in time, then, following Gelfand, Banerjee, and Gamerman (2005), for each t = 1,…, T, we could assume

$${\beta }_i(\mathbf{s},t)={\gamma }_i{\beta }_i(\mathbf{s},t-1)+{\nu }_i(\mathbf{s},t)i=0,1,$$ (13)

where the innovations ν_i(s, t) are correlated mean-zero GPs defined as:

$$\left(\begin{array}{c}{\nu }_0(\mathbf{s},t)\\ {\nu }_1(\mathbf{s},t)\end{array}\right)=\mathbf{A}\left(\begin{array}{c}{v}_0(\mathbf{s},t)\\ v_1(\mathbf{s},t)\end{array}\right)$$

with the v_i(s, t) as above. In addition, for this model, we set β_i(s, 0) = 0, for i = 0, 1. In both (12) and (13), we might envision A = A_t with A_t independent across time.

With two different ways in which time dependence can be modeled for each of the time varying parameters, β_{0, t}, β_{1, t}, β₀(s, t), and β₁(s, t), we can formulate four different versions of the spatio-temporal downscaler model. In experiments carried out with ozone concentration data for 2001 (Berrocal et al. 2010b), the spatio-temporal downscaler model with all time varying parameters nested within time yielded the best predictive performance. The flexibility to choose daily decay parameters is better than the introduction of autoregressive structure in the β's. In addition, fitting conditionally independent daily models is computationally much faster. Hence, in what follows we only consider this specification.

3.2.2 The GMRF smoothed downscaler

To extend the GMRF smoothed downscaler model to the space-time setting, we assume that

$$Y(\mathbf{s},t)={\stackrel{\sim }{\beta }}_0(\mathbf{s},t)+{\beta }_{1,t}\stackrel{\sim }{V}(B,t)+\epsilon (\mathbf{s},t)\epsilon (\mathbf{s},t)\stackrel{\mathit{\text{ind}}}{\sim }N(0,{\tau }^2),$$ (14)

where we decompose β̃₀(s, t) as β̃₀(s, t) = β_{0, t} + β_{0, t}(s). Potential temporal dependence models for β_{0, t}, β_{1, t} and the single GP β₀(s, t) can take the forms described in Section 3.2.1. Extending the measurement error model (4), we have:

$$x(B,t)={\mu }_t+V(B,t)+\eta (B,t),$$ (15)

where $\eta (B,t)\stackrel{\mathit{\text{ind}}}{\sim }N(0,{\sigma }^2)$ and, then Ṽ(B, t) = μ_t + V(B, t)

To model the temporal dependence in the latent field Ṽ(B, t), as before, we consider two cases. In the first, we assume that for each t, the V_t = {V(B, t)} are independent replicates over time of a Gaussian Markov random field provided with a conditional autoregressive prior, that is, for each t:

$$V(B_i,t)|\{V(B_j,t):j\ne i\}\sim N(\sum _{j\in \delta B_i}\frac{V[B_j,t]}{m_i},\frac{{\xi }^2}{m_i}).$$ (16)

In a second case, we assume that the g-dimensional random vectors V_t, t = 1,…, T, have an AR(1) structure in time. Therefore, for each t

$${\mathbf{V}}_t=\rho {\mathbf{V}}_{t-1}+{\mathit{\kappa }}_t,$$ (17)

where κ_t = {κ(B, t)} is a Gaussian Markov random field with a conditional autoregressive structure and V₀ = {V(B, 0)} ≡ 0. As noted above, we only consider the model where the β_{0, t}, β_{1, t}, β₀(s, t), and the V_t = {V(B, t)} are independent in time.

3.2.3 The smoothed downscaler using spatially varying random weights

Extending (7), we assume that:

$$Y(\mathbf{s},t)={\stackrel{\sim }{\beta }}_0(\mathbf{s},t)+{\beta }_{1,t}\stackrel{\sim }{x}(\mathbf{s},t)+\epsilon (\mathbf{s},t)\epsilon (\mathbf{s},t)\sim N(0,{\tau }^2),$$ (18)

where β̃₀(s, t) = β_{0, t} + β₀(s, t). Potential models for the time varying parameters β_{0, t}, β_{1, t} and β₀(s, t) are as in Section 3.2.1 and 3.2.2. To define x̃(s, t), straightforward extension of (8) yields

$$\stackrel{\sim }{x}(\mathbf{s},t)=\sum _{k=1}^g{w}_k(\mathbf{s},t)x(B_k,t),$$ (19)

where the weights w_k(s, t) are random and varying both in space and time. Again, we let r_k, k = 1,…, g denote the centroids of the g numerical model grid cells. First, we introduce independent latent mean-zero GPs, Q(r, t), t = 1,…, T, with exponential covariance structure, decay parameter ϕ_Qt and variance ${\sigma }_Q^2$. Then, the weights w_k(s, t) take the form:

$$w_k(\mathbf{s},t):=\frac{\mathcal{K}(\mathbf{s}-{\mathbf{r}}_k;{\psi }_t)\cdot exp(Q[{\mathbf{r}}_k;t])}{{\sum }_{l=1}^g\mathcal{K}(\mathbf{s}-{\mathbf{r}}_l;{\psi }_t)\cdot exp(Q[{\mathbf{r}}_l;t])},$$ (20)

where 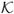(s − r_k; ψ_t) = exp(−ψ_t |s − r_k|), an exponential kernel with decay parameter ψ_t. This model allows the flexibility of spatially and temporally varying weights.

In an alternative formulation, the weights can be specified dynamically by assuming that the latent GP Q(r, t) follows an AR(1) process in time, i.e.,

$$Q(\mathbf{r},t)=\gamma Q(\mathbf{r},t-1)+\lambda (\mathbf{r},t)$$ (21)

with λ(r, t) independent GPs, Q(r, 0) ≡ 0 and the weights as in (20). Again, we only consider the γ = 0 case, i.e. independent Q surfaces over time. As in the static setting, we impose a sum to 0 constraint on each of the GPs Q(r, t), t = 1,…, T.

4. Model fitting

4.1 Priors

All the downscaler models introduced in Section 3 arise as a Bayesian hierarchical formulation and are completely specified given priors for all the parameters. In this section, we briefly discuss the priors adopted for the various model parameters.

First, we consider the static case. Global calibration of the numerical model output results from β₀ and β₁ for which we employ a bivariate normal prior with prior mean equal to (0 1)′ and a diagonal prior covariance matrix with very large diagonal entries corresponding to vague prior variances. For the coregionalization matrix A introduced in the downscaler model in (3) we specify a prior via its entries. More precisely, we place vague lognormal priors on the diagonal terms of A, as they are related to the variances of the local adjustments β₀(s) and β₁(s) and a vague normal prior on the off-diagonal element A₂₁. For all models, we adopt standard conjugate inverse gamma priors for all the variance terms, that is, for τ², σ², ξ², ${\sigma }_{{\beta }_0}^2,{\sigma }_Q^2$. In particular for ${\sigma }_Q^2$ we chose an inverse gamma prior with prior scale equal to 2 and with prior mean equal to 1.0. With more interest in smoothing than in measurement error, we place a rather informative prior on σ² specified so as to produce a posterior mean for σ² smaller, on average, than that of ξ², hence allowing for more variability in V(B) than in η(B).

For the GMRF smoothed downscaler model, we assign a vague normal prior to μ with prior mean equal to the average, over all grid cells B, of the numerical model output, x(B). Similar definition was adopted in the spatio-temporal case; for each t = 1,…, T, the prior mean for μ_t was taken to be equal to the average of x(B, t).

Regarding priors for the decay parameters, it is not possible to consistently estimate all the spatial covariance parameters under weak priors (Zhang 2004). In light of this, we adopted the following strategy: we used a continuous prior—an inverse gamma—for the marginal variance, while we used a discrete prior placed on a grid of values for the decay parameters. That is, for ϕ₀ and ϕ₁, we placed a discrete uniform prior on the grid of values, 0.0015, 0.001, 0.01, 0.05, and 0.1, corresponding, respectively, to practical ranges of about 3000, 2000, 300, 60, and 30 km. In the spatio-temporal case, we assumed that for each t, ϕ_{0, t}, and ϕ_{1, t} followed the same discrete uniform prior.

We could adopt the above specifications for the spatial decay parameters ψ and ϕ_Q in the downscaler with spatially varying random weights. However, we chose to keep them fixed. We set ψ equal to 0.08 yielding an exponential kernel with a range of approximately 36 km, that is three 12-km grid cells. Essentially, only first, second, and third order grid cell neighbors contribute nonnegligibly to the weighted average x̃(s) at s. Experiments with ψ's in the neighborhood of 0.08 didn't reveal sensitivity in terms of predictive performance.

The parameter ϕ_Q determines the smoothness of the process Q(r) and, thus, affects the smoothness of the weights w_k(s) as s moves across the spatial domain. It is clear that the smaller ϕ_Q is, the smoother realizations of Q(r) will be and thus, through (9), resulting weights may be less site-specific than we wish. So, we set ϕ_Q equal to 0.12 (larger than ψ), which corresponds to a range of approximately 24 km, i.e., two 12-km grid cells. Experiments with daily decay parameters ψ_t and ϕ_Qt yielded no distinguishable gain in model performance.

4.2 Computational details

We fit each of the downscaler models presented in Sections 3.1.1, 3.1.2, and 3.1.3 using a Markov Chain Monte Carlo (MCMC) algorithm. Previous experience with the downscaler (Berrocal et al. 2010b) suggested that we keep only the local intercept adjustment β₀(s) different from zero. Thus, we have a single GP and all priors are conjugate.

In the smoothed downscaler using spatially varying random weights, the posterior distribution of the latent GP Q(r) does not have a closed form. Hence, it is necessary to use a Metropolis–Hastings algorithm within the MCMC algorithm where we impose the sum to 0 constraint “on the fly” after each MCMC iteration (Besag et al. 1995). Moreover, we also face a dimensionality problem. To obtain a new sample of weights at each iteration, it is necessary to derive a realization of the latent process Q(r) at the g numerical model grid cell centroids r_k. Given the size of g, to reduce the computational burden associated with the sampling of the weights in (9) and (20), respectively, we replace Q(r_k) and Q(r_k, t), respectively, with the predictive processes (Banerjee et al. 2008) Q̃(r_k) and Q̃(r_k, t). We used m = 648 knots thinned from the centroids of the overall set of 40,044 CMAQ grid cells by systematically selecting knots every 8 rows and 8 columns. So many knots selected in a space-filling fashion avoids concern regarding knot selection issues (see Banerjee et al. 2008). More details on predictive processes and our implementation are provided in the Appendix.

Extension of the MCMC algorithm to the space-time setting is straightforward when the time varying parameters are independent across time. However, we still fit a joint model due to the common variance parameters, e.g., τ², σ², ξ², ${\sigma }_Q^2$. If some of the time varying parameters evolve dynamically in time, fitting requires embedding the Forward Filtering Backward Sampling (FFBS, Carter and Kohn 1994; West and Harrison 1999) algorithm within the MCMC algorithm. Finally, we accommodated missingness in the training dataset by using data augmentation to fill in the missing Y(s, t) at each MCMC iteration under the assumption that the missingness is ignorable.

5. Results

We discuss results for the spatio-temporal versions of the three downscaler models where all the time varying parameters are assumed to be independent across time along with an ordinary kriging model obtained from (10) by setting β̃₁(s, t) equal to 0. As mentioned in Section 2, we fit the models to 700 training sites and we assess the predictive performance of the various models at 100 hold-out sites. We evaluate the out-of-sample predictive performance of each model in terms of Predictive Mean Square Error (PMSE), averaged across space and time, Predictive Mean Absolute Error (PMAE), averaged across space and time, the average length of the 95% predictive interval, averaged across space time, and the empirical coverage of the 95% predictive interval. Table 1 presents results for these statistics for the four models. All downscaler models yield predictions with much lower PMSE and PMAE than an ordinary kriging model, demonstrating the benefit of using the information contained in the CMAQ output. In turn, both the GMRF smoothed downscaler and the smoothed downscaler using spatially varying random weights provide substantial improvement over the downscaler, supporting the need to account for error in the association that links the observation at a site s, Y(s), to the numerical model output at the grid cell B that contains s. In particular, the GMRF smoothed downscaler provides a 5.3% and a 1.9% reduction, respectively, in PMSE and PMAE over the downscaler, while the smoothed downscaler using spatially varying random weights yields a 14.5% and 5.7% improvement, respectively, in PMSE and PMAE. It is noteworthy that the improvement in PMSE and PMAE of the GMRF smoothed downscaler and of the smoothed downscaler with spatially varying weights over the downscaler model is larger at sites that are farther from monitoring training sites (figure available in online supplementary material).

Table 1.

Predictive Mean Squared Error (PMSE), Predictive Mean Absolute Error (PMAE), average length of the 95% predictive interval, and empirical coverage of the 95% predictive interval for the numerical model CMAQ, the new regressor x̃(s, t), an ordinary kriging model, the downscaler, the GMRF smoothed downscaler and the smoothed downscaler with spatially varying random weights

Model	PMSE	PMAE	Average length of 95% PI	Empirical coverage of 95% PI
CMAQ model	135.9	9.1	—	—
x̃(s, t)	124.2	8.7	—	—
Ordinary kriging	60.9	5.8	30.6	94.8%
Downscaler	53.1	5.3	30.4	94.9%
GMRF smoothed downscaler	50.3	5.2	29.4	94.9%
Smoothed downscaler with spatially varying random weights	45.4	5.0	27.7	95.0%

Spatial plots of the posterior mean of {x̃(r_k, t)}_{k=1,…, g}, {Ṽ(B_k, t)}_{k=1,…, g} and of the CMAQ model output {x(B_k, t)}_{k=1,…, g} for July 4, 2001 for a subregion of the Eastern US are shown in Figure 3. Both the GMRF smoothed downscaler and the smoothed downscaler using spatially varying random weights yield surfaces that are smoother than the original CMAQ output and, as Table 1 indicates, are better associated with the monitoring data. All three downscaler models yield predictions of ozone concentration over the entire spatial domain. However, differently from the numerical model output, the three downscaler models produce predictions that are better calibrated than CMAQ itself.

Figure 3.

Spatial maps of: (a) the square root of the CMAQ output, x(B, t), (b) the posterior mean of Ṽ(B, t), and (c) the posterior mean of x̃(B, t), for July 4, 2001 for a subregion in the Northeast.

Figure 4 shows the observed ozone concentration on August 9, 2001 at monitoring sites located in two subregions of the Eastern US along with the posterior predictive mean of ozone concentration resulting from the smoothed downscaler with spatially varying random weights. The predictive surfaces displayed in panels (b) and (d) reproduce the spatial gradient that is visible in the monitoring station data and tend to agree rather well with the observational data.

Figure 4.

(a)–(c) Observed ozone concentration (ppb) on August 9, 2001 in two subregions of the Eastern US. (b)–(d) Posterior predictive mean of ozone concentration on August 9, 2001 as yielded by the smoothed downscaler with spatially varying random weights.

All three downscaler models provide information on the daily local and global bias of the CMAQ model output through β_{0, t}, β_{1, t} and β₀(s, t). Though all the downscaler models have been fitted to ozone concentration on the square root scale, inspection of the posterior mean and 95% credible intervals for β_{0, t} and β_{1, t} clearly indicates that there is a need for calibration of CMAQ since for most days during the three months of June, July, and August 2010, all three models yield posterior estimates for β_{0, t} and β_{1, t} significantly different from 0 and 1, respectively.

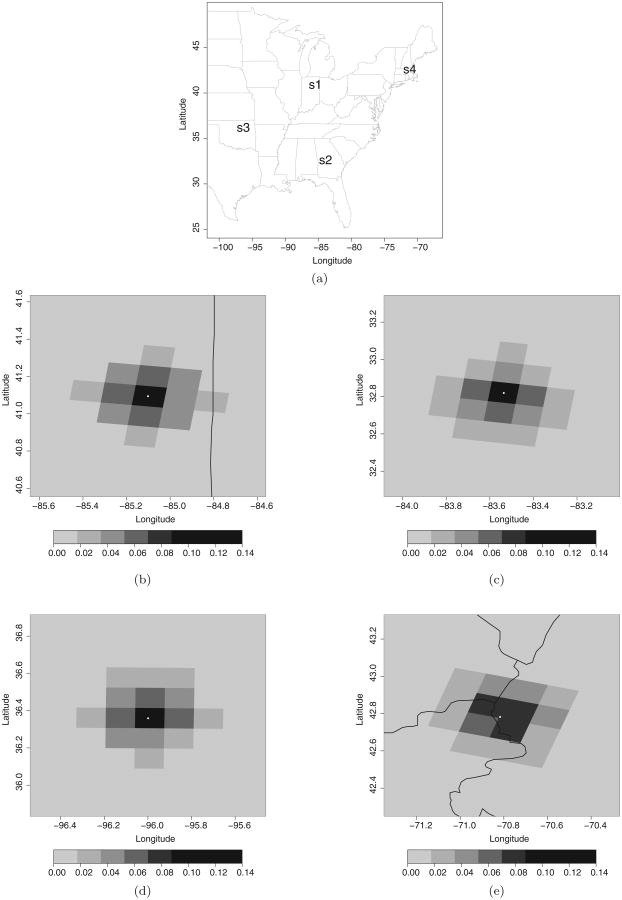
Spatial plots of the weights w_k(s, t) for July 4, 2001, associated with four sites located in the Eastern US and depicted in Figure 5(a) are shown in Figures 5(b)–(e). In each plot, the location of the site within the numerical model grid cell is marked with a dot. As Figures 5(b)–(e) illustrate, the weights have a different orientation and magnitude from site to site.

Figure 5.

(a) Location of the four sites for which we are displaying the posterior predictive mean of the spatially varying random weights w_k (s, t). (b)–(e) Posterior predictive mean of the spatially varying random weights w_k (s, t) for sites: (b) s₁; (c) s₂; (d) s₃; and (e) s₄ on July 4, 2001.

In particular, sites s₁, s₂ and s₃ assign a larger weight to the grid cell B where they lie, while site s₄ assigns similar weights to three numerical model grid cells, including the one in which it lies. In addition, the weights reveal different directionalities for the different sites. The weights w_k(s, t) not only vary in space, but they also vary in time. This is evident by inspecting the posterior mean of the weights w_k(s, t) at the same four sites using two additional days—July 20 and August 9, 2001 (figure available in the supplementary online material). These days were chosen because they are characterized by different conditions in terms of variability in the observed ozone concentration data as illustrated in Figure 2.

Finally, we investigated whether the new regressor, x̃(s, t), is better correlated with the monitoring data, i.e., it explains the observational data better than the numerical model output itself. In this regard, we have computed the daily correlation between Y(s, t) and, respectively, the numerical model output x(B, t), the posterior mean of ṼB, t), and the posterior mean of x̃(s, t) where B still denotes the grid cell containing s. Table 2 reports values of these correlations for the three selected days of July 4, July 20, and August 9, 2001. We see that x̃(s, t) has a higher correlation with Y(s, t) than x(B, t) and Ṽ(B, t).

Table 2.

Correlation between the square root of the observed ozone concentration at the training sites, Y(s, t), and the square root of the CMAQ output, x(B, t), the posteriormeanof Ṽ(B, t) where s ∈ B, and the posterior mean of x̃(s, t) for three days in the summer of 2001: July 4, July 20, and August 9, 2001

Day	x(B, t)	Posterior mean of Ṽ(B, t)	Posterior mean of x̃(s, t)
07/04/2001	0.52	0.59	0.61
07/20/2001	0.76	0.80	0.81
08/09/2001	0.78	0.85	0.86

6. Discussion

We have presented two extensions of our earlier downscaler approach that smooth the computer model output for insertion into a linear regression with spatially varying coefficients. These regressions provide daily interpolated exposure surfaces, assimilating the observed station data with the computer model output. Through a hold-out sample 5% and 15% improvement in predictive mean square error emerges for these new models relative to the original downscaler. Furthermore, greater improvement in predictive performance is found at sites that are far from the monitoring sites.

These new models are more demanding to fit than the original downscaler. However, the GMRF smoothed downscaler can take advantage of the associated convenient full conditional updating while the smoothed downscaler with spatially varying random weights can be implemented using dimension reduction through predictive processes. User-friendly software for fitting the latter model is available on request. Again, fitting a daily fusion model that requires stochastic integration is infeasible with more than 40, 000 grid cells much less across thetimeofanentireozone season.Furthermore, despite being uncalibrated, CMAQ contains useful information for predicting ozone concentration at unmonitored sites: all downscaler models yielded a substantial improvement in out-of-sample predictive performance over an ordinary kriging model.

Both extensions of the downscaler model can be used in conjunction with an environmental exposure analysis. If the health data is point-referenced, then the health outcome at s could be modeled as a function of ozone concentration at s, where the ozone concentration at s is the posterior predictive mean obtained from the model. Similarly, if the health outcome is aggregated over an area, then it could be regressed on the posterior predictive mean of the average ozone concentration over the area. Arguably better is a joint Bayesian approach that models exposure and health outcome jointly and induces a conditional model for outcome given exposure.

Further work is following two tracks. One notes that the primary US EPA air quality standard for ozone is specified in terms of the fourth highest daily maximum across the year exceeding a particular threshold. Using these new models, we would like to provide predictive distributions to assess compliance with respect to this criterion. A second track seeks to develop conditional CAR models using weights that are driven by a GP. That is, given the GP realization, we will define the weights to yield a valid Gaussian CAR model. This enables CAR models with random, spatially varying weights. Allowing directionality in weights enables improved reconstruction of blurred images using GMRF's. We will report on this in a forthcoming manuscript.

Appendix

A.1 Predictive Process Models

In this appendix we provide a brief review on predictive process models and we illustrate how predictive processes can be employed in the smoothed downscaler model with spatially varying random weights to ease computation.

Let Y(s), s ∈ 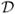, denote a spatial process, not necessarily Gaussian. The classical geostatistical model decomposes Y(s) as follows:

$$Y(\mathbf{s})=\mu (\mathbf{s})+w(\mathbf{s})+\epsilon (\mathbf{s})\epsilon (\mathbf{s})\stackrel{\mathit{\text{ind}}}{\sim }N(0,{\tau }^2),$$ (A.1)

where μ(s) represents the mean structure of Y(s), and w(s) is modeled as a mean-zero GP with covariance function C(·, ·; θ). Inference on the covariance parameter θ is computationally challenging if a large number of observations is available.

The predictive process model addresses this problem by replacing w(s) in (A.1) with the predictive process w̃(s) defined as follows. Let ${\mathbf{r}}_1^{\ast },\dots ,{\mathbf{r}}_m^{\ast }$ be m pre-specified sites, or knots, in 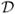and let w* denote the m × 1 vector ${(w({\mathbf{r}}_1^{\ast }),\dots ,w({\mathbf{r}}_m^{\ast }))}^{\prime }$. Then, for each s ∈ 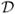, the predictive spatial process w̃(s) derived from the parent process w(s) is defined as

$$\stackrel{\sim }{w}(\mathbf{s})=c^{\prime }(\mathbf{s};\mathit{\theta })\cdot {\mathbf{C}}^{\ast -1}(\mathit{\theta })\cdot {\mathbf{w}}^{\ast },$$ (A.2)

where c(s; θ) is the m × 1 vector with ith component equal to $C(\mathbf{s},{\mathbf{r}}_i^{\ast };\mathit{\theta }),i=1,\dots ,m$, C*(θ) is the m × m matrix with (i, j)th element equal to $C({\mathbf{r}}_i^{\ast },{\mathbf{r}}_j^{\ast };\mathit{\theta })$ and w* ∼ MVN_m(0, C*(θ)).

In other words, the predictive process w̃(s) is the projection of the original spatial process w(s) onto the m-dimensional space generated by w*. Simulation experiments assessing the performance of predictive process models on knots location has shown little sensitivity of results on knots selection, particularly if the knots are chosen on a regular grid with small spacing relatively to the range of the parent process w(s).

In the smoothed downscaler model with spatially varying weights, we introduce predictive processes to alleviate computation when working with the complete CMAQ model output consisting of g=40,044 grid cells. In this situation, as mentioned in Section 4.2, rather than working with the full 40,044-dimensional vectors (Q[r_k])_{k=1,…, g} and (Q[r_k, t])_{k=1,…, g}, we replace Q(r_k) and Q(r_k, t), respectively, with Q̃(r_k) and Q̃(r_k, t) defined using (A.2) and m(=648) dimensional vectors Q* and ${\mathbf{Q}}_t^{\ast }$. Then, at each MCMC iteration, we update the m-dimensional random vector ${\mathbf{Q}}^{\ast }={(Q[{\mathbf{r}}_1^{\ast }],\dots ,Q[{\mathbf{r}}_m^{\ast }])}^{\prime }$ and ${\mathbf{Q}}_t^{\ast }={(Q[{\mathbf{r}}_1^{\ast },t],\dots ,Q[{\mathbf{r}}_m^{\ast },t])}^{\prime }$, respectively, by block-updating, using four blocks of dimension 162 and a random-walk multivariate normal proposal with diagonal covariance matrix and proposal variance appropriately chosen to achieve an acceptance rate of 25 − 40%. We then update the predictive process Q̃(r_k), k = 1,…, g (respectively, Q̃[r_k, t]) and the corresponding new sets of weights w_k(s), k = 1,…, g (respectively, w_k(s, t), k = 1,…, g) for each site s, and we accept or reject the new proposed value following the conventional Metropolis-Hastings scheme. The conditional distributions of the remaining parameters are sampled directly.

A.2 Full Conditionals

Here we provide full conditionals for V_t and ${\mathbf{Q}}_t^{\ast }$ in, respectively, the GMRF smoothed downscaler and the smoothed downscaler with spatially varying random weights. To facilitate exposition, we present full conditionals for the case of no missing data. Extension to handle missing data is straightforward.

For each t, let Y_t = (Y [s₁, t],…, Y[s_n, t])′ denote the n × 1 vector of observations of ozone concentrations for day t and β_0t denote the n × 1 vector β_0t = (β₀[s₁, t],…, β₀[s_n, t])′. Let ${\mathbf{Y}}_t^{(B_i)}$ and ${\mathit{\beta }}_{0t}^{(B_i)}$ denote, respectively, the n_i × 1 vectors (Y[s_j, t])_{j=1,…, ni} and (β₀[s_j, t])_{j=1,…, ni} with s_j ∈ B_i. For each t and i = 1,…, g, from (14), (15), and (16), it follows that the full conditional distribution [V(B_i, t)|{V(B_j, t), j ≠ i}, μ_t, β_{0, t}, β_{1, t}, β_0t, ξ², τ², σ², Y_t, x(B_i, t)] is a $N({\gamma }_i,{\varsigma }_i^2)$ distribution with

$${\varsigma }_i^2={(\frac{n_i{\beta }_{1,t}^2}{{\tau }^2}+\frac{m_i}{{\xi }^2}+\frac{1}{{\sigma }^2})}^{-1}$$

and

$${\gamma }_i={\varsigma }_i^2\cdot \left\{\frac{{\beta }_{1,t}}{{\tau }^2}{\mathbf{1}}^{\prime }\right({\mathbf{Y}}_t^{(B_i)}-{\beta }_{0,t}\mathbf{1}-{\beta }_{1,t}{\mu }_t\mathbf{1}-{\mathit{\beta }}_{0t}^{(B_i)})+(\sum _{j\in \delta B_i}\frac{V(B_j,t)}{{\xi }^2})+(\frac{x(B_i,t)-{\mu }_t}{{\sigma }^2}\left)\right\},$$

where 1 is a n_i × 1 vector of all 1's.

Now we derive the full conditional distribution of ${\mathit{Q}}_t^{\ast }$ in the smoothed downscaler model using spatially varying random weights. For each t = 1,…, T, let Q̃(r_k, t), k = 1,…, g denote the predictive spatial process derived from the parent process Q(r, t). Then, from (A.2), for each k = 1,…, g

$$\stackrel{\sim }{Q}({\mathbf{r}}_k,t)=c^{\prime }({\sigma }_Q^2,{\varphi }_{Q_t})\cdot {\mathbf{C}}^{\ast -1}({\sigma }_Q^2,{\varphi }_{Q_t})\cdot {\mathbf{Q}}_t^{\ast }.$$ (A.3)

We indicate with $\mathbf{e}{\stackrel{\sim }{\mathbf{Q}}}_t^d$ the g × g diagonal matrix with (k, k)th element exp(Q̃(r_k, t)), and with J the g × g matrix of all 1's. Let K_t indicate the n × g matrix K_t = ( 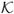[s_i − r_j; ψ_t])_{i=1,…, n;j=1,…, g} and let W_t denote the n × g matrix of spatially varying weights W_t = (w_j [s_i, t])_{i=1,…, n;j=1,…, g}. Then, from (20) it follows that

$${\mathbf{W}}_t=\frac{{\mathbf{K}}_t\cdot e{\stackrel{\sim }{\mathbf{Q}}}_t^d}{({\mathbf{K}}_t\cdot e{\stackrel{\sim }{\mathbf{Q}}}_t^d)\circ \mathbf{J}},$$ (A.4)

where ∘ indicates the Schur product of matrices and the above division of matrices is element-wise.

The Gaussian prior specification for the parent process Q(r, t), and the likelikood in (18) imply that the full conditional distribution $[{\mathbf{Q}}_t^{\ast }|{\beta }_{0,t},{\beta }_{1,t},{\mathit{\beta }}_{0t},{\tau }^2,{\sigma }_Q^2,{\varphi }_{Q_t},{\psi }_t,{\mathbf{Y}}_t]$, t = 1,…, T is

$$[{\mathbf{Q}}_t^{\ast }|{\beta }_{0,t},{\beta }_{1,t},{\mathit{\beta }}_{0t},{\tau }^2,{\sigma }_Q^2,{\varphi }_{Q_t},{\psi }_t,{\mathbf{Y}}_t]\propto \frac{1}{{({\tau }^2)}^{\frac{n}{2}}}\times exp\{-\frac{1}{2}{({\mathbf{Y}}_t-{\beta }_{0,t}\mathbf{1}-{\beta }_{1,t}{\mathbf{W}}_t{\mathbf{X}}_t-{\mathit{\beta }}_{0t})}^{\prime }{({\tau }^2\mathbf{I})}^{-1}({\mathbf{Y}}_t-{\beta }_{0,t}\mathbf{1}-{\beta }_{1,t}{\mathbf{W}}_t{\mathbf{X}}_t-{\mathit{\beta }}_{0t})\}\cdot \frac{1}{{\left|{\mathbf{C}}^{\ast }\right({\sigma }_Q^2,{\varphi }_{Q_t}\left)\right|}^{\frac{1}{2}}}exp\{-\frac{1}{2}\left({\mathbf{Q}}_t^{{\ast }^{\prime }}{\mathbf{C}}^{\ast -1}\right({\sigma }_Q^2,{\varphi }_{Q_t}\left){\mathbf{Q}}_t^{\ast }\right)\},$$

where X_t is the g × 1 vector X_t = (x(B₁, t)…x(B_g, t))′, I is the n × n identity matrix and W_t is as in (A.4).