Abstract
Skewed data is the main issue in statistical models in healthcare costs. Data transformation is a conventional method to decrease skewness, but there are some disadvantages. Some recent studies have employed generalized linear models (GLMs) and Cox proportional hazard regression as alternative estimators.
The aim of this study was to investigate how well these alternative estimators perform in terms of bias and precision when the data are skewed. The primary outcome was an estimation of population means of healthcare costs and the secondary outcome was the impact of a covariate on healthcare cost. Alternative estimators, such as ordinary least squares (OLS) for Ln(y) or Log(y), Gamma, Weibull and Cox proportional hazard regression models, were compared using Monte Carlo simulation under different situations, which were generated from skewed distributions.
We found that there was not one best model across all generated conditions. However, GLMs, especially the Gamma regression model, behaved well in the estimation of population means of healthcare costs. The results showed that the Cox proportional hazard model exhibited a poor estimation of population means of healthcare costs and the β1 even under proportional hazard data. Approximately results are consistent by increasing the sample size. However, increasing the sample size could improve the performance of the OLS-based model.
Keywords: Skewed data, Generalized linear models (GLMs), Cox proportional hazard regression, Ordinary least squares (OLS) model, Transformation, Healthcare cost, Monte Carlo simulation
Background
Statistical models are often used in many healthcare economics and policy studies. The main issues in such studies are the estimation of mean population healthcare costs and finding the best relationship between costs and covariates through regression modeling [1]. However, these cannot be implemented by simple statistical models as the healthcare costs data have specific characterizations [2]. Healthcare costs data demonstrate the substantial positive skewness and are sometimes characterized by the use of large resources with zero cost [3]. These specifications of data impose a number of difficulties in using standard statistical analysis, such as implementing linear regression causes unreliable results [2].
Two-part models based on mixture models are performed when excess zeroes are present in data [3]. Further, logarithmic (or other) transformations are commonly used to decrease the skewness and drive them close to normal distribution, in order to implement linear regression models. The logarithmic transformation with ordinary least squares (OLS) regression is a very common approach in applied economics. However, it also presents several drawbacks. One of these drawbacks is that the predictions are not robust enough to detect the heteroscedasticity in the transformed scale [1,4]. The general consensus is that estimating the mean cost using a logarithmic regression model leads to biased estimation [2,4-6].
An alternative approach is using nonlinear regression models, of which exponential conditional mean (ECM) models in generalized linear models (GLMs) are examples [7]. Generally, GLMs extend the linear modeling framework to allow response variables that are not normally distributed. In healthcare studies, generalized linear modeling through log-link function avoids the weakness and problems of OLS regression. In addition, the Cox proportional hazards model has been a controversial issue for healthcare data modeling. It has been used as a special flexible model for skewed healthcare data in many studies [8,9].
In recent years, extensive research efforts have been done to propose suitable regression methods for the analysis of skewed healthcare data [1,3,10,11]. Many studies also set out a clear framework for comparing these methods from a variety of aspects [5,6,12,13]. Moreover, a few have provided prominent reviews of the statistical methods for analyzing healthcare data [2,7].
However, there is no comparative study that investigates the different methods using different sample sizes. This paper was conducted to compare the proposed statistical models in the available literature using different sample sizes. We specifically focused on comparing proposed statistical models for positive skewed healthcare costs, but not zero mass problems. It was developed based on a Monte Carlo simulation to find appropriate methods to get the unbiased and precise estimates of the mean costs. This aspect is particularly important in the literature [5,13]. Furthermore, in this paper, the coefficient estimations of covariates are also evaluated in our simulations using different sample sizes.
Methods
Let y i denote healthcare expenditures for person i, and x i denote the set of covariates, including the intercept. We estimated the following models.
Ordinary least square based on log transformation
It is common to use linear regression models for the log of costs in healthcare expenditures. Logarithmic transformation is most commonly used to decrease skewness and to make the distribution more symmetric and closer to normality. The log regression model is as follows:
Where it was assumed that E(xε) = 0 and E(ε) = 0, since predicting costs on the original scale is primary objective so:
If the error term is distribution, it is a log-normal case, and then:
However, if the error term is not normally distributed, but is homoscedastic, then the smearing estimator is applied.
Generalized linear models
GLMs are a broad class of statistical models for relating non-normal dependent variables to linear combinations of predictor variables. An invertible link function (g (.)) converts the expectation of the response variable, E (Y i ), to the linear predictor:
The ECM model is a special type of GLM with log-link function, and can be viewed as a nonlinear regression model:
Weibull and Gamma regression models are assumed as two special types of ECM model; β values were estimated here using quasi-maximum likelihood estimation. The exponential distribution was considered to be a special case of the Weibull and Gamma regression models when the shape parameter was equal to 1.
Cox proportional hazard model
The Cox proportional hazard model is based on hazard and survival functions, instead of ECM or direct estimation of E (y|x). It is a semi-parametric model because it does not specify the baseline hazard function:
Where h 0(y) is the baseline hazard, estimated using the Breslow method. The main issue in this model, which should be considered, is the proportional hazard assumption. This means that the hazard ratio of two individuals is independent of time [14]. Note that the interpretation of the estimated coefficients in this model is based on hazard ratio rather than the covariate effect on the mean.
Comparing model performance
The interested estimations are evaluated as follows:
Two statistics were calculated to evaluate the quality of cost predictions using above mentioned models. The first was the mean prediction error (MPE), which measures the bias and predictive accuracy, and the second was the mean absolute prediction error (MAPE):
Actually, MPE indicates how the mean of predicted healthcare expenditures from a particular model compares with the mean of healthcare costs. Models with lower values of MPE have smaller biases than models with higher values. However, MAPE indicates how values of individual predicted healthcare expenditures from a particular model compare with values of actual healthcare expenditures in the sample [6].
Mean square of error (MSE) and 95% confidence interval of the estimate of β1 coefficient were calculated to evaluate the accuracy and precision of the estimated parameter. A more precise estimator should be closer to the true value. A Goodness of fit test provided by Hosmer-Lemeshow test and the Akaike information criteria (AIC) used as an aid to choosing between competing models. Lower values of the AIC indicate the preferred model criterion were also used to evaluate. The mean of the residuals across deciles of x was also plotted in order to assess a systematic bias in the predictions.
Simulation study
To compare the performance of the alternative models, a Monte Carlo simulation was used to show how each estimator behaves under different conditions of skewness that are common in healthcare expenditure studies.
To determine the effect of the level of skewness on the estimated outcome, some skewed probability density function (pdf), such as log-normal, Gamma and Weibull distribution, was used as a data-generating mechanism. To assess how the sample size affects the estimations, 10,000 times batch samples (n = 25, 50, 100, 500 and 1,000) were examined by comparing all models mentioned in the previous section. All generated data were standardized according to Basu et al., in which β 0 was considered as intercept, estimated assuming E(y) = 1.
Log-normal data generation
The true model assumed is as follows:
Where x is uniform (0, 1), ε ∼ N(0, σ 2), in which σ 2 = 0.5, 1.0, 1.5, and β 1 = 1 were used. β 0 was estimated based on E(y) =1:
The skewness of log-normal models is an increasing function of the variance as follows:
We considered σ 2 = 0.5, 1, 1.5 and 2.
Gamma data generation
The pdf of Gamma distribution is:
Where b = exp(β 0 + β 1 x) and α are the scale and shape parameters, respectively. The mean is equal to αb and the skewness is a decreasing function of the shape parameter, as follows:
Where x is uniform (0, 1), β 1 = 1 and β 0 was estimated so that E(y) = 1. Also, we used the assumption that α = 0.5, 1, 2 and 4 in the data generating process.
Weibull data generation
Weibull data generation is considered as a function of the data-generating mechanism, which has proportional hazard properties. It was used to generate proportional hazard data, since the Cox proportional hazards model is based on this assumption:
Where b = exp(β 0 + β 1 x) and α are the scale and shape parameters, respectively. The mean is equal to and the skewness is also a decreasing function of the shape parameter, as follows:
Shape parameter was considered as 0.5, 1 and 5 in this scenario. The proportional hazards assumption was evaluated in all of the simulations.
Results
Mean, standard deviation, skewness and kurtosis for the y in various data-generating mechanisms are presented in Table 1. Based on this result, the log-normal and Weibull models provided greater skewness than the Gamma model. It should be noted that the skewness of data from the log-normal and Gamma models increased monotonically as the sample size increased.
Table 1.
Simple statistics of y
| Mean | Std. Dev. | Coefficient of skewness | Coefficient of kurtosis | ||
|---|---|---|---|---|---|
| Log normal σ2=0.5 | 1.000 | 0.827 | 1.615 | 5.890 | |
| Log normal σ2=1 | 1.000 | 1.200 | 2.070 | 7.684 | |
| Log normal σ2=1.5 | 1.000 | 1.524 | 2.368 | 9.017 | |
| Log normal σ2=2 | 1.000 | 1.813 | 2.585 | 10.057 | |
| n=25 | Gamma α=0.5 | 1.000 | 1.402 | 1.962 | 6.885 |
| Gamma α =1 | 1.000 | 1.022 | 1.544 | 5.400 | |
| Gamma α =2 | 1.000 | 0.760 | 1.247 | 4.565 | |
| Gamma α =4 | 1.000 | 0.576 | 1.040 | 4.051 | |
| Wiebull α=0.5 | 1.000 | 1.939 | 2.592 | 9.902 | |
| Wiebull α =1 | 1.000 | 1.028 | 1.565 | 5.488 | |
| Wiebull α =5 | 1.000 | 0.363 | 0.668 | 3.131 | |
| Log normal σ2=0.5 | 1.000 | 0.841 | 1.992 | 8.305 | |
| Log normal σ2=1 | 1.000 | 1.251 | 2.669 | 12.101 | |
| Log normal σ2=1.5 | 1.000 | 1.626 | 3.132 | 15.086 | |
| Log normal σ2=2 | 1.000 | 2.060 | 3.476 | 17.481 | |
| n=50 | Gamma α=0.5 | 1.000 | 1.433 | 2.350 | 9.558 |
| Gamma α =1 | 1.000 | 1.049 | 1.824 | 7.064 | |
| Gamma α =2 | 1.000 | 0.769 | 1.459 | 5.691 | |
| Gamma α =4 | 1.000 | 0.579 | 1.192 | 4.788 | |
| Wiebull α=0.5 | 1.000 | 2.073 | 3.334 | 16.015 | |
| Wiebull α =1 | 1.000 | 1.047 | 1.846 | 7.182 | |
| Wiebull α =5 | 1.000 | 0.361 | 0.666 | 3.234 | |
| Log normal σ2=0.5 | 1.000 | 0.868 | 2.339 | 11.213 | |
| Log normal σ2=1 | 1.000 | 1.307 | 3.293 | 18.377 | |
| Log normal σ2=1.5 | 1.000 | 1.736 | 3.983 | 24.446 | |
| Log normal σ2=2 | 1.000 | 2.159 | 4.512 | 29.521 | |
| n=100 | Gamma α=0.5 | 1.000 | 1.466 | 2.681 | 12.454 |
| Gamma α =1 | 1.000 | 1.071 | 2.064 | 8.819 | |
| Gamma α =2 | 1.000 | 0.781 | 1.615 | 6.665 | |
| Gamma α =4 | 1.000 | 0.588 | 1.292 | 5.328 | |
| Wiebull α=0.5 | 1.000 | 2.178 | 4.095 | 24.487 | |
| Wiebull α =1 | 1.000 | 1.074 | 2.074 | 8.861 | |
| Wiebull α =5 | 1.000 | 0.370 | 0.626 | 3.054 | |
| Log normal σ2=0.5 | 1.000 | 0.888 | 2.892 | 18.063 | |
| Log normal σ2=1 | 1.000 | 1.364 | 4.667 | 40.650 | |
| Log normal σ2=1.5 | 1.000 | 1.880 | 6.206 | 65.574 | |
| Log normal σ2=2 | 1.000 | 2.420 | 7.508 | 89.605 | |
| n=500 | Gamma α=0.5 | 1.000 | 1.492 | 3.106 | 17.456 |
| Gamma α =1 | 1.000 | 1.076 | 2.320 | 11.267 | |
| Gamma α =2 | 1.000 | 0.789 | 1.764 | 7.819 | |
| Gamma α =4 | 1.000 | 0.594 | 1.369 | 5.826 | |
| Wiebull α=0.5 | 1.000 | 2.293 | 5.650 | 51.600 | |
| Wiebull α =1 | 1.000 | 1.077 | 2.317 | 11.208 | |
| Wiebull α =5 | 1.000 | 0.374 | 0.573 | 2.884 | |
| Log normal σ2=0.5 | 1.000 | 0.882 | 3.030 | 20.532 | |
| Log normal σ2=1 | 1.000 | 1.387 | 5.167 | 53.191 | |
| Log normal σ2=1.5 | 1.000 | 1.914 | 7.197 | 94.542 | |
| Log normal σ2=2 | 1.000 | 2.492 | 9.016 | 137.859 | |
| n=1000 | Gamma α=0.5 | 1.000 | 1.495 | 3.192 | 18.720 |
| Gamma α =1 | 1.000 | 1.078 | 2.367 | 11.805 | |
| Gamma α =2 | 1.000 | 0.791 | 1.786 | 8.018 | |
| Gamma α =4 | 1.000 | 0.597 | 1.381 | 5.909 | |
| Wiebull α=0.5 | 1.000 | 2.313 | 6.179 | 65.070 | |
| Wiebull α =1 | 1.000 | 1.078 | 2.360 | 11.684 | |
| Wiebull α =5 | 1.000 | 0.373 | 0.575 | 2.872 |
The results in Tables 2, 3, 4, 5 and 6 were based on 10,000 times batch replication, in sample sizes of 25, 50, 100, 500 and 1,000, respectively. These tables show the results of the estimates of population means and β1 for each model under the various data-generating processes. Minimum deviance (MPE) and absolute deviance (MAPE) of predicting the value of the response variable (health-care costs) considered as adequacy of methods.
Table 2.
Alternative estimator results for log-normal, gamma and weibull distributions for n=25
| Data | Estimator | MPE | MAPE | MSE(β) | 95% CI | AIC | Prob. H.Lsignif | |
|---|---|---|---|---|---|---|---|---|
| Lower | upper | |||||||
| Log normal σ2=0.5 | OLS for Ln(y) | -0.13903 | 0.58026 | 0.28579 | 0.798 | 1.214 | 56.527 | 0.0484 |
| Gamma | -0.00070 | 0.53623 | 0.24738 | 0.765 | 1.221 | 43.796 | 0.0453 | |
| Weibull | -0.11815 | 0.57319 | 0.25534 | 0.742 | 1.236 | 45.032 | 0.0493 | |
| Cox | -1.45570 | 3.85240 | 6.77976 | -1.823 | -1.089 | 114.191 | 0.0522 | |
| Log normal σ2=1 | OLS for Ln(y) | -0.14087 | 0.80071 | 0.57158 | 0.715 | 1.303 | 73.856 | 0.0467 |
| Gamma | -0.00259 | 0.74803 | 0.47688 | 0.637 | 1.332 | 49.636 | 0.0432 | |
| Weibull | -0.02790 | 0.75177 | 0.51067 | 0.635 | 1.333 | 49.889 | 0.0451 | |
| Cox | -1.02151 | 3.67692 | 4.79504 | -1.374 | -0.670 | 115.543 | 0.0581 | |
| Log normal σ2=1.5 | OLS for Ln(y) | -0.14266 | 0.96247 | 0.85736 | 0.651 | 1.371 | 83.992 | 0.0481 |
| Gamma | -0.00667 | 0.90470 | 0.69826 | 0.523 | 1.427 | 48.094 | 0.0440 | |
| Weibull | 0.08439 | 0.85470 | 0.76599 | 0.553 | 1.407 | 47.547 | 0.0442 | |
| Cox | -0.83058 | 3.61682 | 4.04647 | -1.179 | -0.483 | 116.007 | 0.0544 | |
| Log normal σ2=2 | OLS for Ln(y) | -0.14384 | 1.08909 | 1.14315 | 0.597 | 1.429 | 91.184 | 0.0485 |
| Gamma | -0.01478 | 1.03115 | 0.91562 | 0.420 | 1.514 | 43.316 | 0.0429 | |
| Weibull | 0.19665 | 0.91580 | 1.02132 | 0.484 | 1.470 | 42.107 | 0.0414 | |
| Cox | -0.71755 | 3.58418 | 3.63860 | -1.06 | -0.373 | 116.245 | 0.0536 | |
| Gamma α=0.5 | OLS for Ln(y) | -0.30508 | 1.10870 | 4.184 | 0.327 | 1.646 | 112.098 | 0.1269 |
| Gamma | -0.00608 | 0.93533 | 1.831 | 0.514 | 1.405 | 40.684 | 0.0468 | |
| Weibull | 0.22314 | 0.86661 | 2.132 | 0.509 | 1.426 | 41.359 | 0.0455 | |
| Cox | -0.70630 | 3.61984 | 3.532 | -1.054 | -0.359 | 116.236 | 0.0534 | |
| Gamma α =1 | OLS for Ln(y) | -0.16364 | 0.76291 | 1.424 | 0.626 | 1.380 | 85.253 | 0.0727 |
| Gamma | -0.00141 | 0.70474 | 0.854 | 0.687 | 1.289 | 51.104 | 0.0470 | |
| Weibull | -0.01889 | 0.70780 | 0.858 | 0.686 | 1.290 | 51.072 | 0.0481 | |
| Cox | 1.07902 | 3.67304 | 4.794 | -1.412 | -0.714 | 115.454 | 0.0546 | |
| Gamma α =2 | OLS for Ln(y) | -0.14447 | 0.55706 | 0.567 | 0.779 | 1.240 | 62.351 | 0.0545 |
| Gamma | -0.00064 | 0.51805 | 0.422 | 0.760 | 1.203 | 45.250 | 0.0461 | |
| Weibull | -0.11319 | 0. 54472 | 0.406 | 0.773 | 1.202 | 45.302 | 0.0485 | |
| Cox | 1.52397 | 3.95791 | 6.794 | -1.887 | -1.161 | 113.989 | 0.0583 | |
| Gamma α =4 | OLS for Ln(y) | -0.13872 | 0.40613 | 0.248 | 0.847 | 1.166 | 42.011 | 0.0479 |
| Gamma | -0.00020 | 0.37338 | 0.208 | 0.851 | 1.150 | 32.861 | 0.0431 | |
| Weibull | -0.12969 | 0.40265 | 0.200 | 0.840 | 1.151 | 33.311 | 0.0471 | |
| Cox | -2.18196 | 4.31535 | 10.402 | -2.572 | -1.792 | 111.303 | 0.0486 | |
| Wiebull α=0.5 | OLS for Ln(y) | -0.34517 | 1.36816 | 3.73002 | 0.251 | 1.761 | 119.821 | 0.1253 |
| Gamma | -0.02216 | 1.15326 | 1.73985 | 0.296 | 1.600 | 22.472 | 0.0448 | |
| Weibull | 0.43461 | 0.95799 | 2.23442 | 0.349 | 1.581 | 22.094 | 0.0408 | |
| Cox | -0.51486 | 3.57624 | 2.98777 | -0.948 | -0.082 | 116.549 | 0.0531 | |
| Wiebull α =1 | OLS for Ln(y) | -0.16807 | 0.76539 | 0.93251 | 0.626 | 1.380 | 85.164 | 0.0702 |
| Gamma | -0.00210 | 0.70482 | 0.56343 | 0.676 | 1.290 | 51.009 | 0.0492 | |
| Weibull | -0.01845 | 0.70757 | 0.55860 | 0.675 | 1.291 | 50.971 | 0.0502 | |
| Cox | -1.04789 | 3.75803 | 4.92479 | -1.489 | -0.607 | 115.443 | 0.0526 | |
| Wiebull α =5 | OLS for Ln(y) | -0.13691 | 0.20584 | 0.03730 | 0.926 | 1.076 | 4.692 | 0.0526 |
| Gamma | -0.00006 | 0.17590 | 0.03153 | 0.930 | 1.068 | 0.040 | 0.0412 | |
| Weibull | -0.08524 | 0.18546 | 0.02234 | 0.935 | 1.059 | -2.112 | 0.0470 | |
| Cox | -5.24388 | 7.34860 | 40.76941 | -5.785 | -4.703 | 96.674 | 0.0526 | |
Table 3.
Alternative estimator results for log-normal, gamma and weibull distributions for n=50
| Data | Estimator | MPE | MAPE | MSE(β) | 95% CI | AIC | Prob. H.Lsignif | |
|---|---|---|---|---|---|---|---|---|
| Lower | upper | |||||||
| Log normal σ2=0.5 | OLS for Ln(y) | -0.06472 | 0.56174 | 0.14414 | 0.901 | 1.109 | 110.247 | 0.0403 |
| Gamma | -0.00024 | 0.54325 | 0.12915 | 0.880 | 1.112 | 84.882 | 0.0377 | |
| Weibull | -0.11401 | 0.58013 | 0.13512 | 0.865 | 1.119 | 87.987 | 0.0416 | |
| Cox | -1.37774 | 3.67486 | 5.99725 | -1.550 | -1.206 | 292.456 | 0.0507 | |
| Log normal σ2=1 | OLS for Ln(y) | -0.06560 | 0.77896 | 0.28826 | 0.861 | 1.153 | 144.905 | 0.0375 |
| Gamma | -0.00084 | 0.75579 | 0.24681 | 0.809 | 1.169 | 97.178 | 0.0332 | |
| Weibull | -0.01498 | 0.75773 | 0.27025 | 0.809 | 1.169 | 97.694 | 0.0344 | |
| Cox | -0.96876 | 3.53907 | 4.20450 | -1.135 | -0.803 | 295.126 | 0.0536 | |
| Log normal σ2=1.5 | OLS for Ln(y) | -0.06646 | 0.93700 | 0.43240 | 0.830 | 1.188 | 165.178 | 0.0346 |
| Gamma | -0.00204 | 0.91116 | 0.35880 | 0.743 | 1.219 | 94.667 | 0.0309 | |
| Weibull | 0.10499 | 0.85852 | 0.40537 | 0.766 | 1.206 | 93.005 | 0.0298 | |
| Cox | -0.78847 | 3.49213 | 3.52210 | -0.952 | -0.624 | 296.053 | 0.0556 | |
| Log normal σ2=2 | OLS for Ln(y) | -0.06989 | 1.10461 | 0.57653 | 0.803 | 1.217 | 179.5625 | 0.0347 |
| Gamma | -0.00465 | 1.07701 | 0.46796 | 0.680 | 1.266 | 89.735 | 0.0307 | |
| Weibull | 0.23242 | 0.95573 | 0.54049 | 0.730 | 1.238 | 86.227 | 0.0281 | |
| Cox | -0.68152 | 3.46853 | 3.14852 | -0.846 | -0.520 | 296.522 | 0.0504 | |
| Gamma α=0.5 | OLS for Ln(y) | -0.13425 | 1.01591 | 2.105 | 0.675 | 1.334 | 222.881 | 0.1086 |
| Gamma | -0.00197 | 0.94922 | 0.891 | 0.772 | 1.208 | 77.941 | 0.0351 | |
| Weibull | 0.24545 | 0.87554 | 1.055 | 0.770 | 1.219 | 79.168 | 0.0346 | |
| Cox | -0.70741 | 3.51983 | 3.211 | -0.871 | -0.544 | 296.415 | 0.0531 | |
| Gamma α =1 | OLS for Ln(y) | -0.07705 | 0.47464 | 0.702 | 0.813 | 1.190 | 168.791 | 0.0608 |
| Gamma | -0.00047 | 0.28527 | 0.426 | 0.847 | 1.144 | 100.154 | 0.0388 | |
| Weibull | -0.00937 | 0.28340 | 0.428 | 0.847 | 1.145 | 100.134 | 0.0389 | |
| Cox | 1.03789 | 0.33563 | 4.397 | -1.198 | -0.871 | 294.821 | 0.0531 | |
| Gamma α =2 | OLS for Ln(y) | -0.06760 | 0.54581 | 0.278 | 0.886 | 1.125 | 122.363 | 0.0498 |
| Gamma | -0.00026 | 0.53020 | 0.212 | 0.896 | 1.106 | 87.850 | 0.0438 | |
| Weibull | -0.11172 | 0.55696 | 0.201 | 0.893 | 1.106 | 88.214 | 0.0470 | |
| Cox | 1.47746 | 3.80179 | 6.397 | -1.648 | -1.307 | 291.826 | 0.0504 | |
| Gamma α =4 | OLS for Ln(y) | -0.06486 | 0.39403 | 0.123 | 0.927 | 1.087 | 81.482 | 0.0456 |
| Gamma | -0.00003 | 0.38221 | 0.106 | 0.928 | 1.079 | 63.053 | 0.0424 | |
| Weibull | -0.13114 | 0.41234 | 0.103 | 0.923 | 1.080 | 64.471 | 0.0471 | |
| Cox | -2.09719 | 4.10274 | 9.736 | -2.282 | -1.912 | 286.445 | 0.0496 | |
| Wiebull α=0.5 | OLS for Ln(y) | -0.15405 | 1.25405 | 1.89494 | 0.638 | 1.396 | 237.978 | 0.1004 |
| Gamma | -0.00678 | 1.16471 | 0.84376 | 0.652 | 1.304 | 43.032 | 0.0352 | |
| Weibull | 0.47033 | 0.96587 | 1.14195 | 0.690 | 1.296 | 41.454 | 0.0333 | |
| Cox | -0.50825 | 3.47052 | 2.60197 | -0.754 | -0.264 | 297.097 | 0.0504 | |
| Wiebull α =1 | OLS for Ln(y) | -0.07916 | 0.74709 | 0.47373 | 0.819 | 1.199 | 168.664 | 0.0625 |
| Gamma | -0.00076 | 0.72112 | 0.28681 | 0.845 | 1.147 | 99.360 | 0.0416 | |
| Weibull | -0.00859 | 0.72241 | 0.28548 | 0.844 | 1.148 | 99.339 | 0.0418 | |
| Cox | -1.02239 | 3.63137 | 4.43438 | -1.272 | -0.776 | 294.819 | 0.0521 | |
| Wiebull α =5 | OLS for Ln(y) | -0.06425 | 0.18584 | 0.01895 | 0.964 | 1.040 | 7.720 | 0.051 |
| Gamma | -0.00003 | 0.18068 | 0.01658 | 0.967 | 1.035 | -1.858 | 0.0452 | |
| Weibull | -0.08750 | 0.19046 | 0.01142 | 0.969 | 1.029 | -6.490 | 0.0534 | |
| Cox | -5.11234 | 6.96179 | 38.13497 | -5.360 | -4.864 | 256.001 | 0.0493 | |
Table 4.
Alternative estimator results for log-normal, gamma and weibull distributions for n=100
| Data | Estimator | MPE | MPAE | MSE(β) | 95% CI | AIC | Prob. H.Lsignif | |
|---|---|---|---|---|---|---|---|---|
| Lower | upper | |||||||
| Log normal σ2=0.5 | OLS for Ln(y) | -0.03144 | 0.56088 | 0.06312 | 0.953 | 1.049 | 217.5766 | 0.0391 |
| Gamma | -0.00007 | 0.55234 | 0.05761 | 0.942 | 1.052 | 168.199 | 0.0361 | |
| Weibull | -0.11282 | 0.58936 | 0.06098 | 0.935 | 1.057 | 175.260 | 0.0417 | |
| Cox | -1.34295 | 3.32199 | 5.63414 | -1.423 | -1.263 | 716.154 | 0.0481 | |
| Log normal σ2=1 | OLS for Ln(y) | -0.03161 | 0.77499 | 0.12623 | 0.933 | 1.069 | 286.891 | 0.0365 |
| Gamma | -0.00020 | 0.76419 | 0.10963 | 0.907 | 1.081 | 192.904 | 0.0333 | |
| Weibull | -0.00812 | 0.76533 | 0.12196 | 0.908 | 1.080 | 193.907 | 0.0330 | |
| Cox | -0.94387 | 3.19872 | 3.91711 | -1.020 | -0.868 | 722.133 | 0.0479 | |
| Log normal σ2=1.5 | OLS for Ln(y) | -0.03195 | 0.93383 | 0.18935 | 0.917 | 1.085 | 327.438 | 0.0335 |
| Gamma | -0.00038 | 0.92175 | 0.15884 | 0.873 | 1.107 | 189.222 | 0.0300 | |
| Weibull | 0.11681 | 0.86782 | 0.18295 | 0.887 | 1.099 | 185.001 | 0.0294 | |
| Cox | -0.76851 | 3.15738 | 3.26405 | -0.844 | -0.694 | 724.207 | 0.0531 | |
| Log normal σ2=2 | OLS for Ln(y) | -0.03217 | 1.05939 | 0.25247 | 0.904 | 1.098 | 356.206 | 0.0320 |
| Gamma | -0.00068 | 1.04672 | 0.20674 | 0.840 | 1.132 | 172.665 | 0.0283 | |
| Weibull | 0.23968 | 0.92933 | 0.24393 | 0.869 | 1.113 | 163.925 | 0.0276 | |
| Cox | -0.66436 | 3.13647 | 2.90548 | -0.738 | -0.590 | 725.262 | 0.0544 | |
| Gamma α=0.5 | OLS for Ln(y) | -0.06210 | 0.98793 | 0.924 | 0.842 | 1.149 | 444.474 | 0.1015 |
| Gamma | -0.00071 | 0.95946 | 0.382 | 0.899 | 1.099 | 151.970 | 0.0366 | |
| Weibull | 0.25749 | 0.88296 | 0.456 | 0.896 | 1.102 | 154.259 | 0.0380 | |
| Cox | 0.69973 | 3.18874 | 2.997 | -0.700 | -0.626 | 724.990 | 0.050 | |
| Gamma α =1 | OLS for Ln(y) | -0.03843 | 0.74577 | 0.307 | 0.915 | 1.093 | 335.557 | 0.0569 |
| Gamma | -0.00026 | 0.73384 | 0.185 | 0.934 | 1.072 | 196.691 | 0.0391 | |
| Weibull | -0.00460 | 0.73458 | 0.185 | 0.934 | 1.072 | 196.682 | 0.0395 | |
| Cox | -1.02065 | 3.27855 | 4.182 | -1.095 | -0.947 | 721.285 | 0.0518 | |
| Gamma α =2 | OLS for Ln(y) | -0.03271 | 0.54277 | 0.120 | 0.946 | 1.057 | 242.168 | 0.0504 |
| Gamma | -0.00011 | 0.53579 | 0.092 | 0.950 | 1.494 | 171.847 | 0.0434 | |
| Weibull | -0.11069 | 0.56268 | 0.087 | 0.949 | 1.049 | 172.908 | 0.0471 | |
| Cox | -1.44678 | 3.44580 | 6.080 | -1.525 | -1.369 | 714.645 | 0.0503 | |
| Gamma α =4 | OLS for Ln(y) | -0.03138 | 0.39126 | 0.053 | 0.966 | 1.040 | 160.228 | 0.0436 |
| Gamma | -0.00001 | 0.38627 | 0.046 | 0.967 | 1.037 | 122.262 | 0.0403 | |
| Weibull | -0.13163 | 0.41676 | 0.044 | 0.964 | 1.038 | 125.708 | 0.0515 | |
| Cox | -2.05432 | 3.72857 | 9.359 | -2.138 | -1.970 | 702.730 | 0.0506 | |
| Wiebull α=0.5 | OLS for Ln(y) | -0.07169 | 1.20997 | 0.82955 | 0.830 | 1.186 | 473.993 | 0.0833 |
| Gamma | -0.00180 | 1.16992 | 0.36191 | 0.839 | 1.145 | 83.622 | 0.032 | |
| Weibull | 0.48656 | 0.96925 | 0.50264 | 0.856 | 1.138 | 79.302 | 0.0345 | |
| Cox | -0.49779 | 3.13454 | 2.38376 | -0.668 | -0.330 | 726.558 | 0.0485 | |
| Wiebull α =1 | OLS for Ln(y) | -0.03853 | 0.74709 | 0.20739 | 0.915 | 1.093 | 335.3635 | 0.0574 |
| Gamma | -0.00025 | 0.73522 | 0.12587 | 0.928 | 1.068 | 196.7417 | 0.0399 | |
| Weibull | -0.00400 | 0.73582 | 0.12566 | 0.928 | 1.068 | 196.7316 | 0.0397 | |
| Cox | -1.00326 | 3.28425 | 4.16180 | -1.176 | -0.834 | 721.3257 | 0.0505 | |
| Wiebull α =5 | OLS for Ln(y) | -0.03115 | 0.18335 | 0.00829 | 0.983 | 1.019 | 13.476 | 0.0480 |
| Gamma | -0.00001 | 0.18277 | 0.00738 | 0.984 | 1.016 | -7.0357 | 0.0437 | |
| Weibull | -0.08850 | 0.19266 | 0.00503 | 0.986 | 1.014 | -16.598 | 0.0639 | |
| Cox | -5.04559 | 6.57363 | 36.88155 | -5.160 | -4.932 | 636.392 | 0.0472 | |
Table 5.
Alternative estimator results for log-normal, gamma and weibull distributions for n=500
| Data | Estimator | MPE | MPAE | MSE(β) | 95% CI | AIC | Prob. H.Lsignif | |
|---|---|---|---|---|---|---|---|---|
| Lower | upper | |||||||
| Log normal σ2=0.5 | OLS for Ln(y) | -0.00617 | 0.55823 | 0.01166 | 0.991 | 1.011 | 1075.552 | 0.0438 |
| Gamma | -0.000002 | 0.55662 | 0.01079 | 0.989 | 1.011 | 830.756 | 0.0405 | |
| Weibull | -0.11093 | 0.59335 | 0.01155 | 0.987 | 1.011 | 870.429 | 0.0538 | |
| Cox | -1.31086 | 3.10119 | 5.36566 | -1.326 | -1.296 | 5157.713 | 0.0490 | |
| Log normal σ2=1 | OLS for Ln(y) | -0.00625 | 0.76743 | 0.02331 | 0.987 | 1.015 | 1422.125 | 0.0444 |
| Gamma | -0.00002 | 0.76539 | 0.02041 | 0.981 | 1.017 | 953.996 | 0.0380 | |
| Weibull | -0.00211 | 0.76577 | 0.02309 | 0.982 | 1.016 | 958.951 | 0.0382 | |
| Cox | -0.92086 | 3.01376 | 3.71427 | -0.935 | -0.907 | 5189.630 | 0.0543 | |
| Log normal σ2=1.5 | OLS for Ln(y) | -0.00646 | 0.92875 | 0.03497 | 0.985 | 1.019 | 1624.858 | 0.0406 |
| Gamma | -0.00004 | 0.92652 | 0.02935 | 0.974 | 1.022 | 945.716 | 0.0338 | |
| Weibull | 0.12644 | 0.87192 | 0.03464 | 0.978 | 1.020 | 919.644 | 0.0351 | |
| Cox | -0.74999 | 2.98739 | 3.08671 | -0.764 | -0.736 | 5200.723 | 0.0474 | |
| Log normal σ2=2 | OLS for Ln(y) | -0.00665 | 1.05164 | 0.04662 | 0.983 | 1.021 | 1768.699 | 0.0407 |
| Gamma | -0.00006 | 1.04944 | 0.03788 | 0.966 | 1.028 | 867.320 | 0.0316 | |
| Weibull | 0.25187 | 0.93223 | 0.04619 | 0.974 | 1.024 | 813.451 | 0.0371 | |
| Cox | -0.64857 | 2.97510 | 2.74186 | -0.663 | -0.635 | 5206.363 | 0.0500 | |
| Gamma α=0.5 | OLS for Ln(y) | -0.01173 | 0.97145 | 0.170 | 0.966 | 1.026 | 2218.380 | 0.0814 |
| Gamma | -0.00010 | 0.96635 | 0.069 | 0.981 | 1.019 | 745.079 | 0.0395 | |
| Weibull | 0.26621 | 0.88808 | 0.082 | 0.979 | 1.018 | 756.009 | 0.0613 | |
| Cox | -0.69386 | 3.04111 | 2.896 | -0.999 | -0.388 | 5204.358 | 0.050 | |
| Gamma α =1 | OLS for Ln(y) | -0.00739 | 0.73625 | 0.056 | 0.984 | 1.018 | 1669.842 | 0.0582 |
| Gamma | -0.00001 | 0.73405 | 0.034 | 0.987 | 1.014 | 960.724 | 0.0431 | |
| Weibull | -0.00095 | 0.73423 | 0.034 | 0.987 | 1.014 | 960.723 | 0.0438 | |
| Cox | -1.00444 | 3.10634 | 4.035 | -1.019 | -0.990 | 5184.427 | 0.0468 | |
| Gamma α =2 | OLS for Ln(y) | -0.00643 | 0.54150 | 0.022 | 0.999 | 1.013 | 1202.164 | 0.0452 |
| Gamma | -0.00002 | 0.54021 | 0.017 | 0.992 | 1.011 | 844.867 | 0.0403 | |
| Weibull | -0.10982 | 0.56708 | 0.016 | 0.992 | 1.011 | 851.287 | 0.0546 | |
| Cox | -1.42736 | 3.23880 | 5.909 | -1.442 | -1.413 | 5148.590 | 0.0461 | |
| Gamma α =4 | OLS for Ln(y) | -0.00606 | 0.39091 | 0.010 | 0.993 | 1.007 | 792.221 | 0.0443 |
| Gamma | 0.000004 | 0.39006 | 0.008 | 0.993 | 1.007 | 598.026 | 0.0416 | |
| Weibull | -0.13200 | 0.42060 | 0.008 | 0.993 | 1.007 | 617.434 | 0.1017 | |
| Cox | -2.01502 | 3.48489 | 9.092 | -2.031 | -1.999 | 5086.403 | 0.0486 | |
| Wiebull α=0.5 | OLS for Ln(y) | -0.01379 | 1.18150 | 0.15321 | 0.962 | 1.032 | 2362.321 | 0.0606 |
| Gamma | -0.00012 | 1.17416 | 0.06475 | 0.965 | 1.025 | 411.304 | 0.0338 | |
| Weibull | 0.49762 | 0.97207 | 0.09307 | 0.969 | 1.025 | 384.861 | 0.0693 | |
| Cox | -0.49022 | 2.99166 | 2.25145 | -0.563 | -0.421 | 5213.082 | 0.0495 | |
| Wiebull α =1 | OLS for Ln(y) | -0.00741 | 0.73714 | 0.03830 | 0.980 | 1.016 | 1669.173 | 0.0530 |
| Gamma | -0.00002 | 0.73494 | 0.02327 | 0.984 | 1.012 | 961.400 | 0.0421 | |
| Weibull | -0.00082 | 0.73506 | 0.02326 | 0.984 | 1.012 | 961.376 | 0.0418 | |
| Cox | -0.99154 | 3.11589 | 4.00036 | -1.066 | -0.922 | 5184.367 | 0.0473 | |
| Wiebull α =5 | OLS for Ln(y) | -0.00605 | 0.18346 | 0.00153 | 0.996 | 1.004 | 59.7355 | 0.0453 |
| Gamma | -0.000003 | 0.18362 | 0.00138 | 0.997 | 1.003 | -51.535 | 0.0447 | |
| Weibull | -0.08896 | 0.19356 | 0.00093 | 0.997 | 1.003 | -101.476 | 0.2244 | |
| Cox | -5.00813 | 6.36391 | 36.15827 | -5.029 | -4.987 | 4737.774 | 0.0530 | |
Table 6.
Alternative estimator results for log-normal, gamma and weibull distributions for n=1000
| Data | Estimator | MPE | MPAE | MSE(β) | 95% CI | AIC | Prob. H.Lsignif | |
|---|---|---|---|---|---|---|---|---|
| Lower | upper | |||||||
| Log normal σ2=0.5 | OLS for Ln(y) | -0.00311 | 0.55282 | 0.00586 | 0.996 | 1.006 | 2147.649 | 0.0488 |
| Gamma | -0.00001 | 0.55202 | 0.00543 | 0.994 | 1.006 | 1642.073 | 0.0436 | |
| Weibull | -0.10959 | 0.58828 | 0.00583 | 0.994 | 1.006 | 1722.864 | 0.0701 | |
| Cox | -1.30433 | 3.10889 | 5.32271 | -1.312 | -1.296 | 11694.099 | 0.0467 | |
| Log normal σ2=1 | OLS for Ln(y) | -0.00326 | 0.77307 | 0.01172 | 0.995 | 1.009 | 2840.796 | 0.0488 |
| Gamma | -0.00001 | 0.77202 | 0.01028 | 0.990 | 1.008 | 1924.378 | 0.0419 | |
| Weibull | -0.00120 | 0.77225 | 0.01166 | 0.990 | 1.008 | 1934.411 | 0.0417 | |
| Cox | -0.91650 | 3.02844 | 3.68525 | -0.923 | -0.909 | 11757.613 | 0.0467 | |
| Log normal σ2=1.5 | OLS for Ln(y) | -0.00339 | 0.92803 | 0.01759 | 0.994 | 1.010 | 3246.261 | 0.0477 |
| Gamma | -0.00002 | 0.92689 | 0.01477 | 0.986 | 1.010 | 1893.638 | 0.0393 | |
| Weibull | 0.12788 | 0.87225 | 0.01749 | 0.988 | 1.010 | 1839.946 | 0.0433 | |
| Cox | -0.74664 | 3.00457 | 3.06286 | -0.754 | -0.740 | 11779.664 | 0.0479 | |
| Log normal σ2=2 | OLS for Ln(y) | -0.00351 | 1.05067 | 0.02344 | 0.993 | 1.013 | 3533.943 | 0.0463 |
| Gamma | -0.00002 | 1.04957 | 0.01904 | 0.981 | 1.013 | 1738.981 | 0.0354 | |
| Weibull | 0.25118 | 0.92331 | 0.02331 | 0.987 | 1.011 | 1607.688 | 0.0480 | |
| Cox | -0.64582 | 2.99362 | 2.72102 | -0.653 | -0.639 | 11790.872 | 0.0543 | |
| Gamma α=0.5 | OLS for Ln(y) | -0.00551 | 0.96948 | 0.085 | 0.978 | 1.007 | 4435.972 | 0.0845 |
| Gamma | -0.00001 | 0.96709 | 0.034 | 0.989 | 1.008 | 1487.309 | 0.0417 | |
| Weibull | 0.26721 | 0.88856 | 0.041 | 0.989 | 1.007 | 1508.951 | 0.0931 | |
| Cox | -0.69278 | 3.06113 | 2.881 | -0.700 | -0.686 | 11786.66 | 0.0505 | |
| Gamma α =1 | OLS for Ln(y) | -0.00374 | 0.73620 | 0.028 | 0.992 | 1.009 | 3337.268 | 0.0540 |
| Gamma | -0.000001 | 0.73511 | 0.017 | 0.993 | 1.006 | 1919.125 | 0.0420 | |
| Weibull | -0.00042 | 0.73519 | 0.017 | 0.993 | 1.006 | 1919.131 | 0.0417 | |
| Cox | -1.00124 | 3.1238 | 4.015 | -1.008 | -0.994 | 11747.09 | 0.0529 | |
| Gamma α =2 | OLS for Ln(y) | -0.00318 | 0.54246 | 0.011 | 0.995 | 1.006 | 2401.279 | 0.0481 |
| Gamma | -0.00001 | 0.54183 | 0.009 | 0.995 | 1.005 | 1691.20 | 0.0447 | |
| Weibull | -0.10998 | 0.56877 | 0.008 | 0.995 | 1.005 | 1704.418 | 0.0785 | |
| Cox | -1.42245 | 3.24810 | 5.882 | -1.430 | -1.415 | 11675.63 | 0.0533 | |
| Gamma α =4 | OLS for Ln(y) | -0.00305 | 0.39286 | 0.005 | 0.996 | 1.003 | 1581.076 | 0.0455 |
| Gamma | -0.000004 | 0.39244 | 0.004 | 0.997 | 1.003 | 1203.85 | 0.0435 | |
| Weibull | -0.13273 | 0.42318 | 0.004 | 0.997 | 1.004 | 1243.481 | 0.2093 | |
| Cox | -2.00825 | 3. 48492 | 9.047 | -2.016 | -2.000 | 11551.56 | 0.0518 | |
| Wiebull α=0.5 | OLS for Ln(y) | -0.00654 | 1.17692 | 0.07707 | 0.978 | 1.014 | 4722.98 | 0.0643 |
| Gamma | -0.00004 | 1.17347 | 0.03245 | 0.980 | 1.012 | 819.453 | 0.0378 | |
| Weibull | 0.49853 | 0.97136 | 0.04682 | 0.983 | 1.011 | 765.204 | 0.1416 | |
| Cox | -0.48930 | 3.01307 | 2.23645 | -0.543 | -0.439 | 11804.08 | 0.0492 | |
| Wiebull α =1 | OLS for Ln(y) | -0.00361 | 0.73627 | 0.01926 | 0.989 | 1.007 | 3336.686 | 0.0560 |
| Gamma | -0.00001 | 0.73520 | 0.01171 | 0.991 | 1.006 | 1919.109 | 0.0426 | |
| Weibull | -0.00042 | 0.73527 | 0.01170 | 0.991 | 1.005 | 1919.06 | 0.0432 | |
| Cox | -0.99001 | 3.13384 | 3.98134 | -1.044 | -0.940 | 11746.65 | 0.0509 | |
| Wiebull α =5 | OLS for Ln(y) | -0.00301 | 0.18367 | 0.00077 | 0.998 | 1.002 | 117.810 | 0.0397 |
| Gamma | -0.000001 | 0.18377 | 0.00069 | 0.998 | 1.002 | -105.433 | 0.0393 | |
| Weibull | -0.08904 | 0.19371 | 0.00047 | 0.998 | 1.002 | -205.982 | 0.6238 | |
| Cox | -5.00343 | 6.35876 | 36.0715 | -5.014 | -4.992 | 10855.17 | 0.0485 | |
Generally, entire models exhibited lower MPE by declining skewness and increasing sample size. However, the Gamma regression model had the smallest biases across all data-generating processes. Moreover, our results indicated that its ability to predict the expenditures in a small sample size was as good as for large sample sizes. Furthermore, OLS for Ln(y) and Weibull regression models showed a lower bias than the Cox proportional hazard model, even in proportional hazard data-generating process (Figure 1).
Figure 3.
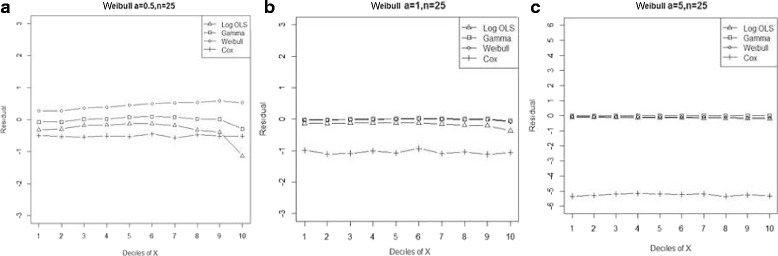
Mean residual from different estimators across deciles of ‘X’ for Weibull data (n=25) with shape parameter a: 0.5, b: 1, c: 5.
Figure 4.
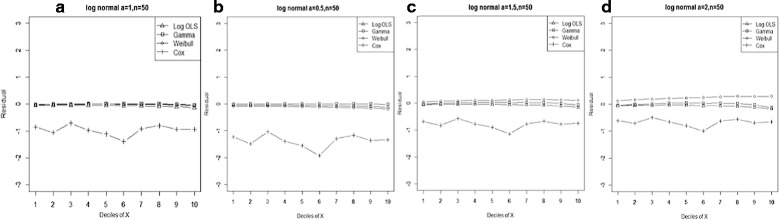
Mean residual from different estimators across deciles of ‘X’ for log-normal data (n=50) with variance a: 0.5, b: 1.0, c: 1.5, d: 2.0.
Figure 5.
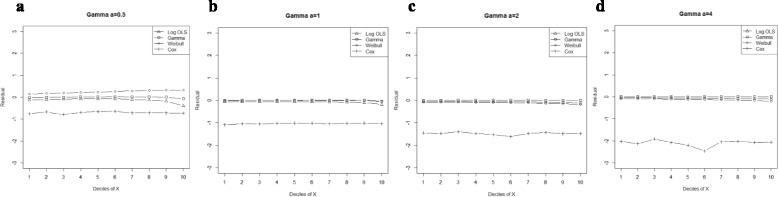
Mean residual from different estimators across deciles of ‘X’ for Gamma data (n=50) with shape parameter a: 0.5, b: 1, c: 2, d: 4.
Figure 6.
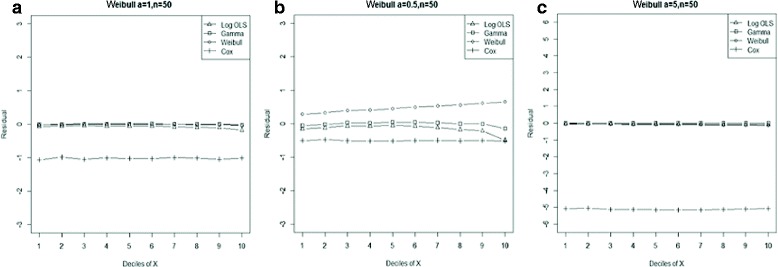
Mean residual from different estimators across deciles of ‘X’ for Weibull data (n=50) with shape parameter a: 0.5, b: 1, c: 5.
Figure 7.
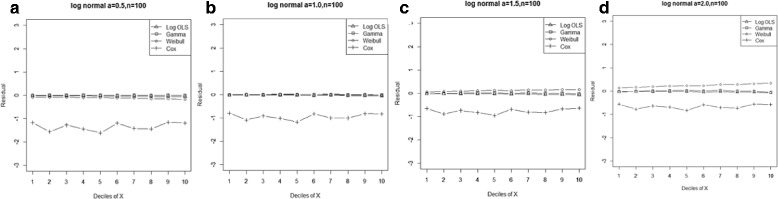
Mean residual from different estimators across deciles of ‘X’ for log-normal data (n=100) with variance a: 0.5, b: 1.0, c: 1.5, d: 2.0.
Figure 8.
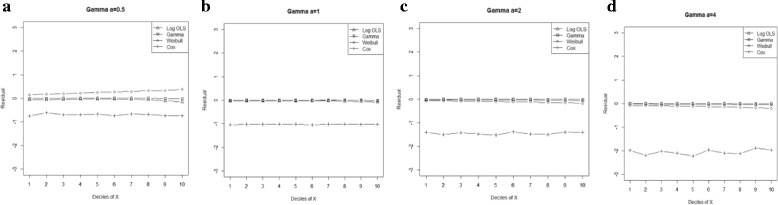
Mean residual from different estimators across deciles of ‘X’ for Gamma data (n=100) with shape parameter a: 0.5, b: 1, c: 2, d: 4.
Figure 9.
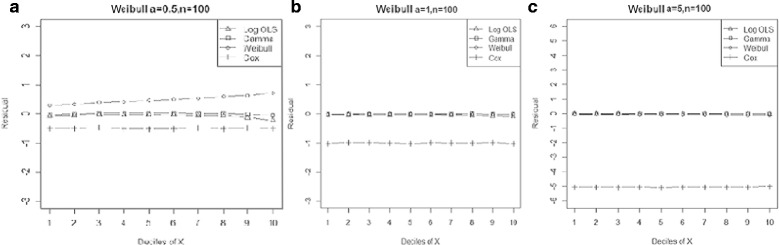
Mean residual from different estimators across deciles of ‘X’ for Weibull data (n=100) with shape parameter a: 0.5, b: 1, c: 5.
Figure 10.
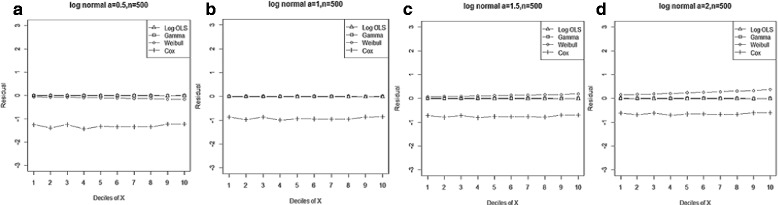
Mean residual from different estimators across deciles of ‘X’ for log-normal data (n=500) with variance a: 0.5, b: 1.0, c: 1.5, d: 2.0.
Figure 11.
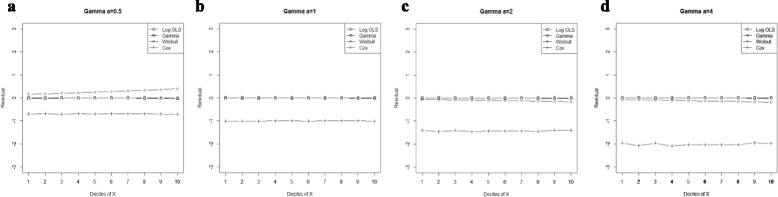
Mean residual from different estimators across deciles of ‘X’ for Gamma data (n=500) with shape parameter a: 0.5, b: 1, c: 2, d: 4.
Figure 12.
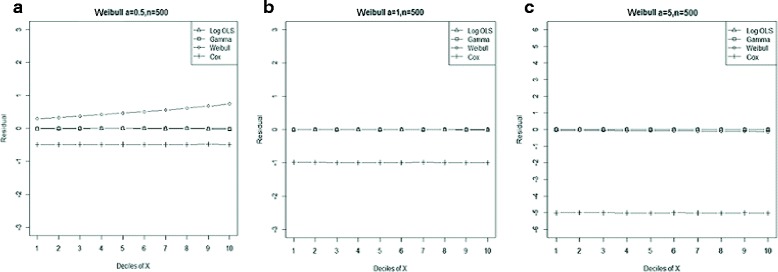
Mean residual from different estimators across deciles of ‘X’ for Weibull data (n=500) with shape parameter a: 0.5, b: 1, c: 5.
Figure 13.
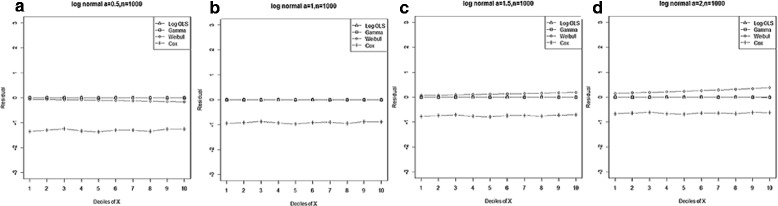
Mean residual from different estimators across deciles of ‘X’ for log-normal data (n=1000) with variance a: 0.5, b: 1.0, c: 1.5, d: 2.0.
Figure 14.
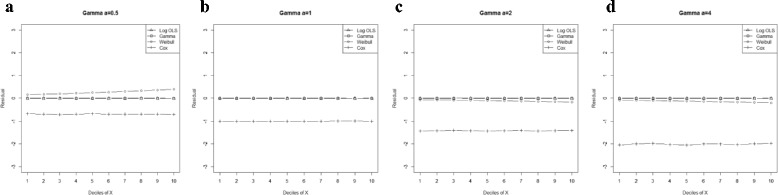
Mean residual from different estimators across deciles of ‘X’ for Gamma data (n=1000) with shape parameter a: 0.5, b: 1, c: 2, d: 4.
Figure 1.
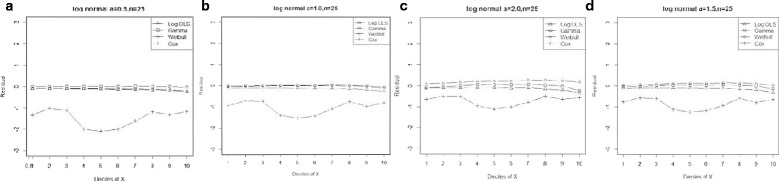
Mean residual from different estimators across deciles of ‘X’ for log-normal data (n=25) with variance a: 0.5, b: 1.0, c: 1.5, d: 2.0.
In addition, evaluating MAPE as an accuracy measure showed that Gamma and Weibull regression models have almost equal MAPE values. In many conditions, such as the log-normal model with σ2 = 1.5, 2, the Gamma model with shape equal to 0.5 (monotonically declining pdf) and the Weibull model with shape equal to 0.5 (linearly increasing hazard), as higher skewness data-generating mechanisms, the MAPE from Weibull regression model was always lower than Gamma regression model.
Interestingly, as the sample size increased, the MAPE of OLS for Ln(y) became very similar to that of the Gamma regression model. However, the MAPE of all models had an insignificant upward trend as the sample size increased.
Since there was also a concern about consistency and precision in the estimates of β1 coefficients, MSE and 95% simulation intervals were investigated. All three regression Gamma and Weibull and OLS for Ln(y) models provided approximately similar MSEs of β1 as data generated using log normal. However, the Gamma regression model showed minimum MSE values. We also found that MSE decreased by reducing skewness and increasing sample size. For the Weibull-generated data, Gamma and Weibull regression models exhibited similar and minimum values of MSE. Under all data-generating mechanisms, 95% simulation intervals were closer to true values in all three regression models. Surprisingly, the Cox proportional hazard model revealed maximum MSE and less accurate 95% simulation intervals, even within proportional hazards data-generating scenario.
Comparison goodness of fit tests (Hosmer-Lemeshow test and AIC criterion) revealed that, under a different range of data conditions, Gamma and Weibull regression models were better behaved. Finally, investigation of the pattern of the residuals as a function of X, which have been implemented by the mean of the residuals across deciles of X, showed more bias for the Cox proportional hazard model across all generated data and sample sizes (see Figures 2-15).
Figure 2.
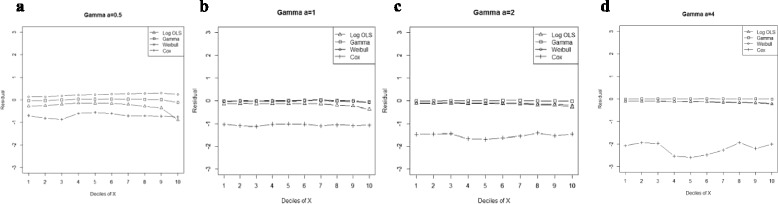
Mean residual from different estimators across deciles of ‘X’ for Gamma data (n=25) with shape parameter a: 0.5, b: 1, c: 2, d: 4.
Figure 15.

Mean residual from different estimators across deciles of ‘X’ for Weibull data (n=1000) with shape parameter a: 0.5, b: 1, c: 5.
Discussion
Although there are many substantial studies addressing the statistical issues in healthcare cost analysis over the last few decades, it is still an important issue that needs further evaluation. In this paper, we assessed the performance of various well-known statistical regression-based models in healthcare expenditure analysis, through different sample sizes and data-generating processes, using a Monte Carlo simulation. Each model was evaluated on 10,000 batch random samples, with 25, 50, 100, 500 and 1,000 sample sizes. Other studies were performed using just one large sample size (such as 10,000) [5,10], while we know the sample size is an important issue in healthcare studies and in precision of model-based estimators.
We found that, by considering the different interest points of various research and various data conditions, different model-based estimators could be used. Indeed, no estimator is considered to be the best across all ranges of data-generating processes. In addition, the accuracy of the results was almost the same in all sample sizes.
However, the GLMs estimated population means more precisely in all data-generating processes and sample sizes. In this respect, our results are consistent with other studies [2,5,6,10]. Comparative studies between log models were evaluated on 1,000 random samples, with a sample size of 10,000. They found almost identical results in estimating the slope β1, but the GLMs were substantially more precise than OLS-based model [5]. In this paper, as the sample size increased, the precision of estimating the mean population and the β1 using an OLS-based model became closer to that of GLMs.
Based on our result, the Gamma regression model provided more accurate estimates of population mean. In other studies, which compare log and Cox proportional hazard models, the Gamma regression model was introduced as the reasonable model across all of the simulation processes [13]. They have also found that the Cox proportional hazard model exhibited good performance when data were generated by distribution with a proportional hazards assumption [13]. In this paper, a Weibull distribution was selected as the proportional hazard data-generating mechanism. In addition, investigating proportional hazards assumption detected that gamma generation process also has produced data with proportional hazard properties but the Cox proportional hazard model showed a poor result within these data generation process. We also found that the Cox proportional hazard model behaved poorly in other data generation scenarios.
Our study has some limitations, including the fact that our focus was on generating skewed data, while kurtosis may have affected the results. Furthermore, the study was limited to fixed covariates.
Conclusions
Selecting the best model is dependent on the interest point of research, which could be the estimated mean of the population or covariate effects. There is no best model among all data conditions. It seems that the GLMs, especially the Gamma regression model, behave well regarding the estimation of population means of healthcare costs in most of the conditions. The results are consistent among all sample sizes; however, increasing sample size leads to improvement in the performance of the OLS-based model.
Based on estimation of the β1, GLMs seems to provide plausible estimations and as the sample size increased, estimated the β1 more precisely in all data-generating processes. Under all data generation, process even proportional hazard data generation scenarios the Cox proportional hazard model provided a poor estimation of mean population and the β1.
Acknowledgements
This study is part of biostatistics MS degree thesis of Fatemeh Pourmotahari and it was supported by the Ahvaz Jundishapur University of Medical Sciences.
Abbreviations
- Prob. H.L.
Hosmer–Lemeshow test
- signif.
At the 5% level
Footnotes
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
ASM contributed to the study design, wrote and revised the manuscript. FP analyzed the data and drafted the manuscript. KAA revised the manuscript. All authors read and approved the final manuscript.
Contributor Information
Amal Saki Malehi, Email: amalsaki@gmail.com.
Fatemeh Pourmotahari, Email: pourmotahari@yahoo.com.
Kambiz Ahmadi Angali, Email: kzfir@yahoo.com.
References
- 1.Gregori D, Petrinco M, Bo S, Desideri A, Merletti F, Pagano E. Regression models for analyzing costs and their determinants in health care: an introductory review. Int J Qual Health Care. 2011;23(3):331–41. doi: 10.1093/intqhc/mzr010. [DOI] [PubMed] [Google Scholar]
- 2.Mihaylova B, Briggs A, O’Hagan A, Thompson SG. Review of statistical methods for analysis healthcare resources and costs. Health Econ. 2011;20:897–916. doi: 10.1002/hec.1653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gilleskie DB, Mroz TA. A flexible approach for estimating the effects of covariates on health expenditures. J Health Econ. 2004;23:391–418. doi: 10.1016/j.jhealeco.2003.09.008. [DOI] [PubMed] [Google Scholar]
- 4.Cantoni E, Ronchetti E. A robust approach for skewed and heavy-tailed outcomes in the analysis of health care expenditures. J Health Econ. 2006;25(2):198–213. doi: 10.1016/j.jhealeco.2005.04.010. [DOI] [PubMed] [Google Scholar]
- 5.Manninga WG, Mullahy J. Estimating log models: to transform or not to transform? J Health Econ. 2001;20:461–94. doi: 10.1016/S0167-6296(01)00086-8. [DOI] [PubMed] [Google Scholar]
- 6.Deb P, Burgess JF. A quasi-experimental comparison of econometric models for health care expenditures. New York: Hunter College Department of Economics; 2003. Report No.: 212.
- 7.Basu A, Manning WG. Issues for the next generation of health care cost analyses. Med Care. 2009;47(7):S109–14. doi: 10.1097/MLR.0b013e31819c94a1. [DOI] [PubMed] [Google Scholar]
- 8.Ravangard R, Arab M, Rashidian A, Akbarisari A, Zare A, Zeraati H. Comparison of the results of cox proportional hazards model and parametric models in the study of length of stay in a tertiary teaching hospital in Tehran. Iran Acta Med Iran. 2011;49(10):650–8. [PubMed] [Google Scholar]
- 9.Jain AK, Strawderman RL. Flexible hazard regression modeling for medical cost data. Biostatistics. 2002;3(1):101–18. doi: 10.1093/biostatistics/3.1.101. [DOI] [PubMed] [Google Scholar]
- 10.Manning WG, Basu A, Mullahy J. Generalized modeling approaches to risk adjustment of skewed outcomes data. J Health Econ. 2005;24:465–88. doi: 10.1016/j.jhealeco.2004.09.011. [DOI] [PubMed] [Google Scholar]
- 11.Faddy M, Graves N, Pettitt A. Modeling length of stay in hospital and other right skewed data: comparison of phase-type, gamma and log-normal distributions. Value Health. 2009;12(2):309–14. doi: 10.1111/j.1524-4733.2008.00421.x. [DOI] [PubMed] [Google Scholar]
- 12.Griswold M, Parmigiani G, Potosky A, Lipscomb J. Analyzing health care costs: a comparison of statistical methods motivated by Medicare colorectal cancer charges. Biostatistics. 2004;1(1):1–23. [Google Scholar]
- 13.Basu A, Manning WG, Mullahy J. Comparing alternative models: log vs Cox proportional hazard? Health Econ. 2004;13:749–65. doi: 10.1002/hec.852. [DOI] [PubMed] [Google Scholar]
- 14.Lee ET, Wang JW. Statistical methods for survival data analysis. 3. New Jersey: John Wiley & Sons; 2003. [Google Scholar]


