A novel approach to analyzing binding data from proteins with two binding sites for the same substrate provides information beyond that accessible with traditional Hill equation analysis.
Abstract
Prokaryotic and eukaryotic Na+-driven transporters couple the movement of one or more Na+ ions down their electrochemical gradient to the active transport of a variety of solutes. When more than one Na+ is involved, Na+-binding data are usually analyzed using the Hill equation with a non-integer exponent n. The results of this analysis are an overall Kd-like constant equal to the concentration of ligand that produces half saturation and n, a measure of cooperativity. This information is usually insufficient to provide the basis for mechanistic models. In the case of transport using two Na+ ions, an n < 2 indicates that molecules with only one of the two sites occupied are present at low saturation. Here, we propose a new way of analyzing Na+-binding data for the case of two Na+ ions that, by taking into account binding to individual sites, provides far more information than can be obtained by using the Hill equation with a non-integer coefficient: it yields pairs of possible values for the Na+ affinities of the individual sites that can only vary within narrowly bounded ranges. To illustrate the advantages of the method, we present experimental scintillation proximity assay (SPA) data on binding of Na+ to the Na+/I− symporter (NIS). SPA is a method widely used to study the binding of Na+ to Na+-driven transporters. NIS is the key plasma membrane protein that mediates active I− transport in the thyroid gland, the first step in the biosynthesis of the thyroid hormones, of which iodine is an essential constituent. NIS activity is electrogenic, with a 2:1 Na+/I− transport stoichiometry. The formalism proposed here is general and can be used to analyze data on other proteins with two binding sites for the same substrate.
INTRODUCTION
Membrane transport proteins serve a key function in living cells by mediating the transport of many different solutes, such as ions, nutrients, and neurotransmitters across biological membranes. Numerous pathological conditions—cystinuria (Fotiadis et al., 2013), glucose–galactose malabsorption (Wright, 2013), hypothyroidism caused by iodide transport defects (Levy et al., 1998; De la Vieja et al., 2007; Paroder-Belenitsky et al., 2011; Portulano et al., 2014)—result from impairments in the function of molecules of this class. Membrane transporters also play a crucial role in the delivery of chemotherapeutic agents and internal radiation (Klutz et al., 2011; Ho et al., 2013) to cancer cells.
Many prokaryotic and eukaryotic transporters exploit the electrochemical gradient of Na+ to translocate their substrates across the membrane. Of those, a significant fraction binds and transports more than one Na+ ion per transport cycle (Caplan et al., 2008; Shi et al., 2008; Abramson and Wright, 2009). Binding assays using a radiotracer in scintillation proximity assays (SPAs) have become a routine procedure for investigating the function of detergent-solubilized transport proteins and, critically, for determining the substrate-binding constants of purified transporters (Pirch et al., 2002; Berry and Price-Jones, 2005; Quick and Javitch, 2007; Harder and Fotiadis, 2012; Khafizov et al., 2012; Zhou et al., 2014).
Conventionally, when more than one Na+ is involved, SPA data are analyzed using the Hill equation (Hill, 1910, 1913; Weiss, 1997; Goutelle et al., 2008) with a non-integer exponent n:
| (1) |
where fn is the fraction of transporter molecules that are occupied by Na+, and Kd is an apparent microscopic dissociation constant. Cases with n > 1 are instances of positive cooperativity, and the resulting curves for fn versus [Na+] are sigmoidal; the Kd value yields the [Na+] at half-saturation. This equation, however, does not describe a true equilibrium situation: there is no real binding reaction that can lead to this expression, as it would have a fractional stoichiometric coefficient. In the case of two binding sites, for example, a fractional Hill coefficient indicates that proteins with only one site occupied represent a significant fraction of the molecules in equilibrium, especially at low [Na+].
Here, we propose a novel way of analyzing SPA data obtained from experiments with transporters that bind Na+ at two sites. The method is exemplified by analyzing experimental SPA data from the Na+/I− symporter (NIS). This approach, which takes into account binding to individual sites, provides information not accessible with the traditional Hill equation analysis.
MATERIALS AND METHODS
Protein purification
293-H cells grown in suspension were transduced with a lentiviral vector containing a rat NIS cDNA construct with an HA tag at the N terminus and a His8 tag and a streptavidin-binding protein (IBA GmbH) tag at the C terminus. I− transport levels were comparable to those in FRTL-5 cells, a line of rat thyroid–derived cells that express NIS endogenously (Dai et al., 1996). A membrane fraction prepared from 293 cells was solubilized with 40 mM n-dodecyl-β-d-maltopyranoside (DDM; Anatrace) and purified via Strep-Tactin affinity chromatography. The S353A/T354A NIS mutant was expressed and purified using the same procedures.
Binding experiments
Binding experiments were performed using the SPA technique (Quick and Javitch, 2007). Affinity-purified NIS (WT or mutant) was bound to Cu2+ chelate YSi scintillation SPA beads (PerkinElmer) via the C-terminal His8 tag. 250 µg SPA beads was used per assay, in a volume of 100 µl. Experiments consisted of competing bound 22Na+ with cold Na+ at the specified concentrations. The assay buffer consisted of 100–600 mM Tris/Mes, pH 7.5, 20% glycerol, 0–500 mM NaCl (equimolar replacement with Tris/Mes), 1 mM TCEP, and 0.1% DDM with 250 ng of affinity-purified NIS. [22Na]Cl (1,017 mCi/mg; PerkinElmer) and the indicated concentrations of cold NaCl were added to the bead solution simultaneously with the protein. Nonspecific binding was determined in the presence of 800 mM imidazole. All binding assays were performed in white-walled, clear-bottomed 96-well plates and quantitated in a photomultiplier (Wallac; PerkinElmer) tube counter (MicroBeta; PerkinElmer) after overnight equilibration.
Analysis of NIS SPA data
All readings were background-subtracted and then normalized using the following relation:
where fx is the fraction of NIS molecules for which the bound 22Na+ has been displaced by cold Na+ at a [Na+] = X; and C0, CX, and C500 are the counts per minute at cold [Na+] = 0, [Na+] = X, and [Na+] = 500 mM.
RESULTS AND DISCUSSION
Non-integer Hill coefficients
The equation proposed by Hill (Hill, 1910, 1913; Dahlquist, 1978; Weiss, 1997; Goutelle et al., 2008) can be written as
and can be considered to represent the equilibrium for the reaction
“where Ka is the equilibrium constant and n is a whole number > 1” (Hill, 1913), and Y is the fraction of protein molecules that have n ligands bound.
This reaction and its associated equilibrium constant imply that the protein (P) has n binding sites, and the ligand (L) must bind to the n sites simultaneously: binding of L to a single site of the protein does not take place. The exponent in this equation is called the Hill coefficient.
In many cases, a better fit to the experimental data can be achieved by using a non-integer Hill coefficient, yielding the equation,
Unfortunately, this equation does not represent an actual reaction; it just says that L can bind to one site and that binding to one site affects the affinity of the other site for L. A value of n > 1 indicates positive cooperativity; an n < 1 indicates negative cooperativity.
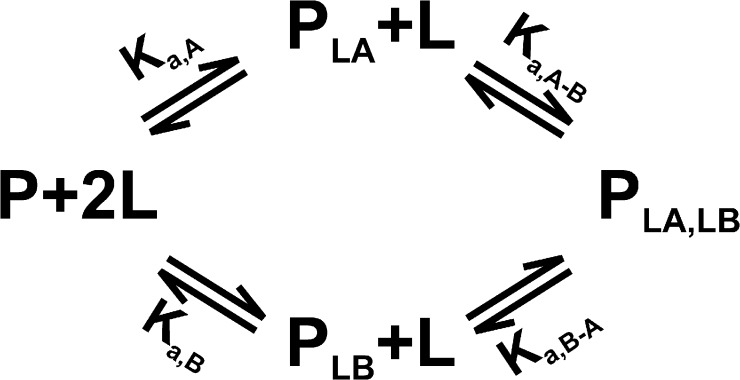
A more general case would be one in which the protein has two nonequivalent sites and L can bind to either site first and then bind to the other. The two sites will, in general, have different affinities for the ligand, and the affinity for binding to a second site may be enhanced (positive cooperativity) or reduced (negative cooperativity) when the other site is already occupied. The reaction scheme for the general case involving two sites, A and B, is represented in Fig. 1, where Ka,A and Ka,B are the association constants for the binding of L to the empty protein, Ka,A−B is the association constant for binding L to site B when site A is occupied, and Ka,B−A is the association constant for binding L to site A when site B is occupied. Note that only three of the four constants are needed because the upper and the lower paths lead to the same species, and therefore Ka,A · Ka,A−B = Ka,B · Ka,B−A. Introducing ϕ, a unitless enhancement/reduction factor, we can write Ka,A−B = Ka,B · ϕ and Ka,B−A = Ka,A · ϕ. For positive cooperativity, ϕ > 1, and ϕ < 1 corresponds to negative cooperativity (ϕ = 1 means independent sites).
Figure 1.
Binding of a ligand L to a protein P with two cooperative binding sites (sites A and B). The association constants for the empty protein are Ka,A and Ka,B, and those for binding of the second ligand are Ka,A−B and Ka,B−A.
The fraction of doubly occupied molecules can be written as
| (2a) |
and the fraction of singly occupied molecules as
| (2b) |
Introducing the new constants
| (3) |
| (4) |
yields
| (5a) |
and
| (5b) |
(The sum of Eqs. 5a and 5b is similar to the Adair equation (Adair et al., 1925) but subjected to the conditions given by Eqs. 3 and 4.)
The normalized signal from an experimental measurement sig(L) is given by
| (6) |
where sr is the ratio of the signal when one L is bound to that when two L’s are bound.
The values of Kp and Kx can be obtained by a least-squares fit of normalized experimental data. Eqs. 3 and 4 can then be used to solve for Ka,A and Ka,B as a function of ϕ. This yields a quadratic equation with solutions
| (7a) |
where we choose the plus sign for Ka,A and the minus sign for Ka,B. Because Ka,A and Ka,B must be real numbers, the expression within the square root “sq”
| (7b) |
or
| (7c) |
must be positive.
Three cases have to be considered: ϕ = 1, ϕ > 1, and ϕ < 1. The case ϕ = 1 corresponds to two independent sites (no cooperativity). If sq = 0, Ka,A = Ka,B = 1/2 Kp and corresponds to two independent identical sites; otherwise, Ka,A > Ka,B.
The case ϕ > 1 corresponds to positive cooperativity. The condition which is equivalent to defines a minimum value of such that ϕmin,p ≤ ϕ < ∞. In contrast, the case ϕ < 1 corresponds to negative cooperativity. The condition or also defines a minimum value of but in this case, ϕmin,p ≤ ϕ < 1.
In both cases, when ϕ = ϕmin, sq = 0; therefore, A symmetrical homodimer, for example, may correspond to this case if the single sites can bind independently, but once a site is occupied, the affinity for the second site is enhanced/reduced.
In the case of positive cooperativity, there is another limiting case. It corresponds to the situation where ϕ is very large, making Ka,A approach Kp and Ka,B approach 0 (from Eq. 7a). This case corresponds to absolute sequential binding (i.e., the ligand does not bind to site B unless site A is already occupied).
After the values of Kp and Kx are obtained by fitting the experimental data, combinations of values of Ka,A and Ka,B can be obtained as a function of the allowed values of ϕ. Although the information obtained is only a range of possible values for the affinities of sites A and B of the empty protein for the ligand, and with Ka,B = Kp – Ka,A.
This analysis provides more information than just the single value that is obtained from the Hill equation using non-integer exponents. Furthermore, the values of Ka,A, Ka,B, and are constrained by Eqs. 3 and 4 and the conditions imposed by Eq. 7. In addition, the formulation corresponds to a well-defined binding mechanism. (The dissociation constant, obtained by computing Kx−1/2, is similar to the Kd obtained from the Hill equation.) One issue that may seem puzzling is that Ka.B approaches zero (and Kd,B approaches ∞) as Ka,A approaches Kp. Why does it still correspond to a two-site situation? The answer is simple. Both Ka,B and ϕ are a function of (Kp − Ka,A); Ka,B is directly proportional and ϕ is inversely proportional, such that That is, as Ka,B approaches zero, Ka,B · ϕ remains bound, and the second site has a finite dissociation constant when site A is occupied. Because Ka,A varies only within a factor of 2, Ka,B · ϕ also varies within a factor of 2.
Because the equations were derived as a function of [L], the concentration of free ligand, they work directly in cases in which [L] is very close to Ladded, the concentration of ligand added at each experimental point. SPA, in which the amount of protein is much less than the amount of ligand, and fluorescence measurements performed with concentration of protein [P] << Kd satisfy this condition.
In the case of SPA experiments with 22Na (L = Na+), the transporter with two Na+ ions bound and the two species with one Na+ bound all produce a signal. Because the signal from the molecules with one Na+ is half that from the fully occupied transporter (sr = 0.5 in Eq. 6), the normalized SPA signal is proportional to the sum of the fraction of molecules with two Na+ ions bound and half the fraction of molecules with one Na+ bound:
Summing these two signals, we obtain
| (8) |
Eq. 8 assumes a maximum signal fraction of 1.0. Because of experimental and normalization errors, it is best to include a numerator multiplier SPAmax, which can also be fitted to the data. The value of the fitted SPAmax should remain close to 1.0.
Sodium binding by WT NIS SPA data
NIS is the key plasma membrane protein that mediates active I− transport in the thyroid gland, the first step in the biosynthesis of the thyroid hormones, of which iodine is an essential constituent (Dai et al., 1996). NIS mutations have been linked to iodide transport defects, which lead to congenital hypothyroidism, deficit in the central nervous system development, and mental retardation if patients are not treated soon after birth (Dohán et al., 2002; De la Vieja et al., 2004, 2005; Paroder-Belenitsky et al., 2011; Li et al., 2013; Paroder et al., 2013; Portulano et al., 2014). NIS couples the inward “uphill” translocation of I− against its electrochemical gradient to the inward “downhill” transport of Na+ down its electrochemical gradient. NIS activity is electrogenic, with a 2:1 Na+/I− transport stoichiometry (Eskandari et al., 1997). It is able to accumulate iodide from serum concentrations orders of magnitude below its Kd. We have recently shown that at physiological Na+ concentrations, ∼79% of all NIS molecules have two Na+ ions bound, and are therefore ready to bind and transport I− (Nicola et al., 2014).
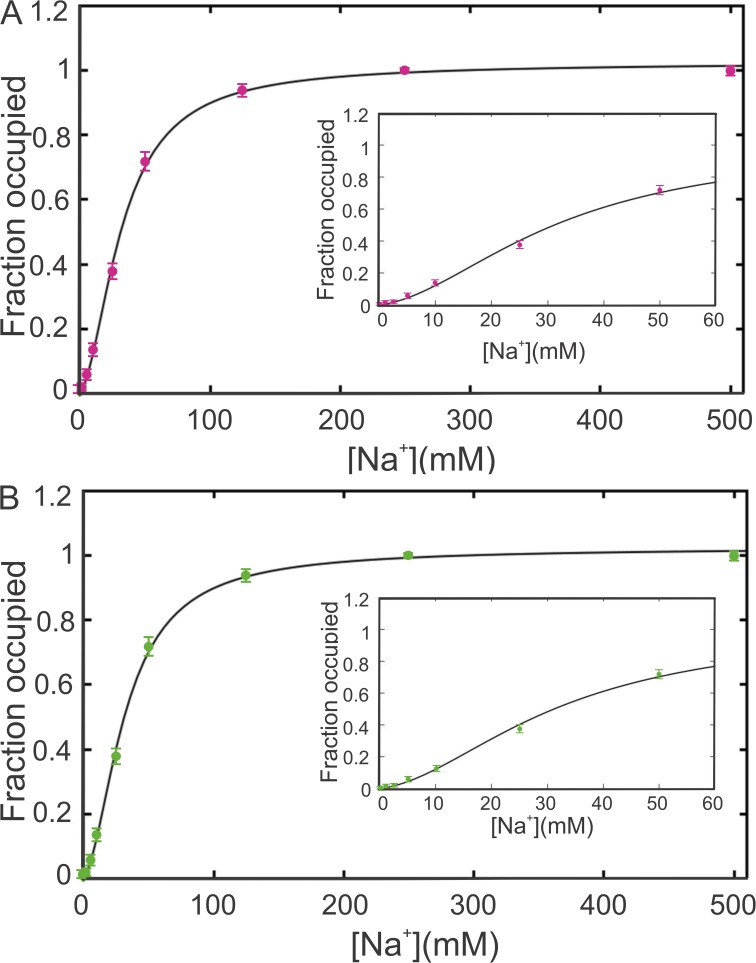
SPA experiments were performed to determine the affinity of Na+ binding by NIS. NIS, like many other transporters in its family, has two independent binding sites for Na+; both Na+ ions that bind to NIS are used to transport I−. The fx values, obtained and normalized as detailed in Materials and methods, were fitted to Eq. 8 as a function of [Na+] to obtain the Kp and Kx values (Fig. 2 A). The agreement between the calculated values (Fig. 2 A, continuous curve) and the experimental data is excellent for fx values in the range of 0–1.0; m is the number of experimental data points, and p is the number of parameters.
Figure 2.
Na+ binding by WT NIS. (A) SPA data for Na+ binding by NIS fitted by Eq. 8. Data were collected and analyzed as described in Materials and methods. Values represent the means ± SE from three independent experiments performed in triplicate. The inset shows the fit at low [Na+], where the cooperativity is more pronounced. (B) SPA data for Na+ binding by WT NIS fitted using the Hill equation with a non-integer coefficient (Eq. 1). The data were fitted with a Kd of 31.8 mM and an n value of 1.74. The inset shows the fit at low [Na+], where the cooperativity is more pronounced.
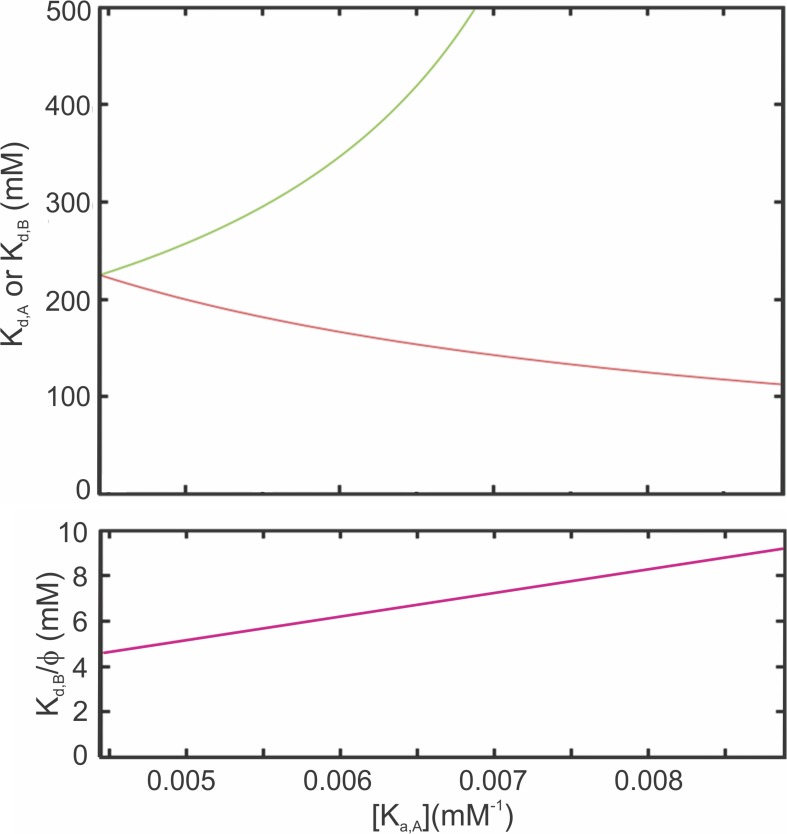
The extremes of the ranges provide examples of the combinations of affinities compatible with the data (Fig. 3, top and bottom). If Kd,A = Kd,B = 225 mM (Kd,X = 1/Ka,X) (Fig. 3, top), binding to a second site becomes highly favorable, with Kd,B/ϕ = 4.5 mM (Fig. 3, bottom), a 50-fold enhancement. At the other extreme, when Kd,A approaches 112.5 mM (i.e., Kd,B approaches infinity), Kd,B/ϕ becomes 9.2 mM, corresponding to a very large enhancement. The actual values for NIS must fall within this range, somewhere between these two extremes.
Figure 3.
Ranges of dissociation constants for Na+ binding by WT NIS. (Top) Dissociation constants for Na+ binding by empty WT NIS—Kd,A (red) and Kd,B (green)—as a function of the allowed values for the association constant Ka,A. (Bottom) Enhanced dissociation constant for the second site when the first site is already occupied.
This analysis shows that the values of the dissociation constants for empty NIS, Kd,A, and Kd,B (Fig. 3, top, left side) are compatible at one extreme, with both sites having the same affinity (Kd,A = Kd,B = 225 mM), and as the affinity of one of the sites (for example, site A) increases, that of the other must decrease to remain compatible with the experimental data. As Kd,A decreases, the value of Kd,B increases dramatically, approaching infinite as Kd,A approaches 112.5 mM (= 1/Kp). However, because of the cooperativity, Kd,B/ϕ becomes highly favorable when site A is occupied (range of 4.6–9.2 mM; Fig. 3, bottom, left side). These values are very similar to those obtained by a statistical thermodynamic analysis of kinetic data (Kd,A = 137 mM and Kd,B = 22.4 mM) (Nicola et al., 2014).
It should be noted that the dissociation constant for the first site (Kd,A) and the enhanced dissociation constant for the second site (Kd,B/ϕ) are always known within a factor of 2. Furthermore, if additional information becomes available—for example, from binding data for affinity mutants—the values of all three constants (Kd,A, Kd,B, and Kd,B/ϕ) can be obtained.
The same data fitted to Eq. 1 (Fig. 2 B) gave a Kd value of 31.9 mM and an n of 1.74. This Kd is highly similar to the geometric mean of Kd,A and Kd,B/ϕ (= 32.1 mM). Although the two equations yield fits of similar quality (see below), there is much more information in the values in Fig. 3 than in the two numbers obtained from fitting the data to the Hill equation.
Sodium binding by S353A/T354A NIS SPA data
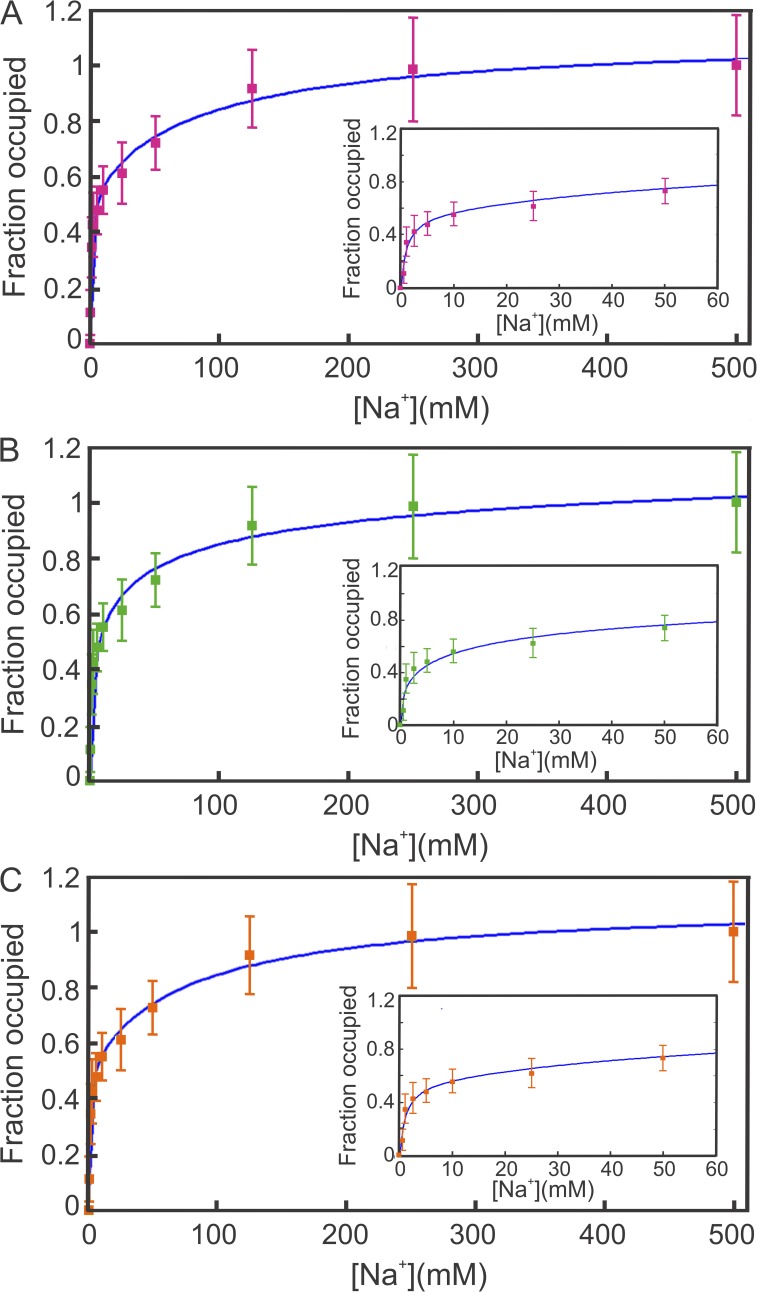
The S353A/T354A NIS mutant was studied as a possible example of a NIS molecule that may bind a single Na+ ion. Residues S353 and T354 were studied because the NIS mutant T354P causes iodide transport defect (Levy et al., 1998), and were identified as residues that are part of the coordination of one of the Na+ ions (De la Vieja et al., 2007), like the corresponding residues in the bacterial leucine transporter LeuT (Yamashita et al., 2005). Alanine substitutions at NIS positions 353 and 354 abolish I− transport (De la Vieja et al., 2007). To determine whether or not the lack of transport activity is caused by a lack of Na+ binding, we generated the double mutant S353A/T354A and measured, using SPA, the binding of Na+ to this NIS mutant. Surprisingly, the mutant binds two Na+ ions, but the binding curve (Fig. 4 A) fails to show the positive cooperativity between the sites observed for the WT (Fig. 2 A).
Figure 4.
Na+ binding by S353A/T354A NIS. (A) SPA data for Na+ binding by S353A/T354A NIS fitted by Eq. 8. Data were collected and analyzed as described in Materials and methods. Values represent the means ± SE from two independent experiments performed in triplicate. The inset shows the fit at low [Na+], where the cooperativity is more pronounced. (B) SPA data for Na+ binding by S353A/T354A NIS fitted by the Hill equation with a non-integer coefficient (Eq. 1). The data were fitted with a Kd of 20.6 mM and an n value of 0.42. The inset shows the fit at low [Na+], where the cooperativity is more pronounced. (C) SPA data for Na+ binding by S353A/T354A NIS fitted for two independent sites. The data were fitted with a Kd,A of 0.90 mM and a Kd,B of 80.5 mM. The inset shows the fit at low [Na+], where the effect of having two sites—one with high affinity and one with low affinity—is more pronounced.
The SPA data were fitted and analyzed using three different formalisms: (1) fit to Eq. 8 followed by the analysis proposed above (Figs. 4 A and 5); (2) fit to Hill equation (Eq. 1) (Fig. 4 B); and (3) fit assuming two independent sites (Fig. 4 C). The three formalisms fit the experimental data extremely well. Interestingly, the fit to Eq. 1 yields a single Kd = 20.6 mM and a Hill coefficient of 0.42. There is little information in these values besides a general Kd,50 and the indication of negative cooperativity (n ≤ 1). Furthermore, the fact that the value of n is smaller than the minimum value (1/N = 0.5) expected for negative cooperativity (Abeliovich, 2005) suggests that Eq. 1 is not an appropriate model for ligand binding to this NIS mutant.
Figure 5.
Ranges of dissociation constants for Na+ binding by S353A/T354A NIS. (Top) Dissociation constants for Na+ binding by empty NIS—Kd,A (cyan) and Kd,B (red)—as a function of the allowed values for the association constant Ka,A. Kd,A = 1/Ka,A varies between 1.98 and 0.99 mM. (Bottom) Kd,B = 1/(Kp − Ka,A) (red) as a function of Ka,A also begins at 1.98 mM (Kp /2; left side of graph) and increases slowly until approximately Ka,A = 0.8 mM−1. As Ka,A approaches Kp, Ka,B approaches infinity (bottom graph, right). In contrast, although Kd,B/ϕ (cyan) begins at 43.78 mM when site A is occupied (negative cooperativity), it only increases to 87.68 mM when Ka,A = Kp (right side of graph).
Analysis using the equations presented above yields a range of Kd values for the first site (Kd,A) between 0.99 and 1.98 mM (Fig. 5, top). For most of this range, the dissociation constant for binding Na+ to site B when site A is not occupied remains small (Kd,B = 4.75 mM at Ka,A = 0.88 mM−1; Kd,B = 6.23 mM at Ka,A = 0.85 mM−1; Fig. 5), but it increases rapidly as Ka,A approaches Kp. Negative cooperativity is manifested in binding to site B when site A is occupied (Kd,B/ϕ; Fig. 5, bottom, cyan). In this situation, Kd,B/ϕ, the dissociation constant for site B when site A is occupied, varies between 43.84 and 87.68 mM (Fig. 5, bottom, cyan). The values on the right side of the graph, 0.99 and 87.68 mM, are highly similar to those obtained by fitting two independent sites (0.90 and 80.48 mM). The similarity between these sets of values reflects the fact that, under these conditions, the two models describe similar situations: in both cases, site B starts binding after site A is substantially occupied. The analysis based on the formalism introduced here, however, describes other situations that are equally compatible with the data from SPA experiments. As mentioned before, analysis with the Hill equation provides much less information.
Equivalence of fitting by the two equations
It could be argued that the similarity between the quality of the fit using the Hill equation with a non-integer coefficient and that using the equations proposed here (i.e., similar rmsresid values) is a coincidence because of the particular values of the constants and n in the case of NIS. To test this possibility, we computed points with the Hill equation (Eq. 1) using values for n ranging from 1.7 to 1.9 and a Kdn value of 0.001. The points in each individual curve were fitted by least squares using Eq. 8 (Fig. 6). The equation fits the calculated points with an rmsresid of <0.004, indicating that the two equations can fit the same data equally well.
Figure 6.
Fitting by Eq. 8 of points generated by Eq. 1. Points were generated using Eq. 1 with n values of 1.7 (mauve ovals), 1.8 (blue triangles), and 1.9 (green squares), and a Kdn of 1,000 (Kan = 0.001). Each set of points was fitted using Eq. 8, resulting in the mauve, cyan, and blue curves, respectively.
Analysis of data obtained by other experimental methods
The formalism presented here can be used to analyze data obtained by other methods, for example, fluorescence (Reyes et al., 2013). In this case, f versus [L] data can be fitted by least squares to a version of Eq. 8 modified to take into account the fact that the signal with one L bound may not be half the signal when two L’s are bound. The modified equation has the form
where S1 is the fraction of the signal that occurs in response to binding of a single L (sr in Eq. 6). The value of S1 can be estimated as part of the least-squares fit. The results obtained can be analyzed as described above. As mentioned earlier, these equations can be used when [L] ≈ Ladded. In the case of fluorescence, this condition is met when [P] << Kd.
Summary of the approach
The equations for binding of a ligand to an allosteric macromolecule with two sites can be derived using three parameters, Ka,A, Ka,B, and ϕ (the enhancement of the affinity for binding the ligand to one of the sites that results from binding the ligand to the other site) (Hines et al., 2014), where Ka,A−B = Ka,B · ϕ and Ka,B−A = Ka,A · ϕ (Fig. 1). Fitting the experimental data to the three parameters in Eqs. 2a and 2b results in many combinations of parameters compatible with the data (Hines et al., 2014). The simple variable change shown in Eqs. 3 (Kp = Ka,A + Ka,B) and 4 (Kx = Ka,A · Ka,B · ϕ) results in equations with only two parameters (Kp and Kx; Eqs. 5a and 5b) that fit the data much more stably. Once the values of Kp and Kx are obtained by least squares or other methods, Ka,A and Ka,B can be obtained as the two roots of a quadratic equation (Eq. 7a). Choosing A (arbitrarily) as the site with the higher affinity (the plus sign in Eq. 7a), the solutions are bound by the conditions and The binding affinity of site B for the ligand when site A is occupied can be obtained as Therefore, even when Ka,B approaches zero, remains finite. The results are a set of values for Ka,A, Ka,B, and Ka,B · ϕ (Kd,A, Kd,B, and Kd,B/ϕ), in which Kd,A and Kd,B/ϕ are known within a factor of 2. This information, along with the fact that the values correspond to a well-defined binding reaction, makes the values obtained by this procedure ideally suited for establishing correlations with structural and computational results. Because Ka,A and Ka,B · ϕ are known within a factor of 2, the free energies of binding ΔGa,A and ΔGa,A−B, calculated as −RTln K, are known within ∼0.4 Kcal/mol (= RTln 2). Additional information can be obtained from the values of ϕ. The free energy of the interaction between the two sites (ΔgA,B) can be calculated as −RTln (ϕ).
Conclusions
In summary, we present a method for analyzing binding data from a protein that binds the same ligand at two sites. In the case of a symmetric homodimer, the analysis provides values for the two binding constants: that for binding to the empty protein at either of the two sites (Kd,A and Kd,B), and that for binding to the second site when the first site is occupied (Kd,B/ϕ). In the case in which the two sites on the protein are different, the approach provides bounded pairs of possible values for the same constants. This information is missed when using the Hill equation with a non-integer coefficient. We tested the usefulness of the equations we propose by analyzing SPA data for NIS. In the case of WT NIS, the Hill equation fit gives a Kd of 31.8 mM and an n of 1.74 (Fig. 2 B). The approach presented here indicates that Na+ binds to the first site with an affinity between 112.5 and 225 mM, and to the second site—once the first site is occupied—with an affinity between 9.2 and 4.6 mM. Although the square root of the product of the constants (32.2 mM) is highly similar to the Hill equation Kd, significant additional information is provided by the values obtained using the new approach. Thus, as opposed to the Hill equation, which provides n, an indication of cooperativity, and an overall Kd-like constant, the approach presented here provides narrowly bounded ranges of pairs of the values of all Kds necessary to fully describe binding of the ligand. This formalism can also be used to analyze data of proteins that bind the same substrate at two binding sites.
Acknowledgments
We thank Drs. D. Leahy and A. Lau for critical reading of the manuscript and insightful discussions.
This study was supported by National Institutes of Health (grant DK-41544 to N. Carrasco).
The authors declare no competing financial interests.
Eduardo Rios served as editor.
Footnotes
Abbreviations used in this paper:
- NIS
- Na+/I− symporter
- SPA
- scintillation proximity assay
References
- Abeliovich H. 2005. An empirical extremum principle for the Hill coefficient in ligand-protein interactions showing negative cooperativity. Biophys. J. 89:76–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abramson J., and Wright E.M.. 2009. Structure and function of Na+-symporters with inverted repeats. Curr. Opin. Struct. Biol. 19:425–432. 10.1016/j.sbi.2009.06.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adair G.S., Block A.V., and Field H.J.. 1925. The hemoglobin system: VI. The oxygen dissociation curve of hemoglobin. J. Biol. Chem. 63:529–545. [Google Scholar]
- Berry J., and Price-Jones M.. 2005. Measurement of radioligand binding by scintillation proximity assay. Methods Mol. Biol. 306:121–137. [DOI] [PubMed] [Google Scholar]
- Caplan D.A., Subbotina J.O., and Noskov S.Y.. 2008. Molecular mechanism of ion-ion and ion-substrate coupling in the Na+-dependent leucine transporter LeuT. Biophys. J. 95:4613–4621. 10.1529/biophysj.108.139741 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dahlquist F.W. 1978. The meaning of Scatchard and Hill plots. Methods Enzymol. 48:270–299. 10.1016/S0076-6879(78)48015-2 [DOI] [PubMed] [Google Scholar]
- Dai G., Levy O., and Carrasco N.. 1996. Cloning and characterization of the thyroid iodide transporter. Nature. 379:458–460. 10.1038/379458a0 [DOI] [PubMed] [Google Scholar]
- De la Vieja A., Ginter C.S., and Carrasco N.. 2004. The Q267E mutation in the sodium/iodide symporter (NIS) causes congenital iodide transport defect (ITD) by decreasing the NIS turnover number. J. Cell Sci. 117:677–687. 10.1242/jcs.00898 [DOI] [PubMed] [Google Scholar]
- De la Vieja A., Ginter C.S., and Carrasco N.. 2005. Molecular analysis of a congenital iodide transport defect: G543E impairs maturation and trafficking of the Na+/I− symporter. Mol. Endocrinol. 19:2847–2858. 10.1210/me.2005-0162 [DOI] [PubMed] [Google Scholar]
- De la Vieja A., Reed M.D., Ginter C.S., and Carrasco N.. 2007. Amino acid residues in transmembrane segment IX of the Na+/I− symporter play a role in its Na+ dependence and are critical for transport activity. J. Biol. Chem. 282:25290–25298. 10.1074/jbc.M700147200 [DOI] [PubMed] [Google Scholar]
- Dohán O., Gavrielides M.V., Ginter C., Amzel L.M., and Carrasco N.. 2002. Na+/I− symporter activity requires a small and uncharged amino acid residue at position 395. Mol. Endocrinol. 16:1893–1902. 10.1210/me.2002-0071 [DOI] [PubMed] [Google Scholar]
- Eskandari S., Loo D.D., Dai G., Levy O., Wright E.M., and Carrasco N.. 1997. Thyroid Na+/I− symporter. Mechanism, stoichiometry, and specificity. J. Biol. Chem. 272:27230–27238. 10.1074/jbc.272.43.27230 [DOI] [PubMed] [Google Scholar]
- Fotiadis D., Kanai Y., and Palacín M.. 2013. The SLC3 and SLC7 families of amino acid transporters. Mol. Aspects Med. 34:139–158. 10.1016/j.mam.2012.10.007 [DOI] [PubMed] [Google Scholar]
- Goutelle S., Maurin M., Rougier F., Barbaut X., Bourguignon L., Ducher M., and Maire P.. 2008. The Hill equation: a review of its capabilities in pharmacological modelling. Fundam. Clin. Pharmacol. 22:633–648. 10.1111/j.1472-8206.2008.00633.x [DOI] [PubMed] [Google Scholar]
- Harder D., and Fotiadis D.. 2012. Measuring substrate binding and affinity of purified membrane transport proteins using the scintillation proximity assay. Nat. Protoc. 7:1569–1578. 10.1038/nprot.2012.090 [DOI] [PubMed] [Google Scholar]
- Hill A.V. 1910. Proceedings of the Physiological Society: January 22, 1910. The possible effects of the aggregation of the molecules of hæmoglobin on its dissociation curves. J. Physiol. 40:iv–vii. 10.1113/jphysiol.1910.sp001386 [DOI] [Google Scholar]
- Hill A.V. 1913. The Combinations of haemoglobin with oxygen and with carbon monoxide. I. Biochem. J. 7:471–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hines K.E., Middendorf T.R., and Aldrich R.W.. 2014. Determination of parameter identifiability in nonlinear biophysical models: A Bayesian approach. J. Gen. Physiol. 143:401–416. 10.1085/jgp.201311116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho A.L., Grewal R.K., Leboeuf R., Sherman E.J., Pfister D.G., Deandreis D., Pentlow K.S., Zanzonico P.B., Haque S., Gavane S., et al. . 2013. Selumetinib-enhanced radioiodine uptake in advanced thyroid cancer. N. Engl. J. Med. 368:623–632. 10.1056/NEJMoa1209288 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khafizov K., Perez C., Koshy C., Quick M., Fendler K., Ziegler C., and Forrest L.R.. 2012. Investigation of the sodium-binding sites in the sodium-coupled betaine transporter BetP. Proc. Natl. Acad. Sci. USA. 109:E3035–E3044. 10.1073/pnas.1209039109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klutz K., Willhauck M.J., Wunderlich N., Zach C., Anton M., Senekowitsch-Schmidtke R., Göke B., and Spitzweg C.. 2011. Sodium iodide symporter (NIS)-mediated radionuclide ((131)I, (188)Re) therapy of liver cancer after transcriptionally targeted intratumoral in vivo NIS gene delivery. Hum. Gene Ther. 22:1403–1412. 10.1089/hum.2010.158 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy O., Ginter C.S., De la Vieja A., Levy D., and Carrasco N.. 1998. Identification of a structural requirement for thyroid Na+/I− symporter (NIS) function from analysis of a mutation that causes human congenital hypothyroidism. FEBS Lett. 429:36–40. 10.1016/S0014-5793(98)00522-5 [DOI] [PubMed] [Google Scholar]
- Li W., Nicola J.P., Amzel L.M., and Carrasco N.. 2013. Asn441 plays a key role in folding and function of the Na+/I− symporter (NIS). FASEB J. 27:3229–3238. 10.1096/fj.13-229138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicola J.P., Carrasco N., and Amzel L.M.. 2014. Physiological sodium concentrations enhance the iodide affinity of the Na+/I− symporter. Nat. Commun. 5:3948 10.1038/ncomms4948 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paroder V., Nicola J.P., Ginter C.S., and Carrasco N.. 2013. The iodide-transport-defect-causing mutation R124H: a δ-amino group at position 124 is critical for maturation and trafficking of the Na+/I− symporter. J. Cell Sci. 126:3305–3313. 10.1242/jcs.120246 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paroder-Belenitsky M., Maestas M.J., Dohán O., Nicola J.P., Reyna-Neyra A., Follenzi A., Dadachova E., Eskandari S., Amzel L.M., and Carrasco N.. 2011. Mechanism of anion selectivity and stoichiometry of the Na+/I− symporter (NIS). Proc. Natl. Acad. Sci. USA. 108:17933–17938. 10.1073/pnas.1108278108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pirch T., Quick M., Nietschke M., Langkamp M., and Jung H.. 2002. Sites important for Na+ and substrate binding in the Na+/proline transporter of Escherichia coli, a member of the Na+/solute symporter family. J. Biol. Chem. 277:8790–8796. 10.1074/jbc.M111008200 [DOI] [PubMed] [Google Scholar]
- Portulano C., Paroder-Belenitsky M., and Carrasco N.. 2014. The Na+/I− symporter (NIS): Mechanism and medical impact. Endocr. Rev. 35:106–149. 10.1210/er.2012-1036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quick M., and Javitch J.A.. 2007. Monitoring the function of membrane transport proteins in detergent-solubilized form. Proc. Natl. Acad. Sci. USA. 104:3603–3608. 10.1073/pnas.0609573104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reyes N., Oh S., and Boudker O.. 2013. Binding thermodynamics of a glutamate transporter homolog. Nat. Struct. Mol. Biol. 20:634–640. 10.1038/nsmb.2548 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi L., Quick M., Zhao Y., Weinstein H., and Javitch J.A.. 2008. The mechanism of a neurotransmitter:sodium symporter—inward release of Na+ and substrate is triggered by substrate in a second binding site. Mol. Cell. 30:667–677. 10.1016/j.molcel.2008.05.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss J.N. 1997. The Hill equation revisited: uses and misuses. FASEB J. 11:835–841. [PubMed] [Google Scholar]
- Wright E.M. 2013. Glucose transport families SLC5 and SLC50. Mol. Aspects Med. 34:183–196. 10.1016/j.mam.2012.11.002 [DOI] [PubMed] [Google Scholar]
- Yamashita A., Singh S.K., Kawate T., Jin Y., and Gouaux E.. 2005. Crystal structure of a bacterial homologue of Na+/Cl−-dependent neurotransmitter transporters. Nature. 437:215–223. 10.1038/nature03978 [DOI] [PubMed] [Google Scholar]
- Zhou X., Levin E.J., Pan Y., McCoy J.G., Sharma R., Kloss B., Bruni R., Quick M., and Zhou M.. 2014. Structural basis of the alternating-access mechanism in a bile acid transporter. Nature. 505:569–573. 10.1038/nature12811 [DOI] [PMC free article] [PubMed] [Google Scholar]