Significance
The intuitive and popular idea of a balance of nature has been criticized, because species interactions may generate nonequilibrium dynamics, such as oscillations and chaos. However, field evidence of chaos in ecosystems is rare. We report on a coastal community that has displayed striking fluctuations in the abundances of barnacles, mussels, and algae for more than 20 y. Data analysis reveals that these fluctuations reflect a cyclic succession alternating between stabilizing and chaotic dynamics during the species replacement. These results are supported by a simple patch-occupancy model, which predicts very similar dynamics when exposed to seasonal variation. Our findings provide a field demonstration of nonequilibrium coexistence of competing species through a cyclic succession at the edge of chaos.
Keywords: chaos, coexistence, cyclic succession, rock–paper–scissors dynamics, rocky intertidal community
Abstract
Although mathematical models and laboratory experiments have shown that species interactions can generate chaos, field evidence of chaos in natural ecosystems is rare. We report on a pristine rocky intertidal community located in one of the world’s oldest marine reserves that has displayed a complex cyclic succession for more than 20 y. Bare rock was colonized by barnacles and crustose algae, they were overgrown by mussels, and the subsequent detachment of the mussels returned bare rock again. These processes generated irregular species fluctuations, such that the species coexisted over many generations without ever approaching a stable equilibrium state. Analysis of the species fluctuations revealed a dominant periodicity of about 2 y, a global Lyapunov exponent statistically indistinguishable from zero, and local Lyapunov exponents that alternated systematically between negative and positive values. This pattern indicates that the community moved back and forth between stabilizing and chaotic dynamics during the cyclic succession. The results are supported by a patch-occupancy model predicting similar patterns when the species interactions were exposed to seasonal variation. Our findings show that natural ecosystems can sustain continued changes in species abundances and that seasonal forcing may push these nonequilibrium dynamics to the edge of chaos.
Since ancient times, it is often argued that undisturbed ecosystems will approach some form of stable equilibrium, at which the populations of the species are maintained at relatively constant numbers (1, 2). However, ecological studies have criticized this idea of “the balance of nature” by pointing out that species abundances in natural ecosystems may remain in a perpetual state of change (3–5). For instance, intransitive competition can lead to a cyclic succession, supporting continued changes in community composition as the dominance is passed on from one species to another in an eternal loop (6–10). Recent theory predicts that seasonal forcing of a cyclic succession can produce quasiperiodic and chaotic species fluctuations (11, 12). Chaos has attracted ecologists’ attention, because it limits the long-term predictability of species abundances (13) and because these nonequilibrium dynamics can potentially sustain a high biodiversity (9). Chaos is predicted by various mathematical models (9, 14–16) and has been found in laboratory experiments with insect populations (17), microbial food webs (18), and plankton communities (5). However, field evidence of chaos in natural ecosystems is rare (19–21) and has never been documented in relation to cyclic succession.
Chaos is commonly described as bounded aperiodic dynamics of a deterministic system that exhibits sensitive dependence on initial conditions (22). Sensitivity to initial conditions implies that small initial differences will grow exponentially in time, such that long-term prediction becomes impossible. In practice, however, a clear distinction between deterministic and stochastic fluctuations is often impossible, because the intrinsic dynamics of natural systems are influenced by exogenous stochastic variation. For instance, species fluctuations are not only caused by competition and predation but also affected by “environmental noise” generated by stochastic variation in weather conditions. During recent decades, considerable advances have been made in the analysis of chaos in the presence of noise (23–25). In particular, sensitive dependence on initial conditions can be estimated for noisy systems using Lyapunov exponents that quantify the extent to which environmental perturbations are amplified (or damped) by the intrinsic dynamics of the system.
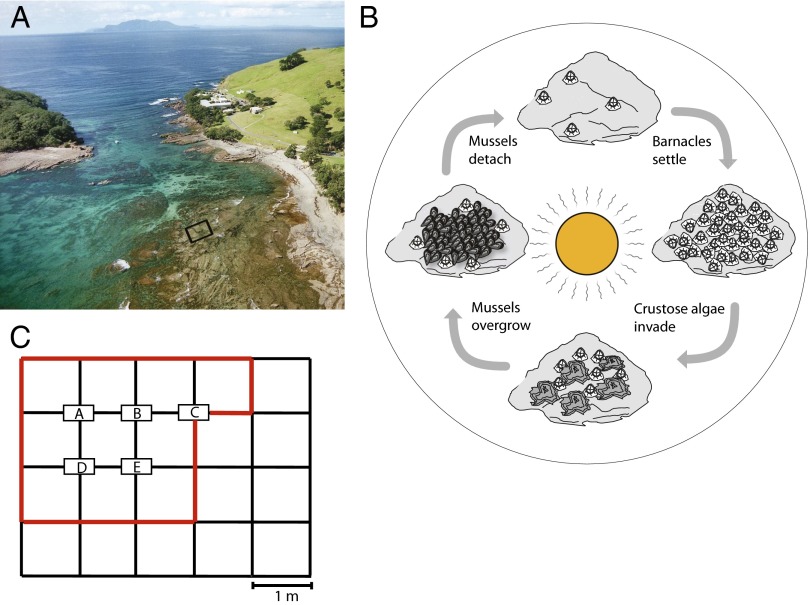
Here, we investigate the species dynamics of a rocky intertidal community in the Cape Rodney-Okakari Point Marine Reserve on the North Island of New Zealand (Fig. 1A). This reserve was established in 1975 as the first marine reserve in New Zealand. It offers ideal conditions for long-term studies of species interactions, because anthropogenic impacts have been kept to a minimum for several decades (26, 27). The rocky intertidal community is dominated by three sessile species: the honeycomb barnacle Chamaesipho columna (Spengler, 1790), the crustose brown alga Ralfsia cf confusa (described as Pseudolithoderma sp. in ref. 28), and the little black mussel Xenostrobus pulex (Lamarck, 1819). Interactions between these species have been described in previous studies (28–30). Barnacles colonize bare rock by gregarious settlement, developing extensive sheets that cover the rocky surface (29). Crustose algae settle on top of the barnacles but do not harm them. Rather, the crustose algae leave space for the barnacles’ waving cirri and benefit from nutrients released by barnacles (28). Xenostrobus mussel larvae cannot settle on smooth bare rock, but they settle gregariously on top of barnacles and crustose algae (29, 30). Xenostrobus mussels subsequently develop a dense carpet, killing the barnacles underneath. After the dead barnacles detach from the underlying rock, the mussel carpet is no longer anchored to any solid surface, and it is washed away by the daily tides (29). Hence, bare rock becomes available again, and the species succession starts anew (Fig. 1B).
Fig. 1.
The rocky intertidal community. (A) Aerial view of the study site at Goat Island Bay. (B) Cyclic succession at the rocky intertidal site. First, barnacles settle on bare rock, and second, crustose algae invade. Third, mussels settle on top of the barnacles and crustose algae, forming a dense carpet that smothers the barnacles and algae underneath. Fourth, the mussels detach, bare rock becomes available again, and the cycle restarts. Drawn by Jan van Arkel (University of Amsterdam, Amsterdam, The Netherlands). (C) Time series were obtained from a permanent grid consisting of 20 plots and five nodes (A–E). The percentages of cover of barnacles, crustose algae, and bare rock were monitored in the plots, whereas mussel cover was estimated from photographs of the nodes. Ten plots and five nodes within the red line were used for the time series analysis.
This paper analyzes the species fluctuations resulting from this hypothesized cyclic succession. Species abundances (expressed as percentage of cover) were monitored on a monthly basis for more than 20 y using a permanent grid (Fig. 1C and SI Appendix, Figs. S1–S5). We use the time series to determine common periodicities in the species fluctuations indicative of a cyclic succession and estimate local and global Lyapunov exponents as indicators of the potential presence of chaos. Finally, we compare the obtained results against a simple patch-occupancy model to assess whether the species interactions described above can, indeed, produce a cyclic succession characterized by chaotic species fluctuations.
Results
Time Series Analysis.
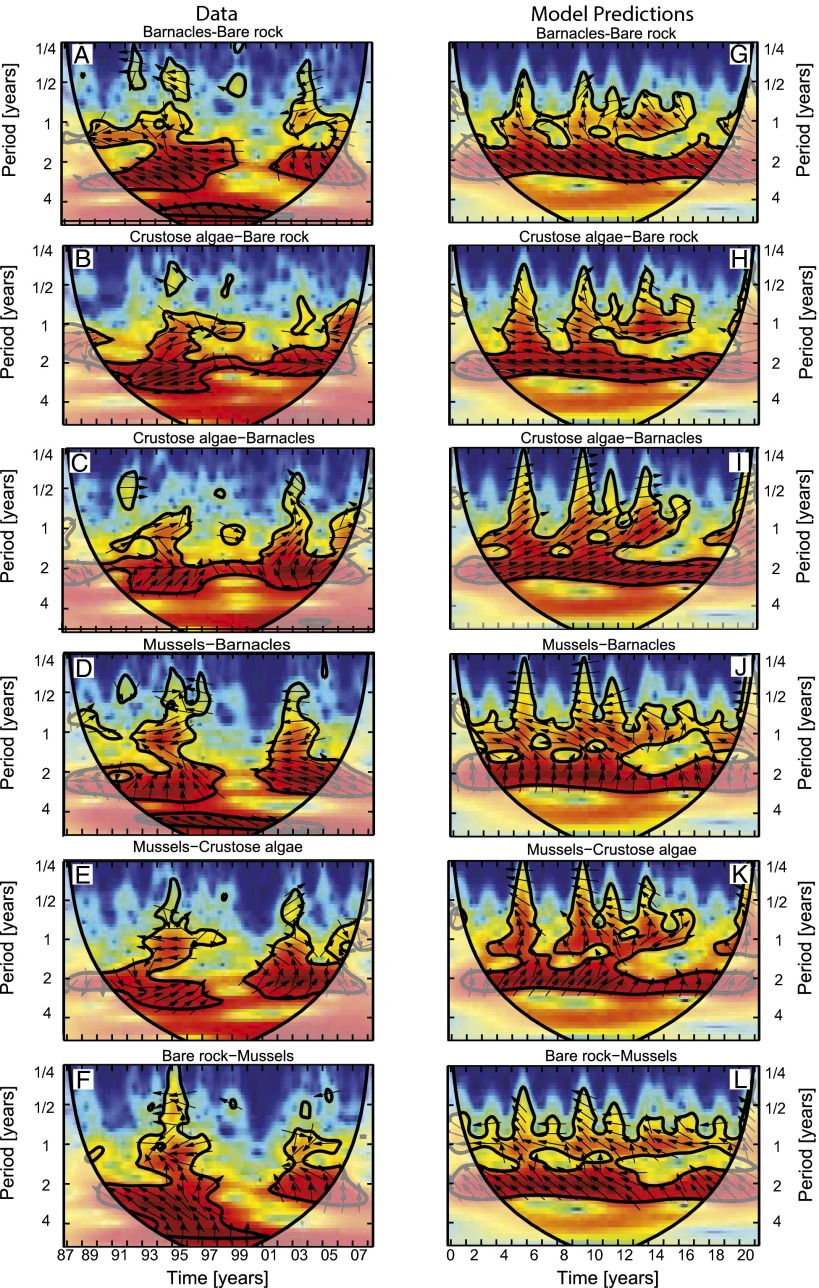
The species showed striking fluctuations (Fig. 2). In some years, the rocks were almost completely covered by barnacles, whereas in other years, crustose algae or mussels dominated the ecosystem. To investigate these species fluctuations in further detail, we first applied cross-wavelet analysis (31) to analyze common periodicities and phase delays in a pairwise comparison of the species. Cross-wavelet spectra revealed a dominant periodicity of ∼2 y in the fluctuations of all species pairs (Fig. 3 A–F). Arrows in Fig. 3 in significant regions of the cross-wavelet spectrum of barnacles and bare rock represent phase angles of 90–180° (Fig. 3A), indicating that it took 6–12 mo for barnacles to fully colonize the bare rock. Likewise, the cross-wavelet spectrum of mussels and barnacles showed phase angles of 90–180° (Fig. 3D), indicating that it also took 6–12 mo for mussels to form a dense carpet covering the barnacles. The crustose algae seemed to act as coplayers, tracking the barnacles with a delay of a few months and disappearing when the mussels formed a dense carpet (Figs. 2 B–D and 3 C and E). Arrows in Fig. 3 in the cross-wavelet spectrum of bare rock and mussels pointed mainly upwards (Fig. 3F), indicating that dense mussel carpets gave way to bare rock in ∼6 mo, and the cycle could start anew. Hence, cross-wavelet analysis confirmed the cyclic nature of the species succession, with bare rock → barnacles and crustose algae → mussels → bare rock.
Fig. 2.
Time series observations of (A) sea surface temperature, (B) barnacles, (C) crustose algae, (D) mussels, and (E) bare rock.
Fig. 3.
Cross-wavelet spectra of all species pairs. Cross-wavelet spectra of (A–F) the observed time series (Fig. 2 B–E) and (G–L) the model predictions (Fig. 5 H–K). The spectra show how common periodicities in the fluctuations of two species (y axis) change over time (x axis). Color indicates cross-wavelet power (from low power in blue to high power in red), which measures to what extent the fluctuations of the two species are related. Black contour lines enclose significant regions, with >95% confidence that cross-wavelet power exceeds red noise. Arrows indicate phase angles between the fluctuations of the two species. Arrows pointing right represent in-phase oscillations (0°), and arrows pointing upward indicate that the first species lags the second species by a quarter period (90°). Shaded areas on both sides represent the cone of influence, where edge effects may distort the results.
However, this cyclic species replacement produced quite irregular species fluctuations. We, therefore, estimated global and local Lyapunov exponents to assess the potential presence of chaos in the time series data. A positive Lyapunov exponent indicates divergence of nearby trajectories, which is widely regarded as the hallmark of chaos (22). The global Lyapunov exponent is concerned with the average rate of trajectory divergence (convergence) over the entire attractor of the dynamical system, whereas local Lyapunov exponents measure the rate of trajectory divergence (convergence) over only a short stretch of time. The Lyapunov exponents were estimated from the Jacobian matrices of a generalized additive model (GAM) (32) fitted to the data to estimate the deterministic skeleton of the dynamics (5, 23, 33). This analysis yielded a positive global Lyapunov exponent of λ = +1.1 y−1 (with a two-sided 95% bootstrap confidence interval of −0.18 to +2.39 y−1) that did not differ significantly from zero. However, the local Lyapunov exponents alternated between positive and negative values (Fig. 4). These results indicate that the community dynamics were at the edge of chaos, shifting back and forth between chaotic and stabilizing dynamics during the cyclic succession.
Fig. 4.
Time series of the local Lyapunov exponent (LLE). The LLE is calculated as the average rate of trajectory divergence (or convergence) over a time span of 180 d.
Patch-Occupancy Model.
The multiannual periodicity, the phase relationships between the species, and the global and local Lyapunov exponents all suggest that the cyclic interactions in this system generated complex dynamics. To test this hypothesis further, we built a simple patch-occupancy model (34, 35) based on the species interactions in this intertidal community (Fig. 1B). The model can be interpreted as the mean field approximation of a stochastic spatial model (36) that describes the rocky habitat as a large set of small patches, each of which can be occupied by a single individual. Let B0 be the cover (i.e., the fraction of patches occupied) by barnacles without crustose algae, and let BA be the cover by barnacles overgrown with crustose algae. Furthermore, let A be the coverage by crustose algae, let M be the coverage by mussels, and let R be the coverage by bare rock. The model reads (SI Appendix)
| [1] |
| [2] |
| [3] |
| [4] |
| [5] |
where cBR is the colonization rate of barnacles on bare rock; cAB and cAR are the colonization rates of crustose algae on barnacles and bare rock, respectively; cM is the colonization rate of mussels on barnacles and crustose algae; and mB, mA, and mM are the mortality rates of barnacles, crustose algae, and mussels, respectively.
The crusts of crustose algae and carpets of black mussels at our study site were sensitive to desiccation during warm days in summer (29), whereas barnacles seemed less temperature-sensitive. Mortality rates of mussels and crustose algae were, therefore, forced by seasonal temperature fluctuations (Fig. 2A), with high mortality in summer and low mortality in winter:
| [6] |
where the scaling coefficient α represents the strength of seasonal forcing, Tmean is the mean annual sea surface temperature of 17.1 °C measured at the research site, and Tmax is the temperature of 20.5 °C measured at the warmest day of the year (February 1; i.e., at t = 32 d).
Without seasonality, the model predicts damped species oscillations, with a periodicity of ∼1.5 y, that gradually converge to a stable coexistence equilibrium (Fig. 5 A–F). In contrast, regular seasonal forcing of the community dynamics induced sustained species fluctuations in a chaotic fashion (Fig. 5 G–L). These results are confirmed by a bifurcation analysis, which shows stable equilibrium without seasonal forcing, periodic community dynamics for weak seasonal forcing, and chaotic dynamics for strong seasonal forcing (SI Appendix, Fig. S15).
Fig. 5.
Model simulations with the patch-occupancy model. (A–E) Without seasonal forcing, the species show damped oscillations that eventually settle down to equilibrium, and (F) the attractor is a stable spiral point. (G–K) With seasonal forcing, the species show sustained irregular oscillations characterized by (L) a strange attractor typical of chaotic systems. For the seasonally forced simulations, the first 30 y were discarded to remove initial transients. The chaotic attractor in L was obtained by running the model for 100 y. Parameter values are provided in SI Appendix, Table S1.
The patch-occupancy model is clearly too simple for accurate quantitative prediction of the observations. Qualitatively, however, cross-wavelet analysis of the seasonally forced model simulations revealed similar features as the cross-wavelet spectra of the real data, with a similar dominant periodicity of ∼2 y and similar phase relationships (compare Fig. 3 G–L with Fig. 3 A–F). Calculation of the Lyapunov exponent for 1,000 simulated time series of 21 y generated by the patch-occupancy model yielded a positive average value of λ = +0.82 y−1 (with 95% of values in the interval of +0.17 to +1.50 y−1), which is strikingly similar to the value estimated for the observed time series. Moreover, the local Lyapunov exponents predicted by the model also alternated between positive and negative values (SI Appendix, Fig. S12). Hence, qualitatively, the main features of the observed complex cyclic succession were captured quite well by a simple patch-occupancy model with seasonal forcing.
Discussion
Our findings show that natural ecosystems can sustain a complex cyclic succession for many years. The cycle starts with bare rock, which serves as substrate for barnacles and to a lesser extent, crustose algae as well but not Xenostrobus mussels, which cannot settle on the smooth rocky surface. In turn, the established barnacles provide suitable substrate for the crustose algae and mussels. The mussels take over and smother the barnacles underneath. After the barnacles are killed, the mussel carpet detaches from the underlying rock, and bare rock becomes available again. These replacements lead to a cyclic succession (Fig. 1B), in which all three species are sustained, but none of the species can stabilize its population. Because these matrix-forming sessile species provide the template on which the community is built, the continued alternations in their species composition are likely to have major implications for many other species (e.g., chitons, limpets, sea stars, and whelk) inhabiting these rocky intertidal communities.
Cyclic species fluctuations are not necessarily driven by deterministic processes. In fact, in many rocky intertidal communities, the mussel cover is occasionally disrupted by strong storms and other major disturbances that clear the mussel dominance and reset the succession (37–39). Such recurrent external disturbances can be a main driver of irregular species fluctuations (40). An interesting example is provided by a recent study of the mussel Mytilus californianus, in which disturbances had a particularly strong effect at high mussel abundance, a phenomenon that was called density-linked stochasticity (41). However, our mussel species, X. pulex, is a small mussel that forms compact mats that are never more than one individual thick and closely packed. As a consequence, mussel mats of X. pulex offer very little resistance to lateral water movement. Even after the largest storms, we never saw any damage or disturbance to mussel mats in our study area. This observation is confirmed by the data, which did not reveal distinct population crashes at high mussel abundance and showed that the loss of mussel dominance was not related to storms or wave action (SI Appendix, Figs. S6–S9). Instead, disappearance of the mussels was a gradual process that took several weeks to months (SI Appendix, Fig. S8). In line with previous studies (29), we observed that the dense carpet of Xenostrobus mussels gradually peeled off after the parietal plates of the dead barnacles detached from the underlying rock. Dislodged pieces of mussel carpet were carried away by the daily tidal motion. Hence, rather than a stochastic process induced by storms, in our study, the loss of mussel dominance seems to be a largely deterministic process in which mussels kill the underlying barnacles, which subsequently leads to dislodgement of the dead barnacles and the mussels attached to them.
We also investigated the possible impact of other sources of stochasticity, such as the role of environmental noise generated by the observed day-to-day temperature fluctuations. Forcing the patch-occupancy model with both daily and seasonal temperature variation produced similar dynamical behavior as seasonality only (SI Appendix, Fig. S14). Hence, according to the patch-occupancy model, seasonal environmental forcing is a major driver of the observed species fluctuations, whereas stochastic environmental noise in the form of daily temperature fluctuations enhanced the variability but did not alter the main qualitative dynamical features of the cyclic succession.
The robustness of our results was further investigated in various ways. For instance, we tested the ability of GAMs to estimate Lyapunov exponents from artificially generated noisy time series with similar features as our data, which showed that our approach can successfully identify the transition from noisy periodic dynamics to noisy chaos (SI Appendix, Fig. S15). Furthermore, additional analyses show that qualitatively similar results are obtained if (i) air temperature instead of water temperature is used as the environmental forcing variable and (ii) the patch-occupancy model is extended with a small density-independent influx of barnacle, algal, and mussel recruits (SI Appendix, Figs. S16–S18).
The observed cyclic succession resembles rock–paper–scissors (RPS) dynamics, a game-theoretical concept producing a cyclic succession as rock beats scissors, scissors beats paper, and paper beats rock (8). RPS dynamics has been reported for several other ecological systems (7, 42–44). In these ecological examples, the different strategies in the RPS game are usually represented by different species or phenotypes actively outcompeting each other in a cyclic fashion. In contrast, the RPS dynamics in our system contain real rock as one of the successional stages. Of course, our rock does not actively exclude other species. Instead, the rocky surface becomes dominant in a passive fashion as the mussel carpet gradually peels off after it has killed the barnacles and crustose algae underneath, thereby providing new substrate for the recolonization by barnacles and thus, turning the dynamics into a cyclic pattern.
Our results differ from a classic example of RPS dynamics among Escherichia coli bacteria on agar plates, where local dispersal and spatial pattern formation were essential to sustain the cyclic succession (43). In our system, mussels and barnacles produce planktonic larvae that can be dispersed over large distances, and the sessile life stages were almost uniformly distributed across the entire observation grid (SI Appendix, Figs. S2–S5). Instead of pattern formation by local dispersal, seasonal forcing seemed to provide the flywheel driving the cyclic succession. Interestingly, seasonal forcing of the community dynamics generated complex rather than regular species fluctuations. Hence, our results provide field evidence for the recent theoretical prediction (11, 12) that seasonal forcing can push a cyclic succession into a quasiperiodic and chaotic regime.
It is known that nonlinear systems can have very long chaotic transients before they settle at a stable equilibrium (25, 45). Could our data be an example? We can never be certain if an ecosystem's observed behavior will persist past the period of observation; the best that we can do is make projections by modeling the processes underlying the dynamics. In our case, the patch-occupancy model always settles onto a chaotic attractor when seasonal forcing becomes strong enough. This behavior suggests that our data show persistent chaos and not just a decades-long transient.
However, our data do not show full-blown chaos. Instead, we found a near-zero global Lyapunov exponent and local Lyapunov exponents that varied systematically between negative and positive values. These results provide an intriguing example of a biological system at the edge of chaos, alternating between stabilizing and chaotic dynamics during cyclic changes in species composition. In natural systems exposed to environmental variation, this situation produces irregular and effectively chaotic population trajectories, because environmental noise is amplified whenever the local Lyapunov exponent is positive. Similar shifts between chaotic and stabilizing dynamics have also been observed in measles epidemics of large cities (46) and the population fluctuations of voles in northern Fennoscandia (21), although our study is probably the first report, to our knowledge, in a multispecies context. These observations suggest that dynamic transitions between irregularity and order might be quite common in ecosystems and perhaps, especially in multispecies communities where sessile species overgrow their neighbors (e.g., in rocky intertidal communities, coral reefs, microbial biofilms, and terrestrial vegetation). Long-term studies of species fluctuations in natural ecosystems are exceptional. However, our findings illustrate that such studies are essential to improve our understanding of the complex community dynamics in the myriad ecosystems characterizing our planet.
Materials and Methods
Data.
The study was located at Goat Island Bay (36°16′ S, 174°48′ E) in the Cape Rodney-Okakari Point Marine Reserve on the North Island of New Zealand. Species abundances, expressed as percentage of cover, were sampled on an approximately monthly basis using a permanent grid consisting of 20 plots of 1 m2 each and five nodes of 0.15 m2 each (Fig. 1C). Percentages of cover of barnacles, crustose algae, and bare rock were estimated in the plots, whereas mussel cover was estimated from photographs of the nodes. Species fluctuations were highly synchronous across all 20 plots of the entire permanent grid (SI Appendix, Figs. S2–S5). For consistency, however, we decided to use data only from 10 plots adjacent to five nodes in our time series analysis. A weather station provided daily records of sea surface temperature, wave height, and wind run. The species and weather data are provided in Dataset S1.
Global and Local Lyapunov Exponents.
The Lyapunov exponent for environmentally forced systems is also known as the “conditional Lyapunov exponent.” Conditional Lyapunov exponents measure trajectory divergence (or convergence) caused by the intrinsic dynamics of a system when exposed to external forcing (21). We used a Jacobian method (5, 23, 33) to estimate conditional Lyapunov exponents of the time series. Jacobian methods are based on the development of a deterministic model (also called the deterministic skeleton) that captures the intrinsic dynamics of the system.
We used our deterministic skeleton as a statistical model that merely served to describe the observed dynamics with a minimum number of biological assumptions. In discrete time, a deterministic model of our community can be written as a system of four difference equations describing the dynamics of barnacles (B), algae (A), mussels (M), and bare rock (R) forced by the observed temperature fluctuations. However, this 4D system resulted in an overspecified model, because the summed percentage of cover of barnacles, mussels, and bare rock remained near 100%. Hence, we removed bare rock as a model variable to simplify the model to a forced 3D system:
| [7] |
| [8] |
| [9] |
where Tt is the temperature at time t, Δt is the time step of the model, and the function fi (with i = B, A, M) describes the changes in percentage of cover of the species. This general model makes few biological assumptions but does take into account observations at our research site that crustose algae and mussels were sensitive to temperature, whereas barnacles were not (29). The model used the same time step of Δt = 30 d as the time series data.
We applied GAMs (32) with thin-plate spline functions using the mgcv package of R, version 3.01 to estimate the unknown function fi for each species. The GAMs included main effects of the three species and pairwise interaction terms, with temperature as a covariate in the models for algae and mussels. Complexity of the spline functions was selected by generalized cross-validation 1.8 (GCV1.8), a modification of the GCV criterion, in which model degrees of freedom were overweighted by a factor of 1.8 to avoid overfitting (33). The GAMs captured the observed time series well (SI Appendix, Fig. S10).
The global conditional Lyapunov exponent, λ, was calculated from the Jacobian matrices J1, …, JN of the model evaluated along the observed time series trajectory (23):
| [10] |
where N is the number of data points in the time series, || || is the Euclidean vector norm, and v0 is a unit vector. The Jacobian matrices include partial derivatives with respect to the intrinsic variables B, A, and M, whereas external forcing by temperature is incorporated by evaluating these Jacobian matrices at the data points (Bj, Aj, Mj, and Tj, where j = 1, …, N) of the time series. Thus, the global conditional Lyapunov exponent measures the extent to which the intrinsic dynamics amplify or dampen the effects of external temperature fluctuations. Time series of the nine elements in the Jacobian matrix are shown in SI Appendix, Fig. S11.
Local Lyapunov exponents (21, 23, 47) were also calculated from Eq. 10. Whereas the global Lyapunov exponent measures the average trajectory divergence over the entire length of the time series, local Lyapunov exponents measure local trajectory divergence over only a short stretch of the time series. In our case, the local Lyapunov exponent calculated the local trajectory divergence over 180 d, which corresponded to six consecutive data points (N = 6) at time intervals of Δt = 30 d.
Additional details on the calculation of Lyapunov exponents and their confidence intervals are provided in SI Appendix.
Patch-Occupancy Model.
Parameter values of the patch-occupancy model were estimated from the time series (SI Appendix, Fig. S13 and Table S1). All model simulations were performed in Matlab (The Mathworks) using an Euler solver with a time step of 0.1 d.
Supplementary Material
Acknowledgments
We thank the many people who assisted with the collection of the time series over the years. We also thank the reviewers for constructive comments, M. J. Kehoe for discussions on the patch-occupancy model, J. van Arkel for drawing Fig. 1B, and M. Ballantine for help with SI Appendix, Fig. S1. J.H. thanks the Turner-Kirk Charitable Trust for supporting his sabbatical at the Isaac Newton Institute of the University of Cambridge. The research of E.B. and J.H. was supported by the Division of Earth and Life Sciences of the Netherlands Organization for Scientific Research (NWO). The research of S.P.E. is supported by National Science Foundation Grants DEB-1353039 and DEB-1256719.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. A.H. is a guest editor invited by the Editorial Board.
See Commentary on page 6252.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1421968112/-/DCSupplemental.
References
- 1.Egerton FN. Changing concepts of the balance of nature. Q Rev Biol. 1973;48(2):322–350. [Google Scholar]
- 2.Zimmerman C, Cuddington K. Ambiguous, circular and polysemous: Students’ definitions of the “balance of nature” metaphor. Public Underst Sci. 2007;16(4):393–406. [Google Scholar]
- 3.Elton CS. Animal Ecology and Evolution. Clarendon; Oxford: 1930. [Google Scholar]
- 4.Pimm SL. The Balance of Nature? Ecological Issues in the Conservation of Species and Communities. Univ of Chicago Press; Chicago: 1991. [Google Scholar]
- 5.Benincà E, et al. Chaos in a long-term experiment with a plankton community. Nature. 2008;451(7180):822–825. doi: 10.1038/nature06512. [DOI] [PubMed] [Google Scholar]
- 6.May RM, Leonard WJ. Nonlinear aspects of competition between three species. SIAM J Appl Math. 1975;29(2):243–253. [Google Scholar]
- 7.Buss LW, Jackson JBC. Competitive networks: Nontransitive competitive relationships in cryptic coral reef environments. Am Nat. 1979;113(2):223–234. [Google Scholar]
- 8.Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge Univ Press; Cambridge, United Kingdom: 1998. [Google Scholar]
- 9.Huisman J, Weissing FJ. Biodiversity of plankton by species oscillations and chaos. Nature. 1999;402(6760):407–410. [Google Scholar]
- 10.Laird RA, Schamp BS. Competitive intransitivity promotes species coexistence. Am Nat. 2006;168(2):182–193. doi: 10.1086/506259. [DOI] [PubMed] [Google Scholar]
- 11.Rand RH, Yazhbin M, Rand DG. Evolutionary dynamics of a system with periodic coefficients. Commun Nonlinear Sci Numer Simul. 2011;16(10):3887–3895. [Google Scholar]
- 12.Ruelas RE, Rand DG, Rand RH. Nonlinear parametric excitation of an evolutionary dynamical system. Proc Inst Mech Eng C. 2012;226(8):1912–1920. [Google Scholar]
- 13.Hastings A, Hom CL, Ellner S, Turchin P, Godfray HCJ. Chaos in ecology: Is mother nature a strange attractor? Annu Rev Ecol Syst. 1993;24:1–33. [Google Scholar]
- 14.May RM. Stability and Complexity in Model Ecosystems. Princeton Univ Press; Princeton: 1973. [PubMed] [Google Scholar]
- 15.Hastings A, Powell T. Chaos in a three-species food chain. Ecology. 1991;72(3):896–903. [Google Scholar]
- 16.Vandermeer J. Loose coupling of predator-prey cycles: Entrainment, chaos, and intermittency in the classic MacArthur consumer-resource equations. Am Nat. 1993;141(5):687–716. [Google Scholar]
- 17.Costantino RF, Desharnais RA, Cushing JM, Dennis B. Chaotic dynamics in an insect population. Science. 1997;275(5298):389–391. doi: 10.1126/science.275.5298.389. [DOI] [PubMed] [Google Scholar]
- 18.Becks L, Hilker FM, Malchow H, Jürgens K, Arndt H. Experimental demonstration of chaos in a microbial food web. Nature. 2005;435(7046):1226–1229. doi: 10.1038/nature03627. [DOI] [PubMed] [Google Scholar]
- 19.Tilman D, Wedin D. Oscillations and chaos in the dynamics of a perennial grass. Nature. 1991;353(6345):653–655. [Google Scholar]
- 20.Hanski I, Turchin P, Korpimäki E, Henttonen H. Population oscillations of boreal rodents: Regulation by mustelid predators leads to chaos. Nature. 1993;364(6434):232–235. doi: 10.1038/364232a0. [DOI] [PubMed] [Google Scholar]
- 21.Turchin P, Ellner SP. Living on the edge of chaos: Population dynamics of Fennoscandian voles. Ecology. 2000;81(11):3099–3116. [Google Scholar]
- 22.Strogatz SH. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Perseus; Cambridge, MA: 1994. [Google Scholar]
- 23.Ellner S, Turchin P. Chaos in a noisy world: New methods and evidence from time-series analysis. Am Nat. 1995;145(3):343–375. [Google Scholar]
- 24.Turchin P. Complex Population Dynamics: A Theoretical/Empirical Synthesis. Princeton Univ Press; Princeton: 2003. [Google Scholar]
- 25.Lai YC, Tél T. Transient Chaos: Complex Dynamics on Finite Time Scales. Springer; New York: 2011. [Google Scholar]
- 26.Ballantine WJ, Langlois TJ. Marine reserves: The need for systems. Hydrobiologia. 2008;606(1):35–44. [Google Scholar]
- 27.Ballantine B. Fifty years on: Lessons from marine reserves in New Zealand and principles for a worldwide network. Biol Conserv. 2014;176:297–307. [Google Scholar]
- 28.Williamson JE, Rees TAV. Nutritional interaction in an alga-barnacle association. Oecologia. 1994;99(1-2):16–20. doi: 10.1007/BF00317078. [DOI] [PubMed] [Google Scholar]
- 29.Luckens PA. Competition and intertidal zonation of barnacles at Leigh, New Zealand. N Z J Mar Freshw Res. 1975;9(3):379–394. [Google Scholar]
- 30.Novak M. Estimating interaction strengths in nature: Experimental support for an observational approach. Ecology. 2010;91(8):2394–2405. doi: 10.1890/09-0275.1. [DOI] [PubMed] [Google Scholar]
- 31.Grinsted A, Moore JC, Jevrejeva S. Application of cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process Geophys. 2004;11(5/6):561–566. [Google Scholar]
- 32.Wood SN. Generalized Additive Models: An Introduction with R. Chapman & Hall/CRC; Boca Raton, FL: 2006. [Google Scholar]
- 33.Nychka D, Ellner S, Gallant AR, McCaffrey D. Finding chaos in noisy systems. J R Stat Soc Series B Stat Methodol. 1992;54(2):399–426. [Google Scholar]
- 34.Hastings A. Disturbance, coexistence, history, and competition for space. Theor Popul Biol. 1980;18(3):363–373. [Google Scholar]
- 35.Tilman D. Competition and biodiversity in spatially structured habitats. Ecology. 1994;75(1):2–16. [Google Scholar]
- 36.Durrett R, Levin SA. Stochastic spatial models: A user's guide to ecological applications. Philos Trans R Soc Lond B Biol Sci. 1994;343(1305):329–350. [Google Scholar]
- 37.Dayton PK. Competition, disturbance, and community organization: The provision and subsequent utilization of space in a rocky intertidal community. Ecol Monogr. 1971;41(4):351–389. [Google Scholar]
- 38.Lubchenco J, Menge BA. Community development and persistence in a low rocky intertidal zone. Ecol Monogr. 1978;48(1):67–94. [Google Scholar]
- 39.Paine RT, Levin SA. Intertidal landscapes: Disturbance and the dynamics of pattern. Ecol Monogr. 1981;51(2):145–178. [Google Scholar]
- 40.Wootton JT. Local interactions predict large-scale pattern in empirically derived cellular automata. Nature. 2001;413(6858):841–844. doi: 10.1038/35101595. [DOI] [PubMed] [Google Scholar]
- 41.Wootton JT, Forester JD. Complex population dynamics in mussels arising from density-linked stochasticity. PLoS ONE. 2013;8(9):e75700. doi: 10.1371/journal.pone.0075700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sinervo B, Lively CM. The rock-paper-scissors game and the evolution of alternative male strategies. Nature. 1996;380(6571):240–243. [Google Scholar]
- 43.Kerr B, Riley MA, Feldman MW, Bohannan BJM. Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors. Nature. 2002;418(6894):171–174. doi: 10.1038/nature00823. [DOI] [PubMed] [Google Scholar]
- 44.Cameron DD, White A, Antonovics J. Parasite-grass-forb interactions and rock-paper-scissor dynamics: Predicting the effects of the parasitic plant Rhinanthus minor on host plant communities. J Ecol. 2009;97(6):1311–1319. [Google Scholar]
- 45.Hastings A. Transients: The key to long-term ecological understanding? Trends Ecol Evol. 2004;19(1):39–45. doi: 10.1016/j.tree.2003.09.007. [DOI] [PubMed] [Google Scholar]
- 46.Ellner SP, et al. Noise and nonlinearity in measles epidemics: Combining mechanistic and statistical approaches to population modeling. Am Nat. 1998;151(5):425–440. doi: 10.1086/286130. [DOI] [PubMed] [Google Scholar]
- 47.Abarbanel HDI, Brown R, Kennel MB. Local Lyapunov exponents computed from observed data. J Nonlinear Sci. 1992;2(3):343–365. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.