Electric-field–induced assembly and propulsion of chiral colloidal clusters

Significance

Although colloids have been used as molecular analogues for understanding how simple building blocks can assemble into functional materials, they are mostly spherical with isotropic properties. We are still far from truly accessing the diversity of structures desired for either fundamental understanding or technological application. Here, we report the electric-field–directed assembly of asymmetric colloids into clusters that exhibit a ubiquitous type of symmetry in nature: the chirality. We further demonstrate that the chirality induces unbalanced hydrodynamic flow, which causes rotational propulsion of chiral clusters that are fully dictated by their handedness. Both the assembly and propulsion mechanisms discovered can be universal and applied to other types of asymmetric particles. They are also useful in modeling active matter and making microengines.

Abstract

Chiral molecules with opposite handedness exhibit distinct physical, chemical, or biological properties. They pose challenges as well as opportunities in understanding the phase behavior of soft matter, designing enantioselective catalysts, and manufacturing single-handed pharmaceuticals. Microscopic particles, arranged in a chiral configuration, could also exhibit unusual optical, electric, or magnetic responses. Here we report a simple method to assemble achiral building blocks, i.e., the asymmetric colloidal dimers, into a family of chiral clusters. Under alternating current electric fields, two to four lying dimers associate closely with a central standing dimer and form both right- and left-handed clusters on a conducting substrate. The cluster configuration is primarily determined by the induced dipolar interactions between constituent dimers. Our theoretical model reveals that in-plane dipolar repulsion between petals in the cluster favors the achiral configuration, whereas out-of-plane attraction between the central dimer and surrounding petals favors a chiral arrangement. It is the competition between these two interactions that dictates the final configuration. The theoretical chirality phase diagram is found to be in excellent agreement with experimental observations. We further demonstrate that the broken symmetry in chiral clusters induces an unbalanced electrohydrodynamic flow surrounding them. As a result, they rotate in opposite directions according to their handedness. Both the assembly and propulsion mechanisms revealed here can be potentially applied to other types of asymmetric particles. Such kinds of chiral colloids will be useful for fabricating metamaterials, making model systems for both chiral molecules and active matter, or building propellers for microscale transport.

Chirality is a fundamental concept presented ubiquitously in the molecular world. For example, small molecules such as the amino acids, phospholipids, and sugars with specific handedness build many biomacromolecules whose chirality is essential to living organisms. Although the right- and left-handed molecules are identical in chemical composition, the catalytic activity (1), pharmacological impact (2, 3), biological recognition (4), and optical response (5) can be strikingly different. Extending the chiral structure to microscopic objects such as colloids has become increasingly desirable for several reasons. First, the chiral arrangement of colloidal particles can exhibit unusually strong optical, electric, and magnetic responses (6–10) that are not manifested either at the single-particle level or in achiral forms. Therefore, chiral clusters can be potentially used to build metamaterials (11–14) with exotic properties or sensors for detection of molecules. Second, chiral particles can be conveniently characterized by real-time optical microscopy. As the macroscopic analog of chiral molecules, they can be used to study fundamental questions related to the crystallization (15) or enantiomeric separation (16, 17) of a racemic mixture. Last but not least, chiral structures have been extensively exploited by microorganisms (18, 19) for locomotion in their typically low Reynolds number environment. Artificial motors with similar structures (20) that can propel through fluids could revolutionize many modern technologies, including targeted drug delivery (21–23), cell manipulation (24), miniaturized surgeons (25), and self-assembly of superstructures (26). In addition, driven propulsion of concentrated chiral colloidal clusters could also serve as a well-controlled system for the study of collective behavior of active matter (27, 28).

Current strategies to make chiral structures are primarily based on photo or E-beam lithography (29, 30), glancing-angle deposition (31), chemical etching (32), or templating methods using chiral molecules such as DNA (33). Nature, however, assembles simple and achiral building blocks into chiral structures with exquisite functionality. Although challenging, such a capability is desirable for making functional materials efficiently. As illustrated by several theoretical studies recently (34–36), particles with anisotropic interactions could potentially offer an appealing route. Here we report our work using alternating current (AC) electric fields to direct the assembly of achiral building blocks, i.e., asymmetric colloidal dimers, into chiral clusters. Interestingly, the broken symmetry in chiral clusters also results in an unbalanced electrohydrodynamic flow surrounding them. They behave like micropropellers and rotate in opposite directions according to their handedness.

Results and Discussion

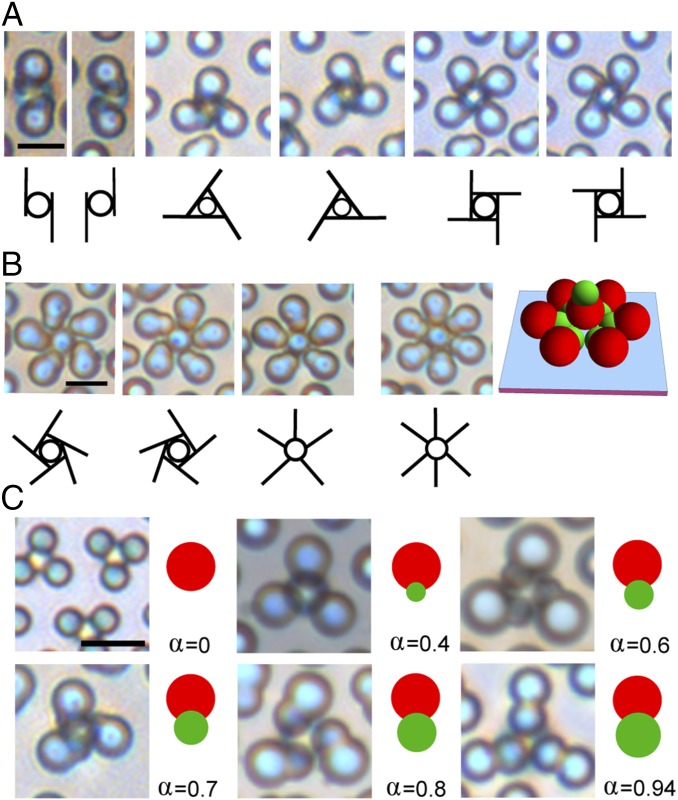
Fig. 1A, Inset shows the building blocks that we use in experiments. They are synthetic polystyrene dimers with asymmetric lobes ($R_1$ = 1.27 µm and $R_2$ = 0.89 µm) (37). An aqueous suspension (in deionized water) of dimers is sandwiched between top and bottom indium-tin-oxide (ITO) glasses, which are separated by a gap of ∼100 µm. An AC electric field is then applied across the gap (see Materials and Methods for more details). Fig. 1A shows a representative picture where dimers are subjected to a perpendicular electric field of 11 V_pp/100 µm and 600 Hz. The field strength is high enough to align some dimers with the field direction (e.g., the standing dimers highlighted in red circles), whereas others keep lying on the substrate (in the blue circles). The fact that not all dimers align with the applied field can be attributed to the attractive interaction between dimers and the electrode through the “dipole-image dipole” force (37, 38). A major part of the image is, however, filled with clusters assembled by several dimers. Fig. 1 B and C shows sequential z scans of two such clusters. Combined with the geometric parameters of the asymmetric dimers, these images allow us to reconstruct the 3D configurations of both clusters. Each one is essentially composed of four dimers, with three of them lying on the substrate, forming the “petals.” Each of the lying dimers points its small lobe toward the center and almost contacts its neighbors tangentially. The petals associate closely with a central standing dimer that is lifted from the substrate. Such a unique packing allows the formation of chiral clusters. Depending on the rotation direction of the petals, we designate the tetrameric clusters in Fig. 1 B and C as a right-handed and a left-handed cluster, respectively. Clearly, each tetramer cannot be mapped on its mirror image by planar rotation and translation. Although the chirality is primarily determined by the arrangement of the lying dimers, we also find that the central standing dimer in all chiral clusters always orients its small lobe toward the substrate.

Fig. 1.

Chiral colloidal clusters assembled from asymmetric dimers under AC electric fields (peak-to-peak voltage $V_{pp}=$ 11 V and $\omega =$ 600 Hz). (A) A large field of view of chiral tetramers. (A, Inset) SEM image showing the asymmetric dimer building blocks. (Scale bar: 5 µm.) (B and C) z scans (unit: micrometers, moving away from the bottom substrate) of the right- and left-handed chiral tetramers, respectively.

The chiral clusters are not just limited to tetramers. As shown in Fig. 2A, clusters with two, three, and four petals are also observed with approximately equal populations of right and left handedness. Clusters can still be formed when the number of petals increases to five and six, as shown in Fig. 2B. However, the chirality becomes ill-defined. For example, although a few chiral clusters with five petals can be observed, achiral clusters are more commonly found. In comparison, all clusters with four or fewer petals are chiral. With six petals in a cluster, we observe only achiral clusters. Moreover, our z-scan images reveal that the central dimer in those clusters orients its large lobe toward the substrate, as shown by the schematic in Fig. 2B. Although we have observed colloidal tetramers assembled from spherical particles before (39), those clusters intrinsically possess rotational symmetry and are achiral. Therefore, it is reasonable to infer that the chirality we observe here arises from the geometric asymmetry of dimer particles. Shown in Fig. 2C are clusters formed from asymmetric dimers synthesized with a wide range of aspect ratios. Not surprisingly, the resulting clusters are chiral only for intermediate values of aspect ratios. When the aspect ratio $R_2/R_1$ approaches zero (i.e., a sphere) or one (i.e., a symmetric dimer), the chirality disappears.

Fig. 2.

The chirality depends on both the geometry and orientation of dimers. (A) Chiral clusters (trimer, tetramer, and pentamer) with an increasing number of petals. The central dimer orients its small lobe toward the substrate. (B) Chiral/achiral clusters with five and six petals. The central dimer orients its large lobe toward the substrate. (C) Colloidal tetramers formed from dimers with different aspect ratios, $\alpha =R_2/R_1$. (Scale bars for A–C: 5 µm.)

A fundamental question to address is what drives the assembly of achiral building blocks (i.e., the dimers) into chiral clusters. Movie S1 shows the dynamic formation of chiral clusters. Upon the application of an AC electric field in the low-frequency regime (200 Hz $<\omega <$ 2,000 Hz), lying dimers are attracted one by one to a central standing dimer that is slightly lifted from the substrate (i.e., out of focus). This initial attraction from a distance is likely caused by the electrohydrodynamic (EHD) flow of solvent (40, 41). The applied AC field induces mobile charges near the electrode. The field-induced dipole on the dimer perturbs the vertically applied electric field and generates a locally tangential field, which acts on the induced charges and drives the EHD flow of solvent along the electrode. Such flow, as observed in spherical colloids, can often induce particle aggregation (40, 41). However, EHD flow alone typically causes close-packed aggregation of all particles rather than chiral clusters with well-separated distance. As indicated in Movie S1, when three lying dimers join in the cluster, they rearrange into an equilibrated chiral configuration. Considering that dimers are polarized under electric fields (primarily due to mobile ions surrounding the particle), the final configuration of a cluster is likely controlled by the induced dipolar interactions between dimers.

We thus develop a theoretical model for the electrostatic energy of colloidal clusters in different configurations, which can predict whether the minimum energy configuration is chiral or achiral for a given set of experimental conditions. As illustrated in Fig. S1, for a given cluster configuration, we approximate individual lobes on dimer particles as spheres. The dimers are subject to an applied electric field ${\mathbf{E}}_0\left(\mathbf{r}\right)=-\mathbf{\nabla }{\psi }_0\left(\mathbf{r}\right)$. They are surrounded by solvent, whose properties are characterized by the dielectric constant $\epsilon$ and Debye length ${\kappa }^{-1}$. Each sphere $i$ with radius $R_i$ is located at the position ${\mathbf{r}}_i$. The polarizability of the sphere $i$ can be expressed as ${\alpha }_i=4\pi {\epsilon }_0\epsilon R_i^3{K}_i$, where $K_i$ is the polarization coefficient that can be calculated both analytically (42) and numerically (43). Two spheres representing the lobes on the same dimer are subject to the geometric constraint of fixed bond length $L=\left|{\mathbf{r}}_i-{\mathbf{r}}_j\right|$. The interaction between dimers and the conducting substrate is accounted for by using image dipoles beneath the electrode. The dipole on sphere $i$, ${\mathbf{p}}_i$, is induced by the sum of electric fields that are both applied externally and generated by neighboring dipoles; i.e.,

$${\mathbf{p}}_i={\alpha }_i\left[{\mathbf{E}}_0\left({\mathbf{r}}_i\right)+{\displaystyle \sum _{j\ne i}{\mathbf{E}}_{\text{ind},j}\left({\mathbf{r}}_i\right)}\right],$$ [1]

where ${\mathbf{E}}_{\text{ind},j}\left(\mathbf{r}\right)=\mathbf{T}(\mathbf{r}-{\mathbf{r}}_j)\cdot {\mathbf{p}}_j$ is the field generated by the induced dipole j. Here the kernel for the dipole field is given by $\mathbf{T}\left(\mathbf{r}\right)=\left(3\mathbf{r}\mathbf{r}-\mathbf{I}\right)/4\pi \epsilon {\epsilon }_0{\left|\mathbf{r}\right|}^3$. Because the induced dipoles interact mutually and respond to local electric fields, we need to solve for them self-consistently. For a given set of spatial configurations of particles, the induced dipoles of each lobe can be obtained by solving a system of linear equations for ${\mathbf{p}}_i$,

$${\mathbf{p}}_i={\displaystyle \sum _j{\mathbf{A}}_{ij}}\cdot {\mathbf{E}}_0\left({\mathbf{r}}_j\right),$$ [2]

where ${\mathbf{A}}_{ij}={\left[{\alpha }_i^{-1}{\delta }_{ij}-\mathbf{T}\left({\mathbf{r}}_i-{\mathbf{r}}_j\right)\left(1-{\delta }_{ij}\right)\right]}^{-1}$ is a collective polarizability tensor for the entire system of colloidal spheres. An example of all dipoles calculated for a chiral tetramer is shown in Fig. S1C. Although they primarily point in the direction that is antiparallel with the applied field (because of the negative polarization coefficient), they are slightly tilted due to the impact of neighboring dipoles.

Once ${\mathbf{p}}_i$ is obtained, the electrostatic energy $U_e$ for the system of dimers can then be written

$$U_e\left(\left\{{\mathbf{r}}_i;{\mathbf{p}}_i\right\}\right)=\frac{1}{2}\left[-{\displaystyle \sum _i{\mathbf{p}}_i}\cdot {\mathbf{E}}_0-\frac{1}{2}{\displaystyle \sum _{i\ne j}{\mathbf{p}}_i}\cdot \mathbf{T}\left({\mathbf{r}}_i-{\mathbf{r}}_j\right){\mathbf{p}}_j+\frac{1}{2}{\displaystyle \sum _i{\mathbf{p}}_i}\cdot {\alpha }_i^{-1}\cdot {\mathbf{p}}_i\right].$$ [3]

The energy $U_e$ includes both dipole–applied field and dipole–dipole interactions. The outermost factor 1/2 in Eq. 3 arises from the fact that the total system includes contributions from both real particles and their image dipoles. Although other electrostatic (e.g., screened Coulomb) and electrohydrodynamic interactions could, in principle, be included, our model hypothesis is that the cluster structure and chirality are dominated by and can be explained at a simplest level in terms of induced dipolar interactions including image effects.

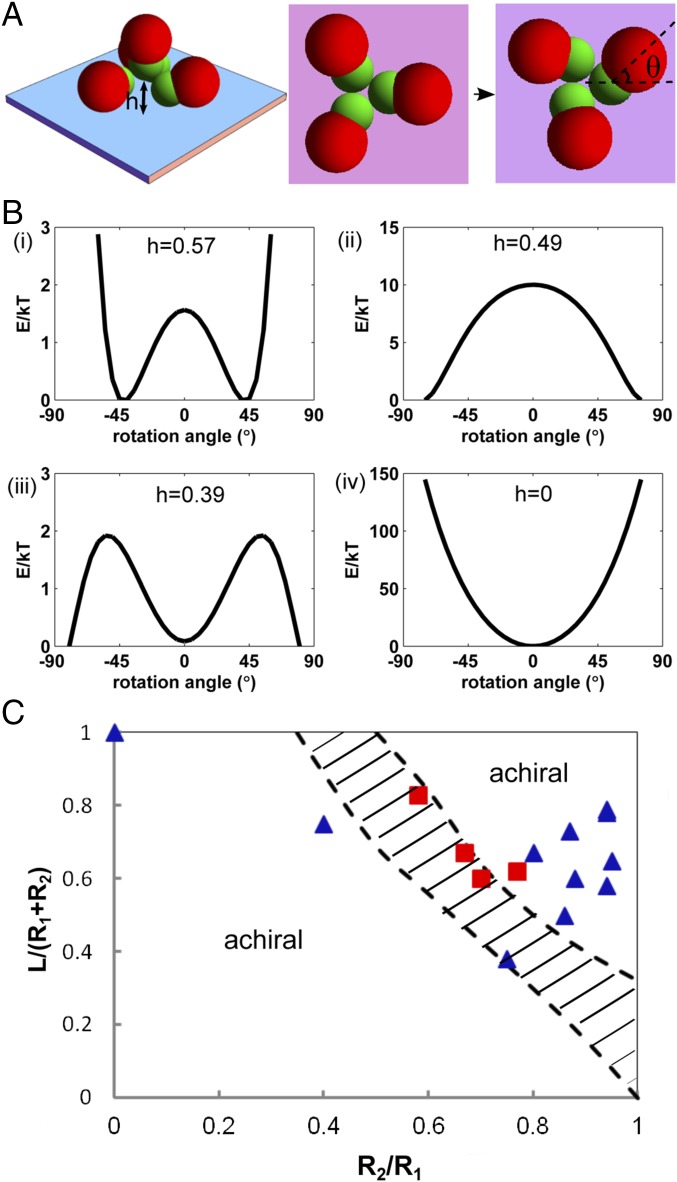
Parameters used in the calculations correspond to the typical experiment conditions: $R_1=1.27$ µm, $R_2=0.89$ µm, ${\zeta }_1={\zeta }_2=-60$ mV, $\epsilon =78$, $E_{\text{rms}}=$ 70 V/mm, and $\omega =$ 1,000 Hz. The polarization coefficient $K_i$ for particle $i$ is calculated based on the low-frequency thin double-layer polarization theory (42). Fig. 3A shows two important geometric parameters describing the structure of chiral clusters. $h$ is the separation between the central standing dimer and the substrate, scaled by the large lobe diameter $2R_1$, and $\theta$ is the rotation angle between the bottom petals and a predefined horizontal axis. By varying $h$, the central dimer–substrate separation will be changed. The separation between small lobes in the petals will be adjusted accordingly (Fig. 3A) with the constraint that the small lobe in the central standing dimer is in tangential contact with all other small lobes of the petal dimers. This is justified by our microscopic observation in Fig. 1 B and C. When $h$ is at its maximum value (e.g., $h$ ∼ 0.57 for $R_2/R_1=0.7$), the central dimer is lifted farthest from the substrate and all four small lobes form a close-packed tetrahedron. The rotation angle $\theta$ in Fig. 3A characterizes the degree of chirality. Any nonzero value of $\theta$ will introduce chirality, whereas the maximal value of $\theta$ for a given $h$ corresponds to the configuration where all petals are packed closely. As shown in Fig. 3B, by varying both $h$ and $\theta$, we can study their impacts on the electrostatic energy of a tetrahedral cluster and hence on the chirality. We note that the minimum energy level of each curve in Fig. 3B is chosen to be zero.

Fig. 3.

The electrostatic energy of chiral and achiral clusters for varying geometric parameters. (A) Two parameters that characterize the cluster configuration. $h$ is the separation between the central dimer and the substrate; $\theta$ is the angle of the petal rotation. For clarity, the central dimer is not shown. (B) The electrostatic energy of a tetramer vs. rotation angle for different $h$. All geometric and electric-field parameters in the calculation correspond to the typical experiment conditions shown in Fig. 1. See text for details. (C) The theoretical phase diagram for chiral clusters (shaded area enclosed by the dashed lines), as predicted by the induced electrostatic model. Red squares and blue triangles indicate chiral and achiral clusters observed in experiments, respectively.

The electrostatic energy of a tetramer is found to depend sensitively on $\theta$ for a given $h$. As shown in Fig. 3 B, i, when $h$ ∼ 0.57, the energy decreases as $\left|\theta \right|$ increases. When $\left|\theta \right|$ reaches ∼45°, the energy becomes minimal. Further increasing $\left|\theta \right|$ causes the energy to rise quickly. It reaches the global maximum when $\left|\theta \right|\sim 60°$, beyond which the petals will physically overlap with each other, representing unrealistic configurations. Clearly, Fig. 3 B, i predicts that a chiral tetramer (with a rotation angle $\left|\theta \right|\sim 45°$) is more energetically favorable than the achiral configuration (with $\theta =0°$). The symmetry of the energy curve also indicates that both right- and left-handed tetramers can be formed with equal probabilities, consistent with experimental observations. An analysis of the dominant contribution to the electrostatic energy indicates that the chirality is largely due to an out-of-plane dipolar attraction between the central standing dimer and the bottom petals. For a given $h$, with increasing $\theta$, the smaller separation between the central dimer and surrounding petals results in a stronger out-of-plane dipolar attraction between them. However, as $\theta$ increases, the petals become closer to each other. As a result, the in-plane dipolar repulsion between them will increase. Therefore, the optimum angle of petal rotation is primarily determined by the competition between the out-of-plane dipolar attraction and the in-plane repulsion. We emphasize that the inclusion of image dipoles is important in our calculation. Otherwise, an achiral configuration becomes more stable. As $h$ decreases, the attraction becomes weaker and the repulsion becomes stronger. At $h$ ∼ 0.39, the energy difference between an achiral ($\theta$ = 0) and a chiral cluster vanishes. With even smaller $h$, the achiral configuration becomes more favorable. To compare all subplots in Fig. 3B directly, we replot them in an absolute energy scale, as shown in Fig. S2. It is clear that the tetramer energy decreases as the central dimer is lifted farther away from the substrate. The global minimum energy configuration among all different $h$ and $\theta$ corresponds to a chiral tetramer with maximum lift in the central dimer ($h$ ∼ 0.57) and chirality angle of $\left|\theta \right|\sim 45°$. Both results are in excellent agreement with our optical characterization of the chiral structures shown in Fig. 1 and the measurement of chirality angle, which is ∼48° ± 2° for tetramers.

We now extend our electrostatic energy calculation to clusters with different numbers of petals, ranging from two to five. For a fixed number of petals but with varying $h$, we again find that the global minimum energy configuration has the central dimer lifted to the maximum height from the substrate while its small lobe maintains contact with the other small lobes in the petals. As for tetramers, this is also consistent with our optical characterization. As shown in Fig. S3, our calculation further shows that the chiral configuration is more energetically favorable for both trimers and tetramers. The model also predicts chirality angles of 60° for chiral trimers, which agrees well with our experimental measurement (∼64° ± 3°). For both pentamers and hexamers, our model predicts that the achiral configuration has the lowest energy, even when the central standing dimer orients its smaller lobe toward the substrate. This again largely supports our experimental observation that the majority of chiral clusters observed in experiments are trimers and tetramers. Only a few chiral pentamers and hexamers are observed near the transition frequency (∼2,000 Hz) where clusters start to disassemble. Because the dipolar repulsion between petals increases dramatically when the number of petals increases, the petals need to be separated from each other as far as possible for a large number of petals, which eventually leads to the achiral configuration. The stability of chiral clusters (i.e., the energy difference between the chiral and achiral configurations) is also enhanced with increasing field strength, as demonstrated in the energy calculation shown in Fig. S4. Our experimental observation is also consistent with the calculation. In fact, one can fix the chiral clusters permanently on the substrate by combining the AC electric field and short pulses of direct current (DC) field, as shown in Movie S1, part 3.

As shown in Fig. 2C, the geometric parameters of the dimers are important for determining chirality. Therefore, we calculate a theoretical chirality phase diagram based on our model of induced electrostatic interactions. Here we characterize a dimer with two (dimensionless) geometric parameters: the aspect ratio $R_2/R_1$ and the bond length $L/(R_1+R_2)$, where $L$ is the center-to-center distance between two lobes in a dimer. As illustrated in Fig. 3C, the shaded regime enclosed by two dashed lines corresponds to the parameter space that favors the formation of chiral clusters, based on our theory. To test this prediction, we systematically synthesize more than 10 samples of dimers with different geometric parameters and assemble them under electric fields. The experimental results are displayed in blue and red symbols in Fig. 3C to represent the formation of achiral and chiral clusters, respectively. They agree well with the phase boundaries predicted by our theory, especially considering that our model takes into account only the induced dipolar interactions and image effects.

We emphasize that the dimers in the present study possess only geometric asymmetry, which also results in small differences in polarization coefficient $K_i$ but large differences in polarizability ${\alpha }_i$ between two lobes. They are not, however, the only type of dimers that can form chiral clusters. For example, asymmetric dimers linked by a magnetic belt can assemble into both chiral clusters and helical chains due to the competition between magnetic interactions and steric hindrance (6). Even if the dimers are geometrically symmetric, they can still form chiral clusters if they possess significant asymmetry in the polarization coefficient. As shown in Fig. S5, chiral tetramers are more energetically favorable when one lobe has either negligible or opposite sign of polarization coefficient. Such kinds of dimers can be possibly synthesized when two lobes have different chemical compositions or zeta potentials.

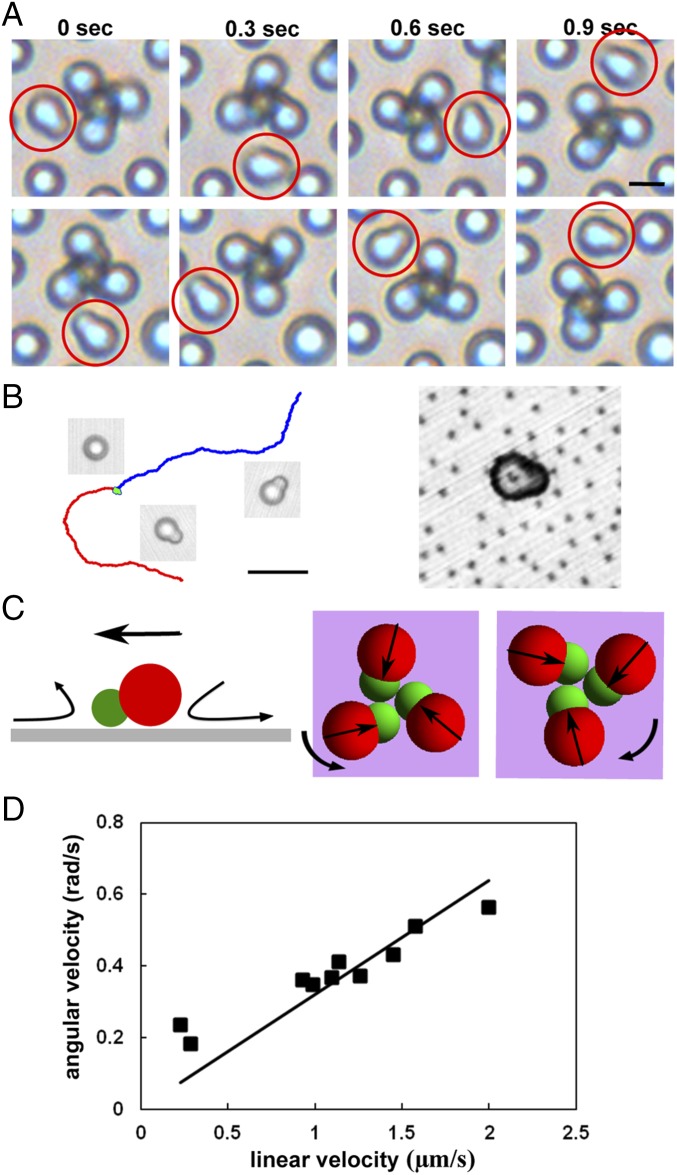
One unique feature of the chiral clusters obtained here is that they are not static after being assembled: They rotate continuously within the plane that is perpendicular to the applied AC field. As shown in Movie S2 and Fig. 4A, the right-handed clusters rotate counterclockwise and the left-handed clusters rotate clockwise, without exception. In contrast, the achiral clusters do not rotate. This rotation is hypothesized to arise from a torque generated by the unbalanced EHD flow of solvent surrounding the chiral clusters. It is known that a polarized particle near the electrode perturbs the vertically applied field and generates a tangential field, which acts on the diffusive ions and drives the EHD flow of solvent along the electrode (40, 41). For a spherical particle or a standing dimer, such flow is symmetric and no particle propulsion is observed in dilute suspension (Movie S3, part 1). However, when the geometrical symmetry is broken, e.g., an asymmetric lying dimer, the EHD flow surrounding the particle can be unbalanced, which in principle can induce its propulsion. Indeed, this is what we have observed, as illustrated by the particle trajectory in Fig. 4B and displayed in Movie S3, part 2.

Fig. 4.

The rotation of chiral clusters under AC fields. (A) Experimental snapshots show that right- and left-handed tetramers rotate in opposite directions (V_pp = 11 V and 560 Hz). The highlighted dimer, as a passive tracer particle, moves with the tetramer. (Scale bar: 3 µm.) (B) Trajectories of three dimer particles (within 18.6 s) with their respective snapshots showing both particle orientation and propelling direction. Green: a standing dimer. Blue and red: two different lying dimers. (Scale bar: 10 µm.) (C) Schematic showing that the unbalanced electrohydrodynamic (EHD) flow of solvent along the electrode can propel an individual asymmetric dimer and cause a chiral cluster to rotate. For clarity, the central dimer in the cluster is not shown. Straight arrows indicate the EHD flow direction surrounding a dimer. (D) The correlation between the angular velocity ${\mathrm{\Omega }}_0$ of a tetramer and the linear velocity $U$ of an individual propelling dimer under the same experimental conditions. Squares, experiment; solid line, theory.

To further probe the EHD flow surrounding an asymmetric dimer, we purposely adhere a dimer particle on the substrate and use small (500 nm) polystyrene spheres as tracers. As can be seen in Movie S4, the solvent is directed toward the smaller lobe but moves away from the larger lobe. The asymmetric distribution of tracer particles can also be seen clearly in Fig. 4B. Such an unbalanced electrohydrodynamic flow will cause the dimer to propel with its smaller lobe pointing forward if it is not immobilized on the substrate, as observed in Movie S3. Clearly, when the asymmetric dimers form into chiral clusters, the EHD flow is also unbalanced due to the broken chiral symmetry. As illustrated schematically in Fig. 4C, the EHD flow and the resulting drag force along each petal can generate a net torque that rotates the chiral clusters deterministically according to their handedness. The predicted rotation directions are consistent with our experimental observation. Apparently, the EHD flow surrounding an achiral cluster is well balanced and does not generate a net torque. Therefore, no rotation should be expected. To further prove our hypothesis that the broken symmetry in EHD flow surrounding individual dimers causes the chiral clusters to rotate, we measure both the linear velocity of an individually propelling dimer $U$ and the angular speed of a chiral tetramer ${\mathrm{\Omega }}_0$ under the same experimental conditions. Fig. 4D shows that two velocities are linearly correlated. In fact, one can estimate the slope theoretically. The details are shown in SI Text and Fig. S6. Briefly, the torque $T$ required to induce rotation is $8\pi \mu R^3{\mathrm{\Omega }}_0$, where $\mu$ is the water viscosity and $R$ is an effective radius of the chiral cluster if we approximate it as a sphere. $T$ is generated by the drag force on each petal; i.e., $T=N{F}_d{L}_a$, where $N$ is the number of petals, $F_d=6\pi \mu \left(R_1+R_2\right)U$ is the drag force on one petal, and $L_a$ is the arm length, i.e., the distance between the center of mass of a cluster and the long axis of one petal. Therefore, the ratio between ${\mathrm{\Omega }}_0$ and $U$ is

$$\frac{{\mathrm{\Omega }}_0}{U}=\frac{3N\left(R_1+R_2\right)L_a}{4R^3}.$$ [4]

Given the lobe sizes $R_1$ and $R_2$, $L_a$ can be calculated geometrically. Eq. 4 is represented by the solid line in Fig. 4D, with $N=3$, $R_1=1.27$ µm, $R_2=0.89$ µm, and $R\sim 2R_1$. Clearly, it matches well the experimental results. In addition, two characteristic features of the EHD flow velocity, as a nonlinear electrokinetic phenomenon, are its dependence on the square of the applied electric field strength and its negative correlation with the frequency (40). As shown in Fig. S7, both features are observed in experimental measurement of the chiral cluster’s angular speed.

It is noted that we obtain a racemic mixture of chiral clusters because they have the same electrostatic energy. Chiral purity is, however, desirable in many applications. One potential strategy is to separate the mixture into enantiopure colloids. Because our clusters exhibit deterministic rotation based on handedness, one could possibly separate them by superimposing a helical flow field (16) or a chirally patterned substrate (44), which rectifies the motion of right- and left-handed clusters along different paths. Another strategy is to build the desirable chirality during assembly, hence avoiding the need for separation. Movie S5 demonstrates such a proof of concept. Initially, the right-handed cluster is stable at 600 Hz. When we increase the frequency to 1,800 Hz, it becomes unstable and the chirality fluctuates due to Brownian motion. At the moment when the chirality switches to left handed, we quickly decrease the frequency back to 600 Hz so that it is locked in. Although it is done manually here, the tuning process can be performed automatically based on image processing and a feedback loop. By further combining this method with microfluidics, one could possibly make chiral clusters one by one with controlled handedness.

In conclusion, we report the directed assembly of achiral building blocks, i.e., asymmetric dimers, into a family of chiral colloidal clusters under the influence of AC electric fields. Supported by both experimental observation and theoretical calculations based on a simple model of induced electrostatic interactions including surface image effects, we show that the chiral configuration, under appropriate experimental conditions, is energetically favorable because of the out-of-plane dipolar attraction between the central dimer and surrounding petals. Moreover, the chiral clusters exhibit active rotational propulsion in response to the perpendicularly applied electric field, with its rotation direction fully dictated by the cluster chirality. This surprising propulsion can be attributed to the broken symmetry in the electrohydrodynamic flow of solvent surrounding those clusters. The clusters obtained in our study represent colloidal molecules with chiral symmetry. They could be used as the building blocks for colloidal arrays with exotic optical responses or as macroscopic analogs for the study of separation of chiral molecules. The broken symmetry could also be further exploited to build colloidal robots for microscale propulsion in a low Reynolds number environment.

Materials and Methods

Materials.

Styrene, divinylbenzene (DVB), sodium 4-vinylbenzenesulfonate, polyvinylpyrrolidone (PVP) (M_r ∼ 40,000), and SDS are purchased from Sigma-Aldrich. The 3-(trimethoxysily)propyl acrylate (TMSPA) is purchased from TCI. The thermal initiator V65 was purchased from Wako Chemicals. All chemicals are used as received except that both styrene and divinylbenzene are purified by aluminum oxide before use.

Synthesis of the Asymmetric Colloidal Dimers.

The synthetic route to make asymmetric polystyrene dimers is reported in our previous publication (45). In brief, dispersion polymerization is adopted for making polystyrene spheres. Subsequently, an aqueous emulsion made of 4 mL 5 wt% PVP, 0.5 mL 2 wt% SDS, 1 mL styrene, 0.05 mL DVB, 0.05 mL TMSPA, and 0.02 g V65 is used to swell 1 mL 20 wt% polystyrene spheres for 24 h. Afterward, the swollen seeds are put in a 70 °C oil bath overnight for cross-linking and polymerization. The cross-linked polystyrene spheres are cleaned four times via centrifugation before a second swelling step. A similar emulsion of PVA, SDS, TMSPA, sodium 4-vinylbenzenesulfonate, and V65 with varied amounts of styrene is used to swell the cross-linked polystyrene spheres for 24 h. A second lobe will emerge during the swelling stage. Polymerization at 70 °C for 12 h will make dimer particles. The amount of styrene used during the second swelling stage can be varied to make asymmetric dimers with different aspect ratios and bond lengths. The dimers are negatively charged because of the sulfonate functional groups on surfaces. Their zeta potentials are measured to be ∼ −60 mV.

Directed Assembly Under AC Electric Fields.

Before the assembly, colloidal dimers are cleaned by centrifugation three times and finally dispersed in deionized water. A total of 10 µL of dimer solution is injected carefully with a pipette into the chamber formed by two pieces of ITO glass slides (Sigma-Aldrich). A 100-µm-thick polyester film is used as the spacer. Careful cleaning of ITO slides is necessary. They are first immersed in acetone and then in isopropyl alcohol with sonication for 10 min each. The ITO slides are further cleaned by oxygen plasma for at least 2 min. To prevent the irreversible adhesion between dimers and substrates, ITO slides are made negatively charged by immersing them in a mixture of 0.5 M potassium chloride and 5 mg/mL poly-sodium 4-styrene sulfonate solution for 10 min under sonication. Finally they are rinsed with deionized water thoroughly. An AC electric field is then applied perpendicularly to the ITO surfaces by using a function generator (RTGOL DG1022). The assembly experiments are performed on an inverted microscope (Olympus IX71) equipped with both a QImaging Retiga-2000R color camera and a Silicon Video 642 high-speed camera.

Tracing the Electrohydrodynamic Flow Surrounding Asymmetric Dimers.

One drop of the dimer suspension is first spread evenly on the surface of an ITO substrate. The droplet is then dried by natural evaporation and the asymmetric dimers stick on the ITO surface due to Van der Waals attraction. A total of 10 µL of 0.2% (wt/vol) 500-nm fluorescent polystyrene spheres (Life Technology; F8813) is then added to the substrate. This solution is sandwiched between two electrodes by putting spacers in between.