Abstract
Ionic concentrations fluctuate significantly during epileptic seizures. In this study, using a combination of in vitro electrophysiology, computer modeling, and dynamical systems analysis, we demonstrate that changes in the potassium and sodium intra- and extracellular ion concentrations ([K+] and [Na+], respectively) during seizure affect the neuron dynamics by modulating the outward Na+/K+ pump current. First, we show that an increase of the outward Na+/K+ pump current mediates termination of seizures when there is a progressive increase in the intracellular [Na+]. Second, we show that the Na+/K+ pump current is crucial in maintaining the stability of the physiological network state; a reduction of this current leads to the onset of seizures via a positive-feedback loop. We then present a novel dynamical mechanism for bursting in neurons with a reduced Na+/K+ pump. Overall, our study demonstrates the profound role of the current mediated by Na+/K+ ATPase on the stability of neuronal dynamics that was previously unknown.
Keywords: Na+/K+ pump, seizure, epilepsy, ion concentrations, STDN, intracellular Na+, extracellular K+
ion movements form the physical basis for electrical activity in the brain. Differences in ionic concentration and charge between intracellular and extracellular spaces lead to ionic currents. These differences are maintained by various ionic pumps that transport ions across the neuronal membrane. The sodium/potassium pump (Na+/K+ ATPase) transports three Na+ ions to the extracellular space and brings two K+ ions into the cytoplasm at each cycle, thus maintaining the electrochemical gradient of Na+ and K+ across the cell membrane. Since the net effect of the pump at each cycle of operation is transporting one positive ion out of a neuron, the pump generates an outward current, which influences the membrane potential. Whereas the electrogenic nature of this current was established in the past (Thomas 1972), very few studies have examined its role in neuronal activity. Furthermore, this pump current has been either assumed to be constant or completely ignored in many of the previous computational studies. This would be a reasonable assumption, provided ion concentrations do not vary significantly. However, during the episodes of a seizure, intense electrical activity leads to large variations of ion concentrations (Somjen 2002). In this paper, we focus on the role of the current generated by the Na+/K+ pump in neuronal dynamics.
Balance between currents generated by active pumps and passive channels is crucial to the stability of the resting state of neurons. Changes in the pump activity have been hypothesized as the cause of seizures (Donaldson et al. 1972; Grisar et al. 1992; Vaillend et al. 2002). Indeed, a partial block of the Na+/K+ pump by a cardiac glycoside, such as Ouabain, leads to epileptiform events (Donaldson et al. 1971, 1972). Furthermore, genetic studies have identified alternations in the Na+/K+ pump gene that are associated with epileptic activity in animal studies (Clapcote et al. 2009) and in epileptic patients (Gallanti et al. 2008).
Whereas there is a sufficient body of evidence linking changes in the Na+/K+ pump to the development of epilepsy, mechanisms by which pump activity may influence epileptogenesis are not well understood. It was suggested that a reduction in the performance of glial Na+/K+ pump would result in dysregulation of the extracellular potassium ion concentration ([K+]o), which in turn, leads to seizures (Grisar 1984). Changes in the Na+/K+ pump that reduce its affinity to K+ ions have been observed in some cases of epilepsy (Grisar et al. 1992). Changes in both the excitability of inhibitory neurons and properties of inhibitory postsynaptic potentials have been reported in conditions of reduced Na+/K+ pump functioning (Haglund and Schwartzkroin 1990; Ross and Soltesz 2000; Vaillend et al. 2002), suggesting that the Na+/K+ pump can contribute to reduction of inhibition. Finally, application of a low dose of Ouabain, causing partial blocking of the Na+/K+ pump, leads to the changes in membrane potential and input resistance of excitatory neurons, even when the [K+]o remained well controlled (Vaillend et al. 2002), suggesting intrinsic ion concentration changes due to reduced Na+/K+ pump activity.
We previously proposed a role for the intracellular [Na+] ([Na+]i) accumulation in seizure termination (Krishnan and Bazhenov 2011). The goal of this new study is to characterize the direct role of the current mediated by the Na+/K+ pump in the onset and termination of seizures. With the use of a combination of computational modeling and in vitro recordings, we found that an increase of [Na+]i during seizure leads to pump activation and an associated increase of the outward pump current. This increase alone was sufficient to explain the termination of seizures. Furthermore, even a small reduction in the Na+/K+ pump current triggered epileptiform activity. We further found that epileptiform activity induced by the Na+/K+ pump reduction was characterized by a previously unknown bursting mechanism. Our study predicts that when there are large changes in electrical activity, such as during sleep or epilepsy, the outward current mediated by the Na+/K+ pump plays a critical role in maintaining stability of cell dynamics.
METHODS
Computational models.
The pyramidal (PY) cells and fast-spiking inhibitory interneurons (INs) were modeled with a conductance-based, two-compartmental model, as described previously (Mainen and Sejnowski 1996). The following equations describe the voltage equations for the two compartments (also see appendix)
| (1) |
where Vd and Vs are the voltage of the dendritic and somatic compartments, and Idleak is the leak current in the dendritic compartment that includes sodium, potassium, and chloride leak currents. All leak currents were of the form gl (El − V), where gl is the maximal conductance, El is the reversal potential, and V is the voltage of the corresponding compartment [maximal conductance for leak currents was set as following: PY: potassium (gKl) = 0.044, sodium (gNal) = 0.02, chloride (gcll) = 0.01; IN: gKl = 0.048, gNal = 0.0215, gcll = 0.003]. Isleak is the leak current in the axosomatic compartment, which included potassium and sodium leaks (PY: gKl = 0.042, gNal = 0.0198; IN: gKl = 0.048, gNal = 0.0225). IdInt and IsInt are the sums of intrinsic currents for dendrite and axosomatic compartments. The IdPump and IsPump are the sums of Na+ and K+ ionic currents (INaPump and IKPump), mediated by the Na+/K+ pump for dendritic and axosomatic compartments. The scaling coefficient is set as α = 1 for all conditions unless specified. The axosomatic and dendritic compartments were coupled (gc = 0.1 nS), and the coupling conductance was scaled, based on surface area of each compartment (ss = 10−6 cm2, sd = 1.65 10−4 cm2). As in previous studies (Mainen and Sejnowski 1996), the axosomatic conductances are assumed to be sufficiently strong to change the somatic membrane voltage almost instantaneously; thus there is no capacitance for the axosomatic compartment in this model. This assumption allows the use of a larger integration step size, resulting in increased computational efficiency, while still replicating realistic neuronal activity (Chen et al. 2012). A fourth-order Runge-Kutta method was used for all integration. The currents from the Na+/K+ pump determined by [Na+]i and [K+]o are given by the following equations (Kager et al. 2000)
| (2) |
where Imax = 20 mA/cm2 is the maximal flux for the Na+/K+ pump and was chosen such that activity of the pump compensates for the leak currents at equilibrium. The constant coefficients (2 and 3) Imax are used to maintain the relationship between Na+ and K+ ions transported by the pump (Glitsch 2001). The dependence of the pump on [Na+]i and [K+]o was given by a sigmoidal function (in variable A) that is known to capture the experimental data available for the activity of the Na+/K+ pump (Läuger 1991), with Koα = 2.5 mM, and Naiα = 20 mM. Intrinsic currents and their conductances were identical to those used in our previous model [described in Krishnan and Bazhenov (2011) and appendix]. The dendritic compartment of PY neurons contained slow currents: high-threshold calcium, calcium-activated potassium, slowly activating potassium (M-current), persistent sodium, hyperpolarization-activated depolarizing mixed cationic (H-current), voltage-gated sodium, and leak. The somatic compartment included voltage-gated sodium, delayed-rectifier potassium, persistent sodium, slowly activating potassium currents, and leak currents. The IN cells include voltage-gated sodium, delayed-rectifier potassium, and leak currents in the soma; dendrites have voltage-gated sodium, H-current, and leak currents. The inhibitory neurons were modeled to describe a fast-spiking neuron without spike adaptation (Markram et al. 2004) and did not include any of the other slow currents.
Ion concentration dynamics.
The model incorporated the concentration dynamics of calcium ion ([Ca2+])i, [K+]i, [K+]o, [Na+]i, [Na+]o, and negatively charged chloride ion ([Cl−])i. The concentration for each ion is determined by a sum of factors, such as the leak current, intrinsic currents, pump currents, extracellular diffusion, and glial activity. The evolution of [K+]o, which is determined by three components—neuron's intrinsic and pump currents (I∑KInt + IKPump), glial activity (G), and diffusion from neighboring neurons or compartments—is mathematically described by the following equations
| (3) |
| (4) |
| (5) |
where k = 10, k1 = 0.0008, [K+]oth = 15, F = 96,489 C/mol, and factor d = 0.15 determines the ratio of the volume of the extracellular compartment to the surface area. These parameters were based on the previous studies (Kager et al. 2000). [K+]oc is the concentration of [K+] in the extracellular space of the adjacent compartment (in the case of the dendritic compartment, [K+]oc corresponds to the [K+]o of the axosomatic compartment and vice versa), and [K+]o−1 and [K+]o+1 are the concentrations for neighboring cells [−1 for previous and +1 for next cell in a one-dimensional (1D) network]. For the neurons on the boundary, the neighboring neuron on one side is taken as the neighbor for both sides (mirror boundaries). Variable [B] represents the buffer in the glia cells ([B]max = 500) following Kager et al. (2000). The δ are scaled diffusion coefficients: δo = δi = D/Δx, where D = 6 × 10−6 cm2/s is the diffusion constant, and Δx = 100 μm is distance, which is approximately the size of one synaptic footprint (10 neurons) in the cortex. Similarly, other ion concentrations are described by the combination of intrinsic activity and activity of the neighboring neuron through diffusion. The equations for [K+]i, [Na+]i, and [Na+]o ions are as follows
| (6) |
| (7) |
| (8) |
where [K+]ic is the [K+]i of the adjacent compartment of the same cell.
Similar to the [K+]o, the [Cl−]i was determined by intrinsic current and the potassium-dependent KCC2 cotransporter. It is described by the following equation
| (9) |
where I∑ClInt is the sum of Cl− currents, [Cl−]∞ = 5 mM, τKocl = 0.08, τCl∞ = 20,000, and k = 100. These values are chosen to match the relationship between [K+]o and [Cl−]i due to the change in the KCC2 cotransporter (Payne et al. 2003). The [Ca2+]i is given by (Mainen and Sejnowski 1996)
| (10) |
where τca = 300, Dca = 0.85, and IHVA is the high-threshold Ca2+ current. The ion concentrations influence the neuron's dynamics through their action on the reversal potential, and the reversal potentials for currents are determined by the Nernst equation for ions passing through the following channels
| (11) |
where e0 = 26.64, EK, ENa, Ecl, and EH are reversal potentials for K+, Na+, and Cl− ions and H-current, respectively. In the model with an external source of potassium to mimic slice conditions (see Fig. 4), the equation for [K+]o was modified as follows
| (12) |
where [K+]ext = 3.5 mM, and τext = 5 s.
Fig. 4.
Bifurcation analysis explains termination of seizure in a single-cell model. A: bifurcation diagram depicts minimum (blue) and maximum (green) Vd values plotted against the bifurcation parameter [K+]o. [Na+]i was fixed at 20 mM, [K+]i and [Na+]o were fixed at 130 mM, and [Cl−]i was fixed at 10 mM; solid and dashed branches correspond to increasing or decreasing [K+]o, respectively. B: voltage traces of a single neuron for selected values of [K+]o ([Na+]i = 20 mM and [Cl−]i = 10 mM). Red and black dots represent local voltage minima and maxima, respectively (which were used in A). ε = 0.5 was used to illustrate the activity in the bistable region ([K+]o = 7.5 mM plot). Top, left: the neuron displayed low-frequency spiking activity. Bottom, right: each burst consisted of high-frequency oscillations, followed by a depolarized block and a prolonged hyperpolarization. The green and blue markers indicate the global maxima and minima, whereas red and black indicate the local maxima and minima. C: calcium ion concentration ([Ca2+]-Vd) phase-space projection, showing 1-dimensional (1D) quiescent (green line, Meq) and a 2D tonic-spiking (attracting yellow and blue surfaces, Mlc) manifold for [K+]o = 75 mM, ([Na+]i = 20 mM and [Cl−]i = 10 mM), which is spanned, respectively, by stable and unstable periodic orbits of the model. The neuron exhibited bistability of coexisting spiking (blue trajectory, marked as S) and bursting (black trajectory) regimes. The yellow part of the 2D manifold (Mlc) is a local attraction basin for tonic spiking. Initial conditions were chosen on the blue part of Mlc, unstable for tonic oscillations, resulting in the onset of the bursting activity (black trajectory). Solid and dashed segments of the 1D quiescent manifold (green line, Meq) correspond to stable and unstable equilibria (quiescent states). The solid red line (<Vd>) represents the effective potential curve made by averaging variables of periodic orbits spanning the 2D manifold Mlc; its end points identify the underlying bifurcations: subcritical Andronov-Hopf (AH) and homoclinic (at point X). The solid, orange line ([Ca2+]i′ = 0) is the slow nullcline; [Ca2+]i decreases (increases) below (above) this line. The red sphere indicates the location of an unstable equilibrium state at the intersection of Meq with this slow nullcline. Points Y, K, and Z indicate the hyperpolarized knee point on Meq and that of <Vd> and the intersection of the curve <Vd> with the slow nullcline [Ca2+]i′ = 0, respectively. Inset shows the 3D phase space, where mINa is the activation variable of the voltage-sensitive sodium current. D: (Ca2+-Vd) phase-space projection showing the critical manifolds for [K+]o = 90 mM ([Na+]i = 20 mM and [Cl−]i = 10 mM); other descriptions are same as for C. E: bifurcation diagram of the quiescent states in the Na+-K+ space. Solid and dashed lines indicate saddle-node (SN) and AH bifurcations, respectively, for different strengths of the Na+/K+ pump current. F: the arrangement of the critical manifolds near termination of seizure ([K+]o = 90 mM; [Na+]i = 20 mM in equation for reversal potential and [Na+]i = 22 mM in equation for Na+/K+ pump current; and [Cl−]i = 10 mM). Black line indicates bursting activity. The blue line (S) on the 2D manifold Mlc indicates the tonic-spiking solution that is unreachable from physiological initial conditions; other descriptions are the same as in C.
Synaptic connections.
The small network (shown in Fig. 1, and see Fig. 4) consisted of 10 PY and two IN neurons. The large network (see Fig. 6) included 100 PY and 25 IN neurons. These numbers resulted in 17% (20%) of INs in the small (large) network, which is close to estimates from neuroanatomical studies [e.g., Markram et al. (2004)]. In both networks, the synaptic connectivity had a local topology with different local footprints for each connection (radii of local connectivity for PY-PY = 5, PY-IN = 1, IN-PY = 5). A fast α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) and slow voltage-dependent N-methyl-d-aspartate (NMDA) synapses were used for connections between PY neurons and from PY to IN. The inhibitory connections from IN to PY were mediated by fast GABA synapses [total conductance: gAMPA(PY-PY) = 9 nS; gNMDA(PY-PY) = 0.9 mS; gAMPA(PY-IN) = 3.0 nS; gNMDA(PY-IN) = 0.3 nS; gGABA(IN-PY) = 9 nS]. Afferent excitatory input (gPY = 1.1 nS; gIN = 1.1 nS) was modeled by the Poisson process with mean frequency f = 140 Hz for both PYs and INs in simulations of the strophanthidin (STDN) effect and in the large network. This resulted in an average firing rate of 0.5 Hz during the resting state of the network.
Fig. 1.
Illustration of all of the methods used in this study. STDN, strophanthidin; [Na+]i, intracellular sodium ion concentration; [K+]o, extracellular potassium ion concentration.
Fig. 6.
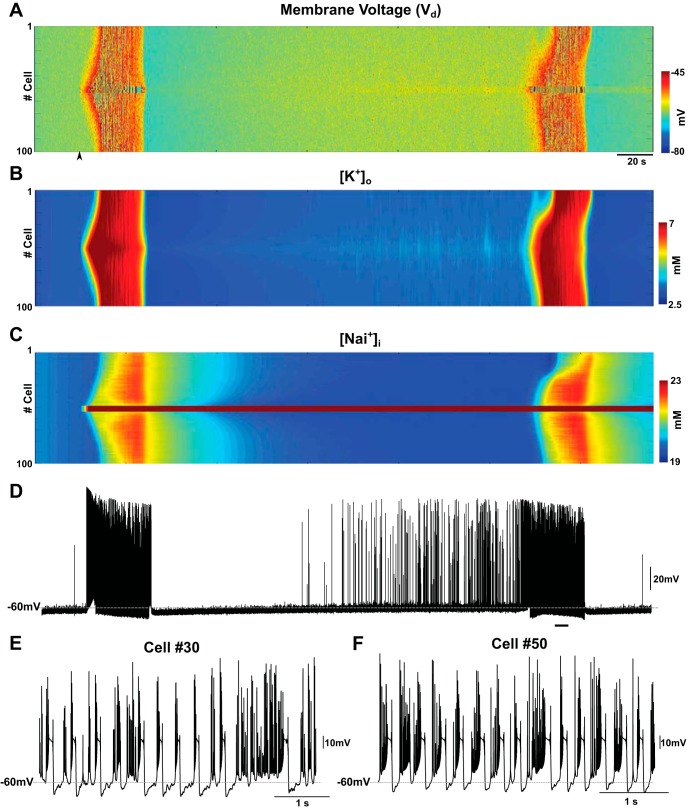
Local reduction of the Na+/K+ pump triggers seizure-like activity in the scaled-up network. A: raster plot of activity in the network of 100 PYs and 25 INs. The Na+/K+ pump was reduced for PY neurons #48–52 at time = 50 s (black arrow), leading to recurrent seizure-like activity that initiated and terminated spontaneously. B and C: time evolution of [K+]o and [Na+]i, respectively. D: membrane voltage of the representative neuron in the middle of the network (cell #50). E: activity of the neuron #30 during the 2nd episode of seizure, marked by a black line in D. F: activity in the neuron #50 for the same period as in E.
Bifurcation analysis.
All bifurcation analyses were performed on a single, isolated PY neuron model with fixed ion concentrations. To detect and continue the slow-motion, tonic-spiking, and quiescent manifolds in the 14D phase space of the model with several time scales, we used the technique proposed in Channell et al. (2007) and Shilnikov (2012). A faux parameter, caip, was introduced in the equation for [Ca2+]i, which is the slowest dynamical variable in the model. Its dynamics were governed by the following equation
| (13) |
where ϵ = 0.01. The condition d[Ca2+]i/dt = 0 defines the slow nullcline (manifold, see Fig. 3D; also see Figs. 4, C, D, and F, and 7, C and D). Variations of caip, which shift the slow nullcline, allowed tonic-spiking and quiescent manifolds to be detected in the phase space for given parameters of the model. We reduced the rate of changes for the slow variable by introducing a parameter ϵ for the sake of better visualizations of the state transitions.
Fig. 3.
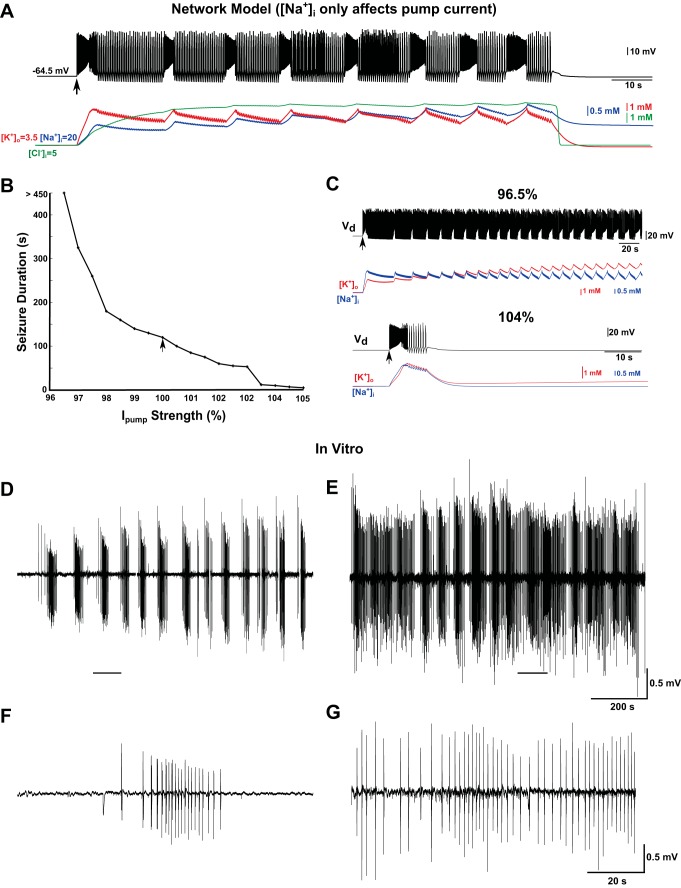
Na+/K+ pump current contributes to termination of seizure. A: activity in the network model with fixed reversal potential for Na+; the only effect of Na+ is on the Na+/K+ pump current. Top: the curve shows the dendritic membrane voltage of a single representative PY neuron. After brief transient input (marked by a black arrow), the network demonstrated seizure-like activity, followed by alternations between tonic and bursting states. The seizure terminated after ∼120 s. Bottom: plots show time evolution of ion concentrations. B: duration of seizure increased with decreasing strength of Na+/K+ pump current (Ipump). C: dynamics of a single PY neuron for 2 different strengths of the Na+/K+ pump current. Top: 96.5% of the control strength; bottom: 104% of the control strength. Vd, voltage of the dendritic compartment. D: periodic epileptiform activity induced by an increase of [K+]o (10 mM KCl) in vitro. E: bath application of 400 nM STDN in addition to 10 mM KCl inhibited the Na+/K+ pump and increased the duration of epileptiform events. Note almost continuous seizure-like activity. F: 1 epileptiform event (zoom-in from D). G: continuous activity after STDN application (zoom-in from E).
Fig. 7.
Bifurcation analysis reveals mechanisms of seizure initiation in a single-cell model. A: bifurcation diagram depicts minimum (blue) and the maximum (green) Vd values plotted against the bifurcation parameter [K+]o in the model with 50% Na+/K+ pump-current reduction (the ion concentrations were fixed at [Na+]i = 20 mM and [Cl−]i = 10 mM). Solid and dashed branches correspond to increasing and decreasing [K+]o, respectively. Red and black dots denote local minima and maxima of voltage, respectively. Note that transition from silent state to bursting now occurs for very low levels of [K+]o ([K+]o ∼ 2.6 mM). B: characteristic voltage traces of a single neuron for few selected values of [K+]o ([Na+]i = 20 mM and [Cl−]i = 10 mM) and reduced Na+/K+ pump current illustrate different dynamical states: periodic, quasiperiodic, bursting. Top, right: slow-frequency modulation of the spiking activity. Bottom: low-frequency spikes whose frequency progressively increased before transition to depolarization block. C: (Ca2+-Vd) phase space depicting the arrangement of the 1D quiescent (green line, Meq) and 2D tonic-spiking (yellow, Mlc) manifolds for [K+]o = 75 mM in conditions of Na+/K+ pump-current reduction. For [K+]o = 7.5 mM, only the periodic orbit or torus (blue curve) solutions were stable. Solid and dashed segments of the 1D manifold represent stable and unstable equilibria (quiescent states), respectively. The neuron exhibits a monostable, tonic-spiking activity, corresponding to the blue trajectory (S) near the fold on Mlc. Note that the intersection point (Z) of the <Vd> curve of effective potentials with the slow nullcline [Ca2+]i′ = 0 is below its knee point K and that the homoclinic point X coincides with the knee point Y on the manifold Meq, thus indicating homoclinic SN bifurcation [SN on invariant circle (SNIC)]; other descriptions are the same as in Fig 4, C. D: rearrangement of the critical manifolds supports bursting for [K+]o = 90 mM in conditions of 50% Na+/K+ pump-current reduction. The bursting trajectory (black) repeatedly switches between the hyperpolarized quiescent branch of Meq and the 2D tonic-spiking manifold (Mlc) glued to the knee point (Y) through a SNIC bifurcation. Note that the knee point K of the effective potential curve <Vd> moved above its intersection point K with the slow nullcline [Ca2+]i′ = 0 to promote persistent bursting.
Equilibrium curves in the biparameter diagram (see Fig. 3D) were found by continuation of the vector function of equation dX/dt = F (X, [K+]o, [Na+]i) (Doedel et al. 1997; Kuznetsov 1995). Bifurcation analysis of the model was performed using the software package Content (Kuznetsov 1998).
Preparation of hippocampal slices.
Acute hippocampal slices were prepared from C57BL/6J postnatal days 14–30 mice (The Jackson Laboratory, Bar Harbor, ME). Mice were anesthetized and decapitated according to University of California, Riverside, Institutional Animal Care and Use Committee-approved protocols. The brain was removed rapidly and sliced at 300 μm using a Leica VT1200 vibratome in ice-cold, low [Ca2+], high sucrose-dissecting solution. The slices were recovered in normal artificial cerebrospinal fluid (ACSF) for 1 h at 32°C and then stored at room temperature for further use.
Brain slices were perfused continuously with ACSF (3–5 ml/min flow rate) containing (in mM) 125 NaCl, 2.5 KCl, 25 NaHCO3, 1.25 NaH2PO4, 1 MgCl2, 2 CaCl2, 25 D-glucose, and 10 sucrose, pH 7.4. Continuous oxygenation was maintained with 95% O2–5% CO2 gas mix. The standard dissecting solution contained (in mM) 87 NaCl, 2.5 KCl, 25 NaHCO3, 1.25 NaH2PO4, 4 MgCl2, 0.5 CaCl2, 10 D-glucose, and 75 sucrose. All chemicals were from Fisher Scientific (Waltham, MA) unless specified otherwise. Epileptiform activity was induced by elevating [K+]o to 10 mM or by adding STDN into ACSF bath solution at 200–1,000 nM concentrations or both.
Recordings from hippocampal slice.
In this study, we used a modification of the loose-seal techniques (Katz et al. 1981). Compared with the tight-seal patch clamp, loose-seal recordings induce no damage to neurons (Roberts and Almers 1992). Briefly, series resistance and pipette capacitance were compensated in the bath using auto mode of the MultiClamp 200B (Molecular Devices, Sunnyvale, CA) amplifier, and the pipette was advanced into mice hippocampal slices to the depth of ∼100 μm. A healthy-looking principal neuron was selected and carefully approached to ∼1 μm distance. Positive pipette pressure was then dropped to zero, and the pipette was slowly advanced to the neuronal membrane. Pipette resistance increased from ∼1 MΩ to ∼20 MΩ upon contact with the neuronal membrane. No additional compensations were used. We performed recordings in >20 independent experiments; responses to STDN were always observed in slices that previously responded to bath application of 10 mM KCl. Slices with no pharmacological stimulation remained silent with occasional random spiking activity.
In the experiments with STDN and 10 mM KCl (see Fig. 3, D–G), multielectrode array (MEA) recordings were performed using 60 channel-perforated arrays from Multi Channel Systems (Baden-Württemberg, Germany). Hippocampal slices were prepared, as described above, and placed on the array so that the hippocampus covered most of the recording electrodes. We performed recordings in three independent experiments. Exact placement of MEA was photographed for further analysis. All MEA recordings were done at 32°C. Data were acquired and preliminarily analyzed by MC_Rack tools (Multi Channel Systems), and channels of interest were exported to pCLAMP10 (Molecular Devices) and Matlab (MathWorks, Natick, MA) for further analysis and plotting.
RESULTS
We previously reported a model of epileptiform activity in a network of conductance-based neurons with variable [Na+]i, [K+]i, [Na+]o, and [K+]o, as well as [Cl−]i and [Ca2+]i (Krishnan and Bazhenov 2011). Ionic concentrations influence intrinsic activity and firing rate of a neuron by their action on the reversal potential; in turn, intrinsic currents contribute to the changes in ion concentrations. This feedback loop has been shown to determine neuronal stability (Fröhlich et al. 2010) and seizure dynamics (Barreto and Cressman 2011; Bazhenov et al. 2004; Cressman et al. 2009; Krishnan and Bazhenov 2011).
In our model, a brief, depolarizing stimulus led to an increase in the firing rate, followed by transient elevation of [K+]o. When the stimulus was sufficiently large (in terms of amplitude or duration), a positive-feedback loop between neuronal firing and [K+]o led to a further increase in [K+]o and initiated sustained, seizure-like activity (Fig. 2A). This electrical event then terminated spontaneously, and its termination was found to be correlated with the progressive accumulation of [Na+]i (Fig. 2B) (Krishnan and Bazhenov 2011). In agreement with previous studies (Fröhlich et al. 2006), [K+]o oscillated between 7 and 9 mM during the course of the seizure (Fig. 2B), whereas [Cl−]i increased during the initial phase and stabilized at ∼10 mM until the termination (Fig. 2B). The increase of [K+]o was associated with high-frequency spiking during the tonic spiking (or fast runs) phase (Fig. 2A). The [K+]o decreased during clonic (or bursting) activity (Fig. 2A) due to prolonged intervals of silence between bursts. These dynamics were shown to arise from bistability between tonic spiking and bursting for a range of [K+]o (Fröhlich et al. 2006; Krishnan and Bazhenov 2011). Intracellular recordings in vivo from cortical neurons during spike-and-wave seizure episodes have identified both tonic-spiking and bursting modes of activity (Timofeev and Steriade 2004). Below, we used a combination of mathematical modeling, bifurcation analysis, computer simulations, and in vitro recordings to dissect the effects of the Na+/K+ pump during a seizure on 1) dynamics of the Na+ and K+ reversal potentials and 2) dynamics of the outward current mediated by the Na+/K+ pump because of its electrogenic nature.
Fig. 2.
Spontaneous termination of seizure in the network model. A, top: image plot of the membrane voltage of all pyramidal (PY) neurons (light colors indicate depolarized potentials) from the network of 10 PY and 2 interneuron (IN) cells; bottom (in black): activity of a single representative PY neuron from the network (neuron #5). Transient direct current (DC) stimulation (2 s) was applied to all PY cells (indicated by large, black arrow). The membrane voltage revealed several state transitions between tonic (fast runs; bottom right) and clonic (bursting; bottom left) periods before termination of seizure-like activity. B: time evolution of [K+]o (red curve), [Na+]i (blue curve), and intracellular chloride concentration ([Cl−])i (green curve).
Role of Na+/K+ pump in termination of seizures: simulation and experiment.
We previously found that [Na+]i would reach its maximum just before seizure termination (Krishnan and Bazhenov 2011). A progressive increase of [Na+]i during seizures could have a dual effect on the neuronal activity. First, an increase of [Na+]i escalates the outward current generated by the Na+/K+ pump due to the pump sensitivity to [Na+]i. Second, it reduces the reversal potential of Na+. To identify which of these two contributions is critical for the termination of a seizure, we simulated a small network of 10 PY neurons and two INs in which the pump current was dependent on [Na+]i, but the reversal potential of Na+ was fixed (Fig. 3). All ion concentrations were assumed to be dynamical variables in these simulations (similar to Fig. 2). Seizure-like activity was triggered by transient input and lasted for ∼15 s but still terminated spontaneously (Fig. 3A). This suggests that the outward current mediated by the Na+/K+ pump was sufficient to cause termination of seizure. Although the change in the reversal potential of Na+ was not required for termination, it contributed to decreasing the seizure duration. Additionally, higher [Na+]i concentrations (22 mM) were necessary for seizure termination when the reversal potential was fixed (compare Fig. 2B with Fig. 3A).
To establish further the role of the Na+/K+ pump current on the termination of a seizure, we scaled the pump current by different values (Fig. 3B). When the Na+/K+ pump current was reduced, seizure duration was prolonged. Seizure lasted the entire simulation period (>450 s in Fig. 3C) for pump-current values <96% of the baseline current that was used in previous simulations. Increases in pump-current strength resulted in the opposite trend. The same stimulus used to elicit seizures in the model with a normal pump failed to initiate seizure when the pump current was >104% of the baseline level.
The relationship between the Na+/K+ pump and seizure duration was tested in vitro in hippocampal slices by blocking the Na+/K+ pump using STDN. First, the [K+]o in the bath solution was elevated up to 10 mM, which led to recurrent episodes of seizure (Fig. 3D). Each episode of seizure-like activity lasted 20–50 s (Fig. 3F). Then, a low concentration of STDN (400 nM) was applied. STDN was shown to block the Na+/K+ pump activity partially at such low concentrations (Ballerini et al. 1997). Application of STDN led to a significant increase of the seizure duration (Fig. 3E), including long episodes of continuous seizure-like activity (Fig. 3G). These data support our model predictions and confirm the critical role of the Na+/K+ pump in termination of seizures.
Tonic spiking, bursting, and bistability in a model of a single PY neuron: simulation.
In our model, repeated transitions between tonic firing and bursting due to changes in [K+]o were required for prolonged seizure activity. To identify a mechanism for these transitions, we carried out a bifurcation analysis on a single PY neuron under different levels of the ionic concentrations. First, we examined the dynamics of a single PY neuron as a function of [K+]o when all other ion concentrations were fixed ([Na+]i = 20 mM, [Cl−]i = 10 mM, [K+]i and [Na+]o = 130 mM). The neuronal model was simulated until it reached steady-state activity. We then computed the global and local maxima and minima of the membrane voltage.
The maxima and minima of the membrane voltage were plotted as a function of the bifurcation parameter ([K+]o; Fig. 4A). An occurrence of a single branch due to the same maximum and minimum values indicates a nonoscillatory state (either at hyperpolarized quiescence or in a depolarization block); oscillations are revealed by the occurrence of two or more branches. Tonic-spiking and bursting activity can be quantitatively differentiated by the number of such branches, as well as by the minimum value of the membrane voltage, which is more negative during bursting than during tonic spiking. To identify bistable behavior in a single neuron model, we examined the neuronal activity as the bifurcation parameter [K+]o was increased or decreased within the same range (Fig. 4A). Hysteresis or bistability occurs when transitions between tonic spiking and bursting take place at different parameter values for the increasing and decreasing conditions.
For values of [K+]o, ranging from 4.2 to 6 mM, the neuron displayed low-frequency spiking activity (Fig. 4B). At [K+]o values slightly higher than 6 mM, we observed spike doublets, whereas a further increase in [K+]o resulted in continuous spiking at higher frequency. Bursting was first observed at [K+]o > 7.8 mM, with each burst consisting of high-frequency oscillations, followed by a depolarized block and a prolonged hyperpolarization (Fig. 4B). For a narrow range of [K+]o between 7.3 and 7.8 mM, the PY neuron exhibited bistability due to the coexistence of tonic-spiking and bursting activity. In the full system with varying ion concentrations (Fig. 2), this bistability was responsible for continuous transitions between tonic-spiking and bursting states.
The origin of bistability between tonic-spiking and bursting activity: bifurcation analysis.
To explore further the dynamical mechanisms underlying tonic spiking and bursting, we disclosed the so-called slow-motion or critical manifolds in the 14D phase space of the isolated neuron with fixed ion concentrations (Fig. 4, C and D). In models, allowing slow and fast dissection of variables, the organization and interaction of these manifolds determine the dynamics and the shape of voltage waveform. To compute the critical manifolds, we introduced a “faux-sweeping” parameter (caip) in the equation for the slowest variable of the model ([Ca2+]i); this was after freezing [Na+], [Cl−], and [K+] (Channell et al. 2007; Shilnikov et al. 1998, 2001). The [Ca2+]i was allowed to vary, and by sweeping caip, the manifolds (2D tonic spiking and 1D quiescent) were identified using parameter continuation of equilibrium states and periodic orbit solutions of the given dynamical system (Kuznetsov 1995). An advantage of the faux-sweeping approach is that it reveals critical manifolds in a high-dimensional phase space of the full system, with multiple time scales for given parameter values (Shilnikov 2012). Figure 4C shows the critical manifolds projected onto the parameter plane of [Ca2+]i and the dendritic voltage variables. In this figure, a 1D quiescent manifold, denoted by Meq, comprised of equilibrium states (resting states of the neuron), is shown. Also shown is a 2D tonic-spiking manifold, denoted by Mlc, which is spanned by stable and unstable periodic orbits of the model.
A stable periodic orbit on the 2D manifold Mlc is associated with continuous tonic-spiking activity, whereas a stable equilibrium state on the 1D manifold Meq corresponds to a quiescent state of a neuron, which can be hyper- or depolarized depending on the voltage level. A transitive solution, which slowly traverses and quickly switches between the tonic-spiking and quiescent manifolds or between hyper- and depolarized branches of the manifold Meq, represents repetitive bursting. Bifurcations of the tonic-spiking orbits and equilibrium states in the neuron model determine the topology and stability of the manifolds and consequently, the voltage trace waveforms of a neuron. In what follows, we demonstrated how such bifurcations and rearrangements of both manifolds could regulate the activity of the neuron for different ion concentrations.
To understand why the neuron remains in a quiescent state or exhibits tonic-spiking or bursting activity for a given configuration of the manifolds, we introduced the auxiliary concept of a slow nullcline, on which the [Ca2+]i dynamics reverse its direction: from increasing to decreasing and vice versa. In the phase-space projection depicted in Fig. 4C, the slow nullcline is represented (denoted by [Ca2+]i′ = 0), crossing the critical manifolds. Its intersection with the 1D manifold Meq corresponds to a quiescent state of the neuron. The slow nullcline sets a threshold that determines whether [Ca2+]i will slowly increase (above the nullcline) or decrease (below the nullcline) for given values of the membrane potential. Depending on the voltage level at the intersection of the slow nullcline with the 2D tonic-spiking manifold Mlc, the neuron can stably exhibit various types of spiking or bursting activity or become bistable. As such, examination of the [Ca2+]i slow nullcline is vital for understanding the aggregate dynamics of the neuron.
Figure 4C illustrates the tonic-spiking and quiescent manifolds in the 2D (Ca2+-Vd) projection of the phase space for [K+]o = 7.5 mM and [Na+]i = 20 mM. This ion concentration configuration fosters bistability of tonic-spiking and bursting activity in the neuron due to the coexistence of two attractors. Tonic-spiking activity corresponds to a stable periodic orbit, shown in a section of Mlc; any initial condition belonging to this section of the tonic-spiking manifold led to this tonic-spiking attractor. Bursting occurred through recurring switching between hyperpolarized and depolarized branches of the 1D quiescent manifold Meq, which was mediated by variations of [Ca2+]i. At hyperpolarized voltage values, [Ca2+]i decreased due to deactivation of the voltage-gated Ca2+ channels and Ca2+ pump operation. The voltage abruptly increased when [Ca2+]i concentration reached a low, critical value (at ∼0.008 mM), corresponding to the knee on the hyperpolarized branch of the manifold Meq (Fig. 4C; point Y). The convergence to the depolarized branch of the quiescent manifold was oscillatory, thereby giving rise to high-frequency spiking at the onset of each burst. Activation of voltage-gated Ca2+ channels at depolarized voltage values led to the progressive increase of [Ca2+]i until it reached ∼0.013 mM. Beyond this value of [Ca2+]i, the depolarized branch became unstable due to a subcritical Andronov-Hopf (AH) bifurcation. At such high levels of [Ca2+]i, activation of the Ca2+-dependent K+ current prevented the neuron from maintaining depolarized voltages (near an unstable equilibrium state). This, in turn, drove the neuron voltage to a hyperpolarized state and initiated another cycle of bursting.
Figure 4D depicts the manifolds when the [K+]o was increased to 9 mM. Unlike the previous case, this configuration of the critical manifold makes bistability impossible due to the relative shift of the tonic-spiking manifold Mlc with respect to the knee (Fig. 4D; point Y) toward higher values of [Ca2+]i. In this configuration, there was no attracting section on Mlc (as in Fig. 4C) to support stable tonic spiking, and therefore, bursting with fast transient spikes became the only activity of a neuron. Corresponding bursting voltage traces are presented in Fig. 4B. The aforementioned changes described in the 2D and 1D manifolds completely account for the tonic-spiking and bursting dynamics observed in the neuron model.
Next, we applied bifurcation analysis to explore the mechanisms by which the current mediated by the Na+/K+ pump influences seizure termination. First, we carried out a biparametric bifurcation analysis of neuron dynamics, with [K+]o and [Na+]i as the control parameters, while keeping all other ion concentrations fixed. We previously found two boundaries separating different activity types [see Fig. 4 in Krishnan and Bazhenov (2011)]. The left boundary (Fig. 4E) represents a saddle-node (SN) bifurcation, corresponding to the transition from the hyperpolarized silent state to spiking. The right boundary, which is due to AH bifurcation, corresponds to the transition from spiking to a depolarized block state. In this study, we explored how these boundaries depend on the Na+/K+ pump current. The SN and AH boundaries confined the region in the parameter plane that corresponds to the occurrence of spiking and/or bursting activity. Outside of this region, the neuron reached either hyperpolarized (for lower values of [K+]o) or depolarized (for higher values of [K+]o) quiescent states. The reduction of the strength of the Na+/K+ pump current transformed the SN and AH boundaries, leading to an expansion of the region of spiking and bursting activity to higher [Na+]i values. Expansion of this region, through the reduction of the effectiveness of pump, led to delayed (or even prevented) termination of seizure. This bifurcation analysis suggests that the strength of the Na+/K+ pump current controls the excitability of the neuron by affecting the regions of quiescent and oscillatory dynamics.
Lastly, we examined the critical manifolds and slow [Ca2+] nullcline under conditions leading to the termination of a seizure. Therefore, we elevated [Na+]i to 22 mM, which corresponds to the value of [Na+]i before the termination in simulations shown in Fig. 3A. To examine the direct effect of the Na+/K+ pump current, the reversal potential of Na+ was fixed at its baseline value, and [K+]o was fixed at 7.5 mM; thus an increase of [Na+]i in this model only affected the Na+/K+ pump current. The (Ca2+-Vd) phase-space projection for this condition is shown in Fig. 4F. Whereas this configuration (similar to Fig. 4C) supports bistability of the neuron, the occurrence of spiking activity in the neuron was practically impossible because of the location of the stable periodic orbit relative to the critical manifolds. Even though the regions of bursting and spiking overlapped in the parameter space, the latter was unreachable from any physiologically feasible, initial state (to reach the spiking orbit, there needed to be a sudden shift in all slow currents), and hence, the neuron stably exhibited only bursting activity. Thus in conditions of high [Na+]i, with bursting as the only possible solution, the [K+]o decreased progressively, leading to termination of the seizure through direct transition from bursting to silence. This analysis suggests that an increase in the Na+/K+ pump current over the course of seizure gives rise to the loss of transitions to tonic spiking, which in turn, results in termination of seizure.
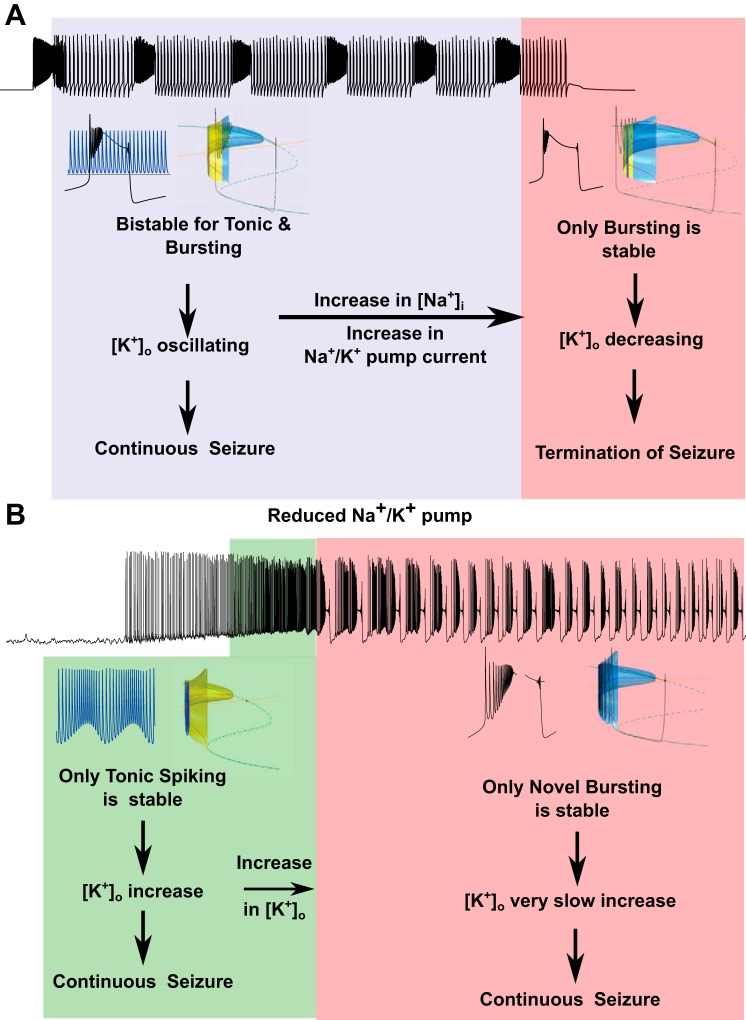
In summary, with the use of computational and bifurcation techniques, we showed that 1) bistability between tonic-spiking and bursting states of a single neuron contributes to sustained seizure by mediating transitions between tonic and clonic states, and 2) termination of seizure due to accumulation of intracellular Na+ occurs when bursting becomes the only stable state of a neuron (Fig. 8A).
Fig. 8.
Summary diagram illustrates effects of the ion concentration changes and pump reduction on the neuronal dynamics.
Onset of seizure after blocking Na+/K+ pump: experiment.
Since the Na+/K+ pump has a significant role in the termination of a seizure, we can predict that it also may be critical in maintaining a stable resting state, and its reduction could trigger a seizure. To test this hypothesis, we performed extracellular recordings from the stratum pyramidale in a hippocampal slice using STDN to block the Na+/K+ pump. In contrast to the previous experiment, here, we maintained normal physiological bath concentration of [K+]o (2.5 mM KCl), so the slice only exhibited low-frequency, spontaneous unit activity before application of STDN. Recurrent seizure-like activity was observed following administration of 500 nM STDN (Fig. 5, A–D). As we reported previously, the CA3 region was characterized by earlier onset and higher amplitude of epileptic bursts compared with other hippocampal areas (Krishnan et al. 2013). Each seizure lasted 5–10 s, with epochs of seizure-like activity separated by 3–5 s periods of silence (Fig. 5A). Closer examination showed two different types of activity during seizure: the first, continuous spiking activity, and the second, burst-like activity (Fig. 5, B and C). The bursts lasted up to 100 ms with varying interspike intervals (ISIs) in the range of 4–8 ms. The ISI histogram showed a peak at very low ISIs, corresponding to ISI within a burst, followed by another main peak at ∼200 ms, corresponding to ISIs between isolated spikes or bursts (Fig. 5D). Overall, the ISI histogram showed that STDN-induced epileptiform activity exhibits a unique bursting mode in hippocampal neuronal networks.
Fig. 5.
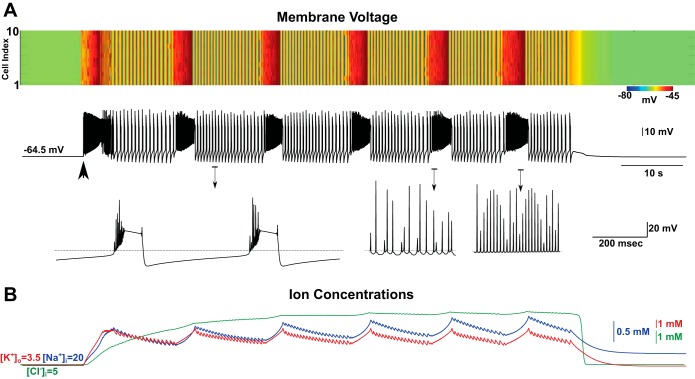
Decrease of the Na/K pump performance triggers seizure. A: juxtacellular recording of a single PY neuron from the CA3 region in a hippocampal slice. Application of 500 nM STDN triggers epileptiform activity. B and C: neuron activity at expanded time scales. Bar (B) indicates time period expanded in C. Note single burst event (C). D: distribution of interspike intervals (ISIs) in vitro after STDN application. The peak near 0 indicates ISIs within burst events. E: simulation of in vitro-like conditions. Membrane voltage of a single representative PY neuron from the network (10 PY and 2 IN cells) after Na+/K+ pump performance was reduced to 50%. Arrow indicates time moment when pump was alternated. F: dynamics of [K+]o (red), [Na+]i (blue), and [Cl−]i (green). G and H: simulated activity at expanded time scales. Bar (G) indicates time period expanded in H. I: distribution of ISIs in the model after the Na+/K+ pump was alternated. Note peak distribution similar to in vitro data (compare with D).
Network model of reduced Na+/K+ pump shows transition to spontaneous seizures.
Next, we simulated a network of 10 PY and two INs, with Na+/K+ pump activity reduced under conditions that were similar to the experimental setup shown in Fig. 5, A–D. In these simulations, [Na+]o, [K+]o, [Na+]i, [K+]i, [Ca2+]i, and [Cl−]i were all dynamic variables. An external source of [K+]ext = 3.5 mM was used for the entire simulation (see methods for details) to mimic the conditions of the in vitro experiment, where the [K+]o concentration is controlled by the perfusion system. To simulate spontaneous background activity observed in vitro, we also introduced random synaptic input to all neurons generating membrane-potential fluctuations and occasional spiking (Fig. 5E).
Reduction of the Na+/K+ pump activity triggered paroxysmal bursting in the network (Fig. 5E) and changes in the ion concentrations. Immediately following reduction of the Na+/K+ pump (reduced by 50% in strength), there was a brief period of continuous spiking, followed by bursting activity. The values [K+]o, [Na+]i, [Ca2+]i, and [Cl−]i were increased progressively until saturation (Fig. 5F).
Closer examination of the burst structure in these conditions (Fig. 5H) revealed a period (first 50–100 ms) of low-frequency spiking (∼5 Hz), followed by a short period (∼50 ms) of fast (up to 100 Hz)-spiking activity. It was then followed by a period of depolarization block. The later part was similar to what we observed previously (Krishnan and Bazhenov 2011) during bursting, triggered by elevated [K+]o (Fig. 2), but the initial low-frequency spiking component of the bursts was a new phenomenon. The corresponding ISI histogram is shown in Fig. 5I. This ISI distribution was similar to that obtained based on experimental data (compare with Fig. 5D) and showed a high-frequency peak at ∼10 ms, followed by several smaller peaks and a declining number of events with increasing ISI values. Both in vitro data and model simulations showed a distinct ISI distribution when seizure-like activity was triggered by elevated [K+]o. Qualitative similarity between in vitro recordings and model data suggests that the model captures the main underlying mechanism of bursting. Later, we examined the origin of the bursting triggered by pump reduction using bifurcation analysis.
Local reduction of the Na+/K+ pump triggers epileptiform activity in vivo: simulation.
Can a local reduction of the Na+/K+ pump trigger a generalized seizure? In a network with only 5% of neurons having 50% pump reduction, we observed a focal initiation of seizures that propagated to entire network (Fig. 6, neurons #48–52 had 50% pump reduced). The onset of each seizure episode was spontaneous and triggered by a group of neurons where pump performance was reduced (Fig. 6A). Similar to what we observed in the smaller network, [K+]o, [Na+]i, and [Cl−]i increased during seizure (Fig. 6, B and C; [Cl−]i not shown). This network model also showed spontaneous termination of epileptiform activity. After the termination of seizures, the network displayed a postictal depression state, characterized by reduced spiking and [K+]o level falling below baseline. This was then followed by a progressive increase of activity and another episode of seizure after ∼400 s. Whereas [K+]o and [Cl−]i returned to preictal levels after the first episode of seizure, [Na+]i remained high for the neurons with reduced pump activity (Fig. 6C). The neurons with reduced pump activity again showed earlier bursting compared with the rest of the network. The burst structure of these neurons (Fig. 6, E and F) was similar to that described in the small network model after pump reduction (Fig. 5). Other neurons displayed bursting that was similar to that in the small network with elevated [K+]o (Fig. 2).
Mechanisms of bursting mode in conditions of reduced Na+/K+ pump: bifurcation analysis.
To reveal the mechanisms underlying the novel type of bursting, shown in Fig. 5, we examined bifurcations of a single, isolated PY neuron under fixed ion concentration conditions and 50% reduction of Na+/K+ pump activity (Fig. 7). The bifurcation diagram revealed a structure (Fig. 7A) that was different from that presented in Fig. 4. The onset of spiking activity was shifted to much lower values of [K+]o: the characteristic transition from silence to tonic spiking occurred at [K+]o ∼ 2.5 mM. The spiking persisted up to [K+]o ∼ 7 mM; however, the amplitude of spikes reduced as [K+]o increased. The bifurcation diagram also revealed multiple local minima and maxima for [K+]o values between 7.1 and 8.4 mM; this was a manifestation of the slow-frequency modulation of the spiking activity (Fig. 7B). The emergence of such voltage waveforms is associated with a torus bifurcation (Neiman et al. 2011; Shilnikov et al. 1998, 2001; Wojcik and Shilnikov 2011). A newborn, 2D stable torus is covered by trajectories whose voltage minima and maxima densely fill out the indicated interval of [K+]o. Torus breakdown gave rise to the bursting activity beyond [K+]o = 8.4 mM. In contrast to the intact Na+/K+ pump condition examined previously (Fig. 4), the onset of each burst included several low-frequency spikes whose frequency progressively increased before transition to depolarization block (Fig. 7B).
As described previously, we computed the critical manifolds corresponding to quiescence and spiking activities for 50% reduction of Na+/K+ pump condition (Fig. 7, C and D). For [K+]o = 7.5 mM, only the periodic orbit or torus (Fig. 7C) solutions were stable. This indicates that the neuron was monostable, showing robust spiking with slow modulation. This structure contrasts the bistable manifolds observed for [K+]o = 7.5 mM in the intact pump conditions (Fig. 4C). Analysis of the tonic-spiking manifold revealed the key properties differentiating between these conditions. In the intact pump condition, the point of contact of the 2D manifold Mlc with an unstable section of the quiescent manifold Meq corresponded to a homoclinic bifurcation of a saddle (Fig. 4C; point X). In the model with a reduced pump, the 2D manifold Mlc touches the hyperpolarized knee (Fig. 7C; point Y), which corresponded to a homoclinic bifurcation of an SN equilibrium state. As pump activity was progressively reduced in the model, the 2D manifold progressively shifted to the left toward lower values of [Ca2+]i, until it reached the low knee point of the 1D manifold.
The increase of [K+]o from 7.5 to 9.0 mM led to a new form of bursting (Fig. 7D). In this regime, the trajectory smoothly traversed from the stable, 1D hyperpolarized branch (corresponding to the interburst silence) directly to the 2D tonic-spiking manifold (corresponding to fast spiking in the onset of bursting). Since there is no stable periodic orbit on the manifold at [K+]o = 9.0 mM, the neuron exhibited episodes of spiking until [Ca2+]i reached the critical value of ∼0.0105 mM, which corresponded to the fold of the 2D tonic-spiking manifold Mlc. After such, the trajectory switched to the depolarized branch of the quiescent manifold. Here, the dynamics were similar to the case of the intact Na+/K+ pump at [K+]o = 9.0 mM. In Fig. 7, C and D (compare with Fig. 4, C and D), the <Vd>-labeled curve represents the averaged voltage and [Ca2+]i variables on the tonic-spiking manifold Mlc. It can also be defined as an effective potential threshold. Observe the characteristic knee point (denoted by point K) due to the fold of Mlc. The location (height) of this knee point relative to the level of the slow nullcline [Ca2+]i′ = 0 in the phase space controls the bifurcations underlying transitions between tonic-spiking and bursting activity in the neuron. In the reduced pump condition, the curve <Vd> ended at the knee point through a homoclinic SN bifurcation [SN on invariant circle (SNIC); Fig. 7D], whereas it terminates through a homoclinic saddle bifurcation at lower [K+]o values (Fig. 4D). Analysis of the bifurcation diagrams in Fig. 7, C and D, reveals that depending on whether the knee point K of the effective potential line <Vd> is situated below or above the slow nullcline [Ca2+]i′ = 0 in the phase space, the neuron exhibits tonic-spiking or bursting activity. If the knee point K is above the nullcline, then during spiking, an average (over the spike duration) voltage can become depolarized sufficiently enough to trigger an increase of [Ca2+]i, thus making the tonic-spiking episode initiate the burst onset. Otherwise, the voltage keeps oscillating around the effective threshold, corresponding to a stable [Ca2+] concentration that maintains continuous spiking activity in the neuron at [K+]o = 7.5 mM.
This analysis explains why reduction of the pump activity prevents the termination of seizures. Even after [Na+]i increases, a neuron produces enough spikes in the bursting mode to prevent [K+]o from decreasing. Therefore, a neuron becomes stable in the new bursting state characterized by multiple spikes near the onset of burst, and such bursting activity lasts continuously.
DISCUSSION
The Na+/K+ pump plays a critical role in maintaining the physiological concentration gradients of Na+ and K+ ions and therefore, the reversal potentials of Na+ and K+ currents. Furthermore, this pump is electrogenic, and the net effect of its action is to remove a positive charge from a neuron at each cycle of pump operation. The hyperpolarizing effect of the outward pump current becomes significant when there are large fluctuations in ion concentrations, such as during seizure or sleep. Our previous study revealed that [Na+]i reaches its maximum just before the termination of seizure (Krishnan and Bazhenov 2011). In this study, we found that the increase of [Na+]i triggers activation of the Na+/K+ pump, and the current it generates becomes the main cause for termination of seizure and postictal depression state. To understand the mechanisms involved in seizure terminations, we performed a detailed bifurcation analysis of the model dynamics. It revealed a novel mechanism of bursting associated with the change in the pump performance and explained the appearance of epileptiform activity when the pump was blocked in slice experiments.
In our model, the transient increase of the [K+]o (e.g., triggered by a short, depolarizing pulse) initiated seizure-like, synchronized activity. This activity was sustained due to the presence of bistability between the tonic and bursting states for a range of [K+]o, which led to repetitive transitions between tonic-spiking and bursting activities (Fig. 2). In the presence of a normal and operational Na+/K+ pump, an increase of [Na+]i over the course of a seizure led to a new dynamical state, where only bursting was stable, which promoted termination of seizures. In the phase space of the model, this transition was caused by the shift of the 2D critical manifold regulating tonic-spiking oscillations. It made a periodic orbit representing fast-spiking activity unreachable, leading to the continuous decrease of [K+]o and termination of seizure. Prediction of this model is that when the Na+/K+ pump current is reduced, duration of the epileptiform events would increase. Indeed, we found in experiments with mice hippocampal slices that application of the Na+/K+ pump antagonist STDN to the slice preparation exhibiting recurrent periodic seizures increased seizure duration and transformed it to almost continuous epileptiform activity.
Whereas there is no direct evidence for an increase in [Na+]i during seizure, several observations support such a possibility. First, [Na+]i is known to increase under continuous neuronal activity (Fleidervish et al. 2010). Second, the [Na+]o is known to decrease during seizure (Dietzel et al. 1982), which reflects the opposite change to intracellular concentration. Finally, [K+]o is known to reduce below baseline following termination of seizure, which suggests elevated Na+/K+ pump activity due to elevated [Na+]i. An increase of [Na+]i during a seizure would decrease the Na+ reversal potential, causing reduced excitability. This can promote termination of epileptiform activity. In this study, we found, however, that the main contribution of [Na+]i change to the termination of seizures was associated with activation of the Na+/K+ pump and an increase of the outward pump current rather than with a decrease of the Na+ reversal potential.
We found that onset and termination of seizures is associated with specific bifurcations of the underlying dynamical systems and may be triggered by change in the ion concentrations. Our findings and several previous studies (Barreto and Cressman 2011; Cressman et al. 2009; Fröhlich and Bazhenov 2006) provide support to growing evidence that a seizure represents a distinct dynamical state of the neuronal network and the bifurcations of that system may explain transitions from normal to pathological state. Recent experimental evidence with human recordings and neural mass models further provide support for the idea that spontaneous termination of seizures occurs due to bifurcation or critical transition (Kramer et al. 2012). Whereas the mass model used in Kramer et al. (2012) involves a neural population rather than the detailed network used in this study, both studies suggest that bifurcation can explain transitions between seizure and normal states. Further multiscale modeling will be required to identify the relationship between the dynamical processes at different levels.
We found that the electrogenic property of the Na+/K+ pump plays an important role in maintaining the physiologically stable state of a neuron. Since the pump is active during the resting state, the Na+/K+ pump current is balanced with other ionic currents available at rest. Reduction of the pump performance may lead to a loss of the stable resting state, causing onset of seizure. This effect was demonstrated both in the model simulations and the in vitro experiments. When the Na+/K+ pump current was reduced, a smaller elevation of [K+]o was sufficient for the onset of spiking. Additionally, bursting activity with a unique topology was found at higher [K+]o (Fig. 7D). This bursting mechanism generated enough spiking activity to prevent [K+]o from decreasing, thus promoting continuous bursting. Bifurcation analysis of the critical manifolds in the phase space of the model revealed that reduction of the Na+/K+ pump activity led to a different organization of the manifolds in the phase space. It results, initial long periods of spiking activity at each burst onset followed by periods of depolarization block before the neuron switched to the hyperpolarized state.
To test this model's prediction, a Na+/K+ pump blocker, STDN, was applied in vitro to mouse hippocampal slices. We found that this triggered epileptiform activity, where PY neurons showed a bursting pattern similar to that found in the computational model with a reduced Na+/K+ pump current. In vitro, application of STDN led both to reduction of the Na+/K+ pump current and the accumulation of [K+]o and [Na+]i. Whereas it would be impossible to separate these effects in vitro, our model predicts that the main epileptogenic effect of STDN can be associated with a reduction of the current mediated by the Na+/K+ pump. In an earlier study, a continuous application of Oubain on a single neuron revealed several distinct forms of activity (Zandt et al. 2013), which were attributed to the different trajectories in [K+]o and [Na+]i space. Experimental conditions are certainly more complex than the model simplification, and the other factors, such as glia and network interactions, could interact with Na+/K+ pump activity in determining evolution of the neuron's activity.
When the performance of the Na+/K+ pump was reduced for only a small group of neurons in a network model, epileptiform activity originated from this population and then spread to the entire network. These seizure-like events repeated every few minutes and were preceded by brief periods of high-frequency activity, generated by neurons with a reduced Na+/K+ pump. This finding may explain previous experimental studies that described the appearance of high-frequency events before the seizure onset (Worrell and Gotman 2011).
There are several limitations to our current study. We mainly focused on examining the effect of the pump changes on excitatory neurons, assuming that it provides the main contribution to the network dynamics. The pump dynamics in the glia cells were not modeled. One of the primary consequences of the glial pump changes would be regulation of [K+]o. Furthermore, the volume of the extracellular and intracellular space was maintained to be constant in the model, and it is known to vary during seizure. Nevertheless, the primary goal of our study was to highlight the important role of Na+/K+ pump activity on the single-cell and network dynamics. To this date, very few studies concerning neuron dynamics incorporate the effects of the Na+/K+ pump to the model simulations [e.g., Arganda et al. (2007), Kager et al. (2002), and Yu et al. (2012)].
There is growing evidence of the importance of the Na+/K+ pump on neural activity and its impact on cognitive processes and brain diseases. It has been shown that [Na+]i accumulates even after short periods of spiking (Fleidervish et al. 2010); thus the Na+/K+ pump current could contribute to slow spike adaptations, which have been shown to be involved in stimuli processing in leech neurons (Arganda et al. 2007). Whereas an exact origin of this phenomena is not known, our study suggests that the Na+/K+ pump current may increase when [Na+]i is elevated and could contribute to the electrical properties of neurons during sensory processing or intrinsic oscillations.
The role of the Na+/K+ pump on various neurological and psychiatric diseases has been studied extensively [see, e.g., Rose and Valdes (1994)]; however, the contribution of the electrogenic property of the pump is still not well characterized. It was suggested that reduction of the Na+/K+ pump is one of the main alterations contributing to bipolar disorder (El-Mallakh and Wyatt 1995), which is characterized by severe mood swings between periods of major depression and periods of mania. Alternations of the Na+/K+ pump gene are known to occur in bipolar disorder (Goldstein et al. 2009) and familial hemiplegic migraine (Tavraz et al. 2008), which is a rare, severe, autosomal-dominant subtype of migraine with aura. In one model of bipolar disorder (El-Mallakh and Wyatt 1995), a mild reduction of the Na+/K+ pump was sufficient to explain the manic symptoms due to hyperexcitability of neurons. Lithium, which is the most commonly used drug to treat manic symptoms, is known to stabilize neuronal hyperexcitability. Future studies are required to characterize the effect of lithium on the Na+/K+ pump. Whereas we present our results to explain mechanisms of epileptic seizures, our findings can be generalized to other brain disorders when activity of the Na+/K+ ATPase is affected.
Reduced Mg2+ is known to cause seizures and is widely used in experimental setups for induction of epileptiform activity through unblocking of NMDA receptors. It is also known that Mg2+ is required for the functioning of the Na+/K+ pump (Rose and Valdes 1994). Thus a reduction of Mg2+ could potentially facilitate seizures through its effect on the Na+/K+ pump. It has been shown that brain injury, such as that occurring in head trauma, leads to delayed depolarization due to changes to the Na+/K+ pump (Tavalin et al. 1997). Whereas previous studies of head trauma emphasized the role of synaptic mechanisms (Houweling et al. 2005), future studies are required to explore the role of the Na+/K+ pump on the development of pathological excitability following traumatic brain injury.
To conclude, our study highlights the importance of the electrogenic property of the Na+/K+ pump in maintaining stability of neuron dynamics. It reveals the necessity of including the pump current in neuronal models, especially when ion concentrations fluctuate significantly, such as during epileptic seizures or synchronized sleep oscillations.
GRANTS
Support for this study was provided by the National Institutes of Health (Grants R01 NS059740, R01 NS081243, R01 EB009282, and R01 MH099645 to M. Bazhenov) and by National Science Foundation Grant DMS-1009591, Russian Foundation for Basic Research Grant 11-01-00001, the grant in the agreement of August 27, 2013, N 02.B.49.21.0003, between the Ministry of Education and Science of the Russian Federation and Lobachevsky State University of Nizhni Novgorod (Sections 2–4), and Russian Science Foundation Grant 14-41-00044 at Lobachevsky State University of Nizhni Novgorod (to A. Shilnikov).
DISCLOSURES
The authors have no competing interests.
AUTHOR CONTRIBUTIONS
Author contributions: A.S. and M.B. conception and design of research; G.P.K. and G.F. performed experiments; G.P.K. and G.F. analyzed data; G.P.K., G.F., A.S., and M.B. interpreted results of experiments; G.P.K. prepared figures; G.P.K., A.S., and M.B. drafted manuscript; A.S. and M.B. edited and revised manuscript; A.S. and M.B. approved final version of manuscript.
Appendix
Intrinsic currents used in a single neuron model.
In general, all intrinsic currents were given by
where Gi is the maximal conductance, m and h are gating variables, and Ei is the reversal potential. The gating variables are given by either its steady-state value (m∞, h∞) or by the following differential equations
The set of intrinsic currents of the axosomatic compartment (IsInt) consisted of voltage-gated sodium (PY: GNa = 3,450 mS/cm2; IN: GNa = 3,800 mS/cm2) and delayed-rectifier potassium (PY and IN: GKv = 200 mS/cm2) currents. The axosomatic compartment of the PY neuron also included persistent sodium (GNap = 3.5 mS/cm2) and sodium-activated potassium (GKNa = 1.3 mS/cm2) channels. The dendritic compartment had high-threshold calcium (ICa), calcium-activated potassium (IKCa), slowly activating potassium (IKm), persistent sodium (INap), hyperpolarization-activated, depolarizing-mixed cationic (Ih), potassium leak, and mixed cationic leak (PY: GCa = 0.016, GKCa = 3.5, GKm = 0.01, GNap = 3.5, Gh = 0.1 mS/cm2; IN: Gh = 0.1 mS/cm2) conductances.
The following set of equations describes the evolution of intrinsic currents and gating variables over time. If not otherwise cited, all of the equations are derived from earlier works (Bazhenov et al. 2004; Mainen and Sejnowski 1996).
Voltage-sensitive sodium current
where, ϕ = 2.95 is a correction factor for temperature (Mainen and Sejnowski 1996). The correction factor had the same value (ϕ = 2.95) in all other currents.
Delayed-rectifier potassium current
where
Persistent sodium current (Alzheimer et al. 1993)
Mixed cation current
Sodium-sensitive potassium current (Wang et al. 2003)
Slowly activating potassium current
High-threshold calcium current
Calcium-sensitive potassium current
Synaptic connections and network topology.
All synaptic currents were modeled by first-order activation schemes (Destexhe et al. 1994; Timofeev 2000) and are given by
where θ (x) is the Heaviside function, and t0 is the time of spike. The parameters for the neurotransmitter pulse [T] were amplitude A = 0.5 and duration tmax = 0.3 ms. The rate constants, α and β, were α = 10 ms and β = 0.25 ms for GABA-A synapses and α = 0.94 ms and β = 0.18 ms for AMPA synapses.
A short-term synaptic depression was included, in which the maximal synaptic conductance was multiplied by a depression variable (D ≥ 1) (Tsodyks and Markram 1997). This variable represents the amount of available synaptic resources and was varied based on the following equation
where U = 0.07 is the fraction of resources used per action potential, τ = 700 ms is the time constant of recovery of the synaptic resources, Di is the value of D just before the ith event, and (t − ti) is the time since the ith event.
Methods used in bifurcation analysis.
Bifurcation analysis provides methods to study qualitative changes of the behavior of a model, represented by a dynamical system, as its control parameters are changed. In the context of neuroscience, such changes are transitions among activity types including bursting, tonic spiking, and quiescence. Neuron dynamics can be described by a set of equations, dX/dt = F(X,α), where X is a vector representing dynamical variables of the model, and α represents a vector of control parameters, such as ion concentrations, maximal conductances, etc. The bifurcation analysis model is concerned with the evolution and stability of equilibrium states and periodic orbits of the dynamical systems as α is varied.
Often, neuronal systems may have slow and fast variables, such as concentration of [Ca2+]i (slow) and activation gates of spiking currents (fast). Dynamics of such slow-fast systems are determined by and centered around the attracting pieces of the so-called slow-motion manifolds, composed of equilibria, and limit cycles of its fast subsystem that constitute the backbones of bursting patterns in a neuronal model. A typical Hodgkin-Huxley model possesses a pair of such manifolds: quiescent and tonic spiking. With the use of the parameter-continuation technique (Kuznetsov 1995), implemented in software packages, such as CONTENT and MATCONT, and tailored specifically for slow-fast neuron models (Shilnikov 2012), one can detect and follow the corresponding branches of equilibria and tonic-spiking periodic orbits in the phase space. A neuron model can be treated as slow-fast system x′ = F(x,z) and z′ = μ G(x,z,α), where 0 < μ <<1; x and z are fast and slow dynamic variables; and α is a control parameter shifting the slow nullcline, given by G(x,α) = 0, in the phase space. An intersection of G(x,z,α) = 0 and F(x,z) = 0 in the phase space is an equilibrium state of the system. One can detect branches of the equilibrium states by varying α. In a similar manner, after having found a stable periodic orbit φ(t,X0,z), corresponding to tonic-spiking activity in the neuron at some α, using the parameter continuation approach, one can identify a cylinder-shaped surface Mlc corresponding to the tonic spiking manifold in the phase space of the neuronal model (Shilnikov 2012; Shilnikov and Kolomiets 2008). The topology and reciprocal location and interaction of these manifolds determine the dynamics of neuronal models generating specific voltage oscillations (Izhikevich 2007).
In this study, following a “faux” parameter approach (Channell et al. 2007), we introduced an auxiliary parameter in the equation of the slow [Ca2+] variable to sweep and locate the above manifolds in the 14D phase space of the given model. The topology of the tonic-spiking manifold discovered in this neuron model is unique and has not yet been reported in literature (Ermentrout and Terman 2010). It is shown in Fig. 4. Its feature is the fold on the tonic-spiking manifold Mlc that gives rise to bistability of tonic spiking and bursting in the model, as well as the onset of a 2D torus corresponding to quasiperiodic (modulation) dynamics of the cell at the transition between tonic spiking and bursting activity (Wojcik 2011).
We identified several types of bifurcations in this study, including various SN, AH, and torus bifurcations. These bifurcations determined the dynamics of the neuron under different conditions. The exact definitions of these bifurcations and relation to neuronal system are covered extensively in previous books (Ermentrout and Terman 2010; Izhikevich 2007; Shilnikov et al. 1998, 2001).
In this study, bifurcation analysis was carried out for the 14D system {which included Vd, activation and deactivation of voltage-sensitive sodium current in soma and dendrite (mINa, hINa, mINaD, hINaD), activation of somatic delayed-rectifier potassium current (mIK), activation of dendritic slowly activating potassium current (mIKm), activation of dendritic and somatic persistent sodium current (mINaps, mINad), activation and inactivation of dendritic high-threshold calcium current (mIHVA, hIHVA), activation of calcium-sensitive potassium current (mIKca), activation of mixed cation current (mIh), and [Ca2+]i}. The exact code, which was used in the software CONTENT (Kuznetsov 1998), for performing all of the main bifurcation analyses presented in this paper is available at the ModelDB site (https://senselab.med.yale.edu/ModelDB/default.cshtml).
REFERENCES
- Alzheimer C, Schwindt PC, Crill WE. Modal gating of Na+ channels as a mechanism of persistent Na+ current in pyramidal neurons from rat and cat sensorimotor cortex. J Neurosci 13: 660–673, 1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arganda S, Guantes R, De Polavieja GG. Sodium pumps adapt spike bursting to stimulus statistics. Nat Neurosci 10: 1467–1473, 2007. [DOI] [PubMed] [Google Scholar]
- Ballerini L, Bracci E, Nistri A. Pharmacological block of the electrogenic sodium pump disrupts rhythmic bursting induced by strychnine and bicuculline in the neonatal rat spinal cord. J Neurophysiol 77: 17–23, 1997. [DOI] [PubMed] [Google Scholar]
- Barreto E, Cressman JR. Ion concentration dynamics as a mechanism for neuronal bursting. J Biol Phys 37: 361–373, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bazhenov M, Timofeev I, Steriade M, Sejnowski TJ. Potassium model for slow (2–3 Hz) in vivo neocortical paroxysmal oscillations. J Neurophysiol 92: 1116–1132, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Channell P Jr, Cymbalyuk G, Shilnikov A. Applications of the Poincaré mapping technique to analysis of neuronal dynamics. Neurocomputing 70: 2107–2111, 2007. [Google Scholar]
- Chen JY, Chauvette S, Skorheim S, Timofeev I, Bazhenov M. Interneuron-mediated inhibition synchronizes neuronal activity during slow oscillation. J Physiol 590: 3987–4010, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clapcote SJ, Duffy S, Xie G, Kirshenbaum G, Bechard AR, Schack VR, Petersen J, Sinai L, Saab BJ, Lerch JP, Minassian BA, Ackerley CA, Sled JG, Cortez MA, Henderson JT, Vilsen B, Roder JC. Mutation I810N in the alpha3 isoform of Na+,K+-ATPase causes impairments in the sodium pump and hyperexcitability in the CNS. Proc Natl Acad Sci USA 106: 14085–14090, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cressman JR, Ullah G, Ziburkus J, Schiff SJ, Barreto E. The influence of sodium and potassium dynamics on excitability, seizures, and the stability of persistent states: I. Single neuron dynamics. J Comput Neurosci 26: 159–170, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A, Mainen ZF, Sejnowski TJ. Synthesis of models for excitable membranes, synaptic transmission and neuromodulation using a common kinetic formalism. J Comput Neurosci 1: 195–230, 1994. [DOI] [PubMed] [Google Scholar]
- Dietzel I, Heinemann U, Hofmeier G, Lux HD. Stimulus-induced changes in extracellular Na+ and Cl− concentration in relation to changes in the size of the extracellular space. Exp Brain Res 46: 73–84, 1982. [DOI] [PubMed] [Google Scholar]
- Doedel EJ, Champneys AR, Fairgrieve TF, Kuznetsov YA, Sandstede B, Wang X. AUTO 97: Continuation and Bifurcation Software for Ordinary Differential Equations (with HomCont). Montreal, Canada: Concordia University, 1997. (Technical Report). [Google Scholar]
- Donaldson J, Minnich J, Barbeau A. Ouabain-induced seizures in rats: regional and subcellular localization of 3 H-ouabain associated with Na + -K + -ATPase in brain. Can J Biochem 50: 888–896, 1972. [DOI] [PubMed] [Google Scholar]
- Donaldson J, St-Pierre T, Minnich J, Barbeau A. Seizures in rats associated with divalent cation inhibition of NA + -K + -ATP'ase. Can J Biochem 49: 1217–1224, 1971. [DOI] [PubMed] [Google Scholar]
- El-Mallakh RS, Wyatt RJ. The Na, K-ATPase hypothesis for bipolar illness. Biol Psychiatry 37: 235–244, 1995. [DOI] [PubMed] [Google Scholar]
- Ermentrout GB, Terman DH. Mathematical Foundations of Neuroscience. New York: Springer, 2010, vol 35. [Google Scholar]
- Fleidervish IA, Lasser-Ross N, Gutnick MJ, Ross WN. Na+ imaging reveals little difference in action potential-evoked Na+ influx between axon and soma. Nat Neurosci 13: 852–860, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fröhlich F, Bazhenov M. Coexistence of tonic firing and bursting in cortical neurons. Phys Rev E Stat Nonlin Soft Matter Phys 74: 031922, 2006. [DOI] [PubMed] [Google Scholar]
- Fröhlich F, Bazhenov M, Timofeev I, Steriade M, Sejnowski TJ. Slow state transitions of sustained neural oscillations by activity-dependent modulation of intrinsic excitability. J Neurosci 26: 6153–6162, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fröhlich F, Sejnowski TJ, Bazhenov M. Network bistability mediates spontaneous transitions between normal and pathological brain states. J Neurosci 30: 10734–10743, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallanti A, Tonelli A, Cardin V, Bussone G, Bresolin N, Bassi MT. A novel de novo nonsense mutation in ATP1A2 associated with sporadic hemiplegic migraine and epileptic seizures. J Neurol Sci 273: 123–126, 2008. [DOI] [PubMed] [Google Scholar]
- Glitsch HG. Electrophysiology of the sodium-potassium-ATPase in cardiac cells. Physiol Rev 81: 1791–1826, 2001. [DOI] [PubMed] [Google Scholar]
- Goldstein I, Lerer E, Laiba E, Mallet J, Mujaheed M, Laurent C, Rosen H, Ebstein RP, Lichtstein D. Association between sodium- and potassium-activated adenosine triphosphatase alpha isoforms and bipolar disorders. Biol Psychiatry 65: 985–991, 2009. [DOI] [PubMed] [Google Scholar]
- Grisar T. Glial and neuronal Na+-K+ pump in epilepsy. Ann Neurol 16: S128–S134, 1984. [DOI] [PubMed] [Google Scholar]
- Grisar T, Guillaume D, Delgado-Escueta AV. Contribution of Na+,K(+)-ATPase to focal epilepsy: a brief review. Epilepsy Res 12: 141–149, 1992. [DOI] [PubMed] [Google Scholar]
- Haglund MM, Schwartzkroin PA. Role of Na-K pump potassium regulation and IPSPs in seizures and spreading depression in immature rabbit hippocampal slices. J Neurophysiol 63: 225–239, 1990. [DOI] [PubMed] [Google Scholar]
- Houweling AR, Bazhenov M, Timofeev I, Steriade M, Sejnowski TJ. Homeostatic synaptic plasticity can explain post-traumatic epileptogenesis in chronically isolated neocortex. Cereb Cortex 15: 834–845, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich EM. Dynamical Systems in Neuroscience. Cambridge, MA: The MIT Press, 2007. [Google Scholar]
- Kager H, Wadman WJ, Somjen GG. Conditions for the triggering of spreading depression studied with computer simulations. J Neurophysiol 88: 2700–2712, 2002. [DOI] [PubMed] [Google Scholar]
- Kager H, Wadman WJ, Somjen GG. Simulated seizures and spreading depression in a neuron model incorporating interstitial space and ion concentrations. J Neurophysiol 84: 495–512, 2000. [DOI] [PubMed] [Google Scholar]
- Katz DC, Rose FA, Erk Y, Spira M. A one-suture end-to-side microvascular sleeve anastomosis: preliminary report. J Microsurg 3: 15–19, 1981. [DOI] [PubMed] [Google Scholar]
- Kramer MA, Truccolo W, Eden UT, Lepage KQ, Hochberg LR, Eskandar EN, Madsen JR, Lee JW, Maheshwari A, Halgren E. Human seizures self-terminate across spatial scales via a critical transition. Proc Natl Acad Sci USA 109: 21116–21121, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan GP, Bazhenov M. Ionic dynamics mediate spontaneous termination of seizures and postictal depression state. J Neurosci 31: 8870–8882, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan GP, Filatov G, Bazhenov M. Dynamics of high-frequency synchronization during seizures. J Neurophysiol 109: 2423–2437, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuznetsov Y. Elements of Applied Bifurcation Theory. New York: Springer-Verlag, 1995, p. 664. [Google Scholar]
- Kuznetsov YA. CONTENT—Integrated Environment for Analysis of Dynamical Systems. Tutorial. École Normale Supérieure de Lyon, Rapport de Recherche UPMA-98-224, 1998. [Google Scholar]
- Läuger P. Electrogenic Ion Pumps. Sunderland, MA: Sinauer Associates, 1991. [Google Scholar]
- Mainen ZF, Sejnowski TJ. Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 382: 363–366, 1996. [DOI] [PubMed] [Google Scholar]
- Markram H, Toledo-Rodriguez M, Wang Y, Gupta A, Silberberg G, Wu C. Interneurons of the neocortical inhibitory system. Nat Rev Neurosci 5: 793–807, 2004. [DOI] [PubMed] [Google Scholar]
- Neiman AB, Dierkes K, Lindner B, Han L, Shilnikov AL. Spontaneous voltage oscillations and response dynamics of a Hodgkin-Huxley type model of sensory hair cells. J Math Neurosci 1: pii: 11, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payne JA, Rivera C, Voipio J, Kaila K. Cation-chloride co-transporters in neuronal communication, development and trauma. Trends Neurosci 26: 199–206, 2003. [DOI] [PubMed] [Google Scholar]
- Roberts WM, Almers W. Patch voltage clamping with low-resistance seals: loose patch clamp. Methods Enzymol 207: 155–176, 1992. [DOI] [PubMed] [Google Scholar]
- Rose AM, Valdes R. Understanding the sodium pump and its relevance to disease. Clin Chem 40: 1674–1685, 1994. [PubMed] [Google Scholar]
- Ross ST, Soltesz I. Selective depolarization of interneurons in the early posttraumatic dentate gyrus: involvement of the Na(+)/K(+)-ATPase. J Neurophysiol 83: 2916–2930, 2000. [DOI] [PubMed] [Google Scholar]
- Shilnikov A. Complete dynamical analysis of a neuron model. Nonlinear Dyn 68: 305–328, 2012 [Google Scholar]
- Shilnikov A, Kolomiets M. Methods of the qualitative theory for the Hindmarsh-Rose model: a case study. A tutorial. Int J Bifurcat Chaos 18: 2141–2168, 2008. [Google Scholar]
- Shilnikov LP, Shilnikov AL, Turaev DV, Chua LO. Methods of Qualitative Theory in Nonlinear Dynamics (World Scientific Series on Nonlinear Science), Part I. Hackensack, NJ: World Scientific, 1998. [Google Scholar]
- Shilnikov LP, Shilnikov AL, Turaev DV, Chua LO. Methods of Qualitative Theory in Nonlinear Dynamics (World Scientific Series on Nonlinear Science), Part II. Hackensack, NJ: World Scientific, 2001. [Google Scholar]
- Somjen GG. Ion regulation in the brain: implications for pathophysiology. Neuroscientist 8: 254–267, 2002. [DOI] [PubMed] [Google Scholar]
- Tavalin SJ, Ellis EF, Satin LS. Inhibition of the electrogenic Na pump underlies delayed depolarization of cortical neurons after mechanical injury or glutamate. J Neurophysiol 77: 632–638, 1997. [DOI] [PubMed] [Google Scholar]
- Tavraz NN, Friedrich T, Durr KL, Koenderink JB, Bamberg E, Freilinger T, Dichgans M. Diverse functional consequences of mutations in the Na+/K+-ATPase alpha2-subunit causing familial hemiplegic migraine type 2. J Biol Chem 283: 31097–31106, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas R. Electrogenic sodium pump in nerve and muscle cells. Physiol Rev 52: 563–594, 1972. [DOI] [PubMed] [Google Scholar]
- Timofeev I, Grenier F, Bazhenov M, Sejnowski TJ, Steriade M. Origin of slow cortical oscillations in deafferented cortical slabs. Cereb Cortex 10: 1185–1199, 2000. [DOI] [PubMed] [Google Scholar]
- Timofeev I, Steriade M. Neocortical seizures: initiation, development and cessation. Neuroscience 123: 299–336, 2004. [DOI] [PubMed] [Google Scholar]
- Tsodyks MV, Markram H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc Natl Acad Sci USA 94: 719–723, 1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaillend C, Mason SE, Cuttle MF, Alger BE. Mechanisms of neuronal hyperexcitability caused by partial inhibition of Na+-K+-ATPases in the rat CA1 hippocampal region. J Neurophysiol 88: 2963–2978, 2002. [DOI] [PubMed] [Google Scholar]
- Wang XJ, Liu Y, Sanchez-Vives MV, McCormick DA. Adaptation and temporal decorrelation by single neurons in the primary visual cortex. J Neurophysiol 89: 3279–3293, 2003. [DOI] [PubMed] [Google Scholar]
- Wojcik J, Shilnikov A. Voltage interval mappings for activity transitions in neuron models for elliptic bursters. Physica D 240.14: 1164–1180, 2011. [Google Scholar]
- Worrell G, Gotman J. High-frequency oscillations and other electrophysiological biomarkers of epilepsy: clinical studies. Biomark Med 5: 557–566, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu N, Morris CE, Joós B, Longtin A. Spontaneous excitation patterns computed for axons with injury-like impairments of sodium channels and Na/K pumps. PLoS Comp Biol 8: e1002664, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zandt BJ, Stigen T, ten Haken B, Netoff T, van Putten MJ. Single neuron dynamics during experimentally induced anoxic depolarization. J Neurophysiol 110: 1469–1475, 2013. [DOI] [PubMed] [Google Scholar]