Deterministic identification of specific individuals from GWAS results

Abstract

Motivation: Genome-wide association studies (GWASs) are commonly applied on human genomic data to understand the causal gene combinations statistically connected to certain diseases. Patients involved in these GWASs could be re-identified when the studies release statistical information on a large number of single-nucleotide polymorphisms. Subsequent work, however, found that such privacy attacks are theoretically possible but unsuccessful and unconvincing in real settings.

Results: We derive the first practical privacy attack that can successfully identify specific individuals from limited published associations from the Wellcome Trust Case Control Consortium (WTCCC) dataset. For GWAS results computed over 25 randomly selected loci, our algorithm always pinpoints at least one patient from the WTCCC dataset. Moreover, the number of re-identified patients grows rapidly with the number of published genotypes. Finally, we discuss prevention methods to disable the attack, thus providing a solution for enhancing patient privacy.

Availability and implementation: Proofs of the theorems and additional experimental results are available in the support online documents. The attack algorithm codes are publicly available at https://sites.google.com/site/zhangzhenjie/GWAS_attack.zip. The genomic dataset used in the experiments is available at http://www.wtccc.org.uk/ on request.

Contact: winslett@illinois.edu or zhenjie@adsc.com.sg

Supplementary information: Supplementary data are available from Bioinformatics online.

1 Introduction

Genome-wide association studies (GWAS) (Hunter et al., 2007; Scott et al., 2007; Sladek et al., 2007; Yeager et al., 2007; Zeggini et al., 2007) are widely used to identify loci in the human genome associated with a specific diseases. The basis of these studies is to associate single-nucleotide polymorphisms (SNPs) or genotypes with the disease phenotype in a case–control design (Hunter et al., 2007). Although a scientific article may present GWAS results at low precision (e.g. correlation between genotypes shown only in a heat map), detailed and accurate results are often available upon request. It is standard to protect the privacy of the participating subjects by keeping patient identities confidential.

Since GWAS results are statistical in nature, until recently most researchers believed that it is safe to share and publish such de-identified results. This belief was challenged by recent bioinformatics research (Homer et al., 2008; Wang et al., 2009), which shows that it is theoretically possible to re-identify individual participants using only aggregate genomic data. Notably, Homer et al. (2008) describe the first such method based on statistical hypothesis testing. This method requires aggregate information from many genotypes (e.g. tens of thousands) to obtain high confidence regarding an individual’s presence in the aggregate. In contrast, a GWAS usually publishes statistics for a much smaller number of genotypes. Therefore, using the approach suggested by Homer et al., access to the whole genotype association dataset would be necessary to accomplish this identification. Access to such complete datasets is restricted and limited only to qualified biomedical researchers with proper vetting (e.g. refer to NIH’s policy for sharing GWAS data, http://grants.nih.gov/grants/guide/notice-files/NOT-OD-07-088.html.). Wang et al. (2009) propose a more ambitious approach that aims to find all genotypes for every patient in the GWAS. This attack, however, rarely succeeds, because the number of unknowns far exceeds the number of known values. In fact, Wang et al. (2009) report only one particular synthetic GWAS involving 174 SNPs and 100 patients on which the attack succeeded. A follow-up study (Zhou et al., 2011) tested this attack with GWAS instances from randomly selected sets of SNPs and did not find any instance on which the attack succeeded. We conclude that none of the existing methods poses a direct threat to GWAS participants’ privacy based on the data that is presented in standard publications.

In data security, the development of effective countermeasures requires the identification of a successful attack algorithm. In this article, we devise a strong privacy attack on published GWAS results, which successfully identifies specific patients by using a strategy of constructing deterministic proofs of study inclusion.

2 Methods

2.1 Preliminaries and problem definition

A typical GWAS recruits two groups of individuals: cases (denoted by D^c) and controls (denoted by D^t). Cases are patients of the disease under investigation, and controls are similar people without the disease. Usually, each SNP has two possible alleles, called the major allele (i.e. the more common allele on the SNP) and the minor allele (the rarer one). Let A denote the major allele and a be the minor allele, {AA, Aa, aa} are the three possible genotypes. Among the three basic models, AA and Aa are taken as the same in the dominant model, aa and Aa are not distinguished in the recessive model and only the additive model takes Aa as an individual genotypes (Haines and Pericak-Vance, 2006). Thus, GWAS with two genotypes is the typical case and is the focus of this work. For the simplicity of presentation, the two genotypes are denoted as 0 (major genotype)/1 (minor genotype), as used in previous studies, e.g. Fraser et al. (2005); Hinney et al. (2007); Ozeki et al. (2011).

Suppose that the GWAS results involve d loci of the human genome, denoted as $\{g_1,g_2,\cdots ,g_d\}$. In genetic model with two genotypes, e.g. the dominant model and the recessive model, we represent the genomic information of an individual by a d-dimensional binary vector x_i, in which each binary variable x_ij represents the genotype of x_i on g_j. Let N^c and N^t be the total number of cases and controls, respectively. For each genotype g_j, we define the following four counts of individuals: $n_j^c$ (respectively $m_j^c$), number of cases having genotype 0(respectively 1) on g_j; $n_j^t$ (respectively $m_j^t$), number of controls having genotype 0(respectively 1) on g_j.

A typical GWAS result includes N^c, N^t and the following three important statistics: the genotype frequency for each genotype, the genotype–disease association of each genotype and the pairwise correlation for each pair of genotypes.

2.1.1 Genotype frequency

The frequency of a minor genotype g_j = 1 is usually computed by $F_j=\frac{n^c+n^t}{N^c+N^t}$, i.e. the ratio between the total number of individuals having the minor genotype on g_j and the total number of GWAS participants.

2.1.2 Genotype–disease association

GWAS commonly uses the following equation to measure the association between a genotype (let g_j) and the disease under study: $V_j=\frac{{(n_j^c{N}^t+n_j^c{N}^c-F_j{N}^c)}^2}{(N^c+N^t-F_j)F_j{N}^c{N}^t}$. The asymptotical distribution of V_j is a ${\chi }^2$ distribution with freedom degree 1, following the standard procedure (McDonald, 2009). The P value of the insignificant difference is thus $1-{\chi }^2\left(d_j,1\right)$, in which we abuse ${\chi }^2(·,·)$ to denote the accumulative distribution function of ${\chi }^2$ with specific degree of freedom. In the following, we assume that the GWAS publishes the P values defined above, denoted as $P(V_j)$, which is true for many GWASs today. Note that our attack is not limited to this particular definition of genotype–disease association but works on any definition in which $n_j^c$ can be expressed as a function of V_j, N^c, N^t and F_j, such as the one above.

2.1.3 Genotype–genotype correlation

For each pair of loci (say g_j and g_k), there are four possible combinations of genotypes, which are (0,0) (i.e. g_j = 0 and g_k = 0), (0,1), (1,0) and (1, 1). Let $M_{jk}^{00},M_{jk}^{01},M_{jk}^{10}$ and $M_{jk}^{11}$ denote the number of cases having each of these four combinations, respectively. The correlation between g_i and g_j can be measured as follows: $V_{jk}=\frac{{(M_{jk}^{11}{M}_{jk}^{00}-M_{jk}^{10}{M}_{jk}^{01})}^2}{\left(M_{jk}^{11}+M_{jk}^{10}\right)\left(M_{jk}^{01}+M_{jk}^{11}\right)\left(M_{jk}^{00}+M_{jk}^{01}\right)\left(M_{jk}^{00}+M_{jk}^{10}\right)}$. Similar to V_j, V_jk also follows the asymptotical ${\chi }^2$ distribution, with degree of freedom 1. Therefore, the corresponding P value, $P(V_{jk})=1-{\chi }^2(V_{jk},1)$ is published as part of GWAS results.

We assume that the attacker possesses a candidate set D and the genomic information of each individual in D. By ‘genomic information’, we mean the set of genotypes published in the GWAS results. We distinguish two situations, closed world and open world. Under closed world assumption, the candidate set D is always a superset of the GWAS cases D^c, i.e. $D^{\text{c}}\subseteq D$. Such a candidate set can be obtained, for instance by a curious staff member of the hospital or research center where the GWAS was conducted. Note that the candidate set D can contain much more people than the GWAS cases D^c, e.g. D can be the set of all individuals whose genome sequences are stored in the hospital or research center. On the other hand, under the open world assumption, the patients in D^c may not be completely covered by the candidate set D known by the adversary. Later, we will analyze the effectiveness of our approach under these two assumptions, respectively.

Given the above assumption, the goal of the attacker is to identify individuals in D that belong to the cases of the GWAS based on the GWAS statistics. The formal definition of the attack problem is summarized as follows.

Definition 1 —

GWAS Privacy Attack Problem

Given candidate set D and GWAS statistics $\{F_j,V_j,V_{jk}\}$, identify as many samples in D as possible that belong to D^c.

2.2 Framework

Assume that the study has identified a set of loci that are associated with the disease, and a set of statistics are published on the genotypes. The published statistics includes the frequency of the minor genotype on each identified locus; the P value of the genotype–disease association for each identified locus and the P value of the genotype–genotype correlation for each pairs of identified loci. Based on the published statistics, a three-step framework is devised to identify specific individuals from GWAS results, recovering the co-occurrence matrices $\{M^{11},M^{10},M^{01},M^{00}\}$, finding presence proofs ρ and finally re-identifying cases from candidates. The framework is summarized in the Algorithm 1.

Algorithm 1. GWAS attack.

Input: D, candidate case set; F_j, frequency of the minor genotypes on g_j; $P(V_j)$, P value of the association between g_j and the disease; $P(V_{jk})$, P value of the correlation between g_i and g_k.

1: Step 1: Recovering the co-occurrence matrices $\{M^{11},M^{10},M^{01},M^{00}\}$. using F_j, $P(V_j)$ and $P(V_{jk})$.

2: Step 2: Finding presence proofs ρ using $\{M^{11},M^{10},M^{01},M^{00}\}$.

3: Step 3: Re-identifying cases from candidates D based on proofs ρ.

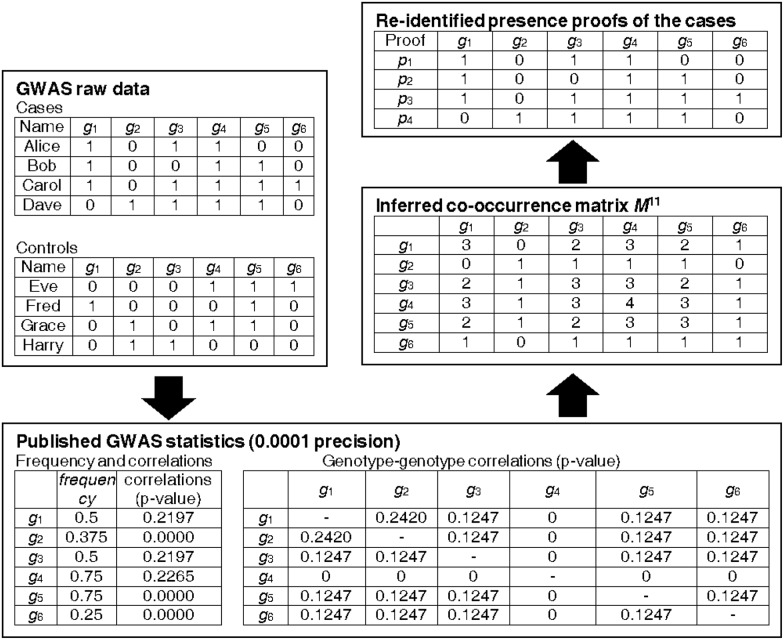
Figure 1 presents an example of GWAS results and an overview of the attack on the example. As shown in the left part of Figure 1, the study has identified a set of loci, and for each locus, the GWAS publishes its minor genotype frequency, the association between the loci and the disease and the genotype–genotype correlation. As shown in right part of Figure 1, our privacy attack attempts to reverse the above process. The attack first infers the co-occurrence matrices from the published statistics, which contains aggregate information about the cases in the GWAS (only the M¹¹ is given in the Figure for the space limitation). Then, the attack applies an iterative data mining algorithm with the matrices to recover sets of genotype subsequences that must occur in the cases, which we call presence proofs in this article. Each presence proof contains characteristics of an individual’s genome who is one of the cases. Finally, given the genotypes of a particular candidate, the attack checks whether that individual is known to be among the cases, by checking whether their genotypes match any presence proof. In the following, we elaborate on these three steps.

Fig. 1.

Example of GWAS result publication and the privacy attack. Top left: part of the raw data of the GWAS, which contains genome sequences for study participants. Bottom: published results of the GWAS, which lists the genotypes of interest, their frequencies and correlation with the disease, as well as the correction between each pair of these genotypes. Right column: the proposed privacy attack, which first recovers a co-occurrence matrix from the published statistics (only M¹¹ is given for space limitation) and uses this matrix to build presence proofs, i.e. sets of genotypes that must be present among the cases

2.3 Step 1: recovering the co-occurrence matrix

Recovering the co-occurrence matrices $\{M^{11},M^{10},M^{01},M^{00}\}$ is the first step of the attack. Note that there are four correlated co-occurrence matrices, M¹¹, M¹⁰, M⁰¹ and M⁰⁰. For each pair of loci (say g_j and g_k), $M_{jk}^{11}$ in matrix M¹¹ is the number of cases having minor genotype on both g_j and g_k, i.e. g_j = 1 and g_k = 1. Similarly, M¹⁰, M⁰¹ and M⁰⁰ contain elements on the number of cases with corresponding combination of g_j and g_k.

Moreover, the diagonal element $M_{jj}^{11}$ in the matrix M¹¹ represents the number of cases with a minor genotype on g_j, i.e. g_j = 1. These diagonal elements can thus be derived directly using the published minor genotype frequency F_j, the genotype–disease association $P(V_j)$ and the number of cases N^t. This step is trivial if the GWAS results contain the frequency computed on the cases only, as multiplying each F_j with the total number of cases N^c would yield the corresponding value in $M_{jj}^{11}$. Hence, we focus on the case where the minor genotype frequency is computed based on all participants of the GWAS. From the published P value for the genotype–disease association of each locus (say g_j), we derive the corresponding value of V_j. Then, using V_j, N^c (i.e. total number of cases), N^t (total number of controls) and F_j, we solve $M_{jj}=n_j^c$ from the definition of V_j.

An off-diagonal element in the matrix, i.e. $M_{jk}^{11}(j\ne k)$, represents the number of cases with both a minor genotypes on g_j and a minor genotypes on g_k, i.e. g_i = 1 and g_k = 1. Once we have M_jj and M_kk ready, we can solve M_jk from the definition of $P(V_{jk})$, using the existing numbers of $P(V_{jk})$ and $M_{jj}^{11}$.

When the matrix M¹¹ is completely recovered, it is straightforward to recover the other three matrices M¹⁰, M⁰¹ and M⁰⁰. For M⁰¹, the recovery is based on the equation $M_{jk}^{01}=M_{kk}^{11}-M_{jk}^{11}$, i.e. the number of cases with major genotype g_j and minor genotype g_k, equals the number of cases with minor genotype g_k minus the number of cases with minor genotype g_j and minor genotype g_k. Similarly, we have $M_{jk}^{10}=M_{jj}^{11}-M_{jk}^{11}$ and $M_{jk}^{00}=N^c-M_{jk}^{11}-M_{jk}^{01}-M_{jk}^{10}$. Thus, $M_{jk}^{00},M_{jk}^{01}$ and $M_{jk}^{10}$ can be recovered, when accurate numbers in $M_{jk}^{11}$ are available.

When the published statistics are exact, all values of Ms can be computed by solving simple mathematical equations. When these statistics are only available with limited precision, the computation of Ms is more complicated. Moreover, it is possible that some values in these matrices cannot be uniquely determined. When this happens, we discard all rows and columns of Ms that contain at least one undetermined value and proceed with the remaining sub-matrices. In the supporting document, we provide a rigorous analysis of the sufficient conditions for co-occurrence matrix recovery, in terms of the precision of the statistics contained in the GWAS results. Moreover, when two genotypes are from different chromosomes, the co-occurrence value between them cannot be uniquely determined and corresponding value is discarded like that of the limited precision case.

The above statistics are also closely related to the SNP-based statistics. For example, in the dominant model, {AA, Aa} are denoted as 0 and aa is denoted as 1. Then we have $\frac{1}{2}{M}_{ij}^{aa}\hspace{0.17em}\le \hspace{0.17em}{M}_{ij}^{11}\hspace{0.17em}\le \hspace{0.17em}{M}_{ij}^{aa}$, e.g. the number of minor genotype is bounded by the number of minor alleles. Here, $M_{jk}^{aa}$ is the number of cases having minor allele a on both g_j and g_k. When a is a rare variant, $M_{ij}^{aa}$ will be small enough to provide a tight bound of $M_{ij}^{11}$.

2.4 Step 2: finding presence proofs

The second step of the attack uses the inferred co-occurrence matrices to construct presence proofs. A presence proof (or designated as simply ‘proof’) is a set of genotypes, such that at least one patient in the cases has exactly these genotypes. The number of genotypes in a presence proof is called the length of the proof. An example length-3 presence proof is $p=\langle g_1=1,g_2=0,g_3=1\rangle$. We say that an individual x matches a presence proof, if and only if, x’s genome contains all the genotypes of the proof. For example, to match the above presence proof p, an individual’s genome must have minor genotype (i.e. genotype 1) on g₁ and g₃ and major genotype (i.e. genotype 0) on g₂. We call the number of cases matching a proof its frequency. The formal definition of presence proof and matching between a presence proof and an individual are given as follows.

Definition 2 —

Presence Proof and Proof Match

A presence proof is a quintuple $\rho =(s_{\rho },I_{\rho },A_{\rho },l_{\rho },u_{\rho })$, where $1\hspace{0.17em}\le \hspace{0.17em}{s}_{\rho }\hspace{0.17em}\le \hspace{0.17em}d$, called the length of ρ, is the number of genotypes involved in ρ, $I_{\rho }=\{j_1,j_2,\dots ,j_{s_{\rho }}\}$ are the indices of the involved loci, $A_{\rho }=\{a_1,a_2,\dots ,a_{s_{\rho }}\}\in {\{0,1\}}^{s_{\rho }}$ are the genotypes of the proofs on the corresponding loci, $l_{\rho }$ and $u_{\rho }$ are the lower bound and upper bound on the frequency of ρ. An individual x_i matches a presence proof ρ, if, for each $j\in I_{\rho }$, the genotype of x_i on g_j is identical to the corresponding genotype in A_ρ.

Based on the above definition, this step aims to identify presence proofs by iteratively building longer proofs from shorter ones, using a novel algorithm that resembles a priori (Agrawal et al., 1994), a commonly used data mining strategy. In the following, we use the notation $D_c^{\rho }$ to denote the set of GWAS cases that match a proof ρ. Clearly, $l_{\rho }\hspace{0.17em}\le \hspace{0.17em}|D_c^{\rho }|\hspace{0.17em}\le \hspace{0.17em}{u}_{\rho }$. Let ${\mathcal{L}}_s$ (called length-s proofs) denote the set of presence proofs, we are going to find that involve exactly s genotypes. The algorithm initializes with ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$, which can be trivially obtained from the co-occurrence matrix. Specifically, there are two length-1 proofs for each locus g_j: (1, {j}, {0}, $n_j^c,n_j^c$) and (1, {j}, {0}, $m_j^c,m_j^c$). Regarding ${\mathcal{L}}_2$, for each pair of loci g_j and g_k, there are four proofs: $(2,\{j,k\},\{0,0\},M_{jk}^{00},M_{jk}^{00}),(2,\{j,k\},\{0,1\},M_{jk}^{01},M_{jk}^{01}),(2,\{j,k\},\{1,0\},M_{jk}^{10},M_{jk}^{10})$ and $(2,\{j,k\},\{1,1\},M_{jk}^{11},M_{jk}^{11})$.

We now describe the iterative procedure that builds a proof of length s + 1 from two proofs of length s. Given two presence proofs ρ and π of length s, i.e. $s_{\rho }=s_{\pi }=s$, we say ρ and π share the same prefix, iff. (i) I_ρ and I_π share the same first s – 1 genotypes, (ii) the last genotype in I_ρ is different than the last one in I_π and (iii) A_ρ and A_π share the same first s – 1 genotypes. A new presence proof σ of length s_σ = s + 1 is constructed by merging ρ and π, denoted as $\sigma =\rho ○\pi$; specifically, I_σ contains all s indices of I_ρ, plus one more which is the last index in I_π; similarly, A_σ contains all s genotypes of A_ρ, as well as the last genotype in A_π.

It remains to compute l_σ and u_σ, i.e. the lower bound and upper bound on the frequency of the candidate proof σ. We first define the intersection ξ of ρ and π (denoted as $\xi =\rho ·\pi$) as the prefix that ρ and π share in common, i.e., $s_{\xi }=s-1,I_{\xi }$ consists of the first s – 1 indices of I_ρ and A_ξ consists of the first s – 1 indices of A_ρ. Since ξ is shorter than ρ and π, it must have been generated before ρ and π in our algorithm, which means that the l_ξ and u_ξ are already known. The following lemma shows how to compute l_σ and u_σ. The proof of the lemma is given in the support online documents.

Lemma 1 —

Given presence proofs ρ and π that share the same prefix, their concatenation $\sigma =\rho ○\pi$, and their intersection $\xi =\rho ·\pi$. Let j_ρ and a_ρ be the last index and genotype in ρ, and j_π and a_π be the last index and genotype in π. We have

$$|D_c^{\sigma }|\hspace{0.17em}\le \hspace{0.17em}\min \{|D_c^{\rho }|,|D_c^{\pi }|,M_{j_{\rho }{j}_{\pi }}^{a_{\rho }{a}_{\pi }}\}$$ (1)

$$|D_c^{\sigma }|\hspace{0.17em}\ge \hspace{0.17em}|D_c^{\rho }|+|D_c^{\pi }|-|D_c^{\xi }|.$$ (2)

Accordingly, we have:

$$u_{\sigma }=\min \left\{u_{\rho },u_{\pi },M_{j_{\rho }{j}_{\pi }}^{a_{\rho }{a}_{\pi }}\right\}$$ (3)

$$l_{\sigma }=l_{\rho }+l_{\pi }-u_{\xi }$$ (4)

We summarize the presence proof generation procedure in Algorithm 2. The algorithm first generates presence proofs of lengths 1 and 2 from the co-occurrence matrix. Then, it iteratively generates new proofs of length m + 1, by concatenating two proofs of length m that share the same prefix. The algorithm terminates when an empty level is generated.

Algorithm 2. Generate presence proofs.

Input: M, the co-occurrence matrix.

1: Build length-1 and length-2 presence proofs ${\mathcal{L}}_1$ and ${\mathcal{L}}_2$.

2: while ${\mathcal{L}}_s\ne \varnothing$ do

3:  Initialize an empty ${\mathcal{L}}_{s+1}$

4:  for each pair of ρ and π in ${\mathcal{L}}_s$ sharing length s – 1 prefix do

5:   Construct a new presence proof $\sigma =\rho ○\pi$

6:   Find the presence proof $\xi =\rho •\pi$

7:   Set j_ρ and a_ρ be the last index and genotype in ρ

8:   Set j_π and a_π be the last index and genotype in π

9:   Set $l_{\sigma }=l_{\rho }+l_{\pi }-u_{\xi }$

10:   Set $u_{\sigma }=\min \{|D_c^{\rho }|,|D_c^{\pi }|,M_{j_{\rho }{j}_{\pi }}^{a_{\rho }{a}_{\pi }}\}$

11:    if $l_{\sigma }>0$ then

12:  Add σ to ${\mathcal{L}}_{s+1}$

13:  Increment s by 1

14: Return all presence proofs

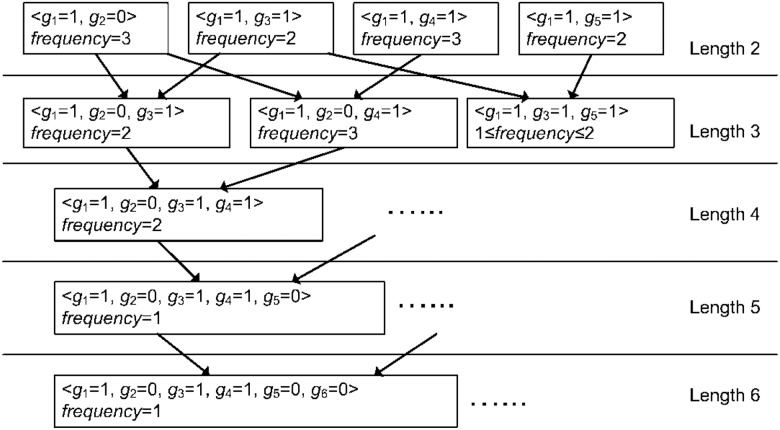
Figure 2 presents an example of the iterative generation of proofs, for the GWAS data shown in Figure 1. We start with length 1 proofs, which are single genotypes on the loci included in the co-occurrence matrix M. In our example, there are 12 such proofs, i.e. genotype 0 and 1 for each of g₁, g₆. The frequency of each of these proofs is derived directly from the diagonal values of M, e.g. the frequency of $\langle g_1=1\rangle$ is $M_{11}^{11}=3$. We discard proofs with zero frequency, e.g. $\langle g_4=0\rangle$, as they do not match any patient in the cases. Next, we construct length-2 presence proofs (e.g. $\langle g_1=1,g_2=0\rangle$), each by combining two length-1 proofs (e.g. $\langle g_1=1\rangle$ and $\langle g_2=0\rangle$). We compute the frequency of each length-2 proof as well, from the frequencies of length-1 proofs and the co-occurrence matrix. For instance, the frequency of $\langle g_1=1,g_2=0\rangle$ is computed by subtracting $M_{12}^{11}$ (the number of cases with minor genotype on both g₁ and g₂) from the frequency of $\langle g_1=1\rangle$. Again, we discard zero-frequency proofs. A proof of length $s\hspace{0.17em}\ge \hspace{0.17em}2$ is built by merging (i.e. taking the set union of all genotypes) two proofs of length $s-1$ that differ in exactly one genotype. For example $\langle g_1=1,g_2=0,g_3=1,g_4=1\rangle$ can be built by merging $\langle g_1=1,g_2=0,g_3=1\rangle$ and $\langle g_1=1,g_2=0,g_4=1\rangle$. In general, the frequency of a proof with length at least 3 cannot be computed directly from the co-occurrence matrix. Instead, we derive a lower bound and an upper bound for each such proof as shown in Lemma 1. We discard proofs with a frequency lower bound of 0, since they might not match any case. The iterative process continues until no additional proofs can be obtained. In the supporting document, we provide an analysis of the probability of obtaining a proof of a given length, based on the characteristics of the genomic domain.

Fig. 2.

Presence proofs (length-2 and longer) and their generation. The attack also infers the frequency of each proof. When the frequency cannot be uniquely determined, the attack derives an upper bound and a lower bound for the frequency (as shown for the rightmost proof of length 3). A proof of length l is generated by combining two proofs of length l-1 that differ in exactly one genotype

2.5 Step 3: re-identifying cases from candidates

Given the genome sequence of a suspected study participant, the final step of the attack is to check whether the suspect is among the cases in the GWAS. From the set of presence proofs obtained in the previous step, we discard each proof that is a subset of another proof. Then we match the suspect’s genome sequence against each proof; if an exact match is found, then we declare the suspect to be a case. When the genome sequence of the suspect is known before the attack begins, we can significantly speed up processing by only generating proofs that match the suspect’s genome sequence.

Given the set of all presence proofs generated in Step 2, we discard each proof whose genotypes are a subset of another proof. Among the remaining proofs, we retain only those whose upper bound and lower bound are both 1, i.e. each of them matches exactly one case. The resulting proofs are used to identify cases from candidates. Specifically, if exactly one candidate matches one such proof, we output this candidate as a case in the GWAS. The following theorem ensures that the result of our attack contains no false positive, under the condition that adversary’s candidate set contains all the cases (i.e. closed world assumption). The proof of the theorem is provided in the support online documents.

Theorem 1 —

Under closed world assumption, if the proof ρ satisfies $l_{\rho }=1$ and there is only one matching individual in the target set, then this individual must be a case in the GWAS.

Under open world assumption, our approach could falsely report candidates in D as patients in D^c. However, our discussion in supporting online documents shows that the lengths of the proofs are usually sufficiently long. This forbids the output of false-positive candidates with high probability, as these candidates need to match a true patient not included in D on a large number of genotypes.

Although Algorithm 2 is capable of generating all presence proofs, its computational costs might be too high for a GWAS that publishes a large number of genotypes, due to the exponential number of possible combinations. In the following, we present an optimized algorithm (which we call candidate matching) that only generates necessary presence proofs for a given candidate set, rather than enumerates all proofs.

Candidate matching is accomplished by building an appropriate first layer ${\mathcal{L}}_2$ (originally done on the first line of Algorithm 2), based on the target candidate sample x_i as Formula 5. The rest of the algorithm runs in exactly the same way as Algorithm 2 does.

$${\mathcal{L}}_2=\left\{\left(1,\{j,k\},\{x_{ij},x_{ik}\},M_{jk}^{x_{ij}{x}_{ik}},M_{jk}^{x_{ij}{x}_{ik}}\right)\right\}$$ (5)

To reduce the computational cost, the candidate matching method finds discriminative genotypes before the generation of presence proofs. As the frequency of proofs on the samples is mostly dependent on the co-occurrence counts of the genotypes, we run the genotype selection based on the heuristic that a genotype is more discriminative if the numbers of co-occurrence of the genotype together with other genotypes are consistently smaller. This brings us a simple minimal mutual co-occurrences genotype selection strategy working as follows. First, we calculate the genotype co-occurrence for each genotype in the candidate. If it is a major genotype, we have $h_j={\sum }_{1\hspace{0.17em}\le \hspace{0.17em}k\hspace{0.17em}\le \hspace{0.17em}d,k\hspace{0.17em}\ne \hspace{0.17em}j}\left(M_{jk}^{00}+M_{jk}^{01}\right)$, otherwise, we have $h_j={\sum }_{1\hspace{0.17em}\le \hspace{0.17em}k\hspace{0.17em}\le \hspace{0.17em}d,k\hspace{0.17em}\ne \hspace{0.17em}j}\left(M_{jk}^{10}+M_{jk}^{11}\right)$. The algorithm returns genotypes with minimal h_j and feeds these genotypes to the proof generation procedure.

3 Results and discussions

To evaluate the effectiveness of the privacy attack, we test it on eight datasets from the Wellcome Trust Case Control Consortium (WTCCC). All DNA samples in these datasets are collected using the 500K Affymetrix chip, and each sample contains genome sequence on 394 747 loci. In Table 1, we list the abbreviation, the target disease and the number of cases in each dataset. We simulate seven different GWASs by using the NBS dataset as the controls and one of the seven other datasets as the cases. The reference population is the set of individuals that appear in any of the eight datasets. In each simulated GWAS, we pick a certain number of genotypes uniformly at random and publish the P values of their genotype–disease correlations and the correlations between each pair of these genotypes. By default, each published value has a precision of 0.001, and different levels of precision are tested.

Table 1.

WTCCC datasets used in the experiments

Dataset	Case/control	Disease	No. of patients
HT	Case	Hypertension	1952
BD	Case	Bipolar disorder	1868
CAD	Case	Coronary artery disease	1926
CD	Case	Crohn’s disease	1748
RA	Case	Rheumatoid arthritis	1860
T1D	Case	Type 1 diabetes	1963
T2D	Case	Type 2 diabetes	1924
NBS	Control	None	1458

For computational efficiency, we select a subset of the published loci with minimal mutual co-occurrences and run the privacy attack on this subset. To evaluate the accuracy of the attack, we iteratively consider each member of the reference population as a suspect. We label the suspect as a positive result if at least one presence proof is found in the DNA of the suspect, but nowhere else in the reference population. Otherwise the result is negative, meaning that the suspect is not re-identified as being among the cases. Intuitively, the attack is effective if it returns positive results for the cases and negative answers for other members of the reference population. We repeat the GWAS simulation and attack for 10 different randomly selected sets of published genotypes for each dataset and report the average results. Table 2 summarizes the parameters investigated in the experiments.

Table 2.

Experimental setup for the GWAS simulations

Parameter	Values of the parameters
Case dataset	HT, BD, CAD, CD, RA, T1D, T2D
Control dataset	NBS
No. of loci used in the attack	10, 12, 14, 16, 18
No. of published loci	25, 50, 75, 100, 125
Precision	0.1, 0.01, 0.001, 0.0001, 0.00001

To evaluate the effect of the attack, the experiments vary the number of published loci, the number of loci used in the attack and the precision of the statistics published by the GWAS. Default values of the parameters in bold

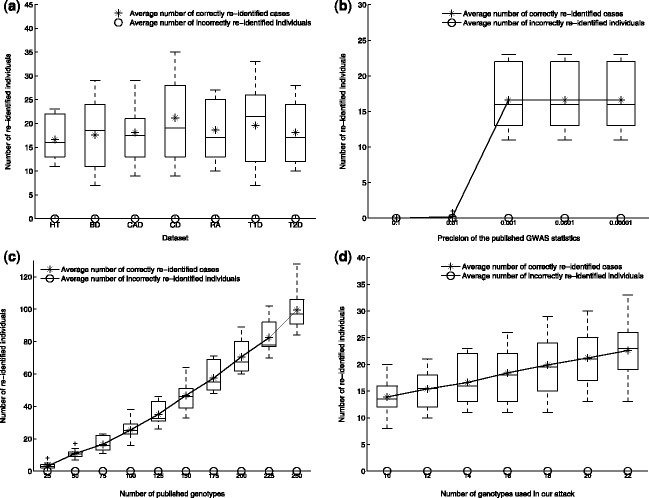
Figure 3 shows that on average, the attack successfully re-identifies 15 cases when 75 genotypes are involved in the GWAS results, of which just 14 are exploited in the attack. In other words, 14 genotypes out of 75 suffice to find unique patterns in 1% of the cases, patterns that distinguish them from everyone else in the reference population. Just as importantly, the attack does not falsely re-identify anyone from the reference population. In the Supplementary Document, we prove that when the reference dataset includes all cases, then the attack will not incur any false positive. We also show that when this assumption does not hold, e.g. some of the cases are not in the reference dataset, false positives are theoretically possible, but unlikely.

Fig. 3.

The number of re-identified cases in the seven WTCCC datasets, averaged across 10 trials with randomly selected sets of published genotypes. The asterisks show the average number of correct re-identifications. The boxes show the median, 25% quantile, 75% quantile, maximum and minimum numbers of correct re-identifications. Overall, the attack correctly re-identifies at least 10 cases with more than 75% probability, and on average re-identifies 15 cases, which is approximately 1% of all cases. No incorrect re-identifications occurred. (a) Results on the seven datasets, with default parameter values listed in Table 2. (b) Results with different precisions of the published statistics on the HT dataset, with other parameters fixed to their default values. (c) Results when varying the number of published genotypes on the HT dataset, with other parameters fixed to default values. (d) Results with varying numbers of genotypes used in the attack on the HT dataset, with other parameters fixed to default values. The Supplementary Document contains additional experimental results

Figure 3 also shows that the number of re-identified cases grows rapidly as the number of published genotypes increases. This is important because today’s GWAS studies already typically report more than 100 loci in the publication (Sladek et al., 2007; Zeggini et al., 2007), which would tend to boost the re-identification rate significantly. Meanwhile, when the number of published genotypes is fixed, the number of re-identified cases increases with the number of loci used in the attack, at the expense of computation time. In addition, Figure 3 also contains results with varying levels of precision for each published value in the GWAS results. As long as the precision remains above 0.001, the number of re-identified cases tends to be stable; in contrast, when the precision level falls below 0.01, the attack is unable to re-identify any case.

To simulate a real attack, we also test the effectiveness of our attack on the WTCCC dataset with the genotypes published by Scott et al. (2007). Because of the different source of the DNA data employed by Scott et al., only 36 out of the 306 genotypes discussed in their article are available in the WTCCC datasets. We therefore apply our attack to these 36 genotypes, using the T2D dataset as cases, NBS as controls, and the other six datasets as the reference population. As shown in Figure 4, the attack determines that 12 people from the WTCCC datasets are among the T2D cases, using 14 genotypes that the attack selected from among the 36 available. The attack does not mistakenly re-identify anyone from the reference population as being among the cases. The number of re-identifications is only slightly lower than that achieved with twice as many randomly selected genotypes in Figure 3, further confirming the effectiveness of the attack.

Fig. 4.

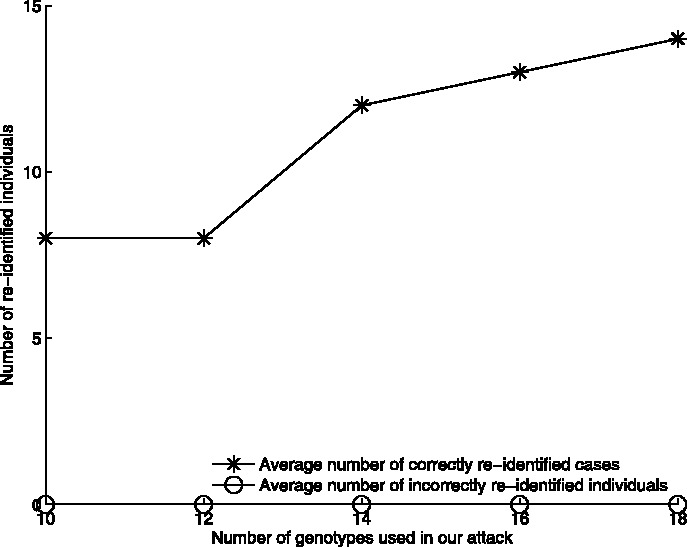
The number of re-identified cases from the T2D dataset, based on the 36 SNPs published in Fraser et al. (2005) that are also available in the WTCCC dataset. The attack re-identifies a dozen cases on average, which is slightly fewer than when the published data is for 75 randomly selected genotypes. The number of re-identified cases gradually grows when more genotypes are used in the attack. The Supplementary Document contains additional results obtained by running the same experiment on other datasets of WTCCC

Note that the above results are based on dominant/recessive coding of the genotypes. When there are a lot rare variants, our method can also be extended to the additive model. Let M and $\mathcal{M}$ denote the co-occurrence matrices on the recessive model (binary coding, 0 for AA, 1 for {Aa, aa}) and the additive model (three states coding, 0 for AA, 1 for Aa and 2 for aa), respectively. Then, we have $M_{ij}^{00}={\mathcal{M}}_{ij}^{00},M_{ij}^{01}={\mathcal{M}}_{ij}^{01}+{\mathcal{M}}_{ij}^{02},M_{ij}^{10}={\mathcal{M}}_{ij}^{10}+{\mathcal{M}}_{ij}^{20},M_{ij}^{11}={\mathcal{M}}_{ij}^{11}+{\mathcal{M}}_{ij}^{12}+{\mathcal{M}}_{ij}^{21}+{\mathcal{M}}_{ij}^{22}$. When the variant on loci g_i is rare, ${\mathcal{M}}_{ij}^{12},{\mathcal{M}}_{ij}^{22}$ will be small enough to ensure that the statistics on the additive model is a good estimation of that that on the recessive model.

4 Conclusion

To sum up, the privacy attack described in this article poses a potential threat to the privacy of patients participating in a GWAS. One effective countermeasure is to lower the precision of the published statistics, e.g. publish only a heat map for the correlation between different genotypes and never reveal their precise values. Meanwhile, since the attack’s power grows with the number of genotypes, studies should minimize the number of SNPs included in the published results. Finally, a promising direction for protecting GWAS results with strong privacy guarantees is differential privacy techniques (Johnson and Shmatikov, 2013), which inject random noise into the statistical results. The current state-of-the-art is able to publish a handful of genotypes with the highest correlations with the disease with strong privacy guarantees and good accuracy. However, some limitations of the method need to be addressed in the future, e.g. the method is only applicable to binary coding of the genotypes, the method incurs prohibitively high error rates when a larger number of genotypes are involved in the published results.

With the availability of direct-to-consumer genetic tests that report genotypes associated with medical or physical traits, personal genetic marker data are becoming widely accessible and even public. Medical institutions are considering collecting prospective genomic data on patients in large scale for both research and potentially clinical purposes. It is therefore important for effective security measures to be in place as these data become accessible. We present the first successful attack algorithm using minimum genotype sets and several effective counter measures. This strategy represents a framework for future genetic privacy defenses.

Funding

This project was supported by the Wellcome Trust under award 076113. Cai and Hao were supported by the National Natural Science Foundation of China [61100148]. Winslett, Xiao, Yang and Zhang were supported by SERC 102-158-0074 from A*STAR in Singapore. Xiao was also supported by SUG Grant [M58020016] and AcRF Tier 1 Grant RG 35/09 from Nanyang Technological University. Yang was also supported by the New Faculty Startup Grant from Hamad Bin Khalifa University. Zhou was partially supported by National Natural Science Foundation of China under grant No. 61272380.

Conflict of Interest: none declared.