The assembly of miRNA-mRNA-protein regulatory networks using high-throughput expression data

Abstract

Motivation: Inference of gene regulatory networks from high throughput measurement of gene and protein expression is particularly attractive because it allows the simultaneous discovery of interactive molecular signals for numerous genes and proteins at a relatively low cost.

Results: We developed two score-based local causal learning algorithms that utilized the Markov blanket search to identify direct regulators of target mRNAs and proteins. These two algorithms were specifically designed for integrated high throughput RNA and protein data. Simulation study showed that these algorithms outperformed other state-of-the-art gene regulatory network learning algorithms. We also generated integrated miRNA, mRNA, and protein expression data based on high throughput analysis of primary trophoblasts, derived from term human placenta and cultured under standard or hypoxic conditions. We applied the new algorithms to these data and identified gene regulatory networks for a set of trophoblastic proteins found to be differentially expressed under the specified culture conditions.

Contact: ysadovsky@mwri.magee.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Complex and adaptive biological systems exhibit homeostatic resilience. They are also capable of adopting a new steady state in response to endogenous or exogenous cues, and must therefore harbor robust transcriptional and translational regulatory networks. Network signals are transmitted within the cell, tissue or organismal environment. MicroRNA regulatory networks represent an important component of the adaptive cellular response (De Lella Ezcurra et al., 2012; Tay et al., 2014). There are extensive descriptions of the derivation of miRNA regulatory networks using experimental or computational methods. Experimental approaches are based on profiling and manipulation of signals, such as miRNAs knockdown/overexpression and assessment of mRNA expression changes, or on enrichment approaches, where miRNAs and mRNAs are pulled down with the Argonaute 2 protein, as in HITS-CLIP (Chi et al., 2009) or PAR-CLIP experiments (Hafner et al., 2010). These approaches are used for searching miRNA-mRNA binding sites and the interactions among the selected transcripts. Computational methods, such as TargetScan (Lewis et al., 2005), miRDB (Wang and El Naqa, 2008) and PicTar (Krek et al., 2005), are largely based on in silico strategies, where the miRNA’s mRNA targets are predicted by thermodynamic analysis of miRNA sequence and evolutionary conserved potential binding sites (e.g. in the 3′ UTR) with the mRNA transcripts. Each of these approaches has advantages and disadvantages. For example, the experimental approaches can definitively address the regulatory relations between miRNAs and target mRNAs, and hence tend to serve as a gold standard, yet they are also expensive and tedious. In addition, enrichment for miRNA and mRNA by pull-down approaches may not imply a functional interaction. In silico approaches are fast and relatively cheap, but may provide an extensive list of possible miRNA-mRNA interactions, and fall short of inferring dynamic relations between miRNAs and mRNAs in any specific cell type or tissue.

Unlike the experimental and the in silico approaches, the statistical approaches derive regulatory relations among miRNAs and mRNAs through analysis of miRNA and mRNA expression data. In particular, linear regression-based methods have been employed in the search of miRNAs that directly regulate targeted mRNAs in a specific system (Le and Bar-Joseph, 2013; Lu et al., 2011; Stanhope et al., 2009). In these methods, the log expression of an mRNA is assumed to be expressed as a linear combination of the log expression of miRNAs targeting that mRNA, and/or the product of the log expression of the targeting miRNAs and Argonaute transcripts. Various model selection methods, including stepwise model selection using information criterion score, L₁ norm regularization based Lasso algorithm (Tibshirani, 1996), can be used to identify miRNAs that are significant predictors of target mRNAs. These selected miRNAs are assumed to be regulators of the target mRNA. The main advantages of these regression-based methods are that (i), they can utilize observational expression data that were generated for other purposes in order to derive the miRNA regulatory network for a particular system, and (ii), they can be used, with little or no modification, to identify the targets of any non-coding RNAs (ncRNAs). However, a major weakness inherent to the implementation of these methods to miRNA regulatory networks is their inability to distinguish between (partial) correlation and causation. Therefore, even when the assumptions of these algorithms were satisfied, miRNAs discovered using these algorithms will not only contain species that regulate target mRNAs, but also miRNAs concomitantly regulated with the target mRNA or with the protein product of the target mRNA. See a hypothetical miRNA/mRNA/protein regulatory network in Supplementary Fig. S1.

In the past two and half decades, there have been rapid developments in research on learning causal relations from observational data (Pearl, 2000; Spirtes et al., 2000). A variety of causal learning algorithms have been proposed, including score-based algorithms, constraint-based algorithms, local learning algorithms, algorithms allowing latent variables, cyclic causal relations, time-series data and non-Gaussian numeric data (Aliferis et al., 2003; Chickering, 2002; Chu and Glymour, 2008; Richardson, 1996; Shimizu et al., 2011; Spirtes et al., 1999). These causal learning algorithms seem particularly suitable for inferring gene regulatory networks from high throughput gene expression data. However, applying causal learning algorithms to the construction of gene regulatory networks raises two major obstacles: (i) the regulatory networks are extremely complex, involving thousands of mRNAs, ncRNAs, proteins, and other molecular species, and (ii), the sample size of the ncRNA, mRNA and protein expression data may be small, often magnitudes less than the number of analyzed variables.

In this article, we propose two new causal learning algorithms for inference of local ncRNA-mRNA-protein regulatory networks. Given a target mRNA/protein, these algorithms identify the molecular species that directly regulate the target, and the molecular species that are directly regulated by the target. These algorithms use a score-based, local learning strategy to address the challenges of a large number of ncRNA-mRNA-protein sets in the network. The first algorithm, called the Markov Blanket Search for mRNA Regulatory Networks (MBSmRN), requires knowledge of the molecular species that are directly regulated by the target molecule, and is specifically designed for identifying direct regulators of mRNAs. The second algorithm, called the Markov Blanket Search for Non-Gaussian Integrated Genomic data (MBSNIG), requires the expression data for the target molecular species to be ‘count data’ (e.g. sequencing count data for miRNA/mRNA expression, and mass spectral count data for protein expression), and can be applied to ncRNA-mRNA-protein expression data generated from most experimental designs.

We evaluated the performance of these two algorithms using simulated data, and compared them with two representative algorithms, the general purpose Max-Min Hill-Climbing (MMHC) algorithm for local causal discovery (Tsamardinos et al., 2006), and the Lasso regression based algorithm for miRNA regulatory networks (Lu et al., 2011; Stanhope et al., 2009). The MMHC algorithm starts with a constraint based local learning algorithm, Max–Min Parents and Children (Tsamardinos et al., 2003), to derive for each variable, a list of candidate parents and children (CPC) of that variable. This algorithm then orients and, possibly, trims the edges connecting the target variable and its CPC using a score based hill-climbing algorithm. The Lasso regression-based algorithm selects a set of miRNAs and proteins that best predict the expression of the target mRNA/protein using the Lasso-based feature selection method. The selected miRNAs/proteins are considered the direct regulators of the target mRNA/protein. We also applied our new algorithms to an integrated miRNA-mRNA-protein expression data set from experiments using primary human placental trophoblasts that were exposed for 72 h to standard culture conditions or to hypoxia (O₂ < 1%), which mimics physiologically relevant placental injury (Oh et al., 2011; Roh et al., 2005). We selected 78 target mRNA/protein pairs and, for each of them, identified the miRNAs and proteins that directly regulated the target mRNA and protein.

2 Methods

Methods related to placentas and trophoblast cultures, expression microarrays for mRNA and miRNA, proteomic analysis using mass-spectrometry, data processing and related references are a part of the Supplementary materials.

2.1 Score-based learning of local gene regulatory network

We developed two algorithms for learning local ncRNA/mRNA/protein regulatory networks. These algorithms are termed the MBSmRN and MBSNIG. Akin to current regression model-based methods for miRNA targets and other causal learning algorithms for genetic regulatory networks (Le and Bar-Joseph, 2013; Le et al., 2013; Lu et al., 2011; Stanhope et al., 2009), these two new algorithms assume that (i), the relation between a target mRNA or protein and its regulators is approximately linear, and (ii), if one molecule X is a direct regulator of another molecule Y, then Y cannot be a direct or indirect regulator of X. The MBSmRN algorithm is based on linear (mixed effect) models for the log expression of each target molecular species, while the MBSNIG algorithm is based on generalized linear (mixed effect) models for the count of each target. The independent variables in these models include the log expression of the ncRNAs and proteins, as well as external factors related to the experiment. In the model for protein targets, the independent variables also included the log expression of the mRNA transcript that encoded the target protein. When the data are grouped, the grouping factor could serve as a random effect of the model. Argonaute-2 could also be included in the model.

For illustration, consider the miRNA, mRNA and protein data for trophoblasts cultured in standard or hypoxic conditions described earlier. Because the measurements of miRNAs and mRNAs were continuous microarray data, while the measurements of proteins were mass spectrometry count data, we used linear mixed effect models for target mRNAs:

$$G_{i,k,t}=g_i+{\sum }_j{b}_{i,j}{M}_{j,k,t}+{\sum }_j{c}_{i,j}\text{log}\left(P_{j,k,t}\right)+{\sum }_h{d}_{i,h}{\delta }_{h,t}+S_{i,k}+{\epsilon }_{i,k,t}$$ (1)

and generalized linear mixed effect models for target proteins:

$$\text{log}\left(E\left[P_{i,k,t}\right]\right)=p_i+a_i{G}_{i,k,t}+{\sum }_j{b}_{i,j}{M}_{j,k,t}+{\sum }_j{c}_{i,j}\text{log}\left(P_{j,k,t}\right)+{\sum }_h{d}_{i,h}{\delta }_{h,t}+S_{i,k}+{\epsilon }_{i,k,t}$$ (2)

In the above equations, P_i,k,t and G_i,k,t represent the count of the ith protein and the log expression of its mRNA transcript in a sample obtained from the kth placenta and exposed to the tth condition, M_j,k,t represents the log expression of the jth miRNA in the same sample, δ_h,t is the Kronecker delta function where δ_h,t = 1 if h = t, and δ_h,t = 0 otherwise, S_i,k represents the kth placenta on the ith protein. The parameters g_i and p_i represent the (hypothetical) overall expression of the ith mRNA and ith protein in the placenta, respectively, a_i, b_ij and c_ij represent the effect of G_ikt, M_jkt and P_jkt on the target, and d_ih represents the effect of the hth condition on the target. Finally, ε_i,k,t represents an independent random error. Note that Argonaute-2 protein and its interaction with miRNAs were not incorporated in the above models because this protein had an extremely low expression level, and was nearly constant across all trophoblast samples in our experiment data. For simplicity, among all types of ncRNAs we only included miRNAs as candidate regulators in our model.

Once the statistical models for the experimental data were specified [e.g. as in equations (1) and (2)], the MBSmRN and MBSNIG algorithms identified the ncRNAs and proteins that directly regulated a target mRNA or protein through the inferences on the Markov blankets of the target RNA or protein. Roughly speaking, given a set of random variables V, and a variable X in V, the Markov blanket of X in V is the minimum set of variables in V such that conditional on which X is independent of all other variables in V. (For the definition of Markov blanket and a brief introduction to the graphic models based causal learning, see Spirtes et al., 2000). Assume the experimental data could be represented by linear (mixed effect) models similar to Equation (1). Let V be the set of all ncRNAs and proteins, Ch(T_i) (‘children’) be the set of all molecular species that were regulated directly by the target T_i, the MBSmRN algorithm identified ncRNAs and proteins that directly regulated target T_i:

MBSmRN algorithm:

1. Identify MB(T_i; V), the Markov blanket for the target T_i from the set V of all ncRNAs and proteins, using the information about Ch(T_i) and the splitting algorithm for Markov Blanket with known direct effects (SAMB-KDE).

2. Identify Pa(T_i) = MB(T_i; MB(T_i; V) \ Ch(T_i)), the Markov blanket for target T_i from variables in MB(T_i) \ Ch(T_i), using model selection method. These are the candidate ncRNAs and proteins that directly regulate target T_i.

MBSmRN requires knowledge about the molecular species directly regulated by the target. In practice, this information is usually only available for mRNAs. Therefore MBSmRN is primarily designed for the identification of direct regulators of mRNAs. The input data for MBSmRN could be either continuous expression data, such as those produced by microarray, or count data, such as those produced by sequencing or Mass Spectrometry.

The MBSNIG algorithm requires that the expression of the target RNA or protein to be measured as count data. It utilizes the non-Gaussian property of the count data to orient the direction of regulation between the target and the ncRNAs and proteins in its Markov blanket. The MBSNIG algorithm identifies the ncRNAs and proteins that directly regulate the target RNA or protein, and the RNAs and proteins that are regulated by that target. Assuming the experimental data can be represented by generalized linear (mixed effect) models similar to Equation (2), the MBSNIG algorithm has the following two steps:

MBSNIG algorithm:

1. Identify MB(T_i; V), the Markov blanket for target T_i from the set V of all ncRNAs and proteins, and in case target T_i is a protein, the mRNA transcript for T_i, using the general SAMB (SAMB-G).

2. Identify the set of ncRNAs and proteins that directly regulate target T_i, and the set of RNAs and proteins regulated by target T_i, by applying the Partial Orientation of the Markov Blanket for a non-Gaussian variable (POMB-NG) algorithm to MB(T_i; V).

Note that in step 2, the RNAs and proteins that are regulated by target T_i, identified by the POMB-NG algorithm, consist of all RNAs and proteins regulated directly by T_i, as well as those RNAs and proteins in MB(T_i; V), the Markov blanket of T_i, that are regulated indirectly by T_i.

We developed two divide and conquer algorithms to identify the Markov blankets for a target mRNA or protein from a causal sufficient dataset as subroutines employed by the MBSmRN and MBSNIG algorithms. The first algorithm, called ‘the SAMB with known direct effects’ (SAMB-KDE), requires the prior knowledge of the variables that are directly regulated by the target. Utilizing this prior knowledge, the algorithm divides the search space of the Markov Blanket into manageable parts, while ensuring that the union of lists of variables derived from all parts is a superset of the Markov blanket of the target. This union then is searched using a model selection procedure to identify the Markov blanket of the target. This algorithm is used in step 1 of the MBSmRN algorithm, with the assumption that the only direct effect of a target mRNA is its encoded protein.

The second algorithm, called the ‘general SAMB’, is a general purpose Markov blanket search algorithm. This algorithm first uses the divide and conquer approach to derive a list of variables containing all direct causes of the target variable, then augments this list with variables that include all spouses of the target variable, and finally performs a model selection procedure on this augmented list, to derive the Markov blanket for the target variable. It is used in step 1 of the MBSNIG algorithm.

Note that both the SAMB-KDE and the SAMB-G subroutines do not specify the model selection method to be used. Users can choose from diverse model selection methods, such as a stepwise method based on information score, or Lasso. Therefore, their time complexity may vary based on the choice of model selection method.

We also developed an algorithm for the POMB-NG, used in step 2 of the MBSNIG algorithm. Given the Markov blanket MB(T_i; V) for a non-Gaussian target variable T_i, this algorithm utilizes the non-Gaussian property of target T_i to determine, for all variables in the Markov blanket MB(T_i; V) of T_i, whether they are direct causes of T_i, or direct and indirect effects of T_i, or neither. The detail of the above three algorithms, their time complexity, and the proof of their correctness can be found in the Supplementary material (Auxiliary algorithms and Supplementary Fig. S2).

We used the resampling method to improve the stability of the results from the MBSmRN and MBSNIG algorithms (Friedman et al., 1999). Based on data structure, either resampling with replacement (bootstrap) or resampling without replacement could be used. The MBSmRN and MBSNIG algorithms were applied to each resampled dataset. Only the ncRNAs and proteins identified by the MBSmRN and MBSNIG algorithms in multiple resampled datasets were considered candidate RNAs and proteins directly regulating or being regulated by the target.

The two algorithms could be modified to incorporate other a priori information. For example, a user’s assumption that among all proteins only transcription factors may be considered direct regulators of target mRNAs can be accommodated by restricting the search of the MBSmRN algorithm to the set of all ncRNAs and all transcription factors. Similarly, if a user believes that miRNAs regulate only those mRNAs with perfect matches to the seed of the miRNAs, the user could also limit the search of the MBSmRN algorithm to the set of all proteins and all those miRNAs with seeds perfectly matching to the target mRNA.

3. Results

3.1 Simulation study

We evaluated the performance of the MBSmRN and MBSNIG algorithms using simulated data, and compared it to that of two representative algorithms, the general purpose MMHC algorithm for local causal discovery (Tsamardinos et al., 2006), and the Lasso regression-based algorithm for miRNA regulatory network (Lu et al., 2011; Stanhope et al., 2009). (Note that Stanhope et al. used the Akaike information criterion (AIC) score-based feature selection method, and used mRNA expression as a surrogate for protein expression). Traditionally, to evaluate the performance of a causal learning algorithm, one needs to consider several parameters, including the number of direct causal relations correctly identified by the algorithm, the number of direct causal relations falsely identified by the algorithm, and the number of direct causal relations whose direction was correctly determined by the algorithm (Spirtes and Meek, 1995). Nonetheless, as our main purpose was to identify the direct regulators of a target mRNA/protein, we sought to evaluate the algorithm’s performance by the accuracy of its prediction of a target’s regulators. We transformed the search for direct regulators of an mRNA/protein target into a binary classification problem of determining, for all measured ncRNA/proteins, which are direct regulators of the target mRNA/protein, and which are not.

To illustrate, consider a dataset D consisting of measurement for a set V of ncRNAs, mRNAs and proteins. We sought to identify the direct regulators of a target mRNA/protein T ∈ V using using an algorithm F. We first generated m resampled datasets from D, and applied algorithm F to each of the m samples. Let S₁,$\dots$ S_m be the m sets of candidate regulators of T identified by algorithm F from the resampled datasets. We then counted, for each observed variable X in V, how many times it was included in these m sets of candidate regulators: f(X) = Σ^m_i = 1 1_Si X), where 1_Si is the indicator function for set S_i. Then we constructed a classifier based on algorithm F, so that it would classify a ncRNA or protein X as a direct regulator of T if f(X) ≥ c for some pre-determined cutoff c.

The performance of a binary classifier can be conveniently evaluated by either the receiver operating characteristic (ROC) curve or the Precision-Recall (PR) curve (Davis and Goadrich, 2006), which could be considered as plots of the true positive rate against false positive rate (ROC) or PR for various values of cutoff c. In the context of regulator network learning, where the number of non-regulators (negative cases) far exceeds the number of true regulators (positive cases), it is highly desirable for a classifier to have high specificity to limit the number of false positives to an acceptable level. Therefore, the PR curve would be preferred. Nevertheless, the ROC curve could also be used if we restrict the ROC over a range of high specificity, (e.g. between 0.95 and 1).

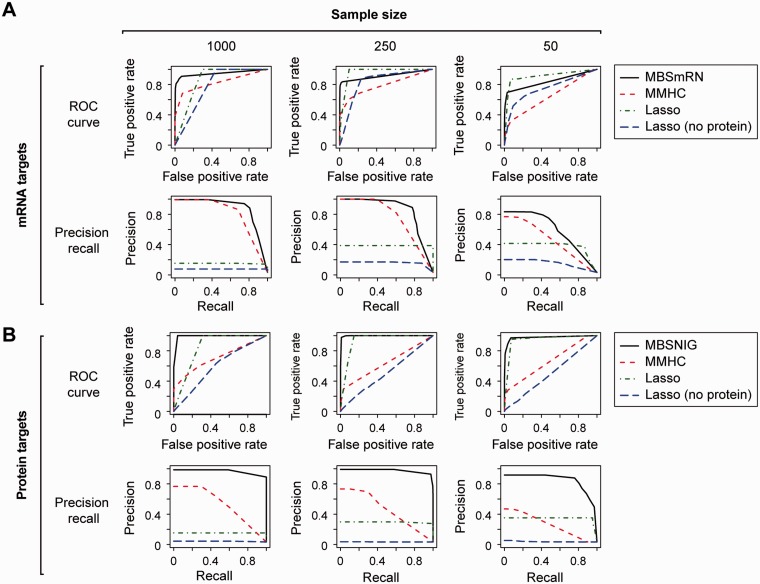
We created four simulated miRNA/mRNA/protein regulatory networks, each consisting of 40 miRNAs, 80 mRNAs and 80 proteins that are encoded by the mRNAs, based on Equations (1) and (2). For each network, we generated random samples of sample size 1250, 250 and 50, respectively. For each sample we generated 25 datasets by sampling without replacement, and evaluated the performance of MBSmRN (for mRNAs), MBSNIG (for proteins), MMHC and Lasso-based algorithms on these resampled datasets, using the method described earlier. Because the original Lasso-based algorithm derived the regulators of mRNAs from the expression of mRNAs and miRNAs, we also evaluated the Lasso-based algorithm on the trimmed simulation data, where the protein data had been removed. We found that the MBSNIG algorithm performed extremely well in predicting the regulators of proteins, even when the sample size was only 50, as shown in the ROC curve and PR curve for MBSNIG in Fig. 1 and Supplementary Figs. S5–7.

Fig 1.

The PR curves and ROC curves of the competing regulatory network learning algorithms for direct regulators of (A) mRNA targets and (B) protein targets, based on the data generated using the first simulated network

The performance of the MBSNIG algorithm for identifying regulators of target proteins was also vastly superior to the MMHC and the Lasso regression-based algorithms. For all simulated networks, the average area under the Precision Recall curve (AUPRC) of the MBSNIG-based classifier for 30 target proteins was already 0.89 when sample size was 50, and reached almost 0.99 when sample size was 250 and 1000. This compared with an average AUPRC of 0.3 and 0.4 at sample size 50, and 0.5 and 0.33 at sample size 250, respectively for classifiers based on the MMHC and the Lasso algorithm (Supplementary Tables S1–4). We also observed a similar difference in partial area under the ROC curve (pAUC), over the range of specificity between 0.95–1, between MBSNIG and the other two algorithms (Table 1 and Supplementary Tables S2–4).

Table 1.

Comparison of the partial AUC of competing regulatory network learning algorithms for the first simulated network. mean.pAUC.1 and mean.pAUC.2 are the average of partial AUC over 30 target mRNAs/proteins for the first and the second algorithm, respectively

Alg1	Alg2	Sample size	Target	mean.pAUC.1	mean.pAUC.2	wilcox. pval
MBSmRN	MMHC	1250	mRNA	0.9226	0.8487	0.01463
MBSmRN	Lasso	1250	mRNA	0.9226	0.6130	8.41E-09
MBSmRN	Lasso (no protein)a	1250	mRNA	0.9226	0.5328	2.38E-11
MMHC	Lasso	1250	mRNA	0.8487	0.6130	1.29E-07
MBSmRN	MMHC	250	mRNA	0.9068	0.8228	0.005421
MBSmRN	Lasso	250	mRNA	0.9068	0.8169	0.009452
MBSmRN	Lasso (no protein)	250	mRNA	0.9068	0.6112	2.42E-09
MMHC	Lasso	250	mRNA	0.8228	0.8169	0.80688
MBSmRN	MMHC	50	mRNA	0.8182	0.6849	0.000688
MBSmRN	Lasso	50	mRNA	0.8182	0.8502	0.41131
MBSmRN	Lasso (no protein)	50	mRNA	0.8182	0.6388	3.17E-06
MMHC	Lasso	50	mRNA	0.6849	0.8502	8.77E-06
MBSNIG	MMHC	1250	Protein	0.9970	0.7391	6.09E-10
MBSNIG	Lasso	1250	Protein	0.9970	0.5905	2.64E-12
MBSNIG	Lasso (no protein)	1250	Protein	0.9970	0.5070	2.35E-12
MMHC	Lasso	1250	Protein	0.7391	0.5905	5.59E-05
MBSNIG	MMHC	250	Protein	0.9967	0.7067	4.10E-11
MBSNIG	Lasso	250	Protein	0.9967	0.7460	1.12E-11
MBSNIG	Lasso (no protein)	250	Protein	0.9967	0.5029	1.52E-12
MMHC	Lasso	250	Protein	0.7067	0.7460	0.420141
MBSNIG	MMHC	50	Protein	0.9372	0.6214	7.56E-09
MBSNIG	Lasso	50	Protein	0.9372	0.8257	7.04E-05
MBSNIG	Lasso (no protein)	50	Protein	0.9372	0.5080	2.90E-11
MMHC	Lasso	50	Protein	0.6214	0.8257	1.05E-06

^aLasso algorithm is applied to simulation data with the protein data removed.

The MBSmRN algorithm also performed better than the MMHC and Lasso-based regression algorithms in identifying regulators of target mRNAs, although the performance advantage was not as large as the MBSNIG algorithm for proteins (Fig. 1 and Supplementary Figs. S5–7). Measured by AUPRC, the performance of the MBSmRN-based classifier was always higher than that of the MMHC algorithm. Measured by pAUC, at a sample size of 250 and 1250, the MBSmRN algorithm also exhibited significantly higher performance than the Lasso regression-based algorithms. At a sample size of 50, the pAUC of the Lasso regression-based algorithm was slightly better, although the difference was not statistically significant. Note that the performance of the Lasso-based algorithm significantly deteriorated as the sample size increased, which is not surprising, given that this regression-based algorithm was incorrect, as discussed earlier. We also noted that after removing the protein data, the Lasso-based algorithm’s performance was severely affected.

We also estimated the computational time needed for these algorithms. Using an Intel Xeon 3.5 Ghz CPU with six threads, at sample size of 50, for each mRNA target, the MBSmRN algorithm required nearly 5 s, Lasso required ∼1 s, and MMHC <1 s. For each protein target, the MBSNIG algorithm required ∼100 s, Lasso ∼2 s and MMHC <1 s. The long computational times of the MBSmRN and MBSNIG algorithms largely reflected poor performance of the iteration loop in R, which was the language we used for these new algorithms. An implementation of these algorithms in other languages, such C or Java, could improve the algorithms’ computation speed by one or two magnitudes.

3.2 Application

From the integrated miRNA-mRNA-protein dataset for trophoblasts cultured in standard or hypoxic conditions, we detected the expression of 231 miRNAs, 26 223 mRNAs and lincRNAs, and 3268 proteins. Among them, we identified 215 miRNAs and 20 381 mRNAs and lincRNAs that were differentially expressed during the time course and/or between standard or hypoxic culture conditions. Using the generalized linear mixed effect model, we also found 324 differentially expressed proteins. The heatmaps for these differentially expressed miRNAs, mRNAs, and proteins are shown in Supplementary Figure S3.

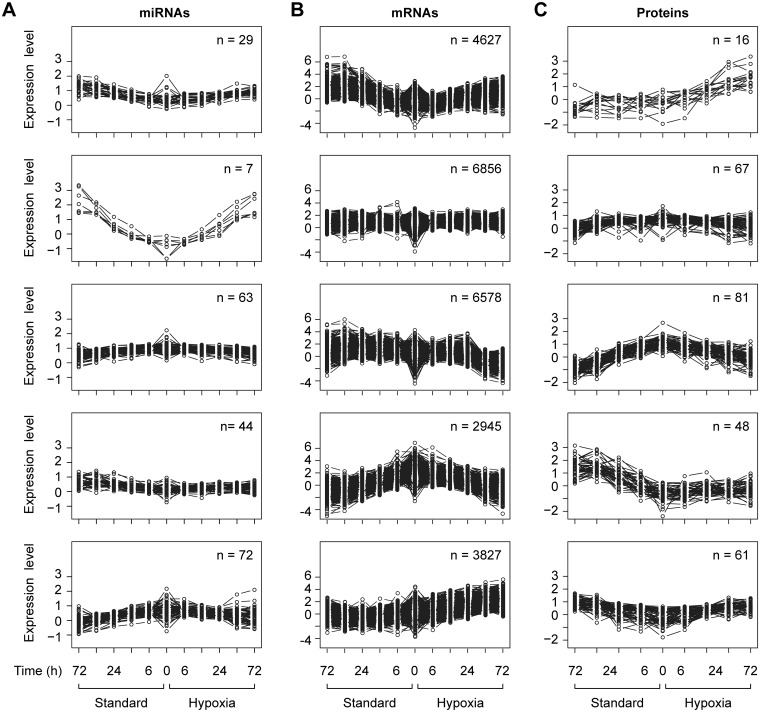
The clustering of differentially expressed miRNAs/mRNAs/proteins, (Fig. 2), revealed common expression patterns: Relative to time 0, some miRNA/mRNA/protein sets were up-regulated throughout the experimental time course in both standard and hypoxic conditions, while others were down-regulated under both conditions. Other sets were down-regulated under standard conditions but up-regulated in hypoxia; and some were up-regulated in standard conditions but down-regulated in hypoxia. A pathway analysis of these different groups of proteins revealed the enrichment of network functions involved in energy production, lipid metabolism and small molecule biochemistry. Among molecular and cellular functions, the most abundant were cellular growth and proliferation (51 of 78 proteins, analyzed by Interactive pathways analysis, Ingenuity Systems). The multi-dimension scaling plots of all expressed miRNAs, mRNAs and proteins highlighted patterns of mRNA/protein expression profiles in trophoblasts cultured in standard or hypoxic conditions over the time course (Supplementary Fig. S4).

Fig. 2.

Plots of clusters of differentially expressed miRNAs/mRNAs/proteins. A miRNA/mRNA/protein is considered differentially expressed if its expression had changed during the time course under either the standard or hypoxic conditions. Expression values are averaged over the four placentas. Each plot represents a cluster of miRNAs/mRNAs/proteins obtained using k-means algorithm. The number of clusters were selected to cover interesting patterns of miRNA/mRNA/proteins expression, such as all members in a cluster were upregulated or downregulated in both conditions, or altered in one of the condition, and altered in the opposite direction in the other condition. Please note that some clusters did not follow any of these patterns. Also, note that there is no correlation among the three plots in the same row. They represent clustering of miRNAs, mRNAs and proteins, respectively

We selected 78 proteins that were differentially expressed over the time course, and/or between the standard and hypoxic conditions by both the generalized linear mixed effect models and the maanova algorithm (Kerr and Churchill, 2001). They all had a minimal average spectral count of 2 over all protein samples. We generated an integrated regulatory network for each of these 78 proteins and their respective mRNA transcripts using the MBSmRN and MBSNIG algorithms. Representative networks are shown in Supplementary Figure S8. Supplementary Figure S9 provides plots of the expression of the miRNAs, mRNAs and proteins in these networks, Supplementary Tables S5 and S6 provide the detailed information about the networks. We found that among the 231 expressed miRNAs, 132 miRNAs were present in the regulatory networks of the 78 mRNAs, and 62 miRNAs were present in the regulatory networks for the 78 proteins, with 31 miRNAs common to the networks for mRNAs and proteins. Interestingly, there was no significant correlation between the list of miRNAs that directly regulated the mRNAs and the list of miRNAs that directly regulated the proteins (P = 0.23, Fisher exact test).

4. Discussion

The examination of gene regulatory networks requires the distinction between intracellular and multicellular (tissue or cultured cells) regulation. An intracellular regulatory network describes, within an individual cell, how variable levels of ncRNA, mRNA and protein molecules interact with each other and, in particular, how the level of some molecules affects the expression of other molecules. The study of regulatory networks at the cellular level is often modeled by differential equations based on production and degradation rates of molecules. These models usually involve a small number of variables, and are applied to single cell expression data (Munsky et al., 2012). Multicellular regulation, on the other hand, centers on changes of total expression of some molecules in a collection of cells, such as tissues or cultured cells, and their impact on total expression of other molecules. As previously shown (Chu, 2008), causal learning algorithms cannot derive intracellular level regulatory networks using observational expression data, such as high throughput miRNA, mRNA and protein data, generated from multicellular systems. However, because of the complexity of regulation at the individual cell level and the extensive communication among cells, it is usually impossible to analytically infer a model of multicellular regulation from knowledge of intracellular regulation. Nevertheless, it is feasible to use high throughput expression data to infer regulation of ncRNA, mRNA, and protein at the multicellular level, which is the focus of the work described here. We proposed two new causal learning algorithms for the inference of local ncRNA/mRNA/protein regulatory networks from high throughput expression profiling data. We applied these algorithms to study primary human trophoblasts cultured in standard culture condition or in hypoxia. Notably, hypoxia was selected for its relevance to the pathobiology of placental trophoblasts during human pregnancy (Oh et al., 2011; Roh et al., 2005).

To address the challenge of a large number of ncRNA/mRNA/proteins species and a small number of biological samples that is typical of high throughput data, the two new algorithms adopted a score-based local causal learning strategy. They first executed a score-based search to identify the Markov blanket for the target mRNA/protein, and then conducted a score-based search to select the set of direct causes of the target mRNA/protein from the Markov blanket. They inferred the Markov blanket and the direct causes for each target mRNA/protein separately, without presenting a complete causal structure that covers all ncRNAs, mRNAs and proteins. When compared with the score-based global causal learning algorithms, such as the Greedy Equivalence Search (GES) algorithm (Chickering, 2002), our new algorithms are computationally efficient and allow the learning of local causal structure. When compared with the constraint-based causal learning algorithms, such as the PC algorithm (Spirtes et al., 2000), our algorithms have higher sensitivity, because they do not require a large number of simultaneous statistical tests.

The MBSmRN algorithm utilizes the prior knowledge that in most cases, a protein product is the only direct target of an mRNA. This allows the use of the Splitting algorithm for the Markov Blanket with known direct effects (SAMB-KDE) in the MBSmRN algorithm, and enables the identification of the sets of direct causes and direct effects from the Markov blanket for an mRNA transcript using a model selection method. In the MBSNIG algorithm, we took advantage of the non-Gaussian distribution of the count data (e.g. protein data generated by mass spectrometry), and developed the POMB-NG data algorithm. As the next generation sequencing technology becomes more affordable, more and more ncRNA and mRNA count data will be available. The MBSNIG algorithm can be applied to these sequencing data to identify the direct regulators of a target ncRNA/mRNA.

Our simulation study showed that the MBSmRN and MBSNIG algorithms are clearly superior to two competing algorithms: the MMHC algorithm and the Lasso regression-based algorithm. In particular, when searching for direct regulators of a target protein, the MBSNIG algorithm performed very well at a sample size of 50, which is comparable to the number of samples we have collected for the study of trophoblasts response to the two culture conditions over a 72 h time-course. Interestingly, at the smallest simulated sample size (50), Lasso regression-based algorithm performed at least as well as the MBSmRN algorithm for identifying regulators of mRNA targets. This is a typical example of the trade-off between variance and bias: when the sample size is extremely small, due to its simplistic approach to regulatory network learning, the Lasso-based algorithm was able to compensate for the strong inherent bias by the low variance of the estimated model.

We applied the new algorithms to integrated miRNA-mRNA-protein expression data for primary human trophoblasts. We believe that a well-designed study for miRNA regulatory networks should include protein expression data in addition to miRNA and mRNA expression data. This is primarily because, as discussed earlier and confirmed by the simulation study, missing protein data make it impossible to distinguish miRNAs that regulate target mRNAs from miRNAs co-regulated with the target mRNA, hence diminishing the performance of regulatory learning algorithms. Moreover, without protein data, it would be impossible to identify those miRNAs that directly affect the translation of proteins irrespective of mRNA degradation (Baek et al., 2008).

One of the main weaknesses of the new algorithms is the linearity assumption, which was needed in order to address the challenges of a small sample size and high network complexity. Theoretically, we could remove the linearity assumption and generalize our algorithms by using nonparametric density estimation methods to derive the Markov blankets for mRNAs and proteins. However, because of the curse of dimensionality, this might never be practical for the study of gene regulatory networks. The other assumption, the no-feedback assumption, could be removed if we adopted a modified Cyclic Causal Discovery (CCD) algorithm (Richardson, 1996). However, the output of the CCD algorithm, which is called a partial ancestral graph, usually does not allow an intuitive biological interpretation. Alternatively, when time series data are available, dynamic Bayesian networks could be used to model the feedback relation (Perrin et al., 2003). However, we would then have to assume stationarity and the correct choice of time points for measurement (Chu and Glymour, 2008; Li et al., 2011; Yan et al., 2010). The combination of the linearity and no-feedback assumptions limit the application of our algorithms to cases where the regulators have an approximately linear effect on its target, and the target does not directly regulate its regulators.

We also highlight that the protein library size could affect the performance of our two new algorithms. When the library size is small, some proteins may not be detected. If these proteins happened to be closely involved in the regulation of the target mRNA or protein, like protein₂ in our schematic example (Supplementary Fig. S1), our algorithms might incorrectly identify miRNAs co-regulated with the target mRNA or protein as regulators of the target mRNA or protein. Despite the above limitations, we believe the new algorithms will provide a useful tool for biologists who are investigating biological networks and seek to identify direct regulators of mRNAs and proteins.

Funding

This work was supported by the Pennsylvania Department of Health Formula Research Fund (to T.J.C.); David Scaife Foundation (to T.P.C.); and National Institutes of Health (R01HD065893 and R21HD071707, to Y.S.).

Conflict of Interest: none declared.