Precision and Error of Three-dimensional Phenotypic Measures Acquired from 3dMD Photogrammetric Images

Abstract

The genetic basis for complex phenotypes is currently of great interest for both clinical investigators and basic scientists. In order to acquire a thorough understanding of the translation from genotype to phenotype, highly precise measures of phenotypic variation are required. New technologies, such as 3D photogrammetry are being implemented in phenotypic studies due to their ability to collect data rapidly and non-invasively. Before these systems can be broadly implemented the error associated with data collected from images acquired using these technologies must be assessed. This study investigates the precision, error, and repeatability associated with anthropometric landmark coordinate data collected from 3D digital photogrammetric images acquired with the 3dMDface System. Precision, error due to the imaging system, error due to digitization of the images, and repeatability are assessed in a sample of children and adults (N=15). Results show that data collected from images with the 3dMDface System are highly repeatable and precise. The average error associated with the placement of landmarks is sub-millimeter; both the error due to digitization and to the imaging system are very low. The few measures showing a higher degree of error include those crossing the labial fissure, which are influenced by even subtle movement of the mandible. These results suggest that 3D anthropometric data collected using the 3dMDface System are highly reliable and therefore useful for evaluation of clinical dysmorphology and surgery, analyses of genotype-phenotype correlations, and inheritance of complex phenotypes.

Introduction

The past twenty years have revealed a remarkable amount of information pertaining to the genetic causes of human disease and the inheritance of phenotypic traits. As evidence accumulates for genetic complexity and the interaction of numerous contributing loci in many human traits and non-Mendelian diseases [Risch, 2000], it is becoming increasingly evident that significant phenotypic variation is the rule rather than the exception. Appreciation for the complexity of interactive gene networks (including signals, receptors, activators, inhibitors, second messengers, transcription factors, structural genes, etc.) in the formation of complex traits is growing as we begin to unravel the molecular underpinnings of phenotypic variability and of observed phenotypic variation. With this awareness comes the necessary entry of precise, quantitative analyses of the phenotype into studies of inheritance.

Regardless of the mode of inheritance, most phenotypes demonstrate a distribution of expression within a population rather than a uniform manifestation. Many discrete syndromes with divergent genetic causes have comparable phenotypes revealing patterns of traits that co-occur, and there is great variation in the phenotypic expression of certain syndromes, even within families. Such variants within a single known disorder are usually attributed to environmental influence, genetic background, degrees of penetrance or expressivity, but little has been done to quantify the fundamental nature of these patterns of phenotypic variation. If we are ever to understand the contributions of all participants along the continuum that translates genotype into phenotype, the remarkable success in molecular biology that has been driven by the study of genes must be matched by equally inventive studies of the phenotype. Precise measures of phenotypes at various points in ontogeny and innovative methods of analysis are integral to discovering the nature of developmental contributions to expressed phenotypic variation.

Anthropometry, the biological science of measuring size, weight, and proportions of the human body [Farkas, 1994b], provides objective and valuable lessons about how to assess and characterize phenotypic variation and dysmorphology in any species. Craniofacial anthropometry is performed on the basis of measures taken between landmarks defined on surface features of the head, face, and ears. Traditionally, anthropometric measurements have been acquired through direct measurement of a subject in a clinical setting, using calipers or metric tape to measure distances or arcs between landmarks [Farkas, 1994a]. However, the collection of quantitative data directly from young children, especially those with associated developmental disability, can be challenging and time-consuming for both the child and the investigator. Traditional anthropometry requires that each measurement be taken individually, requiring physical contact with the subject over a period of several minutes. Digitizers have been used to collect 3D coordinate data directly from human subjects but natural movements of the body at rest (e.g., breathing), and a person’s inability to sit motionless result in coordinate data sets fraught with large motion errors. Recent technologies such as laser surface scanning and 3D photogrammetry have provided a potential solution to these difficulties. Digital data sets can be acquired rapidly and non-invasively while simultaneously being archived for future analysis.

One such system of 3D photogrammetry is the 3dMD digital imaging system, which captures 3D surface images in 2 milliseconds (Fig.1). Before any system can be implemented in quantitative studies of patient populations, the error in producing an image and error in taking measures from the images produced must be evaluated. Though studies on an ideally shaped phantom have shown the 3dMD system to be valid and highly repeatable, a study of a sample of human subjects under realistic data collection conditions is required to accurately determine the impact of various sources of error, including that due to biological variation, on the measures collected. Precision is defined here as the average absolute difference between repeated measures of the same image. Error is defined here as the proportion of total variance attributable to a particular factor. Repeatability is a measure of precision relative to the magnitude of actual biological differences between individuals. Here, we test the repeatability of the images obtained by 3dMD photogrammetry technology, and the precision and measurement error of landmark data collected from these images.

Figure 1.

Surfaces acquired by the 3dMD system. All surfaces were produced from the same image. Surfaces are shown at different orientations to illustrate 3D nature of the data. Left: smooth 3D geometry with texture map applied; middle: 3D wireframe geometry data (polygonal mesh surface); Right: smooth 3D geometry data.

Materials & Methods

A. 3dMD technology

Briefly, the 3dMD system works by projecting random light patterns on the subject of interest (in our case the human face). The subject is captured with multiple precisely synchronized digital cameras set at various angles in an optimum configuration. Because multiple cameras are used there is no need for post-data capture “stitching” of multiple images from various angles into a single composite. Thus, this technology removes a potential source of error in creating a valid 3D representation of the subject at the time of data acquisition. Three dimensional surface geometry and texture are acquired nearly simultaneously. Algorithms developed by 3dMD integrate the various images obtained to produce a single 3D image (Fig. 1). These images can then be visualized and analyzed on a PC using the 3dMD software. A complete summary of the 3dMD system is available online: http://3dMD.com.

B. Study sample and 3dMD image acquisition

The study sample consists of a total of 15 subjects. This number includes seven morphologically normal adults (all over 25 years of age), two children with Down syndrome (ages 4 and 7 years), five children with corrected craniosynostosis (ages 4 months, 10 months, 1 year, 1 ½ years, 3 ½ years, and 4 years), and one morphologically normal child (age 4 years). 3dMD surface images were acquired on a single day at Johns Hopkins University School of Medicine following approved IRB protocols. Two images of each subject were acquired to test the repeatability of the images produced by the 3dMDface system. For each image, the child sat alone or on the lap of a parent. As in standard photography, an investigator held a toy or bright object to attempt to get the child to hold his/her head up and look at the camera. Once acquired, the image was reconstructed and reviewed in less than a minute so that a decision could be made regarding the acceptability of the image. Unacceptable images (i.e., those containing motion artifacts, those in which the subject turned to the side) were deleted and acceptable images were saved as permanent files.

C. Landmark data collection

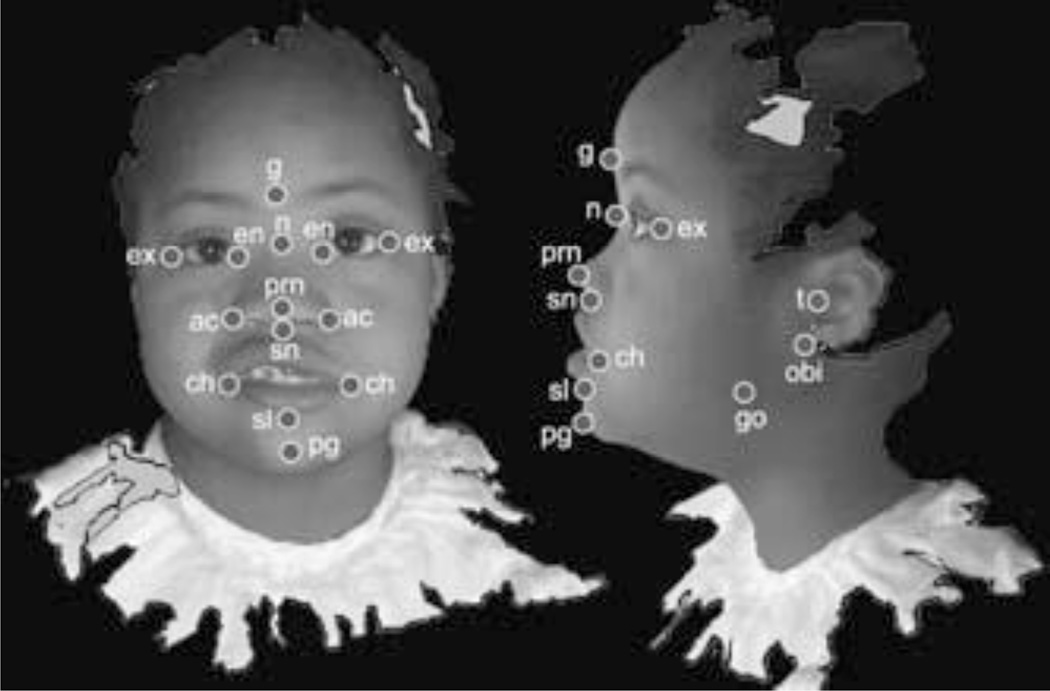
The 3dMD PC-based software allows the user to reconstruct, manipulate and analyze surface images in 3D space. 3D wireframe, smooth surface, and texture map information are combined to render a 3D reconstruction of each image using the 3dMD PC-based software (Fig. 1). All 3D reconstructions were manipulated in 3D space to determine those measures that could be collected from all images. Twenty standard anthropometric landmarks (6 midline and 7 bilateral) were identified on the face and ears following definitions outlined by Farkas [1994a] (Fig. 2) as those appropriate for this study. 3D coordinate locations of these landmarks were collected by a single observer using the 3dMD software. Although linear measures can be collected directly from the images, any error in a linear distance (or angle) will be a function of the error at the endpoints (i.e., landmarks). For this reason, we focus first on the error in the placement of 3D landmarks.

Figure 2.

Landmarks collected from 3dMD images. Landmarks are illustrated on 2D facial and lateral views taken from screenshots of an example 3dMD image, though actual data are 3D. Glabella (g), Nasion (n), Pronasale (prn), Subnasale (sn), Sublabiale (sl), Pogonion (pg), Endocanthion left and right (en), Exocanthion left and right (ex), Alar curvature (ac), Chelion (ch), Tragion (t), Otobasion inferius (obi), Gonion (go).

For each image, the X, Y, and Z axes are established at the time of image acquisition. Given our setup and the positioning of patients directly in front of and facing the camera system, the X-axis is oriented along the mediolateral plane, Y along the superoinferior plane, and Z along the anteroposterior plane. Once an image is produced, the operator can manipulate it in 3D space, but the local coordinate system (created during image acquisition) remains internally consistent regardless of the orientation of the image on the computer screen. This allows direct comparison of the various trials of 3D landmark data collected from a single image without the need for registration of the various data sets through superimposition (i.e., rotation, translation). Landmark data were collected twice from each image by a single investigator, with a minimum of 24 hours elapsing between measurement trials to prevent memory-biased placement of landmarks. Each data collection trial was checked for overt or gross errors, such as switching right and left.

D. Statistical analysis

Statistical analyses were designed following Kohn and Cheverud [1992] and Richtsmeier et al. [1995]. In this design, measurement error in the collection of landmark coordinate data is attributed to three sources: precision, error due to the imaging device, and error due to digitization.

Precision is defined here as the average absolute difference between repeated measures of the same image. Estimates of precision from various data collection trials of a single image can be calculated local to each landmark without superimposition along three orthogonal axes because the coordinate system of the image does not change between data collection episodes. Precision was calculated for each landmark along each of three coordinate axes for each image. Measures of precision were averaged across images and across subjects (Table I; measures of precision for each image are available from the authors upon request) and represent variation in landmark placement over images and subjects along each of the three axes. For this study, we consider values below 1mm highly precise, between 1mm and 2mm precise, and greater than 2mm less precise. The goal of a particular study will dictate the degree of precision required. For example, a study of ear shape among two-year-old males requires greater precision than a comparison of facial width between male and female adults.

TABLE I.

Precision of Each Landmark Along Each of Three Axes, Calculated Across Individuals and Scans

Landmark name	Abbreviation	X axis mediolateral	Y axis superoinferior	Z axis anteroposterior
Glabella	g	0.988	4.03b	1.40a
Nasion	n	0.432	1.35a	0.710
Pronasale	prn	0.309	0.721	0.168
Subnasale	sn	0.242	0.186	0.408
Sublabiale	sl	0.715	0.631	0.442
Pogonion	pg	0.695	0.660	0.587
Left endocanthion	len	0.291	0.336	0.198
Left exocanthion	lex	0.576	0.278	0.568
Left alar curvature	lac	0.435	0.703	0.337
Left chelion	lch	0.401	0.212	0.273
Left tragion	lt	0.437	0.727	1.44a
Left otobasion inferius	lobi	0.283	0.358	0.482
Left gonion	lgo	2.14b	4.05b	3.16b
Right endocanthion	ren	0.339	0.228	0.172
Right exocanthion	rex	0.416	0.319	0.392
Right alar curvature	rac	0.311	0.617	0.332
Right chelion	rch	0.441	0.204	0.308
Right tragion	rt	0.388	1.44a	1.50a
Right otobasion inferius	robi	0.254	0.457	0.625
Right gonion	rgo	1.45a	4.10b	2.95b
Grand mean		0.827

^aIndicates error of greater than 1 mm.

^bIndicates values of greater than 2 mm. Landmark definitions can be found in Farkas [1994b].

In contrast, error is defined here as the proportion of total variance attributable to a particular factor, calculated using an analysis of variance (ANOVA). Error due to the imaging device is the proportion of total variance explained by differences in multiple images of the same subject. Error due to digitization is the proportion of total variance explained by differences in multiple digitizations (data collection episodes) of the same image. Because we must compare patterns of variance across images and across subjects, all of which exist in various coordinate systems, we conducted this analysis using interlandmark linear distances (LDs), rather than landmark coordinate data. By comparing interlandmark linear distances across images and across subjects, we avoid the necessity of any preconceived assumptions about variance patterns. We calculated all possible linear distances (LDs) between the 20 landmarks (n=190) for each digitization (n=2) of each image (n=30). These LDs were used as dependent variables in separate, nested analyses of variance (ANOVA) with two effect terms: 1) subject and 2) image nested within subject. The proportion of the total variance due to the different subjects represents the between-subject variance. The proportion of the total variance due to differences between the two images of the same subject represents the within-subject variance, or error due to the imaging system. The residual error term represents the error due to digitization.

Finally, the amount of acceptable error is addressed by an analysis of repeatability. Repeatability is a measure of precision relative to the magnitude of actual biological differences between individuals. For this analysis, we calculated repeatability for each LD using ANOVA to determine the proportion of total variance in a given LD explained by between-subjects differences [modified from Kohn and Cheverud, 1992]. Statistical significance was addressed by calculating the F statistic, the ratio of between-subject variance to within-subject variance.

results

A. Precision

Precision was calculated for each landmark along each of three axes. The grand mean of the precision calculated across subjects along all axes for all landmarks is 0.827 mm. Values range between 0.17mm and 4.10mm, with a median value of 0.44mm. These results show that on average, the landmarks assessed in this study are located with a very high degree of precision using the 3dMD system. Fourteen of the 20 landmarks display a very high degree of precision, showing error of less than 1mm along each of the three coordinate axes averaged over subjects and scans (Table I). Three of the 20 landmarks show error greater than 1mm, but less than 2mm (nasion, left and right tragion), with the three remaining landmarks having error greater than 2mm (glabella, left and right gonion). Results for these six landmarks are discussed below.

The three landmarks showing error greater than 1mm, but less than 2mm along at least one axis include nasion, right tragion and left tragion (Table I). Right tragion shows error greater than 1mm along two axes (1.44mm along SI axis and 1.50mm along AP axis), with lower error along the third axis (0.39mm). Left tragion shows error greater than 1mm along only one axis (1.44mm on the AP axis), with lower error along the other two axes (0.44mm along ML axis and 0.73mm on the SI axis). Similarly, nasion shows precision greater than 1mm only along one axis (1.35mm on the SI axis), with lower error along the other two axes (0.43mm along ML axis and 0.71mm along the AP axis). This result suggests that nasion is easily located on the mediolateral and anteroposterior axes, but less consistently located superoinferiorly, while the inconsistency in locating left tragion falls along the anteroposterior dimension.

The three landmarks displaying markedly decreased precision (error greater than 2mm) along one or more axes include glabella, right gonion and left gonion (Table I). Glabella shows decreased precision along the Y-axis (superoinferior plane; 4.03mm), with higher precision on the X and Z axes (0.99 and 1.40mm, respectively). This result suggests that glabella is located along the mediolateral and anteroposterior axes with little difficulty, but locating this landmark consistently along the superoinferior axis poses a greater challenge. The error for left gonion ranges from 2.14 to 4.05mm; similarly right gonion shows error from 1.44 to 4.10mm. Gonion is inconsistently located along all three axes.

B. Error due to digitization

Error due to digitization is expressed as a proportion of the total variance observed for each of the 190 LDs. The mean value averaged across all 190 LDs is 0.9%, meaning that on average less than 1% of the total observed variance is explained by error due to digitization. However, seven of the LDs show error due to digitization in excess of 5% (Table II). These results indicate that for most landmarks, a very small proportion of the total error is due to the observer. Of the seven LDs with error due to digitization in excess of 5%, four have glabella as an endpoint. This suggests inconsistency in the observer’s superoinferior location of the landmark glabella. The three remaining LDs denote distances spanning gonion to otobasion inferius (both right and left), and gonion to chelion on the left side. Relative to gonion, otobasion inferius is located superiorly along the plane of the mandibular ramus. Chelion is located anteriorly along the plane of the mandibular body relative to gonion. The increased error in the combination of these LDs indicates the inconsistent placement of gonion along the planes of the ramus and body of the mandible.

TABLE II.

Linear Distances (LDs) for Which Error Due to Digitization is Greater Than 5% of the Total Variance Across all Scans and all Subjects

LD	MSsubject	MSscan(subject)	MSdigitization	% error due to digitization
g-lex	98.98	2.95	5.61	5.2
g-ren	66.76	4.98	10.03	12.3
g-len	69.21	4.99	10.53	12.4
g-n	67.13	11.07	15.69	16.7
lgo-lch	142.22	17.35	8.74	5.2
lgo-lobi	308.55	17.68	20.03	5.8
rgo-robi	180.59	31.33	17.18	7.5

Columns 2, 3, and 4 show the mean squared error (MS) values for each error term. Column 5 shows the percentage of the total error that is due to digitization. For all LDs, between-subject variance was significantly greater than within-subject error variance (α=0.01). Landmark names are keyed to Table I and Figure 2.

C. Error due to imaging system

Error due to imaging system is also expressed as a proportion of the total variance observed in the 190 LDs. The mean value averaged across all 190 LDs is 1.5%, meaning that on average, only 1.5% of the total observed variance is explained by error due to the imaging system. The proportion of the total variance due to differences between the two scans for each subject was less than 5% for 180 of the 190 LDs. This indicates that a very small proportion of the total error is due to the imaging system.

A total of 11 LDs show error due to imaging in excess of 5% of the total variance observed (Table III). Six of these LDs connect the lower lip or mandible to landmarks located superior to the lips. The positions of the mandible and lips change with facial expression, breathing, and speaking, potentially altering the relative locations of landmarks located on these structures more so than landmark pairs that do not cross the mouth. A proper test of error due to imaging requires that the moving parts of the subject remain stable with relation to one another. Unfortunately, facial expression is bound to change at least slightly between scans of the same individual, whether it is due to opening/closing of the mouth, pursing of the lips, speaking, or breathing.

TABLE III.

Linear Distances (LDs) for Which Error Due to Imaging was Greater Than 5% of the Total Variance Across all Data Collection Episodes

LD	MSsubject	MSscan(subject)	MSdigitization	% error due to imaging	Influenced by facial expression	Influenced by shadows
lgo-lobi	308.55	17.68	20.03	5.1	F	S
lgo-lch	142.22	17.35	8.74	10.2	F	S
rgo-rt	463.08	46.90	22.68	7.3	F	S
rgo-rch	218.89	19.56	8.29	5.7	F	S
rgo-robi	180.59	31.33	17.18	12.8	F	S
lch-sl	147.18	9.44	0.56	5.5	F
rt-robi	113.00	6.30	2.19	5.2		S
g-len	69.21	4.99	10.53	5.2
g-ren	66.76	4.98	10.03	5.7
g-n	67.13	11.07	15.69	11.4
pg-sl	29.92	3.17	1.36	7.7

Columns 2, 3, and 4 show the mean squared error (MS) values for each error term. Column 5 shows the percentage of the total error that is due to imaging. LDs marked as F in the sixth column may be influenced by differences in facial expression between images; those marked as S in the last column may be influenced by differences in shadows, shine, and lighting between images. Landmark names are keyed to Table I and Figure 2.

Of the 11 LDs showing greater than 5% error due to imaging, six have an endpoint at either right or left tragion, gonion, or otobasion inferius (Table III). The operator’s placement of these landmarks may be influenced by shadows cast by hair, clothing or the helix of the ear, potentially obscuring detail. Although subtle movements of the entire head (while keeping the jaw and facial expression stable) between scans will not necessarily increase error due to imaging, these movements may alter these shadows, changing the appearance of these areas and consequently the perceived location of the landmarks.

Three other LDs in this category have glabella as one endpoint, extending to nasion, right endocanthion and left endocanthion. However, for these three linear distances, the error due to imaging was exceeded by the error due to digitization, suggesting that this variance was an effect of error in the placement of the landmarks. These three LDs are very small (averaging approximately 15 mm in the children included in this study), with even slight deviation in the location of one endpoint representing a large proportion of that LD.

D. Repeatability

The between-subject variance was significant relative to within-subject error (α=0.001) for every LD considered here, indicating that sources of error (imaging and digitization) were insufficient to obscure differences between the individuals in this study. Repeatability exceeded 95% for 181 of the 190 LDs considered. The other nine LDs had repeatability values ranging from 80% to 95%, and are all represented as having high error due to imaging (Table III).

Discussion

Our study demonstrates that images captured by the 3dMD system are highly repeatable and that 3D landmark data can be acquired with a high degree of precision using the 3dMD system. In general, the error associated with the placement of landmarks on the 3dMD images is sub-millimeter, comparable to that found in studies of other imaging systems [e.g., Kohn et al., 1995; Weinberg et al., 2004]. Further, both the error due to digitization (observer error) and error due to the imaging system are very low, also comparable to other studies [e.g., Kohn et al., 1995]. These results show that anthropometric landmark data collected from the 3dMD imaging system are highly reliable. The few exceptions are discussed below.

The landmarks glabella and left and right gonion show the highest degree of error from all three sources. In fact, the mean of the precision decreases by nearly half, falling to 0.431mm if these three landmarks are excluded from the calculation (from 0.827mm with all 20 landmarks included). These landmarks have been shown by previous studies of other 3D photogrammetric imaging systems to be problematic [e.g., Weinberg et al., 2004]. We discuss the possible reasons for the increased error associated with these landmarks below.

First, glabella is defined by Farkas [1994a] as the most prominent midline point between the eyebrows. The standard orientation for collection of glabella is the Frankfurt horizontal, defined by Farkas [1994a] as the plane connecting porion (or tragion) and orbitale (lowest point on the lower margin of the orbit), with orbitale identified by palpation. Without palpation, the perception of where orbitale lies may change between data collection trials from the same image, altering the subject’s orientation between scans. Though the 3dMD software allows the user to manipulate the images in 3D space, it is impossible to orient the head in exactly the same way each time, under any circumstances, even using this software. The solution to the problem of orientation is not simple. Our approach has been to avoid the use of any landmarks whose identity is based on orientation of the subject. However, if these landmarks are required by a research design, a device could be used to position the subject’s head stably and uniformly between scans. Problems associated with this solution include: 1) the device may obscure portions of the head that are of interest; and 2) individuals may perceive the stabilizing device as invasive. A second possibility is to mark orbitale on the subject using palpation prior to imaging, reducing the variation around this landmark. Weinberg et al. [2004] found in their study of another system that precision was increased when landmarks were marked prior to image acquisition. This may be a valuable strategy for some study populations; however, we found in our study that most children were resistant to having their faces marked in this way.

Second, the landmark gonion is problematic for many reasons. Gonion is defined by Farkas [1994a] as the most lateral point on the mandibular angle, identified by palpation. The angle of the mandible is difficult to locate precisely without direct palpation, which is not possible in any form of indirect data collection. Additionally, the error for this landmark may be high due, at least in part, to relatively increased anatomical variation of the mandible; i.e., variation of the mandibular angle, degree and placement of local fatty tissues. Also, the position of the entire mandible itself may shift with changes in facial expression. Although position of the mandible does not change the location of this landmark on the mandible itself, it shifts the landmark’s location relative to the rest of the head, altering measures between gonion and landmarks above the labial fissure. Weinberg et al. [2004] found similar results in their study of another 3D system. If gonion is necessary to a given study, we suggest palpation and marking the subject prior to image acquisition if the subject is amenable to the physical contact required. We also suggest analyzing measures that include mandibular landmarks separately from those acquired from the rest of the head to avoid this type of error.

Finally, landmarks located on the ears (tragion, otobasion inferius) are difficult to place precisely, because the subject’s hair often casts shadows or obscures these features. We suggest that loose hair should be pulled away from the face and ears if these landmarks are to be used in analysis. For this study we used the 3dMDface System that has two modular units (six cameras) and captures approximately 180-degrees of digital information. The 3dMDcranial System is configured with four modular units for a 360-degree full head capture, with each unit containing three digital machine vision cameras for a total of 12 cameras. Use of the 3dMDcranial system may increase the precision of landmarks on the ears, which are at the margin of the volume captured by 3dface system. The 3dMDface System can be upgraded to the 3dMDcranial System at any time.

Our results represent the error associated with landmark data collection from images acquired of actual people (children and adults) under realistic conditions. This study sample represents a wide age-range, introducing a large degree of biological variability. When the data acquired from the children included in the study sample are assessed without the adult individuals, the relative degree of error due to digitization increases. This increase is partially due to the reduction in biological variation of the sample after removal of the adults. However, the increased error is noted particularly in LDs crossing the labial fissure, indicating that the children in the sample substantially altered their facial expressions between the time of the first and second image acquisition. This result again illustrates error that is inherent in direct digitization of humans using a digitizer and the necessity to analyze measures that include mandibular landmarks separately from those acquired from the rest of the head.

The potential problems contributing to data errors described here (i.e., shadows, the need to palpate and mark certain landmarks, facial expression) are not unique to 3dMD, but are inherent to indirect anthropometry in general. Our results are comparable to studies of error in other 3D systems [e.g., Ayoub et al., 2003; Kohn and Cheverud, 1995; Kohn et al., 1995; Weinberg et al., 2004]. Though our discussion has focused on some of the problems encountered in the acquisition of landmark data from digital images, we emphasize that our results show that these data are highly repeatable and precise. In fact, the benefits of indirect anthropometry far outweigh the problems. First, the time required from the subject is minimal. Once the subject is seated in the appropriate place, the photo is captured in less than 2 milliseconds and the subject is then free to move. Second, the acquisition of the 3dMD images is entirely noninvasive. Third, images can be reviewed immediately to determine whether additional images are required. These factors are extremely important when working with children, especially those with any cognitive deficit or with developmental delay. Reducing the amount of time that any child has to sit still is a major benefit. Fourth, the image data can be archived indefinitely for future study, allowing the user to return to the original images repeatedly to check for errors or to collect supplementary data, whether they are additional anthropometric landmarks, surface areas, volumes, curves, arcs, or any other quantitative measure. Alternate dimensions such as linear distances and angles can also be measured directly on the images, or estimated from landmark coordinate data collected from these images. Finally, the landmark data presented in this study were collected by a trained observer but even so, a learning curve was noticed while training with the new technology. Before implementing any system of data collection, we recommend that the investigator be fully trained and perform his/her own error study to ensure precise and accurate results within any given research design.

Conceivably, the measures recorded by the 3dMD system are directly comparable to published norms. However, it should be noted that the 3dMD system is a non-contact system, while traditional anthropometric data sets are collected through direct measurement of individuals using calipers and/or measuring tape. We place landmarks on image surfaces, while anthropometricians use steel calipers and tapes that can slightly deform the skin with manual pressure. For this reason, we anticipate that LDs calculated from our 3D landmarks may show a slight difference when compared to the same measures taken by more traditional means. Weinberg et al. [2004] found that many of the 19 measures they obtained using 3D photogrammetric images from another imaging system were reduced relative to the same measures acquired with calipers. Further study is required to determine whether this holds true for 3dMD or other imaging systems, and whether there is a systematic difference for which a correction factor could be calculated to make these 3D measures directly comparable to those acquired by direct anthropometry. The inability to use published controls in conjunction with indirect anthropometry data sets would be a drawback of these new technologies.

The raw data acquired by 3D photogrammetry consists of thousands of three-dimensional points that define a complex surface. Though these data sets are informative and useful for purposes of visual comparison either by eyeballing, visualizing “mean surfaces,” or morphing between surfaces, no methods currently exist for statistical hypothesis testing of similarity of complex surfaces captured in these enormous data sets. Hammond et al. [2004] used these types of surface data sets in a test of pattern recognition using data from human faces. In that application, a small number of landmarks (i.e.,11) were initially collected manually on all scans. These landmarks were used to “guide” the formation of a dense correspondence between a common set of points across all faces in the study group. A correspondence of as many as 10,000 points, consisting of the nodes of a mesh superimposed over each form with the 11 original biological points as anchors, can be made in this way across all subjects. Importantly, the correspondence between the 11 original landmarks across all subjects is biological, while the correspondence between the thousands of points in the dense mesh is mathematical. Any errors in the placement of the original landmarks will be echoed in the larger data sets of points that cover the entire surface. The specific placement of surface points within the dense set is a function of the topography of the surface, the distance among the original manually located points, and the mathematical algorithm used to generate the mesh. Only the most general biological correspondence between points within the dense set is preserved across subjects. For this reason, the correspondence of surfaces between subjects is as much a function of mathematics as it is biology. Whether these denser data sets are useful to an investigator depends upon the research question being posed.

Knowledge of the developmental genetic basis for particular aspects of complex phenotypes is fundamental to our understanding of the translation of genotype into phenotype. Not surprisingly, attention has been focused on the roles of individual genes as the absolute source of specific phenotypes. Genes do not act in isolation, but mutually interact within developmental pathways. As the elements of gene networks implicated in development become clearer, the various components and their regulatory elements can be ranked in terms of their probable involvement in the underlying phenotypic variability. Whether analyzed in a model system or in the human population at large, quantitative studies of phenotypic variation at various points in ontogeny are needed to complete our understanding of the effects of known genetic factors and to uncover the influence of those not yet known to us. Modern geometric morphometric methods are available for the analysis of 3D phenotypic data sets [e.g., Marcus et al., 1996; Richtsmeier et al., 1992; Richtsmeier et al., 2002] and more traditional methods of morphological analysis have already proven extremely valuable in explanation of the genotype-phenotype continuum [e.g., Darvasi, 1998; Falconer and Mackay, 1996; Flint and Mott, 2001; Lynch and Walsh, 1995], and in the assessment of surgical outcome [e.g, Sloan et al., 1997]. 3D photogrammetry, when used appropriately and in an informed manner, is one means for acquiring large amounts of accurate phenotypic data in relatively short periods of time in the interest of adding to this growing body of information.