Abstract
In genetics, pleiotropy describes the genetic effect of a single gene on multiple phenotypic traits. A common approach is to analyze the phenotypic traits separately using univariate analyses and combine the test results through multiple comparisons. This approach may lead to low power. Multivariate functional linear models are developed to connect genetic variant data to multiple quantitative traits adjusting for covariates for a unified analysis. Three types of approximate F-distribution tests based on Pillai–Bartlett trace, Hotelling–Lawley trace, and Wilks’s Lambda are introduced to test for association between multiple quantitative traits and multiple genetic variants in one genetic region. The approximate F-distribution tests provide much more significant results than those of F-tests of univariate analysis and optimal sequence kernel association test (SKAT-O). Extensive simulations were performed to evaluate the false positive rates and power performance of the proposed models and tests. We show that the approximate F-distribution tests control the type I error rates very well. Overall, simultaneous analysis of multiple traits can increase power performance compared to an individual test of each trait. The proposed methods were applied to analyze (1) four lipid traits in eight European cohorts, and (2) three biochemical traits in the Trinity Students Study. The approximate F-distribution tests provide much more significant results than those of F-tests of univariate analysis and SKAT-O for the three biochemical traits. The approximate F-distribution tests of the proposed functional linear models are more sensitive than those of the traditional multivariate linear models that in turn are more sensitive than SKAT-O in the univariate case. The analysis of the four lipid traits and the three biochemical traits detects more association than SKAT-O in the univariate case.
Keywords: pleiotropy analysis, rare variants, common variants, association mapping, quantitative trait loci, complex traits, functional data analysis, multivariate linear models
Introduction
In genetics, pleiotropy describes the genetic effect of a single gene on multiple phenotypic traits [Razeto-Barry et al., 2011; Stearns, 2010; Williams, 1957]. For instance, phenylketonuria is a human disease that affects multiple systems but is caused by one gene defect. The disease can cause mental retardation, seizures, and reduced hair and skin pigmentation, and can be caused by any of a large number of mutations in a single gene that codes for the enzyme phenylalanine hydroxylase. Basically, a pleiotropic gene may have an effect on multiple traits simultaneously. The underlying mechanism of pleiotropy is the effect of a gene on metabolic pathways that affect different phenotypes. The phenotypic traits caused by pleiotropy are often correlated due to the genetic correlations, which need to be dealt with properly [Solovieff et al., 2013].
Pleiotropy is common and pervasive in the genome [Sivakumaran et al., 2011]. In a viewpoint published recently, the authors found that the American College of Medical Genetics and Genomics (ACMG) recommended a list of 56 genes for which incidental findings should be sought and reported in clinical exome and genome sequencing [Kocarnik and Fullerton, 2014]. Of the 56 ACMG genes, 43 (77%) had multiple associated phenotypes listed, with an average of 3.5 phenotypes per gene. Hence, it is important to study pleiotropy and to develop novel statistical methods to analyze pleiotropic traits.
One way to analyze the phenotypic traits caused by pleiotropy is to analyze the traits one by one. This approach may lead to low power since it ignores the extra information obtained by combining multiple traits in one unified analysis [Kiezun et al., 2012; Manolio et al., 2009]. In the literature, statistical methods for simultaneous analysis of multiple traits are available. However, the research focus on association analysis between a single nucleotide polymorphism (SNP) and multiple traits [Ferreira and Purcell, 2009; Jung et al., 2008; Klei et al., 2008; O’Reilly et al., 2012; Wu et al., 2013; Yan et al., 2013; Zheng et al., 2012]. In this article, we are interested in a combined association analysis between a pleiotropic gene rather than a single SNP and multiple quantitative traits. A genetic region may contain multiple genetic variants (usually a large number of variants identified by high throughput sequencing technology) that jointly affect the phenotypic traits. Therefore, the problem is to analyze multiple traits and high dimensional variant data. The question is how to build models that can effectively be used to test the association between the traits and the variants in one combined test, instead of many tests of association between one trait and one variant a time.
In a genome-wide association study (GWAS), the genome is scanned by testing for association of millions of individual SNPs with the trait [Manolio et al., 2009; McCarthy et al., 2008]. This strategy suffers from low power and multiple comparison problems [Dudbridge and Gusnanto, 2008]. There has been great interest in developing gene-based or region-based association tests. For instance, burden tests and kernel-based approaches were developed to analyze rare variants [Bansal et al., 2010]. Burden tests collapse rare variants in a genetic region to be a single variable that is used to test for association with the phenotypes [Han and Pan, 2010; Li and Leal, 2008; Madsen and Browning, 2009; Morgenthaler and Thilly, 2007;Morris and Zeggini, 2010; Price et al., 2010; Zawistowski et al., 2010]. The kernel-based tests aggregate the association between variants and phenotypes via a kernel matrix adjusting for covariates, which measures the similarity between individuals [Lin and Schaid, 2009; Mukhopadhyay et al., 2010; Neale et al., 2011;Wessel and Schork, 2006]. It is noteworthy that the sequence kernel association test (SKAT) and its optimal unified test (SKAT-O) have higher power than quite a few burden tests [Lee et al., 2012; Wu et al., 2011].
In Fan et al. [2013] and Luo et al. [2012], functional linear models were proposed to model the genetic effect as a smooth function. Luo et al. [2012] developed χ2-distributed score statistics to test the association at the gene level and Fan et al. [2013] used F -distributed tests adjusting for covariates. Fan et al. [2013] showed that the F -tests are more powerful than the popular SKAT and SKAT-O. In this paper, we build multivariate functional linear models to test the association between the multiple traits and the multiple variants in a genetic region. One motivation is the superior performance of the functional linear models in analyzing a single quantitative trait, and this merit should be useful for analyzing multiple traits.
In addition to burden tests and kernel-based approaches to analyze rare variants, several gene-based association test procedures are available in the literature to test for association between one or multiple traits and variant data [Guo et al., 2012; Lehne et al., 2011; Li et al., 2011; Purcell et al., 2007; Wang et al., 2007; Zhang et al., 2010]. In these procedures, the genetic data are viewed as discrete variables and the genetic effects are modeled as discrete coefficients of individual genetic markers such as SNPs. In Fan et al. [2013] and Luo et al. [2012], the genetic effects were treated as a function of genetic positions of the genetic markers and genetic data were viewed as stochastic functions [Ross, 1996]. Therefore, the philosophy of functional linear models is different from that of the other approaches. Most likely, the functional linear models can better use the linkage disequilibrium (LD) information of the dense genetic data, which leads to high power level while controlling type I error rates accurately.
To apply functional data analysis techniques to gene-based association analysis of complex diseases, the challenge is to build models and test statistics properly. We need to develop valid hypothesis testing procedures to test the association [Fan et al., 2013, 2014]. To our knowledge, Kong et al. [2014] is the only paper to deal with the hypothesis testing of functional linear models, except for Fan et al. [2013, 2014]. Kong et al. [2014] calculates type I error rates at a 0.05 level, by using 5,000 simulated replicates. In short, there has been very limited research on the hypothesis testing of functional regression models. Since we target both candidate gene and genome-wide analysis, we need more research to build valid test statistics which perform well and control false positives rigorously. It is noteworthy that likelihood ratio tests (LRT) were found to inflate type I error rates in both Fan et al. [2013] and Kong et al. [2014], while F-distributed tests generated accurate type I error rates. Therefore, it is not obvious or straightforward to apply classical testing procedures since we need to make sure that type I error rates are properly controlled in genetics studies. In summary, the research is very novel and the problem is important.
The organization of the paper is as follows. We first introduce the theoretical multivariate functional linear models and their revised version for analyzing real data, and build approximate F-test statistics to test association based on multivariate analysis theory. The proposed methods are applied to analyze (1) lipid traits in eight European cohorts, and (2) biochemical traits in the Trinity Students Study. Simulation analysis is performed to evaluate the false positive rates and power performance of the proposed models and tests.
Materials and Methods
Consider n individuals who are sequenced in a genomic region that has m variants. For each individual, we assume that there are L quantitative trait phenotypes, L ≥ 1. In Fan et al. [2013], functional linear models were built to perform association analysis between the m genetic variants and each phenotypic trait individually. In this article, the research goal is to model association between the m genetic variants and the L phenotypic traits as a whole. We assume that the m variants are located in a region with ordered genetic positions 0 ≤ t1 < ⋯ < tm = T. To make the notation simpler, we normalize the region [t1, T] to be [0, 1]. For the i-th individual, let yiℓ (ℓ = 1, 2, …, L) denote her/his quantitative traits, Gi = (Xi(t1), …, Xi(tm))′ denote her/his genotypes of them variants, and Zi = (zi1, …, zic)′ denote her/his covariates. Hereafter in this article,′ denotes the transpose of a vector or matrix. For the genotypes, we assume that Xi(tj) (= 0, 1, 2) is the number of minor alleles of the individual at the j -th variant located at the position tj.
Traditional Multivariate Linear Models
We assume that the quantitative traits are normally distributed. To model the relationship between the ℓ-th trait and the m variants, one may perform a canonical correlation analysis by following multivariate linear model
| (1) |
where αℓ0 is the overall mean, αℓ = (αℓ1, …, αℓc)′ is a c × 1 column vector of regression coefficients of covariates, βℓj is the genetic effect of genetic variant j, and εiℓ is an error term. For each i, the error vector εi = (εi1, …, εiL)′ is normally distributed with a mean vector of zeros and a L × L variance-covariance matrix Σ. Moreover, ε1, …, εn are assumed to be independent.
The analysis of model (1) can be readily done using the manova() function in R, which allows both multiple SNPs and multiple phenotypes to be analyzed jointly as well as the incorporation of covariates. Before fitting the model (1), the QR decomposition can be applied to the genotype data to remove the redundancy. One problem of the model (1) is that it may not be powerful when the number of genetic variants is large. Moreover, the model (1) can only model the LD between the traits and each of the genetic variants as well as the pair-wise LD between the genetic variants, but it can not model higher order LD among the genetic variants [Jung et al., 2008].
Beta-Smooth Only Multivariate Functional Linear Models
In this paper, we propose the following model to build the relation between the ℓ-th trait and the m variants
| (2) |
where βℓ(tj) is the genetic effect at the genetic position tj, and the other terms are similar to those in the multivariate linear regression model (1). It is noteworthy that there is only one difference between model (1) and model (2). That is, the genetic effect coefficient βℓj in model (1) does not depend on the genetic position tj, while βℓ(tj) in model (2) depends on the genetic position tj.
In the model (2), βℓ(tj) is introduced as the genetic effect at the position tj. In this article, we assume that the genetic effect function βℓ(t) is a function of the genetic position t. Therefore, βℓ(tj), j = 1, 2, …, m, are the values of function βℓ(t) at the m variant positions. The genetic effect function βℓ(t) is assumed to be smooth. One may expand it by B-spline or Fourier or linear spline basis functions. Formally, let us expand the genetic effect function βℓ(t) by a series of Kβ basis functions ψk(t), k = 1, …, Kβ as βℓ(t) = (ψ1(t), …, ψKβ (t))(βℓ1, …, βℓKβ)′ = ψ(t)′ βℓ, where βℓ = (βℓ1, …, βℓKβ)′ is a vector of coefficients βℓ1, …, βℓKβ and ψ(t) = (ψ1(t), …, ψKβ (t))′. We consider three types of basis functions: (1) linear spline basis ψ(t) = (1, t, (t – κ3)+, …, (t − κKβ)+)′, where κ3, …, κKβ are knots in the interval [0, 1], and (t − κk)+ indicates if t is larger than κk, i.e. (t − κk)+ = 0 if t ≤ κk and 1 if t > κk; (2) the B-spline basis: ψk(t) = Bk(t), k = 1, …, Kβ; and (3) the Fourier basis: ψ1(t) = 1, ψ2r+1(t) = sin(2πrt), and ψ2r(t) = cos(2πrt), r = 1, …, (Kβ − 1)/2. Here for the Fourier basis, Kβ is taken as a positive odd integer [de Boor, 2001; Ferraty and Romain, 2010; Horváth and Kokoszka, 2012; Ramsay et al., 2009; Ramsay and Silverman, 2005].
Replacing βℓ(tj) by the expansion, the model (2) can be revised as
| (3) |
where (ψ1(tj), …, ψKβ (tj)). In the model (2) and its revised version (3), we use the raw genotype data Gi = (Xi(t1), …, Xi(tm))′ directly in the analysis. In addition, we assume that the genetic effect function βℓ(t) is smooth. Hence, the models are called beta-smooth only approach.
General Multivariate Functional Linear Models
In this section, we build standard functional linear models to connect genetic variants to the phenotypic traits [Ramsay and Silverman, 2005]. The model (2) is one version of functional linear models and is easy to understand. To introduce the standard functional linear models, we view the i-th individual’s genotype data as a genetic variant function (GVF) as Xi(t), t ∈ [0, 1], in addition to treating the genetic effects as functions βℓ(t). Notice that the sample includes n discrete realizations or observations Gi = (Xi(t1), …, Xi(tm))′ of the human genome. By using the genetic variant information Gi, we may estimate the related genetic variant function Xi(t), which will be discussed below. To relate the genetic variant functions to the phenotypic traits adjusting for covariates, we consider the following multivariate functional linear model
| (4) |
where βℓ(t) is the genetic effect of genetic variant function Xi(t) at the position t, and the other terms are similar to those in the beta-smooth only model (2). In the above model, the integration term is used to replace the summation term in the beta-smooth only model (2). It turns out that model (2) performs very similarly to the model (4) in our real data analysis and simulation studies.
Estimation of Genetic Variant Function
To estimate the genetic variant functions Xi(t) from the genotypesGi, we use two methods: (1) an ordinary linear square smoother; (2) a functional principal component analysis (FPCA) technique [Fan et al., 2013; Goldsmith et al., 2011]. The ordinary linear square smoother method assumes that the genetic variant functions are smooth, while no smoothness is assumed by the FPCA technique. In the following, we briefly describe the two approaches.
Let φk(t), k = 1, …, K, be a series of K basis functions, such as the B-spline basis and Fourier basis functions. Let Φ denote the m by K matrix containing the values φk(tj), where j ∈ 1, …, m. Using the discrete realizations Gi = (Xi(t1), …, Xi(tm))′, we may estimate the genetic variant function Xi(t) using an ordinary linear square smoother as follows [Ramsay and Silverman, 2005, Chapter 4]
| (5) |
where φ(t) = (φ1(t), …, φK (t))′. To introduce the main idea of FPCA, let ΣX (s, t) be the covariance function of the genetic variant functions. Note that the covariance function ΣX (s, t) can be estimated by the observed genotype data Gi = (Xi(t1), …, Xi(tm))′, i = 1, 2 …, n [Ramsay and Silverman, 2005; Horváth and Kokoszka, 2012]. Let be the spectral decomposition of ΣX (s, t), where λ1 ≥ λ2 ≥ ⋯ are the nonincreasing eigenvalues and φk(t), k = 1, 2, …, are the corresponding orthonormal eigenfunctions. An approximation for Xi(t), based on a truncated Karhunen–Loève expansion, is
| (6) |
where K is the truncation lag, , and again φ(t) = (φ1(t), …, φK (t))′. Also notice that cik can be estimated by the observed genotype data.
Revised Multivariate Functional Linear Model
First, consider the case of expanding Xi(t) by the ordinary linear square smoother. As in the beta-smooth only case, the genetic effect βℓ(t) is expanded by a series of basis functions ψk(t), k = 1, …, Kβ, as βℓ(t) = (ψ1(t), …, ψKβ (t))(βℓ1, …, βℓKβ)′ = ψ(t)′ βℓ. Replacing Xi(t) in (4) by X̂i(t) in (5) and βℓ(t) by the expansion, we have a revised functional linear model
| (7) |
where . In the above revised regression model, one needs to calculate Φ[Φ′Φ]−1 and in order to get Wi. In the statistical packages R or Matlab, there are readily available codes to calculate them [Ramsay et al., 2009].
In the case of FPCA, we denote , where (ci1, …, ciK) and φ(t) are given by (6), and ψ(t) = (1, t, (t − κ3)+, …,(t − κKβ)+)′ is a vector of linear spline basis functions to expand the genetic effect functions. Then, the revised model in the case of FPCA is
| (8) |
Approximate F-distribution Tests of Association
Consider the multivariate linear model (1) and the revised regression models (3), (7), and (8). Models (7) and (8) are multivariate multiple linear regressions that model the genetic effect of genetic variant functions for the L phenotypic traits simultaneously adjusting for covariates. To test the association between the m genetic variants and the quantitative traits as a group, the null hypothesis is H0 : βℓ = (βℓ1, …, βℓKβ)′ = 0, ℓ = 1, …, L. We may test the null H0 : β1 = … = βL = 0 by approximate F-distribution tests based on Pillai–Bartlett trace, Hotelling–Lawley trace, and Wilks’s Lambda using standard statistical approaches [Anderson, 1984; Fox, 2008; Fox and Weisberg, 2011; Morrison, 2005; Rao, 1973].
If we only have one quantitative trait, i.e. L = 1, the three approximate F-distribution tests based on Pillai–Bartlett trace, Hotelling–Lawley trace, and Wilks’s Lambda are equivalent to the F-test statistics of the standard multiple linear regression. Thus, the models proposed in this article and the related approximate F-distribution tests extend the models and the F-test statistics in Fan et al. [2013].
Parameters of Functional Data Analysis
In the data analysis and simulations, we used the functional data analysis procedure in the statistical package R. We use two functions in library fda of R package as follows to create basis:
basis = create.bspline.basis
(norder = order, nbasis = bbasis)
basis = create.fourier.basis
(c(0,1), nbasis = fbasis)
The three parameters were taken as order = 4, bbasis = 15, fbasis = 25 in all data analysis and simulations to ensure that the type I error rates were properly controlled. Specifically, the order of B-spline basis was 4, and the number of basis functions of B-spline was K = Kβ = 15; the number of Fourier basis functions was K = Kβ = 25. In the data analysis and simulations of FPCA, the number of knots of the linear spline basis was taken as Kβ = 10 and the truncation lag K = 20. To ensure that the results are valid and stable, we tried a wide range of parameters that 10 ≤ K = Kβ ≤ 25 and the results are very close to each other (data not shown).
Application to Real Data
Lipid Traits in Eight European Cohorts
We analyzed lipid traits from eight European cohorts, where five are from Finland [Finland United States Investigation of NIDDM Genetics (FUSION Stage 2) [Scott et al., 2007], FIN-D2D 2007 (D2d-2007) [Kotronen et al., 2010], The Finnish Diabetes Prevention Study (DPS) [Tuomilehto et al., 2001], METabolic Syndrome in Men (METSIM) [Stancakova et al., 2009], and The Dose Responses to Exercise Training Study (DRs EXTRA) [Kouki et al., 2012], two are from Norway [Nord-Trondelag Health Study 2 and Tromso 4 (HUNT and Tromso) [Holmen et al., 2003; Jacobsen et al., 2012], and one from Germany [The DIAbetes GENetic Study (DIAGEN)] [Schwarz et al., 2006]. The two Norwegian cohorts were combined into one study for a joint analysis. The genotype data were from Metabochip genotyping, which was designed to fine map regions that have been associated with metabolic traits [Altshuler et al., 2010]. For each cohort, 54,741 genetic variants were genotyped, located in 97 genetic regions across the 22 autosomes. For our analysis, we utilized the existing literature as a reference for gene selection and found that 22 gene regions were fine mapped [Li et al., 2014; Liu et al., 2014; Morris et al., 2012; Scott et al., 2012; Voight et al., 2010; Zeggini et al., 2008]. We used Builder Mar. 2006 (NCBI36/hg18) to determine gene positions and 5 kb was used to extend the gene region on each side of a gene. The summary of 22 genes and the number of genetic variants in each gene region are given in Supplementary Table S1.
Four lipid traits were analyzed: high-density lipoprotein (HDL) levels, low-density lipoprotein (LDL) levels, triglycerides (TG), and total cholesterol (CHOL). The sample sizes for each combination of seven studies and four trait are provided in Supplementary Table S2. For each trait, inverse normal rank transformation was performed to ensure that the normality assumption was valid. For all studies except for METSIM, age, sex, and type 2 diabetes status were used as covariates. For METSIM, age and type 2 diabetes status were used as covariates since no female was included in the study. A significance threshold of P < 3.1 × 10–6 was taken from Liu et al. [2014] (corresponding to 0.05/16,153 and allowing for the number of genes tested therein).
Table 1 reports significant results of association analysis of five European studies in the regions of APOE and LDLR genes. At the significance threshold of P < 3.1 × 10–6, we detected association at APOE in the five European studies: D2d-2007, FUSION Stage 2, Norway, DIAGEN, and METSIM. At LDLR, association was detected in one study of METSIM. For the studies of D2d-2007 and FUSION Stage 2, two traits (LDL and CHOL) and their bivariate combination (LDL, CHOL) showed association with APOE by our F-approximation tests as well as SKAT-O. For the studies of Norway, DIAGEN, and METSIM, LDL and the trivariate combination (LDL, TG, CHOL) were associated with APOE. For the study of Norway, CHOL and bivariate combinations of (LDL, TG), (LDL, CHOL), and (TG, CHOL) were associated with APOE.
Table 1.
Results of association analysis of lipid traits in five European studies in the regions of APOE and LDLR genes using the F-approximation based on Pillai– Bartlett trace
| P -values of the F-approximation based on Pillai-Bartlett Trace | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Basis of both GVF and βℓ(t) | Basis of beta-smooth only | Multivariate Model (1) |
P-values of SKAT-O |
||||||
| Study | Gene | Traits | B-sp basis | Fourier basis | FPCA | B-sp basis | Fourier Basis | ||
| D2d-2007 | APOE | LDL | 1.89 × 10−25 | 9.02 × 10−25 | 3.47 × 10−23 | 1.89 × 10−25 | 9.02 × 10−25 | 2.85 × 10−24 | 5.87 × 10−13 |
| CHOL | 9.09 × 10−18 | 3.01 × 10−17 | 1.27 × 10−16 | 9.09 × 10− 18 | 3.01 × 10− 17 | 7.97 × 10− 17 | 1.72 × 10− 9 | ||
| LDL, CHOL | 1.21 × 10−20 | 2.08 × 10−19 | 1.90 × 10−19 | 1.21 × 10−20 | 2.08 × 10−19 | 7.91 × 10−19 | X | ||
| FUSION | APOE | LDL | 4.34 × 10−10 | 2.24 × 10−11 | 3.15 × 10−10 | 4.34 × 10−10 | 2.24 × 10−11 | 3.42 × 10−11 | 8.61 × 10−14 |
| Stage 2 | CHOL | 1.34 × 10−12 | 4.92 × 10−13 | 3.18 × 10−12 | 1.34 × 10−12 | 4.92 × 10−13 | 8.70 × 10−13 | 1.64 × 10−12 | |
| LDL,CHOL | 1.20 × 10−7 | 1.29 × 10−8 | 4.65 × 10−8 | 1.20 × 10−7 | 1.29 × 10−8 | 1.75 × 10−8 | X | ||
| Norway | APOE | LDL | 3.79 × 10−28 | 1.90 × 10−27 | 7.15 × 10−26 | 3.79 × 10−28 | 1.90 × 10−27 | 6.05 × 10−27 | 6.21 × 10−6 |
| TG | 5.69 × 10−4 | 3.94 × 10−4 | 6.80 × 10−5 | 5.69 × 10−4 | 3.95 × 10−4 | 6.55 × 10−4 | 5.55 × 10−2 | ||
| CHOL | 2.12 × 10−14 | 6.15 × 10−14 | 2.46 × 10−13 | 2.12 × 10−14 | 6.15 × 10−14 | 1.35 × 10−13 | 3.00 × 10−3 | ||
| LDL,TG | 1.42 × 10−25 | 8.16 × 10−25 | 9.55 × 10−25 | 1.42 × 10−25 | 8.16 × 10−25 | 4.72 × 10−24 | X | ||
| LDL,CHOL | 8.12 × 10−29 | 1.64 × 10−27 | 6.88 × 10−28 | 8.12 × 10−29 | 1.64 × 10−27 | 6.70 × 10−27 | X | ||
| TG,CHOL | 5.32 × 10−20 | 1.46 × 10−19 | 1.46 × 10−20 | 5.32 × 10−20 | 1.46 × 10−19 | 6.08 × 10−19 | X | ||
| LDL,TG,CHOL | 1.18 × 10−24 | 3.06 × 10−23 | 1.13 × 10−24 | 1.18 × 10−24 | 3.06 × 10−23 | 1.68 × 10−22 | X | ||
| DIAGEN | APOE | LDL | 7.84 × 10−7 | 3.31 × 10−6 | 5.82 × 10−6 | 7.84 × 10−7 | 3.31 × 10−6 | 5.76 × 10−6 | 2.37 × 10−1 |
| TG | 3.51 × 10−3 | 8.53 × 10−3 | 1.09 × 10−3 | 3.51 × 10−3 | 8.53 × 10−3 | 1.23 × 10−2 | 7.59 × 10−2 | ||
| CHOL | 1.91 × 10−3 | 5.61 × 10−3 | 1.77 × 10−2 | 1.91 × 10−3 | 5.61 × 10−3 | 7.38 × 10−3 | 4.73 × 10−1 | ||
| LDL,TG | 1.78 × 10−8 | 1.76 × 10−7 | 2.76 × 10−8 | 1.78 × 10−8 | 1.76 × 10−7 | 4.47 × 10−7 | X | ||
| LDL,CHOL | 1.24 × 10−9 | 1.44 × 10−8 | 5.06 × 10−8 | 1.24 × 10−9 | 1.44 × 10−8 | 3.24 × 10−8 | X | ||
| TG,CHOL | 2.99 × 10−6 | 2.49 × 10−5 | 6.76 × 10−6 | 2.99 × 10−6 | 2.49 × 10−5 | 4.51 × 10−5 | X | ||
| LDL,TG,CHOL | 1.81 × 10−10 | 4.43 × 10−9 | 1.83 × 10−9 | 1.81 × 10−10 | 4.43 × 10−9 | 1.19 × 10−8 | X | ||
| METSIM | APOE | LDL | 1.85 × 10−5 | 1.98 × 10−5 | 9.71 × 10−7 | 1.85 × 10−5 | 1.98 × 10−5 | 3.45 × 10−5 | 1.25 × 10−4 |
| TG | 2.80 × 10−2 | 3.43 × 10−2 | 7.66 × 10−2 | 2.80 × 10−2 | 3.43 × 10−2 | 3.96 × 10−2 | 4.04 × 10−1 | ||
| CHOL | 1.87 × 10−2 | 1.84 × 10−2 | 4.33 × 10−3 | 1.87 × 10−2 | 1.84 × 10−2 | 2.73 × 10−2 | 5.43 × 10−2 | ||
| LDL,TG | 2.70 × 10−7 | 3.45 × 10−7 | 1.47 × 10−7 | 2.70 × 10−7 | 3.45 × 10−7 | 7.77 × 10−7 | X | ||
| LDL,CHOL | 3.87 × 10−5 | 5.63 × 10−5 | 2.84 × 10−6 | 3.87 × 10−5 | 5.63 × 10−5 | 9.45 × 10−5 | X | ||
| LDL,TG,CHOL | 1.09 × 10−6 | 2.08 × 10−6 | 8.30 × 10−7 | 1.09 × 10−6 | 2.08 × 10−7 | 3.91 × 10−6 | X | ||
| LDLR | LDL | 1.72 × 10−4 | 2.20 × 10−5 | 9.42 × 10−6 | 1.72 × 10−4 | 2.20 × 10−5 | 4.01 × 10−5 | 1.50 × 10−2 | |
| CHOL | 3.47 × 10−4 | 2.97 × 10−6 | 1.31 × 10−5 | 3.47 × 10−4 | 2.97 × 10−6 | 5.67 × 10−6 | 5.79 × 10−3 | ||
| LDL,CHOL | 3.24 × 10−5 | 2.99 × 10−7 | 2.02 × 10−6 | 3.24 × 10−5 | 2.99 × 10−7 | 7.83 × 10−7 | X | ||
Notes: The associations that attain a threshold significance of P < 3.1 × 10−6 are highlighted in bold [Liu et al. 2014]. The results of “Basis of both GVF and βℓ(t)” were based on smoothing both GVF and genetic effect functions βℓ(t) of model (7), the results of “FPCA Approach” were based on FPCA approach of model (8), the results of “Basis of beta-Smooth Only” were based on smoothing βℓ(t) only approach of model (3), and the P-values of SKAT-O were based of R Package SKAT. GVF, genetic variant function.
For the studies of DIAGEN and METSIM, neither TG nor CHOL showed significant association with APOE at the significance threshold of P < 3.1 × 10–6. However, the bivariate combinations and trivariate combinations were significantly associated with APOE. The bivariate combination (TG, CHOL) also showed association with APOE in the DIAGEN study despite the fact that neither TG nor CHOL was significant in the univariate analysis. For the gene LDLR, CHOL showed a significant association while LDL did not; the bivariate combination (LDL, CHOL) also was significantly associated with LDLR.
In general, our F-approximation tests are more sensitive than the F-approximation tests of the multivariate linear model (1) which in turn is more sensitive than SKAT-O in the univariate case. SKAT-O only detected association of two traits (LDL and CHOL) with APOE in two studies, D2d-2007 and FUSION Stage 2. In comparison, the F-approximation tests of the multivariate linear model (1) detected more association than SKAT-O in the univariate case between two traits (LDL and CHOL) and APOE in the study of Norway. Generally, the P -values of our F-approximation tests are smaller than those of the F-approximation tests of the multivariate linear model (1). In the study of DIAGEN, the F-approximation tests of the multivariate linear model (1) did not detect any association between LDL [or (TG, CHOL)] and APOE. In the METSIM study, the F-approximation tests of the multivariate linear model (1) did nor detect any association between LDL [or (LDL, CHOL) or (LDL, TG, CHOL)] and APOE, and between CHOL and LDLR.
Biochemical Traits in the Trinity Students Study
We performed a pleiotropy analysis of 36 SNP variants in one enzyme gene region on three biochemical traits (denoted by A, B, and C) in a sample of 2,232 individuals from the Trinity Students Study. Since the raw traits were not normally distributed, we transformed the three traits by inverse normal rank transformation. We adjusted for three factors: gender, another chemical compound known to affect these biochemical traits as a continuous covariate, and a dichotomous covariate to indicate if supplements containing these biochemical factors was used.
In Fan et al. [2013], the three traits were analyzed individually and the results were compared with both SKAT and SKAT-O. In this article, we analyzed four combinations of the three traits: three bivariate combinations (A, B), (A, C), (B, C), and one trivariate combination (A, B, C). We tested the association between the transformed individual traits and the 36 SNPs by approximate F-test statistics of bivariate and trivariate linear models using B-spline basis, Fourier basis, and linear spline basis functions. For convenience of comparison, we also present the results of the univariate functional linear models of Fan et al. [2013], as well as those of SKAT-O.
Table 2 presents the P -values of the F-approximation tests based on the Pillai–Bartlett trace for the SNP data of the enzyme gene of the Trinity Students Study. We present the results of four combinations of the three traits on the bottom of the Table 2: (A, B), (A, C), (B, C), and (A, B, C). The four combinations of (A, B), (A, C), (B, C), and (A, B, C) provided much stronger results than those of univariate analysis individually since the P -values of the approximate F-distribution test statistics in the bottom four columns of Table 2 were much smaller than the F-test statistics of the individual univariate analyses of the three traits, A, B, and C. For all three traits, A, B, and C, the results of the univariate F-distributed tests are far better than those of SKAT-O [Table 2 and Fan et al., 2013]. Again, the P -values of our F-approximation tests are smaller than those of the F-approximation tests of the multivariate linear model (1).
Table 2.
Results of association analysis of three traits of the Trinity Students Study in the region of an enzyme gene using the F-approximation based on Pillai–Bartlett trace
| P -values of the F-approximation based on Pillai−Bartlett trace | |||||||
|---|---|---|---|---|---|---|---|
| Basis of both GVF and βℓ(t) | Basis of beta-smooth only | Multivariate Linear Model (1) |
P-values of SKAT-O |
||||
| Traits | B-spline basis | Fourier basis | FPCA | B-spline basis | Fourier basis | ||
| A | 1.73 × 10−13 | 7.89 × 10−13 | 1.54 × 10−15 | 1.73 × 10−13 | 7.89 × 10−13 | 2.84 × 10−12 | 2.16 × 10−10 |
| B | 3.44 × 10−13 | 1.80 × 10−11 | 1.58 × 10−13 | 3.44 × 10−13 | 1.80 × 10−11 | 1.23 × 10−10 | 2.72 × 10−5 |
| C | 1.11 × 10−11 | 9.91 × 10−10 | 8.67 × 10−11 | 1.11 × 10−11 | 9.91 × 10−10 | 3.78 × 10−9 | 1.25 × 10−5 |
| (A, B) | 2.14 × 10−20 | 3.14 × 10−18 | 3.00 × 10−21 | 2.14 × 10−20 | 3.14 × 10−18 | 7.67 × 10−17 | X |
| (A, C) | 1.08 × 10−17 | 9.53 × 10−16 | 9.29 × 10−18 | 1.08 × 10−17 | 9.53 × 10−16 | 4.46 × 10−15 | X |
| (B, C) | 6.54 × 10−15 | 9.51 × 10−12 | 1.19 × 10−14 | 6.54 × 10−15 | 9.51 × 10−12 | 1.05 × 10−10 | X |
| (A, B, C) | 2.30 × 10−21 | 5.87 × 10−18 | 3.74 × 10−21 | 2.30 × 10−21 | 5.87 × 10−18 | 1.56 × 10−16 | X |
Notes: The associations that attain a threshold significance of P < 3.1 × 10−6 are highlighted in bold [Liu et al. 2014]. The results of “Basis of both GVF and βℓ(t)” were based on smoothing both GVF and genetic effect functions βℓ(t) of model (7), the results of “FPCA Approach” were based on FPCA approach of model (8), the results of “Basis of beta-Smooth Only” were based on smoothing βℓ(t) only approach of model (3), and the P -values of SKAT-O were based of R Package SKAT. GVF, genetic variant function
Summary and Observation of Real Data Analysis
In summary, our association analyses of lipid traits and biochemical traits reveal that we may get a better picture by carrying out both univariate association analysis and multivariate pleiotropy analysis. Although the univariate analysis of separate traits may provide useful information despite not reaching a rigorous significance level like P < 3.1 × 10–6, combining the phenotypic traits into a multivariate analysis can produce stronger results, often reaching the genome-wide association threshold.
The results of beta-smooth only are identical or similar to those of smoothing both the genetic variant functions Xi(t) and the genetic effect function βℓ(t) in Tables 1 and 2. Therefore, whether the genetic variant functions are smoothed or not does not have much impact on the results as noted in Fan et al. [2013, 2014]. We also analyzed the data by the F-approximation tests based on the Wilks’s Lambda and Hotelling–Lawley trace. The results of F-approximation tests based on the Wilks’s Lambda and Hotelling–Lawley trace are similar to those of Table 2, although the P -values are slightly different (data not shown).
Empirical Genetic Effects of Genetic Variants
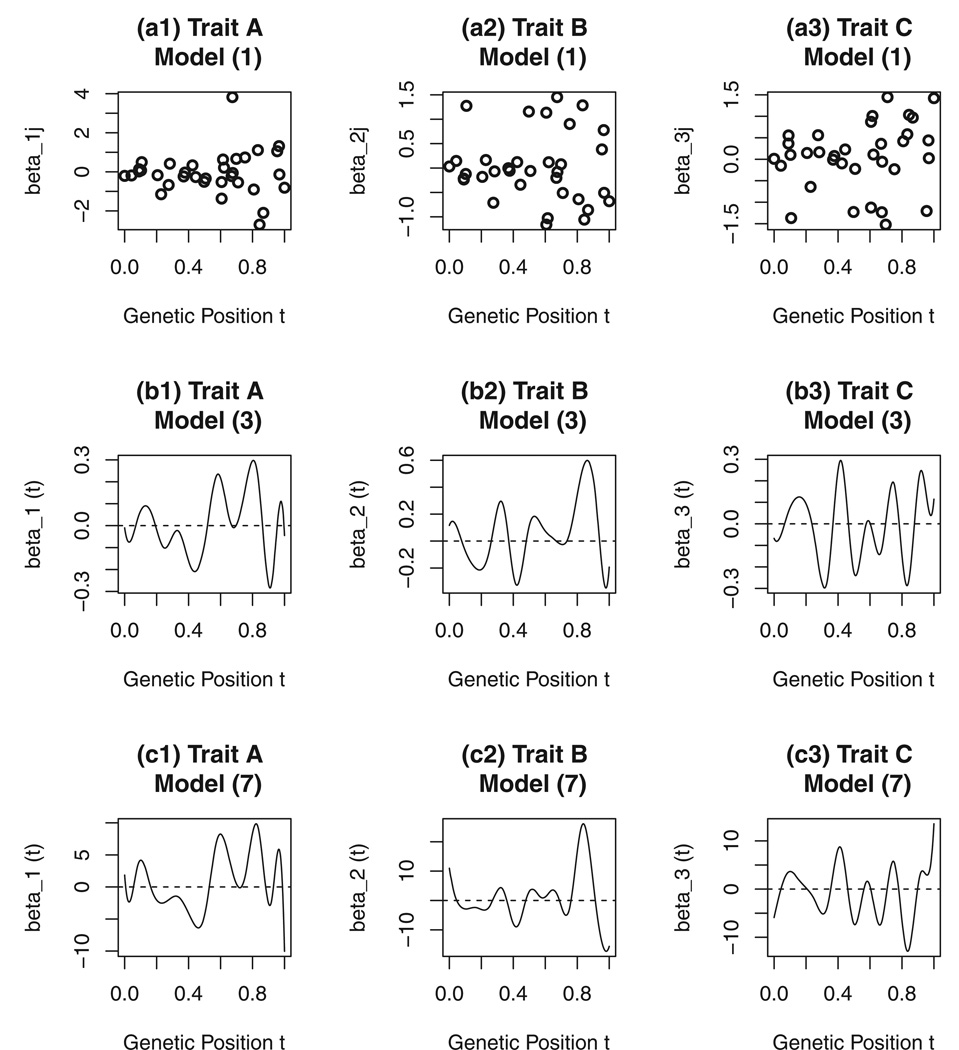
To understand the genetic effect of genetic variants, we use the three biochemical traits in The Trinity Students Study as an example. Figure 1 shows genetic effect coefficients βℓj of the multivariate linear model (1) and genetic effect functions βℓ(t) of functional linear models (3) and (7) against the genetic position. In the plots (a1), (a2), and (a3), the genetic effect coefficients βℓj of model (1) are shown. In the plots (b1), (b2), and (b3), the genetic effect functions βℓ((t) of model (3) are shown. In the plots (c1), (c2), and (c3), the genetic effect functions βℓ((t) of model (7) are shown. In the plots (a1), (a2), and (a3) of Figure 1, the genetic effect coefficients are large for quite a few variants. The genetic effect functions βℓ((t) shown in the plots (b1), (b2), (b3), (c1), (c2), and (c3) show that the genetic effects are large in wide regions.
Figure 1.
The genetic effect coefficients βℓj of multivariate linear model (1) and genetic effect functions βℓ(t) of functional linear models (3) and (7) against the genetic position t for the three biochemical traits in the trinity students study. In the plots (a1), (a2), and (a3), the genetic effect coefficients βℓj of model (1) are shown. In the plots (b1), (b2), and (b3), the genetic effect functions βℓ((t) of model (3) by B-spline basis functions are shown. In the plots (c1), (c2), and (c3), the genetic effect functions βℓ((t) of model (7) by B-spline basis functions are shown.
In addition, we analyzed the four lipid traits and the three biochemical traits by using each single variant versus some phenotype combinations reported in Tables 1 and 2. The results are reported in supplementary files. For instance, the file Trinity (A,B,C) manova.csv contains manova() results of the three biochemical trait combination (A, B, C) vs. each SNP. For each case, multiple variants are associated with the traits. Hence, a combined analysis using multiple variants simultaneously makes sense.
A Simulation Study
Simulations were performed to evaluate the performance of the proposed methods when sample sizes range from 500 to 2,000.As in Lee et al. [2012] and Wu et al. [2011], the cutoff of rare variants was taken as minor allele frequency (MAF) < 0.03. We used the sequence data used in Lee et al. [2012] and Wu et al. [2011] for two scenarios in empirical power and type I error calculations: (1) the causal variants are all rare; (2) the causal variants are both rare and common. The sequence data are with European ancestry from 10,000 chromosomes covering 1 Mb regions using the calibrated coalescent model programmed in COSI [Schaffner et al., 2005]. Specifically, the sequence data were generated using COSI’s calibrated best-fit models, and the generated European haplotypes mimick CEPH Utah individuals with ancestry from northern and western Europe in terms of site frequency spectrum and LD pattern [Fig. 4 in Schaffner et al., 2005; The International HapMap Consortium, 2007]. Genetic regions of 3 kb length were randomly selected in the simulations for type I error calculation and power calculations.
Figure 4.
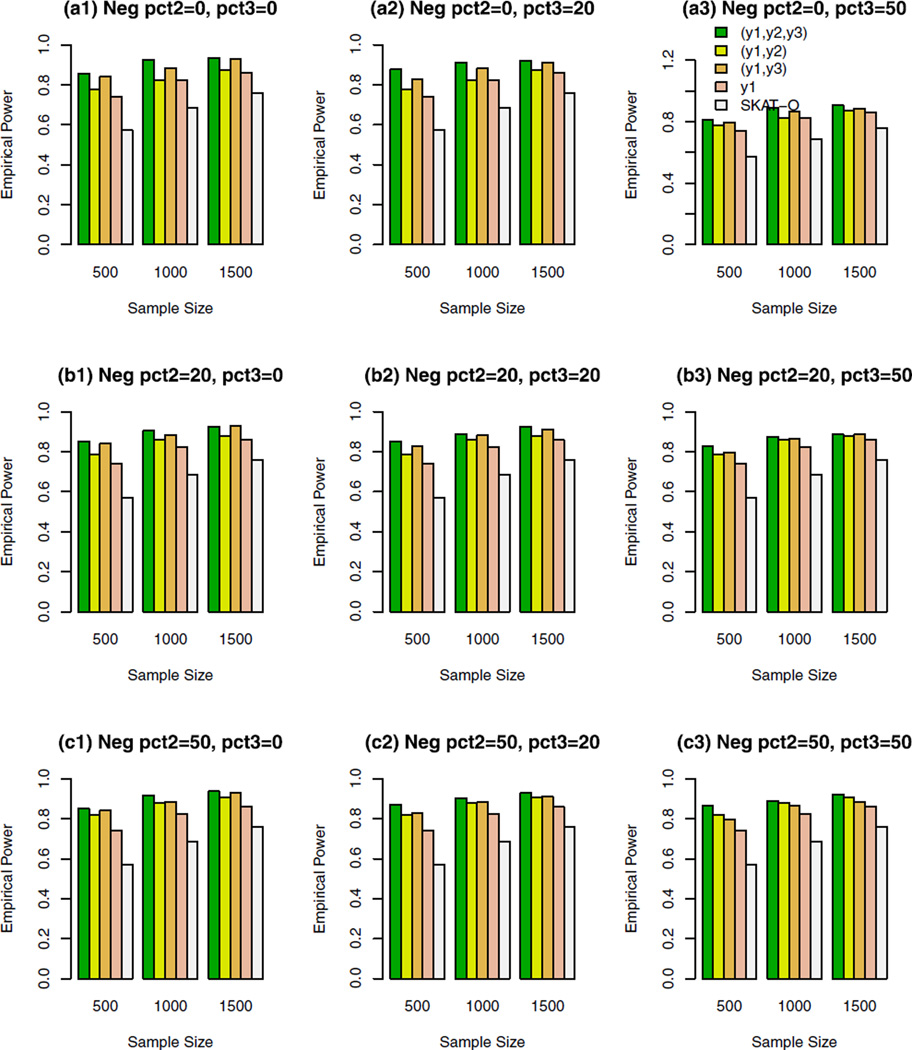
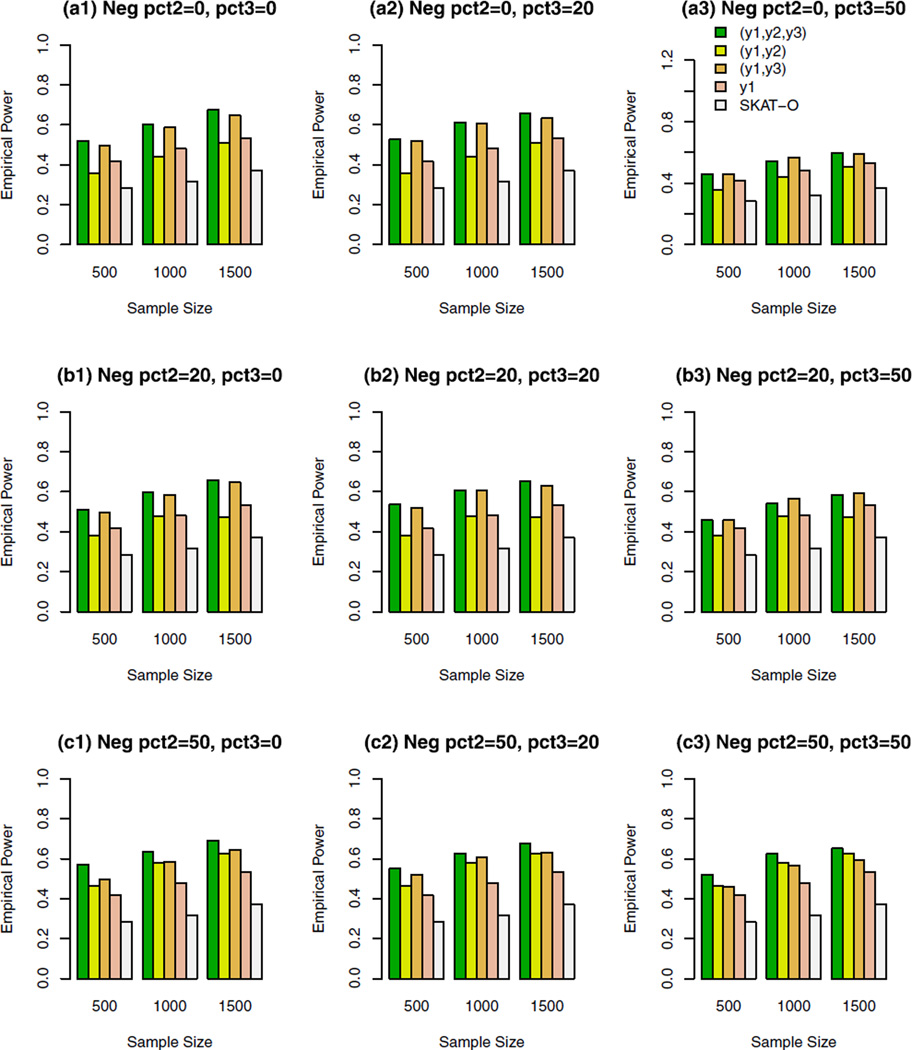
The empirical power of the approximate F-distribution test of model (3) using B-spline basis based on Pillai–Bartlett trace and SKAT-O at α = 0.01, when causal variants were both rare and common and 10% of the variants were causal. For the trait y1, 20%/80% causal variants had negative/positive effects; pct2 represents the percentage of negative effect causal variants for trait y2; and pct3 represents the percentage of negative effect causal variants for trait y3.
Type I error Simulations
To evaluate whether the proposed models and tests control false positive rates accurately, we generated phenotype datasets by using the model
| (9) |
where z1 is a dichotomous covariate taking values 0 and 1 with a probability of 0.5, z2 is a continuous covariate from a standard normal distribution N(0, 1), and (ε1, ε2, ε3)′ follows a normal distribution with a mean vector of 0 and a 3 × 3 variance-covariance matrix
| (10) |
The 3 × 3 variance-covariance matrix Σ is taken from an empirical analysis of the three traits of The Trinity Students Study. To obtain genotype data, 3 kb subregions were randomly selected in the 1 Mb region and the ordered genotypes were these genetic variants in the 3 kb subregions. For the scenario that the causal variants are all rare, only rare variants were used; and for the scenario that the causal variants are both rare and common, all variants in the selected subregions were used. Notice that the trait values are not related to the genotypes, and so the null hypothesis holds. The sample sizes of the datasets were taken as 500, 1,000, 1,500, 2,000, respectively. For each sample size case, 106 phenotype– genotype datasets were generated to fit the proposed models and to calculate the approximate F-test statistics and related P -values. Then, an empirical type I error rate was calculated as the proportion of 106 P -values that were smaller than a given α level (i.e. 0.05, 0.01, 0.001, and 0.0001, respectively).
Empirical Power Simulations
For empirical power simulations, we assumed that 10% or 5% of the variants were causal. We considered two scenarios: (1) the causal variants are all rare, i.e. the causal variants’ MAF < 0.03, and (2) the causal variants are both rare and common. Again, we randomly selected 3 kb subregions to obtain causal variants for the phenotype values. Once a 3 kb subregion was selected from the 1 Mb region, a subset of P causal variants located in the 3 kb subregion was then randomly selected to obtain ordered genotypes (X(t1), …, X(tp)). Then, we generated the quantitative traits by
| (11) |
where z1, z2, and (ε1, ε2, ε3)′ are the same as in the type I error model (9), and the βs are additive effects for the causal variants defined as follows. We used |βij| = ci | log10(MAFj)|/2, where MAFj was the MAF of the j -th variant. When 10% of the variants were causal, c1 = log(7), c2 = log(6), c3 = log(5), respectively; when 5% of the variants were causal, c1 = log(10), c2 = log(8.5), c3 = log(7), respectively. For each setting, 1,000 datasets were simulated to calculate the empirical power levels as the proportion of P -values that are smaller than a given α level (i.e. 0.05, 0.01, and 0.001, respectively).
Type I Error Simulation Results
In our simulations, we calculated the empirical type I error rates for the approximate F-distribution test statistics based on Pillai–Bartlett trace, Hotelling–Lawley trace, and Wilks’s Lambda. For the F-approximation test statistics based on the Pillai–Bartlett trace, the empirical type I error rates are reported in Table 3 for the scenario that the causal variants are all rare, and Table 4 for the scenario that the causal variants are both rare and common. The results of three combinations of traits are reported, two bivariate combinations (y1, y2) and (y1, y3), and one trivariate combination (y1, y2, y3). For each entry of empirical type I error rates, we generated 106 datasets. Results of four different α = 0.05, 0.01, 0.001, and 0.0001 nominal levels were reported.
Table 3.
Empirical type I error rates of the approximate F-distribution tests based on Pillai–Bartlett trace, when the causal variants are all rare
| Sample size |
Nominal level α |
Basis of both GVF and βℓ(t) | Basis of beta-smooth only | ||||
|---|---|---|---|---|---|---|---|
| Traits | B-sp basis | Fourier basis | FPCA | B-sp basis | Fourier basis | ||
| (y1, y2, y3) | 500 | 0.05 | 0.049282 | 0.049516 | 0.049293 | 0.049195 | 0.049204 |
| 0.01 | 0.009733 | 0.009693 | 0.009622 | 0.009624 | 0.009702 | ||
| 0.001 | 0.001002 | 0.000994 | 0.000980 | 0.001009 | 0.001004 | ||
| 0.0001 | 0.000095 | 0.000075 | 0.000108 | 0.000083 | 0.000093 | ||
| 1,000 | 0.05 | 0.050011 | 0.049819 | 0.050006 | 0.050015 | 0.049966 | |
| 0.01 | 0.009851 | 0.009859 | 0.009909 | 0.009945 | 0.009826 | ||
| 0.001 | 0.000948 | 0.000904 | 0.000952 | 0.000910 | 0.000948 | ||
| 0.0001 | 0.000083 | 0.000090 | 0.000101 | 0.000082 | 0.000084 | ||
| 1,500 | 0.05 | 0.049846 | 0.050224 | 0.049697 | 0.049762 | 0.049856 | |
| 0.01 | 0.009845 | 0.010014 | 0.009838 | 0.009850 | 0.009810 | ||
| 0.001 | 0.000954 | 0.001003 | 0.000964 | 0.000909 | 0.000949 | ||
| 0.0001 | 0.000096 | 0.000010 | 0.000088 | 0.000097 | 0.000096 | ||
| 2,000 | 0.05 | 0.049693 | 0.049824 | 0.049889 | 0.049695 | 0.049681 | |
| 0.01 | 0.009900 | 0.009846 | 0.009897 | 0.009926 | 0.009897 | ||
| 0.001 | 0.000989 | 0.000992 | 0.000969 | 0.001003 | 0.000989 | ||
| 0.0001 | 0.000110 | 0.000105 | 0.000097 | 0.000094 | 0.000110 | ||
| (y1, y2) | 500 | 0.05 | 0.049681 | 0.049472 | 0.049346 | 0.049573 | 0.049645 |
| 0.01 | 0.009778 | 0.009907 | 0.009569 | 0.009763 | 0.009772 | ||
| 0.001 | 0.000943 | 0.000961 | 0.000957 | 0.000959 | 0.000957 | ||
| 0.0001 | 0.000101 | 0.000086 | 0.000098 | 0.000099 | 0.000104 | ||
| 1,000 | 0.05 | 0.049793 | 0.049820 | 0.049460 | 0.049938 | 0.049808 | |
| 0.01 | 0.009785 | 0.009740 | 0.009958 | 0.009922 | 0.009784 | ||
| 0.001 | 0.000966 | 0.000990 | 0.000920 | 0.000938 | 0.000961 | ||
| 0.0001 | 0.000098 | 0.000099 | 0.000092 | 0.000079 | 0.000095 | ||
| 1,500 | 0.05 | 0.050169 | 0.049950 | 0.049825 | 0.049801 | 0.050154 | |
| 0.01 | 0.009881 | 0.009938 | 0.009812 | 0.009925 | 0.009885 | ||
| 0.001 | 0.000960 | 0.001010 | 0.000964 | 0.000961 | 0.000958 | ||
| 0.0001 | 0.000099 | 0.000101 | 0.000090 | 0.000109 | 0.000010 | ||
| 2,000 | 0.05 | 0.049463 | 0.049961 | 0.049920 | 0.049857 | 0.049463 | |
| 0.01 | 0.009974 | 0.009931 | 0.010001 | 0.010122 | 0.009970 | ||
| 0.001 | 0.001011 | 0.001014 | 0.000980 | 0.001023 | 0.001010 | ||
| 0.0001 | 0.000098 | 0.000109 | 0.000086 | 0.000113 | 0.000098 | ||
| (y1, y3) | 500 | 0.05 | 0.049204 | 0.049216 | 0.049195 | 0.049222 | 0.049189 |
| 0.01 | 0.009713 | 0.009889 | 0.009728 | 0.009886 | 0.009717 | ||
| 0.001 | 0.000998 | 0.000928 | 0.001031 | 0.000998 | 0.000998 | ||
| 0.0001 | 0.000091 | 0.000096 | 0.000090 | 0.000099 | 0.000090 | ||
| 1,000 | 0.05 | 0.050154 | 0.050095 | 0.050087 | 0.050063 | 0.050098 | |
| 0.01 | 0.009961 | 0.009991 | 0.009986 | 0.010047 | 0.009962 | ||
| 0.001 | 0.001010 | 0.000970 | 0.001030 | 0.000977 | 0.001020 | ||
| 0.0001 | 0.000092 | 0.000102 | 0.000108 | 0.000097 | 0.000097 | ||
| 1,500 | 0.05 | 0.049919 | 0.050195 | 0.049950 | 0.049533 | 0.049929 | |
| 0.01 | 0.009863 | 0.010141 | 0.009930 | 0.009982 | 0.009859 | ||
| 0.001 | 0.000999 | 0.000981 | 0.000985 | 0.000977 | 0.000994 | ||
| 0.0001 | 0.000110 | 0.000095 | 0.000109 | 0.000099 | 0.000107 | ||
| 2,000 | 0.05 | 0.049750 | 0.049626 | 0.049673 | 0.049641 | 0.049791 | |
| 0.01 | 0.009928 | 0.009844 | 0.009865 | 0.009813 | 0.009937 | ||
| 0.001 | 0.000981 | 0.000960 | 0.000957 | 0.000965 | 0.000981 | ||
| 0.0001 | 0.000098 | 0.000087 | 0.000098 | 0.000105 | 0.000098 | ||
Notes: The results of “Basis of both GVF and βℓ(t)” were based on smoothing both GVF and genetic effect functions βℓ(t) of model (7), the results of “FPCA approach” were based on the FPCA approach of model (8), and the results of “Basis of beta-smooth only” were based on the smoothing βℓ(t) only approach of model (3).
Table 4.
Empirical type I error rates of the approximate F-distribution tests based on Pillai–Bartlett trace, when the causal variants are both rare and common
| Sample size |
Nominal level α |
Basis of both GVF and βℓ(t) | Basis of beta-smooth only | ||||
|---|---|---|---|---|---|---|---|
| Traits | B-sp basis | Fourier basis | FPCA | B-sp basis | Fourier basis | ||
| (y1, y2, y3) | 500 | 0.05 | 0.049276 | 0.049309 | 0.049354 | 0.049172 | 0.049258 |
| 0.01 | 0.009762 | 0.009775 | 0.009700 | 0.009746 | 0.009790 | ||
| 0.001 | 0.000932 | 0.000948 | 0.000916 | 0.000958 | 0.000954 | ||
| 0.0001 | 0.000084 | 0.000077 | 0.000075 | 0.000091 | 0.000076 | ||
| 1,000 | 0.05 | 0.049608 | 0.049845 | 0.049651 | 0.049669 | 0.049811 | |
| 0.01 | 0.009775 | 0.009781 | 0.009818 | 0.009771 | 0.009812 | ||
| 0.001 | 0.000947 | 0.000963 | 0.001013 | 0.000943 | 0.000971 | ||
| 0.0001 | 0.000089 | 0.000102 | 0.000081 | 0.000090 | 0.000104 | ||
| 1,500 | 0.05 | 0.049501 | 0.050344 | 0.049806 | 0.049521 | 0.050273 | |
| 0.01 | 0.009954 | 0.009984 | 0.009865 | 0.009942 | 0.009987 | ||
| 0.001 | 0.000988 | 0.000977 | 0.000962 | 0.000990 | 0.000993 | ||
| 0.0001 | 0.000107 | 0.000101 | 0.000093 | 0.000106 | 0.000095 | ||
| 2,000 | 0.05 | 0.049660 | 0.049636 | 0.049661 | 0.049672 | 0.049679 | |
| 0.01 | 0.009869 | 0.010023 | 0.009904 | 0.009872 | 0.010014 | ||
| 0.001 | 0.000957 | 0.001042 | 0.000968 | 0.000956 | 0.001045 | ||
| 0.0001 | 0.000097 | 0.000107 | 0.000103 | 0.000097 | 0.000109 | ||
| (y1, y2) | 500 | 0.05 | 0.049599 | 0.049487 | 0.049746 | 0.049512 | 0.049432 |
| 0.01 | 0.009807 | 0.009784 | 0.009733 | 0.009821 | 0.009825 | ||
| 0.001 | 0.000982 | 0.000956 | 0.000945 | 0.000977 | 0.000978 | ||
| 0.0001 | 0.000109 | 0.000090 | 0.000080 | 0.000109 | 0.000091 | ||
| 1,000 | 0.05 | 0.049727 | 0.049620 | 0.050035 | 0.049759 | 0.049642 | |
| 0.01 | 0.009847 | 0.009777 | 0.009820 | 0.009851 | 0.009731 | ||
| 0.001 | 0.001011 | 0.000976 | 0.000938 | 0.001010 | 0.000972 | ||
| 0.0001 | 0.000098 | 0.000126 | 0.000093 | 0.000099 | 0.000126 | ||
| 1,500 | 0.05 | 0.049868 | 0.049992 | 0.049918 | 0.049875 | 0.049984 | |
| 0.01 | 0.010013 | 0.009943 | 0.009946 | 0.010005 | 0.009948 | ||
| 0.001 | 0.001009 | 0.000997 | 0.000966 | 0.001002 | 0.001002 | ||
| 0.0001 | 0.000089 | 0.000100 | 0.000096 | 0.000090 | 0.000099 | ||
| 2,000 | 0.05 | 0.049785 | 0.050148 | 0.050102 | 0.049811 | 0.050090 | |
| 0.01 | 0.010006 | 0.009923 | 0.009908 | 0.009999 | 0.009932 | ||
| 0.001 | 0.001037 | 0.001016 | 0.000979 | 0.001036 | 0.001015 | ||
| 0.0001 | 0.000106 | 0.000094 | 0.000097 | 0.000106 | 0.000095 | ||
| (y1, y3) | 500 | 0.05 | 0.049691 | 0.049598 | 0.049754 | 0.049757 | 0.049519 |
| 0.01 | 0.009734 | 0.009874 | 0.009773 | 0.009755 | 0.009925 | ||
| 0.001 | 0.000914 | 0.000923 | 0.000976 | 0.000925 | 0.000920 | ||
| 0.0001 | 0.000095 | 0.000083 | 0.000089 | 0.000097 | 0.000089 | ||
| 1,000 | 0.05 | 0.049754 | 0.050020 | 0.049954 | 0.049743 | 0.050016 | |
| 0.01 | 0.010023 | 0.010007 | 0.009983 | 0.010012 | 0.009965 | ||
| 0.001 | 0.000972 | 0.001001 | 0.001023 | 0.000976 | 0.001014 | ||
| 0.0001 | 0.000085 | 0.000096 | 0.000088 | 0.000083 | 0.000108 | ||
| 1,500 | 0.05 | 0.049688 | 0.050607 | 0.049659 | 0.049719 | 0.050506 | |
| 0.01 | 0.009953 | 0.010013 | 0.009880 | 0.009956 | 0.010013 | ||
| 0.001 | 0.000966 | 0.001021 | 0.000992 | 0.000966 | 0.001013 | ||
| 0.0001 | 0.000100 | 0.000107 | 0.000103 | 0.000099 | 0.000105 | ||
| 2000 | 0.05 | 0.049685 | 0.049387 | 0.049816 | 0.049686 | 0.049378 | |
| 0.01 | 0.009975 | 0.009861 | 0.009697 | 0.009965 | 0.009863 | ||
| 0.001 | 0.000972 | 0.000994 | 0.000991 | 0.000974 | 0.000987 | ||
| 0.0001 | 0.000082 | 0.000108 | 0.000101 | 0.000083 | 0.000106 | ||
Notes: The results of “Basis of both GVF and βℓ(t)” were based on smoothing both GVF and genetic effect functions βℓ(t) of model (7), the results of “FPCA approach” were based on the FPCA approach of model (8), and the results of “Basis of beta-smooth only” were based on the smoothing βℓ(t) only approach of model (3).
For the approximate F-distribution test statistics based on the Pillai–Bartlett trace of the multivariate functional linear models, all empirical type I error rates are around the nominal α levels (columns 4–8 of Tables 3 and 4). Therefore, the approximate F-distribution test statistics control type I error rates correctly over all sample sizes and all significance levels. Thus, the approximate F-distribution test statistics can be useful in whole genome and whole exome association studies. Notice that the proposed methods control type I error rates accurately for moderate sample size cases of 500. The empirical type I error rates for the approximate F-distribution tests based on Hotelling–Lawley trace and Wilks’s Lambda are similar to those of the approximate F-distribution tests based on Pillai–Bartlett trace (data not shown).
Statistical Power of the Proposed Tests and SKAT-O
We compared the power performance of the proposed approximate F-distribution tests of bivariate and tri-variate models with the performance of F-tests of univariate models and SKAT-O based on the simulated COSI sequence data. Using B-spline basis functions, the empirical power levels of the approximate F-distribution tests of model (3) based on Pillai–Bartlett trace are reported in the figures both in the main text and in the Supplementary Materials, as well as those of F-tests and SKAT-O using the trait values of y1 at α = 0.01.
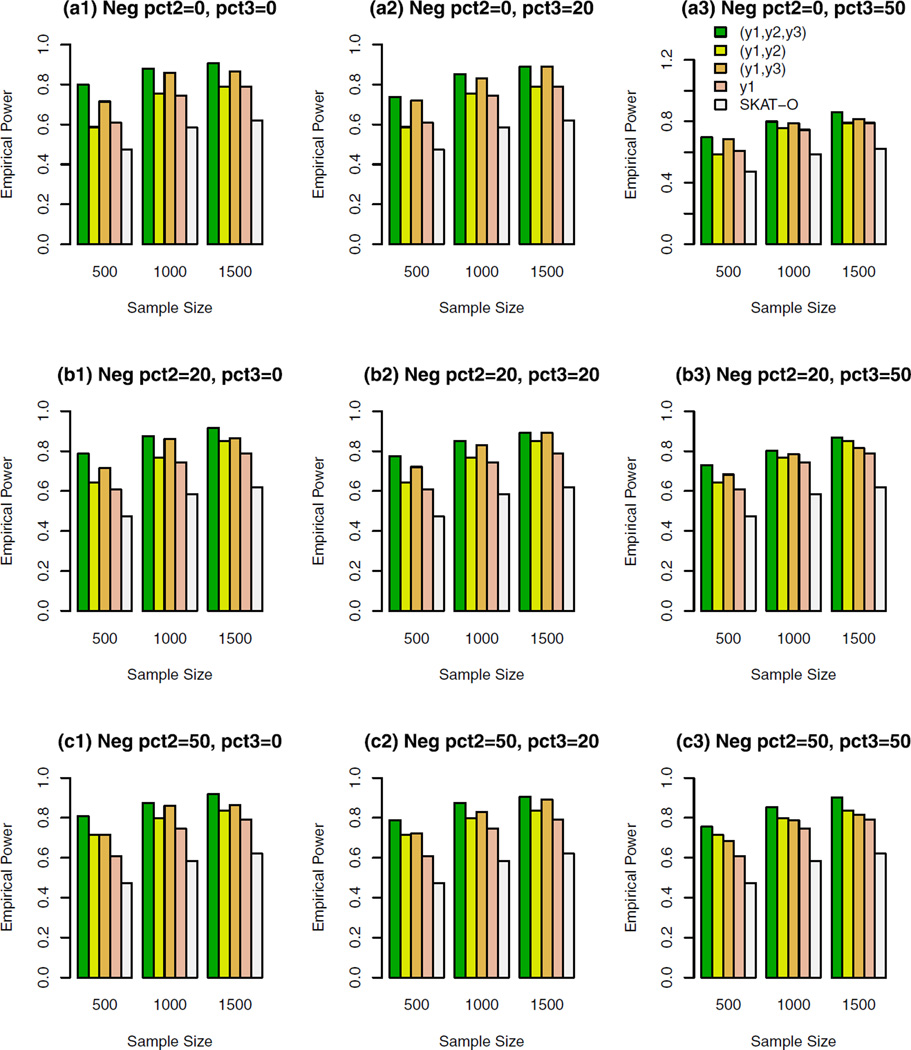
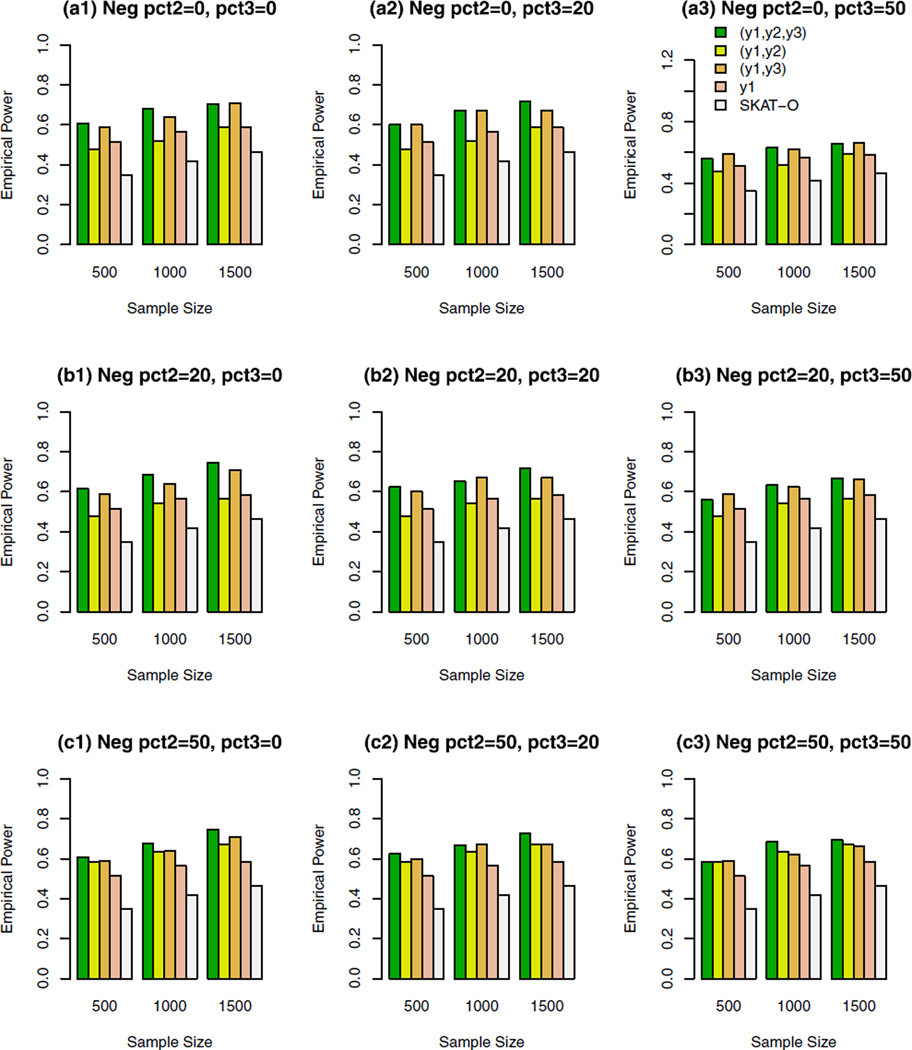
For the trait y1, 20%/80% causal variants had negative/ positive effects in Figures 2–5. In the Supplementary Figures S1–S4, all causal variants had positive effects for the trait y1. In the Supplementary Figures S5, S6, S7, and S8, 50%/50% causal variants had negative/positive effects for the trait y1. For the trait y2 in each figure, all causal variants had positive effects in the top graphs [(a1), (a2), and (a3)], 20%/80% causal variants had negative/positive effects in the middle graphs [(b1), (b2), and (b3)], and 50%/50% causal variants had negative/positive effects in the bottom graphs [(c1), (c2), and (c3)]. For the trait y3 in each figure, all causal variants had positive effects in the left column graphs [(a1), (b1), and (c1)], 20%/80% causal variants had negative/ positive effects in the middle column graphs [(a2), (b2), and (c2)], and50%/50%causal variants had negative/positive effects in the right column graphs [(a3), (b3), and (c3)].
Figure 2.
The empirical power of the approximate F-distribution test of model (3) using B-spline basis based on Pillai–Bartlett trace and SKAT-O at α = 0.01, when causal variants were only rare and 10% of the variants were causal. For the trait y1, 20%/80% causal variants had negative/positive effects; pct2 represents the percentage of negative effect causal variants for trait y2; and pct3 represents the percentage of negative effect causal variants for trait y3.
Figure 5.
The empirical power of the approximate F-distribution test of model (3) using B-spline basis based on Pillai–Bartlett trace and SKAT-O at α = 0.01, when causal variants were both rare and common and 5% of the variants were causal. For the trait y1, 20%/80% causal variants had negative/positive effects; pct2 represents the percentage of negative effect causal variants for trait y2; and pct3 represents the percentage of negative effect causal variants for trait y3.
In Figures 2, 3, and Supplementary Figures S1, S2, S5, and S6, the causal variants are only rare variants. In Figures 4, 5, and Supplementary Figures S3, S4, S7, and S8, the causal variants can be both rare and common. In the legend of all the figures, “(y1, y2, y3)” represents the empirical power bar when all three traits (y1, y2, y3) are used for a trivariate analysis, “(y1, y2)” represents the empirical power bar when two traits (y1, y2) are used for a bivariate analysis, “(y1, y3)” represents the empirical power bar when two traits (y1, y3) are used for a bivariate analysis, “y1” represents the empirical power bar when only one trait y1 is used for a univariate analysis, and “SKAT-O” represents the power level of the trait y1 by SKAT-O.
Figure 3.
The empirical power of the approximate F-distribution test of model (3) using B-spline basis based on Pillai–Bartlett trace and SKAT-O at α = 0.01, when causal variants were only rare and 5% of the variants were causal. For the trait y1, 20%/80% causal variants had negative/positive effects; pct2 represents the percentage of negative effect causal variants for trait y2; and pct3 represents the percentage of negative effect causal variants for trait y3.
As documented in Fan et al. [2013], the F-distributed test statistics of univariate y1 functional linear models have much higher power levels than SKAT-O. The power levels of the approximate F-distribution tests of bivariate (y1, y2), (y1, y3), and trivariate (y1, y2, y3) models are generally higher than those of the F-tests of univariate y1 models. Therefore, it is advantageous to perform multivariate analysis to gain power. Note the power levels of the approximate F-distribution tests of bivariate (y1, y2) models were similar to or slightly lower than those of the F-tests of univariate y1 models, when all the causal variants had positive effects in the top graphs [(a1), (a2), and (a3)] or 20%/80% causal variants had negative/positive effects in the middle graphs [(b1), (b2), and (b3)] for the trait y2 in Supplementary Figures S1–S4. This is mainly due to a high correlation 0.6 between traits y1 and y2, and the degrees of freedom of the approximation F-distribution tests of bivariate models are higher than those of the univariate F-tests. When the correlation decreases, one may gain power by performing bivariate and trivariate analyses after compensating for higher degrees of freedom of the approximate F-distribution tests.
The empirical power levels of the approximate F-distribution tests of model (3) based on Hotelling–Lawley trace and Wilks’s Lambda are similar to those of the approximate F-distribution test based on Pillai–Bartlett trace (data not shown). In our empirical power calculations, we also used Fourier basis functions for model (3), which provided similar results to those reported in the figures. In addition, we have performed empirical power calculations using model (7) and FPCA model (8). The results are similar to those based on model (3). In short, the performance of the F-approximate distributions of models (3), (7), and (8) is very stable and robust, no matter whether it is based on Pillai–Bartlett trace, or Hotelling–Lawley trace, or Wilks’s Lambda.
Discussion
In this paper, we develop multivariate functional linear models and hypothesis testing procedure to test association between multiple quantitative traits and multiple genetic variants in one genetic region. We first introduce a simple beta-smooth only model (2) and its revised version (3) by using the genetic data directly, which assumes that the genetic effects βℓ(t) are smooth functions while no assumption is made about the genetic data. Treating the genetic data as stochastic functions (i.e. genetic variant functions), we propose model (4) to connect the stochastic functions to phenotype adjusting for covariates. By using modern state-of-the-art functional data analysis techniques, the observed high dimension genetic variant data are used to estimate the genetic variant functions based on B-spline or Fourier basis functions or FPCA[de Boor, 2001; Ferraty and Romain, 2010; Horváth and Kokoszka, 2012; Ramsay et al., 2009; Ramsay and Silverman, 2005]. Then, the estimated genetic variant functions are used to build multivariate linear regressions (7) and FPCA model (8) for practical applications. Three types of approximate F-distribution tests based on Pillai–Bartlett trace, Hotelling–Lawley trace, and Wilks’s Lambda are introduced to test association between multiple quantitative traits and multiple genetic variants using standard multivariate analysis theory [Anderson, 1984; Fox, 2008; Fox and Weisberg, 2011; Morrison, 2005; Rao, 1973].
The proposed methods were applied to analyze four lipid traits in eight European cohorts and three biochemical traits in data from the Trinity Students Study. The approximate F-distribution tests provided much more significant results than those of F-tests of univariate analysis and SKAT-O for the three biochemical traits. The analysis of the four lipid traits and the three biochemical traits detected more association than SKAT-O in the univariate case. Generally, the approximate F-distribution tests of the proposed functional linear models are more sensitive than those of traditional multivariate linear models (1) which in turn are more sensitive than SKAT-O in the univariate case. In this paper, we only detected association between three lipid traits (LDL, CHOL, and TG) and two genes (APOE and LDLR). It is possible that more significant results could be detected in a metaanalysis by a combining multiple studies in a unified analysis. However, the multivariate functional linear models of metaanalysis are not well-studied in terms of type I error and power performance evaluation. More research is necessary in the future.
Extensive simulations were performed to evaluate the false positive rates and power performance of the proposed models and tests. To evaluate if the approximate F-distribution tests control false positive rates accurately, four nominal levels were used, i.e. α = 0.05, 0.01, 0.001, 0.0001, and five sample sizes were taken, i.e. n = 500, 1, 000, 1, 500, 2, 000. For each combination of a nominal level and a sample size, 106 datasets were generated to calculate the empirical type I error rates. Therefore, our evaluation is very extensive. Since the empirical type I error rates are all around the nominal levels, in particular at α = 0.0001, the proposed models and the related approximate F-tests can be used in both whole genome or whole exome association studies and candidate gene analysis. We show that the approximate F-distribution tests control the type I error rates very well. Generally, simultaneous analysis of multiple traits can increase power performance compared to an individual test of each trait unless the traits are strongly correlated. The proposed multivariate functional linear models lead to a combined analysis of the multiple traits, and the proposed procedure reduces the number of tests compared to the individual trait analysis.
In addition to the three types of the approximate F-distribution tests, we actually evaluated the approximate Fdistribution test based on Roy’smaximumroot, and spherical F-test as well as its corrected versions [Box, 1954; Greenhouse and Geisser, 1959; Huynh and Feldt, 1976]. However, they all inflated type I error rates. Hence, we did not perform power comparisons for them. In conclusion, the approximate F-distribution tests based on Pillai–Bartlett trace, Hotelling– Lawley trace, and Wilks’s Lambda are recommended for data analysis of the genetic community.
In this article, we used three traits in the simulation study and analyzed four lipid traits and three biochemical traits in the data analysis. In some settings, it is likely that a gene might affect a larger number of traits such as imaging data. This problem needs in-depth investigations in future studies.
Supplementary Material
Acknowledgment
Two anonymous reviewers and the editors, Dr. Shete and Dr. Cordell, provided very good and insightful comments for us to improve the manuscript. We greatly thank the European cohort investigators and the Trinity Students Study (NICHD, NHGRI, Trinity College, Dublin and the Health Research Board of Ireland) investigators for letting us analyze the data and use them as examples. Dr. Stringham and Dr. Teslovich kindly sent us the data of the European cohorts and patiently answered many questions about the cohorts, and we greatly appreciated them. This study was supported by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development (Ruzong Fan, Yifan Wang, Aiyi Liu, and James L. Mills), and by the Intramural Research Program of the National Human Genome Research Institute (Alexander F. Wilson and Joan E. Bailey-Wilson), National Institutes of Health, Bethesda, MD. We thank Dr. Seunggeun Lee who sent us their simulation program of SKAT and sequence data generated by Dr. Yun Li using program COSI. This study utilized the high-performance computational capabilities of the Biowulf Linux cluster at the National Institutes of Health, Bethesda, MD (http://biowulf.nih.gov).
Footnotes
Supporting Information is available in the online issue at wiley onlinelibrary.com.
This article has been contributed to by US Government employees and their work is in the public domain in the USA.
Computer Program
The methods proposed in this paper are implemented by using procedure of functional data analysis (fda) in the statistical package R. The R codes for data analysis and simulations are available from the web http://www.nichd.nih.gov/about/org/diphr/bbb/software/fan/Pages/default.aspx
References
- Altshuler DM, Lander ES, Ambrogio L, Bloom T, Cibulskis K, Fennell TJ, Gabriel SB, Jaffe DB, Shefler E, Sougnez CL. A map of human genome variation from population scale sequencing. Nature. 2010;467:1061–1073. doi: 10.1038/nature09534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson TW. An Introduction to Multivariate Statistical Analysis. Second Edition. New York: John Wiley & Sons; 1984. [Google Scholar]
- Bansal V, Harismendy O, Tewhey R, Murray SS, Schork NJ, Topol EJ, Frazer KA. Accurate detection and genotyping of SNPs utilizing population sequencing data. Genome Res. 2010;20:537–545. doi: 10.1101/gr.100040.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Box GEP. Some theorems on quadratic forms applied in the study of analysis of variance problems I. effect of inequality of variance in the one-way classification. Annal Math Stat. 1954;25(2):290–302. [Google Scholar]
- de Boor C. A Practical Guide to Splines, revised version. Applied Mathematical Sciences 27. New York: Springer; 2001. [Google Scholar]
- Dudbridge F, Gusnanto A. Estimation of significance thresholds for genome-wide association scans. Genet Epidemiol. 2008;32(3):227–234. doi: 10.1002/gepi.20297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan R, Wang Y, Mills JL, Wilson AF, Bailey-Wilson JE, Xiong M. Functional linear models for association analysis of quantitative traits. Genet Epidemiol. 2013;37:726–742. doi: 10.1002/gepi.21757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan R, Wang Y, Mills JL, Carter TC, Lobach I, Wilson AF, Bailey-Wilson JE, Weeks DE, Xiong M. Generalized functional linear models for case-control association studies. Genet Epidemiol. 2014;38:622–637. doi: 10.1002/gepi.21840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferraty F, Romain Y. The Oxford Handbook of Functional Data Analysis. New York: Oxford University Press; 2010. [Google Scholar]
- Ferreira MAR, Purcell SM. A multivariate test of association. Bioinformatics. 2009;25:132–133. doi: 10.1093/bioinformatics/btn563. [DOI] [PubMed] [Google Scholar]
- Fox J. Applied Regression Analysis and Generalized Linear Models. Second Edition. Los Angeles: Sage; 2008. [Google Scholar]
- Fox J, Weisberg S. An R Companion to Applied Regression. Second Edition. Los Angeles: Sage; 2011. [Google Scholar]
- Goldsmith J, Bobb J, Crainiceanu CM, Caffo B, Reich D. Penalized functional regression. J Comput Graph Stat. 2011;20:830–851. doi: 10.1198/jcgs.2010.10007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenhouse SW, Geisser S. On methods in the analysis of profile data. Psychometrika. 1959;24:95–112. [Google Scholar]
- Guo X, Liu Z, Wang X, Zhang H. Genetic association test for multiple traits at gene level. Genet Epidemiol. 2012;37:122–129. doi: 10.1002/gepi.21688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han F, Pan W. A data-adaptive sum test for disease association with multiple common or rare variants. Hum Hered. 2010;70:42–54. doi: 10.1159/000288704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmen J, Midthjell K, Krüger O, Langhammer A, Holmen TL, Bratberg GH, Vatten L, Lund-Larsen PG, et al. The Nord-Trndelag Health Study 1995–97 (HUNT 2): objectives, contents, methods and participation. Nor J Epidemiol. 2003;13:19–32. [Google Scholar]
- Horváth L, Kokoszka P. Inference for Functional Data With Applications. New York: Springer; 2012. [Google Scholar]
- Huynh H, Feldt LS. Estimation of the box correction for degrees of freedom from sample data in randomized block and split-plot designs. J Edu Stat. 1976;1(1):69–82. [Google Scholar]
- Jacobsen BK, Eggen AE, Mathiesen EB, Wilsgaard T, Njolstad I. Cohort profile: the Tromso Study. Int J Epidemiol. 2012;41:961–967. doi: 10.1093/ije/dyr049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung JS, Zhong M, Liu L, Fan RZ. Bi-variate combined linkage and association mapping of quantitative trait loci. Genet Epidemiol. 2008;32:396–412. doi: 10.1002/gepi.20313. [DOI] [PubMed] [Google Scholar]
- Kiezun A, Garimella K, Do R, Stitziel NO, Neale BM, McLaren PJ, Gupta N, Sklar P, Sullivan PF, Moran JL, et al. Exome sequencing and the genetic basis of complex traits. Nat Genet. 2012;44:623–630. doi: 10.1038/ng.2303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klei L, Luca D, Devlin B, Roeder K. Pleiotropy and principal components of heritability combine to increase power for association analysis. Genet Epidemiol. 2008;32:9–19. doi: 10.1002/gepi.20257. [DOI] [PubMed] [Google Scholar]
- Kocarnik JM, Fullerton SM. Returning pleiotropic results from genetic testing to patients and research participants. J Am Med Assoc. 2014;311(8):795–796. doi: 10.1001/jama.2014.369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong D, Staicu A, Maity A. Classical testing in functional linear models. 2014 doi: 10.1080/10485252.2016.1231806. http://www4.stat.ncsu.edu/~staicu/Research.html. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kotronen A, Yki-Järvinen H, Männistö S, Saarikoski L, Korpi-Hyöväalti E, Oksa H, Saltevo J, Saaristo T, Sundvall J, Tuomilehto J, et al. Non-alcoholic and alcoholic fatty liver disease—two diseases of affluence associated with the metabolic syndrome and type 2 diabetes: the FIN-D2D survey. BMC Public Health. 2010;10:237. doi: 10.1186/1471-2458-10-237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kouki R, Schwab U, Lakka TA, Hassinen M, Savonen K, Komulainen P, Krachler B, Rauramaa R, et al. Diet, fitness and metabolic syndrome—the DR’s EXTRA study. Nutr Metab Cardiovasc Dis. 2012;22:553–560. doi: 10.1016/j.numecd.2010.10.008. [DOI] [PubMed] [Google Scholar]
- Lee S, Emond MJ, Bamshad MJ, Barnes KC, Rieder MJ, Nickerson DA, Christiani DC, Wurfel MM, Lin X NHLBI GO Exome Sequencing Project—ESP Lung Project Team. Optimal unified approach for rare-variant association testing with application to small-sample case-control whole-exome sequencing studies. Am J Hum Genet. 2012;91:224–237. doi: 10.1016/j.ajhg.2012.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehne B, Lewis CM, Schlitt T. From SNPs to genes: disease association at the gene level. PLoS One. 2011;6(6):e20133. doi: 10.1371/journal.pone.0020133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li B, Leal SM. Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am J Hum Genet. 2008;83:311–321. doi: 10.1016/j.ajhg.2008.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li MX, Gui HS, Kwan JS, Sham PC. GATES: a rapid and powerful gene-based association test using extended Simes procedure. Am J Hum Genet. 2011;88(3):283–293. doi: 10.1016/j.ajhg.2011.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li S, Mukherjee B, Taylor JMG, Rice KM, Wen X, Rice JD, Stringham HM, Boehnke M. The role of environmental heterogeneity in meta-analysis of gene-environment interactions with quantitative traits. Genet Epidemiol. 2014;38:416–429. doi: 10.1002/gepi.21810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin WY, Schaid DJ. Power comparisons between similarity-based multilocus association methods, logistic regression, and score tests for haplotypes. Genet Epidemiol. 2009;33:183–197. doi: 10.1002/gepi.20364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu DJ, Peloso GM, Zhan X, Holmen OL, Zawistowski M, Feng S, Nikpay M, Auer PL, Goel A, Zhang H, et al. Meta-analysis of gene-level tests for rare variant association. Nat Genet. 2014;46:200–204. doi: 10.1038/ng.2852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo L, Zhu Y, Xiong M. Quantitative trait locus analysis for next-generation sequencing with the functional linear models. J Med Genet. 2012;49:513–524. doi: 10.1136/jmedgenet-2012-100798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madsen BE, Browning SR. A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet. 2009;5:e1000384. doi: 10.1371/journal.pgen.1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, McCarthy MI, Ramos EM, Cardon LR, Chakravarti A, et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy MI, Abecasis GR, Cardon LR, Goldstein DB, Little J, Ioannidis JP, Hirschhorn JN. Genome-wide association studies for complex traits: consensus, uncertainty and challenges. Nat Rev Genet. 2008;9(5):356–369. doi: 10.1038/nrg2344. [DOI] [PubMed] [Google Scholar]
- Morgenthaler S, Thilly WG. A strategy to discover genes that carry multi-allelic or mono-allelic risk for common diseases: a cohort allelic sums test (CAST) Mutat Res. 2007;615:28–56. doi: 10.1016/j.mrfmmm.2006.09.003. [DOI] [PubMed] [Google Scholar]
- Morris AP, Zeggini E. An evaluation of statistical approaches to rare variant analysis in genetic association studies. Genet Epidemiol. 2010;34:188–193. doi: 10.1002/gepi.20450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris AP, Voight BF, Teslovich TM, Ferreira T, Segre AV, Steinthorsdottir V, Strawbridge RJ, Khan H, Grallert H, Mahajan A, et al. Large-scale association analysis provides insights into the genetic architecture and pathophysiology of type 2 diabetes. Nat Genet. 2012;44:981–990. doi: 10.1038/ng.2383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrison DF. Multivariate Statistical Methods. Fourth Edition. California: Thomson; 2005. [Google Scholar]
- Mukhopadhyay I, Feingold E, Weeks DE, Thalamuthu A. Association tests using kernel-based measures of multi-locus genotype similarity between individuals. Genet Epidemiol. 2010;34:213–221. doi: 10.1002/gepi.20451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale BM, Rivas MA, Voight BF, Altshuler D, Devlin B, Orho-Melander M, Kathiresan S, Purcell SM, Roeder K, Daly MJ. Testing for an unusual distribution of rare variants. PLoS Genet. 2011;7:e1001322. doi: 10.1371/journal.pgen.1001322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Reilly PF, Hoggart CJ, Pomyen Y, Calboli FCF, Elliott P, Jarvelin MR, Coin LJM. Multiphen: joint model of multiple phenotypes can increase discovery in GWAS. PLoS One. 2012;7(5):e34861. doi: 10.1371/journal.pone.0034861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Kryukov GV, de Bakker PIW, Purcell SM, Staples J, Wei LJ, Sunyaev SR. Pooled association tests for rare variants in exon-resequencing studies. Am J Hum Genet. 2010;86:832–838. doi: 10.1016/j.ajhg.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, de Bakker PI, Daly MJ, Sham PC. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81(3):559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsay JO, Hooker G, Graves S. Functional Data Analysis With R and Matlab. New York: Springer; 2009. [Google Scholar]
- Ramsay JO, Silverman BW. Functional Data Analysis. Second Edition. New York: Springer; 2005. [Google Scholar]
- Rao CR. Linear Statistical Inference and Its Applications. Second Edition. New York: John Wiley & Sons; 1973. [Google Scholar]
- Razeto-Barry P, Diaz J, Cotoras D, Vasquez RA. Molecular evolution, mutation size and gene pleiotropy: a geometric reexamination. Genetics. 2011;187(3):877–885. doi: 10.1534/genetics.110.125195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross SM. Stochastic Processes. Second Edition. New York: John Wiley & Sons; 1996. [Google Scholar]
- Schaffner SF, Foo C, Gabriel S, Reich D, Daly MJ, Altshuler D. Calibrating a coalescent simulation of human genome sequence variation. Genome Res. 2005;15:1576–1583. doi: 10.1101/gr.3709305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz PE, Towers GW, Fischer S, Govindarajalu S, Schulze J, Bornstein SR, Hanefeld M, Vasseur F, et al. Hypoadiponectinemia is associated with progression toward type 2 diabetes and genetic variation in the ADIPOQ gene promoter. Diabetes Care. 2006;29:1645–1650. doi: 10.2337/dc05-2123. [DOI] [PubMed] [Google Scholar]
- Scott LJ, Mohlke KL, Bonnycastle LL, Willer CJ, Li Y, Duren WL, Erdos MR, Stringham HM, Chines PS, Jackson AU, et al. A genome-wide association study of type 2 diabetes in Finns detects multiple susceptibility variants. Science. 2007;316:1341–1345. doi: 10.1126/science.1142382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott RA, Lagou V, Welch RP, Wheeler E, Montasser ME, Luan J, Magi R, Strawbridge RJ, Rehnberg E, Gustafsson S, et al. Large-scale association analyses identify new loci influencing glycemic traits and provide insight into the underlying biological pathways. Nat Genet. 2012;44:991–1005. doi: 10.1038/ng.2385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sivakumaran S, Agakov F, Theodoratou E. Abundant pleiotropy in human complex diseases and traits. Am J Hum Genet. 2011;89(5):607–618. doi: 10.1016/j.ajhg.2011.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solovieff N, Cotsapas C, Lee PH, Purcell SM, Smoller JW. Pleiotropy in complex traits: challenges and strategies. Nat Rev Genet. 2013;14(7):483–495. doi: 10.1038/nrg3461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stancakova A, Javorsky M, Kuulasmaa T, Haffner SM, Kuusisto J, Laakso M, et al. Changes in insulin sensitivity and insulin release in relation to glycemia and glucose tolerance in 6,414 Finnish men. Diabetes. 2009;58:1212–1221. doi: 10.2337/db08-1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stearns FW. One hundred years of pleiotropy: a retrospective. Genetics. 2010;186(3):767–773. doi: 10.1534/genetics.110.122549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The International HapMap Consortium. A second generation human haplotype map of over 3.1 million SNPs. Nature. 2007;449:851–861. doi: 10.1038/nature06258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuomilehto J, Lindströmb J, Eriksson JG, Valle TT, Hämäläinen H, Ilanne-Parikka P, Keinänen-Kiukaanniemi S, Laakso M, Louheranta A, Rastas M, et al. Prevention of type 2 diabetes mellitus by changes in lifestyle among subjects with impaired glucose tolerance. N Engl J Med. 2001;344:1343–1350. doi: 10.1056/NEJM200105033441801. [DOI] [PubMed] [Google Scholar]
- Voight BF, Scott LJ, Steinthorsdottir V, Morris AP, Dina C, Welch RP, Zeggini E, Huth C, Aulchenko YS, Thorleifsson G, et al. Twelve type 2 diabetes susceptibility loci identified through large-scale association analysis. Nat Genet. 2010;42:579–589. doi: 10.1038/ng.609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K, Li M, Bucan M. Pathway-based approaches for analysis of genome-wide association studies. Am J Hum Genet. 2007;81(6):1278–1283. doi: 10.1086/522374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wessel J, Schork NJ. Generalized genomic distance-based regression methodology for multilocus association analysis. Am J Hum Genet. 2006;79:792–806. doi: 10.1086/508346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams GC. Pleiotropy, natural selection, and the evolution of senescence. Evolution. 1957;11:398–411. [Google Scholar]
- Wu C, Zheng G, Kwak M. A joint regression analysis for genetic association studies with outcome stratified samples. Biometrics. 2013;69:417–426. doi: 10.1111/biom.12012. [DOI] [PubMed] [Google Scholar]
- Wu MC, Lee S, Cai T, Li Y, Boehnke M, Lin X. Rare-variant association testing for sequencing data with the sequence kernel association test. Am J Hum Genet. 2011;89:82–93. doi: 10.1016/j.ajhg.2011.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan T, Li Q, Li Y, Li Z, Zheng G. Genetic association with multiple traits in the presence of population stratification. Genet Epidemiol. 2013;37(6):571–580. doi: 10.1002/gepi.21738. [DOI] [PubMed] [Google Scholar]
- Zawistowski M, Gopalakrishnan S, Ding J, Li Y, Grimm S, Zöllner S. Extending rare-variant testing strategies: analysis of noncoding sequence and imputed genotypes. Am J Hum Genet. 2010;87:604–617. doi: 10.1016/j.ajhg.2010.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeggini E, Scott LJ, Saxena R, Voight BF, Marchini JL, Hu T, de Bakker PIW, Abecasis GR, Almgren P, Andersen G, et al. Wellcome Trust Case Control Consortium. Meta-analysis of genome-wide association data and large-scale replication identifies additional susceptibility loci for type 2 diabetes. Nat Genet. 2008;40:638–645. doi: 10.1038/ng.120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Liu CT, Wang X. An association test for multiple traits based on the generalized Kendallâs tau. J Am Stat Assoc. 2010;105(490):473–481. doi: 10.1198/jasa.2009.ap08387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng G, Wu C, Kwak M, Jiang W, Joo J, Lima JAC. Joint analysis of binary and quantitative traits with data sharing and outcome-dependent sampling. Genet Epidemiol. 2012;36(3):263–273. doi: 10.1002/gepi.21619. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.