MEGADOCK: An All-to-All Protein-Protein Interaction Prediction System Using Tertiary Structure Data

Abstract

The elucidation of protein-protein interaction (PPI) networks is important for understanding cellular structure and function and structure-based drug design. However, the development of an effective method to conduct exhaustive PPI screening represents a computational challenge. We have been investigating a protein docking approach based on shape complementarity and physicochemical properties. We describe here the development of the protein-protein docking software package “MEGADOCK” that samples an extremely large number of protein dockings at high speed. MEGADOCK reduces the calculation time required for docking by using several techniques such as a novel scoring function called the real Pairwise Shape Complementarity (rPSC) score. We showed that MEGADOCK is capable of exhaustive PPI screening by completing docking calculations 7.5 times faster than the conventional docking software, ZDOCK, while maintaining an acceptable level of accuracy. When MEGADOCK was applied to a subset of a general benchmark dataset to predict 120 relevant interacting pairs from 120 x 120 = 14,400 combinations of proteins, an F-measure value of 0.231 was obtained. Further, we showed that MEGADOCK can be applied to a large-scale protein-protein interaction-screening problem with accuracy better than random. When our approach is combined with parallel high-performance computing systems, it is now feasible to search and analyze protein-protein interactions while taking into account three-dimensional structures at the interactome scale. MEGADOCK is freely available at http://www.bi.cs.titech.ac.jp/megadock.

1. INTRODUCTION

Protein-protein interactions (PPIs) occur when two or more proteins bind together, often to perform their biological functions. PPIs have been extensively investigated from the perspectives of biochemistry, quantum chemistry, and molecular dynamics. PPIs are at the core of cellular processes, and investigating PPIs is crucial for understanding cell biology. Several methods to determine PPIs have been developed for this purpose. Moreover, one of the main goals of proteome and interactome analyses is to identify proteins with the potential to bind and interact with each other; this is called PPI screening. High-throughput but noisy methods, such as the yeast two-hybrid system [1], or precise but low-throughput methods, such as fluorescence resonance energy transfer (FRET) [2], have been frequently used as experimental methods for PPI screening. There are also computational methods for PPI prediction [3-12]. Some successful methods include those based on sequence [3-5], evolutionary [6, 7], and domain interaction information [8, 9]. However, the performance of these computational methods is highly dependent on known PPI information. Because protein structure provides fundamental information about function, computational PPI screening methods based on the known structures of protein complexes are also being considered [10-12]. However, these methods can only detect interacting protein pairs resembling those of known protein complexes. Therefore, they do not completely reflect the structural basis of PPIs.

In structural biology, computational methods, such as atomic-level molecular-dynamics simulations, have been primarily applied to analyze in detail the mechanisms of individual known protein interactions. However, these methods are not applicable to large-scale analyses required in systems biology, because the analyses are expensive to perform. Rigid-body protein docking methods have been applied as the initial stage for large-scale PPI network prediction [13-15]. Besides providing a useful technique to help study fundamental biomolecular mechanisms, docking tools to predict PPIs are emerging as promising complementary approaches to rational drug design [16].

Rigid-body protein-protein docking is implemented in various ways, including Fast Fourier Transform (FFT) convolution of 3D voxel space as proposed by Katchalski-Katzir [17] (MolFit [17,18], FTDock [19], PIPER [20], and ZDOCK [21-24]), and others consider shape complementarity of local surface structure (PatchDock [25], LZerD [26], Hex [27, 28]). RosettaDock [29, 30], BiGGER [31], FireDock [32], FiberDock [33], and EigenHex [34] also take flexibility of main- and side-chains into account. Some of these flexible docking methods have successfully predicted protein complexes of targets used in the protein-complex structure prediction, community-wide experiment called Critical Assessment of Prediction of Interactions (CAPRI). CAPRI is a blind prediction competition that does not release the structure of the protein complex judged by CAPRI assessors until after the submission of a target [35, 36]

Wass, et al. reported that the score distribution generated by the rigid-body protein-protein docking tool Hex showed significant differences between known interacting pairs and non-binding pairs when they used only shape complementarity for the scoring function [13]. Nonetheless, more investigation is required on the features of the computational methods, such as the scoring functions that best fit the problem and the parameter spaces that produce better predictions. Here, we consider rigid-body docking by taking into account electrostatic forces as well as shape complementarity. Such docking-based prediction of PPI has an advantage, because it also produces several candidates for presumable docking poses. This provides insights into how the two predicted proteins undergo interactions according to their structural properties.

ZDOCK has been by far the most successful among the rigid docking tools [21-24]. ZDOCK employs voxel models in which protein complexes are divided into three-dimensional (3D) voxels and scored by the correlation functions of each discrete function. The ZDOCK scoring function comprises pairwise shape complementarity (PSC), electrostatics,and interface atomic contact energy score (IFACE) [24] for estimating desolvation free energy, and eight correlation functions are calculated by FFT. Generally, FFT-based docking tools that search the entire 3D grid space for presumable docking positions perform better than local search-based tools. With more correlation functions, it is possible to incorporate more features to evaluate docking pose, although the number of the correlation functions linearly affects calculation speed.Matsuzaki, et al. applied ZDOCK to PPI screening and predicted whether two proteins interact by analyzing the high-scoring decoys produced by a rigid docking process [14]. Yoshikawa, et al. also developed a PPI screening method and used ZDOCK and their original post-docking process called affinity evaluation and prediction (AEP) [15]. However, to search the entire interactome space using these methods involves combinations of 1,000 proteins (1-M combinations). Therefore, acceleration of docking calculations is crucial.

In the present study, we describe the development of a rigid-body docking-based method for PPI screening based on exhaustive calculations of pseudo-binding energies among pairs of target proteins that can be applied to PPI prediction problems of mega-order data. Further, to enable applications to 1-M combinations, we developed efficient FFT-based protein-protein docking software called MEGADOCK, which is designed for exhaustive PPI screening. MEGADOCK searches the relevant interacting protein pairs by conducting protein-protein docking between the tertiary structures of the target proteins and then analyzing the distributions of high-scoring decoys (candidate protein complexes) (Fig.1).

Fig. (1).

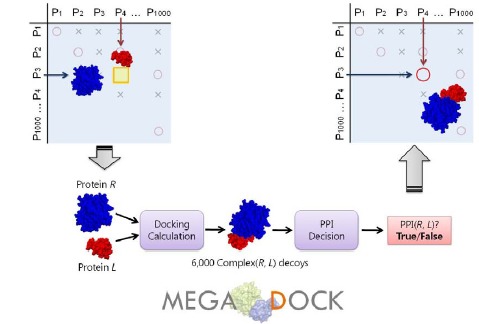
Scheme for all-to-all protein-protein interaction predictions. Using a given structural dataset of target proteins, all the combinations of two protein pairs are examined by docking and post-processing of the docking score distributions. All the pairs predicted to interact will then be used to construct protein-protein interaction networks

By introducing a novel scoring function called the real Pairwise Shape Complementarity score (rPSC), we successfully reduced the computation times for protein docking. Moreover, our software was implemented and made suitable for running on massively parallel computing environments using MPI and OpenMP libraries. This makes it feasible to target a mega-order number of protein pairs.

In the present study, we used MEGADOCK without the desolvation free energy term, which is incorporated into the ZDOCK scoring function. The MEGADOCK calculation time decreased significantly with small differences in the performance of docking pose prediction. The performance of our PPI screening system was comparable to that of a study using ZDOCK for the same purpose [14] when it was applied to a general “benchmark” dataset that included confirmed pairs of proteins exhibiting biological interactions.

2. METHODS

Figure1 and Table 1 show the overall procedures for PPI prediction employing the MEGADOCK system. MEGADOCK consists of two segments called “docking calculation”and “PPI decision.” The “docking calculation segment” performs all-to-all docking and generates high-scoring decoys for all possible combinations of the given protein structures. Subsequently, the “PPI decision segment” analyzes the structural distributions of high-scoring decoys for each pair of proteins and decides if the given two proteins can interact. Finally, a possible PPI network is obtained that connects the positively predicted PPIs.

Table 1.

The proposed all-to-all protein-protein interaction prediction method

i)	All-to-all docking by MEGADOCK that outputs 2,000xt decoys (t: number of decoys recorded per rotation).
ii)	Reranking according to the energy calculation of the high scoring decoys recorded by process (i), the number of decoys is reduced to 1,000. These decoys have the lowest energy score assigned by the reranking.
iii)	Clustering according to the structural similarity of the decoys.
iv)	Calculation of affinity scores for each protein-pair according to the highest docking score of the decoy included in the clusters that have more than m* data.
v)	Prediction of protein pairs that have the potential to interact, with E > E* evaluated as an interacting pair.

2.1. Dataset

To evaluate the docking pose prediction and PPI screening performances, we used a general benchmark dataset called ZLAB Benchmark 2.0 [37] and 4.0 [38]. Each dataset includes two sets of protein-complex data (bound and unbound). The bound set includes structures acquired from the crystal structure of a target protein complex divided into two chains (receptor and ligand). The unbound set includes structures taken from the free form of corresponding protein structures in the bound dataset. We applied parameter optimization of our docking scoring functions using 23 complexes from the ZLAB Benchmark 2.0 (Table 2). Docking pose prediction was evaluated using all 176 complexes from ZLAB Benchmark 4.0. Evaluation of PPI screening performance was conducted on each of the 44 complexes (called the small dataset, Table 3). These were selected from ZLAB Benchmark 2.0 for optimization of the parameter t (described below) and 120 complexes (called the large dataset, Table 4) from ZLAB Benchmark 4.0 to evaluate larger datasets, which consisted of a pair of monomeric proteins (this selection of data was prepared based on a personal communication with Dr. Ryotaro Koike and Dr. Motonori Ota. All the complexes selected consisted of two monomers).

Table 2.

The 23 complex structures selected from the ZLAB Benchmark 2.0 dataset for the selected weighted parameter.

Rigid-body (21)

1AK4, 1AVX, 1AY7, 1B6C, 1CGI, 1D6R, 1E96, 1EAW, 1EWY, 1GCQ, 1GHQ, 1HE1, 1KAC, 1KTZ, 1PPE, 1SBB, 1UDI, 2PCC, 2SIC, 2SNI, 7CEI

Medium Difficulty (2)

1ACB, 1GRN

Table 3.

The 44 complex structures selected from the ZLAB Benchmark 2.0 dataset (small dataset).

Rigid-body (34)

1AK4, 1AVX, 1AY7, 1B6C, 1BUH, 1BVN, 1CGI, 1D6R, 1DFJ, 1E6E, 1E96, 1EAW, 1EWY, 1F34, 1FC2, 1FQJ, 1GCQ, 1GHQ, 1HE1, 1KAC, 1KTZ, 1KXP, 1KXQ, 1MAH, 1PPE, 1QA9, 1SBB, 1TMQ, 1UDI, 2BTF, 2PCC, 2SIC, 2SNI, 7CEI

Medium Difficulty (6)

1ACB, 1GRN, 1HE8, 1I2M, 1M10, 1WQ1

Difficult (4)

1ATN, 1FQ1, 1H1V, 1IBR

Table 4.

The 120 complex structures selected from the ZLAB Benchmark 4.0 dataset (large dataset).

Rigid-body (79)

1AK4, 1AVX, 1AY7, 1B6C, 1BUH, 1BVN, 1CGI, 1CLV, 1D6R, 1DFJ, 1E6E, 1E96, 1EAW, 1EFN, 1EWY, 1F34, 1FC2, 1FFW, 1FLE, 1FQJ, 1GCQ, 1GHQ, 1GL1, 1GLA, 1GPW, 1GXD, 1H9D, 1HE1, 1J2J, 1JTG, 1KAC, 1KTZ, 1KXP, 1KXQ, 1MAH, 1N8O, 1OC0, 1OPH, 1OYV, 1PPE, 1PVH, 1QA9, 1R0R, 1S1Q, 1SBB, 1T6B, 1TMQ, 1UDI, 1US7, 1XD3, 1YVB, 1Z0K, 1Z5Y, 1ZHH, 1ZHI, 2A5T, 2A9K, 2ABZ, 2AJF, 2B42, 2BTF, 2FJU, 2G77, 2HLE, 2HQS, 2I25, 2J0T, 2O8V, 2OOB, 2OUL, 2PCC, 2SIC, 2SNI, 2UUY, 2VDB, 3D5S, 3SGQ, 7CEI, BOYV

Medium Difficulty (23)

1ACB, 1GRN, 1HE8, 1I2M, 1JIW, 1LFD, 1M10, 1MQ8, 1NW9, 1R6Q, 1SYX, 1WQ1, 1XQS, 2AYO, 2CFH, 2H7V, 2HRK, 2J7P, 2NZ8, 2OZA, 2Z0E, 3CPH, 4CPA

Difficult (18)

1ATN, 1BKD, 1F6M, 1FQ1, 1H1V, 1IBR, 1IRA, 1JK9, 1PXV, 1R8S, 1Y64, 1ZLI, 1ZM4, 2C0L, 2I9B, 2IDO, 2O3B, 2OT3

2.2. Docking Calculation Segment

Historical Overview of the MEGADOCK Docking Segment 

Here, we mainly used MEGADOCK version 2.1 with a scoring function that includes a shape complementarity (rPSC) term and an electrostatics term. The first version of MEGADOCK (version 1.0) incorporated only a shape complementarity scoring function proposed by Katchalski-Katzir, et al. [17]. MEGADOCK 2.0 employs an improved shape complementarity score model, rPSC. An electrostatics term is added to the MEGADOCK 2.1 scoring function with the same number of FFTs as that in MEGADOCK 2.0.

Shape complementarity of Katchalski-Katzir and rPSC with voxel model

We consider one protein of the docking-target protein pairs as a receptor (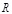) and the other protein as a ligand (). Each protein is first allocated on a 3D voxel space with grid-point spacing of 1.2 Å. The scores are then assigned to each voxel according to the location in a protein, such as the surface or core.

The Katchalski-Katzir’s shape complementarity score G used in MEGADOCK 1.0, is represented as follows:

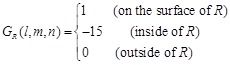(1)

(2)

G_R, and G_L values are assigned to the receptor and ligand voxels, respectively. The docking score SC is given by:

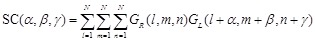(3)

Here 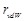represents the van der Waals radius of an atom, and (α, β, γ) is a vector of the ligand translation. In MEGADOCK 2.0, we introduced the following novel scoring function called rPSC (Fig. 2) for the shape complementarity term instead of the Katchalski-Katzir shape complementarity score:

Fig. (2).

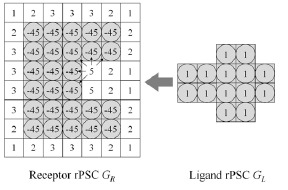
The real Pairwise Shape Complementarity (rPSC) score. The model consists of three-dimensional voxels. The model is shown in two dimensions for simplicity. The voxels with the square and a circle interlace correspond to the area occupied by proteins, while the voxels with only the squares represent unoccupied space. Voxels with a score of 0 are not shown.

(4)

(5)

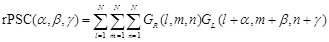(6)

The parameters of these functions are optimized using the structural data of 23 complexes (Table 2).

Combination of rPSC and electrostatics for FFT-based docking

In addition to shape complementarity scores, we used the electrostatic interactions of each amino acid residue as a physicochemical score. The electric field 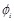is assigned to each voxel 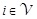as follows:

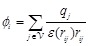(7)

(8)

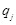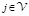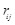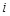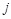Here is the charge of a voxel; ; , the Euclidean distance 1 between voxels and ; and 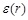, a distance-dependent dielectric function. The electrostatic terms 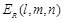and are decided according to the charge of each voxel, q(l, m, n), and the atoms in the residues are assigned charges according to CHARMM19 [39].

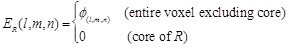, (9)

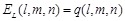, (10)

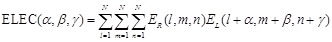
(11)

Considering these two terms, the docking score 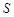of MEGADOCK 2.1 is represented as follows:

, (12)

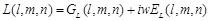, (13)

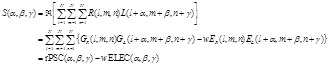
(14)

here 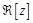represents the real part of 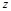. In order to search for the best docking poses, the possible ligand orientations are exhaustively examined with 3,600 rotation angles in 15-degree steps. For each rotation, the ligand is translated into 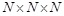patterns for 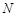voxels. The decoys that yield the highest 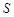for each rotation are recorded. In this manner, a total of 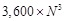docking poses are evaluated for one protein pair. The weight parameter w is set to 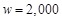, a figure obtained by optimization by conducting preliminary experiments using the data shown in Table 2.

For direct execution of simple convolution sums, 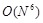calculations are required. In contrast, the calculation order obtained using the fast Fourier transform (FFT) algorithm for discrete Fourier transforms (DFTs) and inverse discrete Fourier transforms (IFTs) is reduced to [17]. The score 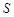for the Fourier transform is:

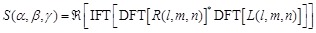
(15)

Here 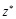represents the complex conjugation of 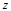. We used FFTW [40] for the FFT routine.

The advantage of rPSC is that it represents a real number; therefore, we can place a physicochemical parameter in the imaginary part. Moreover, it is possible to calculate a score with only one complex number for each voxel. By decreasing the number of required DFT/IFT operations, the docking calculation is expected to be faster than using the conventional docking software, ZDOCK.

Number of Decoys Sampled Per Rotation

Conventional software typically records the highest-scoring decoy obtained by all the translation patterns for each ligand rotation, because it is well known that analyses of more than one decoy per rotation do not significantly contribute to an improvement of docking pose predictions. In contrast, we assumed that in the PPI screening problem, the distributions of high-scoring decoys provide important information for the analyses. Hence, MEGADOCK allows the user to input the number of decoys 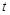that should be recorded per ligand rotation to obtain a larger number of high-scoring decoys.

2.3. PPI Screening Segment

MEGADOCK predicts the relevant PPIs according to the affinity scores calculated by the post-processing of all the docking results.

Reranking of Decoys

By default, the docking segment of the system outputs high-scoring decoys from 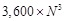ligand rotations and translations. In the present study, we conducted docking with t = 3, and the output was 6,000 decoys. However, some decoys with high docking scores often exhibit high binding energies when assessed using detailed methods. To reduce such unwanted structures, we applied reranking of the high-scoring decoys. This process collects near-native decoys with high ranking, thereby excluding decoys with unrealistically high binding energies. We used ZRANK [41] because it calculates the binding energy of each decoy based on the van der Waals, electrostatic, and desolvation energies among the atoms in close contact.

Clustering of Decoys and PPI Prediction

Matsuzaki et al.developed a PPI screening system by post-processing docking outputs. In this method, a clustering analysis is applied, and clusters of decoys are generated according to their structural similarities [14]. The dissimilarities between two decoys are defined using differences in atomic coordinates. The dissimilarities are the sums of the ligand and receptor terms. The ligand term is defined as the three-dimensional Euclidean distance between the central coordinates of ligands in the decoys when the receptor positions are superposed. The receptor term is defined as the distance of receptors in the decoys calculated in the same manner used for the ligand term while the ligand positions are superimposed. Clustering was conducted using a group-average method to produce 20 clusters for each docking pair. We applied this method to the reranked decoys in the following manner:

1. Let the number of clusters be n_C (here we used 20 as n_C). We defined the following variables indexed by i for each cluster.

2. For each cluster C_i, the decoy with the highest rank given by ZRANK was selected as the representative decoy.

3. When a set of 1,000 highest-ranked decoys was assumed to represent the population, the Z-score of the docking score of the representative decoy is denoted by s_i.

4. The number of data elements in the cluster C_i is denoted by C_i. The Z-score of C_i, when the population is assumed to be n_C clusters, is denoted by m_i.

5. Define the set of clusters C’ whose members have m_i above the cutoff point m^* (Eq. 16). The maximum s_i over the set C’was defined as the affinity evaluation value, E (Eq. 17), in the following manner:

(16)

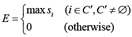(17)

After the value E is assigned to all possible combinations of the candidate proteins, the possible interacting protein pairs can be determined with the cutoff for E at E* as follows:

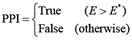(18)

2.4. Large-Scale Parallel Computing

MEGADOCK was parallelized with the message passing interface (MPI) library and OpenMP. Because the calculations for each pair are almost independent, we can parallelize an all-to-all exhaustive PPI prediction task using several methods on hundreds or thousands of CPU cores. The user can specify the numbers of receptor and ligand protein data to be assigned to a single processor after considering the memory capacity. We tested this data parallelization using 192 to 4,608 cores. When a processor is assigned for data comprising receptors and ligands, it calculates FFT for the first ligand with each possible rotation. The FFT results are repeatedly employed for docking with all receptors to avoid redundant calculations. Subsequently, the process is repeated times.

MEGADOCK has an option to avoid DFT calculations and upload precalculated DFT results from the “FFT protein structure library” onto the hard drives. This approach is effective in a system with high I/O performance, and in experiments, we recorded speeds that were three-times faster than simple exhaustive calculations. The FFT routine in MEGADOCK only uses base-3 and base-5 logarithms in addition to base-2 to minimize the volume of the target 3-D cube. However, if we choose too many logarithmic bases, it is necessary to prepare many precalculated FFT models in the library, because protein pairing is unknown a priori. In contrast, if we use graphics processing unit (GPU) acceleration, it is better to simply repeat FFT calculations on a GPU with the most adequate combinations of logarithmic bases. We considered this in our preliminary study when we implemented our system with the aim of high computing power rather than I/O performance (unpublished data).

2.5. Evaluation of Prediction Performance

Docking Pose Prediction

To evaluate docking pose performance, we conducted a redocking and unbound docking experiments using the ZLAB Benchmark dataset. We used the root mean square deviation (RMSD) of the ligand protein (Ligand RMSD), which is the RMSD of the predicted ligand position, and that of the crystal complex structure calculated for all the atoms when the receptor positions are superimposed to determine the accuracy of MEGADOCK’s docking predictions. The RMSDs of the unbound structures were calculated only for residues that were aligned by pairwise alignment of the amino acid sequences between the bound and the unbound structures. We compared five values to determine the docking performance produced by the methods listed above as follows:

• #NND: Number of near-native decoys (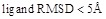) in the 3,600 highest-scoring decoys.

• Best Rank: The rank of the first near-native decoy.

• L-RMSD: The ligand RMSD [Å] of the “Best Rank” decoy.

• Success Rate: The percentage of cases with near-native decoys for a given number N_d of top-ranked predictions per test case.

• Avg Min L-RMSD: The average of minimum L-RMSD for a given number of top-ranked predictions per test case. L-RMSD is calculated by the following procedures:

-   Given the ligand RMSD of a decoy 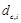for complex c 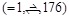with the rank i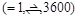th of the docking score, the 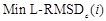is defined as follows: Min L-RMSD_c(i) = min{d_c,1,d_c,2,…,d_c,i} (19)

-   The mean of MinL-RMSD_c(i),Avg Min L-RMSD(i), was used to represent the overall docking performance:

(20)

-   TheAvg Min L-RMSD plot is drawn with the number of predictions i along the x-axis and 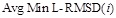along the y-axis. The smaller value of the area under the curve shows the highly ranked closer structures that were similar to the native structure, thereby indicating better performance of the docking pose prediction.

PPI Prediction

Each prediction of the possibilities of interactions in a given protein pair was evaluated as true positive (TP), false positive (FP), true negative (TN), and false negative (FN). For the benchmark data, we assumed 44 TP interactions in the small dataset and 120 TP interactions in the large dataset, where each protein interacts exclusively with one partner from the same crystal structure as the protein complex. The overall performance of the screening system was evaluated by employing the F-measure, the harmonic mean of the Precision (#TP/(#TP + #FP)), and Recall (#TP/(#TP + #FN)). We also show the Accuracy ((#TP + #TN)/(#TP + #FN + #FP + #TN)) to compare PPI prediction performance here with previous work [15]; however, the Accuracy value is not appropriate for evaluating the all-to-all PPI prediction with small positives and large negatives.

3. RESULTS AND DISCUSSION

We applied the most recent version (2.1) of MEGADOCK to docking pose prediction and PPI screening problems. Figure 3 shows examples of docking predictions generated by MEGADOCK 2.1

Fig. (3).

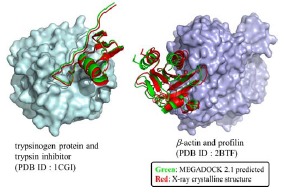
Complex-structure predicted by docking (left: 1CGI; right: 2BTF). Proteins shown by the surface correspond to receptors, whereas those shown by ribbon representations correspond to ligands from both bound structures. Green ligands show the prediction by MEGADOCK, whereas red ligands represent structures determined using X-ray crystallography. (The color version of the figure is available in the electronic copy of the article).

The structure on the left corresponds to the PDB data 1CGI, for which we obtained a Ligand RMSD value of 1.02 Å for the highest-ranked decoy. The structure on the right shows the decoy ranked 221 generated by the redocking of 1KTZ (the Ligand RMSD value = 1.59 Å).

By comparing the performance of MEGADOCK 2.1 to MEGADOCK 1.0 (Katchalski-Katzir shape complementarity), MEGADOCK 2.0 (rPSC), and ZDOCK version 3.0 (PSC, electrostatics, IFACE), we show that the MEGADOCK 2.1 (rPSC, electrostatics) scoring function effectively improves docking pose prediction performance without the desolvation free energy term (section 3.1). The improvement of calculation time compared with ZDOCK 3.0 stated in Section 3.3 shows the PPI screening results. In Section 3.4, we discuss possible improvements to achieve better screening performance on an unbound dataset. In Section 3.5, we describe the application our system to the reconstruction of a known biological pathway.

3.1. Accuracy of Docking Pose Prediction

To evaluate docking pose prediction performance, we conducted redocking (bound docking) and unbound docking with the ZLAB Benchmark 4.0 dataset [38]. We compared the performances of four different docking methods as follows.

1. MEGADOCK 1.0 (Katchalski-Katzir shape complementarity)

2. MEGADOCK 2.0 (rPSC)

3. MEGADOCK 2.1 (rPSC and electrostatics)

4. ZDOCK 3.0 (PSC, electrostatics and IFACE)

To compare with ZDOCK, we set the MEGADOCK parameters of t = 1 and 3,600 decoys. The results are shown in Table S1 ^{(393.2KB, pdf)} (bound set) and Table S2 ^{(393.2KB, pdf)} (unbound set).

The incorporation of the rPSC score for the shape complementarity representation resulted in larger #NND and smaller Best Rank values in many complexes using MEGADOCK 2.1 than in the case of simpler shape complementarity representations (MEGADOCK 1.0). Moreover, by adding the electrostatic force to the scoring function with rPSC, we achieved better Best Rank and #NND values. Here, comparison of the sum of #NND values showed that MEGADOCK 2.1 yielded values of 633 in the bound set and 162 in the unbound set. Both values are higher than those obtained with MEGADOCK 2.0 (613 in the bound and 150 in the unbound sets). By examining the Best Rank values, MEGADOCK 2.1 successfully predicted at least one near-native decoy for 128 protein complexes in the bound set and 23 complexes in the unbound set in the top 100 scored decoys. These values are higher than those generated using MEGADOCK 2.0 (115 in the bound set and 17 in the unbound set). With MEGADOCK 2.1, we obtained near-native decoys that were not achieved with only shape complementarity scoring (MEGADOCK 1.0 and 2.0), such as in 1KTZ (bound, Table S1 ^{(393.2KB, pdf)} ) or 1Z0K (unbound, Table S2 ^{(393.2KB, pdf)} ).

Figure 4 shows a comparison of the Success Rates. A docking method worked well when the area is larger in the left part of the graph. While MEGADOCK 2.1 was less successful when compared with ZDOCK 3.0, incorporation of the electrostatic term clearly improved the docking success rate. Figure 5 shows a comparison of the Avg Min L-RMSD. The docking accuracy of MEGADOCK can be improved, for example, by incorporating a desolvation term in the scoring function. Figure 5 shows further that unbound docking is still a difficult problem for a rigid-docking approach. Both ZDOCK and MEGADOCK failed to generate decoy sets that included near-native decoys whose RMSD compared with the correct binding form was <5 Å of the Avg Min L-RMSD for 176 benchmark protein pairs.

Fig. (4).

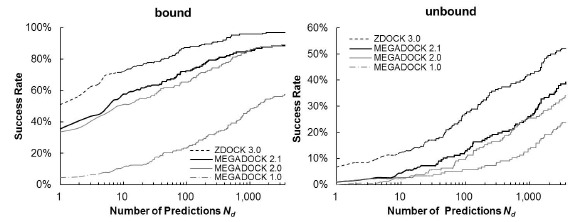
Success rate of MEGADOCK and ZDOCK for all test cases of ZLAB Benchmark 4.0. The success rate was defined as the percentage of cases with an L-RMSD <5 Å for a given number of top-ranked docking predictions per test case.

Fig. (5).

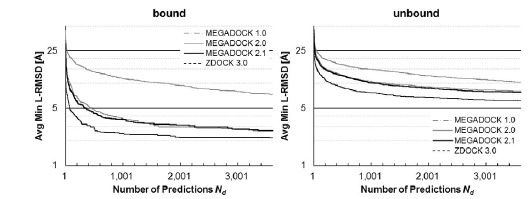
Avg Min L-RMSD of MEGADOCK and ZDOCK for all test cases of ZLAB Benchmark 4.0. Avg Min L-RMSD represents the value given by Eq. (20).

One promising approach for solving this problem is the use of cross-docking among structure ensembles. Such an approach requires a larger number of dockings and is therefore more expensive to compute. The number of docking predictions to be considered will also be larger. Such difficulties can be solved by simple data parallelizing using a massively parallel computing environment. The latest version of MEGADOCK includes the option to enable thread parallelization for each docking process. Process parallelization using MPI makes it possible to calculate the number of docking jobs in parallel on a PC cluster system.

3.2. Docking Calculation Time

Table 5 shows the average time consumed for docking the ZLAB Benchmark 4.0 dataset. All the calculations were conducted on the TSUBAME 2.0 supercomputing system, Tokyo Institute of Technology, Japan, which consists of two 2.93 GHz Intel Xeon processors (6 cores × 2) and 32 GB RAM with operational nodes connected via an InfiniBand and Gigabit Ethernet. An average of 16.6 min was required for each docking calculation using one CPU core. FFT consumed approximately 80% of the total docking time. Here the scoring function with only shape complementarity (MEGADOCK 2.0) consumed 14.7 min (average), and hence, the time for FFT was estimated as 11.8 min. The addition of a correlation function using the FFT results led to calculation times that were 1.8-times longer than the simple scoring function, or an 11.8-min increase. In the proposed rPSC method, by avoiding the addition of FFT, the time increase was suppressed to approximately 1.9 min, which represents an 84% reduction in time compared with simple FFT addition.Table 5 also shows that the average docking time for MEGADOCK was approximately 7.5-times faster than ZDOCK 3.0. This improvement is crucial for analyzing exhaustive docking problems in which the number of required docking jobs increases in a combinatorial manner.

Table 5.

Calculation times for MEGADOCK and ZDOCK.

	MEGADOCK 1.0	MEGADOCK 2.0	MEGADOCK 2.1	ZDOCK 3.0
Average (s.d.) [min]	13.3 (10.1)	14.7 (10.8)	16.6 (11.8)	124.6 (94.1)
6Increase over ZDOCK 3.0	9.37	8.48	7.51	(1.0)

3.3. Screening of Relevant Interacting Protein Pairs by All-to-All Docking

We conducted docking and PPI prediction processes on all combinations of all receptors and all ligand structures (44 × 44 = 1,936and 120 × 120 = 14,400 combinations of the small and large datasets, respectively) according to the procedure listed in Table 1.The PPI screening experiments were conducted using the TSUBAME 2.0 supercomputer system; clustering 1,000 high-scoring decoys averaged 8 min, and the calculation time spent for reranking is shown in Table 6.

Table 6.

Calculation times for ZRANK reranking.

Decoys recorded per rotation (t)	1	2	3	5	10	20
Number of decoys (2000 × t)	2,000	4,000	6,000	10,000	20,000	40,000
Calculation time [min]	3.1	6.2	9.2	15.2	30.4	60.8

Table 7 shows the performance of the PPI prediction with the small dataset. The performance was improved by introducing the reranking process rather than using the docking results alone. Moreover, the F-measure value of 0.415 (Precision 0.447, Recall 0.386, Accuracy 0.975) was calculated using docking parameter (t = 3) that led to the best performance. The performance of the application using the large dataset generated an F-measure value of 0.231 (Precision 0.500, Recall 0.150, Accuracy 0.992) using this setting (t = 3) with the PPI prediction parametersm* = 0.0, E* = 7.3 (see Table 8). Although the large dataset included the small dataset, the effect on performance was small. The performance on the 76×76 test dataset (excluded the small dataset from the large dataset) generated an F-measure value of 0.276.

Table 7.

Results of 44 × 44 protein-protein interaction predictions.

Decoys recorded per rotation (t)		1	2	3	5	10	20
Predictions without reranking	Precision	0.563	0.435	0.474	0.429	0.409	0.450
	Recall	0.205	0.227	0.205	0.205	0.205	0.205
	F-measure	0.300	0.299	0.286	0.277	0.273	0.281
Predictions with reranking	Precision	-	0.375	0.447	0.320	0.347	0.318
	Recall	-	0.409	0.386	0.364	0.386	0.318
	F-measure	-	0.391	0.415	0.340	0.366	0.318

Table 8.

Comparison of the results of protein-protein interaction predictions for the ZLAB Benchmark dataset with MEGA-DOCK and other methods.

Method	Size	Precision	Recall	Accuracy	F-measure
MEGADOCK	120×120	0.500	0.150	0.992	0.231
ZDOCK+Clustering [14]	120×120	0.310	0.225	0.989	0.261
ZDOCK+AEP [15] †	84×84	0.035	0.274	0.902	0.063
ZDOCK+ZRANK+Clustering	120×120	0.474	0.225	0.991	0.301

^†Note: Values for ZDOCK+AEP were taken from reference [15].

Yoshikawa, et al. have shown the prediction performance of their method as an F-measure value of 0.063, Accuracy value of 0.902 on the 84 × 84 bound dataset used AEP [15] (Table 8). Our result here (F-measure value of 0.231 with 0.992 Accuracy on the 120 × 120 bound dataset) is significantly better. Table 8 also shows the comparison of the results of MEGADOCK and ZDOCK with or without post-processing. The proposed post-process (adding ZRANK) improved the prediction performance of MEGADOCK and ZDOCK.

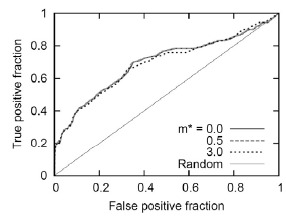
The receiver-operator characteristics (ROC) curve [42] with the large dataset andt = 3 is shown in Fig.6. The ROC curve plots TP and FP fractions and shows the tradeoff between them. A completely random prediction would lead to a diagonal line from the left-bottom to the top-right corners of the plot. The points above the diagonal line represent a scenario in which the prediction is better than random. The ROC curve in Fig.6 shows clearly that when m* = 0.0 to 3.0,the predictions generated by our method are better than random.

Fig. (6).

Evaluation of the docking post-processing system ( t = 3, reranking used). The ROC curves for varying the threshold m* and E* values are shown. The x-axis represents the false-positive fraction (#FP/ (#FP+ #TN)) and the y-axis represents the true-positive fraction (#TP/ (#TP+ #FN)). Random predictions are indicated by the diagonal.

Figure 7 shows a heat map obtained from our PPI prediction method (t = 3). We setthe clustering parameter m* to 0.0 and the threshold value E* to 7.3. The red cells and green cells indicate corresponding pairs predicted as positive and negative, respectively. The red cells placed on the diagonal line indicate TPs; the green cells on the diagonal line indicate FNs. The red cells off the diagonal show FPs.

Fig. (7).

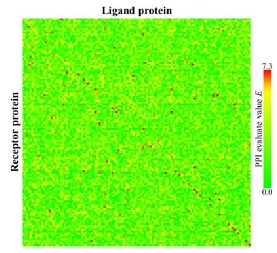
The 120 * 120 map of protein-protein interaction prediction results. The red cells are those for which E is > E*(= 7.3). The cells have been arranged in alphabetical order for each category (Rigid-body, Medium Difficulty, and Difficult) for all axes according to Table 4.

We also conducted all-to-all docking and PPI predictions using the unbound 120 × 120 large dataset. The performance here generated an F-measure value of 0.0390 (Precision 0.0471, Recall 0.0333, Accuracy 0.981) with the PPI prediction parametersm* = 3.0and E* = 6.3. The F-measure value was much worse when compared with that of the bound large dataset, whereas it was slightly better than a random prediction of the F-measure value of 0.0164. We conducted the same analysis using ZDOCK but also failed to acquire a better F-measure value (0.0415).

3.4. Toward Developing a Method Applicable to Unbound Data

The poor performance using unbound data is caused by the high dependence of our current method on the docking scoring function. It assumes that the correct binding structures will score higher than the incorrect docking forms. Nevertheless, we assumed that that the significant docking scores might be difficult to achieve with the unbound structures, because they are not expected to exhibit exact shape complementarity as expected for the redocking of the bound structures.

To improve the PPI prediction of unbound structures, some additional analysis is required as follows: (i) including not only the best decoy’s score but also use a group of highly ranked decoys to calculate E, and (ii) analyzing the distributions of the high scoring decoys with respect to the interaction residues while improving the docking scoring function.

Another promising approach to PPI prediction using the unbound dataset is to use cross-docking with the ensemble structures. In unbound pairs, shape complementarity-based docking scores are not significantly high in high-ranked decoys, because the receptor and ligand protein structures do not possess exact shape complementarity. By sampling some possible protein structures, and if successful, form a structure that is closer to the bound form, the PPI prediction process can be improved. There are some successful outcomes that use ensemble docking, and much effort was made to generate better structure sampling starting from the unbound form of the proteins [43, 44]. As efforts mature that attempt to convert unbound docking problems to those similar for bound docking, our method can provide the link to structural docking to predict possible binding pairs.

It should be noted that the datasets used contain much larger number of “False” pairs(14,280) than “True” pairs (120), making it difficult to achieve a high level of reliable PPI prediction. For example, by using the smaller dataset, we tried dividing our data according to subcellular localization obtained from the Uniprot database (Table S3 ^{(393.2KB, pdf)} -S5 ^{(393.2KB, pdf)} ). The performance of our method varied according to the sub-datasets. While we did not see major improvement in the case of nuclear localization (Figure S1 ^{(393.2KB, pdf)} ), a higher F-measure value was observed for proteins localized to the mitochondrion (Figure S2 ^{(393.2KB, pdf)} ) and Golgi apparatus (Figure S3 ^{(393.2KB, pdf)} ). Although our method aims at primary screening of PPI from large protein structure datasets, we think that we can improve the performance of our method using additional information regarding protein features.

3.5. Application to a Pathway Reconstruction Problem

As a case study using actual biological data, we applied our method to the structures of proteins that are components of the bacterial chemotaxis pathways, which represent a typical target in systems biology, which has been extensively studied over the past several decades. Therefore, we assumed that most of the essential protein-protein interactions are known.

Proteins structures for components of the bacterial chemotaxis pathways (in the KEGG pathway, IDs: eco02030, stm020230, tma02030 for species of Escherichia coli, Salmonellatyphimurium, and Thermatogamaritimae were collected from the PDB. The structures were first screened according to the following criteria as in the protein-protein docking benchmark [45] as follows: (i) experimental method, X-ray diffraction, resolution better than 3.25 Å; and (ii) polypeptides comprising more than 30 amino acid residues. Data for mutants and synthetic polypeptides were excluded. Structural data for only the ligand-binding domain of membrane proteins, which are located in the periplasm, were also excluded, because the other proteins in the pathway localize to the cytoplasm. Each PDB file was divided into data for each polypeptide chain, which in most cases corresponded to a single protein species. Finally, data that could not be ranked with ZRANK were excluded. Using this procedure, we obtained 89 protein structures, which correspond to 13 proteins (CheA, CheB, CheC, CheD, CheR, CheW, CheX, CheY, CheZ, Tsr, FliM, FliG, FliN). We used multiple structural data for each protein where possible. The list of the structural data used is described in Table S6 ^{(393.2KB, pdf)} .

The docking parameter (t: decoys recorded per ligand rotation) was set tot = 3, and we used the PPI prediction parametersm* = 0.0 and E* = 7.3 from which we obtained the best F-measure value in the benchmark data. In cases where one or more structural data elements for a protein species were available, we calculated the scores of the PPI prediction (E) using all the data. When we found at least one positive evaluation between relevant protein pairs, we judged the pair as interacting. We obtained an F-measure score of 0.364 (recall = 0.3, precision = 0.462) for this system. However, the best performance of the PPI prediction in the chemotaxis pathway was the F-measure value of 0.524 with the PPI prediction parameter E* = 7.1 without post-process clustering. This score was better than the result for of a previous study, which used ZDOCK (F-measure value of 0.414 with m* = 2.0, E* = 7.6)[14]. Although MEGADOCK performed better than ZDOCK using the chemotaxis dataset, we cannot determine the significance, because the dataset contains only 13 proteins. The proteins in the dataset cover a limited range of functions; for example, many of them function as kinases or phosphatases. Therefore, it is more helpful to discuss the performance of docking engines using their performances on the benchmark dataset, which covers comprehensively the domains and functions of proteins from the available structures. Future work will include the improvement of the clustering methods and parameter optimization to improve the accuracy of the PPI predictions. It is also important to considerthe characteristics of the target dataset.

4. CONCLUSIONS

We describe here the development of an exhaustive PPI screening system called “MEGADOCK” that conducts docking and post-analysis on protein tertiary structural data. To facilitate more comprehensive searches, we introduced a novel scoring function rPSC, which represents shape complementarity and electrostatic interactions between target proteins with only one correlation function. MEGADOCK was shown to be 7.5-times faster than the conventional ZDOCK 3.0 software while maintaining acceptable docking prediction accuracies. By employing an advanced computing environment, such as using several thousands of CPU cores, our method enables the analysis of a pathway-level problem in a few days. In addition, many scientific calculations have recently benefited from the very high arithmetic capabilities of modern GPUs [46]. Employing a GPU-based docking technique [28, 47, 48] may be interesting given the current situation where GPU-based high performance computers are often present in the Top500 computing website that lists the most powerful commercially available computer systems [49].

For the detection of the relevant interacting protein pairs, we obtained an F-measure value of 0.231 when our method was applied to a subset of a general benchmark dataset. We also applied the proposed system to the comprehensive and highly curated bacterial chemotaxis protein dataset. We generated an F-measure value of 0.364 using the same parameter set that yielded the best F-measure value for the benchmark data.

We are applying our methods to proteins related to the epidermal growth factor receptor signaling pathway. Besides its importance in the proliferation and function of normal cells, when this pathway is altered, inappropriate signaling contributes to the pathogenesis of human cancers. Here the problem size is approximately , and MEGADOCK is designed specifically to work in large-scale parallelized computing environments.

Our future work will include the quantitative representation of the reliability of the prediction for each detected PPI. Moreover, we will try to apply our PPI prediction system to protein-RNA interactions, which was the subject of one of our previous studies, but without post-processing [50]. We will try to combine our novel hydrophobic interaction function [51] with MEGADOCK. We believe that integrating our prediction approach into conventional bioinformatics methods, such as those based on nucleotide sequencing should be useful.

CONFLICT OF INTEREST

The authors confirm that this article content has no conflicts of interest.

SUPPLEMENTARY MATERIALS

The Supplementary materials contain additional tables (Tables S1 ^{(393.2KB, pdf)} , S2 ^{(393.2KB, pdf)} , S3 ^{(393.2KB, pdf)} , S4 ^{(393.2KB, pdf)} , S5 ^{(393.2KB, pdf)} , and S6 ^{(393.2KB, pdf)} ) and figures (Figures S1 ^{(393.2KB, pdf)} , and S3 ^{(393.2KB, pdf)} ) referred to in the main article as follows: Table S1 ^{(393.2KB, pdf)} , docking prediction performance of MEGADOCK and ZDOCK for bound docking testcases in ZLAB Benchmark 4.0; Table S2 ^{(393.2KB, pdf)} , docking prediction performance of MEGADOCK and ZDOCK for the unbound docking testcases in ZLAB Benchmark 4.0; Table S3 ^{(393.2KB, pdf)} , the divided dataset, which includes proteins located in the nucleus; Table S4 ^{(393.2KB, pdf)} , the divided dataset, which includes proteins located to the mitochondrion; Table S5 ^{(393.2KB, pdf)} , divided dataset, which includes proteins located to the Golgi apparatus; Table S6 ^{(393.2KB, pdf)} , the chemotaxis dataset derived from the PDB; Figure S1 ^{(393.2KB, pdf)} , results of the PPI predictions with the nuclear protein subdataset; Figure S2 ^{(393.2KB, pdf)} , results of the PPI predictions with the mitochondrial protein subdataset; and Figure S3, results of the PPI predictions with the Golgi apparatus subdataset.