Abstract
Real-time ultrasound thermography has been recently demonstrated on commercially-available diagnostic imaging probes. In vitro experimental results demonstrate high sensitivity to small, localized temperature changes induced by subtherapeutic focused ultrasound. Most of the published results, however, are based on a thermally-induced echo strain model that assumes infinitesimal change in temperature between imaging frames. Under this assumption, the echo strain is computed using a lowpass axial differentiator which is implemented by a finite impulse response (FIR) digital filter. In this paper, we introduce a new model for temperature estimation which employs a recursive axial filter that acts as a spatial differentiator-integrator of echo shifts. The filter is derived from first principles and it accounts for a nonuniform temperature baseline when computing the spatial temperature change between two frames. This is a major difference from the previously proposed infinitesimal echo strain filter (δ-ESF) approach. We show that the new approach can be implemented by a first-order infinite impulse response (IIR) digital filter with depth-dependent spatial frequency response. Experimental results in vitro demonstrate the advantages over the δ-ESF approach in terms of suppressing the spatial variations in the estimated temperature without resorting to ad hoc lowpass filtering of echo strains. The performance of the new recursive echo strain filter (RESF) is also illustrated using echo data obtained during sub-therapeutic localized heating in the hind limb of Copenhagen rat in vivo. In addition to the RESF, we have used an adaptive spatial filter to remove motion and deformation artifacts during real-time data collection. The adaptive filtering algorithm is described and comparisons with uncompensated estimated spatio-temporal temperature profiles are given. The results demonstrate the feasibility of in vivo ultrasound thermography with high sensitivity and specificity.
I. Introduction
Ultrasound thermography has proved to be a promising modality for non-invasive monitoring and control of temperature during thermal therapy. Local temperature changes create shifts due to physical and apparent displacements. The former is the result of thermal expansion while the rather is related to the local changes in speed of sound. Using an infinitesimal model for thermal expansion and a linear temperature dependency assumption for the speed of sound, Simon et al [1] suggested a model that lumped these two effects in a single equation which related the echo strain to the induced temperature change. We call this the δ-ESF model. Similar results were reported in [2] where the requirement for a good thermal expansion model was also explained. Based on the δ-ESF model and using the speckle tracking method explained in [1], authors in [3] demonstrated the real-time tracking of the temperature change in vivo using the integrated imaging-therapy system described in [4]. This model has also been confirmed by other groups [5],[6] and [7] where some limitations have been addressed as well as solutions for some of the common problems such as the thermoacoustic lens effect have been suggested [8]. In addition to the time domain method, spectral domain tracking of the temperature has been suggested [9],[10]. Although the derivations in these models include the spatial dependency of the temperature change, the final result is similar to the δ-ESF in time domain and does not account for the temperature gradients. Additionally, methods which are not based on displacement estimation have been proposed in [11], [12] and [13] with varying degrees of development in terms of real-time implementation and spatial and temporal resolution.
In spite of successful implementation of the δ-ESF model by many groups, ignoring the nonuniform temperature baseline can cause unrealistic temperature fluctuations at the focus. When these effects are combined with the thermal lens artifacts, without using any ad hoc lowpass filtering, the specificity of the ultrasound thermography can degrade significantly. In this paper we propose a new derivation of the temperature estimation based on the echo shifts. In this derivation, instead of infinitesimal changes the commutative effect of the thermal expansion is considered for modeling the physical shifts. This results in a recursive echo strain filter which was first introduced in [14]. we show that the final temperature reconstruction filter has the form of a differentiator-integrator as opposed to a pure differentiator used in the δ-ESF model. It is shown that the integrator part acts as a low pass filtering process which is derived from the local tissue properties and is effective in reducing inconsistent temperature fluctuations due to temperature gradients as well as ripples due to thermal lens effect without additional filtering.
In case of in vivo temperature estimation, in addition to the modeling errors, deformations caused by natural motions such as breathing, gasping and blood pulsation can introduce non-thermal displacements in the same spatial and temporal frequency bands as the true temperature change. Methods based on frame-to-frame decorrelation were presented in [15] and [16]. Even though these methods are suitable for detecting large motions, they are not applicable for tracking of fast temperature changes with high frame rate speckle tracking. The results presented in [17] and [18] showed that post processing of the temperature using a two dimensional filter inspired by the bio-heat equation can further reduce some of the inconsistencies including the ripples caused by the thermal lens effect and sudden transitions due to mechanical stresses. However due to shared bandwidth of the artifacts and the temperature field, a filtering mechanism with spatial and temporal selectivity is preferred. Using the global availability of the motion strain and adaptive filtering techniques, a method is presented which can significantly reduce most of the motion related artifacts.
The organization of this paper is as follows. In section II we present the new model for the ultrasound echo shift thermography. Section III describes a motion compensation algorithm based on an adaptive filter technique for dealing with natural deformation artifacts during in vivo temperature estimation. Material and methods are described in section IV. Phantom experiment as well as in vivo results are presented in section V. Section VI concludes the paper with a brief summary of achievements and future works.
II. Temperature Estimation Model
Localized heating of tissue in the order of few millimeters in each dimension creates echo shifts due to local changes in the speed of sound and thermal expansion. While the change in echos due to speed of sound variations is unidirectional with respect to temperature change (i.e. scatterers always appear closer to the transducer at higher temperatures when the speed of sound increases with temperature), tissue displacement due to thermal expansion is directional such that all the points between the transducer and the center of focused heating move toward the transducer while the points behind the center of heating are pushed away from the center. The infinitesimal echo strain filter presented in [1] does not take this directionality of the thermal expansion behavior into account. For a point between the transducer and heating center located at depth z at baseline temperature of θ, the round-trip time delay of the echoes can be calculated as
| (1) |
where c(ξ; θ) is the depth and temperature dependent speed of sound. Temperature change creates both apparent and physical changes in the estimated delay. The former is caused by the change in speed of sound while the latter is a result of tissue thermal expansion. Hence the frame-to-frame change in the delay can be written as
| (2) |
where Δθ is the differential change in temperature at depth z and T is the frame (wall clock) time. Assuming a linear model for the change in speed of sound and thermal expansion
| (3) |
and hence
| (4) |
| (5) |
Ignoring the second order approximation terms, this can be further simplified as
| (6) |
A closed form solution of equation (6) is presented in Appendix A where temperature change and speed of sound are both considered as functions of depth and time. Although the final solution is interesting in terms of the reconstruction model in the spatial domain and it corroborates with a simpler model which follows, the implementation requires nonuniform sampling transformation and successive updating of speed of sound and temperature field in an iterative fashion. A simpler model can be derived by assuming small variations in the speed of sound and differentiating both sides of the equation (6) with respect to z
| (7) |
Substituting for ∂a by c∂t/2 in (7) results in the simplified equation:
| (8) |
where t is the propagation delay based on (1). Note that the second term in (8) is an approximation of the second term in (7) (by dropping the term with 1/c2 dependence).
In general, equation (8) is a nonlinear differential equation which can be solved numerically. However, for complexity reasons we would like to form a simpler implementation of the algorithm using only ordinary digital filters. For this reason the depth variable z is replaced by a constant depth z0. By taking Fourier transform from both sides of the equation (8) with respect to the variable t and rearranging the terms
| (9) |
where and are the Fourier transforms of Δθ and δτ respectively and we defined τ = 2z0/c as a constant.
The δ-ESF model presented in [1] was based on the infinitesimal length changes which resulted in the following reconstruction model in the frequency domain
| (10) |
which acts as a pure differentiator operator on the echo shifts independent of any variations in the temperature baseline. The slope of this differentiator is defined based on the tissue thermal coefficients. Equation (9), on the other hand, has the form of a differentiator-integrator which can be implemented as an IIR filter in the axial direction or can be combined with time accumulation to form a spatial-temporal filter. It is interesting to note that, at low frequencies, the filter behaves like a differentiator, which is consistent with the δ-ESF model in (10)1. At higher frequencies, however, the filter has a flat response with a gain of 2/ατ. The cutoff frequency of the filter is also a function of the thermal expansion and the change in speed of sound coefficients. This result is still attractive from the real-time implementation point of view. Even though the derivation accounted for the inhomogeneous baseline, the final result does not relay on explicit knowledge of this baseline. The discrete time equivalent of the reconstruction filter in (9) can be derived by using the bilinear transformation [19],[20]
| (11) |
where Ts is the sampling time of the RF data. Hence
| (12) |
where and are the z transforms of Δθ and δτ respectively. Equation (12) resembles an IIR filter in the axial direction on the displacement data, the main reason that we call this the RESF model. The gain and location of the pole of this filter are defined by α, β (tissue dependent) and τ = 2z0/c in which zo is the effective length over which the recursion implied by (12) occurs. A very small z0 results in a model that approaches the C-ESF model.
Fig. 1 shows the frequency response of the reconstruction filters based on the δ-ESF model and the RESF model with different z0 values where we used α = 1 × 10−4 °C−1 and β = 1 × 10−3 °C-1 [21], [1]. As it can be seen from the plots, as z0 approaches zero, the RESF model approaches the δ-ESF model.
Fig. 1.
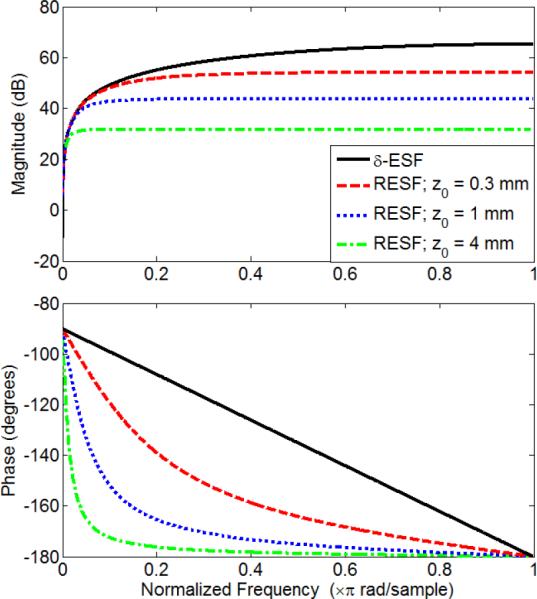
Frequency response of the RESF model for different depths along with the δ-ESF response for α = 10−4 and β = 10−3. Solid black: the δ-ESF model, dashed red: the RESF model with z0 = 0.3 mm, dotted blue: the RESF model with z0= 1 mm and dash-dotted green: the RESF model with z0= 4 mm.
For given values of α and β, The effective recursion length, z0, defines the amount of smoothing implied by the integrator part in (12). In monitoring of hyperthermia using HIFU, for example, z0 can be in the order of the extent of the therapy beam in the imaging plane; typically in the millimeter range.
III. Adaptive Motion Compensation
Natural motions such as breathing, gasping and pulsation in vivo can cause significant artifacts in the estimated temperature. These artifacts are due to the strain pattern induced by the mechanical stress on the tissue and the area for which the artifacts manifest depends on the extent of the motion and connectivity of the different parts of the underlying tissue. For example, the strain pattern caused by gasping can spread over a wide range of the imaging plane such that when using the speckle tracking algorithm regions of strong strain can be detected in almost entire imaging plane. pulsation of small vessels, on the other hand, can create a more localized pattern. The strong time correlation of these patterns and the fact that most of these artifacts appear as strong foci with quasi-cyclic temporal patterns suggest that we can use strain information from outside the target region of ultrasound thermography to correct for the errors occurring within this region using adaptive filter techniques.
Let us assume the estimated temperature in the axial-lateral grid point (m, n) and time index k to be θ(m,n,k). The artifactual temperature of a point outside the heated region due to a strong deformation strain is denoted as θa(mi, ni, k) and we collect N such points for interference compensation. Before heating starts, for each time index k, the error is defined as
| (13) |
where ai(m, n)'s are the coefficients of the adaptive filter for grid point (m,n). Using a Normalized Least Mean Squares (NLMS) method this error is used to find the optimal value of the coefficient vector a(m, n) = [ai(m,n), a2(m,n), aN(m,n)] using the update equation,
| (14) |
where tfoci(k) = [θa(mi, ni, k), θa(m2, n2, k), αa(mN, nN, k)]T is a N × 1 vector containing the artifactual temperature data of each training point at time k and μ is the step size of the gradient descent algorithm used for training of the adaptive filter coefficients. The training phase stops as soon as the artifactual temperature values drop below a defined threshold. Once heating starts the corrected temperature field is calculated as follows
| (15) |
where θc is the motion compensated temperature field and are the entries of the coefficient vector calculated at the last iteration of the NLMS algorithm during the training phase. Fig. 2 depicts the diagram of this process where green dots represent the deformation foci and the red dot represents a point from the target region for temperature estimation.
Fig. 2.
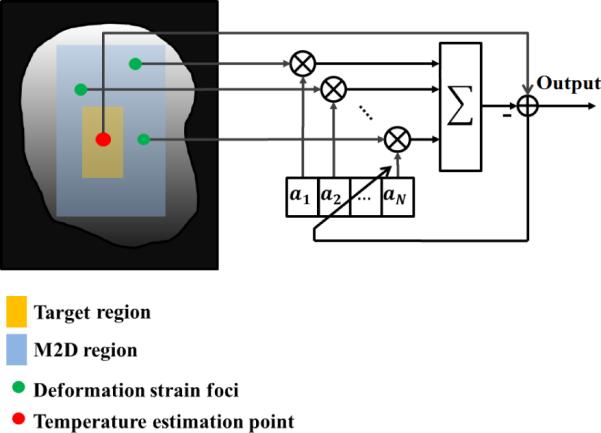
Adaptive filter configuration. N observation points are selected outside the heated region based on pre-heating analysis of tissue motions and deformations (Green dots). A temperature reference point is selected from the heated region (Red dot) based on the target of the focus and/or the analysis of the initial heating rate immediately after the HIFU pulse is applied. The error function shown in the schematics controls the adaptation according to NLMS method [22],[23].
IV. Materials and Methods
A. Experiment Setup and Data Acquisition
1) Wire Heating in Tissue-mimicking Phantom
A thin resistive Nichrome wire (32 AWG) was embedded in a tissue mimicking phantom which was prepared based on the method described in [24]. The wire was 15 cm long with 4.5 ohms resistance. A 3V DC source was applied to both ends of the wire which created around 667 milliamps of current for 13 seconds. RF data was acquired before, during and after the heating in a plane cross sectional to the wire in M2D mode2. RF data was collected using a L14-5/38 linear array (LA) probe and the SonixRP machine with research interface (Ultrasonix, BC, CA). A needle thermocouple (HYP-1 Omega, Philadelphia, PA) was inserted into the phantom very close to the heating wire. During experiment, temperature data from the thermocouple was collected at 100 frames per second. A schematic of the experiment setup is shown in Fig. 3.
Fig. 3.
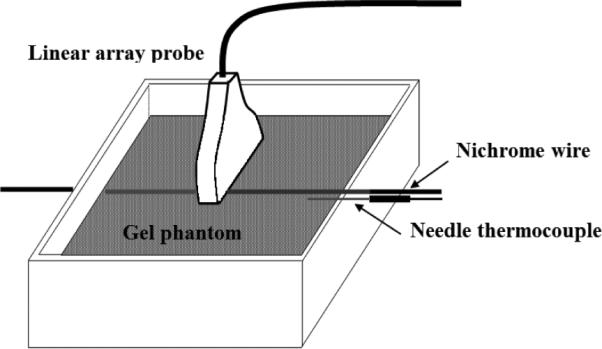
Experiment setup used for imaging of the resistive wire in gel phantom
2) Sub-therapeutic heating in the hind limb of Copenhagen rat in vivo
The M2D data was acquired at 40 MHz sampling rate and about 91 frames per second during sub-therapeutic HIFU shots in the hind limb of a Copenhagen rat as described in [17]. The HIFU shots were created using a 64-element DMUA transducer (Imasonic, FR) operating at 3.5 MHz as described in [25]. The M2D data was acquired using a linear array (HST 15-8, Ultrasonics, BC, CA) and as described in [4], which allowed for relatively high frame rates at the expense of smaller lateral extent of the image. The animal was partially submerged in a temperature controlled (34° C) degassed water and anesthetized using Ketamine and Xylazine under University of Minnesota approved IACUC protocol. This combination often results in deep anesthesia which appear to change the breathing pattern of the animal. For example, the animal gasps for air at semi-regular intervals after each period of low breathing activity. These gasps are often separated by periods of 1.5 - 2 seconds and result in significant displacements and strains throughout the hind limb that present as temperature artifacts. Frame rates in the 80 - 200 frames per second range were found to be necessary for capturing the transients of tissue motion and deformation due to pulsation, breathing as well as the radiation force effects of the pulsed HIFU beams.
B. Data Processing
In all experiments the M2D data was collected before, during and after the heating procedure for use in calculating the incremental displacement using speckle tracking algorithm as presented in [1]. A kernel length of about 9λ (1.84 mm) was used for both experiments where λ is the wavelength of the diagnostic imaging waveform operating at 7.5 MHz. The incremental displacement field was passed through the axial filter described in (12). For in vivo experiments α and β were set to 3 × 10−4 °C−1 and 2 × 10−3 °C−1, respectively based on the average values of thermal coefficients for soft tissue [21],[26]. For gel phantom experiment α and β were set to 2 × 10−4 °C−1 and 2 × 10−3 °C−1, respectively based on the average values from the slow heating experiments of the tissue mimicking phantoms reported in [1] and [27]. The integrator part of the axial filter in (12) was also applied in the reverse direction to compensate for the group delay. After performing the axial processing, the data is passed through a frame-to-frame accumulator followed by a low-pass filer with the cut off frequency of 1.5 Hz to create the final estimated temperature. In each experiment, the baseline temperature was measured and used to map the estimated temperature rise to the absolute temperature.
In order to compare the RESF temperature reconstruction model with the δ-ESF model, the displacement data was also processed using a wide-band axial differentiator and temporal accumulator as described in [1] for the case of the phantom experiment. In both in vitro and in vivo experiments, we exclude the use of any 2D filtering post temperature calculations. For example, the (2D+Time) BHTE-inspired filter proposed in [18] was not used here. This approach was effective in removing temperature artifacts inconsistent with the physical model of temperature evolution in tissue media. However, the objective of this paper is to show that the new formulation removes some of these artifacts by virtue of the filtering step implied by equation (12).
V. Results and Discussion
To show the improvements achieved by the the RESF model and rule out other sources of interference and artifacts, we first present the phantom results.
A. Heated wire in a tissue mimicking phantom
In order to demonstrate the ability of the RESF method in correcting some of the temperature artifacts seen in the δ-ESF model, we first present the results for heating the thin resistive wire embedded in the tissue mimicking phantom. Fig. 4 shows the axial-lateral distribution of the estimated temperature using (a) the δ-ESF model and (b) the RESF model. While the δ-ESF model shows rapid temperature fluctuations and ripples due to thermal lens effect, the RESF model has created a more localized 2-D temperature map consistent with the expected temperature distribution around the heated wire. Fig. 5(a) shows the axial distribution of the estimated temperature using the δ-ESF model and the RESF model with different values of z0. As it can be seen the RESF suppresses most of the rapid fluctuations close to the heating center, partly caused by the thermal lens effect. Fig. 5(b) shows the axial distribution of the estimated temperature using the RESF model with z0 = 6 mm at different time instances during heating and cooling cycles. It can be seen that the RESF model has resulted in a localized temperature map with a subtle elevation in the temperature distribution tail during cooling cycle which can be attributed to the diffusion process. Fig. 6 shows the thermocouple data along with the estimated temperature of a point at similar distance from the wire. As it can be seen there is a good agreement between the two data sets in terms of the extent of temperature change without using additional scaling. The estimated temperature rise and fall also show strong consistency with the thermocouple data.
Fig. 4.
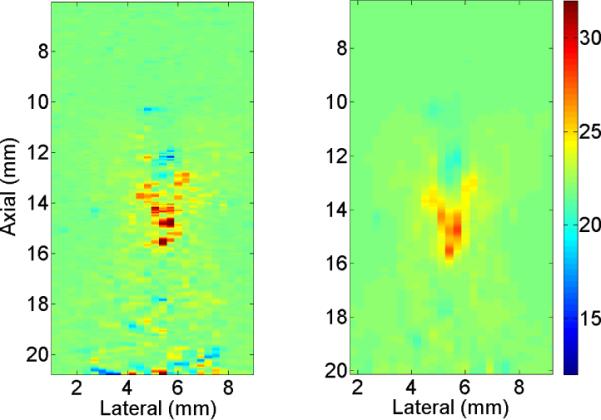
Axial-lateral distribution of the estimated temperature around the heated wire using (a) δ-ESF model and (b) RESF model at peak temperature
Fig. 5.
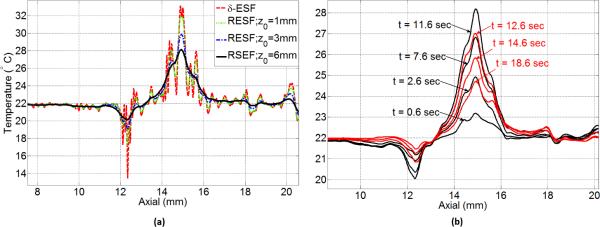
Axial distribution of the estimated temperature around the heated wire (a) estimated temperature based on RESF model for z0 = 1 mm, z0= 3 mm and z0 =6 mm along with δ-ESF result (b) estimated temperature based on the RESF model with z0 =6 mm at different heating (solid black) and cooling (solid red) time instances
Fig. 6.

Ultrasound estimated temperature (solid black) and thermocouple reading (dotted red) very close to the heated wire
B. In vivo results
We present the results of applying a sub-therapeutic HIFU shot in the hind limb of a Copenhagen rat in vivo. The displacement data was passed through the temperature reconstruction filter in (12) with z0= 6 mm. This value of z0 provided best results when combined with the adaptive motion compensation technique. The result was then processed by the band-limited accumulator in the temporal direction to create the final temperature estimate.
Sub-therapeutic HIFU started after one second of baseline measurements and was on for 750 ms. The total duration of data recording was 4 seconds where three sporadic gasps occurred within the data collection interval. Mechanical deformation foci were observed throughout the imaging plane and one location was selected using a simple threshold on the strain data where 33 points were selected as the interference inputs to the algorithm. Classic NLMS algorithm with step size of μ = 0.5 was implemented on the artifactual (before HIFU was applied) temperature data to train the coefficients of the filter for each grid point in the target region. The update process stopped once the artifactual temperature dropped below 38° C where the baseline temperature was 34°C. Fig. 7 shows the axial-temporal distribution of the estimated temperature profile before and after applying the motion compensation method. First of all, the spatial distribution of the temperature seems to be consistent with the focus of the HIFU beam which was at 40 mm. Ripple artifacts due to the thermal lens effect are considerably reduced by using the mew model. In Fig. 7 (a) it can be seen that three strong gasps caused erroneous temperature estimates at three different time instances right at the heating focus and 2 mm beyond the focus. The motion compensation method has successfully canceled the effect of these gasps without scarifying the spatial distribution of the temperature. Fig. 8 (a) and (b) show the axial-lateral distribution of the estimated temperature before and after applying the motion compensation overlaid on 50 dB B-mode image at the second gasp time instance. The heterogeneity of the tissue can be observed in this image where the skin and connective tissues have created hyperechoic regions while muscle tissues appeared as uniform defused scattering areas. The overlaid temperature map in Fig. 8 (a) shows three regions with significant temperature rise. Fig. 8 (b) shows the same temperature map after applying the correction where a confined temperature rise is seen and the artifact are significantly reduced. Fig. 8 (c) shows the time profile of a point close to the focus. The NLMS algorithm is able to converge in a fraction of second. It is seen that while the corrected temperature preserves most of the unaffected parts of the temperature profile, large temperature errors in the order of 4°C (almost 40% of the peak temperature change) are corrected.
Fig. 7.
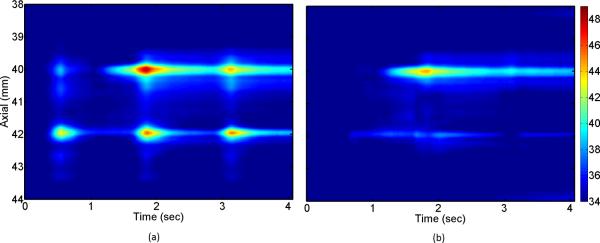
Spatio-temporal temperature profiles obtained (a) before (b) after applying the motion compensation algorithm. In both cases the new derivation is used without any post processing.
Fig. 8.
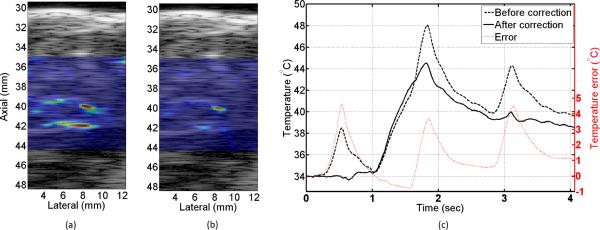
Temperature profiles at t = 1.7 sec obtained (a) before (b) after using the motion compensation method overlaid on a 50 dB B-mode iamge. (c) Temporal profile of the estimated temperature before (dashed black) and after (solid black) motion correction along with the difference (dotted red).
VI. Conclusion
In this paper we presented the RESF model for temperature estimation based on the ultrasound echo shifts. In this model, instead of infinitesimal changes, the cumulative effect of thermal expansion was used to relate the echo shifts to the temperature changes which enabled the incorporation of the temperature gradient in the derivations. The final formulation was shown to be in the form of a differentiator-integrator filter with parameters defined by the physical properties of tissue and heating source. The results of using the RESF model in the heated wire phantom showed consistent axial distribution of the temperature as well as strong agreement with the thermocouple readings without additional scaling. Compared to the δ-ESF model presented previously, the RESF model was shown to be less sensitive to the rapid fluctuations caused by ignoring temperature gradients as well as propagation artifacts including the thermal lens effect. It was also shown that the RESF model can change to the δ-ESF model via changing an effective recursion length variable z0. We then used the RESF model for estimating the temperature during sub-therapeutic HIFU shots in the hind limb of a Copenhagen rat in vivo. Due to gasping significant artifacts were introduced to estimated temperature. Using an adaptive filter technique we presented a motion compensation method which takes advantage of the global availability of the mechanical deformation patterns to train the coefficients of a corrective filter. By using these coefficients and the data from outside the target region we showed that the effect of gasps can be significantly reduced without sacrificing the spatial and temporal distribution of the temperature. When combined by spatial temporal filtering approaches, these results suggest the suitability of ultrasound thermography for in vivo applications as long as good assumptions about local tissue formation and physical properties can be made.
Acknowledgment
The authors would like to thank Dr. Dalong Liu for his efforts in the design of the M2D system, Dr. Jeunghwan Choi and Prof. John Bischof for helping with the animal study and Dr. Andrew J. Casper, Alyona Haritonova and Elias Welken-Resman for help during the experiment and discussions.
This work was funded in part by grant EB009750 from the National Institutes of Health and in part by a Minnesota Futures grant from the university o1 Minnesota's office of vice president for research.
Biography
 Mahdi Bayat (S'12, M'14) received his B.Sc. in electrical engineering from Iran University of Science and Technology, Tehran, Iran in 2004 and his M.S. and Ph.D. in electrical engineering from the University of Minnesota, Twin Cities, in 2014. Dr. Bayat is currently a postdoctoral research fellow at Ultrasound Imaging Lab, Mayo clinic, Rochester, MN. His research interests are in statistical signal processing with applications to therapeutic and diagnostic ultrasound.
Mahdi Bayat (S'12, M'14) received his B.Sc. in electrical engineering from Iran University of Science and Technology, Tehran, Iran in 2004 and his M.S. and Ph.D. in electrical engineering from the University of Minnesota, Twin Cities, in 2014. Dr. Bayat is currently a postdoctoral research fellow at Ultrasound Imaging Lab, Mayo clinic, Rochester, MN. His research interests are in statistical signal processing with applications to therapeutic and diagnostic ultrasound.
 John R. Ballard (S'02, M'12) received his B.S. degree in electrical engineering in 2005 from Michigan State University, East Lansing, and M.S. and Ph.D. degrees in electrical engineering, in 2007 and 2012 respectively, from the University of Minnesota, Twin Cities. Dr. Ballard previously was a postdoctoral researcher in the Ultrasound Imaging and Signal Processing Laboratory at the University of Minnesota where he worked on minimal and noninvasive surgery with a particular focus on the use of HIFU for oncological and cardiovascular applications. Currently, Dr. Ballard is a Senior Innovation Fellow at the Medical Devices Center at the University of Minnesota. His research interests are in signal processing, IP development, and Class I and Class II medical device development for use in cardiology, intensive care, medical imaging and at home monitoring.
John R. Ballard (S'02, M'12) received his B.S. degree in electrical engineering in 2005 from Michigan State University, East Lansing, and M.S. and Ph.D. degrees in electrical engineering, in 2007 and 2012 respectively, from the University of Minnesota, Twin Cities. Dr. Ballard previously was a postdoctoral researcher in the Ultrasound Imaging and Signal Processing Laboratory at the University of Minnesota where he worked on minimal and noninvasive surgery with a particular focus on the use of HIFU for oncological and cardiovascular applications. Currently, Dr. Ballard is a Senior Innovation Fellow at the Medical Devices Center at the University of Minnesota. His research interests are in signal processing, IP development, and Class I and Class II medical device development for use in cardiology, intensive care, medical imaging and at home monitoring.
 Emad S. Ebbini (S'82, M'90, SM'08, F'11) Received his B.Sc. in EE/communications in 1985 from the University of Jordan, and his M.S. and Ph.D. in EE from the University of Illinois at Urbana-Champaign in 1987 and 1990. From 1990 until 1998, he was on the faculty of the EECS department at the University of Michigan Ann Arbor. Since 1998, he has been with the ECE department at the University of Minnesota. In 1993, he received the NSF Young Investigator Award for his work on new ultrasound phased arrays for imaging and therapy. He was a member of AdCom for the IEEE Ultrasonics, Ferroelectrics, and Frequency Control between 1994 and 1997. In 1996, he was a guest editor for a special issue on therapeutic ultrasound in the IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. He was an associate editor for the same transactions from 1997 - 2002. He is a member of the standing technical program committee for the IEEE Ultrasonics Symposium. He served as a member of the Board of the International Society for Therapeutic Ultrasound (2002 - 2011) and is currently serving as its President (2012 - 2015). His research interests are in signal and array processing with applications to biomedical ultrasound and medical devices.
Emad S. Ebbini (S'82, M'90, SM'08, F'11) Received his B.Sc. in EE/communications in 1985 from the University of Jordan, and his M.S. and Ph.D. in EE from the University of Illinois at Urbana-Champaign in 1987 and 1990. From 1990 until 1998, he was on the faculty of the EECS department at the University of Michigan Ann Arbor. Since 1998, he has been with the ECE department at the University of Minnesota. In 1993, he received the NSF Young Investigator Award for his work on new ultrasound phased arrays for imaging and therapy. He was a member of AdCom for the IEEE Ultrasonics, Ferroelectrics, and Frequency Control between 1994 and 1997. In 1996, he was a guest editor for a special issue on therapeutic ultrasound in the IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. He was an associate editor for the same transactions from 1997 - 2002. He is a member of the standing technical program committee for the IEEE Ultrasonics Symposium. He served as a member of the Board of the International Society for Therapeutic Ultrasound (2002 - 2011) and is currently serving as its President (2012 - 2015). His research interests are in signal and array processing with applications to biomedical ultrasound and medical devices.
Appendix A Closed form solution of the thermal-echo displacement equation
At high frame rates where the change in temperature is very small, equation (6) becomes
| (16) |
where the temperature field θ(z, T) is considered as a two dimensional function and variable T represents the time progress along M2D frames. The first term in the right hand side of (16) represents the change in echo shifts due to the thermal expansion while the second term represents the variations due to the change in speed of sound. By replacing c(z; θ) with c(z, T) and noticing that the differential in (16) is due to time progress we have
| (17) |
The time derivative of the echo location in (17) can be regarded as the incremental displacement in the speckle tracking algorithm as explained in [1]. Given that the variations of speed of sound with temperature is known, in its general form, equation (17) represents a non-homogeneous nonlinear integro-differential equation of temperature distribution over time and space. A consistent solution for this equation should satisfy the bio-heat equation with given boundary and initial conditions. Taking Fourier transform from both sides of (17) with respect to variable z
| (18) |
Considering β as a constant and defining φ = (∂θ/∂T)/c we have
| (19) |
where θ = Fz {φ}. Alternatively
| (20) |
Equation (20) is a solvable ODE with the following closed form solution
| (21) |
and taking inverse Fourier transform
| (22) |
The last equation relates the temperature rate to the incremental displacement via baseline speed of sound which can be in turn updated sequentially. Considering that equation (22) is derived with minor assumptions about change in speed of sound and temperature heterogeneity, it still resembles the form of a differentiator-integrator suggested by (9) with appropriate assumptions about α and β.
Footnotes
The difference in the scaling factors is due the fact that in [1] the thermal expansion was included in the differential length element as dζ(θ + δθ) = dζ(θ)(1 + αδθ) whereas here it is modeled as an overall length decrease in the integral limit in (1) as z(θ + Δθ) = z(θ)(1 - αΔθ). Nevertheless, both models result in a similar reconstruction filter at low frequencies and as long as β is much larger than a as shown in Fig. 1.
M2D-mode simply refers to acquiring RF data frames with limited extent in a straightforward extension of the familiar M-mode imaging.
Contributor Information
Mahdi Bayat, Department of Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN, 55455 USA. He is now with the Ultrasound Imaging Lab at Mayo Clinic, Rochester, MN, 55905 USA.
John R. Ballard, Medical Devices Center, University of Minnesota, Minneapolis, MN, 55455 USA..
Emad S. Ebbini, Department of Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN, 55455 USA..
REFERENCES
- 1.Simon C, VanBaren P, Ebbini ES. Two-dimensional temperature estimation using diagnostic ultrasound. IEEE Trans. Ultrason., Ferro-elect., Freq. Contr. 1998 Jul;45:989–1000. doi: 10.1109/58.710592. [DOI] [PubMed] [Google Scholar]
- 2.Maas-Moreno R, Damianou CA. Noninvasive temperature estimation in tissue via ultrasound echo shifts. Part I. Theoretical model. The Journal of the Acoustical Society of America. 1996;100:2514–2521. doi: 10.1121/1.417359. [DOI] [PubMed] [Google Scholar]
- 3.Liu D, Jeong J, Ballard J, Bischof J, Ebbini ES. Real-time Monitoring of Thermal and Mechanical Response to Sub-therapeutic HIFU Beams In Vivo. Proc. IEEE Ultrason. Symp. 2010:2254–2257. [Google Scholar]
- 4.Liu D, Ebbini ES. Real-time 2-D temperature imaging using ultrasound. IEEE Trans Biomed Eng. 2010 Jan;57(1):12–16. doi: 10.1109/TBME.2009.2035103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Miller NR, Bamber JC, Meany PM. Fundamental limitations of noninvasive temperature imaging by means of ultrasound echo strain estimation. Ultrasound in Medicine and Biology. 2002;28:1319–1333. doi: 10.1016/s0301-5629(02)00608-7. [DOI] [PubMed] [Google Scholar]
- 6.Souchon R, Bouchoux G, Maciejko E, Lafon C, Cathignol D, Bertrand M, Chapelon J-Y. Monitoring the formation of thermal lesions with heat-induced echo-strain imaging: A feasibility study. Ultrasound Med. Biol. 2005 Feb;31(2):251–259. doi: 10.1016/j.ultrasmedbio.2004.11.004. [DOI] [PubMed] [Google Scholar]
- 7.Varghese T, Zagzebski JA, Chen Q, Techavipoo U, Frank G, Johnson C, Wright A, Lee FT., Jr Ultrasound monitoring of temperature change during radiofrequency ablation: preliminary in-vivo results. Ultrasound in Med. and Biol. 2002;28:321 – 329. doi: 10.1016/s0301-5629(01)00519-1. [DOI] [PubMed] [Google Scholar]
- 8.Pernot M, Tanter M, Bercoff J, Waters K, Fink M. Temperature estimation using ultrasonic spatial compounding. IEEE Trans. Ultrason., Ferroelect., Freq. Contr. 2004;51(5):606–615. [PubMed] [Google Scholar]
- 9.Seip R, VanBaren P, Cain C, Ebbini ES. Non-invasive real-time multipoint temperature control for ultrasound phased array treatments. IEEE Trans. Ultrason., Ferroelect., Freq. Contr. 1996;43:1063–1073. [Google Scholar]
- 10.Nasiri Amini A, Ebbini ES, Georgiou T. Noninvasive estimation of tissue temperature via high-resolution spectral analysis techniques. IEEE Trans. Biomedical Engineering. 2005;52(2):221–228. doi: 10.1109/TBME.2004.840189. [DOI] [PubMed] [Google Scholar]
- 11. Martin Arthur R, Straube William L., Trobaugh Jason W., Moros Eduardo G. In vivo change in ultrasonic backscattered energy with temperature in motion-compensated images. International Journal of Hyperthermia. 2008;24(5):389–398. doi: 10.1080/02656730801942199. [DOI] [PubMed] [Google Scholar]
- 12.Clarke RL, Bush NL, Ter Haar GR. The changes in acoustic attenuation due to in vitro heating. Ultrasound in Med. and Biol. 2003;29:127135. doi: 10.1016/s0301-5629(02)00693-2. [DOI] [PubMed] [Google Scholar]
- 13.Techavipoo U, Varghese T, Chen Q, Stiles TA, Zagzebski JA, Frank GR. Temperature dependence of ultrasonic propagation speed and attenuation in excised canine liver tissue measured using transmitted and reected pulses. J. Acoust. Soc. Am. 2004;115:2859–2865. doi: 10.1121/1.1738453. [DOI] [PubMed] [Google Scholar]
- 14. Bayat M, Ballard JR, Ebbini ES. Ultrasound thermography in vivo: A new model for calculation of temperature change in the presence of temperature heterogeneity. Ultrasonics Symposium (IUS), 2013 IEEE International. July 2013. :116–119. [Google Scholar]
- 15.Simon C, VanBaren P, Ebbini ES. Motion compensation algorithm for non- invasive two-dimensional temperature estimation using diagnostic pulse-echo ultrasound. doi: 10.1109/58.710592. [DOI] [PubMed] [Google Scholar]
- 16.Daniels MJ, Varghese T. Dynamic frame selection for in vivo ultrasound temperature estimation during radiofrequency ablation. Phys. Med. Biol. 2010 Aug;55(16):4735–4753. doi: 10.1088/0031-9155/55/16/008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Liu D, Ballard JR, Haritonova A, Choi J, Bischof J, Ebbini ES. Real-time Monitoring of Thermal and Mechanical Tissue Response to Modulated Phased-array HIFU Beams In Vivo. Int Symp on Therapeutic Ultrasound. 2011;1481:227–232. [Google Scholar]
- 18.Ebbini ES. Noninvasive two-dimensional temperature imaging for guidance of thermal therapy. Int. Symp. Biomed. Imaging (ISBI) 2006:884–887. [Google Scholar]
- 19.Proakis JG, Rader CM, Ling F, Nikias CL, Moonen M, Proudler IK. Algorithms for Statistical Signal Processing. Printice-Hall; 2001. [Google Scholar]
- 20.Bayat M, Ballard JR, Ebbini ES. Ultrasound thermography: a new temperature reconstruction model and in-vivo results. International Symposium on Therapeutic Ultrasound (ISTU) 2014 Apr; [Google Scholar]
- 21.Duck FA. Physical Properties of Tissues. Academic Press; London: 1990. [Google Scholar]
- 22.Bayat M, Ballard JR, Ebbini ES. Adaptive motion compensation for in vivo ultrasound temperature estimation. Ultrasonics Symposium (IUS), 2013 IEEE International. 2013 Jul;:1797–1800. [Google Scholar]
- 23.Haykin Simon. Adaptive Filter Theory. Printice-Hall Information and System Science Series; 2002. [Google Scholar]
- 24.Nightingale KR, Palmeri ML, Nightingale RW, Trahey GE. On the feasibility of remote palpation using acoustic radiation force. J. Acoust. Soc. Am. 2001 Jul;110:625–634. doi: 10.1121/1.1378344. [DOI] [PubMed] [Google Scholar]
- 25.Casper AJ, Liu Dalong, Ballard JR, Ebbini ES. Real-time implementation of a dual-mode ultrasound array system: In vivo results. Biomedical Engineering, IEEE Transactions on. 2013 Oct;60(10):2751–2759. doi: 10.1109/TBME.2013.2264484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.NCRP Report no. 113: Exposure criteria for medical diagnostic ultrasound: I. criteria based on thermal mechanics. Tech. Rep., Natioanl Council on Radiation Protectin and Measurements. 1992 [Google Scholar]
- 27.Liu Dalong. Ph.D. thesis. University of Minnesota; 2010. Real-time Imaging of Thermal and Mechanical Tissue Response to Focused Ultrasound. [Google Scholar]


