Using Cross-Classified Multilevel Models to Disentangle School and Neighborhood Effects: An Example Focusing on Smoking Behaviors among Adolescents in the United States

Abstract

Background

Despite much interest in understanding the influence of contexts on health, most research has focused on one context at a time despite the reality that individuals have simultaneous memberships in multiple settings.

Method

Using the example of smoking behavior among adolescents in the National Longitudinal Study of Adolescent Health, we applied cross-classified multilevel modeling (CCMM) to examine fixed and random effects for schools and neighborhoods. We compared the CCMM results with those obtained from a traditional multilevel model (MLM) focused on either the school and neighborhood separately.

Results

In the MLMs, 5.2% of the variation in smoking was due to differences between neighborhoods (when schools were ignored) and 6.3% to differences between schools (when neighborhoods were ignored). However in the CCMM examining neighborhood and school variation simultaneously, the neighborhood-level variation was reduced to 0.4%.

Conclusion

Results suggest that using MLM, instead of CCMM, could lead to overestimating the importance of certain contexts and could ultimately lead to targeting interventions or policies to the wrong settings.

INTRODUCTION

There is much interest among epidemiologists in understanding multilevel phenomena, or how features of the physical and psychosocial environment in which individuals live, learn, work, and play influence individual health, disease, and behavior [1, 2]. The growth and interest in multilevel analyses has been facilitated by conceptual developments in multilevel theory [3–6] as well as statistical advancements in multilevel statistical modeling [7–10]. Although multilevel theory posits that multiple contexts (e.g., residential environments, schools, workplaces, hospitals, or other “areas”) influence individual and population health simultaneously, most empirical applications have studied contexts in isolation and the majority of studies have focused on neighborhoods. An emphasis on single contexts, and more specifically neighborhoods, is problematic for at least two reasons. First, it ignores the reality that individuals simultaneously belong to multiple settings that could each independently affect their health. For example, focusing on the influence of neighborhood factors on adolescent health behaviors ignores the influence of schools, which may be a more influential context in teens’ lives. Second, results from studies assessing a single context may be misleading, as the effect of one context can be over- or under-estimated depending on what context is ignored.

The objective of our study was to provide a methodological demonstration of cross-classified multilevel models (CCMM), also sometimes referred to as “multilevel cross-classified models, or ‘cross-classified random effect models”, in disentangling the role of two critical influences on adolescent tobacco use: schools and neighborhoods. CCMM allows researchers to incorporate non-hierarchical nesting structures, where individuals are simultaneously nested within multiple non-hierarchical settings. Thus, rather than modeling the effect of either the school or neighborhood setting, as would be done in a traditional two-level multilevel model (MLM), application of a CCMM enables researchers to simultaneously examine the fixed and random effects corresponding to the school and neighborhood settings. Simultaneous examination of schools and neighborhoods, in particular, is important because both settings can influence health behaviors through multiple pathways, including policies, normative behaviors, access to resources, and the like [11, 12]. In this paper, our intention was to provide a methodological demonstration of the CCMM method and show where and how results from a CCMM might deviate from a traditional multilevel model focused on a single context. A methodological application and applied example of CCMM is warranted, given the underrepresentation of CCMM in the epidemiology literature relative to MLM (see for example [13–19]).

Our demonstration proceeded in several steps. We first modeled our outcome using a traditional multilevel modeling (MLM) approach that included only one context (neighborhood or school) per model. In other words, we modeled the school as a random effect, ignoring the neighborhood in one MLM and then modeled the neighborhood as a random effect, ignoring the school in a second MLM. We then modeled tobacco use using CCMM, which simultaneously accounts for the influence of schools and neighborhoods. We compared both the fixed (i.e., population average effects) and random effects (i.e., variance in the outcome) in models assuming a two level hierarchy (MLM) versus those allowing for multiple non-hierarchical memberships (CCMM). The fixed effects we examined were individual-, school-, and neighborhood-level demographic indicators, including socioeconomic status and race/ethnicity. These fixed effect estimates are informative for determining the extent to which both the predictor of interest is associated with the outcome and the degree to which the predictor of interest reduces between-level variation. Finally, in our CCMM, we compared the relative variance contribution of schools and neighborhoods. By comparing variance contributions (i.e., random effects) across models, we are able to evaluate the extent to which inclusion of the fixed effect variables helped to explain the observed between-school and between-neighborhood variation in smoking.

To increase the use of CCMM, and make the processes of analyzing cross-classified data more transparent, we provide readers with instructions on how to implement the CCMM in MlwIN (refer to Technical Appendix: Part 1 online) and through MlwIN as implemented via STATA (refer to Technical Appendix: Part 2 online).

MATERIALS AND METHODS

Data

Data for the study came from the National Longitudinal Study of Adolescent Health (Add Health), a nationally representative school-based longitudinal survey focusing on the health and behavior of adolescents in middle and high school (grades 7–12; ages 12–18) who were first interviewed in 1994–1995 (Wave 1) [20]. To ensure selected schools were representative of US schools, researchers stratified schools by census region, urbanicity, size, type, and ethnic background of the student body (i.e., percent White) prior to systematic random sampling. From a sampling frame of 26,666 schools, investigators selected a sample of 80 high schools and 52 middle schools for participation. A systematic random sample of high schools along with feeder schools (i.e., middle schools whose students matriculate at the selected high school) was selected. A total of 134 schools (79%) participated. These schools represented the spectrum of schools available to U.S. students, including private schools requiring tuition, parochial or religious based schools, and free public schools of which there are schools of choice (i.e., any student can attend), magnet schools (i.e., schools that typically are available to students via an exam) and neighborhood schools. An in-school survey was completed by 90,118 students. A random sample of these 90,118 students (as well as all students who were eligible to complete the in-school survey, but were absent on the day of administration) were invited to complete a more detailed in-home interview. 20,745 students completed the in-home interview (over 75% of those asked to participate did so). In addition, 17,670 caregivers provided information at Wave 1. AddHealth was an appropriate dataset to use in the current analysis, as the sample was large and comprised individuals who attended distinct school units and lived in distinct residential neighborhoods (as defined by Census tracts, or the relatively stable, geographic groupings of between 1,200–8,000 people, which vary by size, that are created by the United States Census Bureau https://www.census.gov/geo/reference/gtc/gtc_ct.html; defining neighborhoods based on Census tracts is commonplace among studies in the United States) [6].

Our analyses are based on an analytic sample of 16,070 youth who attended 128 schools and lived in 2,111 census tracts. This analytic sample was derived after eliminating youth (n=660) in the non-nationally-representative sample (i.e., who attended schools sampled for genetic analyses) or from schools that did not provide demographic data. We also removed youth who were missing data on the outcome measure (n=139 excluded) or predictors and covariates (n=1,425). These 1,425 participants did not differ with respect to smoking behaviors from those who were included in our analysis with respect to age sex, race, or parental education. However, participants missing information about public assistance tended to be smokers (34% smokers compared to 26% with information on public assistance; p=0.002).

We restricted the analysis to youth who were white, black, or Hispanic, excluding 2,451 students of other races, given that students in other racial/ethnic groups were not sufficiently represented in Add Health to obtain robust group estimates (Native Americans n=104, <1%; Asians n=1,176, 6%; Other n=1,171, 6%). Although Add Health is a longitudinal study, we conducted a cross-sectional analysis because the majority of youth resided in the same neighborhood and school in Wave II as they did in Wave I, and because Wave III and Wave IV were conducted when most youth had graduated from high school and so were no longer uniformly in two different contexts.

Measures

Outcomes: Smoking

In the Wave 1 In-Home survey, youth reported the number of days in the past month they smoked cigarettes. We coded responses to this question into both a continuous (ranging from 1–30, i.e. the number of days in past month) and binary outcome variable (yes/no had ever smoked in the past month) based on previous studies [21, 22].

Predictors: Socioeconomic Status (SES)

SES was obtained at the individual, school, and neighborhood level. At the individual-level, SES was determined based on parent receipt of public assistance and parent education. We used data from either the youth or caregiver interview to capture receipt of public assistance (1=mother currently receiving public assistance, such as welfare; 0=not) and highest level of parent education (defined as the maximum level of education by the resident mother, resident father, or resident step-father/partner; 1=parent did not have at least a high school diploma or equivalent; 0=parent had completed high school/equivalent). At the school-level, we created a continuous measure of school-level SES using individual-level data. Use of individual-level data was required as information about school-level SES was not directly available. We calculated the proportion of students within each school whose mother had received public assistance or did not have a high school degree or equivalent. At the neighborhood level, we used data from the 1990 Census to create a neighborhood-level SES measure indicating the proportion of residents within each neighborhood who had received public assistance or did not have at least a high school degree or equivalent.

Covariates

Adjusted models included the following individual-level covariates: age (continuous), sex (male=0; female=1), and self-reported race/ethnicity (1=non-Hispanic white; 2=non-Hispanic black; 3=Hispanic). We also adjusted for the percentage of students in either the school or the neighborhood who were white.

Analysis

We fit three sets of models in the current analysis. The first two models used a traditional two-level multilevel model. As described in detail elsewhere [7–10], the traditional multilevel model assumes a two-level multilevel data structure, where observations are hierarchically nested, such that members of the lower level (i.e., level one) are nested in one and only one entity at the higher level (i.e., level two). Thus, we began by fitting a two-level “school only” multilevel model (ignoring the neighborhood), where the outcome (denoted y) for a person (denoted i) nested in a given school (denoted j) was modeled as:

$${\mathrm{y}}_{\mathrm{ij}}={\beta }_0+{\beta }_{\mathrm{xij}}+{\mathrm{u}}_{0\mathrm{j}}+{\mathrm{e}}_{0\mathrm{ij}}$$ Equation 1

In Equation 1, the fixed effect parameter β₀ refers to the overall mean outcome y across all schools and β_xij refers to a vector of individual-level covariates. The random effect parameter u_oj refers to the random effect for school (assumed to be normally distributed with a mean of 0 and variance ${\sigma }_{\mathit{uo}}^2$), and e_oij refers to the random effect for the individual.

Second, we ran a two-level “neighborhood only” multilevel model (ignoring school), where the outcome (denoted y) for a person (denoted i) nested in a given neighborhood (denoted k) was modeled as:

$${\mathrm{y}}_{\mathrm{ik}}={\beta }_0+{\beta }_{\mathrm{xik}}+{\mathrm{u}}_{0\mathrm{k}}+{\mathrm{e}}_{0\mathrm{ik}}$$ Equation 2

The fixed and random effect parameters in Equation 2 have an identical interpretation as Equation 1, except they now refer to neighborhoods (instead of schools). Though the two-level multilevel modeling strategy marks a significant advancement over traditional regression models in which context is ignored, it is not flexible enough to accommodate multiple non-nested contexts at once.

The third model we fit was the CCMM. In a CCMM, individuals (denoted i) simultaneously belong to two non-nested contexts, here school (denoted j) and neighborhood (denoted k). Thus our outcome (denoted y) for a person i nested in school j and neighborhood k is modeled as:

$${\mathrm{y}}_{\mathrm{i}(\mathrm{jk})}={\beta }_0+{\mathrm{u}}_{0\mathrm{j}}+{\mathrm{u}}_{0\mathrm{k}}+{\mathrm{e}}_{0\mathrm{i}(\mathrm{j}\mathrm{k})}$$ Equation 3

In Equation 3, which presents a null or intercept-only CCMM (i.e., a model without covariates), the fixed effect parameter, β₀, refers to the overall mean outcome y across all schools and neighborhoods, u_oj refers to the random effect for schools, u_ok refers to the random effect for the neighborhood, and e_oi(jk) refers to the random effect for the individual with the combination of j school and k neighborhood. Like a traditional multilevel model, the CCMM variance parameters are assumed to be independent of each other and normally distributed, with a mean of 0 and variance that is estimated (i.e., ${\sigma }_{\mathit{uo}}^2$).

This CCMM null model can be extended to include predictors or covariates (i.e., fixed effects) at each level of analysis. For example, we included two indicators of SES; the first was a measure of receipt of public assistance at the individual ( ${\beta }_{1_{\mathit{oi}(\mathit{jk})}}$), school ( ${\beta }_{2_{\mathit{oj}}}$), and neighborhood-level ( ${\beta }_{3_{\mathit{ok}}}$):

$${\mathrm{y}}_{\mathrm{i}(\mathrm{jk})}={\mathrm{\beta }}_0+{\mathrm{\beta }}_{1_{\mathrm{oi}(\mathrm{jk})}}+{\mathrm{\beta }}_{2_{\mathrm{oj}}}+{\mathrm{\beta }}_{3_{\mathrm{ok}}}+{\mathrm{u}}_{\mathrm{oj}}+{\mathrm{u}}_{\mathrm{ok}}+{\mathrm{e}}_{\mathrm{oi}(\mathrm{jk})}$$ Equation 4

The parameters in Equation 4 are interpreted differently than Equation 1. For example, ${\beta }_{2_{\mathit{oj}}}$refers to the average effect of school-level parent receipt of public assistance controlling for individual and neighborhood parent receipt of public assistance, and ${\beta }_{3_{\mathit{ok}}}$refers to the average effect of neighborhood-level parent receipt of public assistance controlling for individual and school parent receipt of public assistance. The interpretation of each random effect parameter is the same, except each estimate now controls for the parent receipt of public assistance predictors in the model.

Our analyses proceeded in three steps. First, to partition the variance in number of days smoked into within and between components and estimate an intraclass correlation coefficient (ICC; i.e., the proportion of variation in the outcome that was due to differences across schools and neighborhoods, rather than differences across students), we estimated a null model for each model type: school-only multilevel model (Equation 1), neighborhood-only multilevel model (Equation 2), and the CCMM (Equation 3) (Table 2, Model 1). These ICC estimates were obtained for the school-only multilevel model, neighborhood-only multilevel model, and CCMM. The ICCs in the school-only and neighborhood-only multilevel model were generated by dividing the between-level random effect by the total variance. In the CCMM, we calculated ICCs for the school and neighborhood level, which are referred to as the intra-neighborhood (i.e., correlation in outcome between two youth who live in the same neighborhood, but attend different schools; this was calculated by dividing the neighborhood-level random effect by the total variance, or the sum of the three variance components) and intra-school correlation coefficient (i.e., correlation in outcome between two youth who attend the same school, but live in different neighborhoods; this was calculated by dividing the school-level random effect by the total variance). We also calculated an intracell correlation, referring to the correlation in outcome of two students who live in the same neighborhood and attend the same school; this was calculated by summing the between-level variances, i.e., for the neighborhood and school, by the total variance. Subsequently, we estimated a model that contained individual-level predictors and covariates (Model 2). By including these individual-level variables, we were able to evaluate the extent to which the between-level variance estimates (i.e., random effect parameters) could be explained by the observed individual characteristics across schools and neighborhoods. We then fit a school-only model and CCMM containing individual-level variables as well as the school-level measures of SES and race/ethnicity (Model 3) and a neighborhood-only model and CCMM containing individual-level variables combined with the neighborhood-level measures of SES and race/ethnicity (Model 4). Finally, we fit a CCMM containing all individual-, school-, and neighborhood-level variables (Model 5).

Table 2.

Nested Models Describing Association between Predictors and Number of Days Smoked in the Past 30 Days in the National Longitudinal Study of Adolescent Health (N=16,070)

	Model 1			Model 2
Fixed Effect Estimates	School Only	Neighborhood Only	Cross-Classified	School Only	Neighborhood Only	Cross-Classified
Intercept (SE)	3.8 (0.23)	3.94 (0.11)	3.88 (0.22)	−6.94 (0.84)	−7.42 (0.73)	−6.91 (0.84)
Individual-level
Age				0.80 (0.70, 0.90)	0.85 (0.76, 0.93)	0.80 (0.70, 0.90)
Female				0.06 (−0.22, 0.34)	0.02 (−0.26, 0.30)	0.06 (−0.22, 0.34)
Public Assistance				0.76 (0.27, 1.25)	0.84 (0.34, 1.34)	0.74 (0.26, 1.24)
High School degree				−0.21 (−0.66, 0.25)	−0.15 (−0.62, 0.29)	−0.21 (−0.67, 0.23)
Race
White				Ref	Ref	Ref
Black				−4.28 (−4.73, −3.86)	−4.57 (−4.96, −4.16)	−4.29 (−4.71, −3.86)
Hispanic				−1.98 (−2.49, −1.48)	−2.86 (−3.32, −2.38)	−1.99 (−2.50, −1.48)
School-level
Public Assistance
High School Degree
Percent White
Neighborhood-level
Public Assistance
High School Degree
Percent White
Random Effect Estimates
U3 neighborhood (SE)		4.58 (3.66, 5.65)*	0.46 (0.13, 0.88)*		1.59 (1.03, 2.26)*	0.24 (0.06, 0.61)*
U2 school (SE)	5.44 (4.04, 7.19)*		5.36 (3.95, 7.07)*	2.12 (1.48, 2.97)*		2.08 (1.42, 2.92)*
U1 individual (SE)	83.1 (81.3, 85.0)*	84.0 (82.1, 85.9)*	82.7 (80.9, 84.6)*	80.7 (79.0, 82.5)*	81.1 (79.3, 83.0)*	80.5 (78.8, 82.3)*
Fit Statistics
DIC	–	–	116736	–	–	116259

Model 1 presents the results for a null model (i.e., no covariates) for each model type: school-only multilevel model, neighborhood-only multilevel model, and the cross-classified multilevel model. Model 2 presents the same models as Model 1, except Model 2 includes individual-level predictors and covariates. For the fixed effect estimates, cell entries are parameter (beta) estimates and credible intervals. The intercept is presented as parameter estimate and standard error (SE). Random effects are presented as estimate and credible intervals. DIC refers to Deviance Information Criterion, a measure of model fit and complexity and is only reported for the cross-classified models.

Significant random effects are indicated by

^*(p<0.05).

All analyses were conducted in MLwiN version 2.29 via Stata version 13 (College Station, TX) with Bayesian estimation procedures as implemented via Markov Chain Monte Carlo (MCMC) methods using Metropolis-Hastings algorithm [23]. We used a Bayesian estimation procedure with non-informative priors, because others have shown that estimates of random effects in binary models using maximum-likelihood procedures tend to be biased [24] and computationally intensive [25] and that MCMC is preferable when two sets of random effects are estimated, when there is concern about the correlation between random effects, and when there are some instances of a small number of individuals per cluster. Model fit was evaluated using the Deviance Information Criterion (DIC), which is a test statistic produced by the MCMC procedure that refers to the model complexity and “badness of fit” [26]. Higher DIC values indicate a poorer fitting model. We calculated a linear regression for the continuous outcome and a logistic regression for the binary smoking variable; no other link functions (e.g., log) were available in MlwiN. Parameter estimates (betas or odds ratios, OR) and 95% credible intervals (CI, which are the confidence intervals generated using Bayesian procedures) are presented for fixed and random effect parameters. We examined residual plots at each level of analysis to evaluate model diagnostics on the variance parameter; this enabled us to test model assumptions, detect outliers and influence points on model fit. Analyses were conducted using unweighted data, as weighting techniques for cross-classified methods have not been established [9]. A non-weighted analysis is also appropriate as our emphasis was on tests of association, rather than deriving nationally representative estimates, and we adjusted our analyses for sample characteristics and thus reduced the heterogeneity in the sample [27].

RESULTS

The AddHealth data were well-suited to cross-classified analyses. An average of 125.5 (sd=116.5) youth per school completed an In-Home survey (minimum=18; maximum=1,012). In each neighborhood, an average of 7.6 (sd=18.5) youth completed an In-Home survey (minimum=1; maximum=260). There were 970 (of 2,111) census tracts that contained only one youth respondent. There was an average of 20.2 (sd=22.0) census tracts per school (minimum=1; maximum=175), an average of 1.22 (sd=0.42) schools per census tract (minimum=1; maximum=3), and 2,584 different combinations of school and neighborhood contexts. Thus, there was no clear hierarchical nesting of schools within neighborhoods (or vice versa).

Table 1 presents descriptive statistics on individuals in the total sample as well as by smoking status. 26% of youth (n=4,162) smoked at least once in the past month, with smokers reporting smoking an average of 16.2 days per month (sd=12.3). The sample was balanced in terms of sex (49% male). The majority of participants were white (58%) and were in mid-adolescence (mean age=15.6; sd=1.7). Parent SES was relatively high, as only 10% of mothers were currently receiving public assistance and only 13% had less than a high school education. Smokers were more likely than non-smokers to be white (p<0.001), older in age; p<0.001), and have a parent without at least a high school degree (p=0.05). No differences were found when comparing smokers to non-smokers by sex or receipt of public assistance. Among smokers, whites reported smoking more days than either Blacks or Hispanics (p<0.001) as did those whose parent did not receive public assistance (p=0.005) and who were older (p<0.0001).

Table 1.

Descriptive Statistics on Individuals (n=16,070) in the National Longitudinal Study of Adolescent Health (AddHealth)

Demographic Characteristics	Total Sample (n=16,070)	Non-Smokers 11,908 (74%)	Smokers 4,162 (26%)	p-value†	Number of Days Smoked Median (IQR)	p-value††
Child Sex
Male	7,948 (49%)	5,847 (49%)	2,101 (50%)	0.13	15.0 (27.0)	0.74
Female	8,122 (51%)	6,061 (51%)	2,061 (50%)		15.0 (27.0)
Mother Received Public Assistance
No	14,502 (90%)	10,753 (90%)	3,749 (90%)	0.68	15.0 (27.0)	0.005
Yes	1,568 (10%)	1,155 (10%)	413 (10%)		10.0 (28.0)
Parent Obtained High School Degree
No	2,120 (13%)	1,608 (14%)	512 (12%)	0.05	12.0 (28.0)	0.31
Yes	13,950 (87%)	10,300 (86%)	3,650 (88%)		15.0 (27.0)
Child Race
White	9,387 (58%)	6,304 (53%)	3,083 (74%)	<.0001	20.0 (26.0)	<.0001
Black	3,817 (24%)	3,348 (28%)	469 (11%)		4.0 (12.0)
Hispanic	2,866 (18%)	2,256 (19%)	610 (15%)		10.0 (27.0)
Child Age
11–13	2,299 (14%)	1,991 (17%)	308 (7%)	<.0001	5.0 (18.0)	<.0001
14–16	8,352 (52%)	6,194 (52%)	2,158 (52%)		15.0 (27.0)
17+	5,419 (34%)	3,723 (31%)	1,696 (41%)		20.0 (25.0)

Cell entries are reported as n (%) comparing smokers to non-smokers. Number of days smoked among those who smoke within demographic groups is reported as median interquartile range (IQR) due to the bimodal distribution.

^†Chi-square tests or t-test where appropriate comparing smokers to non-smokers within demographic groups.

^††Wilcoxon rank-sum test or Kruskal-Wallis test where appropriate comparing median number of days reporting smoking across demographic groups.

^†††Child Age is presented here as categories, however, it was modeled as a continuous variable in our models.

The schools and neighborhoods in this sample were diverse. Schools varied significantly with respect to their SES. Across the 128 schools, the average percentage of students whose mothers had received public assistance was 10.4% (sd=9.4; minimum=0; maximum=45.4%), the average percentage whose parents did not have at least a high school education was 11.5% (sd=10.4; minimum=0%; maximum=55.8%) and the average percentage reporting White race was 47.5% (sd=25.5; minimum=0%; maximum=85.9%). Similarly, across the 2,111 neighborhoods, the average percentage of students whose mothers had received public assistance was 10.8% (sd=10.0; minimum=0; maximum=67.5%), the average percentage of residents without at least a high school education was 29.2% (sd=16.1; minimum=0%; maximum=78.7%) and the average percentage reporting white race was 66.6% (sd=33.3; minimum=0%; maximum=100%). The average number of days smoked (school mean=3.73; sd=2.50; neighborhood mean=3.76; sd=7.15) and percentage of respondents who were considered smokers (school mean=23.9%; sd=11.0; neighborhood mean=23.4%; sd=33.6) was similar across neighborhoods and schools. However, as shown in Figure 1 and Figure 2, there was considerable variability within and between these contexts with respect to youth smoking. For example, in some neighborhoods almost 80% of youth were smokers, whereas in others 0% were smokers (Figure 2). Moreover, as shown in Figure 3, schools differed with respect to both the average number of days youth smoked and the variability (minimum and maximum) in numbers of days smoked. Thus, smoking behaviors were not uniform, but rather varied as a result of neighborhood or school context.

Figure 1. Distribution of the Number of Days Reported Smoking in the Past 30 Days Across Schools (N=128) and Neighborhoods (N=2,111 neighborhoods).

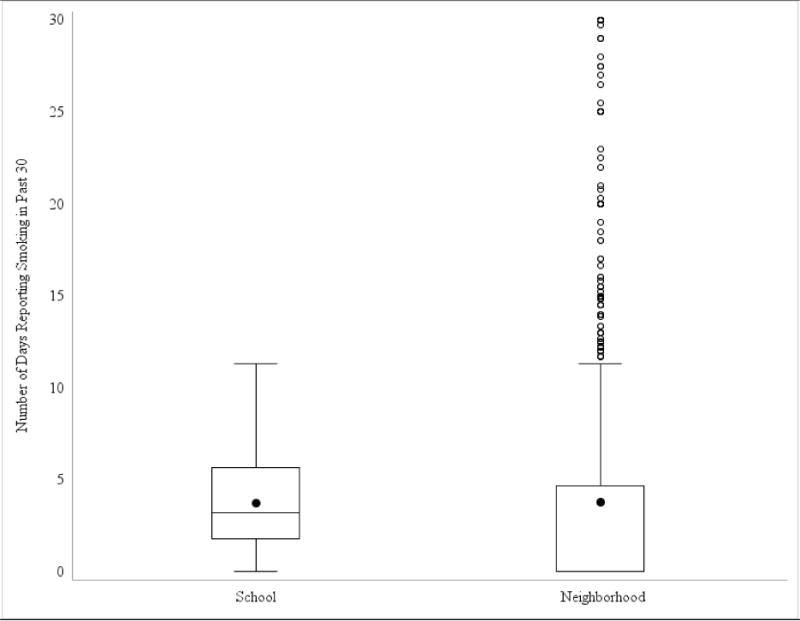
Box plots are presented depicting the number of days youth reported smoking in the past 30 across all schools and neighborhoods. The solid colored dot represents the mean. Horizontal lines in the boxes represent the first quartile, the median, and the third quartile of the distribution of smoking values. Vertical lines depict the 1.5 times the interquartile range of smoking for each school or neighborhood in the sample. Dots outside depict outlying values. The large number of outliers for neighborhoods was due largely to the neighborhoods including only a small number of respondents.

Figure 2. Distribution of the Proportion of Youth Reporting Smoking in the Past 30 Days Across Schools (N=128) and Neighborhoods (N=2,111 neighborhoods).

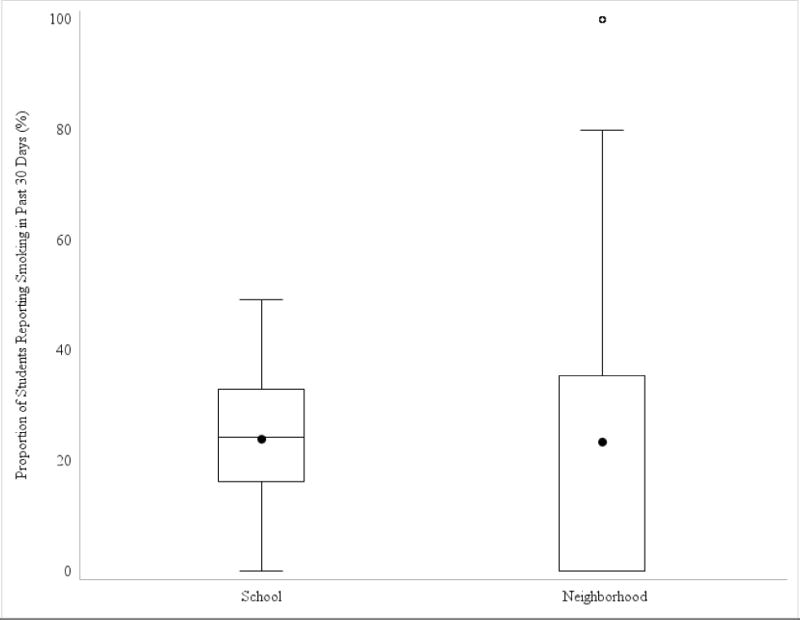
Box plots are presented depicting the proportion of youth reporting smoking in the past 30 across all schools and neighborhoods. The solid colored dot represents the mean. Horizontal lines in the boxes represent the first quartile, the median, and the third quartile of the distribution of smoking values. Vertical lines depict the 1.5 times the interquartile range of smoking for each school or neighborhood in the sample. Dots outside depict outlying values.

Figure 3. Distribution of the Number of Days Youth Reported Smoking in the Past 30 Within and Between Schools (N=128 schools).

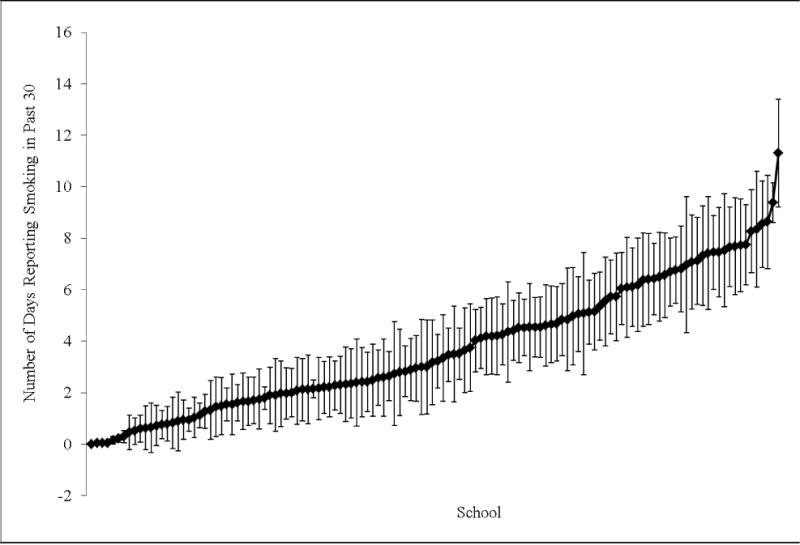
Dots represent the mean number of days youth reported smoking within each school. 95% bounds around the mean based on the standard deviation (SD) of number of days smoked are also presented. Values are sorted from left to right by lowest school mean. 95% confidence intervals may extend into the negative range when the mean smoking days within a school is not significantly different from zero.

The data were also well suited to cross-classified analyses based on the observed differences in contexts youth experienced. That is, youth did not always attend schools that reflected the demographic makeup of their neighborhoods. Though there were moderate to high correlations between school and neighborhood demographic characteristics (r=0.556; p<0.0001 for school and neighborhood percent receiving public assistance; r=0.587; p<0.001 for school and neighborhood parental education; r=0.705; p<0.001 for school and neighborhood percent of population identified as white), the correlations varied across these indicators and provided evidence of some discordance between the neighborhood and school. Indeed, after dichotomizing the public assistance measure to differentiate poor schools and neighborhoods from non-poor schools and neighborhoods (using a cut-point of 10% of more of the population receiving public assistance to denote a high poverty setting, similar to previous studies [28]), we found close to one-quarter of all youth lived in incongruent settings. That is, 13.7% (n=2.200) of youth lived in a low poverty neighborhood, but attended a high poverty school and 10% (n=1.645) lived in a high poverty neighborhood, but attended a low poverty school. A McNemar’s chi-square test of the agreement between the neighborhood and school poverty measures was significant (chi-square 80.1; P<0.0001), indicating that there was not perfect agreement between school and neighborhood poverty.

Multilevel models with smoking as continuous outcome

Table 2 and Table 3 present the results of a series of models for the school-only multilevel model, neighborhood-only multilevel model, and the CCMM predicting the number of days smoked. In our null model (Table 2, Model 1), the random effects for the school-only ( ${\sigma }_{u0j}^2$=5.44) and neighborhood-only model ( ${\sigma }_{u0k}^2$=4.58) were similar. However, in the CCMM, the between-level variance in smoking was driven largely by the school ( ${\sigma }_{u0j}^2$=5.36) and not by the neighborhood ( ${\sigma }_{u0k}^2$=0.46). Comparable ICC values were obtained for the school-only (6.1%) and neighborhood-only multilevel model (5.2%), indicating that the majority of the variability was attributable to individual characteristics. In the CCMM, the intra-neighborhood correlation was 0.52% and the intra-school correlation was 6.1%. Finally, the intracell correlation coefficient, or the correlation in smoking behavior between two youth who live in the same neighborhood and attend the same school, was 6.5%.

Table 3.

Nested Models Describing Association Between Predictors and Number of Days Smoked in the Past 30 Days in the National Longitudinal Study of Adolescent Health (N=16,070)

	Model 3		Model 4		Model 5
Fixed Effect Estimates	School Only	Cross-Classified	Neighborhood Only	Cross-Classified	Cross-Classified
Intercept (SE)	−8.26 (0.96)	−8.24 (0.97)	−8.62 (0.86)	−7.67 (1.02)	−8.43 (1.04)
Individual-level
Age	0.81 (0.71, 0.91)	0.81 (0.71, 0.91)	0.85 (0.76, 0.93)	0.80 (0.70, 0.90)	0.81 (0.72, 0.91)
Female	0.07 (−0.20, 0.34)	0.06 (−0.22, 0.34)	0.02 (−0.25, 0.3)	0.06 (−0.22, 0.34)	0.06 (−0.21, 0.34)
Public Assistance	0.70 (0.20, 1.18)	0.69 (0.19, 1.20)	0.81 (0.31, 1.31)	0.72 (0.22, 1.23)	0.68 (0.19, 1.18)
High School degree	−0.24 (−0.69, 0.21)	−0.24 (−0.69, 0.22)	−0.19 (−0.64, 0.29)	−0.19 (−0.64, 0.28)	−0.21 (−0.68, 0.24)
Race
White	Ref	Ref	Ref	Ref	Ref
Black	−4.10 (−4.55, −3.64)	−4.11 (−4.56, −3.63)	−4.19 (−4.70, −3.7)	−4.20 (−4.72, −3.68)	−4.11 (−4.63, −3.61)
Hispanic	−1.81 (−2.33, −1.29)	−1.80 (−2.32, −1.27)	−2.71 (−3.18, −2.24)	−2.00 (−2.51, −1.48)	−1.83 (−2.36, −1.30)
School-level
Public Assistance	0.07 (0.02, 0.12)	0.07 (0.02, 0.12)			0.07 (0.02, 0.12)
High School Degree	−0.04 (−0.08, 0.01)	−0.04 (−0.08, 0.004)			−0.04 (−0.09, 0.0001)
Percent White	0.02 (0.003, 0.03)	0.02 (0.003, 0.03)			0.02 (0.002, 0.03)
Neighborhood-level
Public Assistance			0.03 (−0.01, 0.06)	0.01 (−0.03, 0.05)	−0.005 (−0.04, 0.03)
High School Degree			−0.01 (−0.02, 0.01)	0.01 (−0.01, 0.03)	0.01 (−0.01, 0.03)
Percent White			0.01 (0.004, 0.02)	0.01 (−0.005, 0.02)	0.0002 (−0.01, 0.01)
Random Effect Estimates
U3 neighborhood (SE)		0.17 (0.04, 0.42)*	1.52 (0.96, 2.18)*	0.16 (0.03, 0.37)*	0.25 (0.05, 0.52)*
U2 school (SE)	1.83 (1.22, 2.64)*	1.78 (1.15, 2.59)*		2.06 (1.39, 2.91)*	1.71 (1.10, 2.48)*
U1 individual (SE)	80.7 (79.0, 82.5)*	80.6 (78.8, 82.3)*	81.1 (79.3, 83.0)*	80.6 (78.8, 82.3)*	80.5 (78.8, 82.3)*
Fit Statistics
DIC	–	116258	–	116261	116265

Model 3 presents the results of the school-only multilevel model and CCMM containing individual-level variables as well as the school-level measure of SES and race/ethnicity. Model 4 presents the results of the neighborhood-only multilevel model and CCMM containing individual-level variables combined with the neighborhood-level measure of SES and race/ethnicity. Model 5 presents the results of a CCMM containing all individual-, school-, and neighborhood-level variables. For the fixed effect estimates, cell entries are parameter (beta) estimates and credible intervals. The intercept is presented as parameter estimate and standard error (SE). Random effects are presented as estimate and credible intervals. DIC refers to Deviance Information Criterion, a measure of model fit and complexity and is only reported for the cross-classified models.

Significant random effects are indicated by

^*(p<0.05).

When individual-level covariates were added to these three models (Table 2, Model 2), the between-level variance declined by more than half relative to Model 1 (school-only ${\sigma }_{u0j}^2$=2.12; neighborhood only ${\sigma }_{u0k}^2$=1.59; and CCMM ( ${\sigma }_{u0j}^2$=0.24; ${\sigma }_{u0k}^2$=2.08). This decline suggests that the between-level variation in smoking was due largely to the observed individual characteristics across schools and neighborhoods.

Model 3 (see Table 3) introduced school-level SES indicators and covariates into the school-only multilevel model and CCMM. When these school-level variables were added, the school-level variance declined slightly compared to Model 2 for both the school-only ( ${\sigma }_{u0j}^2$=1.83 from 2.12) and CCMM ( ${\sigma }_{u0j}^2$=1.78 from 2.08). The neighborhood-level variance in the CCMM of Model 3 decreased slightly relative to the CCMM in Model 2 ( ${\sigma }_{u0k}^2$=0.17 from 0.24). There was a modest association detected between the percentage of students in the school whose mother had received public assistance and number of cigarettes smoked in the school-only (β=0.07) or CCMM (β=0.07). There was no association detected between the percentage of students whose parents did not have a high school degree in the school-only multilevel model (β=−0.04) or CCMM (β=−0.04). There was also a very small association for the percentage of students who were white in the school-only multilevel (β=0.02) or CCMM (β=0.02).

Model 4 (see Table 3) introduced neighborhood-level SES indicators and covariates into the neighborhood-only multilevel model and CCMM. Adding these variables led to a slight decrease in neighborhood-level variance for the neighborhood-only multilevel model ( ${\sigma }_{u0k}^2$=1.52 from 1.59) and a larger decrease in the CCMM ( ${\sigma }_{u0k}^2$=0.16 from 0.24). The school-level variance in the CCMM of Model 4 was nearly identical ( ${\sigma }_{u0j}^2$=2.06 compared to 2.08). Neighborhood-level values of public assistance were not associated with number of cigarettes smoked for either the neighborhood-only (β=0.03) or CCMM (β=0.01), nor were neighborhood values for residents without a high school degree for either the neighborhood-only (β=−0.01) or CCMM (β=0.01), or percentage white for either the neighborhood-only (β=0.01) or CCMM (β=0.01).

Results of Model 5 (see Table 3), which introduced both school- and neighborhood-level SES indicators and covariates into the CCMM, showed that the neighborhood-level variance increased compared to Model 4 ( ${\sigma }_{u0k}^2$=0.25 from 0.16). The school-level variance declined slightly compared to Model 4 ( ${\sigma }_{u0j}^2$=1.71 from 2.06). Modest associations between school-level public assistance (β=0.07) and percentage white (β=0.02) persisted, as did the lack of association between any of the neighborhood-level indicators.

Post-hoc evaluation of these models suggested the results were robust. With the exception of the neighborhood random effect estimates, all other standard errors were small relative to the parameter estimates, suggesting the variances were estimated with a good level of precision. However, the standard errors for the variance components were inflated in the multilevel models in particular. The fixed effect estimates were similar between the CCMM and multilevel models. Residual plots suggested that the model assumptions were not violated in our final model.

Multilevel models with smoking as binary outcome

Web Table 1 and Web Table 2 present the results of models with smoking as a binary outcome. The same overall conclusions can be drawn from these models as the models focusing on the outcome for number of days reported smoking. Figure 4 presents the variance estimates at the school- and neighborhood-level for the school-only multilevel model, neighborhood-only multilevel model, and CCMM predicting odds of smoking. As seen in this Figure, the school- (Model 3) and neighborhood-only multilevel models (Model 4) both identify a modest degree of between-level variation. In other words, the school-level multilevel model suggests there is a significant degree of between-school variation in the odds of smoking, while the neighborhood-level multilevel model suggests there is a significant degree of between-neighborhood variation in the odds of smoking. However, the results of the CCMM (Model 5) suggest that the between-level variation in smoking is driven primarily by school-level variation and not neighborhood-level variation.

Figure 4. Variance Estimates at the School- and Neighborhood-level for the School-only Multilevel Model, Neighborhood-only Multilevel Model, and Cross-Classified Multilevel Model Predicting Odds of Smoking.

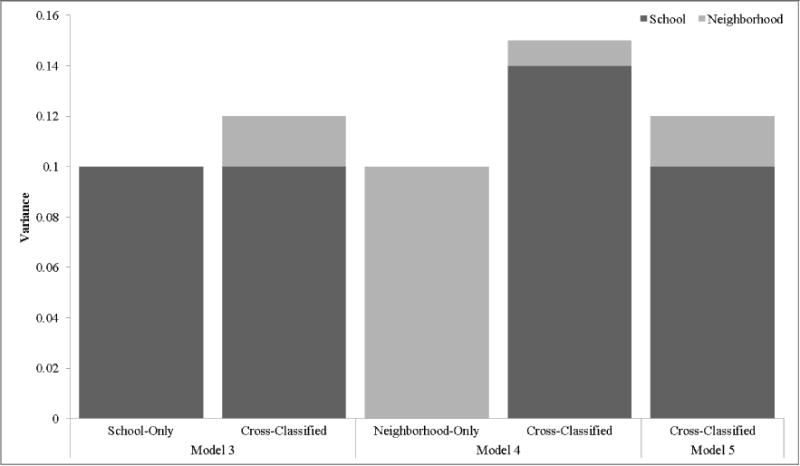
Model 3 includes individual-level covariates as well as school-level SES indicators and covariates. Model 4 includes neighborhood-level covariates as well as neighborhood-level SES indicators and covariates. Model 5 includes individual-level, school-level, and neighborhood-level SES indicators and covariates. All variance estimates shown were statistically significant with the exception of the neighborhood effect in cross-classified Models 3 and 4.

Sensitivity Analysis

We ran a sensitivity analysis to address possible concerns regarding the distribution of students in schools versus neighborhoods. Using Model 5 for both outcomes, we evaluated whether similar results would be obtained if we included an indicator variable adjusting for the number of youth in each neighborhood (0=included more than 1 respondent; 1=included only one respondent). This allowed us to determine whether the neighborhoods with only one respondent (n=970) had a different effect on smoking relative to the neighborhoods that contained a greater number of respondents. As shown in Web Table 3, there was no relationship between the indicator variable and either the continuous (β=0.44; CI=−0.17, 1.05) or binary smoking outcome (OR=1.06; CI=0.89, 1.24). Fixed and random effect parameters in the models including the indicator variable were also nearly identical to the final CCMM. These findings suggest our results were not influenced by one-respondent neighborhoods.

DISCUSSION

This paper demonstrated the value of cross-classified multilevel models (CCMM) to ascertain the quantitative importance of more than one context simultaneously. One very salient finding emerged from the current study. We found that two-level multilevel models that do not account for other non-nested contexts in which individuals are embedded can produce misleading results. In the current case, which focused on adolescent smoking, we found that the role of neighborhoods was overestimated. Specifically, the two-level multilevel model that examined neighborhoods without considering schools suggested that 5.2% of the variation in smoking was due to differences between neighborhoods. However, the neighborhood variation was reduced to 0.52% after running a CCMM that considered the role of schools. Thus, had we estimated only a neighborhood-level multilevel model, and not estimated a CCMM that accounted for the random effect of both schools and neighborhoods, we would have misattributed more of the variance in smoking to neighborhoods and missed the contribution of schools. These results are consistent with previous studies, which have found that failing to account for cross-classified data structures will produce biased variance estimates, such that the variance associated with the omitted level (e.g., school) will be attributed to the included level (e.g., neighborhood) [29]. Model misspecification will be most problematic when there is substantial between-level variation in the higher level unit that is omitted [30] and when the two higher-level units are independent [29].

Results from our methodological demonstration of CCMM should be evaluated in light of several limitations. First, the analyses are based on a nationally-representative sample of adolescents drawn from a study that selected youth using school-based sampling. As a result, the number of individuals per neighborhood was smaller than the number of individuals per school, with some neighborhoods only having one respondent. The fact that we did observe meaningful cross-classification of neighborhood and school units, combined with the finding that there was significant neighborhood-level variation in smoking to be explained in the two-level multilevel model, suggests that data sparseness was likely not an issue here. While it is possible our results reflect the greater number of individuals per school rather than neighborhood, we think this is unlikely, as preliminary analyses we conducted in Add Health using CCMM to examine other health outcomes did find meaningful effects for neighborhoods (results available from the author). However, future research should conduct simulation work and also use the CCMM framework in neighborhood-based studies to evaluate the degree to which sampling methods contribute to these findings.

Second, AddHealth Wave 1 data were also collected more than a decade ago. Although these data may be considered old, AddHealth remains the only nationally-representative sample of adolescents in the US and one of very few in which school and neighborhood level data are available. AddHealth was therefore an appropriate dataset to demonstrate the value of the CCMM framework. Third, we did not complete a detailed investigation into the predictors of smoking, as our example was intended to be a methodological and practical illustration of the CCMM. Inclusion of other potentially relevant factors, when modeled as fixed effects, such as smoking-related policies, measures of social cohesion, will be important for shedding light on the determinants of smoking behavior as well as the between-school and between-neighborhood differences in smoking. Fourth, there are limitations with using Census tracts to define neighborhoods. Although Census Tracts are an imperfect measure to define neighborhoods, they are most commonly used in multilevel research [6]. Future studies should expand upon traditional boundaries of neighborhood to focus on other aspects of the residential environment (e.g., activity spaces; neighborhoods as defined by residents rather than administrative datasets). Finally, our school-level measures of socioeconomic status are limited in that they were aggregated directly from individual-level data. This may be problematic, particularly as our measure of public assistance was based on whether mothers’ (and not fathers’) reported receiving assistance. Though a common approach in multilevel research [6], future studies should use administrative or school-level data when available in order to avoid the concerns about the indicators being a reflection of the students in the sample.

What implications can be drawn from our findings? First, our results emphasize the need to extend current analytic approaches from the basic multilevel model to examine cross-classification. Although there have been some studies using CCMM (see for example [13–19]), the CCMM method is not being used nearly as much as it should be, most likely due to a lack of applied examples. Greater use of CCMM in epidemiology is highly plausible, given the fact that many epidemiological studies collect data in a way that support investigation of cross classification.

Second, our results suggest that given the observed differences in results between the multilevel models and CCMM, scrutiny may be needed to evaluate the strength of prior epidemiological studies on the social determinants of health focusing solely on one context. In the AddHealth sample alone, the majority of studies have examined the role of neighborhoods on adolescent smoking, with much fewer focusing on schools. No studies that we are aware of have used CCMM applied to smoking in AddHealth. How should we interpret this extant research in light of our findings? Although much more research is needed, results of the current study reveal that it is possible that the fixed and random effects identified in previous studies are misleading. We think this is a possibility as even our null CCMM, which did not include any predictors at all, found that the variance attributed to smoking for neighborhoods and schools differed from the conclusions that would have been reached using a traditional MLM, where only one random effect was modeled.

The reasons why CCMM has not been widely are unclear. However, what is known is that few studies have tried to explicitly disentangle the role of one context from another, including neighborhoods and schools [31]. Considerably more work in this area is needed, particularly to help guide the investment of limited public health resources. Without having clear data showing that one context is more important than another (or that both are equally important), the field runs the risk of implementing misguided policies and interventions to contexts that may not be capable of having large effects on reducing health risk and promoting health outcomes.

In summary, this paper provides a framework that we hope will spark more critical evaluations of multilevel analyses that do not account for other potentially relevant contexts. The CCMM methods described here can be extended to many other health outcomes, and at other stages in the lifecourse, to evaluate the role of social contexts on health and ultimately lead to the development of interventions to improve population-level health.