Direct estimation of differential networks

Abstract

It is often of interest to understand how the structure of a genetic network differs between two conditions. In this paper, each condition-specific network is modeled using the precision matrix of a multivariate normal random vector, and a method is proposed to directly estimate the difference of the precision matrices. In contrast to other approaches, such as separate or joint estimation of the individual matrices, direct estimation does not require those matrices to be sparse, and thus can allow the individual networks to contain hub nodes. Under the assumption that the true differential network is sparse, the direct estimator is shown to be consistent in support recovery and estimation. It is also shown to outperform existing methods in simulations, and its properties are illustrated on gene expression data from late-stage ovarian cancer patients.

1 Introduction

A complete understanding of the molecular basis of disease will require characterization of the network of interdependencies between genetic components. There are many types of networks that may be considered, such as protein-protein interaction networks or metabolic networks (Emmert-Streib and Dehmer, 2011), but the focus in this paper is on transcriptional regulatory networks. In many cases, interest centers not on a particular network but rather on whether and how the network changes between disease states. Indeed, differential networking analysis has recently emerged as an important complement to differential expression analysis (de la Fuente, 2010; Ideker and Krogan, 2012). For example, Hudson et al. (2009) studied a mutant breed of cattle known to differ from wild-type cattle by a mutation in the myostatin gene. Myostatin was not differentially expressed between the two breeds, but Hudson et al. (2009) showed that a differential network analysis could correctly identify it as the gene containing the causal mutation. In another example, using an experimental technique called differential epistasis mapping, Bandyopadhyay et al. (2010) demonstrated large-scale changes in the genetic networks of yeast cells after perturbation by a DNA-damaging agent.

Transcriptional networks are frequently modeled as Gaussian graphical models (Markowetz and Spang, 2007). Gene expression levels are assumed to be jointly Gaussian, so that two expression levels are conditionally independent given the other genes if and only if the corresponding entry of the precision matrix, or the inverse covariance matrix, is zero. Representing gene expression levels as nodes and conditional dependency relationships as edges in a graph results in a Gaussian graphical model (Lauritzen, 1996). A differential network can be modeled as changes in this graph structure between two conditions.

However, there may be cases where the conditional dependency relationships between pairs of genes change in magnitude but not in structure. For example, two genes may be positively conditionally dependent in one group but negatively conditionally dependent in the other. The supports of the precision matrices of the two groups would be identical, and would not reflect these potentially biologically significant differences in magnitude. Instead, in this paper two genes are defined to be connected in the differential network if the magnitude of their conditional dependency relationship changes between two groups. More precisely, consider independent observations of expression levels of p genes from two groups of subjects: X_i = (X_i1, . . . , X_ip )^T for i = 1, . . . , n_X from one group and Y_i = (Y_i1, . . . , Y_ip )^T for i = 1, . . . , n_Y from the other, where X_i ~ N(μ_X, Σ_X) and Y_i ~ N(μ_Y , Σ_Y ). The differential network is defined to be the difference between the two precision matrices, denoted ${\Delta }_0={\Sigma }_Y^{-1}-{\Sigma }_X^{-1}$. The entries of Δ₀ can also be interpreted as the differences in the partial covariances of each pair of genes between the two groups. This type of model for a differential network has been adopted by others as well, for example in Li et al. (2007), Danaher et al. (2013), and an unpublished technical report by Städler and Mukherjee (arxiv:1308.2771).

2 Previous approaches

There are currently two main types of approaches to estimating Δ₀. The most straightforward one is to separately estimate ${\Sigma }_X^{-1}$ and ${\Sigma }_Y^{-1}$ and then to subtract the estimates. A naive estimate of a single precision matrix can be obtained by inverting the sample covariance matrix. However, in most experiments the number of gene expression probes exceeds the number of subjects. In this high-dimensional data setting, the sample covariance matrix is singular and alternative methods are needed to estimate the precision matrix. Theoretical and computational work has shown that estimation is possible under the key assumption that the precision matrix is sparse, meaning that each row and each column has relatively few nonzero entries (Friedman et al., 2008; Ravikumar et al., 2008; Yuan, 2010; Cai et al., 2011).

The second type of approach is to jointly estimate ${\Sigma }_X^{-1}$ and ${\Sigma }_Y^{-1}$, taking advantage of an assumption that they share common features. For example, Chiquet et al. (2011), Guo et al. (2011), and Danaher et al. (2013) penalized the joint log-likelihood of the X_i and Y_i using penalties such as the group lasso (Yuan and Lin, 2006) and group bridge (Huang et al., 2009; Wang et al., 2009), which encourage the estimated precision matrices to have similar supports. Danaher et al. (2013) also introduced the fused graphical lasso, which uses a fused lasso penalty (Tibshirani et al., 2005) to encourage the entries of the estimated precision matrices to have similar magnitudes.

However, most of these approaches assume that both ${\Sigma }_X^{-1}$ and ${\Sigma }_Y^{-1}$ are sparse, but real transcriptional networks often contain hub nodes (Barabási and Oltvai, 2004; Barabási et al., 2011), or genes that interact with many other genes. The rows and columns of ${\Sigma }_X^{-1}$ and ${\Sigma }_Y^{-1}$ corresponding to hub nodes have many nonzero entries and violate the sparsity condition. The method of Danaher et al. (2013) is one exception that does not require individual sparsity. Its estimates ${\widehat{\Sigma }}_X^{-1}$ and ${\widehat{\Sigma }}_Y^{-1}$ minimize

$$\sum _{g\in \{X,Y\}}{n}_g\{\log \det {\Sigma }_g^{-1}-\mathrm{tr}\left({\widehat{\Sigma }}_g{\Sigma }_g^{-1}\right)\}-{\lambda }_1\sum _{g\in \{X,Y\}}\sum _{j\ne k}\mid {\omega }_{jk}^g\mid +{\lambda }_2\sum _{jk}\mid {\omega }_{jk}^X-{\omega }_{jk}^Y\mid ,$$ (1)

where ${\widehat{\Sigma }}_X$ and ${\widehat{\Sigma }}_Y$ are sample covariance matrices of the X_i and Y_i, ${\omega }_{jk}^X$ and ${\omega }_{jk}^Y$ are the (j, k)th entries of ${\Sigma }_X^{-1}$ and ${\Sigma }_Y^{-1}$, and det(·) and tr(·) are the determinant and trace of a matrix, respectively. The first term of (1) is the joint likelihood of the X_i and Y_i and the second and third terms comprise a fused lasso-type penalty. The parameters λ₁ and λ₂ control the sparsity of the individual precision matrix estimates and the similarities of their entries, respectively, and when λ₁ is set to zero (1) does not require ${\widehat{\Sigma }}_X^{-1}$ or ${\widehat{\Sigma }}_Y^{-1}$ to be sparse. A referee also pointed out that a recently introduced method (Mohan et al., 2012) were also designed for estimating networks containing hubs. However, theoretical performance guarantees for these methods have not been derived.

The direct estimation method proposed in this paper does not require ${\Sigma }_X^{-1}$ and ${\Sigma }_Y^{-1}$ to be sparse and does not require separate estimation of these precision matrices. Theoretical performance guarantees are provided for differential network recovery and estimation, and simulations show that when the separate networks include hub nodes, direct estimation is more accurate than fused graphical lasso or separate estimation.

3 Direct estimation of difference of two precision matrices

3.1 Constrained optimization approach

Let |·| denote element-wise norms and let ∥·∥ denote matrix norms. For a p × 1 vector a = (a₁, . . . , a_p)_T, define |a|₀ to be the number of nonzero elements of a, ${\mid a\mid }_1={\sum }_j\mid a_j\mid ,{\mid a\mid }_2={\left({\sum }_j{a}_j^2\right)}^{1∕2}$, and |a|_∞ = max_j |a_j|. for a p × p matrix A with entries a_jk, define |A|₀ be the number of nonzero entries of A, |A|₁ = Σ_j,k |a_jk|, |A|_∞ = max_j,k |a_jk|, ∥A∥₁ = max_k Σ_j |a_jk|, ∥A_∞ = max_j Σ_k |a_jk|, ∥A∥₂ = sup_|a|2≤1 |Aa|₂, and ${\Vert A\Vert }_F={\left({\sum }_{j,k}{a}_{jk}^2\right)}^{1∕2}$.

Let ${\widehat{\Sigma }}_X=n_X^{-1}{\sum }_i(X_i-\stackrel{‒}{X}){(X_i-\stackrel{‒}{X})}^T$, where $\stackrel{‒}{X}=n_X^{-1}{\sum }_i{X}_i$, and let ${\widehat{\Sigma }}_Y$ be defined similarly. Since the true Δ₀ satisfies Σ_X Δ₀Σ_Y − (Σ_X − Σ_Y) = 0, a sensible estimation procedure would solve ${\widehat{\Sigma }}_X\Delta {\widehat{\Sigma }}_Y-({\widehat{\Sigma }}_X-{\widehat{\Sigma }}_Y)=0$ for Δ. When min(n_X, n_Y ) < p there are an infinite number of solutions, but accurate estimation is still possible when Δ₀ is sparse. Motivated by the constrained ${\ell }_1$ minimization approach to precision matrix estimation of Cai et al. (2011), one estimator can be obtained by solving

$$\arg \min {\mid \Delta \mid }_1\text{subject to}{\mid {\widehat{\Sigma }}_X\Delta {\widehat{\Sigma }}_Y-{\widehat{\Sigma }}_X+{\widehat{\Sigma }}_Y\mid }_{\infty }\le {\lambda }_n$$

and then symmetrizing the solution. This is equivalent to a linear program, as for any three p × p matrices A, B, and C, $\mathrm{vec}\left(ABC\right)=(C^T\otimes A)\mathrm{vec}\left(B\right)$, where $\otimes$ denotes the Kronecker product and vec(B) denotes the p² × 1 vector obtained by stacking the columns of B. Therefore Δ₀ could be estimated by solving and then symmetrizing

$$\arg \min {\mid \Delta \mid }_1\text{subject to}{\mid ({\widehat{\Sigma }}_Y\otimes {\widehat{\Sigma }}_X)\mathrm{vec}\left(\Delta \right)-\mathrm{vec}({\widehat{\Sigma }}_X-{\widehat{\Sigma }}_Y)\mid }_{\infty }\le {\lambda }_n.$$ (2)

This approach directly estimates the difference matrix without even implicitly estimating the individual precision matrices. The key is that sparsity is assumed for Δ₀ and not for ${\Sigma }_X^{-1}$ or ${\Sigma }_Y^{-1}$. Direct estimation thus allows the presence of hub nodes in the individual networks and can still achieve accurate support recovery and estimation in high dimensions, as will be discussed in Section 4. A similar direct estimation approach was also proposed by Cai and Liu (2011) for high-dimensional linear discriminant analysis. Linear discriminant analysis depends on the product of a precision matrix and the difference between two mean vectors, and Cai and Liu (2011) showed that direct estimation of this product is possible even in cases where the precision matrix or the mean difference are not individually estimable.

3.2 A modified problem

The linear program (2) has a p² × p² constraint matrix ${\widehat{\Sigma }}_Y\otimes {\widehat{\Sigma }}_X$ and can become computationally demanding for large p. A modified procedure can alleviate this burden by requiring the estimate to be symmetric. Denote the (j, k)th entry of a matrix Δ by δ_jk, and define β to be the p(p + 1)/2 × 1 vector with β = (δ_{jk)1≤j≤k≤p}. Estimating a symmetric Δ is thus equivalent to estimating β, which has only p(p + 1)/2 parameters. Define the p² × p(p + 1)/2 matrix S with columns indexed by 1 ≤ j ≤ k ≤ p and rows indexed by l = 1, . . . , p and m = 1, . . . , p, so that each entry is labeled by S_lm,jk. For j ≤ k, let S_jk,jk = S_kj,jk = 1, and set all other entries of S equal to zero. For example, when p = 3,

$$S=\left(\begin{array}{cccccc}\hfill S_{11,11}\hfill & \hfill S_{11,12}\hfill & \hfill S_{11,13}\hfill & \hfill S_{11,22}\hfill & \hfill S_{11,23}\hfill & \hfill S_{11,33}\hfill \\ \hfill S_{21,11}\hfill & \hfill S_{21,12}\hfill & \hfill S_{21,13}\hfill & \hfill S_{21,22}\hfill & \hfill S_{21,23}\hfill & \hfill S_{21,33}\hfill \\ \hfill S_{31,11}\hfill & \hfill S_{31,12}\hfill & \hfill S_{31,13}\hfill & \hfill S_{31,22}\hfill & \hfill S_{31,23}\hfill & \hfill S_{31,33}\hfill \\ \hfill S_{12,11}\hfill & \hfill S_{12,12}\hfill & \hfill S_{12,13}\hfill & \hfill S_{12,22}\hfill & \hfill S_{12,23}\hfill & \hfill S_{12,33}\hfill \\ \hfill S_{22,11}\hfill & \hfill S_{22,12}\hfill & \hfill S_{22,13}\hfill & \hfill S_{22,22}\hfill & \hfill S_{22,23}\hfill & \hfill S_{22,33}\hfill \\ \hfill S_{32,11}\hfill & \hfill S_{32,12}\hfill & \hfill S_{32,13}\hfill & \hfill S_{32,22}\hfill & \hfill S_{32,23}\hfill & \hfill S_{32,33}\hfill \\ \hfill S_{13,11}\hfill & \hfill S_{13,12}\hfill & \hfill S_{13,13}\hfill & \hfill S_{13,22}\hfill & \hfill S_{13,23}\hfill & \hfill S_{13,33}\hfill \\ \hfill S_{23,11}\hfill & \hfill S_{23,12}\hfill & \hfill S_{23,13}\hfill & \hfill S_{23,22}\hfill & \hfill S_{23,23}\hfill & \hfill S_{23,33}\hfill \\ \hfill S_{33,11}\hfill & \hfill S_{33,12}\hfill & \hfill S_{33,13}\hfill & \hfill S_{33,22}\hfill & \hfill S_{33,23}\hfill & \hfill S_{33,33}\hfill \end{array}\right)=\left(\begin{array}{cccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right).$$

When Δ is symmetric some calculation shows that $({\widehat{\Sigma }}_Y\otimes {\widehat{\Sigma }}_X)\mathrm{vec}\left(\Delta \right)=({\widehat{\Sigma }}_Y\otimes {\widehat{\Sigma }}_X)S\beta$. Furthermore, if ${\beta }_0={\left({\delta }_{jk}^0\right)}_{1\le j\le k\le p}$, where ${\delta }_{jk}^0$ is the (j, k)th entry of Δ₀, by Lemma A1 β₀ is the unique solution to $S^T({\Sigma }_Y\otimes {\Sigma }_X)S\beta -S^T\mathrm{vec}({\Sigma }_X-{\Sigma }_Y)=0$. Therefore one reasonable approach to estimate a sparse β₀ in high dimensions is to solve

$$\widehat{\beta }=\arg \min {\mid \beta \mid }_1\text{subject to}{\mid S^T({\widehat{\Sigma }}_Y\otimes {\widehat{\Sigma }}_X)S\beta -S^T\mathrm{vec}({\widehat{\Sigma }}_X-{\widehat{\Sigma }}_Y)\mid }_{\infty }\le {\lambda }_n.$$

However, the inequality constraints can be improved. Let E be the p × p matrix such that $\mathrm{vec}\left(E\right)=({\widehat{\Sigma }}_Y\otimes {\widehat{\Sigma }}_X)S\beta$. These constraints treat the diagonals and off-diagonals of $E-({\widehat{\Sigma }}_X-{\widehat{\Sigma }}_Y)$ differently, with the diagonals constrained roughly half as much as the off-diagonals.

Therefore the remainder of this paper considers the estimate of Δ₀ obtained by solving

$$\begin{array}{cc}\hfill \widehat{\beta }=\arg \min {\mid \beta \mid }_1\text{subject to}& {\mid S^T\widehat{\Sigma }S\beta -S^T\widehat{b}\mid }_{O\infty }\le {\lambda }_n\hfill \\ \hfill \text{and}& {\mid S^T\widehat{\Sigma }S\beta -S^T\widehat{b}\mid }_{D\infty }\le {\lambda }_n∕2,\hfill \end{array}$$ (3)

where $\widehat{\Sigma }={\widehat{\Sigma }}_Y\otimes {\widehat{\Sigma }}_X$, $\widehat{b}=\mathrm{vec}({\widehat{\Sigma }}_X-{\widehat{\Sigma }}_Y)$, and for a p(p+1)/2 × 1 vector c, |c|_O∞ denotes the sup-norm of the entries of c corresponding to the off-diagonal elements of its matrix form, and |c|_D∞ is the sup-norm of the entries corresponding to the diagonal elements. The matrix form of $\widehat{\beta }$ will be denoted by $\widehat{\Delta }$. Compared to (2), (3) requires only a p(p + 1)/2 × p(p + 1)/2 constraint matrix, but requires a stronger theoretical condition to guarantee support recovery and estimation consistency, which is discussed in Section 4.

3.3 Implementation

The estimator (3) can be computed by slightly modifying code from the R package flare, recently developed by X. Li, T. Zhao, X. Yuan, and H. Liu to implement a variety of high dimensional linear regression and precision matrix estimation methods. Their method uses the alternating direction method of multipliers; for a thorough discussion see Boyd et al. (2011). To apply their algorithm, rewrite (3) as

$$\widehat{\beta }=\underset{r,\beta }{\arg \min }f\left(r\right)+{\mid \beta \mid }_1\text{subject to}r+S^T\widehat{\Sigma }S\beta =S^T\widehat{b},$$

where f(r) equals infinity if |r|_O∞ > λ_n or |r|_D∞ > λ_n/2 and zero otherwise. The augmented Lagrangian is then

$$L_p(r,\beta ,y)=f\left(r\right)+{\mid \beta \mid }_1+u^T(r+S^T\widehat{\Sigma }S\beta -S^T\widehat{b})+(\rho ∕2){\Vert r+S^T\widehat{\Sigma }S\beta -S^T\widehat{b}\Vert }_2^2,$$

where u is the Lagrange multiplier and ρ > 0 is a penalty parameter specified by the user. The alternating direction method of multipliers obtains the solution using the updates

$$\begin{array}{cc}\hfill r^{(t+1)}=& \underset{r}{\arg \min }{\Vert u^t∕\rho +S^T\widehat{b}-S^T\widehat{\Sigma }S{\beta }^t-r\Vert }_2^2∕2+f\left(r\right)∕\rho ,\hfill \\ \hfill {\beta }^{t+1}=& \underset{\beta }{\arg \min }{\Vert u^t∕\rho -r^{t+1}+S^T\widehat{b}-S^T\widehat{\Sigma }S\beta \Vert }_2^2∕2+{\mid \beta \mid }_1∕\rho ,\hfill \\ \hfill u(t+1)=& u^t+\rho (S^T\widehat{b}-r^{t+1}-S^T\widehat{\Sigma }S{\beta }^{t+1}),\hfill \end{array}$$

for each iteration t. The flare package incorporates several strategies to speed convergence, such as using a closed-form expression for r^t+1, using a hybrid coordinate descent and linearization procedure to obtain β^t+1, and dynamically adjusting ρ at each iteration.

The direct estimation approach can be tuned using an approximate Akaike information criterion. For the loss functions

$$L_{\infty }\left({\lambda }_n\right)={\mid {\widehat{\Sigma }}_X\widehat{\Delta }\left({\lambda }_n\right){\widehat{\Sigma }}_Y-{\widehat{\Sigma }}_X+{\widehat{\Sigma }}_Y\mid }_{\infty },L_F\left({\lambda }_n\right)={\Vert {\widehat{\Sigma }}_X\widehat{\Delta }\left({\lambda }_n\right){\widehat{\Sigma }}_Y-{\widehat{\Sigma }}_X+{\widehat{\Sigma }}_Y\Vert }_F,$$ (4)

where $\widehat{\Delta }\left({\lambda }_n\right)$ makes explicit the dependence of the estimator on the tuning parameter, λ_n is chosen to minimize

$$(n_X+n_Y)L\left({\lambda }_n\right)+2k,$$ (5)

where L(λ_n) represents either L_∞ or L_F and k is the effective degrees of freedom, which can be approximated by $k={\mid \widehat{\beta }\mid }_0$, or the number of nonzero elements in the upper triangle of $\widehat{\Delta }$. The loss functions (4) focus on the supremum and Frobenius norms in light of Theorems 2 and 3 in Section 4, but other norms could be used as well.

4 Theoretical properties

Let ${\sigma }_{jk}^X$ and ${\sigma }_{jk}^Y$ be the (j, k)th entries of Σ_X and Σ_Y , respectively. Define ${\sigma }_{\max }^X={\max }_j{\sigma }_{jj}^X$ and ${\sigma }_{\max }^Y={\max }_j{\sigma }_{jj}^Y$. Good performance of direct estimation requires the following conditions.

Condition 1

The true difference matrix Δ₀ has s < p nonzero entries in its upper triangle, and |Δ₀|₁ ≤ M, where M does not depend on p.

Condition 2

With s defined as in Condition 1, the constants ${\mu }_X={\max }_{j\ne k}\mid {\sigma }_{jk}^X\mid$ and ${\mu }_Y={\max }_{j\ne k}\mid {\sigma }_{jk}^Y\mid$ must satisfy $\mu =4\max ({\mu }_X{\sigma }_{\max }^Y,{\mu }_Y{\sigma }_{\max }^X)\le {\sigma }_{\min }^S{\left(2s\right)}^{-1}$, where ${\sigma }_{\min }^S={\min }_{j,k}({\sigma }_{jj}^Y{\sigma }_{jj}^X,{\sigma }_{jj}^X{\sigma }_{jj}^X+2{\sigma }_{kj}^Y{\sigma }_{jk}^X+{\sigma }_{jj}^Y{\sigma }_{kk}^X)$.

Condition 1 requires the difference matrix to have essentially constant sparsity, which is reasonable because genetic networks are not expected to differ much between two conditions. Condition 2 requires that the true covariances between the covariates are not too high, and can hold even when ${\Sigma }_X^{-1}$ and ${\Sigma }_Y^{-1}$ are not sparse. Actually it is sufficient to require only that the magnitude of the largest off-diagonal entry of $S^T({\Sigma }_Y\otimes {\Sigma }_X)S$ be less than ${\sigma }_{\min }^S∕2s$, but Condition 2 is more interpretable.

Condition 2 is closely related to the mutual incoherence property introduced by Donoho and Huo (2001), but is more complicated in the current setting because it involves a linear function of the Kronecker product of two covariance matrices. Solving (2) instead of (3) would require only $\max ({\mu }_X{\sigma }_{\max }^Y,{\mu }_Y{\sigma }_{\max }^X)\le {\min }_{j,k}\left({\sigma }_{jj}^X{\sigma }_{kk}^Y\right){\left(2\tilde{s}\right)}^{-1}$, with s̃ equal to the total number of nonzero entries of Δ₀. If in addition ${\sigma }_{jj}^X={\sigma }_{jj}^Y=1$ for all j, max(μ_X, μ_Y) ≤ (2s̃)⁻¹ would be required, which is similar to imposing the usual mutual incoherence condition on Σ_X and Σ_Y . Condition 2 is more restrictive, but (3) is easy to compute and still gives good finite-sample results.

Under these conditions, a thresholded version of the direct estimator $\widehat{\Delta }$ can successfully recover the support of Δ₀. Let the (j, k)th entries of Δ₀ and $\widehat{\Delta }$ be ${\delta }_{jk}^0$ and ${\widehat{\delta }}_{jk}^{}$, respectively. For a threshold τ_n > 0 define the estimator

$${\widehat{\Delta }}_{{\tau }_n}=\left\{{\widehat{\delta }}_{jk}I(\mid {\widehat{\delta }}_{jk}\mid >{\tau }_n)\right\}.$$

Let the (j, k)th entry of ${\widehat{\Delta }}_{{\tau }_n}$ be ${\widehat{\delta }}_{jk}^{{\tau }_n}$, and define the function

$$\mathrm{sgn}\left(t\right)=\{\begin{array}{cc}1,\hfill & t>0,\hfill \\ 0,\hfill & t=0,\hfill \\ -1,\hfill & t<0.\hfill \end{array}\phantom{\}}$$

Then if $\mathcal{M}\left({\widehat{\Delta }}_{{\tau }_n}\right)=\{\mathrm{sgn}\left({\widehat{\delta }}_{jk}^{{\tau }_n}\right):j=1,\dots ,p,k=1,\dots ,p\}$ and $\mathcal{M}\left({\Delta }_0\right)=\{\mathrm{sgn}\left({\delta }_{jk}^0\right):j=1,\dots ,p,k=1,\dots ,p\}$ are vectors of the signs of the entries of the estimated and true difference matrices, respectively, the following theorem holds.

Theorem 1

Suppose Conditions 1 and 2 hold, and let ${\sigma }_{\min }^S$ and μ be defined as in Condition 2. If min(n_X, n_Y ) > log p,

$${\tau }_n\ge \frac{1}{{\sigma }_{\min }^S}\left\{1+\frac{{\sigma }_{\min }^S}{{\sigma }_{\min }^S-(2s-1)\mu }\right\}\{M(\mid {\sigma }_{l^{\prime }l}^X\mid +\mid {\sigma }_{m^{\prime }m}^Y\mid +C)+1\}8C{\left\{\frac{\log p}{\min (n_X,n_Y)}\right\}}^{1∕2},$$

and ${\min }_{j,k:{\delta }_{jk\ne 0}^0}\mid {\delta }_{jk}^0\mid >2{\tau }_n$, then $\mathcal{M}\left({\widehat{\Delta }}_{{\tau }_n}\right)=\mathcal{M}\left({\Delta }_0\right)$ with probability at least 1 − 8p^−τ, where C is defined in Lemma A2 in the Appendix.

Theorem 1 states that with high probability, ${\widehat{\Delta }}_{{\tau }_n}$ can recover not only the support of Δ₀ but also the signs of its nonzero entries, as long as those entries are sufficiently large. In other words, in the context of genetic networks, ${\widehat{\Delta }}_{{\tau }_n}$ can correctly identify genes whose conditional dependencies change in magnitude between two conditions, as well as the directions of those changes, as long as min(n_X, n_Y ) is large relative to log p. In practice the threshold τ_n can be treated as a tuning parameter. In simulations and data analysis τ_n was set to 0 · 0001.

A thresholding step is natural in practice because small entries of $\widehat{\Delta }$ are most likely noisy estimates of zero. This step could be avoided by imposing an irrepresentability condition on ${\Sigma }_X\otimes {\Sigma }_Y$ , similar to those assumed in the proofs of the selection consistencies of the lasso (Meinshausen and Bühlmann, 2006; Zhao and Yu, 2006) and the graphical lasso (Ravikumar et al., 2008). However, these types of conditions are stronger than the mutual incoherence-type property assumed in Condition 2, as discussed in Lounici (2008). The thresholded estimators are pursued in this paper because of their milder theoretical requirements.

In addition to identifying the entries of ${\Sigma }_X^{-1}$ and ${\Sigma }_Y^{-1}$ that change, $\widehat{\Delta }$ can correctly quantify these changes, in the sense of being consistent for Δ₀ in the Frobenius norm.

Theorem 2

Suppose Conditions 1 and 2 hold and define ${\sigma }_{\min }^S$ and μ as in Condition 2. If min(n_X, n_Y ) > log p and

$${\lambda }_n=\{M(\mid {\sigma }_{l^{\prime }l}^X\mid +\mid {\sigma }_{m^{\prime }m}^Y\mid +C)+1\}4C{\left\{\frac{\log p}{\min (n_X,n_Y)}\right\}}^{1∕2},$$

then

$${\Vert \widehat{\Delta }-{\Delta }_0\Vert }_F\le \frac{{\left(5s\right)}^{1∕2}}{{\sigma }_{\min }^S}\left\{1+\frac{{\sigma }_{\min }^S}{{\sigma }_{\min }^S-(2s-1)\mu }\right\}2{\lambda }_n$$

with probability at least 1 − 8p^−τ, where C is defined in Lemma A2.

The proofs of Theorems 1 and 2 rely on the following bound on the element-wise ${\ell }_{\infty }$ norm of the estimation error.

Theorem 3

Suppose Conditions 1 and 2 hold, and define ${\sigma }_{\min }^S$ and μ as in Condition 2. If min(n_X, n_Y ) > log p and

$${\lambda }_n=\{M(\mid {\sigma }_{l^{\prime }l}^X\mid +\mid {\sigma }_{m^{\prime }m}^Y\mid +C)+1\}4C{\left\{\frac{\log p}{\min (n_X,n_Y)}\right\}}^{1∕2},$$

then

$${\mid \widehat{\Delta }-{\Delta }_0\mid }_{\infty }\le \frac{1}{{\sigma }_{\min }^S}\left\{1+\frac{{\sigma }_{\min }^S}{{\sigma }_{\min }^S-(2s-1)\mu }\right\}2{\lambda }_n$$

with probability at least 1 − 8p^−τ, where C is defined in Lemma A2 in the Appendix.

Similar theoretical properties have been derived for separate and joint approaches to estimating differential networks (Cai et al., 2011; Guo et al., 2011). However, these require sparsity conditions on each Σ⁻¹, such as ∥Σ⁻¹∥_∞ ≤ M′ < ∞, which can be violated if the individual networks contain hub nodes. In contrast, Theorems 1–3 can still hold in the presence of hubs.

5 Simulations

5.1 Settings

Simulations were conducted to compare direct estimation (3), fused graphical lasso (1), and separate estimation using the procedure of Cai et al. (2011). Data were generated with p = 40, 60, 90, and 120 and X₁, . . . , X_nX and Y₁, . . . , Y_nY were generated from N(0, Σ_X) and N(0, Σ_Y ), respectively, with n_X = n_Y = 100.

For each p, the support of ${\Sigma }_X^{-1}$ was first generated according to a network with p(p − 1)/10 edges and a power law degree distribution with an expected power parameter of 2, which should mimic real-world networks (Newman, 2003). This still gives a relatively sparse network, since only 20% of all possible edges are present, but the power law structure creates hub nodes, which make certain rows and columns nonsparse.

The value of each nonzero entry of ${\Sigma }_X^{-1}$ was next generated from a uniform distribution with support [−0 · 5, −0 · 2] ∪ [ [0 · 2, 0 · 5]. To ensure positive-definiteness, each row was divided by two when p = 40, three when p = 60, four when p = 90, and five when p = 120. The diagonals were then set equal to one and the matrix was symmetrized by averaging it with its transpose. The differential network Δ₀ was generated such that the largest 20%, by magnitude, of the connections of the top two hub nodes of ${\Sigma }_X^{-1}$ changed sign between ${\Sigma }_X^{-1}$ and ${\Sigma }_Y^{-1}$. In other words, Δ₀ was a sparse matrix, with zero entries everywhere except for 20% of the entries in two rows and columns.

Each method was tuned using an approximate Akaike information criterion. Direct estimation was tuned using (5) and one of the loss functions in (4). For a fair comparison fused graphical lasso was tuned in the same way, after searching across all combinations of three values of λ₁ and 10 values of λ₂. Small values of λ₁ were used because the true precision matrices were nonsparse. Separate estimation was tuned by searching across 10 different values of the tuning parameter to minimize ${\mathrm{AIC}}_X=n_X\mathrm{tr}\left({\widehat{\Sigma }}_X{\widehat{\Omega }}_X\right)-n_X\log \det \left({\widehat{\Omega }}_X\right)+2{\mid {\widehat{\Omega }}_X\mid }_0$, where ${\widehat{\Sigma }}_X$ was the sample covariance matrix of the X and ${\widehat{\Omega }}_X$ was the estimated precision matrix. The same was done for the Y_i, with AIC_Y defined similarly. Results were averaged over 250 replications.

5.2 Results

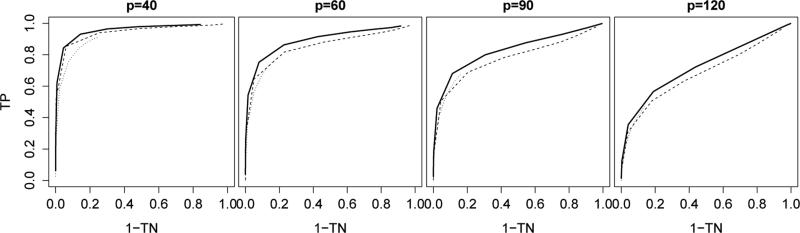
Figure 1 illustrates the receiver operating characteristic curves of the three estimation methods. Let ${\widehat{\delta }}_{jk}$ be the (j, k)th entry of a given estimator $\widehat{\Delta }$ and let ${\delta }_{jk}^0$ be the (j, k)th entry of the true Δ₀. The true positive and negative rates of $\widehat{\Delta }$ were defined as

$$\mathrm{TP}=\frac{{\sum }_{jk}I({\widehat{\delta }}_{jk}\ne 0\text{and}{\delta }_{jk}^0\ne 0)}{{\sum }_{jk}I({\delta }_{jk}^0\ne 0)},\mathrm{TN}=\frac{{\sum }_{jk}I({\widehat{\delta }}_{jk}=0\text{and}{\delta }_{jk}^0=0)}{{\sum }_{jk}I({\delta }_{jk}^0=0)},$$

respectively. Different points on the curves correspond to different tuning parameter values. The curves for the fused graphical lasso estimator (1) were plotted by varying λ₂. The λ₁ parameter, which controls the sparsity of the individual precision matrix estimates, was fixed at a small value because the individual matrices were not sparse. For a fair comparison with the thresholded direct estimator, the fused graphical lasso was thresholded at 0 · 0001. The separate estimator performed poorly and its curves were not plotted. Figure 1 shows that direct estimation compared favorably to fused graphical lasso.

Figure 1.

Receiver operating characteristic curves for support recovery of ${\Delta }_0={\Sigma }_Y^{-1}-{\Sigma }_X^{-1}$; solid line: thresholded direct estimator; dashed line: thresholded fused graphical lasso estimator with λ₁ = 0; dotted line: fused graphical lasso estimator with λ₁ = 0 · 1

The true discovery and nondiscovery rates of the three estimators were studied as well, and were defined as

$$\mathrm{TD}=\frac{{\sum }_{jk}I({\widehat{\delta }}_{jk}\ne 0\text{and}{\delta }_{jk}^0\ne 0)}{{\sum }_{jk}I({\widehat{\delta }}_{jk}\ne 0)},\mathrm{TND}=\frac{{\sum }_{jk}I({\widehat{\delta }}_{jk}=0\text{and}{\delta }_{jk}^0=0)}{{\sum }_{jk}I({\widehat{\delta }}_{jk}=0)},$$

respectively. These rates were taken to be zero when their denominators were equal to zero. In the analysis of genomic data minimizing the number of false discoveries is a major concern. The direct and fused graphical lasso estimators were thresholded at 0 · 0001 and the separate estimator was thresholded at 0 · 0002. In all settings, the true nondiscovery rates of the direct and fused graphical lasso estimators were close to 100%; separate estimation frequently did not identify any zero entries in the differential network. The true discovery rates are reported in Table 1, which also compares the effects of tuning using different loss functions (4). For direct estimation, tuning using L_∞ gave the best true discovery rates for smaller p while L_F was preferrable for larger p. For fused graphical lasso, L_∞ was always the better choice. Using either L_∞ or L_F , direct estimation performed well compared to fused graphical lasso and separate estimation, especially for larger p.

Table 1.

Average true discovery rates over 250 simulations. Standard errors are in parentheses

	${\widehat{\Delta }}_{{\tau }_n}$		${\widehat{\Delta }}_{FGL{\tau }_n}$
p	L∞	LF	L∞	LF	${\widehat{\Delta }}_{S{\tau }_n}$
40	77(16)	29(16)	83(12)	27(17)	2(0)
60	76(19)	66(21)	74(19)	65(30)	1(0)
90	66(25)	80(31)	55(26)	12(28)	1(0)
120	48(39)	61(45)	33(25)	1(7)	1(0)

The direct and fused graphical lasso estimators were tuned using (5) and either L1 or LF from (4); ${\widehat{\Delta }}_{{\tau }_n}$: thresholded direct estimator; ${\widehat{\Delta }}_{FGL{\tau }_n}$: thresholded fused graphical lasso estimator; ${\widehat{\Delta }}_{S{\tau }_n}$: thresholded separate estimator.

The Frobenius norm estimation accuracies of the unthresholded estimators tuned using different loss functions are reported in Table 2. The results of tuning using L_∞ or L_F were comparable. Direct estimation was much more accurate than separate estimation and slightly more accurate than fused graphical lasso. It is possible for direct estimation to simultaneously give markedly better support recovery but similar estimation compared to fused graphical lasso because estimation error depends on the magnitudes of the estimated entries, while support recovery depends only on whether they are nonzero. For example, suppose $\widehat{\Delta }$ had the same support as the true Δ₀, but each nonzero entry had magnitude 0 · 01. Then under the p = 120 simulation setting, ${\Vert \widehat{\Delta }-{\Delta }_0\Vert }_F=1\cdot 56$. The estimation error of this $\widehat{\Delta }$ is even higher than to those in Table 2, but it exactly recovers the true support.

Table 2.

Average estimation errors in Frobenius norm over 250 simulations. Standard errors are in parentheses

	$\widehat{\Delta }$		${\widehat{\Delta }}_{FGL}$
p	L∞	LF	L∞	LF	${\widehat{\Delta }}_S$
40	1·67(0·13)	1·46(0·22)	1·72(0·06)	1·50(0·15)	12·96(0·78)
60	1·68(0·07)	1·62(0·11)	1·68(0·05)	1·69(0·06)	28·45(2·01)
90	1·68(0·04)	1·71(0·03)	1·68(0·03)	1·72(0·03)	57·30(2·75)
120	1·55(0·02)	1·55(0·01)	1·54(0·02)	1·55(0·00)	102·84(4·06)

The direct and fused graphical lasso estimates were tuned using (5) with either L_∞ or L_F from (4); $\widehat{\Delta }$: direct estimator; ${\widehat{\Delta }}_{FGL}$: fused graphical lasso estimator; ${\widehat{\Delta }}_S$: separate estimator.

The good performance of direct estimation came at the price of some computational convenience. The memory required by the large constraint matrix behaves like O(p⁴), though the simulations generally needed no more than one gigabyte of memory when p = 120. In an unpublished technical report, Hong and Luo (arxiv:1208.3922) proved the global linear convergence of the alternating direction method of multipliers applied to problems like (3). However, each iteration of the proposed algorithm requires roughly O(sp⁴) computations, where s is the number of nonzero entries in the upper triangle of Δ₀, as defined in Condition 1. The simulations required on average 51, 853, 6231, and 51589 seconds when p = 40, 60, 90, and 120, respectively. On the other hand, these memory and time requirements are still reasonable in practice. Recently, H. Pang, H. Liu, and R. Vanderbei have developed an even faster algorithm for constrained ${\ell }_1$-minimization problems such as (3), available in the R package fastclime, which should reduce the computational burden of direct estimation.

6 Gene expression study of ovarian cancer

The proposed approach was applied to gene expression data collected from patients with stage III or IV ovarian cancer. Using these data, Tothill et al. (2008) identified six molecular subtypes of ovarian cancer, which they labeled C1 through C6. They found that the C1 subtype, characterized by differential expression of genes associated with stromal and immune cell types, was associated with much shorter survival times.

The proposed direct estimation procedure was applied to investigate whether this poor prognosis sub-type was also associated with differential wiring of genetic networks. The subjects were divided into a C1 group, with 78 patients, and a C2–C6 group, with 113 patients. Several pathways from the KEGG pathway database (Ogata et al., 1999; Kanehisa et al., 2012) were studied to determine if any differences in the conditional dependency relationships of the gene expression levels existed between the subtypes. All probesets corresponding to the same gene symbol were first averaged to get gene-level expression measurements.

Direct estimation and fused graphical lasso were tuned using (5) with the loss function L_∞ because in simulations this gave the best results for fused graphical lasso and good results for direct estimation. Separate estimation was tuned as described in Section 3.3. The direct and fused graphical lasso estimators were thresholded at 0 · 0001 to recover the differential network. The separate estimator was not simply thresholded at 0 · 0002 because simulations showed that this method gave poor true discovery rates. Instead, two genes were defined as being linked in the differential network if they were connected in one group but not the other, or if they were connected in both groups but their conditional dependency relationship changed sign. The procedure of Cai et al. (2011) thresholded at 0 · 0001 was used to recover the individual networks.

Two illustrative examples are reported in Fig. 2. Only genes included in at least one edge, or which saw a change in partial variance between the two subtypes, were included in the figures. In the results of separate estimation, only genes in the differential network estimated by direct estimation were labeled. To interpret the results, the most highly connected genes in the differential networks were considered to be important.

Figure 2.

Estimates of the differential networks between ovarian cancer subtypes. The direct and fused graphical lasso estimators were thresholded and the separate estimator was further sparsified; see text. Black edges show increase in conditional dependency from ovarian cancer subtype C1 to subtypes C2–C6, gray edges show decrease. (a)–(c): KEGG 04350, TGF-β pathway, (d)–(f): KEGG 04210, Apoptosis pathway. (a)–(e) tuned using L_∞ with (5), (f) tuned with λ₁ = 0 and λ₂ to give the same number of edges as (d); see text. Separate estimator not shown for apoptosis pathway.

Figures 2(a)–2(c) illustrate estimates of the differential network of the TGF-β signaling pathway, which at 82 genes is larger than the sample size of the C1 group. Direct estimation suggested the presence of two hub genes, COMP and THBS2, which have both been found to be related to resistance to platinum-based chemotherapy in epithelial ovarian cancer (Marchini et al., 2013). Fused graphical lasso gave the same number of edges in the differential network as direct estimation and only suggested the importance of COMP. It was hard to draw meaningful conclusions from the results of separate estimation because the denseness of the estimated network made it difficult to identify a small number of important genes.

Figures 2(d)–2(f) give the estimates for the apoptosis pathway, which at 87 genes was also larger than sample size of the C1 group. The separate estimator again resulted in a dense network and is not included in Fig. 2. Direct estimation pointed to BIRC3 and TNFSF10 as being important genes. Indeed, TNFSF10 encodes the TRAIL protein, which has been studied a great deal because of its potential as an anticancer drug (Yagita et al., 2004; Bellail et al., 2009), and in particular as a therapy for ovarian cancer (Petrucci et al., 2012; Kipps et al., 2013). BIRC3 can inhibit TRAIL-induced apoptosis (Johnstone et al., 2008) and has also been considered for use as a therapeutic target in cancer (Vucic and Fairbrother, 2007). Figure 2(e) shows the fused graphical lasso estimator tuned in the same way as the direct estimator, and suggests only BIRC3 as being important. For a fairer comparison with direct estimation, Fig. 2(f) depicts the fused graphical lasso estimator after fixing λ₁ = 0 and adjusting λ₂ to achieve the same level of sparsity as Fig. 2(d). The result is similar to Fig. 2(d), though it suggests that BIRC3 and PRKAR2B, a protein kinase, are important, rather than BIRC3 and TRAIL.

7 Discussion

Instead of modeling a differential network as the difference of two precision matrices, as proposed above, another possibility is to use the difference between two directed acyclic graphs. These graphs are natural models for single transcriptional regulatory networks, with nodes representing gene expression levels and edges indicating how the nodes are causally related to each other. Biological changes to a network can be thought of as interventions on some of its nodes, which results in changes to the graphical structure; see the unpublished technical report by Hauser and Bühlmann (arxiv:1303.3216) and references therein. Frequently, however, only observational data are available for gene expression, so it is difficult to estimate the underlying causal structures (Kalisch and Bühlmann, 2007; Maathuis et al., 2009). It would be interesting to develop a direct estimation method for differential networks with interventional data.

For method (3) to have good properties in high dimensions, Δ₀ must be sparse. While reasonable, this assumption will be violated if the biological differences between two groups manifest as global changes that affect a large number of gene-gene dependencies. If some proportion of these global changes are of sufficient magnitude, the method should still be able to detect their presence, though it may not recover all of the changes or accurately estimate their magnitudes. The most challenging case for the proposed method occurs when the network changes are numerous but small. A new statistic could be defined to quantify the degree of global change between two precision matrices, but so far there is little consensus as to what statistic might be most biologically meaningful.

Finally, while the focus has been on directly estimating the difference between two precision matrices, there are situations where interest may center on how a transcriptional regulatory network differs between K conditions, where K > 2. The proposed method could of course be used to estimate all pairwise differential networks, but this could be time-consuming. Another possibility would be to estimate the difference between each precision matrix and some common precision matrix, which could be taken to be the inverse of the pooled covariance matrix of all K groups. In other words, if ${\widehat{\Sigma }}_k$ were the sample covariance matrix of the kth group, let ${\widehat{\Sigma }}_P={\sum }_k{w}_k{\widehat{\Sigma }}_k$ be some weighted average of the ${\widehat{\Sigma }}_k$ and consider solving

$${\widehat{\Delta }}_k=\arg \min {\mid \Delta \mid }_1\text{subject to}{\mid {\widehat{\Sigma }}_k\Delta {\widehat{\Sigma }}_P-{\widehat{\Sigma }}_k+{\widehat{\Sigma }}_P\mid }_{\infty }\le {\lambda }_n.$$

If the difference matrix ${\Delta }_k={\Sigma }_P^{-1}-{\Sigma }_k^{-1}$ were sparse, where ${\Sigma }_P=E\left({\widehat{\Sigma }}_P\right)$ and ${\Sigma }_k^{-1}$ is the precision matrix of the kth group, ${\widehat{\Delta }}_k$ would be a direct estimate of Δ_k. The differential network between the jth and kth group could then be estimated as ${\widehat{\Delta }}_j-{\widehat{\Delta }}_k$.

APPENDIX: PROOFS OF THEOREMS

Lemma 1

The matrix $S^T({\Sigma }_Y\otimes {\Sigma }_X)S$ is invertible, where Σ_Y and Σ_X are p × p covariance matrices and S is defined in Section 3.2.

Proof

Since Σ_X and Σ_Y are positive-definite, there exists a full-rank matrix Σ^1/2 such that ${\Sigma }_Y\otimes {\Sigma }_X={\left({\Sigma }^{1∕2}\right)}^T{\Sigma }^{1∕2}$. Furthermore, from its construction S has full column rank, so rank(S) = p(p+ 1)/2. Therefore

$$\mathrm{rank}\left\{S^T({\Sigma }_Y\otimes {\Sigma }_X)S\right\}=\mathrm{rank}\left\{S^T{\left({\Sigma }^{1∕2}\right)}^T{\Sigma }^{1∕2}S\right\}=\mathrm{rank}\left({\Sigma }^{1∕2}S\right)=\mathrm{rank}\left(S\right).$$

Since $S^T({\Sigma }_Y\otimes {\Sigma }_X)S$ is p(p + 1)/2 × p(p + 1)/2, it is full rank and therefore invertible.

The next lemma comes from the proofs of Theorems 1(a) and 4(a) in Cai et al. (2011).

Lemma 2

Let X_i = (X_i1, . . . , X_ip)^T for i = 1, . . . , n be independent and identically distributed random vectors with E(X_i) = (μ₁, . . . , μ_jT , and let X̄ = n⁻¹X_i and $\widehat{\Sigma }=n^{-1}{\sum }_i(X_i-\stackrel{‒}{X}){(X_i-\stackrel{‒}{X})}^T$. If there exists some 0 < η < 1/4 such that log p/n ≤ η and $E\left\{e^{t{\left(X_{ij-{\mu }_j}\right)}^2}\right\}\le K\le \infty$ for all |t| ≤ η and j = 1, . . . , p, then

$${\mid \widehat{\Sigma }-\Sigma \mid }_{\infty }\le C{(\log p∕n)}^{1∕2}$$

with probability at least 1 − 4p^−τ, where C = 2η ⁻²(2 + τ + η⁻¹ e²K²)² and τ > 0.

Lemma 3

Let $\Sigma ={\Sigma }_Y\otimes {\Sigma }_X$. Label the entries of S_TΣS as ${\sigma }_{j^{\prime }{k}^{\prime },jk}^S(1\le j^{\prime }\le k^{\prime }\le p;1\le j\le k\le p)$. Then

$$\begin{array}{cc}{\sigma }_{j^{\prime }{k}^{\prime },jk}^S={\sigma }_{k^{\prime }k}^Y{\sigma }_{j^{\prime }j}^X+{\sigma }_{k^{\prime }j}^Y{\sigma }_{j^{\prime }k}^X+{\sigma }_{j^{\prime }k}^Y{\sigma }_{k^{\prime }j}^X+{\sigma }_{j^{\prime }j}^Y{\sigma }_{k^{\prime }k}^Y,\hfill & j^{\prime }\ne k^{\prime },j\ne k,\hfill \\ {\sigma }_{j^{\prime }{k}^{\prime },jj}^S={\sigma }_{k^{\prime }j}^Y{\sigma }_{j^{\prime }j}^X+{\sigma }_{j^{\prime }j}^Y{\sigma }_{k^{\prime }j}^X,\hfill & j^{\prime }\ne k^{\prime },j=k,\hfill \\ {\sigma }_{j^{\prime }j,jk}^S={\sigma }_{j^{\prime }k}^Y{\sigma }_{j^{\prime }j}^X+{\sigma }_{j^{\prime }j}^Y{\sigma }_{j^{\prime }k}^X,\hfill & j^{\prime }=k^{\prime },j\ne k,\hfill \\ {\sigma }_{j^{\prime }{j}^{\prime },jj}^S={\sigma }_{j^{\prime }j}^Y{\sigma }_{j^{\prime }j}^X\hfill & j^{\prime }=k^{\prime },j=k.\hfill \end{array}$$

Proof

Label the entries of Σ as σ_l′m′,lm(l′ = 1, . . . , p; m′ = 1, . . . , p; l = 1, . . . , p; m = 1, . . . , p) and the entries of S as S_lm,jk(l = 1, . . . , p; m = 1, . . . , p; 1 ≤ j ≤ k ≤ p), as in Section 3.3. By the definition of the Kronecker product, ${\sigma }_{l^{\prime }{m}^{\prime },lm}={\sigma }_{m^{\prime }m}^Y{\sigma }_{l^{\prime }l}^X$, and ${\sigma }_{j^{\prime }{k}^{\prime },jk}^S={\sum }_{l^{\prime },m^{\prime },l,m}{S}_{l^{\prime },m^{\prime },j^{\prime }{k}^{\prime }}{\sigma }_{l^{\prime },m^{\prime },lm}{S}_{lm,jk}$, so the lemma follows from the definition of the entries of S.

Proof of Theorem 3

Let the entries of Δ₀ be denoted ${\delta }_{jk}^0$, and define the p(p + 1)/2 × 1 vector ${\beta }_0={\left({\delta }_{jk}^0\right)}_{1\le j\le k\le p}$. Define Σ as in Lemma A3, $\widehat{b}=\mathrm{vec}({\widehat{\Sigma }}_X-{\widehat{\Sigma }}_Y)$, b = vec(Σ_X − Σ_Y ), and $h=\widehat{\beta }-{\beta }_0$. The bound on ${\mid \widehat{\Delta }-{\Delta }_0\mid }_{\infty }={\mid h\mid }_{\infty }$ is obtained following Lounici (2008).

Denote the ath component of S^T ΣSh by (S^TΣSh)_a, the (a, b)th entry of S^TΣS by ${\sigma }_{ab}^S$, and the bth component of h by h_b. Also let $\mu ={\max }_{a\ne b}\mid {\sigma }_{ab}^S\mid$. Then ${\left(S^T\Sigma Sh\right)}_a={\sum }_{b=1}{\sigma }_{ab}^S{h}_b={\sigma }_{aa}^S{h}_a+{\sum }_{b\ne a}{\sigma }_{ab}^S{h}_b$, which implies

$$\mid {\sigma }_{aa}^S{h}_a\mid \le {\mid S^T\Sigma Sh\mid }_{\infty }+\mu \mid {\sigma }_{ab}^S\mid \sum _{b\ne a}\mid h_b\mid .$$ (6)

The diagonal terms ${\sigma }_{aa}^S$ can be relabeled as ${\sigma }_{jk,jk}^S$, where j may equal k, and from Lemma A3 must satisfy ${\sigma }_{jk,jk}^S\ge {\sigma }_{\min }^S$, with ${\sigma }_{\min }^S$ defined in Condition 2. The off-diagonal terms ${\sigma }_{ab}^S$, a ≠ b can be relabeled as ${\sigma }_{j^{\prime }{k}^{\prime },jk}^S$ with j′ ≠ j or k′ ≠ k, and from Lemma A3 must satisfy ${\sigma }_{j^{\prime },k^{\prime },jk}^S\le 4\max ({\mu }_X{\sigma }_{\max }^X,{\mu }_Y{\sigma }_{\max }^Y)=\mu$, with μ_X and μ_Y defined in Condition 2. Using these facts, and Condition 2, (6) becomes

$${\mid h\mid }_{\infty }\le \frac{1}{{\sigma }_{\min }^S}\left({\mid S^T\Sigma Sh\mid }_{\infty }+\frac{{\sigma }_{\min }^S}{2s}{\mid h\mid }_1\right).$$ (7)

The method of Cai et al. (2010b) is used to bound |h|₁. Let T₀ be the set of indices corresponding to the support of β₀, and for any p × 1 vector a = (a₁, . . . , a_p)^T let a_T0 be the vector with components a_T0j = 0 for j ∉/ T₀ and a_T0j = a_j for j ∈ T₀.

First it must be shown that β₀ is in the feasible set with high probability. Since X_i and Y_i are both Gaussian, they satisfy the conditions of Lemma A2 and thus ${\mid {\widehat{\Sigma }}_X-{\Sigma }_X\mid }_{\infty }$ and ${\mid {\widehat{\Sigma }}_Y-{\Sigma }_Y\mid }_{\infty }$ are both less than C{log p/ min(n_X, n_Y)}^1/2 with probability at least 1 − 8p^−τ. Then

$$\begin{array}{cc}\hfill {\mid S^T\widehat{\Sigma }S{\beta }_0-S^T\widehat{b}\mid }_{\infty }& \le {\mid S^T(\widehat{\Sigma }-\Sigma )S{\beta }_0\mid }_{\infty }+{\mid S^T(\widehat{b}-b)\mid }_{\infty }\hfill \\ \hfill & \le {\Vert S^T\Vert }_{\infty }{\mid \widehat{\Sigma }-\Sigma \mid }_{\infty }{\Vert S\Vert }_1{\mid {\beta }_0\mid }_1+{\Vert S^T\Vert }_{\infty }({\mid {\widehat{\Sigma }}_X-{\Sigma }_X\mid }_{\infty }+{\mid {\widehat{\Sigma }}_Y-{\Sigma }_Y\mid }_{\infty })\hfill \\ \hfill & \le 4M{\mid \widehat{\Sigma }-\Sigma \mid }_{\infty }+4C{\{\log p∕\min (n_X,n_Y)\}}^{1∕2},\hfill \end{array}$$

where ∥S∥₁ = 2 by the definition of S and |β₀|₁ ≤ M by Condition 1. Next, from the proof of Lemma A3, each entry of Σ can be written as ${\sigma }_{l^{\prime }l}^X{\sigma }_{m^{\prime }m}^Y$, so

$$\begin{array}{cc}\hfill \mid {\widehat{\sigma }}_{l^{\prime }l}^X{\widehat{\sigma }}_{m^{\prime }m}^Y-{\sigma }_{l^{\prime }l}^X{\sigma }_{m^{\prime }m}^Y\mid & =\mid {\sigma }_{l^{\prime }l}^X({\widehat{\sigma }}_{m^{\prime }m}^Y-{\sigma }_{m^{\prime }m}^Y)+({\widehat{\sigma }}_{l^{\prime }l}^X-{\sigma }_{l^{\prime }l}^X){\sigma }_{m^{\prime }m}^Y+({\widehat{\sigma }}_{l^{\prime }l}^X-{\sigma }_{l^{\prime }l}^X)({\widehat{\sigma }}_{m^{\prime }m}^Y-{\sigma }_{m^{\prime }m}^Y)\mid \hfill \\ \hfill & \le [\mid {\sigma }_{l^{\prime }l}^X\mid +\mid {\sigma }_{m^{\prime }m}^Y\mid +C{\{\log p∕\min (n_X,n_Y)\}}^{1∕2}]C{\{\log p∕\min (n_X,n_Y)\}}^{1∕2}\hfill \\ \hfill & \le (\mid {\sigma }_{l^{\prime }l}^X\mid +\mid {\sigma }_{m^{\prime }m}^Y\mid +C)C{\{\log p∕\min (n_X,n_Y)\}}^{1∕2},\hfill \end{array}$$

since min(n_X, n_Y ) > log p. Then β₀ is feasible with probability at least 1 − 8p^−τ if ${\lambda }_n=\{M(\mid {\sigma }_{l^{\prime }l}^X\mid +\mid {\sigma }_{m^{\prime }m}^Y\mid +C)+1)4C{\{\log p∕\min (n_X,n_Y)\}}^{1∕2}$.

Now |h|₁ can be bounded. By the definition of (3), ${\mid {\beta }_0\mid }_1-{\mid \widehat{\beta }\mid }_1\ge 0$. This implies that ${\mid {\beta }_{0T_0}\mid }_1-({\mid {\widehat{\beta }}_{T_0}\mid }_1+{\mid {\widehat{\beta }}_{T_0^c}\mid }_1)\ge 0$. Using the triangle inequality, ${\mid {\beta }_{0T_0}-{\widehat{\beta }}_{T_0}\mid }_1\ge {\mid {\widehat{\beta }}_{T_0^c}\mid }_1$, or in other words, ${\mid h_{T_0^c}\mid }_1\le {\mid h_{T_0}\mid }_1$. Therefore ${\mid h\mid }_1\le 2{\mid h_{T_0}\mid }_1\le 2s^{1∕2}{\mid h_{T_0}\mid }_2$. To bound |h_T0|₂, observe following Cai et al. (2009) that for any s-sparse vector c,

$$\mid c^T{S}^T\Sigma Sc\mid \ge \sum _a{\sigma }_{aa}^S{c}_a^2-\mid \sum _{a\ne b}{\sigma }_{ab}^S{c}_a{c}_b\mid \ge {\sigma }_{\min }^S{\mid c\mid }_2^2-\mu \sum _{a\ne b}\mid c_a{c}_b\mid \ge {\sigma }_{\min }^S{\mid c\mid }_2^2-\mu (s-1){c\mid }_2^2.$$

This implies that

$$\begin{array}{cc}\hfill \mid h_{T_{0}T}^{}{S}^T\Sigma Sh\mid & \ge \mid h_{T_0}^T{S}^T\Sigma S{h}_{T_0}\mid -\mid h_{T_0}^T{S}^T\Sigma S{h}_{T_0^c}\mid \ge \{{\sigma }_{\min }^S-(s-1)\mu \}{\mid h_{T_0}\mid }_2^2-\mid \sum _{a,b}{\sigma }_{ab}^S{h}_{T_{0}a}{h}_{T_0^{c}b}\mid \hfill \\ \hfill & \ge \{{\sigma }_{\min }^S-(s-1)\mu \}{\mid h_{T_0}\mid }_2^2-\mu {\mid h_{T_0}\mid }_1{\mid h_{T_0^c}\mid }_1\ge \{{\sigma }_{\min }^S-(s-1)\mu \}\mid h_{T_0}\}{\mid h_{T_0}\mid }_2^2-\mu {\mid h_{T_0}\mid }_1^2\hfill \\ \hfill & \ge \{{\sigma }_{\min }^S-(2s-1)\mu \}{\mid h_{T_0}\mid }_2^2.\hfill \end{array}$$

Together with $\mid h_{T_0}^T{S}^T\Sigma Sh\mid \le {\mid h_{T_0}\mid }_1{\mid S^T\Sigma Sh\mid }_{\infty }\le s^{1∕2}{\mid h_{T_0}\mid }_2{\mid S^T\Sigma Sh\mid }_{\infty }$, this implies that

$${\mid h\mid }_1\le 2s^{1∕2}{\mid h_{T_0}\mid }_2\le \frac{2s{\mid S^T\Sigma Sh\mid }_{\infty }}{{\sigma }_{\min }^S-(2s-1)\mu },$$

so (7) becomes

$${\mid h\mid }_{\infty }\le \frac{1}{{\sigma }_{\min }^S}\left\{1+\frac{{\sigma }_{\min }^S}{{\sigma }_{\min }^S-(2s-1)\mu }\right\}{\mid S^T\Sigma Sh\mid }_{\infty }.$$

Bounding |S^TΣSh|_∞ uses the proof that β₀ is feasible, because

$$\begin{array}{cc}\hfill {\mid S^T\Sigma Sh\mid }_{\infty }& ={\mid S^T\Sigma S\widehat{\beta }-S^{T}b\mid }_{\infty }\hfill \\ \hfill & \le {\mid S^T\widehat{\Sigma }S\widehat{\beta }-S^T\widehat{b}\mid }_{\infty }+{\mid S^T(\widehat{\Sigma }-\Sigma )S{\widehat{\beta }}_1\mid }_{\infty }+{\mid S^T(\widehat{b}-b)\mid }_{\infty }\hfill \\ \hfill & \le {\lambda }_n+{\Vert S^T\Vert }_{\infty }{\mid \widehat{\Sigma }-\Sigma \mid }_{\infty }{\Vert S\Vert }_1{\mid {\beta }_0\mid }_1+{\Vert S^T\Vert }_{\infty }({\mid {\widehat{\Sigma }}_X-{\Sigma }_X\mid }_{\infty }+{\mid {\widehat{\Sigma }}_Y-{\Sigma }_Y\mid }_{\infty })\hfill \\ \hfill & \le {\lambda }_n+\{4M(\mid {\sigma }_{l^{\prime }l}^X\mid +\mid {\sigma }_{m^{\prime }m}^Y\mid +C)+4{\{\log p∕\min (n_X,n_Y)\}}^{1∕2}=2{\lambda }_n\hfill \end{array}$$

when ${\mid {\widehat{\Sigma }}_X-{\Sigma }_X\mid }_{\infty }$ and ${\mid {\widehat{\Sigma }}_Y-{\Sigma }_Y\mid }_{\infty }$ are both less than C{log p/ min(n_X, n_Y)}^1/2.

Proof of Theorem 1

Let ${\widehat{\delta }}_{jk}^{{\tau }_n}$ be the (j, k)th entry of ${\widehat{\Delta }}_{{\tau }_n}$. Then

$$\mathrm{pr}\{\mathcal{M}\left({\widehat{\Delta }}_{{\tau }_n}\right)=\mathcal{M}\left({\Delta }_0\right)\}=\mathrm{pr}\{\underset{j,k:{\delta }_{jk}^0=0}{\max }\mid {\widehat{\delta }}_{jk}^{{\tau }_n}\mid =0\cap \underset{j,k:{\delta }_{jk}^0>0}{\min }{\widehat{\delta }}_{jk}^{{\tau }_n}>0\cap \underset{j,k:{\delta }_{jk}^0<0}{\max }{\widehat{\delta }}_{jk}^{{\tau }_n}<0\}.$$

Suppose ${\delta }_{jk}^0>0$. Then ${\widehat{\delta }}_{jk}={\delta }_{jk}^0-({\widehat{\delta }}_{jk}-{\delta }_{jk}^0)>2{\tau }_n-{\tau }_n$ with probability going to 1, by Theorem 3, so ${\widehat{\delta }}_{jk}^{{\tau }_n}={\widehat{\delta }}_{jk}>0$. Next suppose ${\delta }_{jk}^0<0$. Then ${\widehat{\delta }}_{jk}={\delta }_{jk}^0-({\widehat{\delta }}_{jk}-{\delta }_{jk}^0)<-2{\tau }_n+{\tau }_n$ with probability going to 1, so ${\widehat{\delta }}_{jk}^{{\tau }_n}={\widehat{\delta }}_{jk}<0$. Finally for ${\delta }_{jk}^0=0,\mid {\widehat{\delta }}_{jk}\mid =\mid {\widehat{\delta }}_{jk}-{\delta }_{jk}^0\mid \le {\tau }_n$ with probability going to 1, so ${\widehat{\delta }}_{jk}^{{\tau }_n}=0$.

Proof of Theorem 2

Solutions to this type of ${\ell }_1$-constrained optimization problem have ${\mid h_{T_0}\mid }_1\ge {\mid h_{T_0^c}\mid }_1$. Cai et al. (2010a) used this property of h, along with their Lemma 3, to show that ${\mid h\mid }_2\le 2{\mid h_{T_0\cup T^{\ast }}\mid }_2$, where T* is the set of indices corresponding to the s/4-largest components of $h_{T_0^c}$. Then ${\mid h\mid }_2\le 2{\left(1.25s\right)}^{1∕2}{\mid h\mid }_{\infty }$, and combining this with Theorem 3 completes the proof.