Inferring Stable Acquisition Durations for Applications of Perfusion Imaging in Oncology

Abstract

Tissue perfusion plays a critical role in oncology. Growth and migration of cancerous cells requires proliferation of networks of new blood vessels through the process of tumor angiogenesis. Many imaging technologies developed recently attempt to measure characteristics pertaining to the passage of fluid through blood vessels, thereby providing a noninvasive means for cancer detection, as well as treatment prognostication, prediction, and monitoring. However, because these techniques require a sequence of successive imaging scans under administration of intravenous imaging tracers, the quality of the resulting perfusion data depends on the acquisition protocol. In this paper, we explain how to infer stability for stochastic curve estimation. The topic is motivated by two recent attempts to determine stable acquisition durations for acquiring perfusion characteristics using dynamic computed tomography, wherein inference used inappropriate statistical methods. Notably, when appropriate statistical techniques are used, the resulting conclusions deviate substantially from those previously reported in the literature.

Introduction

Many imaging technologies developed recently attempt to measure characteristics pertaining to the passage of fluid through blood vessels, thereby providing a noninvasive means to quantify vascular features.¹ Perfusion is of particular interest in oncologic imaging, where tissue, and in particular tumor perfusion, plays a critical role. The growth and migration of cancerous cells requires proliferation of networks of new blood vessels through the process of tumor angiogenesis, triggering modifications to the vasculature of the surrounding host tissue. In principle, measurements obtained from perfusion imaging provide physiological correlates for neovascularization induced by tumor angiogenesis.²

Thus, many investigators in cancer biology and oncology are attempting to use these features to better understand the pathophysiological processes at play in the tumor microenvironment. Ultimately, these efforts aim to identify biomarkers based on perfusion phenotypes that could be uti-lized for cancer detection, disease prognostication, as well as prediction and monitoring of therapeutic response to intervention.^3–6

Perfusion computed tomography (CTp) is one such functional imaging technology that enables noninvasive observation and quantification of perfusion characteristics. Physiological models have been developed to quantify a variety of perfusion characteristics (such as tumor blood volume, capillary permeability) that derive from measuring temporal changes in contrast enhancement obtained from CT images acquired over a period of time during intravenous administration of a contrast medium.⁷ Consequently, CTp provides a quantitative basis for evaluating vasculature heterogeneity. The functional imaging technology has been utilized in a number of organs and tumors, including the prostate, colorectal, head and neck, lung, liver, and normal tissue.

Because such techniques require a sequence of successive scans under intravenous administration of a contrast medium, the quality of the resulting perfusion data depends on the manner in which the data is acquired. When specifying an acquisition protocol, investigators must determine several factors that could affect the quality of the resultant perfusion measurements. For example, one important factor involves the delineation of the preenhancement setpoint, or time/image at which the arterial up-slope is considered to first occur.^8,9 In order to avoid excessive radiation exposure, patients are not scanned continuously, but rather at regular intervals over the course of the acquisition. Thus, investigators must determine the interscan subsampling interval to use in the acquisition. In a recent study,¹⁰ the length of the subsampling intervals was shown to significantly impact the resulting perfusion characteristics. In addition, investigators must determine an acquisition duration, or the extent of time for which the patient must undergo repeated scanning, that yields stable quantification of the perfusion characteristics. To limit radiation exposure, the acquisition duration should be minimized. Moreover, because the tissue type may be unknown before the diagnosis, any proposed duration of acquisition must ensure stable quantification of CTp characteristics for both malignant and healthy tissues before CTp can be used for detection and prognostication.

In the cases of two recent attempts to determine stable acquisition duration for acquiring perfusion characteristics in body tumors using dynamic CT,^11,12 recommendations were put forth that were inferred using statistical methods that are inappropriate for addressing this objective. In this context, the investigators implemented t-tests between CTp values obtained at discrete acquisition durations using a traditional hypothesis-testing framework. Information pertaining to neighboring scans was ignored in the inference, and stability was concluded in the absence of significant differences for tests between successive scans. In the case of one study,¹² conclusions were also based on measures of linear dependence between pairs of intrapatient observations at successive scans.

It is well known that the traditional formulation of the hypothesis-testing problem considers equality of effects under the null hypothesis, with the alternative hypothesis character-izing inequality. The corresponding P-value provides a measure of evidence against the null hypothesis, not for it. Because the roles assumed by the null and alternative statements are logically asymmetric, equivalence should not be inferred from the absence of a significant difference, since, intuitively, any underpowered study would inevitably reach this conclusion. Moreover, it has been well described that measures of linear dependence are misleading and inappropriate for evaluating equivalence or “agreement”.¹³ A proper analysis requires an equivalence-testing framework that measures the evidence against nonequivalence in relation to a prespecified equivalence region.

In addition, the pairwise approaches to inference utilized in both studies ignore temporal trends in the data, masking stabilization as a function of acquisition time. Notably, when appropriate statistical techniques are applied, conclusions deviate substantially from those provided by the aforementioned authors.¹⁴ Heretofore, an appropriate method for inferring stable acquisition durations for acquiring imaging biomarkers from dynamic imaging modalities has yet to be explained. Nor has the concept of “equivalence testing”¹⁵ been appreciated by the oncologic imaging community. In this paper, we explain how statistical modeling can be used to infer stable domains for stochastic curve estimation.

The ideas in this paper are presented in the following sequence. First we present the general method. Thereafter, we demonstrate the method by evaluating acquisition durations for a perfusion biomarker acquired in metastatic sites to the liver as well as healthy liver tissue using semiparametric model inference. We provide concluding remarks in the last section.

Inferring Stable Acquisition Durations from Stochastic Curves

This section presents a formal definition for stability as well as a general approach to inference based on equivalence testing.

Stability criterion

Let t > 0 denote the acquisition duration, and let f (t) characterize the nonstochastic mapping of a perfusion-based biomarker as a function of t. Let $f^{\prime }(t)={\lim }_{u\to 0}\frac{f(t+u)-f(u)}{t}$ denote the derivative or velocity of the function at acquisition time t. f’(t) characterizes the infinitesimal rate of change in f (t) with respect to the change in acquisition time t. Mapping f (t) is considered to be δ-stable, δ > 0, at acquisition time point t₀ if

$$|f(t_0)-f(t*)|<\delta ,\text{for all}t*>t_0.$$ (1)

The function has attained stability at time t if its velocity is bounded within a neighborhood of zero for all subsequent time points. Thus, stability condition (1) is satisfied for all δ > 0 if f’(t) reaches a steady state (or is time invariant) beyond t₀: f’(t*) = 0, for all t* > t₀. Therefore, we can evaluate acquisition durations for time invariance by fitting smooth curves to the observed data and conducting inference on the corresponding derivatives to assess their relative proximity to zero as a function of time.

Stability inference

Let y_t denote a stochastic response variable associated with a perfusion biomarker acquired for one patient region. A general nonparametric additive model applies local regression to a low-dimensional projection of the data. For example, we may assume that a one-to-one transformation of y, g(y), varies symmetrically about mean f(t) with random error ε and constant error variance $Var(\epsilon )={\sigma }_{\epsilon }^2$,

$$g(y_t)=f(t)+\epsilon ,\text{where}E(\epsilon )=0\text{and}Var(\epsilon )={\sigma }_{\epsilon }^2.$$ (2)

Mapping f (t) represents an arbitrary function of time, which can be estimated using smoothing splines or lowess.¹⁶

The traditional approach to statistical analysis through hypothesis testing is valid when the aim of an experiment is to evaluate the evidence for differences among experimental conditions. However, the condition of “stability” is actually a statement of equivalence. A proper analysis requires an equivalence-testing framework that measures the evidence against nonequivalence in relation to a prespecified “equivalence” region.

Let τ > 0 denote the maximum observation period, 0 < t < τ, and let L_α(t) and U_α(t) denote the lower and upper bounds of the 100(1 − α)% simultaneous confidence band (CB_1−α) for f’(t) over the interval (t, τ). Statistically, one should infer that f (t) is stable at acquisition duration t₀ at significance level α if the corresponding CB_1−α encompassing all subsequent acquisition durations are contained within a sufficiently small neighborhood of zero (−λ, λ), that is

$$-\lambda <L_{\alpha }(t*)\text{and}{U}_{\alpha }(t*)<\lambda ,\text{for all}t*>t_0.$$

The approach is analogous to testing null hypotheses of nonequivalence with equivalence region (−λ, λ). The boundary parameter λ represents the minimal magnitude of deviation that is meaningful in the context of the analysis. This may be specified as a scaled multiple of the estimated residual error standard deviation.

Case Study in CT Perfusion

In this section, we demonstrate the method for stability inference presented in the previous section using semiparameteric regression with implementation to the perfusion characteristic most commonly utilized in oncology, namely blood flow (BF). Specifically, spline regression is used to avoid prespecification of a parametric form for the underlying functional relationships, which are often unknown. As demonstrated in Ref. 14, deconvolution modeling of dynamic CT requires acquisition durations of sufficient length in order to achieve accurate quantification of a patient’s perfusion characteristics. Before attaining steady states, these models yield biomarkers that are characterized by periods of noisy fluctuation. The dynamic periods are explained in part by the initial absorption of contrast. Ensuring stable quantification for the various perfusion scanning applications in oncology requires the implementation of acquisition protocols that use acquisition durations that yield relative time-invariant mappings. We will use the statistical model to flexibly estimate the mean velocity in the presence of stochastic curves. The stability criterion will be used to infer a minimum stabilization time for blood flow when acquired in metastatic sites in liver as well as healthy liver.

CT perfusion data

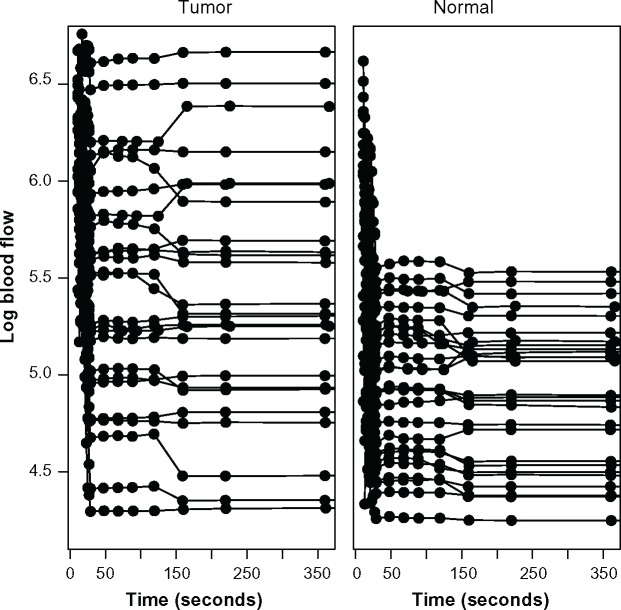
The study collected data on 16 patients with neuroendocrine liver metastases in whom CTp had been undertaken on a target lesion in the liver. CT perfusion images were obtained from a dual-phase protocol spanning a duration of 590 seconds. BF was acquired using a deconvolution analysis with the distributed parameter physiological model.^7,17,18 BF is the rate measured as milliliters per minute per 100 grams of liver tissue (mL/min per 100 g). The dataset analyzed here consisted of 59 eight-slice cine images temporally sampled at 0.5 seconds from the phase 1 acquisition, together with 8 anatomically matched images from the phase 2 acquisition. A final BF value was obtained for each region of interest (ROI) by averaging across each of the eight CT slice images. There were 25 separate ROIs where BF was obtained in liver metastases and 27 separate ROIs where BF was obtained in normal liver tissue. The observed BF values were transformed to the log scale for the purpose of adjusting for conditionally asymmetric residual error at a given acquisition time and to mitigate heteroskedasticity as a function of acquisition time. Figure 1 provides the scatterplots of the observed log BF as a function of acquisition time for both types of tissue. Solid lines connect observations acquired from the same ROI, while dots characterize the observed scan times. The figure suggests that BF tends to be both elevated and more heterogenous in tumor sites when compared to normal liver.

Figure 1.

Scatterplots of log blood flow measurements from the liver perfusion study in tumor (left) and normal liver (right) as functions of acquisition time. Solid lines connect repeated observations obtained from the same region of interest; dots characterize scan times.

Semiparametric model

We model the CTp curves using penalized splines due to their smoothness properties and the fact that a unified framework for computing simultaneous confidence bands has recently been established.¹⁹ Our case study analysis uses a truncated polynomial following the mixed model framework established by Ruppert et al.²⁰, thereby enabling direct estimation and inference on the derivatives of the CTp curves as a function of acquisition duration.

Penalized spline regression

A spline basis is in essence a linear combination of piecewise polynomials. Let s denote a K × 1 vector of knot locations. At time t, a truncated polynomial spline basis of degree D is defined as

$$f(t)={\beta }_0+{\beta }_{1}t+,\cdots ,+{\beta }_D{t}^D+{\displaystyle \sum _{k=1}^K{u}_k{(t-S_k)}_{+}^D},$$ (3)

where ${(t-s)}_{+}^D={(t-s)}^{D}1(t>s)$ for the indicator function 1(). Note that, when restricted to each region of the time domain, the function is a Dth degree polynomial. f(t) is smooth for all t for D > 0. Unlike polynomials that possess all derivatives over the entire domain, splines possess all derivatives only at points that are not knots. The extent to which the spline is differentiable at a knot depends on the degree of the spline. For example, statistical inference with D = 1 approximates the derivative f’(t), with a step function over the time axis partition failing to yield continuity. In general, a Dth degree spline has no more than D − 1 continuous derivatives.

Penalized estimation uses constrained optimization to attempt to strike a balance between smoothness and a close fit to the data.²⁰ In the mixed model representation, the spline coefficients u₁,…,u_K, are modeled as independent and identically distributed (i.i.d.) random effects with variance ${\sigma }_u^2$, and thus can be estimated using restricted maximum likelihood estimation (REML). Importantly, asymptotic simultaneous confidence bands can be obtained using Hotelling’s volume-of-tube formula.¹⁹

Let y_i denote an m_i × 1 vector of BF measurements acquired at times t_i for the ith ROI. In addition, let y denote the column vector obtained from stacking each y_i, i = 1,…, n. In our study, m_i varies between 15 and 17. Adopting the mixed model notation provided by Ruppert et al.²⁰, the semiparametric model is defined using design matrices X and Z corresponding to fixed and random components of the additive model, respectively,

$$\mathrm{y}=\mathbf{X}\beta +\mathbf{Zu}+\epsilon ,$$ 4

where $\epsilon \sim N(0,{\sigma }_e^2)$, $u\sim N(0,{\sigma }_u^2)$, cov(ε, u) = 0, X = (1, t, t²,…,t^D), $Z[{(t-s_1)}_{+}^D,\dots ,{(t-s_K)}_{+}^D]$, and u is the K × 1 vector of spline coefficients defined in (3). Let θ = (β, u) and define matrices

$$C=\left(X,Z\right),\text{and}D=\left(\begin{array}{cc}{0}_{D+1}& 0\\ 0& I_K\end{array}\right).$$

After estimating the variance components with REML, we can obtain the estimated best linear unbiased predictor (BLUP) of f (t), which follows as $\widehat{f}(t)=H(\widehat{\varphi })y,$ where $H(\widehat{\varphi })=\left[C{\left(C^{T}C+\frac{1}{\widehat{\varphi }}D\right)}^{-1}{C}^T\right]$ and $\widehat{\varphi }={\widehat{\sigma }}_u^2/{\widehat{\sigma }}_{\epsilon }^2$. As ϕ increases, ${\sigma }_u^2$ becomes large relative to ${\sigma }_e^2$, and therefore the fit attributes more total variation to an increasingly complex relationship. Conversely, as ϕ decreases, the fit becomes more smooth, as more of the total variation is attributed to random fluctuation.

In addition, the residual sum-of-squared (RSS) errors can be used for cross validation, $RSS={\displaystyle {\sum }_{i=1}^n{\left\{\left(I_n-H(\widehat{\varphi })\right)y\right\}}_i^2}$, or to conduct model criticism for comparing knot locations or among spline bases of varying degrees using Akaike’s information criterion: $AIC=\log (RSS)+2D{F}_{fit}(\widehat{\varphi })/n$, where $D{F}_{fit}(\widehat{\varphi })=tr\left\{H(\widehat{\varphi })\right\}\in [D+1,D+K+1]$.

Derivative inference

Point and interval estimators can be derived for the rate of change as a function of acquisition time. Let g denote a G × 1 vector of grid points or acquisition times of interest on interval [0, τ], and let C_g = (X_g, Z_g) denote the corresponding design matrix such that X_g and Z_g are the column design matrices that result from application of the derivative operation to f(g):

$$\begin{array}{l}{X}_g={\left[0,1,2g_j,\dots ,D{g}_j^{(D-1)}\right]}_{1\le j\le G}{}_{,}\text{and}\\ Z_g={\left[D{\left(g_j-s_1\right)}_{+}^{D-1},\dots ,D{\left(g_j-s_K\right)}_{+}^{D-1}\right]}_{1\le j\le G}{}_{.}\end{array}$$

The estimated BLUP for the derivative ${\widehat{f}}^{\prime }(\mathit{g})$, at each point in g, follows as

$${\widehat{f}}^{\prime }(\mathit{g})=C_g{\left(C^{T}C+\frac{1}{\widehat{\varphi }}D\right)}^{-1}{C}^{T}y$$ 5

Using the mixed model formulation, Ruppert et al.²⁰ demonstrated that the corresponding large sample covariance of ${\widehat{f}}^{\prime }(\mathit{g})-{\widehat{f}}^{\prime }(\mathit{g})$ follows as

$$V_g(\widehat{\varphi })={\widehat{\sigma }}_{\epsilon }^2{C}_g{\left(C^{T}C+\frac{1}{\widehat{\varphi }}D\right)}^{-1}{C}_g^T.$$ 6

Thus, approximate 100(1 − α)% interval estimators can be computed by selecting an appropriate asymptotically justified critical value $c_g^{*}$,

$${\widehat{f}}^{\prime }(\mathit{g})\pm c_g^{*}\sqrt{V_g(\widehat{\varphi })}.$$ 7

A 100(1 − α)% pointwise confidence interval results from fixing $c_g^{*}$ at the (1 − α/2)th quantile of a Student’s t-distribution with n − DF_fit degrees of freedom. Krivobokova et al.¹⁹ use Hotelling’s volume-of-tube formula to derive an approximate simultaneous CB_1−α, whereby asymptotically the critical value is selected to satisfy

$${\mathrm{Pr}}_y\left(\underset{g\in (0,\tau )}{\max }\frac{|H{(\varphi )}^T\epsilon +m(\mathit{g})|}{{\sigma }_{\epsilon }\Vert H(\varphi )\Vert }\ge c_g^{*}\right)=\alpha ,$$

where ε = y − Cθ and m(g) accounts for bias due to shrinkage, m(g) = H(ϕ)^TCθ − Cθ.

Results

Acquisition durations for BF from the liver perfusion study were inferred for CTp curves obtained in metastatic sites as well as regions of healthy liver (from the left or right lobes). For each tissue type, penalized spline regression analysis was implemented using truncated polynomial spline bases of D = 1, 2, 3. Our analysis used the package AdaptFitOS in statistical software R to implement REML and to select $c_g^{*}$ for the resulting simultaneous confidence bands.

Knots were placed at evenly spaced quantiles of the observed acquisition time points. While, in principle penalized spline estimators are robust to knot selection, because the sample sizes are rather small, the total number of knots were selected using the “corrected” version of AIC provided by Hurvich and Simonoff,²¹

$$AI{C}_c=\log (RSS)+\frac{2\left\{D{F}_{fit}\left(\widehat{\varphi }\right)+1\right\}}{n-D{F}_{fit}\left(\widehat{\varphi }\right)-2}.$$

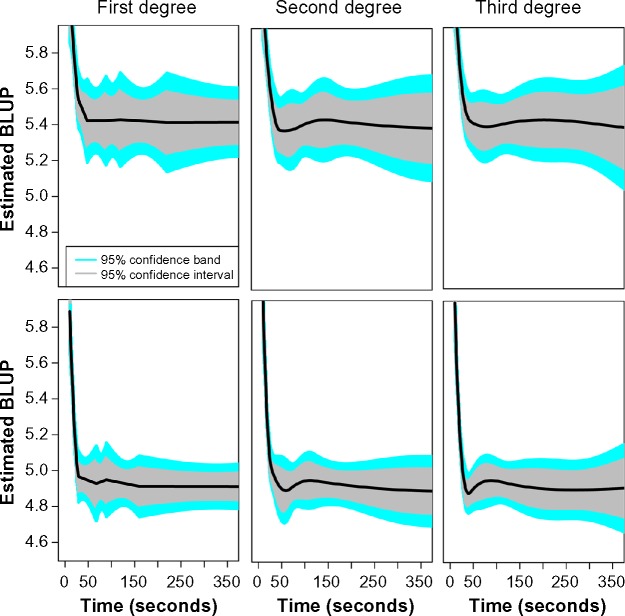
AIC_c was also used to compare goodness of fit among splines of varying degree. Table 1 provides the AIC “optimal” numbers of knots for each spline degree and analysis in tumor and normal sites. In addition, the resulting AIC_c and RSS are provided for each model. Figure 2 plots the point and interval estimates for the BF maps obtained in tumor (top) and normal liver (bottom), as functions of acquisition time. The third-degree truncated polynomial basis clearly resulted in a smooth fit when compared to the piecewise linear model (first degree). An intermediate degree of smoothness is evident for the fit corresponding to the second-degree spline. As evident in Table 1, the first-degree spline yielded the best tradeoff between goodness of fit and model complexity as defined by AIC_c in tumor. For sites in normal liver, the extent of enhanced smoothness provided by the third-degree polynomial yielded the best tradeoff.

Table 1.

Statistical summaries obtained from semiparametric regression analysis of log blood flow from the liver perfusion study using penalized splines with truncated polynomial bases of specified degree. Boldfaced values mark the spline degrees that achieved minimum AIC_c.

TISSUE TYPE	NUMBER KNOTS			AICC			RESIDUAL SS
	SPLINE DEGREE			SPLINE DEGREE			SPLINE DEGREE
	1	2	3	1	2	3	1	2	3
Tumor	13	10	8	4.896	4.899	4.898	129.53	130.00	129.80
Normal	11	9	8	4.387	4.387	4.385	77.88	78.05	77.86

Figure 2.

Estimated best linear unbiased predictors of log blood flow as functions of acquisition time in tumor (top) and normal liver (bottom) using penalized spline regression with truncated polynomial bases of specified degree. Estimated curves are represented by solid black lines. Shaded regions characterize interval estimates.

Figure 3 provides the resultant estimated BLUP for the derivatives and the corresponding CB_0.95, with an equivalence region (red) defined by ±0.5. The residual error standard deviation was estimated to be approximately 0.55 in tumor and 0.42 in normal tissue. Therefore, λ = 0.5 was chosen so that stability was measured in relation to the evidence that the mean curve varied less than approximately 1 standard deviation of random error. Using the approach described in the previous section, we concluded that CTp provides sufficiently stable characterization of BF when acquired for at least 220 seconds. Stabilization was evident sooner in normal liver, where a duration of 131 seconds yielded stable acquisition. This is not surprising, since, as noted in Figure 1, tissue perfusion tends to be more heterogeneous in regions undergoing tumor angiogenesis.

Figure 3.

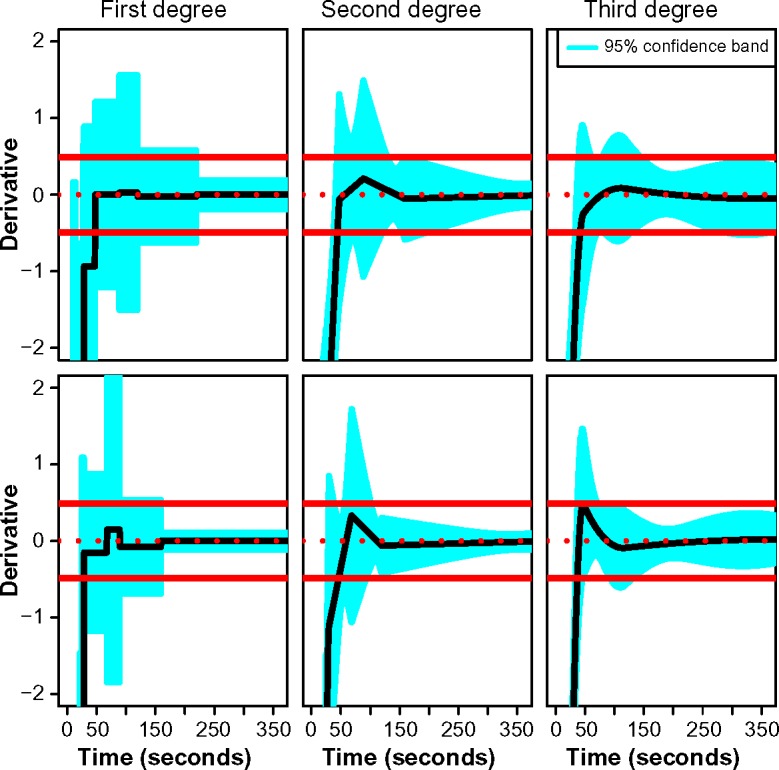
Estimated best linear unbiased predictors of the derivatives as functions of acquisition time in tumor (top) and normal liver (bottom) using penalized spline regression with truncated polynomial bases of specified degree. Point estimates are represented by solid black lines. Shaded regions characterize 95% simultaneous confidence bands over the entire acquisition duration. Red lines are used to depict an equivalence region defined by the neighborhood contained within ±0.5.

Discussion

In this paper, we described a statistically justified model-based approach for inferring stability for estimation of stochastic curves that eventually attain steady states. The effort was motivated in the oncologic imaging setting in the context of evaluating acquisition protocols for functional modalities that depend on a sequence of scans to acquire biomarkers that char-acterize biological processes associated with tumor angiogenesis. The approach was used to select acquisition durations that yield stable characterizations of a perfusion biomarker when acquired in metastatic sites in liver as well as normal liver tissue. It is important that the oncologic community recognize and use appropriate methods of inference when evaluating acquisition protocols for functional imaging modalities so that these promising technologies realize their full potential as tools for constructing biomarkers for guiding cancer detection, prognostication, and treatment selection.