Measuring Psychosocial Environments Using Individual Responses: an Application of Multilevel Factor Analysis to Examining Students in Schools

Abstract

Interest in understanding how psychosocial environments shape youth outcomes has grown considerably. School environments are of particular interest to prevention scientists as many prevention interventions are school-based. Therefore, effective conceptualization and operationalization of the school environment is critical. This paper presents an illustration of an emerging analytic method called multilevel factor analysis (MLFA) that provides an alternative strategy to conceptualize, measure, and model environments. MLFA decomposes the total sample variance-covariance matrix for variables measured at the individual level into within-cluster (e.g., student level) and between-cluster (e.g., school level) matrices and simultaneously models potentially distinct latent factor structures at each level. Using data from 79,362 students from 126 schools in the National Longitudinal Study of Adolescent to Adult Health (formerly known as the National Longitudinal Study of Adolescent Health), we use MLFA to show how 20 items capturing student self-reported behaviors and emotions provide information about both students (within level) and their school environment (between level). We identified four latent factors at the within level: (1) school adjustment, (2) externalizing problems, (3) internalizing problems, and (4) self-esteem. Three factors were identified at the between level: (1) collective school adjustment, (2) psychosocial environment, and (3) collective self-esteem. The finding of different and substantively distinct latent factor structures at each level emphasizes the need for prevention theory and practice to separately consider and measure constructs at each level of analysis. The MLFA method can be applied to other nested relationships, such as youth in neighborhoods, and extended to a multilevel structural equation model to better understand associations between environments and individual outcomes and therefore how to best implement preventive interventions.

Introduction

Schools are one of the most important social institutions in the lives of youth. Today, schools are no longer solely formal educational institutions, but instead are the settings where numerous health- and development-oriented prevention and intervention activities take place (Greenberg et al. 2003; Rones and Hoagwood 2000) and students acquire knowledge and learn skills in both cognitive and social-emotional domains (Eccles and Roeser 2011; Jones et al. 2011). Many well-known and successful prevention efforts have been implemented in schools, including Positive Behavioral Interventions and Support (PBIS) designed to promote school mental health and prevent student disruptive behaviors (Bradshaw et al. 2009). School-based interventions have become popular among prevention scientists as schools offer a unique opportunity to promote, at a population level, the health and well-being of youth. Schools serve more than 95 % of the nation’s youth for 6 hours per day (or upward of 40 % of student’s waking time during the school year) and at least 11 continuous years of their lives (Aud et al. 2010).

In addition to providing the infrastructure necessary to deliver prevention programs, schools have been increasingly recognized as important environments in and of themselves for shaping youth health and development. Indeed, a growing number of studies has linked characteristics of the school environment to educational (e.g., academic performance, engaged learning, and drop out) and non-educational outcomes (e.g., behavioral problems and psychological well-being) (Cohen and Geier 2010; Cohen et al. 2009). The school environment (also referred to throughout this manuscript and in the literature as school climate) can be defined as the overarching construct encompassing both objective and subjective features of the school setting, including the following: order, safety, and discipline; peer norms, values, and expectations; the culture of teaching, learning, and academics; quality of the school facilities and other resources; student’s level of connection and attachment to school; relationships between students, teachers, and staff; and collective student characteristics and behaviors (Anderson 1982; Cohen et al. 2009; Zullig et al. 2010). This paper focuses on these last two elements (social relationships within the school and the collective psychological and emotional characteristics and behaviors of students within the school), which we refer to as the school psychosocial environment.

Researchers have used a variety of approaches, including focus groups, observations, interviews, and surveys conducted with students, teachers, staff, and/or parents, to measure aspects of the school psychosocial environment. To date, school psychosocial environments have most often been measured through students’ self-report. These student self-report measures are easy to administer, demonstrate good psychometric properties, and assess several dimensions of the school environment (see for example Brand et al. 2003; Haynes et al. 2001; National School Climate Center). Thus far, researchers typically develop one of two types of variables based on these measures: (1) student-level variables that capture student’s perceptions and (2) aggregated scores that capture school-wide experiences (e.g., mean levels of perceived school climate within a school). These variables can be constructed with little difficulty and have most often been used in single-level or multilevel analyses as observed predictors of student-level and school-level outcomes.

Although the construction of such variables has provided a solid foundation for documenting the role of school psychosocial environments on various youth outcomes, there are challenges associated with how school psychosocial environments are currently (1) conceptualized, (2) operationalized, and (3) analyzed. These challenges impact prevention science research, as they potentially restrict the empirical refinement of etiologic theory regarding the role of school settings on student health and behavior and may therefore limit the development, implementation, and evaluation of school-based interventions designed to influence such etiological factors. First, the school psychosocial environment is often conceptualized solely in terms of the perceptions individuals have about their setting. Specifically, researchers frequently define school psychosocial environments in terms of the positive or negative feelings and attitudes students have in relation to their school. However, school environments, like any organizational setting, can be conceptualized not just with respect to the perceptions of students about their school but also with respect to the characteristics of individuals that make up the school (e.g., students’ attitudes, beliefs, behaviors, and demographic features). In other words, the social and psychological environment of an organization, including a school, can be understood in terms of the collection of behaviors, beliefs, and attitudes of people within the environment. Indeed, theories from organizational climate research illustrate how climates are defined and influenced by the traits of people within the setting (James et al. 2008). Moreover, school psychosocial environments are often conceptualized as a single-level phenomenon, either operating at the level of students or the school. However, school psychosocial environments could be even better understood as a two-level phenomenon, operating at both the level of students and the school (Anderson 1982; Van Horn 2003). Thus, by conceptualizing and measuring school psychosocial environments as a source of both school-level and student-level (co)variation, researchers will be better able to identify new dimensions of school psychosocial environments that may be relevant for targeting and implementing prevention efforts (i.e., to individual students, to whole schools, or both) and studying the role of school settings.

Second, existing research on school psychosocial environments tends to rely on single variables (e.g., single items corresponding to a feature of the school psychosocial environment) or composites (e.g., a single variable denoting the individual or school-wide average for a set of items capturing the school psychosocial environment). This is a narrow approach. Instead, prevention scientists can adopt a more complex representation of the variables that capture school psychosocial environments—at both the level of students and schools—by examining multivariable systems. In this regard, factor analytic approaches are helpful. In factor analysis, a measurement model is specified, which characterizes the relationship between an unobserved latent factor and a set of observed indicator variables that are presumed to be caused by the unobserved latent factor. Through a measurement model, factor analytic methods enable a more complex understanding of the constructs of interest, as the quality of the indicators as well as relationships between latent factors can be examined (Brown 2006; Kline 2010). Also, since the model includes a parameter that captures unique variance, factor analytic models partially account for measurement error, which regression models do not. Factor analytic methods are also preferable to simple aggregation (e.g., calculating school-level means directly from student data), as aggregation ignores student-level measurement error and within-school variability (Shinn 1990) and treats all indicators as exchangeable.

Finally, and related to the second issue, most prior research on school psychosocial environments has relied on a single-level operationalization and analytic strategy to document the effects of school settings on a given outcome (Dunn et al. 2014). For example, many multilevel studies have been conducted using data where the school psychosocial environment was assessed using surveys of students. In such instances, researchers have constructed a derived variable (Diez Roux 2002) or school-level measure of the psychosocial environment by averaging student responses to items on a given scale and then subsequently averaging those individual means across students in the same school; these school-level means then serve as the predictors in subsequent multilevel analyses. Researchers have also used factor analytic approaches to determine whether multiple items tapping the school psychosocial environment can be grouped together in a common construct; these factor analyses are typically conducted such that latent factors are constructed only at the student level. Multilevel studies with either derived variables or based on factor analytic approaches follow directly from the conceptualization of the school psychosocial environment as a single-level phenomenon (i.e., operating primarily on either students or school) (Van Horn 2003). A single-level perspective is limited in that it mixes or conflates what is occurring at each level. In other words, a single-level perspective completely dissociates—in the analytic model—the student behavior from the collective behavior in that it does not allow for the explicit modeling of behavior covariation at the student-level and collective behavior covariation at the school level. The conflation of student- and school-level processes and phenomenon may not only have methodological impacts, such as model misspecification with respect to the factor configuration and latent structure, but it can also lead to the generation of inaccurate theories and ultimately misidentified intervention targets. In particular, single-level measurement and analytic approaches may induce an ecological fallacy, such that incorrect inferences could be inferred when interpreting a school-level treatment effect on the aggregate behavior score as evidence of effect on student-level behavioral outcomes. To address these limitations, methodological techniques that allow for the specification of a fully multilevel measurement model are needed.

This paper uses an analytic method called multilevel factor analysis (MLFA) (Dedrick and Greenbaum 2011; Dyer et al. 2005; Reise et al. 2005; Toland and De Ayala 2005) to address the above challenges by providing an alternative approach for conceptualizing, measuring, and modeling environments. MLFA is similar to all factor analytic methods in that it seeks to capture the shared variance among an observed set of variables in terms of a potentially smaller number of unobserved constructs or latent factors (Brown 2006; Kline 2010). However, MLFA differs from a traditional factor analysis in one major way: it is multilevel. Unlike a single-level exploratory or confirmatory factor analysis, which estimates latent factors at only one level (i.e., the individual or contextual level), or a random-effect factor analysis, which decomposes the variance of the level-one factor into within and between components (Marsh et al. 2009), MLFA decomposes the total sample variance-covariance matrix into within-cluster (i.e., individual level, within an environment) and between-cluster (i.e., environment level) matrices and simultaneously models distinct latent factor structures at each of these levels (Hox 2010; Muthen 1991, 1994).

There are many methodological and practical implications of MLFA. By allowing for the possibility of two different latent factor structures at the two levels, researchers are better able to understand the variation in structure and meaning that exists between individuals within an environment, as well as between environments, rather than assuming that the factor structure is the same at both levels. Thus, MLFA may help researchers avoid making the erroneous assumption that a given set of items performs the same at each level of analysis or that a given construct means the same thing at each level of analysis; these assumptions would not be detected using hierarchical or multilevel modeling techniques with derived variables or with single-level or random-effect factor analyses. Moreover, MLFA can also be useful for generating new theories regarding the role of environments on youth health and development outcomes. As many large-scale prevention based data collection efforts occur through cluster-based sampling, MLFA can provide an opportunity to study psychosocial environments using data collected at the individual level.

In this paper, we apply the MLFA method using data ascertained from students within schools. As stated previously, we focus on measuring the school psychosocial environment using student-level self-reports of attitudes (about themselves), behaviors, and emotions, as this domain of the school environment seems more often relegated to single-level or derived variable approaches than some of its companion domains. However, the MLFA approach could be effectively used to model other domains of the school environment as well as other settings, such as neighborhoods, hospitals, and workplaces.

Methods

Participants

Data for this study came from the National Longitudinal Study of Adolescent to Adult Health (Add Health, formerly known as the National Longitudinal Study of Adolescent Health), a longitudinal survey focusing on the health and behaviors of adolescents in grades 7–12 (Harris 2013). Add Health, although not including instruments specifically designed to measure the school psychosocial environment, is useful for this application of MLFA as it uses a nationally representative sample of adolescents and includes an array of student-level measures that should directly reflect psychosocial characteristics of the school and the students themselves. Add Health researchers began collecting data for a nationally representative sample in 1994–1995 (wave 1) using schools as the primary sampling unit. To ensure that selected schools were representative of US schools, researchers stratified schools by census region, urbanicity, size, type, and ethnic background of the student body (i.e., percent white) prior to systematic random sampling. From a sampling frame of 26,666 schools, investigators selected a sample of 80 high schools and 52 middle schools for participation. School administrators of these 132 schools were asked to administer an in-school survey to their students at wave 1. Of these 132 schools, 128 (96.97 %) participated in the in-school survey, resulting in a sample of 83,135 students. Given our concerns that the underlying characteristics of the school environment may differ for students attending a boarding school compared to those who did not, we eliminated one private boarding school from our analysis, which included responses from 888 students. We also removed one school that did not have demographic data reported on it; this school included responses from 61 students. Our analytic sample therefore consisted of responses from 82,186 students who attended 126 schools. Across the 126 schools, an average of 652.27 students per school (SD=504.41) completed a survey (minimum=29; maximum=2,546). The analytic sample was balanced in terms of sex (50.4 % female; 49.6 % male) and grade level (13.9 % grade 7; 13.3 % grade 8; 20.8 % grade 9; 19.6 % grade 10; 17.2 % grade 11; and 15.2 % grade 12), was racially/ethnically diverse (46.6 % white; 12.6 % black; 15.8 % Hispanic; 19.4 % multiracial), and included mostly native-born students (90.5 % native).

Materials and Procedure

In-School Questionnaire

The in-school questionnaire was completed by all participating students within each school. It asked youth to self-report on a variety of topics, including their health status, friendships, household structure, social and demographic characteristics, expectations for the future, self-esteem, and school-year extracurricular activities. It contained more than 200 items (most items were focused on relationships with parents and friendship network structure) and was administered during a 45–60-min class period between September 1994 and April 1995. Parents were notified prior to the date the survey was administered and could advise their children not to participate. Questionnaires were optically scanned following completion. The questionnaire consisted of predominately individual items rather than groups of existing measures. Response options for all items were on Likert scales, ranging from a four-point to a nine-point scale. The Likert scales captured agreement (e.g., ranging from 1 = strongly agree to 4=strongly disagree) or frequency (e.g., ranging from 0=never to 4=everyday).

We selected a subset of 21 items from the in-school questionnaire for the current analyses (refer Table 1). These items were selected because they were hypothesized to capture the social and psychological characteristics of students and also reflect the psychosocial environment of their school. These 21 items generally tapped three broad domains: (1) relationships (e.g., student’s ability to get along with teachers and other students), (2) behaviors (e.g., tobacco, alcohol, and drug use; time spent on homework; truancy; and physical fighting), and (3) attitudes/feelings (e.g., beliefs about themselves and feelings of sadness). As our purpose was to demonstrate the utility of the MLFA approach to specifically model school psychosocial environment, we did not consider other measures in the data set that might reflect other domains of school climate (e.g., physical environment and teaching and learning environment) although this general technique could certainly be applied to a larger multidomain item set.

Table 1.

Items from the National Longitudinal Study of Adolescent Health (Add Health) in-school questionnaire

Item	Original response options	Revised response option
Since school started this year, how often have you had trouble	0=never; 1=just a few times=2=about once a week; 3=almost everyday; 4=everyday; 9=multiple response;	0=never; 1=just a few times; 2=about once a week or more
1. Getting along with your teachers
2. Paying attention in school
3. Getting your homework done
4. Getting along with other students
5. In general, how hard do you try to do your school work well?	1=I try very hard to do my best; 2=I try hard enough, but not as hard as I could; 3=I don’t try very hard; 4=I never try at all	1=I try very hard to do my best; 2=I try hard enough, but not as hard as I could; 3=I don’t try very hard or I never try at all
During the past 12 months, how often did you	0=never; 1=once or twice; 2=once a month or less; 3=2 or 3 days a month; 4=once or twice a week; 5=3 to 5 days a week; 6=nearly everyday	0=never; 1=once or twice; 2=more than twice a month
6. Smoke cigarettes
7. Get drunk
8. Skip school without an excuse
In the past month, how often	0=never; 1=rarely; 2=occasionally; 3=often; 4=everyday	0=never; 1=rarely or occasionally; 2=often or everyday
9. did you feel really sick
10. did you feel depressed or blue
11. did you have trouble relaxing
12. were you moody
13. did you cry a lot
14. were you afraid of things
How strongly do you agree or disagree with each of the following statements:	1=strongly agree; 2=agree; 3=neither agree nor disagree; 4=disagree; 5=strongly disagree	0=strongly agree/agree; 1=neither; 2=strongly disagree/disagree
15. I have a lot of good qualities.
16. I have a lot to be proud of.
17. I like myself just the way I am.
18. I feel like I am doing everything just right.
19. I feel socially accepted.
20. I feel loved and wanted.
21. During the past year, how often have you gotten into a physical fight?	0=never; 1=1or 2 times; 2=3–5 times; 3=6 or 7 times; 4=more than 7	0=never; 1=once or twice; 2=more than twice a month

All of these items were taken from the in-school questionnaire

Data Analyses

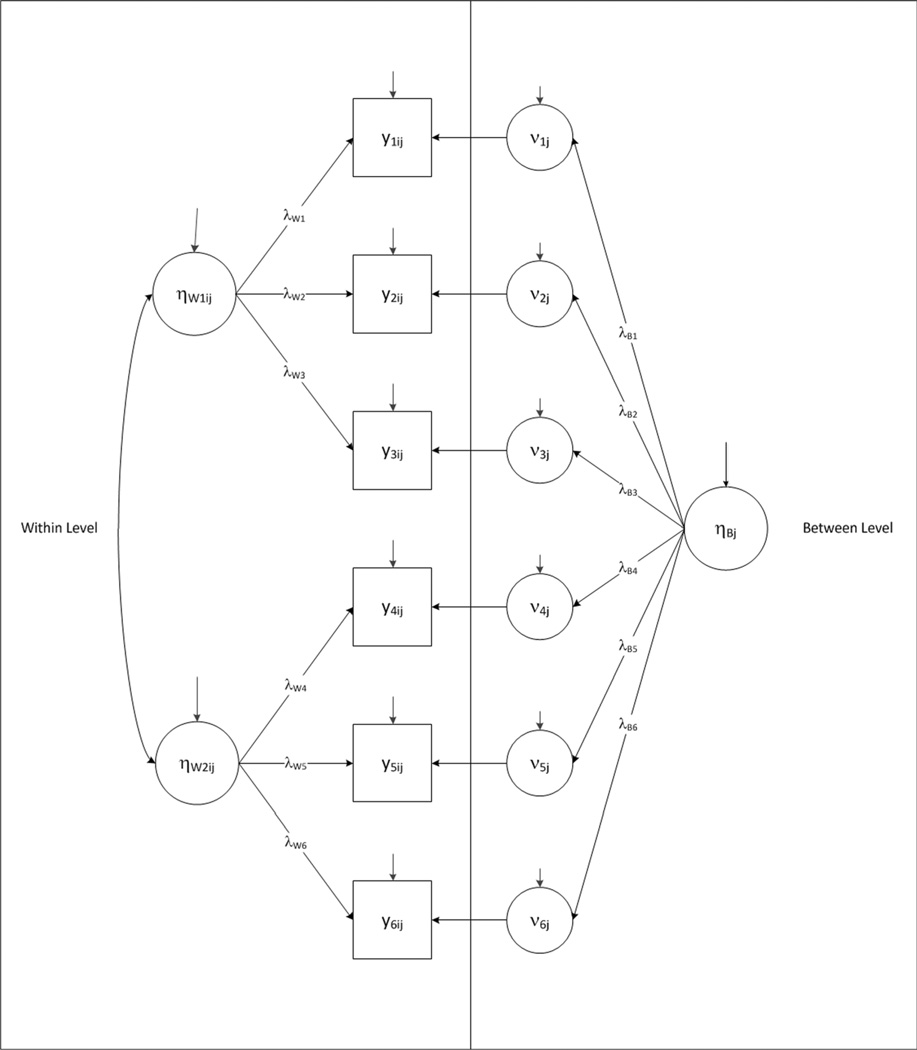
Our primary analyses utilize two variations of MLFA: multilevel exploratory factor analysis (ML-EFA) and multilevel confirmatory factor analysis (ML-CFA). Figure 1 presents a hypothetical ML-CFA with six observed indicator variables, a standard two-factor structure at the within level, and a standard one-factor structure at the between level. In this figure, there are two separate measurement models—one at the within level (e.g., individual students within a school) and the other at the between level (e.g., between schools). At the within level, the individual response for student i in school j on the m^th observed indicator variable, represented with a rectangle labeled y_mij, is a function of one of the two student-specific latent factors, represented with circles labeled η_W1ij and η_W2ij, a random intercept, represented by a circle labeled ν_mj, and a random error term, indicated by a small unanchored arrow pointing to y_mij. The factor loadings, λ_W1, …, λ_W6, estimate the direction and size of the association between the within-level latent factors and the observed variables. This model can be expressed in matrix notation as:

$${\mathbf{y}}_{ij}={\mathbf{\nu }}_j+{\mathbf{\Lambda }}_W{\mathbf{\eta }}_{Wij}+{\mathbf{\epsilon }}_{ij},$$ (1)

where ${\mathbf{\epsilon }}_{ij}\widetilde{\mathrm{i}.\mathrm{i}.\mathrm{d}.}\mathrm{M}\mathrm{V}\mathrm{N}(\mathbf{0},{\mathbf{\theta }}_{\epsilon }),{\mathbf{\eta }}_W\widetilde{\mathrm{i}.\mathrm{i}.\mathrm{d}.}\mathrm{M}\mathrm{V}\mathrm{N}(\mathbf{0},{\mathbf{\Psi }}_W)$, and Cov(ε_ij, η_Wij)=0.

Fig. 1.

Multilevel factor analysis (MLFA). The components of a MLFA are illustrated above. This figure presents two separate measurement models—the within level (i.e., individuals within an environment) and the between level (i.e., between environments). At the within level, two individual-specific latent factors, η_W1ij and η_W2ij, influence the individual’s responses on six items (or observed variables) (y_1ij, y_2ij, …, y_6ij). At the between level, one school-specific latent factor,η_Bj, influences the school response means,ν_mj, that in turn influence the individual’s responses. The direction and size of the factor influences at each level are described by the λ_Ws and λ_Bs, respectively. Each item is measured imperfectly and thus has a residual indicated by the small vertical arrows in the diagram. The residual refers to the unique variance in the item not explained by or related to the latent factor; this unique variance is a combination of measurement error and other unique sources of variability

At the between level, the intercept for school j corresponding to the m^th observed indicator variable, represented by a circle labeled ν_mj, is a function of the school-specific latent factor, represented with circle labeled η_Bj, and a random error term, indicated by a small unanchored arrow pointing to ν_mj. The random intercept refers to the expected value of the indicator for school j at the mean of η_Bj. The factor loadings, λ_B1, …, λ_B6, estimate the direction and size of the association between the between-level latent factors and the random intercepts of the observed variables. This between-school model can be expressed in matrix notation as follows:

$${\mathbf{\nu }}_j=\mathbf{\gamma }+{\mathbf{\Lambda }}_B{\mathbf{\eta }}_{Bj}+{\mathbf{\zeta }}_j,$$ (2)

where ${\mathbf{\zeta }}_j\widetilde{\mathrm{i}.\mathrm{i}.\mathrm{d}.}\mathrm{M}\mathrm{V}\mathrm{N}(\mathbf{0},{\mathbf{\theta }}_{\zeta }),{\mathbf{\eta }}_B\widetilde{\mathrm{i}.\mathrm{i}.\mathrm{d}.}\mathrm{M}\mathrm{V}\mathrm{N}(\mathbf{0},{\mathbf{\Psi }}_B)$, and Cov(ζ_j, η_Bj)=0. In a standard ML-CFA, the assumption of conditional independence is typically imposed such that θ_ε and θ_ζ are both diagonal matrices. Combing Eqs. 1 and 2, one can see that in a ML-CFA, responses to items by a student i in school j are a function of student-level traits, school-level traits, and variability unique to student i and to school j:

$${\mathbf{y}}_{ij}=\mathbf{\gamma }+{\mathbf{\Lambda }}_W{\mathbf{\eta }}_{Wij}+{\mathbf{\Lambda }}_B{\mathbf{\eta }}_{Bj}+{\mathbf{\zeta }}_j+{\mathbf{\epsilon }}_{ij}.$$ (3)

To showcase the utility of the MLFA approach, we used a split-sample cross-validation approach, beginning with a multilevel exploratory factor analysis (ML-EFA) on the first random split of the sample (calibration sample), followed by a multilevel confirmatory factor analysis (ML-CFA), informed by the ML-EFA, on the second random split of the sample (validation sample). Researchers begin by conducting an EFA when the goal is to identify the factor structure underlying a set of variables; thus, an EFA is conducted when there are no a priori hypotheses about the number of latent factors or the relationships between each factor and the indicators (Brown 2006; Kline 1994). This was our case because we were seeking to group together items that were not already part of an existing scale. ML-EFA involves an EFA approach applied separately but simultaneously to the within-level item covariance matrix and the between-level item covariance matrix. In a CFA, researchers have a priori hypotheses about the number of factors and the factor configuration and want to test the validity of a hypothesized model by evaluating the model data consistency. For both analyses, we used a categorical factor analysis, a type of analysis designed for ordinal data. In contrast to a continuous factor analysis, a categorical factor analysis does not require that indicators are continuous or that any distributional assumptions such as normality are met (Flora and Curran 2004). Both EFA and CFA models with categorical indicators use the sample-based polychoric correlation matrix for the observed indicators (in essence, the correlations that would have been observed between the ordinal indicators if their underlying continuous responses were instead measured).

To conduct the ML-EFA and ML-CFA, we began by randomly dividing the sample of students, all of whom had data on at least one item, into two halves; this split was made after stratifying students by school, to ensure that school assignment was distributed identically across the two groups. In the first half (calibration sample) we conducted a ML-EFA; in the second half (validation sample), we conducted a ML-CFA. We also used the ML-EFA to trim the item set into a smaller number of indicators and used the ML-CFA to cross-validate the ML-EFA results in a second split-half sample. Use of split samples is common practice in factor analysis.

Across all models, we evaluated goodness-of-fit using the model chi-squared test, normed comparative fit index (CFI; Bentler 1990), root mean square error of approximation (RMSEA; Steiger 1990), and the standardized root mean square residual (SRMR; Muthén and Muthén 1998). These statistics provide information about the overall fit of the model and the model data consistency (comparing the model-estimated within- and between-level correlation matrices to the within- and between-level sample correlations). Acceptable model fit was determined by a non-significant chi-squared test, CFI values greater than 0.95, and RMSEA and SRMR values below 0.10 (Kline 2010). The CFI, RMSEA, and SRMR values were given more emphasis than the chi-squared test, as the chi-squared test statistic is often significant (implying significant misfit of the model to the data) when the sample size is large. In the MLFA, a SRMR is provided at both the within and between levels. There are no established guidelines for interpreting the SRMR at the between level. Thus, we considered the guidelines typically applied for single-level analyses (≤0.10) and also examined the residuals for the between-level correlation matrix, which can signal particular regions of and systematic patterns of misfit.

We began these analyses by collapsing response options to all items. We did this to eliminate response categories that were infrequently endorsed and thus provided little information about individual-level variability. We created three response options for all items; the collapsed response options appear in the right-side column of Table 1, alongside the original response options. Examination of the polychoric correlation matrix for collapsed items was nearly identical to the original scaling, confirming that a negligible amount of information was lost by the category collapsing.

We conducted all analyses using Mplus software version 6.1. Mplus handles missing data, under the missing at random assumption (MAR), using the weighted least squares with mean and variance adjustment (WLSMV) estimator, which allows missingness to be a function of the observed covariates, but not observed outcomes, as is the case for full information maximum likelihood. When there are no covariates in the model, this is analogous to pairwise present analysis (Muthén and Muthén 1998). We also calculated intraclass correlation coefficients (ICCs) for each item, which indicate the proportion of variance in each observed indicator variable that is due to differences between schools.

These analyses were guided by both theory, broadly related to child development and specifically to school environments, and empirical findings. In both the ML-EFA and ML-CFA, we used WLSMV as the estimation method. We also included weights and stratification variables to adjust for student non-response, the unequal probability of selection of schools, and account for the clustering of students in school. In the ML-EFA, we applied a geomin oblique rotation method, allowing the factors to be correlated. To determine the final model for the ML-EFA, we followed an iterative process whereby we first focused on the within-level results and then proceeded to focus on the between-level results. Specifically, we looked at a variety of different within-level solutions (e.g., between 1 and 7 factors) that were generated with an unstructured between level; the unstructured between level is a model that is fully saturated (perfect fit model) at the between level, meaning that all random item intercepts are allowed to correlate with each other. After deciding on one or two candidate factor enumerations based on overall fit, we then examined several different between-level solutions where the within level was unstructured. Essentially, we considered both the between-level and within-level results so that we would not mistakenly exclude an item that may have disparate performance across levels (e.g., performing poorly at the within level, but well on the between level). For the ML-EFA, we used scree plots, number of eigenvalues greater than one, and model goodness-of-fit statistics to help guide us in deciding the final number of factors to retain at both the within and between levels. After reaching a small number of candidate within- and between-level factor enumerations, we examined the ML-EFA solutions for all possible combinations (e.g., three within-level factors with one between-level factor and three within-level factors with two between-level factors), evaluating each combined within- and between-level factor enumeration according to overall fit as well as substantive interpretability and utility. We examined the performance of each individual item at both the within and between levels because it is at this juncture in conventional single-level EFA that items may be trimmed if they fail to load significantly on any of the factors or if they load significantly on all the factors. We considered trimming items based on magnitude of factor loadings, statistical significance, ratio of the smallest to largest factor loading, etc. Using the final ML-EFA solution, we fit a ML-CFA to the validation half of the split sample, using a model specification wherein any non-statistically significant cross-loadings or cross-loading smaller that 0.32 (standardized) in the ML-EFA were fixed at zero in the ML-CFA (Tabachnick and Fidell 2001). We trimmed items and cross-loadings to develop a parsimonious solution; this is commonplace in factor analysis (Brown 2006; Kline 2010). Our decision to exclude items was made on a similar basis: items that loaded strongly with statistically significant loadings greater than 0.50 on one item at the within and/or between level or items with statistically significant cross-loadings of at least 0.32 on two items at both the within and/or between level were retained. Since the ML-EFA solution provides standardized factor loadings by default, we presented and interpreted standardized factor loadings in the ML-CFA.

We found a small degree of missingness across the items, ranging from a low of 5.13% (does not try hard in school) to a high of 12.95 % (feeling accepted). We included participants with data on at least one item in all analyses, resulting in a total sample of 79,362. The split-half samples (“sample 1,” the calibration sample used for the ML-EFA; “sample 2,” the validation sample used for the ML-CFA) were balanced on demographics, including sex (50.04 % female sample 1; 50.19 % female sample 2), grade level (13.38 % grade 7 sample 1; 13.57%grade 7 sample 2; 15.52% grade 12 sample 1; 15.40 % grade 12 sample 2), and race/ethnicity (18.83 % Hispanic sample 1; 18.80 % Hispanic sample 2). Each sample also contained a similar number of students in each school (sample 1: n=39,669; sample 2: n=39,693).

Results

Intraclass Correlation Coefficients

Table 2 presents ICC estimates from each split sample. ICCs ranged from small to large in magnitude, with 0.9 % of the variation for feeling afraid being due to differences across schools in sample 1, compared to 17.5 % for getting drunk. The remaining variance (1 minus the ICC) was due to differences between students within a school. ICCs were very similar across the split samples. Although most of the variability in these items was due to differences within, rather than between schools, there was considerable variability among the indicators as to the proportion of variation explained between schools. The discrepancy in ICC values across items suggests that school-level sources of variation do not operate uniformly across items. These differences in relative student- and school-level variation also hint at possible differences in the relationship between these items at the two levels of analysis.

Table 2.

Estimated intraclass correlation coefficients (ICCs) for each observed indicator variable in each split sample (n=79,362)

	Intraclass correlation coefficient (ICC)
Observed indicator variables	Sample one (n=39,669)	Sample two (n=39,693)
Trouble paying attention	0.021	0.034
Trouble getting homework done	0.021	0.029
Trouble getting along with teachers	0.038	0.035
Trouble getting along with other students	0.069	0.052
Skipping school	0.126	0.111
Does not try hard in school	0.071	0.068
Getting into a physical fight	0.036	0.035
Smoking cigarettes	0.092	0.141
Getting drunk	0.175	0.202
Feel blue	0.064	0.040
Cried a lot	0.019	0.014
Were moody	0.043	0.036
Trouble relaxing	0.018	0.019
Afraid of things	0.009	0.012
Not doing everything right	0.032	0.030
Not proud of self	0.023	0.027
Does not like oneself	0.026	0.027
Does not feel socially accepted	0.010	0.009
Feels unloved and unwanted	0.020	0.015
Does not have good qualities	0.017	0.018
Feel really sick	0.011	0.014

ICC refers to the proportion of variance in the observed variable that is due to differences across schools

Correlations

Table 3 presents the within- and between-level correlations, in the first randomly split sample (the results from the second randomly split sample are very similar). Correlations among indicators were as high as r=0.720 at the within level and r= 0.924 at the between level. The average correlations at the within and between levels were very similar (mean within-level correlation=0.250, mean between-level correlation=0.243). Most notable, and underscoring the value of the MLFA approach, was the finding that there were differences (in both magnitude and direction) in the correlations between items at the within and between levels. For example, the items fight and drunk were correlated 0.39 at the within level, but −0.53 at the between level.

Table 3.

Correlations among the 21 indicator variables at the within level (below the diagonal) and the between level (above the diagonal)

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
1 TRTEACH	1.00	0.50	0.62	0.91	−0.58	0.83	−0.14	−0.37	−0.44	−0.58	−0.58	−0.59	−0.43	−0.32	0.29	−0.23	−0.03	0.05	−0.34	−0.60	−0.65
2 TRPAYAT	0.63	1.00	0.80	0.34	0.23	0.08	0.39	0.15	0.26	0. 0.21	0.37	0.16	−0.18	0.03	0.13	0.46	0.44	−0.10	0.09	0.19	0.21
3 TRHOMEW	0.56	0.73	1.00	0.60	−0.02	0.32	0.46	0.01	0.07	−0.04	0.03	−0.10	−0.21	−0.07	0.25	0.29	0.39	0.04	0.11	−0.10	−0.13
4 TRALONG	0.57	0.59	0.57	1.00	−0.74	0.90	−0.33	−0.42	−0.63	−0.85	−0.72	−0.78	−0.68	−0.39	−0.07	−0.27	0.14	0.15	−0.43	−0.73	−0.73
5 TRYHARD	0.17	0.23	0.24	0.08	1.00	−0.72	0.63	0.76	0.78	0.88	0.82	0.88	0.55	0.27	0.03	0.40	0.35	0.18	0.56	0.85	0.88
6 FIGHT	0.27	0.17	0.16	0.24	0.22	1.00	−0.30	−0.29	−0.53	−0.76	−0.63	−0.68	−0.45	−0.34	0.19	−0.22	0.09	0.19	−0.16	−0.61	−0.70
7 TRUANT	0.20	0.22	0.22	0.13	0.39	0.34	1.00	0.65	0.72	0.59	0.57	0.52	0.32	0.03	0.27	0.43	0.48	0.08	0.57	0.52	0.51
8 CIG	0.21	0.20	0.18	0.13	0.33	0.33	0.51	1.00	0.91	0.54	0.79	0.77	0.31	0.19	0.29	0.61	0.54	0.17	0.63	0.71	0.74
9 DRUNK	0.21	0.19	0.16	0.11	0.36	0.39	0.60	0.68	1.00	0.80	0.79	0.78	0.56	0.27	0.44	0.63	0.37	0.02	0.60	0.71	0.73
10BLUE	0.07	0.15	0.11	0.11	0.14	0.07	0.21	0.25	0.21	1.00	0.82	0.92	0.70	0.26	0.32	0.51	−0.09	−0.09	0.57	0.86	0.84
11RELAX	0.10	0.17	0.13	0.12	0.14	0.11	0.21	0.22	0.19	0.63	1.00	0.87	0.62	0.58	−0.02	0.56	0.45	0.22	0.67	0.84	0.86
12MOODY	0.09	0.16	0.10	0.12	0.14	0.10	0.22	0.24	0.22	0.61	0.56	1.00	0.66	0.27	0.23	0.48	0.13	0.05	0.56	0.87	0.90
13CRY	0.03	0.09	0.07	0.08	0.00	−0.01	0.13	0.19	0.14	0.62	0.48	0.55	1.00	0.40	0.54	0.49	0.02	0.21	0.72	0.62	0.64
14AFRAID	0.06	0.13	0.11	0.10	0.03	−0.01	0.10	0.12	0.08	0.48	0.45	0.44	0.60	1.00	0.07	0.28	0.23	0.16	0.41	0.43	0.37
15SICK	0.11	0.13	0.11	0.11	0.05	0.11	0.17	0.17	0.15	0.35	0.35	0.36	0.38	0.30	1.00	0.46	−0.03	0.02	0.32	0.14	0.01
16ACCEPT	0.05	0.10	0.08	0.17	0.13	0.07	0.10	0.12	0.05	0.37	0.32	0.27	0.25	0.24	0.20	1.00	0.68	0.38	0.69	0.55	0.61
17WANTED	0.11	0.14	0.11	0.15	0.22	0.17	0.18	0.21	0.16	0.39	0.34	0.28	0.23	0.21	0.20	0.69	1.00	0.68	0.91	0.60	0.43
18GQUAL	0.09	0.14	0.10	0.13	0.22	0.11	.19	0.23	0.17	0.31	0.29	0.23	0.23	0.20	0.19	0.55	0.59	1.00	0.69	0.38	0.28
19PROUD	0.13	0.17	0.16	0.14	0.27	0.14	0.24	0.28	0.22	0.39	0.33	0.28	0.26	0.23	0.23	0.58	0.65	0.72	1.00	0.80	0.58
20LIKESLF	0.05	0.13	0.10	0.08	0.19	0.04	0.14	0.20	0.14	0.44	0.35	0.35	0.34	0.29	0.24	0.56	0.55	0.56	0.63	1.00	0.90
21RIGHT	0.06	0.17	0.14	0.08	0.28	0.06	0.19	0.20	0.17	0.43	0.36	0.36	0.31	0.30	0.22	0.55	0.53	0.49	0.56	0.72	1.00

TRTEACH trouble getting along with teachers, TRPAYAT trouble paying attention, TRHOMEW trouble getting homework done, TRALONG trouble getting along with other students, TRYHARD does not try hard, FIGHT getting into physical fights, TRUANT skipping school, CIG smoking cigarettes, DRUNK getting drunk, BLUE feel blue, RELAX trouble relaxing, MOODY were moody, CRY cried a lot, AFRAID afraid of things, SICK feel really sick, ACCEPT does not feel socially accepted, WANTED feels unloved and unwanted, GQUAL does not have good qualities, PROUD not proud of self, LIKESLF does not like oneself, RIGHT not doing everything right

Multilevel Factor Analysis

Multilevel Exploratory Factor Analysis

We began by conducting a ML-EFA in the first randomly divided sample using the 21 items. As previously noted, we began by conducting a ML-EFA, rather than ML-CFA due to the lack of prior reporting of the number of factors underlying these items at the student or school level. To determine the number of factors, we looked at the scree plot and examined the number of eigenvalues greater than one (following Kaiser’s criteria). We found four eigenvalues greater than one at the within level, suggesting a four-factor solution; the scree plot suggested a five-factor solution. We also found four eigenvalues greater than one at the between level. The between-level scree plot suggested a four-factor solution.

In examining the results for between a one- and five-factor solution at the within level, with an unstructured between level, we found the models with less than four factors had inadequate model fit. We therefore more closely examined the four- (χ²=5,293.889; df=132; p<0.00001; CFI=0.979; RMSEA=0.031; SRMR_within=0.029) and five-factor within-level solutions (χ²=2547.780; df=115; p<0.00001; CFI=0.990; RMSEA=0.023; SRMR_within=0.021). In evaluating these models, we concluded that the four-factor model was the best fitting both empirically and conceptually. It had good fit statistics and four interesting and distinct factors. In contrast, although the fit of the five-factor solution was good, the fifth factor was not meaningful, as it consisted entirely of cross-loadings and did not have a sufficient number of items per factor to yield a distinct factor. Thus, on the basis of empirical findings and theoretical insights, we chose the four-factor solution as our within-level solution.

We next examined the results for between a one- and four-factor solutions at the between level, within an unstructured within level. Here, we found the models with less than three factors had inadequate model fit. However, the three- (χ²= 247.819; df=150; p<0.00001; CFI=1.000; RMSEA=0.004; SRMR_between=0.082), and four-factor solutions (χ²=162.346; df=132; p=0.0374; CFI=1.000; RMSEA=0.002; SRMR_between=0.056) did have good fit. Upon closer inspection of the three- and four-factor solutions, we found the three-factor solution provided more meaningful information than the four-factor solution. Specifically, the fourth factor provided by the four-factor solution did not provide a unique factor; it consisted entirely of cross-loadings. We therefore chose the three-factor solution as our between-level solution.

Before proceeding to the ML-CFA, we examined the ML-EFA model with four-factor within and three-factor between solution and trimmed any items that lacked convergent validity at both the within and between levels. Specifically, we considered the deletion of the item sick (“In the past month, how often did you feel really sick”), as this item had low loadings at both the within and between levels with several large correlation residual values at both levels. We reran the ML-EFA excluding the item sick to evaluate whether the model fit and functioning of other items would change. Results of the sensitivity analysis revealed that the fit of the overall model was comparable after removing the item sick (χ²=5,566.936; df=249; p<0.0001; CFI=0.978; RMSEA= 0.023; SRMR_within=0.029; SRMR_between=0.065). However, the SRMR_between statistic decreased from 0.082 to 0.065 (a decline of 21 %). The functioning of the remaining items was the same across the two models (with and without sick). Given that the removal of this item did not affect the functioning of the remaining items and its low loading relative to other items on the same factor, we decided to proceed by removing the item sick from our analyses. Although there were some items that performed poorly at either the within or between level, these remaining items were not considered for removal as all of them performed well in the factor structure for at least one of the levels. For example, the item “afraid of things” had a relatively weak loading at the between level, but a relatively high loading at the within level.

Final ML-EFA Solution

Table 4 presents the rotated factor loadings for the final ML-EFA solution. At the within level, we named each factor as follows: (1) “school adjustment” to refer to the extent to which students report having difficulty adapting to the role of being a student; (2) “externalizing” to correspond to externalizing symptoms; (3) “internalizing” to describe internalizing symptoms; and (4) “self-esteem” to refer to students’ negative judgments of and attitudes toward themselves. Each factor consisted of at least three standardized loadings above 0.39. High factor loadings indicate a high reliability of that item as an indicator of the corresponding factor. The factors were modestly correlated with one another, ranging from r=0.14 (for school adjustment with internalizing) to r=0.44 (for internalizing with self-esteem). The communalities, which refer to the proportion of an indicator’s total variance that is accounted for by the factor solution, ranged from a low of 24.1 % (for fighting) to a high of 78.9 % (for drunk). Simple structure was generally achieved, as most items did not cross-load (e.g., the item did not have a significant loading on more than one factor). However, there were some items that had cross-loadings at the between level; this was expected given the noticeably higher correlations among the items at the between level compared to the within level. This reinforces the need for an analytic model that does not require a simple structure at either level or the same factor enumeration and configuration.

Table 4.

Factor loadings of items for the multilevel exploratory factor analysis (ML-EFA)

	Within-level				Between-level
	Factor 1 School adjustment	Factor 2 Externalizing	Factor 3 Internalizing	Factor 4 Self-esteem	Factor 1 Collective school adjustment	Factor 2 Psychosocial environment	Factor 3 Collective self-esteem
Trouble paying attention	0.861	0.000	0.040	0.012	0.980	0.009	−0.161
Trouble getting homework done	0.808	−0.006	0.010	0.002	0.903	−0.289	−0.009
Trouble getting along with teachers	0.731	0.077	−0.026	−0.040	0.616	−0.797	−0.010
Trouble getting along with other students	0.722	−0.035	0.010	0.024	0.523	−1.013	0.167
Skipping school	0.050	0.670	0.026	0.028	0.488	0.508	0.040
Does not try hard in school	0.089	0.390	−0.082	0.204	0.080	0.890	0.011
Getting into a physical fight	0.179	0.418	−0.079	0.015	0.261	−0.868	0.308
Smoking cigarettes	0.002	0.730	0.089	0.022	0.199	0.664	0.215
Getting drunk	−0.044	0.905	0.035	−0.055	0.244	0.817	−0.016
Feel blue	−0.016	0.089	0.749	0.106	0.064	1.007	−0.273
Cried a lot	−0.010	−0.065	0.831	−0.051	−0.228	0.679	0.134
Were moody	0.004	0.135	0.702	0.000	0.016	0.950	−0.100
Trouble relaxing	0.024	0.102	0.660	0.075	0.118	0.871	0.123
Afraid of things	0.060	−0.103	0.670	−0.005	−0.124	0.363	0.198
Not doing everything right	−0.010	−0.022	0.153	0.710	−0.026	0.892	0.151
Not proud of self	0.012	0.113	−0.030	0.802	0.018	0.489	0.769
Does not like oneself	−0.044	−0.049	0.150	0.769	−0.051	0.834	0.330
Does not feel socially accepted	0.042	−0.107	0.048	0.739	0.264	0.427	0.379
Feels unloved and unwanted	0.022	0.023	0.006	0.761	0.353	0.011	0.904
Does not have good qualities	−0.011	0.089	−0.077	0.790	−0.093	−0.076	0.828
Factor correlations	1.000				1.000
	0.277	1.000			0.204	1.000
	0.139	0.194	1.000		0.217	0.227	1.000
	0.177	0.251	0.444	1.000

All factor loadings in an EFA are standardized. High EFA loadings appear in bold

χ² =5566.936; df=249; p<0.0001; CFI=0.978; RMSEA=0.023; SRMR_within=0.029; SRMR_between=0.065

At the between level, we named the three latent factors as follows: (1) “collective school adjustment” to refer to the shared variation between random intercepts at the school level for a nearly identical item set to the school adjustment factor at the within level, with the addition of truant and feeling unloved/ unwanted at the between level; (2) “psychosocial environment” to refer to the shared variation between random intercepts for nearly all the item representing the collective behaviors, attitudes, emotions, and relations at the school level; and (3) “collective self-esteem” to refer to the shared variation between random intercepts at the school level for a nearly identical item set to the self-esteem factor at the within level, with the exclusion of right at the between level. As the values of the loadings for the school adjustment and self-esteems factors at the within and between levels were similar in sign but not identical in pattern or magnitude, we use the same general labels (i.e., “school adjustment” and “self-esteem”), but modify with the term “collective” rather than “aggregate” in an effort to differentiate these factors from a derived variable or aggregate approach. All three between-level factors are similarly correlated with one another (r=0.20−0.23). Communalities ranged from 49.6 % (crying) to a 98.6 % (feeling blue).

The results of the ML-EFA suggested three findings. First, student reports of more problems related to functioning in school (e.g., trouble paying attention and trouble getting along with teachers) were driven by both a student’s own underlying level of school adjustment and membership in schools with higher average levels of school adjustment problems across the student population. Similarly, student reports of lower evaluations of self-worth (e.g., not liking oneself and feeling unloved) were driven by both a student’s own underlying level of self-esteem and membership in schools with lower average levels of self-esteem across the student body. Student negative reports across nearly all the socioemotional and behavioral items were driven by the students’ own underlying levels of school adjustment, externalizing, internalizing, and self-esteem problems and membership in schools with poorer psychosocial environments. Interestingly, three of the items that load positively on the within-level factors loaded negatively on the between level psychosocial environment factor, specifically trteach (trouble getting along with teachers), tralong (trouble getting along with other students), and fight (getting into a physical fight). This suggests that there may be elements of the school psychosocial environment, such as levels of control and coercion, that may attenuate overt aggression and social discord while also exacerbating engagement, internalizing, and self-valuing problems across the student body.

We reran the final ML-EFA stratified by school type (middle school versus high school) and also stratified by specific grade levels and found the pattern and direction of loadings at both the within and between levels to be robust, suggesting that our results were not confounded by age.

As shown in Table 4, there were six items that cross-loaded on the between level. Additionally, as shown in Table 4, not all items loaded strongly on factors at both the within and between levels. For example, the item afraid loaded quite highly on the third within-level factor (loading=0.670), but quite low on the between-level factors (the highest loading it had was 0.363). Conversely, and as noted previously, the item tryhard loaded modestly at within level (loading=0.390), but very highly at the between level (loading=0.890). The same was also true for the item fight (within loading=0.418; between loading=−0.868). Moreover, while the first and third factor on the between level were nearly the same in loading pattern to the within level, the values of the loadings were distinct (note: fitting a ML-CFA model constraining the loadings for the school adjustment items and self-esteem items to be equal across levels resulted in a significant decrement in fit and overall poor fit to the data). Given the value and direction of the loadings for the psychosocial environment factor, it was not merely a simple convergence of within level factors at the between level (in other words, fitting a ML-CFA model with a four-factor simple structure at the between level matching the within level resulted in a significant decrement in fit and overall poor fit to the data). This emphasizes that not only can items function differently when there is a similar factor structure at the within and between levels, but also that the factor structure can be distinctly different at each level.

Multilevel Confirmatory Factor Analysis

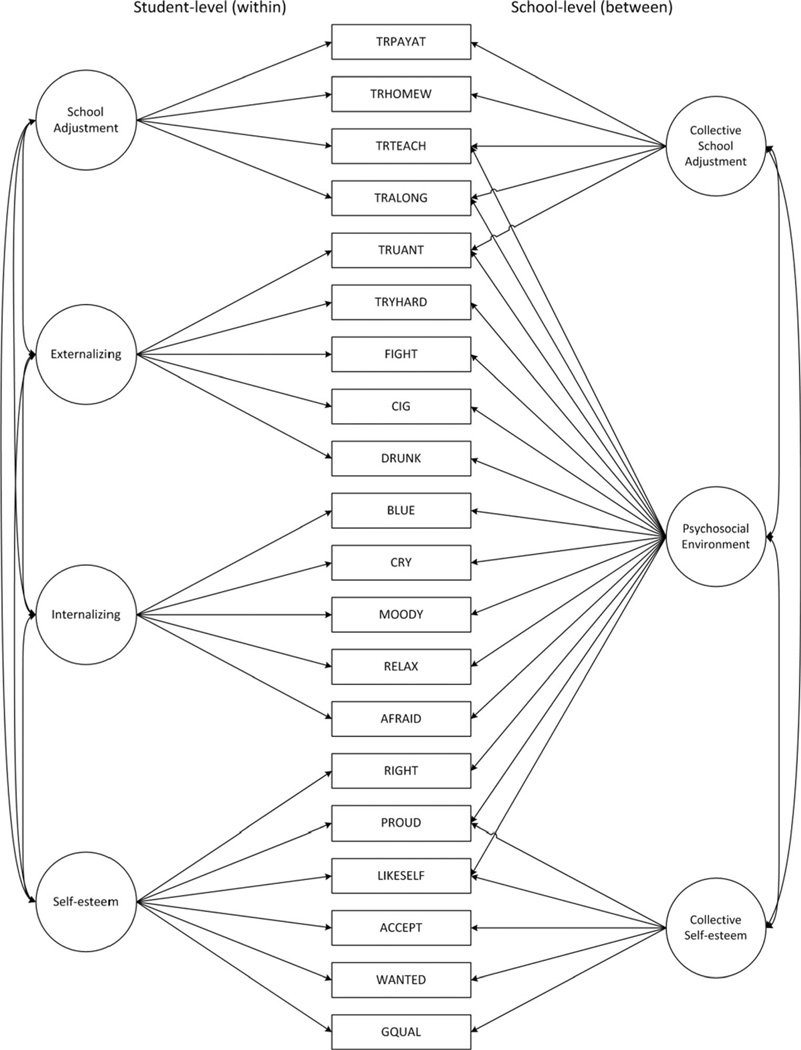
With the 20 variables retained from our ML-EFA, we conducted a ML-CFA in the second randomly divided sample (validation sample). We specifically fit a four-factor within and three-factor between solution, seeking to validate the ML-EFA results. As shown in Table 5 (and Fig. 2), the fit of the ML-CFA was good (χ²=6,138.098; df=326; p<0.0001; CFI=0.975; RMSEA=0.021; SRMR within=0.051; SRMR between=0.120). Factor loadings in the CFA were similar to the EFA. Although they were slightly higher in some cases, this was expected given that CFA estimates tend to be higher as a result of fixing cross-loadings to zero. Only a few indicators showed a notable difference between the EFA and CFA. For example, at the between level, the cross-loadings for not feeling socially accepted and feeling unwanted were nearly zero and not statistically significant.

Table 5.

Standardized factor loadings of items for the multilevel confirmatory factor analysis (ML-CFA)

	Within level				Between level
	Factor 1 School adjustment	Factor 2 Externalizing	Factor 3 Internalizing	Factor 4 Self-esteem	Factor 1 Factor 2 Collective school adjustment	Factor 2 Psychosocial environment	Factor 3 Collective self-esteem
Trouble paying attention	0.859				1.000
Trouble getting homework done	0.806				0.756
Trouble getting along with teachers	0.718				0.664	−0.743
Trouble getting along with other students	0.726				0.533	−0.883
Skipping school		0.700			0.261	0.618
Does not try hard in school		0.566				0.936
Getting into a physical fight		0.442				−0.616
Smoking cigarettes		0.784				0.776
Getting drunk		0.820				0.825
Feel blue			0.857			0.945
Cried a lot			0.735			0.701
Were moody			0.718			0.935
Trouble relaxing			0.720			0.913
Afraid of things			0.621			0.630
Not doing everything right				0.785		0.777
Not proud of self				0.825		0.367	0.766
Does not like oneself				0.816		0.711	0.250
Does not feel socially accepted				0.732		ns	0.819
Feels unloved and unwanted				0.761	ns		0.992
Does not have good qualities				0.741			0.755
Factor correlations	1.000				1.000
	0.404	1.000			0.119	1.000
	0.184	0.266	1.000		0.559	0.251	1.000
	0.209	0.326	0.541	1.000

Notes. χ² =6138.098; df=326; p<0.0001; CFI=0.975; RMSEA=0.021; SRMR_within=0.051; SRMR_between=0.120. Results shown fix two Heywood cases (non-significant negative residuals) at zero

Fig. 2.

Results of multilevel confirmatory factor analysis (ML-CFA). Latent factors are denoted by circles, observed indicators by rectangles. TRPAYAT trouble paying attention; TRHOMEW trouble getting homework done, TRTEACH trouble getting along with teachers, TRALONG trouble getting along with other students, TRUANT skipping school, TRYHARD does not try hard, FIGHT getting into physical fights, CIG smoking cigarettes, DRUNK getting drunk, BLUE feel blue, CRY cried a lot, MOODY were moody, RELAX trouble relaxing, AFRAID afraid of things, RIGHT not doing everything right, PROUD not proud of self, LIKESLF does not like oneself, ACCEPT does not feel socially accepted, WANTED feels unloved and unwanted, GQUAL does not have good qualities

Discussion

The purpose of this paper was to apply a fully multilevel strategy to model school psychosocial environment using individual-level data. Results of this study illustrate the strengths of MLFA in settings where individual-level data may capture one or more distinctly different constructs at each level of analysis. This practical illustration also showcases the broader utility of MLFA as an analytic tool that could be useful to prevention scientists when measuring and modeling individual and environmental-level features on the basis of data collected from individuals.

We found evidence to suggest the factor structure underlying observed variables may differ at the level of students and schools. That is, we found four latent factors at the within level (school adjustment, externalizing symptoms, internalizing symptoms, and self-esteem). Three factors emerged at the school level, two of which represented school-level collective analogues of the individual-level (school adjustment and self-esteem) factors and one of which represented a distinct construct of psychosocial environment. The finding that there were different latent factor structures at the student and school levels highlights the need for prevention theory and practice related to schools (and other contexts targeted by prevention scientists, such as neighborhoods) to separately consider and measure phenomenon at each level of analysis. In other words, our results underscore the need to consider a fully multilevel measurement model. Had we assumed the indicators of student attitudes and behaviors covaried in the same way at the school level as they do at the student level, we would have simply specified a four-factor model at the within level with random factor intercepts at the between level. In so doing, we would have produced a poorly fitting measurement model.

Moreover, our finding that there were differences in the sign of the relationships between the school-level psychosocial environment factor and the school-level social relationship indictors compared to the factor loadings at the student level is also important. These results suggest that if we found a school-based intervention that positively affected the school-level psychosocial environment factor but ignored the different factor structure at the student level, we might incorrectly infer that the positive effect would translate to more positive observed outcomes for all the psychosocial indicators at the student level.

In terms of prevention science practice, these findings suggest that interventions may need to be tailored to the specific level where change is intended. Thus, it may not be reasonable to assume an intervention operating at one level will have “trickle-up” or “trickle-down” effects on the other, non-directly intervened upon level. For example, targeting the self-esteem of individual students could influence the levels of school self-esteem, as these factors share common items. In contrast, targeting the psychosocial environment of the school could impact a broad range of student attitudes and behaviors, although some changes that may appear favorable with respect to certain problems (e.g., overt aggression and relational aggression) could negatively impact other psychosocial outcomes.

Beyond its conceptual and methodological advantages, there are several applied benefits of MLFA (Dunn et al. 2014). Most notable is the fact that MLFA can be easily incorporated into research studies where individuals are sampled through clustering methods and items are collected from students that could provide information about environment-level phenomenon. Many prevention and intervention studies focused on children and adolescents already collect data from youth nested in school and neighborhood environments. However, very few explicitly study how the school environment, in particular, is linked to youth outcomes. Using MLFA, researchers can model the effects of contexts on youth outcomes, even when data were not designed for such purposes. Thus, MLFA provides an opportunity for prevention researchers to study psychosocial environments by using data collected from individuals. This may allow researchers to use fewer resources, while making the most out of their data collection efforts. This is particularly salient in today’s economic and political context, where data collection efforts in schools have been constrained by shrinking educational budgets and a culture of high stakes testing.

Given the limited number of studies published using MLFA, we offer a few recommendations. First, as noted previously, researchers using the MLFA should trim items only after examining how each item performs on both levels so that items are only trimmed if it does not function at both levels. It would be problematic to eliminate an item on the basis of its loading at only one level; both levels must be examined simultaneously. Otherwise, there is a risk of removing an item that has a weak loading on one level, but a strong loading on another. Second, although it may be tempting to use techniques to account for the lack of independence in the observations (e.g., the type=complex command in Mplus), rather than conducting a MLFA, using such a model under circumstances where there are distinct measurement structures at each level may lead to serious model misspecification.

This study has several strengths. Data come from a large, nationally representative survey of youth. We therefore had a very large sample size from which to conduct these analyses and can generalize results to diverse populations. However, there were some limitations. For example, although the sample of students was large, the number of schools they were drawn from was moderate. In addition, we intentionally limited our item set to those specifically hypothesized to reflect the school psychosocial environment. However, a more expansive model including items spanning the other domains of school climate could be specified. By examining more traditional school climate constructs, in combination with the constructs identified here, researchers could develop new insights that expand our understanding of school climate. Given the subjective nature of factor analysis, there may also be limitations to how we labeled each factor. Of course, as with any factor analysis, our final model is by no means the only latent variable model that would be consistent with this data. Arriving at and cross-validating the MLFA with this data neither proves the existence of these particular factors nor validates our labeling and substantive interpretation of the factors. Future research is needed to identify whether these are the best labels for these factors.

In summary, this study contributes to the literature by showing how data collected from individuals can be used to provide information about the settings to which they belong. The MLFA method provides researchers with a unique tool to guide the development of theory, research, and practice on school and other environments.