Abstract
To make an optimal decision we need to weigh all the available options, compare them with the current goal, and choose the most rewarding one. Depending on the situation an optimal decision could be to either “explore” or “exploit” or “not to take any action” for which the Basal Ganglia (BG) is considered to be a key neural substrate. In an attempt to expand this classical picture of BG function, we had earlier hypothesized that the Indirect Pathway (IP) of the BG could be the subcortical substrate for exploration. In this study we build a spiking network model to relate exploration to synchrony levels in the BG (which are a neural marker for tremor in Parkinson's disease). Key BG nuclei such as the Sub Thalamic Nucleus (STN), Globus Pallidus externus (GPe) and Globus Pallidus internus (GPi) were modeled as Izhikevich spiking neurons whereas the Striatal output was modeled as Poisson spikes. The model is cast in reinforcement learning framework with the dopamine signal representing reward prediction error. We apply the model to two decision making tasks: a binary action selection task (similar to one used by Humphries et al., 2006) and an n-armed bandit task (Bourdaud et al., 2008). The model shows that exploration levels could be controlled by STN's lateral connection strength which also influenced the synchrony levels in the STN-GPe circuit. An increase in STN's lateral strength led to a decrease in exploration which can be thought as the possible explanation for reduced exploratory levels in Parkinson's patients. Our simulations also show that on complete removal of IP, the model exhibits only Go and No-Go behaviors, thereby demonstrating the crucial role of IP in exploration. Our model provides a unified account for synchronization, action section, and explorative behavior.
Keywords: Basal Ganglia, Izhikevich neurons, synchronization, n-arm bandit task, exploration
Introduction
Imagine a situation where you would like to dine out and are in search of suitable restaurants. Some restaurants you know for sure are good, and others you have no idea about. In other words you have two fundamentally different options of which one is to order your favorite dish and play it safe (i.e., “exploit”) while the other is to try something new (i.e., “explore”). Further, an unexpected weather change would force you to stay at home (i.e., a No Go decision). How does our brain make a decision in such a scenario? Depending on the situation, an optimal decision could be to either explore, exploit or to take no action (Cohen et al., 2007; Prescott et al., 2007).
A group of subcortical structures collectively called the Basal ganglia (BG) play an important role in many cognitive processes (Gurney et al., 2001a,b; Humphries and Gurney, 2002; Chakravarthy et al., 2010; Schroll et al., 2012; Yucelgen et al., 2012; Chersi et al., 2013) including decision making and action selection. The BG circuit includes the neo-striatum (caudate and putamen), Globus pallidus (externa, GPe, and interna, GPi), subthalamic nucleus (STN), and substantia nigra (pars compacta, SNc and pars reticulata, SNr). BG receive inputs from the cortex through the striatum and STN (Maurice et al., 1998; Aravamuthan et al., 2007) and project through SNr and GPi, the output nuclei of BG, via thalamus (Albin et al., 1989) to motor and executive areas of the cortex (Steiner and Tseng, 2010). Classically BG pathways are segregated into the indirect pathway (IP) constituting a part of the striatum, GPe and STN projecting to GPi (Gerfen and Surmeier, 2011) and the direct pathway (DP) constituting the projection from the striatum to GPi (Gerfen and Surmeier, 2011). The final “action selection” is based on the combined contributions of the two pathways at output nuclei (Smith et al., 1998). The effect of dopamine (DA) on BG pathways and decision making has been well known (Rogers, 2010). Under low DA conditions, IP is more active than DP leading to “No-Go” behavior (Frank, 2005) whereas in high DA conditions DP is more active than IP leading to “Go” (Chevalier and Deniau, 1990). But this traditional explanation of action selection in binary terms of Go/No Go misses out “exploration” and its possible neural substrates out of the picture.
The ability to switch between explorative and exploitative behavior during decision making drew the attention of neuroscientists to study and characterize the corresponding anatomical substrates. It has been suggested that the pallidum, in its interactions with the noradrenergic system, controls the balance between exploration-exploitation (Russell et al., 1992; Aston-Jones et al., 1994; Doya, 2002). Humphries et al. (2007) argue that the brainstem specifically medial reticular formation (mRF) might be the substrate for action selection (Humphries et al., 2007). Schroll et al. (2012) presented a model of working memory sub-served by the cortico-basal-ganglia-thalamic loops where exploration in the model was obtained by the addition of noise to neural dynamics, but no anatomical substrate was suggested (Schroll et al., 2012). Chersi et al. (2013) simulate the role of BG and prefrontal cortex in goal-oriented learning vs. habitual learning and hypothesize that exploration emerges during the “up” state of striatal neurons (Chersi et al., 2013). Shouno et al. (2009) built a spiking network model of BG where the IP selects an action and the DP determines the timing of the selected action. Though the model was able to show exploration in terms of variability in action selection, there was no component of learning in the network (Shouno et al., 2009). Stewart et al. (2012) simulated the rat bandit task experiment using leaky integrate and fire model of cortex and BG where the spiking activity of ventral striatum during a response was measured. Though the model showed behavioral learning, anatomical substrate for exploration was not suggested (Stewart et al., 2012). A recent study by Humphries et al. (2012) suggest the role of tonic DA in setting the exploitation- exploration tradeoff (Humphries et al., 2012) in basal ganglia. Among computational models of BG, very few simulated the neural substrates for exploration within the BG system. The study by Archibald et al. (2013a) on PD patients indicates a decrease in exploration behavior compared to healthy controls during a visuo-spatial task (Archibald et al., 2013a,b).
Chakravarthy et al. (2010) suggested that STN-GPe loop, a coupled excitatory-inhibitory network in the IP, might be the substrate for exploration (Chakravarthy et al., 2010). It is well known that coupled excitatory-inhibitory pools of neurons can exhibit rich dynamic behavior like oscillations and chaos (Borisyuk et al., 1995; Sinha, 1999). This hypothesis has inspired models simulating various BG functions ranging from action selection in continuous spaces (Krishnan et al., 2011), reaching movements (Magdoom et al., 2011), spatial navigation (Sukumar et al., 2012), precision grip (Gupta et al., 2013), and gait (Muralidharan et al., 2013) in normal and Parkinsonian conditions. Using a network of rate-coding neurons, Kalva et al. (2012) showed that exploration emerges out of the chaotic dynamics of the STN-GPe system (Kalva et al., 2012). Most rate coded models, by design, fail to capture dynamic phenomena like synchronization found in more realistic spiking neuron models (Terman et al., 2002; Park et al., 2010, 2011). Synchronization within BG nuclei had gained attention since the discovery that STN, GPe, and GPi neurons show high levels of synchrony in Parkinsonian conditions (Bergman et al., 1994; Bevan et al., 2002; Hammond et al., 2007; Tachibana et al., 2011; Weinberger and Dostrovsky, 2011). This oscillatory activity was found to be present in two frequency bands, one around the tremor frequency [2–4 Hz] and another in [10–30 Hz] frequency (Weinberger and Dostrovsky, 2011). Park et al. (2011) report the presence of intermittent synchrony between STN neurons and its Local field potentials (LFP), recorded using multiunit activity electrodes from PD patients undergoing Deep Brain Stimulation (DBS) surgery (Park et al., 2011) which is absent in healthy controls.
One of the key objectives of the current study is to use a 2D spiking neuron model to understand and correlate STN-GPe's synchrony levels to exploration. As the second objective, we apply the above-mentioned model to the n-armed bandit problem of Daw et al. (2006) and Bourdaud et al. (2008) with the specific aim of studying the contributions of STN-GPe dynamics to exploration. The proposed model shares some aspects of classical RL-based approach to BG modeling. For example, dopamine signal is compared to reward prediction error (Schultz, 1998). Furthermore, DA is allowed to control cortico-striatal plasticity [47], modulate the gains of striatal neurons (Kliem et al., 2007; Hadipour-Niktarash et al., 2012) and influence the dynamics of STN-GPe by modulating the connections (Kreiss et al., 1997; Fan et al., 2012).
The paper is organized as follows. Section Methods: Model Details describes the model architecture and equations used in the simulations. Section Results presents the results. Implications of the modeling study are discussed in the final section.
Methods: model details
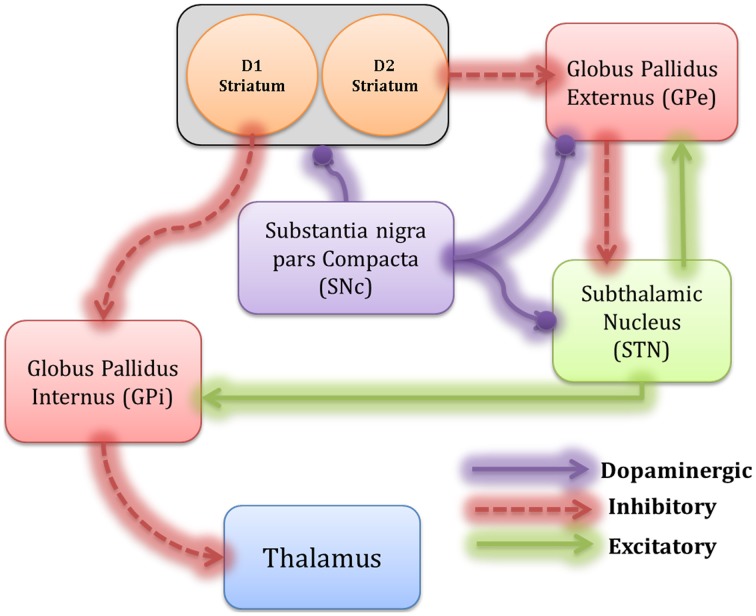
The model consists of the striatum, STN, GPe, GPi, and SNc (Figure 1). Modeling details of various BG nuclei are described below. All the simulations were coded using MATLAB v2012.
Figure 1.
The architecture of the proposed spiking neural Basal Ganglia model, which includes Striatum, GPe, GPi, STN, thalamus, and SNc. The inhibitory connections are represented by dotted lines and the excitatory connections by solid lines. The modulatory effect of DA is shown by the solid line with a ball.
Striatum
Striatal neurons display irregular firing patterns during wakeful stage (Stern et al., 1998; Mahon et al., 2006) which was accounted by modeling the striatal (both D1 and D2) output as Poisson process. The presynaptic potentials due to this striatal output [D1R expressing and D2R expressing medium spiny neurons (MSNs), (Kreitzer, 2009)] was represented as 2 unconnected pools (50 × 50 each) that give rise to GABAergic current from D1 striatum to GPi (Gerfen et al., 1990; Gurney et al., 2001a; Gerfen and Surmeier, 2011) and D2 striatum to GPe neurons (Gerfen et al., 1990) respectively.
Izhikevich neuron model
Izhikevich spiking neuron models have an advantage of being computationally inexpensive compared to biophysical models yet capable to capture various neuronal properties such as firing rate and spike pattern (Izhikevich, 2003) which is absent in rate coded models. The key modules in BG circuit including GPe, STN, and GPi (Figure 1) were modeled using Izhikevich neuron models arranged in a 2D lattice (= 50 × 50) consisting of 2500 neurons each. The Izhikevich parameters (a, b, c, d) for STN neuron were adapted from (Michmizos and Nikita, 2011), GPe and GPi neurons were modeled as tonically spiking Izhikevich neurons (Izhikevich, 2003). The external current (Ix) was adjusted to match the published firing frequencies of these neuronal types (Modolo et al., 2007). The values of the Izhikevich parameters are given in Table 1.
Table 1.
Gives the values and the description of the parameters used in the model and simulation.
| Parameter | Values with description | |||
|---|---|---|---|---|
| STN | GPe | GPi | ||
| Izhikevich parameters | a = 0.005, b = 0.265, c = −65, d = 1.5 | a = 0.1, b = 0.2, c = −65, d = 2 | a = 0.1, b = 0.2, c = −65, d = 2 | |
| External current (I) | ISTN = 30 | IGPe = 10 | IGPi = 10 | |
| StrD1→GPi | 0.8 | Synaptic weight between D1 striatum and GPi | ||
| WStrD2→GPe | 1 | Synaptic weight between D2 striatum and GPe | ||
| DA | 0.1–0.9 in increments of 0.1 | |||
| AD1 | 10 | Amplitude of GABAergic current from D1 striatum to GPi neurons due to DA | ||
| AD2 | 7.5 | Amplitude of GABAergic current from D2 striatum to GPe neurons due to DA | ||
| λStr | 7.5 | Slope of the Gain functions (cD1 and cD2) | ||
| Mg2+ | 1 nM | Concentration of Magnesium ions in nM | ||
| EAMPA | 0 mv | Synaptic potential of AMPA receptor-associated channel | ||
| ENMDA | 0 mV | Synaptic potential of NMDA receptor-associated channel | ||
| EGABA | −60 mV | Synaptic potential of GABA receptor-associated channel | ||
| wsg | 1 | Synaptic weight for excitatory STN to GPe projection | ||
| wgs | 20 | Synaptic weight for inhibitory GPe to STN projection | ||
| cd2 | 0.1 | Parameter that affects the STN→GPe (wsg) and GPe→STN(wgs) weights | ||
| τAMPA | 6 ms | Time decay constant for AMPA receptor | ||
| τNMDA | 160 ms | Time decay constant for NMDA receptor | ||
| τGABA | 4 ms | Time decay constant for GABA receptor | ||
| τNMDA_GPi | 67 ms | Time decay constant for NMDA receptor of GPi neurons | ||
| rs | 1 | Radius of STN laterals Gaussian | ||
| rg | 0.5 | Radius of GPe laterals Gaussian | ||
| cD21 | 0.1 | Parameter that affects the radius of STN and GPe laterals | ||
| AGPe | 1 | Synaptic strength within GPe laterals | ||
| ASTN | 0.2 | Synaptic strength within STN laterals | ||
| nlatSTN− | 5 | # of lateral connections considered in STN neurons | ||
| nlatGPe− | 11 | # of lateral connections considered in GPe neurons | ||
| wSTN→GPi | 1.15 | Synaptic weight between STN and GPi | ||
STN, Sub Thalamic Nucleus; GPe, Globus Pallidus Externa; GPi, Globus Pallidus Interna.
| (1) |
| (2) |
| (3) |
where, vxij = membrane potential, uxij = membrane recovery variable, ISynij = total synaptic current received, Ixij = external current applied to neuron x at location (i, j), vpeak = maximum voltage set to neuron (+30 mv) with x being STN or GPe or GPi neuron.
Synaptic connections
The synaptic connectivity between the nuclei was considered as one to one as in Dovzhenok and Rubchinsky (2012) and was modeled as (similar to Humphries et al., 2009)
| (4) |
| (5) |
The effect of voltage-dependent magnesium channel on NMDA current (Jahr and Stevens, 1990) was modeled as,
| (6) |
where, τRecep = decay constant for synaptic receptor, ERecep = receptor associated synaptic potential (Recep = AMPA/GABA/NMDA), Sxij = Spiking activity of neuron “x” at time “t,” hx→yij = gating variable for the synaptic current from “x” to “y,” Wx→y = synaptic weight from neuron “x” to “y,” Mg2+ = Magnesium ion concentration and Vyij = membrane potential of the neuron “y” for the neuron at the location (i, j) The time constants of GABA, AMPA, and NMDA in STN and GPe were chosen from (Götz et al., 1997) are given in Table 1. All the synaptic connections with their respective variables are described in Table 2 and the values of parameters are given in Table 1.
Table 2.
Gives a description of all the synaptic variables of various synaptic currents modeled using Equations (4) and (8) in Section Synaptic Connections.
| Variable | Description |
|---|---|
| hStrD1x→GPiij | Gating variables for GPi neuron due to GABAergic projections from D1 striatum. “x” represents the input #. For example, if there are 2 inputs presented to the model, x = 1, 2 |
| hStrD2x→GPeij | Gating variable for GPe neuron due to GABAergic projections from D2 striatum |
| hAMPA→GPeij/hNMDA→GPeij | Gating variable for GPe neuron due to glutamatergic input from STN due to either NMDA or AMPA receptor |
| hGABA→STNij | Gating variable for STN neuron due to GABAergic input from GPe neuron |
| hAMPA→STNij/hNMDA→STNij | Gating variable for STN neuron due to glutamatergic input from its collaterals due to either NMDA or AMPA receptor |
| hGABA→GPeij | Gating variable for GPe neuron due to GABAergic input from its collaterals. |
| IStrD1→GPiij | Inhibitory GABAergic current to GPi neuron from D1 striatum |
| IStrD2→GPeij | Inhibitory GABAergic current to GPe neuron from D2 striatum |
| IAMPA→GPeij/INMDA→GPeij | Excitatory glutamatergic current (AMPA/NMDA) from STN neuron to GPe neuron |
| IGABA→STNij | Inhibitory GABAergic current from GPe neuron to STN neuron |
| IAMPAlatij/INMDAlatij | Excitatory glutamatergic current (AMPA/NMDA) from STN neuron to STN neuron due to collateral synapses |
| IGABAlatij | Inhibitory GABAergic current from GPe neuron to GPe neuron due to collateral synapses |
| SGPeij | Spiking activity of GPe neuron at location (i, j) at time “t” |
| SSTNij | Spiking activity of STN neuron at location (i, j) at time “t” |
| SDxyij | Spiking activity of striatum at location (i, j) at time “t.” The variable “y” represents either D1 striatum (=1) or D2 striatum (=2) for an input stimulus “x” |
TN, Sub Thalamic Nucleus; GPe, Globus Pallidus Externa; GPi, Globus Pallidus Interna.
Lateral connections in STN and GPe neurons
Various anatomical studies show the presence of collaterals in STN (Kita et al., 1983) and GPe (Kita and Kita, 1994) neurons. Gillies et al. (2002) show, using a computational model, how various neural firing patterns could emerge due to collaterals in STN (Gillies and Willshaw, 1998). The lateral connections in the current network were modeled as Gaussian neighborhoods. Each neuron (in STN/GPe) receives collateral synaptic input from a fixed number of neighboring neurons located in a 2D grid of size nxn.
Effect of DA on synaptic structural plasticity of STN and GPe neurons
Behavioral learning can lead to synaptic structural changes either in dendrites or in signaling pathways (Caroni et al., 2012). Axonal and dendritic spine elongation and reduction in various areas of brain such as neo-cortex and hippocampus is well known (Richards et al., 2005; Gogolla et al., 2007; Caroni et al., 2012). Interestingly, this structural plasticity has also been observed in dorsal and ventral striatum of BG due to DA depletion (Meredith et al., 1995). Structurally, an increase in synaptic strength could be due to increase in the number of contacts or number of dendritic spines (Mckinney, 2010) which is associated with an increase in NMDA current (Tian et al., 2007). The burst firing in STN neurons observed under PD conditions is hypothesized to be due to increased NMDA currents (Zhu et al., 2005; Shen and Johnson, 2010). Also, Robertson et al. (1990) show a reduction in GABA-A receptor expression levels in GPe neurons of MPTP primates (Robertson et al., 1990), an area that receives projections from SNc (Smith and Kieval, 2000). A decrease in GABA-A levels has also been shown to be correlated to decrease in the number of dendritic spines in neurons (Pallotto and Deprez, 2014). A study by Fan et al. (2012) showed a greater proliferation of synapses from GPe to STN neuron in 6-OHDA rats compared to controls (Fan et al., 2012).
Considering the above mentioned experimental results, one may expect dopamine-dependent plasticity in STN and GPe neurons. Experimental studies have shown the synaptic currents from collaterals (inhibitory or excitatory) follow Gaussian distribution (Lukasiewicz and Werblin, 1990). It has been observed during experimental recordings that low DA levels increase the synchrony levels within STN neurons (Bergman et al., 1994, 1998). Theoretically, such behavior can be observed in any excitatory neurons when their lateral connections are strengthened (Hansel et al., 1995). Moreover, GPe neurons also show synchrony (Bergman et al., 1998) at low DA conditions and such a behavior in inhibitory neurons can be observed when their collateral strength is decreased (Wang and Rinzel, 1993). Taking these theoretical and experimental results into account, we assume that the width of the collateral spread to be modulated by DA levels.
Accordingly, the width of Gaussians in STN and GPe laterals (Section Lateral connections in STN and GPe neurons) in the model was assumed to be modulated by DA and modeled as,
| (7) |
| (8) |
where rs = constant variance of STN Gaussian, rg = constant variance of GPe Gaussian, Rs = changed variance of STN Gaussian due to the effect of dopamine, Rg = changed variance of GPe Gaussian due to the effect of dopamine, cD21 = a constant that determines the effect of DA on STN and GPe laterals, wm→mij = lateral weight matrix of neuron “m” at location (i,j), dij,pq = distance from center neuron (p,q), Rm = Rg(or) Rs, Am = strength of lateral synapse, m = STN or GPe neuron. All parameter values are given in Table 1.
The inhibitory (excitatory) collateral current developed in GPe (STN) neurons are governed by Equation (8). The effect of “Bij” is valid only for NMDA synapses made by STN collaterals but not for GABAergic synapses.
Experimental data suggests that DA causes post-synaptic effects on glutamatergic and GABA currents in STN and GPe respectively (Smith and Kieval, 2000; Cragg et al., 2004; Fan et al., 2012). Thus, we included a factor (cd2), which regulates the effect of the DA, on synaptic currents between STN and GPe, as in Equation (9). This leads to a decrease in the regulated current with increase in DA, as observed in Kreiss et al. (1997).
| (9) |
where the synapses are GPe→STN and STN→GPe. A similar method for DA-dependent synaptic modulation on striatal neurons was used in Humphries et al. (2009).
Total synaptic currents received by each neuron
Total synaptic currents received by GPe neurons.
The total synaptic current received by a GPe neuron at lattice position (i, j) is the summation of GABAergic input from the D2-expressing striatal MSNs (Gerfen et al., 1990) Equation (5), glutamatergic current from STN considering both AMPA and NMDA currents (Götz et al., 1997) Equation (5) and the inhibitory lateral current form other GPe neurons Equation (8). The influence of DA on the GABAergic current from D2 striatum to GPe neuron (Hadipour-Niktarash et al., 2012) was accounted by the variable cD2.
| (10) |
| (11) |
where, IGABAlatij = the inhibitory lateral GABAergic current from other GPe neurons, INMDA→GPeij = excitatory glutamatergic current from STN neuron due to NMDA receptor, IAMPA→GPeij = excitatory glutamatergic current from STN neuron due to AMPA receptor, IStrD2→GPeij = inhibitory GABAergic current from D2 striatum, cD2 = Gain parameter that affects the GABAergic D2 striatal current.
Total synaptic currents received by STN neurons.
The total synaptic current received by an STN neuron at lattice position (i, j) is summation of GABAergic current from GPe neurons (Fan et al., 2012) Equation (5) and glutamatergic input (both AMPA and NMDA) from other STN (Kita et al., 1983) Equation (8).
| (12) |
Where, INMDAlatij = excitatory glutamatergic current from collateral STN neurons due to NMDA receptor, IAMPAlatij = excitatory glutamatergic current from collateral STN neurons due to AMPA receptor, IGABA→STNij = inhibitory GABAergic current from GPe neuron.
Total synaptic currents received by GPi neurons.
The total synaptic current received by a GPi neuron at lattice position (i,j) is a summation of GABAergic currents from D1 striatal neurons (Gerfen et al., 1990)and glutamatergic (both AMPA and NMDA) input from STN neurons (Gerfen and Surmeier, 2011). The increase in GABAergic current from D1 striatum to GPi neurons due to DA modulation (Kliem et al., 2007) was taken into account by the variable cD1.
| (13) |
| (14) |
Where, INMDA→GPiij = excitatory glutamatergic current from STN neuron due to NMDA receptor, IAMPA→GPiij = excitatory glutamatergic current from STN neuron due to AMPA receptor, IStrD1→GPiij = inhibitory GABAergic current from D1 striatum, cD1 = Gain parameter that affects the GABAergic striatal current.
Synchronization
The phenomenon of neural synchrony has attracted the attention of many computational and experimental neuroscientists in the recent decades (Pinsky and Rinzel, 1995; Plenz and Kital, 1999; Hauptmann and Tass, 2007; Kumar et al., 2011; Park et al., 2011). It is believed that partial synchrony helps in the generation of various EEG rhythms such as alpha and beta (Izhikevich, 2007). Studying synchrony in neural networks has been gaining importance due to its presence in normal functioning (coordinated movement of the limbs) and in pathological states (e.g., synchronized activity of CA3 neurons in the hippocampus during an epileptic seizure) (Pinsky and Rinzel, 1995). Plenz and Kitai (1998) proposed that STN-GPe might act as a pacemaker (Plenz and Kital, 1999), a source for generating oscillations in pathological conditions such as Parkinson's disease. Park et al. (2011) report the presence of intermittent synchrony between STN neurons and its Local field potentials (LFP), recorded using multiunit activity electrodes from PD patients undergoing DBS surgery (Park et al., 2011). They also calculated the duration of synchronized and desynchronized events in neuronal activity by estimating transition rates, which were obtained with the help of first return maps plotted using phase of neurons (Park et al., 2010, 2011). To observe how dopamine changes synchrony in STN-GPe, we calculated the phases of individual neurons as defined in (Pinsky and Rinzel, 1995).
The phase of jth neuron was calculated as follows,
| (15) |
| (16) |
where, tj,k and tj,k+1 are the onset times of kth and k + 1th spike of the jth neuron Tj,k ∈ [tj,k, tj,k+1], ∅j (t) = Phase of jth neuron at time “t,” Rsync is the synchronization measure 0 ≤ Rsync = 1,θ = Average phase of neurons, N = total number of neurons in the network.
Action selection using the race model
Action selection is modulated by BG output nucleus GPi which projects back to the cortex via the thalamus. We have used the race model (Vickers, 1970) for the final action selection where an action is selected when temporally integrated neuronal activity of the output neurons crosses a threshold (Frank, 2006; Frank et al., 2007; Humphries et al., 2012).
The dynamics of the thalamic neurons is as follows,
| (17) |
| (18) |
where, zk (t) = integrating variable for kth stimulus, fGPik (t) = normalized and reversed average firing frequency of GPi neurons receiving kth stimulus from striatum, fmaxGPi = highest firing rate among the GPi neurons, SGpikij = neuronal spikes of GPi neurons receiving kth stimulus, N = number of neurons in a single row/column of GPi array (=50), T = duration of simulation.
The first neuron (zk) among k stimuli to cross the threshold (=0.15) represents the action selected. All the variables representing neuron activity are reset immediately after each action selection.
Binary action selection task
The first task we simulated was the simple binary action selection similar to Humphries et al. (2006), where two competing stimuli were presented to the model (Humphries et al., 2006). The input firing frequency is thought to represent “saliency,” with higher frequencies representing higher salience (Humphries et al., 2006). The response of striatal output to cortical input falls in the range of a few tens of Hz (Sharott et al., 2012). Therefore the frequencies that represent the 2 actions were assumed to be around 4 Hz (stimulus #1) and 8 Hz (stimulus #2). Spontaneous output firing rate of the striatal neurons (without input) is assumed to be around 1 Hz (Plenz and Kitai, 1998; Sharott et al., 2012). Selection of higher salient stimulus among the available choices could be considered as “exploitation” while selecting the less salient one as “exploration” (Sutton and Barto, 1998). So the action selected is defined as “Go” if stimulus #2 (more salient) is selected, “explore” if stimulus #1(less salient) is selected and “No Go” if none of them is selected.
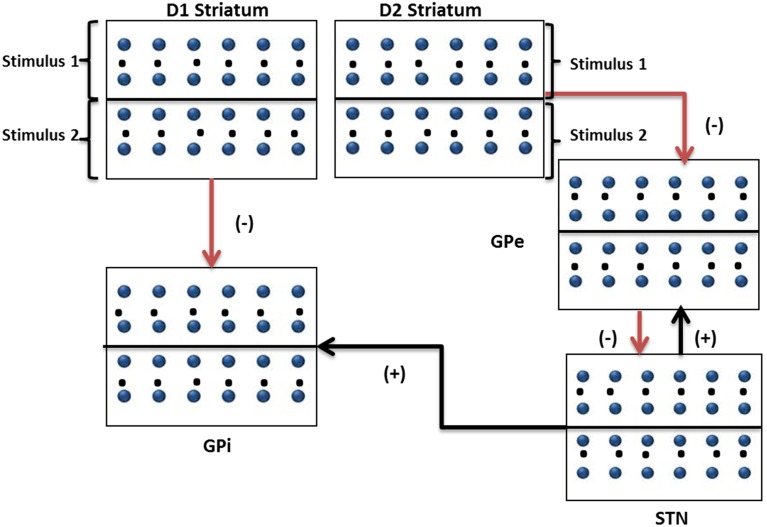
The inputs were given spatially such that the neurons in the upper half of the lattice receive stimulus #1 and lower half the other (Figure 2). The striatal outputs from D1 and D2 neurons of the striatum are given as input to GPi and GPe modules respectively with the projection pattern as shown in Figure 2. Poisson spike trains corresponding to Stimulus #1 were presented as input to neurons (1–1250) and were fully correlated among themselves. Similarly, Poisson spike trains corresponding to Stimulus #2 were presented as input to neurons (1251–2500) and were fully correlated among themselves. Stimulus #1 and #2 are presented for an interval of 100 ms between 100 and 200 ms; at other times uncorrelated spike trains at 1 Hz are presented to all the striatal neurons. The values of the parameters used synaptic weight to implement the binary action selection problem are given in Table 1.
Figure 2.
Modeling the binary action selection task. The figure shows a pictorial representation of inputs to striatal, GPi, GPe, and STN networks (50*50) depicting D1 and D2 neuronal pools and their projections to GPi and GPe networks. Stimulus #1 and Stimulus #2 are the inputs with frequencies representing saliency.
The N-armed bandit task
We now describe the 4-arm bandit task (Daw et al., 2006; Bourdaud et al., 2008) used to study exploratory and exploitatory behavior. In this experimental task, subjects were presented with 4 arms where one among them is to be selected in every trial for a total of 300 trials. The reward/payoff for each of these slots was obtained from a Gaussian distribution whose mean changes from trial to trial with payoff ranging from 0 to 100. The payoff, ri.k associated with the ith machine at the kth trial was drawn from a Gaussian distribution of mean μi,k and standard deviation (SD) σ0. The payoff was rounded to the nearest integer, in the range [0, 100]. At each trial, the mean is diffused according to a decaying Gaussian random walk. The trial was defined as an “exploitatory” trial if highest reward giving arm was selected else defined as an “exploratory” trial.
The payoffs generated by the slot machines are computed as follows,
| (19) |
| (20) |
| (21) |
where, μi,k is the mean of the Gaussian distribution with standard deviation(σ0) for ith machine during kth trial. λm and θm control the random walk of mean (μi,k) and e ~ N(0, σ2d) is obtained from Gaussian distribution of mean 0 and standard deviation σd. ri,k and r'i,k are the payoffs before and after rounding to nearest integer respectively. The initial value of mean payoff, μi,0, is set to a value of 50. All the values for the parameters λm, θm, σd, σ0 were adapted from (Bourdaud et al., 2008).
To make an optimal decision, the subjects need to keep track of rewards associated with each of the 4 arms. The subject's decision to either explore or exploit would depend on this internal representation which would closely resemble the actual payoff that is being obtained. It is quite difficult to identify whether the subject made an exploratory decision or an exploitative one just by observing the EEG and selected slot data. A subject-specific model is required to classify their decisions and identify the strategy (Daw et al., 2006; Bourdaud et al., 2008). Keeping this in mind, Bourdaud et al. (2008) used a “behavioral model” that uses the soft-max principle of RL to fit the selection pattern of human subjects. The parameter “β” of the behavioral model was adjusted such that the final selection pattern matches that of individual subjects in the experiment (refer Appendix A and Table A.1 in Supplementary Material for details). The parameter “β” which controls the exploration level in the behavioral model is tuned to match % exploitation obtained for each of the 8 subjects (1 subject's data was discarded because of artifacts); 2 out of the 8 subjects had similar exploration levels. Hence, a total of 6 subjects' data is taken to account to check the performance of the proposed spiking BG model.
Strategy for slot machine selection
To simulate the experiment, we utilized the concepts of RL and combined the dynamics of BG model to select an optimally rewarding slot in each trial. Experimental data show that BG receives reward related information in the form of dopaminergic input to striatum (Niv, 2009; Chakravarthy et al., 2010). Cortico-striatal plasticity changes due to dopamine (Reynolds and Wickens, 2002) were incorporated in the model by allowing DA signals modulate the Hebb-like plasticity of cortico-striatal synapses(Surmeier et al., 2007).
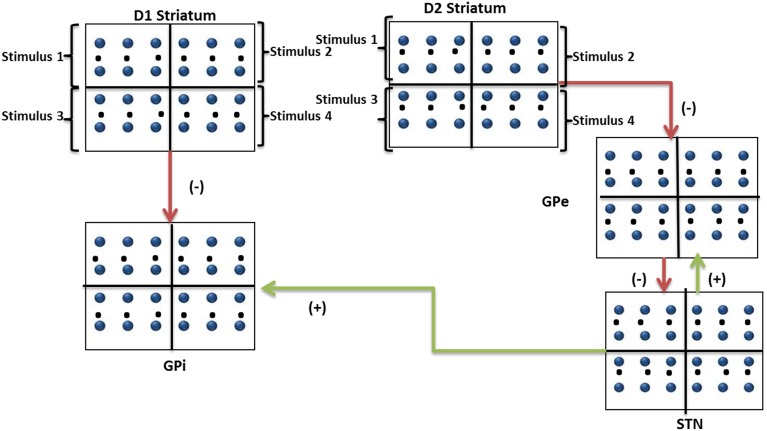
The architecture of the proposed network model is depicted in Figure 3. The output of striatum (both D1 and D2 parts) was divided equally into 4 quadrants which receive input from corresponding stimulus. The stimuli are associated with 2 weights (wD1i,0, wD2i,0) initialized with equal value of 50 which represent the cortico-striatal weights of D1 and D2 MSNs in the striatum. Each of the cortico-striatal weight represents the saliency (in terms of striatal spike rate) for that corresponding arm. These output spikes generated from each of the D1 and D2 striatum project to GPi and GPe respectively. The final selection of an arm is made as in Section Action Selection Using the Race Model. The reward ri,k received for the selected slot was sampled from Gaussian distribution with mean μi,k and SD (σ0) Equation (19).
Figure 3.
Modeling the n-armed bandit task. The figure shows a pictorial representation of inputs to striatal, GPi, GPe, and STN networks (50*50) depicting D1 and D2 neuronal pools and their projections to GPi and GPe networks. Stimulus #1, Stimulus #2, Stimulus #3, and Stimulus #4 are the 4 arms whose saliencies are represented in their cortico-striatal weights.
Using the obtained reward (ri,k), the expected value of the slots, inputs to D1 and D2 striatum are updated using the following equations:
| (22) |
| (23) |
The expected value (Vk) for kth trial is calculated as
| (24) |
The received payoff (Rek) for kth trial is calculated as
| (25) |
The error (δ) for kth trial is defined as
| (26) |
where, wD1i,k are the cortico-striatal weights of D1 striatum for ith machine in kth trial, wD2i,k are the cortico-striatal weights of D2 striatum for ith machine for kthtrial, ri,k is the reward obtained for the selected ith machine for kth trial, xinpi,k is the binary input vector representing the 4 slot machines, e.g., if the first slot machine is selected xinpi,k = [1 0 0 0], η (=0.3) is the learning rate of D1 and D2 striatal MSNs, Rek is the recieved payoff for selected slot for kth trial,Vk is the expected value for selected slot for kth trial
The cortico-straital weights are updated Equations (22) and (23) using the error term “δ” Equation (26). The reward related information in the form of dopaminergic input to striatum has been correlated to the error (δ) (Niv, 2009; Chakravarthy et al., 2010). The δ calculated from the Equation (26) has both positive and negative values with no upper and lower boundaries but the working DA range in the model was limited to small positive values (0.1–0.9). Hence, a mapping from δ to DA is defined as follows,
| (27) |
where, DA is the dopamine signal within range of 0.1–0.9, λ is the slope of sigmoid (=0.2), δk is the error obtained for kth trial Equation (26), sig () is the sigmoid function given by equation:
| (28) |
To verify whether a rewarding slot is selected, delta (δk) as described in Equation (26) was calculated which keeps track of expected and actual payoff.
Results
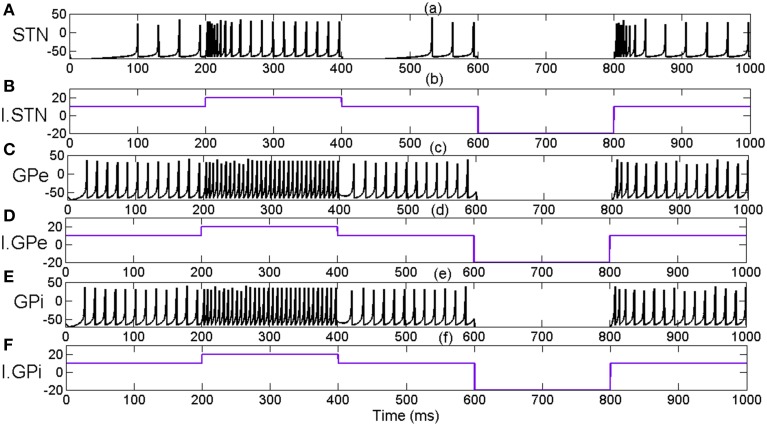
We have investigated if the chosen Izhikevich parameters for STN, GPe and GPi displayed biological properties of corresponding neurons (Figure 4). The distinctive property of inhibitory rebound in STN (Hamani et al., 2004) was observed in simulation which was absent in GPe and GPi neurons. The firing rate of STN, GPe and GPi neurons increased when increasing current inputs (Ixij) as observed in experimental recordings (Magnin et al., 2000; Thibeault and Srinivasa, 2013).
Figure 4.
Indicates the effect of external applied current (Ixij) on neuronal firing pattern and rates of STN, GPe and GPi neurons. (A) Membrane potential of STN neuron for applied current (B), I.STN. (C) Membrane potential of GPe neuron for applied current (D), I.GPe (E) Membrane potential of GPi neuron for applied current (F), I.GPi. X-axis indicates the time of simulation in milliseconds.
We then present results from 3 sets of simulation studies starting with the characterization of the dynamics of STN-GPe network (Simulation set 1). A key idea explored in this study is that the dynamics of STN-GPe critically influence action selection by BG, particularly in the component of exploration. Therefore, we characterize STN-GPe network dynamics in terms of firing frequency and synchronization measure, Rsync. Following that, we present results from the simple binary action selection task (Simulation set 2) where the presence of 3 regimes (Go/explore/No-Go) in action selection is demonstrated revealing the interplay of IP and DP in action selection. Then we present results from the n-arm bandit task (Simulation set 3). The amount of exploration obtained from experimental data was comparable to that of BG model by changing the IP weight.
Simulation set 1: STN-GPe circuit dynamics and synchrony
Pathological oscillations of STN and GP have been associated with various PD symptoms (Bergman et al., 1994; Brown et al., 2001; Levy et al., 2002; Brown, 2003; Litvak et al., 2011; Park et al., 2011; Dovzhenok and Rubchinsky, 2012). Correlated neural firing patterns in STN and GPi can be seen in both experimental conditions of dopamine depletion and in Parkinsonian conditions (Bergman et al., 1994; Nini et al., 1995; Magnin et al., 2000; Brown et al., 2001). Using a conductance based model of STN and GPe system, Terman et al. (2002) demonstrated a variety of rhythmic behaviors by varying the connectivity patterns between STN and GPe (Terman et al., 2002). In the present model we assume that the connections within and between STN and GPe are dopamine-dependent (Cragg et al., 2004) and show increased synchronized behavior under conditions of reduced dopamine, resembling the situation in dopamine-deficient conditions of Parkinson's disease. No inputs were given to STN-GPe network; dopamine (DA) was varied as a parameter Equations (7) and (9) and neural dynamics in the two systems was studied.
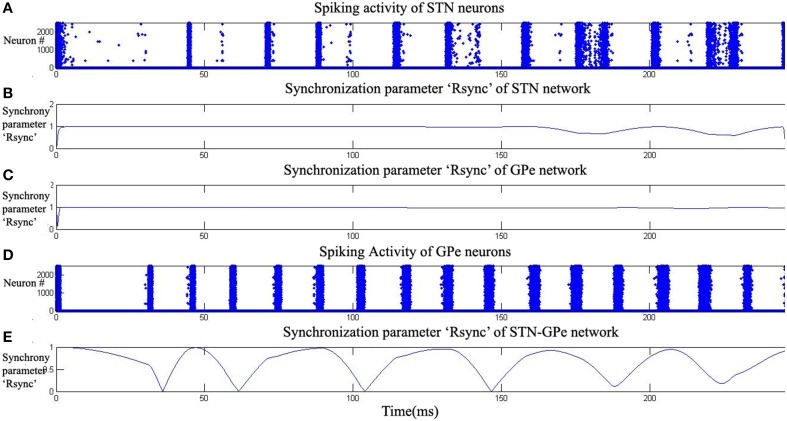
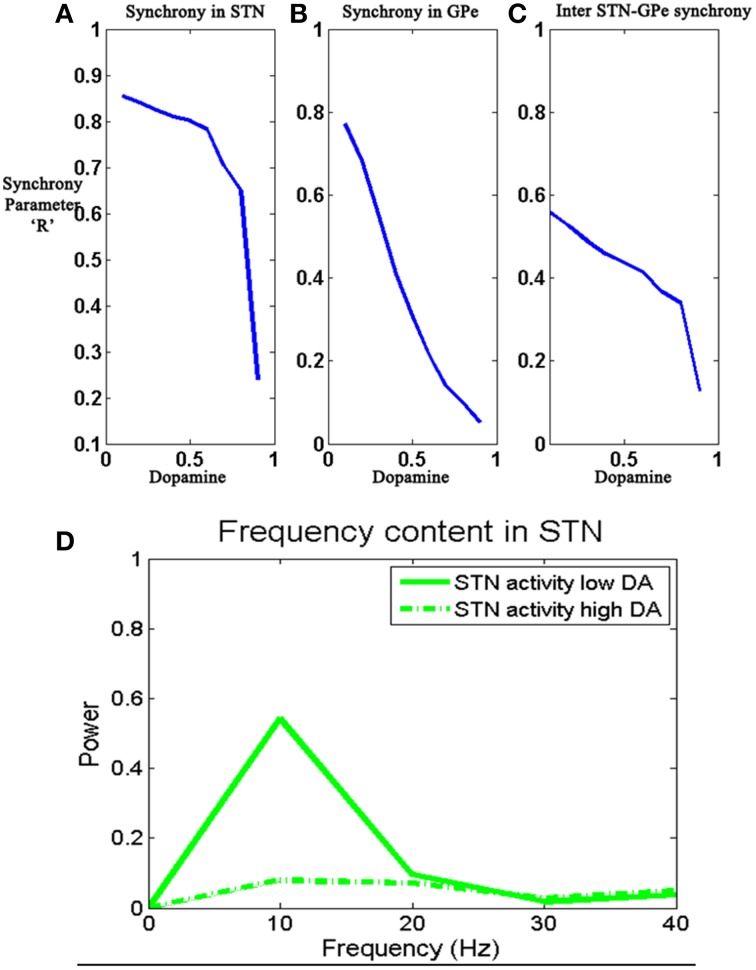
The firing patterns in both STN and GPe varied from synchronized to desynchronized states as levels of dopamine are increased from 0.1 (low) to 0.9 (high) (Figures 5–7). Synchronization parameter “Rsync” as described in Section Action Selection Using the Race Model, Equation (16), is calculated within STN (RsyncSTN) neurons, GPe (RsyncGPe) neurons and also between STN and GPe (RsyncSTNGPe) neurons (Figure 9). For low value of DA (0.1), we observed that both RsyncSTN (Figure 5B) and RsyncGPe (Figure 5C) were high (=1). The value of RsyncSTNGPe (Figure 5E) oscillated between 0 and1 indicating an alternating pattern of synchrony, which is observable in raster plots (Figures 5A,D).
Figure 5.
Highly synchronized activity of STN-GPe system at low dopamine level (DA = 0.1). Plots (A,D) raster plots indicate the activity of STN and GPe neurons with time. Plots (B,C,E) indicate the synchronization parameter (Rsync) calculated for STN, GPe and STN-GPe respectively.
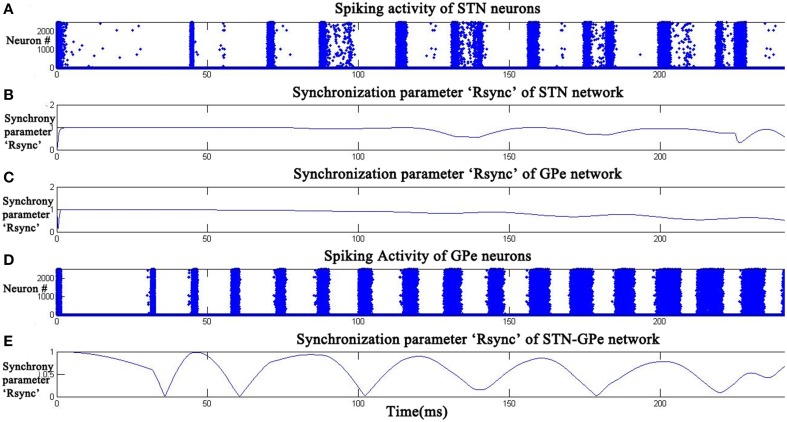
As DA value was increased to an intermediate level (0.5), a decrease in the value of RsyncSTN (Figure 6B) and RsyncGPe (Figure 6C) was observed with time. The decrement in the amplitude of oscillatory pattern in RsyncSTNGPe (Figure 6E) indicates the presence of synchronized and desynchronized firing patterns of the neurons. This can be observed in the raster plots of STN and GPe neurons (Figures 6A,D) which show the beginning of desynchronized behavior.
Figure 6.
STN-GPe Network became desynchronized at intermediate dopamine level (DA = 0.5). Raster plots (A,D) indicate the activity of STN and GPe neurons with time. Plots (B,C,E) indicate the synchronization parameter (Rsync) calculated for STN, GPe, and STN-GPe respectively.
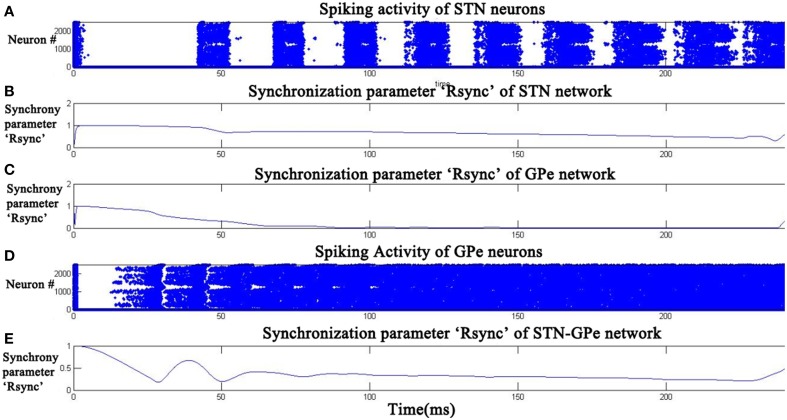
At high DA (0.9), RsyncSTN (Figure 7B) has decreased to an average value of 0.3 and RsyncGPe (Figure 7C) reached an average value of 0.1. The oscillatory pattern in RsyncSTNGPe (Figure 7E) is completely absent at high DA indicating a desynchronized firing pattern, which can also be seen in the raster plots of STN and GPe neurons (Figures 7A,D).
Figure 7.
Desynchronized activity of STN- GPe neurons at high dopamine level (DA = 0.9). Raster plots (A,D) indicate the activity of STN and GPe neurons with time. Plots (B,C,E) indicate the synchronization parameter (Rsync) calculated for STN, GPe, and STN-GPe respectively.
The average firing rate of the neurons in the network was calculated using the following equation:
| (29) |
where, k = denotes STN/GPe, f = average firing rate of the STN/GPe network for a simulation time of 1 s, Skij(t) = Spiking activity of neuron at (i,j) in the network defined by “k,” N = total number of neurons (50∗50), T = simulation time (1 s).
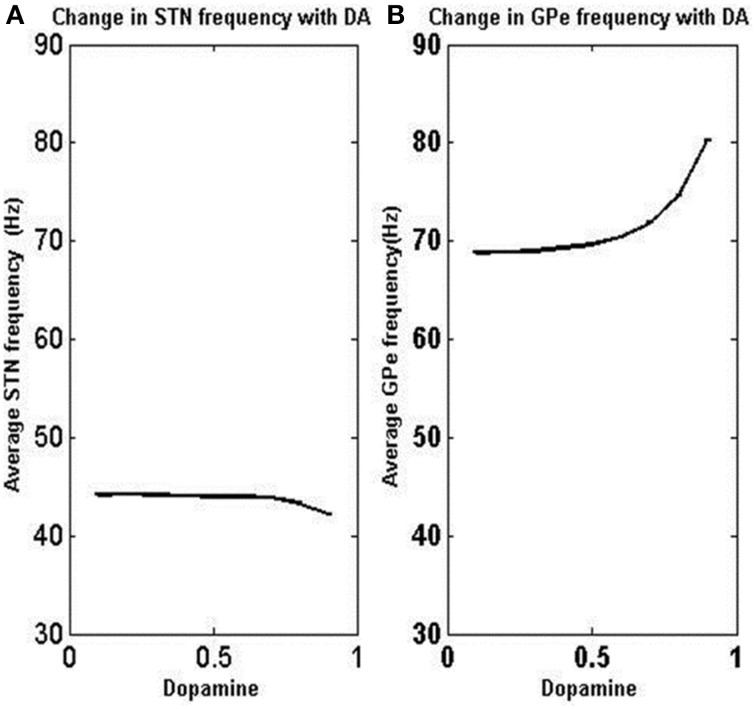
The firing rate of STN neurons decreased from a range of 45–50 Hz (due to bursting) at low DA(0.1) to 35–40 Hz at high DA (0.9) (Figure 8A). Similarly the frequency of GPe neurons increased from about 60–70 Hz at low DA (0.1) to 80–90 Hz at high DA (0.9) (Figure 8B). The simulated firing rates of STN and GPe neurons match with reports from electrophysiological studies (Magnin et al., 2000; Benazzouz et al., 2002) where an increase and decrease in firing rate was observed for STN and GPe respectively in Parkinsonian conditions and vice versa for normal conditions.
Figure 8.
Variation of average firing rate of STN and GPe neurons with DA levels. As the dopamine level is increased, the firing rate increased in GPe neurons but decreased in STN neurons. X-axis indicates the level of dopamine and y-axis is the firing rate of respective neurons. (A) Shows the change in STN frequency with increase in DA level. (B) Shows the change in GPe frequency with increase in DA level.
Under low DA conditions, the contribution of excitatory lateral current is higher in STN, thereby increasing overall firing rate (Figure 8A) and synchrony (Figure 9A) which is observed in general excitatory neurons (Hansel et al., 1995) and such synchrony was found to be absent at high DA levels. GPe neurons show a synchronized firing pattern with decreased lateral synaptic weights at low DA level (Figure 9B) (Wang and Rinzel, 1993). On the contrary, a high lateral inhibition at high DA prevents the neighborhood neurons from firing at the same time, thereby producing a desynchronized firing pattern.
Figure 9.
Shows the change in the 3 synchronization values RsyncSTN (A), RsyncGPe (B), and RsyncSTNGPe (C) oscillatory activity in STN neurons (D) with the value of DA (0.1–0.9). Simulations show reduced synchronization within STN and GPe networks, and also between STN and GPe networks, as DA is increased.
The effect of DA on the synchronization of STN and GPe neurons was studied by estimating the values ofRsyncSTN, RsyncGPe RsyncSTNGPe for increasing values of DA (0.1–0.9). The 3 “Rsync” values showed a decrease in amplitude with an increase in DA level (Figures 9A–C) and the oscillatory activity at low and high DA levels was shown in Figure 9D. Under low DA conditions, GPe activity follows STN activity (Plenz and Kital, 1999) thus forming a pacemaker kind of circuit, which could be the source of STN-GPe oscillations. One of the suspected reasons of bursting activity in STN is the decreased inhibition from GPe neurons (Plenz and Kital, 1999) at low DA levels. This feature is captured by the model since GPe firing rates are smaller for lower DA levels. The STN neurons showed oscillatory around the frequency of 10 Hz at low DA but was absent at high DA level (Kang and Lowery, 2013).
Simulation set 2: binary action selection
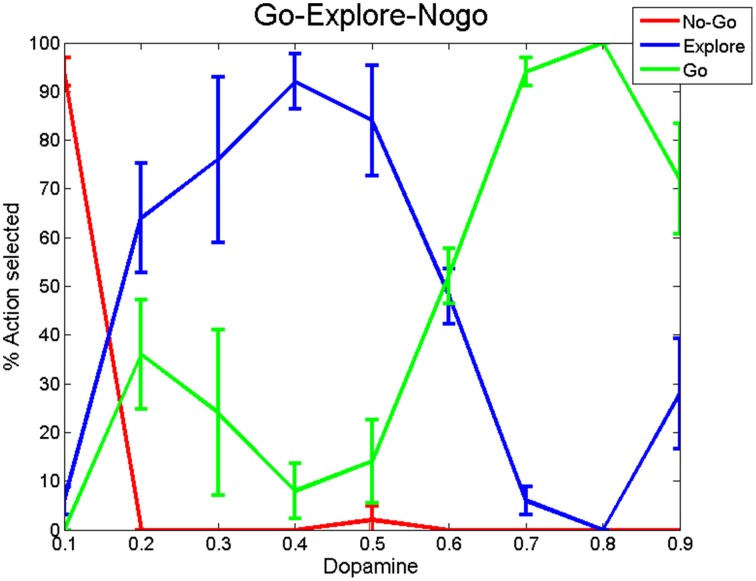
The simulation was run for a period of 250 ms, out of which the input stimuli (assumed to be projected from cortex) is given during the time interval 100–200 ms. A background input around 1 Hz was given during the rest of the simulation. The striatal network with 2500 neurons is divided into two equal sections such that the neurons in the first section (1–1250) received Stimulus #1 and the rest(1251–2500) received Stimulus #2 (Figure 2). Seeking to understand how dopamine affects action selection, we varied the dopamine level from 0.1 (low) to 0.9 (high) and observed which of the 2 inputs was selected at different dopamine levels. The action selected is classified into Go/Explore/No-Go depending on which stimulus is selected: it is “Go” if the stimulus with higher salience is selected, “Explore” if the other stimulus is selected, and “No-Go” if no input is selected.
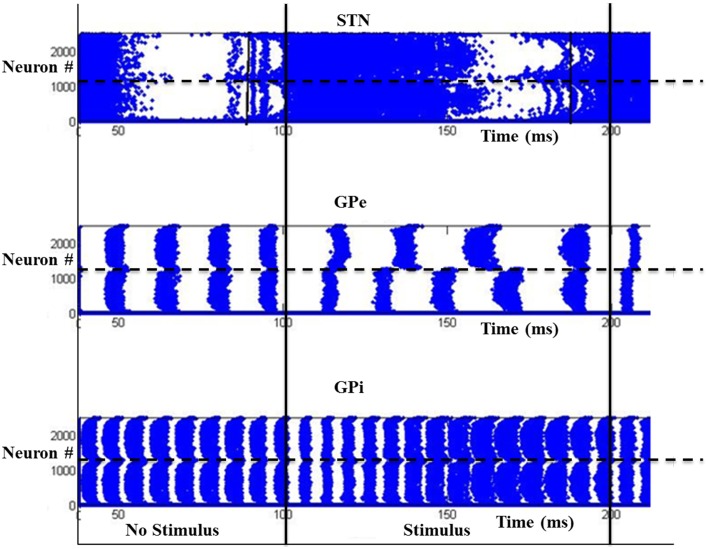
We studied the pattern of action selection as a function of DA level. In low DA state, the activity of STN is high (Figure 10) thus increasing the activity of GPi (Figure 10); an overactive GPi inhibits the thalamus and therefore no action is selected (Figure 10). We thus have a “No-Go” case under low DA conditions.
Figure 10.
Activity of the model at low DA (=0.1) with high firing rate in GPi activity where x-axis represent the time of spiking and y-axis is the spatial representation of 2500 neurons. S1 and S2 are the two stimuli given spatially to the striatum.
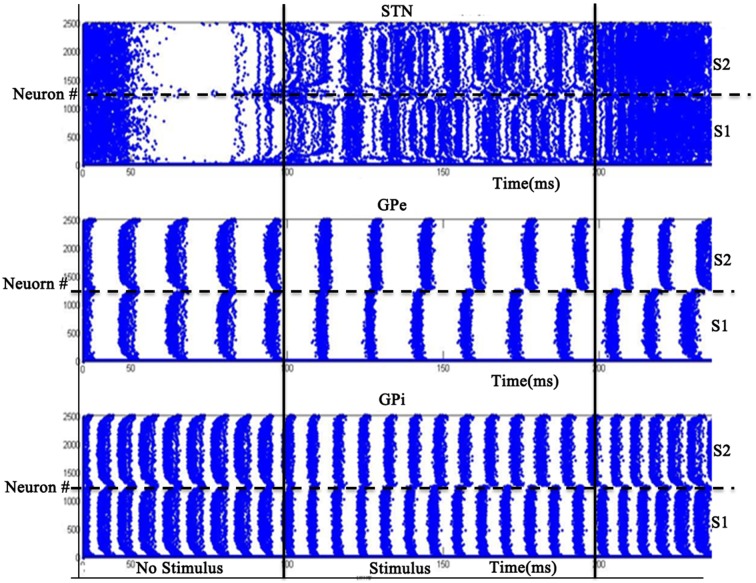
At intermediate levels of dopamine (0.4–0.6), GPi neurons dynamically segregate into two pools, those corresponding to Stimulus #1 and #2 respectively. Neurons in either pool fire in strong synchrony among themselves, while the two pools fire in alternation (Figure 11). The alternation is more visible in GPe and GPi and not so much in STN. This alternation, as we will see below, introduces variability in action selection, even though there is no change in input stimulus. We interpret this variability as a form of exploration in action selection because the burst of activity for the neuron pool corresponding to one action increases the probability of its selection, while simultaneously preventing the selection of the other action. We interpret this dynamical regime corresponding to intermediate DA levels as the “explore” regime.
Figure 11.
Model Activity at intermediate DA (=0.5) with alternating behavior in GPi activity. Where x-axis represents the time of spiking and y-axis is the spatial representation of 2500 neurons. S1 and S2 represent the 2 stimuli given to the network spatially.
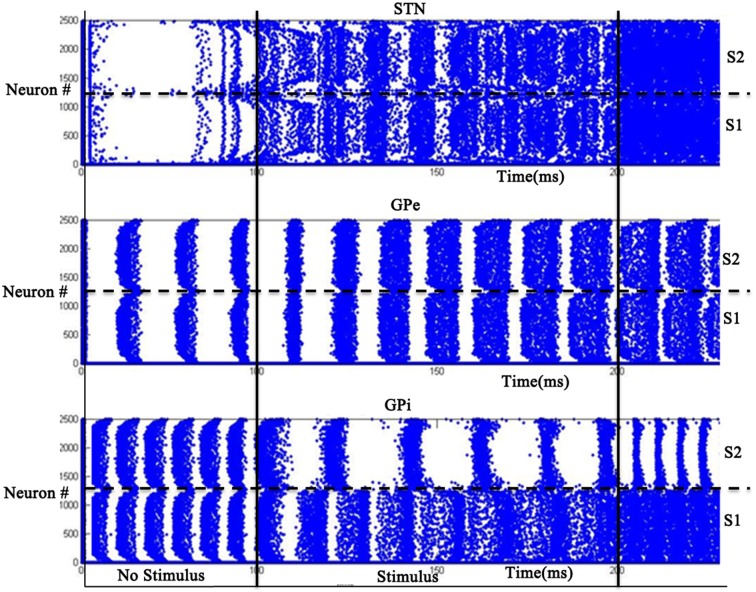
For high dopamine levels (Figure 12), the activity of D1 striatum is high and the DP dominates the IP. The stronger input (Stimulus #2) is selected always as it reaches the threshold sooner. Thus higher dopamine levels correspond to the “Go” regime.
Figure 12.
Model Activity at high DA (=0.9) state where x-axis represents the time of spiking and y-axis is the spatial representation of 2500 neurons. S1 and S2 represent the 2 stimuli which were given spatially to the network.
Simulations were run for 100 trials and the percentage of actions selected under each regime (Go, Explore and No-Go) was calculated for dopamine levels ranging from low (0.1) to high (0.9) (Figure 13). From Figure 13, we may note that the probability of No-Go, where no action is selected, decreases with increase in dopamine; probability of Go increases with dopamine; the peak of exploration is found at intermediate levels of dopamine.
Figure 13.
Percentage of action selection observed in the Go, No-Go, and Explore regimes averaged over 200 trials with DP and IP weight values at wSTN→GPi = 1.15 and wStr→GPi = 0.8. We ran the simulation for 100 trials and segmented in to 4 bins (25 trials each). We then calculated the variance of each regime across all DA levels.
To check the influence of other structures on action selection, we removed the STN projections to GPi, which is best done by omitting the first two terms on the right side of Equation (13). The resulting decision plot exhibited only Go and No-Go with a completely flat Explore regime (Figure B1-b in Supplementary Material Appendix B). The above result suggests that the IP is crucial for exploration. Then we studied how various aspects of the STN-GPe network affect exploration. Changes in GPe lateral connections did not alter exploration levels (results not shown). We then varied the strength of STN-lateral connections and found that at very high values, the system shows very little exploration (Figure B1-a in Supplementary Material Appendix B). STN lesions in 6-OHDA and MPTP animals are known to relieve the symptoms of PD and initiate motor movements (Baunez et al., 1995) but results in multiple deficits while performing attentional and choice tasks such as increase in reaction time and decrease in exploration levels (Baunez et al., 1995, 2001; Baunez and Robbins, 1997). So we studied the effect of STN lesions on exploration and found that as the size of lesion is increased the amount of exploration decreased. We have added the result for a lesion patch of 20 × 20 neurons (Figure B1-c in Supplementary Material) where the lesion was created at the center of the STN neuron lattice. This was achieved by setting the spiking activity of the corresponding neurons to zero (=0). To investigate the effect of STN laterals on exploration, we increased the strength of STN laterals and calculated % exploration at intermediate levels [0.4–0.6] by applying the binary action selection problem. We increased strength of STN laterals from [0.05 to 0.25] with a step of 0.05. We have observed that at low and high levels, the system does not show exploration but peaks for a range of strengths. The result is shown in Figure B2 in Supplementary Material Appendix B.
Simulation set 3: the N-armed bandit task
The decision making ability of the BG model was checked by comparing its performance with behavioral model, representation of experimental data in the n-armed bandit task (n = 4). The task was simulated for a total of 300 trials. The payoff pattern of the 4 arms for 300 trials calculated using the Equations (19)–(21) is shown in Supplementary Material Figure A1.
Parameter “delta”
The difference between the received payoff and estimated payoff from the BG model, the error (δbgk) was calculated for each trial. These results were compared with the error (δbek) obtained from the behavioral model (Bourdaud et al., 2008). The performance of BG model was found to be comparable to behavioral model, which was reflected in the difference between the expected values (V) obtained from behavioral model and the BG model, defined as ebebgk = Vbg-Vbe, where Vbg and Vbe are expected values obtained from BG and behavioral model. The average and SD of the 3 errors (δbgk, δbek, ebebgk) obtained by simulating both behavioral and BG model are listed in Table 3 for all the 6 subjects.
Table 3.
Errors obtained from behavioral model (δbek) and BG (δbgk) model independently and a comparison of the errors obtained from the 2 models (ebebgk).
| Subject | δbg | δbe | ebebg |
|---|---|---|---|
| 1 | 4.68 ± 4.74 | 5.27 ± 4.36 | 4.40 ± 4.49 |
| 2 | 5.04 ± 4.15 | 5.80 ± 4.59 | 3.95 ± 4.02 |
| 3 | 5.52 ± 5.05 | 5.88 ± 6.10 | 4.27 ± 6.12 |
| 4 | 5.05 ± 4.15 | 5.18 ± 4.27 | 4.31 ± 4.20 |
| 5 | 4.89 ± 4.13 | 5.85 ± 5.21 | 4.63 ± 4.51 |
| 6 | 4.45 ± 3.52 | 6.06 ± 5.55 | 4.68 ± 4.55 |
Column 2 shows error (δbgk) values for each of the 6 subjects in BG model. Column 3 shows the error obtained from behavioral model (δbek) of Bourdaud et al. (2008). Column 4 indicates the difference in error (ebebgk) which is the difference between the expected values (Vbg, Vbe) calculated from the 2 models.
δ bg, error obtained from BG model; δ be, error obtained from Behavioral model; ebebg, difference between Vbg and Vbe.
Percent exploitation
In addition to payoff error (δ), another measure that we used to compare performance of BG model with the experimental data, which measures “percentage exploitation.” It is defined as the percentage number of times the highest (expected) reward yielding action (calculated over 300 trials) was selected. For example in a trial “k” if highest reward is obtained from slot 4, and if the model also selects slot 4 then the trial resulted in exploitation; else it is exploration. We calculated the average percentage exploitation values for 10 sessions, where each session consists of 300 trials.
Subject to subject exploration variability was accounted by varying the “temperature” parameter β in the behavioral model Equation (A.8) (Appendix A in Supplementary Material). The parameter “β” controls the exploit-explore balance (higher β implies greater exploitation). Since the indirect pathway (IP) dynamics drives exploration in the BG model, we expected that varying the strengths of the direct pathway (DP) (decreasing wStr→GPi) and the indirect pathway (increasing wSTN→GPi) would give similar results in terms of decreased % exploitation levels.
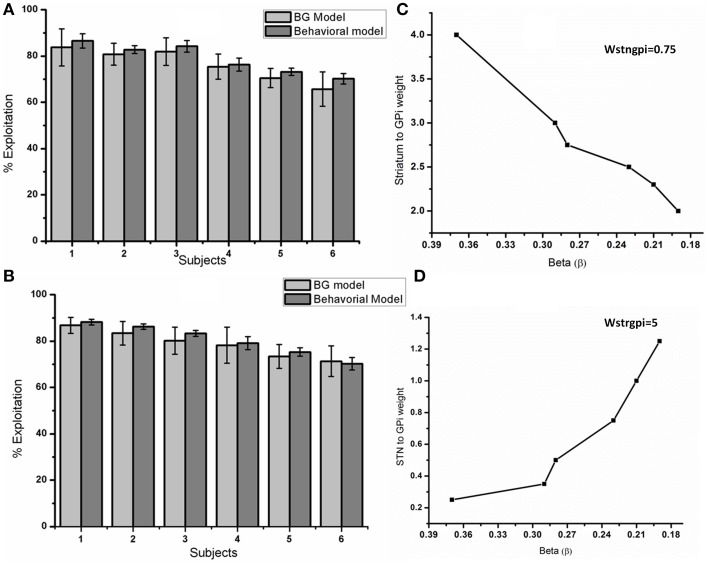
The performance of BG model was compared with the behavioral model in terms of % exploitation shown in the Figure 14. Figure 14A shows the % percentage exploitation as the Y-axis with x-axis as individual subjects, which relates to corresponding beta (β) values in behavioral and DP weight values in BG model. Holding wSTN→GPi constant at 0.75, we varied wStr→ GPi over the range of [2, 4] in steps of 0.25 to match the exploitation levels of the subjects. The relationship between the DP weights (wStr→GPi,) and beta (β) is plotted in Figure 14C. Similarly % percentage exploitation for changing beta (β) and increasing (wSTN→GPi) was plotted in Figure 14B. A decrease in wStr→ GPi implies reduced influence of DP relative to IP, resulting in greater exploration. Similarly one can be control exploration by varying the strength of the IP (wSTN→GPi). Holding wStr→GPi, constant at value (=5), we varied wSTN→GPi over the range of [0.25, 1.25]. The individual weight values for corresponding beta's have been plotted in Figure 14D.
Figure 14.
Compares the performance of BG model with the behavioral model. (A) Shows the percentage exploitation obtained for each of the 6 subjects from BG and behavioral model. Y axis represents percentage exploitation and X axis represents a subject which is a specific beta value (β) in behavioral model and the DP weight (wStr→ GPi) in the BG model. The relationship between beta's (β) of the behavioral model and DP weights (wStr→ GPi) with a constant wSTN→GPi value (=0.75) used to attain (A) are shown in (C). (B) Y axis represents percentage exploitation and X axis represents a subject which is a specific beta value (β) in behavioral model and the IP weight (wSTN→GPi) in the BG model. The relationship between beta's (β) of the behavioral model and IP weights (wSTN→GPi) of BG model with a constant wStr→ GPi value of (=5) used to attain (B) are shown in (D).
To simulate the performance of PD subjects in the above model, we clamped the delta (δ) to a negative value (-20) (simulating low levels of DA) and checked the performance. We observed that the % exploitation decreased (=44%) compared to normals. The decrease in the performance of the PD off condition might be due to decreased exploration leading to the selection of suboptimal choice.
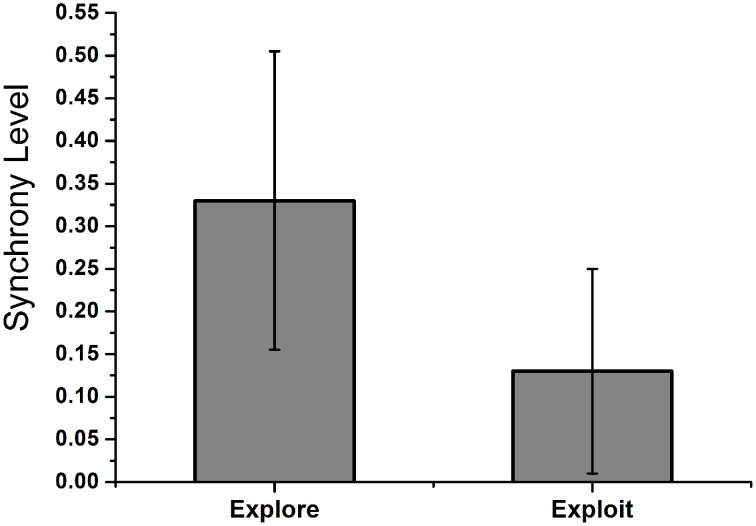
In the binary action selection task (Section Simulation Set 2: Binary Action Selection), we observed that the level of exploration could be related to the synchrony levels in STN neurons. So we classified each of the 300 trials into either exploratory or exploitatory and then checked the corresponding synchrony levels in STN neurons. The synchrony levels for exploitatory case was observed to be significantly lower (=0.13 ± 0.12) than exploratory ones (=0.33 ± 0.176). Independent 2 sample t-test was conducted between synchrony parameter “Rsync” for exploratory and exploitatory trials. With a P-value of 0.002, we could say that there is a statistically significant difference between the 2 mean “Rsync” values. The bar plot for mean “Rsync” for explore and exploit trials is shown in Figure 15.
Figure 15.
Shows the mean “Rsync” value of STN neurons during exploratory and exploitatory trials during the n-arm bandit task. The trials were segregated in to exploitatory or exploratory and the corresponding “Rsync” value of STN neurons was calculated. The exploitatory trials were high DA (0.7–0.9) levels where as exploratory ones around intermediate levels (0.4–0.6).
Discussion
The goal of this model was to understand the role of the BG in explorative behavior as well as the occurrence of synchrony in PD conditions. Studies on exploration-exploitation tradeoff show the importance of these processes during decision making (Sutton and Barto, 1998; Cohen et al., 2007; Humphries et al., 2012; Laureiro-Martãnez et al., 2013). Experimental studies conducted by the Baunez group also suggest a role for STN in exploration where they observed that STN lesions tend to alter the choice made by rats (Baunez et al., 2001). These results emphasize the importance of studying exploration and the corresponding neural substrates at the subcortical level.
Exploration in action selection is usually modeled as being driven by noise or a stochastic mechanism (Cohen et al., 2007; Moustafa and Gluck, 2011; Schroll et al., 2012). The STN-GPe loop of BG has been proposed to act as a pacemaker (Plenz and Kital, 1999) capable of producing synchronized oscillations at low DA levels (PD) (Brown et al., 2001; Bevan et al., 2002) and desynchronized spiking activity at high DA level. In an earlier study, using a rate-coded neural network model of BG (Kalva et al., 2012), we have shown that the STN-GPe system exhibits chaos and fixed point dynamics as two network parameters (w = strength of connections between STN and GPe; σ = strength of lateral connections within STN and GPe) are varied. This trend reached its peak when the STN-GPe system was located on the border between chaos and ordered regimes, viz., the “edge of chaos.” From the facts that synchrony plays an important role in PD and DA levels influence the synchrony levels in STN-GPe, we developed a spiking neuron network model of BG to study the relation between synchrony and exploration by simulating simple (binary action selection) and complex decision making (n-armed bandit task). The model also showed oscillatory activity in STN-GPe neurons at low DA level known to correlate to PD tremor (Bevan et al., 2002).
The STN-GPe loop and exploration-exploitation dynamics
One of the aims of the present study is to show that the complex dynamics of STN-GPe system contributes to exploration and can be correlated to the synchrony levels in the STN-GPe loop. So we studied the STN-GPe loop dynamics (Section Simulation Set 1: STN-GPe Circuit Dynamics and Synchrony) without input from D2 striatum for increasing levels of dopamine (Figures 5–7). As we are interested in studying the role of synchrony in exploration, we characterized the dynamics of STN-GPe in terms of synchronization and oscillatory activity (Figure 9). Due to the observations that STN and GPe neurons show synchrony (asynchrony) at low(high) DA levels (Bergman et al., 1994, 1998) and such behavior in excitatory-inhibitory networks is observed when the excitatory lateral connection is high and inhibitory is low (Lukasiewicz and Werblin, 1990). Considering the above observations we assume the DA modulates the width of Gaussians of STN and GPe collaterals. The results tally with the general observation from electrophysiology that at higher levels of dopamine, the STN-GPe system shows desynchronized activity and under dopamine-deficient conditions exhibits synchronized bursts (Bergman et al., 1994; Gillies and Willshaw, 1998; Park et al., 2011). It is also consistent with the experimental finding that dopamine-deficiency results in an increase of correlations in firing patterns of STN neurons (Brown et al., 2001; Benazzouz et al., 2002; Levy et al., 2002; Willshaw and Li, 2002; Brown, 2003; Foffani et al., 2005). Some computational modeling effort has investigated the link between STN, GPe oscillations and PD tremor (Bevan et al., 2002), an idea that also has strong experimental support with regard to the STN-GPe circuit (Nini et al., 1995; Hurtado et al., 1999; Levy et al., 2002; Brown, 2003; Park et al., 2010). We observed that STN activity showed oscillatory activity with a frequency (=10 Hz) which falls under the beta frequency range observed in experimental PD study (Weinberger and Dostrovsky, 2011).
Role of STN-GPe in binary action selection task
We then used the same model to simulate the binary action selection task (similar to Humphries et al., 2006). Here, we presented two stimuli as inputs to the model (Figure 1). The firing rate of the stimulus was represented as its saliency (Humphries et al., 2006) where selection of higher one was defined as “exploitation/Go” and lesser one as “exploration/Explore” and not selecting any of the inputs as “No-Go.” In the BG model of Kalva et al. (2012) some action is always chosen—thus it does not have a “No-Go” regime (Kalva et al., 2012). The current Izhikevich BG network showed No-Go at low DA levels (0.1–0.3) and Go at high DA levels (0.7–0.9) consistent with the classical picture of BG function. Along with this a peak in “Explore” at intermediate levels of DA (0.4–0.6) was also observed (Figure 13). At intermediate levels of DA, the neuronal pools of STN corresponding to the 2 inputs were firing out of phase which was also observed in GPe and GPe neurons. This anti-phase spiking behavior of GPi neurons became the source of randomness in deciding which stimulus would finally get selected. In other words, the neuronal pool ahead in alternation crossed the threshold first and that corresponding action got selected. This exploratory behavior was controlled by the strength of laterals in STN neurons (ASTN). As the strength of lateral connections was increased, the exploratory action selection percentage peaked and decreased on further increment (Figure B2 in Supplementary Material Appendix B). Increased ASTN leads to high synchrony among STN neurons which is one of characteristic feature observed in PD patients (Park et al., 2010, 2011). From the above observations we may suggest that the decrease in exploration levels in PD subjects (Archibald et al., 2013a) could be due to increased lateral strength in STN neurons value. We found at high lateral synaptic strength, the system switched only between Go and No-Go regimes (Figure B1a in Supplementary Material). To check whether any other module in the network is influencing exploration in the system, we removed the STN to GPi connection (which effectively eliminated the IP). This omission rendered the system to display only Go and No-Go regimes (no exploration) (Figure B1b in Supplementary Material). We also studied the effect of STN lesions on exploration and found as the size of lesion increased the system's exploratory behavior decreased. This result is in agreement with study conducted by Baunez et al. (2001) where they found a decrease in explorative behavior of rats while performing a choice reaction task (Baunez et al., 2001).
Complex decision making: N-armed bandit task
In the n-arm bandit task, the aim of the subject was to maximize the reward by selecting best (highest reward giving) slot in each trial and their performance was measured in terms of amount of exploitative behavior. To make sense of the experimental data, a behavioral model was used to estimate which trial was explorative or exploitative. A similar model was used by Daw et al. (2006) to analyze their fMRI data (Daw et al., 2006). The behavioral model uses the classical soft-max principle (Equation A.8 Appendix A in Supplementary Material) and the parameter “β” controls the level of exploration. Though the behavioral model helps in analyzing the experimental data, it does not elaborate on underlying neural mechanism of exploration due to constraint of being abstract. Apart from understanding the neural mechanism for exploration, the model can also be used to study decision making ability in Parkinsonian conditions and predict the effect of various drugs (L-Dopa, DA agonist) and STN–DBS. We attempted to explain the decision making mechanism in terms of synchrony levels in STN-GPe neurons. When subjected to the binary action selection task, the spiking network model of BG showed exploration at intermediate levels of DA controlled by STN-GPe synchrony levels. So the amount of exploration in the model was controlled by adjusting the synaptic weights in DP (wStr→ GPi) and IP pathway (wSTN→GPi).
The results of behavioral model of Bourdaud et al. (2008) were approximated in 2 ways: (1) Increasing wSTN→GPi while holding wStr→ GPi constant; this would increase exploration since the the GPi neurons are now more strongly influenced by STN and (2) Decreasing wStr→ GPi while keeping wSTN→GPi constant, which has the same effect of increasing wSTN→GPi.
Two parameters (δ and % exploitation) were compared to check the accuracy of the model to account for experimental results. Individual performance of behavioral and BG models were checked by calculating delta (δ),TD error Equation (27) which indicates how well the model is able to track the actual reward pattern from the slots (Table 3). If the BG model is able to replicate the experimental results, the “δ” obtained from BG and behavioral (measure of experimental results) should be correlated. So we calculated the error ebebg between the two delta's (δbg and δbe) to check the accuracy and found the error to be low (Table 3). We also conducted 2 sample t-test on the delta values obtained from BG and behavioral model. An “H” value of (=0) for the test cases indicates that both delta's are from distribution of equal means. In other words, the difference/error between the 2 model expected values is low. The second measure was percentage exploitation i.e., the percentage number of times the model selects the slot with the highest expected payoff (Figure 14). The results obtained from BG model closely match with the behavioral model reinforcing the theory that STN-GPe could be a source for exploration at sub-cortical level. The synchrony level in STN was also found to be statistically different (P = 0.002) during exploratory vs. exploitatory trials. The “Rsync” value (Figure 15) during exploitatory trial (=0.13 ± 0.12) at high DA levels showed a desynchronized behavior leading to the selection of highest reward slot. During exploratory trials, synchrony level of (=0.33 ± 0.175) was observed in STN neurons which is similar to that as observed during binary action selection at intermediate DA level. This intermediate synchrony levels gave rise to the alternating pattern, source of randomness in the model leading to an exploratory behavior.
From these results, we would to emphasize that the exploratory behavior in the system can be controlled by collateral connection strength in STN neurons by changing the synchrony levels in the system. These results suggest that STN-GPe system of BG might be the possible exploratory substrate at subcortical level. Cortical structures also play a critical role in decision making (Bechara et al., 1994; Fellows and Farah, 2003; Clark et al., 2004; Ragozzino, 2007). Many research groups have been working to characterize the anatomical substrates of exploration and exploitation during decision making (Daw et al., 2006; Bourdaud et al., 2008; Pearson et al., 2009, 2010; Laureiro-Martãnez et al., 2013). The ability to modulate the oscillatory activity in STN-GPe neurons by cortex through the hyper-direct pathway has also been suggested and modeled (Kang and Lowery, 2013). Since most classical models of basal ganglia do not include the connection between GPe and GPi (Albin et al., 1989; Delong, 1990) but recent studies by (Nambu et al., 2005) indicate the presence of this pathway. Modeling studies such as (Coulthard et al., 2012) showed the role of BG in decision making without including this specific connection in their model. Though the presence of this pathway has been found out anatomically, the functional significance is yet to be explored. Considering these in to account, we have not included GPe-GPi connection in the model. As a part of future work we would like to integrate cortical areas and the inhibitory GPe-GPi connection with the current model and study the rich dynamics in the system.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fnins.2015.00191/abstract
References
- Albin R. L., Young A. B., Penney J. B. (1989). The functional anatomy of basal ganglia disorders. Trends Neurosci. 12, 366–375. 10.1016/0166-2236(89)90074-X [DOI] [PubMed] [Google Scholar]
- Aravamuthan B., Muthusamy K., Stein J., Aziz T., Johansen-Berg H. (2007). Topography of cortical and subcortical connections of the human pedunculopontine and subthalamic nuclei. Neuroimage 37, 694–705. 10.1016/j.neuroimage.2007.05.050 [DOI] [PubMed] [Google Scholar]
- Archibald N. K., Hutton S. B., Clarke M. P., Mosimann U. P., Burn D. J. (2013a). Visual exploration in Parkinson's disease and Parkinson's disease dementia. Brain 136, 739–750. 10.1093/brain/awt005 [DOI] [PubMed] [Google Scholar]
- Archibald N. K., Hutton S. B., Clarke M. P., Mosimann U. P., Burn D. J. (2013b). Visual exploration in Parkinson’s disease and Parkinson’s disease dementia. Brain 136, 739–750. 10.1093/brain/awt005 [DOI] [PubMed] [Google Scholar]
- Aston-Jones G., Rajkowski J., Kubiak P., Alexinsky T. (1994). Locus coeruleus neurons in monkey are selectively activated by attended cues in a vigilance task. J. Neurosci. 14, 4467–4480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baunez C., Humby T., Eagle D. M., Ryan L. J., Dunnett S. B., Robbins T. W. (2001). Effects of STN lesions on simple vs choice reaction time tasks in the rat: preserved motor readiness, but impaired response selection. Eur. J. Neurosci. 13, 1609–1616. 10.1046/j.0953-816x.2001.01521.x [DOI] [PubMed] [Google Scholar]
- Baunez C., Nieoullon A., Amalric M. (1995). In a rat model of parkinsonism, lesions of the subthalamic nucleus reverse increases of reaction time but induce a dramatic premature responding deficit. J. Neurosci. 15, 6531–6541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baunez C., Robbins T. W. (1997). Bilateral lesions of the subthalamic nucleus induce multiple deficits in an attentional task in rats. Eur. J. Neurosci. 9, 2086–2099. 10.1111/j.1460-9568.1997.tb01376.x [DOI] [PubMed] [Google Scholar]
- Bechara A., Damasio A. R., Damasio H., Anderson S. W. (1994). Insensitivity to future consequences following damage to human prefrontal cortex. Cognition 50, 7–15. 10.1016/0010-0277(94)90018-3 [DOI] [PubMed] [Google Scholar]
- Benazzouz A., Breit S., Koudsie A., Pollak P., Krack P., Benabid A. L. (2002). Intraoperative microrecordings of the subthalamic nucleus in Parkinson's disease. Mov. Disord. 17, S145–S149. 10.1002/mds.10156 [DOI] [PubMed] [Google Scholar]
- Bergman H., Feingold A., Nini A., Raz A., Slovin H., Abeles M., et al. (1998). Physiological aspects of information processing in the basal ganglia of normal and parkinsonian primates. Trends Neurosci. 21, 32–38. 10.1016/S0166-2236(97)01151-X [DOI] [PubMed] [Google Scholar]
- Bergman H., Wichmann T., Karmon B., Delong M. (1994). The primate subthalamic nucleus. II. Neuronal activity in the MPTP model of parkinsonism. J. Neurophysiol. 72, 507–520. [DOI] [PubMed] [Google Scholar]
- Bevan M. D., Magill P. J., Terman D., Bolam J. P., Wilson C. J. (2002). Move to the rhythm: oscillations in the subthalamic nucleus–external globus pallidus network. Trends Neurosci. 25, 525–531. 10.1016/S0166-2236(02)02235-X [DOI] [PubMed] [Google Scholar]
- Borisyuk G. N., Borisyuk R. M., Khibnik A. I., Roose D. (1995). Dynamics and bifurcations of two coupled neural oscillators with different connection types. Bull. Math. Biol. 57, 809–840. 10.1007/BF02458296 [DOI] [PubMed] [Google Scholar]
- Bourdaud N., Chavarriaga R., Galán F., Del R Millan J. (2008). Characterizing the EEG correlates of exploratory behavior. IEEE Trans Neural Syst. Rehabil. Eng. 16, 549–556. 10.1109/TNSRE.2008.926712 [DOI] [PubMed] [Google Scholar]
- Brown P. (2003). Oscillatory nature of human basal ganglia activity: relationship to the pathophysiology of Parkinson's disease. Mov. Disord. 18, 357–363. 10.1002/mds.10358 [DOI] [PubMed] [Google Scholar]
- Brown P., Oliviero A., Mazzone P., Insola A., Tonali P., Di Lazzaro V. (2001). Dopamine dependency of oscillations between subthalamic nucleus and pallidum in Parkinson's disease. J. Neurosci. 21, 1033–1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caroni P., Donato F., Muller D. (2012). Structural plasticity upon learning: regulation and functions. Nat. Rev. Neurosci. 13, 478–490. 10.1038/nrn3258 [DOI] [PubMed] [Google Scholar]
- Chakravarthy V., Joseph D., Bapi R. S. (2010). What do the basal ganglia do? A modeling perspective. Biol. Cybern. 103, 237–253. 10.1007/s00422-010-0401-y [DOI] [PubMed] [Google Scholar]
- Chersi F., Mirolli M., Pezzulo G., Baldassarre G. (2013). A spiking neuron model of the cortico-basal ganglia circuits for goal-directed and habitual action learning. Neural Netw. 41, 212–224. 10.1016/j.neunet.2012.11.009 [DOI] [PubMed] [Google Scholar]
- Chevalier G., Deniau J. (1990). Disinhibition as a basic process in the expression of striatal functions. Trends Neurosci. 13, 277–280. 10.1016/0166-2236(90)90109-N [DOI] [PubMed] [Google Scholar]
- Clark L., Cools R., Robbins T. W. (2004). The neuropsychology of ventral prefrontal cortex: decision-making and reversal learning. Brain Cogn. 55, 41–53. 10.1016/S0278-2626(03)00284-7 [DOI] [PubMed] [Google Scholar]
- Cohen J. D., Mcclure S. M., Angela J. Y. (2007). Should I stay or should I go? How the human brain manages the trade-off between exploitation and exploration. Philos. Trans. R. Soc. B: Biol. Sci. 362, 933–942. 10.1098/rstb.2007.2098 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coulthard E. J., Bogacz R., Javed S., Mooney L. K., Murphy G., Keeley S., et al. (2012). Distinct roles of dopamine and subthalamic nucleus in learning and probabilistic decision making. Brain 135, 3721–3734. 10.1093/brain/aws273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cragg S. J., Baufreton J., Xue Y., Bolam J. P., Bevan M. D. (2004). Synaptic release of dopamine in the subthalamic nucleus. Eur. J. Neurosci. 20, 1788–1802. 10.1111/j.1460-9568.2004.03629.x [DOI] [PubMed] [Google Scholar]
- Daw N. D., O'doherty J. P., Dayan P., Seymour B., Dolan R. J. (2006). Cortical substrates for exploratory decisions in humans. Nature 441, 876–879. 10.1038/nature04766 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delong M. R. (1990). Primate models of movement disorders of basal ganglia origin. Trends Neurosci. 13, 281–285. 10.1016/0166-2236(90)90110-V [DOI] [PubMed] [Google Scholar]
- Dovzhenok A., Rubchinsky L. L. (2012). On the Origin of Tremor in Parkinson's Disease. PLoS ONE 7:e41598. 10.1371/journal.pone.0041598 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doya K. (2002). Metalearning and neuromodulation. Neural Netw. 15, 495–506. 10.1016/S0893-6080(02)00044-8 [DOI] [PubMed] [Google Scholar]
- Fan K. Y., Baufreton J., Surmeier D. J., Chan C. S., Bevan M. D. (2012). Proliferation of external globus pallidus-subthalamic nucleus synapses following degeneration of midbrain dopamine neurons. J. Neurosci. 32, 13718–13728. 10.1523/JNEUROSCI.5750-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fellows L. K., Farah M. J. (2003). Ventromedial frontal cortex mediates affective shifting in humans: evidence from a reversal learning paradigm. Brain 126, 1830–1837. 10.1093/brain/awg180 [DOI] [PubMed] [Google Scholar]
- Foffani G., Bianchi A., Baselli G., Priori A. (2005). Movement−related frequency modulation of beta oscillatory activity in the human subthalamic nucleus. J. Physiol. 568, 699–711. 10.1113/jphysiol.2005.089722 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank M. J. (2005). Dynamic dopamine modulation in the basal ganglia: a neurocomputational account of cognitive deficits in medicated and nonmedicated Parkinsonism. J. Cogn. Neurosci. 17, 51–72. 10.1162/0898929052880093 [DOI] [PubMed] [Google Scholar]
- Frank M. J. (2006). Hold your horses: a dynamic computational role for the subthalamic nucleus in decision making. Neural Netw. 19, 1120–1136. 10.1016/j.neunet.2006.03.006 [DOI] [PubMed] [Google Scholar]
- Frank M. J., Samanta J., Moustafa A. A., Sherman S. J. (2007). Hold your horses: impulsivity, deep brain stimulation, and medication in parkinsonism. Science 318, 1309–1312. 10.1126/science.1146157 [DOI] [PubMed] [Google Scholar]
- Gerfen C. R., Engber T. M., Mahan L. C., Susel Z., Chase T. N., Monsma F., et al. (1990). D1 and D2 dopamine receptor-regulated gene expression of striatonigral and striatopallidal neurons. Science 250, 1429–1432. 10.1126/science.2147780 [DOI] [PubMed] [Google Scholar]
- Gerfen C. R., Surmeier D. J. (2011). Modulation of striatal projection systems by dopamine. Annu. Rev. Neurosci. 34, 441. 10.1146/annurev-neuro-061010-113641 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillies A., Willshaw D. (1998). A massively connected subthalamic nucleus leads to the generation of widespread pulses. Proc. R. Soc. Lond. Ser. B Biol. Sci. 265, 2101–2109. 10.1098/rspb.1998.0546 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillies A., Willshaw D., Li Z. (2002). Subthalamic-pallidal interactions are critical in determining normal and abnormal functioning of the basal ganglia. Proc. Biol. Sci. 269, 545–551. 10.1098/rspb.2001.1817 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gogolla N., Galimberti I., Caroni P. (2007). Structural plasticity of axon terminals in the adult. Curr. Opin. Neurobiol. 17, 516–524. 10.1016/j.conb.2007.09.002 [DOI] [PubMed] [Google Scholar]
- Götz T., Kraushaar U., Geiger J., Lübke J., Berger T., Jonas P. (1997). Functional properties of AMPA and NMDA receptors expressed in identified types of basal ganglia neurons. J. Neurosci. 17, 204–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta A., Balasubramani P. P., Chakravarthy V. S. (2013). Computational model of precision grip in Parkinson's disease: a utility based approach. Front. Comput. Neurosci. 7:172. 10.3389/fncom.2013.00172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gurney K., Prescott T. J., Redgrave P. (2001a). A computational model of action selection in the basal ganglia. I. A new functional anatomy. Biol. Cybern. 84, 401–410. 10.1007/PL00007984 [DOI] [PubMed] [Google Scholar]
- Gurney K., Prescott T. J., Redgrave P. (2001b). A computational model of action selection in the basal ganglia. II. Analysis and simulation of behaviour. Biol. Cybern. 84, 411–423. 10.1007/PL00007985 [DOI] [PubMed] [Google Scholar]
- Hadipour-Niktarash A., Rommelfanger K. S., Masilamoni G. J., Smith Y., Wichmann T. (2012). Extrastriatal D2-like receptors modulate basal ganglia pathways in normal and parkinsonian monkeys. J. Neurophysiol. 107, 1500–1512. 10.1152/jn.00348.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamani C., Saint-Cyr J. A., Fraser J., Kaplitt M., Lozano A. M. (2004). The subthalamic nucleus in the context of movement disorders. Brain 127, 4–20. 10.1093/brain/awh029 [DOI] [PubMed] [Google Scholar]
- Hammond C., Bergman H., Brown P. (2007). Pathological synchronization in Parkinson's disease: networks, models and treatments. Trends Neurosci. 30, 357–364. 10.1016/j.tins.2007.05.004 [DOI] [PubMed] [Google Scholar]
- Hansel D., Mato G., Meunier C. (1995). Synchrony in excitatory neural networks. Neural Comput. 7, 307–337. 10.1162/neco.1995.7.2.307 [DOI] [PubMed] [Google Scholar]
- Hauptmann C., Tass P. A. (2007). Therapeutic rewiring by means of desynchronizing brain stimulation. Biosystems 89, 173–181. 10.1016/j.biosystems.2006.04.015 [DOI] [PubMed] [Google Scholar]
- Humphries M. D., Khamassi M., Gurney K. (2012). Dopaminergic control of the exploration-exploitation trade-off via the basal ganglia. Front. Neurosci. 6:9. 10.3389/fnins.2012.00009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphries M. D., Lepora N., Wood R., Gurney K. (2009). Capturing dopaminergic modulation and bimodal membrane behaviour of striatal medium spiny neurons in accurate, reduced models. Front. Comput. Neurosci. 3:26. 10.3389/neuro.10.026.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphries M. D., Stewart R. D., Gurney K. N. (2006). A physiologically plausible model of action selection and oscillatory activity in the basal ganglia. J. Neurosci. 26, 12921–12942. 10.1523/JNEUROSCI.3486-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphries M., Gurney K. (2002). The role of intra-thalamic and thalamocortical circuits in action selection. Network 13, 131–156. 10.1080/net.13.1.131.156 [DOI] [PubMed] [Google Scholar]
- Humphries M., Gurney K., Prescott T. (2007). Is there a brainstem substrate for action selection? Philos. Trans. R. Soc. B Biol. Sci. 362, 1627–1639. 10.1098/rstb.2007.2057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurtado J. M., Gray C. M., Tamas L. B., Sigvardt K. A. (1999). Dynamics of tremor-related oscillations in the human globus pallidus: a single case study. Proc. Natl. Acad. Sci. U.S.A. 96, 1674–1679. 10.1073/pnas.96.4.1674 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich E. M. (2003). Simple model of spiking neurons. IEEE Trans. Neural Netw. 14, 1569–1572. 10.1109/TNN.2003.820440 [DOI] [PubMed] [Google Scholar]
- Izhikevich E. M. (2007). Dynamical Systems in Neuroscience. Cambridge, MA: The MIT press. [Google Scholar]
- Jahr C. E., Stevens C. F. (1990). Voltage dependence of NMDA-activated macroscopic conductances predicted by single-channel kinetics. J. Neurosci. 10, 3178–3182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalva S. K., Rengaswamy M., Chakravarthy V. S., Gupte N. (2012). On the neural substrates for exploratory dynamics in basal ganglia: a model. Neural Netw. 32, 65–73. 10.1016/j.neunet.2012.02.031 [DOI] [PubMed] [Google Scholar]
- Kang G., Lowery M. M. (2013). Interaction of oscillations, and their suppression via deep brain stimulation, in a model of the cortico-basal ganglia network. IEEE Trans. Neural Syst. Rehabil. Eng. 21, 244–253. 10.1109/TNSRE.2013.2241791 [DOI] [PubMed] [Google Scholar]
- Kita H., Chang H., Kitai S. (1983). The morphology of intracellularly labeled rat subthalamic neurons: a light microscopic analysis. J. Comp. Neurol. 215, 245–257. 10.1002/cne.902150302 [DOI] [PubMed] [Google Scholar]
- Kita H., Kita S. (1994). The morphology of globus pallidus projection neurons in the rat: an intracellular staining study. Brain Res. 636, 308–319. 10.1016/0006-8993(94)91030-8 [DOI] [PubMed] [Google Scholar]
- Kliem M. A., Maidment N. T., Ackerson L. C., Chen S., Smith Y., Wichmann T. (2007). Activation of nigral and pallidal dopamine D1-like receptors modulates basal ganglia outflow in monkeys. J. Neurophysiol. 98, 1489–1500. 10.1152/jn.00171.2007 [DOI] [PubMed] [Google Scholar]
- Kreiss D. S., Mastropietro C. W., Rawji S. S., Walters J. R. (1997). The response of subthalamic nucleus neurons to dopamine receptor stimulation in a rodent model of Parkinson's disease. J. Neurosci. 17, 6807–6819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreitzer A. C. (2009). Physiology and pharmacology of striatal neurons. Annu. Rev. Neurosci. 32, 127–147. 10.1146/annurev.neuro.051508.135422 [DOI] [PubMed] [Google Scholar]
- Krishnan R., Ratnadurai S., Subramanian D., Chakravarthy V. S., Rengaswamy M. (2011). Modeling the role of basal ganglia in saccade generation: Is the indirect pathway the explorer? Neural Netw. 24, 801–813. 10.1016/j.neunet.2011.06.002 [DOI] [PubMed] [Google Scholar]
- Kumar A., Cardanobile S., Rotter S., Aertsen A. (2011). The role of inhibition in generating and controlling Parkinson's disease oscillations in the basal ganglia. Front. Syst. Neurosci. 5:86. 10.3389/fnsys.2011.00086 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laureiro-Martãnez D., Canessa N., Brusoni S., Zollo M., Hare T., Alemanno F., et al. (2013). Frontopolar cortex and decision-making efficiency: comparing brain activity of experts with different professional background during an exploration-exploitation task. Front. Hum. Neurosci. 7:927. 10.3389/fnhum.2013.00927 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy R., Ashby P., Hutchison W. D., Lang A. E., Lozano A. M., Dostrovsky J. O. (2002). Dependence of subthalamic nucleus oscillations on movement and dopamine in Parkinson's disease. Brain 125, 1196–1209. 10.1093/brain/awf128 [DOI] [PubMed] [Google Scholar]
- Litvak V., Jha A., Eusebio A., Oostenveld R., Foltynie T., Limousin P., et al. (2011). Resting oscillatory cortico-subthalamic connectivity in patients with Parkinson's disease. Brain 134, 359–374. 10.1093/brain/awq332 [DOI] [PubMed] [Google Scholar]
- Lukasiewicz P. D., Werblin F. S. (1990). The spatial distribution of excitatory and inhibitory inputs to ganglion cell dendrites in the tiger salamander retina. J. Neurosci. 10, 210–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magdoom K., Subramanian D., Chakravarthy V. S., Ravindran B., Amari S.-I., Meenakshisundaram N. (2011). Modeling basal ganglia for understanding Parkinsonian reaching movements. Neural Comput. 23, 477–516. 10.1162/NECO_a_00073 [DOI] [PubMed] [Google Scholar]
- Magnin M., Morel A., Jeanmonod D. (2000). Single-unit analysis of the pallidum, thalamus and subthalamic nucleus in parkinsonian patients. Neuroscience 96, 549–564. 10.1016/S0306-4522(99)00583-7 [DOI] [PubMed] [Google Scholar]
- Mahon S., Vautrelle N., Pezard L., Slaght S. J., Deniau J.-M., Chouvet G., et al. (2006). Distinct patterns of striatal medium spiny neuron activity during the natural sleep–wake cycle. J. Neurosci. 26, 12587–12595. 10.1523/JNEUROSCI.3987-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maurice N., Deniau J.-M., Glowinski J., Thierry A.-M. (1998). Relationships between the prefrontal cortex and the basal ganglia in the rat: physiology of the corticosubthalamic circuits. J. Neurosci. 18, 9539–9546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mckinney R. A. (2010). Excitatory amino acid involvement in dendritic spine formation, maintenance and remodelling. J. Physiol. 588, 107–116. 10.1113/jphysiol.2009.178905 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meredith G., Ypma P., Zahm D. (1995). Effects of dopamine depletion on the morphology of medium spiny neurons in the shell and core of the rat nucleus accumbens. J. Neurosci. 15, 3808–3820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michmizos K. P., Nikita K. S. (2011). Addition of deep brain stimulation signal to a local field potential driven Izhikevich model masks the pathological firing pattern of an STN neuron, in Engineering in Medicine and Biology Society, EMBC, 2011 Annual International Conference of the IEEE (Boston, MA: IEEE; ), 7290–7293. [DOI] [PubMed] [Google Scholar]
- Modolo J., Mosekilde E., Beuter A. (2007). New insights offered by a computational model of deep brain stimulation. J. Physiol. Paris 101, 56–63. 10.1016/j.jphysparis.2007.10.007 [DOI] [PubMed] [Google Scholar]
- Moustafa A. A., Gluck M. A. (2011). A neurocomputational model of dopamine and prefrontal–striatal interactions during multicue category learning by Parkinson patients. J. Cogn. Neurosci. 23, 151–167. 10.1162/jocn.2010.21420 [DOI] [PubMed] [Google Scholar]
- Muralidharan V., Balasubramani P. P., Chakravarthy V. S., Lewis S. J., Moustafa A. A. (2013). A computational model of altered gait patterns in parkinson's disease patients negotiating narrow doorways. Front. Comput. Neurosci. 7:190. 10.3389/fncom.2013.00190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nambu A., Tachibana Y., Kaneda K., Tokuno H., Takada M. (2005). Dynamic model of basal ganglia functions and Parkinson's disease, in The Basal Ganglia VIII, eds Bolam J. P., Ingham C. A., Magill P. J. (Springer; ), 307–312. [Google Scholar]
- Nini A., Feingold A., Slovin H., Bergman H. (1995). Neurons in the globus pallidus do not show correlated activity in the normal monkey, but phase-locked oscillations appear in the MPTP model of parkinsonism. J. Neurophysiol. 74, 1800–1805. [DOI] [PubMed] [Google Scholar]
- Niv Y. (2009). Reinforcement learning in the brain. J. Math. Psychol. 53, 139–154. 10.1016/j.jmp.2008.12.005 [DOI] [Google Scholar]
- Pallotto M., Deprez F. (2014). Regulation of adult neurogenesis by GABAergic transmission: signaling beyond GABAA-receptors. Front. Cell. Neurosci. 8:166. 10.3389/fncel.2014.00166 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park C., Worth R. M., Rubchinsky L. L. (2010). Fine temporal structure of beta oscillations synchronization in subthalamic nucleus in Parkinson's disease. J. Neurophysiol. 103, 2707–2716. 10.1152/jn.00724.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park C., Worth R. M., Rubchinsky L. L. (2011). Neural dynamics in parkinsonian brain: the boundary between synchronized and nonsynchronized dynamics. Phys. Rev. E 83:042901. 10.1103/physreve.83.042901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearson J. M., Hayden B. Y., Raghavachari S., Platt M. L. (2009). Neurons in posterior cingulate cortex signal exploratory decisions in a dynamic multioption choice task. Curr. Biol. 19, 1532–1537. 10.1016/j.cub.2009.07.048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearson J. M., Heilbronner S. R., Barack D. L., Hayden B. Y., Platt M. L. (2010). Posterior cingulate cortex: adapting behavior to a changing world. Trends Cogn. Sci. 15, 143–151. 10.1016/j.tics.2011.02.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinsky P. F., Rinzel J. (1995). Synchrony measures for biological neural networks. Biol. Cybern. 73, 129–137. 10.1007/BF00204051 [DOI] [PubMed] [Google Scholar]
- Plenz D., Kitai S. T. (1998). Up and down states in striatal medium spiny neurons simultaneously recorded with spontaneous activity in fast-spiking interneurons studied in cortex–striatum–substantia nigra organotypic cultures. J. Neurosci. 18, 266–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plenz D., Kital S. T. (1999). A basal ganglia pacemaker formed by the subthalamic nucleus and external globus pallidus. Nature 400, 677–682. 10.1038/23281 [DOI] [PubMed] [Google Scholar]
- Prescott T. J., Bryson J. J., Seth A. K. (2007). Introduction. Modelling natural action selection. Philos. Trans. R. Soc. B Biol. Sci. 362, 1521–1529. 10.1098/rstb.2007.2050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ragozzino M. E. (2007). The contribution of the medial prefrontal cortex, orbitofrontal cortex, and dorsomedial striatum to behavioral flexibility. Ann. N.Y. Acad. Sci. 1121, 355–375. 10.1196/annals.1401.013 [DOI] [PubMed] [Google Scholar]
- Reynolds J. N. J., Wickens J. R. (2002). Dopamine-dependent plasticity of corticostriatal synapses. Neural Netw. 15, 507–521. 10.1016/S0893-6080(02)00045-X [DOI] [PubMed] [Google Scholar]
- Richards D. A., Mateos J. M., Hugel S., De Paola V., Caroni P., Gähwiler B. H., et al. (2005). Glutamate induces the rapid formation of spine head protrusions in hippocampal slice cultures. Proc. Natl. Acad. Sci. 102, 6166–6171. 10.1073/pnas.0501881102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson R., Clarke C., Boyce S., Sambrook M., Crossman A. (1990). The role of striatopallidal neurones utilizing gamma-aminobutyric acid in the pathophysiology of MPTP-induced parkinsonism in the primate: evidence from [3H] flunitrazepam autoradiography. Brain Res. 531, 95–104. 10.1016/0006-8993(90)90762-Z [DOI] [PubMed] [Google Scholar]
- Rogers R. D. (2010). The roles of dopamine and serotonin in decision making: evidence from pharmacological experiments in humans. Neuropsychopharmacology 36, 114–132. 10.1038/npp.2010.165 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell V., Allin R., Lamm M., Taljaard J. (1992). Regional distribution of monoamines and dopamine D1-and D2-receptors in the striatum of the rat. Neurochem. Res. 17, 387–395. 10.1007/BF00974582 [DOI] [PubMed] [Google Scholar]
- Schroll H., Vitay J., Hamker F. H. (2012). Working memory and response selection: a computational account of interactions among cortico-basalganglio-thalamic loops. Neural Netw. 26, 59–74. 10.1016/j.neunet.2011.10.008 [DOI] [PubMed] [Google Scholar]
- Schultz W. (1998). Predictive reward signal of dopamine neurons. J. Neurophysiol. 80, 1–27. [DOI] [PubMed] [Google Scholar]
- Sharott A., Doig N. M., Mallet N., Magill P. J. (2012). Relationships between the firing of identified striatal interneurons and spontaneous and driven cortical activities in vivo. J. Neurosci. 32, 13221–13236. 10.1523/JNEUROSCI.2440-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen K.-Z., Johnson S. W. (2010). Ca2+ Influx through NMDA-Gated channels activates ATP-Sensitive K+ currents through a nitric oxide–cGMP pathway in subthalamic neurons. J. Neurosci. 30, 1882–1893. 10.1523/JNEUROSCI.3200-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shouno O., Takeuchi J., Tsujino H. (2009). A spiking neuron model of the basal ganglia circuitry that can generate behavioral variability, in The Basal Ganglia IX, eds Groenewegen H. J., Voorn P., Berendse H. W., Mulder A. B., Cools A. R. (New York, NY: Springer; ), 191–200. [Google Scholar]
- Sinha S. (1999). Noise-free stochastic resonance in simple chaotic systems. Phys. A Stat. Mech. Appl. 270, 204–214. 10.1016/S0378-4371(99)00136-318517494 [DOI] [Google Scholar]
- Smith Y., Beyan M. D., Shink E., Bolam J. P. (1998). Microcircuitry of the direct and indirect pathways of the basal ganglia. Neuroscience 86, 353–388. [DOI] [PubMed] [Google Scholar]
- Smith Y., Kieval J. Z. (2000). Anatomy of the dopamine system in the basal ganglia. Trends Neurosci. 23, S28–S33. 10.1016/S1471-1931(00)00023-9 [DOI] [PubMed] [Google Scholar]
- Steiner H., Tseng K. Y. (2010). Handbook of Basal Ganglia Structure and Function: A Decade of Progress. London: Elsevier. [Google Scholar]
- Stern E. A., Jaeger D., Wilson C. J. (1998). Membrane potential synchrony of simultaneously recorded striatal spiny neurons in vivo. Nature 394, 475–478. 10.1038/28848 [DOI] [PubMed] [Google Scholar]
- Stewart T. C., Bekolay T., Eliasmith C. (2012). Learning to select actions with spiking neurons in the basal ganglia. Front. Neurosci. 6:2. 10.3389/fnins.2012.00002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sukumar D., Rengaswamy M., Chakravarthy V. S. (2012). Modeling the contributions of Basal ganglia and Hippocampus to spatial navigation using reinforcement learning. PLoS ONE 7:e47467. 10.1371/journal.pone.0047467 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Surmeier D. J., Ding J., Day M., Wang Z., Shen W. (2007). D1 and D2 dopamine-receptor modulation of striatal glutamatergic signaling in striatal medium spiny neurons. Trends Neurosci. 30, 228–235. 10.1016/j.tins.2007.03.008 [DOI] [PubMed] [Google Scholar]
- Sutton R. S., Barto A. G. (1998). Reinforcement Learning: an Introduction. Cambridge: Cambridge University Press. [Google Scholar]
- Tachibana Y., Iwamuro H., Kita H., Takada M., Nambu A. (2011). Subthalamo−pallidal interactions underlying parkinsonian neuronal oscillations in the primate basal ganglia. Eur. J. Neurosci. 34, 1470–1484. 10.1111/j.1460-9568.2011.07865.x [DOI] [PubMed] [Google Scholar]
- Terman D., Rubin J., Yew A., Wilson C. (2002). Activity patterns in a model for the subthalamopallidal network of the basal ganglia. J. Neurosci. 22, 2963–2976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thibeault C. M., Srinivasa N. (2013). Using a hybrid neuron in physiologically inspired models of the basal ganglia. Front. Comput. Neurosci. 7:88. 10.3389/fncom.2013.00088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian L., Stefanidakis M., Ning L., Van Lint P., Nyman-Huttunen H., Libert C., et al. (2007). Activation of NMDA receptors promotes dendritic spine development through MMP-mediated ICAM-5 cleavage. J. Cell Biol. 178, 687–700. 10.1083/jcb.200612097 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vickers D. (1970). Evidence for an accumulator model of psychophysical discrimination. Ergonomics 13, 37–58. 10.1080/00140137008931117 [DOI] [PubMed] [Google Scholar]
- Wang X.-J., Rinzel J. (1993). Spindle rhythmicity in the reticularis thalami nucleus: synchronization among mutually inhibitory neurons. Neuroscience 53, 899–904. 10.1016/0306-4522(93)90474-T [DOI] [PubMed] [Google Scholar]
- Weinberger M., Dostrovsky J. O. (2011). A basis for the pathological oscillations in basal ganglia: the crucial role of dopamine. Neuroreport 22, 151. 10.1097/WNR.0b013e328342ba50 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willshaw D., Li Z. (2002). Subthalamic–pallidal interactions are critical in determining normal and abnormal functioning of the basal ganglia. Proc. Biol. Sci. 269, 545–551. 10.1098/rspb.2001.1817 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yucelgen C., Denizdurduran B., Metin S., Elibol R., Sengor N. S. (2012). A biophysical network model displaying the role of basal ganglia pathways in action selection, in Artificial Neural Networks and Machine Learning–ICANN 2012 (Berlin; Heidelberg: Springer; ), 177–184. [Google Scholar]
- Zhu Z.-T., Munhall A., Shen K.-Z., Johnson S. W. (2005). NMDA enhances a depolarization-activated inward current in subthalamic neurons. Neuropharmacology 49, 317–327. 10.1016/j.neuropharm.2005.03.018 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.