The elastic free energy of a tandem modular protein under force

Abstract

Recent studies have provided a theoretical framework for including entropic elasticity in the free energy landscape of proteins under mechanical force. Accounting for entropic elasticity using polymer physics models has helped explain the hopping behavior seen in single molecule experiments in the low force regime. Here, we expand on the construction of the free energy of a single protein domain under force proposed by Berkovich et al. to provide a free energy landscape for N tandem domains along a continuous polypeptide. Calculation of the free energy of individual domains followed by their concatenation provides a continuous free energy landscape whose curvature is dominated by the worm-like chain at forces below 20 pN. We have validated our free energy model using Brownian dynamics and reproduce key features of protein folding. This free energy model can predict the effects of changes in the elastic properties of a multidomain protein as a consequence of biological modifications such as phosphorylation or the formation of disulfide bonds. This work lays the foundations for the modeling of tissue elasticity, which is largely determined by the properties of tandem polyproteins.

Introduction

Force spectroscopy studies have uncovered the basic elements of how proteins respond to a stretching force; domains unfold and refold in a time and force dependent manner [1–3]. The Bell model and the formalism of barrier crossing developed by Kramers were widely applied to understand the force dependency of these transitions. However, such models were developed to describe the rupture of bonds over length scales of only a few Angstroms, where changes in entropy do not play a significant role [4]. Using these models to explain protein unfolding-refolding reactions under force, where molecules extend and collapse over tens of nanometers, led to paradoxical results [5]. The departure of experimental findings from simple two-state behavior motivated the development of new theories that considered changes in entropy as a crucial component of the free energy [5, 6]. These models included the laws of polymer physics in the unfolding of a single protein domain under a stretching force and demonstrated the force dependency of the unfolding rates and protein elongation. However, it was not clear how to extend these concepts to construct the elastic free energy of a multi-domain protein where many of these individual modules are arranged in tandem.

Models of tandem modular proteins are becoming increasingly important as these proteins are identified as determinant factors of tissue elasticity and modulators of cell signaling [7–9]. It remains poorly understood how the mechanical behavior of single molecules scales to an overall material property such as tissue elasticity. Here, we generalize the concepts described by Berkovich et al. [5] and show how to construct the elastic free energy of a tandem modular protein as a function of force. We perform Brownian dynamics simulations of the resulting free energy landscape and reproduce key experimental benchmarks of protein unfolding such as the Arrhenius dependency of the rates, the force dependency of the step size, and the force range at which domain refolding is favored over unfolding. Our model predicts that the effects of complex biological modifications, such as disulfide bond formation, can be incorporated into the free energy by simply changing the polymer properties. Thus, describing the elastic free energy of large tandem modular proteins is an important step towards understanding the origins and regulation of tissue elasticity and its function during animal motion [10–12].

Materials and Methods

A free energy model for tandem modular proteins is developed here by extrapolating the procedures described in Berkovich et al. [5]. This model was defined for only one domain, but here we propose a numerical method to concatenate the free energy landscape to any number of identical protein domains N.

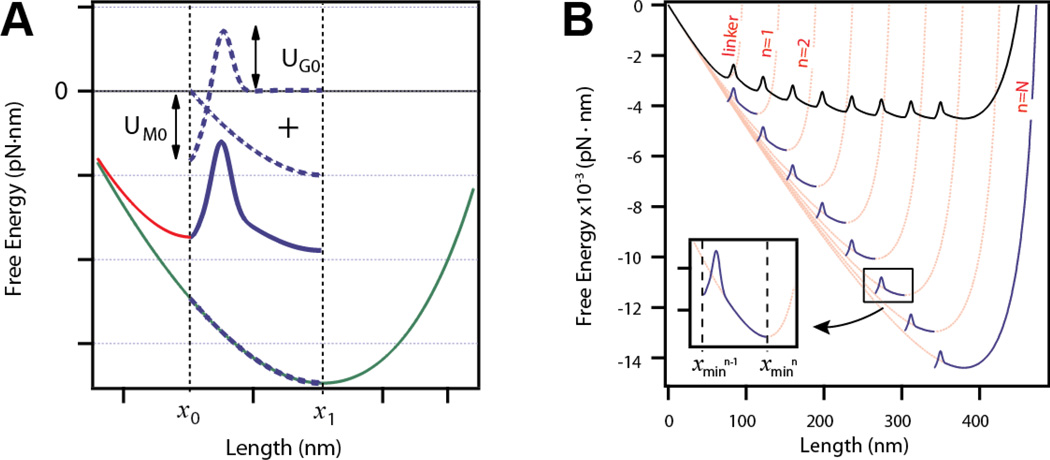
The free energy of a polyprotein can be described by the summation of three distinct components: the entropic elasticity of the polymer chain under force U^WLC (Eq. (S1)), a short range potential representing the hydrophobic interactions that drive folding U^M (Eq. (S2)), and an entropic barrier caused by removal of available polypeptide configurations between the collapsed and folded states U^G (Eq. (S3)). Here the worm-like chain (WLC) model is used to approximate the entropic elasticity of the polypeptide [6, 13]. The entropic elasticity is controlled by two parameters: the increase in contour length ΔL_c and persistence length p. The free energy of a single domain along its pulling coordinate is defined by the summation of these three energy contributions in Eq. (1). A plot of the free energy of a single protein domain constructed from these three components (dashed lines) is shown in Figure 1A (solid line).

$$U(x)=U^{WLC}(x,\mathrm{\Delta }{L}_c)+U^M(x+R_c)+U^G(x)$$ (1)

The energy landscape is defined within the range x₀ ≤ x ≤ x₁. At short extensions, the free energy is dominated by the Morse potential and the protein lies in its native state at x₀. With application of enough force, mechanical unfolding drives the protein to an extended conformation with an energy located at the entropic minimum x₁ according to Eq. (S1).

Figure 1. Method of the construction of the elastic free energy of a tandem modular protein.

A) Construction of the free energy for a single domain unfolding and extending. The free energy of unfolding and extending a domain is constructed from three elements (dotted lines): a Morse well of U_M0 depth, a Gaussian barrier of U_G0 height, and a WLC potential of contour length ΔL_c (green line) from which only the section between x₀ and x₁ is considered. The red curve represents the initial extension to x₀ calculated from the WLC with a contour length L₀. B) Expansion of the free energy model to a polyprotein with N number of domains. The pink lines correspond to WLC curves calculated for an octamer polyprotein at a force F = 20 pN, and for contour length n ·ΔL_c, where n is the number of unfolded domains, ΔL_c = 19 nm, and p = 0.4 nm. At each contour length the WLC has a minimum that serves as the obligatory starting point for the next segment. Segments (thick blue lines) are constructed by adding a Morse well and a Gaussian barrier to the entropic elasticity as described in the text and in Figure 1A within the range x_n−1 to x_n (insert). The WLC for the linker is also shown in the plot (L₀ =42 nm and p_f =10 nm, extended at F = 20 pN). The final free energy profile is constructed by concatenating all segments at their boundaries (thick black line).

In order to generalize this result for tandem modular proteins, we consider the effect of unfolding a second domain in the protein. At constant force F, unfolding a second domain increases the total length of the polymer by ΔL_c such that the total contour length of the polymer is 2·ΔL_c. The entropic minimum of this polymer chain is now located at a new extension x₂. Thus, extending a polymer with N unfolded domains is well described by Eq. (S1) with a contour length of n·ΔL_c where 1 ≤ n ≤ N, and an entropic minimum located at extension x_n (pink curves; Figure 1B).

Figure 1B is a graphical representation of how to construct the free energy landscape of a tandem polyprotein from the segments comprising the free energy of each individual domain. Prior to unfolding, the second domain lies in the minimum of a Morse potential located at x₁ and must cross a transition state barrier at x₁ + x_b. After unfolding, the second domain lies at its entropic minimum x₂. Thus, we sum the three energetic components as described in Eq. (1) over the range [x₁, x₂] for a polymer with contour length 2·ΔL_c. For a protein with N folded domains, the free energy is divided into several segments, defined by the evaluation of Eq. (1) on [x_n−1, x_n] for n = 1, 2, … N (blue curves, Fig. 1B). A general expression for the free energy of any segment n is provided here:

$$U_n(x)=U^{WLC}(x,n\mathrm{\Delta }{L}_c)+U^M(x-x_{n-1}+R_c)+U^G(x-x_{n-1}),x_{n-1}\le x\le x_n$$ (2)

Furthermore, we assume that the free energy must be continuous at the boundaries of each segment, so that the entropic minimum of the extended domain coincides with the minimum Morse energy of the subsequent folded domain. This is numerically achieved by concatenating all the segments to satisfy the following boundary condition (black curve; Figure 1B).

$$U_{n-1}(x_{n-1})=U_n(x_{n-1}),1\le n\le N$$ (3)

As shown in Figure 1B, a polypeptide with N structured domains (black curve) has a different energy compared to an unstructured polypeptide with an equivalent contour length (pink curve, n = N) due to Eq. (3) [14]. Finally, we append to the free energy a stiff segment representing N tandem folded domains plus any polymer linkers used for attachment chemistry to the probe (red curve, Figure 1A and B). The free energy for this segment is calculated using only the WLC (Eq. (S1)) with a high persistence length (Table S1) on the range [0, x₀].

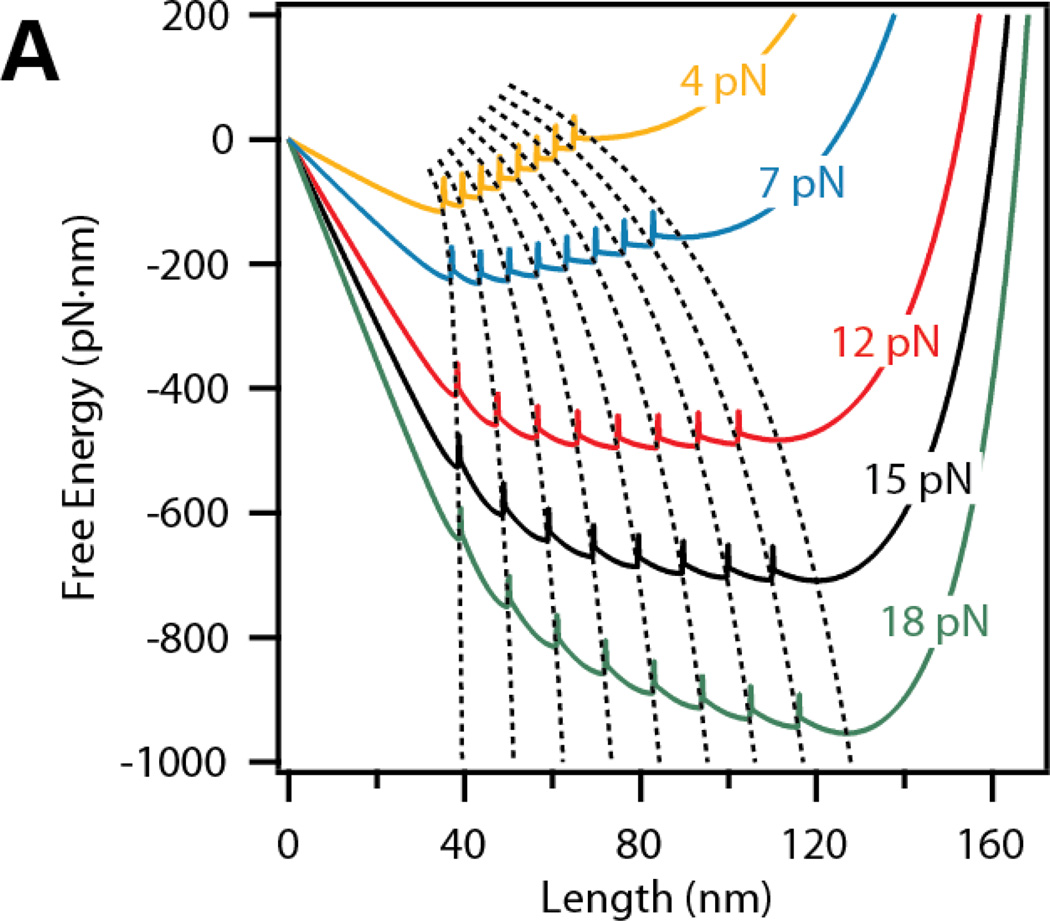
The resulting continuous free energy landscape for a tandem modular protein with N=8 domains is shown in Figure 2. The free energy was calculated at several forces: 4, 7, 12, 15 and 18 pN. As the force applied to the polypeptide increases, the location of the entropic minima x_n increases according to the WLC model (Figure 2A, dashed lines). The trajectories of the minima as a function of force will be referred to here as E-curves. For a protein with N=8 domains, there are N+1 E-curves representing the entropic minima of the linker plus 1 to 8 unfolded domains. Upon a change in force, the polypeptide is driven to the same local minimum within the new free energy curve; hence, tracking the E-curve. Thereafter, the polyprotein diffuses towards the global energy minimum at that force.

Figure 2. Representation of the E-curves describing the trajectory of the minimum of each domain as a function of force.

The free energy for eight tandem repeats displays nine local minima, corresponding to 0 – 8 unfolded domains. The global minimum of the free energy shifts from 0 domains unfolded to 8 domains unfolded as the force is increased from 4 to 18 pN. E-curves are represented by dashed lines that track the free energy minima through different forces.

Brownian dynamics are suitable for generating extension vs time trajectories of a polypeptide with conditions designed to mimic those present in single molecule experiments. The diffusion of the system along its elastic free energy can be simulated with Brownian dynamics using the over-damped Langevin equation [5].

$$\dot{x}(x)=-\frac{D}{k_{B}T}\frac{\partial U(x)}{\partial x}+{(2D)}^{\frac{1}{2}}\mathrm{\Gamma }(t),$$ (4)

where D is the self-diffusion coefficient [6, 15] and Γ(t) is a white noise associated with the surrounding thermal environment of the molecule, described here by <Γ(t)> = 0 and < Γ(t)Γ(t’) > = δ (t – t’). U(x) is the elastic free energy of the entire polymer at a constant force as described by Eqs. (2)–(3). Given that the free energy does not have an analytical form, we evaluate Eqs. (2)–(3) for a polypeptide of N=8 domains over a range of forces from 2 to 40 pN prior to the simulations. These free energy profiles provide look-up tables for the Brownian dynamics simulations at a given force. The parameters used for the free energy model and Brownian dynamics are given in the supplementary materials (Table S1).

Additionally, we study the force dependency of the unfolding rates as a function of force. We generated 20–30 unfolding traces using Brownian dynamics (Eq. (4)) at forces from 20 to 100 pN. The traces were summed, normalized, and fit with a single exponential (Figure S2A). The error for each measured rate was estimated using bootstrapping methods [16].

Results

It has been proposed before how to include the effect of entropic elasticity in the free energy of a single protein domain [5]. Here we expand this model to a tandem polyprotein and explore its consequences in the free energy landscape. This model proposes that the free energy landscape of tandem polyproteins is highly dependent on the polymer elastic properties. We provide a numerical method for how to expand the model from the energy of one domain [5, 6] to the total free energy of N number of domains.

There are several salient features of the free energy constructed using the methods described above. Due to the entropic elasticity, the model predicts that the distances between the local minima are equidistant at a given force and scale with the force according to the WLC (Eq. (S1)). Furthermore, the change in free energy upon unfolding is different for any domain n within the energy landscape, because it depends on the local curvature of the entropic elasticity (Figure 1B). For instance at 20 pN the change in free energy between x₀ and x₁ is greater than between x₇ and x₈.

The position of the global minimum free energy determines the most likely end-to-end length of the polyprotein at any given force. This position is highly dependent on the parameters of the entropic elasticity and the attractive Morse potential. Moreover, the rates depend mainly on the local slope of the free energy, transition state barrier, and diffusion coefficient D. Hence, we can predict the kinetics and steady state behavior of a polyprotein under force with Brownian dynamics.

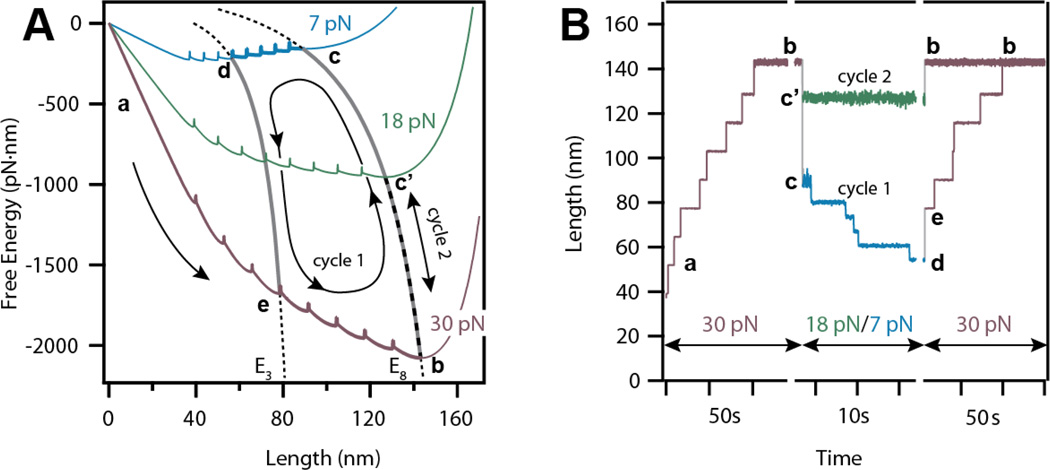
We employ various force protocols to explore the free energy of the polyprotein using Brownian dynamics. Figure 3A shows two examples of how a tandem modular protein of eight domains responds to a change in force by diffusing along its free energy landscape (cycle 1 and 2). In adjacent Figure 3B, traces obtained from Brownian dynamics simulations show how the end-to-end length of the polyprotein changes in response to the force-pulse protocol (cycle 1 and 2) defined in Figure 3A.

Figure 3. Force-protocols to explore the free energy landscape of a tandem protein using Brownian dynamics.

A) Free energies and E-curves depicting the trajectory of a single unfolding-refolding-unfolding Brownian Dynamics simulation. Movement along a single free energy may result in folding or unfolding while diffusion along an E-curve changes the end-to-end length of the protein without folding events. B) Traces obtained from Brownian dynamics simulations for two different cycles (cycle 1 and 2). The first cycle considers the total unfolding at 30 pN from a to b, followed by a quench of 7 pN causing diffusion along the E8 curve to c, and a final refolding of five domains from c to d. For the second cycle, the refolding force is reduced to 18 pN instead of 7 pN, causing the shortening of the polyprotein from b to c’ without refolding any domains.

In both cases the protein is first unfolded at a high force of 30 pN, displaying 12.9 nm step-increases in the measured end-to-end length, as it travels on its energy landscape toward the global minimum (a→b). In the first case (cycle 1), the force is quenched to 7 pN. At this force, the protein undergoes a fast entropic collapse of approximately 54 nm as it travels along E₈ from 30 pN to 7 pN (b→c). This fast entropic collapse is followed by a series of five downward steps of 6.5 nm in the protein end-to-end length. These steps represent individual refolding events, which occur as the protein diffuses towards its global minimum along its 7 pN energy landscape from the entropic minimum x₈ to x₃ (c→d). In the subsequent high force pulse (30 pN) the polymer chain stretches and five domains unfold once more (d→e→b). In an alternative force protocol (cycle 2), the force is quenched to 18 pN. In this case the unfolded protein only experiences entropic collapse due to the change in force, and no domains refold since the global energy minimum rests on the E₈ curve (b→c’→b). Force protocols do not need to jump between distinct values of force, as performed here. A powerful feature of this free energy model is the ability to predict protein dynamics in response to an arbitrary force perturbation. Brownian dynamics with several non force-clamp perturbations demonstrate the flexibility of our method (Figure S3).

The results of the Brownian dynamics simulations over a broad range of forces reveal several important features of mechanical protein unfolding. At any given force, unfolding or refolding of a protein domain results in stepwise changes in the end-to-end length due to the equidistant spacing of the local free energy minima. Thus, we are able to reproduce the scaling of the step size with the WLC that is seen experimentally (Figure S1) [17]. Furthermore, we examine the force dependency of the unfolding rates obtained from the average of simulated traces at different forces (see Methods). The unfolding rates show typical Arrhenius behavior, $k=k_0\text{exp}\left(\frac{F·\mathrm{\Delta }x}{k_{B}T}\right)$, that is observed experimentally [4, 16]. Our fit parameters for the Arrhenius equation were found to be k₀ = 3.3 · 10⁻³s⁻¹ and Δx = 0.25 nm (Figure S2B). It is notable that we recover the same distance to the transition state that was set during the construction of our free energy (Δx = x_b = 0.25 nm).

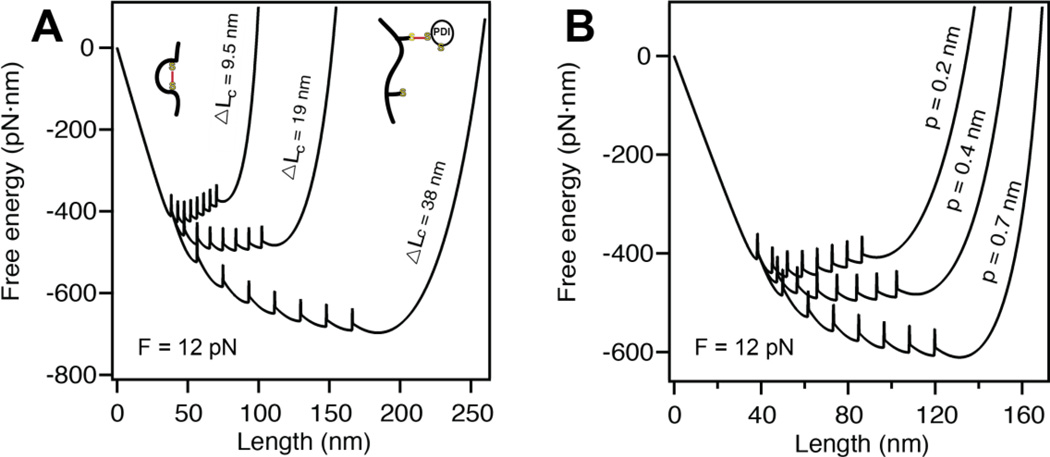
The model acts as a powerful predictive tool of the effect of certain biological processes on proteins folding under force. For example, it has been shown that introducing a disulfide bond into a protein domain accelerates the rate of folding several times and increases the stability of the folded state. In this case, the disulfide bond does not affect the mechanical clamp, but only serves to shorten the contour length ΔL_C [18]. Our model predicts that reducing ΔL_C shifts the global minimum free energy towards the folded state, in agreement with these experimental findings (Figure 4A). At low forces, our model also predicts that the presence of a disulfide bond would make the protein more difficult to unfold.

Figure 4. Altering the parameters of the entropic elasticity affects protein folding.

A) Decreasing the contour length of our polyprotein from ΔL_c = 38 nm to ΔL_c = 9.5 nm, shifts the global minimum free energy from favoring the completely unfolded state to the completely folded state at a constant force of F =12 pN. Hence, the rate of folding is considerably increased by the decreasing ΔL_c. B) A similar effect is captured by altering the persistence length at a constant force of F = 12 pN. Increasing the stiffness of the polymer from p = 0.2 nm to p = 0.7 nm also shifts the minimum free energy from fully folded to fully unfolded.

Alternatively, it has been demonstrated that the persistence length of a protein can be modified through post-translational modifications such as phosphorylation [19, 20]. According to our model, changing p is expected to alter the kinetics of unfolding/folding. Figure 4B shows the effects of stiffening and softening the polyprotein chain by increasing and decreasing p respectively. Increasing the persistence length from p = 0.2 nm to p = 0.7 nm shifts the global minimum energy from the completely folded state to the completely unfolded state.

Discussion

The Bell model was originally intended to explain the forced dissociation of adhesive bonds, where the transition state energy is lowered by an amount directly proportional to the applied force [4]. As force spectroscopy techniques were developed to study folding/unfolding reactions in proteins and nucleic acids molecules, the Bell model was further expanded to explain their dynamics as a function of force. However these reactions, in which molecules extend and collapse over tens of nanometers, have a high entropic cost due to stretching of the polypeptide chain which is not accounted for by the Bell model. Previous results by Berkovich et al. emphasized the role of entropic elasticity in the free energy landscape of a single folded domain under force [5]. In this manuscript, we provide a formalism to expand his methods to constructing the free energy landscape of a polyprotein of any number of domains, N. We achieve this by constructing a piece-wise free energy landscape, with each segment consisting of energy contributions from entropic elasticity, an attractive potential, and an entropic barrier. The resulting free energy landscape is tightly linked to the polymer properties of the polypeptide, which are modeled by the WLC. As a consequence, our model incorporates the dominant effects of entropic work in extending a polypeptide and predicts the force dependency of the step size during unfolding or refolding. This effect is not included in other free energy models to date [21–23].

Brownian dynamics on the proposed free energy landscape shows advancements over previous theoretical framework using Monte Carlo simulations [24]. Because Brownian dynamics evaluates the derivative of the potential surface, it is sensitive not only to transition state barriers but also to the shape and slope of the underlying free energy (Eq. (4)). As seen in Figure 4, although the barriers to folding are not modified, decreasing the contour length or persistence length raises the slope of the free energy, resulting in the increased of the rate of folding. Thus, our model predicts the kinetics of the polyprotein upon changes in its polymer properties without prior knowledge of the rates, which is required in Monte Carlo simulations.

Constructing an accurate representation of the free energy of modular proteins along the pulling coordinate in a physiological range of forces (1–10 pN [8, 17]) is a crucially important effort in biology. The discovery that massively large tandem polyproteins are responsible for the elasticity of muscle and other tissues has shifted our view on the molecular origins of tissue elasticity and its regulation [7, 9, 25, 26]. While it is currently challenging to study the mechanical characteristics of polyproteins with hundreds of structured domains using single molecule force spectroscopy, as in the case with the muscle protein titin, our model has the ability to determine the elastic properties of a polyprotein with any number of domains. The next goal in developing this model is to be able to establish the effects of point mutations, other post-translational modifications, and domains with heterogeneous stability on the free energy landscape. We will ultimately use our findings to develop the first full-scale model of muscle tissue elasticity to be able to predict the severity of diseases in muscles resulting from abnormal protein regulation and from genetic mutations that alter domain stability.