Abstract
Objective
A mechanistic, physiologically-based pharmacokinetic (PK/PD) model was developed to describe the biphasic insulin release and evaluate the racial effects on the glucose– insulin kinetics in response to intravenous glucose.
Methods
Fifteen African-American and 18 Caucasian children and adolescents between 8 and 18 years of age were enrolled in the study. Intravenous bolus of glucose (250 mg/kg) was administered and blood samples collected at frequent intervals for three hours following the glucose injection. A nonlinear mixed-effect population kinetic analysis with covariate structure was performed using Monolix.
Results
A significantly higher initial insulin secretion from a readily releasable pool, which is responsible for the first-phase insulin secretion, was detected in African-Americans compared to Caucasians (p < 0.05).
Conclusions
The proposed kinetic model is able to describe the glucose-stimulated insulin response, account for the first-phase insulin release and identify a racially-based pharmacokinetic difference in insulin’s biphasic secretion behavior. It is hypothesized that the first-phase insulin component may play an important role in the development of type 2 diabetes. The proposed mechanistic model provides a quantitative analysis of the biphasic insulin release that may be useful in the early detection of diabetes.
Keywords: First-phase insulin, Beta-cell, Ethnicity, Intravenous glucose tolerance test, Insulin modeling, Pharmacokinetics, Pharmacodynamics
1. Introduction
The prevalence of obesity and type 2 diabetes among children is increasing in U.S., and this problem is greater in African-American children compared to Caucasian children [1]. A number of recent reports have demonstrated that nondiabetic African-Americans have increased insulin resistance [2–5] which is a risk factor for developing type 2 diabetes [6,7]. Increased insulin secretion in African-Americans may compensate for or precede the insulin resistance [2,8–10]. In any event, it appears that there is an inherent difference in glucose and insulin metabolism between these two populations.
In our previous study [11] a nonparametric approach was used to analyze insulin dynamics by means of data from frequently sampled intravenous glucose tolerance tests (FSIVGTT). That study indicated that race, as a major covariate, only affects the insulin concentration in the first-phase for non-obese subjects. As first demonstrated by Cerasi and Luft in vivo [12], insulin secretion in response to glucose exhibits a biphasic pattern. Much effort has been devoted to understanding the underlying mechanisms of the biphasic release because of the apparent association between the onset of type 2 diabetes and the loss of the first-phase [12,13].
The objectives of this study are to kinetically evaluate the biphasic insulin release based on current knowledge of the beta-cell insulin physiology, and to apply population kinetic analysis principles to differentiate the kinetic parameters that contribute to the difference in insulin secretion between African-American and Caucasian. A wide variety of models have been used to study the glucose and insulin dynamics. The often applied minimal model [14] has been used for several decades due to its capability of estimating indices of insulin sensitivity. However, the minimal model does not represent the early insulin secretion, accurately. The early first-phase data points are commonly not included in the minimal model analysis. Thus, the minimal model is not suitable for analyzing the early phase release. Only few models have been proposed to describe insulin secretion based on the mechanism of a biphasic insulin secretion. Grodsky modeled multiple insulin pools in beta-cells [15]. They studied the phasic insulin secretion both in vitro and in vivo and suggested a two-compartment model to describe the biphasic secretion. However, the model only successfully simulated the first-phase secretion under certain levels of glucose stimulation. A more elaborate model with a biphasic mechanism of insulin secretion has been proposed by Gupta et al. [16]. However due to the greater complexity of that model the parameters that relate to first-or second-phase release are difficult to evaluate in a population kinetic framework.
In this work, the physiological mechanism of biphasic secretion is specifically considered in the PK/PD analysis, with a strong structural connection to current knowledge of the beta-cell insulin physiology. Compared to other models that consider a biphasic insulin models, the proposed model is simpler in structure and number of parameters and includes physiologically based parameters closely related to the important biphasic insulin secretion. Insulin concentrations obtained from FSIVGTT in the two racial groups were simultaneously analyzed in a population modeling framework using the Monolix software [17] according to the proposed mechanistic kinetic model. A specific covariate structure was used in the population analysis enabling the identification of distinct differences in physiologically relevant kinetic parameters between African-American and Caucasian youths.
2. Subjects and methods
2.1. Subjects
The database used here were the same as the one used in our previous noncompartmental analysis [11] except 5 subjects were excluded due to missing first- or second-phase. The FIVGTT analysis involved 15 healthy African-American (3 females and 12 males), age 13.7 ± 2.55 (mean ± SD), and 18 healthy Caucasian children (8 females and 10 males), age 14.1 ± 2.90. The BMI of African-Americans is 25.6 ± 4.63, which is significantly (p < 0.05) higher comparing to that of 21.5 ± 4.13 of Caucasians. The study was conducted in accordance with the guidelines in The Declaration of Helsinki and the protocol approved by the Ohio State University Office of Responsible Research.
2.2. Sampling procedure
Subjects received their routine diet for at least 3 days before the glucose tolerance test and then were admitted at 8 AM after 10 h fasting to the General Clinical Research Center, Ohio State University. On the morning of the test, a bolus glucose of 250 mg/kg was administered within 1 min through an intravenous catheter at time 0. Blood samples were collected at −10, 0, 2, 4, 6, 8, 10, 12, 14, 16, 19, 22, 27, 32, 42, 52, 62, 72, 82, 92, 102, 122, 142,162 and 182 min relative to the glucose administration at time 0.
2.3. Laboratory analysis
Plasma glucose was measured by the YSI model 2300 glucose analyzer (Yellow Springs Instruments, Yellow Springs, OH). The coefficient of variation (CV) of this method is <2%. Plasma insulin was measured in the CORE laboratory of the GCRC using a double antibody radioimmunoassay (Coat-A-Count kit manufactured by Siemens Medical Solutions Diagnostics, Los Angeles, CA). The sensitivity of the insulin assay was 2.5 µU/ml. The intra-and inter-assay CV were 6% and 10%, respectively.
2.4. PK/PD modeling
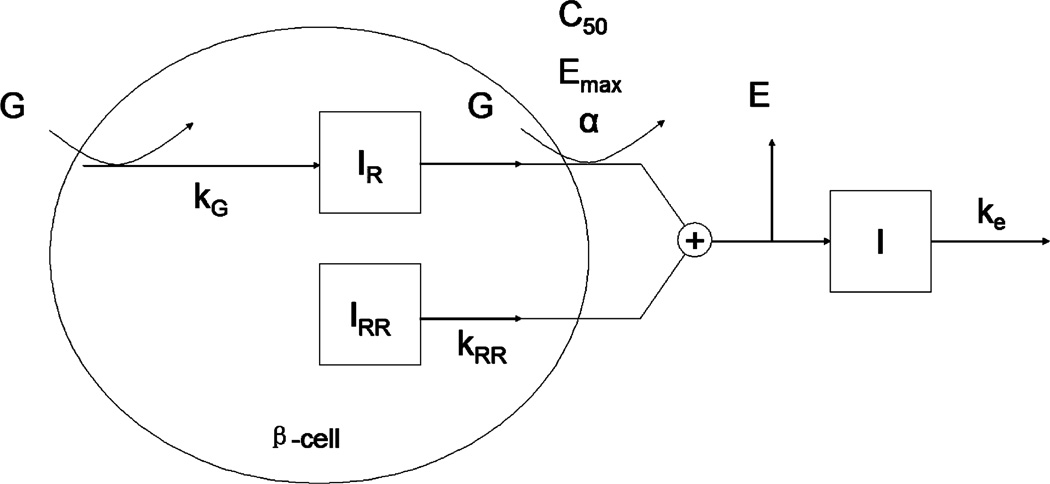
A physiologically based mathematical model was developed to describe plasma insulin concentration in response to an acute glucose challenge during FIVGTT. The model considers the physiologic mechanism of biphasic secretion of insulin at the beta-cell level. The model (Fig. 1) includes two insulin pools in the beta-cells, which store the biosynthesized insulin granules and account for the biphasic nature of insulin secretion. One pool, here denoted the reserved insulin pool (IR), governs the second-phase insulin secretion and the other denoted the readily releasable insulin pool (IRR) governs the first-phase insulin secretion.
Fig. 1.
Schematic of the proposed PK/PD model. G represents the glucose; IR, IRR and I represent reserved insulin, readily releasable insulin and plasma insulin respectively. E denotes the extraction ratio of insulin by liver. kG, ke and kRR are rate constants; C50, Emax and α are the parameters in the Hill equation.
Eq. (1) describes the second-phase insulin secretion from the IR pool. It considers a rate of formation of IR proportional to the plasma glucose concentration (CG) and a release of insulin empirically described by a Hill equation:
| (1) |
with kG denoting the first-order formation rate constant, and the Emax, C50 and α the Hill equation parameters, while IR_0 is the estimated initial condition of the IR pool.
The insulin in the readily releasable pool (IRR) has been “primed” (prepared for release) for ready release according to the biphasic secretion mechanism. The readily releasable insulin can in response to the glucose stimulation be released at a relatively fast rate compared to that in the IR pool, to form the first-phase. The change in IRR is given by:
| (2) |
where kRR is a first-order rate constant and IRR_0 is the estimated initial condition of the IRR pool.
The insulin from the beta-cells (IR and IRR pools) needs to go through the liver prior to its entry into the circulation. A fraction of insulin described by the extraction ratio E is removed by the liver. The plasma is considered as a single compartment for insulin with first-order elimination kinetics. Accordingly, the rate of change in the plasma insulin concentration is described by:
| (3) |
where CI is the plasma insulin concentration, CI_0 is the initial plasma insulin concentration, ke is a first-order elimination rate constant, V is the distribution volume of insulin in plasma and Pe has been introduced to represent the expression of (1 − E)/V to avoid identifiability problems.
2.5. Population PK/PD modeling
A nonlinear mixed-effect model was used for the population analysis in which the insulin concentration profile is described by the above set of differential equations, and random effects account for variability between-and within-subjects. Let yij denotes the j-th observed plasma insulin concentration of subject i at time tij (i = 1, …, n, j = 1,…, k), then the nonlinear mixed-effect model is written as:
| (4) |
where f is the PK/PD model consisting of the solution to the differential Eqs. (1)–(3), g is the residual error model, εij is the coefficient of the error model following a normal distribution with mean 0 and variance 1.
Various residual error models were investigated for the population analysis and the choice made based on the likelihood ratio test and plots of goodness-of-fit. As possibilities we consider the function g (Eq. (4)) to have the following constant, proportional and combined forms:
| (5) |
| (6) |
| (7) |
with ϕi being a p-dimensional vector of individual parameters for subject i assumed to be log-normally distributed, ensuring non-negativity in the estimation. Race was evaluated as a categorical covariate to explain between-subject variability in the kinetic parameters. To describe racial effects, ϕi was modeled with the following covariate structure:
| (8) |
where ci is a categorical vector corresponding to the ethnicity of subject i (African-American was used as reference class); β is a vector of coefficients of size p; μ is a vector of population means for parameters with length p; ηi represents the random effect assumed to follow a normal distribution with mean of zero and Ω is a diagonal variance matrix of the random effects. Significance of the racial effect on parameters was evaluated by the Wald test at a significance level of 0.05.
2.6. Data analysis
The data from all the subjects were simultaneously analyzed using the open-source free computer software Monolix, standalone version 3.1 developed by INRIA, France [17]. The population parameters were estimated based on the maximum likelihood estimation (MLE). A Stochastic Approximation Expectation Maximization (SAEM) algorithm coupled with Markov Chain Monte Carlo (MCMC) [18–21] procedure was used for MLE estimation of the parameters of the population model without the use of approximations in the estimation of the likelihood. We made use of Monolix because its algorithm showed much better convergence properties compared to the software NONMEM VI which failed to converge in our case. The Hastings–Metropolis algorithm was applied to compute conditional means and conditional standard deviations of the individual parameters. The glucose concentrations were represented by a linear spline interpolation.
3. Results
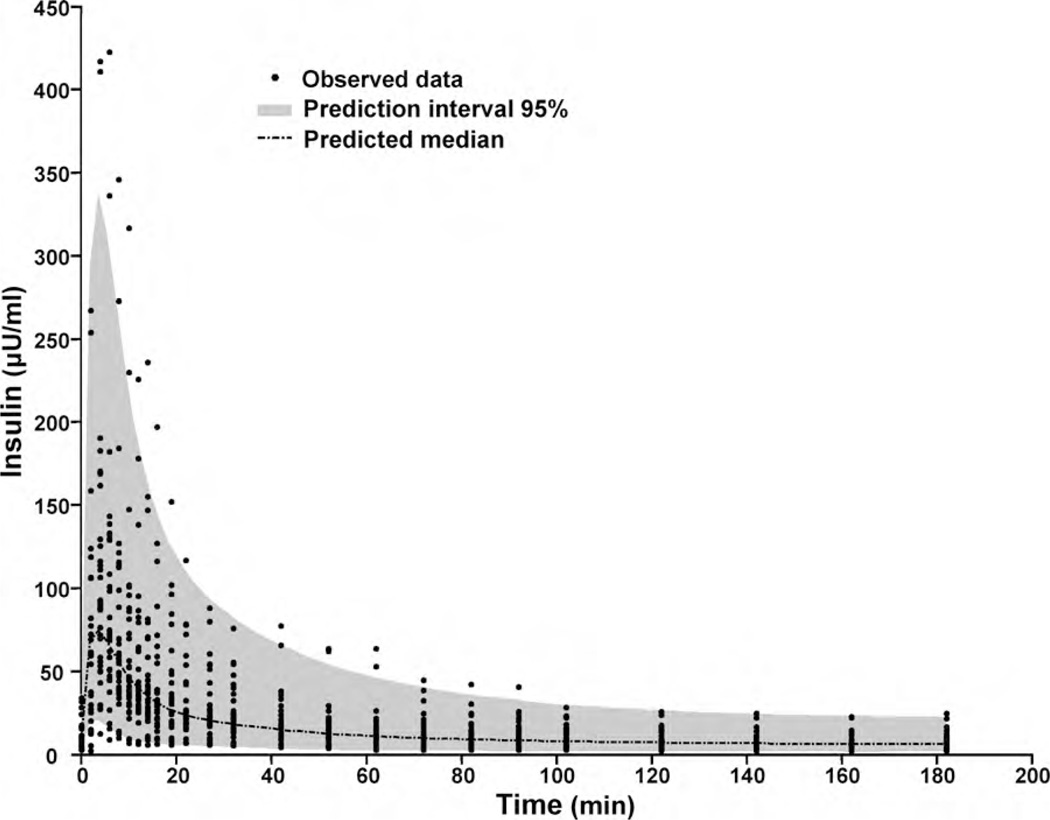
No racial difference in HOMA-IR was found between the African-American (2.60 ± 1.92) and Caucasian groups (2.04 ± 1.87) indicating similar insulin sensitivity. The residual error in the nonlinear mixed-effect population kinetic analysis was best described with a proportional model. Population estimates of parameters and between-subject variability (standard deviation) are presented in Table 1. A visual predictive check (VPC) with 1000 simulated dataset was performed. The simulated median and the 95% confidence interval are given in Fig. 2 together with the observed insulin concentrations. The VPC plot provides good evidence of the adequacy of the model.
Table 1.
Population estimates of the proposed PK/PD model using Monolix.
| Parameters | Estimate | RSE (%)a |
|---|---|---|
| kG (min−1) | 0.24 | 21 |
| Emax (min−1) | 0.0185 | 16 |
| C50 (mg/dl) | 73.8 | 6 |
| Pe (L−1) | 0.0581 | 25 |
| ke (min−1) | 0.194 | 12 |
| kRR (min−1) | 0.499 | 0.2 |
| α | 4.05 | 13 |
| IR0 (µU) | 4530 | 34 |
| CI_0 (µU/ml) | 8.7 | 12 |
| kR·IR (µU/min)‡ | 1580b | 31 |
| β_kRIR | −0.922 | 27 |
| b | 0.185 | 3 |
| Standard deviation of parameters | ||
| kG | 0.296 | |
| Emax | 0.189 | |
| C50 | 0.224 | |
| Pe | 0.146 | |
| ke | 0.505 | |
| kRR | 0.216 | |
| α | 0.278 | |
| IR0 | 0.403 | |
| CI_0 | 0.659 | |
| kR·IR (African-American) | 0.608 | |
| kR·IR (Caucasian) | 0.699 |
RSE, relative standard error.
The value is for African-American which is used as reference.
kR·IR of Caucasian is calculated as: 1580 × exp(−0.922) = 628.
p = 0.00016.
Fig. 2.
Visual predictive check of the population PK/PD model. Comparison of the observed concentrations with the median and 95% interval predicted for 1000 simulated datasets computed from the estimated population PK/PD model.
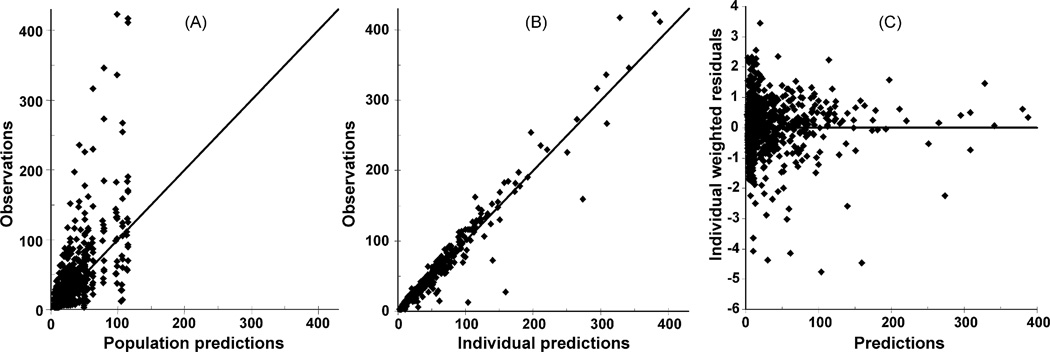
In the present investigation race as a covariate was incorporated in the structure of population model (Eq. (8)). Inclusion or deletion of covariate was determined by a Wald test at a significance level of 0.05.Wefirst applied the covariate of race to all parameters. It was then found that the initial value of the IRR pool (IRR_0) is significantly associated (p < 0.05) with race, and racial effect on the rate constant of kRR is close to significant (p = 0.064). If only the parameter kRR or IRR_0 is considered in the covariate structure, then race shows a significant relationship. Accordingly, the derived parameter kRIR = kRR·IRR_0, which provides a metric for the initial first-phase insulin secretion from beta-cell, was used in the population analysis. In this way race was found to have a significant effects on kRIR, resulting in a 63% decrease in kRIR for Caucasians compared with African-Americans. Fig. 3 shows the goodness-of-fit plots for this model. Apart from the high observed plasma insulin, the population predicted insulin concentrations and observations are clustered around the line of identity (Fig. 3A). Plotting the individual predictions against the observations for insulin (Fig. 3B) reduces the scattering around the line of identity as indicating that the population kinetic analysis is able to explain the variability in the insulin response. The scatter plot of population weighted residual against predicted concentrations of insulin (Fig. 3C) indicates that the residuals are randomly distributed. Thus, the population model appears to adequately describe the biphasic insulin dynamics.
Fig. 3.
Goodness-of-fit plots of population model. (A) Observed insulin concentrations vs. population predictions, (B) observed insulin concentrations vs. individual predictions, and (C) weighted residuals vs. population.
4. Discussion
The current study combines a nonlinear mixed-effect population modeling approach and a physiologically based PK/PD model for analyzing insulin behavior in response to glucose stimulation. The structure of the PK/PD model contains expressions to describe the physiologic mechanism of insulin’s biphasic secretion. The population PK/PD modeling with the covariate analysis approach enables identification of parameters specific to the difference found in the first-phase insulin secretion between African-American and Caucasian youths [11].
4.1. PK/PD modeling rationale
The insulin release from the beta-cells involves the arrangement of insulin into secretory granules, trafficking of the insulin-containing granules to the plasma membranes and exocytosis from the beta-cell [22]. The release of insulin from the b-cells has been found to follow a biphasic time-course consisting of a rapid and transient first-phase followed by a slowly developing and sustained second-phase. The underlying mechanisms of the biphasic pattern are still poorly understood in spite of the fact that biphasic release of insulin has been known for more than 40 years [12]. One explanation proposed by a number of studies [15,23–26] suggests that the biphasic release is due to the existence of at least two distinct pools of insulin granules in beta-cells. Based on their release competence or proximity to the plasma membrane it is proposed that the granules belonging to the readily releasable pool (IRR) can be rapidly discharged without any further modification and thus is responsible for the first-phase insulin secretion; the second-phase release is due to the insulin granules in the reserved pool (IR) which have to be translocated to the membrane and primed before they can be released.
The PK/PD model presented in this work subscribes to this current cellular biology understanding of the kinetic mechanism governing insulin biphasic secretion. Specifically, the IRR and IR pools of insulin are included in the proposed model (Fig. 1) to consider this mechanism. Upon glucose stimulation, the granules in the IRR pool are secreted from beta-cells at a faster rate compared to the IR pool, and thus form the first-phase release.
Glucose is the main physiological regulator of insulin production and secretion in the beta-cells [27–29]. Several studies [15,26,30] have reported that the magnitude of the peak of the first-phase is varying with the level of glucose, while the shape and the transient nature of the peak remain unchanged. Thus, the size of IRR should be associated with the glucose level. However, we could not estimate the dependence of IRR on the glucose dose since only one level of glucose stimulation was tested in our study subjects. For the effect of glucose on the second-phase, we assume the production rate of insulin in IR to be proportional to the glucose concentration. The relationship between glucose and insulin release from the IR pool was analyzed by using several PK/PD relationships, including the Hill function with or without sigmoidicity and a simple linear function. In order to determine a reasonable empirical structure for the population analysis as a first step, glucose and insulin data were fitted individually using WINFUNFIT which is a Windows version evolved from the FUNFIT program [31]. Our analysis suggests that the model using the Hill function with sigmoidicity best describes the insulin dynamics during FSIVGTT based on the Akaike information criteria [32] and graphical comparisons of fits.
4.2. Model parameters
The extraction ratio parameter E influences the amount of insulin that reaches the systemic circulation. Approximately 50% (E = 0.5) of insulin secreted from beta-cell is extracted by the liver, but the value of E may change with the glucose level [33]. Instead of estimating E, which is not possible based on the current data, our PK/PD analysis estimates the Pe parameter, which “encapsulates” the E and V parameters (Pe = (1 − E) /V). The average value of V has been reported to be 10 l [34]. Thus, the value of Pe calculated according to these references is about 0.05, which is in agreement with the population estimate of Pe based on our model which is 0.0581 with a 95% confidence interval of 0.0436–0.0773 l−1. Thus, our results do not indicate a significant change in Pe in response to a glucose challenge.
The ke has been reported from 0.1 to 0.3 min−1 [35,36]. Our population ke estimate of 0.194 min−1 falls into this range, which corresponds to an insulin half-life time of 3.57 min with a 95% confidence interval of 1.33–6.93 min.
In the proposed model, the initial amount of IR is treated as an estimated parameter and not calculated assuming an initial steady state condition. The rational for this is the fact that the basal insulin level is not a stable parameter because the insulin concentration in blood changes in a pulsatile manner. At the fasting state, the contribution of the pulsatile insulin secretion has been found to be at least at least 75% of the total insulin secretion [37].
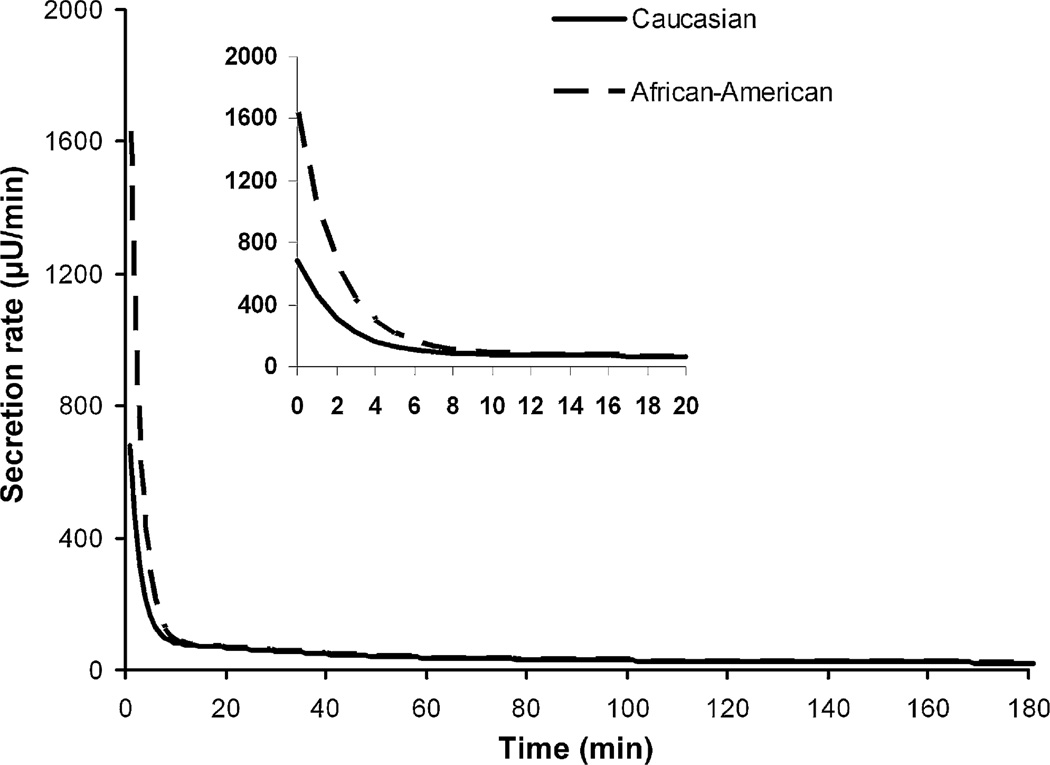
Higher insulin concentrations in the first-phase in the African-American subjects were detected compared to Caucasians [11] which may indicate beginning signs of progression towards insulin resistance and a pre-diabetic state in the African-American group. Increased insulin secretion in the African-Americans may also compensate for or precede the insulin resistance [2,8–10]. The increase in insulin level may be caused by an increase in insulin secretion from IRR and/or IR, or a decreased insulin removal via the extraction from the liver or elimination from plasma. Our covariate analysis suggests that the difference is due to the insulin secretion from the IRR pool. The significant racial difference (p < 0.05) in the initial insulin secretion (kRIR) from the beta-cells resulted in the difference in the secretion profiles found in the first-phase. Secretion profiles from beta-cell (Fig. 4) during FSIVGTT can be reconstructed using population parameters and averaged glucose concentrations. No significant association was found between race and the insulin elimination, and race and insulin extraction by liver.
Fig. 4.
Beta-cell secretion profile during FSIVGTT for African-American (dotted line) and Caucasian (solid line) according to population parameters and averaged glucose concentrations.
The present analysis is based on FSIVGTT experiments. Research is currently in progress to test the applicability of the model for analyzing OGTT data to possibly broaden the applicability of the analysis.
4.3. Other possible factors
Because of the significant difference in the BMI parameter between the two racial groups the difference in degree of obesity cannot be ruled out as possible alternative explanation for the kinetic difference found between the two groups. A better balanced study is needed to investigate that possibility. Possible differences in other factors that have not been determined in this study such as physical activity that was found to be a possible contributor [38], or genetic factors may also need to be considered.
In summary, the proposed mechanistic PK/PD model is able to describe the biphasic release of insulin in response to a glucose challenge. The population analysis allowed an estimation of the variability of the parameters relating to the important biphasic release and enabled the effect of race on the parameters to be evaluated. A significant difference between races was identified in the derived parameter kR·IR that relates to the first-phase insulin release. Our result is supported by our previous exploratory nonparametric analysis of the insulin–glucose kinetics where we found African-Americans to have a higher insulin concentration in the first-phase compared to Caucasians [11]. The proposed kinetic model in this work offers an opportunity to quantify the biphasic characteristic of insulin release and provides a mechanistic and quantitative understanding of the first-phase release, which has been found to play an important role in the development of type 2 diabetes.
Footnotes
Conflict of interest
There are no conflicts of interest.
REFERENCES
- 1.Wang Y, Beydoun MA. The obesity epidemic in the United States—gender age, socioeconomic, racial/ethnic, and geographic characteristics: a systematic review and meta-regression analysis. Epidemiol Rev. 2007;29:6–28. doi: 10.1093/epirev/mxm007. [DOI] [PubMed] [Google Scholar]
- 2.Goran MI, Bergman RN, Cruz ML, Watanabe R. Insulin resistance and associated compensatory responses in african-american and Hispanic children. Diabetes Care. 2002;25:2184–2190. doi: 10.2337/diacare.25.12.2184. [DOI] [PubMed] [Google Scholar]
- 3.Uwaifo GI, Nguyen TT, Keil MF, Russell DL, Nicholson JC, Bonat SH, et al. Differences in insulin secretion and sensitivity of Caucasian and African American prepubertal children. J Pediatr. 2002;140:673–680. doi: 10.1067/mpd.2002.124312. [DOI] [PubMed] [Google Scholar]
- 4.Arslanian S. Insulin secretion and sensitivity in healthy African-American vs American white children. Clin Pediatr (Phila) 1998;37:81–88. doi: 10.1177/000992289803700204. [DOI] [PubMed] [Google Scholar]
- 5.Arslanian S, Suprasongsin C. Differences in the in vivo insulin secretion and sensitivity of healthy black versus white adolescents. J Pediatr. 1996;129:440–443. doi: 10.1016/s0022-3476(96)70078-1. [DOI] [PubMed] [Google Scholar]
- 6.Lillioja S, Mott DM, Spraul M, Ferraro R, Foley JE, Ravussin E, et al. Insulin resistance and insulin secretory dysfunction as precursors of non-insulin-dependent diabetes mellitus. Prospective studies of Pima Indians. N Engl J Med. 1993;329:1988–1992. doi: 10.1056/NEJM199312303292703. [DOI] [PubMed] [Google Scholar]
- 7.Warram JH, Martin BC, Krolewski AS, Soeldner JS, Kahn CR. Slow glucose removal rate and hyperinsulinemia precede the development of type II diabetes in the offspring of diabetic parents. Ann Int Med. 1990;113:909–915. doi: 10.7326/0003-4819-113-12-909. [DOI] [PubMed] [Google Scholar]
- 8.Duck MM, Hoffman RP. Impaired endothelial function in healthy African-American adolescents compared with Caucasians. J Pediatr. 2007;150:400–406. doi: 10.1016/j.jpeds.2006.12.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Preeyasombat C, Bacchetti P, Lazar AA, Lustig RH. Racial and etiopathologic dichotomies in insulin hypersecretion and resistance in obese children. J Pediatr. 2005;146:474–481. doi: 10.1016/j.jpeds.2004.12.014. [DOI] [PubMed] [Google Scholar]
- 10.Arslanian SA, Saad R, Lewy V, Danadian K, Janosky J. Hyperinsulinemia in african-american children: decreased insulin clearance and increased insulin secretion and its relationship to insulin sensitivity. Diabetes. 2002;51:3014–3019. doi: 10.2337/diabetes.51.10.3014. [DOI] [PubMed] [Google Scholar]
- 11.Xie L, Hoffman RP, Veng-Pedersen P. Noncompartmental pharmacokinetics analysis of glucose-stimulated insulin response in African-American and Caucasian youths. Biopharm Drug Dispos. 2009;30:117–125. doi: 10.1002/bdd.652. [DOI] [PubMed] [Google Scholar]
- 12.Cerasi E, Luft R. The plasma insulin response to glucose infusion in healthy subjects and in diabetes mellitus. Acta Endocrinol (Copenh) 1967;55:278–304. doi: 10.1530/acta.0.0550278. [DOI] [PubMed] [Google Scholar]
- 13.Davies MJ, Rayman G, Grenfell A, Gray IP, Day JL, Hales CN. Loss of the first phase insulin response to intravenous glucose in subjects with persistent impaired glucose tolerance. Diab Med. 1994;11:432–436. doi: 10.1111/j.1464-5491.1994.tb00302.x. [DOI] [PubMed] [Google Scholar]
- 14.Bergman RN, Phillips LS, Cobelli C. Physiologic evaluation of factors controlling glucose tolerance in man: measurement of insulin sensitivity and beta-cell glucose sensitivity from the response to intravenous glucose. J Clin Invest. 1981;68:1456–1467. doi: 10.1172/JCI110398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Grodsky GM. A threshold distribution hypothesis for packet storage of insulin and its mathematical modeling. J Clin Invest. 1972;51:2047–2059. doi: 10.1172/JCI107011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gupta N, Hoffman RP, Veng-Pedersen P. Pharmacokinetic/pharmacodynamic differentiation of pancreatic responsiveness in obese and lean children. Biopharm Drug Dispos. 2005;26:287–294. doi: 10.1002/bdd.461. [DOI] [PubMed] [Google Scholar]
- 17.Monolix. 2008 http://software.monolix.org/; [Google Scholar]
- 18.Panhard X, Samson A. Extension of the SAEM algorithm for nonlinear mixed models with 2 levels of random effects. Biostatistics. 2009;10:121–135. doi: 10.1093/biostatistics/kxn020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kuhn E, Lavielle M. Maximum likelihood estimation in nonlinear mixed effects models. Ann Stat. 2005;49:1020–1038. [Google Scholar]
- 20.Kuhn E, Lavielle M. Coupling a stochastic approximation version of EM with an MCMC procedure. ESAIM P&S. 2004;8:115–131. [Google Scholar]
- 21.Delyon B, Lavielle M, Moulines E. Convergence of a stochastic approximation version of the EM algorithm. Ann Stat. 1999;27:94–128. [Google Scholar]
- 22.Halban PA. Structural domains and molecular lifestyles of insulin and its precursors in the pancreatic beta cell. Diabetologia. 1991;34:767–778. doi: 10.1007/BF00408349. [DOI] [PubMed] [Google Scholar]
- 23.Bratanova-Tochkova TK, Cheng H, Daniel S, Gunawardana S, Liu YJ, Mulvaney-Musa J, et al. Triggering and augmentation mechanisms, granule pools, and biphasic insulin secretion. Diabetes. 2002;51(Suppl. 1):S83–S90. doi: 10.2337/diabetes.51.2007.s83. [DOI] [PubMed] [Google Scholar]
- 24.Daniel S, Noda M, Straub SG, Sharp GW. Identification of the docked granule pool responsible for the first phase of glucose-stimulated insulin secretion. Diabetes. 1999;48:1686–1690. doi: 10.2337/diabetes.48.9.1686. [DOI] [PubMed] [Google Scholar]
- 25.O’Connor MD, Landahl H, Grodsky GM. Comparison of storage- and signal-limited models of pancreatic insulin secretion. Am J Physiol. 1980;238:R378–R389. doi: 10.1152/ajpregu.1980.238.5.R378. [DOI] [PubMed] [Google Scholar]
- 26.Grodsky GM, Curry D, Landahl H, Benet L. Further studies on the dynamic aspects of insulin release in vitro with evidence for a two-compartmental storage system. Acta Diabetol Lat. 1969;6(Suppl. 1):554–578. [PubMed] [Google Scholar]
- 27.Melloul D, Marshak S, Cerasi E. Regulation of insulin gene transcription. Diabetologia. 2002;45:309–326. doi: 10.1007/s00125-001-0728-y. [DOI] [PubMed] [Google Scholar]
- 28.Jarrett RJ, Keen H, Track N. Glucose and RNA synthesis in mammalian islets of Langerhans. Nature. 1967;213:634–635. doi: 10.1038/213634a0. [DOI] [PubMed] [Google Scholar]
- 29.Permutt MA, Kipnis DM. Insulin biosynthesis. I. On the mechanism of glucose stimulation. J Biol Chem. 1972;247:1194–1199. [PubMed] [Google Scholar]
- 30.Dean PM. Ultrastructural morphometry of the pancreatic cell. Diabetologia. 1973;9:115–119. doi: 10.1007/BF01230690. [DOI] [PubMed] [Google Scholar]
- 31.Pedersen PV. Curve fitting and modeling in pharmacokinetics and some practical experiences with NONLIN and a new program FUNFIT. J Pharmacokinet Biopharm. 1977;5:513–531. doi: 10.1007/BF01061732. [DOI] [PubMed] [Google Scholar]
- 32.Akaike H. A new look at the statistical model identification. IEEE Trans Automat Control. 1974;19:716–723. [Google Scholar]
- 33.Field JB. Extraction of insulin by liver. Annu Rev Med. 1973;24:309–314. doi: 10.1146/annurev.me.24.020173.001521. [DOI] [PubMed] [Google Scholar]
- 34.Home PD, Massi-Benedetti M, Shepherd GA, Hanning I, Alberti KG, Owens DR. A comparison of the activity and disposal of semi-synthetic human insulin and porcine insulin in normal man by the glucose clamp technique. Diabetologia. 1982;22:41–45. doi: 10.1007/BF00253868. [DOI] [PubMed] [Google Scholar]
- 35.Sherwin RS, Kramer KJ, Tobin JD, Insel PA, Liljenquist JE, Berman M, et al. A model of the kinetics of insulin in man. J Clin Invest. 1974;53:1481–1492. doi: 10.1172/JCI107697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Volund A, Polonsky KS, Bergman RN. Calculated pattern of intraportal insulin appearance without independent assessment of C-peptide kinetics. Diabetes. 1987;36:1195–1202. doi: 10.2337/diab.36.10.1195. [DOI] [PubMed] [Google Scholar]
- 37.Juhl C, Grofte T, Butler PC, Veldhuis JD, Schmitz O, Porksen N. Effects of fasting on physiologically pulsatile insulin release in healthy humans. Diabetes. 2002;51(Suppl 1):S255–S257. doi: 10.2337/diabetes.51.2007.s255. [DOI] [PubMed] [Google Scholar]
- 38.Ku CY, Gower BA, Hunter GR, Goran MI. Racial differences in insulin secretion and sensitivity in prepubertal children: role of physical fitness and physical activity. Obes Res. 2000;8:506–515. doi: 10.1038/oby.2000.63. [DOI] [PubMed] [Google Scholar]