Abstract
Tin monosulfide (SnS) is a naturally p-type semiconductor with a layered crystal structure, but no reliable n-type SnS has been obtained by conventional aliovalent ion substitution. In this work, carrier polarity conversion to n-type was achieved by isovalent ion substitution for polycrystalline SnS thin films on glass substrates. Substituting Pb2+ for Sn2+ converted the majority carrier from hole to electron, and the free electron density ranged from 1012 to 1015 cm−3 with the largest electron mobility of 7.0 cm2/(Vs). The n-type conduction was confirmed further by the position of the Fermi level (EF) based on photoemission spectroscopy and electrical characteristics of pn heterojunctions. Density functional theory calculations reveal that the Pb substitution invokes a geometrical size effect that enlarges the interlayer distance and subsequently reduces the formation energies of Sn and Pb interstitials, which results in the electron doping.
Control of carrier polarity conversion in semiconductor is important to produce high-performance semiconductor devices such as solar cells and light emitters, and is actually utilized in conventional semiconductors such as Si and compound semiconductors. On the other hand, it is known that such bipolar doping is not attained easily in other semiconductors; e.g., most of oxide semiconductors are of naturally n-type, and it is difficult to obtain p-type conduction in the same materials as known e.g. for SnO2, and vice versa e.g. for Cu2O. To date, several, but a limited number of doping routes have been recognized and employed. For ionic semiconductors, aliovalent ion substitution and off-chemical stoichiometry are known well; e.g., substitution of Zn2+ with Ga3+ increased the electron density in ZnO1, and Cu vacancy increased the hole density in Cu2O2. Further, H doping is now recognized as an important and effective route for n-type doping in oxide semiconductors3. For organic semiconductors and devices, chemical doping, which is caused by partial charge transfer originating from different electron affinities of constituent atoms/functional groups, is important4. The most popular route for carrier polarity conversion is aliovalent ion substitution; actually, n-type conversion of SnO was realized by substituting Sb3+ ions for the Sn2+ ions5. However, up to now, this route has not been succeeded in many semiconductors, such as SnS.
SnS is a naturally p-type semiconductor with hole densities of 1015–1018 cm−3 and the high mobilities ~90 cm2/(Vs)6,7. It has a layered crystal structure along the a-axis direction as shown in Fig. 1a, which belongs to the orthorhombic lattice (the space group Pnma, No. 62). Due to its reasonable small bandgap of ~1.07 eV8 and strong optical absorption coefficients above the bandgap (>105 cm−1), SnS is expected to be a promising absorber material for low-cost thin-film solar cells. Thus, numerous n-type materials, including CdS9,10, SnS211, FeS212, TiO213, ZnO14, and amorphous- Si15, have been employed for fabricating heterojunction SnS-based solar cells. However, the highest energy conversion efficiency reported up to now is limited to ~4%16,17, which is much lower than the theoretically-predicted value of 24%18. The low efficiency might suffer from the unfavorable band alignments and the large lattice mismatches in the heterojunction structures19,20. Fabricating a homojunction solar cell with p-SnS/n-SnS structure would solve this problem.
Figure 1. Structure of 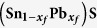 films.
films.
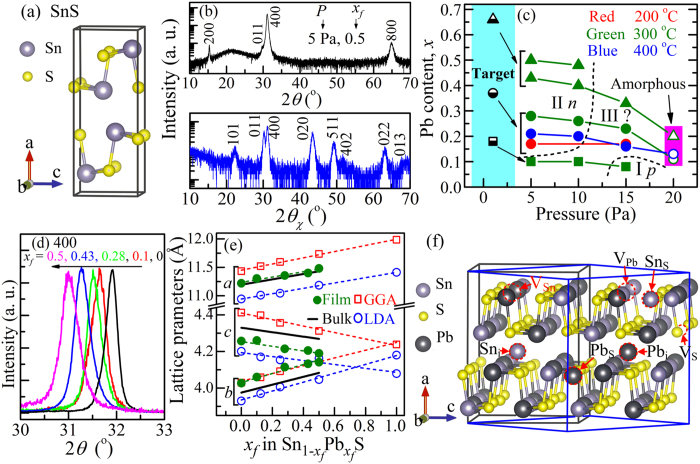
(a) Crystal structure of pure SnS. (b) Out-of-plane (top panel) and in-plane (bottom panel) synchronous scan XRD patterns of 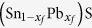 film with xf = 0.5 grown at 300 °C and 5 Pa. (c) Pb content (xt for target, xf for thin films) as a function of pressure, substrate temperature, and xt. The half-filled symbols indicate the targets, the closed circles the orthorhombic phase crystalline films, and the open symbols amorphous films. (d) 400 out-of-plane XRD diffraction peaks of the
film with xf = 0.5 grown at 300 °C and 5 Pa. (c) Pb content (xt for target, xf for thin films) as a function of pressure, substrate temperature, and xt. The half-filled symbols indicate the targets, the closed circles the orthorhombic phase crystalline films, and the open symbols amorphous films. (d) 400 out-of-plane XRD diffraction peaks of the 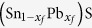 films grown at 300 °C with various xf values. (e) Lattice parameters (a, b, c) of
films grown at 300 °C with various xf values. (e) Lattice parameters (a, b, c) of 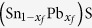 films as a function of xf. The closed circles indicate those obtained with the thin films, the solid lines are those of bulk (Sn1–xPbx)S taken from ref. 25, and the open symbols are the calculation results obtained by DFT in this work. The dashed straight lines are guides for eyes. (f) (Sn1-xPbx)S supercell model used for DFT calculations. The black line box draws the (Sn16–nPbn)S16 supercell model used for calculating the lattice parameters in Fig. 1e. The blue line box draws the (Sn16Pb16)S32 supercell model used for defect calculations in Fig. 4, where the intrinsic defect models examined in this study are indicated also in the figure.
films as a function of xf. The closed circles indicate those obtained with the thin films, the solid lines are those of bulk (Sn1–xPbx)S taken from ref. 25, and the open symbols are the calculation results obtained by DFT in this work. The dashed straight lines are guides for eyes. (f) (Sn1-xPbx)S supercell model used for DFT calculations. The black line box draws the (Sn16–nPbn)S16 supercell model used for calculating the lattice parameters in Fig. 1e. The blue line box draws the (Sn16Pb16)S32 supercell model used for defect calculations in Fig. 4, where the intrinsic defect models examined in this study are indicated also in the figure.
With this line, much effort has been devoted to obtaining n-type SnS materials by substituting the Sn2+ ions with aliovalent ions with the charge state of 3+. Dussan et al. report that Bi3+-doped SnS exhibits n-type conduction when the Bi concentration is larger than 50%21. Whereas, a Bi2S3 impurity phase, which is also n-type, was observed in their heavily Bi-doped SnS films22. Sajeesheesh et al. claim that n-type SnS thin films are obtained by chemical spray pyrolysis, but their result might be due to a significant n-type Sn2S3 impurity phase in the films23. Very recently, Sinsermsuksakul et al. tried to obtain n-type SnS by Sb3+ doping; however, except for great increase in the electrical resistance of the SnS film, no n-type conduction was observed24. That is, no reliable n-type SnS material has yet been reported.
In this work, we succeeded in fabricating reliable n-type SnS films by isovalent Pb2+ doping. We found that the doping mechanism is strikingly different from the conventional doping routes such as ion substitution, off-stoichiometry, and chemical doping. Substitution for the Sn2+ ion with a larger Pb2+ ion increases the interlayer distance in SnS, and this geometrical effect induces the formation of Sn/Pb interstitials easier, and the interstitial ions work as donors.
We deposited 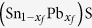 films (xf: film chemical composition) by pulsed laser deposition (PLD) on SiO2 glass substrates in a H2S gas flow to control the chemical stoichiometry ([Sn] + [Pb]): [S] (the parentheses denote the concentrations), where the H2S pressure (P) was a variable parameter.
films (xf: film chemical composition) by pulsed laser deposition (PLD) on SiO2 glass substrates in a H2S gas flow to control the chemical stoichiometry ([Sn] + [Pb]): [S] (the parentheses denote the concentrations), where the H2S pressure (P) was a variable parameter. 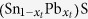 polycrystalline disks with the target chemical composition xt = 0.18, 0.37, and 0.66 were used as ablation targets. X-ray fluorescence (XRF) spectroscopy confirmed that these xt produced thin films with xf = 0.08–0.5. The details of experimental and calculation are found in method part of this paper.
polycrystalline disks with the target chemical composition xt = 0.18, 0.37, and 0.66 were used as ablation targets. X-ray fluorescence (XRF) spectroscopy confirmed that these xt produced thin films with xf = 0.08–0.5. The details of experimental and calculation are found in method part of this paper.
Results and discussion
First, we confirmed the film structures by X-ray diffraction (XRD). Figure 1b shows a typical out-of-plane 2θ/ω synchronous scan (top panel) and an in-plane synchronous 2θχ/φ scan (bottom panel) XRD patterns of the 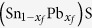 film with xf = 0.5 grown at substrate temperature (Ts) = 300 °C and P = 5 Pa. The out-of-plane XRD pattern exhibited strong 200, 400 and 800 diffractions of the orthorhombic structure, which is the same as that of pure SnS in Fig. 1a, along with a weak 011 diffraction. As seen in Figure S1 (supplementary information), orthorhombic
film with xf = 0.5 grown at substrate temperature (Ts) = 300 °C and P = 5 Pa. The out-of-plane XRD pattern exhibited strong 200, 400 and 800 diffractions of the orthorhombic structure, which is the same as that of pure SnS in Fig. 1a, along with a weak 011 diffraction. As seen in Figure S1 (supplementary information), orthorhombic 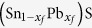 films were obtained at P ≤ 15 Pa (corresponding to the closed symbols in Fig. 1c); while, amorphous films were obtained when P was increased to 20 Pa (the open symbols in Fig. 1c). The in-plane synchronous 2θχ/φ scan (bottom panel) shows powder-like patterns with all possible hkl diffractions, suggesting that the film did not have in-plane orientation. It was further confirmed by in-plane rocking patterns (φ scan at fixed 2θχ, data not shown); all the data showed that the crystallized films did not have a preferential orientation in plane. These results indicate that the
films were obtained at P ≤ 15 Pa (corresponding to the closed symbols in Fig. 1c); while, amorphous films were obtained when P was increased to 20 Pa (the open symbols in Fig. 1c). The in-plane synchronous 2θχ/φ scan (bottom panel) shows powder-like patterns with all possible hkl diffractions, suggesting that the film did not have in-plane orientation. It was further confirmed by in-plane rocking patterns (φ scan at fixed 2θχ, data not shown); all the data showed that the crystallized films did not have a preferential orientation in plane. These results indicate that the 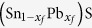 films were polycrystalline films with a strong 100 preferential orientation normal to the substrate. No impurity phase was detected both in the out-of-plane and the in-plane XRD patterns.
films were polycrystalline films with a strong 100 preferential orientation normal to the substrate. No impurity phase was detected both in the out-of-plane and the in-plane XRD patterns.
Figure 1c shows the variation of xf as functions of P, Ts and xt. It is seen that all the xf values were smaller than the xt values of the corresponding targets, and the xf values decreased with increasing P. As seen for the target with xt = 0.37, the maximum amount of Pb was incorporated when the films were grown at Ts = 300 °C. We, therefore, employed Ts = 300 °C hereafter.
The crystallized region in Fig. 1c is classified further to three regions as indicated by the dashed lines. Region I is “p-type region” (high P ≥ 15 Pa at low xf < 0.1), where the films still exhibited p-type conduction with low hole densities (Nh) and low hole mobilities (μh) (measured by Hall effect, details will be discussed for Fig. 2). n-type 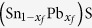 films were obtained in Region II (“n-type region”, xf ≥ 0.15 at low P ≤ 10 Pa). The electron density (Ne) and mobility (μe) changed largely with xf and P, which will be discussed later on. Region III is the intermediate region (“highly-resistive region”, low xf & low P, and high xf & high P), where the films exhibited very high resistivity >105 Ω·cm, and the Hall effect measurements did not give definite Hall voltage signs.
films were obtained in Region II (“n-type region”, xf ≥ 0.15 at low P ≤ 10 Pa). The electron density (Ne) and mobility (μe) changed largely with xf and P, which will be discussed later on. Region III is the intermediate region (“highly-resistive region”, low xf & low P, and high xf & high P), where the films exhibited very high resistivity >105 Ω·cm, and the Hall effect measurements did not give definite Hall voltage signs.
Figure 2. Electrical and electronic properties.
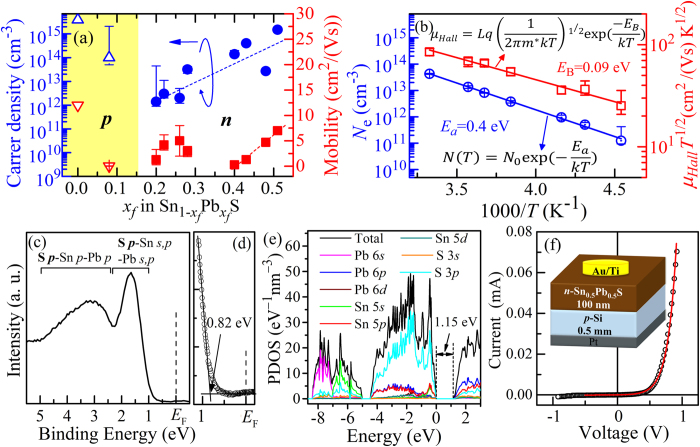
(a) Carrier density and mobility of 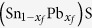 films as a function of xf measured by Hall effect. (b) Temperature dependences of electron density (Ne, blue line) and mobility (μe, red line) of n-type
films as a function of xf measured by Hall effect. (b) Temperature dependences of electron density (Ne, blue line) and mobility (μe, red line) of n-type 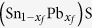 film with xf = 0.48. (c,d) UPS spectrum of n-type (Sn0.5Pb0.5)S film. (d) shows a magnified view near EF. (e) Projected DOS of (Sn0.5Pb0.5)S calculated by DFT with GGA functionals. (f) I-V characteristics of n-(Sn0.5Pb0.5)S/p-Si pn heterojunction. Inset shows the device structure.
film with xf = 0.48. (c,d) UPS spectrum of n-type (Sn0.5Pb0.5)S film. (d) shows a magnified view near EF. (e) Projected DOS of (Sn0.5Pb0.5)S calculated by DFT with GGA functionals. (f) I-V characteristics of n-(Sn0.5Pb0.5)S/p-Si pn heterojunction. Inset shows the device structure.
Here, we discuss the doping structure of Pb. Figure 1d shows the variation of the out-of-plane 400 diffraction angles 2θ400 obtained by 2θ/ω synchronous scan as a function of xf. The 2θ400 value shifted to lower angles as xf increased, indicating that the a-axis expanded with increasing xf. The lattice parameters obtained from the out-of-plane 400 and the in-plane 020 and 011 diffraction angles are summarized as a function of xf in Fig. 1e. As xf increased from 0 to 0.5, the a and b values increased linearly from 1.12 to 1.14 nm and from 0.403 to 0.414 nm, respectively, whereas the c value decreased from 0.426 to 0.419 nm; i.e., the interlayer distance (corresponding to the a value) increased. The solid lines in Fig. 1e represent the lattice parameters of the(Sn1–xPbx)S bulk sample reported by Leute et al.25. The a values of our films are almost the same as those of the bulk samples. However, the b and c values exhibited non-negligible deviations from the bulk values; i.e., the b-axis was expanded while the c-axis shrunken compared from the bulk values. The reason is not clear, but defects in the polycrystalline films would cause the structural difference. Figure 1e also compares the variation of the lattice parameters with those obtained by density functional theory (DFT) calculations (the open symbols) performed with the (Sn16–nPbn)S16 supercell model (Pb substitution model) indicated by the black line box in Fig. 1f. Here, local density approximation (LDA) and generalized gradient approximation (GGA) functionals are compared. As will be seen later, GGA provides better description about the electronic structure; however, here we can see that the experimental results for the Pb substitution model were within the variation of the functionals (typically, the ground-state lattice parameters by DFT include errors within 2–3%). That is, this model, where the Sn sites are substituted by Pb, explains the experimental structure well, and strongly supports that the Pb dopants are successfully incorporated to the Sn sites in the SnS lattice. We also confirmed that the films are uniform in microstructures and chemical compositions, and no segregation (e.g., a Pb-rich impurity phase) was detected by atomic force microscopy (AFM), field-emission scanning electron microscopy (FE-SEM), and electron-probe microanalysis (EPMA) (supplementary information Figure S2 and Table S1).
Figure 2a shows Hall effect measurement results as a function of xf. The pure SnS film showed p-type conduction with Nh ~ 4.1 × 1015 cm−3 and μh ~ 12 cm2/(Vs). The 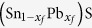 film with xf = 0.08 fabricated at P = 15 Pa still showed p-type conduction but with the low Nh ~ 1.0 × 1014 cm−3 and the very small μHall in the order of 10−2 cm2/(Vs). When xf ≥ 0.2, n-type conductions were observed for the films fabricated at P = 5 and 10 Pa. For the n-type
film with xf = 0.08 fabricated at P = 15 Pa still showed p-type conduction but with the low Nh ~ 1.0 × 1014 cm−3 and the very small μHall in the order of 10−2 cm2/(Vs). When xf ≥ 0.2, n-type conductions were observed for the films fabricated at P = 5 and 10 Pa. For the n-type 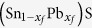 film with xf = 0.2, Ne and μHall were 1.4 × 1012 cm−3 and 1.3 cm2/(Vs), respectively. Ne increased with increasing xf and reached 2.0 × 1015 cm−3 for xf = 0.5. μe was not changed largely when xf < 0.3 (Ne < 3.2 × 1013 cm−3). At xf values >0.4, μe increased almost linearly, and the maximum value of 7.0 cm2/(Vs) was obtained for xf = 0.5.
film with xf = 0.2, Ne and μHall were 1.4 × 1012 cm−3 and 1.3 cm2/(Vs), respectively. Ne increased with increasing xf and reached 2.0 × 1015 cm−3 for xf = 0.5. μe was not changed largely when xf < 0.3 (Ne < 3.2 × 1013 cm−3). At xf values >0.4, μe increased almost linearly, and the maximum value of 7.0 cm2/(Vs) was obtained for xf = 0.5.
Figure 2b shows temperature dependences of Ne and μe for the 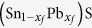 film with the room-temperature Ne of 4.3 × 1013 cm−3 (xf = 0.48 grown at 10 Pa). The Ne shows a thermally-activated behavior with an active energy of Ea ~ 0.4 eV. From a simple approximation in the impurity region Ne = (NDNC)1/2exp[–(EC – ED)/(2kBT)] (ND is the donor density, NC the conduction band effective density of states (DOS), EC – ED the donor level measured from the conduction band minimum EC, kB the Boltzmann constant), EC – ED and ND are estimated to be ~0.8 eV and 2.5 x 1021 cm−3 (NC = 2.8 x 1019 cm−3 is taken from Si), respectively. More accurate estimation was performed based on the total DOS obtained by the DFT calculation and the semiconductor statistics26, which provided EC – ED = 0.75 eV, EC – EF = 0.30 eV, and ND = 1.0 × 1021 cm−3, agreeing well with the above simple estimation and guaranteeing that the film is in the impurity region in this measurement temperature range. On the other hand, although EF was closer to EC as in usual n-type semiconductors, the donor level ED was closer to the valence band maximum energy (EV) rather than EC, showing that the n-type doping in the
film with the room-temperature Ne of 4.3 × 1013 cm−3 (xf = 0.48 grown at 10 Pa). The Ne shows a thermally-activated behavior with an active energy of Ea ~ 0.4 eV. From a simple approximation in the impurity region Ne = (NDNC)1/2exp[–(EC – ED)/(2kBT)] (ND is the donor density, NC the conduction band effective density of states (DOS), EC – ED the donor level measured from the conduction band minimum EC, kB the Boltzmann constant), EC – ED and ND are estimated to be ~0.8 eV and 2.5 x 1021 cm−3 (NC = 2.8 x 1019 cm−3 is taken from Si), respectively. More accurate estimation was performed based on the total DOS obtained by the DFT calculation and the semiconductor statistics26, which provided EC – ED = 0.75 eV, EC – EF = 0.30 eV, and ND = 1.0 × 1021 cm−3, agreeing well with the above simple estimation and guaranteeing that the film is in the impurity region in this measurement temperature range. On the other hand, although EF was closer to EC as in usual n-type semiconductors, the donor level ED was closer to the valence band maximum energy (EV) rather than EC, showing that the n-type doping in the 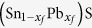 films is a bit different from the usual n-type semiconductors.
films is a bit different from the usual n-type semiconductors.
As shown by the red line in Fig. 2b, μe decreased with decreasing the temperature, and the ln(μHalT1/2)–T−1 plot exhibited a good straight line in the whole T range, suggesting that the electron transport in the film was dominated by grain boundary (GB) potential barriers as proposed by Seto et al.27, where electron transport is disturbed by potential barriers formed due to the electrons trapped at acceptor-type defects at the GBs. The GB potential barrier height EB is estimated to be approximately 0.09 eV (the equation is given in Fig. 2b27). From this result, we can estimate the potential electron mobility μ0 (i.e., the ideal value when no GB affects the carrier transport) by extrapolating EB to zero (i.e., μ0 = μHall exp(EB/kT)), which gives μ0 ~ 1.6 × 102 cm2/(Vs).
Figure 2c shows a valence band structure of a (Sn0.5Pb0.5)S film measured by ultraviolet photoemission spectroscopy (UPS). A sharp peak at 1–2 eV and a broad peak at 2.5–4.5 eV can be observed, agreeing with the projected DOS (PDOS) calculated by DFT in Fig. 2e. The valence band consists mainly of S 3p orbitals, which slightly hybridized with Sn 5s, Sn 5p, Sn 5d, Pb 6s, Pb 6p, and Pb 6d orbitals. As seen in Fig. 2d, the observed EF of the (Sn0.5Pb0.5)S film is located at 0.82 eV above VBM. From the bandgap value of 1.15 eV (will be discussed for Fig. 3), the EC – EF value is estimated to be 0.33 eV, closer to conduction band minimum (CBM).
Figure 3. Optical properties.
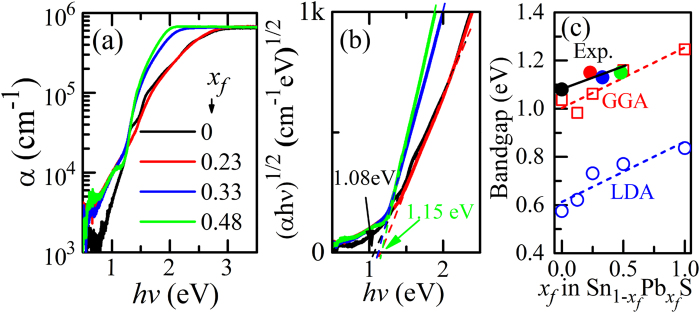
(a) Typical optical absorption spectra and (b) (αhν)1/2 – hν plots (indirect-transition model) of 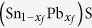 films with various xf (the xf values are indicated in the figure (a)). The values in (b) indicate the optical bandgaps obtained from the straight regions in the (αhν)1/2 – hν plots. (c) Variation of optical bandgaps with xf. Those calculated by DFT with LDA and GGA functionals are also shown.
films with various xf (the xf values are indicated in the figure (a)). The values in (b) indicate the optical bandgaps obtained from the straight regions in the (αhν)1/2 – hν plots. (c) Variation of optical bandgaps with xf. Those calculated by DFT with LDA and GGA functionals are also shown.
To further confirm the n-type conduction of these films, n-type (Sn0.5Pb0.5)S/p-type Si pn heterojunction was prepared (the device structure is shown in the inset to Fig. 2f). The n-(Sn0.5Pb0.5)S film and the p-Si wafer used had Ne = 2 × 1015 and Nh = 5 × 1015 cm−3, respectively. The current–voltage (I–V) characteristic of the pn junction (Fig. 2f) showed a clear rectifying characteristic, further supporting the n-type conduction of the 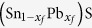 film. The band alignment of this pn heterojunction (supplementary information Figure S3) gives the built-in potential (Vbi) of 0.76 eV. This Vbi roughly explains the experimental threshold voltage of the pn heterojunction ~0.67 V obtained by extrapolating the straight line region in Fig. 2f.
film. The band alignment of this pn heterojunction (supplementary information Figure S3) gives the built-in potential (Vbi) of 0.76 eV. This Vbi roughly explains the experimental threshold voltage of the pn heterojunction ~0.67 V obtained by extrapolating the straight line region in Fig. 2f.
Figures 3a and b show typical optical absorption spectra and (αhν)1/2 – hν plots (the indirect-transition model) of the 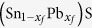 films fabricated at the various conditions, respectively. The pure SnS film (the black line in (a)) exhibited very weak subgap absorption, and the bandgap estimated from the (αhν)1/2–hν plot is 1.08 eV, agreeing well with the literature theoretical value of ~1.07 eV8. The bandgaps estimated from (b) are shown in Fig. 3c as a function of xf, showing that the bandgap value increased with xf. Comparing with the calculated bandgap values, it is concluded that the GGA functional reproduces the experimental values better than LDA.
films fabricated at the various conditions, respectively. The pure SnS film (the black line in (a)) exhibited very weak subgap absorption, and the bandgap estimated from the (αhν)1/2–hν plot is 1.08 eV, agreeing well with the literature theoretical value of ~1.07 eV8. The bandgaps estimated from (b) are shown in Fig. 3c as a function of xf, showing that the bandgap value increased with xf. Comparing with the calculated bandgap values, it is concluded that the GGA functional reproduces the experimental values better than LDA.
Here, we like to discuss the origin of the n-type doping in the 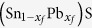 films. It is known that Pb ions favor to take +2 and +4 oxidation states, and the latter would explain the n-type doping if Pb4+ substitutes the Sn2+ site. However, the above DFT calculations for the (Sn32–nPbn)S32 supercell models indicated that the Pb substitutions at the Sn site (denoted PbSn) generate no free charges because the Pb is ionized to Pb2+. We also confirmed by X-ray photoemission spectroscopy (XPS) that the calibrated energy level of Pb 4f7/2 in the
films. It is known that Pb ions favor to take +2 and +4 oxidation states, and the latter would explain the n-type doping if Pb4+ substitutes the Sn2+ site. However, the above DFT calculations for the (Sn32–nPbn)S32 supercell models indicated that the Pb substitutions at the Sn site (denoted PbSn) generate no free charges because the Pb is ionized to Pb2+. We also confirmed by X-ray photoemission spectroscopy (XPS) that the calibrated energy level of Pb 4f7/2 in the 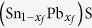 with xf = 0.5 was 137.55 eV and close to that in a reference PbS (137.15 eV), which supports that the oxidation state of the Pb incorporated in the
with xf = 0.5 was 137.55 eV and close to that in a reference PbS (137.15 eV), which supports that the oxidation state of the Pb incorporated in the 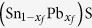 films is +2 (supplementary information Figure S4). This result in turn indicates that the doping mechanism by this Pb substitution is not an aliovalent ion substitution, and the conventional substitution models do not explain the n-type doping in the
films is +2 (supplementary information Figure S4). This result in turn indicates that the doping mechanism by this Pb substitution is not an aliovalent ion substitution, and the conventional substitution models do not explain the n-type doping in the  films.
films.
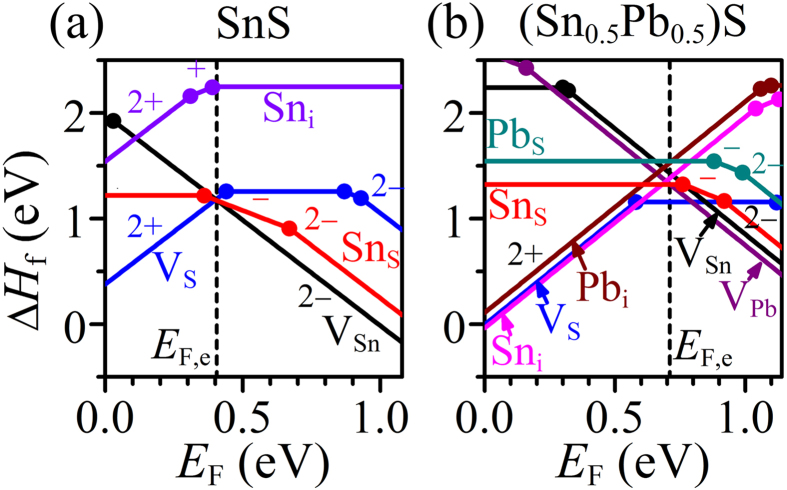
Here, we discuss the microscopic mechanism of the n-type doping by the Pb substitution. Firstly, we should remind that the n-type conduction was obtained only when a film was grown under the S-poor condition (i.e., at low P). We calculated the formation enthalpies (ΔHf) of intrinsic defects in the pure SnS and the (Sn0.5Pb0.5)S models (the blue line box in Fig. 1f) under the S-poor limit condition as a function of EF by DFT calculations as shown in Fig. 4a and b, respectively. Vacancies (VS, VSn, VPb), anti-site defects (SnS, PbS), interstitials (Sni, Pbi) were examined (see Fig. 1f for the models) with the defect charge states from 2+ to 2−. These calculations employed LDA functionals not GGA in order to compare with the previously-reported results for pure SnS by Vidal et al..28 The present result of the pure SnS model (Fig. 4a) is almost the same as their results; i.e., the most stable charge state of VS transits from 2+ to 0 at EF ~ 0.4 eV, corresponding to the charge transfer energy level of ε2+/0. The most stable defect changed from VS2+ to SnS− & VSn2− at EF ~ 0.4 eV. As VS2+ acts as a doubly-ionized donor while SnS− and VSn2− are ionized acceptors, suggesting that SnS is intrinsically a compensated p-type semiconductor. For quantitative analysis, the equilibrium EF (EF,e) at 400 °C (i.e., we assume the defect structures at the growth temperature were frozen to room temperature) was calculated by considering all the ΔHf values and the semiconductor statistics, giving EF,e – EV = 0.41 eV with [VS2+] = 5.0 × 1015, [VSn2−] = 3.9 × 1015, and [SnS−] = 5.2 × 1015 cm−3 for the SnS model. This means that the free electrons were generated from VS2+ at 1.0 × 1016 cm−3 but compensated by larger amounts of holes generated from VSn2− and SnS− at 1.3 × 1016 cm−3, resulting in the p-type conduction. It should be noted that the Sni has a very large ΔHf and is not likely formed in pure SnS.
Figure 4. Formation enthalpies ΔHf of intrinsic defects calculated at S-poor limit.
Calculated ΔHf for (a) pure SnS and (b) (Sn16Pb16)S32 models as a function of EF at S-poor limit. The values in the figures represent the charge states of the defects in the DFT calculations. The black dashed lines represent the equilibrium EF (EF,e) calculated self-consistently.
For the (Sn0.5Pb0.5)S model in Fig. 4b, although the ΔHf values of VS2+,0 remained unchanged, that of Sni2+ was reduced and that of VSn2− increased significantly compared to those in the pure SnS, which is because the interlayer distance (corresponding to the a-axis length) and the b-axis lattice parameters were increased by the Pb substitution (as also observed experimentally in Fig. 1e). Similar ΔHf behaviors were found also for Pbi2+ and VPb2−, respectively. That means, this geometrical alternation makes the generation of the donor Sni2+ and Pbi2+ easier whereas suppresses the generation of the acceptor VSn2− and VPb2−, suggesting n-type doping. The EF,e calculation at 300 °C gave EF,e – EV = 0.71 eV with [VSn2−] = 5.5 × 1013, [VPb2−] = 4.6 × 1014, [Sni2+] = 6.1 × 1014, and [Pbi2+] = 3.2 × 1013 cm−3. Note that the VS has the charge neutral state at this EF,e, and does not contribute to carrier doping. Consequently, the free holes were generated at 1.0 × 1015 cm−3, while the larger amounts of free electrons were generated at 1.3 × 1015 cm−3, resulting in n-type doping. Finally, we conclude that Sni and Pbi are the most plausible origin of the n-type conduction in the 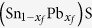 films.
films.
Summary
In summary, n-type conduction in SnS was achieved by isovalent Pb substitution with the maximum electron mobility of 7 cm2/(Vs). DFT calculations proposed a new doping model where the Pb substitution at the Sn sites induces the formation of Sni and/or Pbi and produces donors. To date, carrier polarity control in semiconductor is achieved mainly by aliovalent ion substitution, off chemical stoichiometry, chemical doping and so on. This work revealed that substitution by an isovalent ion can also induce carrier doping by a two-step indirect mechanism through a geometrical effect and subsequent formation of charged defects.
The present finding provides a novel idea for carrier doping. Even keeping the same crystal structure and the ion charges, easiness of impurity doping, in particular for atoms/ions with largely-different sizes, depends significantly on the lattice parameters and the internal atomic coordinates, which can be altered also by impurity doping. Further, although substitution doping usually requires aliovalent ion doping to alter the carrier polarity or concentration, geometrical doping has more flexibility because isovalent ion doping would also work for carrier doping.
This way of thinking would provide more flexibility to explore new doping routes, open a new way for controlling carrier polarity and density in novel semiconductors in which conventional aliovalent ion substitution is difficult.
Methods
Film fabrication
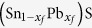 films of 100–200 nm in thickness were grown on SiO2 glass substrates by pulsed laser deposition (PLD) using a KrF excimer laser (248 nm in wavelength, 3–6 J/cm2 of laser energy density, and 10 Hz of repetition rate) with
films of 100–200 nm in thickness were grown on SiO2 glass substrates by pulsed laser deposition (PLD) using a KrF excimer laser (248 nm in wavelength, 3–6 J/cm2 of laser energy density, and 10 Hz of repetition rate) with 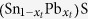 polycrystalline targets in a H2S gas flow to control the S stoichiometry. The base pressure of the growth chamber was 1 × 10−5 Pa. Ts was varied from 200 to 400 °C, and P of an Ar/H2S mixing gas (80/20%) from 5 to 20 Pa.
polycrystalline targets in a H2S gas flow to control the S stoichiometry. The base pressure of the growth chamber was 1 × 10−5 Pa. Ts was varied from 200 to 400 °C, and P of an Ar/H2S mixing gas (80/20%) from 5 to 20 Pa.
Characterization
The crystalline phase and crystal structure of the obtained films were characterized by X-ray diffraction (XRD, radiation source = Cu Kα). Optical properties were obtained by measuring transmittance (Tr) and reflectance (R) spectra. The absorption coefficient (α) was estimated by α = ln[(1−R)/Tr]/d, where d is the film thickness. Electrical properties of the SnS films were analyzed by Hall effect measurements using the van der Pauw configuration with an AC modulation of magnetic field. The Pb content in the films (xf) were determined by X-ray fluorescence (XRF) spectroscopy calibrated by the chemical compositions obtained by inductively-coupled plasma-atomic emission spectroscopy (ICP-AES). The valence band structures were observed by UPS (excitation source = He I, 21.2 eV), where the films were protected in an Ar atmosphere during the transfer from the PLD chamber to the UPS chamber. The oxidation state of Pb was examined by x-ray photoemission spectroscopy (XPS, Mg Kα).
Calculation
Stable crystal/defect structures, their electronic structures, and formation energies of intrinsic defects were calculated by density functional theory (DFT) calculations with local density approximation (LDA) and generalized gradient approximation (GGA) PBE96 functionals using the Vienna Ab initio Simulation Package (VASP 5.3.3)29. The plane wave cutoff energy was set to 323.3 eV. A 32-atoms supercell model ((Sn16–nPbn)S16, black line in Fig. 1f) and a 4 × 6 × 5 k-mesh were used for the calculations of structural properties and electronic structures. The defect calculations were performed using a 64-atoms model ((Sn16Pb16)S32, blue line in Fig. 1f) and a 3 × 3 × 3 k-mesh. The procedure for calculating the defect ΔHf along with the general corrections followed the methodology reviewed by Zunger et al.30,31. The equilibrium Fermi levels (EF,e) were determined using the calculated density of states (DOS) by solving semiconductor statistic equations self-consistency so as to satisfy the charge neutrality condition32.
Additional Information
How to cite this article: Ran, F.-Y. et al. n-type conversion of SnS by isovalent ion substitution: Geometrical doping as a new doping route. Sci. Rep. 5, 10428; doi: 10.1038/srep10428 (2015).
Supplementary Material
Acknowledgments
F.-Y. Ran and T. Kamiya were supported by Funding Program for Next Generation World-Leading Researchers (NEXT Program, Project #GR035). This work was supported also by the New Energy and Industrial Technology Development Organization (NEDO) under the Ministry of Economy, Trade and Industry (METI) and by the Element Strategy Initiative to Form Core Research Center and the Ministry of Education, Culture, Sports, Science and Technology (MEXT).
Footnotes
Author Contributions H.Hosono, T.K. and F-Y.R. proposed the concepts and designed the experiments. F-Y.R. carried out the experiments and the data analyses. H.Hiramatsu participated in the data analyses. Z.X. and T.K. performed the calculation work and the analyses. F-Y.R. and Y.T. performed UPS and XPS measurements. F-Y.R., Z.X. and T.K. wrote the manuscript with help from all the co-authors.
References
- Ko H. J. et al. Ga-doped ZnO films grown on GaN templates by plasma-assisted molecular-beam epitaxy. Appl. Phys. Lett. 77, 3761–3763 (2000). [Google Scholar]
- Raebiger H., Lany S. & Zunger A. Origins of the p-type nature and cation deficiency in Cu2O and related materials. Phys. Rev. B 76, 045209 (2007). [Google Scholar]
- Chen L.-Y. et al. Hydrogen-doped high conductivity ZnO films deposited by radio-frequency magnetron sputtering. Appl. Phys. Lett. 85, 5628–5630 (2004). [Google Scholar]
- Méndez H. et al. Doping of Organic Semiconductors: Impact of Dopant Strength and Electronic Coupling. Angew. Chem. Int. Edit. 52, 7751–7755 (2013). [DOI] [PubMed] [Google Scholar]
- Hosono H., Ogo Y., Yanagi H. & Kamiya T. Bipolar Conduction in SnO thin films. Electrochem. Solid-State lett. 14, H13–H16 (2011). [Google Scholar]
- Albers W., Haas C. & Maesen van der F. The preparation and the optical perperties of SnS crystals. J. Phys, Chem. Solids 15, 306–310 (1960). [Google Scholar]
- Mathews N. R., Anaya H. B. M., Cortes-Jacome M. A., Angeles-Chavez C. & Toledo-Antonio J. A. Tin sulfide thin films by pulse electrodeposition: structural, morphological, and optical properties. J. Electrochem. Soc. 157, H337–H341 (2010). [Google Scholar]
- Ran F.-Y., Xiao Z., Hiramatsu H., Hosono H. & Kamiya T. Growth of high-quality SnS epitaxial films by H2S flow pulsed laser deposition. Appl. Phys. Lett. 104, 072106 (2014). [Google Scholar]
- Ramakrishna Reddy K. T., Koteswara Reddy N. & Miles R. W. Photovoltaic properties of SnS based solar cells. Sol. Energy Mater. Sol. Cells 90, 3041–3046 (2006). [Google Scholar]
- Bashkirov S. A., Gremenok V. F., Ivanov V. A. Lazenka V. V. & Bente K. Tin sulfide thin films and Mo/p-SnS/n-CdS/ZnO heterojunctions for photovoltaic applications. Thin Solid Films 520, 5807–5810 (2012). [Google Scholar]
- Sánchez-Juárez A. Tiburcio-Silver A. & Ortiz A. Fabrication of SnS2/SnS heterojunction thin film diodes by plasma-enhanced chemical vapor deposition. Thin Solid Films 480, 452–456 (2005). [Google Scholar]
- Berry N. et al. Atmospheric-pressure chemical vapor deposition of iron pyrite thin films. Adv. Energy Mater. 2, 1124–1135 (2012). [Google Scholar]
- Wang Y., Gong H., Fan B. H. & Hu G. X. Photovoltaic behavior of nanocrystalline SnS/TiO2. J. Phys. Chem. C 114, 3256–3259 (2010). [Google Scholar]
- Ichimura M. & Takagi H. Electrodeposited ZnO/SnS heterostructures for solar cell application. Jpn. J. Appl. Phys. 47, 7845 (2008). [Google Scholar]
- Jiang F., Shen H. L., Wang W. & Zhang L. Preparation of SnS film by sulfurization and SnS/a-Si heterojunction solar cells J. Electrochem. Soc. 159, H235 – H238 (2012). [Google Scholar]
- Sinsermsuksakul P. et al. Enhancing the efficiency of SnS solar cells via band-offset engineering with a zinc oxysulfide buffer layer. Appl. Phys. Lett. 102, 053901 (2013). [Google Scholar]
- Steinmann V. et al. 3.88% efficient tin sulfide solar cells using congruent thermal evaporation. Adv. Mater. 26, 7488–7492 (2014). [DOI] [PubMed] [Google Scholar]
- Schneikart A., Schimper H.–J., Klein A. & Jaegermann W. Efficiency limitations of thermally evaporated thin-film SnS solar cells.J. Phys. D: Appl. Phys. 46, 305109 (2013). [Google Scholar]
- Sun L. et al. Band alignment of SnS/Zn(O,S) heterojunctions in SnS thin film solar cells. Appl. Phys. Lett. 103, 181904 (2013). [Google Scholar]
- Cai X., Zeng S. & Zhang B. Fabrication and characterization of InGaN p-i-n homojunction solar cell. Appl. Phys. Lett. 95, 173504 (2009). [Google Scholar]
- Dussan A., Mesa F. & Gordillo G. Influence of microstructural heterogeneity on the scaling between flow stress and relative density in microcellular Al–4.5% Cu. J. Mater. Sci. 45, 2403–2407 (2010). [Google Scholar]
- Gordillo G., Botero M. & Oyola J. S. Synthesis and study of optical and structural properties of thin films based on new photovoltaic materials. Microelectron J 39, 1351–1353 (2008). [Google Scholar]
- Sajeesh T. H.; Warrier A. R.; Kartha C. S. & Vijayakumar K. P. Optimization of parameters of chemical spray pyrolysis technique to get n and p-type layers of SnS. Thin Solid Films 518, 4370–4374 (2010). [Google Scholar]
- Sinsermsuksakul P. et al. Antimony-doped tin(II) sulfide thin films. Chem. Mater. 24, 4556–4562 (2012). [Google Scholar]
- Leute V., Behr A., Hünting C. & Schmidtke H. M. Phase diagram and diffusion properties of the quasibinary system (Sn, Pb) S. Solid State Ionics 68, 287–294 (1994). [Google Scholar]
- Sze S. M. & Ng K. K. Physics of Semiconductor Devices Ch. 1 (John Wiley & Sons, Inc., Hoboken, New Jersey, 2007). [Google Scholar]
- Seto J. Y. W. The electrical properties of polycrystalline silicon films. J. Appl. Phy. 46, 5247–5254 (1975). [Google Scholar]
- Vidal J. et al. Band-structure, optical properties, and defect physics of the photovoltaic semiconductor SnS. Appl. Phys. Lett. 100, 032104 (2012). [Google Scholar]
- Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basic set. Phys. Rev. B 54, 11169 (1996). [DOI] [PubMed] [Google Scholar]
- Lany S. & Zunger A. Assessment of correction methods for the bandgap problem and for finite-size effects in supercell defect calculations: Case studies for ZnO and GaAs. Phys. Rev. B 78, 235104 (2008). [Google Scholar]
- Lany S. & Zunger A. Accurate prediction of defect properties in density functional supercell calculations. Modelling Simul. Mater. Sci. Eng. 17, 084002 (2009). [Google Scholar]
- Laks D. B., Van de Valle C. G., Neumark G. F., Blöchl P. E. & Pantelides S. T. Native defects and self-compensation in ZnSe. Phys. Rev. B 45, 10965 (1992). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.